教学项目：判断三角形类型程序的测试

合集下载

教学项目：判断三角形类型程序的测试

教学项目：判断三角形类型程序的测试需求：（程序的规格说明要求）有一个程序，用来判断一个三角形的类型。

输入三个整数a、b和c分别作为三角形的三条边的边长，通过程序来判断由这三条边构成的三角形类型是等边三角形、等腰三角形、一般三角形还是非三角形(不能构成一个三角形)。

用决策表法对该程序进行测试。

分析：等价类划分法和边界值分析方法的局限性等价类划分法和边界值分析方法比较适合输入变量或输入条件相互独立的情况，但是当输入变量或输入条件相互依赖、相互制约的时候，采用等价类划分法和边界值分析方法是难以描述的，测试效果也很难保障。

在一些数据处理问题当中，某些操作的实施依赖于多个逻辑条件的组合，即：针对不同逻辑条件的组合值，分别执行不同的操作。

决策表很适合于处理这类问题。

分析：什么是决策表？1、决策表也称判定表，是分析和表达多逻辑条件下执行不同操作的情况的工具。

2、决策表能够将复杂的问题按照各种可能的情况全部列举出来，简明并避免遗漏，设计出完整的测试用例集合。

在所有的黑盒测试方法中，基于决策表（也称判定表）的测试是最为严格、最具有逻辑性的测试方法。

知识点：采用决策表法设计测试用例的步骤：(1)列出所有的条件桩和动作桩。

(2)确定规则的个数。

有n个条件（每个条件取真、假值的情况）的决策表有2n个规则。

(3)填入条件项。

(4)填入动作项，得到初始决策表。

(5)简化决策表，合并相似规则(相同动作)。

如果两条或多条规则的动作项相同，条件项只有一项不同，则可以将该项合并，合并后的条件项用符号“-”表示，说明执行的动作与该条件的取值无关，称为无关条件。

(6)根据决策表设计测试用例。

一条规则一个测试用例，排除掉不可能的规则。

解答：(1)列出所有的条件桩和动作桩。

条件桩—列出问题的所有条件。

（通常认为列出的条件的先后次序无关紧要）动作桩—列出问题规定的可能采取的操作。

（这些操作的排列顺序没有约束）运用决策表设计测试用例时，可将条件理解为输入，将动作理解为输出。

软件测试三角形类型判断程序实验报告

南通大学
软件测试
——三角形类型判断
学院：计算机科学与技术学院
班级：软外1 1 1
学号： 1113122022
姓名：王治
一、实验题目
测试三角形类型判断程序
二、实验开发工具：
Eclipse、JUnit、Ant
三、编码实现三角形类型判断程序：
class Triangle{
private double a, b, c;
public Triangle ( double a, double b, double c ){ this.a = a;
this.b = b;
this.c = c;
}
/*
返回值为1表示是等边三角形
返回值为2表示是等腰三角形
返回值为3表示是其他种类三角形
返回值为-1表示不能构成三角形
*/
public int type (){
//to be added
}
四、设计测试用例
建立一个被JUnit测试的类
建立对应的JUnit Test类
不能构成三角形的测试用例
构成等边三角形的测试用
构成等腰三角形的测试用例
构成其他种类三角形的测试用例
三角形有一条边是非正数
四、编写ant脚本驱动测试用例。

经典黑盒测试（判断三角形的形状）

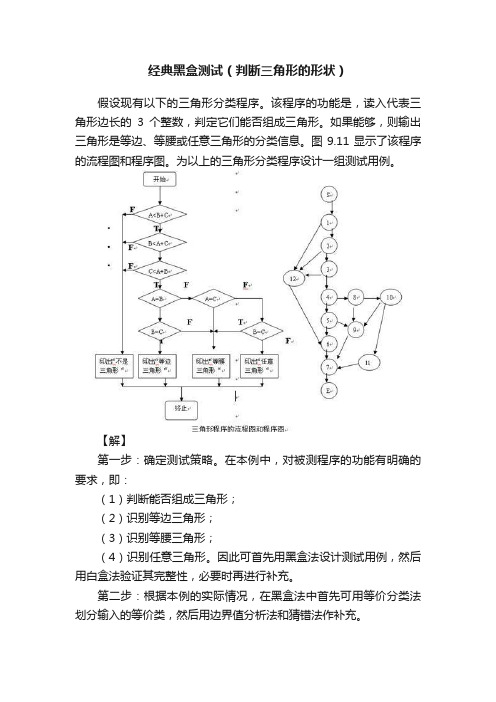
经典黑盒测试（判断三角形的形状）假设现有以下的三角形分类程序。

该程序的功能是，读入代表三角形边长的3个整数，判定它们能否组成三角形。

如果能够，则输出三角形是等边、等腰或任意三角形的分类信息。

图9.11显示了该程序的流程图和程序图。

为以上的三角形分类程序设计一组测试用例。

【解】第一步：确定测试策略。

在本例中，对被测程序的功能有明确的要求，即：（1）判断能否组成三角形；（2）识别等边三角形；（3）识别等腰三角形；（4）识别任意三角形。

因此可首先用黑盒法设计测试用例，然后用白盒法验证其完整性，必要时再进行补充。

第二步：根据本例的实际情况，在黑盒法中首先可用等价分类法划分输入的等价类，然后用边界值分析法和猜错法作补充。

等价分类法：有效等价类输入3个正整数：(1)3数相等(2)3数中有2个数相等，比如AB相等(3)3数中有2个数相等，比如BC相等(4)3数中有2个数相等，比如AC相等(5)3数均不相等(6)2数之和不大于第3数，比如最大数是A(7)2数之和不大于第3数，比如最大数是B(8)2数之和不大于第3数，比如最大数是C无效等价类：(9)含有零数据(10)含有负整数(11)少于3个整数(12)含有非整数(13)含有非数字符边界值法：(14)2数之和等于第3数猜错法：(15)输入3个零(16)输入3个负数第三步：提出一组初步的测试用例，如下表所示：第四步：用白盒法验证第三步产生的测试用例的充分性。

结果表明，上表中的前8个测试用例，已能满足对被测程序图的完全覆盖，不需要再补充其他的测试用例。

软件测试-判断三角形形状路径白盒测试

三角形白盒测试要求要求：,其他1 ) 自备 C 语言程序(可从 C 语言程序设计的教科书上摘录若干典型程序C++ 、C# 、Java 程序均可)；#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){int a,b,c;printf(" 输入三角形的三个边 :");scanf("%d %d %d",&a,&b,&c);if(a<=0||b<=0||c<=0)printf(" 不符合条件，请重新输入 a,b,c\n");else if(a+b<=c||abs(a-b)>=c)printf("不是三角形\n");else if(a==b&&a==c&&b==c)printf("这个图为等边三角形\n");else if(a==b||a==c||b==c)printf（"这个图为等腰三角形\n"）;elseprintf（"这个图为一般三角形\n"）;2）根据该程序绘制对应的程序流程图;/ 幟沖迈〃軾已等堆卄琳::矗歴# 输山养赠〃诚日等山/ / 输出水呈/3）分别根据程序流程图给出符合语句覆盖、判定覆盖、条件覆盖、路径覆盖以及判定/条件覆盖和条件组合覆盖的的测试用例以及预期的运行结果；语句覆盖判断覆盖条件覆盖判定1 : 1-1(a<=0) 1-2(b<=0) 1-3(c<=0)判定2: 2-1(a+b<=c) 2-2(|a-b|>=c) 判定3: 3-1(a==b)判定4: 4-1(a==c)判定5: 5-1(a==c)判定 6: 6-1(b==c)判定/条件覆盖、条件组合覆盖、路径覆盖4）根据程序流程图画出流图，并确定线性独立路径的基本集合，然后给出符合各集合的测试用例；路径1: 1-2-3路径2: 1-2-4-5-7-9-12-13路径3: 1-2-4-5-7-9-10-13路径4: 1-2-4-5-7-10-13 路径5: 1-2-4-5-8-10-13。

判断三角形类型的程序

判断三角形类型的程序三角形是几何学中的一个基本概念，它是由三条线段组成的闭合图形。

根据三角形的边长和角度，我们可以将它们分为不同的类型。

在本文中，将介绍如何编写一个程序来判断三角形的类型。

我们需要了解三角形的基本概念。

三角形的边可以分为三个部分：两条边和一个底边。

而三个角则是由这三条边所形成的。

根据三角形的边长和角度，我们可以将三角形分为以下几种类型：等边三角形、等腰三角形、直角三角形、钝角三角形和锐角三角形。

在编写程序之前，我们需要确定程序的输入和输出。

输入应该是三角形的三条边长，而输出则应该是三角形的类型。

根据输入的三条边长，我们可以使用一些条件判断语句来确定三角形的类型。

下面是一个简单的示例程序：```pythondef triangle_type(a, b, c):if a == b == c:return "等边三角形"elif a == b or a == c or b == c:return "等腰三角形"elif a**2 + b**2 == c**2 or a**2 + c**2 == b**2 or b**2 + c**2 == a**2:return "直角三角形"elif a**2 + b**2 < c**2 or a**2 + c**2 < b**2 or b**2 + c**2 < a**2:return "钝角三角形"else:return "锐角三角形"a = float(input("请输入三角形的第一条边长："))b = float(input("请输入三角形的第二条边长："))c = float(input("请输入三角形的第三条边长："))print("这是一个", triangle_type(a, b, c))```在上述的程序中，我们首先定义了一个函数`triangle_type`，它接受三个参数a、b、c，分别代表三角形的三条边长。

软件测试作业三角形判定

实验报告
课程名称：软件测试
实验项目：判断三角形
专业班级：软件0505班
姓名：
学号：
指导教师：**
沈阳工业大学实验报告
（适用计算机程序设计类）
专业班级：软件学院学号：姓名：实验名称：
附件A 沈阳工业大学实验报告
（适用计算机程序设计类）
专业班级：软件0505 学号：姓名：实验步骤或程序：
1.设计窗口
2.设计结构
ModelMain是程序的主入口，主要实现窗口的建立，从键盘接收三个变量，调用Triangle 类的构造方法和判断方法，并打印出结果。

Judge是一个判断接口定义了3个方法
Triangle是三角形类，实现了Judge接口
3.设计接口
4.实现内部功能
5.输出结果。

三角形程序白盒测试

请输入能构成三角形的整数。
执行路径：1-2-3-7-12
请输入能构成三角形的整数。
Case35
a=’g’，b=’6’，c=’h’
请输入能构成三角形的整数。
执行路径：1-2-3-7-12
请输入能构成三角形的整数。
Case36
a=’h’，b=’发’，c=’52’
请输入能构成三角形的整数。
执行路径：1-2-3-7-12
a=’5.3’，b=’3.0’，c=’2.3’
请输入能构成三角形的整数。
满足：F4,T5,F6
请输入能构成三角形的整数。
Case14
a=’6’，b=’2.3’，c=’3
请输入能构成三角形的整数。
满足：T4,F5,T6
请输入能构成三角形的整数。
Case15
a=’2’，b=’3’，c=’5’
请输入能构成三角形的整数。
执行路径：1-2-3-7-12
请输入能构成三角形的整数。
Case21
a=’1’，b=’2’，c=’3’
请输入能构成三角形的整数。
执行路径：1-2-3-4-5-7-12
请输入能构成三角形的整数。
Case22
a=’15’，b=’2’，c=’5’
请输入能构成三角形的整数。
执行路径：1-2-3-4-5-7-12
Case1
a=’三’，b=’角’，c=’形’
请输入能构成三角形的整数。
执行路径：1-2-3-7-12
请输入能构成三角形的整数。
Case2
a=’5’，b=’2’，c=’2’
请输入能构成三角形的整数。
执行路径：1-2-3-4-5-6-9-10-12
请输入能构成三角形的整数。
Case3

判定三角形的程序及黑盒白盒测试

判定三角形的程序及黑盒白盒测试LtD黑盒白盒测试实验报告学院：计算机科学与工程专业：软件工程姓名：张子晗软件测试方案测试目的1.练习并掌握软件测试管理的一般过程与步骤2.掌握测试管理的人工过程和能通过相关管理软件实现以下操作：1)创立和管理多个测试组和用户2)配置测试环境，编写详细测试方案，安排测试进度3)实施测试，执行测试4)对测试进行评估测试题目关于三角形问题的测试测试方法1.对于主题进行黑盒测试，测试内容包括等价类划分测试，边界值分析测试，决策表方法使用。

2.对于主题进行白盒测试，测试内容包括语句覆盖测试，分支覆盖测试，条件覆盖测试，分支/条件覆盖测试，条件组合覆盖测试以及根本路径测试。

测试资料1.黑盒测试：黑盒测试也称功能测试，它是通过测试来检测每个功能是否都能正常使用。

在测试中，把程序看作一个不能翻开的黑盒子，在完全不考虑程序内部结构和内部特性的情况下，在程序接口进行测试，它只检查程序功能是否按照需求规格说明书的规定正常使用，程序是否能适当地接收输入数据而产生正确的输出信息。

黑盒测试着眼于程序外部结构，不考虑内部逻辑结构，主要针对软件界面和软件功能进行测试。

黑盒测试是以用户的角度，从输入数据与输出数据的对应关系出发进行测试的。

很明显，如果外部特性本身设计有问题或规格说明的规定有误，用黑盒测试方法是发现不了的。

2.白盒测试：白盒测试又称结构测试、透明盒测试、逻辑驱动测试或基于代码的测试。

白盒测试是一种测试用例设计方法，盒子指的是被测试的软件，白盒指的是盒子是可视的，你清楚盒子内部的东西以及里面是如何运作的。

"白盒"法全面了解程序内部逻辑结构、对所有逻辑路径进行测试。

"白盒"法是穷举路径测试。

在使用这一方案时，测试者必须检查程序的内部结构，从检查程序的逻辑着手，得出测试数据。

贯穿程序的独立路径数是天文数字。

采用什么方法对软件进行测试呢?常用的软件测试方法有两大类:静态测试方法和动态测试方法。

白盒测试实验报告_三角形(2)

白盒测试实验报告——三角形
一、实验目的
（1）巩固白盒测试技术，能熟练应用控制流覆盖方法设计测试用例；
（2）学习测试用例的书写。

二、实验内容
判断三角形类型
输入三个整数a、b、c，分别作为三角形的三条边，通过程序判断这三条边是否能构成三角形？如果能构成三角形，则判断三角形的类型（等边三角形、等腰三角形、一般三角形）。

要求输入三个整数a、b、c，必须满足以下条件：1≤a≤200；1≤b≤200；1≤c≤200。

要求：
为测试该程序的方便，请将三角形判断的算法尽量放入一个函数中。

（1）画出程序的流图；
（2）分别以语句覆盖、判定覆盖、条件覆盖、判定条件覆盖、条件组合覆盖设计测试用例，并写出每个测试用例的执行路径
要求：设计测试用例时，每种覆盖方法的覆盖率应尽可能达到100%
（3）请采用基本路径测试方法对程序进行测试，并给出具体测试用例信息。

（4）通过你的测试，请总结你所使用测试方法发现的Bug。

三、实验要求
（1）根据题目要求编写测试用例
（2）撰写实验报告
（3）有关的实现程序请附到实验报告中
（4）实验报告命名规则：学号后两位+姓名_白盒实验
四、实验报告
（1）程序代码：
7.
8.
（2）程序的流图：
（4）判定覆盖；
（5）条件覆盖：
（6）判定/条件覆盖；
（8）基本路径覆盖；
附录：测试用例书写格式（语句覆盖为例）。

小学四年级数学教案：三角形的分类与判断

小学四年级数学教案：三角形的分类与判断三角形的分类与判断一、教学目标1.知识目标：掌握三角形的定义和性质，能够准确判断三角形的类型。

2.能力目标：培养学生的逻辑思维和分析能力，训练学生准确判断三角形的能力。

3.情感目标：培养学生对数学的兴趣和爱好，激发学生学习数学的积极性。

二、教学重点难点教学重点：掌握三角形的定义和性质。

教学难点：分析判断三角形的类型。

三、教学方法1.讲授法：讲解三角形的定义、性质及分类。

2.图像分析法：通过图像分析判断三角形的类型。

3.实践操作法：通过练习题和课堂活动，让学生巩固和拓展所学知识。

四、教学过程1.导入通过学生生活中的实例，引入三角形的概念和定义，如衣服、书包等物体的造型，让学生理解三角形的基本构造。

2.讲授(1)三角形的定义：三边所组成的图形叫做三角形。

(2)三角形的性质：①三角形的三条边可以组成三个内角，三个内角的和为180度。

②一个三角形的任何两边的长度之和大于第三边的长度。

③等腰三角形的两边相等，两角一定相等。

④等边三角形的三条边都相等，三个内角也相等，每个内角都是60度。

(3)三角形的分类：①按边长分：●等边三角形：三边长度都相等。

●等腰三角形：两边长度相等。

●普通三角形：三边长度都不相等。

②按角度分：●锐角三角形：三个内角都是锐角。

●直角三角形：其中一个内角是90度。

●钝角三角形：其中一个内角是钝角，大于90度。

3.图像分析(1)通过图像分析，判断下列三角形的类型：(2)学生自主练习，尝试判断不同类型的三角形。

4.实践操作(1)完成练习题，帮助学生巩固所学知识。

(2)进行小组活动，以小组为单位，运用所学知识完成任务，提高学生的合作与竞争精神。

五、教学总结通过本节课的学习，学生掌握了三角形的定义、性质和分类。

通过图像分析和实践操作，培养了学生的逻辑思维和判断能力。

帮助学生建立数学学习的兴趣和爱好，提高学生的学习热情和积极性。

软件测试判断三角形形状白盒测试黑盒测试

淮海工学院计算机工程学院实验报告书课程名：《软件工程导论》题目：软件测试学号： 511020825姓名：薛思雨一、实验目的与要求1、掌握软件测试2、掌握白盒测试方法3、掌握黑盒测试方法（边界值分析和等价类划分）4、掌握自动化测试软件和方法二、实验内容或题目1）试画出：给定四边形的四条边，判断这个四边形是普通四边形、平等四边形、菱形的流程图，给出详细设计结果与C语言代码，对其使用白盒和黑盒测试技术分别设计测试用例（包括所有白盒测试的覆盖、黑盒测试的边界值分析与等价类划分）。

然后，使用测试用例进行实际测试，并给出测试结果；（或输入三条边，判断三条边组成的图形是一般三角形、等腰三角形、直角三角形、等边三角形，亦或不能构成三角形，其它要求同四边形）2）了解一些典型的自动化测试软件和方法，建议有条件可下载、安装Mercury Interactive公司的负载测试工具LoadRunner、功能测试工具WinRunner和测试管理工具TestDirector；IBM-Rational公司的测试套件Rational Suite TestStudio的Rational Robot、Rational TestManagerhe、Rational Quantify等工具，了解软件的使用方法。

3) 课内认真完成实验报告，禁止抄袭。

三、实验步骤与源程序第一题：1. 根据题目画流程图核心流程图：源代码：#include<stdio.h>void main(void){int a,b,c,k;printf("请输入三角形的三边长(0-100):");scanf("%d %d %d",&a,&b,&c);if((a>=1&&a<=100)&&(b>=1&&b<=100)&&(c>=1&&c<=100)) {if((a+b>c)&&(a+c>b)&&(b+c>a)){if((a==b&&b!=c)||(a==c&&c!=b)||(b==c&&a!=b))k=1;if(a==b&&a==c)k=2;if((a*a+b*b==c*c)||(a*a+c*c==b*b)||(c*c+b*b==a*a))k=3;switch(k){case 1:printf("等腰三角形\n");break;case 2:printf("等边三角形\n");break;case 3:printf("直角三角形\n");break;default:printf("一般三角形\n");break;}}elseprintf("不能构成三角形\n");}elseprintf("警告：无效输入！！\n");}第二题：1.打开虚拟机，启动Windows XP Professional。

软件测试

软件测试实验报告课程名称：软件测试实验项目：判断三角形专业班级：姓名：学号:指导教师：一．实验题目输入三个整数作为三边的边长构成三角形，分别用等价类方法和判定表方法构造测试用例进行测试（注：三角形可能为一般三角形，等腰三角形，等边三角形）二．设计程序代码如下：#include<iostream>#include <math.h>using namespace std;void main(){cout<<"输入三边边长："<<endl;int a,b,c;cin>>a;cin>>b;cin>>c;if(a+b>c&&a+c>b&&b+c>a&&fabs(a-b)<c&&fabs(a-c)<b&&fabs(b-c)<a){if(a==b&&b==c){cout<<"可构成等边三角形："<<endl;}else if(a==b||a==c||b==c){cout<<"可构成等腰三角形"<<endl;}else{cout << "可构成普通三角形" << endl;}}else cout<<"不能构成三角形"<<endl;}三．等价类划分：(1)划分等价类：输入条件有效等价类无效等价类是否三角形的三条边a>0 （1）b>0 （2）c>0 （3）a+b>c (4)b+c>a (5)a+c>b (6)a-b<c （7）b-c<a （8）a-c<b （9）a<=0 （10）b<=0 （11）c<=0 （12）a+b<=c (13)b+c<=a (14)a+c<=b (15)a-b>=c （16）b-c>=a （17）a-c>=b （18）是否等腰三角形a=b (19)b=c (20)a=c(21)a≠b AND b≠c ANDa≠c (22)a=b AND b=c AND a≠b (24)是否等边三角形a=c(23) b≠c (25)a≠c(26)(2)．测试用例设计：序号 a b c 覆盖等价类输出1 4 5 6 123456789 构成一般三角形2 3 4 5 6 7 8 9 10 -2 1 11 -2 11 1 -21 1 43 1 11 2 15 1 22 5 15 2 1101112131415161718不能构成三角形111213 6 6 78 6 66 8 61 2 3 4 5 6 7 8 9 191 2 3 4 5 6 7 8 9 201 2 3 4 5 6 7 8 9 21等腰三角形14 4 5 6 1 2 3 4 5 6 7 8 9 22 非等腰三角形15 4 4 4 1 2 3 4 5 6 7 8 9 23 等边三角形161718 4 3 33 5 34 4 51 2 3 4 5 6 7 8 9 241 2 3 4 5 6 7 8 9 251 2 3 4 5 6 7 8 9 26非等边三角形四：判定表方法1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17条件a.>0 0 1 1 1 1 1- 1 1 1 1 1 1 1 1 1 1 1b>0 - 0 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1c>0 - - 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 a+b>c - - - 0 1 1 1 1 1 1 1 1 1 1 1 1 1 b+c>a - - - - 0 1 1 1 1 1 1 1 1 1 1 1 1 a+c>b - - - - - 0 1 1 1 1 1 1 1 1 1 1 1 a-b<c - - - - - - 0 1 1 1 1 1 1 1 1 1 1 b-c<a -- - - - - - - 0 1 1 1 1 1 1 1 1 1 a-c<b - - - - - - - - 0 1 1 1 1 1 1 1 1 a=b - - - - - -- - - - 1 1 1 1 0 0 0 0 b=c - - - - - - - - - 1 1 0 0 1 1 0 0 a=c - - - - - - - - - 1 0 1 0 1 0 1 0 不能构成三角1 1 1 1 1 1 1 1 1动作形等腰三角形1 1 1等边三角形1一般三角形1不可能1 1 1（2）测试用例设计：测试用例id a b c 预期输出1 -1 3 4 不能构成三角形2 2 -3 3 不能构成三角形3 2 3 -2 不能构成三角形4 1 35 不能构成三角形5 6 2 3 不能构成三角形6 2 4 1 不能构成三角形7 5 2 2 不能构成三角形8 2 5 2 不能构成三角形9 5 2 1 不能构成三角形10 3 3 3 等边三角形11 ？？？无效12 ？？？无效13 3 3 5 等腰三角形14 ？？？无效15 5 4 4 等腰三角形16 2 1 2 等腰三角形17 4 2 5 一般三角形。

实验六_三角形问题的基本路径测试

实验六三角形问题的基本路径测试一、实验目的1.掌握程序控制流图的画法。

2.掌握环路复杂度的计算方法。

3.掌握利用基本路径法进行白盒测试的方法。

二、实验任务1．理解三角形问题的命题。

三角形问题是软件测试文献中广泛使用的一个例子。

三角形问题：输入三个整数a、b和c分别作为三角形的三条边，通过程序判断有这三条边构成的三角形类型是：等边三角形、等腰三角形、一般三角形或非三角形。

主要代码如下：1.If (inta >= intb + intc)2. Or (intb >= inta + intc)3. Or (intc >= intb + inta) Then4. strMsg = "非三角形"5.Else6. If (inta = intb)7. And (intb = intc) Then8. strMsg = "等边三角形"9. Else10. If (inta = intb)11. Or (inta = intc)12. Or (intc = intb) Then13. strMsg = "等腰三角形"14. Else15. strMsg = "普通三角形"16. End If17. End If18.End If19.MsgB ox(strMsg, rmation, "三角形问题") //输出判断结果2．利用基本路径测试法对三角形问题进行测试用例设计。

三、实验步骤1．理解三角形问题中各种三角形的判断方法。

2．根据上面的代码画出程序的控制流图。

（注意：复合条件语句，需改复合条件的判断为一系列单个条件的嵌套）3．计算环路复杂度。

4．求出基本路径组合。

5．设计测试用例（按照表1的形式，设计用例）。

表1：用例设计表四、实验报告要求1．实验报告中“实验内容”应包含（1）程序控制流图；（2）环路复杂度计算结果；（3）基本路径集合；（4）测试用例设计（按表1填写）。

《三角形特征判断程序》测试计划

三角形特征判断程序测试计划---韩春晖2012年4月12日修订历史记录目录1.简介 (2)1.1目的 (3)1.2背景 (3)1.3范围 (3)2.测试提交文档 (3)3.测试进度 (3)4.测试资源 (4)4.1人力资源 (4)4.2测试坏境 (4)4.3测试工具 (4)5.测试策略 (5)6问题严重度描述 (5)7附录：项目任务 (6)1.简介1.1目的三角形测试判断程序测试：这份测试计划书是为了测试C语言程序能否运行成功，以达到预期效果,然后给出正确答案或提示错误。

1.2背景项目的名称：三角形特征判断程序测试项目产品名称：C语言程序—判断三角形的测试项目组织者：第一组产品用户：ST1201班产品设计者：第一组产品运行者：第一组1.3范围根据软件行业标准，制定测试计划、测试方案，包括收集测试方法、测试用例及手工测试工具等。

本测试主要针对C语言程序实现功能进行测试，对长度有特殊比例模块进行重点测试。

2.测试提交文档（1）测试计划文档（2）测试用例文档（3）测试报告文档3.测试进度4.1人力资源下表列出了在此项目的人员配备方面所做的各种假定。

4.2测试坏境下表列出了测试的系统坏境4.3测试工具次项目将列出测试使用的工具：由于本测试很简单，故只测试功能测试。

具体功能测试6问题严重度描述7附录：项目任务以下是一些与测试有关的任务：✧制定测试计划⏹确定测试需求⏹制定测试策略⏹生成测试计划✧设计测试⏹准备工作量分析文档⏹确定并说明测试用例⏹确定测试过程，并建立测试过程的结构✧实施测试⏹通过编程创建测试脚本⏹建立外部数据集✧执行测试✧执行测试过程✧评估测试的执行情况✧恢复暂停的测试✧核实结果✧调查意外结果✧记录缺陷✧对测试进行评估✧评估测试用例覆盖✧评估代码覆盖✧分析缺陷✧确定是否达到了测试完成标准与成功标准。

判断三角形程序的测试报告

判断三角形程序的测试报告姓名：郭新宇学号：110402420041、三角形问题输入三个整数a、b、c分别作为三角形的三条边现通过程序判断由三条边构成的三角形的类型为等边三角形、等腰三角形、一般三角形、特殊的还有直角三角形，以及不构成三角形。

现在要求输入三个整数a、b、c必须满足以下条件条件1 1≤a<100 条件4 a<b+ c条件2 1≤b<100 条件5 b<a+ c条件3 1≤c<100 条件6 c<a+ b如果输入值a、b、c不满足条件1、条件2和条件3 程序给出“边的取值超出允许范围”的信息。

如果输入值a、b、c 满足条件1、条件2和条件3则输出下列四种情况之一1如果不满足条件4、条件5和条件6中的一个则程序输出为“非三角形”。

2如果三条边相等则程序输出为“等边三角形”。

3如果恰好有两条边相等则程序输出为“等腰三角形”。

4如果三条边都不相等则程序输出为“一般三角形”。

2、测试目的：通过测试，判断程序是否达到预期的要求，程序是否存在问题。

3、测试用例设计依据和方法：等价类方法和边界值方法。

4、测试用例设计分析1,、有效数据位1到1002、输出结果：非三角形，等腰三角形，等边三角形，直角三角形，一般三角形或XX 的值不在允许范围内5、测试用例表操作过程序号输入及操作说明期望的测试值评价标准实测结果11,2,4非三角形非三角形非三角形25,5,5等边三角形等边三角形等边三角形33,4,5直角三角形直角三角形直角三角形42，3,3 等腰三角形等腰三角形等腰三角形56,7,9一般三角形一般三角形一般三角形6-1,5,5 a 的值不在允许范围内a 的值不在允许范围内a 的值不在允许范围内附：程序代码#include <stdio.h>void main(){int a,b,c;printf("请输入三个整数，用逗号分隔！");scanf("%d,%d,%d",&a,&b,&c);if((a<=0)||(b<=0)||(c<=0)){if(a<=1)printf("a 的值不在取值范围内！");else if (b<=1)printf("b 的值不在取值范围内！");else if (c<=1)printf("c 的值不在取值范围内！");}else if ((a>=100)||(b>=100)||(c>=100)){if (a>=100)printf("a 的值不在取值范围内！");else if (b>=100)printf("b 的值不在取值范围内！");else if (c>=100)printf("c 的值不在取值范围内！");}else if ((a+b<=c)||(b+c<=a)||(a+c<=b))printf("非三角形！");else if ((a==b)&&(b==c)&&(a==c))printf("等边三角形！");else if (((a==b)&&(a!=c))||((a==c)&&(a!=b))||((c==b)&&(a!=c))) printf("等腰三角形！");else if (a*a==b*b+c*c||b*b==a*a+c*c||c*c==a*a+b*b)printf("直角三角形！");else printf("一般三角形！");}。

【C语言程序设计】C语言判断三角形的类型！

【C语⾔程序设计】C语⾔判断三⾓形的类型！根据输⼊的三⾓形的三条边判断三⾓形的类型，并输出其⾯积和类型。

算法思想⾸先判断其两边之和是否⼤于第三边，若⼤于则判断可以构成三⾓形，再进⼀步判断该三⾓形是什么三⾓形，并计算这个三⾓形的⾯积；否则不能构成三⾓形。

①从键盘输⼊三⾓形的三条边。

②判断两边之和是否⼤于第三边。

③若条件成⽴则判断可构成三⾓形，计算其⾯积，并判断其类型；否则判断其不能构成三⾓形。

④在类型判断中⾸先判断其是否三边相等，条件成⽴则判断其为等边三⾓形；否则判断其是否有两边相等，条件成⽴则判断其为等腰三⾓形；否则判断其是否有两边的平⽅和等于第三边的平⽅，条件成⽴则判断其为直⾓三⾓形；否则判断其为普通三⾓形。

程序代码#include <stdio.h>#include <math.h>int main(){float a,b,c;float s,area;printf("请输⼊三⾓形的三条边:\n");scanf("%f,%f,%f",&a,&b,&c);if(a+b>c&&b+c>a&&a+c>b){s=(a+b+c)/2;area=(float)sqrt(s*(s-a)*(s-b)*(s-c));printf("三⾓形的⾯积是：%f\n" ,area);if(a==b&&a==c)printf("三⾓形是等边三⾓形\n");else if(a==b||a==c||b==c)printf("三⾓形是等腰三⾓形\n");else if((a*a+b*b==c*c)||(a*a+c*c==b*b)||(b*b+c*c==a*a))printf("三⾓形是直⾓三⾓形\n");elseprintf("三⾓形是普通三⾓形\n");}elseprintf("不能构成三⾓形\n");return0;}调试运⾏结果输⼊为 3，3，3 时，对应的输出情况如下所⽰：请输⼊三⾓形的三条边:3,3,3三⾓形的⾯积是：3.897114三⾓形是等边三⾓形输⼊为 3，4，5 时，对应的输出情况如下所⽰：请输⼊三⾓形的三条边:3,4,5三⾓形的⾯积是：6.000000三⾓形是直⾓三⾓形总结①在本实训之前必须知道三⾓形的相关知识，⽐如，怎么判断输⼊的三边是否能构成三⾓形、三⾓形的⾯积计算⽅法等。

三角测试作业

android:hint="请输入第一条边长a"/>
取得a，b，c的数值，并得到浮点型和整数型
StringvalueA=edgeA.getText().toString().trim();
StringvalueB=edgeB.getText().toString().trim();
StringvalueC=edgeC.getText().toString().trim();
提示：请输入a
输入长度不正确
a=--，b=--，c=A
提示：请输入a
输入长度不正确
0<a<=200
b不是整型数值
c不是整型数值
a=2，b=B，c= A
提示：b不在值域内
提示：b不是整数
a<=0||a>200||--
b不是整型数值
c不是整型数值
a=-2，b=B，c= A
提示：a不在值域内
提示：a不是整数
两边相等时，判断为等腰三角形
输入a=201，b=201，c=202，判断为等腰三角形
三边都相等时，判断为等边三角形
输入a=201，b=201，c=201，判断为等边三角形
4、代码修改
代码功能
原代码
修改后代码
限制a，b，c输入的都为数字
<EditText
android:id="@+id/edgeA"android:layout_width="match_parent"android:layout_height="wrap_content"android:hint="请输入第一条变长a"/>
提示：c不在值域内

三角形判定测试

⑤：输入数据为（6,6,6），期待值pan（）为4，test（）为1
3.将所有测试用例放到Junit test suite内
4.
六、实验反思
这个实验发现自己的不足，有很多操作步骤不是很清楚，Java的不熟悉让自己对操作非常生疏，一些技术性的东西也不是很明白，希望下次能顺利地完成实验任务。
2.改实验用了5组测试用例进行测试
①：输入数据为（1,0,1），期待值pan（）为-4，test（）为-4
②：输入数据为（1,3,1），期待值pan（）为4，test（）为0
③：输入数据为（3,3,1），期待值pan（）为4，test（）为2
④：输入数据为（3,4,5），期待值pan（）为4，test（）为3
软件测试技术基础
实
验
报
告
姓名：周湘洁
学号：20127386
班级：计算机2班
指导老师：余波
完成时间：2015.4.18
实验一：单元测试框架Junit
一、实验目的：
1.通过测试员输入的数据人工动态测试三角形的判定
2.让同学们了解Junit的使用
二、实验环境：
1.windows+eclipse
三、实验内容：
if((a>0&&a<100)&&(b>0&&b<100)&&(c>0&&c<100)){
return4;
}else{
return-4;
}
}
publicinttest(){
booleanIsTraingle;
if((a<b+c)&&(b<a+c)&&(c<a+b)){

测试设计_判断三角形类型问题

判断三角形类型问题测试设计一、需求分析1、本程序用于判断三角形的类型。

2、程序的输入：三角形的三边由手工输入，再进行判断；需要注意的是，本程序只接受数值类型的输入，而且程序要求输入的范围在200以内，所以最好输入200以内的数，但是对超出200以外的数，本程序也要作特别的处理，对于要求以内的数，程序会做出正确的处理。

3、特殊要求：如果三条边能组成三角形（指范围在200以内的边），必须以绘图的方式把三角形画出来，对于其他输入也要做出相应处理4、演示从输入数据到输出类型和图形的整个过程二、概要设计根据以上的分析，可以抽象出7种三角形的类型：三条边中任意一条边超过限定值（200）或小于限定值（1）、输入的三条边无法组成三角形、等边三角形、普通等腰三角形、普通三角形、普通直角三角形和等腰直角三角形。

对于直角三角形的处理为：由于是手工输入，无法输入开根号的无限循环小数，以达到组成三角形的目的。

所以，可以规定其中任意两条边平方和与第三条边的平方之差在正负0.07之内，就已经是直角三角形了。

判断类型的过程如下：三、代码部分代码主要分为两部分：核心类（判定三角形的类型以及花三角行等等）以及界面类部分，其中界面类部分由于采用VB，其中的一些按钮之类的类是开发环境本生自带的类，是已经集成的，所以，我没有编写代码。

代码具体如下：（1）、核心类代码：1—1（2）、界面类代码：2—12—2三角形问题———需求检查表三角形弱健壮等价类测试用例及其输出:测试用例a b c预期输出WN1303030等边三角形WN2303036等腰三角形WN3304050直角三角形WN4303840普通三角形WN5342011无法组成三角形WN6303042.4264等腰直角三角形WR1-23434a取值不在允许的范围内WR234-234b不取值不在允许的范围内WR33434-2c取值不在允许的范围内WR42053434a取值不在允许的范围内WR53420534b不取值不在允许的范围内WR63434205c取值不在允许的范围内三角形边界值_健壮性测试用例及其输出:基于决策表的测试(三角形问题)三角形问题决策表决策表1：决策表2：基于决策表的用例:用例ID a b c预期输出规则条数统计ID1253060非三角形256ID2412412非三角形128ID3235020非三角形64ID4273033普通三角形1ID5304050直角三角形1ID6305040直角三角形1ID7503040直角三角形1ID8？？？不可能1ID9？？？不可能1ID10？？？不可能1ID11？？？不可能1ID12353535等边三角形1ID13？？？不可能1ID14？？？不可能1ID15？？？不可能1ID16？？？不可能1ID17？？？不可能1ID18？？？不可能1ID19？？？不可能1ID20？？？不可能1ID21？？？不可能1ID22？？？不可能1ID23？？？不可能1ID24？？？不可能1ID25303042.4264等腰直角三角形1ID26？？？不可能1ID27303037等腰三角形1ID28？？？不可能1ID29？？？不可能1ID30？？？不可能1ID31？？？不可能1ID32？？？不可能1ID33？？？不可能1ID343042.426430等腰直角三角形1ID35303730等腰三角形1ID36？？？不可能1ID37？？？不可能1ID38？？？不可能1ID39？？？不可能1ID4042.42463030等腰直角三角形1ID41？？？不可能1ID42？？？不可能1ID44373030等腰三角形1ID45？？？不可能8ID46？？？不可能8ID47？？？不可能8三角形的判定覆盖及用例:根据上述的三角形程序流程图现设计针对判定覆盖(即分支覆盖)性的一组测试用例：用例a b c预期输出第一组-10300248无效第二组15287非三角形第三组142018普通三角形第四组151510普通等腰三角形第五组262626等边三角形第六组304050普通直角三角形第七组100100141.421等腰直角三角形由上述流程图以及给出的七组用例可以看出，给出的用例已经覆盖了所有的判定的分枝。

试验一——判断三角形的类型，并设计测试用例

unexpectedendofjsoninput请尝试刷新页面或更换浏览器重试
试验一 ——判断三角形的类型，并设计测试用例
试验目的：使用JAVA语言编写一个方法，判断三角形为等边等腰或者一般类型，并设计测试用例使用JUnit进行测试。试验工具：Eclipse，12-sources.jar，hamcrest-core-1.3-sources.jar。试验步骤：1.在Eclipse中新建一个工程命名为triangle。 2.在该工程中导入上述两个jar包 3.编写相关程序，以边的长度是否一致判断三角形类型。 4.新建一个新的CLASS，编写测试用例 5.右键点击工程包，点击RUN AS-->JUnit Test，观察测试用例的运行情况试验总结：通过此次试验，熟悉了JUnit的使用方法，尝试了测试用例的设计。

教学项目：判断三角形类型程序的测试