图形学实验一 三维分形(附源代码)
分形图形学实验报告

分形图形学实验报告指导实验报告要求1.实验名称2.实验目的、要求3.实验主要内容(某某算法的实现)4.实验过程(程序流程图、源代码)5.实验结果(附上打印的图形)6.实验小结实验报告一一般分形图形生成实验目的1.Koch曲线、Sierpinski三角形、Cantor集的计算机实现2.掌握用迭代、递归生成分形实验内容及步骤1、Koch曲线函数:plot(x1,y1) –(x2,y2)(画直线函数)sin( )(正弦函数)cos( )(余弦函数)ArcTan( )(反正切函数)2、Sierpinski三角形函数:plot(x1,y1) –(x2,y2)(画直线函数)sin( )(正弦函数)cos( )(余弦函数)3、Cantor集实验报告二L系统语言生成分形图形实验目的1.掌握用L系统语言生成分形2.Koch曲线、Sierpinski三角形、Cantor集的L系统实现实验内容及步骤1.编写程序用L系统语言生成分形图形1)编写程序生成Koch曲线:初始图形是一条线段,生成过程是将线段中间1/3向外折起。
程序伪码如下:KochCurve { ;柯赫曲线Angle 6 ;角度增量是60°Axiom F ;初始图形是一单位线段F=F+F--F+F ;产生式是将线段中间1/3折起} ;结束2)用L系统再次生成Sierpinski三角。
生成Sierpinski三角的伪码如下:Hilbert{ ;Sierpinski三角,1996-12Angle 4Axiom Y ;初始串为任意字母YX=-YF+XFX+FY- ;第一个生成规则Y=+XF-YFY-FX+ ;第二个生成规则,由以上规则不断代换}3)模拟草本植物。
注意这里出现了“括号”——可以方便地表示树枝,伪码如下:HerbPlant { ;生成植物,本程序使用了括号Angle 14Axiom ZZ=ZFX[+Z][-Z]X=X[-FFF][+FFF]FX}实验报告三逃逸时间法生成Mandelbrot 集与Julia集实验目的1.掌握逃逸时间法2.Mandelbrot集与Julia集的计算机实现实验内容及步骤1.编写程序生成Mandelbrot集在复迭代中影响最大的当属迭代z→z^2+c,实际上它只是形式更一般的复解析迭代z_(n+1)=F(z_n)+c的一种, F是一个非线性函数。
matlab画三维图像的示例代码(附demo)

matlab画三维图像的⽰例代码(附demo)当我们学习surface命令时,已经看到了三维作图的⼀些端倪。
在matlab中我么可以调⽤mesh(x,y,z)函数来产⽣三维图像。
⾸先,我们⽤z=cos(x)sin(y)在-2pi ≤x,y≤ 2pi内的图像来看看:[x,y] = meshgrid(-2*pi:0.1:2*pi);z = cos(x).*sin(y);mesh(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')显⽰图像如下:同样⽤mesh命令产⽣z = ye-(x2+y2)的三维图像:[x,y] = meshgrid(-2:0.1:2);z = y.*exp(-x.^2-y.^2);mesh(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')下⾯绘制表⾯带有渐变颜⾊的图像,可以通过 surf 和 surfc 命令实现,只要简单更改上⾯例⼦中的命令为:surf(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')则图像如下所⽰,图像表⾯的颜⾊与⾼度是相称的:若使⽤surfc则会在图像中留下映像:surfc(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')还可以调⽤surfl(命令中的'l'表⽰这是⼀个光照表⾯ lighted surface)命令显⽰三维光照物体的表⾯,可以使⽤这个命令产⽣没有线条的三维图像,图像还可以是彩⾊的或灰度的。
例如仍然产⽣函数z = ye-(x2+y2)的灰度图像,图像中的阴影可设置为flat、interp、faceted:surfl(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')shading interp;colormap(gray);下⾯我们使⽤matlab内置函数来产⽣像球形或圆柱形这样的基本图像,例如:t = 0:pi/10:2*pi;[X,Y,Z] = cylinder(1+sin(t));surf(X,Y,Z),colormap('default');axis square会得到如下图像:试试另⼀个稍微有点不同的函数,阴影设置为faceted:t = 0:pi/10:2*pi;[X,Y,Z] = cylinder(1+cos(t));surf(X,Y,Z),shading faceted;axis square若将阴影设置为shading flat,则图像显⽰为:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
用计算机程序制作三维立体画(精)

用计算机程序制作三维立体画摘要该文介绍了三维立体画的原理和制作方法,并给出了用C 语言编写的源程序。
借助于Pbrush.exe,读者可以自己设计和欣赏各式各样的三维立体画。
目前,市面上正在流行各式各样的立体画,其特点是从外表来看与一般的图案很相似,但是双眼紧盯着注视片刻后,一恍惚之间眼前便出现了画中画——立体像。
笔者第一次看到这种画便被发明者的创意所倾倒。
利用众所皆知的双眼视差原理,竟能在一张平面纸上制造出如此奇幻。
但是立体画本身除了其发明者的灵感和画面创作者的别出心裁之外,其原理上并无神秘之处。
用计算机程序来实现它,可说是易如反掌。
笔者用一个晚上时间,便在微机上用BASIC语言实现了简单形体——平面圆饼的立体画。
当然,要使该程序具有完善的功能,提高其制作速度,还是应该用编译语言(如C语言)来编写。
本文中给出的源程序借助于Windows中的.BMP图形文件,可使大家自己制作任意形态的立体画。
一、立体画的原理看过立体电影的人都知道,当人的双眼分别接收不同视角拍摄的图像时便会产生立体感。
这是由于人眼长期观察的习惯造成的。
和立体电影原理相同的立体摄影风景照片也很早就已出现。
图1中给出了这种立体照片的示意图。
左、右照片分别是人的双眼角度上观察一棱锥体时左右眼看到的图像(图2)。
左眼看到的是棱锥的顶端向右错动了一些的图像,右眼的看到则是棱锥的顶端向左错动了一些的图像。
如果用一张硬卡片隔开两张照片,双眼分别看两张画,会看到一个立体的棱锥体。
这种立体照片的观察方法在测绘学中也早已采用。
但是,目前的三维立体画在形式上与这些很不相同。
它是怎样在同一张画面上呈现立体的呢?首先,分析一下人们是怎样从这些立体画中看出“立体形体”的。
从前面所说的可以知道,人眼要得到立体感,双眼必须有视差,即双眼看到的图像应该有差异。
人们在看立体画时,都有“恍惚”一下的过程。
在这过程中,双眼的视中心发生了错动(如图4)。
这样@@09A04003.GIF;图4左眼看到的是画面的“偏左像”,右眼看到的是画面的“偏右像”。
计算机图形学实验报告(分形图)

实验六:分形图的生成班级11信计2班学号20110502078 姓名刘昱丞分数一、实验目的理解分形图生成的基本原理,掌握几种常见的分形图生成算法,利用TurboC实现Koch 曲线和可以无穷放大的Mandelbrot Set (曼德布洛特集)生成算法。
二、实验内容1.、利用Koch 曲线生成规则,在屏幕上生成一段Koch 曲线。
2/、利用Mandelbrot Set 生成规则,在屏幕上生成可以无穷放大的Mandelbrot Set (曼德布洛特集)三、实验步骤(1)预习教材关于Koch 曲线和可以无穷放大的Mandelbrot Set (曼德布洛特集)的生成原理。
(2)仿照教材关于Koch 曲线和可以无穷放大的Mandelbrot Set (曼德布洛特集)生成算法生成算法,使用TurboC实现该算法。
(3)调试、编译、运行程序。
四、实验要求在下次实验时提交本次试验的实验报告(实验报告包括实验目的、实验内容、实验实现过程、源程序、实验结果、实验体会)。
五、实验过程( 1 ) Koch 曲线的生成规则它的构造是:迭代初始把原线段去掉中间的三分之一,代之以底边在被去线段上的等边三角形的两腰;以后每一步的迭代都是这样的重复。
从以上过程可以清楚地看出,Koch曲线(其它分形集也是如此)可以由简单的图,称为生成元,迭代产生。
在这里,Koch曲线的生成元是:六、实验代码1/、Koch曲线源程序:#include <stdio.h>#include <stdlib.h>#include <math.h>#include <conio.h>#include <graphics.h>#define rad 0.0174532925#define NUMBER 24koch(ax,ay,bx,by)int ax,ay,bx,by;{ float cx,cy,ex,ey,dx,dy,arf,le,c;c=1000; /*30000,20000,10000,5000,1000 tiao jie ci shu */if ((bx-ax)*(bx-ax)+(by-ay)*(by-ay)<c)line(ax,ay,bx,by);else{cx=ax+(bx-ax)/3;cy=ay+(by-ay)/3;ex=bx-(bx-ax)/3;ey=by-(by-ay)/3;koch((int)(ax),(int)(ay),(int)(cx),(int)(cy)); /* koch(ax,ay,cx,cy); */ koch((int)(ex),(int)(ey),(int)(bx),(int)(by));le=sqrt((ex-cx)*(ex-cx)+(ey-cy)*(ey-cy)); /* koch(ex,ey,bx,by); */ arf=atan((ey-cy)/(ex-cx));if((arf>=0 &&(ex-cx)<0)||(arf<=0 &&(ex-cx)<0))arf=arf+3.1415;dy=cy+sin(arf+3.1415/3)*le;dx=cx+cos(arf+3.1415/3)*le;koch((int)(cx),(int)(cy),(int)(dx),(int)(dy)); /*koch(cx,cy,dx,dy);*/ koch((int)(dx),(int)(dy),(int)(ex),(int)(ey)); /* koch(dx,dy,ex,ey); */ }}main(){float xa1,xb1,ya1,yb1;float xa,xb,ya,yb;float dex,dey,dx,dy;float x,y,s1,s2;int steps,k;int gdriver=DETECT,gmode;initgraph(&gdriver,&gmode,"C:\\JMSOFT\\DRV");cleardevice();setbkcolor(BLUE);/* line(400,400,600.4,540.6); */settextstyle(1,0,3);outtextxy(100,100,"Shijiazhuang University");/* koch(340,150,100,150) ; */koch(100,300,500,300) ;getch();closegraph();return 0;}输出结果为:2.、可以无穷放大的Mandelbrot Set (曼德布洛特集)源程序:#include <graphics.h>#include <conio.h>// 定义常量#define ITERATIONS 1000 // 迭代次数,越高,图像越精细#define MAXCOLOR 64 // 颜色数/////////////////////////////////////////////////// 定义复数及乘、加运算/////////////////////////////////////////////////// 定义复数struct COMPLEX{double re;double im;};// 定义复数“乘”运算COMPLEX operator * (COMPLEX a, COMPLEX b){COMPLEX c;c.re = a.re * b.re - a.im * b.im;c.im = a.im * b.re + a.re * b.im;return c;}// 定义复数“加”运算COMPLEX operator + (COMPLEX a, COMPLEX b){COMPLEX c;c.re = a.re + b.re;c.im = a.im + b.im;return c;}/////////////////////////////////////////////////// 定义颜色及初始化颜色/////////////////////////////////////////////////// 定义颜色int Color[MAXCOLOR];// 初始化颜色void InitColor(){// 使用HSL 颜色模式产生角度h1 到h2 的渐变色int h1 = 240, h2 = 30;for(int i=0; i<MAXCOLOR/2; i++){Color[i] = HSLtoRGB((float)h1, 1.0f, i * 2.0f / MAXCOLOR);Color[MAXCOLOR-1-i] = HSLtoRGB((float)h2, 1.0f, i * 2.0f / MAXCOLOR);}}/////////////////////////////////////////////////// 绘制Mandelbrot Set (曼德布洛特集)/////////////////////////////////////////////////void Draw(double fromx, double fromy, double tox, double toy){COMPLEX z, c;int x, y, k; // 定义循环变量for(x = 0; x < 640; x++){c.re = fromx + (tox - fromx) * (x / 640.0);for(y = 0; y < 480; y++){c.im = fromy + (toy - fromy) * (y / 480.0);z.re = z.im = 0;for(k = 0; k < ITERA TIONS; k++){if ( z.re * z.re + z.im * z.im > 4.0 ) break;z = z * z + c;}putpixel(x, y, (k >= ITERA TIONS) ? 0 : Color[k % MAXCOLOR]);}}}/////////////////////////////////////////////////// 主函数/////////////////////////////////////////////////void main(){// 初始化绘图窗口及颜色initgraph(640, 480);InitColor();// 初始化Mandelbrot Set(曼德布洛特集)坐标系double fromx, fromy, tox, toy;fromx = -2.1; tox = 1.1;fromy = -1.2; toy = 1.2;Draw(fromx, fromy, tox, toy);// 捕获鼠标操作,实现放大鼠标选中区域MOUSEMSG m;bool isLDown = false;int selfx, selfy, seltx, selty; // 定义选区while(!kbhit()){m = GetMouseMsg(); // 获取一条鼠标消息switch(m.uMsg){// 按鼠标中键恢复原图形坐标系case WM_MBUTTONUP:fromx = -2.1; tox = 1.1;fromy = -1.2; toy = 1.2;Draw(fromx, fromy, tox, toy);break;// 按鼠标左键并拖动,选择区域case WM_MOUSEMOVE:if (isLDown){rectangle(selfx, selfy, seltx, selty);seltx = m.x;selty = m.y;rectangle(selfx, selfy, seltx, selty);}break;// 按鼠标左键并拖动,选择区域case WM_LBUTTONDOWN:setcolor(WHITE);setwritemode(R2_XORPEN);isLDown = true;selfx = seltx = m.x;selfy = selty = m.y;rectangle(selfx, selfy, seltx, selty);// 按鼠标左键并拖动,选择区域case WM_LBUTTONUP:rectangle(selfx, selfy, seltx, selty);setwritemode(R2_COPYPEN);isLDown = false;seltx = m.x;selty = m.y;if (selfx == seltx || selfy == selty) break;// 修正选区为4:3int tmp;if (selfx > seltx) {tmp = selfx; selfx = seltx; seltx = tmp;} if (selfy > selty) {tmp = selfy; selfy = selty; selty = tmp;}if ( (seltx - selfx) * 0.75 < (selty - selfy) ){selty += (3 - (selty - selfy) % 3);selfx -= (selty - selfy) / 3 * 4 / 2 - (seltx - selfx) / 2;seltx = selfx + (selty - selfy) / 3 * 4;}else{seltx += (4 - (seltx - selfx) % 4);selfy -= (seltx - selfx) * 3 / 4 / 2 - (selty - selfy ) / 2;selty = selfy + (seltx - selfx ) * 3 / 4;}// 更新坐标系double f, t;f = fromx + (tox - fromx) * selfx / 640;t = fromx + (tox - fromx) * seltx / 640;fromx = f;tox = t;f = fromy + (toy - fromy) * selfy / 480;t = fromy + (toy - fromy) * selty / 480;fromy = f;toy = t;// 画图形Draw(fromx, fromy, tox, toy);}}getch();closegraph(); }输出结果为:。
计算机图形学-3D图形绘制代码和截图

实验报告内容:
一、实验设备:
OpenGL 实用工具库文件 glut32.dll,glut.h,glut32.lib
安装 GLUT 库
Copy glut.h
=>VC/include/gl/
glut32.lib =>VC/lib/
glut32.dll =>windows/system32/
二、实验目的、要求: 1.理解 OpenGL 三维观察流水线 2.理解 3D 模式数据结构及绘制方法
②截图:
glMatrixMode(GL_PROJECTION); glLoadIdentity(); // gluPerspective(45.0, float(w) / h, 0.1, 100.0); glFrustum(-1.0,1.0,-1.0,1.0,1.5,20.0); glMatrixMode(GL_MODELVIEW); } void display(void) { glClear(GL_COLOR_BUFFER_BIT); glColor3f(1.0,1.0,1.0); glLoadIdentity();//设置当前矩阵为单位矩阵 gluLookAt(5.0,4.0,9.0,0.0,0.0,0.0,0.0,1.0,0.0); glScalef(2.0,1.0,1.0);//x 方向放大 2 倍 glutWireCube(1); glFlush(); } void main(int argc, char **argv) { glutInit(&argc, argv); glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE); glutInitWindowSize(500,500); glutInitWindowPosition(100,100); glutCreateWindow("3D Cube"); init(); glutReshapeFunc(myReshape); glutDisplayFunc(display); glutMainLoop(); }
图形学实验报告三维图形

图形学课程设计题目:三维真实感图形设计与绘制专业:计算机科学与技术学号姓名:一.一)课程设计目的与要求图形学课程设计的主要目的是让同学们通过图形学的实际问题应用,进一步增强计算机图形学理论的理解、算法应用、图形数据结构设计与图形程序设计等,从而提高图形学实际应用与软件开发能力。
二)课程设计题目三维真实感图形设计与绘制三)问题的提出与需求分析(1)题目内容说明:本题目要求应用OpenGL的光照技术和纹理技术实现一个简单的三维真实感图形的程序设计。
具体要求实现功能:1)通过对话方式实现交互式设计光照模型功能。
2)实现三维模型纹理映射功能。
3)用鼠标跟踪球方法实现三维模型的空间旋转。
(2)技术要点说明1)三维模型显示场景树:将三维可视化模型场景内容分解用一种树或表数据结构描述。
2)实现一个读Targa文件的程序:Targa是一种常见的图像格式文件,该文件通常以未压缩的格式存储图像。
3)实现鼠标跟踪球方法程序。
二.设计思路要设计一个良好的场景和优秀的交互方式,现在虚拟现实场景十分繁多,各种交互方式也五花八门,我们要选择特定的场景,场景要保证两点:一是其新鲜性,让人耳目一新,否则会让人有过于老套的感觉;另外就是其真实度,这是本次课题的着重关注点;在选取选定的场景后,我们要定义各交互方式,在从现有可得到的交互方式案例中提取和创新,以保证开发出来的交互方式可以最大程度的提高人机交互的效率。
场景的规模是必须考虑的,因为设计的时间和人员有限,必须限制场景规模,没有时间和人力去开发过大的场景规模,但是如果场景规模过小,演示系统就无法给人带来非常强烈的真实感冲击,而且过小规模的场景也会限制交互方式的设计和开发;所以定义适当的场景规模,对于课题的成败十分重要。
通过对计算机图形学和三维人机交互方式等相关书籍和文献的阅读和学习,了解和掌握建立真实图形显示系统的过程和三维虚拟场景中人机交互的方式。
三维图形及动画场景的显示,就是把所建立的三维空间模型,经过计算机的复杂处理,最终在计算机二维屏幕上显示的过程,并且在显示的过程要保证其真实感。
图形学实验报告三维几何变换

实验三三维几何变换
班级学号:102055208 姓名:牛慧敏
一、实验目的
(1)掌握三维平移、比例、旋转、对称、和错切5种变换矩阵
(2)掌握三维坐标向屏幕二维坐标变换的公式
二、实验环境
基于windows平台下的计算机一台,Microsoft VC++6.0
三、实验内容
在屏幕中心绘制三维右手坐标系,y轴向右,z轴向上,x轴向前并与z轴逆时针方向的夹角135度,绘制原始立方体,痛过按钮实现平移、比例、旋转、对称、和错切五种变换。
功能说明:
(1)设置原始图形为立方体
(2)实现上、下、左、右、前、后、平移变换
(3)实现放大、缩小比例变换
(4)实现绕x轴,y轴和z轴正向的旋转变换
(5)实现关于xoy平面、yoz
四、实验结果(窗口)。
三维随机分形地形生成

三维随机分形地形生成原文:/fractal.html目录说明:本页所有图像均经过优化以减小尺寸,所以与实际图像会有细微差别。
1. 第一部分:生成随机分形地形1. 介绍2. 自相似3. 一维中点变换4. 高度图5. Diamond-Square 算法6. 蓝天白云7. 其它算法2. 第二部分关于例子源码1. 安装2. 快速起步3. 使用程序4. 代码结构5. 下载源码[Visual C++工程,使用SGI实现的OpenGL](单击标题下载)6. 参考终于找到这个SGI OpenGl地址了:/tools/ocx/ocx_image/opengl2.exe介绍十年前,我参加1986 年*****H 活动,Gavin S. P. Miller 那篇题为Definition and Rendering of Terrain Maps 的论文让我充满敬畏。
该文描述了少数生成分形地形的算法,作者还介绍了一个他们认为更先进的新方法。
开始我被这些算法能够生成难以置信的风景图所震惊!(尽管这些算法被作者认为“漏洞百出”)后来,读过论文,这些算法之简单将我完全打败了。
我从此成为一个分形地形迷。
算法背后的数学可能相当复杂。
然而,完全理解这些数学并不是掌握这些算法的必要条件。
很好,否则我得在解释算法之前讲解所有的数,也许永远也讲不到算法。
此外,关于分形数学的文字材料数以吨计,参见本文本的参考部分会有所帮助。
同样的原因,我不会深入到数学细节,也不包括对分形的广泛总览及它们可被用来做的每样东西。
相反,我将描述分形地形生成背后的概念,并集中仔细讲解我个人最喜欢的”diamond-square”算法。
我将演示如何使用这个算法静态拼嵌高度数据数组,这些数据可用于几何地形数据、地形纹理数据及云纹理映射。
分形有什么用呢?假定你已经知道,那正是你读本文的原因。
随机地形图对飞行模拟或制作背景纹理图(如显示一带远山)十分有用。
生成地形的算法也可用于生成部分云天的纹理图。
计算机图形学实验报告及代码

计算机图形学实验报告及代码第 1 章概述一、教学目标通过本章的学习,使学生能够了解计算机图形学的基本概念、研究内容;当前的发展概况;本门课程的特点和应用。
二、教学要求1.了解计算机图形学的概念和研究内容;2.了解本门课程的发展概况。
三、教学内容提要1. 计算机图形学的研究内容2. 计算机图形学发展概况3. 计算机图形学特点和应用4. 计算机图形学当前研究的课题5. 计算机图形生成和输出的流水线四、教学重点、难点及解决方法本章将主要围绕计算机图形学的基本概念进行介绍,介绍研究内容;当前的发展概况;本门课程的特点和应用等等。
五、课时安排2学时六、教学设备多媒体七、检测教学目标实现程度的具体措施和要求通过课堂提问的方式来检测学生对基本概念的掌握程度。
八、教学内容1.1 计算机图形学的研究内容计算机图形学(Computer Graphics): 研究通过计算机将数据转换为图形,并在专用显示设备上显示的原理、方法和技术的学科。
计算机图形表现形式(1).线条式(线框架图)用线段来表现图形,容易反映客观实体的内部结构,如各类工程技术中结构图的表示,机械设计中零件结构图及电路设计中的电路原理图等。
具有面模型、色彩、浓淡和明暗层次效应,适合表现客观实体的外形或外貌,如汽车、飞机、轮船等的外形设计以及各种艺术品造型设计等。
(2).真实感面模型图形跑车靓照计算机图形分类(空间)(1).二维图形(2D):在平面坐标系中定义的图形(2).三维图形(3D):在三维坐标系中定义的图形计算机图形产生方法(1).矢量法(短折线法)任何形状的曲线都用许多首尾相连的短直线(矢量)逼近。
(2).描点法(像素点串接法)每一曲线都是由一定大小的像素点组成计算机绘图方式:(1)交互式绘图允许操作者以某种方式(对话方式或命令方式)来控制和操纵图形生成过程,使得图形可以边生成、边显示、边修改,直至符合要求为止。
如AUTOCAD等(2)被动式绘图图形在生成过程中,操作者无法对图形进行操作和控制。
计算机图形学期末大作业3D建模

深圳大学实验报告课程名称:计算图形学实验名称:3D建模和真实感图形绘制学院:计算机与软件学院专业:计算机科学与技术报告人:学号:******* 班级: 1同组人:无指导教师:**实验时间:2014年11、12月实验报告提交时间:2014/12/28教务处制一.实验目的1、使用OpenGL创建和动画你自己设计的角色。
2、熟悉3D层次建模和转换。
二.实验步骤1、打开VC6.0打开工作空间modeler.dsw, 可以看到工程的所有工程都包含进来了。
找到sample.cpp并打开。
2、找到sample.cpp中的draw函数,在这个函数中绘制图形。
首先,在一对glPushMatrix()和glPopMatrix()之间用glTranslated函数确定绘制图形坐标系的原点(以下图形的绘制均用到这对函数,后面不再赘述)。
然后用三角形绘制平行四边形的地板,用setDiffuseColor函数设定不同的颜色参数。
主要代码如下:2、为模型绘制背景,即三角旋转阶梯。
同样的,用三角形绘制,使得整个画面看起来像舞台般宽敞华丽。
主要代码如下(为了方便截图,一行代码过长的地方我都做了换行截断):3、在舞台的中心设置柱子。
为了使其更加精致美观,此处用三角形拼接柱子,并且颜色设置成黄白相间,使气氛柔和淡雅。
4、柱子一般都有柱台的。
此处用长方体作为柱台,大气得体。
颜色选择淡蓝色,正好跟柱子的颜色相辉映。
主要代码如下:5、俗话说好事成双。
在同一个层次中,我再绘制了同样的柱子和柱台,使画面呈现对称美。
6、柱子是空心的,得给它加个“盖子”。
为了统一柱子的结构,此处依然用三角形拼接柱子的尖顶,尖顶作为柱子的下一个层次。
如图:主要代码如下:7、柱子上再加个球体,显得气势恢宏。
用drawSphere函数就可以了。
下面是加上两个球体后的效果:8、场景都绘制好了,下面增加人物模型。
此处先画身体,选择圆柱函数来画。
设置上下底的半径,就可以画出一条可爱的小裙子了。
计算机图形学光照与三维图形源代码

viewer[1]+= 1.0;
}
if(key == 'z') {
viewer[2]-= 1.0; }
if(key == 'Z') {
viewer[2]+= 1.0;
}
glutPostRedisplay ();
}
void mouse(int button,int state,int x,int y)
glutMouseFunc(mouse);
glutKeyboardFunc(Keyboard);
glutMainLoop();
return 0;
}
计算机图形学光照与三维图形源代码图形光照代码源程序三维图形光照代码源代码三维立体原代码图形学
#include <glut.h>
#include <math.h>
#include<stdio.h>
static int spin=0;
float a=0.0;
float b=1.0;
float m=0.0,n=0.0;
glEnable(GL_LIGHT0);
}
if (key == '2'){
a+=0.1;
}
if(key =='3'){
b-=0.1;
}
if(key == 'x') {
viewer[0]-= 1.0;
}
if(key == 'X'){
viewer[0]+= 1.0;
}
if(key == 'y'){
C++3D图形变换(含源码,下载后可复制黏贴使用)

实验三 3D图形变换一.实验目的:掌握3D图像的变换,了解多数的3D变换,平移,旋转等几何变换,还有投影变换等知识。
二.实验原理:3D图像的移动,比例变化,旋转等几何变换算法原理及各种投影变换算法原理。
三.实验步骤:一.建立MFC单文档程序,用来编写3D变换。
二.建立Mainframe,并设计,添加相应的ID及映射函数。
三.实验的主要代码:1、设计3维图形平移变换算法的实现程序;void CMyView::OnTranslation(){m_Select=SEL_TS;m_str="平移";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[4][4]=1;my1.A[3][3]=1;my1.A[4][1]=20; //x轴方向上平移my1.A[4][2]=28; //y轴方向上平移my1.A[4][3]=28; //z轴方向上平移my1.Draw();}2、设计3维图形缩放变换算法的实现程序;void CMyView::OnScalingS(){m_Select=SEL_MO;m_str="整体变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[3][3]=1;my1.A[4][4]=0.5;my1.Draw();}void CMyView::OnScalingXyz(){m_Select=SEL_MO;m_str="XYZ变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=2; //x轴方向上比例my1.A[2][2]=1; //y轴方向上比例my1.A[3][3]=2; //z轴方向上比例my1.A[4][4]=1;my1.Draw();}3、设计3维图形旋转变换算法的实现程序。
三维图形的生成计算机图形学源代码及报告

实验报告《计算机图形学》课题:三维图形的生成指导教师:***2013年5月三维图形的生成一.目的1.加深对计算机图形学的理解。
2.熟悉Visual C++ OpenGL的编程方法。
3.学习用编程方法绘制三维图形。
二.实验原理V oid CALLBACK display(void){glClear(GL_COLOR_BUFFER_BIT);glColor3f(1.0,1.0,1.0);glLoadIdentity();glTranslatef(0.0,0.0,-5.0);glScalef(1.0,2.0,1.0);auxWireCube(1.0);glFlush();} //画图void CALLBACK stepDisplay(void){r tri+=0.01;d isplay();}void CALLBACK myReshape(GLsizei w,GLsizei h){g lMatrixMode(GL_PROJECTION);g lLoadIdentity();g lFrustum(-1.0,1.0,-1.0,1.0,1.5,20.0);g lMatrixMode(GL_MODELVIEW);g lViewport(0,0,w,h);} //旋转三.实验步骤1.复习OpenGL语言。
2.编写图形生成程序,分析绘制结果。
四.实验内容#include<gl/glaux.h>#pragma comment(lib,"glaux.lib")#pragma comment(lib,"opengl32.lib")#pragma comment(lib,"glu32.lib")GLfloat rtri=0;1void myinit(void){glShadeModel(GL_SMOOTH);}void CALLBACK display(void){glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清除屏幕及深度缓存glLoadIdentity(); // 重置模型观察矩阵glTranslatef(-1.5,0.0,-6.0); // 左移1.5 单位,并移入屏幕6.0 glRotatef(rtri,0.0,1.0,0.0); // 绕Y轴旋转正方体glBegin(GL_TRIANGLES); // 开始绘制金字塔的各个面glColor3f(1.0f,0.0f,0.0f); // 红色glVertex3f( 0.0f, 1.0f, 0.0f); // 三角形的上顶点(前侧面)glColor3f(0.0f,1.0f,0.0f); // 绿色glVertex3f(-1.0f,-1.0f, 1.0f); // 三角形的左下顶点(前侧面)glColor3f(0.0f,0.0f,1.0f); // 蓝色glVertex3f( 1.0f,-1.0f, 1.0f); // 三角形的右下顶点(前侧面)glColor3f(1.0f,0.0f,0.0f); // 红色glVertex3f( 0.0f, 1.0f, 0.0f); // 三角形的上顶点(右侧面)glColor3f(0.0f,0.0f,1.0f); // 蓝色glVertex3f( 1.0f,-1.0f, 1.0f); // 三角形的左下顶点(右侧面)glColor3f(0.0f,1.0f,0.0f); // 绿色glVertex3f( 1.0f,-1.0f, -1.0f); // 三角形的右下顶点(右侧面)glColor3f(1.0f,0.0f,0.0f); // 红色glVertex3f( 0.0f, 1.0f, 0.0f); // 三角形的上顶点(后侧面)glColor3f(0.0f,1.0f,0.0f); // 绿色glVertex3f( 1.0f,-1.0f, -1.0f); // 三角形的左下顶点(后侧面)glColor3f(0.0f,0.0f,1.0f); // 蓝色glVertex3f(-1.0f,-1.0f, -1.0f); // 三角形的右下顶点(后侧面)glColor3f(1.0f,0.0f,0.0f); // 红色glVertex3f( 0.0f, 1.0f, 0.0f); // 三角形的上顶点(左侧面)glColor3f(0.0f,0.0f,1.0f); // 蓝色glVertex3f(-1.0f,-1.0f,-1.0f); // 三角形的左下顶点(左侧面)glColor3f(0.0f,1.0f,0.0f); // 绿色glVertex3f(-1.0f,-1.0f, 1.0f); // 三角形的右下顶点(左侧面)glEnd();2glTranslatef(0.0f,0.0f,-7.0f); // 先右移再移入屏幕glRotatef(rtri,0.0f,1.0f,0.0f); // 在XYZ轴上旋转立方体glBegin(GL_QUADS); // 开始绘制立方体glColor3f(0.0f,1.0f,0.0f); // 颜色改为蓝色glVertex3f( 1.0f, 1.0f,-1.0f); // 四边形的右上顶点(顶面) glVertex3f(-1.0f, 1.0f,-1.0f); // 四边形的左上顶点(顶面) glVertex3f(-1.0f, 1.0f, 1.0f); // 四边形的左下顶点(顶面) glVertex3f( 1.0f, 1.0f, 1.0f); // 四边形的右下顶点(顶面)glColor3f(1.0f,0.5f,0.0f); // 颜色改成橙色glVertex3f( 1.0f,-1.0f, 1.0f); // 四边形的右上顶点(底面) glVertex3f(-1.0f,-1.0f, 1.0f); // 四边形的左上顶点(底面) glVertex3f(-1.0f,-1.0f,-1.0f); // 四边形的左下顶点(底面) glVertex3f( 1.0f,-1.0f,-1.0f); // 四边形的右下顶点(底面)glColor3f(1.0f,0.0f,0.0f); // 颜色改成红色glVertex3f( 1.0f, 1.0f, 1.0f); // 四边形的右上顶点(前面) glVertex3f(-1.0f, 1.0f, 1.0f); // 四边形的左上顶点(前面) glVertex3f(-1.0f,-1.0f, 1.0f); // 四边形的左下顶点(前面) glVertex3f( 1.0f,-1.0f, 1.0f); // 四边形的右下顶点(前面)glColor3f(1.0f,1.0f,0.0f); // 颜色改成黄色glVertex3f( 1.0f,-1.0f,-1.0f); // 四边形的右上顶点(后面) glVertex3f(-1.0f,-1.0f,-1.0f); // 四边形的左上顶点(后面) glVertex3f(-1.0f, 1.0f,-1.0f); // 四边形的左下顶点(后面) glVertex3f( 1.0f, 1.0f,-1.0f); // 四边形的右下顶点(后面)glColor3f(0.0f,0.0f,1.0f); // 颜色改成蓝色glVertex3f(-1.0f, 1.0f, 1.0f); // 四边形的右上顶点(左面) glVertex3f(-1.0f, 1.0f,-1.0f); // 四边形的左上顶点(左面) glVertex3f(-1.0f,-1.0f,-1.0f); // 四边形的左下顶点(左面) glVertex3f(-1.0f,-1.0f, 1.0f); // 四边形的右下顶点(左面)glColor3f(1.0f,0.0f,1.0f); // 颜色改成紫罗兰色glVertex3f( 1.0f, 1.0f,-1.0f); // 四边形的右上顶点(右面) glVertex3f( 1.0f, 1.0f, 1.0f); // 四边形的左上顶点(右面) glVertex3f( 1.0f,-1.0f, 1.0f); // 四边形的左下顶点(右面) glVertex3f( 1.0f,-1.0f,-1.0f); // 四边形的右下顶点(右面)glEnd(); // 立方体绘制结束3glFlush();}void CALLBACK stepDisplay(void){rtri+=0.01;display();}void CALLBACK myReshape(GLsizei w,GLsizei h) {glMatrixMode(GL_PROJECTION); glLoadIdentity();glFrustum(-1.0,1.0,-1.0,1.0,1.5,20.0); glMatrixMode(GL_MODELVIEW);glViewport(0,0,w,h);}int main(int argc,char** argv){auxInitDisplayMode(AUX_SINGLE|AUX_RGBA); auxInitPosition(0,0,500,500);auxInitWindow("bianhuan");myinit();auxReshapeFunc(myReshape);auxIdleFunc(stepDisplay);auxMainLoop(display);}4五.实验结果:六.实验小结:通过这次实验,更深刻的学习了计算机图形学的编程语言,对于OpenGL的了解更一步。
图形学三视图、正轴测投影c#代码
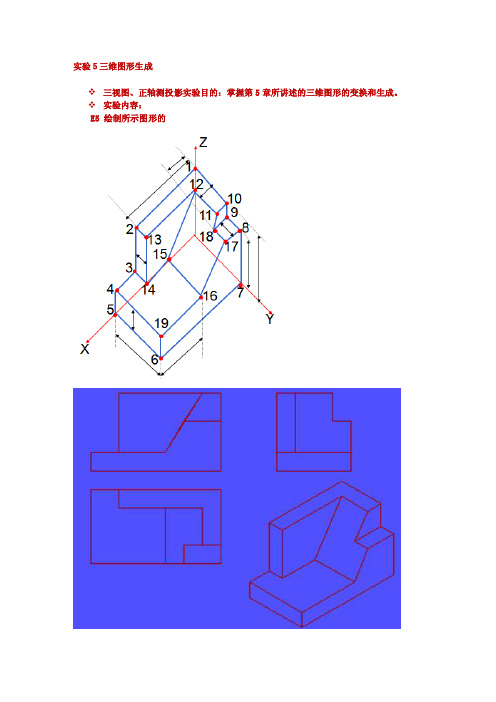
实验5三维图形生成三视图、正轴测投影实验目的:掌握第5章所讲述的三维图形的变换和生成。
实验内容:E5 绘制所示图形的Form1.csusing System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Text;using System.Windows.Forms;namespace E5{//!!说明:主视图有两点连线不对,应该是坐标连线的问题,但连线太多所以没找到是哪两点连错。
public partial class Form1 : Form{int x0 = 150;int z0 = -150;double c = Math.Cos(Math.PI / 2);double s = Math.Sin(Math.PI / 2);double c1 = Math.Cos(Math.PI / 4);double s1 = Math.Sin(Math.PI / 4);Matrix[] p3d = new Matrix[20];//三维顶点Matrix[] p3dv = new Matrix[20];//主视图顶点Matrix[] p3dw = new Matrix[20];//侧视图顶点Matrix[] p3dh = new Matrix[20];//俯视图顶点Matrix[] p3dc = new Matrix[20];//正轴侧顶点/* double[,] p = new double[17,4]{{0,0,42,1},{55,0,42,1},{55,0,10,1},{70,0,10,1},{70,0,0,1},{70,40,0,1},{0,40,0,1},{0,40,27,1},{0,30,27,1},{0,30,42,1},{10,30,42,1},{10,10,42,1},{55,10,42,1},{55,10,10,1},{30,10,10,1},{30,40,10,1},{20,40,27,1},{20,30,27,1},{70,40,10,1}}; */void Getp3d(ref Matrix[] p3d)//三维顶点赋值{for(int i=0;i<19;i++){p3d[i]=new Matrix(1,4);//三维顶点}p3d[0].Data = new double[1, 4] { {0,0,42,1} };p3d[1].Data = new double[1, 4] { { 55, 0, 42, 1 } }; p3d[2].Data = new double[1, 4] { { 55, 0, 10, 1 } }; p3d[3].Data = new double[1, 4] { { 70, 0, 10, 1 } }; p3d[4].Data = new double[1, 4] { { 70, 0, 0, 1 } };p3d[5].Data = new double[1, 4] { { 70, 40, 0, 1 } }; p3d[6].Data = new double[1, 4] { { 0, 40, 0, 1 } };p3d[7].Data = new double[1, 4] { { 0, 40, 27, 1 } }; p3d[8].Data = new double[1, 4] { { 0, 30, 27, 1 } }; p3d[9].Data = new double[1, 4] { { 0, 30, 42, 1 } }; p3d[10].Data = new double[1, 4] { { 10, 30, 42, 1 } }; p3d[11].Data = new double[1, 4] { { 10, 10, 42, 1 } }; p3d[12].Data = new double[1, 4] { { 55, 10, 42, 1 } }; p3d[13].Data = new double[1, 4] { { 55, 10, 10, 1 } }; p3d[14].Data = new double[1, 4] { { 30, 10, 10, 1 } }; p3d[15].Data = new double[1, 4] { { 30, 40, 10, 1 } }; p3d[16].Data = new double[1, 4] { { 20, 40, 27, 1 } }; p3d[17].Data = new double[1, 4] { { 20, 30, 27, 1 } }; p3d[18].Data = new double[1, 4] { { 70, 40, 10, 1 } };}public Form1(){InitializeComponent();}private void Form1_Paint(object sender, PaintEventArgs e){Getp3d(ref p3d);//主视图矩阵Matrix Tv = new Matrix(4);Tv.Data = new double[4,4]{{1 , 0 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , 0 , 1}};//侧视图Matrix Tw1 = new Matrix(4); Tw1.Data = new double[4, 4] {{0 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , 0 , 1}};Matrix Tw2 = new Matrix(4); Tw2.Data = new double[4, 4] {{c , s , 0 , 0},{-s , c , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , 0 , 1}};Matrix Tw3 = new Matrix(4); Tw3.Data = new double[4, 4] {{1 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 1 , 0},{x0 , 0 , 0 , 1}};//俯视图//俯视图的投影变换Matrix Th1 = new Matrix(4); Th1.Data = new double[4, 4] {{1 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 0 , 1}};//使H面绕X轴负向旋转90°Matrix Th2 = new Matrix(4);Th2.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , c , -s , 0},{0 , s , c , 0},{0 , 0 , 0 , 1}};//使H面沿Z轴负向平移一段距离z0Matrix Th3 = new Matrix(4);Th3.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , -z0,1}};//正轴侧// 先绕Z轴正向旋转α角//再绕X轴反向旋转β角//将三维形体向XOZ平面(V面)作正投影得到正轴测投影的投影变换矩阵Matrix Tc1 = new Matrix(4);Tc1.Data = new double[4, 4]{{c1 , s1 , 0 , 0},{-s1 , c1 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 0 , 1}};Matrix Tc2 = new Matrix(4);Tc2.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , c1 , -s1 , 0},{0 , s1 , c1 , 0},{0 , 0 , 0 , 1}};Matrix Tc3 = new Matrix(4);Tc3.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 1 , 0},{150 , 0 , 150 , 1}};//矩阵变换for(int i=0;i<19;i++){p3dv[i] = new Matrix(1, 4);//p3dv[i] = p3d[i] * Tv;p3dw[i] = new Matrix(1, 4);//p3dw[i] = p3d[i] * Tw1 * Tw2 * Tw3;p3dh[i] = new Matrix(1, 4);//p3dh[i] = p3d[i] * Th1 * Th2 * Th3;p3dc[i] = new Matrix(1, 4);//p3dc[i] = p3d[i] * Tc1 * Tc2 * Tc3;}Graphics g=e.Graphics;Pen mypen = new Pen(Color.Yellow, 1.0f);//主视图Point[] pp3d=new Point[19];for (int i = 0; i < 18; i++){//矩阵变换为二维坐标pp3d[i].X=Convert.ToInt16( p3dv[i].Data[0,0]); pp3d[i].Y =Convert.ToInt16( p3dv[i].Data[0,2]); }g.DrawLines(mypen, pp3d);// g.DrawLine(mypen, pp3d[0], pp3d[9]);// g.DrawLine(mypen, pp3d[1], pp3d[12]);// g.DrawLine(mypen, pp3d[2], pp3d[13]);// g.DrawLine(mypen, pp3d[3], pp3d[18]);g.DrawLine(mypen, pp3d[7], pp3d[16]);// g.DrawLine(mypen, pp3d[8], pp3d[17]);g.DrawLine(mypen, pp3d[10], pp3d[17]);// g.DrawLine(mypen, pp3d[11], pp3d[14]);// g.DrawLine(mypen, pp3d[15], pp3d[18]);//侧视图Point[] pp3d1 = new Point[18];for (int i = 0; i < 18; i++){pp3d1[i].X = Convert.ToInt16(p3dw[i].Data[0, 0]); pp3d1[i].Y = Convert.ToInt16(p3dw[i].Data[0, 2]); }g.DrawLines(mypen, pp3d1);// pp3d1[19] = pp3d1[0];g.DrawLine(mypen, pp3d1[0], pp3d1[9]);g.DrawLine(mypen, pp3d1[1], pp3d1[12]);g.DrawLine(mypen, pp3d1[2], pp3d1[13]);// g.DrawLine(mypen, pp3d1[3], pp3d1[18]);g.DrawLine(mypen, pp3d1[7], pp3d1[16]);g.DrawLine(mypen, pp3d1[8], pp3d1[17]);g.DrawLine(mypen, pp3d1[10], pp3d1[17]);g.DrawLine(mypen, pp3d1[11], pp3d1[14]);// g.DrawLine(mypen, pp3d1[15], pp3d1[18]);//俯视图Point[] pp3d2 = new Point[18];for (int i = 0; i < 18; i++){pp3d2[i].X = Convert.ToInt16(p3dh[i].Data[0, 0]); pp3d2[i].Y = Convert.ToInt16(p3dh[i].Data[0, 2]); }g.DrawLines(mypen, pp3d2);g.DrawLine(mypen, pp3d2[0], pp3d2[9]);g.DrawLine(mypen, pp3d2[1], pp3d2[12]);g.DrawLine(mypen, pp3d2[2], pp3d2[13]);// g.DrawLine(mypen, pp3d2[3], pp3d2[18]);g.DrawLine(mypen, pp3d2[7], pp3d2[16]);g.DrawLine(mypen, pp3d2[8], pp3d2[17]);g.DrawLine(mypen, pp3d2[10], pp3d2[17]);g.DrawLine(mypen, pp3d2[11], pp3d2[14]);// g.DrawLine(mypen, pp3d2[15], pp3d2[18]);//正轴侧Point[] pp3d3 = new Point[18];for (int i = 0; i < 18; i++){pp3d3[i].X = Convert.ToInt16(p3dc[i].Data[0, 0]); pp3d3[i].Y = Convert.ToInt16(p3dc[i].Data[0, 2]); }//pp3d3[19] = pp3d3[0];g.DrawLines(mypen, pp3d3);g.DrawLine(mypen, pp3d3[0], pp3d3[9]);g.DrawLine(mypen, pp3d3[1], pp3d3[12]);g.DrawLine(mypen, pp3d3[2], pp3d3[13]);// g.DrawLine(mypen, pp3d[3], pp3d[18]);g.DrawLine(mypen, pp3d3[7], pp3d3[16]);g.DrawLine(mypen, pp3d3[8], pp3d3[17]);g.DrawLine(mypen, pp3d3[10], pp3d3[17]);g.DrawLine(mypen, pp3d3[11], pp3d3[14]);// g.DrawLine(mypen, pp3d[15], pp3d[18]);}}}Matrix.csusing System;using System.Collections.Generic;using System.Text;namespace E5{class Matrix{public double[,] Data;public Matrix(){ }public Matrix(int size){this.Data = new double[size, size];}public Matrix(int rows, int cols){this.Data = new double[rows, cols];}public Matrix(double[,] data){Data = data;}public static Matrix operator *(Matrix M1, Matrix M2){int r1 = M1.Data.GetLength(0); int r2 = M2.Data.GetLength(0);int c1 = M1.Data.GetLength(1); int c2 = M2.Data.GetLength(1);// try// {if (c1 != r2){throw new System.Exception("Matrix dimensions donot agree ");}// }double[,] res = new double[r1, c2];for (int i = 0; i < r1; i++){for (int j = 0; j < c2; j++){for (int k = 0; k < r2; k++){res[i, j] = res[i, j] + (M1.Data[i, k] * M2.Data[k, j]); }}}return new Matrix(res);}}}。
三维图形学实验报告

实验一1.(1)三角形:#include<glut.h>// glut.h includes gl.h and glu.hvoid init(void) {glClearColor(0.0, 0.0, 0.0, 0.0);}void reshape(int w, int h) {glViewport(0, 0, (GLsizei)w, (GLsizei)h);glMatrixMode(GL_PROJECTION);// 指定哪一个矩阵是当前矩阵glLoadIdentity();//重置当前指定的矩阵为单位矩阵。
gluOrtho2D(-1.0, 1.0, -1.0, 1.0); // The para are: (left, right, bottom, top) 定义二维正交投影矩阵glMatrixMode(GL_MODELVIEW); //指定哪一个矩阵是当前矩阵}void display(void) {glClear(GL_COLOR_BUFFER_BIT); // Clear the frame bufferglColor3f(0.0, 1.0, 0.0); // Set current color to greenglBegin(GL_POLYGON); // Draw the triangleglVertex2f(-0.7, -0.7);glVertex2f(0.7, -0.7);glVertex2f(0, 0.7);glEnd();glFlush(); // Force to display the new drawings immediately}int main(int argc, char **argv) {glutInit(&argc, argv); // Initialize GLUT function callingsglutInitWindowSize(400, 400);glutInitWindowPosition(200, 100); // in numbers of pixelsglutCreateWindow("Green Triangle");glutDisplayFunc(display); // is created or re-drewinit(); // Invoke this function for initializationglutMainLoop(); // Enter the event processing loopreturn 0; // Indicate normal termination// (Required by ANSI C)}// 操作,定义事件回调函数(2)点:void display(){glClear(GL_COLOR_BUFFER_BIT); // Clear the frame bufferglColor3f(0.0, 1.0, 0.0); // Set current color to greenglPointSize(10.);glBegin(GL_POINTS);glVertex2i(0.5,0.5);glEnd();glFlush(); // Force to display the new drawings immediately }(3)线段:void display(){glClear(GL_COLOR_BUFFER_BIT); // Clear the frame bufferglColor3f(0.0, 1.0, 0.0); // Set current color to greenglLineWidth(3.0);glBegin(GL_LINES);glVertex3f(0., 0., 0.);glVertex3f(0., 1., 0.);glEnd();glFlush(); // Force to display the new drawings immediately }(4)四边形:void display(){glClear(GL_COLOR_BUFFER_BIT); // Clear the frame bufferglColor3f(1.0, 0.0, 0.0); // Set current color to greenglRectf(0.6, 0.3, 0.2, 0.8);int vertex1[] = { 0.6, 0.3};int vertex2[] = { 0.2, 0.8};glRectiv(vertex1, vertex2);glFlush(); // Force to display the new drawings immediately }2.立方体:3.void reshape(int w, int h)4.{5. glViewport(0, 0, w, h);6. glMatrixMode(GL_PROJECTION);7. glLoadIdentity();8. glOrtho(-3.0, 3.0, -3.0, 3.0, -3.0, 3.0);9.}10.void display(){11. glClear(GL_COLOR_BUFFER_BIT); // Clear the frame buffer12. glMatrixMode(GL_MODELVIEW);13. glLoadIdentity();14. gluLookAt(1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);15. glutWireCube(0.5);16. glutSwapBuffers();17. glColor3f(0.0, 1.0, 0.0);18. glBegin(GL_LINE_LOOP); //Green19. glVertex3f(0., 0., 0.); glVertex3f(0., 2, 0.);20. glVertex3f(2, 2, 0.); glVertex3f(2, 0., 0.);21. glEnd();22. glColor3f(1.0, 1.0, 0.0);23. glBegin(GL_LINE_LOOP); //Yellow24. glVertex3f(0., 0., 2); glVertex3f(2, 0., 2);25. glVertex3f(2, 2, 2); glVertex3f(0., 2, 2);26. glEnd();27. glColor3f(0.0, 1.0, 1.0);28. glBegin(GL_LINES); //Cyan29. glVertex3f(0., 0., 0.); glVertex3f(0., 0., 2);30. glVertex3f(0., 2, 0.); glVertex3f(0., 2, 2);31. glVertex3f(2, 0., 0.); glVertex3f(2, 0., 2);32. glVertex3f(2, 2, 0.); glVertex3f(2, 2, 2);33. glEnd();34. glFlush(); // Force to display the new drawings immediately}3.(1)三角形条带void display(){glClear(GL_COLOR_BUFFER_BIT); // Clear the frame bufferGLfloat v0[] = { 0., 0.3 },v1[] = { 0.2, 0.6 },v2[] = { 0.4, 0.3 },v3[] = { 0.5, 0.6 },v4[] = { 0.6, 0.3 },v5[] = { 0.8, 0.6 },glColor3f(1.0);glBegin(GL_TRIANGLE_STRIP);//三角形条带函数glVertex2fv(v0);glVertex2fv(v1);glVertex2fv(v2);glVertex2fv(v3);glVertex2fv(v4);glVertex2fv(v5);glEnd();glFlush(); // Force to display the new drawings immediately }3.(2)三角形扇形GLfloat v0[] = { 0., 0.3 },v1[] = { 0.3, 0.7 },v2[] = { 0.5, 0.65 },v3[] = { 0.5, 0.5},v4[] = { 0.45, 0.4 },v5[] = { 0.3, 0.35 },glColor3f(1.0);glBegin(GL_TRIANGLE_FAN);//共享一个顶点glVertex2fv(v0);glVertex2fv(v1);glVertex2fv(v2);glVertex2fv(v3);glVertex2fv(v4);glVertex2fv(v5);glEnd();glFlush(); // Force to display the new drawings immediately}实验二1.点glColor3f(0.0, 1.0, 0.0);glPointSize(3.);glBegin(GL_POINTS);glVertex3f(0.1, 0.5, 0);glColor3f(1.0, 1.0, 0.0);glPointSize(5.);glBegin(GL_POINTS);glVertex3f(0.5, 0.5, 0);glColor3f(1.0, 0.0, 0.0);glPointSize(10.);glBegin(GL_POINTS);glVertex3f(0.3, 0.4, 0);glColor3f(0.0, 0.0, 1.0);glPointSize(1.);glBegin(GL_POINTS);glVertex3f(0.2, 0.6, 0);glColor3f(1.0, 1.0, 1.0);glPointSize(4.);glBegin(GL_POINTS);glVertex3f(0.3, 0.5, 0);glEnd();glFlush(); // Force to display the new drawings immediately }2.直线glColor3f(0.0, 1.0, 0.0);glLineWidth(1.0);glBegin(GL_LINES);glVertex3f(0.3, 0.1, 0.0);glVertex3f(0.3, 0.5, 0.0);//垂直距离glColor3f(1.0, 1.0, 0.0);glLineWidth(3.);//宽度glBegin(GL_LINES);glVertex3f(0.2, 0.1, 0.0);glVertex3f(0.2, 0.5, 0.0);glColor3f(1.0, 0.0, 0.0);glLineWidth(5.);glBegin(GL_LINES);glVertex3f(0.5, 0.1, 0.0);glVertex3f(0.5, 0.5, 0.0);glEnd();glFlush(); // Force to display the new drawings immediately }3.直线,虚线,点划线glColor3f(1.0, 0.0, 0.0);glLineWidth(2.0);glBegin(GL_LINES);glVertex2f(0.0, 0.3);glVertex2f(0.8, 0.3);glEnd();glColor3f(1.0, 0.0, 0.0);glEnable(GL_LINE_STIPPLE);glLineStipple(1, 0x0101);glLineWidth(2.0);glBegin(GL_LINES);glVertex2f(0.0, 0.5);glVertex2f(0.8, 0.5);glEnd();glColor3f(1.0, 0.0, 0.0);glEnable(GL_LINE_STIPPLE);glLineStipple(1, 0xffcc);glLineWidth(2.0);glBegin(GL_LINES);glVertex2f(0.0, 0.8);glVertex2f(0.8, 0.8);glEnd();4.顶点不同颜色的三角形平滑填充glShadeModel(GL_SMOOTH);glBegin(GL_TRIANGLES);glColor3f(0.0, 0.0, 1.0);glPointSize(5.0);glVertex2f(0.3, 0.3);glColor3f(1.0, 0.0, 0.0);glPointSize(5.0);glVertex2f(0.4, 0.6);glColor3f(1.0, 1.0, 0.0);glPointSize(5.0);glVertex2f(0.5, 0.4);glEnd();5.调用glPolygonMode(face, displayMode); glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);6. 两个正方形混合(1)glEnable(GL_BLEND);glBlendFunc(GL_SRC_ALPHA,GL_ONE_MINUS_SRC_ALPHA);//混合glColor4f(0.0, 1.0, 0.0,0.5); // Set current color to green glRectf(0.6, 0.3, 0.2, 0.8);int vertex1[] = { 0.6, 0.3 };int vertex2[] = { 0.2, 0.8 };glRectiv(vertex1, vertex2);glColor4f(0.0, 0.0, 1.0,0.5); // Set current color to greenglRectf(0.5, 0.2, 0.1, 0.5);int vertex3[] = { 0.5, 0.2 };int vertex4[] = { 0.1, 0.5 };glRectiv(vertex3, vertex4);(2)glEnable(GL_BLEND);glBlendFunc(GL_SRC_ALPHA,GL_ZERO);(3) glEnable(GL_BLEND);glBlendFunc(GL_ONE,GL_ZERO);说明:用函数glBlendFunc(sFactor,dFactor);选择调和因子的值产生不同的混合效果,有GL_ONE,GL_ZERO,GL_SRC_ALPHAGL_DST_ALPHA,GL_ONE_MINUS_SRC_ALPHA等实验三1.平移glMatrixMode(GL_MODELVIEW);glColor3f(1.0, 1.0, 0.0);glRectf(0.6, 0.3, 0.2, 0.8);glColor3f(1.0, 0.0, 0.0);glTranslatef(-0.5,-0.3,0.0);glRectf(0.6, 0.3, 0.2, 0.8);旋转:glColor3f(1.0, 1.0, 0.0);glRectf(0.6, 0.3, 0.2, 0.8)glLoadIdentity();glRotatef(90.0,0.0,0.0,1.0);glRectf(0.6, 0.3, 0.2, 0.8);缩放:glColor3f(0.0, 1.0, 1.0);glLoadIdentity();glScalef(-0.5, 1.0, 1.0);glRectf(0.6, 0.3, 0.2, 0.8);3.桌子绘制void table(){glColor3f(0.0, 1.0, 1.0);glRectf(-0.5, 0.3, 0.5, -0.3);glColor3f(1.0, 1.0, 0.0);glRectf(-0.4, 0.25, 0.4, 0.15);glColor3f(1.0, 1.0, 0.0);glRectf(-0.4, 0.25, -0.3, -0.15);glColor3f(1.0, 1.0, 0.0);glRectf(0.3, 0.25, 0.4, -0.15);glColor3f(1.0, 1.0, 0.0);glRectf(-0.4, -0.15, 0.4, -0.25);glColor3f(1.0, 0.2, 0.0);glRotatef(-45.0, 0.0, 0.0, 1.0);glTranslatef(0.15, 0.35, 0.0);glRectf(-0.3, -0.15, 0.3, -0.25);glLoadIdentity();glColor3f(1.0, 0.2, 0.0);glRotatef(-90, 0.0, 0.0, 1.0);glTranslatef(-0.35, -0.15, 0.0);glRectf(-0.3, -0.15, 0.3, -0.25);glLoadIdentity();glColor3f(1.0, 0.2, 0.0);glRotatef(-90, 0.0, 0.0, 1.0);glTranslatef(-0.65, 0.15, 0.0);glRectf(-0.3, -0.15, 0.3, -0.25);glLoadIdentity();glColor3f(1.0, 0.2, 0.0);glRotatef(-90, 0.0, 0.0, 1.0);glTranslatef(-0.2, 0.6, 0.0);glRectf(-0.3, -0.15, 0.3, -0.25);}void display(){glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT); // Clear the frame buffer glMatrixMode(GL_MODELVIEW);glPushMatrix();glRotatef(-45.0, 0.0, 0.0, 1.0);table();glPopMatrix();glFlush();}4. 编程绘制罗马字母Ⅳ和Ⅹ。
电子科大-计算机学院-三维图形程序设计实验报告-.

实验报告课程名称:三维图形程序设计学院:计算机科学与工程学院专业:计算机科学与技术指导教师:周川学生姓名:郫县卡戴珊学号:2014666666666实验成绩:日期:2016年3月31日电子科技大学计算机学院实验中心电子科技大学实验报告一、实验一:三维图形程序上机操作训练与图元编程二、实验室名称:主楼A2412实验时间:2016年3月31号三、实验目的:1. 掌握VC中OpenGL三维编程环境的建立过程;2. 掌握GLUT编写OpenGL应用程序的基本步骤,熟悉GLUT基于事件驱动的编程模型;3. 掌握不同类型图元的顶点装配方式,并能够利用图元建立简单的几何对象。
四、实验原理:OpenGL编程语言面向对象编程技术五、实验内容:(一)安装、配置和测试OpenGL三维编程环境1. 首先检查Windows操作系统中是否正确安装了Visual Studio集成开发环境:实验要求在Windows XP、Visual C++ 2005平台以上;2. 解压OpenGL.zip到任意目录下;3. 检查OpenGL核心库和实用库及其头文件是否安装正确和完整:检查%VSINSTALLDIR%\VC\PlatformSDK\Include\GL目录下是否存在gl.h、glu.h两个头文件,并从解压得到的GL子目录下拷贝缺少的头文件到该目录下;检查%VSINSTALLDIR%\VC\PlatformSDK\Lib目录下是否存在OpenGL32.lib、GLU32.lib两个库文件,并从解压得到的Lib子目录下拷贝缺少的Lib文件到该目录下;4. 安装GLUT库及其头文件。
从解压得到的GL子目录下拷贝glut.h到%VSINSTALLDIR%\VC\PlatformSDK\Include\GL目录中,从解压得到的Lib子目录下拷贝glut32.lib到%VSINSTALLDIR%\VC\PlatformSDK\Lib下,拷贝glut32.dll到%windir%\system32目录下。
三维空间中的分形

OpenGL的基本函数
8.纹理映射
⑴ 纹理定义 在程序中可以用以下函数定义二维纹理映射: void glTexImage2D(GLenum target,GLint level,GLint components, GLsizei width,Glsizei height,GLint border,GLenum format,GLenum type,const GLvoid *pixels);
16
OpenGL的基本函数
5.光照设置 ⑴ 创建光源(Light Source) 光源有许多特性,如颜色、位置、方向等。可以使用下面的函数定 义光源: void glLight{if}[v](GLenum light , GLenum pname, TYPE param) ⑵ 启动光照 在OpenGL中,必须明确指出光照是否有效或无效。如果光照无效,则 只是简单地将当前颜色映射到当前顶点上去,不进行法向、光源、材质 等复杂计算,那么显示的图形就没有真实感。启动和取消光源的函数如 下: glEnable(GL_LIGHTING);//启动光照 gDisable(GL_LIGHTING);//取消光照
参考书:《分形算法与程序设计》
15
OpenGL的基本函数
4.颜色设置 ⑴ RGBA模式下的颜色定义 在RGBA模式下,利用glColor*命令来定义当前颜色。glColor*命令 有如下几种形式: void glColor3{b s i f d ub us ui}(TYPE r,TYPE g,TYPE b); void glColor4{b s i f d ub us ui}(TYPE r,TYPE g,TYPE b,TYPE a); void glColor3{b s i f d ub us ui}v(TYPE *v); void glColor4{b s i f d ub us ui}v(TYPE *v); ⑵ 在颜色索引模式下的颜色定义 通过调用函数glIndex*()从颜色索引表中选取当前颜色。 void glIndex(s f d i)(c:TYPE); void glIndex(s f d i)v(c:PTYPE); 参考书:《分形算法与程序设计》
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告实验名称:三维分形算法姓名:陈怡东学号:09008406程序使用说明:程序打开后会呈现出3次分形后的四面体,因为考虑到观察效果的清晰所以就用了3次分形作为演示。
与用户的交互:1键盘交互:分别按下键盘上的数字键1,2,3,4可以分别改变四面体的4个面的颜色。
按下字母c(不区别大小写)可以改变视图函数,这里循环切换3种视图函数:glOrtho,glFrustum,gluPerspective,但是改变视图函数后要窗口形状变化后才能显现出来按下字母键q(不区别大小写)可以退出程序2鼠标交互:打开后在绘图的区域按下鼠标左键不放便可以拖动图形的视角,这里为了展现图形的3D效果因此固定了其中一点不放,这样就可以看到3D的效果。
鼠标右击则有弹出菜单显示,其中改变颜色则是同时改变4个面的颜色,本程序中运用了8组配色方案。
改变视图函数也是上述的3种函数,这里的效果立刻显现,但是还有很多问题达不到所要的效果,希望老师能帮忙解决一下。
设计思路:分形算法:把四面体细分成更小的四面体,先找出其6个棱的中点并连接起来,这样就在4个顶点处各有一个小的四面体,原来四面体中剩下的部分应当去掉。
仿效二维的生成方法,我们对保留的四个小四面体进行迭代细分。
这样细分结束后通过绘制4个三角形来绘制每一个剩下的四面体。
交互的实现:键盘交互,即通过对按键的响应写上响应函数实现对视图和颜色的改变。
鼠标交互:通过对鼠标左右按键的实现:该部分只做了必要的介绍,具体实现见代码(附注释)分形算法:void tetra(GLfloat *a,GLfloat *b,GLfloat *c,GLfloat *d)函数实现的是绘制四面体并且给四个面绘上不同的颜色。
以区别开来,函数的实现细节见代码,有注释介绍。
void triangle3(GLfloat *a,GLfloat *b,GLfloat *c)函数用来绘制每个平面细分后的三角形。
其中顶点设置为3维坐标glVertex3fv(a);void divide_tetra(GLfloat *a,GLfloat *b,GLfloat *c,GLfloat *d,int m)细分四面体的函数实现。
前四个参数为传入点的坐标,最后参数m则是细分次数。
先计算六个中点的坐标mid[1][j]=(a[j]+c[j])/2;3次循环则是对x,y,z三个坐标的一次计算,然后再递归调用绘制4个小四面体。
然后是显示回调函数void mydisplay3FX();这跟程序模板差不多不做过多介绍。
分形算法中必要重要的一点是隐藏面的消除。
即书上2.10.3介绍的内容。
对对象进行排序以正确绘制他们的算法称为可见表面算法,也课称为隐藏面消除算法。
这里采用的死Z-缓存算法。
在主程序中申请辅助存储器:一个Z(深度)缓存,为此把初始化代码改为glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB|GLUT_DEPTH);递归结束的时候调用函数:glEnable(GL_DEPTH_TEST);算法在深度缓存中存储信息,所以必须在需要重绘的窗口清空这个缓存。
为此把函数中的清屏操作改为:glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);键盘交互通过键盘回调函数glutKeyboardFunc(myKeyboard)来调用键盘响应函数,响应事件则在void myKeyboard()中具体实现。
分别判断按下的按键的具体值,然后通过改变colors数组的值以及视图函数来改变现实,所用的颜色索引保存在colorChange数组之中。
鼠标交互:其中用到了鼠标事件(mouse event)和移动事件(move event)然后分别通过回调函数glutMouseFunc(myMouse),glutMotionFunc(myMotion);来调用。
代码中对与鼠标单击相应即视角的移动,先通过点击的位置获取点下的坐标,用来判断是否在四面体内部的函数用glReadPixels(x,500-y,1,1,GL_RGB,GL_FLOAT,pix);来实现。
该函数读取点击位置的像素,将获取的结果存入数组pix在后面的判断算法中如果像素不为0则拾取该图形。
该算法的好处是不需要计算复杂的坐标和线段函数而能方便的拾取对象。
缺点则是在内部的白色区域点击不能够拾取图像。
具体代码的实实现函数void myMouse(int btn,int state,int x,int y)移动相应函数void myMotion(int x,int y)首先对于移动过程中获取的坐标与全局变量定义的坐标统一数量级。
所以在代码开头除以150,然后对每个点的坐标以此做改变,并将这次获取的坐标存入x0,y0中作为移动到下一个坐标的起始坐标在移动过程中就不停地循环调用该函数。
程序还对右击的事件弹出菜单做了响应,该响应是通过main函数的glutAttachMenu(GLUT_RIGHT_BUTTON); 代码实现,即将所设计的菜单加到右击事件中。
具体菜单的设计见main函数事件的响应在void main_menu(int),void color_menu(int);两个函数中而color_menu则是作为main_menu中的一个子菜单.其中对不同的事件做了响应小结:该程序中,结合了openGL很多函数的应用,首先是基础现实函数及模板过程的编写。
然后就是分形算法的分析,虽然大部分是参考书中的代码,但是在具体实现时还是加入很多自己的想法。
然后就是与用户的交互,从鼠标和键盘两个角度,加入了一些基本的事件响应,虽然功能不是很强大,但是初始学习的目的已经达到了。
当然在其过程中查阅了网上很多的资料,以及同学之间的讨论。
当然在这过程中还是遇到很多的麻烦的,一是对代码过程的理解不是很深刻,因此有些代码的位置不对导致得不出自己想要的结果。
其次是本身算法的缺陷导致结果的问题。
本程序中对视图函数的变化的代码做的不是很好还是有问题的希望老师能帮助解决一下这些问题!经过这次试验,我对openGL已经有了比较完整的认识,相信这对经后的学习是很有帮助的源代码// 3DFenXing.cpp : 定义控制台应用程序的入口点。
//typedef int BOOL;#define TRUE 1#define FALSE 0#include <iostream>#include <GL/glut.h>#include <stdio.h>#include <stdlib.h>using namespace std;GLfloat ColorsChange[8][3]={{0,0,0},{1,0,0},{0,1,0},{0,0,1},{0,1,1},{1,0,1},{1,1,0},{1,1,1}};GLfloat colors[4][3]={{1,0,0},{0,1,0},{0,0,1},{0,1,1}};GLfloatv[4][3]={{0,0,1},{0,0.942809,-0.333333},{-0.816497,-0.471405,-0.333333},{0.816497,-0.471405,-0.33 3333}};//GLfloatv[4][3]={{0,0,1},{0,0.942809,-0.333333},{-1.916497,-0.471405,-0.333333},{1.916497,-0.471405,-0.33 3333}};int xc,yc;//鼠标按下时点的左边GLfloat xmin=-1.916497;GLfloat xmax=1.916497;GLfloat ymin=-0.471405;GLfloat ymax=0.942809;GLfloat p[3] = {25.0,10.0,25.0};int flat[4]={0};//标记改变哪个面的颜色int Shitu=0;//选取视图函数标记int x0=0;int y0=0;int down=0;double x1=0.0;double y1=0.0;GLfloat *pix=new GLfloat[3];void myReshape(int w,int h);void mydisplay3FX();void main_menu(int);void color_menu(int);int pick_3D(int x,int y);//void myMotion(int x,int y);void myKeyboard(unsigned char key,int x,int y);//定义标记变量BOOL picking = FALSE;//如果处于拾取状态,这位TRUE//BOOL moving=TRUE;//如果处于多边形移动状态,则为TRUEint in_3D=-1;//是否在图形内部int present_color=0;//默认颜色GLsizei wh=500,ww=500;//窗口初始大小int draw_mode =0;//绘制模式void triangle3(GLfloat *a,GLfloat *b,GLfloat *c)//绘制三角形{glVertex3fv(a);glVertex3fv(b);glVertex3fv(c);}void tetra(GLfloat *a,GLfloat *b,GLfloat *c,GLfloat *d){glColor3fv(colors[0]);triangle3(a,b,c);glColor3fv(colors[1]);triangle3(a,c,d);glColor3fv(colors[2]);triangle3(a,d,b);glColor3fv(colors[3]);triangle3(b,d,c);}void divide_tetra(GLfloat *a,GLfloat *b,GLfloat *c,GLfloat *d,int m) {GLfloat mid[6][3];int j;if(m>0){for(j=0;j<3;j++){mid[1][j]=(a[j]+c[j])/2;mid[2][j]=(a[j]+d[j])/2;mid[3][j]=(b[j]+c[j])/2;mid[4][j]=(c[j]+d[j])/2;mid[5][j]=(b[j]+d[j])/2;mid[0][j]=(a[j]+b[j])/2;}divide_tetra(a,mid[0],mid[1],mid[2],m-1);divide_tetra(mid[0],b,mid[3],mid[5],m-1);divide_tetra(mid[1],mid[3],c,mid[4],m-1);divide_tetra(mid[2],mid[4],mid[5],d,m-1);}elsetetra(a,b,c,d);//细分四面}//键盘响应事件void myKeyboard(unsigned char key,int x,int y) {if(key=='1'){//int a=1;if(flat[0]<7){flat[0]++;}elseflat[0]=0;for(int i=0;i<3;i++){colors[0][i]=ColorsChange[flat[0]][i];}}else if(key=='2'){//int a=1;if(flat[1]<7){flat[1]++;}elseflat[1]=0;for(int i=0;i<3;i++){colors[1][i]=ColorsChange[flat[1]][i];}}else if(key=='3'){//int a=1;if(flat[2]<7){flat[2]++;}elseflat[2]=0;for(int i=0;i<3;i++){colors[2][i]=ColorsChange[flat[2]][i];}}else if(key=='4'){//int a=1;if(flat[3]<7){flat[3]++;}elseflat[3]=0;for(int i=0;i<3;i++){colors[3][i]=ColorsChange[flat[3]][i];}}else if(key=='c'|key=='C'){Shitu++;}else if(key=='q'|key=='Q')exit(0);glutPostRedisplay();}//鼠标响应事件void myMouse(int btn,int state,int x,int y){if(btn==GLUT_LEFT_BUTTON&&state==GLUT_DOWN) {//通过按下点的像素拾取图像glReadPixels(x,500-y,1,1,GL_RGB,GL_FLOAT,pix);//只要不是白像素就拾取图形if(pix[0]!=1.0||pix[1]!=1.0||pix[2]!=1.0){if(down==0) //获取按下点坐标{down=1;//标记为鼠标按下//标记下初始位置的值y0=y;x0=x;}elsedown=0;}}if(btn==GLUT_LEFT_BUTTON&&state==GLUT_UP){down=0;}/*int j;y=wh-y;if(btn==GLUT_LEFT_BUTTON&&state==GLUT_DOWN&&!picking&&!moving) {//增加顶点moving=FALSE;if(in_3D>=0){if()}}if(btn==GLUT_LEFT_BUTTON&& state==GLUT_DOWN && picking ){picking=FALSE;//moving=FALSE;j = pick_3D(x,y);if(j >= 0){//polygons[j].used = FALSE;in_3D = 1;glutPostRedisplay();}}*/}//移动图形int pick_3D(int x,int y){//根据每个多边形的包围盒寻找第一个包含拾取位置的多边形if ((x>=xmin) && (x<=xmax) &&(y>=ymin) && (y<=ymax)){in_3D=1;return(in_3D);}else{printf("not in the 3DFenxing\n");return(-1);}}//鼠标移动过程中计算图像的位置void myMotion(int x,int y){if(down==1){x1=(x-x0)/150.0;y1=(y-y0)/150.0;//计算图像各顶点的变化,通过固定不同的点可以达到不同的变换效果v[0][0]=v[0][0]+x1;//v[1][0]=v[1][0]+x1;v[2][0]=v[2][0]+x1;v[3][0]=v[3][0]+x1;v[0][1]=v[0][1]-y1;//v[1][1]=v[1][1]-y1;v[2][1]=v[2][1]-y1;v[3][1]=v[3][1]-y1;x0=x;y0=y;}glutPostRedisplay();}void color_menu(int index){for(int j=0;j<4;j++){for(int i=0;i<3;i++){colors[j][i]=ColorsChange[(j+index)%8][i];}}glutPostRedisplay();}void main_menu(int index){switch(index){case 6:glOrtho(-2.0,2,-2.0,2.0,-10.0,10.0);//变换视图函数1glutPostRedisplay();break;case 7:glFrustum(-2.0,2,-2.0,2.0,0.1,10.0);//变换视图函数2glutPostRedisplay();break;case 9:gluPerspective(50,1,0.10,20);//变换视图函数3glutPostRedisplay();break;case 8: //退出exit(0);}}void myReshape(int w,int h){glViewport(0,0,w,h);//设置观察参数glMatrixMode(GL_PROJECTION);glLoadIdentity();if(w<=h){if((Shitu%2)==0)glOrtho(-2.0,2.0,-2.0*(GLfloat)h/(GLfloat)w,2*(GLfloat)h/(GLfloat)w,-10.0,10.0);elseglFrustum(-2.0,2.0,-2.0,2,0.1,10.0);}else{if ((Shitu)%2==0)glOrtho(-2.0*(GLfloat)w/(GLfloat)h,2*(GLfloat)w/(GLfloat)h,-2.0,2.0,0.1,10.0);elseglFrustum(-2.0,2,-2.0,2.0,0.1,10.0);}glMatrixMode(GL_MODELVIEW);glutPostRedisplay();}void mydisplay3FX(){glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);glBegin(GL_TRIANGLES);glMatrixMode(GL_PROJECTION);glLoadIdentity();if((Shitu%2)==0)glOrtho(-2.0,2.0,-2.0,2,-10.0,10.0);elseglFrustum(-2.0,2.0,-2.0,2,0.1,10.0);glLoadIdentity();glMatrixMode(GL_MODELVIEW);divide_tetra(v[0],v[1],v[2],v[3],3);glEnd();glFlush();}//主入口函数void main(int argc,char **argv){int c_menu;glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB|GLUT_DEPTH);glutInitWindowSize(500,500);glutCreateWindow("3D ");c_menu = glutCreateMenu(color_menu);glutAddMenuEntry("颜色方案1",0);glutAddMenuEntry("颜色方案2",1);glutAddMenuEntry("颜色方案3",2);glutAddMenuEntry("颜色方案4",3);glutAddMenuEntry("颜色方案5",4);glutAddMenuEntry("颜色方案6",5);glutAddMenuEntry("颜色方案7",6);glutAddMenuEntry("颜色方案8",7);glutCreateMenu(main_menu);glutAddSubMenu("变换四面体颜色",c_menu);//glutAddMenuEntry("移动图形",5);glutAddMenuEntry("变换视图函数1",6);glutAddMenuEntry("变换视图函数2",7);glutAddMenuEntry("变换视图函数3",9);glutAddMenuEntry("退出",8);glutAttachMenu(GLUT_RIGHT_BUTTON);glutMouseFunc(myMouse);glutMotionFunc(myMotion);glutKeyboardFunc(myKeyboard);glutReshapeFunc(myReshape);glutDisplayFunc(mydisplay3FX);glEnable(GL_DEPTH_TEST);glClearColor(1.0,1.0,1.0,1.0);glutMainLoop(); }。
