第二章 复变函数的积分
第二章复变函数的积分

f (z)dz lim f (k )(zk zk1)
l
积分n函 数k1
积分路径 一般来说,复变函数的积分值与积分路径有关.
2、复变函数积分计算方法
n
f (z)dz lim f (k )(zk zk1) n k 1
l
1)将复变函数的路积分化为两个实变函数的线积分
2)参数积分法
若积分曲线的参数方程z=z(t) ( ),dz z'(t)dt
则
f (z)dz f [z(t)]z'(t)dt
l
(极坐标法,通常用来计算积分路径为圆弧时的情况)
通常思路:
积分路径l为圆弧: 宗量用指数形式表示:
z z0
z z0 ei
n
n
f (z)dz f (z)dz;l lk
l
k 1 lk
k 1
f (z)dz f (z)dz
lAB
lBA
f (z)dz
l
f (z) dz ; dz
dx2 dy2 ds
l
Ms; M f (z) , s l的长度
用来求积分的估计值
r
1
z3 z
2
dz
z3 z r 1 z2
dz
(1)
z3
z r 1 z2
dz M
dz M
z r
ds Ms
z r
(2)
由(1)(2)式,得:
z3 dz Ms
z r 1 z2
M
1
r
3
r
2
s ds 2 r z r
复变函数积分方法总结

复变函数积分方法总结经营教育乐享选取日期复变函数积分方法总结数学本就灵活多变,各类函数的排列组合会衍生多式多样的函数新形势,同时也具有本来原函数的性质,也会有多类型的可积函数类型,也就会有相应的积分函数求解方法;就复变函数:z=x+iy i2=-1 ,x,y分别称为z的实部和虚部,记作x=Rez,y=Imz; arg z=θθ称为主值-π<θ≤π ,Arg=argz+2kπ ;利用直角坐标和极坐标的关系式x=rcosθ ,y=rsinθ,故z= rcosθ+i rsinθ;利用欧拉公式e iθ=cosθ+isinθ;z=re iθ;1.定义法求积分:定义:设函数w=fz定义在区域D内,C为区域D内起点为A终点为B的一条光滑的有向曲线,把曲线C 任意分成n 个弧段,设分点为A=z 0 ,z 1,…,z k-1,z k ,…,z n =B,在每个弧段z k-1 z k k=1,2…n 上任取一点k 并作和式S n =∑f(k )nk−1z k -z k-1= ∑f(k )nk−1z k 记z k = z k - z k-1,弧段z k-1 z k 的长度δ=max1≤k≤n {S k }k=1,2…,n,当 δ→0时,不论对c 的分发即k 的取法如何,S n 有唯一的极限,则称该极限值为函数fz 沿曲线C 的积分为:∫f(z)dz c=lim δ 0∑f(k )nk−1z k设C 负方向即B 到A 的积分记作 ∫f(z)dz c−.当C 为闭曲线时,fz 的积分记作∮f(z)dz cC 圆周正方向为逆时针方向 例题:计算积分1)∫dz c 2) ∫2zdz c ,其中C 表示a 到b 的任一曲线; 1 解:当C 为闭合曲线时,∫dz c =0. ∵fz=1 S n =∑f(k)n k−1z k -z k-1=b-a ∴lim n 0Sn =b-a,即1)∫dz c =b-a.2当C 为闭曲线时,∫dz c =0. fz=2z;沿C 连续,则积分∫zdz c 存在,设k =z k-1,则∑1= ∑Z n k−1(k −1)z k -z k-1 有可设k =z k ,则∑2= ∑Z n k−1(k −1)z k -z k-1因为S n 的极限存在,且应与∑1及∑2极限相等;所以S n = ∑1+∑2= ∑k−1n z k (z k2−z k−12)=b 2-a 2∴ ∫2zdz c=b 2-a 2定义衍生1:参数法:fz=ux,y+ivx,y, z=x+iy 带入∫f(z)dz c得: ∫f(z)dz c = ∫udx c - vdy + i ∫vdx c + udy 再设zt=xt+iyt α≤t ≤β∫f(z)dz c =∫f(z(t))z(t)́dt βα参数方程书写:z=z 0+z 1-z 0t0≤t ≤1;z=z 0+re i θ,0≤θ≤2π 例题1: ∫z 2dz 3+i 0积分路线是原点到3+i 的直线段解:参数方程 z=3+i t ∫z 2dz 3+i 0=∫[(3+i)t]2[(3+i)t]′dt 1=3+i 3∫t 2dt 1=6+263i例题2: 沿曲线y=x 2计算∫(x 2+iy )dz 1+i解: 参数方程 {x =ty =t 2 或z=t+it 2 0≤t ≤1 ∫(x2+iy )dz 1+i 0=∫(t 2+it 2)(1+2it)dt 1=1+i [∫(t 2dt )dt 10 + 2i ∫t 3dt 1=-16+56i定义衍生2 重要积分结果: z=z 0+ re i θ ,0≤θ≤2π 由参数法可得:∮dz(z−z 0)n+1c =∫ire iθe i (n+1)θr n+12π0d θ=i r n ∫e −inθ1+i 0d θ ∮dz (z−z 0)n+1c={2πi n =00 n ≠0例题1:∮dz z−2|z |=1 例题2:∮dzz−12|z |=1解: =0 解 =2πi2.柯西积分定理法:柯西-古萨特定理:若fzdz 在单连通区域B 内解析,则对B 内的任意一条封闭曲线有:∮f(z)dz c=0 定理2:当f 为单连通B 内的解析函数是积分与路线无关,仅由积分路线的起点z 0与终点z 1来确定;闭路复合定理:设函数fz 在单连通区域D 内解析,C 与C 1是D 内两条正向简单闭曲线,C 1在C 的内部,且以复合闭路Γ=C+C 1所围成的多连通区域G 全含于D 则有:∮f(z)dz Γ=∮f(z)dz c +∮f(z)dz c1=0 即∮f(z)dz c =∮f(z)dz c1推论: ∮f(z)dz c=∑∮f(z)dz ckn k=1 例题:∮2z−1z 2−zdz cC 为包含0和1的正向简单曲线;解: 被积函数奇点z=0和z=1.在C 内互不相交,互不包含的正向曲线c 1和c 2;∮2z−1z 2−zdz c=∮2z−1z (1−z)dz c1+∮2z−1z (1−z)dz c2=∮1z−1+1z dz c1+∮1z−1+1zdz c2=∮1z−1dz c1+∮1zdz c1+∮1z−1dz c2+∮1zdz c2=0+2πi+2πi+0=4πi原函数法牛顿-莱布尼茨公式:定理可知,解析函数在单连通域B 内沿简单曲线C 的积分只与起点z 0与终点z 1有关,即∫f()c d = ∫f()z1zd 这里的z 1和z 0积分的上下限;当下限z 0固定,让上限z 1在B 内变动,则积分∫f()z1zd 在B 内确定了一个单值函数Fz,即Fz= ∫f()z1zd 所以有 若fz 在单连通区域B 内解析,则函数Fz 必为B 内的解析函数,且F(z)́=fz.根据定理和可得∫f(z)z 1z 0dz = Fz 1 - Fz 0. 例题:求∫zcosz 1dz 解: 函数zcosz 在全平面内解析∴∫zcosz 10dz =zsinz |0i -∫sinz 1dz = isin i+cosz |0i =isin i+cos i-1 =ie −1−12i+e −1+12i-1=e -1-1此方法计算复变函数的积分和计算微积分学中类似的方法,但是要注意复变适合此方法的条件; 柯西积分公式法:设B 为以单连通区域,z 0位B 中一点,如fz 在B 内解析,则函数f(z)z−z 0在z 0不解析,所以在B内沿围绕z0的闭曲线C的积分∫f(z)z−z0dzc一般不为零; 取z0位中心,以δ>0为半径的正向圆周|z−z0|=δ位积分曲线cδ,由于fz的连续性,所以∫f(z)z−z0dzc =∫f(z)z−z0dzcδ=2πifz0:若fz在区域D内解析,C为D内任何一条正向简单闭曲线,它的内部完全含于D,z0为C内的任一点,有:fz0=12πi ∮f(z)z−z0dz例题:1∮|z|2∮z(9−z2)(z+i)dz |z|=2解:=2π isin z|z=0=0 解:=∮z9−z2z−(−i)dz|z|=2=2πi z9−z2|z=-i=π5解析函数的高阶导数:解析函数的导数仍是解析函数,它的n阶导数为f n z0=n!2πi ∮f(z)(z−z0)n+1dzn=1,2…其中C为fz的解析区域D内围绕z0的任一条正向简单闭曲线,而它的内部全含于D.例题:∮e zz5dzcC:|Z|=1解:由高阶导数的柯西积分公式:原式=2πi14!e z4|z=π2=πi123.解析函数与调和函数:定义:1调和函数:如果二元实函数φx,y在区域D内具有二阶连续函数,且满足拉普拉斯方程:2φx 2+2φy 2=0,则称φx,y 为区域D 内的调和函数;若fz=u+iv 为解析函数,则u 和v 都是调和函数,反之不一定正确2共轭调和函数:ux,y 为区域内给定的调和函数,我们把是 u+iv 在D 内构成解析函数的调和函数vx,y 称为ux,y 的共轭调和函数;若v 是u 的共轭调和函数,则-u 是v 的共轭调和函数关系:任何在区域D 内解析的函数,它的实部和虚部都是D 内的调和函数;且虚部为实部的共轭调和函数;求解方法:1偏积分法:若已知实部u=ux,y,利用C-R 方程先求得v 的偏导数u x =v y ,两边对y 积分得v=∫u x dy +g(x).再由u y =−v x 又得x ∫vx dy +g(x)́=- u y从而g(x)=∫[−u y−x∫ux dy]dx + Cv=∫u xdy + ∫[−u y−x∫ux dy]dx + C 同理可由vx,y 求ux,y.不定积分法:因为f(z)́=U x +i V x = U x -iU y = V y +iV X 所以fz=∫U (z )dz +c fz=∫V (z )dz +c线积分法:若已知实部u=ux,y,利用C-R 方程可得的dv=vxdx+vydy=-uydx+∫u xdy 故虚部为 v=∫−u ydx +(x ,y )(x0,y 0,)u xdy +C该积分与路径无关,可自选路径,同理已知vx,y 也可求ux,y.例题:设u=x 2-y 2+xy 为调和函数,试求其共轭函数vx,y 级解析函数fz=ux,y+ivx,y 解:利用C-R 条件u x=2x+yu y=-2y+x2ux 2=22uy 2=-2所以满足拉普拉斯方程,有v x=−u y=2y-xv y=ux=2x+y所以v=∫(2y −x)dx +φ(y)=2xy- x 22+φ(y)v y=2x+φ(y)́=2x+y φ(y)́=y φ(y)=y 22+c vx,y=2xy- x 22+y 22+cfz=ux,y+ivx,y=122-i z 2+iC4.留数求积分:留数定义:设z 0为函数fz 的一个孤立奇点,即fz 在去心邻域、0<|z −z 0|<δ ,我们把fz 在z 0处的洛朗展开式中负一次幂项系数c -1称为fz 在z 0处的留数,记为Resfz,z 0即Resfz,z 0=c -1 或者Resfz,z 0=12πi∮f (z )dz c C 为0<|z −z 0|<δ 留数定理:设函数fz 在区域D 内除有限个孤立奇点z 1z 2…z n,其中z k 表示函数f (z )的孤立奇点孤立奇点:定义:如果函数f (z )在z 0不解析,但在z 0某个去心邻域0<|z −z 0|<δ内解析,则称z 0为f (z )的孤立奇点; 例如1z 、e 1z都是以z=0为孤立奇点函数1(z+1)(z+2)以z=-1、z=2为孤立奇点..........在孤立奇点z=z 0的去心邻域内,函数f (z )可展开为洛朗级数 f (z )=∑c n ∞n=−∞(z−z 0)n洛朗级数中负幂项是否存在,若存在是有限项还是无限项,这对fz 在z 0处的奇异性将起着决定性的作用;讨论孤立奇点z 0的类型::若函数fz 在孤立奇点z 0的去心邻域内的洛朗展开式中不含负幂项,即对一切n<0有c n =0,则称z 0是fz 的可去奇点因为没有负幂项,即c -n =0,n=1,2.....故c -1=0;遇到函数fz 的奇点类型是可去奇点 ,一般对函数f (z )求积分一般为零判断可去奇点方法:⑴函数f (z )在某个去心邻域0<|z −z 0|<δ内解析,则z 0是f (z )的可去奇点的充要条件是存在极限lim z→z 0f (z )=c 0,其中c 0是一复常数;⑵在⑴的假设下,z 0是fz 可去奇点的充要条件是:存在r ≤δ,使得fz 在0<|z −z 0|<r 内有界若函数fz 在孤立奇点z 0的去心邻域内洛朗级数展开式中只有有限个负幂项,即有正整数m,c -m ≠0,而当n<-m 时c -n =0 则称z 0是fz 的m 级极点; 其洛朗展开式是:fz=c −m (z−z 0)m +c −m +1(z−z 0)m+1+…+c −1z−z 0+c 0+c 1z-z 0n+m +…+c 0z-z 0n+…这里c -m ≠0,于是在 0<|z −z 0|<δ有fz=c −m (z−z 0)m+c −m +1(z−z 0)m+1+…+c −1z−z 0+c 0+c 1z-z 0n+m +…+c 0z-z 0n +…=1(z−z 0)mφ(z).φ(z)一个在0<|z −z 0|<δ解析,同时φ(z)≠0,则z 0是fz 的m 级极点;判断定理:1fz 在z 0的去心邻域0<|z −z 0|<δ解析,z 0是fz 的m 级极点的充要条件是可以表示成的形式;2z 0是fz 的m 级极点的充要条件是lim z→z 0f(z)=∞.:若函数fz 在孤立奇点z 0的去心邻域内洛朗级数展开式中只有无限个负幂项,则称z 0是fz 的本性奇点判断方法:孤立奇点是本性奇点的充要条件是不存在有限或无穷的极限lim z→z 0f(z);函数在极点的留数:准则一:若z 0为一级极点,则 Resfz,z 0= lim z→z 0f (z )(z −z 0)准则二:做z 0为m 级极点,则 Resfz,z 0=1(m−1)!limz→z 0d m−1dzm−1{z-z 0mfz} 准则三:设fz=P(Z)Q(Z),Pz 以及Qz 都在z 0解析,如果Pz 0=0,Qz 0≠0,则z 0是fz 的一级极点,而且: Resfz,z 0=P(Z 0)Q(Z0)́ 无穷远处的留数:定义:扩充z 平面上设z=∞为fz 上的孤立奇点,即fz 在R<|z |<+∞内解析,C 为圆环绕原点z=0的任一条正向简单闭曲线,则积分值12πi ∮f (z )c −1dz 称为fz 在z=∞处的留数,记作 Resfz, ∞=12πi ∮f (z )c −1dz如果fz,在R<|z |<+∞内的洛朗展开式为fz,=∑c n z n∞n=−∞ 则有Resfz, ∞=-c -1如果fz 在扩充复平面上只有有限个孤立奇点包括无穷远处在内设为z 1,z 2,…,z n ,∞则fz 在各奇点的留数总和为零,即 ∑Res[f(z)dz]n k=1+Resfz, ∞=0; Resfz, ∞=-Resf 1z 1z 2,0 例题:求下列Resfz, ∞的值 1fz=e zz 2−1 2fz=1z (z+1)4(z−4)解:1在扩充复平面上有奇点:±1,∞ ,而±1为fz 的一级极点且Resfz,1=lim z→1(z −1)f(z)=lim z→1e z z+1=12e Resfz,-1= lim z→−1(z −1)f(z)=lim z→1e z z−1=-12e −1 ∵Resfz, ∞ + Resfz,1 + Resfz,-1=0得∴Resfz, ∞=-{ Resfz,1+ Resfz,-1}= 12e −1+e =-sh1 2 由公式Resfz, ∞=-Resf 1z 1z 2,0,而1z 2f 1z = 1z (z+1)4(z−4)以z=0为可去奇点,所以 Resfz, ∞= -Resf 1z 1z 2,0=0 用留数定理计算积分:形如∫R(cosθ,sinθ)2π0d θ的定积分计算;其中R(cosθ,sinθ)为cos θ与sinθ的有理函数;故解这类题是就会联想到复变函数与三角变换的相关知识--欧拉公式,令z=e iθ,dz=izd θ=i e iθ d θ d θ=dz iz sin θ=12i e iθ−e −iθ=z 2−12iz cos θ(e iθ+e −iθ)= z 2+12iz 则∫R(cosθ,sinθ)2π0d θ=∮R[z 2+12iz ,z 2−12iz ]|z |dz iz =∮f (z )dz |z |其中fz= R[z 2+12iz ,z 2−12iz 1iz 然后又留数定理求的积分值为2πi ∑Res[f (z ),z k ]n k=1 其中z k k=1,2, …n 为fz 在单位圆周内的所有孤立奇点; 形如∫R(x)dx +∞−∞的积分计算;其中Rx 为x 的有理函数,且分母的次数至少比分子的高二次,Rx 在实轴上无孤立奇点;则∫R(x)dx +∞−∞=2πi ∑Res Rz,z k ,z k 为上半平面的所有奇点 形如∫R(x)e iax dx +∞−∞=2πi ∑Res R (x )e iax ,z k 其中k 为上半平面的所有奇点 5.总结:以上只是粗略的列举了计算复变积分的方法,还有许多细节性的问题没有一一列举;复变积分的算法对比实函数积分的计算方法,有很多相似的地方,较实函数积分要复杂些;复变的积分变换多是理解性的问题,多做题目可以提高思维的多样性,但容易造成思维定势;理解才是主要解题之道。
数学物理方法第二章复变函数的积分
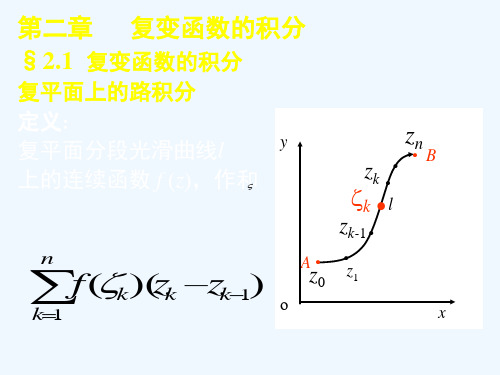
一般而言,复变函数的积分不仅与起点和终点有 关, 同时还与路径有关。
§2.2 柯西(Cauchy)定理
——研究积分与路径之间的关系 (一)单连通域情形 单连通域: 在其中作任何简单闭合围线,围 线内的点都是属于该区域内的点。 单连通区域的Cauchy 定理 :如果函数 f (z) 在闭 单连通区域 B 中单值且解析, 则沿 B 中任 何一个分段光滑的闭合曲线 l (也可以是 B 的 边界 l0 ), 函数的积分为零。
lim f( z z ) k)( k k 1
n
存在且与 k 的选取无关, 则这个和的极限称为 函数 f (z) 沿曲线 l 从 A 到 B 的路积分,记为
即
l
f (z) dz
n k k k 1
z ) d z lim f ( )( z z f(
l n k 1 max | z | 0 k
l 1 l 2
f (z)=Re (z)不是解析函数!
y i l2 o l1 1 l2
I1 Rez d z xd( x iy) 1 xd x i d y i 0 0 2 ( y = 0) (x=1)
1 1
1+i
l1 x
1 I 0 id y x d x 2 0 0 (x=0) ( y=i ) 2
l l l
v u u v d x d y i d x d y s s x y y x
又u、v 满足C-R条件 u v u v , x y y x
y
f ( z ) d z 0
l
B
l
o
复变函数与积分变换第二章:解析函数

u v i x x
偏导数的定义
若沿平行于虚轴的方式 z z z(x 0)
f ( z z ) f ( z ) f ( z ) lim z 0 z [u( x , y y ) iv ( x , y y )] [u( x , y ) iv ( x , y )] lim y 0 i y u( x , y y ) u( x , y ) v ( x , y y ) v ( x , y ) lim i lim y 0 y 0 i y i y
f ' ( z ) ux iv x ux iuy v y iuy v y iv x
函数在区域 D 内解析的充要条件
定理二
函数 f ( z ) u( x , y ) iv ( x , y ) 在其定义
域 D 内解析的充要条件是: uபைடு நூலகம் x , y )与 v ( x , y ) 在 D 内可微, 并且满足柯西-黎曼方 程.
z ( z0 z )( z0 z ) z0 z0 z0 z z0 , z z
z 关键看 , 如果z0 0则极限存在,否则不存在。 z
定理
(1) 在区域 D 内解析的两个函数 f ( z ) 与 g( z ) 的 和、差、积、商 (除去分母为零的点 )在 D 内解析.
(6)
f [ g( z )] f ( w ) g( z ). 其中w g( z )
1 (7) f ( z ) , 其中 w f ( z )与z ( w )是 ( w ) 两个互为反函数的单值 函数, 且 ( w ) 0
微分的概念:
设函数 w f ( z )在 z0 可导, 则 w f ( z0 z ) f ( z0 ) f ( z0 ) z ( z )z ,
复变函数 题库

复变函数题库第一章 复变函数 1. 复数21ii +的指数表示为 主辐角为 三角式为 , z=i ,则Arg z= , 复数z 3/5+4i/5=,则z 为( ), 复数1-的三角式为 , Arg(z+2i)=()2. 复数的指数式 ,复数11ii -+的三角式 ,复数1i e +的三角式 ,z y ix =+的辐角为3. Im(32)i -= ,Re(32)i += ,arg(22)i += ,复数z 16/25+8i/25=的主辐角为4. 内点指 ,外点指 ,边界点指 ,闭区域指 ,柯西-黎曼方程是复变函数可导的 条件5. 推导直角坐标系和极坐标系下的柯西-黎曼第二章 复变函数的积分1. 极坐标系中的柯西-黎曼方程为2. 调和函数的表达式为3. 复连通区域柯西定理的数学表达形式为4. 单连通区域柯西定理的数学表达形式为5. 柯西公式为6.()nl z dz α-=⎰Ñ ,若z 和α为复数,则1l dz z α=-⎰Ñ7. ()()n f z =8. 已知一个解析函数)(z f 的实部是y x sin e u =,求该解析函数9. 已知一个解析函数)(z f 的实部是22u x y xy =-+,(0)0f =,求该解析函数 10. 已知一个解析函数)(z f 的实部是32u 3x xy =-,(0)0f =,求该解析函数 11. 已知一个解析函数)(z f 的虚部是22v yx y=+,求该解析函数 12. 已知一个解析函数)(z f 的实部是u (cos sin )x e x y y y =-,(0)0f =,求该解析函数。
第三章 幂级数展开1. 幂级数11()kk z i k ∞=-∑的收敛圆半径为 ,幂级数1!()k k z k k ∞=∑的收敛圆半径为 ,幂级数1!kk z k k ∞=⎛⎫⎪⎝⎭∑的收敛圆半径为 , 幂级数0k k k e t ∞=∑(其中t为复变数)的收敛圆半径为2. 32382(4)z z z +=-是的 阶极点,z i=是221()(1)f z z =+的 阶极点,00zz e =是的 ,若某函数的展开式为0100000!()()kk k f z z z -=-=-∑,则0z 为该函数的 ,若某函数的展开式为00()!()k f z k z z ∞=-∑,则0z 为该函数的 。
第二章复变函数的积分

第二章 复变函数的积分在微积分学中,微分法与积分法是研究函数性质的重要方法。
同样,在复变函数中,积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。
§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。
若选定C 的两个可能方向中的一个作为正方向,那么就把C 理解为带有方向的曲线,称为有向曲线。
设曲线C 的两个端点为A 与B ,如果从A 到B 的方向作为C 的正方向,那么从B 到A 的方向就是C 的负方向,并把它记作-C 。
在今后的讨论中,常把两个端点中的一个作为起点,另一个作为终点。
除特殊声明外,正方向总是指从起点到终点的方向。
关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时,临近P 点的曲线内部始终位于P 点的左方。
与之相反的方向就是曲线的负方向。
若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==,)(βα≤≤t (2.1) t 为实参数,则规定t 增加的方向为正方向,即由)(αz a =到)(βz b =的方向为正方向。
定义2.1 设函数)(z f w =定义在区域D 内,C 为区域D 内起点为A 终点为B 的一条光滑有向曲线,把曲线C 任意分成n 个弧段,设分点为:B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ(图3.1),作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ,记=∆k s 的长度,}Δ{max 1k nk s δ≤≤=。
当n 无限增加,且δ趋于零时,如果不论对C 的分法及k ζ的取法如何,当n S 有唯一极限,那么称这个极限值为函数)(z f 沿曲线C 的积分,记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( (2.2)图2.1C 称为积分路径,⎰Cdz z f )(表示沿C 的正方向的积分,⎰-C dz z f )(表示沿C的负方向的积分。
数学物理方法第2章复变函数积分-2016方案

(2.1.3)
(2) 化为参数积分计算.设积分曲线L的参数方程为z(t),
将z(t)及dz(t)=z'(t)dt代入式(2.1.4),可得
3
【例2.1.1】计算积分I=
其中曲线L是
(1)沿1+ i 到2+4 i 的直线,见图2.2(a);
(2)沿1+ i 到2+i,再到2+4 i 的折线,见图2.2(b);
§2.2.1 单通区域的柯西定理
定理 若函数f(z)在单通区域D 内解析,则f(z)在D内沿任意 闭曲线的积分为零
∮l f(z)dz = 0 (2.2.1)
证明 这个定理的严格证明比较复 杂, 为简单起见, 我们在“f(z)在D 内连续” 附加条件下证明这个定 理.
先将复变积分化为两个实变积 分的线性叠加
29
这就是解析函数的定积分公式,它与实变 函数中的牛顿-莱布尼茨公式具有相同的形 式。
通常把f(z)的原函数的集合
称f(z)的不定积分,式中C为复常数。
30
(2.2.8)
31
§2.2.3 复通区域的柯西定理
定理 若f(z)在闭复通区域 解析,则f(z)沿所
有内、外边界线(L=L0+ 之和为零
37
【2.2.2】试计算 其中积分回路分别(图2.11) (1) |z-i|=2;(2) |z+i|=2;(3) |z|=3.
38
解 首先,将被积函数分解为部分分式(利用通 分可以凑出来)
≠0
=0
39
40
【例2.2.3】若f(z)=1/(z-a) 在z=a的无心邻域内 连续,积分回路是以a点为圆心的圆弧
由于a点在D内随意变动时,柯西公式依然成立, 有时分别用z和x代替式 (2.3.1)的a和z。将柯西公 式改写为
第1篇 复变函数论-第2章 复变函数积分

Anhui University 在上一章学习了复变函数,重点介绍了解析函数的许多性质,这些性质都是在可导和可微的基础上得出的。
第2章复变函数积分()(,)(,) 若函数在区域内解析则有:f z u x y iv x y D =+1. 解析函数的调和性:解析函数的实部与虚部均满足二维拉普拉斯方程:(由C-R 条件可证明)。
220,0.xx yy xx yy u u u u v v v v ∆≡∇=+=∆≡∇=+=2. 解析函数的共轭性:解析函数的实部与虚部由C-R 方程联系,称为解析函数的共轭性。
具体说只要知道解析函数的实部或者虚部就可求得解析函数。
3. 解析函数的实部与虚部是彼此相互正交的曲线。
0),(),(=∇⋅∇y x v y x u为了深入理解复变函数,本章用积分理论来分析复变函数积分。
基本内容:1、掌握复积分的概念、性质和计算方法;2、掌握解析函数的基本定理-Cauchy定理及其应用;3、掌握解析函数的基本公式-Cauchy公式及其应用2.1 复数函数积分一. 复积分的定义1max 0()lim ()k n k k n C k z f z dz f z ζ→∞=∆→=∆∑∫记作:()w f z l =为被积函数,为积分路径。
二. 复积分存在的条件1max 0()lim ()k n k kn l k z f z dz f z ζ→∞=∆→=∆∑∫由上式可知:一个复积分的实质是两个实积分的和。
实积分存在的条件:(,)(,)分段光滑,,在上连续l u x y v x y l因此复积分存在的条件:分段光滑,在上连续。
()l f z l注1:所说的曲线总是指光滑或逐段光滑曲线。
注2:边界的正方向:规定当观察者沿曲线边界前进时,所围的区域始终在观察者的左手边,则前进的方向为正方向。
rzz<−单连通区域Rzzr<−<复连通区域正方向正方向三. 复积分的性质(1)()d ()d l lf z z f z z −=−∫∫反转积分路径:(2)()d ()d ;() l l kf z z k f z z k =∫∫为复常数(3)[()()]d ()d ()d ;l l l f z g z z f z z g z z ±=±∫∫∫121()(),,k n n k L l f z dz f z dz n l l l ==∑∫∫"(4),若曲线L由段线段组成被积函数的线性可叠加性积分路径的可叠加性(5)|()||()|||L L f z dz f z dz ≤⋅∫∫(6) , () () ()d ()d .设曲线的长度为函数在上满足那么l l l L f z l f z M f z z f z s ML ≤≤≤∫∫积分估值定理四. 计算方法1. 用定义计算2. 通过计算实积分结果表明:被积函数与积分路径有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复积分的牛顿-莱布尼兹公式
记住
务必 记住
世界科技发展史 10万年前火的使用、石制工具 3万年前关于来世、生育等思想 1万年前栽种谷物、动物驯养、陶器出现 5000年前金字塔和庙宇、史前巨石阵 4000年前中国早期的天文学,金属加工,印度数学开 端 3000年前埃及历法 约2000年前后托勒密的天文学和地学 希腊数学家和哲学家毕达哥拉斯(公元前572--公元前 497年)、柏拉图(公元前427年--前347年)和亚里士多 德(公元前384 -- 公元前322)和希腊数学家如欧几里 得(公元前325--公元前265)
典型应用实例
例 3.2.1 计算积分
b
a
z sin z dz
2
【解】 函数 z sin z 2 在 z 平面上解析,
1 易知 cos z 2 为它的一个原函数,根 2
据复积分的牛顿-莱布尼兹公式有
b
a
1 1 2 2 z sin z dz cos z cos a 2 cos b 2 2 2 a
例
sinhz z
2
| z|1
dz
2 i ( n ) dz f (a) n 1 L n! ( z a) f ( z)
–例
• 问题:计算回路积分
2 i ( n ) dz f (a) n 1 L n! ( z a) f ( z)
sinhz z
2
| z|1
dz
• 分析:与推广的柯西公式比较, 可知f(z)=sinh(z),a = 0,n = 1 • 解:由推广的柯西公式
t 1 所以
1
i
z t t 1 zdz d( ) d( ) [1 (1)] 1 i 1 2 2 2 1 2
1 1
2
1
例3.2.4 计算积分
i
0
z sin zdz
【解】 由于
i
z sin z 在复平面内处处解析,
i 0
因而积分与路径无关,可用分部积分法得
y
指出
y R x R
y
r R
O
O
x
O
x
| z | R
y
2
| z | R
y
1
r | z | R
y
O
1
O
x
-R
O
R
x
x
1 arg z 2
Im z 0
| z | R, Im z 0
记住
1 2
记住
3
举例
计算
dz l z 1
dz l z 1
dz l z 3
l 是圆周 z 2
可直接用如下公式:
dz l z 3i
务必 记住
作业(必做)
计算
dz l z 2 1
-2 0
y
2
x 1 2
l 是圆周 z 2
可直接用如下公式: -1
-2
务必 记住
计算
dz l z 2 1
0
l 是圆周 z 2
精美图苑:巴西里約熱內盧救世主耶穌雕像
记住
dz 1、 计算 l z 2 9 , 其中闭合曲线 l
(1)包围3i,不包围 3i (2)包围 3i,不包围 3i (3)包围 3i和3i z - sinz 2、 计算 l 6 dz z
作业(选做)第31页
dz 1、 计算 l z 2 9 , 其中闭合曲线 l
(1)包围3i,不包围 3i (2)包围 3i,不包围 3i (3)包围 3i和3i z - sinz 2、 计算 l 6 dz z
2 i ( n ) dz f (a) n 1 L n! ( z a) f ( z)
z 2 i cosh0 2 i
sinhz
2
| z|1
dz 2 i sinh'(0)
f
(n)
n! ( z) 2 i
f ( ) ( z )
n 1
L
d
作业(必做)
Δ
Ε Ζ
ε
δ ε
对数之基数
系数,方位角,阻 抗,相对粘度 迟滞系数,效率
Θ
Η Θ
ζ
η℩ θ
theta
iota kappa lamb da mu
温度,角度
微小,一点 介质常数
∧
Μ
ι
κ
波长,体积
磁导系数,微,动 摩擦系数,流体粘
例
计算
C
zdz ,其中C为从原点
到点3+4i的直线段.
【解】 直线的方程可写成 或 于是 又因
– 例2
• 问题:计算回路积分
1 dz | z |1 z ( z 2)
• 分析:与柯西公式比较, 可知f(z)= ,a =
例3
• 问题:计算回路积分 • 分析:
| z | 2
1 dz z ( z 1)
记住
记住
记住 或
2 i ( n ) dz f (a) n 1 L n! ( z a) f ( z)
记住
这个定理是柯西(Cauchy)于1825年发表的,古莎(Goursat)于
1900年提出了修改,故又称为柯西-古莎定理.
记住
举例
记住
举例
举例
填“顺时针方向”,“逆时针方向”
据此规定,故有界单连通区域积分的边界线沿 方向。而对于有界复连通区域,外边界取 方向,内边界取 反,内边界取 为边界线的正方向)
z sin zdz zd( cos z)
0
z ( cos z ) 0 ( cos z )dz
i 0
i
icosi sini i(cosi isini) ieii ie1
附:希腊字母读音表及意义
大写 Α Β Γ Γ 小写 α β γ δ 英文读 音 alpha beta gam ma delta epsilo n zeta eta 国际音 标 /'alfa / /'beit ə/ /'gæ mə / /'delt ə/ /ep'si lon/ /'zi:tə / /'i:tə / /'ζi:t ə/ /ai'o ute/ /kæ p ə/ /'læ m də / /mju: / 意义 角度,系数 磁通系数,角度, 系数 电导系数,角度 变动,密度,屈光 度
b
例3.2.2 (非闭合环路积分中的换元积分法)
计算积分
1
i
zdz
【解法1】z 在整个复平面上解析,且
1 2 z z 2
运用复积分的牛顿-莱布尼兹公 式有 1
i
zdz
1 2 1 1 2 z |i [1 (i) 2 ] 1 2 2
【解法2】换元积分法 令 t z 2 ,则当 z i ,有 t 1 ;当 z 1 ,有
C C C
由高等数学理论,其复积分的实部、虚部满足实 积分与路径无关的条件,所以 zdz
1 (3 4i) 2 样的曲线都等于 2
C
的值不论 C 是怎
,这说明有些函数的积分值
与积分路径无关.
作业(必做)
计算
1i
0
( x y ix )dz
2
积分路径是直线段
计算
1i
0
( x y ix )dz
cosh z dz | z| 2 z 1
• 分析:与柯西公式比较,可知f(z)=cosh(z),a = -1 •解:由柯西公 式
f ( z) dz 2 i f (a) za
cosh z dz 2 i cosh( 1) 2 i cosh1 | z| 2 z 1
柯西公式
记住
记住
记住
提问 记住
应用举例
L
f ( z) dz 2 i f (a) za
cosh z dz | z| 2 z 1
1 dz | z |1 z ( z 2)
| z | 2
1 dz z ( z 1)
柯西公式
• 应用举例
– 例1
• 问题:计算回路积分
L
0
3
3
2i 5!
本章小结
• 路积分 – 复变函数的路积分可分解为2个线积分; – 一般情况下,路积分与积分路径有关; • 柯西定理 – 在单连通区域内解析,则路积分与路径无关, 完全由起点和终点决定; – 在复连通区域内解析,则回路积分等于沿回路 里所有内边界线积分之和。 • 柯西公式 n! f ( ) (n) f ( z) d n 1 2 i L ( z )
C
C
f ( z )dz
性质
[ f g ]dx
a
b
b
a
fdx gdx
a a b
[ f g ]dz
C
C
fdz gdz
C C
c a
b
a
f ( x)dx f ( x)dx
b b c a
C
f ( z )dz f ( z )dz
f dx f dx f dx
2
积分路径是直线段
1 (1 i ) 3
精美图苑:吳哥(柬埔寨古都)
记住
CR
R
L
z0
图 3.10
• 单连通区域与多连通区域
