西安交大计算方法b大作业课件
数值计算B大作业---精品模板

课程设计课程名称:数值计算B设计题目:数值计算B大作业学号:姓名:完成时间:题目一:多项式插值某气象观测站在8:00(AM )开始每隔10分钟对天气作如下观测,用三次多项式插值函数(Newton )逼近如下曲线,插值节点数据如上表,并求出9点30分该地区的温度(x=10)。
二、数学原理假设有n+1个不同的节点及函数在节点上的值(x 0,y 0),……(x n ,y n ),插值多项式有如下形式:)())(()()()(n 10n 102010n x -x )(x -x x -x x P x x x x x x -⋯⋯-+⋯⋯+-++=αααα (1) 其中系数i α(i=0,1,2……n )为特定系数,可由插值样条i i n y x P =)((i=0,1,2……n )确定。
根据均差的定义,把x 看成[a,b ]上的一点,可得f(x)= f (0x )+f [10x x ,](0x -x )f [x , 0x ]= f[10x x ,]+f [x,10x x ,] (1x -x )……f[x , 0x ,…x 1-n ]= f [x, 0x ,…x n ]+ f [x , 0x ,…x n ](x —x n )综合以上式子,把后一式代入前一式,可得到:f (x )= f [0x ]+f[10x x ,](0x -x )+ f[210x x x ,,](0x -x )(1x -x )+ …+ f[x, 0x ,…x n ](0x -x )…(x —x 1-n )+ f [x , 0x ,…x n ,x ])(x 1n +ω= N n (x )+)(x n R 其中N n (x )= f[0x ]+f [10x x ,](0x -x )+ f [210x x x ,,](0x -x )(1x -x )+…+ f [x , 0x ,…x n ](0x -x )…(x —x 1-n ) (2))(x n R = f (x)— N n (x )= f [x, 0x ,…x n ,x ])(x 1n +ω (3) )(x 1n +ω=(0x -x )…(x —x n )Newton 插值的系数i α(i=0,1,2……n )可以用差商表示。
西安交通大学《计算方法》课程课件-第五章

特点
(1)速度快:Newton迭代法比简单迭代法收敛快
(2)由于要计算导数,因此计算量稍大
可以使用一点Newton迭代法
x ( k 1)
(k ) (k ) f ( x ) f ( x ) (k ) x( k ) x , k 0,1, 2... (k ) (0) f ( x ) f ( x )
因此,由连续函数的介值定理知, , 必有x* [a, b], 使 ( x* ) 0
即有x* ( x* ), 因此, ( x)在[a, b]中存在不动点x* (2)证明根唯一 __ __ __ 若 ( x)在[a, b]还有一个不动点 x ,使 x = ( x ),则
x x (x ) ( x) q x x x x
第5章 非线性方程求解 5.2 收敛性问题 5.2.1 简单迭代---不动点
证明: (1)证明有根 由条件(2)知,函数 ( x)连续 ,构造辅助函数 ( x) x ( x)
则 ( x)在[a, b]上也连续 ,由条件(1)知 ( a ) a (a) 0 同理 (b) b (b) 0
否则令x
(k )
x ,取I
( k 1)
(k )
=[ x , x( k 1) ]
( k 1)
__
(4)计算区间长度,若 x
x
x( k ) x( k 1) < , 则停止,令x , 输出 2
*
否则,令k k 1, 转(2)
第5章 非线性方程求解 5.2 收敛性问题 5.2.1 简单迭代---不动点
x( k 1) ( x( k ) ), k 0,1, 2,...
(5-3)
《计算方法》PPT课件

就可以得到一个递推公式
uk uk1x ank ,
k=1,2, …,n (1.3)
这样的计算过程只需要计算n次乘法和n次加法。 这种算法和上一种算法相比,不仅逻辑结构简单, 而且计算也明显地减少了。多项式求值的这种算法 称为秦九韶算法(计算框图见图1.2)。
2020/12/7
.
10
1.2 误差的来源及其基本概念
5
2020/. 12/7
5.
⒊得不到准确解时,设法得到近似解
例:求 x a, a 已0知数。
由数学中的极限理论可知,
当lim n
xn
x时(,极限存在)
有:lim n
xn1
lim
n
1 2
( xn
a xn
)
即x 1 ( x a )
2
x
于是 x2 a, a 0, x a
又∵n只能有限,∴x是近似值。
2020/12/7
.
6
在计算方法中,我们还将讨论: ⒋解的特性(近似程度,敛散性) ⒌各种方法的优缺点(速度,存储量) ⒍各种方法的实用范围(收敛范围)
7
2020/. 12/7
7.
⑵ 一个好的方法应具有如下特点:
第一,面向计算机,要根据计算机特点提供实际可行的 有效算法,即算法只能包括加、减、乘、除运算和逻辑运 算,是计算机能直接处理的。
计算方法
1
1.1 计算方法研究的对象和特点
计算方法实际上就是计算机上使用的数值计算方法,所 以这门课程又称为数值计算方法或数值分析。它是专门研究 求解各种数学问题的数值计算方法。现在,由于大多数科学 计算都比较复杂,人工计算无法完成;而计算机科学的迅速 发展和广泛应用提供了解决这些复杂问题的新途径。
计算方法第一讲知识课件

2020/9/27
例:计算多项式: 0 . 0 6 2 5 x 4 0 . 4 2 5 x 3 1 . 2 1 5 x 2 1 . 9 1 2 x 2 . 1 2 9 6 需10次乘法4次加法。
( ( ( 0 . 0 6 2 5 x 0 . 4 2 5 ) x 1 . 2 1 5 ) x 1 . 9 1 2 ) x 2 . 1 2 9 6
2020/9/27
教材与参考书
• 邓建中,刘之行,西安交通大学出版社,《计算方法》 ,2001年
• 李庆扬,关冶 《数值分析原理》,清华大学出版社, 2000年
• 李庆扬,易大义,王能超 《现代数值分析》,高教出版 社,1995年
• Michael T. H. Scientific Computing: An introductory Survey, 清华大学出版社,2001
• Matlews J. H. Numerical Methods Using Matlab, 电子工业 出版社,2002
2020/9/27
第一讲数值分析的意义内容与方法
数值分析或计算方法的历史早于计算机的产生 ,许多(如今仍在使用的)概念与方法由二 十世纪前的伟人给出 Newton (1642-1727) Euler(1707-1783) Lagrange(1736-1813) Laplace(1749-1817) Legendre(1752-1833) Hermite(1822-1901) Gauss(1777-1855) Cauchy(1789-1857) Jacobi(1804-1851) Adams(1819-1892) Chebyshev(1821-1894) Laguerre(18341886)
计算方法课件1(崔丽鸿)

§1.3 绝对误差和相对误差
一.绝对误差 /* absolute error */
设
称
x
——准确值,x * ——近似值。
*
*
e( x ) x x 为 x 的绝对误差(简称误差) | e( x ) | 为 x * 的绝对误差限。
二.相对误差 /* relative error */
14/47
§1.1 引言
算法影响计算的精度
例2
令
设多项式为 ( x-2)9 , 我们来计算其在区间 [1.92, 2.08]上的值。
p(x) = ( x-2)9 q(x) = x9 – 18 x8 + 144 x7 – 672 x6 + 2016 x5 4032 x4 + 5376 x3 – 4608 x2 + 2304 x - 512
NY
BJ
以上是一个病态问题
/* ill-posed problem*/ 关于本身是病态的问题,还是留给数学家去头痛吧!
30/47
蝴蝶效应是气象学家洛伦兹1963年提出来的。其大意 为:一只南美洲亚马孙河流域热带雨林中的蝴蝶,偶 尔扇动几下翅膀,可能在两周后引起美国德克萨斯引 起一场龙卷风。
数值分析
理学院
崔丽鸿
教材:西安交通大学出版社
《计算方法》
作者:邓建中
2/47
主要参考书
1.《数值分析基础教程》,
李庆杨,
高等教育出版社,
2001年第1版
3/47
主要参考书
2.《数值方法和MATLAB实现与应用》, (美) Gerald Recktenwald 著 伍卫国 万群 张辉 等译, 机械工业出版社,
西安交通大学《计算方法》课件-第六章
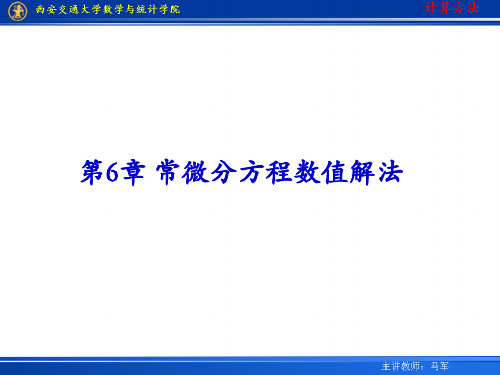
当f (t , y)在区域a t b c y d 中连续 ,且对变量y
满足Lipschitz条件 :对t [a, b] , y1 , y2 [c, d ] , 都有
f (t , y1 ) f (t , y2 ) L y1 y2 (6-2)
其中L为常数 则初值问题(6-1)的解存在且唯一
y(t ) f (t , y (t ))确定了函数y (t )在平面 上的方向场
yi 1 yi hf (ti , yi )是y(ti 1 )的一个近似,即由(ti , yi )到(ti 1 , yi 1 )的 直线段局部近似代替了由(ti , y(ti ))到(ti 1 , y(ti 1 ))的曲线
( 3)可以看出后退Euler方法比Euler方法的结果更好一些
显式方法:由yi直接计算yi 1的算法 隐式方法:不能直接由yi直接计算yi 1,而需要从方程中求解yi 1的算法
第6章 常微分方程数值解法 6.1 常微分方程初值问题的数值方法 6.1.2 多步法
对于微分方程 y f ( t , y( t ))
条件下是
h h2 (b a) y( ) O(h), a b y (i ) 2 i 1 2
N
若初值问题(6-1)通过某一种数值方法得到yN ,则最终误差 E ( y(b), h) y(b) - yN
称为总体截断误差 简记为 EN
第6章 常微分方程数值解法 6.1 常微分方程初值问题的数值方法 6.1.1 Euler方法及其变形
令t0 0, y0 1 yi 1 yi h( yi 2sin ti )进行计算,得到数值解.
程序演示
第6章 常微分方程数值解法
例.用Euler法求解初值问题
西安交大计算方法B2017大作业

计算方法B上机报告姓名:学号:班级:学院:任课教师:2017年12月29日题目一:1.1题目内容某通信公司在一次施工中,需要在水面宽度为20米的河沟底部沿直线走向铺设一条沟底光缆。
在铺设光缆之前需要对沟底的地形进行初步探测,从而估计所需光缆的长度,为工程预算提供依据。
已探测到一组等分点位置的深度数据(单位:米)如下表所示:(1)请用合适的曲线拟合所测数据点;(2)估算所需光缆长度的近似值,并作出铺设河底光缆的曲线图;1.2实现题目的思想及算法依据首先在题目(1)中要实现的是数据的拟合,显然用到的是我们在第三章中数据近似的知识内容。
多项式插值时,这里有21个数据点,则是一个20次的多项式,但是多项式插值随着数据点的增多,会导致误差也会随之增大,插值结果会出现龙格现象,所以不适用于该题目中点数较多的情况。
为了避免结果出现大的误差,同时又希望尽可能多地使用所提供的数据点,提高数据点的有效使用率,这里选择分段插值方法进行数据拟合。
分段插值又可分为分段线性插值、分段二次插值和三次样条插值。
由于题目中所求光缆的现实意义,而前两者在节点处的光滑性较差,因此在这里选择使用三次样条插值。
根据课本SPLINEM算法和TSS算法,采用第三种真正的自然边界条件,在选定边界条件和选定插值点等距分布后,可以先将数据点的二阶差商求出并赋值给右端向量d,再根据TSS解法求解三对角线线性方程组从而解得M值。
求出M后,对区间进行加密,计算200个点以便于绘图以及光缆长度计算。
对于问题(2),使用以下的公式20f (x)2dxf'(x)2dx(x )ds1.3算法结构1. For i 0,1,2, , n12. x kelse i 1 kxx k1〜一〜h; x< x x; x x<13 x xh2h" 〜[M k 1 _ M k (y k 1 M k 1 )x (y k M k —)xVh y6 6 6 61.4 matlab 源程序n=20;x=O:n;y=[9.01 8.96 7.96 7.97 8.02 9.05 10.13 11.18 12.26 13.28 13.32 12.61 11.29 10.229.15 7.90 7.95 8.86 9.81 10.80 10.93];M=y; %用于存放差商,此时为零阶差商h=zeros(1, n+1);c=zeros(1, n+1);d=zeros(1, n+1);a=zeros(1, n+1);b=2*o nes(1, n+1);h(2)=x(2)-x(1);for i=2:n %书本110 页算法SPLINEMh(i+1)=x(i+1)-x(i);c(i)=h(i+1)/(h(i)+h(i+1));a(i)=1-c(i);enda(n +1)=-2; %计算边界条件c(0),a(n+1),采用的是第三类边界条件c(1)=-2;for k=1:3 %计算k阶差商for i=n+1:-1:k+1M(i)=(M(i)-M(i-1))/(x(i)-x(i-k));endif(k==2) %计算2阶差商d(2:n)=6*M(3:n+1); %给 d 赋值endif(k==3)d(1)=(-12)*h(2)*M(4); %计算边界条件d(0),d(n),采用的是第三类边界条件d( n+1)=12*h( n+1)*M( n+1);endendl=zeros(1, n+1);r=zeros(1, n+1);u=zeros(1, n+1);q=zeros(1, n+1);u(1)=b(1);r(1)=c(1);q(1)=d(1);for k=2:n+1 %利用书本49页算法TSS求解三对角线性方程组r(k)=c(k);l(k)=a(k)/u(k-1);u(k)=b(k)-l(k)*r(k-1);q(k)=d(k)-l(k)*q(k-1);endp( n+1)=q( n+1)/u( n+1);for k=n :-1:1p(k)=(q(k)-r(k)*p(k+1))/u(k);endfprintf('三对角线性方程组的解为:');disp(p);%求拟合曲线x1=0:0.1:20; %首先对区间进行加密,增加插值点n1=10* n;x2=zeros(1, n1+1);x3=zeros(1, n1+1);s=zeros(1, n1+1);for i=1: n1+1for j=1: nif x1(i)>=x(j)&&x1(i)<=x(j+1) %利用书本111 页算法EVASPLINE 求解拟合曲线s(x)h(j+1)=x(j+1)-x(j);x2(i)=x(j+1)-x1(i);x3(i)=x1(i)-x(j);s(i)=(p(j).*(x2(i))A3/6+p( j+1).*(x3(i))A3/6+(y(j)-p(j).*((h(j+1))A2/6)).*x2(i)+…(y(j+1)-p(j+1).*(h(j+1))A2/6).*x3(i))/h(j+1);endendendplot(x,-y,'x') %画出插值点hold onplot(x1,-s) %画出三次样条插值拟合曲线hold ontitle('三次样条插值法拟合电缆曲线');xlabel('河流宽度/m');ylabel('河流深度/m');Len gth=0;for i=1: n1L=sqrt((x1(i+1)-x1(i))A2+(s(i+1)-s(i))A2); % 计算电缆长度Len gth=Le ngth+L;endfprintf('电缆长度(m)=');disp(Le ngth);图1. 1三次样条插值法拟合海底光缆曲线山舅 10 -0.70091,922& 0.8703 -山 24斫 0.3520 -0.9224 -1,8224电缆长 l(n)= 26.6656图1.2海底光缆长度结果铺设海底光缆的曲线如图1.1所示由上图可以看出,所得到的曲线光滑,能够较好得反映实际的河沟底部地势 形貌。
西安交通大学《计算方法》课件-第一章
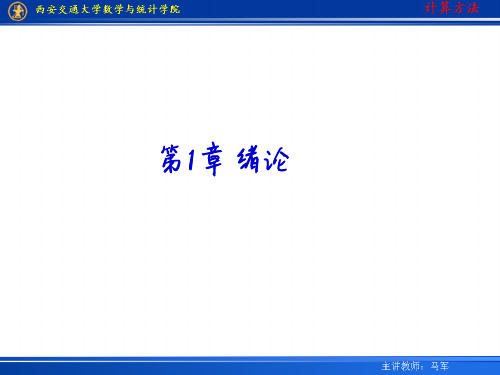
浮点运算原则
(1)避免产生大结果的运算,尤其是避免小数作为除数 参加运算 (2)避免“大”“小”数相加减 (3)避免相近数相减,防止大量有效数字损失 (4)尽可能简化运算步骤,减少运算次数
第1章 绪论
定义 数据相对小的变化引起解的相对大的变化的问题 称为病态问题,否则称为良态问题。
问题的性态就是指问题的解对原始数据扰动的敏感性
第1章 绪论
浮点数系运算误差
(2)计算结果的尾数多于t位数字
在F (2,3,1,2)中
(0.100 20 ) (0.111 20 ) 0.1101 21 (0.100 22 ) (0.111 21 ) 0.1000111 22
需要对结果进行舍入处理,产生的差称为舍入误差
记为F ( , t , L,U )
l
将计算机中所能表示的全体数的集合称为计算机的浮点数系
浮点数系中的数的个数是有限的,其个数为
2( 1) t 1 (U L 1) 1
第1章 绪论
浮点数系的误差
在计算机的浮点数系中,四则运算是非封闭的 为使经过算术运算产生的结果仍然要用浮点数系中的数 表示,因此必须用一个比较接近的数来代替 因此产生误差 称此误差称为舍入误差
第1章 绪论
第1章 绪论
什么是计算方法
《计算方法》介绍基本的数学问题中的主要数值方法, 介绍方法的思想、结构、条件、对输入数据的要求、生成 数据的意义、应注意的事项等 介绍数值计算中的一些最基本的概念 设计常见应用问题的数值处理方法 对数值方法的数值特性进行研究 分析方法的可靠性 分析方法的效率
第1章 绪论
问题的性态
已知问题f ( x)的输入数据只有一个 ,用x来表示 若有两个输入数据x和~ x , 则可以得到两个不同的结果f ( x)和f ( ~ x)
西安交大计算方法B2017大作业

计算方法B上机报告姓名:学号:班级:学院:任课教师:2017年12月29日题目一:1.1题目内容某通信公司在一次施工中,需要在水面宽度为20米的河沟底部沿直线走向铺设一条沟底光缆。
在铺设光缆之前需要对沟底的地形进行初步探测,从而估计所需光缆的长度,为工程预算提供依据。
已探测到一组等分点位置的深度数据(单位:(1)(2)估算所需光缆长度的近似值,并作出铺设河底光缆的曲线图;1.2 实现题目的思想及算法依据首先在题目(1)中要实现的是数据的拟合,显然用到的是我们在第三章中数据近似的知识内容。
多项式插值时,这里有21个数据点,则是一个20次的多项式,但是多项式插值随着数据点的增多,会导致误差也会随之增大,插值结果会出现龙格现象,所以不适用于该题目中点数较多的情况。
为了避免结果出现大的误差,同时又希望尽可能多地使用所提供的数据点,提高数据点的有效使用率,这里选择分段插值方法进行数据拟合。
分段插值又可分为分段线性插值、分段二次插值和三次样条插值。
由于题目中所求光缆的现实意义,而前两者在节点处的光滑性较差,因此在这里选择使用三次样条插值。
根据课本SPLINEM 算法和TSS 算法,采用第三种真正的自然边界条件,在选定边界条件和选定插值点等距分布后,可以先将数据点的二阶差商求出并赋值给右端向量d ,再根据TSS 解法求解三对角线线性方程组从而解得M 值。
求出M 后,对区间进行加密,计算200个点以便于绘图以及光缆长度计算。
对于问题(2),使用以下的公式:20=()L f x ds ⎰20(f x =⎰191(k kk f x +==∑⎰1.3 算法结构1. For n i ,,2,1,0⋅⋅⋅=1.1 i i M y ⇒2. For 2,1=k2.1 For k n n i ,,1, -=2.1.1 i k i i i i M x x M M ⇒----)/()(13. 101h x x ⇒-4. For 1-,,2,1n i =4.1 11++⇒-i i i h x x4.2 b a c c h h h i i i i i i ⇒⇒-⇒+++2;1;)/(11 4.3 i i d M ⇒+165. 0000;;c M d M d n n ⇒⇒⇒λn n n b a b ⇒⇒⇒2;;20μ6. 1111,γμ⇒⇒d b7. For m k ,,3,2 = ! 获取M 的矩阵元素个数,存入m7.1 k k k l a ⇒-1/μ 7.2 k k k k c l b μ⇒⋅-1- 7.3 k k k k l d γγ⇒⋅-1- 8. m m m M ⇒μγ/9. For 1,,2,1 --=m m k9.1 k k k k k M M c ⇒⋅-+μγ/)(110. k ⇒1 ! 获取x 的元素个数存入s 11. For 1,,2,1-=s i11.1 if i x x ≤~then k i ⇒;break else k i ⇒+112. xx x x x x h x x k k k k ˆ~;~;11⇒-⇒-⇒--- y h x h M y x h M y x M x M k k k k k k ~/]ˆ)6()6(6ˆ6[2211331⇒-+-++---1.4 matlab 源程序n=20; x=0:n;y=[9.01 8.96 7.96 7.97 8.02 9.05 10.13 11.18 12.26 13.28 13.32 12.61 11.29 10.22 9.15 7.90 7.95 8.86 9.81 10.80 10.93];M=y; %用于存放差商,此时为零阶差商 h=zeros(1,n+1); c=zeros(1,n+1); d=zeros(1,n+1); a=zeros(1,n+1); b=2*ones(1,n+1); h(2)=x(2)-x(1);for i=2:n %书本110页算法SPLINEM h(i+1)=x(i+1)-x(i);c(i)=h(i+1)/(h(i)+h(i+1)); a(i)=1-c(i); enda(n+1)=-2; %计算边界条件c(0),a(n+1),采用的是第三类边界条件 c(1)=-2;for k=1:3 %计算k 阶差商 for i=n+1:-1:k+1M(i)=(M(i)-M(i-1))/(x(i)-x(i-k)); endif(k==2) %计算2阶差商 d(2:n)=6*M(3:n+1); %给d 赋值 endif(k==3)d(1)=(-12)*h(2)*M(4); %计算边界条件d(0),d(n),采用的是第三类边界条件 d(n+1)=12*h(n+1)*M(n+1); end endl=zeros(1,n+1); r=zeros(1,n+1); u=zeros(1,n+1); q=zeros(1,n+1); u(1)=b(1); r(1)=c(1); q(1)=d(1);for k=2:n+1 %利用书本49页算法TSS求解三对角线性方程组r(k)=c(k);l(k)=a(k)/u(k-1);u(k)=b(k)-l(k)*r(k-1);q(k)=d(k)-l(k)*q(k-1);endp(n+1)=q(n+1)/u(n+1);for k=n:-1:1p(k)=(q(k)-r(k)*p(k+1))/u(k);endfprintf('三对角线性方程组的解为:');disp(p);%求拟合曲线x1=0:0.1:20; %首先对区间进行加密,增加插值点n1=10*n;x2=zeros(1,n1+1);x3=zeros(1,n1+1);s=zeros(1,n1+1);for i=1:n1+1for j=1:nif x1(i)>=x(j)&&x1(i)<=x(j+1) %利用书本111页算法EVASPLINE求解拟合曲线s(x)h(j+1)=x(j+1)-x(j);x2(i)=x(j+1)-x1(i);x3(i)=x1(i)-x(j);s(i)=(p(j).*(x2(i)).^3/6+p(j+1).*(x3(i)).^3/6+(y(j)-p(j).*((h(j+1)).^2/6)).*x2( i)+...(y(j+1)-p(j+1).*(h(j+1)).^2/6).*x3(i))/h(j+1);endendendplot(x,-y,'x') %画出插值点hold onplot(x1,-s) %画出三次样条插值拟合曲线hold ontitle('三次样条插值法拟合电缆曲线');xlabel('河流宽度/m');ylabel('河流深度/m');Length=0;for i=1:n1L=sqrt((x1(i+1)-x1(i))^2+(s(i+1)-s(i))^2); %计算电缆长度Length=Length+L;endfprintf('电缆长度(m)=');disp(Length);1.5 结果与说明铺设海底光缆的曲线如图1.1所示图1. 1三次样条插值法拟合海底光缆曲线由上图可以看出,所得到的曲线光滑,能够较好得反映实际的河沟底部地势形貌。
西安交通大学计算方法B完整版

第一章绪论1.1数值计算现代科学的发展,已导致科学与技术的研究从定性前进到定量,尤其是现代数字计算机的出现及迅速发展,为复杂数学问题的定量研究与解决,提供了强有力的基础。
通常我们面对的理论与技术问题,绝大多数都可以从其物理模型中抽象出数学模型,因此,求解这些数学模型已成为我们面临的重要任务。
一、本课程的任务:寻求解决各种数学问题的数值方法——如何将高等数学的问题回归到初等数学(算术)的方法求解——了解计算的基础方法,基本结构(否则只须知道数值软件)——并研究其性质。
立足点:面向数学——解决数学问题面向计算机——利用计算机作为工具充分发挥计算机的功能,设计算法,解决数学问题例如:迭代法、并行算法二、问题的类型1、离散问题:例如,求解线性方程组bAx=——从离散数据:矩阵A和向量b,求解离散数据x;2、连续问题的离散化处理:例如,数值积分、数值微分、微分方程数值解;3、离散问题的连续化处理:例如,数据近似,统计分析计算;1.2数值方法的分析在本章中我们不具体讨论算法,首先讨论算法分析的基础——误差。
一般来讲,误差主要有两类、三种(对科学计算):1)公式误差——“截断误差”,数学↔计算,算法形成——主观(人为):数学问题-数值方法的转换,用离散公式近似连续的数学函数进行计算时,一般都会发生误差,通常称之为“截断误差”;——以后讨论2)舍入误差及输出入误差——计算机,算法执行——客观(机器):由于计算机的存储器、运算器的字长有限,在运算和存储中必然会发生最末若干位数字的舍入,形成舍入误差;在人机数据交换过程中,十进制数和二进制数的转换也会导致误差发生,这就是输入误差。
这两种误差主要是由于计算机的字长有限,采用浮点数系所致。
首先介绍浮点数系一、计算机上的运算——浮点运算面向计算机设计的算法,则先要讨论在计算机上数的表示。
科学记数法——浮点数:约定尾数中小数点之前的数全为零,小数点后第一个数不能为零。
目前,一般计算机都采用浮点数系,一个存储单元分成首数和尾数:首数l 尾数(位)其中首数存放数的指数(或“阶”)部分,尾数存放有效数字。
西安交大并行计算作业

并行计算与程序设计作业班级:姓名:学号:1.1至1.3节作业1.调试课件中的所有程序,并完成作业,同时在程序结果中需要输出个人信息;代码:Program mainwrite(*,*)'班级:', 'write(*,*)'姓名:',' 'print *,'学号:',''end2.编写一个数值求解方程的程序,方程为4.1x3 −5.3x=11.8,求解区间为(1,5),误差小于1e-6。
代码:a=1b=5if(f(a)*f(b).LT.0) thenwrite(*,*)'inter:(',a,',',b,')'Loop1: do while((abs(f(a)-f(b)).gt.10e-6).and.$ (abs(a-b).gt.10e-6))c=(a+b)/2if(f(a)*f(c).le.0)thenb=celsea=cend ifend do Loop1write(*,*)'x=',celsewrite(*,*)'Please input real interval'end ifendreal function f(x)f=4.1*x**3-5.3*x-11.8end结果:1.4节作业1.采样简单离散求和法求下面积分值:∫x2sin(x)+1xx 1代码:read(*,*) a,b,nh=(b-a)/(2.0*n)s=0.0x=a+hf2=0.0f4=0.0loop1: do i=1,n-1 x=x+hf2=f2+f(x)x=x+hf4=f4+f(x)end do loop1s=h/3.0*(f(a)+f(b)+4.0*f4+2.0*f2)write(*,150) s100 format(1x,'a=',f8.2,2x,'b=',f8.2,$ 2x,'n=',i4)150 format(1x,'s=',f16.7)endreal function f(x)f=x**2/(sin(x)+1)endd ouble precision i,ai,ydouble precision sum=0i=1do 10 while(1/i.gt.1e-5)sum=1/i+sumi=i+110 continuewrite(*,*) 'sum=',sumend结果:1.6节作业1.调试课本中的所有程序;(结果略)2.用双精度型数据计算:∑1x=11+12+13+⋯+1xxx=1直到1x≤10−5代码:double precision sum=0i=1do 10 while(1/i.gt.1e-5)sum=1/i+sumi=i+110 continuewrite(*,*) 'sum=',sumend结果:3.已知三角形三个顶点的坐标分别为A(1.5,2.5),B(-2.5,1), C(1,-1),采用复型数据类型求三角形的面积和重心。
西安交大计算方法

西安交通大学计算方法上机实验班级:(xxx)姓名:(xxx)学号:21116010041.按两种顺序计算y,哪个接近真值?Y = 1000 + + + … +用java 语言编写:public class Add {public static void main(String[] args){double s=0,y=1000;for(double a=1001.0;a<=2000.0;a++){y+=1.0/a;}for(double a=2000.0;a>=1001.0;a--){s+=1.0/a;}s=s+1000;System.out.println("正序和"+s);System.out.println("逆序和"+y);}}运行结果:结论:显然假设是double类型的数据时,先算大数的过程吃掉了末尾的小数被进位所埋没,导致了大数吃小数的误差,按从小到大(从右向左)的计算顺序所得的结果与真值相近,而按从大到小(从左到右)的计算顺序所得的结果与真值的误差较大。
1-18.设(x) = 1 + x + + + … + , 计算(-5)和1/(5),哪个接近?解法一:用JAVA 语言编写:public class second{ public static void main(String[] args){double s1=1 ,s2=1;double e=1,sum=1; //e的初值为1,sum用来存放n!int a=1;while(sum<Math.pow(10, 1000000)){sum=a*sum;e=1.0/sum+e;a++;}double b=1.0/(e*e*e*e*e);System.out.println("较为精确的值1/e^5="+b);for(int i=1;i<=24;i++){s1+=cimi1(i);s2+=cimi2(i);}s1=1.0/s1;System.out.println("1/S24(5)="+s1);System.out.println("S24(-5)="+s2);}public static double cimi1(int ai){double xi=1;for(int i=ai;i>=1;i--){xi=xi*(5.0/i);}return xi;}public static double cimi2(int ai){double xi=1;for(int i=ai;i>=1;i--){xi=xi*(-5.0/i);}return xi;}}运行结果:解法二:用matlab编程并运行,如下:(1)计算(-5)运行结果如下:(2)计算1/(5)运行结果如下:而的真是结果为0.006737946比较得1/(5)的计算结果与真实值更接近解法三:也可以用C++编写:#include "stdafx.h"#include"stdio.h"#include "iostream"using namespace std;int main(int argc, char* argv[]){ int func1(int );double func2(int);double y=0;int i;for(i=1;i<25;i++){ int z=func1(i);double e=func2(i);y+=z/e;}cout<<"----------------------------------------"<<endl;cout<<"1/S(5)的运算结果是:"<<" "<<1.0/(y+1)<<endl;cout<<"----------------------------------------"<<endl;return 0;}int func1(int x){int y=1;int k;for (k=0;k<x;k++)y*=5;return y;}double func2(int n){double y=1;int j;for (j=1;j<=n;j++)y*=j;return y;}运行结果如下图:结论:通过比较上述的几种编程结果,可以看出1/S(5),更接近真实值,而且用matlab更为简便,可以直接利用函数库,并可以轻松的嵌入秦九韶算法,大大减少运算量和时间。
西安交大并行计算理论赵银亮课件第六章

并行分治设计步骤
将输入划分成若干个规模相等的子问题; 同时(并行地)递归求解这些子问题; 并行地归并子问题的解,直至得到原问 题的解。
Batcher归并、排序网络
比较器操作和[0,1]原理 奇偶归并网络 双调归并网络 Batcher排序网络 2D-Mesh上的排序算法
k l k l 与 之差: 2 2 2 2 k l k l k l 0 c* 0, 且为第2( ) ( ) ( ) k l项 2 2 2 2 2 2 1 c* : c** e k l : d k l 0 : 0且分别是第k l -1和k l项
), (b1 , b3 ,..., b m ) (d1 , d 2 ,..., d n
2 1 2 2 2
m 2 2
)
(a2 , a4 ,..., a
), (b2 , b4 ,..., b m ) (e1 , e2 ,..., e n
例:n=8, p=8, C01~C08为前缀和
PRAM求前缀和算法 sequenceT SCAN(sequenceT x, ⊕: T × T → T )
x为B树第k层 Scan返回为C树第k层
y为B树第k-1层
z为C树第k-1层
由z构造出s,也就是 C树第k层
8个 元 素 的 数 据 流 分 析
设计思想
以树的叶结点为输入,中间结点为处理结点, 由叶向根或由根向叶逐层进行并行处理。
示例
求最大值 计算前缀和
算法6.8: SIMD-TC(SM)上求最大值算法
计算方法b

I6
.1268
I7
.1124
I8
.1010
① ②
.6321
.6320
.3679
.3680
.2462
.2643
.2074
.2073
.1704
.1709
.1480
.1455
.1120
.1268
.2160
.1124
-.7280
.1010
由上表可见,方法①中,原始步的误差,随着计算步数的增加被严重地 放大,特别是竟变成负数(注意:被积函数是非负函数),而方法② ~ 则相反;这是因为方法①中,若前步有误差: : I n1 I n1 ,则n步 ~ ~ I 1 n I n n1 1 nI n1 n I n n 误差:
A
(1) J (i ,i i ) 1i 2i
1 2 n 1
2
nin
i1 , i2 ,} in所需的置换次数. J (i1 , i2 ,, in ) 其中 是由{1 , 2, , n}变换到{ 可见每计算一个行列式, 需要 (n 1) n个浮点运算;因此,按 ! n! Grammar方法解方程组约需N (n 2 1) 个浮点运算。当 时 n 20 ,用一个运算速度为 N 9.7 1020
•算法的稳定性
例:计算积分
I n e 1 x n e x dx , n 0, 1,,8
0
1
解:由微积分,有计算公式,
① I n 1 nIn1
② I n 1
1 (1 I n ) n
方法
准确值
I0
.6321
I1
.3679
I2
2462
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《计算方法B》上机实验报告学院:机械工程学院班级:姓名:学号:2015年12月22日1 1.计算以下和式: S = ∑ 8n + 1 - 8n + 4 - 8n + 5 - 8n + 6 ⎪ ,要求: 42 1 1∞ n =0 16n ⎛ ⎫ ⎝ ⎭(1)若保留 11 个有效数字,给出计算结果,并评价计算的算法;(2)若要保留 30 个有效数字,则又将如何进行计算。
实现思想:以上问题出现了近似数相减的问题,为了减小误差,可分别求得减数之和 以及被减数之和,最后将两者相减。
另外,减数与被减数求和均为同号计算, 按照绝对值递增顺序相加可减小舍入误差。
此题中对有效数字有要求,因而计 算时首先需要根据有效数字位数计算得出迭代次数,以保证计算值的精度。
源程序:m=input('输入有效数字个数m='); s0=1;s1=0;s2=0;n=0; %判断迭代次数while s0>=0.5*10^-(m-1)s0=4/(16^n*(8*n+1))-2/(16^n*(8*n+4))-1/(16^n*(8*n+5))- 1/(16^n*(8*n+6)); n=n+1;end%分别求解各项并求和 for k=n-1:-1:0a1=4/(16^k*(8*k+1)); a2=2/(16^k*(8*k+4)); a3=1/(16^k*(8*k+5)); a4=1/(16^k*(8*k+6)); s1=a1+s1; s2=a4+a3+a2+s2; endS=vpa(s1-s2,m)实验结果:11位有效数字计算结果如图1所示;30为有效数字计算结果如图2所示。
图1.11位有效数字计算结果图2.30为有效数字计算结果所示: (1)请用合适的曲线拟合所测数据点;k +1 =0k1. 某通信公司在一次施工中,需要在水面宽度为 20 米的河沟底部沿直线走向铺设一条沟底光缆。
在铺设光缆之前需要对沟底的 地形进行初步探测,从而估计所需光缆的长度,为工程预算提 供依据。
已探测到一组等分点位置的深度数据(单位:米)如下表(2)估算所需光缆长度的近似值,并作出铺设河底光缆的曲线图;算法思想:由于题中所给点数为 20,若采用高次多项式插值将产生很大的误差, 所以拉格朗日或牛顿并不适用。
题中光缆为柔性,可光滑铺设于水底,鉴于此 特性,采用三次样条插值插值法较为合适。
算法结构:三次样条算法结构见《计算方法教程》P110;光缆长度计算公式:l = 20⎰= 19 20∑ ⎰k⎰0源程序:clear; clc; x=0:20;y=[9.01 8.96 7.96 7.97 8.02 9.05 10.13 11.18 12.26 13.28 13.32 12.61 11.29 10.22 9.15 7.90 7.95 8.86 9.81 10.80 10.93]; d=y;plot(x,y,'k.','markersize',15) hold on %%%计算差商 for k=1:2for i=21:-1:(k+1)d(i)=(d(i)-d(i-1))/(x(i)-x(i-k)); endend%%%设定d 的边界条件for i=2:20d(i)=6*d(i+1);endd(1)=0;d(21)=0;%%%带状矩阵求解(追赶法)a=0.5*ones(1,21);b=2*ones(1,21);c=0.5*ones(1,21);a(1)=0;c(21)=0;u=ones(1,21);u(1)=b(1);r=c;yy(1)=d(1);%%%追for k=2:21l(k)=a(k)/u(k-1);u(k)=b(k)-l(k)*r(k-1);yy(k)=d(k)-l(k)*yy(k-1);end%%%赶m(21)=yy(21)/u(21);for k=20:-1:1m(k)=(yy(k)-r(k)*m(k+1))/u(k);end%%%绘制曲线k=1;nn=100;xx=linspace(0,20,nn);l=0;for j=1:nnfor i=2:20if xx(j)<=x(i)k=i;break;elsek=i+1;endendh=1;xbar=x(k)-xx(j);xmao=xx(j)-x(k-1);s(j)=(m(k-1)*xbar^3/6+m(k)*xmao^3/6+(y(k-1)-m(k-1)*h^2/6)*xbar+(y(k)-m(k)*h^2/6)*xmao)/h;sp(j)=-m(k-1)*(x(k)-xx(j))^2/(2*h)+m(k)*(xx(j)-x(k-1))^2/(2*h)+(y(k)-y(k-1))/h-(m(k)-m(k-1))*h/6;l(j+1)=(1+sp(j)^2)^0.5*(20/nn)+l(j);%求解光缆长度end%%%绘图plot(xx,s,'r-','linewidth',1.5)disp(['¹光缆长度为ª',num2str(l(nn+1)),'Ã×'])曲线图如图2-1所示,计算光缆长度如图2-2所示。
图2-1光缆插值曲线图图2-1光缆计算长度显示3.假定某天的气温变化记录如下表所示,试用数据拟合的方法找出这一天的气温变化的规律;试计算这一天的平均气温,并试估计误差。
实现思想:此题中所给数据点数目较多,采用拉格朗日插值法或者牛顿插值法需要很高次的多项式,计算困难,误差大;采用样条插值计算量虽然不大,但是存放参数Mi的量很大,且没有一个统一的数学公式来表示,也不是很方便。
所以可考虑用最小二乘法进行拟合。
计算过程中,分别使用二次函数、三次函数以及四次函数,计算其相应的系数,估算误差并作图比较各个函数之间的区别。
算法结构:(参考课本P123)1.1[形成矩阵Qk]1.2[变换Gk-1到Gk]2.[求解三角方程]3.[计算误差]源代码:clear;clc;x=0:24;y=[15141414141516182020232528313431292725242220181716];m=length(x);n=input('请输入函数的次数');plot(x,y,'k.',x,y,'-')grid;hold on;n=n+1;G=zeros(m,n+1);G(:,n+1)=y';c=zeros(1,n);%建立c来存放σq=0;f=0;b=zeros(1,m);%建立b用来存放β%%%形成矩阵G for j=1:nfor i=1:mG(i,j)=x(1,i)^(j-1);endend%%%建立矩阵Qkfor k=1:nfor i=k:mc(k)=G(i,k)^2+c(k);endc(k)=-sign(G(k,k))*(c(k)^0.5);w(k)=G(k,k)-c(k);%建立w来存放ωfor j=k+1:mw(j)=G(j,k);endb(k)=c(k)*w(k);%%%变换矩阵Gk-1到G kG(k,k)=c(k);for j=k+1:n+1q=0;for i=k:mq=w(i)*G(i,j)+q;ends=q/b(k);for i=k:mG(i,j)=s*w(i)+G(i,j);endendend%%%求解三角方程Rx=h1a(n)=G(n,n+1)/G(n,n);for i=n-1:(-1):1for j=i+1:nf=G(i,j)*a(j)+f;enda(i)=(G(i,n+1)-f)/G(i,i);%a(i)存放各级系数f=0;enda%%%回代过程p=zeros(1,m);for j=1:mfor i=1:np(j)=p(j)+a(i)*x(j)^(i-1);endendplot(x,p,'r*',x,p,'-');E2=0;%用E2来存放误差%%%误差求解for i=n+1:mE2=G(i,n+1)^2+E2;endE2=E2^0.5;disp('误差为');disp(E2);t=0;for i=1:mt=t+p(i);endt=t/m;%%%平均温度disp(['平均温度为',num2str(t),'℃'])实验结果:二次函数拟合,结果如下图所示图3-1二次函数拟合结果三次函数拟合,结果如下图所示图3-2三次函数拟合结果四次函数拟合,结果如下图所示图3-3四次函数拟合结果结果对比:将二次函数、三次函数和四次函数拟合结果绘制在同一个坐标内,如图3-4所示。
其计算误差结果见表3-1所示。
图3-4拟合结果对比分析4.设计算法,求出非线性方程6x5-45x2+20=0的所有实根,并使误差不超过10-4。
算法思想:本题可采用牛顿法迭代求解,令f(x)=6x5-45x2+20,得带格式为x k+1=xk-f ( xk)f'(xk)根据函数图像可以找出根的大致分布区间,带入不同的初值即可解出不同的根.源代码:function y=f2(x)y=6*x.^5-45*x.^2+20;%定义原函数function y=f3(x)y=30*x^4-90*x;%定义原函数倒数i=-5:0.1:5;y=f2(i);plot(i,y)hold onplot(i,0,'-')%画出原函数图像%%Newton法求根x1=input('输入初值');e=10^(-4);%误差设定Nmax=1000;%迭代最大次数限定for n=1:Nmaxf0=f2(x1);if abs(f2(x1))<efprintf('输出的f(x)已经足够小');x=x1;breakelseF0=f3(x1);x=x1-f0/F0;if abs(x-x1)<ebreakelsex1=x;endendendfprintf('输出方程的根x=%2f',x)计算结果:函数图像如图4-1所示。
计算结果分别见图4-2所示。
图4-1函数图像图4-2计算结果根据带入不同的初值,可以求出不同的根,有图4-2可以看出,原函数的根大约有三个,分别是-0.654542、0.681174、1.870799。
5.线性方程组求解。
(1)编写程序实现大规模方程组的高斯消去法程序,并对所附的方程组进行求解。
所附方程组的类型为对角占优的带状方程组。
(2)针对本专业中所碰到的实际问题,提炼一个使用方程组进行求解的例子,并对求解过程进行分析、求解。
算法思想:高斯消去法是利用现行方程组初等变换中的一种变换,将一个不为零的数乘到一个方程后加到另一个方程,使方程组变成同解的上三角方程组,然后再自下而上对上三角方程组求解。
