材料力学答案第三版
材料力学课后习题答案详细

变形厚的壁厚:
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ,试求 C 与 D 两点间的距离改
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作
轴力图。若横截面面积 A1 200mm2 , A2 300mm2 , A3 400mm2 ,并求各横截 面上的应力。
A1 11.503cm2 1150.3mm2
AE
N EA A
366.86 103 N 2 1150.3mm2
159.5MPa
EG
N EG A
357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ,其横截面面尺寸如图所示。荷载
22
N 22 A2
10 103 N 300mm 2
33.3MPa
3
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
材料力学第3版习题答案

材料力学第3版习题答案第一章:应力分析1. 某材料在单轴拉伸下的应力-应变曲线显示,当应力达到200 MPa 时,材料发生屈服。
若材料在该应力水平下继续加载,其应力将不再增加,但应变继续增加。
请解释这一现象,并说明材料的屈服强度是多少?答案:这种现象表明材料进入了塑性变形阶段。
在单轴拉伸试验中,当应力达到材料的屈服强度时,材料的晶格结构开始发生滑移,导致材料的变形不再需要额外的应力增加。
因此,即使继续加载,应力保持不变,但应变会因为材料内部结构的重新排列而继续增加。
在本例中,材料的屈服强度是200 MPa。
第二章:材料的弹性行为2. 弹性模量是描述材料弹性行为的重要参数。
若一块材料的弹性模量为210 GPa,当施加的应力为30 MPa时,其应变是多少?答案:弹性模量(E)与应力(σ)和应变(ε)之间的关系由胡克定律描述,即σ = Eε。
要计算应变,我们可以使用公式ε =σ/E。
将给定的数值代入,得到ε = 30 MPa / 210 GPa =1.43×10^-4。
第三章:材料的塑性行为3. 塑性变形是指材料在达到屈服点后发生的永久变形。
如果一块材料在单轴拉伸试验中,其屈服应力为150 MPa,当应力超过这个值时,材料将发生塑性变形。
请解释塑性变形与弹性变形的区别。
答案:塑性变形与弹性变形的主要区别在于材料在去除外力后是否能够恢复原状。
弹性变形是指材料在应力作用下发生的形状改变,在应力移除后能够完全恢复到原始状态,不留下永久变形。
而塑性变形是指材料在应力超过屈服点后发生的不可逆的永久变形,即使应力被移除,材料的形状也不会恢复到原始状态。
第四章:断裂力学4. 断裂韧性是衡量材料抵抗裂纹扩展的能力。
如果一块材料的断裂韧性为50 MPa√m,试样的尺寸为100 mm×100 mm×50 mm,试样中存在一个长度为10 mm的初始裂纹。
请计算在单轴拉伸下,材料达到断裂的临界应力。
材料力学答案第三版单辉祖
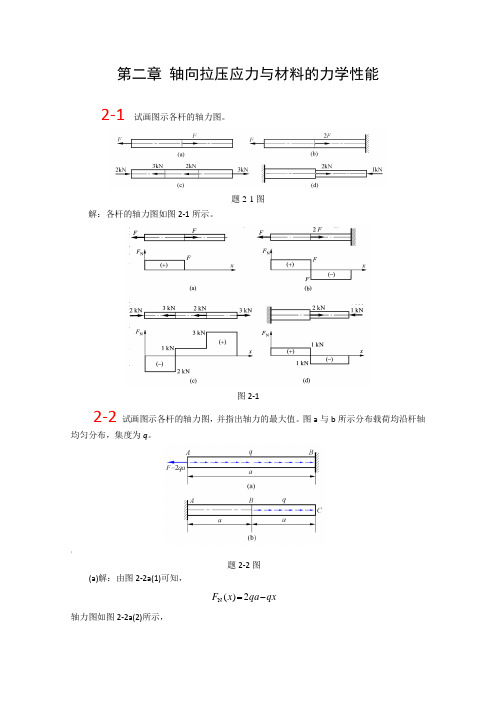
第二章轴向拉压应力与材料的力学性能2-1试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图,并指出轴力的最大值。
图a与b所示分布载荷均沿杆轴均匀分布,集度为q。
;题2-2图(a)解:由图2-2a(1)可知,=2()F-xqxqaN轴力图如图2-2a(2)所示,qa F 2m ax ,N =图2-2a(b)解:由图2-2b(2)可知, qa F =Rqa F x F ==R 1N )($22R 2N 2)()(qx qa a x q F x F -=--=轴力图如图2-2b(2)所示,qa F =m ax N,图2-2b2-3 图示轴向受拉等截面杆,横截面面积A =500mm 2,载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题2-3图解:该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N 10508263=⨯=⨯⨯==-A F σ 》斜截面m -m 的方位角, 50-=α故有MPa 3.41)50(cos MPa 100cos 22=-⋅== ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα杆内的最大正应力与最大切应力分别为MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
题2-5解:由题图可以近似确定所求各量。
~220GPa Pa 102200.001Pa10220ΔΔ96=⨯=⨯≈=εσEMPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
2-7 一圆截面杆,材料的应力-应变曲线如题2-6图所示。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第4章 刚体静力学专门问题

习题4-2图工程力学(工程静力学与材料力学)习题与解答第4章 刚体静力学专门问题4-1 塔式桁架如图所示,已知载荷FP 和尺寸d 、l 。
试求杆1、2、3的受力。
知识点:桁架、求解桁架的截面法 难易程度:一般 解答:截面法,受力如图(a )d l =αtan ,22cos d l d +=α0=∑x F ,0cos 2P =-αF F∴ P222F d d l F +=(拉)0=∑A M ,02P 1=⋅-l F d F ∴ P 12F d l F =(拉)=∑y F ,0sin 231=++αF F FP 33F d lF -=(压)4-2 桁架的载荷和尺寸如图所示。
试求杆BH 、CD 和GD 的受力。
知识点:桁架、求解桁架的节点法 难易程度:一般 解答:1.节点G :=∑y F ,0=GD F2.节点C :=∑y F ,0=HC F3.整体,图(a )0=∑B M ,0405601015R =⨯+⨯-E F 67.26R =E F kN (↑)习题4-4图习题4-3图4.截面法,图(b )0=∑H M ,067.26106055=⨯+⨯--CD F 67.6-=CD F kN (压)=∑y F ,067.266022=+--BH F1.47-=BH F kN4-3 试判断图示结构中所有零杆。
知识点:桁架、零杆与零杆的判断 难易程度:一般 解答:由节点C 知,F1 = F4 = 0再由节点E 知,F10 = 0由节点D 知,F7 = 0 由节点B 知,F13 = 0 再由节点A 知,F11 = 04-4 图示桁架的两部分用铰链K 连接,在铰链K 上作用有集中载荷FP = 10kN 。
试求各杆受力。
解:1.由结构和载荷对称性,只需考虑一半桁架即可。
由节点D ,FDF = 0 再由节点F ,FHF = 0再由节点H ,FHJ = 0 再由节点J ,FKJ = FJF = 0 再由节点F ,FFB = 0 2.节点K (图(a ))=∑y F ,030cos 2P =+︒F F KH77.53P -=-=F F KH kN (受压)∴ 77.5-======CA GC KG DB HD KH F F F F F F kN (压)其余各杆受力均为零。
《工程力学(工程静力学与材料力学)(第3版)》考试试卷(附答案)(10)

工程力学考试答卷(10)1.(5分)结构对称的梁在反对称载荷作用下:弯矩图对称,剪力图反对称;弯矩图反对称,剪力图对称;弯矩图和剪力图都对称;弯矩图和剪力图都反对称。
正确答案是B。
2.(5分)关于材料的力学一般性能,有如下结论,请判断哪一个是正确的:脆性材料的抗拉能力低于其抗压能力;(B)脆性材料的抗拉能力高于其抗压能力;(C)韧性材料的抗拉能力高于其抗压能力;正确答案是A。
(D)脆性材料的抗拉能力等于其抗压能力。
3.(5分)关于斜弯曲的主要特征有以下四种答案,请判断哪一种是正确的。
(A) My≠0,Mz≠0,FNx≠0;,中性轴与截面形心主轴不一致,且不通过截面形心;(B) My≠0,Mz≠0,FNx=0,中性轴与截面形心主轴不一致,但通过截面形心;(C) My≠0,Mz≠0,FNx=0,中性轴与截面形心主轴平行,但不通过截面形心;(D) My≠0,Mz≠0,FNx≠0,中性轴与截面形心主轴平行,但不通过截面形心。
正确答案是B。
4.(5分)两根长度相等、直径不等的圆轴受扭后,轴表面上母线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大剪应力分别为τ1max和τ2max,材料的切变模量分别为G1和G2。
关于τ1max和τ2max的大小,有下列四种结论,请判断哪一种是正确的。
(A)τ1max>τ2max;(B)τ1max<τ2max;(C)若G1>G2,则有τ1max>τ2max;正确答案是C。
(D)若G1>G2,则有τ1max<τ2max。
5.(10分)截面为工字形的立柱受力如图所示。
试求此力向截面形心C平移的结果。
解:r =(-50, 125, 0)mm F =(0, 0, -100)kN F 向C 平移,得 FR =(0, 0, -100)kN1000000.1250.05-)(-=⨯==kj i F r F M M C C=(-12.5, -5, 0)kN ·m6.(10分)图示芯轴AB 与轴套CD 的轴线重合,二者在B 、C 处连成一体;在D 处无接触。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第8章 剪应力分析

2.确定梁内横截面上的最大拉应力和最大压应力;
3.确定梁内横截面上的最大切应力;
4.画出横截面上的切应力流。
知识点:弯曲切应力公式的应用、切应力流
难度:难
解答:
1.图(a):
kN
, kN
剪力与弯矩图如图(b)、(c);
2.形心C位置
MPa
MPa
3. m3
MPa
4.切应力流如图(e)。
(A)下移且绕点O转动;
(B)下移且绕点C转动;
(C)下移且绕z轴转动;
(D)下移且绕 轴转动。
知识点:弯曲中心、薄壁截面梁产生平面弯曲的加载条件
难度:一般
解答:
正确答案是D。
8-19试判断下列图示的切应力流方向哪一个是正确的。
知识点:横向弯曲时梁横截面上的切应力流、弯曲切应力分析方法
难度:难
解答:
(A)细长梁、横截面保持平面;
(B)弯曲正应力公式成立,切应力沿截面宽度均匀分布;
(C)切应力沿截面宽度均匀分布,横截面保持平面;
(D)弹性范围加载,横截面保持平面。
知识点:弯曲时梁横截面上切应力分析
难度:易
解答:
正确答案是B。
公式 推导时应用了局部截面的正应力合成的轴力,该正应力 则要求弯曲正应力公式成立;另外推导时在 时,应用了 沿截面宽度均匀分布假设。
难度:难
解答:
正确答案是D。
8-21简支梁受力与截面尺寸如图所示。试求N-N截面上a、b两点的铅垂方向的切应力以及腹板与翼缘交界处点c的水平切应力。
知识点:弯曲切应力公式的应用、切应力流
难度:难
解答:
FQ = 120kN,形心C位置。
工程材料力学性能 第三版课后题答案(束德林)

工程材料力学性能课后题答案第三版(束德林)第一章单向静拉伸力学性能1、解释下列名词。
(1)弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
(2)滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
(3)循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
(4)包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
(5)解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
(6)塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指材料在外力作用下(如拉伸、冲击等)仅产生很小的变形即断裂破坏的性质。
韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
(7)解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
(8)河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
(9)解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
(10)穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
(11)韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变。
2、说明下列力学性能指标的意义。
答:(1)E(G)分别为拉伸杨氏模量和切边模量,统称为弹性模量表示产生100%弹性变所需的应力。
σ规定残余伸长应力,试样卸除拉伸力后,其标距部分的残余伸长达到规定的原始标距百分比时的应力。
(2)rσ名义屈服强度(点),对没有明显屈服阶段的塑性材料通常以产生0.2%的塑性形变对应的应力作为屈2.0服强度或屈服极限。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第3章 力系的平衡
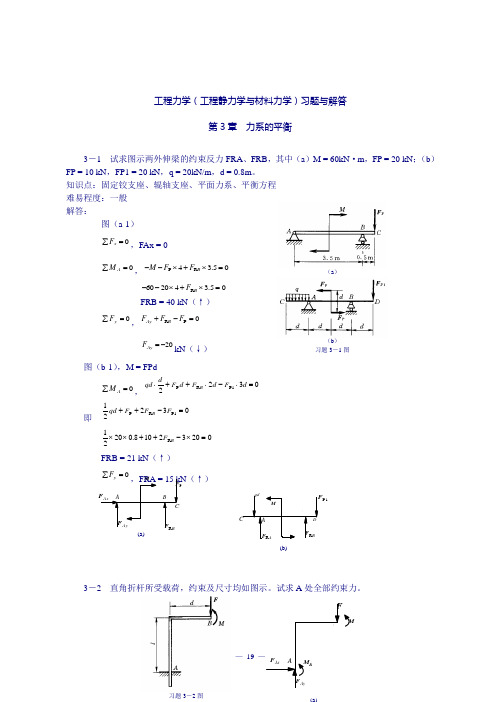
工程力学(工程静力学与材料力学)习题与解答第3章 力系的平衡3-1 试求图示两外伸梁的约束反力FRA 、FRB ,其中(a )M = 60kN ·m ,FP = 20 kN ;(b )FP = 10 kN ,FP1 = 20 kN ,q = 20kN/m ,d = 0.8m 。
知识点:固定铰支座、辊轴支座、平面力系、平衡方程 难易程度:一般 解答:图(a-1) 0=∑x F ,FAx = 00=∑A M ,05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN (↑)=∑y F ,0P R =-+F F F B Ay20-=Ay F kN (↓)图(b-1),M = FPd 0=∑A M ,03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN (↑)=∑y F ,FRA = 15 kN (↑)3-2 直角折杆所受载荷,约束及尺寸均如图示。
试求A 处全部约束力。
A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)(a )(b ) 习题3-1图FMB习题3-3图sF W A F ABF BF AN F(a)知识点:固定端约束、平面力系、平衡方程 难易程度:一般 解答: 图(a ): 0=∑x F ,0=Ax F=∑y F ,=Ay F (↑)0=∑A M ,0=-+Fd M M AM Fd M A -=3-3 图示拖车重W = 20kN ,汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时,车轮A 、B 对地面的正压力。
知识点:固定端约束、平面力系、平衡方程 难易程度:一般解答: 图(a ):0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ,4.6NA =F kN3-4 图示起重机ABC 具有铅垂转动轴AB ,起重机重W = 3.5kN ,重心在D 。
工程材料力学性能 第三版课后题答案(束德林)

工程材料力学性能课后题答案第三版(束德林)第一章单向静拉伸力学性能1、解释下列名词。
(1)弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
(2)滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
(3)循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
(4)包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
(5)解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
(6)塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指材料在外力作用下(如拉伸、冲击等)仅产生很小的变形即断裂破坏的性质。
韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
(7)解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
(8)河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
(9)解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
(10)穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
(11)韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变。
2、说明下列力学性能指标的意义。
答:(1)E(G)分别为拉伸杨氏模量和切边模量,统称为弹性模量表示产生100%弹性变所需的应力。
σ规定残余伸长应力,试样卸除拉伸力后,其标距部分的残余伸长达到规定的原始标距百分比时的应力。
(2)rσ名义屈服强度(点),对没有明显屈服阶段的塑性材料通常以产生0.2%的塑性形变对应的应力作为屈2.0服强度或屈服极限。
刘鸿文材料力学第三版指导与例题习题解答答

刘鸿文材料力学第三版指导与例题习题解答答案1. 概述本文是对《刘鸿文材料力学第三版》一书中的指导与例题习题解答的总结和归纳。
本书是一本材料力学的经典教材,对于材料力学的基本概念和理论有着全面的介绍和解释。
本文将以Markdown文本格式为基础,给出每个章节的指导和例题习题的解答。
2. 引论2.1 材料力学的基本概念材料力学是研究固体材料在力学作用下的变形和破坏规律的学科。
材料力学的基本概念包括应力、应变、弹性、塑性等。
这些基本概念是理解材料力学的关键。
2.1.1 应力与应变应力和应变是材料力学中最基本的概念。
应力是指单位面积上的力,常用符号为σ;应变是单位长度的变形量,常用符号为ε。
2.1.2 弹性与塑性弹性是指材料在受力后能够恢复原来形状和大小的能力;塑性是指材料在受力后会发生永久性变形的能力。
2.2 材料力学的基本原理材料力学的基本原理包括平衡条件、变形规律和破坏准则。
平衡条件是指材料在受力作用下保持力学平衡的条件;变形规律是指材料在受力作用下发生变形的规律;破坏准则是指材料在受力作用下发生破坏的条件。
2.2.1 平衡条件材料在受力作用下保持力学平衡的条件可以通过平衡方程来描述。
平衡方程包括力的平衡方程和力矩的平衡方程。
2.2.2 变形规律材料在受力作用下发生变形的规律可以通过应力-应变关系来描述。
常见的应力-应变关系有胡克定律和牛顿黏弹性模型。
2.2.3 破坏准则材料在受力作用下发生破坏的条件可以通过破坏准则来描述。
破坏准则可以根据材料的性质和应用场景来确定。
3. 第一章:张力、剪力和弯矩3.1 基本概念和基本公式3.1.1 张力、剪力和弯矩的定义张力是指作用在某个材料上的两个相邻截面之间的力;剪力是指作用在某个材料上的两个相邻截面之间的切力;弯矩是指作用在某个材料上的两个相邻截面之间的力矩。
3.1.2 张力、剪力和弯矩的计算公式张力的计算公式为T = F/A,其中T为张力,F为作用在材料上的力,A为材料的横截面积。
材料力学-单祖辉-第三版课后答案-(第九章—第十九章)

σr2 σ1 μ(σ2 σ3)[σ] 将上述各主应力值代入上式,得
σr2 [100.25(42.7)] MPa20.7 MPa[σ] 可见,该铸铁构件满足强度要求。
9-12 图示圆球形薄壁容器,其内径为 D,壁厚为 ,承受压强为 p 之内压。试证明
r3 2 4 2 154.52 414.962 MPa 157.4MPa [ ] b 点处的正应力和切应力分别为
3
σ
M yb Iz
7.80104 (0.140 0.0137)N 7.07105 m2
1.393108
Pa 139.3
MPa
τ
FS S z ( b ) Izδ
130103 2.23104 N 7.07105 0.0085m2
(α1
α2
)ΔT
FN1 E1 A1
FN2 E2 A2
σ1t E1
σ2t E2
(d)
由式(a)可知,
σ1t
A1
σ2t
A2,
σ1t σ2t
A2 A1
δ2 δ1
即
σ1t
δ2 δ1
σ2t
(e)
将方程(e)与方程(d)联立求解,得铜环和钢环内的周向正应力依次为
σ1t
(α1 α2 )E1E2δ2 E1δ1 E2δ2
4.82107
Pa 48.2
MPa
该点也处于单向与纯剪切组合应力状态,其相当应力为
r3 139.32 448.22 MPa169.4MPa[ ] c 点处于纯剪切应力状态,其切应力为
τ
FS S z ,max Izδ
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第9章 应力状态分析

解答:
正确答案是D。
四个应力状态的主应力, 、 、 ;其主力方向虽不全相同,但应变比能与主应力值有关,因此它们的应变比能相同。
9-30关于图示应力状态,有如下论述,试选择哪一种是正确的。
(A)最大主应力为500MPa,最小主应力为100MPa;
(B)最大主应力为500MPa,最大切应力为250MPa;
工程力学(工程静力学与材料力学)习题与解答
第9章 应力状态分析
9-1木制构件中的微元受力如图所示,其中所示的角度为木纹方向与铅垂方向的夹角。试求:
1.面内平行于木纹方向的切应力;
2.垂直于木纹方向的正应力。
知识点:平面应力状态、任意方向面上的应力分析
难度:易
解答:
(a)平行于木纹方向切应力
MPa
垂直于木纹方向正应力
知识点:广义胡克定律、压力容器应力分析
难度:一般
解答:
MPa
MPa
MPa
9-21液压缸及柱形活塞的纵剖面如图所示。缸体材料为钢,E = 205GPa, = 0.30。试求当内压p=10MPa时,液压缸内径的改变量。
知识点:广义胡克定律、压力容器应力分析
难度:难
解答:
缸体上
MPa
MPa
9-22试证明对于一般应力状态,若应力应变关系保持线性,则应变比能
知识点:应力状态的基本概念
难度:一般
解答:
正确答案是B。
MPa
MPa
,为单向应力状态。
9-28试分析图示的四个应力状态是否等价,有下列四种答案。
(A)四者均等价;
(B)仅(a)和(b)等价;
(C)仅(b)、(c)等价;
(D)仅(a)和(c)等价。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第9章 应力状态分析

MPa
MPa
2.
MPa
MPa
9-13图示外径为300mm的钢管由厚度为8mm的钢带沿20°角的螺旋线卷曲焊接而成。试求下列情形下,焊缝上沿焊缝方向的切应力和垂直于焊缝方向的正应力。
1.只承受轴向载荷FP = 250kN;
2.只承受内压p=5.0MPa(两端封闭)
3.同时承受轴向载荷FP = 250kN和内压p=5.0MPa(两端封闭)
难度:一般
解答:
(1)当 = 40℃
mm<
mm<
所以铝板内无温度应力,
(2)当 = 80℃
mm>
mm>
∴ (1)
(2)
所以解得qx = qy=70MPa(压)
, MPa
MPa
9-18对于一般平面应力状态,已知材料的弹性常数E、 ,且由实验测得 和 。试证明:
知识点:广义胡克定律、 三者之间的关系
难度:一般
难度:一般
解答:
正确答案是C。
(A)不满足切应力互等定律;
(B)不满足平衡;
(C)既可满足切应力互等,又能达到双向的平衡;
(D)不满足两个方向的平衡。
9-27微元受力如图所示,图中应力单位为MPa。试根据不为零主应力的数目,它是:
(A)二向应力状态;
(B)单向应力状态;
(C)三向应力状态;
(D)纯切应力状态。
MPa
9-7受力物体中某一点处的应力状态如图所示(图中p为单位面积上的力)。试求该点处的主应力。
知识点:应力圆的应用
难度:难
解答:
应力圆半径
9-8从构件中取出的微元,受力如图所示。试:
1.求主应力和最大切应力;
2.确定主平面和最大切应力作用面位置。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第6章 杆件的内力分析
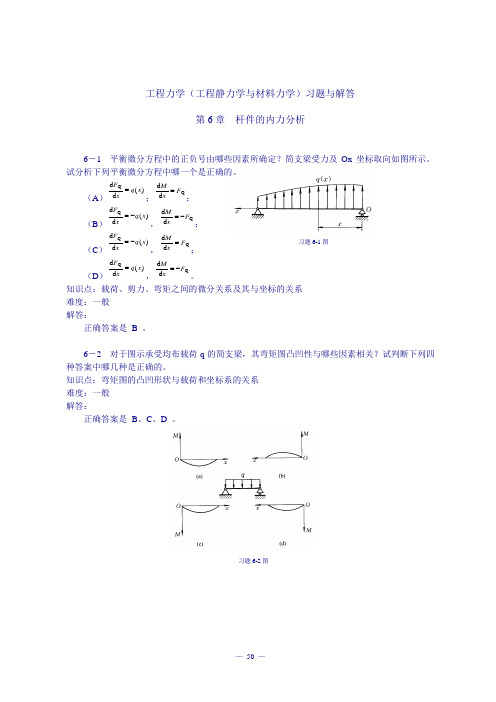
(↑)
弯距图如图示,其中 |
M
|max
ql
2
。
6-13 试作图示刚架的弯矩图,并确定 | M |max 。
习题 6-13 图
1
1
2
1 2
A
B1
Fx 0 , FAx ql
MA 0
ql
l 2
ql 2
FRB
l
0
— 58 —
FRB
3 2
ql
Fy
0 , FAy
3 2
ql 2
(↑)
弯距图如图示,其中 | M |max ql 2 。
D
B
C
1
1
1.5
M (ql2)
A
M (ql2)
D
BC
10.75
D
B
C
1
25
2
32
知识点:梁的剪力图与弯矩图 难度:一般 解答:
Fy 0 , FRA ql (↑)
M A 0 , M A ql 2
MD
0,
ql 2
ql l
ql
l 2
MD
0
MD
3 2
ql 2
| FQ |max ql
|
M
| max
M (x) 1 q x 0 2 4ql x l 2
2ql x 3l 4ql x 5l
(5l x 6l)
M (x) 1 q x 0 2 4ql x l 2
即
2ql x 3l 4ql x 5l
(0 x 6l)
2.弯矩图如图(a); 3.载荷图如图(b); 4.梁的支承为 B、D 处简支(图 b)。
Fx 0 , px FNx 0
《工程力学(工程静力学与材料力学)(第3版)》考试试卷(附答案)(2)

工程力学考试答卷(2)1.(5分)拉压杆件轴向变形公式N F ll EA ∆=的应用条件是:等截面直杆、弹性范围内加载;等截面直杆、弹性范围内加载、力的作用线通过截面形心;等截面直杆、弹性范围内加载、力的作用线通过截面形心沿着杆的轴线; 等截面直杆、力的作用线通过截面形心沿着杆的轴线。
2.(5分)对于建立材料在一般应力状态下的失效判据与设计准则,试选择如下合适的论述。
(A )逐一进行试验,确定极限应力;(B )无需进行试验,只需关于失效原因的假说; (C )需要进行某些试验,无需关于失效原因的假说;(D )假设失效的共同原因,根据简单试验结果。
3.(5分)图示四梁中FP ,、l 、W 、[]σ均相同,不考虑轴力影响。
试判断关于它们强度高低的下述结论中哪一个是正确的。
正确答案是 C 。
正确答案 D(A)强度:图a=图b=图c=图d;(B)强度:图a>图b>图c>图d;(C)强度:图b>图a>图c>图d;正确答案是B。
(D)强度:图b>图a>图d>图c。
4.(5分)提高钢制大柔度压杆承载能力有如下方法.试判断哪一种是最正确的。
(A)减小杆长,减小长度系数,使压杆沿横截面两形心主轴方向的柔度相等;(B)增加横截面面积,减小杆长;(C)增加惯性矩,减小杆长;正确答案是A。
(D)采用高强度钢。
sF WAF ABF BF AN F(a)5.(10分)图示拖车重W = 20kN ,汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时,车轮A 、B 对地面的正压力。
图(a ):0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN0=∑y F ,4.6NA =F kN6.(10分)画出图示梁的剪力图和弯矩图,并确定 max Q ||F 和max||M 。
AB(ql2lFQF 511ADEC B2M 2M M231M2ql=∑A M ,lM F B 2R =(↑)0=∑y F ,lM F A 2R =(↓)lM F 2||max Q =qm8kN ⋅B(a)z(d)M M 2||max =7.(25分)梁的受力及横截面尺寸如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章轴向拉压应力与材料的力学性能2-1试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图,并指出轴力的最大值。
图a与b所示分布载荷均沿杆轴均匀分布,集度为q。
题2-2图(a)解:由图2-2a(1)可知,=2()F-xqxqaN轴力图如图2-2a(2)所示,qa F 2m ax ,N =图2-2a(b)解:由图2-2b(2)可知, qa F =R qa F x F ==R 1N )(22R 2N 2)()(qx qa a x q F x F -=--=轴力图如图2-2b(2)所示,qa F =m ax N,图2-2b2-3 图示轴向受拉等截面杆,横截面面积A =500mm 2,载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题2-3图解:该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N 10508263=⨯=⨯⨯==-A F σ 斜截面m -m 的方位角, 50-=α故有MPa 3.41)50(cos MPa 100cos 22=-⋅== ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα杆内的最大正应力与最大切应力分别为MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
题2-5解:由题图可以近似确定所求各量。
220GPa Pa 102200.001Pa10220ΔΔ96=⨯=⨯≈=εσEMPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
2-7 一圆截面杆,材料的应力-应变曲线如题2-6图所示。
若杆径d =10mm ,杆长l =200mm ,杆端承受轴向拉力F = 20kN 作用,试计算拉力作用时与卸去后杆的轴向变形。
题2-6图解: 255MPa Pa 1055.2m0.010πN102048223=⨯=⨯⨯⨯==A F σ 查上述εσ-曲线,知此时的轴向应变为 %39.00039.0==ε 轴向变形为mm 780m 108700390m)2000(Δ4....l εl =⨯=⨯==-拉力卸去后,有00364.0e =ε, 00026.0p =ε故残留轴向变形为0.052mm m 105.2000260(0.200m)Δ5p =⨯=⨯==-.l εl2-9 图示含圆孔板件,承受轴向载荷F 作用。
已知载荷F =32kN ,板宽b =100mm ,板厚=δ15mm ,孔径d =20mm 。
试求板件横截面上的最大拉应力(考虑应力集中)。
题2-9图解:根据2.0m)100.0m/(020.0/==b d查应力集中因数曲线,得42.2≈K根据 δd b Fσ)(n -=, n max σσK =得64.5MPa Pa 1045.60.015m0.020)(0.100N103242.2)(723n max =⨯⨯⨯⨯=-===-δd b KF K σσ 2-10 图示板件,承受轴向载荷F 作用。
已知载荷F =36kN ,板宽b 1=90mm ,b 2=60mm ,板厚δ=10mm ,孔径d =10mm ,圆角半径R =12mm 。
试求板件横截面上的最大拉应力(考虑应力集中)。
题2-10图解:1.在圆孔处根据111100.090mm 010.01.b d == 查圆孔应力集中因数曲线,得 6.21≈K故有117MPa Pa 1017.1m010.0)010.0090.0(N 10366.2)(82311n 1max 1=⨯=⨯⨯⨯===--δd b F K σK σ 2.在圆角处根据1.50.060mm 090.021===b b d D 2.00.060mm 012.02===b R d R 查圆角应力集中因数曲线,得 74.12≈K故有104MPa Pa 1004.10.010m 0.060N 103674.182322n 2max 2=⨯=⨯⨯⨯===δb F K σK σ 3. 结论MPa 117max =σ(在圆孔边缘处)2-14图示桁架,承受铅垂载荷F 作用。
设各杆的横截面面积均为A ,许用应力均为[σ],试确定载荷F 的许用值[F ]。
题2-14图解:先后以节点C 与B 为研究对象,求得各杆的轴力分别为 F F 2N1=F F F ==N3N2根据强度条件,要求 ][2σ≤AF由此得2][][AF σ=2-15 图示桁架,承受载荷F 作用,已知杆的许用应力为[σ]。
若在节点B 和C 的位置保持不变的条件下,试确定使结构重量最轻的α值(即确定节点A 的最佳位置)。
题2-15图解:1.求各杆轴力设杆AB 和BC 的轴力分别为N1F 和N2F ,由节点B 的平衡条件求得αF F αF F ctan sin N2N1==, 2.求重量最轻的α值由强度条件得ασFA σF A ctan ][ ]sin [21==,α结构的总体积为)ctan sin22(][ctan ][cos ]sin [2211αασFl ασFl αl ασF l A l A V +=+⋅=+=由0d d =αV得01cos 32=-α由此得使结构体积最小或重量最轻的α值为4454opt '= α2-16 图示桁架,承受载荷F 作用,已知杆的许用应力为[σ]。
若节点A 和C 间的指定距离为 l ,为使结构重量最轻,试确定θ的最佳值。
题2-16图解:1.求各杆轴力由于结构及受载左右对称,故有θFF F sin 2N2N1== 2.求θ的最佳值 由强度条件可得θσFA A ]sin [221==结构总体积为θσFlθl θσF l A V ]sin2[cos 2]sin [211=⋅== 由 0d d =θV得0cos2=θ由此得θ的最佳值为45opt =θ2-17图示杆件,承受轴向载荷F 作用。
已知许用应力[σ]=120MPa ,许用切应力[τ]=90MPa ,许用挤压应力[σbs ]=240MPa ,试从强度方面考虑,建立杆径d 、墩头直径D 及其高度h 间的合理比值。
题2-17图解:根据杆件拉伸、挤压与剪切强度,得载荷F 的许用值分别为 ][4π][2t σd F =(a) ][4)(π][bs 22b σd D F -=(b)][π][s τdh F =(c)理想的情况下,s b t ][][][F F F ==在上述条件下,由式(a )与(c )以及式(a )与(b ),分别得d h ][4][τσ=d D bs][][1σσ+= 于是得 1:][4][:][][1::bs τσσσ+=d h D 由此得1:333.0:225.1::=d h D2-18 图示摇臂,承受载荷F 1与F 2作用。
已知载荷F 1=50kN ,F 2=35.4kN ,许用切应力[τ]=100MPa ,许用挤压应力][bs σ=240MPa 。
试确定轴销B 的直径d 。
题2-18图解:1. 求轴销处的支反力由平衡方程0=∑x F 与0=∑y F ,分别得 kN 25cos4521=-= F F F BxkN 25sin452== F F By由此得轴销处的总支反力为kN 435kN 252522.F B =+=2.确定轴销的直径由轴销的剪切强度条件(这里是双面剪)][π22s τd F A F τB≤==得m 0150m 10100104.352][263.τF d B =⨯⨯⨯⨯=≥ππ 由轴销的挤压强度条件][bs b bs σd F d F σB≤==δδ 得m 014750m 102400100104.35][63bs ..σδF d B =⨯⨯⨯=≥结论:取轴销直径15m m m 015.0=≥d 。
2-19图示木榫接头,承受轴向载荷F = 50 kN 作用,试求接头的剪切与挤压应力。
题2-19图解:剪应力与挤压应力分别为MPa 5)m 100.0)(m 100.0(N10503=⨯=τMPa 5.12)m 100.0)(m 040.0(N10503bs =⨯=σ2-20图示铆接接头,铆钉与板件的材料相同,许用应力[σ] =160MPa ,许用切应力[τ] = 120 MPa ,许用挤压应力[σbs ] = 340 MPa ,载荷F = 230 kN 。
试校核接头的强度。
题2-20图解:最大拉应力为MPa 3.153)m )(010.0)(020.0170.0(N1023023max =-⨯=σ 最大挤压与剪切应力则分别为MPa 2300.010m)5(0.020m)(N102303bs =⨯=σMPa 4.146π(0.020m)5N 10230423=⨯⨯⨯=τ2-21 图示两根矩形截面木杆,用两块钢板连接在一起,承受轴向载荷F = 45kN 作用。
已知木杆的截面宽度b =250mm ,沿木纹方向的许用拉应力[σ]=6MPa ,许用挤压应力][bs σ=10MPa ,许用切应力[τ]=1MPa 。
试确定钢板的尺寸δ与l 以及木杆的高度h 。
题2-21图解:由拉伸强度条件 ][)2(σδh b Fσ≤-=得0.030m m 10625001045][263=⨯⨯⨯=≥-.σb F δh(a )由挤压强度条件][2bs bs σb δFσ≤=得mm 9m 0090m 1010250.021045][263bs ==⨯⨯⨯⨯=≥.σb F δ (b )由剪切强度条件 ][2τblFτ≤=得mm 90m 0900m 101250.021045][263==⨯⨯⨯⨯=≥.b F l τ 取m 009.0=δ代入式(a ),得 48mm m 0480m )009.02030.0(==⨯+≥.h 结论:取m m 9≥δ,m m 90≥l ,m m 48≥h 。
2-22 图示接头,承受轴向载荷F 作用。
已知铆钉直径d =20mm ,许用应力[σ]=160MPa ,许用切应力[τ]=120MPa ,许用挤压应力][bs σ=340MPa 。
板件与铆钉的材料相同。
试计算接头的许用载荷。
题2-22图解:1.考虑板件的拉伸强度 由图2-22所示之轴力图可知,4/3 N2N1F F F F ==,][)(1N11σδd b FA F σ≤-==432kN N 104.32N 10160015.0)02002000(][)(56=⨯=⨯⨯⨯=-≤.-.σδd b F][)2(432N22σδd b FA F σ≤-==512kN N 105.12N 10160015.0)040.0200.0(34][)2(3456=⨯=⨯⨯⨯-=-≤σδd b F图2-222.考虑铆钉的剪切强度 8s F F =][π842s τdF A F τ≤==302kN N 1002.3N 101200200π2][π25622=⨯=⨯⨯⨯⨯=≤.τd F3.考虑铆钉的挤压强度][ 4 4bs b bs b σδδσ≤===d F d F F FkN 408N 1008.4N 103400.0200.0154][456bs =⨯=⨯⨯⨯⨯=≤σd F δ结论:比较以上四个F 值,得kN 302][=F2-23 图a 所示钢带AB ,用三个直径与材料均相同的铆钉与接头相连接,钢带承受轴向载荷F 作用。
