遗 传 算 法 详 解 ( 含 M A T L A B 代 码 )
遗传算法遗传算法

(5)遗传算法在解空间进行高效启发式搜索,而非盲 目地穷举或完全随机搜索;
(6)遗传算法对于待寻优的函数基本无限制,它既不 要求函数连续,也不要求函数可微,既可以是数学解 析式所表示的显函数,又可以是映射矩阵甚至是神经 网络的隐函数,因而应用范围较广;
(7)遗传算法具有并行计算的特点,因而可通过大规 模并行计算来提高计算速度,适合大规模复杂问题的 优化。
26
(4)基本遗传算法的运行参数 有下述4个运行参数需要提前设定:
M:群体大小,即群体中所含个体的数量,一般取为 20~100; G:遗传算法的终止进化代数,一般取为100~500; Pc:交叉概率,一般取为0.4~0.99;
Pm:变异概率,一般取为0.0001~0.1。
27
10.4.2 遗传算法的应用步骤
遗传算法简称GA(Genetic Algorithms)是1962年 由美国Michigan大学的Holland教授提出的模拟自然 界遗传机制和生物进化论而成的一种并行随机搜索最 优化方法。
遗传算法是以达尔文的自然选择学说为基础发展起 来的。自然选择学说包括以下三个方面:
1
(1)遗传:这是生物的普遍特征,亲代把生物信息交 给子代,子代总是和亲代具有相同或相似的性状。生 物有了这个特征,物种才能稳定存在。
18
(3)生产调度问题 在很多情况下,采用建立数学模型的方法难以对生
产调度问题进行精确求解。在现实生产中多采用一些 经验进行调度。遗传算法是解决复杂调度问题的有效 工具,在单件生产车间调度、流水线生产车间调度、 生产规划、任务分配等方面遗传算法都得到了有效的 应用。
19
(4)自动控制。 在自动控制领域中有很多与优化相关的问题需要求
10
《基本遗传算法》

(2) 解码
假设某一个体的编码是:
x: bl bl-1 bl-2……b2b1
则对应的解码公式为:
x = umin + (
1
i=l
bi
·2i-1
)
·Umax umin 2l 1
整理ppt
[例] 设 -3.0 ≤ x ≤ 12.1 , 精度要求 =1/10000,由公式: = Umax umin
M——群体大小; F——个体适应度评价函数; s——选择操作算于; c——交叉操作算子: m——变异操作算于; pc——交叉概率; pm——变异概率;
整理ppt
1.3 基本遗传算法描述
Procedure GA
Begin initialize P(0); t=0; while (t<=T) do for i=1 to M do Evaluate fitness of P(t); end for for i=1 to M do Select operation to P(t); end for for i=1 to M/2 do Crossover operation to P(t); end for for i=1 to M do Mutation operation to P(t); end for for i=1 to M do P(t+1) = P(t); end for t=t+1 end while
从而产生出一个新的个体。
基本位变异运算的示例如下所示:
基本位变异
A:1010 1 01010
A’:1010 0 01010
变异点
整理ppt
变异概率
变异是针对个体的某一个或某一些基因座上的基因值执行的,因此变异概率pm 也是针对基因而言,即:
神经网络与遗传算法

10.4 遗传算法
1975年美国Michigan大学J.Holland教授提出。 美国人De.Jong博士将遗传算法应用于函数优化 Goldberg成了遗传算法的框架。
10.4.1遗传算法基本原理
选择适应值高的染色体进行复制,通过 遗传算子:选择、交叉(重组)、变异,来 产生一群新的更适应环境的染色体,形成新 的种群。
遗传算法利用适应值信息,而不需要导数或其它辅助信 息。
遗传算法用适应值评估个体,用遗传算子产生更优后代 ,不需要像神经网络中用梯度公式引导。
隐含并行性:
遗传算法是对N个位串个体进行运算,它隐含 了大量的模式(用通配符#包含的个体)
遗传机器学习
10.5基于遗传算法的分类学习系统
我们研制的遗传分类学习系统GCLS是一种字符串规则 (分类器)的学习系统。
1
总和∑ 平均值 最大值
1754
1.00 4.00
4.0
439
0.25 1.00 1.0
729
0.42 1.66 2.0
选择后的交配 池(下划线部 分交叉)
11001 11011 11011 10000
交叉对象
(随机选 择)
交叉位置
(随机选择 )
新的种群
2
1
11011
1
1
11001
4
3
11000
3
遗传算法是进行群体的搜索。 它对多个个体进行群体搜索,构成一个不断进
化的群体序列,它能找到全局最优解(优于爬 山法)
遗传算法是一种随机搜索方法,三个算子都是 随机操作,利用概率转移规则。
遗传算法的处理对象是问题参变量进行编码的个体,而 不是参变量自身。
参变量编码成位串个体,通过遗传算子进行操作。不是 对参数变量进行直接操作。
遗传算法基础

比例选择法(轮盘赌)
• 基本思想
各个个体被选中的概率与其适应度大小成正比。 设群体大小为 M,个体 i 的适应度大小为F ( xi ) ,则 个体 i 被选中的概率为
Pi =
F ( xi )
∑ F (x )
i =1 i
M
比例选择法(轮盘赌)
• 具体步骤 1)计算各基因适应度值和选择概率 Pi 2)累计所有基因选择概率值,记录中间累 加值S - mid 和最后累加值 sum = ∑ Pi 3)产生一个随机数 N,0〈 N 〈 1 4)选择对应中间累加值S - mid 的基因进 入交换集 5)重复(3)和(4),直到获得足够的基 因。
t i
t i i
n
模式定理
• 选择算子的作用
f (H , t) m( H , t + 1) = m( H , t ) f (t )
若 若
f (H , t) >1,m(H,t)增加 f (t ) f ( H , t ) <1,m(H,t)减少 f (t )
在选择算子的作用下,对于平均适用度高于群体平 在选择算子的作用下, 均适应度的模式,其样本数将增长, 均适应度的模式,其样本数将增长,对于平均适用 度低于群体平均适应度的模式, 度低于群体平均适应度的模式,其样本数将减少
f ( x) f ( x) f ( x) f ( x) f ( x) f ( x)
F(x)
F(x)
F(x)
F(x)=f(x)+C
遗传算法基本要素与实现技术
• 选择算子 • 适应度较高的个体被遗传到下一代群体中 的概率较大,适应度较低的个体被遗传到 下一代群体中的概率较小。 • 选择方法 比例选择法(轮盘赌) 锦标赛选择法
遗传算法

缺点:该算法只是对每个落点进行单独的考虑,没有反应不同组 合所产生的共同效果,所以只是近似的算法,不能获得最优的结果。 基于单个的优化不能保证在整体情况下能获得最大值。 如果对所有的可能方案进行评价,找到最佳方案。例如在N*N的
栅格空间中确定n个 目标的最佳位置,则所要对比的组合高达
2.遗传算法和GIS结合解决空间优化问题
所谓交叉运算,是指对两个相互配对的染色体依据
交叉概率 Pc 按某种方式相互交换其部分基因,从而形 成两个新的个体。
交叉前: 00000|011100000000|10000 11100|000001111110|00101 交叉后: 00000|000001111110|10000 11100|011100000000|00101 染色体交叉是以一定的概率发生的,这个概率记为Pc
行一点或多点交叉的操作,但这样很容易产生断路或环路。针对路径 的具体需要,这里采用只允许在除首、尾结点之外的第一个重复结点位
置交叉且只进行一点交叉的操作方式。例如:设从起始结点1到目标结
点9的一对父代个体分别是G1和G2,分别如下表示: G1(1,3,5,6,7,8,9)
G2(1,2,4,5,8,9)
是一种有效的解最优化问题的方法。 其基本思想是:首先随机产生种群,对种群中的被选中染色体进行交
叉或变异运算生成后代,根据适值选择部分后代,淘汰部分后代,但种群
大小不变。经过若干代遗传之后,算法收敛于最好的染色体,可能是问题 的最优解或次优解。
适应度函数
遗传算法对一个个体(解)的好坏用适应度函数
值来评价,适应度函数值越大,解的质量越好。适应 度函数是遗传算法进化过程的驱动力,也是进行自然
篇论文。此后Holland教授指导学生完成了多篇有关遗传算法研究的论
遗 传 算 法 详 解 ( 含 M A T L A B 代 码 )

遗传算法入门(上)代码中的进化学说与遗传学说写在之前算法所属领域遗传算法的思想解析为什么要用遗传算法?科研现状应用现状遗传算法入门系列文章:(中篇)遗传算法入门(中)实例,求解一元函数最值(MATLAB版)(下篇)遗传算法入门(下)实例,求解TSP问题(C++版)写在之前说明:本想着用大量篇幅写一篇“关于遗传算法的基本原理”作为本系列入门的第一篇,但是在找寻资料的过程中,看到网络上有大量的关于遗传算法的介绍,觉得写的都挺好,所以本文我就简单写点自己的理解。
推荐几篇关于遗传算法的介绍性文章:遗传算法详解(GA)(个人觉得很形象,很适合初学者)算法所属领域相信每个人学习一门知识之前,都会想知道这门知识属于哪一门学科范畴,属于哪一类技术领域?首先对于这种问题,GA是没有绝对的归属的。
算法的定义是解决问题的一种思想和指导理论。
而遗传算法也是解决某一问题的一种思想,用某一编程语言实现这种思想的程序具有很多特点,其中一个便是智能性和进化性,即,不需要大量的人为干涉,程序本身能够根据一定的条件自我筛选,最终得出令人满意的结果。
所以按照这种特性,把它列为人工智能领域下的学习门类毫无疑问是可以的。
遗传算法的思想是借鉴了达尔文的进化学说和孟德尔的遗传学说,把遗传算法说成是一门十足的仿生学一点都不过分。
然而从应用的角度出发,遗传算法是求最优解问题的好方法,如信号处理中的优化、数学求解问题、工业控制参数最优解、神经网络中的激活函数、图像处理等等,所以把遗传算法说成优化范畴貌似也说的过去。
为了方便理解,我们可以暂时将其定位为人工智能–智能优化,这也是很多书中描述遗传算法的惯用词汇。
遗传算法的思想解析遗传算法(gentic algorithms简称GA)是模拟生物遗传和进化的全局优化搜索算法我们知道,在人类的演化中,达尔文的进化学说与孟德尔的遗传学说起着至关重要的理论指导。
每个人作为一个个体组成一个人类种群,正是经历着物竞天择,才会让整个群体慢慢变的更好,即更加适应周围的环境。
2遗传算法介绍

对控制参数的改进
Srinvivas等人提出自适应遗传算法,即PC和Pm 能够随适应度自动改变,当种群的各个个体适应度 趋于一致或趋于局部最优时,使二者增加,而当种 群适应度比较分散时,使二者减小,同时对适应值 高于群体平均适应值的个体,采用较低的PC和Pm, 使性能优良的个体进入下一代,而低于平均适应值 的个体,采用较高的PC和Pm,使性能较差的个体被 淘汰。
对遗传算子的改进
排序选择 均匀交叉 逆序变异
(1) 随机产生一个与个体编码长度 相同的二进制屏蔽字P = W1W2„Wn ; (2) 按下列规则从A、B两个父代个 体中产生两个新个体X、Y:若Wi = 0, 则X的第i个基因继承A的对应基因,Y 的第i个基因继承B的对应基因;若Wi = 1,则A、B的第i个基因相互交换,从 而生成X、Y的第i个基因。
模式阶用来反映不同模式间确定性的 差异,模式阶数越高,模式的确定性就越高,
所匹配的样本数就越少。在遗传操作中,即
使阶数相同的模式,也会有不同的性质,而
模式的定义距就反映了这种性质的差异。
模式定理
模式定理:具有低阶、短定义距以及平 均适应度高于种群平均适应度的模式在子代
中呈指数增长。
模式定理保证了较优的模式(遗传算法
的质量越好。适应度函数是遗传算法进化过
程的驱动力,也是进行自然选择的唯一标准,
它的设计应结合求解问题本身的要求而定。
选择算子
遗传算法使用选择运算来实现对群体中的个体 进行优胜劣汰操作:适应度高的个体被遗传到下一
代群体中的概率大;适应度低的个体,被遗传到下
一代群体中的概率小。选择操作的任务就是按某种 方法从父代群体中选取一些个体,遗传到下一代群
遗传算法应用于组合优化
遗传算法的基本原理和方法

遗传算法的基本原理和⽅法遗传算法的基本原理和⽅法⼀、编码编码:把⼀个问题的可⾏解从其解空间转换到遗传算法的搜索空间的转换⽅法。
解码(译码):遗传算法解空间向问题空间的转换。
⼆进制编码的缺点是汉明悬崖(Hamming Cliff),就是在某些相邻整数的⼆进制代码之间有很⼤的汉明距离,使得遗传算法的交叉和突变都难以跨越。
格雷码(Gray Code):在相邻整数之间汉明距离都为1。
(较好)有意义的积⽊块编码规则:所定编码应当易于⽣成与所求问题相关的短距和低阶的积⽊块;最⼩字符集编码规则,所定编码应采⽤最⼩字符集以使问题得到⾃然的表⽰或描述。
⼆进制编码⽐⼗进制编码搜索能⼒强,但不能保持群体稳定性。
动态参数编码(Dynamic Paremeter Coding):为了得到很⾼的精度,让遗传算法从很粗糙的精度开始收敛,当遗传算法找到⼀个区域后,就将搜索现在在这个区域,重新编码,重新启动,重复这⼀过程,直到达到要求的精度为⽌。
编码⽅法:1、⼆进制编码⽅法缺点:存在着连续函数离散化时的映射误差。
不能直接反映出所求问题的本⾝结构特征,不便于开发针对问题的专门知识的遗传运算算⼦,很难满⾜积⽊块编码原则2、格雷码编码:连续的两个整数所对应的编码之间仅仅只有⼀个码位是不同的,其余码位都相同。
3、浮点数编码⽅法:个体的每个基因值⽤某⼀范围内的某个浮点数来表⽰,个体的编码长度等于其决策变量的位数。
4、各参数级联编码:对含有多个变量的个体进⾏编码的⽅法。
通常将各个参数分别以某种编码⽅法进⾏编码,然后再将他们的编码按照⼀定顺序连接在⼀起就组成了表⽰全部参数的个体编码。
5、多参数交叉编码:将各个参数中起主要作⽤的码位集中在⼀起,这样它们就不易于被遗传算⼦破坏掉。
评估编码的三个规范:完备性、健全性、⾮冗余性。
⼆、选择遗传算法中的选择操作就是⽤来确定如何从⽗代群体中按某种⽅法选取那些个体遗传到下⼀代群体中的⼀种遗传运算,⽤来确定重组或交叉个体,以及被选个体将产⽣多少个⼦代个体。
遗传算法

x为0,1:二进制编码 x为整数:二进制/十进制编码 x为实数:二进制/十进制/实数编码
编码原则:
完备性。问题空间中所有点(侯 选解)都能用遗传算法空间中的 点(染色体)表现; 健全性。遗传算法空间中的染色 体都能对应问题空间中的所有侯 选解; 非冗余性。染色体和侯选解一一 对应。
W z
1 遗传算法的概念
若干 1.0 0.0 最优 执行变异操作获得 个体 4 个体 子代一个新个体
10011
0.144
0.144
个体被选取的概率
Psi f i /
f
j 1
N
0.309
i=i+1
j
i 1,2, , N
i=i+1
适应值的比例变换法
期望值法(个体不多时) 排位次法(个体适应度相近时)
W z
c 0.691 0.055 y 个体3 01000 0.636 基因干预
i=i+1
4.确定指定结果的方法和停止 运行准则
W z
交互
②
1 遗传算法的概念
染色体编码 y=f(x), x∈(x-, x+)
染色体编码,生成初始种群 遗传代数:NEra=0 计算每个个体的适应度 y 收敛否 ? n 进行选择、 杂 交 pc 、 变 异 pm 和 保 留 等遗传操作,生成 新一代种群 NEra=NEra+1 解码 输出结果
n
y 变异前 A1=11001 变异后 基因干预 A’1=11011
人机 交互
②
1 遗传算法的概念
①
遗传操作——保留
使得遗传算法能以概率 1收敛到全局最优解。
对种群进行简单的选择 ( 复制 ) 、杂交和变异操作 是遗传算法的精髓! 停止运行准则
遗传算法详解

1.1.1 基本遗传学基础
遗传算法是根据生物进化的模型提出的一种优化算法。 自然选择学说是进化论的中心内容,根据进化论,生物的 发展进化主要有三个原因,即遗传、变异和选择。
遗传是指子代总是和亲代相似。遗传性是一切生物所共有的 特性,它使得生物能够把其特性、性状传给后代。遗传是生物进 化的基础。
第五页,编辑于星期一:十五点 十七分。
④ 遗传算法的寻优规则是由概率决定的,而非确 定性的。 ⑤ 遗传算法在解空间进行高效启发式搜索,而非盲 目地穷举或完全随机搜索。 ⑥ 遗传算法对所求解的优化问题没有太多的数学 要求。
⑦ 遗传算法具有并行计算的特点,因而可通过大规模并 行计算来提高计算速度。
第六页,编辑于星期一:十五点 十七分。
表6-3列出了交叉操作之后的结果数据,从中可以看出交叉操作的具体过 程。首先,随机配对匹配集中的个体,将位串1、2配对,位串3、4配对;然后, 随机选取交叉点,设位串1、2的交叉点为k=4,二者只交换最后一位,从而 生成两个新的位串,即
串串12:: 10
1 1
1 0
0 0
1 0
பைடு நூலகம்
0 1
1 1
1 0
0 0
A1=0110 | 1 A2=1100 | 0 交叉操作后产生了两个新的字符串为:
A1’=01100
A2’=11001
第十三页,编辑于星期一:十五点 十七分。
一般的交叉操作过程:
图1-2 交叉操作
遗传算法的有效性主要来自于复制和交叉操作。复制虽然能够从旧种群中选择 出优秀者,但不能创造新的个体;交叉模拟生物进化过程中的繁殖现象,通过 两个个体的交换组合,来创造新的优良个体。
遗传算法解释及代码(一看就懂)

遗传算法( GA , Genetic Algorithm ) ,也称进化算法。
遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。
因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识作为遗传算法生物背景的介绍,下面内容了解即可:种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ):包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。
适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。
那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。
这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取);首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。
这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。
遗传算法的研究与应用

研 究 与 开 发
圈圆圈画 圜国国
徐 清振 , 肖成林
(, 南师范 大学计 算机学 院 。 1华 广州 50 3 ; . 16 l 2 华南 理工 大学应用 数学 系 , 广州 504 ) 160
摘 要 : 据遗传 算法 的一 些基本概 念以度 遗传 算法的操 作 流程 , 遗传算 法的繁 殖算 子从数 学上给 出 根 对
体 的选 择 、 叉和变 异 , 中编码 是最重 要的环 节。 交 其
A筹 . 『’ 。 I = -2 n 1. …
唯一对 应着一个 实数 葺, 可按式 ( ) 2 计算 :
X=01 = l -(
,
( 1 】
现 代 () 2 计
于是对 任何 研 长 的 0 l 符 串 A = i -— l -字 b r b, n
设 ( l …, , [ 蜘, 12 … ,, x ,2 )鹭苣 日 = , 。 n 给 X, n 定 精度 为 8则取 m 是满 足式 () , 1 的最小整数 。
几位 的组 合称 为一个基 因 。 叉称染 色体 。然后 再对这
些染 色体 进行某 些操作 实现参数 寻优 。 遗传算 法 中的 基本概 念包括染 色体 的编码 、 数 、 应度 函数 、 色 参 适 染
维普资讯
研究与 开发
其 中 e A) ( 为一 实数 。
因此 , 编码 e 是一种有效的编码 , 但它不是正则
编码 .因为对 n 空 间里 的不 同 向量可 以对应着 相 同
的编 码 串 。
被选中的概率就越大 , 其子孙在下一代产生的个数就 越多。 选择 的方法 根据不 同的 问题 , 用不 同的方案 。 采 最常见的方法有比ቤተ መጻሕፍቲ ባይዱ法 、 排列法和比率排列法 。比侧
最全的遗传概率计算方法(高中生物)

全:遗传概率的计算方法(高中生物)概率是对某一可能发生事件的估计,是指总事件与特定事件的比例,其范围介于0和1之间。
相关概率计算方法介绍如下:一、某一事件出现的概率计算法例题1:杂合子(Aa)自交,求自交后代某一个体是杂合体的概率。
解析:对此问题首先必须明确该个体是已知表现型还是未知表现型。
(1)若该个体表现型为显性性状,它的基因型有两种可能:AA和Aa。
且比例为1∶2,所以它为杂合子的概率为2/3。
(2)若该个体为未知表现型,那么该个体基因型为AA、Aa和aa,且比例为1∶2∶1,因此它为杂合子的概率为1/2。
正确答案:2/3或1/2二、亲代的基因型在未肯定的情况下,其后代某一性状发生的概率计算法例题2:一对夫妇均正常,且他们的双亲也都正常,但双方都有一白化病的兄弟,求他们婚后生白化病孩子的概率是多少?解析:(1)首先确定该夫妇的基因型及其概率?由前面例题1的分析可推知该夫妇均为Aa的概率为2/3,AA的概率为1/3。
(2)假设该夫妇为Aa,后代患病的概率为1/4。
(3)最后将该夫妇均为Aa的概率(2/3×2/3)与假设该夫妇均为Aa情况下生白化病患者的概率1/4相乘,其乘积1/9,即为该夫妇后代中出现白化病患者的概率。
正确答案:1/9三、利用不完全数学归纳法例题3:自交系第一代基因型为Aa的玉米,自花传粉,逐代自交,到自交系第n代时,其杂合子的几率为。
解析:第一代 Aa 第二代 1AA 2Aa 1aa 杂合体几率为 1/2 第三代纯 1AA 2Aa 1aa 纯杂合体几率为(1/2)2 第n代杂合体几率为(1/2)n-1正确答案:杂合体几率为(1/2)n-1四、利用棋盘法例题4:人类多指基因(T)是正常指(t)的显性,白化基因(a)是正常(A)的隐性,都在常染色体上,而且都是独立遗传。
一个家庭中,父亲是多指,母亲正常,他们有一个白化病和正常指的的孩子,则生下一个孩子只患有一种病和患有两种病以及患病的概率分别是()A.1/2、1/8、5/8B.3/4、1/4、5/8C.1/4、1/4、1/2D.1/4,1/8,1/2解析:据题意分析,先推导出双亲的基因型为TtAa(父),ttAa(母)。
TSP、MTSP问题遗传算法详细解读及python实现

TSP、MTSP问题遗传算法详细解读及python实现写在前⾯遗传算法是⼀种求解NPC问题的启发式算法,属于仿⽣进化算法族的⼀员。
仿⽣进化算法是受⽣物⾏为启发⽽发明的智能优化算法,往往是⼈们发现某种⽣物的个体虽然⾏为较为简单,但⽣物集群通过某种原理却能表现出智能⾏为。
于是不同的⼈研究不同的⽣物⾏为原理,受到启发⽽发明出新的仿⽣进化算法。
⽐如免疫优化算法,蚁群算法,模拟退⽕算法等,这些算法以后也会简单介绍。
本⽂的主题是遗传算法,该算法也是受到⽣物⾏为启发。
物竞天择,适者⽣存,优胜劣汰,是该优化算法的核⼼思想。
笔者在业务中需要⽤到遗传算法求解TSP问题,但是⽹上能查找到的资料对遗传算法的讲解不够通俗易懂,往往上来就是遗传变异交叉,对于我这样的初学者来说有点不知所云,于是不得不直接看源码,⼀⾏⼀⾏地理解代码的意思,才弄懂了原理。
这种⽅法对于初学者和编程基础薄弱者颇为困难,⽽且费时费⼒,苦不堪⾔。
同时,由于读者可能熟练掌握的是不同的语⾔,因此若代码是某⼀种语⾔编写的,那么掌握其他语⾔的读者很可能难以吸收,浪费了资源。
此外,⽹上关于TSP问题的资料很多,但是关于MTSP问题的资料却凤⽑麟⾓。
因此有了创作本⽂的意图,旨在⽤最通俗详尽的语⾔深⼊浅出地解释遗传算法解TSP、MTSP问题的原理及应⽤遗传算法解TSP问题原理⼀、TSP问题旅⾏商问题,即TSP问题(Traveling Salesman Problem)⼜译为旅⾏推销员问题、货郎担问题,是数学领域中著名问题之⼀。
假设有⼀个旅⾏商⼈要拜访n个城市,他必须选择所要⾛的路径,路径的限制是每个城市只能拜访⼀次,⽽且最后要回到原来出发的城市。
路径的选择⽬标是要求得的路径路程为所有路径之中的最⼩值。
想要求解出TSP问题的最优解,⽬前唯⼀的⽅法是穷举出所有的路径。
然⽽,路径的数量级是n!,也就是⽬标点数量的阶乘。
当n为14时,n!已经⼤于800亿。
当n更⼤,为30,40 时,更是天⽂数字,即使计算机⼀秒钟计算⼀亿次,其求解时间也远⼤于我们的寿命。
一个公式搞定遗传计算

掌握该方法可以大大缩短做遗传题的时间。
但一定要对哈代--温伯格公式有清楚的认识,才能用这个公式解题,否则反而会影响到你。
从例题和解析中感悟和总结,因为只要自己总结出来的东西才是自己的。
例如自由交配的实质就是配子自由交配等等。
基因频率有关的计算例析基因频率是指某群体中,某一等位基因在该位点上可能出现的基因总数中所占的比率。
对基因频率的计算有很多种类型,不同的类型要采用不同的方法计算。
一、哈代--温伯格公式(遗传平衡定律)的应用当种群较大,种群内个体间的交配是随机的,没有突变发生、新基因加入和自然选择时,存在以下公式:(p+q)2=p2+2pq+q2=1 ,其中p代表一个等位基因的频率,q代表另一个等位基因的频率,p2 代表一个等位基因纯合子(如AA)的频率,2pq代表杂合子(如Aa)的频率,q2代表另一个纯合子(aa)的频率。
例1:已知苯丙酮尿症是位于常染色体上的隐性遗传病。
据调查,该病的发病率大约为1/10000。
请问,在人群中苯丙酮尿症致病基因的基因频率以及携带此隐性基因的杂合基因型频率各是多少?解析:由于本题不知道具体基因型的个体数以及各种基因型频率,所以问题变得复杂化,此时可以考虑用哈代----温伯格公式。
由题意可知aa的频率为1/10000,计算得a的频率为1/100。
又A+a=1,所以A的频率为99/100,Aa的频率为2×(99/100)×(1/100)=99/5000。
答案:1/100,99/5000例2:在阿拉伯牵牛花的遗传实验中,用纯合体红色牵牛花和纯合体白色牵牛花杂交,F1全是粉红色牵牛花。
将F1自交后,F2中出现红色、粉红色和白色三种类型的牵牛花,比例为1:2:1,如果取F2中的粉红色的牵牛花与红色的牵牛花均匀混合种植,进行自由传粉,则后代表现性及比例应该为( )解析:按遗传平衡定律:假设红色牵牛花基因型为AA、粉红色牵牛花基因型为Aa,F2中红色、粉红色牵牛花的比例(AA:Aa)为1:2,即A的基因频率为2/3,a的基因频率为1/3,子代中AA占(2/3)×(2/3)=4/9,Aa占2((2/3)×(2/3)=4/9,aa占(1/3)×(1/3)=1/9答案: 红色:粉红色:白色=4:4:1二、几种计算类型(一).常染色体上的基因,已知各基因型的个体数,求基因频率。
(完整)基本遗传算法

基本遗传算法Holland创建的遗传算法是一种概率搜索算法,它利用某种编码技术作用于称为染色体的数串,其基本思想是模拟由这些串组成的个体进化过程.该算法通过有组织的、然而是随机的信息交换,重新组合那些适应性好的串.在每一代中,利用上一代串结构中适应性好的位和段来生成一个新的串的群体;作为额外增添,偶尔也要在串结构中尝试用新的位和段来替代原来的部分。
遗传算法是一类随机优化算法,它可以有效地利用已有的信息处理来搜索那些有希望改善解质量的串.类似于自然进化,遗传算法通过作用于染色体上的基因,寻找好的染色体来求解问题.与自然界相似,遗传算法对待求解问题本身一无所知,它所需要的仅是对算法所产生的每个染色体进行评价,并基于适应度值来改变染色体,使适应性好的染色体比适应性差的染色体有更多的繁殖机会.第一章遗传算法的运行过程遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象,从任一初始种群(Population)出发,通过随机选择、交叉和变异操作,产生一群更适应环境的个体,使群体进化到搜索空间中越来越好的区域,这样一代一代地不断繁衍进化,最后收敛到一群最适应环境的个体(Individual),求得问题的最优解。
一.完整的遗传算法运算流程完整的遗传算法运算流程可以用图1来描述。
由图1可以看出,使用上述三种遗传算子(选择算子、交叉算子和变异算子)的遗传算法的主要运算过程如下:(1)编码:解空间中的解数据x,作为遗传算法的表现形式。
从表现型到基因型的映射称为编码.遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合就构成了不同的点。
(2)初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。
遗传算法以这N个串结构作为初始点开始迭代。
设置进化代数计数器t←0;设置最大进化代数T;随机生成M个个体作为初始群体P(0)。
(3)适应度值评价检测:适应度函数表明个体或解的优劣性。
遗传算法简单易懂的例子

遗传算法简单实例为更好地理解遗传算法的运算过程,下面用手工计算来简单地模拟遗传算法的各个主要执行步骤。
例:求下述二元函数的最大值:(1) 个体编码遗传算法的运算对象是表示个体的符号串,所以必须把变量x1, x2 编码为一种符号串。
本题中,用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数,所以分别用3位无符号二进制整数来表示,将它们连接在一起所组成的6位无符号二进制数就形成了个体的基因型,表示一个可行解。
例如,基因型 X=101110 所对应的表现型是:x=[ 5,6 ]。
个体的表现型x和基因型X之间可通过编码和解码程序相互转换。
(2) 初始群体的产生遗传算法是对群体进行的进化操作,需要给其淮备一些表示起始搜索点的初始群体数据。
本例中,群体规模的大小取为4,即群体由4个个体组成,每个个体可通过随机方法产生。
如:011101,101011,011100,111001(3) 适应度汁算遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而决定其遗传机会的大小。
本例中,目标函数总取非负值,并且是以求函数最大值为优化目标,故可直接利用目标函数值作为个体的适应度。
(4) 选择运算选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。
一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。
本例中,我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。
其具体操作过程是:•先计算出群体中所有个体的适应度的总和fi ( i=1.2,…,M );•其次计算出每个个体的相对适应度的大小 fi / fi ,它即为每个个体被遗传到下一代群体中的概率,•每个概率值组成一个区域,全部概率值之和为1;•最后再产生一个0到1之间的随机数,依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数。
(5) 交叉运算交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某两个个体之间的部分染色体。
遗传算法

一、遗传算法的原理1.自然遗传与遗传算法①遗传:子代总是和亲代具有相同或相似的性状。
有了这个特征物种才能稳定存在②变异:亲代和子代之间已经子代不同个体之间的差异,称为变异,变异是随机发生的,变异的选择和积累是生命多样性的根源。
③生存斗争和逝者生存:具有适应性变异的个体被保留下来,不具有适应性变异的个体被淘汰,通过一代代的生存环境的选择作用,性状逐渐与祖先有所不同,演变成新的物种。
④自然界对进化中的生物群体提供及时的反馈信息,或称为外界对生物的评价,评价反映了生物的生存机会。
⑤生物进化是一个不断循环的过程,本质上是一种优化过程。
⑥遗传物质以基因的形式排列在染色体上,每个基因有特殊的位置并控制生物的某些特性。
不同的基因组合产生的个体对环境的适应性不一样。
(对应具体问题,把问题可能解编码成向量---染色体,向量的每个元素就是基因)例如:个体染色体9 ---- 1001(2,5,6)---- 010 101 1102.遗传算法①将“优胜劣汰,适者生存”的生物进化原理引入到求解优化问题中。
②从某一随机产生的初始群体出发③按照变异等遗传操作规则不断地迭代④根据每一个体的适应度,保留优良品种,引导搜索过程向最优解逼近。
⑤在这一过程中,通过随机重组编码位串中重要的基因,使新一代的位串集合优于老一代的位串集合,群体中的个体不断进化,逐渐接近最优解,最终达到求解问题的目的。
二、遗传算法的步骤1.步骤:①选择编码策略,把参数集合X和域转换成位串结构空间S;②定义适应函数f(X);③确定遗传策略,包括选择群体大小n,选择、交叉、变异方法,以及确定交叉概率、变异概率等遗传参数;④随机初始化生成群体P;⑤计算群体中个体位串解码后的适应值f(X)⑥按照遗传策略,运用选择(选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。
选择操作是建立在群体中个体的适应度评估基础上的)、交叉(所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。
1遗传算法基本流程图
产 ( H) : 表示 在t 代种群中 存在模式x 的 个 体数目 ;
4 .遗传操作
选择 ( s e l e c t i o n )、交叉 ( c r o s s o v e r )和变异 ( m u t a t i o n )是
遗传算法中的三种基本遗传操作。下面分别加以 介绍。 1 ) 选择操作
东北师范大学硕士学位论文
选择 ( s e l e c t i o n ) ,根据染色体对应的适应度值和问题的要求, 筛选种群中的染色体,染色体的适应度越高,保存下来的概率越大, 反之则越小,甚至被淘汰。选择操作通常选用适应度比例法 ( 轮盘赌 方式) ,它是以适应度的大小为比例进行遗传过程中的父体选择,适应 度越高的个体被选中的机率就越大。也就是处于优势的个体有更多的 繁衍机会。具体做法是:首先计算群体中各个体的适应度,得相应的
东北师范大学硕士学位论文
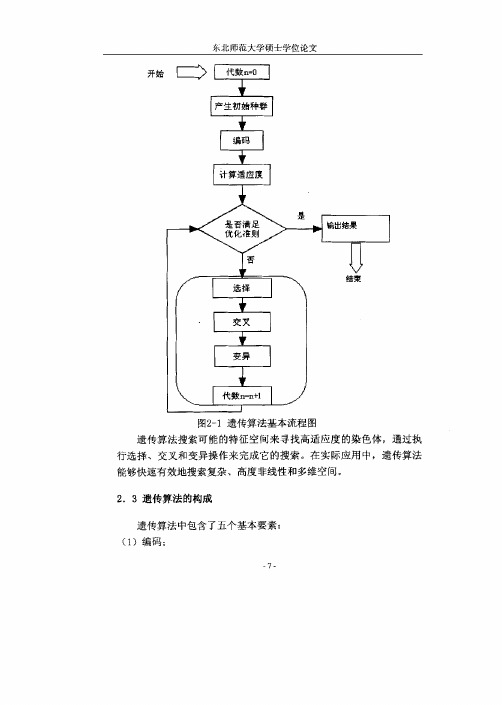
图2 - 1遗传算法基本流程图 遗传算法搜索可能的特征空间来寻找高适应度的染色体,通过执 行选择、交叉和变异操作来完成它的搜索。在实际应用中,遗传算法 能够快速有效地搜索复杂、高度非线性和多维空间。 2 .3遗传算法的构成 遗传算法中包含了五个基本要素: ( 1 ) 编码;
. 是否到了预定算法的最大代数;
东北师范大学硕士学位论文
是否找到某个较优的染色体; 连续几次迭代后得到的解群中最好解是否变化等。
:
2 .4遗传算法的基本理论 遗传算法作为一种复杂问题的智能算法,它的理论基础是— 模 式定理和积木假说。
2 . 4 . 1模式定理
定义 1( 模式) :基于三值字符集{ 0 . 1 ,* }所产生的能描述具有某 些结构相似的 0 . 1 字符串集的字符串称作模式。 定义 2( 模式阶) :模式 H中确定位置的个数称作该模式的模式阶
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
详解MATLAB在最优化计算中的应用(pdf版)第1章 MATLAB语言基础11.1 MATLAB简介11.1.1 MATLAB的产生与发展11.1.2 MATLAB语言的优势11.2 MATLAB入门21.2.1 MATLAB工作环境21.2.2 MATLAB中的数据类型81.2.3 MATLAB语言中的常量与变量111.2.4 MATLAB中的矩阵131.2.5 符号运算201.2.6 关系与逻辑运算221.3 MATLAB中的矩阵运算221.3.1 矩阵的代数运算221.3.2 矩阵的关系与逻辑运算251.3.3 矩阵分析251.4 MATLAB中的图形功能281.4.1 二维图形291.4.2 三维图形331.5 MATLAB工具箱的使用351.5.1 MATLAB工具箱的特点351.5.2 MATLAB工具箱的使用方法351.6 本章小结37第2章 MATLAB程序设计382.1 MATLAB程序设计方法382.1.1 MATLAB中的控制结构382.1.2 MATLAB中的M脚本文件和M函数文件46 2.1.3 MATLAB程序的调试532.2 MATLAB扩展编程552.2.1 调用MATLAB引擎562.3 本章小结73第3章最优化计算问题概论743.1 引言743.1.1 最优化问题的提出743.1.2 最优化理论和方法的产生与发展753.2 最优化问题的典型实例763.2.1 资-源利用问题763.2.2 分派问题773.2.3 投资决策问题793.2.4 多目标规划问题803.3 最优化问题的数学描述813.3.1 最优化问题三要素813.3.2 最优化问题分类823.4 最优化问题的解决方案833.5 本章小结84第4章线性规划854.1 引言854.2 线性规划问题的一般提法854.3 线性规划问题的标准型874.3.1 线性规划问题的一般标准型874.3.2 线性规划问题的矩阵标准型874.3.3 线性规划问题的向量标准型884.3.4 非标准型的标准化884.4 线性规划问题中解的概念894.4.1 基本解904.4.2 可行解、可行域914.4.3 基本可行解914.4.4 最优解914.4.5 实例914.5 线性规划问题的求解924.5.1 图形解法934.5.2 单纯形法944.5.3 人工变量单纯形法1024.6 线性规划问题的MATLAB求解方法107 4.6.1 线性规划问题的MATLAB标准型1074.6.2 线性规划问题求解的MATLAB函数调用108 4.7 线性规划实例1144.7.1 生产计划问题1154.7.2 连续投资问题1174.7.3 配料问题1194.7.4 运输问题1204.7.5 绝对值问题1224.8 本章小结124第5章整数规划1275.1 引言1275.2 整数规划的数学模型1275.2.1 典型的整数规划问题1275.2.2 整数规划问题的数学模型1315.3 整数规划的求解1315.3.1 理论基础1315.3.2 分枝定界法1325.3.3 隐枚举法1365.3.4 匈牙利算法1415.4 整数规划问题的MATLAB求解方法1455.4.1 用MATLAB求解一般混合整数规划问题145 5.4.2 用MATLAB求解0-1规划问题1505.4.3 已给出实例的MATLAB求解1535.5 整数规划的应用实例1575.5.1 计划排班问题1575.5.2 合理下料问题1595.5.3 生产计划问题1625.5.4 背包问题1665.6 本章小结168第6章非线性规划1716.1 引言1716.2 非线性规划问题的数学模型1716.2.1 典型的非线性规划问题1716.2.2 非线性规划问题的数学模型1736.3 理论基础1736.3.1 全局最优解和局部最优解1746.3.2 凸函数和凸规划1746.3.3 无约束非线性规划问题的极值条件1776.3.4 多维有约束非线性规划问题的极值条件179 6.4 非线性规划问题的求解1836.5 一维搜索1856.5.1 一维搜索的基本思想1856.5.2 试探法——黄金分割法1886.5.3 插值法——牛顿法1906.5.4 抛物线法1926.5.5 一维搜索的MATLAB求解1926.6 多维无约束非线性优化1966.6.1 最速下降法1966.6.2 牛顿法1986.6.3 共轭方向法2016.6.4 Powell算法2106.6.5 多维无约束优化的MATLAB求解函数fminunc213 6.6.6 多维无约束优化的MATLAB求解函数fminsearch223 6.7 多维约束非线性优化2266.7.1 拉格朗日乘子法2266.7.2 序列无约束极小化法2286.7.3 近似规划法2346.7.4 多维约束优化的MATLAB求解2366.8 综合实例2526.8.1 商品最优存储方法2536.8.2 产销量的最佳安排2566.9 本章小结258第7章二次规划2627.1 二次规划问题的数学模型2627.2 等式约束的二次规划问题2627.2.1 直接消去法2637.2.2 拉格朗日乘子法2647.3 有效集方法2667.4 Wolfe算法2707.5 Lemke算法2737.6 二次规划问题的MATLAB求解277 7.6.1 输入参数和输出参数2787.6.2 控制参数设置2787.6.3 命令详解2797.6.4 综合实例2817.7 本章小结284第8章多目标规划2868.1 多目标规划问题的数学模型286 8.2 多目标规划问题的解集和象集288 8.2.1 多目标规划的解集2888.2.2 多目标规划的象集2918.3 处理多目标规划的方法2928.3.1 约束法2928.3.2 评价函数法2938.3.3 功效系数法2978.3.4 多目标规划的MATLAB求解300 8.4 线性目标规划3068.4.1 线性目标规划的数学模型309 8.4.2 线性目标规划的求解方法3168.4.3 线性目标规划的MATLAB求解326 8.5 综合实例3338.6 本章小结337第9章图与网络优化3409.1 引言3409.2 基本概念3419.2.1 图的基本概念3419.2.2 树的基本概念3489.3 最短路径问题3539.3.1 两个指定顶点之间的最短路径353 9.3.2 任意两个顶点之间的最短路径356 9.3.3 最短路径问题的MATLAB求解359 9.4 网络最大流问题3639.4.1 基本概念与基本定理3639.4.2 最大流问题的求解3669.5 最小费用最大流3739.5.1 基本概念3739.5.2 最小费用最大流问题的求解374 9.5.3 最小费用最大流的MATLAB求解375 9.6 本章小结379第10章现代智能优化算法简介38210.1 引言38210.2 遗传算法38210.2.1 概述38310.2.2 基本要素38310.2.3 遗传算子38510.2.4 遗传算法的基本步骤38710.2.5 遗传算法的MATLAB实现39110.3 模拟退火算法39710.3.1 模拟退火算法的基本思想39710.3.2 模拟退火的算法步骤39710.3.3 模拟退火算法的参数控制问题400 10.3.4 模拟退火的MATLAB工具箱求解405 10.4 禁忌搜索40910.4.1 局部邻域搜索简介40910.4.2 禁忌搜索的基本原理41010.4.3 禁忌搜索的关键技术41110.4.4 禁忌搜索的MATLAB实现41410.5 本章小结419第11章综合案例42011.1 线性规划——农业改造问题42011.1.1 农业改造问题的建模42011.1.2 农业改造问题的求解42311.2 整数规划——组件配套问题42611.2.1 组件配套问题的建模42611.2.2 组件配套问题的求解42711.3 非线性规划——广告问题42811.3.1 广告问题的建模42911.3.2 广告问题的求解43211.4 多目标规划——投资问题43311.4.1 投资问题的建模43411.4.2 投资问题的求解43511.5 图与网络优化——通信网问题43711.5.1 通信网问题的建模43811.5.2 通信网问题的求解438mutFNs--变异函数表,如['boundaryMutationfunction y = simple_fitness(x)lower = boundarylist[index][0]本部分主要为了了解遗传算法的应用,选择一个复杂的二维函数来进行遗传算法优化,函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为:4.计算S2的增量df = f(S2) - f(S1),其中f(S1)为S1的代价函数。
P_test = NIR(temp(51:end),:)';citys = [randperm(100);randperm(100)]';print('有效进化代数:%s'%(obj_trace.shape[0]))error('Minimum population for running this function is 20');[N, m] = size(intermediate_chromosome);。
