2014-2015年黑龙江省绥化市三校联考高二上学期期中数学试卷及参考答案
黑龙江省绥化市三校2015届高三上学期期中联考英语试卷

黑龙江省绥化市三校2015届高三上学期期中联考英语试卷(时间:120分钟总分:150分Ⅰ卷交答题卡,Ⅱ卷交答题纸)第Ⅰ卷(共105分)第一部分:听力(共20个小题,每小题1.5分,共计30分)第一节听下面5段对话。
每段对话后有一个小题,从题中所给的ABC三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man mean?A. The film was interesting on the whole.B. He had never seen such a terrible film.C. The film wasn’t as good as he had expected.2. What color paper does the girl want?A. Red.B. Pink.C. Blue.3. What is the relationship between the speakers?A. Mother and son.B. Sister and brother.C. Teacher and student.4. How will the woman go home?A. Somebody will drive her home.B. Her father will pick her up.C. She will go back home on foot.5. What are the speakers talking about?A. The government.B. Their payment.C. A strike.第二节听下面5段对话或独白。
每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听每段对话或独白前, 你将有时间阅读各个小题, 每小题5秒钟; 听完后, 各小题将给出5秒钟的作答时间。
黑龙江省绥化市三校2015届高三上学期期中联考地理试卷
黑龙江省绥化市三校2015届高三上学期期中联考地理试卷考试说明:满分100分,考试时间90分钟。
(1)答题前,考生先将自己的条形码在答题卡上贴好;(2)请按照题号顺序在各题目的答题区域内作答,在草稿纸、试题上答题无效。
(3)保持卡面清洁,不得折叠,不要弄破、弄皱,不准使用涂改液、刮纸刀。
第Ⅰ卷(共60分)一、选择题:以下题目四个选项中只有一个正确。
每题2分,共30题,60分。
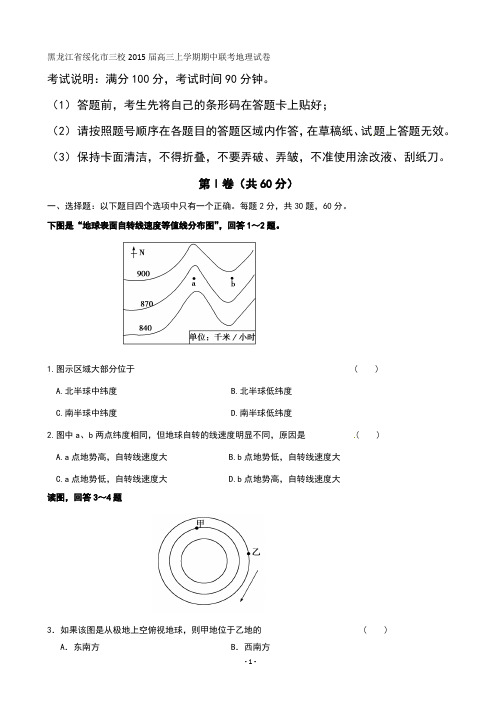
下图是“地球表面自转线速度等值线分布图”,回答1~21.图示区域大部分位于 ( )A.北半球中纬度B.北半球低纬度C.南半球中纬度D.南半球低纬度2.图中a、b两点纬度相同,但地球自转的线速度明显不同,原因是( )A.a点地势高,自转线速度大B.bC.a点地势低,自转线速度大D.b读图,回答3~4题3.如果该图是从极地上空俯视地球,则甲地位于乙地的 ( )A.东南方 B.西南方C.东北 D.西北方4.条件同上题,下列叙述正确的是 ( )A.自转线速度甲地大于乙地B.自转角速度甲地小于乙地C.甲、乙两地地方时相差11小时D.12月22日白昼时间甲地大于乙地根据我国日历显示的信息,回答5~6题。
5.立秋时,太阳直射点的经度为( )A.127°E B.131°E C.120° E D.135°E6.有关此时太阳直射点的位置及其移动方向的说法,正确的是 ( )A.太阳直射点位于赤道上并向南移动B.太阳直射点在赤道以南并向南移动C.太阳直射点在赤道以北并向南移动D.太阳直射点位于赤道上并向北移动7.地震发生时,当地在水中游泳的人会感到 ( ) A.只有前后、左右摇晃 B.只有上下颠簸C.先上下颠簸,后左右摇晃 D.先左右摇晃,后上下颠簸地震波在不同媒介中的传播速度是不同的,科学家们利用这一原理探究地球内部结构。
据此回答8~9题。
8.地震波在地球内部传播时,科学家们发现在距离地面大约2900千米深度处横波速度突然降为零,纵波速度也突然下降,这说明了 ( )A.地球内部存在着岩浆B.该深度上下层次的温度变化明显C.大陆地壳与大洋地壳的厚度不同D.该深度上下层次的物质组成存在很大差异9.人们在生产活动中还常利用地震波 ( )A.传递声音信号B.进行地质探矿C.调查农作物虫害情况D.测量山峰的高度云量是以一日内云遮蔽天空的百分比来表示。
2014-2015黑龙江省绥化市三校高三生物上学期期末联考试题

绥化市三校2015届高三上学期期末联考理科综合能力测试说明:本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
共300分。
考生注意:1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上。
考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
第II卷用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
3.考试结束,监考员将试题卷、答题卡一并收回。
可能用到的相对原子质量:H 1 C 12 O 16 Mg 24 S 32第I卷一、选择题:本卷共13小题。
每小题6分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
1.叶绿体和线粒体的相同点是①可利用光学显微镜观察②水作为生理功能的一种原料③均增大细胞器内的膜面积④可通过转录和翻译控制某些蛋白质的合成⑤产生的ATP可用于各种生命活动A.①②③⑤ B.①②③④ C.①②④⑤ D.②③④⑤2.将水稻培养在含有各种营养元素的培养液中,发现水稻吸收硅多,吸收钙少。
这说明A.水稻培养液中硅和钙的浓度不同B.水稻根细胞对于物质的输入和输出具有选择性C.水稻根细胞吸收硅的能力弱,吸收钙的能力强D.硅是小分子,钙是大分子3.下图是油菜种子在发育和萌发过程中,糖类和油脂的变化曲线。
下列分析错误的是A.干重相等的可溶性糖和油脂,所贮存的能量油脂多于糖B.种子发育过程中,由于可溶性糖更多地转变为油脂,种子需要的氮增加C.种子萌发时,油脂酶的活性很高D.种子萌发时,油脂转变为可溶性糖4.黄曲霉毒素是毒性极强的致癌物质。
有关研究发现它能引起细胞中的核糖体不断从内质网上脱落下来。
这一结果直接导致A.染色体被破坏 B.高尔基体被破坏C.中心体被破坏 D.分泌蛋白质的合成受到影响5.自身免疫病产生的原因是A.人体免疫系统对病原菌的免疫效应B.人体免疫系统对人体正常组织的免疫反应C.人体免疫系统对过敏原的反应D.自身免疫功能缺陷6.下列有关生态学观点的叙述,错误的是A.绿色植物的光合作用是生态系统中最基本的能量固定B.桑基鱼塘生态系统体现了物质循环和能量多级利用的原理C.生态系统的信息传递只发生在生物之间,不会发生在生物与无机环境之间D.生态系统的结构包括组成成分和营养结构第Ⅱ卷三、非选择题:包括必考题和选考题两部分。
高二上学期期中考试数学试卷含答案

高二级上学期期中考试题数学本试卷共8页,22小题,满分150分,考试时间120分钟。
第一部分选择题(共60分)一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知直线l 1:2x +my =2,l 2:m 2x +2y =1,且l 1⊥l 2,则m 的值为( )A .0B .-1C .0或1D .0或-12.若一个圆锥的轴截面是面积为1的等腰直角三角形,则该圆锥的侧面积为( )A.2π B .22π C .2πD .4π3.把正方形ABCD 沿对角线AC 折起,当以A ,B ,C ,D 四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成角的大小为( )A .90°B .60°C .45°D .30°4.若过点(2,1)的圆与两坐标轴都相切,则圆心到直线230x y --=的距离为( )A B C D 5.下列命题中,正确的是( )A .任意三点确定一个平面B .三条平行直线最多确定一个平面C .不同的两条直线均垂直于同一个平面,则这两条直线平行D .一个平面中的两条直线与另一个平面都平行,则这两个平面平行6.已知M (3,23),N (-1,23),F (1,0),则点M 到直线NF 的距离为( )A. 5 B .23 C . 22D .3 37.已知各顶点都在一个球面上的正四棱柱(其底面是正方形,且侧棱垂直于底面)高为4,体积为16,则这个球的表面积是( )A .20πB .16πC .32πD .24π8.直线:20l x y ++=分别与x 轴、y 轴交于A 、B 两点,点P 在圆22(2)2x y -+=上, 则ABP △面积的取值范围是( ) A .[]26,B .[]48,C .D .⎡⎣二、多选题:本题共4小题,每小题5分,共20分.9.若220x x --<是2x a -<<的充分不必要条件,则实数a 的值可以是( ) A .1B .2C .3D .410.已知,αβ是两个不重合的平面,,m n 是两条不重合的直线,则下列命题正确的是( ) A .若//m n m α⊥,,则n α⊥ B .若//,m n ααβ⋂=,则//m n C .若m α⊥,m β⊥,则//αβ D .若,//,m m n n αβ⊥⊥,则//αβ 11.若直线过点(1,2)A ,且在两坐标轴上截距的绝对值相等,则直线l 方程可能为( ) A .10x y -+=B .30x y +-=C .20x y -=D .10x y --=12.已知四棱锥P ABCD -,底面ABCD 为矩形,侧面PCD ⊥平面ABCD ,BC =CD PC PD ===.若点M 为PC 的中点,则下列说法正确的为( )A .BM ⊥平面PCDB .//PA 面MBDC .四棱锥M ABCD -外接球的表面积为36π D .四棱锥M ABCD -的体积为6第二部分非选择题(90分)三、填空题:本题共4小题,每小题5分,共20分.13.命题“20210x x x ∃<-->,”的否定是______________.14.已知直线l 1的方程为23y x =-+,l 2的方程为42y x =-,直线l 与l 1平行且与l 2在y 轴上的截距相同,则直线l 的斜截式方程为________________.15.若直线:l y kx =与曲线:1M y =+有两个不同交点,则k 的取值范围是________________.16.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的体积为____________.四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知直线l 1的方程为x +2y -4=0,若l 2在x 轴上的截距为32,且l 1⊥l 2.(1)求直线l 1与l 2的交点坐标;(2)已知直线l 3经过l 1与l 2的交点,且在y 轴上的截距是在x 轴上的截距的2倍,求l 3的方程.18.(本小题满分12分)四棱锥P-ABCD 的底面ABCD 为直角梯形,AB ∥CD ,AB ⊥AD ,AB =12CD =1,P A ⊥平面ABCD ,P A =AD = 3.(1)求证:PD ⊥AB ;(2)求四棱锥P-ABCD 的体积.19.(本小题满分12分)已知圆C 的圆心坐标为(a ,0),且圆C 与y 轴相切. (1)已知a =1,M (4,4),点N 是圆C 上的任意一点,求|MN |的最小值;(2)已知a <0,直线l 的斜率为43,且与y 轴交于点20,3⎛⎫- ⎪⎝⎭.若直线l 与圆C 相离,求a 的取值范围.20.(本小题满分12分)在直三棱柱ABC-A 1B 1C 1中,AB =5,AC =3,BC =4,点D 是线段AB 上的动点.(1)当点D 是AB 的中点时,求证:AC 1∥平面B 1CD ;(2)线段AB 上是否存在点D ,使得平面ABB 1A 1⊥平面CDB 1?若存在,试求出AD 的长度;若不存在,请说明理由.21. (本小题满分12分) 如图,多面体ABCDEF 中,四边形ABCD 是菱形,060ABC ∠=,FA ⊥平面ABCD ,//,2 2.FA ED AB FA ED ===求二面角F BC A --的大小的正切值;求点E 到平面AFC 的距离;求直线FC 与平面ABF 所成的角的正弦值.22. (本小题满分12分)已知圆22+=9:O x y ,过点()0,2P -任作圆O 的两条相互垂直的弦AB 、CD ,设M 、N 分别是AB 、CD 的中点,(1)直线MN 是否过定点? 若过,求出该定点坐标,若不过,请说明理由; (2)求四边形ACBD 面积的最大值,并求出对应直线AB 、CD 的方程.高二级上学期期中考试题 数学答案及说明一、选择题:1.D ,2.A ,3.C ,4.B ,5.C ,6.B ,7.D ,8.A ,9.BCD ,10.ACD ,11.ABC ,12.BC.二、填空题:13.0x ∀<,2210x x --≤;14.y =-2x -2;15.13,24⎡⎫⎪⎢⎣⎭;16.36π.题目及详细解答过程:一、单选题(本题共8小题,每小题5分,共40分)1.已知直线l 1:2x +my =2,l 2:m 2x +2y =1,且l 1⊥l 2,则m 的值为( ) A .0 B .-1 C .0或1 D .0或-1 解析:因为l 1⊥l 2,所以2m 2+2m =0,解得m =0或m =-1. 答案:D2.若一个圆锥的轴截面是面积为1的等腰直角三角形,则该圆锥的侧面积为( ) A.2π B .22π C .2π D .4π 解析:设底面圆的半径为r ,高为h ,母线长为l ,由题可知,r =h =22l ,则12(2r )2=1,r =1,l =2.所以圆锥的侧面积为πrl =2π. 答案:A3.把正方形ABCD 沿对角线AC 折起,当以A ,B ,C ,D 四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成角的大小为( )A .90°B .60°C .45°D .30°解析:当三棱锥D ABC 体积最大时,平面DAC ⊥平面ABC .取AC 的中点O ,则∠DBO 即为直线BD 和平面ABC 所成的角.易知△DOB 是等腰直角三角形,故∠DBO =45°.答案:C4.若过点(2,1)的圆与两坐标轴都相切,则圆心到直线230x y --=的距离为( )A B C D 【答案】B【解析】由于圆上的点()2,1在第一象限,若圆心不在第一象限, 则圆与至少与一条坐标轴相交,不合乎题意,所以圆心必在第一象限, 设圆心的坐标为(),a a ,则圆的半径为a ,圆的标准方程为()()222x a y a a -+-=.由题意可得()()22221a a a -+-=,可得2650a a -+=,解得1a =或5a =,所以圆心的坐标为()1,1或()5,5,圆心到直线的距离均为121132555d ⨯--==; 圆心到直线的距离均为22553255d ⨯--== 圆心到直线230x y --=的距离均为22555d -==; 所以,圆心到直线230x y --=25. 故选:B .5.下列命题中,正确的是( ) A .任意三点确定一个平面 B .三条平行直线最多确定一个平面C .不同的两条直线均垂直于同一个平面,则这两条直线平行D .一个平面中的两条直线与另一个平面都平行,则这两个平面平行 解析:由线面垂直的性质,易知C 正确. 答案:C6.已知M (3,23),N (-1,23),F (1,0),则点M 到直线NF 的距离为( ) A. 5 B .23 C . 22D .3 3解析:易知NF 的斜率k =-3,故NF 的方程为y =-3(x -1),即3x +y -3=0. 所以M 到NF 的距离为|33+23-3|(3)2+12=2 3. 答案:B7.已知各顶点都在一个球面上的正四棱柱(其底面是正方形,且侧棱垂直于底面)高为4,体积为16,则这个球的表面积是( )A .20πB .16πC .32πD .24π解析:由题意知正四棱柱的底面积为4,所以正四棱柱的底面边长为2,正四棱柱的底面对角线长为22,正四棱柱的对角线为2 6.而球的直径等于正四棱柱的对角线,即2R =2 6.所以R = 6.所以S 球=4πR 2=24π. 答案:D8.直线:20l x y ++=分别与x 轴、y 轴交于A 、B 两点,点P 在圆22(2)2x y -+=上,则ABP △面积的取值范围是( ) A .[]26,B .[]48,C .232⎡⎤⎣⎦,D .2232⎡⎤⎣⎦,【答案】A 【解析】直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,()()2,0,0,2A B ∴--,则22AB =.点P 在圆22(2)2x y -+=上,∴圆心为(2,0),则圆心到直线的距离1202222d ++==.故点P 到直线20x y ++=的距离2d 的范围为2,32⎡⎤⎣⎦,则[]22122,62ABP S AB d d ==∈△.故答案为A.二、多选题(每题5分,共20分)9.若220x x --<是2x a -<<的充分不必要条件,则实数a 的值可以是( ) A .1B .2C .3D .4【答案】BCD【解析】:由220x x --<,解得12x -<<.又220x x --<是2x a -<<的充分不必要条件,(1∴-,2)(2-,)a ,则2a .∴实数a 的值可以是2,3,4.故选:BCD .10.已知,αβ是两个不重合的平面,,m n 是两条不重合的直线,则下列命题正确的是( ) A .若//m n m α⊥,,则n α⊥ B .若//,m n ααβ⋂=,则//m n C .若m α⊥,m β⊥,则//αβ D .若,//,m m n n αβ⊥⊥,则//αβ 【答案】ACD 【解析】若m α⊥,则,a b α∃⊂且a b P =使得m a ⊥,m b ⊥,又//m n ,则n a ⊥,n b ⊥,由线面垂直的判定定理得n α⊥,故A 对; 若//m α,n αβ=,如图,设m AB =,平面1111D C B A 为平面α,//m α,设平面11ADD A 为平面β,11A D n αβ⋂==,则m n ⊥,故B 错;垂直于同一条直线的两个平面平行,故C 对;若,//m m n α⊥,则n α⊥,又n β⊥,则//αβ,故D 对; 故选:ACD .11.若直线过点(1,2)A ,且在两坐标轴上截距的绝对值相等,则直线l 方程可能为( ) A .10x y -+= B .30x y +-= C .20x y -= D .10x y --=【答案】ABC【解析】:当直线经过原点时,斜率为20210k -==-,所求的直线方程为2y x =,即20x y -=; 当直线不过原点时,设所求的直线方程为x y k ±=,把点(1,2)A 代入可得12k -=,或12k +=,求得1k =-,或3k =,故所求的直线方程为10x y -+=,或30x y +-=; 综上知,所求的直线方程为20x y -=、10x y -+=,或30x y +-=. 故选:ABC .12.已知四棱锥P ABCD -,底面ABCD 为矩形,侧面PCD ⊥平面ABCD ,23BC =,26CD PC PD ===.若点M 为PC 的中点,则下列说法正确的为( )A .BM ⊥平面PCDB .//PA 面MBDC .四棱锥M ABCD -外接球的表面积为36π D .四棱锥M ABCD -的体积为6 【答案】BC【解析】作图在四棱锥P ABCD -中:为矩形,由题:侧面PCD ⊥平面ABCD ,交线为CD ,底面ABCDBC CD ⊥,则BC ⊥平面PCD ,过点B 只能作一条直线与已知平面垂直,所以选项A错误;连接AC 交BD 于O ,连接MO ,PAC ∆中,OM ∥PA ,MO ⊆面MBD ,PA ⊄面MBD ,所以//PA 面MBD ,所以选项B 正确;四棱锥M ABCD -的体积是四棱锥P ABCD -的体积的一半,取CD 中点N ,连接PN ,PN CD ⊥,则PN平面ABCD ,32PN =,四棱锥M ABCD -的体积112326321223M ABCD V -=⨯⨯⨯⨯=所以选项D 错误.矩形ABCD 中,易得6,3,3AC OC ON ===,PCD 中求得:16,2NM PC ==在Rt MNO 中223MO ON MN =+=即: OM OA OB OC OD ====,所以O 为四棱锥M ABCD -外接球的球心,半径为3, 所以其体积为36π,所以选项C 正确, 故选:BC三、填空题(每题5分,共20分)13.命题“20210x x x ∃<-->,”的否定是______. 【答案】0x ∀<,2210x x --≤【解析】因为特称命题的否定是全称命题,所以,命题20210x x x ∃<-->,, 则该命题的否定是:0x ∀<,2210x x --≤ 故答案为:0x ∀<,2210x x --≤.14.已知直线l 1的方程为23y x =-+,l 2的方程为42y x =-,直线l 与l 1平行且与l 2在y 轴上的截距相同,则直线l 的斜截式方程为________________.解析:由斜截式方程知直线l 1的斜率k 1=-2,又l ∥l 1,所以l 的斜率k =k 1=-2.由题意知l 2在y 轴上的截距为-2,所以l 在y 轴上的截距b =-2.由斜截式方程可得直线l 的方程为y =-2x -2.答案:y =-2x -215.若直线:l y kx =与曲线()2:113M y x =+--有两个不同交点,则k 的取值范围是________________.解析:曲线M :y =1+1-(x -3)2是以(3,1)为圆心,1为半径的,且在直线y =1上方的半圆.要使直线l 与曲线M 有两个不同交点,则直线l 在如图所示的两条直线之间转动,即当直线l 与曲线M 相切时,k 取得最大值34;当直线l 过点(2,1)时,k 取最小值12.故k 的取值范围是13,24⎡⎫⎪⎢⎣⎭. 答案:13,24⎡⎫⎪⎢⎣⎭16.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的体积为____________.解析:如图,连接OA ,OB .由SA =AC ,SB =BC ,SC 为球O 的直径,知OA ⊥SC ,OB ⊥SC .又由平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,知OA ⊥平面SCB . 设球O 的半径为r ,则OA =OB =r ,SC =2r ,所以三棱锥S ABC 的体积为311323r V SC OB OA ⎛⎫=⨯⋅⋅= ⎪⎝⎭,即r 33=9.所以r =3.所以3344336.33=O V r πππ=⨯=球答案:36π四、解答题(每题5分,共70分)17.(本小题满分10分)已知直线l 1的方程为x +2y -4=0,若l 2在x 轴上的截距为32,且l 1⊥l 2.(1)求直线l 1与l 2的交点坐标;(2)已知直线l 3经过l 1与l 2的交点,且在y 轴上的截距是在x 轴上的截距的2倍,求l 3的方程. 解:(1)设l 2的方程为2x -y +m =0,..........1分因为l 2在x 轴上的截距为32,所以3-0+m =0,m =-3,即l 2:2x -y -3=0.....3分联立⎩⎪⎨⎪⎧x +2y -4=0,2x -y -3=0,得⎩⎪⎨⎪⎧x =2,y =1.所以直线l 1与l 2的交点坐标为(2,1)...........5分 (2)当l 3过原点时,l 3的方程为y =12x ..........6分当l 3不过原点时,设l 3的方程为12x y a a +=...........7分 又直线l 3经过l 1与l 2的交点,所以2112a a+=, 得52a =,l 3的方程为2x +y -5=0...........8分 综上,l 3的方程为y =12x 或2x +y -5=0...........10分18.(本小题满分12分)四棱锥P-ABCD 的底面ABCD 为直角梯形,AB ∥CD ,AB ⊥AD ,AB =12CD =1,PA ⊥平面ABCD ,PA =AD = 3.(1)求证:PD ⊥AB ;(2)求四棱锥P-ABCD 的体积.18.解:(1)证明:因为PA ⊥平面ABCD ,AB ⊂平面ABCD ,所以PA ⊥AB ,..........1分又因为AB ⊥AD ,AD ∩PA =A ,..........3分 所以AB ⊥平面PAD ,..........4分又PD ⊂平面PAD ,..........5分所以AB ⊥PD ...........6分 (2)解:S 梯形ABCD =12(AB +CD )·AD =332,.......8分又PA ⊥平面ABCD ,..........9分所以V 四棱锥P-ABCD =13×S 梯形ABCD ·PA =13×332×3=32...........12分19.(本小题满分12分)已知圆C 的圆心坐标为(a ,0),且圆C 与y 轴相切. (1)已知a =1,M (4,4),点N 是圆C 上的任意一点,求|MN |的最小值; (2)已知a <0,直线l 的斜率为43,且与y 轴交于点20,3⎛⎫- ⎪⎝⎭.若直线l与圆C 相离,求a 的取值范围.19.解:(1)由题意可知,圆C 的方程为(x -1)2+y 2=1...........2分又|MC |=(4-1)2+(4-0)2=5,..........4分 所以|MN |的最小值为5-1=4...........5分(2)因为直线l 的斜率为43,且与y 轴相交于点20,3⎛⎫- ⎪⎝⎭,所以直线l 的方程为y =43x -23.即4x -3y -2=0..........7分因为直线l 与圆C 相离,所以圆心C (a ,0)到直线l 的距离d >r . 则224243a a ->+.........9分又0a <,所以245a a ->-,解得2a >-..........11分 所以a 的取值范围是(-2,0)..........12分20.(本小题满分12分)在直三棱柱ABC-A 1B 1C 1中,AB =5,AC =3,BC =4,点D 是线段AB 上的动点. (1)当点D 是AB 的中点时,求证:AC 1∥平面B 1CD ;(2)线段AB 上是否存在点D ,使得平面ABB 1A 1⊥平面CDB 1?若存在,试求出AD 的长度;若不存在,请说明理由.20.解:(1)证明:如图,连接BC 1,交B 1C 于点E ,连接DE ,则点E 是BC 1的中点,又点D 是AB 的中点,由中位线定理得DE ∥AC 1,.........1分 因为DE ⊂平面B 1CD ,.........2分AC 1⊄平面B 1CD ,.........3分所以AC 1∥平面B 1CD ..........4分(2)解:当CD ⊥AB 时,平面ABB 1A 1⊥平面CDB 1........5分 证明:因为AA 1⊥平面ABC ,CD ⊂平面ABC , 所以AA 1⊥CD ..........6分又CD ⊥AB ,AA 1∩AB =A ,.........7分所以CD ⊥平面ABB 1A 1,因为CD ⊂平面CDB 1,.........8分 所以平面ABB 1A 1⊥平面CDB 1,.........9分故点D 满足CD ⊥AB 时,平面ABB 1A 1⊥平面CDB 1......10分 因为AB =5,AC =3,BC =4,所以AC 2+BC 2=AB 2, 故△ABC 是以角C 为直角的三角形, 又CD ⊥AB ,所以AD =95..........12分22. (本小题满分12分) 如图,多面体ABCDEF 中,四边形ABCD 是菱形,060ABC ∠=,FA ⊥平面ABCD ,//,2 2.FA ED AB FA ED ===求二面角F BC A --的大小的正切值;求点E 到平面AFC 的距离;求直线FC 与平面ABF 所成的角的正弦值.21.解: 作于点G ,连接FG , 四边形ABCD 是菱形,,,为等边三角形,,-----1分平面ABCD ,平面ABCD ,,又,,平面AFG ,BC FG ∴⊥-----2分 G∴为二面角的平面角,------3分----------------------------4分连接AE ,设点E 到平面AFC 的距离为h , 则, ----------------------5分即,也就是,--------------------6分解得:; ------------------------------------------------7分(3)作CH AB ⊥于点H ,连接FH ,ABC ∆为等边三角形,H ∴为AB 的中点,221,3,5,AH CH FH FA AH ===+= FA ⊥平面ABCD ,CH ⊂平面ABCD ,FA CH ∴⊥,----8分 又,CH AB AB AF A ⊥⋂=,CH ∴⊥平面ABF ,-----9分CFH ∴∠为直线FC 与平面ABF 所成的角,-------10分36sin 422CH CFH CF ∴∠===.-----------------12分 22.(本小题满分12分)已知圆22+=9:O x y ,过点()0,2P -任作圆O 的两条相互垂直的弦AB 、CD ,设M 、N 分别是AB 、CD 的中点,(1)直线MN 是否过定点?若过,求出该定点坐标,若不过,请说明理由; (2)求四边形ACBD 面积的最大值,并求出对应直线AB 、CD 的方程.22.解:(1)当直线AB CD 、的斜率存在且不为0,设直线AB 的方程为:()()()112220,,,,y kx k A x y B x y =-≠------------1分由2229+=y kx x y =-⎧⎨⎩得:()221450k x kx +--=--------------------2分 点()0,2P -在圆内,故0∆>. 又 1212222422,21211M M Mx x k k x x x y kx k k k +∴+=∴===-=-+++ 即 2222,11kM k k ⎛⎫- ⎪++⎝⎭--------------------3分AB CD ⊥以1k -代换k 得22222,11k k N k k ⎛⎫-- ⎪++⎝⎭22222222111.22211MNk k k k k k k k k k -+-++∴==+++---------------4分∴直线MN 的方程为:222212121k k y x k k k -⎛⎫+=- ⎪++⎝⎭化简得2112k y x k-=-,故直线MN 恒过定点()01-,--------------------5分 当直线AB CD 、的斜率不存在或为0时,显然直线MN 恒过定点()01-, 综上,直线MN 恒过定点()01-,--------------------.6分 (2) 解法一:圆心O 到直线AB的距离1d =AB ==分 (或由第(1)问得:21AB x =-==以1k -代换k 得CD =)AB CD ⊥∴以1k -代换k 得:CD =分12ACBD S AB CD ∴=⋅==分14=≤= 当且仅当221,1k k k==±时,取等号,故四边形ACBD 面积的最大值为14,--------------------11分对应直线AB 、CD 分别为2,2y x y x =-=--或2,2y x y x =--=-----------12分 解法二:设圆心O 到直线AB 、CD 的距离分别为12,d d 、则22222211229,9AB r d d CD r d d =-=-=-=---------------------7分AB CD ⊥222124d d OP ∴+==--------------------8分()()()2222121221991821818414ACBD S AB CD d d d d OP ∴=⋅=≤-+-=-+=-=-=--------------------10分当且仅当12d d =,即1k =±时,取等号,故四边形ACBD 面积的最大值为14,--------------------11分对应直线AB 、CD 分别为2,2y x y x =-=--或2,2y x y x =--=---------12分。
哈三中2023-2024学年上学期高二期中考试数学试卷含答案解析

哈三中2023—2024学年上 学期高二学年期中考试数学试卷考试说明:(1)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分.考试时间为120分钟;(2)第I 卷,第II 卷试题答案均答在答题卡上,交卷时只交答题卡.第I 卷 (选择题, 共60分)一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.抛物线28y x =−的准线方程为( )A .=2y −B .4x =−C .2x =D .2x =−2.双曲线22916144x y −=的焦点坐标是( )A .(B .(0,C .(5,0),(5,0)−D .(0,5),(0,5)−3.若点P 到点)0,2(的距离比它到直线03=+x 的距离小1,则点P 的轨迹方程是( ) A .x y 82= B .x y 82−= C .y x 82= D .y x 82−=6.已知双曲线22:13x E y −=,直线:1l y kx =+,若直线l 与双曲线E 的两个交点分别在双曲线的两支上,则k 的取值范围是( )A .k <k >B .k <<C .k <或k > D .k <<7.已知抛物线2:2(0)C y px p =>的焦点F 与椭圆2212516x y +=的右焦点重合.斜率为(0)k k >的直线l 经过点F ,且与C 的交点为,A B .若||2||AF BF =,则直线l 的斜率为( )合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.2211B. 若123F MF π∠=,则22123b b =C. 若OM F F 221=则31112221=+e e D. 若212MF MF =则2(1,2]e ∈12.已知O 为坐标原点,12,F F 分别是双曲线2222:1(0,0)x y E a b a b −=>>的左,右焦点,直线4:3l y x =与双曲线E 交于,A B 两点,220F A F B ⋅= .M 为双曲线E 上异于,A B 的点,且,MA MB 与坐标轴不垂直,过2F 作12F MF ∠平分线的垂线,垂足为N ,则下列结论正确的是( ) A .双曲线E 的离心率为B .双曲线E 的渐近线方程是2y x =±C .直线MA 与MB 的斜率之积为4D .若||1ON =,则12AF F ∆的面积为4第Ⅱ卷 (非选择题, 共90分)三、填空题:本大题共4小题,每小题5分,共20分.将答案填在答题卡相应的位置上.点P 为椭圆C 上异于12,A A 的一点,则直线1PA 和2PA 的斜率之积等于_________. 15.已知直线1+−=x y 与椭圆22221(0)x y a b a b+=>>相交于B A ,两点,且线段AB 的中点在直线04:=−y x l 上,则此椭圆的离心率为_______.16.抛物线()220y px p =>的焦点为F ,准线为l ,A B 、是抛物线上的两个动点,且满足0AF BF ⋅=.设线段AB 的中点M 在l 上的投影为N ,则2MN AB 的最大值是 .四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分10分)已知直线:120()l kx y kk R −++=∈,(1,1),(2,1)P Q −−. (1)若经过,P Q 两点的直线与直线l 垂直,求此时直线l 的斜率; (2)1k =时,若点P 关于直线l 的对称点为点P ′,求线段P Q ′的长度.18.(本小题满分12分)已知半径为4的圆C 与双曲线221916x y −=的渐近线相切,且圆心C 在x 轴正半轴上. (1)求圆C 的方程;(2)经过(8,0)点,且斜率为k 的直线l 交圆C 于,A B 两点,若||AB =,求直线l 的方程.19.(本小题满分12分)21.(本小题满分12分)已知双曲线2222:1(0,0)x y C a b a b−=>>的焦点与椭圆22212x y +=的焦点相同,且双曲线C 经过点(1,1)P .(1)求双曲线C 的标准方程;(2)设,A B 为双曲线C 上异于点P 的两点,记直线,PA PB 的斜率为12,k k ,若12(1)(1)1k k −−=.求直线AB 恒过的定点.哈三中2023—2024学年上 学期高二学年期中考试数学答案1. C2. C3. A4. B5. C6. B7. D8. B 9.BCD 10. AB 11. ABD 12. BCD 13.15 14. 3−或13−15.16.17. (1)32k = (2)518.(1) (2)或 解析:(1)因为圆心C 点在轴正半轴上,设圆心C .圆C 的标准方程为:.双曲线的渐近线方程为:.因为双曲线的渐近线与圆C 相切,所以圆心C到双曲线一条渐近线的距离与圆的半径相等。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 语文 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一语文试题(本卷满分150分,答题时间120分钟)一、本大题共13道题,共29分(1—3题,每小题3分;4—13题,每小题2分)。
1.下列各句中,加点的成语使用恰当的一项是()A.湖北省黄金寺村为迎接上级扶贫检查,把几个村的羊群集中到一起,以其规模效益骗取扶贫资金,其手段之恶劣,令人叹为观止。
B.凌南地区虽地域狭窄,物产匮乏,但由于大力开发绿色农业,方寸之地,拓出了发展的空间。
C.得知了徐悲鸿去世的消息,她打开身边珍藏着的悲鸿早年的妙手丹青,不由得泪下如珠。
D. 在我父亲的记忆里,那是一段极为特殊、不堪回首的岁月,人事的变迁如白云苍狗,谁也无法预料。
2.下列各句中,没有语病的一句是()A.为了更好地提高服务质量,我们必须坚持以人为本,最大限度地为旅客创造和谐的候车环境、快乐的人性化服务。
B.校庆在即,学校要求全体师生注重礼仪,热情待客,以带给从全国各地回母校参加庆祝活动的校友感到宾至如归。
C.人才培养的质量是衡量一所大学办得好不好的重要因素,大力提升人才培养水平是高等教育改革发展的战略课题。
D.在现代社会,人与人的交往更加密切,口语交际能力有助于人们加强合作,增进理解,对于个人事业成功也有着重要影响。
3.依次填入下面一段文字横线处的语句,衔接最恰当的一组是()我国是食品生产和消费大国,_____,_____,_____,_____,_____,_____。
这样才能有效解决食品安全领域损害群众利益的突出问题,切实增强消费安全感。
①强化执法措施,严惩违法犯罪分子②食品产业涉及环节多,哪一环出现漏洞都会给食品安全带来严重威胁③创新食品安全监管机制④坚决淘汰劣质企业,以震慑所有企业使之不敢越雷池半步⑤保障食品安全需要生产经营者诚信自律,更需要严格的法律制度约束和有效监管⑥因此,必须保持严厉打击违法违规行为的态势,及时消除各环节的隐患A.②⑥①③④⑤ B.②⑤⑥①④③ C.⑤②⑥③①④ D.⑤⑥②④③①4. 文学常识题:选出表述正确的一项 ( )A. 朱自清,号秋实。
黑龙江省绥化市三校2014-2015学年度高一上学期期中联考数学试题

黑龙江省绥化市三校2014-2015学年度高一上学期期中联考数学试题第I 卷 (选择题, 共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合{|20142015}A x x =≤≤,{|}B x x a =<,若A B ≠⊂,则实数a 的取值范围是( )A.2014a >B.2015a >C. 2014a ≥D.2015a ≥ 2.函数1()f x x x=-的图象关于 ( )A.坐标原点对称B.x 轴对称C. y 轴对称D.直线y x =对称 3.若0.52a =,log 3b π=,2log 0.3c =,则( )A.b c a >>B. b a c >>C. c a b >>D. a b c >> 4.下列各组函数中,表示同一函数的是( )A .2)(|,|)(x x g x x f == B .22)()(,)(x x g x x f ==C .1)(,11)(2+=--=x x g x x x f D .1)(,11)(2-=-⋅+=x x g x x x f5.定义在R 上的函数⎩⎨⎧>---≤-=)0)(2()1()0)(4(log )(2x x f x f x x x f 则)3(f 的值为( )A.1-B.2-C.1D.2 6.若2lg(2)lg lg (,)x y x y x y R -=+∈,则yx的值为 ( )A.4B.1或14 C. 1或4 D.147.已知函数)(x f 为奇函数,且当0>x 时,xx x f 1)(2+=,则)1(-f 等于( )A .2-B .0C .1D .28.函数212()log (12)f x x x =+-的值域为是( )A.[1,0)-B. [1,)-+∞C. (0,1)D. [1,)+∞ 9.函数2()ln(1)f x x x=+-的零点所在的大致区间是 ( )A.(0,1)B. (1,2)C.(2,)eD. (3,4)10.函数1()2y =( )A. 1[1,]2-B. (,1]-∞-C. [2,)+∞D. 1[,2]211.已知函数⎩⎨⎧≥+-<=)0(4)3()0()(x a x a x a x f x 满足对任意12x x ≠,都有1212()()0f x f x x x -<-成立,则a 的范围是 ( )A.1(0,]4 B.(0,1) C.1[,1)4D.(0,3)12.若函数52(20)()log (02)x x f x g x x x ⎧-≤<⎪=⎨-<≤⎪⎩()(是奇函数,当02x ≤<时,()g x 的最大值为 ( ) A.14 B. 34- C. 34 D. 14- 第Ⅱ卷 (非选择题, 共90分)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.) 13.函数43)1ln(2+--+=x x x y 的定义域为__________.14.若()f x 是幂函数,且满足3)2()4(=f f ,则=)21(f __________.15.如果xxx f -=1)1(,则当0≠x 且1≠x 时,=)(x f __________16.函数)(x f 的定义域为A ,若A x x ∈21,且)()(21x f x f =时总有21x x =,则称)(x f 为单函数.例如,函数)(12)(R x x x f ∈+=是单函数.下列命题: ①函数)()(2R x x x f ∈=是单函数;②若)(x f 为单函数,A x x ∈21,且21x x ≠,则)()(21x f x f ≠;③若B A f →:为单函数,则对于任意B b ∈,A 中至多有一个元素与之对应; ④函数)(x f 在某区间上具有单调性,则)(x f 一定是单函数. 其中的正确的是______.(写出所有正确的编号)三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.(本题满分10分)计算:(1)23202151********--+--.)(.)( (2)323396415932455---+-)(log log log18.(本题满分12分)(1)当3=a 时,求B A ,)(B C A U ; (2)若φ=B A ,求实数a 的取值范围.19.(本题满分12分) 已知)()(a x ax xx f ≠-=. (1)若2-=a ,试证)(x f 在)2,(-∞内单调递增;(2)若0>a 且)(x f 在),1(+∞内单调递减,求a 的取值范围.20.(本题满分12分)设)3(log )1(log )(x x x f a a -++=(0>a 且1≠a ),且2)1(=f .(1)求a 的值及)(x f 的定义域. (2)求)(x f 在区间]23,0[上的最大值.21.(本题满分12分)集合A 是由具备下列性质的函数)(x f 组成的: ①函数)(x f 的定义域是),0[+∞; ②函数)(x f 的值域是)4,2[-;③函数)(x f 在),0[+∞上是增函数,试分别探究下列两小题: (1)判断函数)0(2)(1≥-=x x x f 及)0()21(64)(2≥⋅-=x x f x 是否属于集合A ?并简要说明理由;(2)对于(1)中你认为属于集合A 的函数)(x f ,不等式)1(2)2()(+<++x f x f x f 是否对于任意的0≥x 恒成立?请说明理由.22.(本题满分12分)定义:已知函数)(x f 在)](,[n m m n <上的最小值为t ,若m t ≤恒成立,则称函数)(x f 在)](,[n m m n <上具有“DK ”性质.(1)判断函数222+-=x x x f )(在],[21上是否具有“DK ”性质,说明理由.(2)若22+-=ax x x f )(在],[1+a a 上具有“DK ”性质,求a 的取值范围.绥化市三校2014-2015学年度上学期高一期中联考高一期中数学试题一、选择题 BADABD ABBDAC 二、填空题13.(-1,1) 14.31 15.11-x 16.(2)(3) 三、解答题17、(1)1/2 (2)-21 18.(本题满分12分)17.(1)A ∩B={x|-1≤x ≤1或4≤x ≤5}, A ∪(ðU B)={x|-1≤x ≤5}.(2)当a <0时,A=Ø,显然A ∩B=Ø,合乎题意. 当a ≥0时,A ≠Ø,A={x|2-a ≤x ≤2+a},B={x|x 2-5x+4≥0}={x|x ≤1或x ≥4}. 由A ∩B=Ø,得2a 12a 4-⎧⎨+⎩><,解得0≤a <1. 故实数a 的取值范围是(-∞,1). 19.(本题满分12分) (1)证明 任取x 1<x 2<-2, 则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2=2x 1-x 2x 1+2x 2+2.∵(x 1+2)(x 2+2)>0,x 1-x 2<0,∴f (x 1)<f (x 2), ∴f (x )在(-∞,-2)内单调递增. (2)解 任设1<x 1<x 2,则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a =ax 2-x 1x 1-ax 2-a.∵a >0,x 2-x 1>0,∴要使f (x 1)-f (x 2)>0,只需(x 1-a )(x 2-a )>0恒成立,∴a ≤1. 综上所述知a 的取值范围是(0,1].20.(本题满分12分)(1)2=a ,)(x f 的定义域为(-1,3)(2))32(log )(22++-=x x x f ,1=x 取最大值2. 22.(本题满分12分)(1)∵f(x)=x 2-2x+2,x ∈[1,2], ∴f(x)min =1≤1,∴函数f(x)在[1,2]上具有“DK ”性质.(2)f(x)=x 2-ax+2,x ∈[a,a+1], 其对称轴为x= a2. ①当a 2≤a ,即a ≥0时,函数f(x)min =f(a)=a 2-a 2+2=2. 若函数f(x)具有“DK ”性质,则有2≤a 总成立,即a ≥2.②当a<a 2<a+1,即-2<a<0时,f(x)min =f(a 2)=-2a 4+2.若函数f(x)具有“DK ”性质,则有- 2a 4+2≤a 总成立,解得a ∈Ø.③当a2≥a+1,即a ≤-2时,函数f(x)的最小值为f(a+1)=a+3. 若函数f(x)具有“DK ”性质,则有a+3≤a,解得a ∈Ø.综上所述,若f(x)在[a,a+1]上具有“DK ”性质,则a 的取值范围为[2,+∞).。
黑龙江省绥化市三校2014-2015学年度高二上学期期末联考 英语试题 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高二英语试题本试卷分第I卷和第II卷两部分,满分120分,考试时间100分钟第I卷(两部分,共70分)第一部分阅读理解(共两节,满分40分)第一节(共15小题,每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出可以填入空白处的最佳选项。
AKoalas remind people of teddy bears. They have thick fur and large ears. Their broad, flat nose makes them look cute, similar to teddy bears. In fact koalas aren’t cute. They have sharp teeth and very sharp claws! Koalas are marsupials. This means the mother carries her baby in a pocket while it develops, similar to a kangaroo. The baby koala lives in its mother’s pocket for the first six months of its life.The name “koala”comes from a native Australian word that means “no drink”. The koalas get almost all their water from the eucalyptus(桉树)leaves they eat. That’s where they get their food too. Koalas eat only eucalyptus leaves, and only the leaves of certain eucalyptus trees. The eucalyptus trees are where the koalas live. It’s also where they sleep. Koalas sleep about nineteen hours a day!Why do they sleep so much? Some people think it’s because they’re lazy. But koalas aren’t lazy. They sleep so much because there isn’t much nutrition (营养)in eucalyptus leaves. Koalas store hardly any fat, so they must save their energy. One way to do this is to move slowly and sleep a lot.After a day of sleeping they like to move around and eat just after sunset. They live alone most of the time. Koalas are very protective of their trees. If a koala sees another koala eating in its favorite tree, it might tell the other koala to leave by “barking”at it. Koalas do “talk”to each other. Besides barks, the males make a deep grunting sound. The mothers and babies talk in soft clicking sounds. If they get scared they may scream like a baby.1. According to the article, how are koalas and kangaroos alike?A. They both have thick fur.B. They both have sharp teeth.C. They both eat eucalyptus leaves.D. They both carry their young in a pocket.2. The word “koala”comes from a word that means ________.A. no drinkB. moving slowlyC. large earsD. barking loudly3. Why do koalas sleep a lot?A. Their babies need to get much rest.B. They get tired from playing so much.C. Their food does not give them much energy.D. They do not like to be awake when it is warm.4. If an adult koala screams like a baby, he may get ________.A. worriedB. hungryC. scaredD. sleepyBBabysitter WantedI am seeking a babysitter for my 6-month-old son. A few hours on Saturdays and Sundays to help me and then additional times as needed. Applicant should be over 18, responsible, loving, warm, and have experience in caring for babies. The pay is $ 10 an hour.If this sounds like a good fit for you, please reply to: rebecharv @ or call 800-4964. It is urgent!Office Manager wantedOur company is looking for a full-time manager to run the business. Strong skills and some experience are needed in organization and business management.Also, he or she should be familiar with computer.Please send your resume to jim @ californiaaquatics. com or call 800-6978 to apply.Waiter/ Waitress wantedSpecialty Restaurant is looking for an experienced waiter/ waitress. A knowledge of wines and experience in dining are necessary. Must work well under pressure and understand the basics of fine dining and customer service.If you're interested, please contact us at job-tkupe 1329358152 @ craigslist. Org to apply.This is a part-time job. Please, no phone calls about this job!Office Cleaner WantedLooking for Part-time work? A position available in the Mississauga area! Part-time 4 hours per day from 10:00 a.m.-2:00 p.m.Some experience is necessary. Pay: $15 per hour.Reply to: job-p3b7u-1365632206 @ or call 800-81975. The position of a(n) ___________ is full-time job.A. babysitterB. office managerC. waiter/ waitressD. office cleaner6. What can we learn from the passage?A. The office cleaner has to work three hours each day.B. One can apply for a waiter or waitress by telephone.C. Experience is necessary for all these four jobs.D. A babysitter earns $5 more than an office cleaner per hour.7. In which column can we read these messages in the newspaper?A. AdvertisingB. NewsC. EntertainmentD. SportsCHave you ever played the video dance game? Now such games are used to help lose weight!Like many other teenage boys, Jones loved sports. But at 5 feet, 175 pounds, he found his weight a trouble. His doctor wanted him to lose 50 pounds so that he may catch up with the football game by the end of summer.Jones chose the popular dance Revolution video game at home to increase his activity. He had lost about 10 pounds by changing his diet. Now, after two weeks playing the game, he has lost another 10!In West Virginia, 43% of the nearly 6,000 children examined for heart disease risk were considered over-weighted; more than 25% were too fat. “we are in a crisis of childhood obesity not only in West Virginia but in America,” said a researcher.Researchers are looking at the potential for improving effects by using the game. A teacher in West Virginia has been using the video game in her classes since last fall. She reported that the game does improve heart health as well as eye-hand coordination, and her students take the video game as a great alternative to jumping rope or ball games.The US Education Department is putting the game in 20 schools to control childhood obesity. Well, are you going to try such a game to dance away your extra weight?8.Jones’ main problem was that.A.he was too shortB.he was over-weightedC.he lacked the skill in footballD.he didn’t keep a healthy diet9.The underlined word means .A. being unfriendlyB. being unhappyC. being unhealthyD. being overweight10. It can be learned that .A. in West Virginia 25% of the children were too fatB. after playing the game, Jones has lost weightC. the teacher is a failure in using the video gameD. the US Education Department is promoting the game all over the country11. The most suitable title for the passage is .A. Dance Away Your WeightB. Play the Video Dance GameC. Solve the Problem of ObesityD. A Magic Video Dance GameDRecently, a study was carried out to determine who was the greatest American president. Sixty-five presidential historians took part in it, and they judged the past forty-two American leaders based on ten leadership qualities, including public persuasiveness(信服), crisis leadership, management of the economy, moral leadership, and conduct of international relations. The historians also looked at administrative ability (管理能力), relations with Congress, ability to set goals, and the pursuit of equal justice for all. Finally, the experts took into consideration the historical period in which the president lived.The historians chose Abraham Lincoln as American’s greatest president. He had also been named the greatest president in a similar study in 2000.Abraham Lincoln was the president who led the nation through the Civil War in the 1860s, and was able to unite it in the end. He also took the first steps to abolish(废除) slavery in America.Edna Medford, a professor of history at Howard University in Washington, D.C., was an adviser on this study and the earlier one. She says Abraham Lincoln is seen to represent the values the nation most honors, such as truthfulness, moderation, and respect for human rights.The historians put American’s first president, George Washington, second on the list, while Franklin D. Roosevelt, Theodore Roosevelt, and Harry Truman follow in that order. John F. Kennedy, the country’s first Roman Catholic president, is sixth on the list. Like Lincoln, Kennedy was murdered while in office.Among recent presidents, Ronald Reagan was named the tenth best and Bill Clinton rated fifteenth, while the historians put former president George W. Bush at number thirty-six. His father, George H.W. Bush, did much better, being placed at number eighteen.12. We learn from the text that ___________.A. this is the second time Abraham Lincoln has been chosen as America’s greatestpresidentB. Edna Medford didn’t take part in the study conducted in 2000C. George H.W. Bush was thought to have done worse in office than GeorgeW.BushD. Harry Truman was rated the fourth-best president by the study13. Which of the following belong to the ten leadership qualities considered?a. Being able to persuade the public.b. Taking effective measures during a financial crisis.c. Balancing home life and career.d. Pursuing equal justice for all.A. a,b,cB. b,c,dC. a,b,dD. a,c,d14. Who is rated worst among the following four presidents?A. John F. KennedyB. George W. BushC. Bill ClintonD. George Washington15. The text is mainly about ________.A. the ten qualities a great president needsB. how Abraham Lincoln improved the countryC. the values the American nation honors mostD.a study of American presidents第二节:根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 历史 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一历史试题第Ⅰ部分选择题一、每小题只有一项是符合题意的。
(每小题2分,共60分)1.《辛丑条约》标志着中国完全沦为半殖民地半封建社会,主要是因为该条约导致了()A .清政府完全成为列强统治中国的工具B .清政府在财政上完全受制于帝国主义C .清政府在军事上直接受帝国主义威胁D .中国局面完全由帝国主义控制2.语汇出现频率的高低可以反映国家政治经济主题的变化。
下列哪些语汇最有可能出现在1912年元旦中国各报刊上()A.北京、义和团、八国联军、赔款、“新政”B.临时政府、孙中山、共和、三权分立C.新文化、北洋军阀、实业救国、张謇D.革命、中国共产党、长征、改造、抗日3.有人认为辛亥革命是中国社会“从君主到民主”转型的开始。
对此理解错误的是(A. 建立了资产阶级共和国B. 颁布了《中华民国临时约法》C. 推翻了清王朝的专制统治D. 结束了中国的封建统治4.《杂文月刊》曾刊登过一篇名为《中国简史》的文章,其中有:“林则徐说:我销;康有为说:我变;孙中山说:看我的。
”对其正确的认识是()A.反映了近代中国人的救国探索B.都不同程度的阻碍中国近代化进程C.纯属缺乏历史依据的文夸张D.三者的斗争对象和方式基本一致5.《二十世纪中国的崛起》指出:“一个民族的觉醒,通常要有两个条件:第一,这个民族面对着或者经历了以往没有遇到过的严重危机,甚至整个民族被逼到生死存亡的关头,旧格局再也无法继续保持下去;第二,还要这个民族能看到出路,燃烧起新的希望,深信只要奋起救亡,勇于变革,就可以改变目前的艰难处境。
”下列能反映20世纪中国“旧格局再也无法继续保持下去”和“奋起救亡,勇于变革”的史实是()A.《马关条约》的签订和公车上书B.瓜分狂潮和义和团运动C.《辛丑条约》的签订和戊戌变法D.《辛丑条约》的签订和辛亥革命6.章太炎说“长素(康有为)以为‘革命之惨,流血成河,死人如麻,而其事卒不可就’。
黑龙江省绥化市三校2014-2015学年度高一上学期期中联考生物试题

黑龙江省绥化市三校2014-2015学年度高一上学期期中联考生物试题一、选择题(答案写在答题卡上,每题3分,共计60分)1.生命系统的结构层次中哪个层次最大()A.生态系统 B. 种群 C. 生物圈 D.群落2.细胞中含量最多的化合物是( )A蛋白质B淀粉C水D糖原3.组成细胞膜的主要成分是:()A.磷脂、蛋白质、糖类 B.糖类、糖蛋白C.脂质、蛋白质、无机盐 D.磷脂、蛋白质、核酸4.水在生物体的许多化学反应中充当( )A溶剂B催化剂C载体D还原剂5.染色质和染色体的正确关系是()A.同种物质在同一时期的两种形态B. 不同种物质在同一时期的两种形态C. 不同种物质在不同时期的两种形态D. 同种物质在不同时期的两种形态6.某儿童患佝偻病,发烧时就会抽搐,医生建议他平时要()A.新鲜水果和蔬菜B.钙片和维生素DC.谷物种皮D.蛋白质与糖类7.下列关于细胞与生命活动的叙述,错误的是()A.生命活动离不开细胞B.病毒不具有细胞结构,所以它的生命活动与细胞无关C.细胞是生物体结构和功能的基本单位D.生命和细胞难解难分8.下列哪一项不属于细胞膜的功能( )A控制物质进出细胞B将胰岛细胞形成的胰岛素,分泌到胰岛细胞外C提高细胞内化学反应的速率D作为系统的边界,维持细胞内环境的稳定9.细胞通过呼吸作用分解糖类并释放能量,主要是利用()A麦芽糖B核糖C葡萄糖D蔗糖10.夏季酷暑时分,在室外作业的人们应多饮用()A盐汽水B牛奶C纯净水D果汁11.哪种碱基是RNA所没有的()A 腺嘌呤B 鸟嘌呤C胞嘧啶D胸腺嘧啶12..细胞核内行使遗传功能的结构是()A核膜B核孔C染色质 D 核仁13.科学家常用哺乳动物红细胞作材料研究细胞膜的组成,是因为( )A哺乳动物红细胞容易得到B哺乳动物红细胞在水中容易胀破C哺乳动物成熟的红细胞没有核膜、线粒体等膜结构D哺乳动物红细胞的细胞膜在光学显微镜下容易观察到14.洋葱表皮细胞与口腔上皮细胞在结构上的区别是( )A.细胞核B.细胞膜C.细胞质D.细胞壁15.下列关于细胞核的说法,不正确的是( )A细胞核是遗传物质贮存和复制的场所B细胞核控制细胞的代谢和遗传C细胞核位于细胞的中央,所以它是细胞的控制中心D DNA主要存在于细胞核内16.组成蛋白质的基本单位是()A.甘氨酸B.氨基酸C.二肽D.多肽17.下列能与斐林试剂反应生成砖红色沉淀的是()A.葡萄糖B.蛋白质C.脂肪D.核酸18.血红蛋白和叶绿素中含有的重要元素依次是()A.Fe、Mg B.Cu、MgC.Mg、Fe D.Mg、I19.在唾液腺细胞中,参与合成并分泌唾液淀粉酶的细胞器有( )A线粒体、中心体、高尔基体、内质网B内质网、核糖体、叶绿体、高尔基体C内质网、核糖体、高尔基体、线粒体D内质网、核糖体、高尔基体、中心体20.在成人心肌细胞中的数量显著多于腹肌细胞中的数量的细胞器是( )A核糖体 B 线粒体C内质网D高尔基体绥化市三校2014-2015学年度上学期高一期中联考高一生物试题答题卡二、非选择题(每空2分,共计40分,答案填在横线上)21.某小岛,树木杂草茂盛,树上栖息着小益鸟和猫头鹰,地面上有田鼠、青蛙和蛇,此外,还有大量的昆虫、细菌和真菌等,从生命系统的结构层次上分析回答:(1)该岛上全部的猫头鹰组成了。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 地理 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一地理试题一、选择题(每题有一个正确选项,共60分。
1-20每题一分,21-40每题2分)1、下列属于天体的是()嫦娥三号是中国国家航天局嫦娥工程第二阶段的登月探测器,包括着陆器和玉兔号月球车。
2013年12月2日1时30分,嫦娥三号”探测器由长征三号乙运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察。
根据此段材料回答2~4题。
2、嫦娥三号卫星将会飞出( )A.银河系 B.太阳系 C.地月系 D.高层大气层3、中国登月探测器玉兔在月球上可以观测到的现象有( )①绚丽的极光②蓝天白云③一划而过的流星④满天星星⑤日蚀现象⑥昼夜更替A.①②③ B.①③⑥ C.②④⑤ D.④⑤⑥4、中国登月探测器在月球上将探测不到任何生命物质,主要原因之一是月球()A.与太阳的距离不适宜 B.体积质量太小C.缺少重要的矿物质 D.太阳辐射太强5、下列自然现象与太阳辐射有关的是()A.两极地区出现极光 B.煤、石油和天然气的形成C.杭州湾钱塘潮 D.无线电通讯暂时中断、“磁暴”6、哈尔滨和海口两地的自转角速度和线速度相比较,正确的叙述是()A.两地的角速度和线速度都相同B.两地的角速度和线速度都不相同C.角速度相同,线速度海口大于哈尔滨D.角速度相同,线速度海口小于哈尔滨北京时间2013年6月20日上午10点,中国神舟十号宇航员首次在天宫一号太空授课,全国各中小学及时调整课程观看全国直播的“太空环境下的科学实验”。
据此完成7~8题。
7、位于拉萨(29°36′N,91°06′E)的中学生在观看“太空授课”过程中,发现电视信号出现了一段时间的中断,请你分析其原因可能是受()A.太阳辐射的影响B. 太阳活动的影响C.地球公转到远日点附近的影响D.同学们收看节目时正值黑夜8、太空授课直播时,地球的昼夜分布情况最接近下图中的下图是“太阳直射点在地球表面移动示意图”,据此回答9~11题。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 物理 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一物理试题一.单项选择题:(本题共8小题,每小题4分,共32分,每小题只有一个....选项符合题意) 1.下列关于重心、弹力和摩擦力的说法,正确的是 ( ) A .物体的重心一定在物体的几何中心上 B .劲度系数越大的弹簧,产生的弹力越大C .动摩擦因数与物体之间的压力成反比,与滑动摩擦力成正比D .静摩擦力的大小是在零和最大静摩擦力之间发生变化2.某物体同时受到同一平面内的三个共点力作用,在如图所示的四种情况中(坐标纸中每格边长表示1N 的大小的力),该物体所受的合外力大小正确的是( )A .甲图中物体所受的合外力大小等于4NB .乙图中物体所受的合外力大小等于2NC .丙图中物体所受的合外力大小等于0D .丁图中物体所受的合外力大小等于0 3.下列对运动的认识错误的是 ( ) A .亚里士多德认为有力作用在物体上,物体才能运动;没有力的作用,物体就静止 B .伽利略认为如果完全排除空气的阻力,所有的物体将下落得同样快C .伽利略认为,若没有摩擦,在水平面上运动的物体将保持其速度继续运动下去D .牛顿认为力不是维持物体运动的原因,力是改变物体运动状态的原因4.钓鱼岛是中国领土铁证如山,但日本政府一再挑衅,并于今年九月发起购岛闹剧。
对此包括港澳台在内,全国上下共同掀起保岛高潮。
中国人民解放军做为坚强后盾更是频频亮剑,一批批重量级装备纷纷闪亮出场。
国产最先进武装直升机武直-10(WZ-10)已经进行多次试飞,下图为一架WZ-10在钓鱼岛海域拖曳扫雷具进行近岛扫除水雷演习模拟图。
拖曳型扫雷具质量为m ,由于近岛海水的流动对物体产生水平方向的冲击力,使软绳偏离竖直方向,当直升甲乙丙丁F 1 F 2F 3 F 1F 2F 3F 1 F 2 F 3F 1F 2F 3机相对地面静止时,绳子与竖直方向成θ角,已知物体所受的浮力不能忽略,下列说法正确的是 ( )A .绳子的拉力为mgcos θB .绳子的拉力一定大于mgC .物体受到海水的水平方向的作用力等于绳子的拉力D .物体受到海水的水平方向的作用力小于绳子的拉力5.如图所示,将一球用网兜挂在光滑的墙壁上,设绳对球的拉力为F1,墙壁对球的支持力为F 2,当球的半径增大时(设球的质量不变,细绳长度不变) ( ) A .F 1、F 2均不变 B .F 1、F 2均减小 C .F 1、F 2均增大 D .F 1减小,F 2增大6.如图所示,质量为m 的木块A 放在质量为M 的三角形斜劈上,现用大小均为F 、方向相反的水平力分别推A 和B ,它们均静止不动,则( )A .A 与B 之间一定存在摩擦力 B .B 与地面之间一定存在摩擦力C .B 对A 的支持力一定小于mgD .地面对B 的支持力的大小一定等于(M +m )g7. 如图所示,质量分别为M 和m 的物块由相同的材料制成,且M >m ,将它们用通过轻而光滑的定滑轮的细线连接。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 化学 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一化学试题本试卷参考元素相对原子质量: H:1 O:16 Na:23 Cu:64 Fe:56 一.单项选择题(每小题只有一个正确选项,每题2分,共12×2=24分)1、下列物质不能通过化合反应直接制得的是A.FeCl2 B.NaHCO3C.Al(OH)3D.Fe3O42、下列试剂能贮存在磨口玻璃塞的试剂瓶里的是A.HF溶液B.KOH溶液C.盐酸D.水玻璃3、等量镁铝合金粉末分别与下列4种过量的溶液充分反应,放出氢气最多的是A.18mol·L-1H2SO4溶液 B.2mol·L-1H2SO4溶液C.6 mol·L-1KOH溶液 D.3 mol·L-1HNO3溶液4、下列反应,其产物的颜色按红色、红褐色、淡黄色、蓝色顺序排列的是①金属钠在纯氧中燃烧②FeSO4溶液中滴入NaOH溶液并在空气中放置一段时间③FeCl3溶液中滴入KSCN溶液④无水硫酸铜放入医用酒精中A.②③①④ B.③①②④C.③②①④ D.①②③④5、氧化还原反应在生产、生活中具有广泛的用途。
下列生产、生活中的事例不包含氧化还原反应的是A. 常温时浓硫酸能使铝、铁钝化B.点制豆腐C.食物腐败D.燃放鞭炮6、“纳米材料”是指粒子直径在1~100nm之间的材料,纳米碳就是其中的一种。
若将纳米碳均匀地分散到蒸馏水中,对所形成的分散系说法正确的是:(1)是溶液;(2)是胶体;(3)能产生丁达尔效应;(4)能通过滤纸;(5)不能通过滤纸;(6)静置后会析出黑色的沉淀。
A.(1)(4)(6) B.(2)(3)(4) C.(2)(3)(5) D.(3)(4)(6)7、下列实验基本操作(或实验注意事项)中,主要是处于实验安全考虑的是A.实验剩余的药品不能放回原试剂瓶 B.可燃性气体的验纯C.气体实验装置在实验前进行气密性检查 D.滴管不能交叉使用8、下列实验操作中正确的是A.蒸发时,应使混合物中的水分完全蒸干后,才能停止加热B.过滤操作中,漏斗下端管口与烧杯内壁相互接触C.分液时,先把分液漏斗中上层液体从上口倒出,再把下层液体从下口放出D. 萃取时,应选择有机萃取剂,且萃取剂的密度必须比水大9、用NA表示阿伏加德罗常数的值,下列叙述正确的是A.常温常压下,22.4LH2含有的分子数为NAB.25℃、101KPa时,1 mol CO2气体所占有的体积约为22.4LC.标准状况下,4.0g NaOH含有的Na+ 离子数为0.1 NAD.物质的量浓度为0.5mol /L的MgCl2溶液中,含有Cl—个数为1 NA10、下列离子方程式书写正确..的是A.CuSO4溶液与Ba(OH)2溶液反应:Ba2+ + SO42− = BaSO4↓B.NaHSO4溶液和NaHCO3溶液反应:H+ + HCO3− = H2O + CO2↑C.氯化铝溶液中加入过量氨水:Al3+ + 4NH3•H2O = AlO2- + 4NH4+ + 2H2OD.澄清石灰水中通入过量二氧化碳:Ca2+ +2OH +CO2 = CaCO3↓+H2O11、在两个容积相同的密闭容器中,一个盛有NO气体,另一个盛有N2和O2的混合气体。
黑龙江省绥化市三校2014-2015学年度高二上学期期末联考 数学理科试题 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高二数学理科试题试卷说明:1、本试卷满分150分,答题时间120分钟。
2、请将答案直接填涂在答题卡上,考试结束只交答题卡。
第Ⅰ卷(选择题 满分60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.复数z =-3+i2+i的共轭复数是( )A .-1+iB .-1-iC .2+iD .2-i 2.已知命题p :∃x 0∈C ,x 20+1<0,则 ( ) A .¬p :∀x ∈C ,x 2+1≤0 B .¬p :∀x ∈C ,x 2+1<0 C .¬p :∀x ∈C ,x 2+1≥0D .¬p :∀x ∈C ,x 2+1>03.某单位有职工75人,其中青年职工35人,中年职工25人,老年职工15人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本容量为15,则样本中的青年职工人数为 ( )A .7B .15C .25D .35 4.已知一个家庭有两个小孩,则两个孩子都是女孩的概率为( ) A .14 B .13 C .12 D .235.双曲线x 2-y 2m=1的离心率大于2的充分必要条件是( )A .m >12 B .m ≥1 C .m >1 D .m >26.下列命题中,假命题...是( ) A .若命题p 和q 满足p ∨q 为真,p ∧q 为假,,则命题p 与q 必一真一假 B .互为逆否命题的两个命题真假相同C .“事件A 与B 互斥”是“事件A 与B 对立”的必要不充分条件D .若f (x ) =2x ,则f ′(x )=x ·2x -17.阅读右面的程序框图,若输入的n 是100,则输出的变量S 的值是( )A .5 049B .5 050C .5 051D .5 0528.用秦九韶算法求多项式f (x )=7x 7+6x 6+5x 5+4x 4+3x 3+2x 2+x 的值,当x =3时,v 3的值为( )A .789B .262C .86D .279.椭圆满足这样的光学性质:从椭圆的一个焦点发射光线,经椭圆反射后,反射光线经过椭圆的另一个焦点。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 生物 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一生物试题一、单项选择题(1-50,每小题1分;50-55,每小题2分;共60分。
下列每小题所给选项有一项符合题意,请将正确答案的序号填涂在答题卡上)1.如图表示人体细胞中四种主要元素占细胞干重的百分比,其中表示碳元素的是( )A.甲 B.乙 C.丙 D.丁2.下列化合物中含有的化学元素种类最少的一组是( )A.抗体和糖蛋白B.纤维素和脱氧核糖C.性激素和tRNA D.质粒和呼吸酶3.某人身体不适,全身浮肿,去医院做尿液检查时,化验师做了如下操作:①取稀释尿液2 mL;②加0.1 g/mLNaOH溶液1 mL摇匀;③加0.01 g/mL CuSO4溶液4滴,摇匀;④观察结果有紫色出现。
该人可能患有( )A.糖尿病 B.肾小球肾炎 C.脂肪肝 D.过敏性皮炎4.在观察植物细胞的质壁分离和复原的过程中,某同学在视野中看到生活着的洋葱表皮细胞正处于如图所示状态,a、b表示该部位的溶液浓度,由此可以推断 ( )A.可能a>b,细胞渗透吸水B.可能a=b,渗透系统保持动态平衡C.可能a<b,细胞渗透失水D.上述三种情况都有可能5. 下图为细胞亚显微结构示意图,下列有关说法不正确的是()A.此图可用来表示低等植物细胞的亚显微结构B.若此图表示洋葱根尖分生区细胞,应去掉的结构为5、9C.图中含有DNA的结构有3、5、6D.此图若表示动物的性腺细胞,则不应有的结构为1、2、56.“分子伴侣”是一类在细胞中能识别正在合成的多肽或部分折叠的多肽并与多肽的一定部位相结合,帮助这些多肽转运、折叠或组装,但其本身不参与最终产物的形成的蛋白质。
根据所学知识推测“分子伴侣”主要存在于( )A.核糖体 B.内质网 C.高尔基体 D.溶酶体7.下面能发生质壁分离的一组细胞是( )①食用的糖醋蒜细胞②蚕豆叶的表皮细胞③植物的根毛细胞④人的口腔上皮细胞⑤用盐酸解离的洋葱根尖细胞⑥根尖分生区细胞A.①⑤B.②③⑥C.①②③④⑤⑥D.②③8.下列关于细胞内物质组成的叙述不正确的是( )AB.细胞中的化合物都以碳链为基本骨架C.ATP和RNA中都含有腺嘌呤和核糖D .细胞中的酶可多次发挥作用9. 植物细胞吸收物质的方式之一是胞吞作用,具体过程是:当物质吸附在细胞膜上时,细胞膜内陷,形成小囊泡,囊泡地移动过程中在细胞内溶解消失,把物质留在细胞内,或囊泡一直移动将物质交给液泡。
黑龙江省绥化市三校2015届高三上期中联考数学试卷及答案

绥化市三校2015届高三上学期期中联考数学试卷命题人: 高三理数备课组本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分第I 卷 (选择题, 共60分)一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}1|3,|04x A x x B x x -⎧⎫=>=<⎨⎬-⎩⎭,则A B = ( ) A .∅ B .()3,4 C .()2,1- D . ()4,+∞ 2. 复数32ii +(i 为虚数单位)在复平面上对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.已知a 为实数,则“2>a ”是“a a 22>”成立的 ( )A .充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4、已知向量a ()2,1+=m ,b ()1,-=m ,且a //b等于( )AB .2C .320D .325 5.设0.3113211log 2,log ,()32a b c ===,则( ) A .a <b <c B .a <c <b C .b <c <a D .b <a <c6.设等比数列{a n }的前n 项和为S n ,若S 10S 5=12,则S 15S 5= ( )A .34 B . 23 C . 12D .137.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象 ( )A.向右平移6π个单位长度 B. 向右平移3π个单位长度C.向左平移6π个单位长度D. 向左平移3π个单位长度8.已知数列{}n a 中,11=a ,121++=+n a a n n ,则通项n a 等于 ( )A.⎩⎨⎧≥++==2,121 ,12n n n n a n B. 122-=n a n C. 12-=n a n D. 2n a n = 9..已知函数()x x x x f cos 3sin cos )(-=,则( ) A .函数()x f 的周期为π2 B .函数()x f 在区间⎥⎦⎤⎢⎣⎡-6,6ππ上单调 C .函数()x f 的图象关于直线12π-=x 对称D .函数()x f 的图象关于点⎪⎭⎫⎝⎛0,6π对称 10.已知非零向量,a b 满足||3||a b =,且关于x 的函数3211()||22f x x a x a bx =++⋅为R 上增函数,则,a b 夹角的取值范围是 ( ) A 、[0,]2πB 、[0,]3πC 、(,]32ππD 、2(,]33ππ11.)(x f 是定义在),0(+∞上的非负可导函数,且满足()()0xf x f x '-≤,对任意正数b a ,, 若b a <,则必有 ( )A .)()(a bf b af ≤B .)()(b af a bf ≤C .)()(b f a af ≤D .)()(a f b bf ≤12. 设函数()f x 的定义域为D ,若满足:①()f x 在D 内是单调函数; ②存在[],a b D ⊆()b a >,使得()f x 在[],a b 上的值域为[],a b ,那么就称()y f x =是定义域为D 的“定义函数”.若函数2()log ()(0,1)x a g x a t a a =+>≠是定义域为R 的“定义函数”,则t 的取值范围为 ( )A. 1(,)4-∞B. 1(,1)4C. 1(0,)4D. 1(0,]4第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡相应的位置上)13.已知α为第二象限角,sin cos αα+=,则cos 2α= . 14.在ABC ∆中,M 是BC 的中点,AM=1,点P 在AM 上且满足2=,则)(+等于 .15. 已知命题p 不等式|x|+|x-1|>m 的解集为R,命题q 函数f (x)=(52)x m --是减函数.若p 或q 为真命题,p 且q 为假命题,则实数m 的取值范围是 .16 已知函数()f x ,(1,1)x ∈-且(0)0f =,()f x 的导函数为()43cos f x x '=+,如果2(1)(1)0f a f a -+-<,则实数a 的取值范围是 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本大题10分)在△ABC 中,a 、b 、c 分别为内角A 、B 、C 的对边,且222a b c bc =++. (1)求A 的大小;(2)若sin sin 1,2B C b +==,试求△ABC 的面积.18(本大题12分)2a ,5a 是方程027x 12x 2=+-的两根, 数列}a {n 是公差为正数的等差数列,数列}b {n 的前n 项和为n T ,且)N n (b 211T *n n ∈-=. (1)求数列}{n a ,}b {n 的通项公式;(2)记n n n b a c =,求数列}c {n 的前n 项和n S .19.(本小题满分12分)设函数()|1||5|f x x x =++-,∈x R . ⑴ 求不等式()10f x x +≤的解集;⑵ 如果关于x 的不等式2()(2)f x a x --≥在R 上恒成立,求实数a 的取值范围.20.(本题满分12分)已知二次函数()y f x =的图像经过坐标原点,其导函数为()62f x x '=-,数列{}n a 的前n 项和为n S ,点*(,)()n n S n ∈N 均在函数()y f x =的图像上。
黑龙江省绥化市三校2014-2015学年度高二上学期期末联考 物理试题 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高二物理试题试卷说明本试卷满分110分,答题时间90分钟。
请将答案填涂在答题卡上。
一、单项选择题:共7小题,每小题只有一个答案,每题5分,共35分。
1.下列装置没用到带电粒子在磁场中发生偏转的原理的是()(A)磁流体发电机(B)回旋加速器(C)电视显像管(D)示波管2.有Ⅰ、Ⅱ两根不同材料的电阻丝,长度之比为L1∶L2=1∶5,横截面积之比为S1∶S2=2∶3,∶R2=2∶5,则它们的电阻率之比为()电阻之比为R(A)2∶3(B) 3∶4(C) 4∶3(D)8∶33.如图所示,电的电动势为30 V,内电阻忽略不计,一个“6V,12 W”的电灯与一个绕线电阻为2Ω的电动机串联。
已知电路中的电灯正常发光,则电动机输出的机械功率为() (A)36 W (B)40 W (C)48 W (D)60 W4.如图所示,把一个装有导电溶液的圆形玻璃器皿放入磁场中,玻璃器皿的中心放一个圆柱形电极B,与电池的正极相连;沿器皿边缘内壁放一个圆环形电极A,与电池的负极相连。
从器皿上方往下看(俯视),对于导电溶液和溶液中正、负离子的运动,下列说法中正确的是()(A)溶液做逆时针方向运动(B)溶液做顺时针方向运动(C)正离子沿圆形玻璃器皿的半径向边缘移动(D)负离子沿圆形玻璃器皿的半径向中心移动5.现将电池组、滑线变阻器、带铁芯的线圈A、线圈B、电流计及开关如下图连接。
在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左加速滑动时,电流计指针向右偏转。
由此可以推断()(A)线圈A向上移动或滑动变阻器的滑动端P向右加速滑动,都能引起电流计指针向左偏转(B)线圈A中铁芯向上拔出或断开开关,都能引起电流计指针向右偏转(C)滑动变阻器的滑动端P匀速向左或匀速向右滑动,都能使电流计指针静止在中央(D)因为线圈A、线圈B的绕线方向未知,故无法判断电流计指针偏转的方向6.静止在光滑水平面上的条形磁铁左端和轻弹簧连接,轻弹簧的另一端固定在墙上,在条形磁铁的上方偏右位置(如图)固定有通电直导线,电流垂直纸面向内,下列说法正确的是()(A)弹簧被压缩,磁铁对水平面的压力变小(B)弹簧被压缩,磁铁对水平面的压力变大(C)弹簧被拉长,磁铁对水平面的压力变小(D)弹簧被拉长,磁铁对水平面的压力变大7.如图所示,水平放置的平行板电容器,上板带负电,下板带正电,带电小球以速度v0水平射入电场,恰好沿下板边缘飞出。
黑龙江省哈三中2014-2015学年度高二上学期期中考试数学理试卷

哈三中2014—2015学年度上学期 高二学年第一模块数学(理科)试卷命题员: 审题员:考试说明:(1)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分, 满分150分.考试时间为120分钟;(2)第I 卷,第II 卷试题答案均答在答题卡上,交卷时只交答题卡.第I 卷 (选择题, 共60分)一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知曲线C 的方程为2220x xy y -+-=,则下列各点中,在曲线C 上的点是A .(B .()1,2-C .()2,3-D .()3,8 2. 已知A 为圆A :()22125x y -+=的圆心,平面上点P 满足3=PA ,那么点P 与圆A 的位置关系是A .点P 在圆A 上B .点P 在圆A 内C .点P 在圆A 外D .无法确定3. 双曲线221412x y -=的焦点到渐近线的距离为A .B .2CD .1 4. 抛物线22y x =的准线方程为A .12x =-B .12x =C .18y = D .18y =-5.已知点()()0,1,0,1B A -,P 是平面内一动点,直线PB PA ,斜率之积为21-, 则动点P 的轨迹方程为A .2221(1)x y x +=≠±B .2221(1)x y x +=≠± C .2221(1)x y x -=≠± D .2221(1)x y x -=≠± 6. 已知点()y x P ,在圆2220x y x ++=上,则x y +的最小值为1 B.1 C.1 D. 17. 设定点1(0,2)F ,2(0,2)F -,动点P 满足条件124(0)PF PF a a a+=+>,则点P 的轨迹是A .椭圆B .线段C .不存在D .椭圆或线段8. 已知点(8,8)P 在抛物线2:2C y px =(0p >)上,直线l 与抛物线C 相切于点P ,则直线l 的斜率为 A .34 B .43 C .21 D .45 9.若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值 范围为A .[B .(C .[D .( 10. 已知抛物线2:4C y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若3FP FQ =,则||QF =A .1B .43C .53D .211. 过双曲线15322=-y x 的左焦点F 引圆322=+y x 的切线FP 交双曲线右支于点P ,T 为切点,M 为线段FP 的中点,O 为坐标原点,则MT MO -= A.3 B. 5 C. 35- D.35+12. 已知椭圆22182x y +=上一点(2,1)A 和该椭圆上两动点B 、C ,直线AB 、AC 的斜率分别为1k 、2k ,且120k k +=,则直线BC 的斜率k A . 2121-<>k k 或 B . 21-=k C . 21=k D .k 的值不确定 第Ⅱ卷 (非选择题, 共90分)二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡相应的位置上) 13. 已知AB 为过双曲线C 的一个焦点F 且垂直于实轴的弦,且AB 为双曲线C 的实轴长的2倍,则双曲线C 的离心率为___________.14. 顶点在原点,经过圆22:20C x y x +-+=的圆心且准线与x 轴垂直的抛物线方程为 .15. 已知方程1422=+ky x 的曲线是焦点在y 轴上的椭圆,则实数k 的取值范围为____________________.16. 已知圆1)sin 2()cos 2(:221=-+-θθy x C 与圆1:222=+y x C ,在下列说法中:①对于任意的θ,圆1C 与圆2C 始终相切; ②对于任意的θ,圆1C 与圆2C 始终有四条公切线;③直线)(0)52()2(3)3(2:R m m y m x m l ∈=+-+++与圆2C 一定相交于两个不同的点;④Q P ,分别为圆1C 与圆2C 上的动点,则||PQ 的最大值为4. 其中正确命题的序号为_________________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)已知双曲线2222:1(0,0)x y C a b a b-=>>的渐近线方程为:x y 3±=,右顶点为)0,1(.(Ⅰ)求双曲线C 的方程;(Ⅱ)已知直线m x y +=与双曲线C 交于不同的两点B A ,,且线段AB 的中点为()00,y x M .当00≠x 时,求x y 的值.18.(本小题满分12分)已知P 是长轴长为6的椭圆C 上的任意一点,1(2,0)F -,2(2,0)F 是椭圆C 的两个焦点,O 为坐标原点,12OQ PF PF =+,求动点Q 的轨迹方程.19.(本小题满分12分)在直角坐标系xoy 中,曲线562+-=x x y 与坐标轴的交点都在圆C 上. (Ⅰ)求圆的方程;(Ⅱ)求过点()4,220.(本小题满分12分)已知21F F 、为椭圆C :12222=+by a x (>a 过左焦点1F 的直线与C 相交于B A ,方程.21.(本小题满分12分)如图,已知抛物线2:4C x y =,过点(0,2)M 任作一直线与C 相交于,A B 两点,过点B 作y 轴的平行线与直线AO 相交于点D (O 为坐标原点). (Ⅰ)求点D 的纵坐标0y 的值;(Ⅱ)作C 的任意一条切线l (不含x 轴),与直线2y =相交于点1N ,与直线0y y =相交于点2N .求2221||||MN MN -的值.22.(本小题满分12分)已知椭圆1E :22216x y a +=的焦点1F 、2F 在x 轴上,且椭圆1E 经过(,2)(0)P m m ->,过点P 的直线l 与1E 交于点Q ,与抛物线2E :24y x =交于A 、B 两点,当直线l 过2F 时1PF Q ∆的周长为 (Ⅰ)求m 的值和1E 的方程;(Ⅱ)以线段AB 为直径的圆是否经过2E 上一定点,若经过一定点求出定点坐标,否则说明理由.哈三中2014—2015学年度上学期 高二学年第一模块数学(理科)试卷答案一.选择题1.A2.B3.A4.D5.B6.B7.D8.C9.C 10.B 11.C 12.C 二.填空题13.3 14.x y 22= 15.40<<k 16.①③④三.解答题17. (1)1322=-y x (2)3 18.1203622=+y x 19. (1)056622=+--+y x y x(2)112;2+=x y20. 13622=+y x 21. (1)2- (2)822. (1)1675;522=+=y x m (2)()2,1。
黑龙江省绥化市三校2015届高三12月月考化学试题

黑龙江省绥化市三校2015届高三12月月考化学试题2014年12月(考试时间:90分钟 试卷满分:100分 )注意事项:1.答题前,务必将自己的姓名、考号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须将答案书写在专设答题页规定的位置上。
4.所有题目必须在答题卡上作答.在试题卷上答题无效。
5.考试结束后,只交试卷答题卡。
6. 可能用到的数据 相对原子质量: H 1 C12 N14 O16 Zn65 Fe56 Cu64第I 卷 (共42分)一、选择题(本题包括14小题,每小题3分,共42分。
每题只有一个选项符合题意) 1.咖喱是一种烹饪辅料,若白衬衣被咖喱汁玷污后,用普通肥皂洗涤该污渍时会发现,黄色污渍变成红色,经水清洗后红色又变成黄色。
据此现象,你认为咖喱汁与下列何种试剂有相似的化学性质A .品红溶液B .石蕊溶液C .次氯酸钠D .无水硫酸铜 2.下列叙述正确的是A .由同种元素组成的物质一定属于纯净物B .金属氧化物一定是碱性氧化物,非金属氧化物一定是酸性氧化物C .元素的性质随着元素相对原子质量的递增而呈现周期性变化D .氧化物一定只含有两种元素3. 25℃、101 kPa 下,碳、氢气、甲烷和葡萄糖的燃烧热依次是△H = - 393.5 kJ/mol 、 △H =-285.8kJ/mol 、△H = - 890.3 kJ/mol 、△H = - 2 800 kJ/mol ,则下列热化学方程式正确的是A .C (s )+21O 2(g )=CO (g ) △H = - 393.5 kJ/mol B .2H 2(g )+O 2(g )=2H 2O (l ) △H = - 571.6 kJ/molC .CH 4(g )+2O 2(g )=CO 2(g )+2H 2O (g ) △H = - 890.3 kJ/molD .21C 6H 12O 6(s )+3O 2(g )=3CO 2(g )+3H 2O (g ) △H = - 2800 kJ/mol4.能正确表示下列反应的离子方程式是A.Fe3O4溶于足量稀HNO3:Fe3O4+8H+=Fe2++2Fe3++ 4H2OB.NH4HCO3溶液与足量Ba(OH)2溶液混合:HCO3-+Ba2++OH-=BaCO3↓+H2OC.向澄清石灰水中通入少量CO2:OH-+CO2=HCO3-D.将0.2 mol·L-1的NH4Al(SO4)2溶液与0.3 mol·L-1的Ba(OH)2溶液等体积混合:2Al3++3SO42-+3Ba2++6OH-=2Al(OH)3↓+3BaSO4↓5.X、Y为短周期元素,X位于I A族,X与Y可形成化合物X2Y,下列说法正确的是A.X的原子半径一定大于Y的原子半径B.X2Y可能是离子化合物,也可能是共价化合物C.两元素形成的化合物中,原子个数比不可能为11D.X与Y的简单离子不可能具有相同的电子层结构6.N A表示阿伏加德罗常数的值,下列叙述正确的是A.22.4L的CO气体和1mol N2所含的电子数相等B.1L密度为1.84g·cm3 质量分数为98%的硫酸溶液中,所含氢原子数为36.8N AC.在标准状况下,32g氧气和臭氧的混合气体中含氧原子数为2N AD.1mol/L FeCl3溶液中,含有Cl-的数目为3N A7.R2O8n-在一定条件下可以把Mn2+氧化成MnO4-,若反应中R2O8n-变为RO42-,又知反应中氧化剂与还原剂的物质的量之比为5∶2,则n值为A.1 B.2 C.3 D.48.如图所示:,每个编号代表下列物质中的一种物质,凡是用直线相连的两种物质均能发生化学反应。
黑龙江省绥化市三校2014-2015学年度高一上学期期末联考 英语 Word版含答案

绥化市三校2014-2015学年度第一学期期末联考高一英语试题第一部分:听力(共两节,满分20分)第一节(共5小题;每小题1分,满分5分)1. What does the woman do?A. An actressB.A WriterC.A director2.Where will they probably go next?A.To a hotel B.To a post office C.To a restaurant3.When will the man meet the woman?A.At 5:20 B.At 5:30 C. At 5:404.What does the man mean?A.He wants to go for a picnic.B.He doesn’t like the woman’s plan.C.He is too busy to help the woman.5.Where does this conversation most probably take place?A.At the cinema B.On the street C.At home第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答6、7题。
6.Where are probably Aunt Mary and Jim now?A.At their homeB.On the wayC.In the kitchen7.What is new with Jim?A.He has moved away B.He has grown much fatterC.He has grown much taller听第7段材料,回答8至10题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年黑龙江省绥化市三校联考高二(上)期中数学试卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的.1.(5分)命题“若a>b,则a+c>b+c”的逆否命题为()A.若a<b,则a+c<b+c B.若a≤b,则a+c≤b+cC.若a+c<b+c,则a<b D.若a+c≤b+c,则a≤b2.(5分)与曲线=1共焦点,而与曲线=1共渐近线的双曲线方程为()A.=1 B.=1 C.=1 D.=13.(5分)已知双曲线=1(a>0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x4.(5分)函数f(x)=x2﹣2ax+1在(﹣∞,2]上是单调递减函数的必要不充分条件是()A.a≥2 B.a=6 C.a≥3 D.a≥05.(5分)过抛物线y2=﹣x的焦点F的直线交抛物线于A、B两点,且A、B在直线x=上的射影分别M,N,则∠MFN等于()A.45°B.60°C.90°D.以上都不对6.(5分)有下列四个命题:①命题“若xy=1,则x,y互为倒数”的逆命题;②命题“面积相等的三角形全等”的否命题;③命题“若m>1,则x2﹣2x+m=0有实根”的逆否命题;④命题“若A∩B=B,则A⊆B”的逆否命题.其中是真命题的个数是()A.1 B.2 C.3 D.47.(5分)方程mx+ny2=0与mx2+ny2=1(|m|>|n|>0)的曲线在同一坐标系中的示意图应是()A. B.C.D.8.(5分)已知动点P(x,y)满足=,则点P的轨迹是()A.两条相交直线B.抛物线C.双曲线D.椭圆9.(5分)一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于P,直线PF1(F1为椭圆的左焦点)是该圆的切线,则椭圆的离心率为()A.B.C.D.10.(5分)已知点P为抛物线y=x2上的动点,点P在x轴上的射影为M,点A 的坐标是(6,),则|PA|+|PM|的最小值是()A.8 B.C.10 D.11.(5分)若椭圆=1与双曲线=1有相同的焦点F1、F2,P是这两条曲线的一个交点,则△F1PF2的面积是()A.4 B.2 C.1 D.12.(5分)已知A,B是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2(k1k2≠0),若椭圆的离心率为,则|k1|+|k2|的最小值为()A.1 B.C.D.2二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)过椭圆=1的焦点F的弦中最短弦长是.14.(5分)过抛物线y2=﹣12x的焦点作直线l,直线l交抛物线于,A,B两点,若线段AB中点的横坐标为﹣9,则|AB|=.15.(5分)已知圆C过双曲线﹣=1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是.16.(5分)设点P是椭圆=1(a>b>0)与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为.三、解答题:本大题共6小题,共70分,解答应有证明或演算步骤17.(10分)已知半径为5的圆C的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y﹣29=0相切.(1)求圆C的方程;(2)设直线ax﹣y+5=0与圆C相交于A、B两点,求实数a的取值范围.18.(12分)在平面直角坐标系xOy中,直线l与抛物线y2=4x相交于不同的两点A,B.(Ⅰ)如果直线l过抛物线的焦点,求•的值;(Ⅱ)在此抛物线上求一点P,使得P到Q(5,0)的距离最小,并求最小值.19.(12分)已知椭圆的一个顶点为A(0,﹣1),焦点在x轴上,若右焦点到直线x﹣y+2=0的距离为3.(Ⅰ)求椭圆的方程;(Ⅱ)设椭圆与直线y=x+m相交于不同的两点M、N,问是否存在实数m使|AM|=|AN|;若存在求出m的值;若不存在说明理由.20.(12分)如图,已知四棱锥S﹣ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.(Ⅰ)求证:PQ∥平面SCD;(Ⅱ)求二面角B﹣PC﹣Q的大小.21.(12分)设过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q 与点P关于y轴对称,O为坐标原点,若且.(1)求点P的轨迹M的方程;(2)过F(2,0)的直线与轨迹M交于C,D两点,求•的取值范围.22.(12分)如图,椭圆=1(a>b>0)的一个焦点是F(1,0),O为坐标原点.(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,值有|OA|2+|OB|2<|AB|2,求a的取值范围.2014-2015学年黑龙江省绥化市三校联考高二(上)期中数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的.1.(5分)命题“若a>b,则a+c>b+c”的逆否命题为()A.若a<b,则a+c<b+c B.若a≤b,则a+c≤b+cC.若a+c<b+c,则a<b D.若a+c≤b+c,则a≤b【解答】解:把“若a>b,则a+c>b+c”看做原命题,它的逆否命题是题设和结论否定并且要交换位置,∴它的逆否命题是:“若a+c≤b+c,则a≤b”,故选:D.2.(5分)与曲线=1共焦点,而与曲线=1共渐近线的双曲线方程为()A.=1 B.=1 C.=1 D.=1【解答】解:由题意得,曲线=1是焦点在y轴上的椭圆,且c===5,所以双曲线焦点的坐标是(0、5)、(0,﹣5),因为双曲线与曲线=1共渐近线,所以设双曲线方程为,即,则﹣64λ﹣36λ=25,解得λ=,所以双曲线方程为,故选:A.3.(5分)已知双曲线=1(a>0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x【解答】解:双曲线=1(a>0)的实轴长2a、虚轴长:2、焦距长2,成等差数列,所以:4=2a+2,解得a=.双曲线=1的渐近线方程为:y=±x.故选:D.4.(5分)函数f(x)=x2﹣2ax+1在(﹣∞,2]上是单调递减函数的必要不充分条件是()A.a≥2 B.a=6 C.a≥3 D.a≥0【解答】解:∵函数f(x)=x2﹣2ax+1在(﹣∞,2]上是单调递减函数,对称轴x=a∴a≥2,根据充分必要条件的定义可判断:a≥0是必要不充分条件,故选:D.5.(5分)过抛物线y2=﹣x的焦点F的直线交抛物线于A、B两点,且A、B在直线x=上的射影分别M,N,则∠MFN等于()A.45°B.60°C.90°D.以上都不对【解答】解:根据抛物线的方程可知准线方程为x=,由抛物线的性质有|FA|=|MA|,∴∠AMF=∠AFM,同理∠BFN=∠BNF,∵AM∥x轴∥BN,∴∠MFO=∠AMF∴∠AFO=∠MFO,同理可知∠BFN=∠NFO∴∠MFN=∠MFO+∠NF0=90°故选:C.6.(5分)有下列四个命题:①命题“若xy=1,则x,y互为倒数”的逆命题;②命题“面积相等的三角形全等”的否命题;③命题“若m>1,则x2﹣2x+m=0有实根”的逆否命题;④命题“若A∩B=B,则A⊆B”的逆否命题.其中是真命题的个数是()A.1 B.2 C.3 D.4【解答】解:根据倒数的定义,可得“若xy=1,则x、y互为倒数”的逆命题:“若x、y互为倒数,则xy=1”是真命题,①正确;“面积相等的三角形全等”的否命题:“面积不相等的三角形不全等”是真命题,②正确;原命题与逆否命题有相同的真假性,∵方程x2﹣2x+m=0有实根⇔△=4﹣4m≥0⇔m≤1,∴原命题“若m>1,则x2﹣2x+m=0有实根”是假命题,∴③错误;原命题与逆否命题有相同的真假性,∵命题“若A∩B=B,则A⊆B”为假命题,∴④错误.∴真命题的个数是2,故选:B.7.(5分)方程mx+ny2=0与mx2+ny2=1(|m|>|n|>0)的曲线在同一坐标系中的示意图应是()A. B.C.D.【解答】解:方程mx+ny2=0 即y2=﹣,表示抛物线,方程mx2+ny2=1(|m|>|n|>0)表示椭圆或双曲线.当m和n同号时,抛物线开口向左,方程mx2+ny2=1(|m|>|n|>0)表示焦点在y轴上的椭圆,无符合条件的选项.当m和n异号时,抛物线y2=﹣开口向右,方程mx2+ny2=1(|m|>|n|>0)表示双曲线,故选:A.8.(5分)已知动点P(x,y)满足=,则点P的轨迹是()A.两条相交直线B.抛物线C.双曲线D.椭圆【解答】解:令f(x)=,则其几何意义为点(x,y)到(1,2)的距离,令g(x)=,其几何意义为(x,y)点到直线y=3x+4y+12的距离,依题意二者相等,即点到点(1,2)的距离与到定直线的距离相等,进而可推断出P的轨迹为抛物线.故选:B.9.(5分)一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于P,直线PF1(F1为椭圆的左焦点)是该圆的切线,则椭圆的离心率为()A.B.C.D.【解答】解:设F2为椭圆的右焦点由题意可得:圆与椭圆交于P,并且直线PF1(F1为椭圆的左焦点)是该圆的切线,所以点P是切点,所以PF2=c并且PF1⊥PF2.又因为F 1F2=2c,所以∠PF1F2=30°,所以.根据椭圆的定义可得|PF1|+|PF2|=2a,所以|PF2|=2a﹣c.所以2a﹣c=,所以e=.故选:D.10.(5分)已知点P为抛物线y=x2上的动点,点P在x轴上的射影为M,点A 的坐标是(6,),则|PA|+|PM|的最小值是()A.8 B.C.10 D.【解答】解:依题意可知,抛物线y=x2即抛物线2y=x2焦点为(0,),准线方程为y=﹣,只需直接考虑P到准线与P到A点距离之和最小即可,(因为x轴与准线间距离为定值不会影响讨论结果),由于在抛物线中P到准线的距离等于P到焦点的距离,此时问题进一步转化为|PF|+|PA|距离之和最小即可(F为曲线焦点),显然当P、A、F三点共线时|PF|+|PA|距离之和最小,为|FA|,由两点间距离公式得|FA|==10,那么P到A的距离与P到x轴距离之和的最小值为|FA|﹣=故选:B.11.(5分)若椭圆=1与双曲线=1有相同的焦点F1、F2,P是这两条曲线的一个交点,则△F1PF2的面积是()A.4 B.2 C.1 D.【解答】解:不妨设P为双曲线右支上的点,由椭圆的定义可得,PF1+PF2=4,由双曲线的定义,可得,PF1﹣PF2=2,解得PF1=2+,PF2=2﹣,F1F2=2,由于(2)2+(2﹣)2=(2)2,则三角形PF1F2为直角三角形,则面积为:=1,故选:C.12.(5分)已知A,B是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2(k1k2≠0),若椭圆的离心率为,则|k1|+|k2|的最小值为()A.1 B.C.D.2【解答】解:设M(t,s),N(t,﹣s),t∈[0,a],s∈[0,b],A(﹣a,0),B(a,0),k1=,k2=﹣|k1|+|k2|=||+|﹣|≥2=2当且仅当=﹣,即t=0时等号成立.因为A,B是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,M(t,s),N(t,﹣s),即s=b∴|k1|+|k2|的最小值为,∵椭圆的离心率为,∴,∴a=2b∴|k1|+|k2|的最小值为1故选:A.二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)过椭圆=1的焦点F的弦中最短弦长是.【解答】解:由题意设F(),过F的弦中垂直于x轴的弦最短;∴x=时,y=;∴最短弦长为.故答案为:.14.(5分)过抛物线y2=﹣12x的焦点作直线l,直线l交抛物线于,A,B两点,若线段AB中点的横坐标为﹣9,则|AB|=24.【解答】解:∵抛物线的方程为y2=﹣12x,∵2p=12,p=6,∵|AB|=x A+x B+p=x A+x B+6,∵若线段AB的中点M的横坐标为﹣9,∴(x A+x B)=﹣9,∴x A+x B=﹣18,∴|AB|=18+6=24.故答案为:2415.(5分)已知圆C过双曲线﹣=1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是.【解答】解:由双曲线的几何性质易知圆C过双曲线同一支上的顶点和焦点,所以圆C的圆心的横坐标为4.故圆心坐标为(4,±).∴它到中心(0,0)的距离为d==.故答案为:.16.(5分)设点P是椭圆=1(a>b>0)与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为.【解答】解:根据已知条件知P点在y轴右侧;由得,;∵|PF1|+|PF2|=2a,∴由|PF1|=3|PF2|得,;∴,F2(c,0);∴,整理得:a=2,或a=(舍去);∴a2=8b2=8a2﹣8c2;∴7a2=8c2;∴.故答案为:.三、解答题:本大题共6小题,共70分,解答应有证明或演算步骤17.(10分)已知半径为5的圆C的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y﹣29=0相切.(1)求圆C的方程;(2)设直线ax﹣y+5=0与圆C相交于A、B两点,求实数a的取值范围.【解答】解:(1)设圆心为M(m,0)(m∈Z),∵圆C与直线4x+3y﹣29=0相切,且半径为5,∴圆心,到直线4x+3y﹣29=0的距离d=r,即=5,即|4m﹣29|=25,∵m为整数,∴m=1,则所求圆的方程为(x﹣1)2+y2=25;(2)直线ax﹣y+5=0即y=ax+5,代入圆的方程,消去y整理得:(a2+1)x2+2(5a﹣1)x+1=0,∵直线ax﹣y+5=0交圆于A,B两点,∴△=4(5a﹣1)2﹣4(a2+1)>0,即12a2﹣5a>0,解得:a<0或a>,则实数a的取值范围是(﹣∞,0)∪(,+∞).18.(12分)在平面直角坐标系xOy中,直线l与抛物线y2=4x相交于不同的两点A,B.(Ⅰ)如果直线l过抛物线的焦点,求•的值;(Ⅱ)在此抛物线上求一点P,使得P到Q(5,0)的距离最小,并求最小值.【解答】解:(Ⅰ)由题意:抛物线焦点为(1,0)设l:x=ty+1代入y2=4x消去x得y2﹣4ty﹣4=0,设A(x1,y1),B(x2,y2)则y1+y2=4t,y1y2=﹣4∴•=x1x2+y1y2=(ty1+1)(ty2+1)+y1y2=t2y1y2+t(y1+y2)+1+y1y2=﹣4t2+4t2+1﹣4=﹣3.(Ⅱ)设P(x,y),则|PQ|===,∴x=3时,P到Q(5,0)的距离最小,此时,,|PQ|min=4.19.(12分)已知椭圆的一个顶点为A(0,﹣1),焦点在x轴上,若右焦点到直线x﹣y+2=0的距离为3.(Ⅰ)求椭圆的方程;(Ⅱ)设椭圆与直线y=x+m相交于不同的两点M、N,问是否存在实数m使|AM|=|AN|;若存在求出m的值;若不存在说明理由.【解答】解:(Ⅰ)依题意可设椭圆方程为,则右焦点F()由题设,解得a2=3.故所求椭圆的方程为.(Ⅱ)设P为弦MN的中点,由得4x2+6mx+3m2﹣3=0由于直线与椭圆有两个交点,∴△>0,解得:﹣2<m<2.由韦达定理可知:,从而.∴,又|AM|=|AN|,∴AP⊥MN,则,即m=2,因为:﹣2<m<2.所以不存在实数m使|AM|=|AN|.20.(12分)如图,已知四棱锥S﹣ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.(Ⅰ)求证:PQ∥平面SCD;(Ⅱ)求二面角B﹣PC﹣Q的大小.【解答】证明:(1)证明取SC的中点R,连QR,DR.由题意知:PD∥BC且PD=BC;QR∥BC且QP=BC,∴QR∥PD且QR=PD.∴PQ∥DR,又PQ⊄面SCD,∴PQ∥面SCD.(6分)(2)解:以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,则S(0,0,a),B(0,a,0),C(﹣a,a,0),Q(0,a).面PBC的法向量为=(0,0,a),设为面PQC的一个法向量,由,cos<,∴二面角B﹣PC﹣Q的大小为arccos.(12分)21.(12分)设过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q 与点P关于y轴对称,O为坐标原点,若且.(1)求点P的轨迹M的方程;(2)过F(2,0)的直线与轨迹M交于C,D两点,求•的取值范围.【解答】解:(1)∵过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q与点P关于y轴对称,∴Q(﹣x,y),设A(a,0),B(0,b),∵O为坐标原点,∴=(x,y﹣b),=(a﹣x,﹣y),=(﹣x,y),,∵且,∴,解得点P的轨迹M的方程为.(2)设过F(2,0)的直线方程为y=kx﹣2k,联立,得(3k2+1)x2﹣12k2x+12k2﹣3=0,设C(x1,y1),D(x2,y2),则x1+x2=,x1x2=,=(x1﹣2,y1),=(x2﹣2,y2),∴=(x1﹣2)(x2﹣2)+y1y2=(1+k2)(x1﹣2)(x2﹣2)=(1+k2)[x1x2﹣2(x1+x2)+4]=(1+k2)(﹣+4)==+,∴当k2→∞,•的最小值→;当k=0时,•的最大值为1.∴•的取值范围是(,1].22.(12分)如图,椭圆=1(a>b>0)的一个焦点是F(1,0),O为坐标原点.(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,值有|OA|2+|OB|2<|AB|2,求a的取值范围.【解答】解:(Ⅰ)设M,N为短轴的两个三等分点,因为△MNF为正三角形,所以,即1=,解得.a2=b2+1=4,因此,椭圆方程为.(Ⅱ)设A(x1,y1),B(x2,y2).(ⅰ)当直线AB与x轴重合时,|OA|2+|OB|2=2a2,|AB|2=4a2(a2>1),因此,恒有|OA|2+|OB|2<|AB|2.(ⅱ)当直线AB不与x轴重合时,设直线AB的方程为:,整理得(a2+b2m2)y2+2b2my+b2﹣a2b2=0,所以因为恒有|OA|2+|OB|2<|AB|2,所以∠AOB恒为钝角.即恒成立.x1x2+y1y2=(my1+1)(my2+1)+y1y2=(m2+1)y1y2+m(y1+y2)+1==.又a2+b2m2>0,所以﹣m2a2b2+b2﹣a2b2+a2<0对m∈R恒成立,即a2b2m2>a2﹣a2b2+b2对m∈R恒成立.当m∈R时,a2b2m2最小值为0,所以a2﹣a2b2+b2<0.a2<a2b2﹣b2,a2<(a2﹣1)b2=b4,因为a>0,b>0,所以a<b2,即a2﹣a﹣1>0,解得a>或a<(舍去),即a>,综合(i)(ii),a的取值范围为(,+∞).赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
