GDP与经济发展及人口变化关系模型
经济预测报告的主要模型和工具

经济预测报告的主要模型和工具随着社会经济的发展和变化,预测经济发展趋势成为了各界关注的焦点。
经济预测报告是指通过一系列模型和工具对未来经济发展趋势进行预测和分析的报告。
本文将介绍经济预测报告的主要模型和工具,包括GDP预测模型、ARIMA模型、VAR模型、计量经济学方法、人工智能模型以及决策树模型。
一、GDP预测模型GDP预测模型是预测经济增长的主要模型之一。
它基于对GDP与各个经济因素之间关系的分析,通过建立数学模型进行预测。
GDP预测模型的核心理论是经济增长因素模型,该模型包括消费、投资、政府支出和净出口等多个变量。
通过对这些变量进行分析和测量,可以预测未来的GDP增长率。
二、ARIMA模型ARIMA模型是一种时间序列分析模型,常用于短期经济预测。
它基于对历史经济数据的分析,通过寻找数据中的趋势和季节性变化,来预测未来的经济走势。
ARIMA模型包括自回归(AR)部分、差分(I)部分和移动平均(MA)部分。
通过对这三个部分进行组合,可以建立数学模型进行经济预测。
三、VAR模型VAR模型是一种多变量时间序列分析模型,用于预测经济变量之间相互关系。
VAR模型基于向量自回归理论,通过对各个经济变量之间的关系进行建模,来预测未来的经济变化。
VAR模型能够考虑多个经济变量之间的相互影响,因此在预测经济发展趋势方面具有很强的优势。
四、计量经济学方法计量经济学方法是经济预测报告中常用的统计学方法之一。
它通过对大量经济数据进行分析和研究,寻找数据之间的关系和规律。
计量经济学方法主要包括回归分析、相关分析、时间序列分析等。
这些方法能够有效地挖掘数据中的信息,并用于预测未来的经济走势。
五、人工智能模型人工智能技术的发展为经济预测报告带来了新的机遇和挑战。
人工智能模型可以通过对大量经济数据进行学习和分析,建立起复杂的预测模型。
它可以处理大规模和高维度的数据,并挖掘数据中的非线性关系。
人工智能模型的发展为经济预测提供了新的思路和方法。
宏观经济的经济增长模型

宏观经济的经济增长模型在宏观经济学中,经济增长模型被广泛应用于分析和预测一个国家或地区的经济总体增长。
这些模型旨在解释经济增长的原因、推动因素以及对经济体整体产出和生产率的影响。
本文将介绍几种主要的宏观经济的经济增长模型。
一、古典增长模型古典增长模型又称为劳动增长模型,是最早的一种增长模型。
该模型假设经济增长主要由人口增长和劳动生产率的增加所驱动。
其核心假设是,随着劳动力的增加和劳动生产率的提高,国民经济总体产出也会相应增加。
这一模型最早由亚当·斯密等经济学家提出,并在其经济学巨著《国富论》中得到详细阐述。
二、新古典增长模型新古典增长模型是对古典增长模型的改进和扩展。
该模型引入了资本积累的概念,认为资本投资对经济增长起到了重要作用。
新古典增长模型将经济增长解释为劳动力、资本和技术进步共同作用的结果。
在该模型中,资本积累通过提高生产力和劳动生产率,从而推动经济增长。
新古典增长模型主要由罗伯特·索洛等经济学家提出。
三、内生增长模型与古典和新古典增长模型不同,内生增长模型认为技术进步是经济增长的内在推动力,而不是外部因素。
该模型将创新、研发和教育等因素纳入经济增长模型的考虑范畴。
内生增长模型认为,通过增加技术创新和人力资本投资,经济体可以实现持续的经济增长。
这一模型由保罗·罗默和罗默共同开发提出。
四、扩散增长模型扩散增长模型强调技术进步的传播和扩散对经济增长的重要性。
该模型认为,不同国家或地区之间的技术进步可以通过贸易、外商直接投资和人员流动等途径进行传递和扩散,从而促进整体经济的增长。
扩散增长模型主要由保罗·罗默等经济学家提出,并得到了广泛应用和认可。
五、新增长理论新增长理论是对传统经济增长模型的进一步发展和拓展。
该理论认为,技术进步和知识创新对经济增长的推动作用远远大于传统模型所能解释的范畴。
新增长理论强调创新、研发、知识产权保护等因素对经济增长的重要性,并提出了一系列政策建议来促进经济增长。
GDP与经济发展及人口变化关系模型

GDP与经济发展及人口变化关系模型摘要本文讨论了国内生产总值与经济发展及人口变化的关系问题.针对问题一:国内生产总值是衡量经济发展的重要指标,而固定资产投资和进出口贸易的快速发展推动了我国经济的增长,因此有必要站在宏观的角度对我国国内生产总值与固定资产投资及进出口总额的关系进行分析.通过查找数据建立三者之间的基本回归模型,利用matlab进行求解,结果见文中表1.考虑到固定资产投资与进出口总额之间可能存在交互作用,将模型进行改进求解结果见文中表2.对两个模型进行结果的检验和预测,通过分析对比两者的数据得出改进的模型拟合度更高,更符合实际.针对问题二:当经济中总产出、收入和就业连续6个月到一年有明显下降,经济出现普遍收缩时,标志着经济衰退,因此分别建立国内生产总值与财政收入及失业率之间的回归模型.通过模型预测2012年财政收入为103.7925千亿元,同比增长0.0506%,失业率为4.1026% ,同比增长0.0634%.由于0.0506%与0.0634%都是相当小的数字,财政收入和失业率的增幅均是非常微小的,因此在一定程度上不能说明经济有衰退的迹象,只能说明经济涨幅不大.针对问题三:国内生产总值增长率、通货膨胀率和失业率是判断宏观经济运行状况的三个主要指标.通货膨胀率一般是用国内生产总值缩减指数来衡量的,通过奥肯定律可以得出国内生产总值与失业率的关系,进而得出国内生产总值是通过影响通货膨胀率及失业率对经济形势起决定性影响.针对问题四:建立关于人口数量与国内生产总值的自回归分布滞后模型,对其求解结果见文中表7,可以看出人口数量不仅与国内生产总值有关系,而且与其自身前一年的人口数量也存在着紧密的联系.问题一各项经济指标均会随时间的变化而变化,将问题一进行推广建立关于国内生产总值与固定资产投资及进出口总额的混合有限多项式分布滞后模型.此外统计回归模型是用途最广泛的一类随机模型.该模型不仅适用于对各个经济指标间关系的讨论,也可用于产品销售量的预测、教学评估、人口预测.关键词奥肯定律;统计回归模型;经济衰退;自回归分布滞后模型一、问题重述一个国家的国内生产总值往往反映该国的经济发展状况,中国亦无例外.改革开放以来,中国经济持续保持高速发展,特别是近20年更是基本保持10%以上的增长速度.据统计局数据,1979-2010年中国经济的平均增速是9.9%;1991-2010年平均增速是10.5%;2001-2010年平均增速也是10.5%.经过30多年的高速增长,中国经济已变得体量巨大、基数巨大.在2012年之前,我国国内生产总值逐步呈上升趋势,而在2012年的国内生产总值有所放缓,这与我国的经济政策发生变化相关联.请查找资料,利用数学建模给出如下四个问题的探讨:(1)通过一个或两个方面探讨2012年以前中国国内生产总值与其经济变化的关系.(2)中国2012年国内生产总值放缓能否证明经济形势有衰退的迹象.(3)如何评价中国国内生产总值对经济形势的影响.(4)中国人口变化与国内生产总值有无关系.二、问题分析国内生产总值是衡量经济发展的重要指标,它与我国经济及人口的变化均有着一定的联系,根据考虑问题的侧重点不同,以下从四个方面作详细讨论.针对问题一:固定资产投资和进出口贸易的发展,对我国经济的增长起到了推动的作用.但它们对经济增长的拉动作用是否显著,国内生产总值与固定资产投资和进出口总额三者之间存在什么样的关系,是需要进一步统计和检验的.通过查找1992-2011年20年的国内生产总值、进出口贸易额和固定资产投资额(全文数据均来自《中国统计年鉴》)的处理,建立统计回归模型,进而可以分析得出国内生产总值与固定资产投资额和进出口贸易额之间的关系.针对问题二:当经济中总产出、收入和就业连续6个月到一年的明显下降,经济出现普遍收缩时,标志着经济衰退.因此对1992-2011年20年的国内生产总值与财政收入及其与就业率的数据进行分析,分别建立关于国内生产总值与财政收入和国内生产总值与就业率的回归模型,通过预测2012年国内生产总值、财政收入和就业率来判断当国内生产总值放缓时经济是否有衰退的迹象.针对问题三:国内生产总值增长率、通货膨胀率和失业率是判断宏观经济运行状况的三个主要指标.通货膨胀率一般是用国内生产总值缩减指数来衡量的,由此国内生产总值缩减指数可以直接由国内生产总值计算得出.因此可以通过奥肯定律找出失业率与其增长率的函数关系,以此来判断出中国国内生产总值对经济形势的影响.针对问题四:人口总量与国内生产总值是随时间变化而发生改变的.当年的人口总量与最近三年的人口总量和国内生产总值都有关系,因此建立关于从1992年到2011年20年人口总量与国内生产总值的自回归分布滞后模型分析得人口变化与国内生产总值的关系.三、基本假设1.数据以年为基准,不考虑一年内的波动和变化;2.数据均为按当年价格计算的名义值;3.所有数据均真实可靠.四、符号表示与名词解释固定资产投资:是以货币形式表现的在一定时期内全社会建造和购置固定资产的工作量以及与此有关的费用的总称.财政收入:指国家财政参与社会产品分配所取得的收入,是实现国家职能的财力保证.进出口总额:指实际进出我国国境的货物总金额.五、模型建立与求解国内生产总值的增长对经济发展起着越来越重要的作用,因此必须正确认识国内生产总值增长与经济发展之间的关系.在我国,人口问题也不容忽视,它制约着中国经济和社会的发展.下面通过对各问题的分析,建立相应的模型,并求解.文中所有数据见附表一.5.1 国内生产总值与进出口贸易总额和固定资产投资的回归模型基本回归模型 设第t 年的国内生产总值为t G ,固定资产投资为t I ,进出口总额为t E ,t =1,…,n ( n =20).因变量t G 与自变量t I 和t E 的散点图见图1和图2.图1 t G 对t I 的散点图 图2 t G 对t E 的散点图由图1可以看出,随着固定资产投资额的增加,国内生产总值向上弯曲增长的趋势渐缓,图中曲线是用二次函数模型2012=+++t t t G I I βββε (1)拟合的(其中ε是随机误差).而图2中,当进出口总额增大时,国内生产总值向上弯曲增长的趋势加强,图中曲线仍是用二次函数模型2012=+++t t t G E E βββε (2)拟合的.综合上面的分析,结合(1)和(2)建立如下的回归模型2201234=+++++t t t t t G I E I E βββββε (3) 根据附表一的数据,对(3)利用matlab 统计工具箱求解(见附录程序一),得到回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表1=0.9941R 表明t G 的99.41%可由(3)确定,F 值远远超过其检验的临界值,p远小于α,因而模型(3)从整体上看是可用的.将回归系数的估计值代入(3),得到基本回归模型22=27.7677+0.9937+0.7844-0.00004-0.001t t t t t G I E I E (4)模型改进 从表面上看基本模型(4)的拟合度已经很高2=0.9941R ,但模型(4)中回归变量t I 和t E 对因变量t G 的影响是相互独立的.实际中由于t I 和t E 均与t G 存在很大的依赖关系,因此t I 与t E 之间应存在着交互作用会对t G 产生影响.不妨简单地用t I 与t E 的乘积代表它们的交互作用,于是将(3)增加一项,得到22012345=++++++t t t t t t t G I E I E I E ββββββε (5)对(5)求解(见附录程序二) 得到回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表2表2与表1的结果相比,=0.9961R 有所提高,说明(5)比(3)有所改进.并且,所有参数的置信区间,特别是t I 与t E 交互项系数5β的置信区间不包含零点,这就说明t I 与t E 之间存在着交互作用并对t G 产生影响.F 值也远远超过其检验的临界值,p 也远小于α,所以(5)比(3)更符合实际.将回归系数的估计值代入(5),得到改进的回归模型22=17.6708+0.9993+1.2295-0.0138-0.0204+0.0316t t t t t t t G I E I E I E (6)结果分析及预测 从机理上看,对于经济规律作用下的时间序列数据,加入交互项的模型(6)更为合理.将模型(4)和模型(6)的计算值t G 与实际数据t G 的比较以及两个模型的残差t e (=-t t t e G G )表示在表3、图3和图4上.可以看出模型(6)更合适些.表3:模型(4)和模型(6)的计算值G 与残差et G (模型t G (模型48.2305 43.0398 60.2638 58.2552 65.5259 64.6390图3 模型(4),(6)的t G 与t G 图4 模型(4),(6)的t e(注:图3和图4中蓝色表示实际数据,绿色表示模型(4)计算出的数据,红色表示模型(6)计算出的数据)5.2 国内生产总值放缓与经济衰退关系模型分析国内生产总值与财政收入的关系模型 设第t 年财政收入为t F ,画出因变量t F 与自变量t G 的散点图(t =1,…,n ( n =20)),并直接利用matlab 统计工具箱(CFTOOL 命令)拟合曲线见图5.图5 t F 与t G 的散点图 拟合函数的表达式为2012=+++t t t F G G βββε (7)其中(7)各参数的值及其置信区间见表4=0.9986R 表明t F 的99.86%可由(7)确定.RMES 为回归系统的拟合标准差,其越小说明曲线拟合的越好.表4显示 1.72RMES =,因此模型(7)是可用的.将回归系数的估计值代入(7)得到2=-3.381+0.1638+0.0001346t t t F G G (8)查看中国科学院预测科学研究中心关于《2012年我国GDP 预测及宏观经济形势分析》知道预计2012年国内生产总值的增长率为8.5%.因此预计2012年国内生产总值为471.564(千亿元),将其代入(8)得到2012年财政收入为103.7925(千亿元).与2011年财政收入103.740(千亿元)相比,同比增长了0.0506%,因此2012年我国财政收入仍是增长的,只是增长幅度非常小而已.国民生产总值与失业率的关系模型 设第t 年失业率为t U (t =1,…,20),画出因变量t U 与自变量t G 的散点图,并直接利用matlab 统计工具箱(CFTOOL 命令)拟合曲线见图6.图6 t U 与t G 的散点图拟合函数的表达式为222471582------036=+++t t t G G G t U eeeβββββββββε⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(9)其中(9)中各参数的值及其置信区间见表5=0.9412R 表明t F 的94.12%可由(7)确定.0.2103RMES =,因此模型(7)是可用的.将回归系数的估计值代入(7)得到222-41.48-19.41-38.83---8.21421.29 3.965=5.425+4.24-3.141t t t G G G t U eee⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(10)将预计的2012年国内生产总值471.564(千亿元)代入(8)得出2012年失业率为4.1026%,与2011年失业率4.1%相比,同比增长了0.0634%.因此2012年我国公失业率仍是增长的,只是增幅很小而已. 而经济衰退是指当经济中总产出、收入和就业连续6个月到一年的明显下降,经济中很多部门出现普遍收缩,则这种经济下降称为衰退. 0.0634%的增长是很微小的,因此可视为失业率基本没有变化.通过以上讨论分析可得当GDP 增幅减小为8.5%时,财政收入同比增长了0.0506%,失业率同比增长了0.0634%.由于0.0506%与0.0634%都是相当小的数字,因此不能说明经济有衰退的迹象,只能说明经济涨幅不大. 5.3 国内生产总值对经济形势影响关系模型设第t 年经济状况指数为t λ,国内生产总值增长率为t g ,失业变化率为t U ∆.通过奥肯定律:=-0.5(-2.25)t t U g ∆ 可以得出失业率t U 与t g 的关系为=-0.5(-2.25)t t U g dt ⎰ (11)又t λ受t g 及t U 的影响,设i a (i =1,2)分别表示t g 、t U 对t λ的权重,则12=+t t t a g a U λ (12) 由(11)和(12)可得t g 对经济形势影响的关系模型为12=+-0.5(-2.25)t t t a g a g dt λ⎰ (13)通过(13)可得国内生产总值通过对失业率的影响对经济形势起决定性影响. 5.4 中国人口变化与国内生产总值关系模型自回归分布滞后模型 设第t 年人口总数为t P ,(t =1,…,n ( n =33)).数据(见附表二)借鉴计量经济学中的自回归分布滞后模型,首先建立初始模型012132112233t t t t t t t t P G G G P P P ααααβββε-----=+++++++ (14)即当年的人口总量与最近三年的人口总量和国内生产总值都有关系,t ε为随机干扰项.查找近三十年我国人口总量(数据见附表一),利用matlab 进行求解得回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表6=0.99995R 表明t P 的99.995%可由(14)确定,F 值远远超过其检验的临界值,p 远小于α,因而模型(3)从整体上看是可用的.检查参数的置信区间发现1α,2α,3α和3β的置信区间均包含零点,表明回归变量t G ,1t G -,2t G -和3t P -对t P 的影响不太显著.模型改进 由于每年P 和G 的值都分别与其前几年的值有关,且P 与G 两者之间也存在着一定的关系,因此通过对1t G -,2t G -和3t P -逐项剔除后重新拟合并检查其2R ,F 和p 的值及各参数的置信区间,得到最终改进的模型0121t t t P G P βββ-=-+ (15) 求解(15)结果见表7=0.99979R 表明t P 的99.979%可由(15)确定有所提高,表7与表6的结果相比,所有参数的置信区间均不包含零点,F 值也远远超过其检验的临界值,p 也远小于α,所以(16)更符合实际.将回归系数的估计值代入(15)得到1=3351.5-0.0015122+0.98296t t t P G P - (16)从(16)可以看出人口数量不仅与国内生产总值有关系,而且与其自身前一年的人口数量也存在着紧密的联系.结果分析及预测 将用模型(16)的计算值t P 与实际数据t P 的比较以及两个模型的残差t e (=-t t t e P P )表示在表8、图7上.图7 模型(16)'.'t P ,''t P o ,'*'t e表8和图7显示用模型(16)预计的人口数量与实际人口数量非常吻合,因此模型(16)更贴合实际.六、模型评价和推广模型的评价本文在正确查找数据基础上建立了多个统计回归模型.在对原始数据进行拟合时,采用多种方法,对模型不断进行改进,使其愈来愈完善且具有很高的拟合精度.在此基础,对模型作进一步分析讨论得到一系列可靠而实用的信息.但由于时间紧迫以及数据量的不足,部分模型较为粗糙,需要进一步改进. 模型检验通过已有数据进行拟合与比较来检验模型,经检验证实建立的模型对原始数据有很高的拟合度,基本符合模型建立的初衷. 模型的推广推广一:由于各项经济指标都会随时间的变化而变化,针对问题一可以采用混合有限多项式分布滞后模型进行拟合,模型如下:01213212132112233t t t t t t t t t t G I I I E E E G G G ααααβββγγγε-------=++++++++++ 其中i α,i β和i γ为参数,0,1,2,3i =.推广二:统计回归模型是用途最广泛的一类随机模型.该模型不仅适用于对各个经济指标间关系的讨论,也可用于产品销售量的预测、教学评估、人口预测等问题.参考文献[1]姜启源,谢金星,叶俊.数学模型[M].北京:高教出版社,2011.1.[2]国家统计局编.中国统计年鉴(2011)[M].北京:中国统计出版社,2012.2. [3]中国国家统计局网站 /2012-8-15.[4]陈锡康,祝坤福 王会娟.2012年我国GDP 预测及宏观经济形势分析[M]. 北京:高教出版社,2012.1. [5]萨谬尔森,诺德豪斯.经济学[M].北京:高教出版社,2000.6. 附录表一11。
论人口发展与经济增长的系统动力机制

论人口发展与经济增长的系统动力机制作者:倪同春来源:《中国市场》2021年第11期[摘要]目的是探讨人口发展与经济增长的系统动力机制。
方法是文章从人口发展与经济增长的关系出发,建立系统动力模型,对模型进行稳健性检验,分析了该模型的预测功能。
结果是①人口发展和经济增长密切相关;②经济增速的提高,依赖人口发展水平的提升;③出生率决定了就业人数,是保障劳动力供给的重要因素;④要想提高人口质量,必须提高教育支出水平,而这离不开经济增长。
结论是一是短期内应挖掘劳动力和人力资本存量,提高劳动参与率,注重劳动力的技能培训;二是长期内应采取宽松的人口生育政策,提高教育、医疗卫生支出,从而提升人口数量和质量。
[关键词]人口发展;经济增长;系统动力;稳健性;预测功能全面放开“二胎”政策,是对我国计划生育政策的重大调整,结合我国经济社会的发展情况,可见该政策的出台是及时的、必要的。
简单来说,“二胎”政策能增加我国人口数量,积极应对人口老龄化,激发第二次人口红利,继而助推国民经济健康发展。
由此可见,人口发展和经济增长之间具有密切关联。
1 研究背景从全球范围来看,关于人口和经济两者间的关系研究集中在三个方面:一是人口数量和经济增长的关系,乐观的观点认为人口增长会带来新的劳动力、新的知识、新的技术,从而加快经济增长;悲观的观点认为人口增长会造成资本不足,从而限制经济增长;二是人口结构和经济增长的关系,主要探讨年龄结构、劳动力供给、消费、投资、储蓄、进出口、资本流动之间的影响;三是人口质量和经济增长的关系,认为人力资本具有经济增长效应,也有学者持怀疑态度。
实际上,人口的数量、结构、质量,可以统称为人口发展[1]。
正是得益于经济社会的增长,人口才会有所发展;而人口发展又会影响经济增长,两者相互作用、相互影响。
为了得出更加全面、科学的结论,本研究引入系统动力学方法,不仅分析两者的关系,还预测两者的发展趋势。
2 人口发展与经济增长的关系2.1 人口数量对经济增长的影响国外经济学家提出的新古典增长模型中,阐述了资本(K)、技术(A)、劳动力(L)的关系,即Y=A·F(K,L)。
经济增长模型

PPT文档演模板
经济增长模型
• 三、新增长理论
20世纪80年代中期以来逐渐发展的内生增长理 论不断将新古典增长理论中假定的外生因素内生 化,认为这些因素既是推动经济增长的主要力量, 也是经济增长本身的结果。区别于新古典增长理 论,内生增长理论也被称为新增长理论。
•由两部门均衡条 件I=S,得到: •(2)代入(1):
PPT文档演模板
经济增长模型
➢稳态
人均资本存量不再变化时
的资本存
量水平被称为资本的稳定状态水平,简称稳态。
• 在稳态时,由于人均资本存量不变,人均产 出也稳定在一个水平上不再发生变化,人均产 出的增长不再持续。
• 注意:总产出的增长还会以人口增长的速度进 行下去。
但是,没有任何消费的情况是不可能的。 即使一些实行计划经济的国家曾经通过抑制消 费来获取高投资率,但也不可能做到将所有收 入都用于投资。
PPT文档演模板
经济增长模型
那么,采取一个什么样的储蓄率水平是 最好的呢?
n 从经济福利的角度来看,选择一个什么样 的稳定水平,取决于社会的个人福利最大化。
n 对个人而言,他本身并不关心产出和资本 有多少,而是关心可供他消费的产品与服务有 多少。个人福利最大化可以用个人消费的最大 化来表示。
经济增长模型
➢促进经济增长的方法
提高储蓄率和降低人口增长率可以促进经 济增长,但提高储蓄率和降低人口增长率都有 一定的限度。这两种方法对经济的影响都只是 暂时的。
这就意味着依靠以上两种方法来促进人均 产出的长期增长是不可行的。
那么,怎么解释一些国家数百年来人 均收入(产出)不断提高的现象呢?
PPT文档演模板
经济增长模型

生产函数 Y (t) = F (K (t), A(t)L(t)) = Kα ( AL)1−α ,K (t) 资本,L(t) 劳动力,A(t)
技术 要素投入的变化(扩大再生产) 劳动力扩大再生产: L&(t) = nL(t) , n 人口
增长率
技术扩大再生产: A&(t) = gA(t) , g 技术进
sy* = (n + d )k * 用图表示为:
4
关于稳态的几个结论:因为在稳态有 ∆y = 0 ,表示人均 GDP 不增长,那么此 时总的 GDP 增长率( ∆Y Y )=人口增长率 n。即在稳态的增长率与储蓄率 s 无关 (仅仅与 n 有关)。 ※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
P44
专栏
3-2),即
从全部的 ∆y y 增长中不能被要素投入的增长所解释的部分,体现了技术进步的
力量。——注意 P53 页的专栏 3-3,注意 P56 页习题 7(注意 P58 注释 9,已知
Y=AF(K,N),如何去推人均的生产函数 y=f(k))。
Note:书中提到了技术进步对生产函数的两种影响。一种是对 K,N 都产
Y
Y
∆Y = (1 − θ ) • ∆N + θ • ∆K + ∆A P41(2)
Y
N
KA
其含义是:
产出的增长=劳动增长×劳动份额+资本增长×资本份额+技术进步
2.经济增长的人均指标 人均指标主要有两个: ∆y y 表示人均的 GDP 增长率; ∆k k 表示人均机器数 的增长率( k 为人均机器数,又称资本-劳动比率); 必须清楚总量增长指标和人均指标之间的关系:
∆y = θ • ∆k + ∆A P42(4)
我国人口出生率对经济发展的影响

我国人口出生率对经济发展的影响作者:孙启晓来源:《今日财富》2022年第04期经济社会的发展离不开人口资源,把握这两者的相互关系,能为经济发展提供科学依据。
本文从我国人口出生率演变特征及经济发展现状入手,分析了人口资源和经济发展之间的关系,并建立系统动力模型进行预测研究,结果表明:①人口发展和经济增长密切相关,人口发展水平提高,能促进经济增长;②人口出生率决定了就业人数,直接影响劳动力供给水平;③增加教育支出才能提高人口质量,而这离不开经济增长。
基于此,提出建议如下:完善社保体系,调整生育政策,加快经济发展。
我国对于人口出生率与经济发展之间的研究,主要依据“马尔萨斯人口陷阱”理论,该理论明确指出:人口出生率和人们的生活状态密切相关。
国内学者的研究中,利用人口出生率、死亡率、工人工资、人均生产总值等变量进行分析,结果证实人口出生率是经济发展的内生变量。
新时代背景下,我国经济发展取得显著成就,而人口控制成为宏观调控的一个关键因素。
只有深入分析这两者的关联性,将人口出生率维持在合理范围内,才能对经济增长产生积极作用,促进经济社会的可持续发展。
一、我国人口出生率演变特征及经济发展现状(一)人口出生率演变特征依据《中国统计年鉴》和国家统计局的抽样调查数据,我国从1949年至2020年的人口出生率经历了六个阶段:①1949年-1970年是高出生率阶段,人口出生率平均为33.88‰。
②1971年-1979年是出生率大幅下降阶段,人口出生率从1971年的30.65‰降低至1979年的17.32‰。
③1980年-1987年是出生率小幅回升阶段,人口出生率从1980年的18.21‰提升至1987年的23.33‰。
④1988年-2004年是出生率持续下降阶段,人口出生率从1988年的22.37‰降低至2004年的12.29‰。
⑤2005年-2015年是出生率平稳阶段,人口出生率基本维持在12‰左右。
⑥2016年-2020年是出生率二次持续下降阶段,人口出生率从2016年的12.95‰降低至2020年的8.52‰,其中2020年首次跌破10‰。
经济增长索罗模型

gt
资本积累方程不变:
K sY dK
K / K sY / K d
把生产函数用人均产出的形式表述出来: 1
yk A
对等式两边先取对数再求导:
y/ y k/ k (1 ) A/ A
• 平衡增长路径:
由资本积累方程可知当且仅当Y/K的比值为一定值时,K的增 长率是一常数。此外,若Y/K一定,则y/k也一定,而且更重 要的是:y和k以相同比率增长。像这种资本、产出、消费和 人口均按一相同的固定比率增长的情形。 我们把某一变量x沿平衡增长路径的增长率记为 x 则根上面的分析,我们可以得到沿着平衡路径增长时
• 二,现代经济增长理论。
1,哈罗德—多马模型,提出了西方经济增长理论史上第一个经济增长 数学模型。 2,新古典模型(60-70年代)之后陷入低潮。1,分析技术方面的2,实 践方面 3,新增长模型(80年代中后期) 现代经济增长理论经历了从技术外生增长到内生增长,市场结构从完 全竞争到不完全竞争(垄断竞争)的演变。
• • • • • • • •
第1章 导言:经济增长的事实 第2章 索罗模型 第3章 新古典增长理论的实证应用 第4章 创意经济学 第5章 经济增长的引擎 第6章 一个简单的增长与发展模型. 第7章 生经济增长模型 第8章 内生经济增长模型
第1章 导言:经济增长的事实
• 这个世界由不同形态和规模的经济体组组成。有 许多十分富裕的国家,同时也存在一些非常贫困 的国家。一些国家迅速地增长,而一些则根本没 有增长的迹象。此外,一大批国家事实上是处于 这些极端之间.当考虑经济增长与发展的时候,通 过考察以下这些极端案例作为开端是很有帮助的: 富国、穷国以及处于两者间增长迅速的国家。本 章将展示一些与这些分类相关的实证证据——事 实。这样一来,自然就引出了增长与发展的核心 问题。
9.2.2 经济增长模型论: 新古典经济增长模型

基本方程解析
K 2、另一方面,人均资本 k N ln k ln K ln N 两边对时间 求微分 t 1 dk 1 dK 1 dN k dt K dt N dt k K N k K n k K N k K K k k n K K nK K k k K k K K n N k N N 两边同除以 ,得: N K k N K k n k (式2) N
k为人均资本的折旧;
2、 y为人均储蓄,S S y; S 3、k为人均资本量; k 0称为资本深化; 4、k S y n )k说明一定的人均储蓄S y必须用于装备新 ( 工人(量为n k),另一部分必须替换 旧资本(量为 k); 所以,装备新工人和替 换折旧的人均储蓄称资 本广化。 如果 S y n ),k 0,称为资本深化 ( 即资本深化k 人均储蓄S y 资本广化(n )k
人均储蓄
k sy (n )k sy k (n )k
n—人口增长率 δ—资本折旧率,0< δ<1 nk—为增加的人口配备的资本 δk——用于折旧的资本
基本方程解析
1、一方面,存量资本的 变化k取决于净投资 净投资k 总投资I 折旧(设折旧率为 ) K I K K S Y K 又因为均衡条件 S I N 两边同除以劳动量 S SY K S y k (式1) N
三、新古典稳态分析 1、稳态含义:指人均资本k和人均产量y达到一个稳定水平 的长期状态。
三、新古典稳态分析 2、稳态特征: (1)人均资本达到均衡值。△k=0,即人均资本的增量为 零。 (2)人均产量也达到均衡值。△y=0,因为y=f(k)。 (3)人均资本、人均产量不变,并不是总资本、总产量不 变,实际上,由于N以n增长率上升,经济也在增长。此时经 济增长率为:
改革开放以来我国GDP变动与居民收入变动关系实证分析_易晨晨
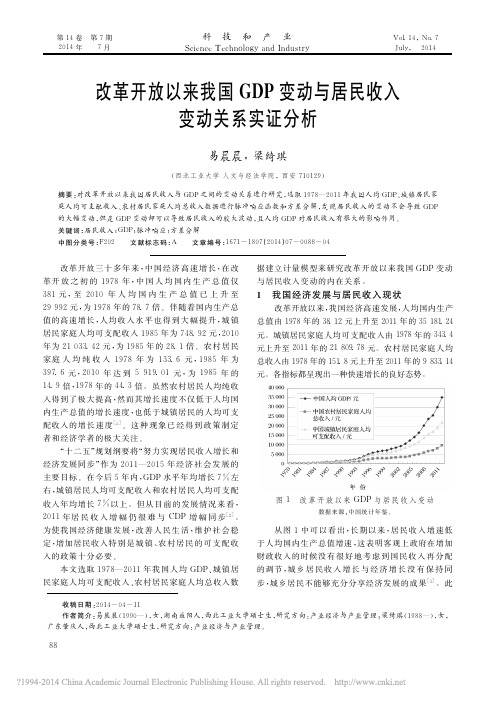
表 1 ADF 检 验 结 果
1% 水 平
5% 水 平
-2.647
-1.953
-2.639
-1.951
-2.639
-1.951
-3.679 -3.661
-2.968 -2.96
-3.654
-2.957
10% 水 平 -1.61 -1.61 -1.61 -2.623 -2.619 -2.617
改革开放三十 多 年 来,中 国 经 济 高 速 增 长,在 改 革开 放 之 初 的 1978 年,中 国 人 均 国 内 生 产 总 值 仅 381 元,至 2010 年 人 均 国 内 生 产 总 值 已 上 升 至 29 992 元 ,为1978 年 的78.7 倍 。 伴 随 着 国 内 生 产 总 值的高速增长,人均 收 入 水 平 也 得 到 大 幅 提 升,城 镇 居 民 家 庭 人 均 可 支 配 收 入 1985 年 为 748.92 元 ,2010 年为21 033.42元,为1985年 的 28.1倍。 农 村 居 民 家 庭 人 均 纯 收 入 1978 年 为 133.6 元,1985 年 为 397.6 元,2010 年 达 到 5 919.01 元,为 1985 年 的 14.9 倍 ,1978 年 的 44.3 倍 。 虽 然 农 村 居 民 人 均 纯 收 入 得 到 了 极 大 提 高 ,然 而 其 增 长 速 度 不 仅 低 于 人 均 国 内 生 产 总 值 的 增 长 速 度 ,也 低 于 城 镇 居 民 的 人 均 可 支 配收入的增 长 速 度 。 [1] 这 种 现 象 已 经 得 到 政 策 制 定 者和经济学者的极大关注。
第 14 卷 第 7 期 2014年 7月
科 技 和 产 业
国内生产总值与经济增长的关系

经济增长通常 是通过比较不 同时期国内生 产总值来计算 的,一般分为 名义增长和实
际增长。
名义增长是指 未考虑物价变 动的经济增长, 实际增长是指 考虑物价变动 的经济增长。
经济增长的衡量指标
国内生产总值(GDP):衡量一个国家或地区一定时期内生产活动的 最终成果,是经济增长的主要衡量指标。
GDP是按照国土原则计算的国内生产总值,包括在中国领土范围内生产的最终产品和劳务的价值。
国内生产总值的计算方法
定义:国内生产总 值是指一定时期内, 一个国家或地区境 内生产活动的总量。
计算方法:国内生 产总值可以通过增 加值法或收入法进 行计算,其中增加 值法较为常用。
增加值法:通过将 各产业部门的增加 值相加得到国内生 产总值。
国际经济环境对国内生产总值与经济增长的影 响
国际贸易:国际 贸易的开放程度 和贸易伙伴的经 济状况对国内生 产总值与经济增 长有直接影响。
汇率:汇率的波 动会影响出口和 进口,进而影响 国内生产总值与
经济增长。
全球经济周期: 全球经济周期的 变化会影响国内 生产总值与经济 增长,例如全球 经济衰退可能导 致国内生产总值 与经济增长放缓。
经济增长能够创造更多的就业机会,提高居民收入水平,促进社会 稳定和民生改善。
经济增长能够推动产业升级和结构调整,提高国家的国际竞争力和可 持续发展能力。
经济增长能够增加政府的财政收入,提高国家对基础设施、教育、 医疗等方面的投入,促进社会福利水平的提高。
国内生产总值与经济增长的实例分 析
不同国家国内生产总值与经济增长的对比分析
YOUR LOGO
国内生产总值与 经济增长的关系
XX,a click to unlimited possibilities
区域经济增长模型

F ( K , L) MPL 2 F ( K , L) MPL FL 0, 0 2 L L L
(3)规模报酬不变,即生产函数满足一次齐次性,可用 公式表示: Y F (K , L) F ( K , L)
一、 单区域增长:索洛模型
罗伯特· 默顿· 索洛( Robert Merton Solow),美国著名经济 学家,1987年诺贝尔经济学奖获得者,1956年发表了其代 表性论文《对经济增长理论的一个贡献》,并由此而成为 经济增长理论的代表,他构建了一个理论模型,该模型对 经济增长机制进行了独特的分析,并最终得出了经济增长 最终将趋于停滞的结论。 一个区域经济增长是通过生产要素的投入而实现的,如果 假定技术水平不变,则经济增长取决于资本和劳动,假定 劳动数量不发生变化,则经济增长唯一地与投资挂起钩来, 而由于资本的折旧最终于导致新增的投资只能满足折旧的 需要,到那时经济增长将停止,达到稳定状态。
Y1
O1
D1
O1 f ( L1 , K1 , Q1 ,...)
D1 f (C1 , I1 ,...)
T1 , R1 , SE1 , IN1 , PO1 , SO1
区域经济内生增长因素的作用关系
二、经济发展的含义
经济发展与经济增长既有联系又有区别,经 济增长是产出的增加(总产出和人均产出);而 经济发展不仅是产出的增加,还要伴随着产出结 构的改善和资源配置(投入结构)的优化。 从规范意义上讲,经济发展还包括政治、社 会体制进步、收入分配的合理化、文化教育水平 的提高以及居民劳动条件和生活条件的改善。
对任意的正数λ成立。这实际上也是生产技术的一个特征,这 一特征保证了生产要素按其边际产量进行分配。 (4)资本(或劳动)趋向于零时,资本(或劳动)的边际产 量趋向于无穷大;资本(或劳动)趋向于无穷大时,资本(或 劳动)的边际产量趋向于零。即:
我国GDP增长与人民就业及生活水平的关系分析

我国GDP增长与人民就业及生活水平的关系分析摘要:在中国经济发展重要阶段,对经济增长模式提出新要求的现在,我组本着经济以人为本的思想,通过对改革开放以来我国GDP增长与人民就业及生活水平的关系的分析,对我国原来的粗放型经济增长模式作出粗浅的考查,再联系现实情况,引出可持续发展的经济增长模式和绿色GDP。
关键词:GDP,名义GDP,实际GDP,绿色GDP,人民生活水平,消费,经济福利,就业人数,就业规模,投入,产出,资源,经济发展模式一、引言 GDP产生于第二次世界大战之后,逐渐被世界各国所采用,是指一个国家在某一既定时期内所生产的最终物品与劳务的市场价值。
它衡量一国的总收入与总支出①,其效应是多方面的,GDP的增长与人民物质生活得水平改善和丰富,就业情况的发展,国家的国际竞争力、吸引力及政治地位等有着密切的联系。
被认为是社会经济福利最好的一个衡量指标。
我国改革开放以来二十多年,创造了国内生产总值年均增长超过8%的世界奇迹。
然而GDP增长的原因很多,有必然原因,有偶然原因,有可持续性增长,有破坏性增长。
对资源破坏性开发,对劳动力破坏性使用,都可能使GDP快速增长。
GDP 是经济运行的结果,这个结果只有定量意义,没有定性意义,不能反映经济运行的质量。
经济要以人为本,在中国的经济社会发展处在一个十分重要关口,对经济增长模式提出新的要求的现在,我们有必要对改革开放以来中国经济增长与人民就业及生活水平的关系进行具体的分析。
模型的建立与修正本文采用了1978-2002年的我国国内GDP、就业和平均工资的相关数据,数据主要来源于中国统计年鉴,如下表:年份国内生产总值国内就业总人数职工平均工资 1978 3624.1 40152 615 1979 4038.2 41024 6681980 4517.8 42361 762 1981 4862.4 43725 772 1982 5294.7 45295 7981983 5934.5 46436 826 1984 7171 48197 974 1985 8964.4 49873 11481986 10202.2 51282 1329 1987 11962.5 52783 1459 1988 14928.3 54334 17471989 16909.2 55329 1935 1990 18547.9 64749 2140 1991 21617.8 65491 23401992 26638.1 66152 2711 1993 34634.4 66808 3371 1994 46759.4 67455 45381995 58478.1 68065 5500 1996 67884.6 68950 6210 1997 74462.6 69820 64701998 78345.2 70637 7479 1999 82067.5 71394 8346 2000 89468.1 72085 93712001 97314.8 73025 10870 2002 104790.6 73740 12422 变量设定:Y:GDP值 :全国就业总人数 :全国的职工平均工资 1模型的设定 (1)初始模型:最小二乘回归:(2)变换模型为对数模型:用最小二乘法回归:lnY=-11.76329+1.338849ln+0.899991ln+ Se: (2.386913) (0.253883) (0.053772) t= -4.928243 5.273493 16.73724 =0.995761 =0.995375 F=2583.852 d=0.654905 可以看出:对数模型的拟合程度更好,具体分析对数模型拟合结果:和都很接近于1,说明模型拟合优度较好。
经济增长模型

∆A = 0 ⇒ ∆A > 0
生的技术进步,即从 A
A。
令
g
=
∆A A
为技术进步引起的增长率,那么
g
产生的影响是:
1)使得 y = f (k) 以 g 的增长率增长(注意 A 的影响是对整个生产函数的影响)
2)使得人均储蓄 sy = sf (k) 以 g 的增长率增长 注意 P53 图 3-7,技术进步作为外生变量导致生产函数曲线整体上移。 此时在稳态, y 和 k 不是不变,而是均以 g 的速率增长——人均指标。而总
y
kA
为
∆y y
=θ
•
∆k k
+
(1−θ )
∆A(对应 A
P52
倒数第
6
行,参见专栏
3-3)。将
∆A A
=
∆k
k
代入该式,我们得到:
g = ∆y = θ • ∆k + (1 −θ ) ∆A = θ • ∆k + (1−θ ) ∆k = ∆k
y
k
A
k
kk
这说明,产出与资本以同样速率增长,人均产出的增长率 ∆y y 与人均资本的
sy* = (n + d )k * 用图表示为:
4
关于稳态的几个结论:因为在稳态有 ∆y = 0 ,表示人均 GDP 不增长,那么此 时总的 GDP 增长率( ∆Y Y )=人口增长率 n。即在稳态的增长率与储蓄率 s 无关 (仅仅与 n 有关)。 ※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
3.戴蒙德模型 拉姆齐-卡斯-库普曼斯模型仍然存在缺陷,即其中的家庭都是神仙,长生 不老,显然与事实不符。戴蒙德修正了这一不足,引入新老家庭的更替,从而将 现实的人口生死更替引入增长模型,使增长模型与现实更为相符。在戴蒙德模型 下,平衡增长路径的资本存量又可以高于黄金律资本存量,维护了索洛模型的结 论。 4.新增长理论 虽然以上三类模型通过不断修正与现实越来越接近,但还是忽视了一个十分 核心的问题。这些模型里的核心变量——技术一直被假设是外生的,技术进步到 底如何发生、与增长是否有内在联系等重要问题都被回避。新增长理论正是针对 这一缺陷,将技术进步视为内生,研究经济增长,具体包括 R&D 模型和人力资 本模型,从而使得经济增长理论研究与现实世界之间的距离进一步得到了缩短。
人口、资源和GDP发展的统计规律
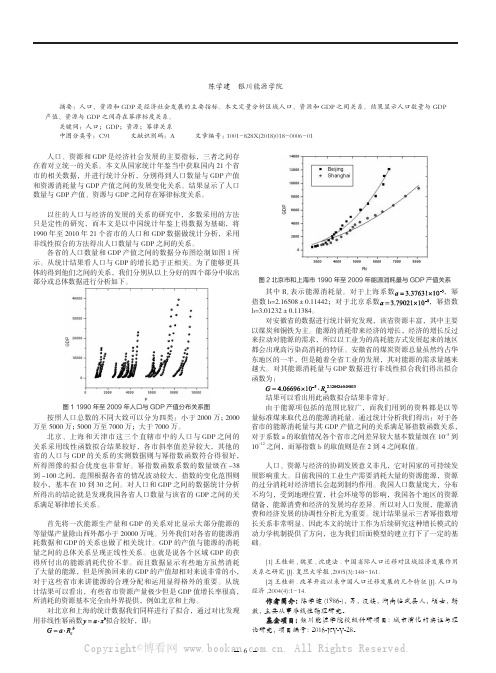
现代经济信息6人口、资源和GDP发展的统计规律陈学建 银川能源学院摘要:人口、资源和GDP 是经济社会发展的主要指标。
本文定量分析区域人口、资源和GDP 之间关系。
结果显示人口数量与GDP 产值、资源与GDP 之间存在幂律标度关系。
关键词:人口;GDP;资源;幂律关系中图分类号:C91 文献识别码:A 文章编号:1001-828X(2018)018-0006-01人口、资源和GDP 是经济社会发展的主要指标,三者之间存在着对立统一的关系。
本文从国家统计年鉴当中获取国内21个省市的相关数据,并进行统计分析,分别得到人口数量与GDP 产值和资源消耗量与GDP 产值之间的发展变化关系。
结果显示了人口数量与GDP 产值、资源与GDP 之间存在幂律标度关系。
一、人口、资源和GDP统计关系以往的人口与经济的发展的关系的研究中,多数采用的方法只是定性的研究,而本文是以中国统计年鉴上得数据为基础,将1990年至2010年21个省市的人口和GDP 数据做统计分析,采用非线性拟合的方法得出人口数量与GDP 之间的关系。
各省的人口数量和GDP 产值之间的数据分布图绘制如图1所示。
从统计结果看人口与GDP 的增长趋于正相关。
为了能够更具体的得到他们之间的关系,我们分别从以上分好的四个部分中取出部分或总体数据进行分析如下。
图1 1990年至2009年人口与GDP 产值分布关系图按照人口总数的不同大致可以分为四类:小于2000万;2000万至5000万;5000万至7000万;大于7000万。
北京、上海和天津市这三个直辖市中的人口与GDP 之间的关系采用线性函数拟合结果较好,各市斜率值差异较大,其他的省的人口与GDP 的关系的实测数据则与幂指数函数符合得很好,所得图像的拟合优度也非常好。
幂指数函数系数的数量级在-38到-100之间,范围根据各省的情况波动较大,指数的变化范围则较小,基本在10到30之间。
对人口和GDP 之间的数据统计分析所得出的结论就是发现我国各省人口数量与该省的GDP 之间的关系满足幂律增长关系。
65岁以上人口占比与gdp的相关分析统计学

65岁以上人口占比与gdp的相关分析统计学65岁以上人口占比,也叫老龄化程度。
从经济学角度看,一个社会或地区65岁以上人口占总人口数的比例越高,说明该地区经济发展水平相对较低,这种情况下,居民消费倾向低,可能导致产业结构单一、经济增长缓慢甚至衰退;反之,则表示该地区的经济处于良性循环状态,并且有着很强的经济潜力和持续的发展动力。
因此,我们可以通过测量65岁以上人口占比与 gdp 的关系来了解各地区人口年龄结构的特点,由此判断其经济发展水平和未来的发展趋势。
本文将利用面板数据模型来分析65岁以上人口占比与我国2015年的gdp 的相关关系。
65岁以上人口占比,即65岁及以上人口所占全部人口数的比重。
它主要反映了一个国家或者地区中老年人口的规模和比例,是衡量该地区人口健康水平和劳动力资源丰富程度的重要指标。
近些年来,随着我国国内人均寿命的不断提升,老年人口已经成为社会上最庞大的群体。
根据第六次人口普查数据显示:我国60岁及以上人口达到2.22亿,占总人口的13.26%,而同期我国15—59岁劳动力人口总数约为10.95亿,也就意味着每四个劳动力人口当中便有1位60岁及以上的老年人。
考虑到实际参加工作的人员多半需要抚养小孩和赡养老人等,目前的老龄化水平仍然远远超出预计。
在今后的几十年里,随着人类寿命的进一步延长,老龄化问题还会更严峻,若干年后,可能会形成少子老龄化的局面。
如何积极应对“未富先老”带来的挑战?合理开发老年人才,切实推动传统产业改革创新,促进经济转型升级,都值得深入研究。
一个国家或地区是否富裕,不仅取决于该地区的 gdp,而且还受到人口年龄结构的影响。
相对于青壮年人口而言,老年人口具有技术陈旧、教育水平低、缺乏适宜的工作岗位等劣势,很难为经济注入新鲜血液,但其具备精力充沛、经验丰富等优势,却又是经济建设不可或缺的宝贵财富。
所以,我们既不能只重视青壮年人口,忽略老年人口,亦不能漠视老年人口,忽略老年人才。
brock模型 公式

brock模型公式 Brock模型公式是一种用于描述人口增长和经济增长之间关系的模型。
该模型由William F. Brock和Stephen J. Durlauf于2001年提出,并在经济学和社会科学领域得到广泛应用。
Brock模型公式可以用来研究和预测社会经济系统的发展趋势,为政策制定者提供决策依据。
一、什么是Brock模型公式? Brock模型公式是一种描述人口和经济增长之间相互作用的数学模型。
该模型通过建立人口变化和经济增长之间的关联,分析二者对彼此的影响。
Brock模型公式被广泛用于研究人口发展趋势和经济增长的关系,有助于理解社会经济系统的运行机制。
二、Brock模型公式的原理: Brock模型公式基于以下假设:人口数量和经济增长率之间存在着相互依赖关系。
经济增长率对人口增长产生影响,而人口增长也对经济增长率产生影响。
该模型通过数学表达式来刻画这种关系,帮助我们理解和预测这两个变量的发展趋势。
三、Brock模型公式的数学表达式:Brock模型公式可以用以下数学表达式来表示: dP/dt = λ*P - μ*P^2 - β*P*Y + α*Y dY/dt = r*Y - γ*Y^2 - ρ*P*Y + δ*P 在上述公式中,P表示人口数量,Y表示经济增长率。
λ、μ、β、α、r、γ、ρ、δ为模型的参数。
其中,λ表示人口增长率,μ表示人口数量受到地理和环境限制的影响,β表示人口对经济增长的影响,α表示人口对经济产出的影响。
r表示GDP增长率,γ表示经济增长受到资源和生产率限制的影响,ρ表示人口对经济增长的影响,δ表示人口对GDP的影响。
四、Brock模型公式的解释与分析:1. 人口增长率对经济增长的影响: 在Brock模型公式中,λ*P项表示人口数量的增长对经济增长的影响。
如果人口增长率较高,将会导致劳动力市场扩大,从而促进经济增长。
反之,如果人口增长率较低,将会对经济增长产生阻碍。
2. 人口对经济产出的影响: 在Brock模型公式中,β*P*Y和α*Y项分别表示人口对经济产出的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GDP与经济发展及人口变化关系模型摘要本文讨论了国内生产总值与经济发展及人口变化的关系问题.针对问题一:国内生产总值是衡量经济发展的重要指标,而固定资产投资和进出口贸易的快速发展推动了我国经济的增长,因此有必要站在宏观的角度对我国国内生产总值与固定资产投资及进出口总额的关系进行分析.通过查找数据建立三者之间的基本回归模型,利用matlab进行求解,结果见文中表1.考虑到固定资产投资与进出口总额之间可能存在交互作用,将模型进行改进求解结果见文中表2.对两个模型进行结果的检验和预测,通过分析对比两者的数据得出改进的模型拟合度更高,更符合实际.针对问题二:当经济中总产出、收入和就业连续6个月到一年有明显下降,经济出现普遍收缩时,标志着经济衰退,因此分别建立国内生产总值与财政收入及失业率之间的回归模型.通过模型预测2012年财政收入为103.7925千亿元,同比增长0.0506%,失业率为4.1026% ,同比增长0.0634%.由于0.0506%与0.0634%都是相当小的数字,财政收入和失业率的增幅均是非常微小的,因此在一定程度上不能说明经济有衰退的迹象,只能说明经济涨幅不大.针对问题三:国内生产总值增长率、通货膨胀率和失业率是判断宏观经济运行状况的三个主要指标.通货膨胀率一般是用国内生产总值缩减指数来衡量的,通过奥肯定律可以得出国内生产总值与失业率的关系,进而得出国内生产总值是通过影响通货膨胀率及失业率对经济形势起决定性影响.针对问题四:建立关于人口数量与国内生产总值的自回归分布滞后模型,对其求解结果见文中表7,可以看出人口数量不仅与国内生产总值有关系,而且与其自身前一年的人口数量也存在着紧密的联系.问题一各项经济指标均会随时间的变化而变化,将问题一进行推广建立关于国内生产总值与固定资产投资及进出口总额的混合有限多项式分布滞后模型.此外统计回归模型是用途最广泛的一类随机模型.该模型不仅适用于对各个经济指标间关系的讨论,也可用于产品销售量的预测、教学评估、人口预测.关键词奥肯定律;统计回归模型;经济衰退;自回归分布滞后模型一、问题重述一个国家的国内生产总值往往反映该国的经济发展状况,中国亦无例外.改革开放以来,中国经济持续保持高速发展,特别是近20年更是基本保持10%以上的增长速度.据统计局数据,1979-2010年中国经济的平均增速是9.9%;1991-2010年平均增速是10.5%;2001-2010年平均增速也是10.5%.经过30多年的高速增长,中国经济已变得体量巨大、基数巨大.在2012年之前,我国国内生产总值逐步呈上升趋势,而在2012年的国内生产总值有所放缓,这与我国的经济政策发生变化相关联.请查找资料,利用数学建模给出如下四个问题的探讨:(1)通过一个或两个方面探讨2012年以前中国国内生产总值与其经济变化的关系.(2)中国2012年国内生产总值放缓能否证明经济形势有衰退的迹象.(3)如何评价中国国内生产总值对经济形势的影响.(4)中国人口变化与国内生产总值有无关系.二、问题分析国内生产总值是衡量经济发展的重要指标,它与我国经济及人口的变化均有着一定的联系,根据考虑问题的侧重点不同,以下从四个方面作详细讨论.针对问题一:固定资产投资和进出口贸易的发展,对我国经济的增长起到了推动的作用.但它们对经济增长的拉动作用是否显著,国内生产总值与固定资产投资和进出口总额三者之间存在什么样的关系,是需要进一步统计和检验的.通过查找1992-2011年20年的国内生产总值、进出口贸易额和固定资产投资额(全文数据均来自《中国统计年鉴》)的处理,建立统计回归模型,进而可以分析得出国内生产总值与固定资产投资额和进出口贸易额之间的关系.针对问题二:当经济中总产出、收入和就业连续6个月到一年的明显下降,经济出现普遍收缩时,标志着经济衰退.因此对1992-2011年20年的国内生产总值与财政收入及其与就业率的数据进行分析,分别建立关于国内生产总值与财政收入和国内生产总值与就业率的回归模型,通过预测2012年国内生产总值、财政收入和就业率来判断当国内生产总值放缓时经济是否有衰退的迹象.针对问题三:国内生产总值增长率、通货膨胀率和失业率是判断宏观经济运行状况的三个主要指标.通货膨胀率一般是用国内生产总值缩减指数来衡量的,由此国内生产总值缩减指数可以直接由国内生产总值计算得出.因此可以通过奥肯定律找出失业率与其增长率的函数关系,以此来判断出中国国内生产总值对经济形势的影响.针对问题四:人口总量与国内生产总值是随时间变化而发生改变的.当年的人口总量与最近三年的人口总量和国内生产总值都有关系,因此建立关于从1992年到2011年20年人口总量与国内生产总值的自回归分布滞后模型分析得人口变化与国内生产总值的关系.三、基本假设1.数据以年为基准,不考虑一年内的波动和变化;2.数据均为按当年价格计算的名义值;3.所有数据均真实可靠.四、符号表示与名词解释固定资产投资:是以货币形式表现的在一定时期内全社会建造和购置固定资产的工作量以及与此有关的费用的总称.财政收入:指国家财政参与社会产品分配所取得的收入,是实现国家职能的财力保证.进出口总额:指实际进出我国国境的货物总金额.五、模型建立与求解国内生产总值的增长对经济发展起着越来越重要的作用,因此必须正确认识国内生产总值增长与经济发展之间的关系.在我国,人口问题也不容忽视,它制约着中国经济和社会的发展.下面通过对各问题的分析,建立相应的模型,并求解.文中所有数据见附表一.5.1 国内生产总值与进出口贸易总额和固定资产投资的回归模型基本回归模型 设第t 年的国内生产总值为t G ,固定资产投资为t I ,进出口总额为t E ,t =1,…,n ( n =20).因变量t G 与自变量t I 和t E 的散点图见图1和图2.图1 t G 对t I 的散点图 图2 t G 对t E 的散点图由图1可以看出,随着固定资产投资额的增加,国内生产总值向上弯曲增长的趋势渐缓,图中曲线是用二次函数模型2012=+++t t t G I I βββε (1)拟合的(其中ε是随机误差).而图2中,当进出口总额增大时,国内生产总值向上弯曲增长的趋势加强,图中曲线仍是用二次函数模型2012=+++t t t G E E βββε (2)拟合的.综合上面的分析,结合(1)和(2)建立如下的回归模型2201234=+++++t t t t t G I E I E βββββε (3) 根据附表一的数据,对(3)利用matlab 统计工具箱求解(见附录程序一),得到回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表1=0.9941R 表明t G 的99.41%可由(3)确定,F 值远远超过其检验的临界值,p远小于α,因而模型(3)从整体上看是可用的.将回归系数的估计值代入(3),得到基本回归模型22=27.7677+0.9937+0.7844-0.00004-0.001t t t t t G I E I E (4)模型改进 从表面上看基本模型(4)的拟合度已经很高2=0.9941R ,但模型(4)中回归变量t I 和t E 对因变量t G 的影响是相互独立的.实际中由于t I 和t E 均与t G 存在很大的依赖关系,因此t I 与t E 之间应存在着交互作用会对t G 产生影响.不妨简单地用t I 与t E 的乘积代表它们的交互作用,于是将(3)增加一项,得到22012345=++++++t t t t t t t G I E I E I E ββββββε (5)对(5)求解(见附录程序二) 得到回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表2表2与表1的结果相比,=0.9961R 有所提高,说明(5)比(3)有所改进.并且,所有参数的置信区间,特别是t I 与t E 交互项系数5β的置信区间不包含零点,这就说明t I 与t E 之间存在着交互作用并对t G 产生影响.F 值也远远超过其检验的临界值,p 也远小于α,所以(5)比(3)更符合实际.将回归系数的估计值代入(5),得到改进的回归模型22=17.6708+0.9993+1.2295-0.0138-0.0204+0.0316t t t t t t t G I E I E I E (6)结果分析及预测 从机理上看,对于经济规律作用下的时间序列数据,加入交互项的模型(6)更为合理.将模型(4)和模型(6)的计算值t G 与实际数据t G 的比较以及两个模型的残差t e (=-t t t e G G )表示在表3、图3和图4上.可以看出模型(6)更合适些.表3:模型(4)和模型(6)的计算值G 与残差et G (模型t G (模型48.2305 43.0398 60.2638 58.2552 65.5259 64.6390图3 模型(4),(6)的t G 与t G 图4 模型(4),(6)的t e(注:图3和图4中蓝色表示实际数据,绿色表示模型(4)计算出的数据,红色表示模型(6)计算出的数据)5.2 国内生产总值放缓与经济衰退关系模型分析国内生产总值与财政收入的关系模型 设第t 年财政收入为t F ,画出因变量t F 与自变量t G 的散点图(t =1,…,n ( n =20)),并直接利用matlab 统计工具箱(CFTOOL 命令)拟合曲线见图5.图5 t F 与t G 的散点图 拟合函数的表达式为2012=+++t t t F G G βββε (7)其中(7)各参数的值及其置信区间见表4=0.9986R 表明t F 的99.86%可由(7)确定.RMES 为回归系统的拟合标准差,其越小说明曲线拟合的越好.表4显示 1.72RMES =,因此模型(7)是可用的.将回归系数的估计值代入(7)得到2=-3.381+0.1638+0.0001346t t t F G G (8)查看中国科学院预测科学研究中心关于《2012年我国GDP 预测及宏观经济形势分析》知道预计2012年国内生产总值的增长率为8.5%.因此预计2012年国内生产总值为471.564(千亿元),将其代入(8)得到2012年财政收入为103.7925(千亿元).与2011年财政收入103.740(千亿元)相比,同比增长了0.0506%,因此2012年我国财政收入仍是增长的,只是增长幅度非常小而已.国民生产总值与失业率的关系模型 设第t 年失业率为t U (t =1,…,20),画出因变量t U 与自变量t G 的散点图,并直接利用matlab 统计工具箱(CFTOOL 命令)拟合曲线见图6.图6 t U 与t G 的散点图拟合函数的表达式为222471582------036=+++t t t G G G t U eeeβββββββββε⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(9)其中(9)中各参数的值及其置信区间见表5=0.9412R 表明t F 的94.12%可由(7)确定.0.2103RMES =,因此模型(7)是可用的.将回归系数的估计值代入(7)得到222-41.48-19.41-38.83---8.21421.29 3.965=5.425+4.24-3.141t t t G G G t U eee⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(10)将预计的2012年国内生产总值471.564(千亿元)代入(8)得出2012年失业率为4.1026%,与2011年失业率4.1%相比,同比增长了0.0634%.因此2012年我国公失业率仍是增长的,只是增幅很小而已. 而经济衰退是指当经济中总产出、收入和就业连续6个月到一年的明显下降,经济中很多部门出现普遍收缩,则这种经济下降称为衰退. 0.0634%的增长是很微小的,因此可视为失业率基本没有变化.通过以上讨论分析可得当GDP 增幅减小为8.5%时,财政收入同比增长了0.0506%,失业率同比增长了0.0634%.由于0.0506%与0.0634%都是相当小的数字,因此不能说明经济有衰退的迹象,只能说明经济涨幅不大. 5.3 国内生产总值对经济形势影响关系模型设第t 年经济状况指数为t λ,国内生产总值增长率为t g ,失业变化率为t U ∆.通过奥肯定律:=-0.5(-2.25)t t U g ∆ 可以得出失业率t U 与t g 的关系为=-0.5(-2.25)t t U g dt ⎰ (11)又t λ受t g 及t U 的影响,设i a (i =1,2)分别表示t g 、t U 对t λ的权重,则12=+t t t a g a U λ (12) 由(11)和(12)可得t g 对经济形势影响的关系模型为12=+-0.5(-2.25)t t t a g a g dt λ⎰ (13)通过(13)可得国内生产总值通过对失业率的影响对经济形势起决定性影响. 5.4 中国人口变化与国内生产总值关系模型自回归分布滞后模型 设第t 年人口总数为t P ,(t =1,…,n ( n =33)).数据(见附表二)借鉴计量经济学中的自回归分布滞后模型,首先建立初始模型012132112233t t t t t t t t P G G G P P P ααααβββε-----=+++++++ (14)即当年的人口总量与最近三年的人口总量和国内生产总值都有关系,t ε为随机干扰项.查找近三十年我国人口总量(数据见附表一),利用matlab 进行求解得回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表6=0.99995R 表明t P 的99.995%可由(14)确定,F 值远远超过其检验的临界值,p 远小于α,因而模型(3)从整体上看是可用的.检查参数的置信区间发现1α,2α,3α和3β的置信区间均包含零点,表明回归变量t G ,1t G -,2t G -和3t P -对t P 的影响不太显著.模型改进 由于每年P 和G 的值都分别与其前几年的值有关,且P 与G 两者之间也存在着一定的关系,因此通过对1t G -,2t G -和3t P -逐项剔除后重新拟合并检查其2R ,F 和p 的值及各参数的置信区间,得到最终改进的模型0121t t t P G P βββ-=-+ (15) 求解(15)结果见表7=0.99979R 表明t P 的99.979%可由(15)确定有所提高,表7与表6的结果相比,所有参数的置信区间均不包含零点,F 值也远远超过其检验的临界值,p 也远小于α,所以(16)更符合实际.将回归系数的估计值代入(15)得到1=3351.5-0.0015122+0.98296t t t P G P - (16)从(16)可以看出人口数量不仅与国内生产总值有关系,而且与其自身前一年的人口数量也存在着紧密的联系.结果分析及预测 将用模型(16)的计算值t P 与实际数据t P 的比较以及两个模型的残差t e (=-t t t e P P )表示在表8、图7上.图7 模型(16)'.'t P ,''t P o ,'*'t e表8和图7显示用模型(16)预计的人口数量与实际人口数量非常吻合,因此模型(16)更贴合实际.六、模型评价和推广模型的评价本文在正确查找数据基础上建立了多个统计回归模型.在对原始数据进行拟合时,采用多种方法,对模型不断进行改进,使其愈来愈完善且具有很高的拟合精度.在此基础,对模型作进一步分析讨论得到一系列可靠而实用的信息.但由于时间紧迫以及数据量的不足,部分模型较为粗糙,需要进一步改进. 模型检验通过已有数据进行拟合与比较来检验模型,经检验证实建立的模型对原始数据有很高的拟合度,基本符合模型建立的初衷. 模型的推广推广一:由于各项经济指标都会随时间的变化而变化,针对问题一可以采用混合有限多项式分布滞后模型进行拟合,模型如下:01213212132112233t t t t t t t t t t G I I I E E E G G G ααααβββγγγε-------=++++++++++ 其中i α,i β和i γ为参数,0,1,2,3i =.推广二:统计回归模型是用途最广泛的一类随机模型.该模型不仅适用于对各个经济指标间关系的讨论,也可用于产品销售量的预测、教学评估、人口预测等问题.参考文献[1]姜启源,谢金星,叶俊.数学模型[M].北京:高教出版社,2011.1.[2]国家统计局编.中国统计年鉴(2011)[M].北京:中国统计出版社,2012.2. [3]中国国家统计局网站 /2012-8-15.[4]陈锡康,祝坤福 王会娟.2012年我国GDP 预测及宏观经济形势分析[M]. 北京:高教出版社,2012.1. [5]萨谬尔森,诺德豪斯.经济学[M].北京:高教出版社,2000.6. 附录表一11。
