博弈论第三章习题
经济博弈论(第三版)复习题及答案%20谢识予著

L 2,0 3,4
R
7、我们用反应函数法来分析这个博弈。先讨论博弈方 1 的选择。根据问题 的假设,如果博弈方 2 选择金额 s2(0≤s2≤10000) ,则博弈方 1 选择 s1 的利益 为: s1 u(s1)= 0
当 S1≤10000 -s2 当 S1≤10000 -s2
因此博弈方 1 采用 s1=1000—s2 时,能实现自己的最大利益 u(s1)= s1=1000— s2。因此 s1=1000—s2 就是博弈方 1 的反应函数。 博弈方 2 与博弈方 1 的利益函数和策略选择是完全相似的,因此对博弈方 1 所选择的任意金额 s1, 博弈方 2 的最优反应策略, 也就是反应函数是 s2=1000- s1。 显然, 上述博弈方 1 的反应函数与博弈方 2 的反应函数是完全重合的,因此 本博弈有无穷多个纳什均衡,所有满足该反应函数,也就是 s1+ s2=10000 的数组 (s1 ,s2)都是本博弈的纯策略纳什均衡。 如果我是两个博弈方中的一个,那么我会要求得到 5000 元。理由是在该博 弈的无穷多个纯策略纳什均衡中, (5000,5000)既是比较公平和容易被双方接 受的,也是容易被双方同时想到的一个,因此是一个聚点均衡。 9、 (1)两个厂商的利润函数为: πi=pqi-ciqi=(a-qi-qj)qi-ciqi 将利润函数对产量求导并令其为 0 得: ∂π i =a-qj-ci-2qi=0 ∂qi 解得两个厂商的反应函数为: qj=(a- qj-ci)/2 或具体写成: q1=(a-q2-c1)/2 q2=(a-q1-c2)/2 (2)当 0<ci<a/2 时, 我们根据上述两个厂商的反应函数,直接求出两个厂商 的纳什均衡产量分别为: a − 2c1 + c 2 3 a + c1 − 2c 2 q2= 3 (3)当 c1<c2<a,但 2c2>a+ c1 时,根据反应函数求出来的厂商 2 产量 q2<0。 这意味着厂商 2 不会生产, 这时厂商 1 成了垄断厂商,厂商 1 的了优产量选择是 利润最大化的垄断产量 a − c1 q1=q* = 2 因此这种情况下的纳什均衡为[(a- c1)/2, 0]。 q1=
博弈论习题(1-4)

博弈论作业题第一章4.“囚徒的困境”的内在根源是什么?举出现实中囚徒困境的具体例子。
5.博弈有哪些分类方法?有哪些主要的类型?9.你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的:你决定开,则0.35的概率你将收益300万元(包括投资),而0.65的概率你将全部亏损掉;如果你不开,则你能保住本钱但也不会有利润。
请你(a )用得益矩阵和扩展表示该博弈;(b )如果你是风险中性的,你会怎样选择?(c )如果你是风险规避的,且期望得益的折扣系数为0.9,你的策略选择是什么?(d )如果你是风险偏好的,期望得益折扣系数为1.2,你的选择又是什么?10. 一逃犯从关押他的监狱中逃走,一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线,看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可少坐10年牢,但一旦被抓住则要加刑10年;看守抓住逃犯能得1000元奖金。
请分别用得益矩阵和扩展形表示该博弈,并作简单分析。
第二章4.求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
博弈方2T 博弈方1B5.下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡?博弈的结果是什么?博弈方2T 博弈方1 M B6.设古诺模型中有n 家厂商。
q i 为厂商i 的产量,Q=q 1+…+q n 为市场总产量。
P 为市场出清价格,且已知P=P(Q)=a-Q (当Q<a 时,否则P=0)。
假设厂商i 生产q i 产量的总成本为C i =C i (q i )=cq i ,也就是说没有固定成本且各厂商的 边际成本都相同,为常数c (c<a )。
假设各厂商同时选择产量,该模型的纳什均衡是什么?当n 趋于无穷大时博弈分析是否仍然有效?7.两寡头古诺模型,P(Q)=a-Q 等与上题相同,但厂商的边际成本不同,分别为c 1和c 2。
如果0<c i <a/2,问纳什均衡产量各位多少?如果c 1<c 2<a ,但2c 2>a+c 1,则纳什均衡产量又为多少?8.甲、乙两公司分属两个国家,在开发某种新产品方面有下面得益矩阵表示的博弈关系(单位:百万美元)。
【博弈论基础】(吉本斯)课后习题答案

混 合 战 略 纳 什 均 衡 矛 盾 , 假 设 不 成 立 , 原 命 题 得 证 。
猪 头 非 整 理 ebwf@
3
Gibbons《博弈论基础》第二章习题解答(部分)
2.1 采用逆向归纳法,先最大化家长的收益:给定孩子的行动 A,来选择自己的行动 B,
MaxV ( I p − B) + k ( I c + B)
2 2 时 , 生 产 qm / 2 的 一 方 的 利 润 为 π 2 = 5(a − c) / 48 , 生 产 qc 的 一 方 的 利 润 为
π 3 = 5(a − c)2 / 36 ; 双 方 都 生 产 qc 时 , 每 一 方 的 利 润 都 为 π 4 = (a − c) 2 / 9 。 以 标 准 式 表 示
2 1 2 2
{( (2w − w ) /(w + w ), (2w
1.14
− w1 ) /( w1 + w2 ) ) , ( (2 w1 − w2 ) /( w1 + w2 ), (2 w2 − w1 ) /( w1 + w2 ) )}
*
证 明 : 在 混 合 战 略 纳 什 均 衡 中 , 参 与 人 i 的 混 合 战 略 为 pi , 其 中 选 择 第 j 个 纯 战 略 sij 的 概 率 为 pij 。 用 反 证 法 证 明 。 假 设 pij > 0 , 且 sij 是 第 一 个 被 重 复 剔 除 劣 战 略 所 剔 除 的 战 略 。 那 么 参 与 人 i 必 定 存 在 另 一
针 对 上 面 的 博 弈 , 设 参 与 人 1 的 战 略 为 ( p,1-p), 参 与 人 2 的 战 略 为 ( q,1-q)。 则 对 于 1 来 说 , 2q* + 4(1 − q* ) = 3q* + 2(1 − q* ) , 得 : q* = 2 / 3 ; 对 于 2 来 说 , 4(1 − p ) = 2 p + 3(1 − p ) , 得 p = 1/ 3 。
博弈论第三次答案全新

第三次作业1、两个人合作开发一项产品,能否成功与两个人的工作态度有关,设成功概率如下:单位的利益。
如果双方采取出发战略,则该博弈无限次重复博弈的均衡是什么?答:该博弈的得益矩阵如下B努力 偷懒A 努力 9/4,9/4 3/2,5/2 偷懒 5/2,3/2 2,2一次性博弈显然是囚徒困境博弈,唯一的均衡是两人都偷懒,双方的得益期望都是2。
在无限次重复博弈中,假设双方为了在共同努力方面实现合作采取如下出发策略:开始时努力,若发现对方偷懒,自己也偷懒,可以分析贴现因子δ符合什么条件可以构成子博弈完美纳什均衡:不偏离:()()δδδ-=+++1491492K K 偏离:()δδδ-+=+++12212252ΛΛ 当满足()δδ-+≥-1221149,即21≥δ时采取这种出发策略是正确的,否则偏离是正确的。
当21≥δ时,双方都采取出发策略是该博弈的子博弈完美纳什均衡,如果21<δ,则上述出发策略组合不是子博弈完美纳什均衡,两人都会采取偷懒的策略。
2、假设无限次重复博弈的阶段博弈是古诺竞争模型,假设两个寡头面对市场需求为 Q =a -p ,不变的单位成本为c ,请计算支持垄断价格作为子博弈精练纳什均衡的结 果的最低贴现因子。
在重复博弈下 合作的收益要大于背叛的收益 即:()22283118c a c a -⎪⎭⎫ ⎝⎛≥⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-δ+2311⎪⎭⎫ ⎝⎛--c a δ 解得179≥δ3、不会4、两个厂商生产相同产品在市场上进行竞争性销售。
第1个厂商的成本函数为11q c =,其中1q 为厂商1的产量。
第2个厂商的成本函数为22cq c =,其中2q 为厂商2的产量,c 为其常数边际成本。
两个厂商的固定成本都为零。
厂商2的边际成本c 是厂商2的“私人信息”,厂商1认为c 在⎥⎦⎤⎢⎣⎡23,21上呈均匀分布。
设市场需求函数为214q q P --=,其中P 为价格,两个厂商都以其产量为纯战略,问纯战略贝叶斯均衡为何?。
博弈论第三章知识题

问题1:如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定,即下图中a 、b 数值不确定。
试讨论本博弈有哪几种可能的结果。
如果本博弈中的“威胁”和“承诺”是可信的,a 或b 应满足什么条件?①0a <,不借—不分—不打;②01a <<,且2b >,借—不分—打; ③1a >,且2b >,借—不分—打(,)a b ; ④0a >,且2b <,借—分—(2,2)问题2:三寡头市场需求函数Q P -=100,其中Q 是三个厂商的产量之和,并且已知三个厂商都有常数边际成本2而无固定成本。
如果厂商1和厂商2同时决定产量,厂商3根据厂商1和厂商2的产量决策,问它们各自的产量和利润是多少?1123111231(100)2(98)q q q q q q q q q π=----=---2123221232(100)2(98)q q q q q q q q q π=----=---(a ,b )(0,4)3123331233(100)2(98)q q q q q q q q q π=----=--- 331230,(98)/2q q q q π∂=⇒=--∂代入,11212122(98)/2,(98)/2q q q q q q ππ=--=--12120,0q q ππ∂∂==∂∂,得***12398/3,49/3q q q === ***1234802/9,2401/9πππ===。
问题3:设两个博弈方之间的三阶段动态博弈如下图所示。
(1)若a 和b 分别等于100和150,该博弈的子博弈完美纳什均衡是什么?(2)T N L --是否可能成为该博弈的子博弈完美纳什均衡路径,为什么?(3)在什么情况下博弈方2会获得300单位或更高的得益?(1)博弈方1在第一阶段选择R ,在第三阶段选择S ,博弈方2在第二阶段选择M 。
(a ,b )50,300(2)不可能。
T N L --带来的利益50明显小于博弈方1在第一阶段R 的得益300;无论a 和b 是什么数值,该路径都不能构成Nash 均衡,不能成为子博弈完美Nash 均衡。
博弈论吉本斯第三章习题答案

(1 +
tp
)×
x
− x
c
−
c x
>
(−1) ×
x
− x
c
+
c x
(1) 与(2)联立,
=〉 tp
>
2c x−c
−2
=
p ---------------------(2)
c = p 带入(1)
仅供参考!!
-2-
E-mail:beckham.23@
Gibbons《博弈论基础》第三章习题解答(部分)
2c − 2x + 2c = cx − c2 c2 + (4 − x)c − 2x = 0
c = −4 + x + 16 + x2 2
x − c = 2x + 4 − x − 16 + x2 = 1 + 4 − 16 + x2
x
2x
2
2x
其中,4 − 16 + x2 = 1 ×
1
= 1×
1
2x
2 4 + 16 + x2 x
3.5
假设参与者 1 的私人信息为 tc ,参与者 2 的私人信息为 tp 。 tc ,tp ∈ (0, x)
正面
反面
正面
1+ tc , -1 -1, 1+ t p
-1, 1
1, -1
反面
当 tc > c 时,参与者 1 选正面;当 t p > p 时,参与者 2 选择反面
因此,参与者 1 选择正面的概率为 x − c ,选背面的概率为 c ;
2
4+ x
博弈论课后习题

第一章导论1、什么是博弈博弈论的主要研究内容是什么2、设定一个博弈模型必须确定哪几个方面3、举出烟草、餐饮、股市、房地产、广告、电视等行业的竞争中策略相互依存的例子。
4、“囚徒的困境”的内在根源是什么举出现实中囚徒的困境的具体例子。
5、博弈有哪些分类方法,有哪些主要的类型6、你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的:你决定开,则的概率你讲收益300万元(包括投资),而的概率你将全部亏损;如果你不开,则你能保住本钱但也不会有利润,请你(a)用得益矩阵和扩展形式表示该博弈;(b)如果你是风险中性的,你会怎样选择(c)如果你是风险规避的,且期望得益的折扣系数为,你的策略选择是什么(d)如果你是风险偏好的,期望得益折算系数为,你的选择又是什么7、一逃犯从关押他的监狱中逃走,一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线,看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可以少坐10年牢,但一旦被抓住则要加刑10年;看守抓住逃犯能得到1000元奖金。
请分别用得益矩阵和扩展形式表示该博弈,并作简单分析。
第二章完全信息静态博弈1、上策均衡、严格下策反复消去法和纳什均衡相互之间的关系是什么2、为什么说纳什均衡是博弈分析中最重要的概念3、找出现实经济或生活中可以用帕累托上策均衡、风险上策均衡分析的例子。
4、多重纳什均衡是否会影响纳什均衡的一致预测性质,对博弈分析有什么不利影响5、下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡博弈的结果是什么6、求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
7、博弈方1和2就如何分10 000元进行讨价还价。
假设确定了以下规则:双方同时提出自己要求的数额S1和S2,0≤s1,s2≤10000,如果s1+s2≤10 000,则两博弈方的要求都得到满足,即分别得到s1和s2,但如果是s1+s2>10 000,则该笔钱就被没收。
问该博弈的纯策略纳什均衡是什么如果你是其中一个博弈方,你会要求什么数额,为什么8、设古诺模型中有n家厂商、qi 为厂商i的产量,Q=q1+…+qn 为市场总产量、P为市场出清价格,且已知P=P(Q)=a-Q(当Q<a时,否则P=0)。
策略博弈习题部分解答

博弈论与政治第三小组作业第二章名词解释:1、理性行为(rational behavior):参与人精于算计并严格按照其最优策略行事。
其中理性有两个重要的内涵:一个人对自己的利益完全了解,并能完美地计算出何种行动可以最大化其利益。
2、不完美信息(imperfect information):在博弈的每一个行动时点上,参与人可能无法获悉决策所需的全部信息。
这包括相关的外部环境——比如天气——的不确定性,以及对方先前或当前的行动。
这类情况称为不完美信息。
3、不完全信息(incomplete information):当一个参与人比另一个参与人了解更多信息时,阴谋诡计就会产生。
这类情况称为不完全信息。
4、合作博弈(cooperative game):博弈论使用两个专门术语来区分协议具有强制力和不具有强制力的情况。
若协议对参与人行为具有强制力,则称此类博弈为合作博弈。
5、非合作博弈(noncooperate game):个体参与人可根据其利益采取行动,则称此类博弈为非合作博弈。
第三章名词解释:1、中间评估函数(intermediate valuation function):赋予非终点结支付的规则被称为中间评估函数。
2、先动优势(firstmover advantage):在博弈的过程中先做决策带来的优势。
先动优势来自于将其自身置于一个优势地位以及迫使其他参与人接受它的承诺能力。
后动优势(second-mover advantage):在博弈的过程中后做决策带来的优势。
后动优势源于自己可对他人选择做出的灵活性。
第四章名词解释:1、占优策略(dominant strategy)、劣策略(dominated strategy):每一个博弈中的参与者通常都拥有不止一个竞争策略,其所有策略的集合构成了该企业的策略集。
在参与者各自的策略集中,如果存在一个与其他竞争对手可能采取的策略无关的最优选择,则称其为占优策略(Dominant Strategy),与之相对的其他策略则为劣势策略。
博弈论第三章习题

问题1:如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定,即下图中a 、b 数值不确定。
试讨论本博弈有哪几种可能的结果。
如果本博弈中的“威胁”和“承诺”是可信的,a 或b 应满足什么条件?①0a <,不借—不分—不打;②01a <<,且2b >,借—不分—打;③1a >,且2b >,借—不分—打(,)a b ;④0a >,且2b <,借—分—(2,2)问题2:三寡头市场需求函数Q P -=100,其中Q 是三个厂商的产量之和,并且已知三个厂商都有常数边际成本2而无固定成本。
如果厂商1和厂商2同时决定产量,厂商3根据厂商1和厂商2的产量决策,问它们各自的产量和利润是多少?1123111231(100)2(98)q q q q q q q q q π=----=---2123221232(100)2(98)q q q q q q q q q π=----=---3123331233(100)2(98)q q q q q q q q q π=----=---331230,(98)/2q q q q π∂=⇒=--∂ 代入,11212122(98)/2,(98)/2q q q q q q ππ=--=--(a ,b ) (0,4)12120,0q q ππ∂∂==∂∂,得***12398/3,49/3q q q ===***1234802/9,2401/9πππ===。
问题3:设两个博弈方之间的三阶段动态博弈如下图所示。
(1)若a 和b 分别等于100和150,该博弈的子博弈完美纳什均衡是什么?(2)T N L --是否可能成为该博弈的子博弈完美纳什均衡路径,为什么?(3)在什么情况下博弈方2会获得300单位或更高的得益?(1)博弈方1在第一阶段选择R ,在第三阶段选择S ,博弈方2在第二阶段选择M 。
(2)不可能。
T N L --带来的利益50明显小于博弈方1在第一阶段R 的得益300;无论a 和b 是什么数值,该路径都不能构成Nash 均衡,不能成为子博弈完美Nash 均衡。
重庆大学博弈论习题及参考答案

第一章完全信息静态博弈第二章完全信息动态博弈第三章 不完全信息静态博弈1、市场进入博弈一个完全垄断企业B 正在垄断一个行业市场,另一个潜在的试图进入该行业的企业A ,称A 为进入者,B 为在位者。
A 不知道B 的成本特征,设B 有两种可能的成本,即高成本和低成本。
两种成本情况下的博弈矩阵如表6.1。
表6.1 市场进入博弈 B高成本 低成本A进入 不进入假定B 知道进入者A 的成本为高成本,且与B 为高成本时的成本相同。
假若信息是完全的,则当B 为高成本时,唯一的精炼纳什均衡为(进入,默认),另一纳什均衡(不进入,斗争)是含有不可置信的威胁。
当B 为低成本时,唯一的纳什均衡为(不进入,斗争),即若A 进入行业,具有低成本优势的B 将通过降低价格将A 逐出市场。
由于存在行业进入成本,所以A 被逐出市场后将有净的10单位进入成本的损失。
当A 不知道B 的成本情况时,他的选择将依赖于他对B 的成本类型的主观概率或先验概率密度。
设A 对B 是高成本的先验概率判断为P ,则A 认为B 为低成本的概率为P -1。
如果A 进入,其期望支付为 )10)(1()40(--+P P 如果1不进入,其期望支付为0。
当且仅当0)10)(1()40(≥--+P P 或51≥P 时,A 选择进入;反之,当51<P 时,A 不进入。
于是,贝叶斯均衡为:(进入,默认),高成本,51≥P ; (进入,斗争),低成本,51≥P ;(不进入,*),51<P其中*表示可以是斗争,也可以是默认。
2、成本信息不对称的古诺博弈之前给出的古诺博弈中,每个厂商的成本函数是共同知识。
这里,我们假设每个厂商的成本函数是私人信息,具体规定如下:两个企业生产相同产品在同一市场上进行竞争性销售,市场需求函数为P a Q -=,0>a ,P 为产品价格,Q 为市场需求量。
假设a 充分大时总有0≥-P a ,企业i 的成本函数为i i i q b C =,其中i C 为企业i 的总成本,i q 为其产量,i b 为其平均成本,i b 为常数且0>i b ,故i b 也是边际成本。
博弈论习题及其解答

一、经典多元线性回归模型
1、多元线性回归模型的一般形式
Yi = b0 + b1 X 1i + b2 X 2i + L bk X ki + U i i = 1, 2,L n
k个解释变量,n期观测值,矩阵形式为:
Y = Xb + U
其中:
Y1 1 X11 L Xk1 U1 b0 1 X12 L Xk 2 Y2 U2 b Y = X = U = b= 1 M M M M M M Y 1 X L X U b 1n kn n n k
该方程组可以写成矩阵形式如下:
X ' X b = X 'Y
∧
求解该方程组得到:
b =
∧
(X
'X
)
1
X 'Y
矩阵微分法
∧ ' Q = ∑e = ∑Yi Yi = ee = Y X b Y X b 2 i ∧ 2 ∧ '
= Y Y Y X b b X Y + b X X b = Y Y 2Y X b+ b X X b
= nσ u2 ( k + 1) σ u2 = ( n k 1) σ u2
所以,U的方差的无偏估计量为:
σ
∧ 2 U
e 'e = n k 1
五、拟合优度检验
1、可决系数的调整
R2 = ESS b' X ' X b n Y = 2 TSS Y 'Y n Y
2 2
∧
∧
2
∧ ∧ ∧ ∧ ∧ ∧ ∧ Y Y = Y 2Y Y + nY = Y 'Y nY = b' X ' X b nY ∑ i ∑ i ∑i 2 ∑Y i Y = ∑Yi 2Y ∑Y i + nY = Y 'Y nY 2 2 2
博弈论各章节课后习题答案 (1)
第一章绪论
1.什么是博弈论?博弈有哪些基本表示方法?各种表示法的基本要素是什么?(见教材)
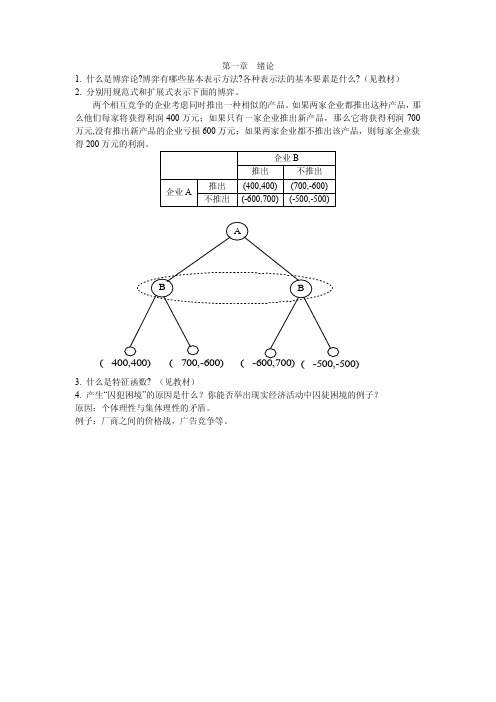
2.分别用规范式和扩展式表示下面的博弈。
两个相互竞争的企业考虑同时推出一种相似的产品。
如果两家企业都推出这种产品,那么他们每家将获得利润400万元;如果只有一家企业推出新产品,那么它将获得利润700万元,没有推出新产品的企业亏损600万元;如果两家企业都不推出该产品,则每家企业获得200万元的利润。
3.什么是特征函数?(见教材)
4.产生“囚犯困境”的原因是什么?你能否举出现实经济活动中囚徒困境的例子?原因:个体理性与集体理性的矛盾。
例子:厂商之间的价格战,广告竞争等。
企业B
推出
不推出企业A 推出
(400,400)(700,-600)不推出(-600,700)(-500,-500)
(。
博弈论各章节课后习题答案

9. 求如图所示完全信息动态博弈的子博弈完美纳什均衡(图中数字(a,b,c)分别表示局中人 1、
2、3 的 收 益 )。
1
A1
A2
3
2
C1
C2
B1
B2
(4,2,3)
(1,7,8) 3
C1
C2 C1
3
C2
(5,4,3) (7,6,6) (2,1,9) (0,4,2)
答:局中人 1 采取 A2 行 动 ,局中人 2 采取行动 B1 时,局中人 3 必然采取 C2 行 动( 因为 3<6), 因而该博弈的顶点只能是(7,6,6)。同样对于局中人 3 右边一个子博弈,必然采取 C1 行动 (9>2),因而该博弈的顶点只能是(2,1,9)。进而原博弈简化为:
的定价,qi是企业i的需求量。假设企业生产没有固定成本,并且边际成本为常数c,c<a.假定博弃 重复无穷多次,每次的价格都立即被观察到,企业使用触发策略。求使垄断价格可以作为完美 均衡结果出现的最低贴现因子δ,并解释δ与n的关系。
分以下几个步骤进行。
1)计算纳什均衡 当企业 i 选择价格 pi,其它企业选择价格 pj(j=1,2,…,n,j≠i)时,企业 i 的利润为: πi = (pi − c)qi = (pi − c)(a − pi + b(p1 + p2 + ⋯ + pi−1 + pi+1 + ⋯ + pn )) ,i=1,2,…,n
∂π2 ∂q 2
= a − q1
− 2q2
− q3
−c=0
∂π3 ∂q3
=
a
− q1
− q2
− 2q3
−c
吉本斯-博弈论基础答案

1 2 的收益贴现到t期可得 1 − δ (a − c) / 8 , 1 2 2 触发战略有效的条件是: 1 − δ (a − c ) / 8 > (a − c) / 4 ,得到: δ > 1/ 2
(可参见谢识予的《经济博弈论》习题解答) 。 2.14 略 2.15 (1)垄断的产量、价格、利润: π=Q(a-Q)-CQ 利润最大化时:a-2Q=C,从而 Q=(a-c)/2. 此时价格为(a-c)/2。 (2)古诺均衡下的产量、价格、利润: π=(a-∑qi) qi -cqi
(*)
因 此 当 增 加 S 时 , U1 ( I c − S ) 会 减 小 , 同 时 , d ( S + B ) / dS > 0 , ∴ S + B 会 增 加 ,
∴ U 2 ( S + B ) 会增加,因为(*)式, U 2 ( S + B ) 增加的幅度比 U1 ( I1 − S ) 减小的幅度大,所以
如果参与者推断自然选择左边博弈的概率23参与者2选l如果参与者推断自然选择左边博弈的概率23参与者2选l和选r无差异如果参与者推断自然选择左边博弈的概率23参与者2选r如果参与者推断自然选择左边博弈的概率23参与者2选l如果参与者推断自然选择左边博弈的概率23参与者2选l和选r无差异如果参与者推断自然选择左边博弈的概率23参与者2选r自然选择左边博弈时参与者1选t参与者2选l
由 一 阶 条 件 ∂π i / ∂qi = 0 , 可 得 : qi = (a − q− i − c) / 2 … … ( 1)
* *
( 1) 式 两 端 乘 以 2, 再 减 qi , 可 得 : qi = a − Q − c … … ( 2), 对 于 任 意 的 i 都 成 立 。
吉本斯《博弈论基础》课后习题答案

对 于 2 来 说 , 4(1− p*) = 2 p* + 3(1− p*) , 得 p* = 1/ 3 。
则 原 博 弈 的 混 合 战 略 纳 什 均 衡 为 : { (1/3, 2/3, 0), (2/3, 0, 1/3) }。 1.12 按 照 1.11 的 解 法 , 可 得 混 合 战 略 纳 什 均 衡 为 : { (2/3, 1/3), (3/4, 1/4) }。 过 程 略 。 1.13 此博弈有两个纯战略纳什均衡、一个混合战略纳什均衡。 纯 战 略 纳 什 均 衡 为 :( 向 企 业 1 申 请 , 向 企 业 2 申 请 );( 向 企 业 2 申 请 , 向 企 业 1 申 请 )。 混合战略纳什均衡为:
{ } ((2w1 − w2 ) /(w1 + w2 ), (2w2 − w1) /(w1 + w2 )) ,((2w1 − w2 ) /(w1 + w2 ), (2w2 − w1) /(w1 + w2 ))
1.14
证 明 : 在 混 合 战 略 纳 什 均 衡 中 , 参 与 人 i 的 混 合 战 略 为 pi* , 其 中 选 择 第 j 个 纯 战 略 sij 的 概
目 要 求 , 即 ( qc , qc )是 唯 一 的 纳 什 均 衡 , 并 且 在 纳 什 均 衡 下 , 每 一 企 业 的 福 利 都 要 比 他 们 相
互合作时低,但两个企业都没有严格劣战略。 1.6
当 0 < c1, c2 < a / 2 时 , 易 求 均 衡 产 量 q1* = (a + c2 − 2c1) / 3 , q2* = (a + c1 − 2c2 ) / 3 。 而 当
为:
博弈论基础吉本斯课后习题答案

Gibbons《 博 弈 论 基 础 》 习 题 解 答 ( CENET)
π1 , π1
qc
π3 ,π2
q’
π1 ,π5
π2 ,π3 π4,π4 π7 ,π6
π5 ,π1 π6 ,π7 π8 ,π8
其 中 , π5 = (a − c)2 /16 , π 6 = (a − c)2 /18 , π 7 = (a − c)2 /12 , π8 = 0 。 此 博 弈 符 合 题
Max A
U
(
I
c
(
A)
+
I
p
(
A)
−
V
'−1
(k
))
一阶条件:
U
'(Ic
+
B*
)[
I
' c
( A)
+
I
' p
(
A)]
=
0
由于 U 是递增又严格凹的,U ' (Ic + B*) ≠ 0
这与孩子的选择可是全家的收入最大化的一阶条件相同:
I
' c
(
A)
+
I
' p
(
A)
=
0
2.2 采用逆向归纳法,先最大化家长的收益:给定的孩子的行动 S,来选择自己的行动 B,
率 为 pi*j 。 用 反 证 法 证 明 。
博弈论第三次答案

第三次作业1、两个人合作开发一项产品,能否成功与两个人的工作态度有关,设成功概率如下:单位的利益。
如果双方采取出发战略,则该博弈无限次重复博弈的均衡是什么?答:该博弈的得益矩阵如下B努力 偷懒A 努力 9/4,9/4 3/2,5/2偷懒 5/2,3/2 2,2 一次性博弈显然是囚徒困境博弈,唯一的均衡是两人都偷懒,双方的得益期望都是2。
在无限次重复博弈中,假设双方为了在共同努力方面实现合作采取如下出发策略:开始时努力,若发现对方偷懒,自己也偷懒,可以分析贴现因子δ符合什么条件可以构成子博弈完美纳什均衡:不偏离:()()δδδ-=+++1491492 偏离:()δδδ-+=+++12212252 当满足()δδ-+≥-1221149,即21≥δ时采取这种出发策略是正确的,否则偏离是正确的。
当21≥δ时,双方都采取出发策略是该博弈的子博弈完美纳什均衡,如果21<δ,则上述出发策略组合不是子博弈完美纳什均衡,两人都会采取偷懒的策略。
2、假设无限次重复博弈的阶段博弈是古诺竞争模型,假设两个寡头面对市场需求为 Q =a -p ,不变的单位成本为c ,请计算支持垄断价格作为子博弈精练纳什均衡的结 果的最低贴现因子。
在重复博弈下 合作的收益要大于背叛的收益 即:()22283118c a c a -⎪⎭⎫ ⎝⎛≥⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-δ+2311⎪⎭⎫ ⎝⎛--c a δ 解得179≥δ3、不会4、两个厂商生产相同产品在市场上进行竞争性销售。
第1个厂商的成本函数为11q c =,其中1q 为厂商1的产量.第2个厂商的成本函数为22cq c =,其中2q 为厂商2的产量,c 为其常数边际成本.两个厂商的固定成本都为零.厂商2的边际成本c 是厂商2的“私人信息”,厂商1认为c 在⎥⎦⎤⎢⎣⎡23,21上呈均匀分布。
设市场需求函数为214q q P --=,其中P 为价格,两个厂商都以其产量为纯战略,问纯战略贝叶斯均衡为何?.给定2q ,厂商1的问题是12111)14( )1(max 1q q q q P q ---=-=π 因)(22c q q =。
博弈论课后习题

第一章导论1、什么是博弈博弈论的主要研究内容是什么2、设定一个博弈模型必须确定哪儿个方面3、举出烟草、餐饮、股市、房地产、广告、电视等行业的竞争中策略相互依存的例子。
4、“囚徒的困境”的内在根源是什么举出现实中囚徒的困境的具体例子。
5、博弈有哪些分类方法,有哪些主要的类型6、你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的:你决定开,则的概率你讲收益300万元(包括投资),而的概率你将全部亏损;如果你不开,则你能保住本钱但也不会有利润,请你(a)用得益矩阵和扩展形式表示该博弈;(b)如果你是风险中性的,你会怎样选择(c)如果你是风险规避的,且期望得益的折扣系数为,你的策略选择是什么(d)如果你是风险偏好的,期望得益折算系数为,你的选择又是什么7、一逃犯从关押他的监狱中逃走,一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线,看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可以少坐10年牢,但一旦被抓住则要加刑10年;看守抓住逃犯能得到1000 元奖金。
请分别用得益矩阵和扩展形式表示该傅弈,并作简单分析。
第二章完全信息静态博弈1、上策均衡、严格下策反复消去法和纳什均衡相互之间的关系是什么2、为什么说纳什均衡是博弈分析中最重要的概念3、找出现实经济或生活中可以用帕累托上策均衡、风险上策均衡分析的例子。
4、多重纳什均衡是否会影响纳什均衡的一致预测性质,对博弈分析有什么不利影响5、下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡暉弈的结果是什么6、求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
7、博弈方1和2就如何分10 000元进行讨价还价。
假设确定了以下规则: 双方同时提出自己要求的数额S1和S2, 0 < si, s2 < 10 000,如果sl+s2 W10 000,则两博弈方的要求都得到满足,即分别得到si和s2,但如果是sl+s2>10 000,则该笔钱就被没收。
博弈论 第三节

纳什均衡作用
纳什均衡被广泛应用于各个领域的研究,尤其在进行 制度分析时,我们可应用它得出一个很重要结论:一 种制度(体制)安排要发生效力,必须是一种纳什均衡。 否则,这种制度安排便不能成立。
贝茨(R.H.Bates,1983)设想过无国家社会的两个大家 庭的情形。X和Y,每家都拥有同样的武力潜能和侵犯倾 向,都拥有相当于10头牛的净财产。每家都有两种行为选 择:侵犯对方行为A,不侵犯对方行为N。两个策略的收 益与另一家的策略选择有关,因而就有四个可能的结果。 下面就是一个假设的收益矩阵:
四分卫
13,-13 10.5,-10.5 1,-1 -2,2
┏━━━━━━━━━━━━━┯━━━━━━━━━━━━━━┓ ┃ │ 家庭X的选择 ┃ ┃ ├──────┬───────┨ ┃ │A(侵犯) │N(不侵犯) ┃ ┠──────┬──────┼──────┼───────┨ ┃ │A(侵犯) │ (4,4) │ (18,2) ┃ ┃家庭Y的选择├──────┼──────┼───────┨ ┃ │N(不侵犯)│ (2,18) │ (10,10) ┃ ┗━━━━━━┷━━━━━━┷━━━━━━┷━━━━━━━┛
6,-6 10,-10
4.5,-4.5 3,-3
1,-1 -2,2
纳什均衡(Nash equilibrium )
纳什均衡(非合作博弈均衡 )指的是博弈中的一个 策略组合,在其他参与人都坚守这个策略组合中的 策略不变的情况下,没有参与人通过改变自己的策 略而得到一个更高的支付。
并不是指所有参与人的支付最优。
寻找纳什均衡的方法
最优策略
重复剔除劣策略 枚举法 最优反应分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题1:如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定,即下图中a 、b 数值不确定。
试讨论本博弈有哪几种可能的结果。
如果本博弈中的“威胁”和“承诺”是可信的,a 或b 应满足什么条件?①0a <,不借—不分—不打;②01a <<,且2b >,借—不分—打;③1a >,且2b >,借—不分—打(,)a b ;④0a >,且2b <,借—分—(2,2)问题2:三寡头市场需求函数Q P -=100,其中Q 是三个厂商的产量之和,并且已知三个厂商都有常数边际成本2而无固定成本。
如果厂商1和厂商2同时决定产量,厂商3根据厂商1和厂商2的产量决策,问它们各自的产量和利润是多少?1123111231(100)2(98)q q q q q q q q q π=----=---2123221232(100)2(98)q q q q q q q q q π=----=---3123331233(100)2(98)q q q q q q q q q π=----=---331230,(98)/2q q q q π∂=⇒=--∂(a ,b ) (0,4)代入,11212122(98)/2,(98)/2q q q q q q ππ=--=--12120,0q q ππ∂∂==∂∂,得***12398/3,49/3q q q === ***1234802/9,2401/9πππ===。
问题3:设两个博弈方之间的三阶段动态博弈如下图所示。
(1)若a 和b 分别等于100和150,该博弈的子博弈完美纳什均衡是什么?(2)T N L --是否可能成为该博弈的子博弈完美纳什均衡路径,为什么?(3)在什么情况下博弈方2会获得300单位或更高的得益?(1)博弈方1在第一阶段选择R ,在第三阶段选择S ,博弈方2在第二阶段选择M 。
(2)不可能。
T N L --带来的利益50明显小于博弈方1在第一阶段R 的得益300;无论a 和b 是什么数值,该路径都不能构成Nash 均衡,不能成为子博弈完美Nash 均衡。
(a ,b ) 50,300(3)由于T N L --不是本博弈的子博弈完美Nash 均衡,因此博弈方2不可能通过该路径实现300单位的得益,唯一有可能实现300单位及以上的得益的路径为L N S --,要使该路径成为子博弈完美Nash 均衡而且博弈方2得到300单位及以上的得益必须300,300a b >≥。
问题4:企业甲和企业乙都是彩电制造商,都可以选择生产低档产品或高档产品,每个企业在四种不同的情况下的利润如以下得益矩阵所示。
如果企业甲先于企业乙进行产品选择并投入生产,即企业乙在决定产品时已经知道企业甲的选择,而且这一点双方都清楚。
(1)用扩展型表示这一博弈。
(2)这一博弈的子博弈完美纳什均衡是什么?扩展型表示的博弈若甲选择高档,乙选择低档,甲得1000元,乙得700元;若甲选择低档,乙选择高档,那么甲得700元,乙得1000元,所以:甲的策略为:选择生产高档产品;乙的策略是:若甲选择高档,乙选择低档;若甲选择低档,乙选择高档。
本博弈的子博弈Nash 均衡是:甲选择生产高档彩电,乙选择生产低档彩电。
问题5:乙向甲索要1000元,并且威胁甲如果不给就与他同归于尽。
当然甲不一定相信乙的威胁。
请用扩展型表示该博弈,并找出纯策略纳什均衡和子博弈完美纳什均衡。
两个纯策略Nash 均衡:(给,实施),(不给,不实施) 实施的威胁不可信,甲在第一阶段选择不给,乙在第二阶段不实施(生命诚可贵);这是子博弈完美纳什均衡;另一个(给,实施)不可信。
问题6:两个寡头企业进行价格竞争博弈,企业1的利润函数是q c aq p ++--=21)(π,企业2的利润函数是p b q +--=22)(π,其中p 是企业1的价格,q 是企业2的价格。
求:(1)两个企业同时决策的纯策略纳什均衡;-1000,1000)(2)企业1先决策的子博弈完美纳什均衡;(3)企业2先决策的子博弈完美纳什均衡;(4)是否存在参数c b a ,,的特定值或范围,使两个企业都希望自己先决策?解:(1)122()02()0p aq c p q b qππ∂=--+=∂∂=--=∂,解得:,p ab c q c =-= 12,b ab c ππ==-(2)22()0q b q π∂=--=∂,代入得到21)p ab c b π=--++(,12)0p ab c pπ∂=--+=∂(,得 p ab c =-,企业1的子博弈完美纳什均衡企业1的定价p ab c =-,企业2的定价q b =,利润也与(1)相同。
与同时选择无异。
(3)将p aq c =-代入222))q b p q b aq c π=--+=--+-((22)0q b a qπ∂=--+=∂(,解得2a q b =+,代入得 22a p abc =+- *12a b b π=+>,2*24a ab c ab c π=+->- (4)只有先决策的利润大于后决策时的利润时才有激励。
①当24a abc ab c +->-0a ⇒≠,企业2希望先决策; ②当2a b b >+时,企业1希望先决策,只要0a <都希望自己先决策。
20,0,0,024a ab b abc ab c >+>->+->,因此当 0,2a ab <>-和c ab <时都能满足,这样才参数范围都希望自己先决策。
问题7:三寡头市场有倒转的需求函数为Q a Q P -=)(,其中321q q q Q ++=,i q 是厂商i 的产量。
每一个厂商生产的边际成本为常数c ,没有固定成本。
如果厂商1先选择产量1q ,厂商2和厂商3观察到1q 后同时选择2q 和3q ,问它们各自的产量和利润是多少?解:[]123()()1,2,3i i a c q q q q i π=----=21232312332020a c q q q q a c q q q q ππ∂=----=∂∂=----=∂ 2311()3q q a c q ==--,代入得1111()3a c q q π=-- 令*11110,()2d q a c dq π==-,代入得:**231()6q q a c ==- *2*2*2123111(),(),()123636a c a c a c πππ=-=-=- 问题8:考虑如下的双寡头市场战略投资模型:企业1和企业2目前情况下的生产成本都是2=c 。
企业1可以引进一项新技术使单位成本降低到1=c ,该项技术需要投资f 。
在企业1作出是否投资的决策(企业2可以观察到)后,两个企业同时选择产量。
假设市场需求函数为q q p -=14)(,其中p 是市场价格,q 是两个企业的总产量。
问上述投资额f 处于什么水平时,企业1会选择引进新技术?解:以未引进技术为基准1121121222(14)2(14)2q q q q q q q q ππ=---=---,令12120q q ππ∂∂==∂∂,得 12124,16q q ππ==⇒==如果引进技术,1121121222(14)(14)2q q q q f q q q q ππ=----=--- 令12120q q ππ∂∂==∂∂,得1211411196,,339q q f π'==⇒=- 只有引进技术后得到的利润大于未引进技术的总利润时,即 196169f ->,即196521699f <-=时企业1才会引进新技术。
问题9:如果学生在考试之前全面复习,考好的概率为90%,如果学生只复习一部分重点,则有50%的概率考好。
全面复习花费的时间1001=t 小时,重点复习只需要花费202=t 小时。
学生的效用函数为:e W U 2-=,其中W 是考试成绩,有高低两种分数h W 和l W ,e 为努力学习的时间。
问老师如何才能促使学生全面复习?解:学生全面复习的期望得益10.9(200)0.1(200)0.90.1200h l h l u w w w w =⨯-+⨯-=+-学生重点复习的期望得益20.5(40)0.5(40)0.50.540h l h l u w w w w =⨯-+⨯-=+-根据激励相容的条件,12u u ≥,所以有0.90.12000.50.540h l h l w w w w +-≥+-所以:0.4()160h l w w -≥故:400h l w w -≥奖学金与学习成绩全面挂钩,才能激励学生的学习;单靠成绩没有这么大的力度。
问题10:某人正在打一场官司,不请律师肯定会输,请律师后的结果与律师的努力程度有关。
假设当律师努力工作(100小时)时有50%的概率能赢,律师不努力工作(10小时)则只有15%的概率能赢。
如果诉讼获胜可得到250万元赔偿,失败则没有赔偿。
因为委托方无法监督律师的工作,因此双方约定根据结果付费,赢官司律师可获赔偿金额的10%,失败则律师一分钱也得不到。
如果律师的效用函数为e m 05.0.-,其中m 是报酬,e 是努力小时数,且律师有机会成本5万元。
求这个博弈的均衡。
解:第三阶段,律师努力的期望得益:0.5200.557.5⨯-⨯=不努力的期望得益:0.1524.50.850.5 3.25⨯-⨯=满足激励相容约束第二阶段:7.5 3.25&7.55>>接受委托并努力工作第一阶段:委托,接受委托,代理人努力工作,那么⨯+⨯=>0.52250.50112.50委托是必然的选择。
打官司的人提出委托,律师接受委托并努力工作。
0,5)赢(225,20)(0,-5)(225,24.5)(0,-0.5)。
