(完整版)平方数的规律及100以内的平方表

合集下载

平方数的规律及以内的平方表

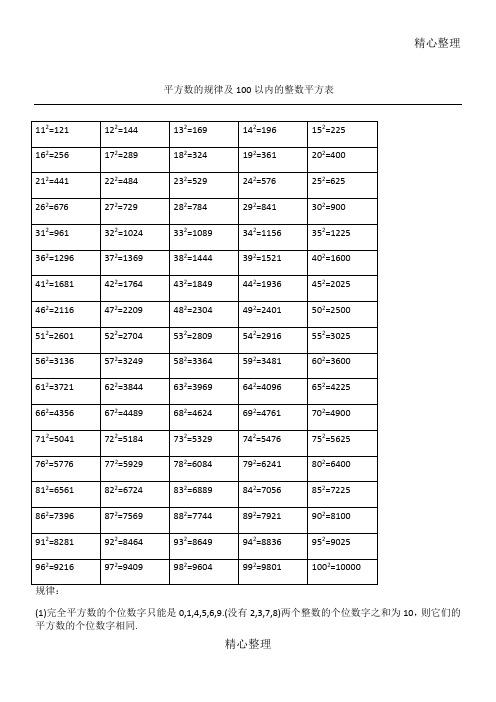
精心整理平方数的规律及100以内的整数平方表(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.,等..a×ab×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

100以内整数的平方及其规律

平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b 例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744 用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744, 112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).1-20的平方数221-40的平方数341-60的平方数461-80的平方数581-100的平方数。

平方数的规律及100以内的平方表

平方数的规律及100以内的整数平方表之欧侯瑞魂创作(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不克不及被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不克不及整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分需要条件是n有奇数个因数(包含1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它自己乘以它自己）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必定是一个为奇数另一个为偶数，不成能同时为奇数或同时为偶数.z和z2肯定都是奇数.五组罕见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841记忆技巧：(a+b)2= a2 + b2+2ab(a－b)2=a2+b2 －2ab|| | || |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超出的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不克不及被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不必检查了，实际上2431=1117.③增加对数字的熟悉程度，比方162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的) 122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及以内的平方表

平方数的规律及以内的平方表The Standardization Office was revised on the afternoon of December 13, 2020平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到√n之间的所有质数是不是n的因子即可，超过√n的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<√2431<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=11×13×17.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

2021年平方数的规律及100以内的平方表

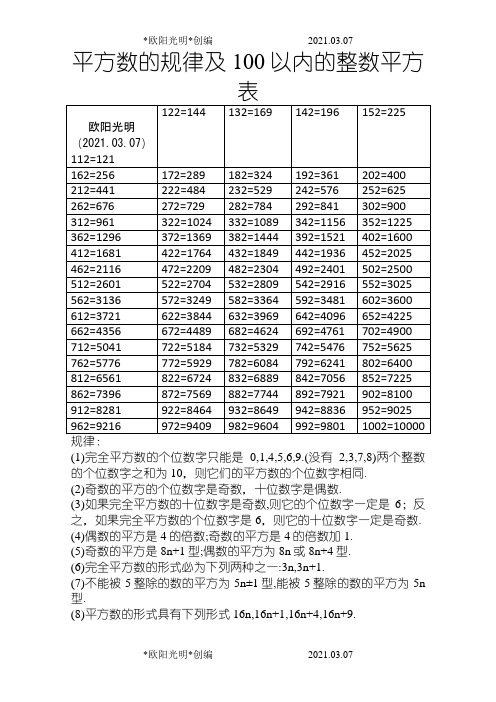
平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数. x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=292 9+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841记忆技巧：(a+b)2= a2 + b2+2ab(a－b)2=a2+b2 －2ab|| | || |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的) 122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及以内的平方表

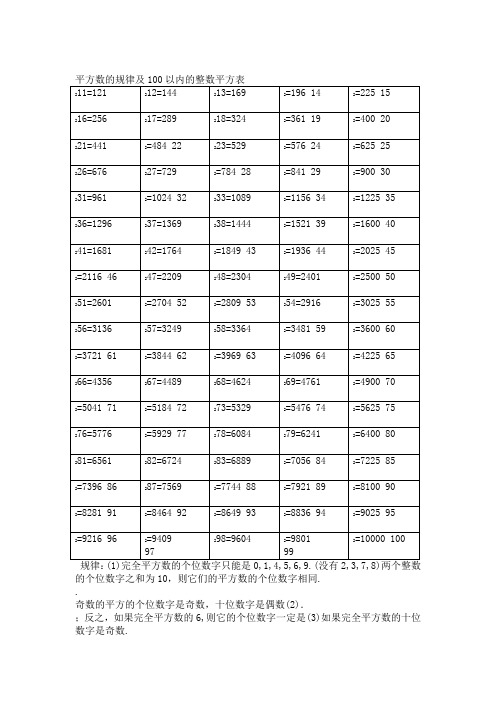
的个位数字之和为10，则它们的平方数的个位数字相同..奇数的平方的个位数字是奇数，十位数字是偶数(2)．；反之，如果完全平方数的6,则它的个位数字一定是(3)如果完全平方数的十位数字是奇数.，则它的十位数字一定是奇数个位数字是61. 4的倍数加4偶数的平方是的倍数;奇数的平方是(4). 8n+4型;偶数的平方为8n或(5)奇数的平方是8n+1型:3n,3n+1.(6)完全平方数的形式必为下列两种之一. 5n型,能被5整除的数的平方为不能被5整除的数的平方为5n±1型(7)16n,16n+1,16n+4,16n+9.(8)平方数的形式具有下列形式2,5,8) 0,1,3,4,6,7,9.(没有(9)完全平方数的各位数字之和的个位数字只能是. a不是完全平方数的平方不能整除a,则(10)如果质数p能整除a,但p.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数n). 和(包括1是完全平方数的充分必要条件是(12)一个正整数nn有奇数个因数或整数乘以它本身乘以它,一个数如果是另一个整数的完全立方（即一个整数的三次方如，方数叫数,也做立们就称这个数为完全立方么本身）,那我.等0,1,8,27,64,125,216,343,512,729,1000222.为一组勾股数+y就称=zx,y,z如果正整数x,y,z满足不定方程x,2必定都是奇数. 和zx,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z五组常见的勾股数：222222222222222+21+15；5=29+12=17=13；720+24；=25；38+4=59+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：222222－2ab －b)(a+b)+b=a=a+b+2ab(a||||||a×ab×b2×a×ba×ab×b2×a×b2222+2×10×3=100+9+60=169=10例：13 =(10+3)+32222－2×90×2=90=8100+4+2－88360=7744 =(90-2)用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，22整3不能被49<<50,2+4+3+1=10所以,=2401<2431<2500=5049是否为质数，因为2431判定除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117. 28210， 16=256=2=1024=2，32③增加对数字的熟悉程度，比如2122=7744, 另外一些特殊结构的数字应该牢记，如=4096=288,6422=484,(121和484从左到右与从右到左看是一样的11=121,22)22222).也左右颠倒a左右颠倒后=961,(a=169,31=441,13=144,2112．。

(完整word版)平方数的规律及100以内的平方表

精心整理平方数的规律及100以内的整数平方表(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.精心整理精心整理(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2=a2+b2+2ab(a－b)2=a2+b2－2ab||||||a×ab×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).精心整理。

100以内整数的平方及其规律

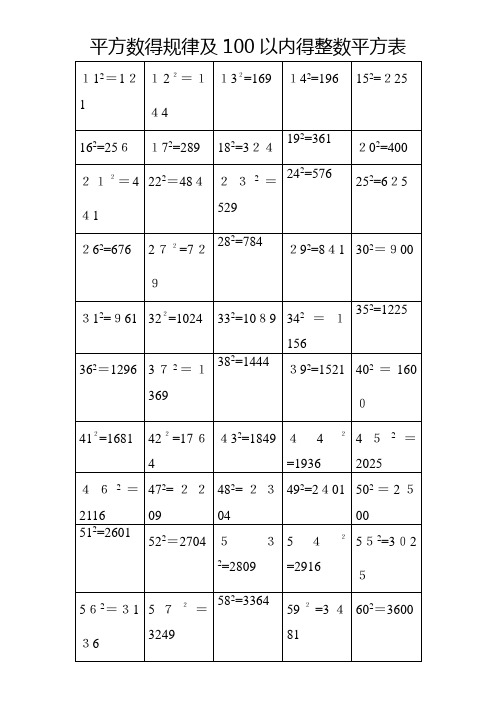
平方数得规律及100以内得整数平方表规律：（１)完全平方数得个位数字只能就是０,１，4,5,6,9、(没有2，3，7，8）两个整数得个位数字之与为1０,则它们得平方数得个位数字相同、（2)奇数得平方得个位数字就是奇数,十位数字就是偶数、(3）如果完全平方数得十位数字就是奇数,则它得个位数字一定就是6;反之，如果完全平方数得个位数字就是6，则它得十位数字一定就是奇数、(4)偶数得平方就是４得倍数；奇数得平方就是4得倍数加1、(5)奇数得平方就是8n+1型;偶数得平方为８n或８n＋4型、（6）完全平方数得形式必为下列两种之一：3n，３ｎ+1、(7)不能被５整除得数得平方为5n±1型,能被5整除得数得平方为5n 型、(８）平方数得形式具有下列形式１6n,16n＋１,16n+4,1６n+９、(9）完全平方数得各位数字之与得个位数字只能就是０,1，3,4，６,7，９、(没有２,5，8）（10）如果质数ｐ能整除a,但ｐ得平方不能整除a,则a不就是完全平方数、(11）在两个相邻得整数得平方数之间得所有整数都不就是完全平方数、（12）一个正整数n就是完全平方数得充分必要条件就是n有奇数个因数（包括1与ｎ)、一个数如果就是另一个整数得完全立方（即一个整数得三次方，或整数乘以它本身乘以它本身)，那么我们就称这个数为完全立方数,也叫做立方数,如０,1，8,27，64,125,216,３4３,512，729，１0０0等、如果正整数x，ｙ，ｚ满足不定方程ｘ2+y２＝ｚ2,就称x，ｙ，z为一组勾股数、x，y必然就是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数、z与z2必定都就是奇数、五组常见得勾股数:32+42=52；5２+12２=132；72+2４2=２52；82+1５２＝172;２０2＋212=29２９＋16=25；25+14４=１69；４9＋5７6=6２5; 64+2２5＝２89；４００＋44１＝84１记忆技巧：(ａ+b)2＝a2＋ｂ２＋2ａb （ａ－b)2=a2 + ｂ2 －2ab｜｜| ｜| ｜ａ×a ｂ×b 2×a×b a×a b×b 2×a ×b例：132＝（10＋3)2=102＋３2+２×10×3=1０0＋9+６0=169 882=(90-２)2＝902+2２－2×９０×2=８1０0＋4—36０=７７4４用处：①训练计算能力，使计算更快更准确；②估计某数得平方根所处得范围，在判定某个较大得数n就是不就是质数时可以缩小其可能因子得筛选范围，只需检查3到之间得所有质数就是不就是n得因子即可，超过得都不必检查了、例如,判定2431就是否为质数,因为４92=240１<2431〈25０0=50２,所以4９＜＜5０，2+4+3＋1＝10不能被３整除，２341得个位既非0又非5，故只需检查7到４7之间得所有质数能否整除2431即可，而53,59，61,6７……等更大得质数都不用检查了，实际上２４31=1117、③增加对数字得熟悉程度，比如16２=2５6=28，３22＝10２4＝2１0,６42=４096=２1２,另外一些特殊结构得数字应该牢记，如８8２=774４，ﻫ１12=12１,2２２=484,（1２1与484从左到右与从右到左瞧就是一样得)ﻫ１２２＝144,21２=４41,１３2=169,３12=9６1,(a左右颠倒后ａ2也左右颠倒）、1—2０得平方数221－40得平方数341-60得平方数461－80得平方数581-100得平方数。

100以内平方表

规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到√n之间的所有质数是不是n的因子即可，超过√n的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<√2431<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=11×13×17.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及以内的平方表

平方数的规律及以内的平方表Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2=a2+b2+2ab(a－b)2=a2+b2－2ab||||||a×a b×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及100以内的平方表(最新编写)

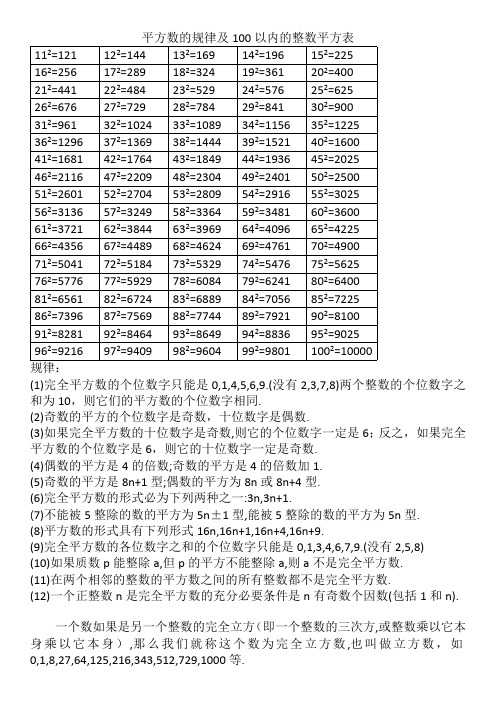
平方数的规律及100以内的整数平方表112=121122=144132=169142=196152=225162=256172=289182=324192=361202=400212=441222=484232=529242=576252=625262=676272=729282=784292=841302=900312=961322=1024332=1089342=1156352=1225362=1296372=1369382=1444392=1521402=1600412=1681422=1764432=1849442=1936452=2025462=2116472=2209482=2304492=2401502=2500512=2601522=2704532=2809542=2916552=3025562=3136572=3249582=3364592=3481602=3600612=3721622=3844632=3969642=4096652=4225662=4356672=4489682=4624692=4761702=4900712=5041722=5184732=5329742=5476752=5625762=5776772=5929782=6084792=6241802=6400812=6561822=6724832=6889842=7056852=7225862=7396872=7569882=7744892=7921902=8100912=8281922=8464932=8649942=8836952=9025962=9216972=9409982=9604992=98011002=10000规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，n超过的都不必检查了.例如，判定2431是否为质数，因为n2431492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.×13×③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

100以内整数的平方与规律

平方数的规律及100以的整数平方表(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).1-20的平方数221-40的平方数341-60的平方数461-80的平方数581-100的平方数。

平方数的规律及以内的平方表

数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8).不是完全平方数a则a,的平方不能整除p但a,能整除p如果质数(10)．.在两个相邻的整数的平方数之间的所有整数都不是完全平方数(11)n).和(包括1一个正整数n是完全平方数的充分必要条件是n有奇数个因数(12)或整数乘以它本身乘以它,一个数如果是另一个整数的完全立方（即一个整数的三次方也叫做立方数，如,本身）,那么我们就称这个数为完全立方数.等0,1,8,27,64,125,216,343,512,729,1000222.为一组勾股数+y就称=zx,y,z如果正整数x,y,z满足不定方程x ,2必定都是奇数. 和zx,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z五组常见的勾股数：222222222222222 +21 ；+4=58 ；5；+12+15=1320 ；7=17+24=253=299+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：22222 2 －2ab =a + b b + 2ab (a(a+b)－= ab) +| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b2222+2×10×3=100+9+60=169 13=10=(10+3)+3例：2222－2×90×2=8100+4=90－88+2=(90-2)360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的都不必检查之间的所有质数是不是n到,只需检查3的因子即可，超过的筛选范围22,所以=2401<2431<2500=50是否为质数，因为了.例如，判定243149<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非49<5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.28210，=1024=2=256=2 ，3216③增加对数字的熟悉程度，比如2122=7744, 另外一些特殊结构的数字应该牢记，如=4096=288 ,6422=484,(121和484从左到右与从右到左看是一样的11=121,22)22222).也左右颠倒a左右颠倒后=961,(a=169,31=441,13=144,2112．。

平方数的规律及100以内的平方表讲解学习

平方数的规律及100以内的平方表平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

100以内平方表

规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及以内的平方表

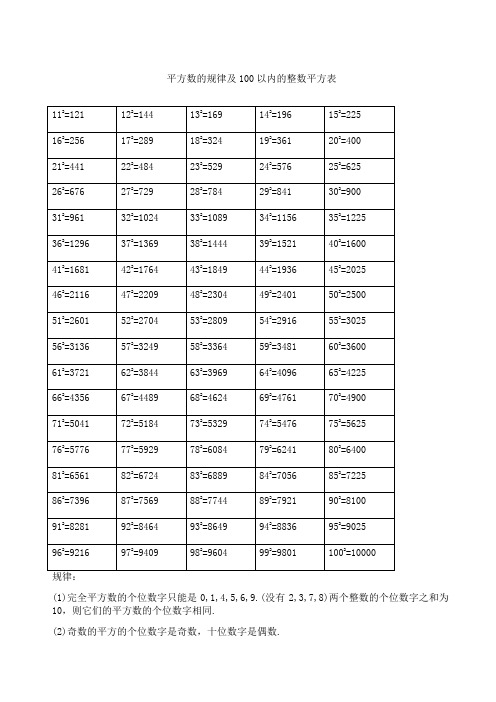
平方数的规律及100以内的整数平方表(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2=a2+b2+2ab(a－b)2=a2+b2－2ab||||||a×a b×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及以内的平方表

平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数. 五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

100以内平方表

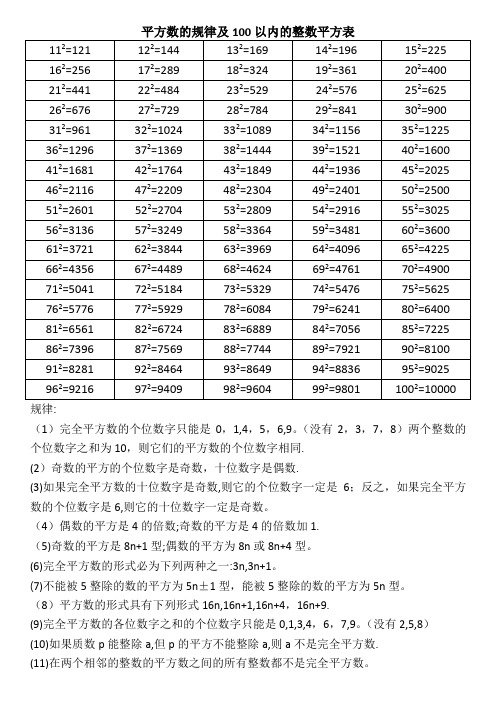
规律:（1）完全平方数的个位数字只能是0，1,4，5，6,9。

（没有2，3，7，8）两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2）奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6,则它的十位数字一定是奇数。

（4）偶数的平方是4的倍数;奇数的平方是4的倍数加1.（5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型。

(6)完全平方数的形式必为下列两种之一:3n,3n+1。

(7)不能被5整除的数的平方为5n±1型，能被5整除的数的平方为5n型。

（8）平方数的形式具有下列形式16n,16n+1,16n+4，16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4，6，7,9。

（没有2,5,8）(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数。

（12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数（包括1和n）。

一个数如果是另一个整数的完全立方（即一个整数的三次方，或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数，也叫做立方数，如0，1,8，27，64,125，216，343，512，729,1000等。

如果正整数x,y,z满足不定方程x2+y2=z2，就称x,y，z为一组勾股数。

x，y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52;52+122=132;72+242=252;82+152=172；202+212=2929+16=25；25+144=169；49+576=625; 64+225=289; 400+441=841记忆技巧：(a+b)2= a2 + b2+2ab(a－b)2=a2+b2 －2ab｜｜｜｜| |a×ab×b2×a×ba×ab×b2×a×b例：132=(10+3）2=102+32+2×10×3=100+9+60=169882=(90-2）2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了。