100以内的平方数与立方数
100以内整数的平方及其规律

平方数的规律及100以内的整数平方表规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b 例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744 用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744, 112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).1-20的平方数221-40的平方数341-60的平方数461-80的平方数581-100的平方数。
1--100平方立方表

21952
24389
27000
立方
原数
31
32
33
34
35
36
37
38
39
40
原数
平方
961
1024
1089
1156
1225
1296
1369
1444
1521
1600
平方
立方
29791
32768
35937
39304
42875
46656
50653
54872
59319
64000
立方
原数
41
42
43
614125
636056
658503
681472
704969
729000
立方
原数
91
92
93
94
95
96
97
98
99
100
原数
平方
8281
8464
8649
8836
9025
9216
9409
9604
9801
10000
平方
立方
753571
778688
804357
830584
857375
884736
912673
2809
2916
3025
3136
3249
3364
3481
3600
平方
立方
132651
140608
148877
157464
166375
175616
185193
1--100平方立方表

72
73
74
75
76
77
78
79
80
原数
平方
5041
5184
5329
5476 |
5625
5776
5929
6084
6241
6400
平方
1、、・ 立方
35791
1
3
37324(
8
389017
405224
421875
4
38976
45653
3
4'
74552
1493039
5
12000
立方
原数
81
82
83
84
学习资料收集于网络,仅供参考
1的平方=1
13=1
2的平方=4
23=8
3的平方=9
33=27
4的平方=16
43=64
5的平方=25
53=125
6的平方=36
63=216
7的平方=49
73=343
8的平方=64
83=512
9的平方=81
93=729
10的平方=100
103=1000
11的平方=121
113=1331
12的平方=144
123=1728
13的平方=169
133=2197
14的平方=196
143=2744
15的平方=225
153=3375
16的平方=256
163=4096
17的平方=289
173=4913
18的平方=324
183=5832
19的平方=361
20的平方=400
平方数的规律及以内的平方表
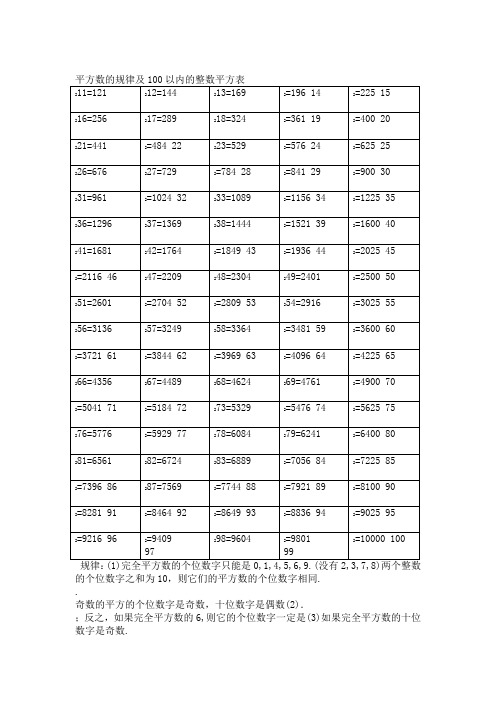
的个位数字之和为10,则它们的平方数的个位数字相同..奇数的平方的个位数字是奇数,十位数字是偶数(2).;反之,如果完全平方数的6,则它的个位数字一定是(3)如果完全平方数的十位数字是奇数.,则它的十位数字一定是奇数个位数字是61. 4的倍数加4偶数的平方是的倍数;奇数的平方是(4). 8n+4型;偶数的平方为8n或(5)奇数的平方是8n+1型:3n,3n+1.(6)完全平方数的形式必为下列两种之一. 5n型,能被5整除的数的平方为不能被5整除的数的平方为5n±1型(7)16n,16n+1,16n+4,16n+9.(8)平方数的形式具有下列形式2,5,8) 0,1,3,4,6,7,9.(没有(9)完全平方数的各位数字之和的个位数字只能是. a不是完全平方数的平方不能整除a,则(10)如果质数p能整除a,但p.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数n). 和(包括1是完全平方数的充分必要条件是(12)一个正整数nn有奇数个因数或整数乘以它本身乘以它,一个数如果是另一个整数的完全立方(即一个整数的三次方如,方数叫数,也做立们就称这个数为完全立方么本身),那我.等0,1,8,27,64,125,216,343,512,729,1000222.为一组勾股数+y就称=zx,y,z如果正整数x,y,z满足不定方程x,2必定都是奇数. 和zx,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z五组常见的勾股数:222222222222222+21+15;5=29+12=17=13;720+24;=25;38+4=59+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:222222-2ab -b)(a+b)+b=a=a+b+2ab(a||||||a×ab×b2×a×ba×ab×b2×a×b2222+2×10×3=100+9+60=169=10例:13 =(10+3)+32222-2×90×2=90=8100+4+2-88360=7744 =(90-2)用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,22整3不能被49<<50,2+4+3+1=10所以,=2401<2431<2500=5049是否为质数,因为2431判定除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117. 28210, 16=256=2=1024=2,32③增加对数字的熟悉程度,比如2122=7744, 另外一些特殊结构的数字应该牢记,如=4096=288,6422=484,(121和484从左到右与从右到左看是一样的11=121,22)22222).也左右颠倒a左右颠倒后=961,(a=169,31=441,13=144,2112.。
(完整word版)平方数的规律及100以内的平方表

精心整理平方数的规律及100以内的整数平方表(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.精心整理精心整理(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2=a2+b2+2ab(a-b)2=a2+b2-2ab||||||a×ab×b2×a×ba×ab×b2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).精心整理。
1--100平方立方表

256
289
324
361
400
平方
立方
1331
1728
2197
2744
3375
4096
4913
5832
6859
8000
立方
原数
21
22
23
24
25
26
27
28
29
30
原数
平方
441
484
529
576
625
676
729
784
841
900
平方
立方
9261
10648
12167
13824
15625
17576
4624
4761
4900
平方
立方
226981
238328
250047
262144
274625
287496
300763
314432
328509
343000
立方
原数
71
72
73
74
75
76
77
78
79
80
原数
平方
5041
5184
5329
5476
5625
5776
5929
6084
6241
6400
平方
立方
357911
19683
21952
24389
27000
立方
原数
31
32
33
34
35
36
37
38
39
40
原数
平方数的规律及100以内的平方表(最新编写)
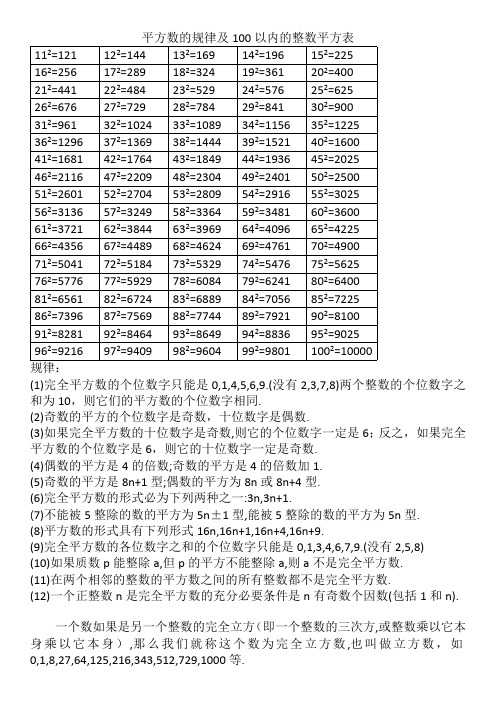
平方数的规律及100以内的整数平方表112=121122=144132=169142=196152=225162=256172=289182=324192=361202=400212=441222=484232=529242=576252=625262=676272=729282=784292=841302=900312=961322=1024332=1089342=1156352=1225362=1296372=1369382=1444392=1521402=1600412=1681422=1764432=1849442=1936452=2025462=2116472=2209482=2304492=2401502=2500512=2601522=2704532=2809542=2916552=3025562=3136572=3249582=3364592=3481602=3600612=3721622=3844632=3969642=4096652=4225662=4356672=4489682=4624692=4761702=4900712=5041722=5184732=5329742=5476752=5625762=5776772=5929782=6084792=6241802=6400812=6561822=6724832=6889842=7056852=7225862=7396872=7569882=7744892=7921902=8100912=8281922=8464932=8649942=8836952=9025962=9216972=9409982=9604992=98011002=10000规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,n超过的都不必检查了.例如,判定2431是否为质数,因为n2431492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.×13×③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
平方数和立方数—解答

可 知 n 是 偶 数 , 所 以 4 mn , 因 而 4 (m2 n 2 m) , 所 以 4 m , 根 据
(k 2 m 4m 4 , m )
4 4
d 4 ,又 k 2m 2 4m 2 4m 应该是完全平方数, ,可知 m ( , 4) d
2 2 所以 k m 4m 4 m 是完全平方数,又因为 ( k m 4m 4 , m ) 1 ,因此 m 是完全
m 2 n 2 m kmn 0 ,这是关于 n 的一元二次方程, k 2m 2 4m 2 4m 应该是完全
平方数,设 (k 2 m 4m 4, m) d ,若 d 1 ,则 m 是一个完全平方数,若 d>1 ,则
mn (m 2 n 2 m) , 可知 d 4 , 因此 d 是偶数, 进而 m 是偶数, (k 2 m 4m 4, m) (m, 4) d ,
2 2 28n 2 1 2 2m ,7n2
m2 1 m 1 m 1 m 1 。所以 m 为正奇数,由于 4 2 2 2
4
4
4
平方数,于是 m 是一个完全平方数。
例 6. 用 (n) 表示正整数 n 的所有不同正因数的个数,已知 24 n 1 ,证明:
24 (n) 。
解:显然, n 1(mod 4) ,故 n 不是完全平方数,从而 n Z ,若 d n ,且
d n
n n n ,这就表明 d 和 是两个不等的因子,从而 n 的因数是两两相 d d
d 2 1 4k (k 1) 8 d 2 1, 又(24, d ) 1 3不整除d d 2 1(mod 3) 。
所以 3 d 2 1 。又 (3,8) 1 ,从而 24 d 2 1 。这样 n 的每一对因子都被 24 整 除,结论成立。
平方数的规律及以内的平方表

数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8).不是完全平方数a则a,的平方不能整除p但a,能整除p如果质数(10)..在两个相邻的整数的平方数之间的所有整数都不是完全平方数(11)n).和(包括1一个正整数n是完全平方数的充分必要条件是n有奇数个因数(12)或整数乘以它本身乘以它,一个数如果是另一个整数的完全立方(即一个整数的三次方也叫做立方数,如,本身),那么我们就称这个数为完全立方数.等0,1,8,27,64,125,216,343,512,729,1000222.为一组勾股数+y就称=zx,y,z如果正整数x,y,z满足不定方程x ,2必定都是奇数. 和zx,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z五组常见的勾股数:222222222222222 +21 ;+4=58 ;5;+12+15=1320 ;7=17+24=253=299+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:22222 2 -2ab =a + b b + 2ab (a(a+b)-= ab) +| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b2222+2×10×3=100+9+60=169 13=10=(10+3)+3例:2222-2×90×2=8100+4=90-88+2=(90-2)360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的都不必检查之间的所有质数是不是n到,只需检查3的因子即可,超过的筛选范围22,所以=2401<2431<2500=50是否为质数,因为了.例如,判定243149<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非49<5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.28210,=1024=2=256=2 ,3216③增加对数字的熟悉程度,比如2122=7744, 另外一些特殊结构的数字应该牢记,如=4096=288 ,6422=484,(121和484从左到右与从右到左看是一样的11=121,22)22222).也左右颠倒a左右颠倒后=961,(a=169,31=441,13=144,2112.。
(完整word版)平方数的规律及100以内的平方表

精心整理平方数的规律及100以内的整数平方表(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.精心整理精心整理(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2=a2+b2+2ab(a-b)2=a2+b2-2ab||||||a×ab×b2×a×ba×ab×b2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).精心整理。
小学数学点知识归纳平方数和立方数

小学数学点知识归纳平方数和立方数在小学数学中,平方数和立方数是基础而重要的概念。
深入理解和应用平方数和立方数对于学生的数学学习和解题能力的提升具有积极的作用。
本文将对平方数和立方数的概念进行归纳总结,并通过实例分析来加深理解。
一、平方数平方数是指某个自然数乘以自身所得到的产品。
比如,1的平方等于1,2的平方等于4,3的平方等于9,以此类推。
我们可以发现每个自然数的平方数都有一个明确的规律,即平方数的间隔是逐渐增加的。
下面是一些比较简单的平方数:1² = 12² = 43² = 94² = 165² = 25通过观察上述例子,我们可以发现平方数的特点:平方数是自然数的两倍加一的结果,而且相邻平方数之间的差值是逐渐增加的。
平方数在实际生活中有广泛的应用。
例如,在图形的构造和计算中,平方数可以帮助我们找到正方形的边长、面积以及顶点等属性。
同时,平方数与平方根的概念密切相关,对于后期数学的学习和理解起到了铺垫的作用。
二、立方数立方数是指一个自然数的立方,即某个自然数乘以自身两次所得到的产品。
比如,1的立方等于1,2的立方等于8,3的立方等于27,以此类推。
下面是一些比较简单的立方数:1³ = 12³ = 83³ = 274³ = 645³ = 125立方数的特点和平方数类似,也有一定的规律可循。
我们可以发现每个自然数的立方数之间的间隔也是逐渐增加的。
立方数在实际生活和数学领域中也有广泛的应用。
例如,在测量和计算物体体积时,我们需要应用立方数的概念。
此外,在几何图形和立体几何的学习中,立方数和立方根的运算也是必不可少的。
总结:平方数和立方数是小学数学中的基础概念,对于培养学生的数学思维和解题能力具有重要意义。
通过观察和分析平方数和立方数的规律,学生可以培养对数学的敏感性和逻辑思维能力,并在实际问题中应用这些概念解决问题。
玩转平方数与立方数五年级下册数学能力提升全攻略

玩转平方数与立方数五年级下册数学能力提升全攻略数学是一个重要的学科,对于学生来说,掌握数学的基本概念和运算技巧至关重要。
在五年级下册的数学学习中,平方数与立方数是一个重要的知识点。
掌握了平方数与立方数的概念和性质,将有助于提升学生的数学能力。
本文将以五年级下册数学教材为基础,为大家介绍玩转平方数与立方数的全攻略。
一、平方数与立方数的概念1. 平方数的定义在数学中,平方数是指某个数的平方,即一个数乘以自己所得到的结果。
例如,1、4、9、16等都是平方数,因为它们分别是1、2、3、4的平方。
2. 立方数的定义立方数是指一个数字的立方,即一个数乘以自己再乘以自己所得到的结果。
例如,1、8、27、64等都是立方数,因为它们分别是1、2、3、4的立方。
二、平方数与立方数的性质1. 平方数的性质(1)连续平方数之间的差是一列奇数。
(2)一个正整数的个位数字只能是0、1、4、5、6、9中的一个,才能使其成为平方数。
(3)一个平方数的十位数字只能是0、1、4、5、6、9中的一个。
2. 立方数的性质(1)连续立方数之间的差是一列等差数列。
(2)一个正整数的个位数字只能是0、1、8、9中的一个,才能使其成为立方数。
(3)一个立方数的十位数字只能是0、1、8、9中的一个。
三、平方数与立方数的运算1. 开平方与平方根开平方是指求一个数的平方根,即找到一个数,使它的平方等于给定的数。
平方根用符号√表示。
例如,√9=3,因为3的平方等于9。
2. 立方与立方根立方是指求一个数的立方根,即找到一个数,使它的立方等于给定的数。
立方根也用符号∛表示。
例如,∛27=3,因为3的立方等于27。
四、练习与拓展1. 平方数与立方数练习(1)判断以下各数是否为平方数:25、37、81、100。
(2)判断以下各数是否为立方数:8、27、64、1000。
2. 平方数与立方数拓展(1)求出100以内的所有平方数与立方数。
(2)找出一个平方数,使得其十位数字为6,个位数字是4。
平方立方表快速记忆方法

平方立方表快速记忆方法引言平方立方表是数学中常用的一张表格,它列出了1到10的数的平方和立方。
学习和记忆平方立方表可以帮助我们在日常计算和解题中节省时间和精力。
本文将介绍一种快速记忆平方立方表的方法。
方法详解1. 理解平方和立方的定义在开始记忆平方立方表之前,我们首先需要理解平方和立方的定义。
平方是指一个数自乘一次,立方是指一个数自乘两次。
例如:2的平方是4,2的立方是8。
2. 记忆平方表的1到10的数字和它们的平方我们首先来记忆平方表中的1到10的数字和它们的平方:1.1的平方等于12.2的平方等于43.3的平方等于94.4的平方等于165.5的平方等于256.6的平方等于367.7的平方等于498.8的平方等于649.9的平方等于8110.10的平方等于100可以使用反复默念和写下这些数字和它们的平方来帮助记忆。
可以选择合适的时间和地点,例如在公交车上或者在睡前默念这些数字。
3. 记忆立方表的1到10的数字和它们的立方接下来,我们来记忆立方表中的1到10的数字和它们的立方:1.1的立方等于12.2的立方等于83.3的立方等于274.4的立方等于645.5的立方等于1256.6的立方等于2167.7的立方等于3438.8的立方等于5129.9的立方等于72910.10的立方等于1000同样地,可以使用反复默念和写下这些数字和它们的立方来帮助记忆。
4. 利用记忆法巩固记忆除了反复默念和写下,我们还可以利用一些记忆法来巩固这些记忆:4.1 关联记忆将数字和它们的平方、立方以及其他与之相关的信息进行关联记忆。
例如,我们可以将数字1和它的平方1想象成一个相似的形状,类似一个“口”字,这样可以帮助记忆1的平方是1。
4.2 编排记忆将数字和它们的平方、立方按照一定的顺序编排起来,形成一个有规律的图形或图像。
例如,我们可以将1的平方和立方放在第一行,2的平方和立方放在第二行,依次类推。
这样的编排可以帮助我们更容易地记忆和回忆。
常用幂次数

常用阶乘数
(定义n的阶乘写作n!。n!=1×2×3×4×···×(n-1)×n)
数字
1
2
3
4
5
6
7
阶乘
1
26Βιβλιοθήκη 24120720
5040
40以内质、合数
常用幂次数
一、平方数
底数
1
2
3
4
5
6
7
8
9
10
平方
1
4
9
16
25
36
49
64
81
100
底数
11
12
13
14
15
16
17
18
19
20
平方
121
144
169
196
225
256
289
324
361
400
底数
21
22
23
24
25
26
27
28
29
30
平方
441
484
529
576
625
676
729
784
841
900
一、质数
2、3、5、7、11、13、17、19、23、29、31、37、41
二、合数
4、6、8、9、10、12、14、15、16、18、20、21、22、24、25、26、27、28、30、32、33、34、35、36、38、39
常用经典因数分解
