30以内平方数、10以内立方数和2-6的高阶幂次数
中国人民解放军文职考试-数字推理复习点
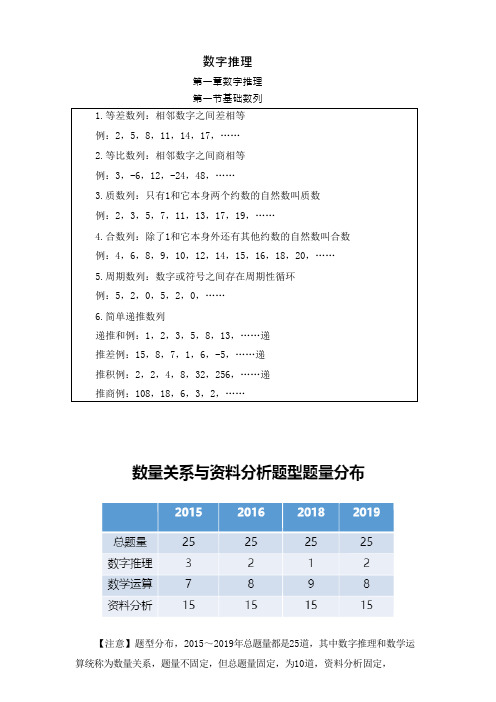
数字推理第一章数字推理第一节基础数列1.等差数列:相邻数字之间差相等例:2,5,8,11,14,17,……2.等比数列:相邻数字之间商相等例:3,-6,12,-24,48,……3.质数列:只有1和它本身两个约数的自然数叫质数例:2,3,5,7,11,13,17,19,……4.合数列:除了1和它本身外还有其他约数的自然数叫合数例:4,6,8,9,10,12,14,15,16,18,20,……5.周期数列:数字或符号之间存在周期性循环例:5,2,0,5,2,0,……6.简单递推数列递推和例:1,2,3,5,8,13,……递推差例:15,8,7,1,6,-5,……递推积例:2,2,4,8,32,256,……递推商例:108,18,6,3,2,……【注意】题型分布,2015~2019年总题量都是25道,其中数字推理和数学运算统称为数量关系,题量不固定,但总题量固定,为10道,资料分析固定,【知识点】内容:1.基础数列:常见数列,可以为特征数列和非特征数列打下基础。
2.特征数列。
3.非特征数列。
特征数量和非特征数列是考试重点。
【知识点】基础数列:1.等差数列:相邻数字之间差相等。
例:2,5,8,11,14,17,……。
可以看到相邻两项都差3,就是公差为3的等差数列,17后面应该跟20。
2.等比数列:相邻数字之间商相等。
例:3,-6,12,-24,48,……。
可以看到相邻两项商值固定,是-2倍关系,是公比为-2的等比数列,所以48后面跟-96。
3.质数列(需要记忆):只有1和它本身两个约数的自然数叫质数。
意思就是一个数只能拆成1和它本身,比如7,只能拆成1*7。
例:2,3,5,7,11,13,17,19,……。
20以内的质数要记住,并形成敏感度,以免比如出现2、3、5、7不认得,后面填错。
注意2是这些质数中的唯一偶数。
4.合数列(需要记忆):除了1和它本身外还有其他约数的自然数叫合数,相比质数列考的比较少。
常用幂次数
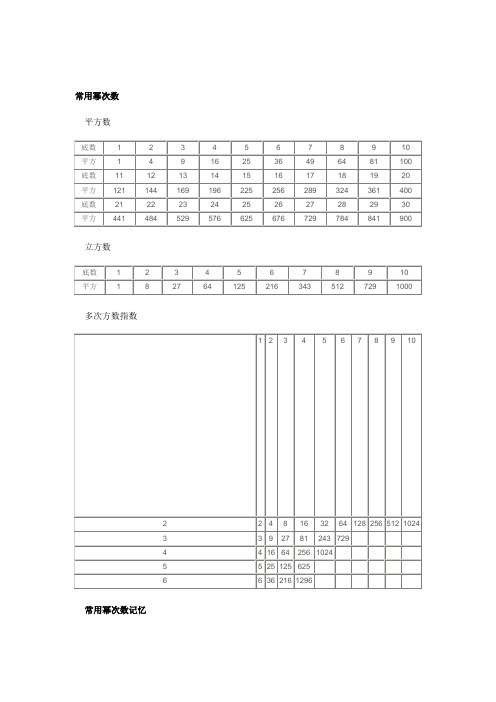
常用幂次数平方数立方数多次方数指数常用幂次数记忆1.对于常用的幂次数字,考生务必将其牢记在心,这不仅对数字推理的解题很重要,对数学运算乃至资料分析试题的迅速、准确解答都起着至关重要的作用。
2.很多数字的幂次数都是相通的,比如729=93=36=272,256=28=44=162等。
3.“21~29”的平方数是相联系的,以25为中心,24与26、23与27、22与28、21与29,它们的平方数分别相差100、200、300、400。
常用阶乘数(定义:n的阶乘写作n!。
n!=1×2×3×4×…×(n-1)×n)200以内质数表2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97101、103、107、109、113、127、131、137、139、149、151、157、163、167、173、179、181、191、193、197、199“质数表”记忆1.“2、3、5、7、11、13、17、19”这几个质数作为一种特殊的“基准数”,是质数数列的“旗帜”,公务员考试中对于质数数列的考核往往集中在这几个数字上。
2.83、89、97是100以内最大的三个质数,换言之80以上、100以下的其他自然数均是合数,特别需要留意91是一个合数(91=7×13)。
3.像91这样较大的合数的“质因数分解”,也是公务员考试中经常会设置的障碍,牢记200以内一些特殊数字的分解有时可以起到意想不到的效果,可将其看作一种特殊意义上的“基准数”。
常用经典因数分解91=7×13111=3×37119=7×17133=7×19117=9×13143=11×13147=7×21153=9×17161=7×23171=9×19187=11×17209=19×11有了上述“基准数”的知识储备,在解题中即可以此为基础用“单数字发散”思维解题。
10以内的数开平方表

10以内的数开平方表第一步:掌握平方数或立方数与结果个位数之间的对应关系。
为了能够快速口算二次方根或三次方根,我们必须要建立平方数或立方数与平方或立方结果的个位数间的对应关系,这样才便于后面的判断和运用。
10以内的立方中,立方数与结果个位数之间是一一对应的关系,这个一一对应的关系需要数量掌握。
在具体运用过程中,如果不能熟练掌握,可以直接列出10以内的立方表来参考。
10以内立方中的一一对应关系由上表格可知,1、4、5、6、9这五个数的立方数与结果个位数是相同的,而2、8、3、7这四个数的立方数与结果个位数是互补的(其和为10),这样我们就可以很轻松的掌握它们之间的一一对应关系了。
2、3、7、8互补,其它同。
为了简洁,可以直接记为“2、3互补,其它同”。
记住以上口诀即可。
2、3互补就是说在立方数与结果个位数的一一对应关系上,2、3都是与其互补数一一对应的,同样地,2、3的互补数也是与2、3一一对应的。
因此“2、3互补”就暗含了2、8和3、7这两对互补数,也就是4个数。
下面我们来看看平方数与结果个位数之间的对应关系。
我们知道1、5、6这三个数的平方数与结果个位数是相同的;2、8这两个互补的数的结果个位数都是4;3、7这两个互补的数的结果个位数都是9;9、1这两个互补的数的结果个位数都是1;4、6这两个互补的数的结果个位数都是6.我们发现了一个规律:互补的两个数结果的个位数是相同的。
因此我们可以根据这个特点来掌握。
比如9,9的补数是1,而1的平方是1,所以9这个平方数的结果个位数是1.再比如结果个位数6与哪几个平方数对应呢?既然6是平方数的结果的个位数,因此可以根据九九乘法表知4和6都满足,并且4和6这两个数是互补的。
强调:以上两个表格必须要熟练地掌握,能达到不需要思考可以直接写出对应的数最好。
第二步:确定被开方数开方结果的位数。
由于一位数的平方和立方大家已经掌握,因此我们根据一位数的平方和立方的结果知道以下内容:1.根据10以内立方中9的立方是729,而10的立方是1000,我们可以得出不超过三位数的数开立方其结果应是一位数。
数字推理第一期

常用幂次数一、平方数底数 1 2 3 4 5 6 7 8 9 10平方 1 4 9 16 25 36 49 64 81 100底数11 12 13 14 15 16 17 18 19 20平方121 144 169 196 225 256 289 324 361 400底数21 22 23 24 25 26 27 28 29 30平方441 484 529 576 625 676 729 784 841 900二、立方数底数 1 2 3 4 5 6 7 8 9 10平方 1 8 27 64 125 216 343 512 729 1000三、多次方数1 2 3 4 5 6 7 8 9 102 2 4 8 16 32 64 128 256 512 10243 3 9 27 81 243 7294 4 16 64 256 10245 5 25 125 6256 6 36 216 1296ps 1、很多数字的幂次数都是相通的,比如729=93=36=272,256=28=44=162等。
2、“21~29”的平方数是相联系的,以25为中心,24与26、23与27、22与28、21与29,他们的平方数分别相差100、200、300、 400。
常用阶乘数(定义 n的阶乘写作n!。
n!=1×2×3×4×···×(n-1)×n )数字 1 2 3 4 5 6 7阶乘 1 2 6 24 120 720 504040以内质、合数(0既不是质数也不是合数)一、质数: 2、3、5、7、11、13、17、19、23、29、31、37、41二、合数: 4、6、8、9、10、12、14、15、16、18、20、21、22、24、25、26、27、28、30、32、33、34、35、36、38、39常用经典因数分解91=7×13 111=3×37 119=7×17 133=7×19 117=9×13 143=11×13147=7×21 153=9×17 161=7×23 171=9×19 187=11×17 209=19×111)等差、等比这种最简单的不用多说,深一点就是在等差、等比上再加、减一个数列,如24,70,208,622,规律为a*3-2=b2)深一愕模型,各数之间的差有规律,如1、2、5、10、17。
(完整版)常用幂次数表格
“相同互补型”两数相乘速算技巧:两个两位数相乘,如果满足下面三个条件当中任意一个(“互补”指相加为10)1. 十位相同、个位互补;2. 十位互补、个位相同;3. 某一个数的十位与个位相同,另一个数的十位与个位互补。
那么:乘积的头=头乂头+相同的数;乘积的尾=尾乂尾如:“ 72X 78”,十位均为“ 7”,相同;个位“ 2”与“ 8”互补所以乘积的头=7X 7 + 7=56,尾=2X 8=16,即72 X 78=5616如:“ 38X 78”,个位均为“ 8”,相同;十位“ 3”与“ 7”互补所以乘积的头=3X 7 + 8=29,尾=8X 8=64,即38 X 78=2964如:“ 22X 46”,前一个数十位与个位都是“2”,后一个数“ 4”与“ 6”互补所以乘积的头=2X 4 + 2=10,尾=2X 6=12,即22 X 46=1012如果是两个三位数相乘,满足下面两个条件当中任意一个也可以使用类似技巧:1. 百位相同,后两位相加为100 (此时“尾”需要占四位);2. 百位、十位相同,个位相加为10。
女口:“ 325X 375”,头=3X 3+3= 12,尾=25X 75 = 1875。
即325X 375= 121875。
女口:“ 232X 238”,头=23X 23+23 = 552,尾=2X 8 = 16。
即卩232X 238= 55216。
如:“ 165 = 165X 165”,头=16X 16+16= 272,尾=5X 5 = 25。
即卩165 = 27225。
两个典型的乘方余数问题李委明“除以10”乘方余数核心口诀【例1】37424"8的末位数字是()。
A.2C.6[答案]B[解析]37424998==>22==>4B.4 D.8【例2】(浙江2007A-1 1 ) 1 2007 + 32007+ 5 2007+ 72007+ 92007的值的个位数是(A.5 C.8B.6 D.9[答案]A2007 ^2007 _2007 —2007 小2007 一小3 _ _>3 小3[解析]1 +3 +5 +7 +9 ==>1+3+5+7+9 ==>1+7+5+3+9==>5o“除以7”乘方余数核心口诀1. 底数除以7留余数;2. 指数除以6留余数(余数为0则看作6)。
安徽省行测讲义第二部分 数量关系数字推理

第二部分数量关系数字推理背景知识数的历史复数分为:实数、虚数。
复数a+bi,当且仅当b=0时,它是实数,当且仅当a=b=0时,它是实数0,当b不等于0时,叫复数,当a=0且b不等于0时,叫做纯虚数。
虚数,人们开始称之为“实数的灵魂”,1637年笛卡儿称为“想像中的数”,1777年瑞士数学家欧拉(Euler,或译为欧勒)开始使用符号i表示虚数的单位。
a+bi(a,b属R)的数叫复数,其中i叫虚数单位。
现在,复数一般用来表示向量(有方向的数量),这在力学、地图学、航空学中的应用是十分广泛的。
虚数越来越显示出其丰富的内容,真是:虚数不虚。
黄金分割比把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。
其比值是一个无理数,取其前三位数字的近似值是0.618。
由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。
实数分为:有理数、无理数。
无理数是实数中不能精确地表示为两个整数之比的数,即无限不循环小数。
如圆周率、2的平方根等。
有理数能写成有限小数和无限循环小数,比如4=4.0, 4/5=0.8, 1/3=0.33333。
有理数:整数(正整数、0、负整数)、分数(正分数、负分数)。
注意:自然数是非负整数集,即是由正整数和0组成。
整数(偶数、奇数)、正整数(1、质数也叫素数、合数)两个相邻整数必为一奇一偶。
除了最小的质数2是偶数以外,其余质数都是奇数。
任何一个合数都可以分解成若干个质因素之积。
有理数有正数、负数之分;整数、分数之分;自然数、小数之分;偶数、奇数之分;质数(素数)、合数之分。
数量关系主要考查考生对数量关系的理解、计算和判断推理的能力。
数字推理的出题形式:数阵型、数列型、数图(表)型。
数字推理备考复习阶段原则掌握:因为数字推理要求考生对数字本身以及数字间的关系有极强的敏感性,这一敏感性需要长时间的训练来养成,很难在几天之内速成。
第一阶段,培养数字敏感性建议考生不要在复习的一开始就急于大量的做题,最好先通过少量做题来培养数字敏感性。
1~30平方立方简便背法

1~30平方立方简便背法在数学的学习中,记住 1 到 30 的平方和立方是一项基础但又有些繁琐的任务。
不过,别担心,这里为您介绍一些简便的背法,帮助您轻松掌握。
首先,咱们来说说 1 到 10 的平方。
1 的平方是 1,2 的平方是 4,3 的平方是 9,4 的平方是 16,5 的平方是 25,6 的平方是 36,7 的平方是 49,8 的平方是 64,9 的平方是 81,10 的平方是 100。
这几个相对简单,多念几遍就能记住。
接下来是 11 到 20 的平方。
11 的平方是 121,12 的平方是 144,13 的平方是 169,14 的平方是 196,15 的平方是 225,16 的平方是 256,17 的平方是 289,18 的平方是 324,19 的平方是 361,20 的平方是400。
对于这一段,咱们可以找一些规律。
比如 11 到 19 的平方,个位数都是 1、4、9、6、5 这几个数字在循环,而十位数每次增加 1,同时结果的百位数就是十位数乘以比它大 1 的数。
再看 21 到 30 的平方。
21 的平方是 441,22 的平方是 484,23 的平方是 529,24 的平方是 576,25 的平方是 625,26 的平方是 676,27 的平方是 729,28 的平方是 784,29 的平方是 841,30 的平方是 900。
这部分可以结合前面的规律,并且多做一些计算练习来加强记忆。
说完平方,咱们再聊聊立方。
1 的立方是 1,2 的立方是 8,3 的立方是 27,4 的立方是 64,5 的立方是 125,6 的立方是 216,7 的立方是 343,8 的立方是 512,9 的立方是 729,10 的立方是 1000。
这里的规律不太明显,更多的是需要反复记忆。
11 到 20 的立方,11 的立方是 1331,12 的立方是 1728,13 的立方是 2197,14 的立方是 2744,15 的立方是 3375,16 的立方是 4096,17 的立方是 4913,18 的立方是 5832,19 的立方是 6859,20 的立方是8000。
