加减,平方,立方1-9次幂常用数据

合集下载

1--100平方立方表

19683
21952
24389
27000
立方
原数
31
32
33
34
35
36
37
38
39
40
原数
平方
961
1024
1089
1156
1225
1296
1369
1444
1521
1600
平方
立方
29791
32768
35937
39304
42875
46656
50653
54872
59319
64000
立方
原数
41
42
43
614125
636056
658503
681472
704969
729000
立方
原数
91
92
93
94
95
96
97
98
99
100
原数
平方
8281
8464
8649
8836
9025
9216
9409
9604
9801
10000
平方
立方
753571
778688
804357
830584
857375
884736
912673
2809
2916
3025
3136
3249
3364
3481
3600
平方
立方
132651
140608
148877
157464
166375
175616
185193

常用幂次数

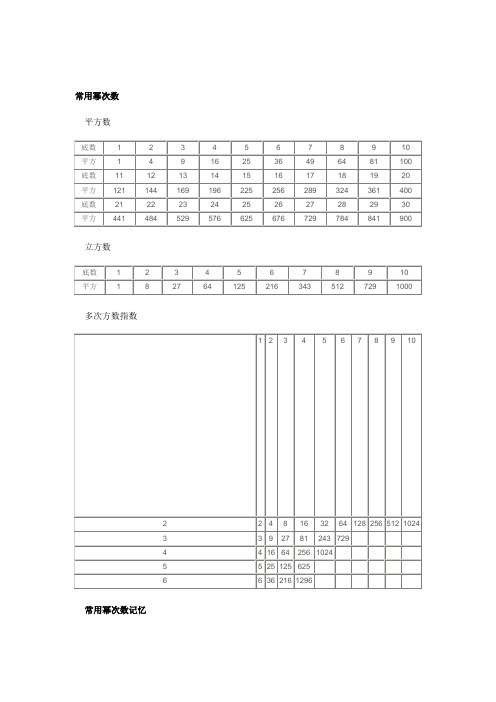
常用幂次数平方数立方数多次方数指数常用幂次数记忆1．对于常用的幂次数字，考生务必将其牢记在心，这不仅对数字推理的解题很重要，对数学运算乃至资料分析试题的迅速、准确解答都起着至关重要的作用。

2．很多数字的幂次数都是相通的，比如729＝93＝36＝272，256＝28＝44＝162等。

3．“21～29”的平方数是相联系的，以25为中心，24与26、23与27、22与28、21与29，它们的平方数分别相差100、200、300、400。

常用阶乘数（定义：n的阶乘写作n!。

n!=1×2×3×4×…×（n-1）×n）200以内质数表2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97101、103、107、109、113、127、131、137、139、149、151、157、163、167、173、179、181、191、193、197、199“质数表”记忆1．“2、3、5、7、11、13、17、19”这几个质数作为一种特殊的“基准数”，是质数数列的“旗帜”，公务员考试中对于质数数列的考核往往集中在这几个数字上。

2．83、89、97是100以内最大的三个质数，换言之80以上、100以下的其他自然数均是合数，特别需要留意91是一个合数（91=7×13）。

3．像91这样较大的合数的“质因数分解”，也是公务员考试中经常会设置的障碍，牢记200以内一些特殊数字的分解有时可以起到意想不到的效果，可将其看作一种特殊意义上的“基准数”。

常用经典因数分解91=7×13111=3×37119=7×17133=7×19117=9×13143=11×13147=7×21153=9×17161=7×23171=9×19187=11×17209＝19×11有了上述“基准数”的知识储备，在解题中即可以此为基础用“单数字发散”思维解题。

平方和立方的公式表

平方和立方的公式表平方和立方的公式是数学中常见且重要的公式。

它们分别用于计算一个数的平方和立方。

在本文中，我们将介绍这两个公式的含义、应用场景以及它们在数学中的重要性。

平方和公式可以用来计算一组数的平方和。

平方和是指将一组数的每个数分别平方，并将所有平方数相加所得到的结果。

平方和公式的数学表示如下：平方和 = a^2 + b^2 + c^2 + ...其中，a、b、c等表示一组数。

这个公式在数学和统计学中有广泛的应用。

例如，在统计学中，可以用平方和公式来计算数据的方差，方差是用来衡量数据离散程度的指标。

平方和公式的应用不仅局限于数学和统计学领域，它还可以在物理学中找到应用。

在牛顿力学中，质点的动能可以通过质点的质量和速度的平方和来计算。

因此，平方和公式在物理学中也具有重要的意义。

与平方和公式类似，立方的公式用于计算一个数的立方。

立方是指将一个数自身连续乘以三次的结果。

立方公式的数学表示如下：立方 = a^3其中，a表示一个数。

立方公式常用于计算几何体的体积。

例如，在计算正方体的体积时，可以利用立方公式将正方体的边长立方来计算。

立方公式在实际应用中也有广泛的用途。

它在物理学中用于计算物体的体积和密度，以及化学中用于计算物质的摩尔质量。

此外，在计算机科学中，立方公式也常用于计算算法的时间复杂度和空间复杂度。

平方和和立方的公式在数学中具有重要的地位。

它们不仅被广泛应用于各个领域，而且也有助于理解和解决实际问题。

通过运用这些公式，我们可以更好地理解数学和科学的本质，更准确地描述和计算各种现象和现实情况。

总结起来，平方和和立方的公式是数学中重要的工具。

它们在数学、统计学、物理学、化学和计算机科学等领域中都有广泛的应用。

了解和掌握这些公式的含义和应用场景，对于提高数学和科学水平，解决实际问题具有重要意义。

谜材-数学名词

谜材-数学名词【数学名词】一字：边、差、长、乘、除、底、点、度、分、高、勾、股、行、和、弧环、集、加、减、积、角、解、宽、棱、列、面、秒、幂、模、球式、势、商、体、项、象、线、弦、腰、圆二字：十位、个位、几何、子集、大圆、小圆、元素、下标、下凸、下凹百位、千位、万位、分子、分母、中点、约分、加数、减数、数位通分、除数、商数、奇数、偶数、质数、合数、乘数、算式、进率因式、因数、单价、数量、约数、正数、负数、整数、分数、倒数乘方、开方、底数、指数、平方、立方、数轴、原点、同号、异号余数、除式、商式、余式、整式、系数、次数、速度、距离、时间方程、等式、左边、右边、变号、相等、解集、分式、实数、根式对数、真数、底数、首数、尾数、坐标、横轴、纵轴、函数、常显变量、截距、正弦、余弦、正切、余切、正割、余割、坡度、坡比频数、频率、集合、数集、点集、空集、原象、交集、并集、差映射、对角、数列、等式、基数、正角、负角、零角、弧度、密位函数、端点、全集、补集、值域、周期、相位、初相、首项、通项公比、公差、复数、虚数、实数、实部、虚部、实轴、虚轴、向量辐角、排列、组合、通项、概率、直线、公理、定义、概念、射线线段、顶点、始边、终边、圆角、平角、锐角、纯角、直角、余角补角、垂线、垂足、斜线、斜足、命题、定理、条件、题设、结论证明、内角、外角、推论、斜边、曲线、弧线、周长、对边、距离矩形、菱形、邻边、梯形、面积、比例、合比、等比、分比、垂心重心、内心、外心、旁心、射影、圆心、半径、直径、定点、定长圆弧、优弧、劣弧、等圆、等弧、弓形、相离、相切、切点、切线相交、割线、外离、外切、内切、内径、外径、中心、弧长、扇形轨迹、误差、视图、交点、椭圆、焦点、焦距、长袖、短轴、准线法线、移轴、转轴、斜率、夹角、曲线、参数、摆线、基圆、极轴极角、平面、棱柱、底面、侧面、侧棱、楔体、球缺、棱锥、斜高棱台、圆柱、圆锥、圆台、母线、球面、球体、体积、环体、环球冠、极限、导数、微分、微商、驻点、拐点、积分、切面、面角极值、三字：被减数、被乘数、被除数、假分数、代分数、质因数、小数点多位数、百分数、单名数、复名数、统计表、统计图、比例尺循环节、近似数、准确数、圆周率、百分位、十分位、千分位万分位、自然数、正整数、负整数、相反数、绝对值、正分数负分数、有理数、正方向、负方向、正因数、负因数、正约数运算律、交换律、结合律、分配律、最大数、最小数、逆运算奇次幂、偶次幂、平方表、立方表、平方数、立方数、被除式代数式、平方和、平方差、立方和、立方差、单项式、多项式二项式、三项式、常数项、一次项、二次项、同类项、填空题选择题、判断题、证明题、未知数、大于号、小于号、等于号恒等号、不等号、公分母、不等式、方程组、代入法、加减法公因式、有理式、繁分式、换元法、平方根、立方式、根指数小数点、无理数、公式法、判别式、零指数、对数式、幂指数对数表、横坐标、纵坐标、自变量、因变量、函数值、解析法解析式、列表法、图象法、指点法、截距式、正弦表、余弦表正切表、余切表、平均数、有限集、描述法、列举法、图示法真子集、欧拉图、非空集、逆映射、自反性、对称性、传递性可数集、可数势、维恩图、反函数、幂函数、角度制、弧度制密位制、定义城、函数值、开区间、闭区间、增函数、减函数单调性、奇函数、偶函数、奇偶性、五点法、公因子、对逆性比较法、综合法、分析法、最大值、最小值、递推式、归纳法复平面、纯虚数、零向量、长方体、正方体、正方形、相交线延长线、中垂线、对预角、同位角、内错角、无限极、长方形平行线、真命题、假命题、三角形、内角和、辅助线、直角边全等形、对应边、对应角、原命题、逆命解、原定理、逆定理对称点、对称轴、多边形、对角线、四边形、五边形、三角形否命题、中位线、相似形、比例尺、内分点、外分点、平面图同心圆、内切圆、外接圆、弦心距、圆心角、圆周角、弓形角内对角、连心线、公切线、公共弦、中心角、圆周长、圆面积反证法、主视图、俯视图、二视图、三视图、虚实线、左视图离心率、双曲线、渐近线、抛物线、倾斜角、点斜式、斜截式两点式、一般式、参变数、渐开线、旋轮线、极坐标、公垂线斜线段、半平面、二面角、斜棱柱、直棱柱、正梭柱、直观图正棱锥、上底面、下底面、多面体、旋转体、旋转面、旋转轴拟柱体、圆柱面、圆锥面、多面角、变化率、左极限、右极限隐函数、显函数、导函数、左导教、右导数、极大值、极小值极大点、极小点、极值点、原函数、积分号、被积式、定积分无穷小、无穷大、连分数、近似数、弦切角四字：混合运算、乘法口诀、循环小数、无限小数、有限小数、简易方程四舍五人、单位长度、加法法则、减法法则、乘法法则、除法法则数量关系、升幂排列、降幂排列、分解因式、完全平方、完全立方同解方程、连续整数、连续奇数、连续偶数、同题原理、最简方程最简分式、字母系数、公式变形、公式方程、整式方程、二次方根三次方根、被开方数、平方根表、立方根表、二次根式、几次方根求根公式、韦达定理、高次方程、分式方程、有理方程、无理方程分数指数、同次根式、异次根式、最简根式、同类根式、常用对数换底公式、反对数表、坐标平面、坐标原点、比例系数、一次函数二次函数、三角函数、正弦定理、余弦定理、样本方差、集合相交等价集合、可数集合、对应法则、指数函数、对数函数、自然对数指数方程、对数方程、单值对应、单调区间、单调函数、诱导公式周期函数、周期交换、振幅变换、相位变换、正弦曲线、余弦曲线正切曲线、余切曲线、倍角公式、半角公式、积化和差、和差化积三角方程、线性方程、主对角线、副对角钱、零多项式、余数定理因式定理、通项公式、有穷数列、无穷数列、等比数列、总和符号特殊数列、不定方程、系数矩阵、增广炬阵、初等变换、虚数单位共轭复数、共轭虚数、辐角主值、三角形式、代数形式、加法原理乘法原理、几何图形、平面图形、等量代换、度量单位、角平分线互为余角、互为补角、同旁内角、平行公理、性质定理、判定定理斜三角形、对应顶点、尺规作图、基本作图、互逆命题、互逆定理凸多边形、平行线段、逆否命题、对称中心、等腰梯形、等分线段比例线段、勾股定理、黑金分割、比例外项、比例内项、比例中项比例定理、相似系数、位似图形、位似中心、内公切线、外公切线正多边形、扇形面积、互否命题、互逆命题、等价命题、尺寸注法标准方程、平移公式、旋转公式、有向线段、定比分点、有向直线经验公式、有心曲线、无心曲线、参数方程、普通方程、极坐标系等速螺线、异面直线、直二面角、凸多面体、祖恒原理、体积单位球面距离、凸多面角、直三角面、正多面体、欧拉定理、连续函数复合函数、中间变量、瞬间速度、瞬时功率、二阶导数、近似计算辅助函数、不定积分、被积函数、积分变量、积分常数、凑微分法相对误差、绝对误差、带余除法、微分方程、初等变换、立体几何平面几何、解析几何、初等函数、等差数列五字：四舍五入法、纯循环小数、一次二项式、二次三项式、最大公约数最小公倍数、代入消元法、加减消元法、平方差公式、立方差公式立方和公式、提公因式法、分组分解法、十字相乘法、最简公分母算数平方根、完全平方数、几次算数根、因式分解法、双二次方负整数指数、科学记数法、有序实数对、两点间距离、解析表达式正比例函数、反比例函数、三角函数表、样本标准差、样本分布表总体平均数、样本平均数、集合不相交、基本恒等式、最小正周期两角和公式、两角差公式、反三角函数、反正弦函数、反余弦函数反正切函数、反余切函数、第一象限角、第二象限角、第三象限角第四象限角、线性方程组、二阶行列式、三阶行列式、四阶行列式对角钱法则、系数行列式、代数余子式、降阶展开法、绝对不等式条件不等式、矛盾不等式、克莱姆法则、算术平均数、几何平均数一元多项武、乘法单调性、加法单调性、最小正周期、零次多项式待定系数法、辗转相除法、二项式定法、二项展开式、二项式系数数学归纳法、同解不等式、垂直平分线、互为邻补角、等腰三角形等边三角形、锐角三角形、钝角三角形、直角三角形、全等三角形边角边公理、角边角公理、边边边定理、轴对称图形、第四比例项外角平分线、相似多边形、内接四边形、相似三角形、内接三角形内接多边形、内接五边形、外切三角形、外切多边形、共轭双曲斜二测画法、三垂线定理、平行六面体、直接积分法、换元积分法第二积分法、分部积分法、混循环小数、第一积分法、同类二次根六字：一元一次方程、一元二次方程、完全平方公式、最简二次根式直接开平方法、半开半闭区间、万能置换公式、绝对值不等式实系数多项式、复系数多项式、整系数多项式、不等边三角形中心对称图形、基本初等函数、基本积分公式、分部积分公式二元一次方程、三元一次方程七字：一元一次不等式、一元二次不等式、二元一次方程组三元一次方程组、二元二次方程组、平面直角坐标系等腰直角三角形、二元一次不等式、二元线性方程组三元线性方程组、四元线性方程组、多项式恒等定律八字及以上：一元一次不等式组、三元一次不定方程、三元齐次线性方程组。

初一数学次方公式大全总结

初一数学上册知识点1 正负数 1.正数：大于0的数。

2.负数：小于0的数。

3.0即不是正数也不是负数。

4.正数大于0，负数小于0，正数大于负数。

(二)有理数 1.有理数：由整数和分数组成的数。

包括：正整数、0、负整数，正分数、负分数。

可以写成两个整之比的形式。

(无理数是不能写成两个整数之比的形式，它写成小数形式，小数点后的数字是无限不循环的。

如：π) 2.整数：正整数、0、负整数，统称整数。

3.分数：正分数、负分数。

(三)数轴 1.数轴：用直线上的点表示数，这条直线叫做数轴。

(画一条直线，在直线上任取一点表示数0，这个零点叫做原点，规定直线上从原点向右或向上为正方向;选取适当的长度为单位长度，以便在数轴上取点。

) 2.数轴的三要素：原点、正方向、单位长度。

3.相反数：只有符号不同的两个数叫做互为相反数。

0的相反数还是0。

4.绝对值：正数的绝对值是它本身，负数的绝对值是它的相反数;0的绝对值是0，两个负数，绝对值大的反而小。

(四)有理数的加减法 1.先定符号，再算绝对值。

2.加法运算法则：同号相加，到相同符号，并把绝对值相加。

异号相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。

互为相反数的两个数相加得0。

一个数同0相加减，仍得这个数。

3.加法交换律：a+b=b+a两个数相加，交换加数的位置，和不变。

4.加法结合律：(a+b)+c=a+(b+c)三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

5.a?b=a+(?b)减去一个数，等于加这个数的相反数。

(五)有理数乘法(先定积的符号，再定积的大小) 1.同号得正，异号得负，并把绝对值相乘。

任何数同0相乘，都得0。

2.乘积是1的两个数互为倒数。

3.乘法交换律：ab=ba4.乘法结合律：(ab)c=a(bc)5.乘法分配律：a(b+c)=ab+ac (六)有理数除法 1.先将除法化成乘法，然后定符号，最后求结果。

2.除以一个不等于0的数，等于乘这个数的倒数。

次方计算公式表

次方计算公式表
次方有两种算法。

第一种是直接用乘法计算，例：3⁴=3×3×3×3=81；第二种则是用次方阶级下的数相乘，例：3⁴=9×9=81。

次方计算公式
1次方
次方最基本的定义是：设a为某数，n为正整数，a的n次方表示为aⁿ，表示n个a连乘所得之结果，如2⁴=2×2×2×2=16。

次方的定义还可以扩展到0次方和负数次方等等。

在电脑上输入数学公式时，因为不便于输入乘方，符号“^”也经常被用来表示次方。

例如2的5次方通常被表示为2^5。

20次方
常数项是零次方项。

任何除0以外的数的0次方都是1 。

如3的0次方是1，-1的0次方也是1，0的0次方没有意义。

注：-1⁰=-1，但是(-1)⁰=1。

前者是用0减1求零次方，后者是对整个-1求零次方。

3负次方
一个数的负次方即为这个数的正次方的倒数。

a^-x=1/a^x
例:2的-1次方=1/2的一次方。

1/2的-1次方=2的一次方。

5的-2次方=1/5的二次方，
1/5的-2次方=5的二次方。

常用幂次数表格

常用幂次数常见数字整除判定法则2、4、8、5、25、125整除判定1. 能被2（或 5）整除的数，末一位数字能被2（或 5）整除；2. 能被4（或 25）整除的数，末两位数字能被4（或 25）整除；3. 能被8（或125）整除的数，末三位数字能被8（或125）整除；4. 一个数被2（或 5）除得的余数，就是其末一位数字被2（或 5）除得的余数5. 一个数被4（或 25）除得的余数，就是其末两位数字被4（或 25）除得的余数6. 一个数被8（或125）除得的余数，就是其末三位数字被8（或125）除得的余数3、9整除判定1. 能被3（或9）整除的数，各位数字和能被3（或9）整除。

2. 一个数被3（或9）除得的余数，就是其各位相加后被3（或9）除得的余数。

11整除判定1. 能被11整除的数，奇数位的和与偶数位的和之差，能被11整除。

“相同互补型”两数相乘速算技巧：两个两位数相乘，如果满足下面三个条件当中任意一个（“互补”指相加为10）：1. 十位相同、个位互补；2. 十位互补、个位相同；3. 某一个数的十位与个位相同，另一个数的十位与个位互补。

那么：乘积的头＝头×头+相同的数；乘积的尾=尾×尾如：“72×78”，十位均为“7”，相同；个位“2”与“8”互补所以乘积的头＝7×7＋7=56，尾＝2×8=16，即72×78=5616如：“38×78”，个位均为“8”，相同；十位“3”与“7”互补所以乘积的头＝3×7＋8=29，尾＝8×8=64，即38×78=2964如：“22×46”，前一个数十位与个位都是“2”，后一个数“4”与“6”互补所以乘积的头＝2×4＋2=10，尾＝2×6=12，即22×46=1012如果是两个三位数相乘，满足下面两个条件当中任意一个也可以使用类似技巧：1. 百位相同，后两位相加为100（此时“尾”需要占四位）；2. 百位、十位相同，个位相加为10。

1到20的平方立方平方根立方根

算数平方根的计算公式为：
由以上公式计算得出1到20的算术平方根分别为：
一、1的算数平方根等于答1
二、2的算数平方根约等于等于1.414
三、3的算数平方根等于1.732
四、4的算数平方根等于2
五、5的算数平方根等于2.236
六、6的算数平方根等于2.449
七、7的算数平方根等于2.645
八、8的算数平方根等于2.828
九、9的算数平方根等于3
十、10的算数平方根等于3.162
十一、11的算数平方根等于3.316
十二、12的算数平方根等于3.464
十三、13的算数平方根等于3.605
十四、14的算数平方根等于3.741
十五、15的算数平方根等于3.872
十六、16的算数平方根等于4
十七、17的算数平方根等于4.123
十八、18的算数平方根等于4.242
十九、19的算数平方根等于4.358
二十、20的算数平方根等于4.472
以上数据结果不是整数时四舍五入精确到第三位小数。

加减,平方,立方1-9次幂常用数据

判定个位数字规律：（1）2的1－9次方个位数字为：2－4－8－6依次循环；（2）3的1－9次方个位数字为：3－9－7－1依次循环；（3）4的1－9次方个位数字为：4－6依次循环；（4）5的任何（非0）次方个位数字均为5；（5）6的任何（非0）次方个位数字均为6；（7）7的1－9次方个位数字为：7－9－3－1依次循环；（8）8的1－9次方个位数字为：8－4－2－6依次循环；（9）9的1－9次方个位数字为：9－1依次循环。

（10）要判定一个数的个位数字是几，只需按照这个数的个位数字的n 次方除以4得出的余数即是这个数的个位数字在次方中的排序位置数字。

（11）4的n次方，9的n次方只需除以2即可得出个位数字。

（12）1、5、6的n次方个位数字均为本身。

20以内加法.5+ 6=11 6+ 6=124+ 7=11 5+ 7=12 6+ 7=13 7+ 7=143+ 8=11 4+ 8=12 5+ 8=13 6+ 8=14 7+ 8=15 8+ 8=16 2+ 9=11 3+ 9=12 4+ 9=13 5+ 9=14 6+ 9=15 7+ 9=16 8+ 9=17 9+ 9=18.20以内减法11-2=911-3=811-4=711-5=611-6=511-7=411-8=311-9=2 12-3=912-4=812-5=712-6=612-7=512-8=412-9=313-4=913-5=813-6=713-7=613-8=513-9=414-5=914-6=814-7=714-8=614-9=515-6=915-7=815-8=715-9=6.16-7=916-8=816-9=7.17-8=917-9=8.18-9=9.19-10=911-30的平方表11*11=121 12*12=144 13*13=169 14*14=196 15*15=225 16*16=256 17*17=289 18*18=324 19*19=361 20*20=400 21*21=441 22*22=484 23*23=529 24*24=576 25*25=625 26*26=676 27*27=729 28*28=784 29*29=841 30*30=9001-15 的立方表1*1*1=1 2*2*2=8 3*3*3=27 4*4*4=64 5*5*5=125 6*6*6=2167*7*7=343 8*8*8=512 9*9*9=729 10*10*10=1000 11*11*11=133112*12*12=1728 13*13*13=2197 14*14*14=274415*15*15=3375。