逻辑代数的基本定律和常用公式
逻辑代数的基本定律及规则2010.9.23

_ _ _
_
_ _
_
三变量最小项的编号
长春理工大学软件学院
最大项
最大项标准式是以“或与”形式出现的标准式。 最大项: 对于一个给定变量数目的逻辑函数, 所有变 量参加相“或”的项叫做最大项。 在一个最大项中, 每个 变量只能以原变量或反变量出现一次。 例如, 一个变量A有二个最大项: (2 ) A, A。
例题:化简函数
AB + AC + BC = AB + AC
F = ABC + AD + C D + BD
F = ABC + AD + C D + BD
= ABC + ( A + C ) D + BD
= AC ⋅ B + AC ⋅ D + BD
= AC ⋅ B + AC ⋅ D
= ABC + AD + C D
最小项
2 n 个最小项。最小项通 以此类推,n变量共有
常用 mi 表示。 最小项标准式:全是由最小项组成的“与或” 式,便是最小项标准式(不一定由全部最小项 组成)。 例如:
F ( ABC ) = A B C + BC + A C = A B C + ABC + A BC + AB C + AB C = ∑ m(0,3,4,6,7)
长春理工大学软件学院
逻辑代数的基本定律及规则
对合律: A = A
冗余律: AB + A C + BC = AB + A C
长春理工大学软件学院
逻辑代数的基本定律及规则
3 基本规则
代入规则:任何一个含有变量A的等式,如果将所有 出现A的位置都用同一个逻辑函数代替,则等式仍然 成立。这个规则称为代入规则。 反演规则:对于任何一个逻辑函数F,想要得到F的反 函数,只需要将F中的所有“·”换成“+”,“+”换 成“·”,“0”换成“1”,“1”换成“0”,原变量换成反 变量,反变量换成原变量。 长春理工大学软件学院
逻辑代数基本定律规则及常用公式

逻辑代数基本定律规则及常⽤公式在四则运算中,我们知道有交换律、结合律以及分配律等。
那么在逻辑运算中,也有它⾃⼰的基本定律,下⾯将介绍逻辑代数运算中的基本定理。
逻辑代数基本定理1.0、1定律0、1定律描述的是单个变量A和0、1之间的运算规则。
其中有以下四条定律:(1)A·0=0,即A和0相与始终为0;(2)A·1=A,即A与1相与结果为A;(3)A+0=A,即A和0相或结果为A;(4)A+1=1,即A和1相或始终为1。
2.重叠律重叠率描述逻辑变量A和其⾃⾝的运算。
(1)A·A=A,即A和⾃⼰相与等于它本⾝;(2)A+A=A,即A和⾃⼰相或亦等于它本⾝。
3.互补律互补律描述A和⾃⾝的反变量¬A之间的关系。
(1)A·¬A=0,即A和⾃⾝反变量相与始终为0;(2)A+¬A=1,即A和⾃⾝反变量相或始终为1。
证明:由于A和¬A之间⾄少有⼀个为0,即⼆者不可能全为1,所以相与得0;同时,A和¬A之间⾄少有⼀个为1,满⾜或运算的“有1出1”,所以相或得0。
4.还原律A的反变量再取反,等于本⾝,即¬(¬A)=A。
5.交换律在此定律及之后的定律中,都将会涉及到两个及以上的逻辑变量。
交换律即两个逻辑变量运算时交换位置,结果不变。
(1)A·B=B·A,即A 与B等于B与A;(2)A+B=B+A,即A或B等于B或A。
6.结合律结合律指三个及以上变量相与或相或时,可以使任意两个变量先进⾏运算,再去和别的变量进⾏运算。
(1)(A·B)·C=A·(B·C),即A与B后再与C,等于B与C后再与A。
(2)(A+B)+C=A+(B+C),即A或B后再或C,等于B或C后再或A。
7.分配律逻辑代数的分配律和四则运算的分配律很类似,但是有⼀些不同。
(1)A·(B+C)=A·B+A·C,即A和B或C相与,等于A和B、C分别相与,然后进⾏或运算;(2)(A+B)·(A+C)=A+B·C,这⼀条定律显得有⼀些特殊,它的结果并不像四则运算中展开后有四项的形式,实际上,我们可以这样的得到:(A+B)·(A+C)=A·A+A·C+A·B+B·C=A+AC+AB+BC=A(1+B+C)+BC=A·1+BC=A+BC。
代数法化简逻辑函数.pdf

AB AC ABC ABC
AB(1 C) AC(1 B)
AB A C
2.1 逻辑代数
三.逻辑代数的基本规则:
u 1.代入规则:任何一个逻辑等式,若将等式两边出现的同一个 变量代之以一个逻辑函数,则等式依然成立。
例 分配律 C (A B) A C B C
如 L= A+BC 则 L´= A B C
F=A+BC F ' A B C
对偶规则的基本内容是:如果两个逻辑函数表达式相等, 那么它们的对偶式也一定相等。
即:若 F = L ,则 F´= L´
下面公式中的公式l和公式2就互为对偶式。
2.1 逻辑代数
2.1 逻辑代数
四.异或的运算定律 与或式
2.1 逻辑代数
u2.反演规则 将一个逻辑函数 L 进行下列变换: ·→+,+ →· 0 → 1,1 → 0 原变量 → 反变量,反变量 → 原变量。
所得新函数表达式叫做L的反函数→ L
利用反演规则,可以非常方便地求得一个函数的反函数的表达式
例 F AC B D 解: F (A C)(B D)
2.1 逻辑代数
吸收定律 A+AB=A
A AB A B
A·(A+B)=A
AA B AB
例 证明吸收律 A AB A B
证: A AB A(B B) AB AB AB AB
AB AB AB AB
A(B B) B(A A) A B
冗余律
例ቤተ መጻሕፍቲ ባይዱ
AB+AC+BC=AB+AC ;
证明 ∵ A⊕ B=C ∴A⊕ B⊕ B=C⊕ B ∴A⊕ 0=C⊕ B ∴C⊕ B=A
逻辑代数的公式与基本定理

序号
公式
序号
公式
规律
1
A·0=0
10
A+1=1
0-1律
2
A·1=A
11
A+0=A
0-1律
3
0 1; 1 0
12
4
A·A= A
13
A A
A+A=A
还原律 重叠律
5
A A 0
14
A A1
互补律
6
A·B=B·A
15
A+B=B+A
交换律
7
A·(B·C) = (A·B)·C
16 A+(B+C)=(A+B)+C 结合律
AB CD ABD(E F) AB CD
被吸收
2.反变量的吸收:
证明: A AB A AB AB
长中含反, 去掉反。
A B(A A) A B
例如: A ABC DC A BC DC 被吸收
3.混合变量的吸收:
证明: AB AC BC
1
AB AC ( A A)BC
2
A AB A B
3
AB AB A
4
A(A+B)= A
AB AC BC AB AC
5
AB AC BCD AB AC
6
AAB AB ; AAB A
规律 吸收律 吸收律
吸收律
1.原变量的吸收: A+AB=A 证明: A+A=BA(1+B=)A•1=A
长中含短,留下短。
利用运算规则可以对逻辑式进行化简。 例如:
8
A·(B+C)=A·B + A·C 17 A+B·C =(A+B) ·(A+C) 分配律
逻辑代数中的基本定律和公式

逻辑代数中的基本定律和公式
逻辑代数是一种用来研究逻辑的数学,它通过使用变元和逻辑公式来描述逻辑系统,它被用来解释和分析许多不同类型的逻辑结构。
它还可以帮助我们理解计算机语言、逻辑设计和许多其他类型的数学理论。
基本定律和公式是逻辑代数的基础,它们用来描述一个逻辑系统的行为。
以下是一些常见的定律和公式:* 交换律:如果A和B是同类元素,则A+B = B+A。
* 结合律:如果A、B和C是同类元素,则A+(B+C)=(A+B)+C。
* 分配率:如果A、B和C是同类元素,则A(B+C)= AB + AC。
* 吸收律:如果A和B是同类元素,则A+AB=A。
* 对立律:如果A是一个元素,则A+ A'=
1,其中A'是A的补充。
* 析取律:如果A和B是同类元素,则A+B'=A'B。
* 推理律:如果A和B是同类元素,则A→B = A'+B。
* 合取律:如果A和B是同类元素,则A+B = A'B'。
这些定律和公式提供了一种方法来描述逻辑系统的行为,这些定律和公式可以用来构建逻辑系统,并且可以用来解释和分析逻辑系统的行为。
它们也可以用来构建计算机语言,并用来解释和分析计算机语言的行为。
因此,我们可以看出,逻辑代数中的基本定律和公式是一种非常重要的工具,它们可以帮助我们理解和分析逻辑系统,也可以帮助我们理解和分析计算机语言的行为。
此外,它们还可以用来解释和分析许多不同类型的逻辑结构。
因此,逻辑代数中的基本定律和公式是一种非常重要的研究工具,它们可以帮助我们理解和探索逻辑系统的行为,从而有助于我们更好地理解和设计逻辑系统。
逻辑代数的基本定律和常用公式

逻辑代数的基本定律和常用公式1、基本定律逻辑代数是一门完整的科学。
与普通代数一样,也有一些用于运算的基本定律。
基本定律反映了逻辑运算的基本规律,是化简逻辑函数、分析和设计逻辑电路的基本方法。
(1)交换律(2)结合律(3)分配律(4)反演律(德·摩根定律)2、基本公式(1)常量与常量(2)常量与变量(3)变量与变量3、常用公式除上述基本公式外,还有一些常用公式,这些常用公式可以利用基本公式和基本定律推导出来,直接利用这些导出公式可以方便、有效地化简逻辑函数。
(1)证明:上式说明当两个乘积项相加时,若其中一项(长项:A·B)以另一项(短项:A)为因子,则该项(长项)是多余项,可以删掉。
该公式可用一个口诀帮助记忆:“长中含短,留下短”。
(2)证明:上式说明当两个乘积项相加时,若他们分别包含互为逻辑反的因子(B和),而其他因子相同,则两项定能合并,可将互为逻辑反的两个因子(B和)消掉。
(3)证明:上式说明当两项相加时,若其中一项(长项:·B)包含另一项(短项:A)的逻辑反()作为乘积因子,则可将该项(长项)中的该乘积因子()消掉。
该公式可用一个口诀帮助记忆:“长中含反,去掉反”。
例如:(4)证明:上式说明当3项相加时,若其中两项(AB和C)含有互为逻辑反的因子(A和),则该两项中去掉互为逻辑反的因子后剩余部分的乘积(BC)称为冗余因子。
若第三项中包含前两项的冗余因子,则可将第三项消掉,该项也称为前两项的冗余项。
该公式可用一个口诀帮助记忆:“正负相对,余(余项)全完”。
例:Welcome !!! 欢迎您的下载,资料仅供参考!。
数字电路知识点汇总

数字电路知识点汇总第1章数字逻辑概论一、进位计数制1.十进制与二进制数的转换2.二进制数与十进制数的转换3.二进制数与16进制数的转换二、基本逻辑门电路第2章逻辑代数表示逻辑函数的方法,归纳起来有:真值表,函数表达式,卡诺图,逻辑图及波形图等几种。
一、逻辑代数的基本公式和常用公式1)常量与变量的关系A+0=A与A=⋅1AA+1=1与0⋅A0=A⋅=0AA+=1与A2)与普通代数相运算规律a.交换律:A+B=B+AA⋅⋅=ABBb.结合律:(A+B)+C=A+(B+C)⋅A⋅B⋅⋅=(C)C()ABc.分配律:)⋅=+A⋅B(CA⋅⋅BA C+A+=+)B⋅)(C)()CABA3)逻辑函数的特殊规律a.同一律:A+A+Ab.摩根定律:BBA+=A⋅A+,BBA⋅=b.关于否定的性质A=A二、逻辑函数的基本规则代入规则在任何一个逻辑等式中,如果将等式两边同时出现某一变量A的地方,都用一个函数L表示,则等式仍然成立,这个规则称为代入规则例如:C⋅+A⊕⊕⋅BACB可令L=CB⊕则上式变成L⋅=C+AA⋅L⊕⊕=LA⊕BA三、逻辑函数的:——公式化简法公式化简法就是利用逻辑函数的基本公式和常用公式化简逻辑函数,通常,我们将逻辑函数化简为最简的与—或表达式1)合并项法:利用A+1A=⋅B⋅,将二项合并为一项,合并时可消去=+A=A或ABA一个变量例如:L=B+BA=(C+)=ACACBBCA2)吸收法利用公式AA⋅可以是⋅+,消去多余的积项,根据代入规则BABA=任何一个复杂的逻辑式例如化简函数L=EAB++DAB解:先用摩根定理展开:AB=BA+再用吸收法L=E+AB+ADB=E B D A B A +++ =)()(E B B D A A +++ =)1()1(E B B D A A +++ =B A +3)消去法利用B A B A A +=+ 消去多余的因子 例如,化简函数L=ABC E B A B A B A +++ 解: L=ABC E B A B A B A +++ =)()(ABC B A E B A B A +++=)()(BC B A E B B A +++=))(())((C B B B A B B C B A +++++ =)()(C B A C B A +++ =AC B A C A B A +++ =C B A B A ++4)配项法利用公式C A B A BC C A B A ⋅+⋅=+⋅+⋅将某一项乘以(A A +),即乘以1,然后将其折成几项,再与其它项合并。
逻辑代数的基本定律及规则

逻辑代数的基本定律及规则文章来源:互联网作者:佚名发布时间:2012年05月26日浏览次数: 1 次评论:[已关闭] 功能:打印本文一、逻辑代数相等:假定F、G都具有n个相同变量的逻辑函数,对于这n个变量中的任意一组输入,如F和G都有相同的输出值,则称这两个函数相等。
在实际中,可以通过列真值表来判断。
二、逻辑代数的基本定律:在逻辑代数中,三个基本运算符的运算优先级别依次为:非、与、或。
由此推出10个基本定律如下:1.交换律A+B=B+A;A·B=B·A2.结合律A+(B+C)=(A+B)+C;A·(BC)=(AB)·C3.分配律A·(B+C)=AB+AC;A+BC=(A+B)·(A+C)4.0-1律A+0=A;A·1=AA+1=1 ;A·0=05.互补律A+=1 ;A·=06.重叠律A·A=A;A+A=A7.对合律=A8.吸收律A+AB=A;A·(A+B)=AA+B=A+B;A·(+B)=ABAB+B=B;(A+B)·(+B)=B9.反演律=·;=+10.多余项律AB+C+BC=AB+C;(A+B)·(+C)·(B+C)=(A+B)·(+C)上述的定律都可用真值表加以证明,它们都可以用在后面的代数化简中。
三、逻辑代数的基本规则:逻辑代数中有三个基本规则:代入规则、反演规则和对偶规则。
1.代入规则:在任何逻辑代数等式中,如果等式两边所有出现某一变量(如A)的位置都代以一个逻辑函数(如F),则等式仍成立。
利用代入规则可以扩大定理的应用范围。
例:=+,若用F=AC代替A,可得=++2.反演规则:已知函数F,欲求其反函数时,只要将F式中所有的“·”换成“+”,“+”换成“·”;“0”换成“1”,“1”换成“0”时,原变量变成反变量,反变量变成原变量,便得到。
逻辑代数中的基本公式、常用公式与基本定理

(1)
(2) A+AB=A
(3)
(4)
1.代入定理:在含有变量A的等式中,将A用一个逻辑表达式代替,等式仍然成立。
2.对偶定理:将某逻辑表达式Y中的与和或对换,0和1对换(所有的“+”运算符都换成“·”,“·”换成“+”,0换成1,1换成0)且保持原来的运算优先顺序,那么就得到一定对偶式 。如果两个逻辑表达式相等,那么它们各自的对偶式也就必然相等。例:
若A·(B+C)=A·B+A·C
则A+BC=(A+B)(A+C
求对偶式时,要保证优先次序不变,否则就会出错。如A+AB=A,求对偶式时如不加括号,得到AA+B=A,从而得到错误的结论:A+B=A
3.反演定理:将某逻辑表达式Y中的与和或对换,0和1对换,原变量和反变量对换,这样得到的表达式就是 。
注意:对偶规则和反演规则的区别:对偶规则不需要将逻辑变量取反,而反演规则重要将逻辑变量取反。
逻辑代数中的基本公式、常用公式与基本定理
基本公式
常用公式
基本定理
(1)基本运算
A·0=0
A·1=A A·A=A
A+0=A A+A=A
A+1=1
(2)交换律
A·B=B·A
A+B=B+A
(3)结合律
A(B·C)=(A·B)·C
A+(B+C)=(A+B)+C
(4)分配律
A·(B+C)=A·B+A·C
(A+B)·(A+C)+A+BC
狄摩根定律在我们日常生活中也有应用,如以下两句话的含意一致的:
逻辑函数的公式化简法

逻辑函数的公式化简法逻辑代数的八个基本定律01律01律交换律结合律分配律(1)A1= A (2)A0= 0 (5)AB= BA (7)A(BC)= (AB) C (3)A+0= A (4)A+1= 1 (6)A+B= B+A (8)A+(B+C)= (A+B)+C(9)A(B+C)= AB+AC (10)A+(BC)= (A+B)(A+C) 0互补律(11) A A = 重叠律(13)AA= A 反演律否定律(17 )Α =(12) A + A =(14)A+A= A1(15) AB = A + BA(16) A + B = A B逻辑代数的常用公式逻辑函数的公式化简法(1)并项法运用公式A + A = 1 ,将两项合并为一项,消去一个变量,如例. Y1 = AB + ACD + A B + A CD= ( A + A ) B + ( A + A )CD = B + CD练习1. 练习1. Y2= BC D + BCD + BC D + BCD= BC ( D + D ) + BC ( D + D )= BC + BC = B= A( BC + BC ) + A( BC + BC )= ABC + ABC + ABC + ABC = AB(C + C ) + AB(C + C )练习2. 练习2. Y3= AB + AB = A( B + B ) = A(2)吸收法吸收法将两项合并为一项,运用公式A+AB=A,将两项合并为一项,消去将两项合并为一项多余的与项。
多余的与项。
例. Y1 = ( A B + C ) ABD + AD= ( A B + C ) B AD + AD = AD[]练习1.Y2 = AB + ABC + ABD + AB (C + D ) 练习1.= AB + AB C + D + (C + D ) = AB[]练习2. 练习2. Y3 = ( A + BC ) + ( A + BC )( A + B C + D)= A + BC(3)消去法消去法运用公式A + A B = A + B,或AB + A C + BC = AB + A C增加必要的乘积项,消去多余的因子例.Y1 = A + A CD + A BC= A + CD + BC练习1. 练习1. Y2 = A + AB + BE= A + B + BE = A+ B + E练习2. 练习2.Y3 = AC + AB + B + C= AC + AB + B C= AC + B C(4)配项法配项法先通过乘以A + A = 1或加上A + A = A ,增加必要的乘积项,再用以上方法化简,如:例. Y1 = AB + A B + BC + B C= AB + A B (C + C ) + BC + B C ( A + A )= AB + A BC + A BC + BC + AB C + A B C= ( AB + AB C ) + ( A BC + BC ) + ( A BC + A B C )= AB + BC + A C练习1. 练习1.Y2 = A BC + A BC + ABC= ( A BC + A BC ) + ( A BC + ABC )= A B (C + C ) + ( A + A) BC= A B + BC练习2. 练习2.Y3 = AB + AC + BCD= AB + AC + BCD ( A + A) = AB + AC + ABCD + ABCD= AB + AC小结逻辑函数的公式化简法A 并项法:将两项合并为一项,并项法:+ A = 1 ,将两项合并为一项,消去多余的项吸收法:吸收法:+ AB = A ,将两项合并为一项,消去将两项合并为一项, A 多余的项A 消去法:消去法:+ AB = A + B , AB + AC + BC = AB + A C 将两项合并为一项,将两项合并为一项,消去多余的项A 配项法:配项法:+ A = 1或加上A + A = A ,再利用以上的方法做题作业P34页2-5,(2)(3)(4)(5)。
1.1逻辑代数的基本运算
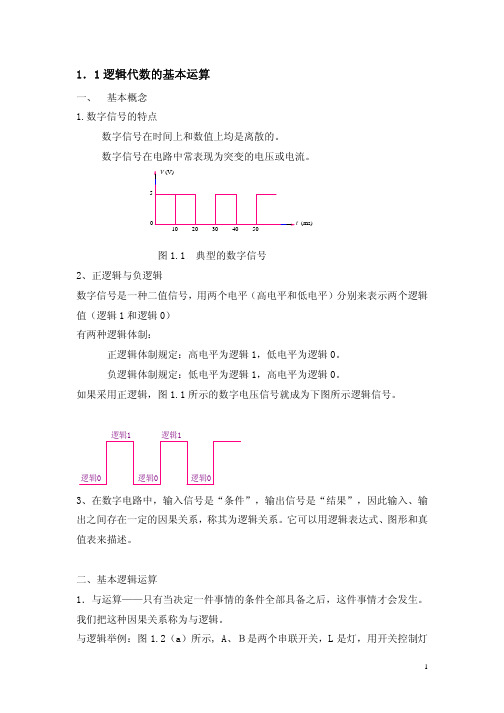
1.1逻辑代数的基本运算一、 基本概念 1.数字信号的特点数字信号在时间上和数值上均是离散的。
数字信号在电路中常表现为突变的电压或电流。
图1.1 典型的数字信号2、正逻辑与负逻辑数字信号是一种二值信号,用两个电平(高电平和低电平)分别来表示两个逻辑值(逻辑1和逻辑0) 有两种逻辑体制:正逻辑体制规定:高电平为逻辑1,低电平为逻辑0。
负逻辑体制规定:低电平为逻辑1,高电平为逻辑0。
如果采用正逻辑,图1.1所示的数字电压信号就成为下图所示逻辑信号。
3、在数字电路中,输入信号是“条件”,输出信号是“结果”,因此输入、输出之间存在一定的因果关系,称其为逻辑关系。
它可以用逻辑表达式、图形和真值表来描述。
二、基本逻辑运算1.与运算——只有当决定一件事情的条件全部具备之后,这件事情才会发生。
我们把这种因果关系称为与逻辑。
与逻辑举例:图1.2(a)所示, A、B是两个串联开关,L 是灯,用开关控制灯逻辑0逻辑1逻辑0逻辑1逻辑0V t (V)(ms)51020304050亮和灭的关系如图2(b)所示。
设1表示开关闭合或灯亮;0表示开关不闭合或灯不亮,则得真值表图2(c)所示V(c)图1.2与逻辑运算(a)电路图(b)真值表(c)逻辑真值表(d)逻辑符若用逻辑表达式来描述,则可写为与运算的规则为: “输入有0,输出为0;输入全1,输出为1”。
数字电路中能实现与运算的电路称为与门电路,其逻辑符号如图(d)所示。
与运算可以推广到多变量:⋅⋅⋅=C B A L ……2.或运算——当决定一件事情的几个条件中,只要有一个或一个以上条件具备,这件事情就发生。
我们把这种因果关系称为或逻辑。
或逻辑举例:如图1.3(a)所示,或运算的真值表如图1.3(b )所示,逻辑真值表如图1.3(c )所示。
若用逻辑表达式来描述,则可写为L =A+B或运算的规则为:“输入有1,输出为1;输入全0,输出为0”。
BA L ⋅=(c)图1.3或逻辑运算(a) 电路图(b)真值表(c)逻辑真值表(d)逻辑符号在数字电路中能实现或运算的电路称为或门电路,其逻辑符号如图(d)所示。
逻辑代数基础

2、不属于单个变量上的反号应保留不变。
Y A( B C ) CD
Y ( A BC)(C D) Y (( AB C ) D) C
Y (((A B)C)D) C
三、 对偶定理
对任何一个逻辑表达式Y 作对偶变换,可得Y的 对偶式YD, YD称为Y的对偶式。 对偶变换: “﹒”→“﹢” 对偶定理:如果两个逻辑式相等, 则它们的对偶式也相等。
1 1
C
0
1
1 0
1 0
1 1 t 1 0 1 1
0
1 0 1
Y
1
0
1
三、逻辑函数的两种标准形式 最小项: 在n变量逻辑函数中,若m为包含n个因子的乘 积项,而且这n个变量都以原变量或反变量的形式在 m 中出现,且仅出现一次,则这个乘积项m称为该 组变量的最小项。 3个变量A、B、C可组成 8(23)个最小项:
“﹢”→“﹒”
“0” → “1”
“1” →“0”
利用对偶规则,可以使要证明及要记忆的公 式数目减少一半。
Y A( B C )
Y A B C
D
Y ( AB CD)
Y (( A B) (C D))
D
(2)式 (12)式
1 A A
0 A A
A( B C ) AB AC
§2.2
逻辑代数中的三种基本运算
一、与逻辑(与运算) 与逻辑:仅当决定事件(Y)发生的所有条件(A,
B,C,…)均满足时,事件(Y)才能发生。表达
式为: Y=ABC…
例:开关A,B串联控制灯泡Y
A A A A E E E E
电路图
BB B B YY Y Y
逻辑代数基础

Y AC AB
AC( B B) AB(C C)
ABC ABC ABC ABC ABC ABC ABC m5 m6 m7
例1:画出 Y AC AB 的卡诺图
Y ABC ABC ABC m5 m6 m7
输入变量 BC 00 A 0 0 1 00 01 11 10 m0 m1 m3 m2 m4 m5 m7 m6 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
② 最小项的性质 对于任意一个最小项,只有一组变量取值使 它的值为1,而在变量取其它各值时,这个 最小项的值都是零; 不同的最小项,使它的值为1的那组变量取 值也不同; 对于变量的同一组取值,任意两个最小项 的乘积为零; 对于变量的同一组取值,所有最小项的逻辑 或为1。
第2章 逻辑代数基础
§2.1 逻辑代数 § 2.2 逻辑函数表达式的形式与变换 §2.3逻辑函数的化简
§2.1逻辑代数的基本规则和定理
逻辑代数(又称布尔代数),它是分析和 设计逻辑电路的数学工具。虽然它和普通代 数一样也用字母表示变量,但变量的取值只 有“0”,“1”两种,分别称为逻辑“0”和逻 辑 “1”。这里“0”和“1”并不表示数量的大小, 而是表示两种相互对立的逻辑状态。
③最小项的编号
注:下标与编码所对应的十进制数值相同
④函数的最小项表达式
将逻辑函数表达式化成一组最小项之和,称为 最小项表达式。任何一个函数均可表达成 唯一的 最小项之和。 如:
L( A, B, C ) ( AB AB C ) AB
( AB A B C ) AB AB ABC AB ABC A BC ABC ABC m3 m5 m 6 m 7 m(3,5,6,7)
1.3.1逻辑代数基本定律和规则

Y A C B D
应用反演规则应注意:
1.保持原来的运算优先顺序,即如果在原函数表达式中,AB 之间先运算,再和其它变量进行运算, 那么非函数的表达式 中,仍然是AB之间先运算。 2.不属于单个变量上的反号应保留不变。
Y AB C D C
Y ( A B)C D C
对偶规则:如果两个逻辑式相等,则它们的对偶式也相等。
Y A(B C) Y AB CD
Y D A BC Y D ( A B) (C D)
利用对偶规则,可以使要证明及要记忆的公式数目减少一半。
1 A A
A(B C) AB AC
0 A A
A BC ( A B)( A C)
例如,在反演律中用BC 去代替等式中的 B,则新的等式仍成立。
BC代替等式中的B
ABC A BC A B C
02
如果将逻辑函数Y 中的所有“·”换成“+”,“+”换成
“·”,“0”换成“1”,“1”换成“0”,而变量保持不变,
则可得到的一个新的函数表达式 Y D, Y D 称为Y 的对偶式。
一
一、逻辑代数的基本定律:有10个基本定律
定律名称 0-1律 自等律 重叠律 互补律 交换律 结合律 分配律 吸收律 反演律 还原律
定律1
A·0=0 A·1=A A·A=A
A A 0
A·B=B·A A·(B·C )=(A·B )·C A·(B+C )=AB+AC
A(A+B )=A
AB A B
(B B
C) C
A (A
B B)
A A B A B A B
摩根定律
A B AB BA 00 0 0 01 0 0 10 0 0 11 1 1
逻辑代数的基本规则

逻辑代数的基本规则
逻辑代数是一种数学系统,用于处理逻辑关系。
以下是逻辑代数的基本规则:
1. 0 和1 规则:0 和1 分别代表逻辑中的假和真。
2. 与运算规则(AND):如果A 和B 都是真,则A AND B 为真;如果A 和B 中至少有一个为假,则A AND B 为假。
3. 或运算规则(OR):如果A 或B 中至少有一个为真,则A OR B 为真;如果A 和B 都为假,则A OR B 为假。
4. 非运算规则(NOT):如果A 为真,则NOT A 为假;如果
A 为假,则NOT A 为真。
5. 分配律:A (B OR C) = (A B) OR (A C),A (B AND C) = (A B) AND (A C)。
6. 结合律:(A OR B) OR C = A OR (B OR C),(A AND B) AND C =
A AND (
B AND C)。
7. 交换律:A OR B = B OR A,A AND B = B AND A。
8. 吸收律:A OR A = A,A AND A = A。
9. 互补律:A OR NOT A = 1,A AND NOT A = 0。
10. 德摩根定律:NOT (A OR B) = (NOT A) AND (NOT B),NOT
(A AND B) = (NOT A) OR (NOT B)。
逻辑代数常用恒等式

逻辑代数常用恒等式逻辑代数是一种数学分支,它研究的是逻辑关系和逻辑运算。
在逻辑代数中,恒等式是一种非常重要的概念,它们可以帮助我们简化逻辑表达式,提高计算效率。
本文将介绍逻辑代数中常用的恒等式,并按照类别进行划分。
1. 布尔恒等式布尔恒等式是逻辑代数中最基本的恒等式,它们描述了布尔代数中的逻辑运算规律。
其中最常用的恒等式有以下几个:(1)交换律:A∧B=B∧A,A∨B=B∨A(2)结合律:(A∧B)∧C=A∧(B∧C),(A∨B)∨C=A∨(B∨C)(3)分配律:A∧(B∨C)=(A∧B)∨(A∧C),A∨(B∧C)=(A∨B)∧(A∨C)(4)德摩根定律:¬(A∧B)=¬A∨¬B,¬(A∨B)=¬A∧¬B2. 德摩根恒等式德摩根恒等式是逻辑代数中非常重要的一类恒等式,它们描述了逻辑运算中的否定关系。
其中最常用的恒等式有以下几个:(1)双重否定律:¬(¬A)=A(2)否定的交换律:¬(A∧B)=¬A∨¬B(3)否定的结合律:¬(A∨B)=¬A∧¬B3. 布尔-德摩根恒等式布尔-德摩根恒等式是布尔恒等式和德摩根恒等式的结合体,它们描述了逻辑运算中的复合关系。
其中最常用的恒等式有以下几个:(1)德摩根第一定律:¬(A∨B)=(¬A)∧(¬B)(2)德摩根第二定律:¬(A∧B)=(¬A)∨(¬B)(3)布尔第一定律:A∨(A∧B)=A(4)布尔第二定律:A∧(A∨B)=A4. 其他恒等式除了以上三类恒等式外,逻辑代数中还有一些其他的恒等式,它们描述了逻辑运算中的特殊情况。
其中最常用的恒等式有以下几个:(1)恒等律:A∨¬A=1,A∧¬A=0(2)同一律:A∨1=1,A∧0=0(3)零律:A∨0=A,A∧1=A总结逻辑代数中的恒等式是逻辑运算中的基本规律,它们可以帮助我们简化逻辑表达式,提高计算效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明: 上式说明当3项相加时,若其中两项(AB和 C)含有互为逻辑反的因子 (A和 ),则该两项中去掉互为逻辑反的因子后剩余部分的乘积(BC) 称为冗余因子。若第三项中包含前两项的冗余因子,则可将第三项消 掉,该项也称为前两项的冗余项。该公式可用一个口诀帮助记忆:“正 负相对,余(余项)全完”。 例:
逻辑代数的基本定律和常用公式
1、基本定律 逻辑代数是一门完整的科学。与普通代数一样,也有一些用于运算的基 本定律。基本定律反映了逻辑运算的基本规律,是化简逻辑函数、分析 和设计逻辑电路的基本方法。 (1)交换律
(2)பைடு நூலகம்合律
(3)分配律
(4)反演律(德·摩根定律)
2、基本公式 (1)常量与常量
(2)常量与变量
(3)变量与变量
3、常用公式 除上述基本公式外,还有一些常用公式,这些常用公式可以利用基本公 式和基本定律推导出来,直接利用这些导出公式可以方便、有效地化简 逻辑函数。 (1) 证明:
上式说明当两个乘积项相加时,若其中一项(长项:A·B)以另一项 (短项:A)为因子,则该项(长项)是多余项,可以删掉。该公式可 用一个口诀帮助记忆:“长中含短,留下短”。 (2) 证明: 上式说明当两个乘积项相加时,若他们分别包含互为逻辑反的因子(B 和 ),而其他因子相同,则两项定能合并,可将互为逻辑反的两个因 子(B和 )消掉。 (3) 证明: 上式说明当两项相加时,若其中一项(长项: ·B)包含另一项(短 项:A)的逻辑反( )作为乘积因子,则可将该项(长项)中的该乘 积因子( )消掉。该公式可用一个口诀帮助记忆:“长中含反,去掉 反”。 例如:
