BODE图画图过程
bode图 nyquist图

系统开环Nyquist图的绘制
例1 已知系统的开环传递函数如下,试绘制系统的 开环Nyquist图。
举例说明
系统开环Nyquist图的绘制
举例说明
例2 已知系统的开环传递函数如下,试绘制系统的 开环Nyquist图,并求与实轴的交点。
Nyquist图与实轴相交时
系统开环Nyquist图的绘制
延迟环节 是不是 最小相位环节 ?
系统开环Bode图的绘制
Bode图的绘制举例
系统开环Bode图的绘制
单回路开环系统Bode图的绘制
系统开环Nyquist图的绘制
概述
K ( n s 1) ( k s 2 k k s 1)
2 2
G( s) s
v
n 1
k 1
举例说明
例3 已知系统的开环传递函数如下,试绘制系统的 开环Nyquist图。
系统开环Nyquist图的绘制
总结
0型系统(v = 0)
G ( j ) K (1 j 1 )(1 j 2 )...(1 j m ) ( j ) (1 jT1 )(1 jT2 )...(1 jTn )
n m
0
A(0) K
只包含惯性环节的0型系统Nyquist图
( 0) 0
A( ) 0
( ) ( n m ) 90
系统开环Nyquist图的绘制
总结
I型系统(v = 1)
G ( j ) K (1 j 1 )(1 j 2 )...(1 j m ) ( j ) (1 jT1 )(1 jT2 )...(1 jTn )
如何绘制伯德图PPT课件

G( j ) 00
(5-63) (5-64)
100 00
900 1800
10 100 1000
图5-11 放大环节的Bode图
如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G( j) 1 j 1 1 e j90 j
7
当有n个积分环节串联时,即
dB L()
G(
j
)
(
1
j
)n
其对数幅频特性为
20 lg
G(
j )
20 lg
1
பைடு நூலகம்n
40
( 5-70 )
0
(5-71)
0.01 0.1
40 dB / dec
1
10
n 20 lg
G( j ) n 900
(5-72) 度 ()
6
设 ' 10 ,则有
20lg ' 20lg 10 20 20lg
dB L()
可见,其对数幅频特性是一条在
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线 (ω 轴),且以每增加十倍频降 低20分贝的速度(-20dB/dec ) 变化的直线。
40
20dB / dec
1
L() dB
bode图怎么绘制

bode图怎么绘制不过在系统辨识工具箱中有相应的函数能够完成该功能。
应该是invfrqs函数。
但这个是由频率响应得到的,所以你的对输入输出信号做傅里叶变换得到频率响应后在用这个函数拟合传递函数。
使用matlab工具箱更为方便和直观:1. 把u,y信号导入到工作空间里。
2. 用ident命令打开matlab系统辨识工具箱,然后点击import data,从新打开界面里导入工作空间的数据。
然后可以通过图形查看该输入输出信号,或者在proprocess进行信号预处理。
3. 根据你的模型在estimate里选择linear parameter models,个人觉得你应该选择ARX 结构,确定阶数,然后进行估计。
4. 在主界面里查看估计模型,并且可以和实际输出比较,看看拟合度。
详细使用方面参考帮助文档System Identification Toolbox User's Guide也只能是拟合吧,拟合的目标也只能是有限的一些典型传递函数。
做过这个,就是拟合吧在sisotool工具里放置合适的零极点,尽量使曲线吻合,得到传递函数我是大概知道实测的曲线的零极点分布的,然后去拟合的,这样好做点如果已经得到Bode plot,就幅度vs频率,相位vs频率曲线,根据+/-20db/dec,+/-40db/dec 渐近线先预测几个pole,zero,double pole double zero,然后再去近似了。
还有几个比较困难的地方是:1)实际系统引入的杂散参数和群延迟特性,才是拟合和预测的难点。
2)实际测量时仪器已经采用了离散化的数字处理手段,还有测量系统处理误差和测量时注入的扰动幅度所引起的误差,对低频还好,对高频都是很大的影响。
3)所以目前已有的模型,多是对1/2开关频率之前的预测,V2等新模型有所改进,但是还是有其局限性以我测试的为例吧,R=1e3; C=1e-7; L=0.1; Rl=1000;magdb_LCR=zeros(1,1e5);% -sL-R-|(1/sC)mag_LCR=zeros(1,1e5);phase_LCR=zeros(1,1e5);freq=(1:1e5);RCplot=zeros(1,1e5);LCRplot=zeros(1,1e5);for f=1:1:1e5LCR=1/((1i*2*pi*f)^2*L*C+1i*2*pi*f*C*Rl+1);LCRplot(f)=LCR;mag_LCR(f)=abs(LCR);magdb_LCR(f)=20*log10(abs(LCR));phase_LCR(f)=angle(LCR)*180/pi;end我用上方的函数写一个已知的传递函数,生成对应频率下的幅值和相位。
如何绘制伯德图.ppt

j?
??
其幅频特性为
1
G ( j? ) ? ?
对数幅频特性是
(5-65) (5-66)
1
20 lg G ( j? ) ? 20 lg ? ? 20 lg ? ?
(5-67)
当 ? ? 0 . 1 时,20 lg G ( j 0 . 1 ) ? ? 20 lg 0 . 1 ? 20 ( dB ) ; 当 ? ? 1 时,20 lg G ( j1) ? ? 20 lg 1 ? 0 ( dB ) ;
当 ? ? 10 时,20 lg G ( j10 ) ? ? 20 lg 10 ? ? 20 ( dB ) 。
6
设 ? ' ? 10 ? ,则有
? 20 lg ? ' ? ? 20 lg 10 ? ? ? 20 ? 20 lg ?
可见,其对数幅频特性是一条 在
dB L(? )
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线
(5-73) (5-74)
? ? 20 lg 1 ? T 2? 2
当 ? ?? 1 时, 20 lg G ( j ? ) ? ? 20 lg 1 ? T 2 ? 2 ? 0 ( dB ) ,
T
当 ? ?? 1 时,20 lg G ( j ? ) ? ? 20 lg 1 ? T 2 ? 2 ? ? 20 lg T ? ( dB )
40
(ω 轴),且以每增加十倍频降
20
? 20 dB / dec
低20分贝的速度( -20dB/dec )
0
0.01
0.1
1
10
?
变化的直线。
? 20
积分环节的相频特性是
? G ( j ? ) ? ? 90 0
实验二:绘制控制系统的Bode图(学生用)

实验二:绘制控制系统的Bode图Bode Graphics of Controlling System一、实验目的1.利用计算机做出开环系统的伯德图;2.观察记录控制系统的开环频域性能;3.控制系统的开环频率特性分析。
二、实验步骤1.在Windows界面上双击matlab图标,即可打开MATLAB命令平台。
2.练习相关M函数(1)伯德图绘图函数:bode(sys)bode(sys,{wmin,wmax})bode(sys,w)[m,p,w]=bode(sys)函数功能:对数频率特性作图函数,即伯德图作图。
格式1:给定开环系统的数学模型对象sys作伯德图,频率向量w自动给出。
格式2:给定变量w的绘图区间为{wmin,wmax}。
格式3:频率向量w由人工给出。
w的单位为[弧度]/秒,可以由命令logspace得到对数等分的w值。
格式4:返回变量格式,不作图。
m为频率特性G(jω)的幅值向量,m=︱G(j)︳。
p为频率特性G(jω)的幅角向量,p=arg[G(jω)],单位为角度(°)。
w为频率向量,单位为[弧度]/秒。
更详细的命令说明,可键入“help bode”在线帮助查阅。
例如,系统开环传递函数为作图程序为num=[10];den=[1 2 10];sys=tf(num,den);bode(sys);grid on上面两句或者直接换为:bode(num,den);绘制伯德图如图1所示。
或者给定人工变量w=logspace(-1,1,32); % w范围和点数n ,下面对该函数做了详细的说明bode(num,den,w); %或者sys=tf(num,den); bode(sys,w);grid on绘制伯德图如图2所示。
图3 伯德图图4 伯德图(2)对数分度函数:logspace(d1,d2)logspace(d1,d2,n)函数功能:产生对数分度向量。
格式1:从10d1到10d2之间作对数等分分度,产生50个元素的对数等间隔向量。
如何绘制伯德图

。
6
设 ' 10 ,则有
20 lg 20 lg 10 20 20 lg
'
(5-68)
dB L( )
可见,其对数幅频特性是一条在 ω =1(弧度/秒)处穿过零分贝线 ( ω 轴),且以每增加十倍频降 低 20 分贝的速度( -20dB/dec ) 变化的直线。 积分环节的相频特性是
对数幅频特性为
20 lg G( j ) 20 lg K
(5-61)
当K>1时,20lgK>0,位于横轴上方;
当K=1时,20lgK=0,与横轴重合;
当K<1时,20lgK<0,位于横轴下方。
4
放大环节的对数幅频特性如图5-11所示,它是一条与角频 率ω 无关且平行于横轴的直线,其纵坐 标为20lgK。
0
100
1000
(5-63)
180
0
放大环节的相频特性是
G( j ) 0
0
图5-11 放大环节的Bode图
(5-64) 如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G ( j ) 1 j j 1
1
e
j 90
2 2 2
(5-85)
相频特性是
G ( j ) arctg 2 1
2 2
dB
40
(5-86)20
0
1 1 10
0
精确特性
40dB / dec
二阶微分环节与振荡节的Bode
1
图关于ω 轴对称,如图5-21 。
第5章4——Bode图
2
1 2 n
2
n
2 arc tg n 2 1 2 n
0 0 ( ) 90 n 180
autocumt@ 22
振荡环节L()
L()dB 40 20 0dB -20
(rad / s)
10 -2
10 -1
1
10
0
2 3 4
10
1
autocumt@
自动控制原理
对数分度:
lg 2 0.301
lg 3 0.4771 lg 4 2lg 2 0.602 lg 5 0.699 lg 6 lg 3 lg 2 0.778
lg 7 0.845 lg 8 3 lg 2 0.903 lg 9 2 lg 3 0.954
()º
(rad / s)
10 -2
autocumt@
10 -1
3
100
10
1
20 10 0
自动控制原理
L() dB -10
-20 -30 -40 900 450
( )
00 0 -450 -900
-1350
完 整 图 二 合 一
-1800
10 -2
autocumt@
[-20] 0.1 0.2
1
2
10 20
[-20]
100
16
5-4 对数频率特性——Bode图
(5)一次微分环节
传递函数: G(S) TS+ 1 频率特性: G ( j ) Tj 1
0 0 1 相频特性 ( ) arctanT 45 T 90
典型环节的Bode图

控制系统的开环频率特性目的:掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点:开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤:1)将开环传递函数表示为时间常数表达形式,计算各个典型环节的交接频率2)求20lgK的值,并明确积分环节的个数ν3)通过(1,20lgK)绘制斜率为-20vdB/dec低频段4)随着频率增加,每遇到一个典型环节的交接频率,就改变一次斜率最小相位系统定义:递函数的零点、极点全部位于S 左半平面,同时又无纯滞后环节的系统称为最小相位系统。
否则就是非最小相位系统。
对数幅频特性与相频特性之间存在确定的对应关系。
对于一个最小相位系统,我们若知道了其幅频特性,它的相频特性也就唯一地确定了。
也就是说:只要知道其幅频特性,就能写出此最小相位系统所对应的传递函数,而无需再画出相频特性。
非最小相位系统高频时相角迟后大,起动性能差,响应缓慢。
对响应要求快的系统,不宜采用非最小相位元件。
Tf函数用来建立实部或复数传递函数模型或将状态方程、或零级增益模型转化成传递函数形式。
sys = tf(num,den)命令可以建立一个传递函数,其中分子和分母分别为num和den。
输出sys 是储存传递函数数据的传递函数目标。
单输入单输出情况下,num和den是s的递减幂级数构成的实数或复数行向量。
这两个向量并不要求维数相同。
如h = tf([1 0],1)就明确定义了纯导数形式h(s)=s。
若要构建多输入多输出传递函数,要分别定义每一个单输入单输出系统的端口的分子与分母。
2 典型环节的伯德图绘制曲线在MA TLAB中实现,利用下述的程序段:num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on2.1 比例环节传递函数:()G s K=频率特性:()G j Kω=对数幅频特性:()20lgL j Kω=对数相频特性:()0ϕω=程序段:num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) holdon结论:放大环节的对数幅频特性是一条幅值为20lgK分贝,且平行于横轴的直线,相频特性是一条和横轴重合的直线。
自动控制理频域伯德图

Lω 20lg1 =0 dB
——低频渐近线为一条0dB的水平直线。
Lω 20lg 1 Tn ω
2
2 2
2ζ T ω
n
2
高频段,即ωTn>>1时
L() 20lg( Tn ) 40lg(Tn )
2 2
当ω增加10倍
ωTn 40 40lgωTn L() 40lg10
相频与ω无关,值为-90°且平行于横轴的直线。
L ( )
20 0
20 0.1 10
1
( )
0 90
0.1
1
10
3 微分因子
G jω jω
微分环节是积分环节的倒数,它们的 曲线斜率和相位移也正好相差一个负号。
L ( )
20
0
20
0.1 20
1
10
( )
90
L() 40lg Tn 40lg1 0(dB)
即高频渐近线是一条斜率为-40dB/dec的直线。 当 ωω 1 时
n
Tn
说明
ω ωn
1 Tn
为二阶系统(振荡环节)的转折频率。
。10
0
0.1
0.2 0. 3
L ( )
dB
-40dB/dec
0 .7 1
10
系统 的相频特性为 90 arctan arctan 2 10
0
W=0
90
0
W=1
W=10 W=无穷大
110.860
123.70
0 90
波德(Bode)图

2 2
低频段( << n)
L( ) 20lg1 0
即低频渐近线为0dB的水平线。 高频段( >> n)
2 L( ) 20lg 1 2 n n 2 2
20 lg 40 lg 40 lg 40 lg n n n
3
通常用L()简记对数幅频特性,也称L() 为增益;用()简记对数相频特性。
对数坐标的优点
幅值相乘、相除,变为相加,相减,简化作图; 对数坐标拓宽了图形所能表示的频率范围 两个系统或环节的频率特性互为倒数时,其对数 幅频特性曲线关于零分贝线对称,相频特性曲线关 于零度线对称
11
20 10
Bode Diagram
= 0.1 = 0.2 = 0.3 = 0.5
L()/ (dB)
0
-10 -20
-30 -40 0
渐近线
= 0.7 = 1.0
-40dB/dec
() / (deg)
-45
-90 -135 -180 0.1
= 0.1 = 0.2 = 0.3
即低频段可近似为0dB的水平线,称为低频渐近线。 高频段( >> 1/T )
L( ) 20lg 1 T 2 2 20lg T 20lg T 20lg
即高频段可近似为斜率为-20dB/dec 的直线,称 为高频渐近线。
7
L()/ (dB)
10 0
10
Bode Diagram 渐近线 -20dB/dec
j 1 i 1 n m
(3)依次作出各环节的Bode图(渐进线); (4)将各环节曲线合成; (5)将对数幅频特性曲线竖直移动20lgKdB.
bode图画图过程
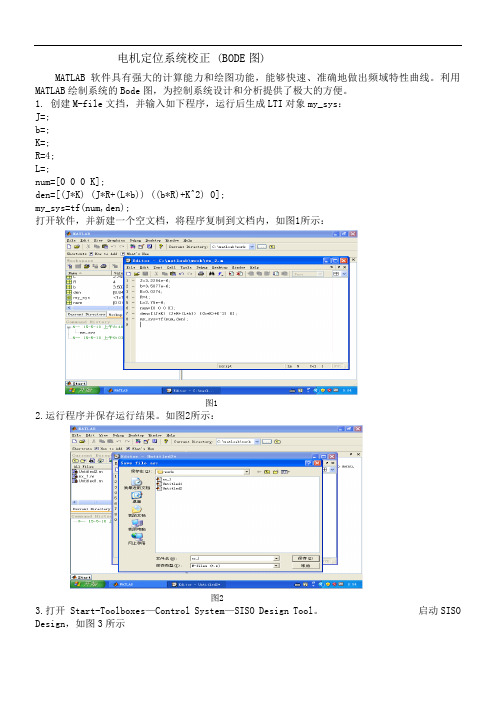
电机定位系统校正 (BODE图)MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB绘制系统的Bode图,为控制系统设计和分析提供了极大的方便。
1. 创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:J=;b=;K=;R=4;L=;num=[0 0 0 K];den=[(J*K) (J*R+(L*b)) ((b*R)+K^2) 0];my_sys=tf(num,den);打开软件,并新建一个空文档,将程序复制到文档内,如图1所示:图12.运行程序并保存运行结果。
如图2所示:图23.打开 Start-Toolboxes—Control System—SISO Design Tool。
启动SISO Design,如图3所示图34. 将my_sys程序导入到SISO Design Tool中,File-Import 如图4所示图45. 在View菜单中,关闭根轨迹显示,只显示开环的Bode图。
如图5所示图56. 加积分环节;加零点(60角频率)将各个参数进行积分:空白处右键—Add Pole/Zero—Integrator。
如图6所示:图67.在magnitude曲线加零点,然后Analysis菜单下Response to Step Command指令。
如图7所示:图78. 在管理反馈界面中,只显示闭环的r与y的关系—LT1 Viewer For SISO Design Tool界面空白处右键—Systems—Closed Loop :r to u (green),如图8所示:图89. 添加零点和极点,如图8所示,并移动极点、零点和线的位置,调整LT1 Viewer For SISO Design Tool窗口中函数图像的变化直到符合Bode图,如图9所示:图 910.用鼠标上下移动观察阶越响应的超调量变化,满足校正要求。
如图10 所示:图1011.从analysis→closed loopbode调用LTI viewer分析闭环BODE图。
控制工程-典型环节的对数坐标图(Bode图)

I 型系统的低频渐近线: L (ω )= 20lgK-20lgω 斜率为-20dB/dec的直线,且与0dB线(横轴)的交点为ω=K
II型系统的低频渐近线: L (ω )= 20lgK-40lg ω 斜率为-40dB/dec的直线,且与0dB线(横轴)的交点为= K
3. dec:十倍频,即频率增加10倍;
4. ±20dB/dec:频率每增加10倍,分贝值增加或下降20;
5. 坐标原点0只是纵坐标的0,横坐标没有0。
南华大学
第四章 系统的频率响应分析
对数相频特性曲线:
∠G(jω)
90° 45°
0
1
10
说明: 1. 横坐标仍然表示ω,仍然按对数均匀分度; 2. 纵坐标为(ω)=∠G(jω),均匀分度; 3.坐标原点0只是纵坐标的0,横坐标没有0。
南华大学
第四章 系统的频率响应分析
5. 用特殊点及趋势或者叠加画对数相频特性曲线。
90 ( )
45
一阶微分环节 2
0
ω1
ω2
-45 惯性环节 1
-90
③ω3
惯性环节
南华大学
第四章 系统的频率响应分析
频率特性的特征量
表征系统动态特性的频域性能指标
零频幅值A(0) 复现频率M与复现带宽0~M 谐振频率r及相对谐振峰值Mr 截止频率b和截止带宽0~b
G
() G( j)
0°
ω
南华大学
第四章 系统的频率响应分析
各典型环节Bode图特点总结:
比例环节 积分环节 微分环节 惯性环节 一阶微分环节 二阶振荡环节 二阶微分环节 延时环节
如何绘制伯德图

2 20 log
A( )
20 log
K
40
K 10
20log K 20log ,
20
当K 1时, 1, L() 0;
20 40
()
1 10 100 K 1
10,L() 20 可见斜率为-20dB/dec 当K 0时, 1, L() 20 log K;
1 10 100
T
2
可见,相角的变化范围从0~180度。
Wednesday, May 29, 2024
17
二阶微分环节的波德图
( )(deg)
180°
1.0
150° 0.7
120° 90°
0.5 0.3 0.2
60° 0.1
30°
0°
L( )(dB)
40dB / Dec
L( ) 20
(dB)
比例环节的bode图
二、典型环节的波德图
⒈ 比例环节:G(s) K, (K 0),G( j) K 幅频特性:A() K;相频特性:() 0
L() / dB
20log K
20log K
20log K
()
180
K 1
K 1 log
0 K 1
对数幅频特性:
0
L() 20lg K 0
0
K 0 log
相频特性:
() K 0
180
Wednesday, May 29, 2024
K 1 K 1 0 K 1
1
积分环节的Bode图
⒉ 积分环节的频率特性:G(s) K
s
频率特性:
G( j )
K
j
K
K
e2
BODE图的讲解(共22张)

1 0.1 ② 2 1
3 5
2
③ 基准线:
1, 20lg 0.032 30dB
斜率 - 20 v 20dB / dec
第14页,共22页。
例1 根据Bode图确定(quèdìng)系统传递函数。
解. 依图有 G(s) K
() G arctan 1 arctan m 90v arctan T1 arctan Tn-v
第10页,共22页。
绘制开环系统Bode图的步骤
⑴ 化G(j)为尾1标准型
⑵ 顺序列出转折频率
例1
G(s)
40(s 0.5) s(s 0.2)( s2 s 1)
100( s 1)
/T 第7页,共22页。
⑹ 振荡(zhèndàng)G环(节s)
n2
s2 2ns n2
G(
j )
1
2 n2
1
j2
n
L( ) 20lg
[1
2 n2
]2
[2
n
]2
( )
arctan 2
n
1 -
2
2 n
1
n
1
n
L() 0
() 0
L( ) 40lg n
() 180
第8页,共22页。
第15页,共22页。
例5 已知 L(),写出G(s),绘制 , G(j)。
解⑴
K( s 1)
G(s) 1
s( s 1)
2
20 log c 20 log 0
2
1
0
1c 2
k1
0
1c 2
⑵ 叠加作图如右
⑶ G( j )
G( j0) 90
如何绘制伯德图PPT课件

是一条斜率为-n×20dB/dec,且在 00
ω =1(弧度/秒)处过零分贝线(ω
0.01 0.1
1
轴)的直线。相频特性是一条与ω 900
无关,值为-n×900且与ω 轴平行的 1800 直线。两个积分环节串联的Bode图
如图5-13所示。
图5-13 两个积分环节串联的Bode图
8
(三) 惯性环节
1
L() dB
40
20
0
0.01 0.1
1
-20
-40
( )
90o
45o
0
0.01 0.1
1
-45o
-90o
10
100
10
100
2
用伯德图分析系统有如下优点: (1) 将幅频特性和相频特性分别作图,使系统(或环
节) 的幅值和相角与频率之间的关系更加清晰;
(2) 幅值用分贝数表示,可将串联环节的幅值相乘变为相 加运算,可简化计算;
一阶微分环节的对数幅频特性如图5-16所示,渐近线的转折频
率 为1,转折频率处渐近特性与精确特性的误差为
,
其误20差lg 均2为正3d分B 贝数,误差范围与惯性环节类似。
相频特性是
当 时, G( j ); arctg
(5-78)
0 G( j0) 00
12
当 1 时,G( j 1) 450 ;
成的折线称为对数幅频特性的渐近线。如图5-14所示。
9
惯性环节的相频特性为
G( j ) arctgT (5-75)
当 0时,G( j0) 00;
当 1 时,G( j 1 ) 450;
5.3 对数频率特性(Bode图)

(5-58)
式中, Li (ω) 和ϕi (ω ) 分别表示各典型环节的对数幅频特性和对数相频特性。 式(5-58)表明,只要能作出 G( jω ) 所包含的各典型环节的对数幅频和对数相频曲线,
将它们进行代数相加,就可以求得开环系统的 Bode 图。实际上,在熟悉了对数幅频特性的
性质后,可以采用更为简捷的办法直接画出开环系统的 Bode 图。具体步骤如下:
5.3 对数频率特性(Bode 图)
5.3.1 典型环节的 Bode 图
1.比例环节
比例环节 G( jω ) = K 的频率特性与频率无关,其对数幅
频特性和对数相频特性分别为
⎧L(ω) = 20 lg K ⎨⎩ϕ(ω) = 0o
(5-50)
相应 Bode 图如图 5-23 所示。
2.微分环节
微分环节 G( jω) = s 的对数幅频特性与对数相频特性
显然,当ω ωn = 1,即ω = ωn 时,是两条渐近线的相交点,所以,振荡环节的自然
频率ωn 就是其转折频率。
振荡环节的对数幅频特性不仅与ω ωn 有关,而且与阻尼比ξ 有关,因此在转折频率附
近一般不能简单地用渐近线近似代替,否则可能引起较大的误差。图 5-27 给出当ξ 取不同 值时对数幅频特性的准确曲线和渐近线,由图可见,当ξ < 0.707 时,曲线出现谐振峰值, ξ 值越小,谐振峰值越大,它与渐近线之间的误差越大。必要时,可以用图 5-28 所示的误
差修正曲线进行修正。
由式(5-55)可知,相角ϕ (ω ) 也是ω ωn 和ξ 的函数,当ω = 0 时,ϕ (ω ) = 0 ;当ω → ∞ 时,ϕ (ω ) = −180o ;当ω = ωn 时,不管ξ 值的大小,ωn 总是等于 − 90o ,而且相频特性 曲线关于 (ωn , − 90°) 点对称,如图 5-27 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电机定位系统校正(BODE图)
MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB^制系统的Bode图,为控制系统设计和分析提供了极大的方便。
1.创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:
J=3.2284e-6;
b=3.5077e-6;
K=0.0274;
R=4;
L=2.75e-6;
num=[0 0 0 K];
den=[(J*K) (J*R+(L*b)) ((b*R)+O2) 0]; my_sys=tf( nu m,de n);
打开Matlab7.0软件,并新建一个空文档,将程序复制到文档内,如图1所示:
图1
2.运行程序并保存运行结果。
如图2所示:
图2
图4
3. 打开 Start-Toolboxes — Control
System — SISO Design Tool
启动SISO Design,如图3所示
4. 将my_sys 程序导入到SISO Design Tool 中, 如图4所示
啪号TW Hi^vicn Toni
P il ■ ErLE ・ Vi, mr r za-ipMi-i k t Dqri £x> al
>
1* E □'l'l. •冷日■丁 11*』]1卜
l>] X o 4 T 11; »M s K 1 m
i
4||'=4Dp
山 watL
a ft — 15-S-IQ Jt 午肌
"■存
-i-s — 15-5-in 上午恥
ny_2F2
c !x|
F L 1« Edu I 上LIM tmp viiK«l&rl 姿kl 尸L C. Tadul
llaJp
II
H n y. L R ann
曲
闻
出田画田田刚
Dur r ■n.l 卫a r nry
CtiaiTijinfl Hi ®f
-15-5-JQ 上牛奔
■■■jip.syg
G ii — 15-5-10 上午和 i
SB (TT = EJS >
尺jgtrt.Hci nr ||T ^ nkm 1rn mfi B * njrtlini
£>■ |si90 ・ui.
fi 1 v f Ja S D .EM 1 色
■'i -Fi'Mii ^mpp+if-slnr
Ci|r TBH.*: n i. B-Bf I arv
^(Bft-olKl fir tiv? for “偷史 俺±&n )埔1口
曲
riw^uefCf rijSr.1
4 fftcrt
图6
5.
在View 菜单中,关闭根轨迹显示,只显示开环的 Bode 图。
如图5所示
-j'K
严为一 L 旷犷10上午欣 ' jy.syft
鼻壬-LE-5-1D ±4=9z
;-■ *y_sj5
'as -iti'r 8 BTO J
(
亘
1Q~
Fr-»*>< icv 「和;汪c
」^i l 5Q CF1 T i^O 1
C ■■ iill . FFI I I H
fVF*inl- PkFA rr n<r 。
尸刑■IjJ'fCn nil i
!~|**U rtH6 Brier fC)
6. 加积分环节;加零点(60角频率)将各个参数进行积分:空白处右键一Add Pole/Zero —Integrator 。
如图6 所示:
> ELSV l?««icri Tutil 匚「陌|IXl
Itl? Eilil K L«JT艶心声注I&ili \5ti伽 felj.
41崑e斗丁鬼二:网壬X打
图6
图8
7. 在 mag nitude 曲线加零点,然后 An alysis 菜单下 Respo nse to Step Comma nd 指令。
如图7所示:
8. 在管理反馈界面中,只显示闭环的r 与y 的关系一LT1 Viewer For SISODesign Tool 界面空白处右键一Systems — Closed Loop : r to u (green ),如图 8 所 示:
4-60
.irn
1*1
□ ILI mr F 「E tJcf'l LI TIE I Q U B l:rp
———_
i
10
呈1- 1
T inpi MC
> 1AT1
□ s 仪丸丄
jll^pwrf
也lifE’l p rH {召eno
弓--'Si i
,l WATlAfl 3时订昨-C
0 ■ ■ 0 好
FSD D««i«
Fll* K&aJl: 姿" 16IWf
经业尸■ ■ Tb-ale 电Lfciw
CuFwit QsfflFiensfflcr
II *11! I -.I
I L
I LS *
鸟| x Q
Ir1
怖艸N3M
I M m h i E'i
驻;三远工
>
Miwrta^Qi
F 卫:・ 3 JOB g F 罪科 * ro-mj 1!
=31 曲 j
图10
9. 添加零点和极点,如图8所示,并移动极点、零点和线的位置,调整LT1 Viewer For SISO Design Tool 窗口中函数图像的变化直到符合 Bode 图,如图9所示:
Fb^jueircy
.Of Wwidtmn »P
|
S3
』LTI Vioer fax 右i.%Q D CD £<11 laol
SS'xi 时
S.L1-V fidLJL Eiw*
WTh (111
ril» Elii N»1F
宝M Q 占忌也|匸;阳I
0当欧g 1品
#'iF^lhid
*Q¥Cd
sdtck^il 陸・l »ro : •】a * -B T
云 砒弋匕E Edktr Fir mrrie d-™r iDPtzr (5
吃 N iTXMl
|j' HQ J'tSfelETl …
IJ1 VlftT f D R T 哎-戶
|
10•用鼠标上下移动观察阶越响应的超调量变化,满足校正要求。
如图
10所示:
7Lla takl Tin
WTiXH.1 EO-TE
A J »
H [;:K Q — p
[二叶■ = I
---- Cyiirri Cbvrpcn: B ^JCT
[ Il * 0-L LWs) 1
1 Si
irU 14
PM ; g
Fiw* iy.4 ■
=TI
1C'
PI 血 sfl-Ti-ns Uz 床tr
幅- n Mill 111 Ij ti :j - A 山,・仆齐 F 口fi pjiita ftr rmilaRcE 口ggctH
3 Ed-i -
——丄巾杏霍.fiCrnerritfCir
如土 >
d - o c 11 小
GM 19.6 :«
I - I -! -»■
宝■止OOP
Lil vbMQf
r | L"i |. | +
IE
两汨点旳(FWI^WJ
Wnridkmns- XP IPrcHI»Mi?Ml
)M&TLXP
11从 analysi 厂closed loopbode 调用 LTI viewer 分析闭环 BODE 图。
如图 11 所示:
通过Bode 图,可以直观的看出系统的幅值/增益随频率变化的特性 及相位 随频特变化的特性。
幅频特性和相频特性是频率域分析最重要的两个参数,系统 的表现如何、是否稳定,几乎完全依赖于这两个特性,因此,分析系统内部的各 部分的Bode 图,就是进行稳定性分析,并根据规则和准则,改变系统参数,设 计出符合要求的稳定的系统。
一个元件、一个网络、一个子系统,只要有输入和 输出,就有对应的幅频和相频特性,就可以做出 Bode 图。
LTI 帖丹叭
由 hM- l iime Ucddh?
J
rujuc
Zdj M - C :\...
|^|17I Vi w^r f m
a 槪片12--M
lilt- Jd: t fjri 己卉 Help D 岂鱼負£
・ JIXI
liTJL Viewex I PI SlliO J .KDL T OO 止 Tl fr-'£<
U -1UJ -2££l 0 a -feo -F-D
B J -J I C'HJUT
ia
a
-ff..BF=IAJ^=£€ ■
ID*
I lMJijenEV llfiQt-vj
图11。
