题型五特殊四边形的动态探究题
09专题五 特殊四边形的动态探究题(PPT课件)

方法指导
把所求线段转化到直角三角形中,再结合已知条件,求出 相关线段的长度,利用勾股定理或锐角三角函数建立等量 关系式进行求解;④检验所求线段的长度是否满足题意; 二是:先判断动点在什么位置时几何图形为特殊图形;再 结合题干信息和特殊图形判定,证明动点在该位置时是特 殊图形;最后根据特殊图形的性质进行求解.
10.又∵BD=CD,∴CD=5.在Rt△DFC中,CF=CD·cos60°
=5 .
2
②解:100.
【解法提示】∵AB=AC,AD⊥BC,∴BD= 1 2
BC=2
5,
∴AD= AB2BD2=4 5,∵AB是⊙O的直径,∴∠AEB=
∠ADB=90°,∴∠ADC=90°,∵∠ACB=∠ACB,
∴△ACD∽△BCE,∴
•10、阅读一切好书如同和过去最杰出的人谈话。2021/9/122021/9/122021/9/129/12/2021 10:30:56 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/122021/9/122021/9/12Sep-2112-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/122021/9/122021/9/12Sunday, September 12, 2021
中考专题数学解答组特殊四边形的动态探究

故答案为2 .
特殊四边形
1.如图,在菱形ABCD中,AB=2,∠DAB=60∘,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为时,四边形AMDN是矩形;
②当AM的值为时,四边形AMDN是菱形.
解答:
∴△ABE≌△CDF(ASA).
(2)当BC=6 时,四边形AECF是菱形.
理由:在Rt△ADC中,∵AD=BC=6 ,DC=6,
∴tan∠DAC=CD:AD= ,
∴∠DAC=30∘,∠ACD=60∘,
∴∠ACF=∠DCF=30∘,
∴DF=CD·tan30∘=2 ,
∴CF=2DF=4 ,AF=AD−DF=6 −2 =4 ,
③∠EFD=90∘时,此种情况不存在.
故当t= 秒或4秒时,△DEF为直角三角形.
3.矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6.
(1)证明:△ABE≌△CDF;
(2)填空:①当BC=时,四边形AECF为菱形;
∴AF=CF,
∵△ABE≌△CDF,
∴BE=DF,
∵AD=BC,
∴AF=CE,
∵AF∥EC,
∴四边形AECF是平行四边形,
∵AF=FC,
∴四边形AECF是菱形.
故答案为6 .
(3)当AN=NE时,∵四边形AECF是菱形,
∴OA=OC,
∴ON∥EC,
∵AN=NE,EM=CM,
∴NM∥AC,
∴四边形ONMC是平行四边形,
题型五 特殊四边形的动态探究题

题型五 特殊四边形的动态探究题试题演练1. 如图,AD 是⊙O 的直径,AD =2BD ,点C 是ACD ︵上的不与A 、D 重合的动点,连接BC ,BA ,AC .(1)求∠ACB 的度数; (2)填空:已知⊙O 半径为4.①当l CD ︵=________时,四边形OBDC 是菱形; ②当l CD ︵=________时,四边形ABDC 是矩形.2. 如图,在Rt △ABC 中,∠ACB =90°,以点A 为圆心,AC 为半径作⊙A ,交AB 于点D ,交CA 的延长线于点E ,过点E 作EF ∥AB 交⊙A 于点F ,连接AF ,BF ,DF . (1)求证:△ABC ≌△ABF ; (2)填空:①当∠CAB 等于______时,四边形ACBF 为正方形; ②当∠CAB 等于________时,四边形ADFE 为菱形.3. (’15郑州模拟)如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°,点C 是AB ︵上异于A 、B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E ,连接DE ,点G 、H 在线段DE 上,且DG =GH =HE .(1)当点C 在AB ︵上运动时,在CD 、CG 、DG 中,长度不变的线段是________,该线段的长度是________;(2)求证:四边形OGCH 是平行四边形; (3)当OD =________时,四边形OGCH 是菱形.4. 如图,CD 是△ABC 的中线,点E 是AF 的中点,CF ∥AB . (1)求证:CF =AD ;(2)若已知AB =10,AC =6,填空:①当BC 长为________时,四边形BFCD 是矩形; ②当BC 长为________时,四边形BFCD 是菱形.5. 如图,在矩形ABCD中,AB=13 cm,AD=4 cm,点E、F同时分别从D、B两点出发,以1 cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).(1)求证:四边形EGFH是平行四边形.(2)填空:①当t为________s时,四边形EGFH是菱形;②当t为________s时,四边形EGFH是矩形.6. 如图,已知Rt△ABC中,∠C=90°,AC=8 cm,BC=6 cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,P,Q运动速度均为2 cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t (单位:s)(0≤t≤4)解答下列问题:(1)在点P,Q运动过程中,平行四边形AQPD的面积是否具有最大值,若有,请求出它的最大值;否则,请说明理由.(2)填空:①当t的值为________s时,平行四边形AQPD为矩形;②当t的值为________s时,平行四边形AQPD为菱形.7. (’15平顶山模拟)如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG;(2)填空:①若∠B=60°,当BC=________AB时,四边形ABFG是菱形;②若∠B=60°,当BC=________AB时,四边形AECG是正方形.8. 如图,在平行四边形ABCD中,对角线BD=8 cm,AC=4 cm,点E从点B出发沿BD方向以1 cm/s的速度向点D运动,同时点F从点D出发沿DB方向以同样的速度向点B运动,设点E、F运动的时间为t(s),其中0<t<8.(1)求证:△BEC≌△DF A;(2)填空:①以点A、C、E、F为顶点的四边形一定是________形;②当t的值为________时,以点A、C、E、F为顶点的四边形为矩形.【答案】1. 解:(1)∵AD 是⊙O 的直径, ∴∠ABD =90°, ∵AD =2BD ,∴在Rt △ABD 中,cos ∠D =BD AD =BD 2BD =12, ∴∠D =60°, ∴∠ACB =∠D =60°;(2)①4π3;②8π3.【解法提示】①当BC ⊥OD 时,∵OB =OD =BD ,∴OE =DE ,∵OD 是半径,BC 是弦,∴BE =CE ,∴四边形OBDC 是菱形,则OD =CD =OC ,∴∠COD =60°,∴lCD ︵=60 π×4180=4π3;②当BC 经过圆心O 时,易得四边形ABDC 是矩形,△AOC 为等边三角形,∴∠COD =180°-60°=120°,∵l CD =120 π×4180=8π3.2. 【思路分析】(1)首先利用平行线的性质得到∠F AB =∠CAB ,然后利用SAS 证得两三角形全等即可;(2)①当∠CAB =45°时,四边形ACBF 为正方形.∠F AB =∠CAB =45°,进而∠F AC =∠AFB =∠ACB =90°,四边形ACBF 为矩形,再由邻边AC =AF 得其为正方形;②当∠CAB =60°时,四边形ADFE 为菱形.根据∠CAB =60°,得到∠F AB =∠AFE =∠CAB =∠AEF =60°,从而得到EF =AD =AE ,利用邻边相等的平行四边形是菱形进行判断.解:(1)证明:∵EF ∥AB , ∴∠E =∠CAB ,∠EF A =∠F AB , ∵∠E =∠EF A , ∴∠F AB =∠CAB , 又∵AF =AC ,AB =AB , ∴△ABC ≌△ABF (SAS); (2)①45° ②60°【解法提示】①当∠CAB =45°时,由(1)知,∠F AB =∠CAB =45°,∠F AC =∠AFB =∠ACB =90°,故四边形ACBF 为矩形,又∵AC =AF ,∴四边形ACBF 为正方形.②当∠CAB =60°时,易得∠F AB =∠AFE =∠CAB =∠AEF =60°,从而得到△AEF 和△ADF 均为等边三角形,∴EF =AD =AE =DF , ∴四边形ADFE 为菱形.3. 【思路分析】(1)由于四边形ODCE 是矩形,而矩形的对角线相等,所以DE =OC ,而CO 是圆O 的半径,这样DE 的长度不变,也就DG 的长度不变;(2)连接OC ,容易根据已知条件证明四边形ODCE 是矩形,然后利用其对角线互相平分和DG =GH =HE ,可以知道四边形CHOG 的对角线互相平分,从而判定其是平行四边形;(3)若四边形OGCH 是菱形,必有OC 与GH 垂直,即可推得DE 、OC 垂直、平分且相等,故得到四边形CDOE 是正方形,在Rt △OCD 中,利用OC =OA =3,OD =CD 运用勾股定理即可求出OD 的长.解:(1)DG ,1.【解法提示】在矩形ODCE 中,DE =OC =3,∵DG =GH =HE ,∴DG =13DE =1.(2)连接OC 交DE 于M .由矩形得OM =CM ,EM =DM .∵DG =HE ,∴EM -EH =DM -DG ,∴HM =MG .∴四边形OGCH 是平行四边形. (3)32 2. 【解法提示】∵四边形OGCH 是菱形,∴OC ⊥GH ,∴OC ⊥DE ,又∵OC =DE ,CM =OM =EM =DM ,∴四边形CDOE 是正方形.∴CD =OD ,∠CDO =90°,∵OA =OC =3,∴OD 2+CD 2=9,2OD 2=9,OD =322.4. 【思路分析】(1)易得DE 是△ABF 的中位线,进而DE //BF ,结合CF ∥AB ,证得四边形BFCD 是平行四边形,从而得到CF =BD =AD ;(2)①当CD ⊥AB ,即CD 是AB 的中垂线时,平行四边形BFCD 有一个角为直角是矩形,此时AC =BC =6;②当∠ACB =90°,CD是直角三角形斜边上的中线,可得CD =AD =BD ,从而平行四边形BFCD 的邻边相等是菱形,此时由勾股定理易得BC 的长.解:(1)证明:∵CD 是△ABC 的中线,点E 是AF 的中点, ∴AD =BD ,AE =FE , ∴DE ∥BF , ∵CF ∥AB ,∴四边形BFCD 是平行四边形, ∴CF =BD , ∴CF =DA . (2)①6 ②8【解法提示】①当CD ⊥AB ,即CD 是AB 的中垂线时,∠CDB =90°,平行四边形BFCD 有一个角为直角是矩形,此时AC =BC =6;②当∠ACB =90°时,CD 是直角△ABC 斜边上的中线,∴CD =AD =BD ,从而平行四边形BFCD 的邻边相等是菱形,此时由勾股定理易得BC =8.5. 【思路分析】(1)易证△ADE ≌△CBF ,进而易得GE ∥HF ,且GE =HF ,所以四边形EGFH 是平行四边形.(2)①四边形EGFH 是菱形,G 是AE 的中点,则GF =GE =GA =12AE ,得到∠AFE =90°,根据DE =AF ,列方程求解;②四边形EGFH 是矩形,易得△ADE ∽△EHC ,则根据AE EC =DECH列方程求解即可.解:(1)∵四边形ABCD 是矩形,∴∠D =∠B =90°,AD =CB ,∵点E 、F 同时分别从D 、B 两点出发,以1 cm/s 的速度沿DC 、BA 向终点C 、A 运动, ∴DE =BF ,∴△ADE ≌△CBF (SAS), ∴AE =CF ,∠DEA =∠EAF =∠CFB , ∵点G 、H 分别为AE 、CF 的中点, ∴GE ∥HF ,且GE =HF ,∴四边形EGFH 是平行四边形.(2)① 132;②8或23.【解法提示】连接EF ,∵四边形EGFH 是菱形,G 是AE 的中点.∴GF =GE =GA =12AE ,∴EF ⊥AB ,∴DE =AF ,∴t =13-t ,∴t =132.②∵四边形EGFH 是矩形,∴∠D =∠EHC =∠AEH =90°,∴∠AED +∠HEC =∠ECH +∠HEC =90°,∴∠AED =∠ECH ,∴△ADE ∽△EHC ,∴AE EC =DE CH ,∴42+t 213-t =t 1242+t 2,解得:t 1=8,t 2=23. 6. 【思路分析】(1)首先利用勾股定理求得AB =10,然后表示出AP ,过P 作PH ⊥AC 于H ,利用△APH ∽△ABC ,利用相似三角形对应边的比相等,表示出AH 的长,然后由平行四边形面积公式,得到平行四边形AQPD 的面积的二次函数表达式,用配方法求最值;(2)①利用矩形的性质得到△APQ ∽△ABC ,利用相似三角形对应边的比相等列出比例式即可求得t 值;②利用菱形的性质得到△AEQ ∽△ACB ,利用相似三角形对应边的比相等列出比例式即可求得t 值.解:(1)∵Rt △ABC 中,∠C =90°,AC =8cm ,BC =6cm , ∴AB =10cm , ∵BP =2t cm ,∴AP =AB -BP =10-2 t ,过P 作PH ⊥AC 于H ,则PH ∥BC , ∴△APH ∽△ABC ,∴PH BC =AP AB ,即PH 6=10-2t 10, ∴PH =35(10-2t ).∵S ▱AQPD =AQ ·PH =2t ·35·(10-2t )=-125t 2+12t =-125(t -52)2+15,∴当t =52s 时,平行四边形AQPD 的面积具有最大值,为15.(2)①209;②2513. 【解法提示】①当▱AQPD 是矩形时,PQ ⊥AC ,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AQ AP=AC AB ,即2t 10-2t =810,解得t =209.∴当t =209时,▱AQPD 是矩形;②当▱AQPD 是菱形时,DQ ⊥AP ,则 △AEQ ∽△ACB ,∴AE AQ =AC AB ,即5-t 2t =810,解得t =2513.∴当t =2513时,▱AQPD是菱形.7. 【思路分析】(1)根据平行四边形和平移的性质得到AB =CD ,AE =CG ,再证明Rt △ABE ≌Rt △CDG 可得到BE =DG ;(2)①要使四边形ABFG 是菱形,须使AB =BF ;根据条件找到满足AB =BF 时,BC 与AB 的数量关系即可; ②当四边形AECG 是正方形时,AE=EC ,由AE =32AB ,可得EC =32AB ,再有BE =12AB 可得BC =3+12AB .解:(1)证明:∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AB =CD .∵AE 是BC 边上的高,且CG 是由AE 沿BC 方向平移而成, ∴CG ⊥AD ,AE =CG , ∴∠AEB =∠CGD =90°.∵在Rt △ABE 与Rt △CDG 中,AE =CG ,AB =CD , ∴Rt △ABE ≌Rt △CDG (HL), ∴BE =DG .(2)①32;②3+12.【解法提示】①当BC =32AB 时,四边形ABFG 是菱形.证明:∵AB ∥GF ,AG ∥BF ,∴四边形ABFG 是平行四边形.∵Rt △ABE 中,∠B =60°,∴∠BAE =30°,∴BE =12AB ,∵BE =CF ,BC =32AB ,∴EF =12AB .∴AB =BF .∴四边形ABFG 是菱形.②BC =3+12AB 时,四边形AECG 是正方形.∵AE ⊥BC ,GC ⊥CB ,∴AE ∥GC ,∠AEC =90°,∵AG ∥CE ,∴四边形AECG 是矩形,当AE =EC 时,矩形AECG 是正方形,∵∠B =60°,∴EC =AE =AB ·sin60°=32AB ,BE =12AB ,∴BC =3+12AB .8. 解:(1)证明:∵四边形ABCD 是平行四边形, ∴AD =BC ,AD ∥BC , ∴∠EBC =∠FDA .在△BEC 和△DF A 中, ⎩⎪⎨⎪⎧BE =DF ,∠EBC =∠FDA ,BC =DA ,∴△BEC ≌△DF A . (2)①平行四边形;②2或6.【解法提示】①平行四边形,理由如下:连接CF ,AE ,由(1)得:∠BEC =∠DF A ,EC =AF ,∴∠FEC =∠AFE ,即EC ∥AF ,∴以点A 、C 、E 、F 为顶点的四边形一定是平行四边形.②2或6,理由如下:∵四边形AECF 为矩形,∴AC =EF ,∵BD =8cm ,AC =4cm ,∴EF =4,BE =2cm 或6cm. ∵速度为1cm/s ,∴t =2或6.。
题型五特殊四边形的动态探究题

题型五特殊四边形的动态探究题试题演练1.如图.初是00的直径,AD=2BD、点C是忌9上的不与乩〃重合的动点,连接处胡,AC.(1)求①的度数;(2)填空:已知00半径为4.①当兀=_ _ —时,四边形处Z疋是菱形;②当龙= ________ 时,四边形力宓是矩形.1)第1题图2.如图,在RtA/l^r中,Z/16»=90o,以点力为圆心,/1C为半径作0儿交/仿于点0交0的延长线于点呂过点F作济'〃.個交O力于点尸,连接力尸,BF, DF.(1)求证:'ABC仝HABF;(2)填空:①当矽等于时,四边形川物为正方形;②当A CAB等于—时,四边形皿应为菱形.第2题图3. C 15模拟)如图,扇形。
矽的半径创=3,圆心角Z/k刃=90°,点C是壶上异于小B 的动点,过点C作CDLOA于点、D,作CE丄OB于点、E,连接甌,点0、〃在线段处上,且DG= GH= HE.(1)当点C在舫上运动时,在⑵CG、加中,长度不变的线段是 ___________ ,该线段的长度是(2)求证:四边形切/是平行四边形;⑶当「时,四边形宓7是菱形.第3题图4.如图.09是△/!%的中线,点E是仰的中点,CF//AB.(1)求证:CF=AD;(2)若已知丿仿=10, /亿、=6,填空:①当腮长为时,四边形以d是矩形;②当腮长为时,四边形刃乙9是菱形.B F第4题图5.如图,在矩形/怡仞中,初=13 cm, AD=4 cm,点£尸同时分别从〃、〃两点出发,以1 cm/s的速度沿化、朋向终点G M运动,点G、〃分别为处;倂'的中点,设运动时间为“s).(1)求证:四边形财〃是平行四边形.(2)填空:①当r为s时,四边形财〃是菱形;②当r为s时,四边形昭〃是矩形.第5题图6.如图,已知RtZkM%中,ZC=90° , AC=8 cm,仇=6 cm.点戶由〃出发沿胡方向向点月匀速运动,同时点0由月出发沿月C方向向点C匀速运动,P、0运动速度均为2 cm/s. 以力0、〃为边作平行四边形AQPD、连接他,交/矽于点£设运动的时间为七(单位:s)(0£W4)解答下列问題:(1)在点只0运动过程中,平行四边形力旳的面积是否具有最大值,若有,请求出它的最大值;否则,请说明理由.(2)填空:①当r的值为s时,平行四边形月如为矩形;②当r的值为s时,平行四边形/K溜为菱形.第6题图7. C 15模拟)如图,在平行四边形丽仞中,处是腮边上的高,将△/!滋沿腮方向平移,使点E与点C重合,得△矶(1)求证:BE=DG;(2)填空:①若ZB=60。
专题5 特殊平行四边形的动点问题

专题5特殊平行四边形的动点问题类型一、一般动点问题【例1】如图,在Rt ABC ∆中,90,60B AC ∠=︒=cm,60A ∠=︒,点D 从点C 出发沿CA 方向以4cm/s 的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以2cm/s 的速度向点B 匀速运动.当其中一个点到达终点时,另一个点也随之停止运动.设点,D E 运动的时间是t s (015)t <≤.过点D 作DF BC ⊥于点F ,连接,DE EF .(1)求证:AE=DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值,如果不能,说明理由;(3)当t 为何值时,△DEF 为直角三角形?请说明理由.【解答】(1)证明:根据题意可知CD=4t ,AE=2t ,∵∠B=90°,∠A=60°,∴∠C=30°,∴DF=21DC=2t.∵AE=2t ,DF=2t ,∴AE=DF.(2)能.理由如下:∵AB ⊥BC ,DF ⊥BC ,∴AE ∥DF.∵AE=DF ,AE ∥DF ,∴四边形AEFD 为平行四边形,∴要使平行四边形AEFD 为菱形,则需AE=AD ,即2t=60-4t ,解得t=10,∴当t=10时,四边形AEFD 为菱形.(3)根据题意可知需分∠EDF=90°或∠DEF=90°两种情况讨论.①当∠EDF=90°时,∵∠EDF=∠B=∠DFE=90°,∴四边形DEBF 是矩形,∴∠DEB=90°,∴∠AED=90°.∵∠AED=90°,∠A=60°,∴∠ADE=30°.∵∠AED=90°,∠ADE=30°,∴AD=2AE ,即60-4t=4t ,解得t=215.②当∠DEF=90°时,∵四边形AEFD 为平行四边形,∴EF ∥AD ,∴∠ADE=∠DEF=90°.∵∠ADE=90°,∠A=60°,∴AD=21AE ,即60-4t=21×2t ,解得t=12.综上所述,当t=215或12时,△DEF 为直角三角形.【例2】如图在平面直角坐标系中,A (16,0)、C (0,8),四边形OABC 是矩形,D 、E 分别是OA 、BC 边上的点,沿DE 折叠矩形,点A 恰好落往y 轴上的点C 处,点B 落B '处。
题型五c特殊四边形的动态探究题

题型五 特殊四边形的动态探究题试题演练1. 如图,AD 是⊙O 的直径,AD =2BD ,点C 是ACD ︵上的不与A 、D 重合的动点,连接BC ,BA ,AC .(1)求∠ACB 的度数;(2)填空:已知⊙O 半径为4.①当l CD ︵=________时,四边形OBDC 是菱形;②当l CD ︵=________时,四边形ABDC 是矩形.2. 如图,在Rt △ABC 中,∠ACB =90°,以点A 为圆心,AC 为半径作⊙A ,交AB 于点D ,交CA 的延长线于点E ,过点E 作EF ∥AB 交⊙A 于点F ,连接AF ,BF ,DF .(1)求证:△ABC ≌△ABF ;(2)填空:①当∠CAB 等于______时,四边形ACBF 为正方形;②当∠CAB 等于________时,四边形ADFE 为菱形.3. (’15模拟)如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°,点C 是AB ︵上异于A 、B的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E ,连接DE ,点G 、H 在线段DE 上,且DG =GH =HE .(1)当点C 在AB ︵上运动时,在CD 、CG 、DG 中,长度不变的线段是________,该线段的长度是________;(2)求证:四边形OGCH 是平行四边形;(3)当OD =________时,四边形OGCH 是菱形.4. 如图,CD 是△ABC 的中线,点E 是AF 的中点,CF ∥AB .(1)求证:CF =AD ;(2)若已知AB =10,AC =6,填空:①当BC 长为________时,四边形BFCD 是矩形;②当BC 长为________时,四边形BFCD 是菱形.5. 如图,在矩形ABCD中,AB=13 cm,AD=4 cm,点E、F同时分别从D、B两点出发,以1 cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).(1)求证:四边形EGFH是平行四边形.(2)填空:①当t为________s时,四边形EGFH是菱形;②当t为________s时,四边形EGFH是矩形.6. 如图,已知Rt△ABC中,∠C=90°,AC=8 cm,BC=6 cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,P,Q运动速度均为2 cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4)解答下列问题:(1)在点P,Q运动过程中,平行四边形AQPD的面积是否具有最大值,若有,请求出它的最大值;否则,请说明理由.(2)填空:①当t的值为________s时,平行四边形AQPD为矩形;②当t的值为________s时,平行四边形AQPD为菱形.7. (’15模拟)如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG;(2)填空:①若∠B=60°,当BC=________AB时,四边形ABFG是菱形;②若∠B=60°,当BC=________AB时,四边形AECG是正方形.8. 如图,在平行四边形ABCD中,对角线BD=8 cm,AC=4 cm,点E从点B出发沿BD方向以1 cm/s的速度向点D运动,同时点F从点D出发沿DB方向以同样的速度向点B运动,设点E、F运动的时间为t(s),其中0<t<8.(1)求证:△BEC≌△DF A;(2)填空:①以点A、C、E、F为顶点的四边形一定是________形;②当t的值为________时,以点A、C、E、F为顶点的四边形为矩形.【答案】1. 解:(1)∵AD 是⊙O 的直径,∴∠ABD =90°,∵AD =2BD ,∴在Rt △ABD 中,cos ∠D =BD AD =BD 2BD =12,∴∠D =60°,∴∠ACB =∠D =60°;(2)①4π3;②8π3.【解法提示】①当BC ⊥OD 时,∵OB =OD =BD ,∴OE =DE ,∵OD 是半径,BC 是弦,∴BE =CE ,∴四边形OBDC 是菱形,则OD =CD =OC ,∴∠COD =60°,∴lCD ︵=60 π×4180=4π3;②当BC 经过圆心O 时,易得四边形ABDC 是矩形,△AOC 为等边三角形,∴∠COD =180°-60°=120°,∵l CD =120 π×4180=8π3.2. 【思路分析】(1)首先利用平行线的性质得到∠FAB =∠CAB ,然后利用SAS 证得两三角形全等即可;(2)①当∠CAB =45°时,四边形ACBF 为正方形.∠F AB =∠CAB =45°,进而∠F AC =∠AFB =∠ACB =90°,四边形ACBF 为矩形,再由邻边AC =AF 得其为正方形;②当∠CAB =60°时,四边形ADFE 为菱形.根据∠CAB =60°,得到∠FAB =∠AFE =∠CAB =∠AEF =60°,从而得到EF =AD =AE ,利用邻边相等的平行四边形是菱形进行判断.解:(1)证明:∵EF ∥AB ,∴∠E =∠CAB ,∠EFA =∠FAB ,∵∠E =∠EF A ,∴∠FAB =∠CAB ,又∵AF =AC ,AB =AB ,∴△ABC ≌△ABF (SAS);(2)①45° ②60°【解法提示】①当∠CAB =45°时,由(1)知,∠F AB =∠CAB =45°,∠FAC =∠AFB =∠ACB =90°,故四边形ACBF 为矩形,又∵AC =AF ,∴四边形ACBF 为正方形.②当∠CAB =60°时,易得∠FAB =∠AFE =∠CAB =∠AEF =60°,从而得到△AEF 和△ADF 均为等边三角形,∴EF =AD =AE =DF , ∴四边形ADFE 为菱形.3. 【思路分析】(1)由于四边形ODCE 是矩形,而矩形的对角线相等,所以DE =OC ,而CO 是圆O 的半径,这样DE 的长度不变,也就DG 的长度不变;(2)连接OC ,容易根据已知条件证明四边形ODCE 是矩形,然后利用其对角线互相平分和DG =GH =HE ,可以知道四边形CHOG 的对角线互相平分,从而判定其是平行四边形;(3)若四边形OGCH 是菱形,必有OC 与GH 垂直,即可推得DE 、OC 垂直、平分且相等,故得到四边形CDOE 是正方形,在Rt △OCD 中,利用OC =OA =3,OD =CD 运用勾股定理即可求出OD 的长.解:(1)DG ,1.【解法提示】在矩形ODCE 中,DE =OC =3,∵DG =GH =HE ,∴DG =13DE =1.(2)连接OC 交DE 于M .由矩形得OM =CM ,EM =DM .∵DG =HE ,∴EM -EH =DM -DG ,∴HM =MG .∴四边形OGCH 是平行四边形.(3)322. 【解法提示】∵四边形OGCH 是菱形,∴OC ⊥GH ,∴OC ⊥DE ,又∵OC =DE ,CM =OM =EM =DM ,∴四边形CDOE 是正方形.∴CD =OD ,∠CDO =90°,∵OA =OC =3,∴OD 2+CD 2=9,2OD 2=9,OD =32 2.4. 【思路分析】(1)易得DE 是△ABF 的中位线,进而DE //BF ,结合CF ∥AB ,证得四边形BFCD 是平行四边形,从而得到CF =BD =AD ;(2)①当CD ⊥AB ,即CD 是AB 的中垂线时,平行四边形BFCD 有一个角为直角是矩形,此时AC =BC =6;②当∠ACB =90°,CD 是直角三角形斜边上的中线,可得CD =AD =BD ,从而平行四边形BFCD 的邻边相等是菱形,此时由勾股定理易得BC 的长.解:(1)证明:∵CD 是△ABC 的中线,点E 是AF 的中点,∴AD =BD ,AE =FE ,∴DE ∥BF ,∵CF ∥AB ,∴四边形BFCD 是平行四边形,∴CF =BD ,∴CF =DA .(2)①6 ②8【解法提示】①当CD ⊥AB ,即CD 是AB 的中垂线时,∠CDB =90°,平行四边形BFCD 有一个角为直角是矩形,此时AC =BC =6;②当∠ACB =90°时,CD 是直角△ABC 斜边上的中线,∴CD =AD =BD ,从而平行四边形BFCD 的邻边相等是菱形,此时由勾股定理易得BC =8.5. 【思路分析】(1)易证△ADE ≌△CBF ,进而易得GE ∥HF ,且GE =HF ,所以四边形EGFH 是平行四边形.(2)①四边形EGFH 是菱形,G 是AE 的中点,则GF =GE =GA =12AE ,得到∠AFE =90°,根据DE =AF ,列方程求解;②四边形EGFH 是矩形,易得△ADE ∽△EHC ,则根据AE EC =DE CH 列方程求解即可.解:(1)∵四边形ABCD 是矩形,∴∠D =∠B =90°,AD =CB ,∵点E 、F 同时分别从D 、B 两点出发,以1 cm/s 的速度沿DC 、BA 向终点C 、A 运动, ∴DE =BF ,∴△ADE ≌△CBF (SAS),∴AE =CF ,∠DEA =∠EAF =∠CFB ,∵点G 、H 分别为AE 、CF 的中点,∴GE ∥HF ,且GE =HF ,∴四边形EGFH 是平行四边形.(2)① 132;②8或23. 【解法提示】连接EF ,∵四边形EGFH 是菱形,G 是AE 的中点.∴GF =GE =GA =12AE ,∴EF ⊥AB ,∴DE =AF ,∴t =13-t ,∴t =132. ②∵四边形EGFH 是矩形,∴∠D =∠EHC =∠AEH =90°,∴∠AED +∠HEC =∠ECH +∠HEC =90°,∴∠AED =∠ECH ,∴△ADE ∽△EHC ,∴AE EC =DE CH ,∴42+t 213-t =t 1242+t2,解得:t 1=8,t 2=23.6. 【思路分析】(1)首先利用勾股定理求得AB =10,然后表示出AP ,过P 作PH ⊥AC 于H ,利用△APH ∽△ABC ,利用相似三角形对应边的比相等,表示出AH 的长,然后由平行四边形面积公式,得到平行四边形AQPD 的面积的二次函数表达式,用配方法求最值;(2)①利用矩形的性质得到△APQ ∽△ABC ,利用相似三角形对应边的比相等列出比例式即可求得t 值;②利用菱形的性质得到△AEQ ∽△ACB ,利用相似三角形对应边的比相等列出比例式即可求得t 值.解:(1)∵Rt △ABC 中,∠C =90°,AC =8cm ,BC =6cm ,∴AB =10cm ,∵BP =2t cm ,∴AP =AB -BP =10-2 t ,过P 作PH ⊥AC 于H ,则PH ∥BC , ∴△APH ∽△ABC ,∴PH BC =AP AB ,即PH 6=10-2t 10,∴PH =35(10-2t ).∵S ▱AQPD =AQ ·PH =2t ·35·(10-2t )=-125t 2+12t =-125(t -52)2+15, ∴当t =52s 时,平行四边形AQPD 的面积具有最大值,为15.(2)①209;②2513. 【解法提示】①当▱AQPD 是矩形时,PQ ⊥AC ,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AQ AP =AC AB ,即2t 10-2t =810,解得t =209.∴当t =209时,▱AQPD 是矩形;②当▱AQPD 是菱形时,DQ ⊥AP ,则 △AEQ ∽△ACB ,∴AE AQ =AC AB ,即5-t 2t =810,解得t =2513.∴当t =2513时,▱AQPD是菱形.7. 【思路分析】(1)根据平行四边形和平移的性质得到AB =CD ,AE =CG ,再证明Rt △ABE ≌Rt △CDG 可得到BE =DG ;(2)①要使四边形ABFG 是菱形,须使AB =BF ;根据条件找到满足AB =BF 时,BC 与AB 的数量关系即可; ②当四边形AECG 是正方形时,AE =EC ,由AE =32AB ,可得EC =32AB ,再有BE =12AB 可得BC =3+12AB . 解:(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB =CD .∵AE 是BC 边上的高,且CG 是由AE 沿BC 方向平移而成,∴CG ⊥AD ,AE =CG ,∴∠AEB =∠CGD =90°.∵在Rt △ABE 与Rt △CDG 中,AE =CG ,AB =CD ,∴Rt △ABE ≌Rt △CDG (HL),∴BE =DG .(2)①32;②3+12.【解法提示】①当BC =32AB 时,四边形ABFG 是菱形. 证明:∵AB ∥GF ,AG ∥BF ,∴四边形ABFG 是平行四边形.∵Rt △ABE 中,∠B =60°,∴∠BAE =30°,∴BE =12AB , ∵BE =CF ,BC =32AB ,∴EF =12AB .∴AB =BF .∴四边形ABFG 是菱形. ②BC =3+12AB 时,四边形AECG 是正方形.∵AE ⊥BC ,GC ⊥CB ,∴AE ∥GC ,∠AEC =90°,∵AG ∥CE ,∴四边形AECG 是矩形,当AE =EC 时,矩形AECG 是正方形,∵∠B =60°,∴EC =AE =AB ·sin60°=32AB ,BE =12AB ,∴BC =3+12AB .8. 解:(1)证明:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∴∠EBC =∠FDA .在△BEC 和△DFA 中, ⎩⎨⎧BE =DF ,∠EBC =∠FDA ,BC =DA ,∴△BEC ≌△DFA .(2)①平行四边形;②2或6.【解法提示】①平行四边形,理由如下:连接CF ,AE ,由(1)得:∠BEC =∠DF A ,EC =AF ,∴∠FEC =∠AFE ,即EC ∥AF ,∴以点A 、C 、E 、F 为顶点的四边形一定是平行四边形.②2或6,理由如下:∵四边形AECF 为矩形,∴AC =EF ,∵BD =8cm ,AC =4cm ,∴EF =4,BE =2cm 或6cm.∵速度为1cm/s ,∴t =2或6.。
09专题五 特殊四边形的动态探究题(word版习题)

专题五 特殊四边形的动态探究题(2019、2019、2019.18、2019、2019.17;2019.22;2019.19;2009.21) 试题演练1. 如图,在△OAB 中,OA =OB ,以点O 为圆心的⊙O 经过AB 的中点C ,直线AO 与⊙O 相交于点E 、D ,OB 交⊙O 于点F ,P 是DF ︵的中点,连接CE 、CF 、BP .(1)求证:AB 是⊙O 的切线. (2)若OA =4,则①当DP ︵长为________时,四边形OECF 是菱形; ②当DP ︵长为________时,四边形OCBP 是正方形.第1题图2. 如图,AB 是⊙O 的直径,点P 是⊙O 上不与A ,B 重合的一个动点,延长P A 到点C ,使AC =AP ,点D 为⊙O 上一点,且满足AD ∥PB ,射线CD 交PB 延长线于点E .(1)求证:△P AB ≌△ACD ; (2)填空:①若AB =6,则四边形ABED 的最大面积为____________;②若射线CD 与⊙O 的另一个交点为F ,连接OF ,则当∠P AB 的度数为________时,以O ,A ,D ,F 为顶点的四边形为菱形.第2题图 3. 如图,已知▱ABCD 中,AD =8 cm ,AB =10 cm ,BD =12 cm.点P 从点A 出发,以1 cm/s 的速度向点B 运动,同时点Q 从点C 出发以相同的速度向点D 运动.设运动时间为t .(1)连接DP 、BQ ,求证:DP =BQ ;(2)填空:①当t为______s时,四边形PBQD是矩形;②当t为______s时,四边形PBQD是菱形.第3题图4.如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于点F,连接OC,AF.(1)求证:△COD≌△BOD;(2)填空:①当∠1=________时,四边形OCAF是菱形;②当∠1=________时,AB=22OD.第4题图5. (2019濮阳模拟)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与斜边AB交于点D,E为BC边的中点,连接DE.(1)求证:DE是⊙O的切线;(2)填空:①若∠B=30°,AC=23,则DE=________;②当∠B=________时,以O,D,E,C为顶点的四边形是正方形.第5题图6.如图,AB为半圆O的直径,C为半圆上一动点,过点C作半圆O的切线l,过点B作BD⊥l,垂足为D,BD与⊙O交于点E,连接OC、CE、AE,AE交OC于点F.(1)求证:△CDE≌△EFC;(2)若AB=4,连接AC.①当AC=________时,四边形OBEC为菱形;②当AC=________时,四边形EDCF为正方形.第6题图7.如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G.(1)求证:GC是⊙F的切线;(2)填空:①若△BCF的面积为15,则△BDA的面积为________;②当∠GCD的度数为________时,四边形EFCD是菱形.第7题图8.如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S 相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.(1)求证:△DCS≌△DBS;(2)若AB=10,AC=6,点P是线段DS上的动点.①连接PC、PB,当PD=_________时,四边形PCSB是菱形;②当PD=_________时,△P AC的周长最小.第8题图9. 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1 cm/s的速度匀速运动,同时动点Q从点C出发以相同的速度沿CA 方向匀速运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为32cm,AC=8 cm,设运动时间为t秒.(1)求证:NQ=MQ;(2)填空:①当t=________时,四边形AMQN为菱形;②当t=________时,NQ与⊙O相切.第9题图10.如图,AB是半圆O的直径,点C是半圆上的一个动点,∠BAC的平分线交圆弧于点D,半圆O在点D处的切线与直线AC交于点E.(1)求证:△ADE∽△ABD;(2)填空:①若ED∶DB=3∶2,则AE∶AB=________;②连接OC、CD,当∠BAC的度数为________时,四边形BDCO是菱形.第10题图11. 如图,AB为⊙O的直径,点D、E位于AB两侧的圆上,射线DC切⊙O于点D.已知点E是圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.(1)求证:CD∥AB;(2)填空:①当∠DAE=________时,四边形ADFP是菱形;②当∠DAE=________时,四边形BFDP是正方形.第11题图12.如图,BC是⊙O的直径,BP=BO,过点P作⊙O的切线交⊙O于点A,点D为劣弧AC上一点,连接OA,AC,AD,CD,AB.(1)求证:△OAP≌△BAC;(2)填空:①若BP=3,则△APC的面积为________;②在①的条件下,当l AD︵=________时,四边形AOCD为菱形.第12题图13.如图,△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E.(1)求证:△OBD≌△OED;(2)填空:①当∠BAC=________时,CA是半圆O的切线;②当∠BAC=________时,四边形OBDE是菱形.第13题图14.如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.(1)求证:BC∥OP;(2)填空:若半圆O的半径等于2,①当AP=________时,四边形OAPC是正方形;②当AP=________时,四边形BODC是菱形.第14题图15.如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上的一点,过点D作DE⊥BC,垂足为F,交直线m于点E,连接CD,BE.(1)求证:CE=AD;(2)填空:当D是AB的中点时,①四边形BECD是________;②当∠A=________时,四边形BECD是正方形.第15题图16.如图,⊙O的半径为4 cm,其内接正六边形ABCDEF,点P,Q同时分别从A、D两点出发,以1 cm/s的速度沿AF、DC向终点F、C运动.连接PB、PE、QB、QE,设运动时间为t(s).(1)求证:四边形PEQB 为平行四边形; (2)填空:①当t =________ s 时,四边形PEQB 为菱形; ②当t =________ s 时,四边形PEQB 为矩形.第16题图答案试题演练1. (1)证明:∵在△ABO 中,OA =OB ,C 是AB 的中点, ∴OC ⊥AB .∵OC 为⊙O 的半径, ∴AB 是⊙O 的切线;(2)解:①π3;【解法提示】要使四边形OECF 为菱形,则OE =OF =CE =CF =OC , ∴△OCE 是等边三角形, ∴∠AOC =60°, 又∵OC ⊥AC ,∴OC =OA ·cos60°=12OA =12×4=2,又∵∠BOD =180°-∠AOC -∠BOC =60°,P 是DF ︵的中点, ∴∠DOP =∠FOP =30°, ∴DP ︵的长=30π2180⋅⋅=π3. ②22π.【解法提示】要使四边形OCBP 为正方形,则∠BOC =∠BOP =45°, 又∵∠AOC =∠BOC ,∴∠AOB =90°,又∵OA =OB ,OC ⊥AB ,∴OC =12AB =22OA =22, 又∵P 是DF ︵的中点, ∴DP ︵=PF ︵,∴DP ︵的长=45π180⋅⋅=22π.2. (1)证明:如解图①,连接BD , ∵AB 为⊙O 的直径, ∴∠APB =∠ADB =90°, ∵AD ∥PB ,∴∠CAD =∠APB =90°, ∴∠P AD =90°,第2题解图①∴∠APB =∠ADB =∠P AD =90°, ∴四边形ADBP 是矩形, ∴AD =PB ,在△P AB 和△ACD 中, ∴△P AB ≌△ACD ; (2)解:①18;【解法提示】①由(1)知,AD =PB ,∵AD ∥PB ,AC =AP ,∴AD =12PE =12(PB +BE ),∴PB =EB ,∴AD =BE ,∵AD ∥PB ,∴四边形ADEB 是平行四边形,∵AB 是⊙O 的直径,其长度不变,∴直线CD 和⊙O 相切时,即点D 到直径AB 的距离等于半径时,四边形ABED 的面积最大,∵AB =6,∴S 四边形ABED 最大=AB×12AB =18. ② 30°或60°.【解法提示】分两种情况考虑:当P A ︵>PB ︵时,如解图②,连接PD ,则PD 为⊙O 的直径,∵四边形ADFO 为菱形,∴OA =AD =DF =FO =OD ,∴△ADO 和△ODF 为等边三角形,∴∠AOD =60°,∵OA =OP ,∴∠P AB =12∠AOD =30°;当P A ︵<PB ︵时,如解图③,连接PD ,AF ,则PD 为⊙O 的直径,∵四边形AODF 为菱形,∴OA =AF =DF =FO =OD ,∴△AOF 和△DOF 为等边三角形,∴∠AOD =120°,∴∠AOP =60°,∵OA =OP ,∴△AOP 为等边三角形,∴∠P AB =60°.第2题解图② 第2题解图③ 3. (1)证明:∵四边形ABCD 是平行四边形, ∴∠A =∠C ,AD =BC . 又∵AP =CQ =t , 在△APD 和△CQB 中, ∴△APD ≌△CQB (SAS), ∴DP =BQ ; (2)解:① 1;【解法提示】如解图①,要使四边形PBQD 是矩形,∴DP ⊥AB ,∴AD 2-AP 2=BD 2-BP 2=DP 2,即82-t 2=122-(10-t )2,解得t =1. ② 2.【解法提示】要使四边形PBQD 为菱形,则BP =DP ,如解图②,过点D 作DH⊥AB 于H ,连接PQ ,与BD 相交于O .由①知BH =10-1=9,cos ∠DBH =BHBD =912=34.在Rt △BOP 中,cos ∠PBO =OB PB ,cos ∠DBH =cos ∠PBO =34,即34=610t ,解得t=2.第3题解图4. (1)证明:∵OD⊥BC,OB=OC,∴∠ODC=∠ODB=90°,∠OCD=∠OBD,在△COD和△BOD中,∴△COD≌△BOD;(2)解:①30°;【解法提示】如解图,要使四边形OCAF是菱形,则OF=AF=OA=AC=OC,即△AOF和△OAC是等边三角形,∴∠2=∠3=60°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠1=30°,∴当∠1=30°时,四边形OCAF是菱形.第4题解图②45°.【解法提示】∵AB=2OB,∴要使AB=22OD,则OD=22OB,∴在Rt△ODB中,sin∠1=ODOB=22,∴∠1=45°,∴当∠1=45°时,AB=22OD.5. (1)证明:如解图,连接OD. ∵AC是⊙O的直径,∴∠ADC=90°,∴∠CDB =90°, 又∵E 为BC 边的中点, ∴DE 为Rt △DCB 斜边的中线,∴DE =CE =12BC . ∴∠DCE =∠CDE . ∵OC =OD , ∴∠OCD =∠ODC ,∴∠ODC +∠CDE =∠OCD +∠DCE =∠ACB =90°, ∴∠ODE =90°. ∵OD 为⊙O 的直径, ∴DE 是⊙O 的切线.第5题解图 (2)解:①3;【解法提示】∵∠B =30°,AC =23,∠BCA =90°,∴tan30°=AC BC ==33,解得:BC =6,则DE =12BC =3. ②45°.【解法提示】∵四边形ODEC 为正方形, ∴∠DEC =∠ACB =90°,DE =EC , 又∵BE =DE ,∴△DBE 是等腰直角三角形, ∴∠B =45°.6. (1)证明:由题意可知,∠D=90°,∵AB为半圆O的直径,∴∠AEB=90°,又∵l为半圆O的切线,∴∠DCO=90°,∴四边形CFED为矩形,∴CF=DE,EF=CD,又∵CE=CE,∴△CDE≌△EFC(SSS);(2)解:①2;【解法提示】若四边形OBEC是菱形,则OC=OB=BE=CE=12AB,∴∠EAB=30°,∴∠COA=∠EBA=60°,∵OC=OA,∴△AOC为等边三角形,∵AB =4,∴AC=2.②2 2.【解法提示】如解图,若四边形EDCF为正方形,则O与F重合,B与E重合,∠AOC=90°,∵OA=OC=2,∴AC=2 2.第6题解图7. (1)证明:∵AB=AD,FB=FC,∴∠B=∠D,∠B=∠BCF.∴∠D=∠BCF,∴CF∥AD.∵CG⊥AD,∴CG⊥CF,又∵FC为⊙F的半径,∴GC是⊙F的切线;(2)解:①60;【解法提示】∵CF∥AD,∴△BCF∽△BDA,∵BFBA=12,S△BCF∶S△BDA=1∶4,∴S△BDA =4S△BCF=4×15=60.②30°.【解法提示】∵四边形EFCD为菱形,∴EF∥BD,∵点F为AB的中点,AB=AD,∴AE=AF,∵AF=EF,∴△AEF是等边三角形,∴∠AEF=60°,∴∠D=60°,∴∠GCD=180°-90°-60°=30°.8. (1)证明:∵点F是弧BC的中点,SF为⊙S的半径,∴SF⊥BC,且E为BC的中点,∴DS是BC的垂直平分线,∴DC=DB.在△DCS和△DBS中,∴△DCS≌△DBS(SSS);(2)解:①7 3;【解法提示】如解图,四边形PCSB是菱形,∴PE=SE,BE=CE,PS⊥BC.∵AB是⊙S的直径,∴AC⊥BC,∵AB=10,AC=6,在Rt△ABC中,由勾股定理可得BC=8,∴BE=4,∵BS=5,∴在Rt△BES中,由勾股定理可得ES=3,∴PS =6,∵由(1)可得DB 是⊙S 的切线,∴BS ⊥DB ,∴∠SEB =∠SBD =90°,∵∠BSE =∠DSB ,∴△EBS ∽△BDS ,∴SB SD =SE SB ,即5SD=35,∴SD =253,∴PD =SD -PS =253-6=73,∴当PD =73时,四边形PCSB 是菱形.第8题解图② 253.【解法提示】∵DS 是BC 的垂直平分线,∴PC =PB ,∴△P AC 的周长=AC +P A +PC =6+P A +PC =6+P A +PB ,当P 、A 、B 三点共线时,P A +PB 最小,即点P 与点S 重合时,△P AC 的周长最小,即周长的最小值为6+10=16,此时PD=SD ,由①知SD =253,∴当PD =253时,△P AC 的周长最小. 9. (1)证明:∵AB 是⊙O 的直径,AB ⊥MN ,∴PM =PN ,∴AB 垂直平分MN ,∴NQ =MQ ;(2)解:①83;【解法提示】AP =t ,CQ =t ,则PQ =8-t -t =8-2t ,∵AQ ⊥MN ,PM =PN ,∴当AP =PQ 时,四边形AMQN 为菱形,即t =8-2t ,解得t =83.②2.【解法提示】如解图,作OH ⊥QN 于H ,OQ =AC -AO -CQ =8-32-t =132-t ,OP =t -32,当ON ⊥QN 时,QN 为⊙O 的切线,∵∠NOQ =∠PON ,∠OPN =∠ONQ ,∴△ONP ∽△OQN ,∴OP ∶ON =ON ∶OQ ,即(t -32)∶32=32∶(132-t ),整理得t 2-8t +12=0,解得t 1=2,t 2=6(舍去),∴t =2时,NQ 与⊙O 相切.第9题解图10. (1)证明:如解图①,连接OD,∵AD是∠BAC的平分线,∴∠EAD=∠DAB,∵AO=OD,∴∠OAD=∠ODA,∴∠EAD=∠ODA,∴OD∥AE,∵DE是半圆O的切线,∴OD⊥DE,∴∠E=90°,∵AB是半圆O的直径,∴∠ADB=90°,∴∠EAD=∠DAB,∠E=∠ADB,∴△ADE∽△ABD;第10题解图①(2)解:①3∶4;【解法提示】由(1)得△ADE∽△ABD,∴EDBD=AEAD,∵ED∶DB=3∶2,∴AE∶AD=3∶2,∴∠EAD=30°,∴∠DAB=30°,∴AD∶AB=3∶2,∴AE∶AB=3∶4.②60°.【解法提示】如解图②,连接OC,CD,OD,当四边形BDCO是菱形时,OD =BD,∴△ODB为等边三角形,∴∠DOB=60°,由(1)得,OD∥AC,∴∠BAC =60°.第10题解图②11. (1)证明:如解图,连接OD,∵射线DC切⊙O于点D,∴OD⊥CD,即∠ODF=90°,∵∠AED=45°,∴∠AOD=2∠AED=90°,即∠ODF=∠AOD,∴CD∥AB;第11题解图(2)解:①67.5°;【解法提示】∵四边形ADFP是菱形,∴AD=AP,∵在Rt△AOD中,OA=OD,∴∠DAO=45°,∴∠ADP=∠APD=180°-45°2=67.5°,∴在△ADE中,∠DAE=180°-∠ADE-∠AED=180°-67.5°-45°=67.5°.②90°.【解法提示】当四边形BFDP是正方形,由题意可知,DE⊥AB时DE经过⊙O 的圆心,∴DE是⊙O的直径,∴∠DAE=90°.12. (1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵P A为⊙O的切线,∴∠OAP=90°,∴∠OAP=∠BAC,∵在Rt△OAP中,BP=BO,∴点B为PO的中点,∴AB=PB=BO,∵OA=OB,∴OA=OB=AB,∴△ABO为等边三角形,∴∠AOP=∠ABC=60°,在△OAP和△BAC中,∴△OAP≌△BAC;(2)解:①273 4;【解法提示】如解图,过点A作AE⊥BC于点E,∵BP=3,OB=OC,∴PC=BP+OB+OC=9.在Rt△AOE中,∵∠AOE=60°,∴AE=OA·sin∠AOE=OA·sin60°=3×32=332.∴S△APC =12PC·AE=12×9×332=2734.第12题解图②π.【解法提示】如解图,连接OD.∵四边形AOCD为菱形,∴AO=AD,∵OA=OD,∴△AOD为等边三角形,∴∠AOD=60°,∴l AD︵=60π3180=π.13. (1)证明:如解图,连接AD,第13题解图∵AB 是半圆O 的直径,∴AD ⊥BC ,又∵AB =AC ,∴∠BAD =∠CAD ,∴BD ︵=ED ︵.∴BD =ED ,在△OBD 和△OED 中,∴△OBD ≌△OED (SSS);(2)解:①90°;【解法提示】当∠BAC =90°,∵AB 为⊙O 的直径,∴CA 是半圆O 的切线.②60°.【解法提示】∵四边形OBDE 为菱形,∴OB =BD ,∵OB =OD ,∴△OBD 是等边三角形,∴∠ABC =60°,∵AB =AC ,∴△ABC 为等边三角形,∴∠BAC =60°.14. (1)证明:如解图,连接OC ,AC ,∵AB 是直径,AM ⊥AB ,∴BC ⊥AC ,AP 是半圆的切线,∵PC 切半圆O 于点C ,∴P A=PC,又∵OA=OC,∴OP⊥AC,∴BC∥OP;第14题解图(2)解:①2;【解法提示】若四边形OAPC是正方形,则OA=AP,∵OA=2,∴AP=2.②2 3.【解法提示】如解图,连接CD,若四边形BODC是菱形,则CB=BO=OD=DC,∵AB=2OB,∠ACB=90°,∴AB=2BC,∴∠BAC=30°,∠ABC=60°,∵BC∥OP,∴∠AOP=∠ABC=60°,又∵∠OAP=90°,OA=2,∴∠OP A=30°,∴OP=4,∴AP=2 3.15. (1)证明:∵∠ACB=90°,DE⊥BC,∴DE∥AC,∵直线m∥AB,∴四边形ACED为平行四边形,∴CE=AD;(2)解:①菱形;【解法提示】∵∠ACB=90°,D为AB的中点,BD=CD=DA,由(1)知,CE =AD,∴CE=CD.∵BD=CD,DE⊥BC,∴CF=BF,∴BE=CE,∴BD=CD =CE=BE,∴四边形BECD是菱形.②45°.【解法提示】要使四边形BECD为正方形,则BD=CD,BD⊥CD,∴∠CBD=45°,∵∠ACB=90°,∴∠A=45°.16. (1)证明:∵正六边形ABCDEF内接于⊙O,∴AB=BC=CD=DE=EF=F A,∠A=∠ABC=∠C=∠D=∠DEF=∠F,∵点P、Q同时分别从A,D两点出发,速度1 cm/s,运动时间为t(s),∴AP=DQ=t,在△ABP和△DEQ中,∴△ABP≌△DEQ(SAS).∴BP=EQ,同理可证,PE=QB,∴四边形PEQB是平行四边形;(2)解:①2;【解法提示】当四边形PBQE为菱形时,PB=PE=EQ=QB,∴△ABP≌△DEQ ≌△FEP≌△CBQ,∴AP=PF=DQ=QC,即t=4-t,得t=2.②0或4.【解法提示】如解图,连接OB,OP.要使四边形PBQE为矩形,则OB=OP.故点P在点A或点F处,即t的值为0或4.第16题解图。
2019年中考数学复习专题五特殊四边形的动态探究

〔1〕求证:AE = DF; 〔2〕四边形AEFD能够成为菱形吗?如果能,求出相应的 t 值;如果不能,说明理由; 〔3〕当 t 为何值时,△DEF 为直角三角形?请说明理由.
第二十三页,共27页。
解:
第二十四页,共27页。
第二十五页,共27页。
谢谢(xiè xie) 大家!
第二十六页,共27页。
第十七页,共27页。
第十八页,共27页。
第ห้องสมุดไป่ตู้九页,共27页。
7.〔2018河师大附中联考〕如图,AB 为⊙O的直径,点 C 为AB 延长线上一点,动点P从点A出发沿 AC 方向以每秒1个 单位长度的速度运动(yùndòng),同时动点 Q 从点C 出发以相 同的速度沿 CA 方向运动(yùndòng),当两点相遇时停止运动 (yùndòng),过点P作 AB 的垂线,分别交⊙O 于点 M 和点 N, ⊙O的半径为 1,设运动(yùndòng)时间为 t 秒.
①假设AB = 4,那么四边形AOPD的最大面积(miàn jī)为 ________;
②连接OD,当∠PBA的度数为________时,四边形BPDO是 菱形.
第二页,共27页。
【解析】 (1) 证明:∵PC = PB,D是AC的中点,∴DP∥AB,
且DP =
AB. ∴∠CPD = ∠PBO.
∵OB = OA = AB,∴DP = OB.∴△CDP
2019年中考数学(shùxué)复 习专题五特殊四边形的动态探
究
第一页,共27页。
典例精析
典例 〔2018河南(hé nán), 如图,AB是半圆O的直径,点P 是1半7〕圆上不与点A,B重合的一个动点,延长BP到点C,使PC = PB,D是AC的中点,连接PD,PO. 〔1〕求证:△CDP △POB; 〔2〕填空:
2019河南中考数学复习课件:攻克专题得高分 专题五 特殊四边形的动态探究题(共10张PPT)

特殊四边形的动 态探究题
典例 例 精析 如图,在△ACE中,AC=CE,⊙O经过点A,C且
与边AE,CE分别交于点 D , FBC ,点B是 DF AC 且 ,连接AB,BC,CD. (1)求证:△CDE≌△ABC; 等边三 (2)填空:若AC为⊙ O的直径,则 例题 角形 图 等腰直角三 ①当△ACE的形状为 时,四边形OCFD为 角形 菱形; ②当△ACE的形状为 ABCD为正方形. 时,四边形 上一点,
∵∠AFC=90°,∴AC=AE,
∵AC=CE,∴AC=AE=CE,即△ACE是等边三
②∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,∴∠ACD=45°,
∵AC=CE,CD⊥AE,∴∠DCE=∠ACD=45°,
∴∠ACE=90°,
∵AC=CE,
∴△ACE是等腰直角三角形.
【方法指导】特殊四边形的动态探究题一般分两种情
2.探究动点的运动时间判定特殊四边形时,要利用转
化的思想将其转化为探究线段的长度判定特殊四边形
进行求解,当在几何图形中要求点的运动时间,则需
求出点运动的路程,即线段的长度,再结合已知速度
即可求解,但要注意所求线段的长度为动点运动所经
过的路径长.
证明∵ DF BC
,∴∠BAC=∠DCF,
∵∠CDE是圆内接四边形ABCD的外角,∴∠CDE= ∠ABC, CDE ABC 在△ CDE和△ABC中, DCE BAC AC CE ∴△CDE≌△ABC(AAS);
(2)【思维教练】①要使四边形OCFD是菱形,则根
据菱形的性质可得到△ACE的边角关系,即可得出
解:①等边三角形;②等腰直角三角形.
【解法提示】如解图,①连接AF,
专题四特殊四边形的动态探究

∴①△若OAEDB正=是4,等则六边四三边边角形形A形O,即PDAE的D=B最OE大C, 面D积E为F4为; ☉O的内接正六边形,点P,Q同时分别从A,D
②在①的条件下,BC= 6 cm时,四边形ADFE的面积是6 cm2.
两点出发,以1 ∴AP=PF=DQ=QC,
∵AO=CO,∠CAB=30°,
cm/s的速度沿AF,DC向终点F,C运动,连接PB,QE,
又呈∵现∠类D类型PC均=∠型为AP解E,二答∴∠题D,C分A=∠利DPC用. 动点运动时间判定特殊四边形
值一般为9分或10分.
例2 ( (1)求证:△CDP≌△POB;
∴∠EOF=120°,
河南商丘名校统一模拟联考)如图,☉O的半径为4 cm,
(2)当AD运动到什么位置时,四边形OEDF是菱形,请说明理由;
( 河南濮阳一模)如图,在Rt△ABC中,∠ACB=90°,以AC为直
径的☉O与斜边AB交于点D,E为BC边的中点,连接DE.
例1 如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的一
个PD动,PO点. 思,连接路BP并导延长引BP到点(C1,使)P已C=P知B,D是一AC的组中对点,连应接 边CP=PB,结合已知条件易得DP
(1)求 EF 的值;
OE
(2)当AD运动到什么位置时,四边形OEDF是菱形,请说明理由;
(3)点D运动过程中,线段EF的最小值为 5 3 (直接写出结果).
解析 (1)作OP⊥EF交EF于点P,则PE=PF= 1 EF,
2
∵∠BAC=60°,
∴∠EOF=120°,
∵OE=OF,
∴∠OEF=∠OFE=30°,
5 cm时,四边形CEDF是矩形;
(∵1O)求A=证OPC:△,∴EC∠DPO,B≌C△AQ=P∠OBO,;设AC. 运动时间为t(s).
特殊四边形的动态探究题
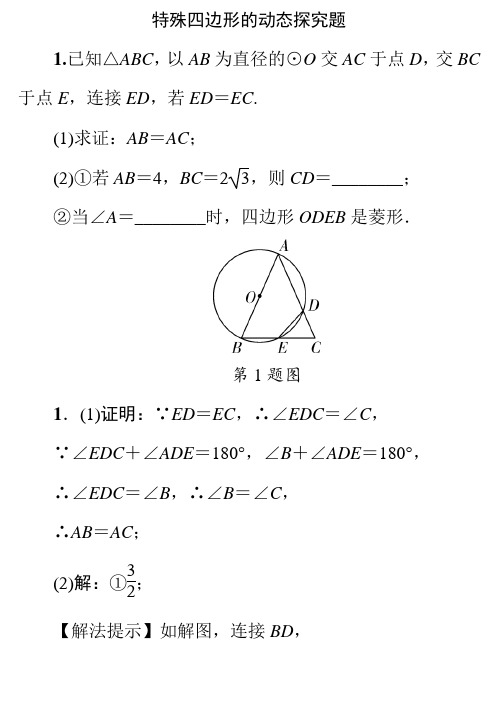
特殊四边形的动态探究题1.已知△ABC ,以AB 为直径的⊙O 交AC 于点D ,交BC 于点E ,连接ED ,若ED =EC .(1)求证:AB =AC ;(2)①若AB =4,BC =23,则CD =________;②当∠A =________时,四边形ODEB 是菱形.第1题图1.(1)证明:∵ED =EC ,∴∠EDC =∠C ,∵∠EDC +∠ADE =180°,∠B +∠ADE =180°, ∴∠EDC =∠B ,∴∠B =∠C ,∴AB =AC ;(2)解:①32;【解法提示】如解图,连接BD ,第1题解图∵AB 为⊙O 的直径,∴BD ⊥AC ,设CD =a ,由(1)知AC =AB =4,则AD =4-a ,在Rt △ABD 中,由勾股定理可得BD 2=AB 2-AD 2=42-(4-a )2,在Rt △CBD 中,由勾股定理可得BD 2=BC 2-CD 2=(23)2-a 2,∴42-(4-a )2=(23)2-a 2,解得a =32,即CD =32. ②60°.【解法提示】如解图,连接OD 、OE ,∵四边形ODEB 是菱形,∴OB =BE ,又∵OB =OE ,∴△OBE 是等边三角形,∴∠OBE =60°,∵OD ∥BE ,∴∠BOD =120°,∴∠A =12∠BOD =60°.2 .如图,在▱ABCD 中,AD =4,AB =5,延长AD 到点E ,连接EC,过点B作BF∥CE交AD于点F,交CD的延长线于点G.(1)求证:四边形BCEF是平行四边形;(2)①当DF=______时,四边形BCEF是正方形;②当GFGD=________时,四边形BCEF是菱形.第2题图2. (1)证明:∵四边形ABCD是平行四边形,∴EF∥BC. ∵BF∥CE,∴四边形BCEF是平行四边形;(2)解:①1;【解法提示】∵四边形BCEF是正方形,∴BF=BC=AD=4,∠FBC=∠AFB=90°,∴AF=AB2-BF2=52-42=3.∵AD=4,∴DF=AD-AF=4-3=1.②45. 【解法提示】∵四边形BCEF是菱形,∴BF=BC=AD=4.∵四边形ABCD是平行四边形,∴CD∥AB,∴GDAB=GFBF,即GFGD=BFAB=45.3.如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.(1)求证:BC∥OP;(2)若半圆O的半径等于2,填空:①当AP=________时,四边形OAPC是正方形;②当AP=________时,四边形BODC是菱形.第3题图3.解:(1)证明:连接OC,AC,如解图所示,∵AB是直径,AM⊥AB,∴BC⊥AC,AP是半⊙O的切线,又∵PC是半⊙O的切线,∴P A=PC,又∵OA=OC,∴OP⊥AC,∴BC∥OP;(2)①2;②2 3.【解法提示】①若四边形OAPC是正方形,则OA=AP,∵OA=2,∴AP=2;②若四边形BODC是菱形,则CB=BO=OD=DC,∵AB=2OB,∠ACB=90°,∴AB=2BC,∴∠BAC=30°,∠ABC=60°,∵BC∥OP,∴∠AOP=∠ABC=60°,又∵∠OAP=90°,OA=2,∴∠OP A=30°,∴OP=4,∴AP=22222-OAOP=2 3.=4-第3题解图4.如图,在△ABC中,∠ACB=90°,线段BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,AF=CE且F不与E重合.(1)求证:△EF A≌△ACE;(2)填空:①当∠B=_________°时,四边形ACEF是菱形;②当∠B=_________°时,线段AF与AB垂直.第4题图4.(1)证明:如解图,第4题解图∵ED是BC的垂直平分线,∴EB=EC,ED⊥BC,∴∠3=∠4,∵∠ACB=90°,∴FE∥AC,∴∠1=∠5,∵∠2与∠4互余,∠1与∠3互余,∴∠1=∠2=∠5,∴AE=CE.又∵AF=CE,∴AE=AF,∴∠5=∠F,在△EF A和△ACE中,AF=AE=EC,∠1=∠2=∠5=∠F,∴△EF A≌△ACE.(2)解:①30;②45.【解法提示】①∵四边形ACEF是菱形,∴AC=CE,∵CE是Rt△ABC斜边AB的中线,∴CE=AE=BE,∴AE=AC=CE,∴△ACE是等边三角形,∴∠1=60°,则∠B=30°,∴当∠B=30°时,四边形ACEF是菱形;②由(1)知△EF A≌△ACE,∴∠AEC=∠EAF,∴AF∥CE,∵AF⊥AB,∴CE⊥AB,∵CE=EB,∴∠3=∠4=45°,∴当∠B=45°时,线段AF与AB垂直.5.如图,AB是⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED,EB,切点分别为点D,B.连接AD并延长交BE延长线于点C,连接OE.(1)试判断OE与AC的关系,并说明理由;(2)填空:①当∠BAC=_________°时,四边形ODEB为正方形;②当∠BAC=30°时,ADDE的值为________.第5题图5.解:(1)OE∥AC,OE=12AC.理由:连接OD,如解图,第5题解图∵DE,BE是⊙O的切线,∴OD⊥DE,AB⊥BC,∴∠ODE=∠ABC=90°,∵OD=OB,OE=OE,∴Rt △ODE≌Rt△OBE(HL),∴∠1=∠2.∵∠BOD=∠A+∠3,OA=OD,∴∠A=∠3,∴∠2=∠A,∴OE∥AC;∵OA=OB,∴EC=EB,∴OE是△ABC的中位线,∴OE=12AC.(2)①45;②3.【解法提示】①要使四边形ODEB是正方形,由ED=EB,∠ODE=∠ABC=90°,只需∠DOB=90°,∴∠A=45°;②过O作OH⊥AD于H,∵∠A=30°,OA=OD,∴∠3=∠A=30°,∴OD,∵∠ODE=90°,∠1=∠3=30°,∴OD,∴ADDE=3.6.如图,将⊙O的内接矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接BC1,∠ACB =30°,AB=1,CC1=x.(1)若点O与点C1重合,求证:A1D1为⊙O的切线;(2)①当x=________时,四边形ABC1D1是菱形;②当x=________时,△BDD1为等边三角形.第6题图6. (1)证明:∵四边形ABCD为矩形,∴∠D=90°,∵把△ACD沿CA方向平移得到△A1C1D1,∴∠A1D1O=∠D=90°,∴A1D1⊥OD1,∴A1D1为⊙O的切线;(2)解:①1;②2.【解法提示】①如解图①,连接AD1,当x=1时,四边形ABC1D1是菱形;第6题解图①理由:由平移得:AB=D1C1,且AB∥D1C1,∴四边形ABC1D1是平行四边形,∵∠ACB=30°,∴∠CAB=60°,∵AB=1,∴AC=2,∵x=1,∴AC1=1,∴AB=AC1,∴△AC1B是等边三角形,∴AB=BC1,∴四边形ABC1D1是菱形;②如解图②所示,当x=2时,△BDD1为等边三角形,第6题解图②则可得BD=DD1=BD1=2,即当x=2时,△BDD1为等边三角形.7. 如图,AB是半圆O的直径,点C是半圆上的一个动点,∠BAC的平分线交圆弧于点D,半圆O在点D处的切线与直线AC交于点E.(1)求证:△ADE∽△ABD;(2)填空:①若ED∶DB=3∶2,则AE∶AB=________;②连接OC、CD,当∠BAC的度数为________时,四边形BDCO是菱形.第7题图7.(1)证明:如解图①,连接OD,∵AD 是∠BAC 的平分线,∴∠EAD =∠DAB ,∵AO =OD ,∴∠OAD =∠ODA ,∴∠EAD =∠ODA ,∴OD ∥AE ,∵DE 是半圆O 的切线,∴OD ⊥DE ,∴∠E =90°,∵AB 是半圆O 的直径,∴∠ADB =90°,∴∠EAD =∠DAB ,∠E =∠ADB ,∴△ADE ∽△ABD ;第7题解图①(2)解:① 3∶4;【解法提示】由(1)得△ADE ∽△ABD ,∴ED BD =AE AD ,∵ED ∶DB =3∶2,∴AE ∶AD =3∶2,∴∠EAD =30°,∴∠DAB =30°,∴AD ∶AB =3∶2,∴AE ∶AB =3∶4.② 60°.【解法提示】如解图②,连接OC,CD,OD,当四边形BDCO是菱形时,OD=BD,∴△ODB为等边三角形,∴∠DOB=60°,由(1)得,OD∥AC,∴∠BAC=60°.第7题解图②8.如图,以△ABC一边AB为直径作⊙O,与另外两边分别交于点D、E,且点D为BC的中点,连接DE.(1)证明:△ABC是等腰三角形;(2)填空:①当∠B=________时,四边形BDEO是菱形;②当∠B=________时,△AOE是直角三角形.第8题图8.(1)证明:连接AD,如解图,∵AB是⊙O的直径,∴∠BDA=90°.∵D为BC的中点,∴BD=DC,∴AB=AC,∴△ABC是等腰三角形;第8题解图(2)解:①60°;②67.5°.【解法提示】①当∠B=60°时,四边形BDEO是菱形.连接OD,如解图,∵∠B=60°,∴△ABC是等边三角形,△OBD是等边三角形,∴△AOE是等边三角形,△DOE 是等边三角形,∴OB=BD=DE=EO, ∴四边形BDEO 是菱形;②若△AOE是直角三角形,只有一种情况,即∠AOE=90°,∵OA=OE,∴∠OAE=∠AEO=45°,由(1)知△ABC 是等腰三角形,∴∠B=∠C=180°-45°2=67.5°.9.如图,在△ABC中,AB=BC=8,O是AB的中点,以O 为圆心,OA 为半径的圆交AC 于D ,E 是AB ︵上的一点,∠C =45°,连接BE ,DE . AF 切圆O 于点A ,交BE 的延长线于点F .(1)求证:BC 是圆O 的切线;(2)填空:①当BE =________时,四边形BDAE 是正方形;②当BF =________时,四边形ODAF 是平行四边形.第9题图9.(1)证明:∵AB =BC ,∠C =45°,∴∠BAC =∠C =45°,∵在△ABC 中,∠ABC =180°-∠BAC -∠C =180°-45°-45°=90°,又∵AB 是过圆心O 的直径,OB ⊥BC ,∴BC 是圆O 的切线;(2)解:① 42;② 4 5.【解法提示】①当DE 经过圆心时四边形BDAE 是正方形,连接BD ,AE ,如解图①,∵AB 是圆O 的直径,∴∠ADB =90°,又∵AB =BC ,∴BD ⊥AC ,A D =DC =BD ,又∵∠ADB =90°,AD =BD ,∴DO ⊥AB ,∴AB ⊥ED ,∵AB =ED ,OA =OB ,OE =OD ,∴四边形BDAE 是正方形.∵AB =8,∴EO =OB =4,∴BE =22BO EO +=16+16=42,∴当BE =42时,四边形BDAE 是正方形;②如解图②,∵四边形ODAF 是平行四边形,∴AF =OD =4,∴BF =22AB AF +=2284+=45,∴当BF =45时,四边形ODAF 是平行四边形.第9题解图① 第9题解图②10.如图,已知平行四边形ABCD 中,AD =8 cm ,AB =10 cm ,BD =12 cm.点P 从点A 出发,以1 cm/s 的速度向点B 运动,同时点Q 从点C 出发以相同的速度向点D 运动.设运动时间为t .(1)连接DP 、BQ ,求证:DP =BQ ;(2)填空:①当t为______s时,四边形PBQD是矩形;②当t为______s时,四边形PBQD是菱形.第10题图10.解:(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=BC.又∵AP=CQ=t,∴△APD≌△CQB (SAS),∴DP=BQ;(2)①1;②2.【解法提示】①如解图①,∵△APD ≌△CQB,∴DP =BQ.∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴AB-AP=CD-CQ,即BP=DQ,∴四边形PBQD是平行四边形.当∠DPB=90°时,则四边形PBQD就是矩形.此时,AD2-AP2=BD2-BP2=DP2,即82-t2=122-(10-t)2,解得t=1;②如解图②,由①知四边形PBQD是平行四边形,当DP =BP 时,则四边形PBQD 就是菱形.此时,连接PQ ,交BD 于点O ,则PQ ⊥BD ,OB =OD =6. 作DH ⊥AB 于H .由①知BH =10-1=9,cos ∠DBH =BH BD =912=34.在Rt △BOP 中,cos ∠PBO =OB PB,cos ∠DBH =cos ∠PBO =34,即34=t 106,解得t =2.第10题解图① 第10题解图②。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题型五特殊四边形的动态探究题试题演练1.如图,AD是O O的直径,AD = 2BD,点C是ACD上的不与A、D重合的动点,连接BC,BA, AC.⑴求/ ACB的度数;(2)填空:已知O O半径为4.时,四边形OBDC是菱形;________ 时,四边形ABDC是矩形.2.如图,在Rt△ ABC中,/ ACB = 90°以点A为圆心,交CA的延长线于点E,过点E作EF // AB交O A于点F,连接AF , BF, DF .⑴求证:△ ABC^A ABF ;⑵填空:①当/ CAB等于 ______ 时,四边形ACBF为正方形;②当/ CAB等于 ________ 时,四边形ADFE为菱形.①当1CD =②当l cD =AC为半径作O A,交AB于点D,£D第2题图3.('郑附模拟)如图,扇形OAB的半径OA= 3,圆心角/ AOB = 90 °点C是AB上异于A、B的动点,过点C作CD丄OA于点D,作CE丄OB于点E,连接DE,点G、H在线段DE 上,且DG = GH = HE.⑴当点C在AB上运动时,在CD、CG、DG中,长度不变的线段是________________ ,该线段的长度是________ ;⑵求证:四边形OGCH是平行四边形;(3)当OD = ________ 时,四边形OGCH是菱形.4.如图,CD是厶ABC的中线,点E是AF的中点,CF // AB.(1)求证:CF = AD;⑵若已知AB= 10, AC = 6,填空:①当BC长为_________ 时,四边形BFCD是矩形;②当BC长为_________ 时,四边形BFCD是菱形.B F第4题图5.如图,在矩形 ABCD 中,AB = 13 cm , AD = 4 cm ,点E 、F 同时分别从 D 、B 两点出发, 以1 cm/s 的速度沿DC 、BA 向终点C 、A 运动,点G 、H 分别为AE 、CF 的中点,设运 动时间为t(s). ⑴求证:四边形 EGFH 是平行四边形. ⑵填空:① 当t 为 _______ s 时,四边形EGFH 是菱形; ② 当t 为 _______ s 时,四边形EGFH 是矩形.E C第5题图Q 由A 出发沿AC 方向向点C 匀速运动,P , Q 运动速度均为2cm/s.以AQ 、PQ 为边作平行四边形 AQPD ,连接DQ ,交AB 于点E.设运动的时间为t (单位:s)(0< tw 4)解答下列问题:(1)在点P , Q 运动过程中,平行四边形 AQPD 的面积是否具有最大值,若有,请求出它的最大值;否则,请说明理由. ⑵填空:①当t 的值为 _________ s 时,平行四边形 AQPD 为矩形; ②当t 的值为 _________ s 时,平行四边形AQPD 为菱形.QC第6题图6.如图,已知Rt △ ABC 中,C = 90 ° AC = 8 cm , BC = 6 cm.点P 由B 出发沿BA 方向向点A 匀速运动,同时点7. ( ' 1平顶山模拟)如图,在平行四边形ABCD中,AE是BC边上的高,将△ ABE沿BC方向平移,使点E与点C重合,得△ GFC.(1)求证:BE = DG ;⑵填空:①若/ B = 60°当BC = ________ AB时,四边形ABFG是菱形;②若/ B = 60°当BC = ________ AB时,四边形AECG是正方形.A G 1)B E F C第7题图8.如图,在平行四边形ABCD中,对角线BD = 8 cm, AC = 4 cm,点E从点B出发沿BD 方向以1 cm/s的速度向点D运动,同时点F从点D出发沿DB方向以同样的速度向点B运动,设点E、F运动的时间为t(s),其中Ov tv 8.(1)求证:△ BEC^A DFA;⑵填空:①以点A、C、E、F为顶点的四边形— -定是 _ _______ 形;②当t的值为_______ 时,以点A、C、E、F为顶点的四边形为矩形.C第8题图【答案】1.解:⑴•/ AD 是O O 的直径,•••/ ABD = 90° •/ AD = 2BD ,•••/ ACB=/ D = 60°⑵①4n ;②8n.【解法提示】 ①当BC 丄OD 时,T OB = OD = BD , • OE = DE , v OD 是半径,BC 是= 坪;②当BC 经过圆心O 时,易得四边形ABDC 是矩形,△ AOC 为等边三角形,•/ COD3=180° — 60°= 120° ••T CD =2.【思路分析】(1)首先利用平行线的性质得到/FAB =/ CAB ,然后利用SAS 证得两三角形全等即可;(2)①当/ CAB = 45°寸,四边形 ACBF 为正方形./ FAB = / CAB = 45° 进而/FAC = / AFB = / ACB = 90°四边形ACBF 为矩形,再由邻边AC = AF 得其为正方形; ②当/ CAB = 60°时,四边形 ADFE 为菱形.根据/ CAB = 60°得到/ FAB = / AFE = / CAB =/ AEF = 60°从而得到EF = AD = AE ,禾U 用邻边相等的平行四边形是菱形进行判断.解:(1)证明:v EF // AB , •••/ E =/ CAB ,/ EFA =/ FAB ,v/ E=/ EFA ,• / FAB = / CAB , 又v AF = AC ,AB = AB , • △ ABC ^A ABF (SAS );⑵①45 ° ②60 °【解法提示】 ①当/CAB = 45°时,由(1)知,/ FAB = / CAB = 45°,/ FAC = / AFB = / ACB =•••在 Rt △ ABD 中, c os / D =BD = A D = BD = 12BD = 2,弦,• BE = CE , •四边形 OBDC 是菱形, 则 OD= CD= OC,•/ COD= 60° •- lCD=甘90°故四边形ACBF为矩形,又•/ AC = AF ,•••四边形ACBF为正方形.②当/ CAB = 60° 时,易得 / FAB = Z AFE = Z CAB = Z AEF = 60° 从而得到△ AEF 和△ ADF均为等边三角形,• EF = AD = AE= DF, •四边形ADFE为菱形.3.【思路分析】(1)由于四边形ODCE是矩形,而矩形的对角线相等,所以DE = OC , 而CO 是圆O的半径,这样DE的长度不变,也就DG的长度不变;(2)连接OC,容易根据已知条件证明四边形ODCE是矩形,然后利用其对角线互相平分和DG = GH = HE,可以知道四边形CHOG的对角线互相平分,从而判定其是平行四边形;(3)若四边形OGCH是菱形,必有OC与GH垂直,即可推得DE、OC垂直、平分且相等,故得到四边形CDOE是正方形,在Rt△ OCD中,利用OC= OA= 3, OD = CD运用勾股定理即可求出OD的长.解:(1)DG, 1.1 【解法提示】在矩形ODCE 中,DE = OC= 3,v DG = GH = HE ,• DG = 3DE = 1.3(2)连接OC交DE于M.由矩形得OM = CM , EM = DM .•/ DG = HE ,• EM —EH = DM —DG , • HM = MG.「.四边形OGCH 是平行四边形.⑶3■ 2.【解法提示】•••四边形OGCH是菱形,• OC丄GH ,• OCX DE,又•/ OC = DE , CM=OM = EM = DM,•四边形CDOE 是正方形.• CD = OD , Z CDO = 90° •/ OA = OC= 3, •••OD2+ CD2= 9, 2OD2= 9, OD = K/2.4.【思路分析】(1)易得DE是厶ABF的中位线,进而DE//BF,结合CF // AB,证得四边形BFCD是平行四边形,从而得到CF = BD = AD ; (2)①当CD丄AB,即CD是AB的中垂线时,平行四边形BFCD有一个角为直角是矩形,此时AC= BC= 6;②当Z ACB = 90° CD是直角三角形斜边上的中线,可得CD = AD = BD,从而平行四边形BFCD的邻边相等是菱形,此时由勾股定理易得BC的长.解:⑴证明:T CD是厶ABC的中线,点E是AF的中点,••• AD = BD , AE = FE ,••• DE // BF ,•/ CF // AB,•四边形BFCD是平行四边形,•CF = BD ,•CF = DA.⑵①6 ②8【解法提示】①当CD丄AB,即CD是AB的中垂线时,/ CDB = 90°平行四边形BFCD 有一个角为直角是矩形,此时AC= BC = 6;②当/ACB = 90°时,CD是直角△ ABC斜边上的中线,• CD = AD = BD,从而平行四边形BFCD的邻边相等是菱形,此时由勾股定理易得BC= 8.5.【思路分析】(1)易证△ ADE CBF,进而易得GE// HF,且GE= HF,所以四边形EGFH是平行四边形. ⑵①四边形EGFH是菱形,G是AE的中点,则GF = GE= GA =殳AE,得到/ AFE = 90 °根据DE = AF,列方程求解;②四边形EGFH是矩形,易得△ ADE EHC,则根据斐=列方程求解即可.EC CH解:(1)•••四边形ABCD 是矩形,•/ D =Z B= 90° AD = CB,•••点E、F同时分别从D、B两点出发,以1 cm/s的速度沿DC、BA向终点C、A运动,•DE = BF ADE ◎△ CBF(SAS),•AE= CF,/ DEA = Z EAF = Z CFB ,•••点G、H分别为AE、CF的中点,•GE// HF,且GE= HF ,•••四边形EGFH 是平行四边形.132⑵①才:②8或2.【解法提示】连接EF ,1•••四边形EGFH 是菱形,G 是AE 的中点.• GF = GE = GA = qAE ,: EF 丄AB ,13• DE = AF , • t = 13- t ,「. t=y.②•••四边形 EGFH 是矩形,•/ D = Z EHC = Z AEH = 90°•••/ AED + / HEC = / ECH + / HEC = 90° AED = / ECH ,6.【思路分析】(1)首先利用勾股定理求得 AB = 10,然后表示出 AP ,过P 作PH 丄AC 于H ,利用△ APHABC ,禾U 用相似三角形对应边的比相等,表示出 AH 的长,然后由平 行四边形面积公式,得到平行四边形AQPD 的面积的二次函数表达式,用配方法求最值;⑵①利用矩形的性质得到△ APQABC ,利用相似三角形对应边的比相等列出比例式即可 求得t 值;②利用菱形的性质得到厶 AEQACB ,利用相似三角形对应边的比相等列出比 例式即可求得t 值.解:(1)•/ Rt △ ABC 中,/ C = 90° AC = 8cm , BC = 6cm , • AB = 10cm ,•/ BP = 2tcm ,• AP = AB — BP = 10 — 2 t , 过P 作PH 丄AC 于H ,贝U PH // BC , • △ APHABC ,• PH = AP 即 PH = 10— 2t …BC — AB , ' 6 — 10 ,3•- PH = 5(10 — 2t).3•/ S AQPD = AQ PH = 2t • - (10 — 2t)5=—敢2+ 12t =— ^(t — 2)2+ 15,5 5 2.AE ■ DE CH , .,42+12 • 13 —t t—,解得: 十+ t 2t 1 = 8, t 2= |.5•••当t =劳时,平行四边形 AQPD 的面积具有最大值,为 15.第6题解图⑵①乎;②嘗【解法提示】 ①当?AQPD 是矩形时,PQ 丄AC ,「. PQ // BC ,•△ APQ ABC ,: AQ =AB ,即於2T 盒,解得t = 20•二当t = 20时,?AQPD 是矩形;②当?AQPD 是菱形时, DQ 丄 AP ,贝U △ AEQACB ,: AQ = AC ,即詈=盒,解得 t =鲁•••当 t =衮时,?AQPD 是菱形.7.【思路分析】(1)根据平行四边形和平移的性质得到 AB = CD , AE = CG ,再证明 Rt △ ABE 也Rt △ CDG 可得到BE = DG ;⑵①要使四边形 ABFG 是菱形,须使AB = BF ;根据条 件找到满足 AB = BF 时,BC 与AB 的数量关系即可; ②当四边形 AECG 是正方形时,AEAB ,可得 EC =-^AB ,再有 BE = 1A B 可得 BC= 丁AB.解:(1)证明:•••四边形 ABCD 是平行四边形,• AD // BC , AB = CD. •••AE 是BC 边上的高,且 CG 是由AE 沿BC 方向平移而成,• CG 丄 AD , AE = CG ,•••/ AEB =Z CGD = 90°• •在 Rt △ ABE 与 Rt △ CDG 中,AE = CG , AB = CD ,• Rt △ ABE 也 Rt △ CDG (HL),3【解法提示】 ①当BC = ^AB 时,四边形ABFG 是菱形./I Q H C• BE = DG.证明:•/ AB // GF , AG // BF ,•••四边形 ABFG 是平行四边形.1•/ Rt △ ABE 中,/ B = 60° BAE = 30° • BE = gAB ,3 1••• BE = CF , BC = gAB ,• EF = J AB.A AB = BF.A 四边形 ABFG 是菱形.②BC =-^2匕AB 时,四边形AECG 是正方形.•••AE 丄 BC, GC 丄 CB ,• AE // GC ,Z AEC = 90°TAG // CE ,•四边形 AECG 是矩形,当 AE = EC 时,矩形 AECG 是正方形B = 60° • EC = AE = AB sin60°= ^AB , BE = gAB , • BC=^2^AB.• AD = BC , AD // BC ,•••/ EBC=Z FDA .在厶BEC 和厶DFA 中, ⑵①平行四边形;②2或6.【解法提示】 ①平行四边形,理由如下:连接 CF , AE ,由(1)得:/ BEC = Z DFA , EC = AF , FEC = Z AFE ,即 EC // AF ,•以点 A 、C 、E 、 F 为顶点的四边形一定是平行四边形 •②2或6,理由如下:•••四边形AECF 为矩形,• AC = EF ,■/ BD = 8cm , AC = 4cm , • EF = 4, BE = 2cm 或 6cm.•••速度为 1cm/s ,「. t = 2 或 6. 8.解:⑴证明:•••四边形 ABCD 是平行四边形,BE= DF ,/ EBC=Z FDA,BC= DA,。
