《三年级奥数》数学最短路线课件
合集下载
《最短路径问题》PPT课件教学
C
你能要自己的语言重新描述一下问题吗？ C是l上一个动点， 当点C在l的什么位置时，AC+BC最小？
探究 如图，点A，B 在直线l 的同侧，点C 是直线上的一个动点，当点C 在l 的什么位置时，AC 与CB 的和最小？
一开始的时候我们就讨论过点A，B在直线异侧的情况， 你还记得是怎么做的吗？ 连接两点，交点就是所求 同侧的情况也能直连接两点吗？不行
拓广探索
在纸上画五个点，使任意三个点组成的三角形都 是等腰三角形 . 这五个点应该怎样画？
拓广探索
如图，△ABC 是等边三角形，BD 是中线，延长BC 至 E，使CE =CD . 求证DB =DE .
拓广探索
如图，△ABC 是等腰三角形，AC =BC，△BDC 和△ACE 分别为等边三角形，AE 与BD 相较于F，连接CF 并延长 ，交AB 于点G . 求证：G 为AB 的中点 .
复习巩固
如图，在△ABC 中，∠ABC =50°，∠ACB =80°，延长 CB至D，使DB =BA，延长BC 至E，使CE =CA，连接 AD，AE .求∠D，∠E，∠DAE 的度数 .
复习巩固 如图，AD =BC，AC=BD，求证：△EAB 是等腰三角形 .
复习巩固
综合应用
试确定如图所示的正多边形的对称轴的条数，一般地 ，一个正n边形有多少条对称轴？
综合应用
如图，从图形Ι 到图形Ⅱ是进行了平移还是轴对称？如果 是轴对称，找出对称轴；如果是平移，是怎样平移？
综合应用
如图，AD是△ABC 的角平分线，DE，DF 分别是△ABD 和△ACD的高 . 求证：AD 垂直平分EF .
综合应用
如图，在等边三角形 ABC 的三边上，分别取点D，E，F ，使AD =BE =CF . 求证△DEF 是等边三角形 .
你能要自己的语言重新描述一下问题吗？ C是l上一个动点， 当点C在l的什么位置时，AC+BC最小？
探究 如图，点A，B 在直线l 的同侧，点C 是直线上的一个动点，当点C 在l 的什么位置时，AC 与CB 的和最小？
一开始的时候我们就讨论过点A，B在直线异侧的情况， 你还记得是怎么做的吗？ 连接两点，交点就是所求 同侧的情况也能直连接两点吗？不行
拓广探索
在纸上画五个点，使任意三个点组成的三角形都 是等腰三角形 . 这五个点应该怎样画？
拓广探索
如图，△ABC 是等边三角形，BD 是中线，延长BC 至 E，使CE =CD . 求证DB =DE .
拓广探索
如图，△ABC 是等腰三角形，AC =BC，△BDC 和△ACE 分别为等边三角形，AE 与BD 相较于F，连接CF 并延长 ，交AB 于点G . 求证：G 为AB 的中点 .
复习巩固
如图，在△ABC 中，∠ABC =50°，∠ACB =80°，延长 CB至D，使DB =BA，延长BC 至E，使CE =CA，连接 AD，AE .求∠D，∠E，∠DAE 的度数 .
复习巩固 如图，AD =BC，AC=BD，求证：△EAB 是等腰三角形 .
复习巩固
综合应用
试确定如图所示的正多边形的对称轴的条数，一般地 ，一个正n边形有多少条对称轴？
综合应用
如图，从图形Ι 到图形Ⅱ是进行了平移还是轴对称？如果 是轴对称，找出对称轴；如果是平移，是怎样平移？
综合应用
如图，AD是△ABC 的角平分线，DE，DF 分别是△ABD 和△ACD的高 . 求证：AD 垂直平分EF .
综合应用
如图，在等边三角形 ABC 的三边上，分别取点D，E，F ，使AD =BE =CF . 求证△DEF 是等边三角形 .
《最短路径问题》PPT课件
A
a 3、连接PA，PB，由对称轴 的性质知，PA= P1A，
P1
PB=P2B
∴先到点A处吃草，再到点B
处饮水，最后回到营地，
这时的放牧路线总路程最
短，即 (PB+BA+AP)min
• 证明：
P2
b ∵ PA1+A1B1+B1P
B1 B
.P
河
= P1A1+A1B1+B1P2 > P1A+AB+BP2
前面和右面
D D1
③
A 1 A1
C1
2
4
B1
AC1 =√52+22 =√29
左面和上面
• 1、如图是一个长方体木块，已知 AB=5,BC=3,CD=4，假设一只蚂蚁 在点A处，它要沿着木块侧面爬到点D 处，则蚂蚁爬行的最短路径是 7 4 。
D
4
C
A
5
B3
• 2、现要在如图所示的圆柱体侧面A点 与B点之间缠一条金丝带（金丝带的宽 度忽略不计），圆柱体高为6cm，底面 圆周长为16cm，则所缠金丝带长度的 最小值为 10cm 。
在河上建一座桥MN，桥造在何处才能使从A到B
的路径最短？（假设河的两岸是平行的直线，桥
要与河垂直）
.A M
作法： 1、将点B沿垂直与河岸的方
向平移一个河宽到E
N
2、. E连接AE交河对岸与点M,则
.点BM为建桥的位置，MN为 所建的桥。
A C
M ND E
B
• 证明： ∵ AC+CD+DB = AC+CD+CE = AC+CE+CD > AE+CD = AM+ME+CD = AM+NB+MN ∴ AC+CD+DB > AM+NB+MN
《最短路径问题》PPT课件
13.4 课题学习 最短路径问题
导入新课
讲授新课
当堂练习
课堂小结
.
1
学习目标
1.体会图形的变化在解决最值问题中的作用，感悟转 化思想．（重点）
2.能利用轴对称解决简单的最短路径问题.（难点）
.
2
导入新课
复习引入 1.如图，连接A、B两点的所有连线中，哪条最短？为什么？
②最短，因为两点之间，线段最短
A．P是m上到A、B距离之和最短的
点，Q是m上到A、B距离相等的点
B．Q是m上到A、B距离之和最短的
点，P是m上到A、B距离相等的点
C．P、Q都是m上到A、B距离之和最
短的点
D．P、Q都是m上到A、B距离相等
的点
.
16
2.如图，∠AOB=30°，∠AOB内有一定点P，且
OP=10．在OA上有一点Q，OB上有一点R．若
△PQR周长最小，则最小周长是（ A ）
A．10
B．15
C．20
D．30
.
17
3.如图，牧童在A处放马，其家在B处，A、B到河岸的距离分 别为AC和BD，且AC=BD,若点A到河岸CD的中点的距离为500 米，则牧童从A处把马牵到河边饮水再回家，所走的最短距离 是 1000 米.
C
D 河
A
B
.
18
则点C 即为所求． ACΒιβλιοθήκη B lB′.
9
问题3 你能用所学的知识证明AC +BC最短吗？
证明：如图，在直线l 上任取一点C′（与点C 不重合），
连接AC′，BC′，B′C′．由轴对称的性质知，
BC =B′C，BC′=B′C′．
∴ AC +BC= AC +B′C = AB′，
导入新课
讲授新课
当堂练习
课堂小结
.
1
学习目标
1.体会图形的变化在解决最值问题中的作用，感悟转 化思想．（重点）
2.能利用轴对称解决简单的最短路径问题.（难点）
.
2
导入新课
复习引入 1.如图，连接A、B两点的所有连线中，哪条最短？为什么？
②最短，因为两点之间，线段最短
A．P是m上到A、B距离之和最短的
点，Q是m上到A、B距离相等的点
B．Q是m上到A、B距离之和最短的
点，P是m上到A、B距离相等的点
C．P、Q都是m上到A、B距离之和最
短的点
D．P、Q都是m上到A、B距离相等
的点
.
16
2.如图，∠AOB=30°，∠AOB内有一定点P，且
OP=10．在OA上有一点Q，OB上有一点R．若
△PQR周长最小，则最小周长是（ A ）
A．10
B．15
C．20
D．30
.
17
3.如图，牧童在A处放马，其家在B处，A、B到河岸的距离分 别为AC和BD，且AC=BD,若点A到河岸CD的中点的距离为500 米，则牧童从A处把马牵到河边饮水再回家，所走的最短距离 是 1000 米.
C
D 河
A
B
.
18
则点C 即为所求． ACΒιβλιοθήκη B lB′.
9
问题3 你能用所学的知识证明AC +BC最短吗？
证明：如图，在直线l 上任取一点C′（与点C 不重合），
连接AC′，BC′，B′C′．由轴对称的性质知，
BC =B′C，BC′=B′C′．
∴ AC +BC= AC +B′C = AB′，
最短路径问题 课件
课题学习 最短路径问题
知识点1：两点在直线异侧时的最短路径问题 【例1】 如图1-13-30-1，在直线l上找一点P，使得 PA+PB的和最小.
解：答图13-30-1,点P即为所求.
知识点2：两点在直线同侧时的最短路径问题 【例2】 如图1-13-30-3,已知直线l和l外两点A,B， 点A,B在l同侧，求作一点P，使点P在直线l上，并且 使PA+PB最短．
解：如答图13-30-6，作点A的对称点A′， 连接A′B，与直线l相交于点C，连接AC， 点C即为所求．
6. 如图1-13-30-9，正方形网格中每个小正方形边 长都是1．在直线l上找一点P，使PB+PC的值最小.
略.
7. 如图1-13-30-10，在平面直角坐标系中，点 A（4，4），B（2，-4）．在y轴上求作一点P，使 PA+PB的值最小.（不写作法，保留作图痕迹）
略.
8. 如图1-13-30-11，∠XOY内有一点P，请在射线OX上 找出一点M，在射线OY上找出一点N，使PM+MN+NP最短．
解：如答图13-30-7,作点P关于OX对称的点 P1，关于OY对称的点P2，连接P1P2，交OX， OY于点M，N，则M,N两点即为所求．
9. 如图1-13-30-12，在△ABC中，AB=AC，AD是BC边 上的高，P是AB边上的一点，请在高AD上找一点E， 使得△PEB的周长最短．
解：作图略, 作点A关于直线l的对称点A′， 连接A′B与直线l交于点P， 则P点即为所求．
4. 如图1-13-30-7，直线l旁有两点A，B，在直线上 找一点CA，B两点的距离相等．
解：如答图13-30-5,点C,点D即为所求.
5. 如图1-13-30-8，l为某河流的南岸线，一天傍晚 某牧童在A处放牛，欲将牛牵到河边饮水后再回到家 B处，牧童想以最短的路程回家．请你在找中画出牛 饮水C的位置．
知识点1：两点在直线异侧时的最短路径问题 【例1】 如图1-13-30-1，在直线l上找一点P，使得 PA+PB的和最小.
解：答图13-30-1,点P即为所求.
知识点2：两点在直线同侧时的最短路径问题 【例2】 如图1-13-30-3,已知直线l和l外两点A,B， 点A,B在l同侧，求作一点P，使点P在直线l上，并且 使PA+PB最短．
解：如答图13-30-6，作点A的对称点A′， 连接A′B，与直线l相交于点C，连接AC， 点C即为所求．
6. 如图1-13-30-9，正方形网格中每个小正方形边 长都是1．在直线l上找一点P，使PB+PC的值最小.
略.
7. 如图1-13-30-10，在平面直角坐标系中，点 A（4，4），B（2，-4）．在y轴上求作一点P，使 PA+PB的值最小.（不写作法，保留作图痕迹）
略.
8. 如图1-13-30-11，∠XOY内有一点P，请在射线OX上 找出一点M，在射线OY上找出一点N，使PM+MN+NP最短．
解：如答图13-30-7,作点P关于OX对称的点 P1，关于OY对称的点P2，连接P1P2，交OX， OY于点M，N，则M,N两点即为所求．
9. 如图1-13-30-12，在△ABC中，AB=AC，AD是BC边 上的高，P是AB边上的一点，请在高AD上找一点E， 使得△PEB的周长最短．
解：作图略, 作点A关于直线l的对称点A′， 连接A′B与直线l交于点P， 则P点即为所求．
4. 如图1-13-30-7，直线l旁有两点A，B，在直线上 找一点CA，B两点的距离相等．
解：如答图13-30-5,点C,点D即为所求.
5. 如图1-13-30-8，l为某河流的南岸线，一天傍晚 某牧童在A处放牛，欲将牛牵到河边饮水后再回到家 B处，牧童想以最短的路程回家．请你在找中画出牛 饮水C的位置．
小学三年级奥数 第22讲最短路线
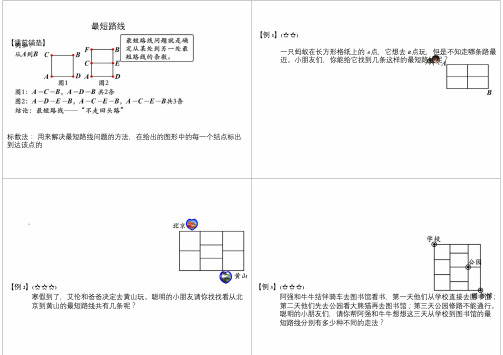
最短路线
【例1】(☆☆)
【课前铺垫】
一只蚂蚁在长方形格纸上的A点，它想去B点玩，但是不知走哪条路最
近。
小朋友们，你能给它找到几条这样的最短路线呢？
标数法：用来解决最短路线问题的方法，在给出的图形中的每一个结点标出
到达该点的
，。
【例2】(☆☆☆)【例3】(☆☆☆)
寒假到了，艾伦和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢？阿强和牛牛结伴骑车去图书馆看书，第一天他们从学校直接去图书馆；第二天他们先去公园看大熊猫再去图书馆；第三天公园修路不能通行。
聪明的小朋友们，请你帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法？
1
【例4】(☆☆☆☆)【例5】(☆☆☆☆☆)
图中的“我爱史老师”有多少种不同的读法。
一只密蜂从A处出发，A回到家里B处，每次只能从一个蜂房爬向右侧
邻近的蜂房而不准逆行，共有多少种回家的方法？
【例6】(☆☆☆☆☆)
城市街道如下图所示，有几处街区有积水不能通行，那么从A到B的最
短路线有几条？
【本讲总结】
最短路线
宗旨：不走冤枉路，就要朝着目标走
方法：标数法
标数法四步：
1．找目标、定方向
2．从起点标数，起点标1
3．按顺序每个点都要标到
4．某点数字＝指向该点箭头
尾巴上的数字相加
注意：
．坏点可以划去或看成
2．必须经过，分段标出
2。
最短路径问题-(PPT课件) 公开课
第十三章 轴对称
故事引入
导入新课
复习旧知
1.如图，连接A、B两点的所有连线中，哪条最短？
①
为什么？
②
②最短，因为两点之间，线段最短
A ③B
2.如图，点P是直线l外一点，点P与该直线l上各点连
接的所有线段中，哪条最短？为什么？
P
PC最短，因为垂线段最短
A BC
Dl
3.如图，如何作点A关于直线l的对称点？
B
A
C
l
联想旧知
B
A
C
l
B′
用旧知解决新知
A
C
l
B
提示：本题也可作A点关于直线l的对称点
典例精析
例1 如图，已知点D、点E分别是等边三角形ABC
中BC、AB边的中点，AD=5，点F是AD边上的动
点，则BF+EF的最小值为（ B ）
A．7.5
B．5
C．4
D．不能确定
解析：△ABC为等边三角形，点D是BC边的中点，即点B与点 C关于直线AD对称.∵点F在AD上，故BF=CF.即BF+EF的最小 值可转化为求CF+EF的最小值，故连接CE即可，线段CE的长 即为BF+EF的最小值.
l2
l2
2.关键： 作对称点，利用轴对称的性质将线段转化， 从而利用“两点之间，线段最短”来解决
作法及思路分析
1.作点A关于直线 l 的对称点A′ ，连接CA′。
B A
l
C
A′
2.由上步可知AC+CB=B_′_A_C_+_C_B_′ ___
思考：当C在直线 l 的什么位置时AC +CB′最短？
3.如图，如何作点A关于直线l的对称点？
故事引入
导入新课
复习旧知
1.如图，连接A、B两点的所有连线中，哪条最短？
①
为什么？
②
②最短，因为两点之间，线段最短
A ③B
2.如图，点P是直线l外一点，点P与该直线l上各点连
接的所有线段中，哪条最短？为什么？
P
PC最短，因为垂线段最短
A BC
Dl
3.如图，如何作点A关于直线l的对称点？
B
A
C
l
联想旧知
B
A
C
l
B′
用旧知解决新知
A
C
l
B
提示：本题也可作A点关于直线l的对称点
典例精析
例1 如图，已知点D、点E分别是等边三角形ABC
中BC、AB边的中点，AD=5，点F是AD边上的动
点，则BF+EF的最小值为（ B ）
A．7.5
B．5
C．4
D．不能确定
解析：△ABC为等边三角形，点D是BC边的中点，即点B与点 C关于直线AD对称.∵点F在AD上，故BF=CF.即BF+EF的最小 值可转化为求CF+EF的最小值，故连接CE即可，线段CE的长 即为BF+EF的最小值.
l2
l2
2.关键： 作对称点，利用轴对称的性质将线段转化， 从而利用“两点之间，线段最短”来解决
作法及思路分析
1.作点A关于直线 l 的对称点A′ ，连接CA′。
B A
l
C
A′
2.由上步可知AC+CB=B_′_A_C_+_C_B_′ ___
思考：当C在直线 l 的什么位置时AC +CB′最短？
3.如图，如何作点A关于直线l的对称点？
小学奥数之最短路线
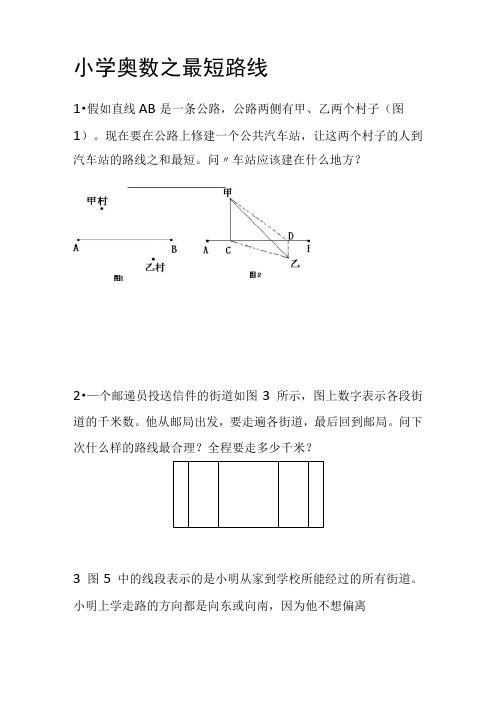
小学奥数之最短路线1•假如直线AB是一条公路，公路两侧有甲、乙两个村子（图1）。
现在要在公路上修建一个公共汽车站，让这两个村子的人到汽车站的路线之和最短。
问〃车站应该建在什么地方？2•—个邮递员投送信件的街道如图3所示，图上数字表示各段街道的千米数。
他从邮局出发，要走遍各街道，最后回到邮局。
问下次什么样的路线最合理？全程要走多少千米？3图5中的线段表示的是小明从家到学校所能经过的所有街道。
小明上学走路的方向都是向东或向南，因为他不想偏离小明家△4．如图8，从甲地到乙地最近的道路有几条？甲学校的方向而走冤枉路。
那么小明从家到学校可以有我少条不同的路线？学校5．某城市的街道非常整齐，如图10所示。
从本南角A 处人匕到东北角B处要求走最近的路并且不能通过十字路口C（正在修路），共有多少种不同的走法？B—6图13是一个街区街道的平面图。
邮递员从邮局出发，跑遍所有街道投送信件。
请你为他安排一条最短的路线，并按图中标出的千米数算出这条路线的长度（单位：千米）。
3邮局14是一个街道平面图。
王宏处到B处，在不走回头路，不走重复路的条件下，可以有多少种不同的路线？请你用交叉点上标数的方法计算一下。
8．从学校到少年宫有4条东西向的马路和3条南北向的马路相通。
如图15，李楠从学校出发，步行到少年宫（只放向9•如图16,从P到Q共有多少咱不同的最短路线？10•如图17所示，某城市的街道图，若从AZ走到B（只能由北向南、由西向东），则共有多少种不同的走法？11．如图18所示，从甲地到乙地，最近的道路有几条？能通车，12•图19为某城市的街道示意图，C处正在挖下水道，不13．如图20所示是一个街道的平面图，在不走回头路、不走重复路和条件下，可以有多少种不同的走法？B。
小学奥数-最短路线
最短路线
1、请你画出从小明家去图书馆的最短路线，并说出理由。
2、一只小蚂蚁想从下图中的点A爬到对边BC。
沿怎样的路线爬行需要的时间最少？在图中画一画。
3、如图，三角形ABC的三条边AB，AC，BC分别表示三条公路。
在D点处有一名士兵接到一个紧急任务，需要他先到达BC公路，然后再到达AB公路。
他怎样走才能以最短的时间完成任务呢？在图中画出路线。
（假设士兵的速度一定）
4、如图，三角形ABC的三条边AB，AC，BC分别表示三条公路。
在D处有一个村庄，现准备修一条通往公路的小路，在图中画出最短的小路。
5、一只小蚂蚁想从下图中的点A爬到对边CD。
你能帮它开辟一条最短的路线，使它尽快到达吗?在图中画一画。
6、一个邮递员投送信件的街道如下图所示，你能帮他设计一条最短路线，使自己从邮局出发，走遍每一条街道并回到邮局吗？
7、如右图，每个小方格的边长是1厘米，一条贪吃的蛇从左下角出发，沿着格线爬行，如果它想吃掉图中的3个“”，最少要爬多远？请你画出路线。
8、下图是一个公园的平面图，A点是出入口，B，C，D，E，F，G，H，I，J是各个景点，你能帮游客设计一条最短路线，使他从出入口出发，走遍每一条路后，最终回到出入口吗?。
最短路径PPT课件
小结
本节课，我们通过什么方法解决了最短 路径问题？在解决问题的过程中，你有 哪些收获？
四边形
菱形OBCD在平面直角坐标系中的位置如图所 示，顶点B（2,0），∠DOB=60°，点E坐标 为 (0, 3)，点P是对角线OC上一个动点，则 EP+BP最短的最短距离是______。
y
D
C
●
P
●
O
B
x
●
13.4 课题学习
最短路径问题
导入新课
复习引入
1.如图，连接A、B两点的所有连线中，哪条最短？为什么？
②最短，因为两点之间，线段最短
①
②
A ③B
2.如图，点P是直线l外一点，点P与该直线l上各点连接的所有
线段中，哪条最短？为什么？
P
PC最短，因为垂线段最短
A BC
Dl
八年级八班同学做游戏，在活动区 域边缘放了一些球(如下图)，小明按 怎样的路线跑，去捡哪个位置的球， 才能最快拿到球跑到目的地A?
M Ｍ１
N
Ｎ１
B
理由:另任作桥M1N１，连接AM１，BN１，A１N１. 由平移性质可知，AM＝A１N，AA１＝MN＝M１N１，AM１＝A１N１.
AM+MN+BN转化为ＡＡ１＋Ａ１Ｂ，而ＡＭ１＋Ｍ１Ｎ１＋ＢＮ１ 转化为ＡＡ１＋Ａ１Ｎ１＋ＢＮ１.
在△A１N１B中，由线段公理知A1N1+BN1＞A1B.
因此ＡＭ１＋Ｍ１Ｎ１＋ＢＮ１＞ AM+MN+BN.
∴CB=CB',C'B=C'B'.
B
∴AC+CB=AC+CB'=AB'。
A
《最短路径问题》微课程最短路径问题ppt
则AC和BC的大小关系是什么？ l
C
A
B
容易得出，AC=BC. 依据“线段垂直平分线上的点到线段两端点的距离相等”.
引出问题
思考：相传古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦.有 一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：从图中的A 地出发，到一条笔直的河边l饮马，然后到B地.到河边什么地方饮马可使他 所走的路线全程最短？ 精通数学、物理学的海伦稍加思索，利用轴对称的知识回答了这个问题.这 个问题后来被称为“将军饮马问题”.
B A
l
这是个实际问题，你能用自己理解的语言描述一下吗？ 如图所示：将A，B 两地抽象为两个点，将河l抽象为一条直线.
∙B A∙
l
那你能用数学语言说明这个问题所表达的意思吗？
如图： 点A，B分别在直线l的同侧，点C是直线l上的一个动点，当点C在什么
位置的时候，AC+BC的值最小？
∙B A∙
l
如果点A，B在直线l的两侧，这时该如何求解？
离是（ B ）
A.900
B.1200
C.1500
D.1800
C
D
A
B
谢谢大家
∙B
A∙
你能证明这个结论吗
∙
l
C
∙ B′
容易得出：连接AB′交直线l于点C，则点C即为所求.
证明：在直线l上任意取一点C′（不与点C重合），连接AC′，BC′，B′C′.
由轴对称的性质可得：BC=B′C，BC′=B′C′，
则AC+BC=AC+B′C=AB′，AC′+BC′=AC′+B′C′.
在△AB′C′中，AB′<AC′+B′C′， 所以AC+BC<AC′+B′C′. 由点C′的任意性可知，AC+BC的值是 最小的，故点C的位置符合要求.
C
A
B
容易得出，AC=BC. 依据“线段垂直平分线上的点到线段两端点的距离相等”.
引出问题
思考：相传古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦.有 一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：从图中的A 地出发，到一条笔直的河边l饮马，然后到B地.到河边什么地方饮马可使他 所走的路线全程最短？ 精通数学、物理学的海伦稍加思索，利用轴对称的知识回答了这个问题.这 个问题后来被称为“将军饮马问题”.
B A
l
这是个实际问题，你能用自己理解的语言描述一下吗？ 如图所示：将A，B 两地抽象为两个点，将河l抽象为一条直线.
∙B A∙
l
那你能用数学语言说明这个问题所表达的意思吗？
如图： 点A，B分别在直线l的同侧，点C是直线l上的一个动点，当点C在什么
位置的时候，AC+BC的值最小？
∙B A∙
l
如果点A，B在直线l的两侧，这时该如何求解？
离是（ B ）
A.900
B.1200
C.1500
D.1800
C
D
A
B
谢谢大家
∙B
A∙
你能证明这个结论吗
∙
l
C
∙ B′
容易得出：连接AB′交直线l于点C，则点C即为所求.
证明：在直线l上任意取一点C′（不与点C重合），连接AC′，BC′，B′C′.
由轴对称的性质可得：BC=B′C，BC′=B′C′，
则AC+BC=AC+B′C=AB′，AC′+BC′=AC′+B′C′.
在△AB′C′中，AB′<AC′+B′C′， 所以AC+BC<AC′+B′C′. 由点C′的任意性可知，AC+BC的值是 最小的，故点C的位置符合要求.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以下赠品教育通用模板
前言
您的内容打在这里，或者通过复制您的文本后，在此框中选择粘贴，并 选择只保留文字。在此录入上述图表的综合描述说明。您的内容打在这 里，或者通过复制您的文本后，在此框中选择粘贴，并选择只保留文字。 在此录入上述图表的综合描述说明。 您的内容打在这里，或者通过复制您的文本后，在此框中选择粘贴，并 选择只保留文字。在此录入上述图表的综合描述说明。您的内容打在这 里，或者通过复制您的文本后。
例题【五】（★ ★ ★ ★ ★ ）
城市街道如下图所示，有几处街区有积水不能通行，那么 从A到B的最短路线有几条？
从起点开始标数，注意积水处都是 坏点，那好把这些点划去或看成0。
例题【五】（★ ★ ★ ★ ★ ）
城市街道如下图所示，有几处街区有积水不能通行，那么 从A到B的最短路线有几条？
111111
例题【一】（★ ★ ）
一只蚂蚁在长方形格纸上的A点，它想去B点玩，但是不知走哪条路 最近。小朋友们，你能给它找到几条这样的最短路线呢？
例题【一】（★ ★ ）
A→C→D→G→B、A→C→F→G→B、 A→E→F→G→B、A→C→F→I→B、 A→E→F→I→B、A→E→H→I→B、
例题【一】（★ ★ ）
标数法
例题【三】（★ ★ ★ ★ ）
图中的“我爱史老师”有多少种不同的读法。
1
1 1 11
起点是“我” 每个字看做“点”（车站） 共有1+4+6+4+1=16（种）
1 234 1 36 14 1
例题【四】（★ ★ ★ ★ ★ ）
一只密蜂从A处出发，A回到家里B处，每次只能从一个蜂房 爬向右侧 邻近的蜂房而不准逆行，共有多少种回家的方法？
您的内容打在这里，或者通过复制您的文本后，在此框中选择粘贴，并 选择只保留文字。在此录入上述图表的综合描述说明。
您的内容打在这里，或者通过复制您的文本后，在此框中选择粘贴，并 选择只保留文字。在此录入上述图表的综合描述说明。
01 点击此处添加标题 02 点击此处添加标题 03 点击此处添加标题
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里，或者 通过复制您的文本后，在 此框中选择粘贴，并选择 只保留文字。在此录入上 述图表的综合描述说明。
点击此处添加标题
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里，或者通过复制您的文本后，在此框中选择粘贴，并 选择只保留文字。在此录入上述图表的综合描述说明。
目录
01
单击添加标题
02
单击添加标题
03
单击添加标题
04
单击添加标题
01 点击添加文字
点击此处添加标题
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里，或者通过复制您的文本后， 在此框中选择粘贴，并选择只保留文字。在此录 入上述图表的综合描述说明。
一只蚂蚁在长方形格纸上的A点，它想去B点玩，但是不知走哪条路 最近。小朋友们，你能给它找到几条这样的最短路线呢？
方法二：标数法
目标：右、下 方向：左、上
1
1
3
2
1
36
知识点睛
步ቤተ መጻሕፍቲ ባይዱ：
1、找目标、定方向 2、从起点标数，起点标1 3、按顺序每个点都要标到
例题【二】（★ ★ ★ ）
寒假到了，艾伦和爸爸决定去黄山玩。聪明的小朋友请你找找看从 北 京到黄山的最短路线共有几条呢？
12 3 4 5 6
目标：右、下 方向：左、上
13 14
5 11 11
155
11
1 6 11 11 11 22
本课总结
宗旨：不走冤枉路，就要朝着目标走 方法：标数法 1．找目标、定方向 2．从起点标数，起点标1 3．按顺序每个点都要标到 4．某点数字＝指向该点箭头 尾巴上的数 字相加 注意： 1．坏点可以划去或看成0 2．必须经过，分段标出
最短路线
三年级 第18课
课前回顾
最短路线问题就是确定从某处到 另一处最短路线的条数。
课前铺垫
课前铺垫
图1：A-C-B,A-D-B 共2条 图2：A-D-E-B,A-C-E-B,A-C-E-B 共3条 结论：最短路线——“不走回头路”
课前铺垫
标数法：
用来解决最短路线问题的方法，在给 出的图形中的每一个结点标出到达该 点的方法数，最后利用相加原则求出 到达目的地方法数。
您的内容打在这里，或者 通过复制您的文本后，在 此框中选择粘贴，并选择 只保留文字。在此录入上 述图表的综合描述说明。
您的内容打在这里，或者 通过复制您的文本后，在 此框中选择粘贴，并选择 只保留文字。在此录入上 述图表的综合描述说明。
您的内容打在这里，或者 通过复制您的文本后，在 此框中选择粘贴，并选择 只保留文字。在此录入上 述图表的综合描述说明。
标数法
例题【二】（★ ★ ★ ）
寒假到了，艾伦和爸爸决定去黄山玩。聪明的小朋友请你找找看从 北 京到黄山的最短路线共有几条呢？
目标：右、下 方向：左、上
1 1
1
1
12
23
2 1
3
4
7
10
老师点睛 箭头很重要，一定逐一标； 步骤要严谨，不能跳着做。
例题【三】（★ ★ ★ ★ ）
图中的“我爱史老师”有多少种不同的读法。
只能从小号码的蜂房爬进相邻 的大号码的蜂房！ 蜜蜂的运动方向是固定的，所 以依然可以采取标数法。
例题【四】（★ ★ ★ ★ ★ ）
一只密蜂从A处出发，A回到家里B处，每次只能从一个蜂房 爬向右侧 邻近的蜂房而不准逆行，共有多少种回家的方法？
1 3 8 21 55
1 2 5 13 34 小蜜蜂从A出发到B处共有89种不同的回家方法!
点击此处添加标题
您的内容打在这里，或者通过复制您的文本 后，在此框中选择粘贴，并选择只保留文字。 在此录入上述图表的综合描述说明。