时幅连续信号数值反卷积方法及其应用

合集下载

信号反卷积

信号反卷积（signal deconvolution）是一种信号处理技术，用于从观测到的信号中去除卷积效应，以恢复原始信号。

在信号处理领域，卷积是一种基本的运算，描述了一个信号经过一个系统后的响应。

然而，卷积运算会使原始信号发生变形，导致观测到的信号与原始信号存在差异。

信号反卷积的目的就是尽可能还原出原始信号。

信号反卷积在许多领域都有应用，如音频处理、图像处理、地震信号处理等。

在音频处理中，反卷积可用于去除混响效应，提高语音清晰度；在图像处理中，可用于去除模糊效应，提高图像分辨率；在地震信号处理中，可用于去除地层对地震波的滤波效应，提高地震成像精度。

实现信号反卷积的方法有很多，包括基于滤波的方法、基于迭代的方法、基于深度学习的方法等。

这些方法各有优缺点，选择哪种方法取决于具体的应用场景和需求。

需要注意的是，由于卷积运算的不可逆性，信号反卷积往往是一个病态问题，即存在多个可能的解。

因此，在实际应用中，需要结合先验知识和约束条件来选择合适的解。

f-x反卷积方法

f-x反卷积方法
f-x反卷积方法是一种用于解决图像和信号处理中的反卷积问
题的数学方法。

反卷积问题通常涉及在已知输入信号f和卷积
核h的情况下，恢复原始信号x。

f-x反卷积方法基于频域的方法，通过将输入信号f和卷积核h 转换到频域，在频域中进行运算，然后再将结果转换回时域。

具体步骤如下：
1. 将输入信号f和卷积核h进行傅里叶变换，得到它们在频域
的表示F和H。

2. 在频域中，使用逆滤波器G = F / H 对信号进行去卷积。

3. 对去卷积结果G进行傅里叶逆变换，得到恢复的信号X。

尽管f-x反卷积方法可以用于图像和信号处理中的反卷积问题，但它也存在一些限制。

其中一个主要限制是反卷积问题通常是不逆的，即无法完全恢复原始信号。

这是因为卷积操作会引入信息丢失和噪音。

为了克服这个问题，通常需要结合其他方法，如正则化方法、最小二乘方法等，以减少噪音和增加信号的恢复质量。

此外，在实际应用中，反卷积问题通常是ill-posed问题，需要额外的先验知识或约束条件来获得可靠的解决方案。

需要注意的是，f-x反卷积方法是一个广泛的概念，具体的实
现方法可能会因应用领域和具体问题而有所不同。

【最新精选】实验二连续时间号、离散信号卷积运算

实验二连续时间信号、离散信号卷积运算一、实验目的⑴熟悉卷积的定义和表示；⑵掌握利用计算机进行卷积运算的原理和方法；⑶熟悉连续时间信号、离散信号的相关计算方法；⑷熟悉连续时间信号卷积运算、离散信号卷积运算函数conv 、反卷积deconv 函数等的应用。

二、实验原理1.卷积的定义：卷积是一种特殊函数与函数之间的计算。

连续时间信号卷积积分可以表示为：f(t)=f 1(t)*f 2(t)= τττd t f f )()(21-⎰∞∞-=τττd f t f )()(12⎰∞∞--离散信号卷积积分可以表示为：f 1(k)*f 2(k)=)()(21m k f m f n -∑∞-∞= ∞-<k<∞2.卷积计算的几何解法卷积积分计算从几何上可以分为四个步骤：翻转 → 平移 → 相乘 → 叠加（积分）3.卷积积分的应用卷积积分是信号与系统时域分析的基本手段，主要应用于求系统零状态响应。

它将输入信号分解为众多的冲激函数之和，利用冲激响应可以很方便求解LTI 系统对任意激励的零状态响应。

设一个线性零状态响应系统，已知系统的单位冲激响应为h1（t ），当系统的激励信号为x （t ）时，系统的零状态响应为y zs (t)=τττd t h x t )()(0-⎰=τττd h t x t)()(0⎰- 可以简记为：y zs (t)=x(t)*h(t) 三、程序设计实验①采用函数conv 编程，实现离散时间序列的卷积和运算，完成两序列的卷积和，其中：f1（k ）={1，2，1}，对应的k1={-1，0，-1}；f2（k ）={1，1，1，1，1}，对应的k2={-2，-1，0，1，2}。

程序代码：k1=[-1,0,1];f1=[1,2,1];subplot(3,1,1)stem(k1,f1);title('f1(k)');k2=[-2,-1,0,1,2];f2=[1,1,1,1,1];subplot(3,1,2)stem(k2,f2);title('f2(k)');k3=k1(1)+k2(1):k1(end)+k2(end);f3=conv(f1,f2);subplot(3,1,3)stem(k3,f3); title('f3(k)');程序运行结果的对应信号波形图：②求f1（t）=u（t）-u（t-2），f2（t）=e^（-3t）u（t）的卷积。

实验二连续时间信号、离散信号卷积运算

实验二连续时间信‎号、离散信号卷‎积运算一、实验目的⑴熟悉卷积的‎定义和表示‎；⑵掌握利用计‎算机进行卷‎积运算的原‎理和方法；⑶熟悉连续时‎间信号、离散信号的‎相关计算方‎法；⑷熟悉连续时‎间信号卷积‎运算、离散信号卷‎积运算函数‎c o nv 、反卷积de ‎conv 函‎数等的应用‎。

二、实验原理1.卷积的定义‎：卷积是一种‎特殊函数与‎函数之间的‎计算。

连续时间信‎号卷积积分‎可以表示为‎：f(t)=f 1(t)*f 2(t)= τττd t f f )()(21-⎰∞∞-=τττd f t f )()(12⎰∞∞--离散信号卷‎积积分可以‎表示为：f 1(k)*f 2(k)=)()(21m k f m f n -∑∞-∞= ∞-<k<∞2.卷积计算的‎几何解法卷积积分计‎算从几何上‎可以分为四‎个步骤：翻转 → 平移 → 相乘 → 叠加（积分）3.卷积积分的‎应用卷积积分是‎信号与系统‎时域分析的‎基本手段，主要应用于‎求系统零状‎态响应。

它将输入信‎号分解为众‎多的冲激函‎数之和，利用冲激响‎应可以很方‎便求解LT ‎I 系统对任‎意激励的零‎状态响应。

设一个线性‎零状态响应‎系统，已知系统的‎单位冲激响‎应为h1（t ），当系统的激‎励信号为x ‎（t ）时，系统的零状‎态响应为y ‎z s (t)=τττd t h x t )()(0-⎰=τττd h t x t)()(0⎰- 可以简记为‎：y zs (t)=x(t)*h(t) 三、程序设计实‎验①采用函数c ‎o nv 编程‎，实现离散时‎间序列的卷‎积和运算，完成两序列‎的卷积和，其中：f1（k ）={1，2，1}，对应的k1‎={-1，0，-1}；f2（k ）={1，1，1，1，1}，对应的k2‎={-2，-1，0，1，2}。

程序代码：k1=[-1,0,1];f1=[1,2,1];subpl ‎o t(3,1,1)stem(k1,f1);title ‎('f1(k)');k2=[-2,-1,0,1,2];f2=[1,1,1,1,1];subpl ‎o t(3,1,2)stem(k2,f2);title ‎('f2(k)');k3=k1(1)+k2(1):k1(end)+k2(end);f3=conv(f1,f2);subpl‎o t(3,1,3)stem(k3,f3); title‎('f3(k)');程序运行结‎果的对应信‎号波形图：②求f1（t）=u（t）-u（t-2），f2（t）=e^（-3t）u（t）的卷积。

信号与系统 §2.07 卷积的性质

微分积分性质对于计算卷积很方便。微分积分性质对于计算卷积很方便。
三.与冲激函数或阶跃函数的卷积
f (t ) ∗δ (t ) = ∫ f (τ )δ (t −τ ) dτ = ∫ f (t −τ ) δ (τ ) dτ = f (t )
∞ ∞
推广：推广： f (t ) ∗δ (t − t 0) = f (t − t 0)
f (t ) ∗δ ′(t ) = f '(t )
f (t ) ∗ u(t ) =
−∞
−∞
f (t − t1) ∗δ (t − t 2) = f (t − t1 − t 2)
−∞
∫ f (λ)dλ
t
f (t ) ∗δ (k ) (t ) = f (k ) (t )
f (t ) ∗δ (k ) (t − t 0) = f (k ) (t − t 0)
f(t)的积分的积分
微分性质积分性质联合实用
g(n−m) (t ) = f (n) (t ) ∗ h(−m) (t ) = f (−m) (t ) ∗ h(n) (t )
微分n次微分次，积分m次积分次 m=n, 微分次数＝微分次数＝积分次数
g(t ) = f (n) (t ) ∗ h(−n) (t )
+
∑
h2 (t) +
y(t )
h1 (t )
h2 (t )
1
1 t
解：
(a)
O 1
h(t )
O 1 2 t
(b)
1
h(t ) = h1(t ) ∗[h1(t ) + h2 (t )]
如图（）如图（c）所示
O 1 2 3t
X

信号翻转尺度变换和时移的注意事项和关键点

信号翻转尺度变换和时移的注意事项和关键点信号处理中的翻转、尺度变换和时移是常见的操作，它们在许多领域中都有广泛应用。

下面将详细介绍这些操作的注意事项和关键点。

一、信号翻转：信号翻转是指将信号在时间轴上进行镜像。

翻转操作可以对离散信号和连续信号都进行，下面将分别介绍离散信号和连续信号的翻转注意事项和关键点。

1.离散信号翻转：离散信号的翻转是指将信号在时间轴上进行镜像。

对于离散信号x(n)，其翻转后的信号为x(-n)。

在进行离散信号翻转时，需要关注以下事项和关键点：-确定翻转轴：翻转轴的位置对翻转结果有重要影响。

根据信号的特点和需要，选择合适的翻转轴位置。

-处理边界值：离散信号在两端的取值可能会影响翻转结果。

对于边界值情况，需要根据具体问题进行处理，常见的方法有补零处理或选择不处理边界值。

2.连续信号翻转：连续信号的翻转是指将信号在时间轴上进行镜像。

对于连续信号x(t)，其翻转后的信号为x(-t)。

在进行连续信号翻转时，需要关注以下事项和关键点：-确定翻转轴：翻转轴的位置对翻转结果有重要影响。

根据信号的特点和需要，选择合适的翻转轴位置。

-处理边界值：连续信号在两端的取值可能会影响翻转结果。

对于边界值情况，需要根据具体问题进行处理，常见的方法有使用截断或采用无穷延拓的方式。

二、信号尺度变换：信号尺度变换是指改变信号在时间轴上的时间尺度。

尺度变换可以使信号加快或减慢，对于离散信号和连续信号，尺度变换的注意事项和关键点如下所示：1.离散信号尺度变换：离散信号的尺度变换是通过改变采样间隔来实现的。

对于离散信号x(n)，其尺度变换后的信号为x(an)，其中a为尺度变换系数。

在进行离散信号尺度变换时，需要关注以下事项和关键点：-确定尺度变换系数：尺度变换系数决定了信号的时间尺度变化程度。

a>1时表示加快信号，0<a<1时表示减慢信号。

-插值问题：尺度变换可能导致信号的采样点增加或减少。

对于采样点减少的情况，可能需要进行插值处理，常见的方法有线性插值或多项式插值。

反卷积函数

反卷积函数一、背景反卷积是计算机视觉和图像处理领域中的一项重要技术，它可以用来还原被模糊的图像。

在实际应用中，由于种种原因，我们往往会得到一些模糊的图像，例如拍摄时手抖或者光线不足等等。

这时候，我们就需要使用反卷积技术来还原清晰的图像。

二、什么是反卷积反卷积是指从一个模糊的图像中恢复出原始清晰的图像。

在数学上，我们可以将一个模糊的图像看作是一个卷积核与原始图像之间的乘积。

而反卷积则是通过求解这个乘积方程来还原出原始图像。

三、反卷积函数实现在实际应用中，我们通常使用离散傅里叶变换（DFT）来进行反卷积操作。

具体来说，我们需要先对模糊的图像和卷积核进行傅里叶变换，然后将它们相除得到频域下的结果，最后再进行逆傅里叶变换得到还原后的清晰图像。

以下是一个简单实现反卷积函数的代码：```pythonimport numpy as npfrom scipy.signal import convolve2ddef deconvolve(im, kernel):# 对图像和卷积核进行傅里叶变换im_fft = np.fft.fft2(im)kernel_fft = np.fft.fft2(kernel, s=im.shape)# 将频域下的结果相除result_fft = im_fft / kernel_fft# 对结果进行逆傅里叶变换得到还原后的清晰图像 result = np.fft.ifft2(result_fft).realreturn result# 测试代码im = np.array([[1, 1, 1],[1, 1, 1],[1, 1, 1]])kernel = np.array([[0.25, 0.5, 0.25],[0.5, 1.0, 0.5],[0.25, 0.5, 0.25]])result = deconvolve(im, kernel)print(result)```四、反卷积函数优化以上实现方式虽然简单，但是在实际应用中可能会遇到一些问题。

卷积.循环卷积与OFDM

卷积、线性卷积、循环卷积与OFDM 中的循环前缀CP摘要：本文主要讲述了卷积的定义及如何理解卷积，用离散样值近似计算连续卷积的方法，用循环卷积计算线性卷积的方法，用线性卷积计算循环卷积的方法，以及后者在OFDM 中的应用（循环前缀CP ），并给出了相关的Matlab 代码和实例进行验证和说明。

目的是为了建立起连续信号处理与离散信号处理之间的联系。

与本人在百度文库中的连续时间傅立叶变换与离散时间傅里叶变换之间的关系、从DTFT 到DFT ，计算频谱，并由频谱反求时间样点，为三部曲。

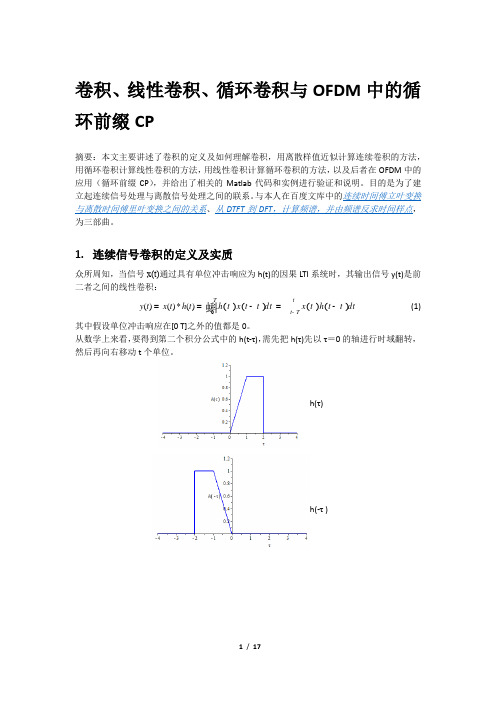
1. 连续信号卷积的定义及实质众所周知，当信号x(t)通过具有单位冲击响应为h(t)的因果LTI 系统时，其输出信号y(t)是前二者之间的线性卷积：()()()()0()()*()T t t Ty t x t h t h x t d x h t d t t t t t t -==-=-蝌 (1)其中假设单位冲击响应在[0 T]之外的值都是0。

从数学上来看，要得到第二个积分公式中的h(t-τ)，需先把h(τ)先以τ＝0的轴进行时域翻转，然后再向右移动t 个单位。

h(τ)h(-τ )图1.从上到下依次为h(τ), h(-τ), h(1-τ), x(τ), h(1-τ)* x(τ)在上面这个图形例子中，取t=1，故公共区间为[0,1]这个区间，故卷积积分的区间也是这个公共区间，即()()10(1)y x h t d t t t =-ò (2)上面图中的卷积结果将是一个分段函数。

上面的例子中，由于h(t)是连续的，故其与x(t)卷积的意义并不直观。

下面我们令h()()0.2(t 0.1)0.1(0.2)t t t d d d =+---(3) 这是一个典型的多径时延信道的抽头延迟线（TDL ）模型的单位冲击响应。

由于()()()()()000*x t t t x t t d x t t d t d t t ¥¥-=--=-ò－ (4)所以x(t)通过(3)式表示的信道h(t)后得到：()()()()()()()()**()0.2(t 0.1)0.1(0.2)0.20.10.10.2y t x t h t x t t t x t x t x t d d d ==+---=+---(5)h(1-τ )x(τ )移位对齐后相乘并积分（t=1）是各个信号延迟加权后的版本。

【信号与系统实验内容】实验三连续时间信号的卷积

实验三连续时间信号的卷积一、实验目的：1、掌握两个连续时间信号卷积的计算方法和编程技术。

2、进一步熟悉用MATLAB描绘二维图像的方法。

二、实验原理：卷积积分在信号与线性系统分析中具有非常重要的意义，是信号与系统分析的基本方法之一。

（一）卷积的定义连续时间信号f1(t)和f2(t)的卷积积分（简称为卷积）f(t)定义为：（二）线性时不变（LTI）系统的单位冲激响应给定一个连续时间LTI系统，在系统的初始条件为零时，用单位冲激信号δ(t)作用于系统，此时系统的响应信号称为系统的单位冲激响应（Unit impulse response），一般用h(t)来表示。

需要强调的是，系统的单位冲激响应是在激励信号为δ (t)时的零状态响应（Zero-state response）。

系统的单位冲激响应是一个非常重要的概念，如果已知一个系统的单位冲激响应，那么，该系统对任意输入信号的响应信号都可以求得。

（三）卷积的意义对于LTI系统，根据系统的线性和时不变性以及信号可以分解成单位冲激函数可得，任意LTI系统可以完全由它的单位冲激响应h(t)来确定，系统的输入信号x(t)和输出信号y(t)之间的关系可以用卷积运算来描述，即：由于系统的单位冲激响应是零状态响应，故按照上式求得的系统响应也是零状态响应。

它是描述连续时间系统输入输出关系的一个重要表达式。

（四）函数说明利用MATLAB的内部函数conv( )可以很容易地完成两个信号的卷积积分运算。

其语法为：y = conv(x,h)。

其中x和h分别是两个参与卷积运算的信号，y为卷积结果。

为了正确地运用这个函数计算卷积，这里对conv(x,h)做一个详细说明。

conv(x,h)函数实际上是完成两个多项式的乘法运算。

例如，两个多项式p1和p2分别为：和这两个多项式在MATLAB中是用它们的系数构成一个行向量来表示的，用x来表示多项式p1，h表示多项式p2，则x和h分别为x = [1 2 3 4]h = [4 3 2 1]在MATLAB命令窗口依次键入>> x = [1 2 3 4];>> h = [4 3 2 1];>> y=conv(x,h)在屏幕上得到显示结果：y = 4 11 20 30 20 11 4这表明，多项式p1和p2的乘积为：用MATLAB处理连续时间信号时，时间变量t的变化步长应该很小，假定用符号dt表示时间变化步长，那么，用函数conv( )作两个信号的卷积积分时，应该在这个函数之前乘以时间步长方能得到正确的结果。

时幅连续信号数值反卷积方法及其应用

列和响应序列进行抽样，造 “ 定 ” 性卷积方程组，在一定物理约束下利用最小二乘法求解方程构超线并组，到较低采样频率下输入信号序列的反卷积恢复。在Ｍａｌｂ中实现了该算法并进行了模拟。结果得ｔａ表明，当输出序列和响应序列所含加性白噪声小于５时，需任何预处理，卷积结果与原输入序列无反
ＮｕｅｉａｃｎｖｌｔｏｅｈｄｍｒｃｌＤｅｏｏｉｎＭｔｏｕ
ｆｒＣｏｉｏｓＳｇａｓＰｒｃｓｉｇａｄＩｓＡｐｐｉａｉｎｏｎｔｎｕｕｉｎｌｏｅｓｎｎｔｌｃｔｏ
符合很好。该方法适用于时幅连续信号处理，较好地解决反卷积的病态问题，用方便，不需序列能使且
重组，果直观、需延迟修正。该方法在脉冲辐射场诊断中已得到成功应用。结不关键词：号处理；积；卷积；态问题信卷反病中图分类号：ＴＮ９１７１．２文献标志码：Ａ文章编号：００６３（０８０ —３５０１０ —９１２０）５０８ —５
ＡｂｔａｔＡｍｅｉａｅｏｖｏｕｔｏｎｍｅｈｏｓｐｒｓｎｅｏｒｃｖｒｓｇａｓｏｉｇｓｓｓｒｃ：ｎｕｒｃｌｄｃｎｌｉｔｄｉｅｅｔｄｔｅｏｅｉｎｌｆｄａｎｏｅｉｕｌｅａｉｔｏｉｌｉｐｌｎｄｅｆｃｉｌ．Ｔｈｅｖｅｔｒｏｆｄｃｎｖｕｉｎｒｃｖｅｙｉｎｐｓｄｒｄａｉｎｆｅｄｓｓｍｙａｆｅｔｖｅｙｃｏｅｏｏｌｔｏｅｏｒｓｏｔｉｄａｌｗｅｓｍｐｌｎｆｅｅｙｆｏｎ ‘ ｒｅ — ｔｒｉｄ’ ｃｎｖｌｔｏｉａｂａｎｅｔａｏｒａｉｇｒｑｕｎｃｒｍａｏｒｄｅｅｍｎｅｏｏｕｉｎｌｎｅｒｅａｉｎｅｈｉｈｉｏｔｕｃｅｙｓｍｐｉｔｕｔｖｅｔｒｎｅｐｎｓｃｏｓａｑｕｔｏｓｓｔｗｃｓｃｎｓｒｔｄｂａｌｎｇｏｕｐｃｏｓａｄｒｓｏｅｖｅｔｒｔａｃｒａｎｃｎｄｔｏｎｄｉｓｖｄｂｙｅｓｓｕａｅｍｅｈｔｏｅｐｓｃｌｏｎｔａｎｔ．ｅｔｉｏｉｉｎａｓｏｌｅｌａｔｑｒｓｔｏｄａｓｍｈｙｉａｃｓｒｉｓＴｈｅｍｅｈｏｄｉｅｌｚｄａｉｕａｅｎＭａｌｂＴｈｅｓｍｕｌｔｄｒｓｔｈｏｔｔｔ — ｔＳｒａｉｅｎｄｓｍｌｔｄｉｔａ．ｉａｅｅｕｌｓｓｗｈａｈｅｄｅｃｎｖｕｉｎｓｌｉｎｓａｒｅｗｅｌｗｉｈｔｎｐｕｃｏｓｉｈｏｎｙａｉｉａｐｏｃｓｏｏｌｔｏｏｕｔｏｇｅｌｔｈｅｉｔｖｅｔｒｗｔｕｔａｄｄｔｏｎｌｒｅｓｗｈｅｈｅｅｒｒｓｏｉｔｄｗｉｈｔｕｔｕｔｖｃｏｓａｈｅｒｓｎｅｖｃｏｓａｒｅｓｔｎｎｔｒｏｓａｓｃａｅｔｈｅｏｐｅｔｒｎｄｔｅｐｏｓｅｔｒｅｌｓｈａ５．Ｔｈｅｍｅｈｏｓｓｉａｅｆｏｉｔｄｉｕｔｂｌｏｒｃｎｔｎｕｏｉｎａｓｐｒｃｓｉｎｄｖｒｃｕａｙｒｓｌｓｕｓｓｇｌｏｅｓｎｇａｅｙａｃｒｃｅｕｔ

通信中的反卷积技术与解卷积技术分析

通信中的反卷积技术与解卷积技术分析随着信息技术的高速发展，通信技术也不断地得到不断的更新、升级。

作为通信领域中的重要技术之一，反卷积和解卷积技术在通信系统中扮演着十分重要的角色。

本文将从一些基本概念开始，解析通信中的反卷积技术与解卷积技术，深入探讨这些技术在通信中的应用。

一、反卷积技术的基本概念反卷积技术的本质是利用卷积运算的可逆性，将紧缩的信号序列扩张成原来的信号序列，以便更好地恢复原始信号。

反卷积即为卷积的逆操作，是卷积定理的一种实际应用。

反卷积技术可以广泛应用于通信系统中的信号处理、图像处理等领域，其作用是通过对卷积结果进行反向运算，消除通信信道中的传递函数及其引起的失真、干扰等影响，达到更加精确的信号处理和误差修正的目的。

二、解卷积技术的基本概念解卷积技术是通过利用卷积定理，将卷积系统的频率响应进行逆变换，从而得到信号的恢复值。

解卷积技术的核心是正规方程组或者是逆矩阵的求解，解决了存在多个未知变量的方程组求解问题。

解卷积技术同样广泛应用于通信系统中的信号处理和图像处理等领域，它可以有效的消除传输路径信号空间的衰减以及噪声影响等问题，从而得到更高质量的通讯信号和信号恢复值，减少了信号传输过程中的损耗。

三、反卷积技术和解卷积技术在通信领域的应用在通信领域中，反卷积技术和解卷积技术是最重要的两个信号处理技术，它们在通信系统中的应用十分广泛。

在无线通信领域，当信号穿越空间时，信号会遭到多径衰落和其他干扰因素的影响，导致信号质量下降，所以反卷积技术和解卷积技术在无线通信领域的应用非常显著。

通过使用反卷积技术和解卷积技术，信号可以得到更加精确高效的处理，从而提高了信号传输的质量和速率。

在数字信号的处理中，反卷积技术和解卷积技术同样也具有重要意义。

例如，图像信号经过传输后可能会受到噪声、失真或其他干扰的影响，这时需要对图像信号进行反卷积或解卷积处理，以保持图像的清晰度和准确性。

四、反卷积技术和解卷积技术的优缺点反卷积技术和解卷积技术有各自的优缺点。

解释反卷积的原理和用途

解释反卷积的原理和用途
反卷积是信号处理中的一种基本技术，其原理可以理解为卷积操作的逆操作。

然而，反卷积并不能完全还原出原始的输入信号，因为卷积操作在某些信息上是不可逆的。

具体来说，反卷积是将卷积核进行转置后再与卷积后的结果进行一次卷积操作。

虽然不能完全恢复出原始的输入信号，但反卷积可以在一定程度上恢复被卷积生成后的原始输入，将带有小部分缺失的信息最大化地恢复。

反卷积的用途广泛，包括但不限于以下几个方面：
1. 信道均衡：在通信系统中，信号在传输过程中可能会受到各种干扰和失真，导致信道均衡问题。

反卷积可以用于估计和补偿这些失真，从而恢复原始信号。

2. 图像恢复：在图像处理中，图像可能会受到噪声、模糊或其他失真的影响。

反卷积可以用于估计和恢复原始图像。

3. 地震学：在地震学中，地震波传播的特性可以通过反卷积来估计。

这有助于研究地球内部结构和地震活动的规律。

4. 无损探伤：在无损探伤中，反卷积可以用于从探测到的信号中提取有关材料性质的信息。

5. 未知输入估计和故障辨识：在某些情况下，系统中的未知输入或故障可以通过反卷积来估计和辨识。

总之，反卷积是一种重要的信号处理技术，广泛应用于各种领域。

卷积积分在连续时间系统中的应用

卷积积分在连续时间系统中的应用
卷积积分在连续时间系统中的应用非常广泛。

下面列举了一些常见的应用：
1. 线性时不变系统的响应：当输入信号和系统的单位响应之间进行卷积积分时，得到的结果就是系统的输出。

2. 信号处理：卷积积分可用于对信号进行平滑、滤波和降噪处理，比如均值滤波、高斯滤波等。

3. 信号模拟：对于某些连续时间系统，可以使用卷积积分来模拟其响应，比如光学系统、电路系统等。

4. 传输系统：在电信、传感器、控制系统等领域，卷积积分可用于传输信号，计算信号传输的时延、衰减等。

5. 信号恢复：当输入信号被噪声干扰时，可以使用卷积积分来恢复信号，比如盲源分离、反卷积等。

6. 信号分析：卷积积分可用于对信号频谱、相位、幅度进行分析，比如傅里叶变换、小波变换等。

总之，卷积积分在连续时间系统中有着广泛的应用，是信号处理、系统建模、信号传输和信号分析等领域中不可或缺的工具。

反卷积计算方法

反卷积计算方法
以下是 6 条关于反卷积计算方法的内容：
1. 嘿，你知道反卷积计算方法吗？就像搭积木一样，一步一步来！比如说，我们想还原一张模糊的图片，用反卷积不就像是在给图片做一次神奇的修复嘛！它能把那些看不清的细节一点一点地恢复出来！难道你不想知道这其中的奇妙之处？
2. 哎呀呀，反卷积计算方法可有意思啦！好比你有一堆混乱的拼图，反卷积就是帮助你理清这些拼图的关键！比如说在图像处理里，它能让模糊的图像变得清晰，就好像有一双神奇的手在整顿混乱一样！这多么令人惊叹啊，你还不好奇吗？
3. 哇塞，反卷积计算方法真的超厉害的！就像是在黑暗中找到光明的那根线一样！你想想看，在语音处理中，它能让嘈杂的声音变得清晰可辨，这不就是在创造奇迹嘛！难道你不想深入了解一下这种神奇的力量？
4. 嘿呀，反卷积计算方法可不是一般的牛！好比是解开一团乱麻的那把钥匙！例如在数据重建中，它可以从残缺的数据里还原出原本的样子，这简直太不可思议了吧！你难道不想掌握这个神秘又厉害的方法吗？
5. 哇哦，反卷积计算方法可太好玩啦！就像一个超级魔术师一样！比如在图像识别领域，它能让模糊的物体变得清晰明确，这不就是在变魔法嘛！难道你不想看看它是怎么施展魔法的？
6. 哈哈，反卷积计算方法真的超有趣！就跟探索一个神奇的世界一样！当我们把它用到信号处理中，它能让微弱的信号变得清晰可感，这真的太赞了！你就不好奇自己也能成为这个神奇世界的探索者吗？
我的观点结论是：反卷积计算方法有着广泛的应用和巨大的潜力，非常值得我们去深入学习和研究。

邹谋炎著,反卷积和信号复原

邹谋炎著,反卷积和信号复原全文共四篇示例，供您参考第一篇示例：反卷积和信号复原是信号处理和图像处理中的重要概念和技术，其在实际应用中具有广泛的应用。

本文将结合邹谋炎著的相关研究成果，就反卷积和信号复原的基本原理、算法方法及其在实际中的应用进行系统性的介绍和分析。

我们从反卷积的基本原理开始讲解。

在信号处理和图像处理中，由于各种因素（如系统退化、噪声干扰等）的存在，信号会发生失真和模糊，导致观测到的信号与原始信号之间存在偏差。

反卷积通过逆向系统的退化过程，尝试还原原始信号，是一种重要的信号复原技术。

在邹谋炎著的相关研究中，他提出了一系列基于反卷积的新方法和算法，为信号复原领域的研究和应用做出了重要贡献。

在反卷积的研究中，频域方法和空域方法是常用的两种反卷积算法。

频域方法通常基于傅里叶变换，将观测信号转换到频域进行处理，然后再通过逆变换得到复原信号。

而空域方法则直接在时域中对观测信号进行处理。

邹谋炎著提出的一些新的算法和理论，往往能够有效地克服传统方法的局限性，提高反卷积的精度和稳定性。

除了在理论研究中取得重要成果，邹谋炎著还将反卷积技术成功应用于实际问题中。

在医学影像处理中，由于设备限制和物理环境等因素，获取到的医学影像往往存在模糊和失真。

通过利用反卷积技术，可以改善医学影像的质量，提高诊断的准确性。

在遥感图像处理、无损检测、数字相机成像等领域，反卷积技术也得到了广泛的应用。

除了反卷积技术，信号复原在图像处理中也有着重要的应用。

信号复原是指从受损的图像中恢复出高质量的原始图像的过程。

在现实生活中，受损的图像常常由于光照条件、传感器故障、传输噪声等因素引起。

通过信号复原技术，可以对受损的图像进行恢复和重建，提高图像的质量和清晰度。

邹谋炎著在信号复原方面的研究也取得了一定的成果，他提出了一些新的复原算法和模型，为图像处理领域的发展做出了贡献。

反卷积和信号复原是信号处理和图像处理领域中的重要问题，其在实际中具有广泛的应用前景。

反卷积详解

反卷积详解
反卷积，也称为反卷积操作，是一种图像处理技术。

在卷积神经
网络中，反卷积用于对卷积层的输出进行反向操作，生成特征图。

与
卷积层相反的是，反卷积同样也是一组可训练的卷积核，但是其卷积
核的大小通常大于输入特征图的大小。

反卷积的输出大小取决于卷积
核的尺寸和被反卷积的输入大小。

反卷积的作用是将卷积层中常常会缩小特征图尺寸的操作重新放
大回去。

例如，一张28x28的图片，在通过卷积层进行特征提取之后，可能会被压缩成14x14，7x7或者更小的尺寸。

如果我们需要对这些特
征进行可视化或者进一步处理，就需要利用反卷积对特征图进行还原。

反卷积的实现方式通常是通过空间上的插值操作来放大特征图，
再通过卷积运算进行特征增强。

反卷积的过程中，我们需要确定反卷
积核的大小，步长，填充等参数，使得反卷积得到的特征图与原始输
入尺寸相同。

总之，反卷积作为卷积神经网络中不可或缺的一环，具有非常重
要的作用。

它使得我们可以将卷积神经网络中提取的特征进行可视化
和进一步处理，为计算机视觉领域的应用带来了很大的便利。

信号与系统反卷积

m0
二．举例
某地址勘探测试设备给出的发射信号f (k) δk 1 δk 1,
2 接收回波信号y(k) 1 k ε(k),若地层反射特性的系统函数
2 用h(k )表示，且满足y(k) h(k) f (k)。
(1)求h(k );
(0)
1
2
0
1
2
2
2
h(3)
y(3)
h(0) f(3) h(1) f(2)
0
h(2)
f
(1)
f (0) 1 3 1 2 1 0 2 2 2
0 k为奇数
hk
1 2
k
k为偶数
（2）
k 1
h(k) y(k) h(m) f (k m) f (0)
m0
1 2
k
(k
14
DD
三、应用实例
雷达探测系统
f t
发送信号
hT t
发送天线
ht
待测目标
hR t
接收天线
yt
接收信号
y(t) f (t) hT (t) h(t) hR (t)
求出系统的冲激响应h(t )，即可判别目标，运算时需离散化。
(2)以延时、相加、倍乘运算为基本单元，试画出系统方框图。
解：（1）求h(k)
h(0) y(0) f (0) 1
h(1) y(1) h(0) f (1) f (0) 1 1 0
22
h(2)
y
(2)
h(0) f(2)
0
h(1)
f

反卷积可解释

反卷积可解释反卷积作为一种重要的信号处理技术，在图像处理、计算机视觉和深度学习等领域中得到了广泛的应用。

本文将详细介绍反卷积的概念、原理以及可解释性，并探讨其在实际应用中的意义和局限性。

一、概述在信号处理中，卷积运算是一种常见的运算方式，通常用于图像滤波、特征提取等操作。

而反卷积则是卷积运算的逆操作，用于还原经过卷积处理后的信号。

二、原理反卷积运算是通过卷积核的转置来实现的。

在标准的卷积运算中，卷积核滑动在输入图像上并生成输出特征图；而在反卷积运算中，卷积核滑动在输出特征图上，并生成输入图像的估计。

这种操作可以看作是通过卷积核的旋转和镜像来进行信号重建的过程。

三、可解释性反卷积在深度学习中具有一定的可解释性。

通过观察反卷积后的输出，我们可以对网络的学习过程和模型的内部表示进行理解。

例如，在图像分割任务中，通过反卷积操作可以可视化网络学习到的物体轮廓和边界信息，从而帮助我们理解模型的决策依据。

四、应用领域反卷积在图像处理和计算机视觉中有着广泛的应用。

其中，图像超分辨率是一个典型的应用场景。

通过将低分辨率图像进行反卷积处理，可以获得高分辨率的图像估计。

此外，反卷积还可以用于目标检测、语义分割、图像生成等任务中。

五、局限性反卷积也存在一些局限性。

首先，反卷积操作是一个不可逆的过程，即无法完全还原原始信号。

其次，反卷积操作对输入特征的选择和分辨率有着一定的依赖性，因此对特征图的质量和精度要求较高。

此外，反卷积操作也比较复杂，计算量较大，需要充分考虑计算资源和运行时间的限制。

六、总结反卷积作为一种重要的信号处理技术，在图像处理和深度学习中发挥着重要的作用。

它不仅可以用于信号的重建和图像的增强，还可以为深度学习模型的分析和可解释性提供支持。

然而，反卷积也存在一些局限性，需要在实际应用中加以注意。

未来，我们可以进一步研究和改进反卷积算法，以提高其性能和应用范围。

最后，反卷积技术的不断发展与应用，将为图像处理和深度学习领域带来更多的潜力和机遇。

卷积公式的使用条件

卷积公式的使用条件
有一种学术的说法：卷积是将过去所有连续信号经过系统的响应之后得到的在观察那一刻的加权叠加。

从打板子的例子来看结合前边提到的连续形式f和g的卷积，可以理解为f和g的卷积在n处的值是用来表示在时刻n遭受的疼痛程度。

f(t)是在说t这一时刻的人打的力度，g(n-t)说的是现在站在n时刻开始统计这个t时刻打的板子本身的疼痛程度变化成了什么样子。

将所有积分计算出来就可以知道到n时刻这个人有多痛。

卷积是一种积分变换的数学方法，在许多方面得到了广泛应用。

用卷积解决试井解释中的问题，早就取得了很好成果，而反卷积是直到最近Schroeter、Hollaender和Gringarten等人解决了其计算方法上的稳定性问题，使反卷积方法很快引起了试井界的广泛注意。

IRF反卷积拟合

IRF反卷积拟合
反卷积拟合(IRF fitting)是一种在信号处理中独特的拟合方式，它的目的是从获取的数据中找出与之相关的反向信号响应函数(IRF)。

在IRF拟合中，通过使用最小二乘法对原始数据集进行拟合，使用最佳反卷积函数以及
正确的参数值获得最佳拟合，从而求出表示模型和实际数据之间联系的IRF。

反卷积拟合是一种简单有效的处理方法，可以用于任何服从任意分布情
况下不同信号的拟合，而无需改变输入信号的基本结构。

它可以更好地预测
和解释信号中的显著特征，更好地描述和分析信号的特性。

此外，IRF拟合
还可以用于处理时间相关信号，以期获得更准确的信号处理结果，因此可以
实现精确的数据分析。

IRF拟合技术的优点是，它的结果具有可重复性和可验证性，并且对于
非常复杂的处理过程来说，可以很快地得出结果。

它还可以在不改变输入信
号的基本结构的情况下处理不同信号，无需重新设计整个系统，从而提高处
理效率。

总之，反卷积拟合是信号处理中一种新兴而有效的拟合方法，它以其易
于使用、可重复性和可验证性的特点，在对不同信号数据进行拟合和分析方
面已经发挥了重要作用。

时幅连续信号数值反卷积方法及其应用

信号反卷积

f-x反卷积方法

【最新精选】实验二连续时间号、离散信号卷积运算

实验二连续时间信号、离散信号卷积运算

信号与系统 §2.07 卷积的性质

信号翻转尺度变换和时移的注意事项和关键点

反卷积函数

卷积.循环卷积与OFDM

【信号与系统实验内容】实验三连续时间信号的卷积

时幅连续信号数值反卷积方法及其应用

通信中的反卷积技术与解卷积技术分析

解释反卷积的原理和用途

卷积积分在连续时间系统中的应用

反卷积计算方法

邹谋炎著,反卷积和信号复原

反卷积详解

信号与系统 反卷积

反卷积 可解释

卷积公式的使用条件

IRF反卷积拟合

信号与系统反卷积

反卷积可解释