内心、外心、重心、垂心定义及性质总结讲解学习
三角形重心垂心外心内心相关性质介绍
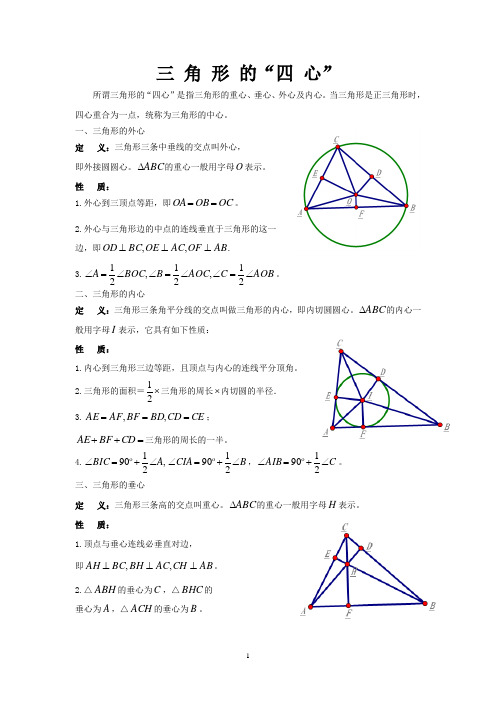
三 角 形 的“四 心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)0=++GC GB GA ;(2))(31PC PB PA PG ++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心: 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心: 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心: 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心: 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.
THANKS
致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求
欢迎您的下载,资料仅供参考。
内心、外心、重心、垂心定义及性质总结讲解学习

内心、外心、重心、垂心定义及性质总结1.内心:(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3重心:(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2 倍。
4垂心:三条高所在直线的交点。
5重心:三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.6垂心:三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.7内心:三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根源;点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定义理当然.8外心:三角形有六元素,三个内角有三边.作三边的中垂线,三线相交共一点.此点定义为“外心”,用它可作外接圆.“内心” “外心”莫记混,“内切” “外接”是关键.保安员服装管理规定一、目的为加强保安队伍的职业化、正规化建设,规范公司保安制服的领用、发放和管理,特制定以下规定:二、范围本规定明确了公司保安制服领用、发放范围,收费及折旧办法等。
三、职责1.财务部负责公司制服的采购。
2.管理部内勤负责公司制服的保管、发放及制服发放名单的统计核实工作。
3.管理部负责员工着装的检查工作。
四、管理内容与要求1.保安制服分类:共分夏装、春秋装、冬装三种,其中含附件有:帽子1顶,腰带1条,领带1条;配饰有:硬肩章、软肩章、胸号、胸徽、帽徽及领带夹等。
1)夏装包括:短袖衬衣、夏裤。
2)春秋装包括:长袖衬衣、春秋套装。
3)冬装包括:棉衣。
2.特勤服分类:共分夏装、春秋装、冬装三种,其中含附件有:帽子1顶;配饰有:肩章、背章、胸号、胸徽、腰带、帽徽等八件套。
1)夏装包括:短袖衬衣、夏裤。
内心、外心、重心、垂心定义及性质总结-外心的定义

内⼼、外⼼、重⼼、垂⼼定义及性质总结-外⼼的定义内⼼、外⼼、重⼼、垂⼼定义及性质总结
1.内⼼:
(1)三条⾓平分线的交点,也是三⾓形内切圆的圆⼼。
(2)性质:到三边距离相等。
2外⼼:
(1)三条中垂线的交点,也是三⾓形外接圆的圆⼼。
(2)性质:到三个顶点距离相等。
3 重⼼:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂⼼:三条⾼所在直线的交点。
5 重⼼: 三条中线定相交,交点位置真奇巧,
交点命名为“重⼼”,重⼼性质要明了,
重⼼分割中线段,数段之⽐听分晓;
长短之⽐⼆⽐⼀,灵活运⽤掌握好.
6 垂⼼: 三⾓形上作三⾼,三⾼必于垂⼼交.
⾼线分割三⾓形,出现直⾓三对整,
直⾓三⾓形有⼗⼆,构成六对相似形,四点共圆图中有,细⼼分析可找清.
7内⼼: 三⾓对应三顶点,⾓⾓都有平分线,
三线相交定共点,叫做“内⼼”有根源;
点⾄三边均等距,可作三⾓形内切圆,
此圆圆⼼称“内⼼”如此定义理当然.
8外⼼: 三⾓形有六元素,三个内⾓有三边.
作三边的中垂线,三线相交共⼀点.
此点定义为“外⼼”,⽤它可作外接圆.
“内⼼”“外⼼”莫记混,“内切”“外接”是关键.如有侵权请联系告知删除,感谢你们的配合!。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心 : 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心 : 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心 : 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心 : 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.。
内心、外心、重心、垂心定义及性质总结

此文档收集于网络,如有侵权请联系网站删除
内心、外心、重心、垂心定义及性质总结
1. 内
心:(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2 外
心:1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重
心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍
4 垂心:三条高所在直线的交点
5 重心: 三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.
6 垂心: 三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直
角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7 内心: 三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根
源;点至三边均等距,可作三角形内切圆,此圆圆心称“内心”如此定
义理当然.
8 外心: 三角形有六元素,三个内角有三边.作三边的中垂线,三线相交共一点.此点定义为“外心” ,用它可作外接圆.“内心”“外心”莫记混,“内切”“外接”是关键.。
三角形重心垂心外心内心相关性质介绍

三 角 形 的“四 心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,.3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)=++;(2))(31++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
最新整理内心、外心、重心、垂心定义及性质总结48783知识讲解

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心 : 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心 : 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心 : 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心 : 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质在三角形中,有四个非常重要的点,它们是:内心、外心、重心和垂心。
这些点的性质在几何学和三角学中都非常重要。
在本文中,我们将对这些点进行定义和它们的性质。
内心内心是一个三角形内部的点。
它是由三条角平分线所确定的点,也就是说,它到三角形三条边的距离相等。
性质1.内心是三角形的唯一的内接圆心。
2.内心到三角形三边的距离相等。
3.连接内心与三角形三个顶点的线段分别垂直于三边。
4.内心和三角形顶点的连线相交于三角形的垂心。
5.内心是三角形的重心、外心和垂心的欧拉线的交点之一。
外心外心是一个三角形外部的点,它是由三边中垂线的交点所确定的点。
外心是三角形外接圆的圆心。
性质1.外心是三角形的唯一的外接圆心。
2.连接外心与三角形三个顶点的线段分别垂直于相应的边。
3.外心到三角形三个顶点的距离相等。
4.三角形的角上的中垂线恰好交于外心。
5.外心到三角形三边的距离相等。
重心重心是由三条中线的交点所确定的点。
性质1.重心到三角形三个顶点的距离相等。
2.连接重心和三角形三个顶点的线段相等。
3.重心将每条中线分成两个部分,中心到三角形各边上的点的距离之和相等。
4.重心是三角形垂心和外心的中点。
5.连接重心与三个角平分线的交点构成的三角形是原三角形的等价三角形。
垂心垂心是由三边的垂线所交的点。
性质1.垂心到三角形三个顶点的线段中,最短的是对应于最大角的那一段。
2.垂心到三角形三个顶点的线段之和是定值,即为三角形的半周长。
3.三角形的顶点与对面边上的垂足之间的线段互相垂直。
4.三角形的三个垂直平分线相交于垂心。
5.垂心是三角形内心、外心和重心的欧拉线的交点之一。
内心、外心、重心和垂心是三角形中非常重要的点。
它们有许多有趣的性质,这些性质在解决各种几何问题时非常有用。
正三角形重心中心垂心外心内心的知识点

正三角形重心中心垂心外心内心的知识点一、知识概述《正三角形重心、中心、垂心、外心、内心》①基本定义:- 重心:说实话,这就像是正三角形的平衡点。
如果把正三角形看作是一块均匀的薄板,从重心这个点吊起来,薄板会水平平衡。
它是三条中线(连接一个顶点和对边中点的线段)的交点。
- 中心:在正三角形里,重心、垂心、外心、内心这四个心是重合的,这个重合的点就叫做中心。
- 垂心:想象一下,从正三角形的每个顶点向对边作垂线,三条垂线的交点就是垂心,这就好比是三角形三条高线(过顶点作对边的垂线段)相交的地方。
- 外心:它是正三角形外接圆的圆心,这个点到三个顶点的距离是相等的。
就像用一个圆刚好把正三角形圈在里面,这个圆的圆心就是外心。
- 内心:这是正三角形内切圆的圆心,内心到三条边的距离相等。
就好像在正三角形里面画一个正好能挨着三条边的圆,这个圆的圆心就是内心。
②重要程度:在三角形相关的几何知识里,这些概念非常重要。
无论是解决几何证明题,还是计算三角形的一些数值,它们都是关键的要素。
就像建房子的基石一样,如果这些概念不清楚,很多关于正三角形更复杂的问题就做不了。
③前置知识:得先把三角形的基础概念搞清楚,像三角形的边、角、顶点这些。
另外,得知道线段的中点怎么找,垂线怎么作,还有圆的一些基本概念,像圆心、半径什么的。
④应用价值:在建筑设计里,如果要设计一个正三角形结构的建筑,这些心的位置可以帮助确定建筑的力学结构平衡点,稳定性布局等。
在机械制造中,处理正三角形形状的零件,这些概念有助于精准定位和设计加工工艺。
二、知识体系①知识图谱:在几何学科里,正三角形的这几个心是三角形性质这一板块的重要内容,和三角形的全等、相似等概念也有着千丝万缕的联系。
②关联知识:和三角形的内角和、等腰三角形的性质等知识是紧密相联的。
比如说,正三角形内角都是60度,这一性质在研究这几个心的位置关系或者计算与这几个心相关的线段长度时有时候也会用到。
③重难点分析:- 掌握难度:我觉得对于初学者来说还是有点难度的。
内心、外心、重心、垂心定义及性质总结[借鉴]
![内心、外心、重心、垂心定义及性质总结[借鉴]](https://img.taocdn.com/s3/m/78232147eef9aef8941ea76e58fafab069dc4404.png)
内心、外心、重心、垂心定义及性质总结[借鉴]内心、外心、重心、垂心是几何学中与三角形相关的四个重要概念。
以下是它们的定义及性质总结:1.内心(Incenter)定义:内心是三角形内切圆的圆心。
性质:o内心到三角形三个顶点的距离相等。
o内心与三角形各边之间的距离等于三角形半周长与内切圆半径之差的一半。
o在内心分线上,任意两边的向量之积等于另外两边向量之积的负值。
2.外心(Excenter)定义:外心是三角形外接圆的圆心。
性质:o外心到三角形三个顶点的距离相等。
o外心与三角形各顶点连线所成的角等于三角形内角和的一半。
o在外心分线上,任意两边的向量之积等于另外两边向量之积的值。
3.重心(Centroid)定义:重心是三角形三条中线的交点。
性质:o重心到三角形三个顶点的距离与到三条中线的距离相等。
o重心与三角形各边之间的距离等于三角形半周长与外接圆半径之差的一半。
o在重心分线上,任意两边的向量之积等于另外两边向量之积的值。
4.垂心(Hypotenuse)定义:垂心是三角形各边上的高线的交点。
性质:o垂心到三角形三个顶点的距离与到三条高的距离相等。
o垂心与三角形各顶点连线所成的角等于三角形内角和的一半。
o在垂心分线上,任意两边的向量之积等于另外两边向量之积的负值。
总结:内心、外心、重心和垂心在几何学中具有特殊的性质和重要性。
这些概念之间的关系可以用于证明定理和解决问题。
对于内心和外心,它们分别与三角形的内切圆和外接圆相关,而重心和垂心则分别与三角形的中线和高的交点相关。
这些概念及其性质在几何学中具有广泛的应用,例如在解决几何问题、绘制图形和证明定理等方面都有重要的应用价值。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总
结
内心、外心、重心、垂心,听起来是不是有点抽象?其实它们就像是几颗星星,各自闪烁却又紧密相连。
首先,内心指的是一个三角形内部的重心,能够很好地代表这个三角形的“平均位置”。
想象一下,就像在一块蛋糕的中心,哪里最甜,在哪里就是内心。
再说外心,顾名思义,它就是三角形外部的一个点,能与三角形的三个顶点连成等边三角形,真是个神奇的概念。
外心的存在就像一位默默无闻的英雄,虽然不在三角形的内部,但却和三角形息息相关。
它总是与角度相关,能够让我们更好地理解三角形的对称性。
接着我们来聊聊重心。
重心是三角形的一个重要概念,大家知道吗?重心就像那颗能量源泉,位于三角形三个顶点连线的交点。
这个位置就是三角形的“心脏”,它的特性在于重心的存在让三角形在任何方向上的稳定性都达到了极致。
换句话说,重心让三角形不管怎样摆放都能保持平衡,简直是个天生的调和者。
最后,我们来看看垂心。
垂心是个有趣的角色,它是三角形各边延长线与对顶角的交点。
想象一下,如果三角形是个舞台,垂心就是那颗最闪亮的
明星。
它的作用在于能够通过高度来实现与三角形的某种关系,真的是个不可或缺的元素。
每当我们把这四个概念结合在一起,便能更深入地了解三角形的奥秘。
总结起来,内心、外心、重心、垂心,这四个概念就像一场精彩的表演,彼此辉映。
它们不仅仅是几何中的抽象符号,更是我们理解空间和形状的钥匙。
无论是学习数学,还是在日常生活中,掌握这些概念都能让我们更加从容自信。
就像一首动听的旋律,每一个音符都不可或缺,让我们一起在这片数学的天地中畅游吧!。
三角形重心垂心外心内心相关性质介绍

三 角 形 的“五 心”所谓三角形的“五心”是指三角形的重心、垂心、外心、旁心及内心。
当三角形是正三角形时,重心、垂心、外心及内心重合为一点,统称为三角形的中心。
一、三角形的外心(1个)定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的外心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21 4.直角三角形的外心在斜边中点。
二、三角形的内心(1个)定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2. CE CD BD BF AF AE ===,,3. 三角形的面积=⨯21三角形的周长⨯内切圆的半w 径.; =++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的旁心(3个) 定 义:三角形的一条内角平分线与其他两个角的外角平分线交于一点,即三角形的旁心。
性 质:1. 旁心到三角形一边及其他两边延长线的距离相等。
即,到三边距离相等。
2. 三角形有三个旁心。
这三个旁心到三角形三条边的延长线的距离相等3. 与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心叫旁心。
四、三角形的垂心定 义:三角形三条高的交点叫垂心。
ABC ∆的垂心一般用字母H 表示。
直角三角形的垂心在直角顶点上。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心1、内心(1)定义:三角形的内心是三角形三条角平分线的交点(或内切圆的圆心)。
(2)三角形的内心的性质①三角形的三条角平分线交于一点,该点即为三角形的内心②三角形的内心到三边的距离相等,都等于内切圆半径r③s=(r是内切圆半径)④在Rt△ABC中,∠C=90°,r=(a+b-c)/2.⑤∠BOC = 90 °+∠A/2 ∠BOA = 90+∠C/2 ∠AOC = 90+∠B/22、外心(1)定义:三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
(2)三角形的外心的性质①三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
③锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合④OA=OB=OC=R⑤∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA⑥S△ABC=abc/4R3、重心(1)三角形的三条边的中线交于一点。
该点叫做三角形的重心。
(2)三角形的重心的性质①重心到顶点的距离与重心到对边中点的距离之比为2:1。
②重心和三角形3个顶点组成的3个三角形面积相等。
③重心到三角形3个顶点距离的平方和最小。
④在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/3⑤重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
⑥重心是三角形内到三边距离之积最大的点。
4、垂心(1)定义:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
(2)三角形的垂心的性质①锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外②三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心③垂心O关于三边的对称点,均在△ABC的外接圆上④△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AO·OD=BO·OE=CO·OF⑤H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形xx的圆心。
(2)性质:到xx距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心:三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.
6 垂心:三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7内心:三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根源;点至xx均等距,可作三角形xx,此圆圆心称“内心”如此定义理当然.
8外心:三角形有六元素,三个内角有xx.作xx的中垂线,三线相交共一点.此点定义为“外心”,用它可作外接圆.“内心”“外心”xx混,“内切”“外接”是关键.
1/ 1。
三角形重心垂心外心内心相关性质介绍资料讲解

三角形重心垂心外心内心相关性质介绍三 角 形 的“四 心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,.3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心 定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质: 1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠οB CIA ∠+=∠2190ο,C AIB ∠+=∠2190ο。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2=== 3.重心的坐标是三顶点坐标的平均值.即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)=++; (2))(31++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
内心、外心、重心、垂心定义及性质总结-外心的定义

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等.
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心:三条中线定相交,交点位置真奇巧,
交点命名为“重心",重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心 : 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清。
7内心 : 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心 : 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心"莫记混,“内切”“外接”是关键.。
内心、外心、重心、垂心定义及性质总结

内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形xx的圆心。
(2)性质:到xx距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心:三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.
6 垂心:三角形上作三高,三高必于垂心交.高线分割三角形,出现直角三对整,直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7内心:三角对应三顶点,角角都有平分线,三线相交定共点,叫做“内心”有根源;点至xx均等距,可作三角形xx,此圆圆心称“内心”如此定义理当然.
8外心:三角形有六元素,三个内角有xx.作xx的中垂线,三线相交共一点.此点定义为“外心”,用它可作外接圆.“内心”“外心”xx混,“内切”“外接”是关键.
1/ 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心 : 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心 : 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,
直角三角形有十二,构成六对相似形,
四点共圆图中有,细心分析可找清.
7内心 : 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心 : 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.保安员服装
管理规定
一、目的
为加强保安队伍的职业化、正规化建设,规范公司保安制服的领用、发放和管理,特制定以下规定:
二、范围
本规定明确了公司保安制服领用、发放范围,收费及折旧办法等。
三、职责
1.财务部负责公司制服的采购。
2.管理部内勤负责公司制服的保管、发放及制服发放名单的统计核实工作。
3.管理部负责员工着装的检查工作。
四、管理内容与要求
1.保安制服分类:共分夏装、春秋装、冬装三种,其中含附件有:帽子1顶,
腰带1条,领带1条;配饰有:硬肩章、软肩章、胸号、胸徽、帽徽及领带夹等。
1)夏装包括:短袖衬衣、夏裤。
2)春秋装包括:长袖衬衣、春秋套装。
3)冬装包括:棉衣。
2.特勤服分类:共分夏装、春秋装、冬装三种,其中含附件有:帽子1顶;
配饰有:肩章、背章、胸号、胸徽、腰带、帽徽等八件套。
1)夏装包括:短袖衬衣、夏裤。
2)春秋装包括:春秋套装。
3)冬装包括:棉衣。
