《普通物理学》PPT课件
合集下载
普通物理学课件:10磁介质中的安培环路定理(普通物理 )

r2 R2 I
H
Ir
2R2
B
Ir 2R2
R
I
H
0
r
r R H2r I
H I B 0I
2r
2r
I R
0
r
H
B
H
I
2R
I 2R
0I 2R
O
R
rO
R
r
在分界面上H 连续, B 不连续
电介质中的
高斯定理
S
E
dS
1
0
S(qຫໍສະໝຸດ qi')1
1
S
E
dS
0
S
q
0
S
P
dS
S (0E P) dS q
S
D 0E P
D dS S
V edV
二、磁场强度、磁感应强度的关系
M mH
B
H M
0
m —
B 0
介质的磁化率
mH
B 0(1 m )H 0r 介质的磁导率
r
B H
B,
H
,
M
之间的关系
M
B
m
H
H M
0
B 0(1 m )H
r
(
1
m
)
B 0r H H
r称为相对磁导率
0r磁导率
P、D、E 之间的关系
P e0E
D 0E P
D ( 1 e ) 0E
r
(1
e
)
D r0E E
称为相对电容率
r
或相对介电常量
例1 一环形螺线管,管内充满磁导率为μ,相对磁导 率为μr的顺磁质。环的横截面半径远小于环的半径。
H
Ir
2R2
B
Ir 2R2
R
I
H
0
r
r R H2r I
H I B 0I
2r
2r
I R
0
r
H
B
H
I
2R
I 2R
0I 2R
O
R
rO
R
r
在分界面上H 连续, B 不连续
电介质中的
高斯定理
S
E
dS
1
0
S(qຫໍສະໝຸດ qi')1
1
S
E
dS
0
S
q
0
S
P
dS
S (0E P) dS q
S
D 0E P
D dS S
V edV
二、磁场强度、磁感应强度的关系
M mH
B
H M
0
m —
B 0
介质的磁化率
mH
B 0(1 m )H 0r 介质的磁导率
r
B H
B,
H
,
M
之间的关系
M
B
m
H
H M
0
B 0(1 m )H
r
(
1
m
)
B 0r H H
r称为相对磁导率
0r磁导率
P、D、E 之间的关系
P e0E
D 0E P
D ( 1 e ) 0E
r
(1
e
)
D r0E E
称为相对电容率
r
或相对介电常量
例1 一环形螺线管,管内充满磁导率为μ,相对磁导 率为μr的顺磁质。环的横截面半径远小于环的半径。
大学普通物理学经典课件——静电场 共75页PPT资料

r 电偶极子的轴 0 电偶极矩(电矩)
p qr0
q
p q
讨论
r0
(1)电偶极子轴线延长线上一点的电场强度
q O q
r0 2 r0 2
E
x
A
E
x
q O q
x r0 2 r0 2
E
A
E
x
1
q
E
ቤተ መጻሕፍቲ ባይዱ
4π 0
(xr0
2)2i
E 4π10(xrq0 2)2i
四 掌握用点电荷和叠加原理以及电势的定义式 求解带电系统电势的方法.
§9.1 电荷 电荷的量子化 电荷守恒定律
一 电荷的量子化
基本性质 1 电荷有正负之分;
2 电荷量子化; 电子电荷 e1.6012 0 1C 9
q ne(n 1 ,2 ,3 , )
3 同性相斥,异性相吸.
强子的夸克模型具有分数电荷( 1 或 2 电子电荷)
E
V
1
4π 0
er
r2
dV
电荷面密度 d q
ds
E
S
1
4π 0
σer r2
ds
电荷线密度 d q
E
l
1
4π 0
re2rddl l
qds
r
P
dE
dl
q
r
dE
P
五
电偶极子的电场强度(自习)
y dqdl ( q )
qR
r 2π R
P
x
ox
1 dl
z
dE
4π 0
高教版《普通物理学》chapter-7ppt课件

qx x2 R2
3/2
方向
返回 退出
讨论
E
4π0
qx x2 R2
3/2
1. 若 x=0,则 E=0,环心处的电场强度为零。
2. 若x>>R, 则有
E q
4π 0 x2
远离圆环处的场强近似等于点电荷的电场强度。
返回 退出
例7-7 求均匀带电圆盘轴线上任一点的电场。设盘
半径为R,电荷面密度为。
解: 均匀带电的薄圆盘可看成由许多带电细圆
电场强度通量E :
通过电场中任一曲面的电场线条数。 1. 均匀电场中通过平面S的电场强度通量
ΨE ES
Ψ E EcS o E sS
返回 退出
2、非均匀电场的电场强度通量
d Ψ E E co d S s E d S
Ψ E SE co d S sS E d S
d Ψ E E d S的正、负取决于面
Fq E ( q )E 0
l
+q。
F
F 。-q
E
电偶极子所受合力为零。 但力矩不为零,力矩为
M F sli n qs E i n p lsE in M pE
电偶极子在均匀外电场中转动。
返回 退出
M pE
F
p
。-q
+。q
F
E
0 π
2
F 。-q
+q。
E
π
F
π
2
- p+
脱氧核糖和磷酸盐交替 连接形成多核苷酸链。
两条核苷酸链通过碱基之间的静电力作用配对 连接形成双螺形结构的DNA分子。
碱基的配对原则是腺嘌令(A)与胸腺嘧啶(T),鸟 嘌呤(G)与胞核嘧啶(C),即AT、TA、GC、CG。
程守洙普通物理学精品PPT课件

3. 温度 T 反映物体冷热程度的物理量,其高低反 映内部分子热运动的剧烈程度。
热力学温标(T:K)与摄氏温标(t:℃): t /℃=T /K-273.16
二、平衡态 准静态过程
平衡态(equilibrium state):在不受外界影响 (即系统与外界没有物质和能量的交换)的条件下, 无论初始状态如何,系统的宏观性质在经充分长时间 后不再发生变化的状态。
=
8
8.31105 273 47
6.67 102 (kg)
漏去氧气的质量为
Δm m m 3.33102 kg
§5-2 分子热运动和统计规律 一、分子热运动的图像
分子热运动:大量分子做永不停息的无规则运动。
布朗运动
分子热运动的图像:
1. 标准状态下 ,气体分子之间的距离大约是分子本 身线度(10-10 m)的10倍左右,可把气体看作是彼 此相距很大间隔的分子集合。
布规律。
例如:伽耳顿板实验
投入一个小球,一次 实验中,小球落入哪个狭 槽是偶然的。
投入大量的小球,落 入各个狭槽的小球数目遵 守一定的统计规律。
为了描述统计规律,引入分布函数:
设第 i 个狭槽的宽度为Δxi ,其中积累的小球 高度为 hi ,则此狭槽内的小球数目ΔNi 正比于小球 占的面积ΔA = hiΔxi 。令 ΔNi =C ΔA = C hi Δxi 则小球该的总数为
2. 分子与分子间的相互作用力,除了在碰撞的瞬间 以外,极为微小。
3. 分子热运动的平均速度约 v = 500 m/s ,
分子的平均碰撞频率约 Z = 1010 /s,
分子的平均自由程约 λ =10-7 m。
返回
二、分子热运动的基本特征 分子热运动的基本特征:分子的永恒运动与频繁 的相互碰撞。
大学普通物理学经典课件——电磁感应.ppt

B
R
E R
B r
E
E
E
r<R
B
R
B dS 0 S
H
L
dl
I
涡旋电场: E dl d B ds
L
dt S
一 位移电流
S2
S1
-+ -+
-+
L -+ I
-
dD dt
+ +
I
-
jc -
-
D
+
+ jc
+
B
AI
例 半经为R,相距 l(l R) 的圆形空气平板电容器,两端
L dI RI
dt
Idt LIdI RI2dt
2r R
l K
t Idt 1 LI 2 t RI 2dt
0
2
0
自感线圈磁能
电
电源反 回路电
源 作 功
抗自感 电动势 作的功
阻所放
出的焦 耳热
Wm
1 2
LI 2
自感线圈磁能
Wm
1 LI 2 2
I
L
L n2V , B nI
如图所示。设直导线中的电流强度为I,导线ab 长为L,a端到直导线的距离为d,求导线ab中的
动生电动势,并判断哪端电势较高。
a
大学物理 普通物理学.ppt

又 N N'
mg
解得
aM
mg sin cos M m sin 2
a
(m M )g sin M m sin 2
[例 2水]质对量小=球m的的阻小力球:在水面f处由k静v开始下沉,
浮力= F ,求任意时刻小球下沉的速度。
解:
o
f
F
v(t) a
x mg
小球运动方程:
mg kv F m dv
分离变量
dt
dv dt mg kv F m
k dv
k dt
mg kv F m
vd(mg kv F ) k
t
dt
0 mg kv F
m0
ln mg kv F k t
mg F
A认为 A
升降机:惯性系
球:受引力自由落体
升降机在自由
g
空间加速上升
B认为:
B F惯
g
两者等价
球受向下惯性力
在引力场中,相对静止电梯自由下落物体的运动 与无引力场中以g向上加速运动的电梯中物体的 运动等效
或: 无引力场中,相对静止电梯静止的物体与有引力 场中以 g 下落的电梯中静止的物体等效
不等效之处:
a'a0
m(a'a0
)
有
F (
定义:F惯
ma0 ) ma'
ma0 ----惯性力
F
F惯
F
ma'
ma' ----非惯性系中的牛二律
说明:
惯性力与真实力有区别
普通物理学-第二章ppt课件

精选ppt
9
返回 退出
§2-2 动量定理 动量守恒定律
一、动量定理 由牛顿运动定律:
Fd(mv)dp
dt dt
dpFdt
t2 t1
Fdt
pp12dp p 2p 1
其中,I
t2
Fdt
表示力对时间的累积量,
叫做冲量(imt1 pulse of force)。
精选ppt
10
返回 退出
Ip2p1
29
近似竖直向上 22
返回 退出
三、动量守恒定律
根据质心运动定律:
F i m aC
若 Fi 0 则 aC 0
即
vC
mivi = 常矢量 m
p mivi mvC=常矢量
i
如果系统所受的外力之和为零,则系统的总动
量保持不变,这个结论叫做动量守恒定律(law of
conservation of momentum)。 精选ppt
若不计重力和其他外力,由动量守恒 定律可得
m ( m v d m ) v ( d v ) ( d m ) v ( u )
略去二阶小量,
dv u dm m
精选ppt
25
返回 退出
dv u dm m
设u是一常量, v2dv m2udm
v1
m1
m
v2
v1
uln m1 m2
设火箭开始飞行的速度为零,质量为m0 ,燃料烧尽时, 火箭剩下的质量为m ,此时火箭能达到的速度是
动量定理(theorem of momentum): 质点在运动
过程中,所受合外力的冲量等于质点动量的增量。
说明
(1) 冲量 I 的方向是所有元冲量 Fdt 的合
普通物理学课件 第九章 电磁感应 电磁场理论

导线内总的动生电动势为
∫ εi =
G (v
×
G B)
⋅
G dl
L
例题9-2 如图已知铜棒OA长L=50m,处在方向垂直 纸面向内的均匀磁场(B =0.01T)中,沿逆时针方向
绕O轴转动,角速率ω=100 πrad/s, 求铜棒中的动生
电动势大小及方向。如果是半径为50cm的铜盘以上 述角速度转动,求盘中心和边缘之间的电势差。
转速为n=10r/s,转轴与磁场方向垂直。求(1)当线
圈由其平面与磁场垂直而转过30°时线圈内的动生
电动势;(2)线圈转动时的最大电动势及该时刻线
圈的位置;(3)由初始位置开始转过1s时线圈内的
动生电动势。
ωO b
解:取顺时针的绕行方向为 正方向,线圈平面与磁场方 向垂直时为计时起点(t=0), 当线圈转过角θ时,通过单
因此,dx小段上的动生电动势为
I
v M
N
x dx
a
l
dε i
=
Bvdx
=
μ0I 2πx
vdx
总的动生电动势为
∫ ∫ εi =
dεi =
a+l a
μ0I vdx 2πx
=
μ0I 2π
vቤተ መጻሕፍቲ ባይዱ
ln
⎛ ⎜⎝
a
+ a
l
⎞ ⎟⎠
=
4.4 ×10−6 V
例题9-4 边长为l=5cm的正方形线圈,在磁感应强度
为B=0.84T的磁场中绕轴转动,线圈铜线的电阻率为 ρ = 1.7×10−8Ω ⋅ m ,截面积S=0.5m2 ,共10匝。线圈
=
−
μ 0lI 0 2π
ln⎜⎛ ⎝
普通物理学上册第七章 ppt课件

精品资料
第7章 静止电荷的电场
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
er
E
1
4π 0
q r2
E
rP
q er
点电荷的电场具有球对称性 。
前页 后页 目录 31
第7章 静止电荷的电场
2. 电场强度的叠加原理
F F 1 F 2 F n
E F F F 11 F F 2 2 F F n n
q 0 q q 00 q q 00
qq 00
E1 E F q0 P
E 1 E 2 E n
前页 后页 目录 19
第7章 静止电荷的电场
普通物理学上册第七 1章.点电荷
形状、体积与观察距离相比可以忽略的带电体。
2.库仑定律
两个静止点电荷之间相互作用力的大小与这两 个点电荷的电荷量的乘积成正比,而与这两个点电 荷之间的距离的平方成反比,作用力的方向沿着这 两个点电荷的连线,同号电荷相互排斥,异号电荷 相互吸引。
Ex4π0a(sin2sin1)
Ey4π0a(cos1cos2)
讨论
带电线无限 长
Ex 0
1 0 2 π
Ey
2π 0a
场强具有轴对称 性
本题完
前页 后页 目录 44
第7章 静止电荷的电场
例3 均匀带电圆环轴线上一点P处的场强。
P解2:59建例立题图6 示直角坐标
系dq在P点的场强
普通物理学优秀PPT

向质点前进的方向。(瞬时)速度的大小等于(瞬
时)速率。
返回 退出
直角坐标系中:
v
dr dt
d dt
(xi
yj
zk )
பைடு நூலகம்
vxi
vy
j
vzk
vx
dx dt
,
vy
dy dt
,
vz
dz dt
速度的大小:
v v
vx2
v
2 y
vz2
返回 退出
八、加速度 加速度是反映速度变化的物理量。 t 时间内,速度增量为:
三、空间和时间 空间(space)反映了物质的广延性,与物体
的体积和位置的变化联系在一起。 时间(time)反映物理事件的顺序性和持续性。
返回 退出
目前的时空范围:宇宙的尺度1026m(~20亿光年) 到微观粒子尺度10-15m,从宇宙的年龄1018s(~200亿
年)到微观粒子的最短寿命10-24s。
2. r 与 r 的区别:
r rB rA rB rA
只当
rA
、rB
同方向时,取等号。
r r
返回 退出
七、速度
速度是反映质点运动的快慢和方向的物理量。
平均速度(average velocity):
v r t
平均速率(average speed):
v s t
平均速度是矢量,其方向与位移的方向相同。平均 速率是标量。平均速度的大小并不等于平均速率。
yj
zk
位矢的大小为:
r r x2 y2 z2
位矢的方向余弦:
cos x cos y cos z
r
r
r
返回 退出
时)速率。
返回 退出
直角坐标系中:
v
dr dt
d dt
(xi
yj
zk )
பைடு நூலகம்
vxi
vy
j
vzk
vx
dx dt
,
vy
dy dt
,
vz
dz dt
速度的大小:
v v
vx2
v
2 y
vz2
返回 退出
八、加速度 加速度是反映速度变化的物理量。 t 时间内,速度增量为:
三、空间和时间 空间(space)反映了物质的广延性,与物体
的体积和位置的变化联系在一起。 时间(time)反映物理事件的顺序性和持续性。
返回 退出
目前的时空范围:宇宙的尺度1026m(~20亿光年) 到微观粒子尺度10-15m,从宇宙的年龄1018s(~200亿
年)到微观粒子的最短寿命10-24s。
2. r 与 r 的区别:
r rB rA rB rA
只当
rA
、rB
同方向时,取等号。
r r
返回 退出
七、速度
速度是反映质点运动的快慢和方向的物理量。
平均速度(average velocity):
v r t
平均速率(average speed):
v s t
平均速度是矢量,其方向与位移的方向相同。平均 速率是标量。平均速度的大小并不等于平均速率。
yj
zk
位矢的大小为:
r r x2 y2 z2
位矢的方向余弦:
cos x cos y cos z
r
r
r
返回 退出
普通物理学课件:0绪论

3 学习内容
3.1 物理学的基本原理、基础知识 3.2 物理学在科学和技术中的应用 3.3 科学方法和创造性思维(图3)
4 怎样学好
4.1 严守纪律 4.2 认真配合老师 4.3 课堂与课外有机结合(t外>=2t内) 4.4 兴趣学习(图4)
5 计分原则
交作业:少交一次扣1分; 不认真扣1分
平时成绩(30%) 签到:缺席一次扣1分 (两次迟到算缺席一次)
总 成 期末成绩(70%) 纪律:被点名一次扣5分 绩
附加成绩(0-5分)
5 大学物理学教材结构
普通物理
力学(1-3) 热学(4-6) 振动与波动(12,13,14) 波动光学(15,16) 电磁学(7,8-11) 量子论(10-13)
预祝配合愉快! 谢 谢!!
图1:物理学在科学中应用的几个例子
普通物理学
第零章 绪 论
1 学习的必要性
1.1 物理学是自然科学的核心学科 (图1)
1.2 技术发展的推动力 1.3 学习的基础
(图2)
1.4 在生活中的应用
等等
2 物理学研究的内容
2.1 物质结构:实物; 场 2.2 物质间相互作用:引力、电磁、强、
弱相互作用 2.3 物质运动:物质的波粒二象性
迈克尔逊干涉仪
电子扫描隧道显微镜
下页1
哈勃望远镜
下页1
追综卫星的激光测距仪
下1
斯坦福直线加速器
中国环流器一号
返回
图2:物理学在技术中的分形图
下页
返回
图3:一些物理学家的照片 下3
图4:一些干涉、衍射图样 4下页
《普通物理学》PPT课件

第一,线性现象一般表现为时空中的平滑运动, 并可用性能良好的函数表示;而非线性现象则表现为 从规则运动向不规则运动的转化和跃变.
第二,线性系统往往表现为对外界的影响成比例 地变化;而非线性系统中参量在一些关节点上的极微 小变化,可引起系统运动形式的决定性改变。
第三,反映在连续介质中的波动上,线性行为表 现为色散引起波包的弥散,导致结构的消失,而非线 性作用却可促使空间规整性结构的形成和维持.
自然界大量存在的相互作用是非线性的,线性作用 只不过是非线性作用在一定条件下的近似.
上页 下页 返回 退出
二、混沌和牛顿力学的内在随机性
1.混沌 由确定性方程描述的简单系统可以出现极为复杂
的貌似随机的无规运动,这就是混沌. 常见的混沌想象
(1)天体力学中的地球上流星的起源问题 太阳系的小行星大部分存在与火星与木星之间,
上页 下页 返回 退出
我们以湍流的形成为例进行说明. 湍流现象是种混沌,它普遍存在于行星和地球大
气、海洋与江河、火箭尾流乃至血液流动等自然现象 之中.流体的运动一般用确定性的流体力学方程描述.
当流体绕过圆柱体流动 时,随着表征流体中外力 与黏性力竞争的雷诺数的 不断增大,当雷诺数达到 某个临界值时,流动中就 出现湍流.当雷诺数Re<1时 ,流动情形如图 (a)所示.增 大流速,使雷诺数Re≈20时, 可看到圆柱体后面出现两 个对称的涡旋,如图(b)
若系统表现为周期运动,那么系统就只有很少 的运动模式,无法应付多变的环境中所出现的种 种突变,这会导致系统损伤和功能失调。
上页 下页 返回 退出
2.内随机性
随机性:在一定条件下,如果系统的某个状态 既可能出现,也可能不出现。
外随机性 系统自身不会出现随机性,随机性来 自系统外部或某些尚不清楚的原因的 干扰作用。
第二,线性系统往往表现为对外界的影响成比例 地变化;而非线性系统中参量在一些关节点上的极微 小变化,可引起系统运动形式的决定性改变。
第三,反映在连续介质中的波动上,线性行为表 现为色散引起波包的弥散,导致结构的消失,而非线 性作用却可促使空间规整性结构的形成和维持.
自然界大量存在的相互作用是非线性的,线性作用 只不过是非线性作用在一定条件下的近似.
上页 下页 返回 退出
二、混沌和牛顿力学的内在随机性
1.混沌 由确定性方程描述的简单系统可以出现极为复杂
的貌似随机的无规运动,这就是混沌. 常见的混沌想象
(1)天体力学中的地球上流星的起源问题 太阳系的小行星大部分存在与火星与木星之间,
上页 下页 返回 退出
我们以湍流的形成为例进行说明. 湍流现象是种混沌,它普遍存在于行星和地球大
气、海洋与江河、火箭尾流乃至血液流动等自然现象 之中.流体的运动一般用确定性的流体力学方程描述.
当流体绕过圆柱体流动 时,随着表征流体中外力 与黏性力竞争的雷诺数的 不断增大,当雷诺数达到 某个临界值时,流动中就 出现湍流.当雷诺数Re<1时 ,流动情形如图 (a)所示.增 大流速,使雷诺数Re≈20时, 可看到圆柱体后面出现两 个对称的涡旋,如图(b)
若系统表现为周期运动,那么系统就只有很少 的运动模式,无法应付多变的环境中所出现的种 种突变,这会导致系统损伤和功能失调。
上页 下页 返回 退出
2.内随机性
随机性:在一定条件下,如果系统的某个状态 既可能出现,也可能不出现。
外随机性 系统自身不会出现随机性,随机性来 自系统外部或某些尚不清楚的原因的 干扰作用。
《普通物理学》课件-第七章 振动
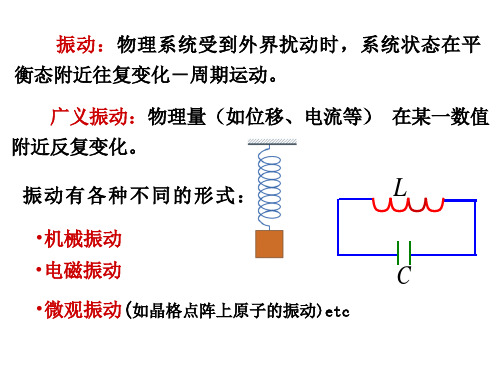
5g
等效劲度系数 (ke) f ke x
f: 恢复力 x: 偏离平衡位置的位移
0
ke m
弹簧的串联和并联
• 串联公式: 1/k = 1/k1 +1/k2
• 并联公式: k = k1 + k2
k1
k2
k1
k2
例:一劲度系数为 k 的弹簧均分为二,试求 均分后两弹簧并联的等效劲度系数 k'。
解:串联公式:
sinθ≈θ (θ<5o 0.3 rad)
O
l
T
当振幅很小时,单摆的振动为简谐振动。
mg
Quasi 1-D restoring force
f = -mgsinθ≈-mgθ= -mgx/l
k = mg/l, ω02 = k/m = g/l ω0 = √g/l
T 2 l
g
单摆实验 可以测g
复摆(物理摆)
A
ωt+
0
xx
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
x Acos(t )
•复数表示:
将xy平面看作一个复平面
矢量端点对应于一个复数 (包含模和辐角)
xt Acost 0
x t Aeit0辐角
eit0 cost 0 i sin t 0
设B的质量为m, A的质量便是γm
A
v0
B
B
第一阶段是弹性碰撞
第二阶段:A做匀速直线运动;B,B '的质心做匀速直线运动,
B,B '相对质心作简谐振动。
弹性碰撞
mvA
mvB
(0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们以湍流的形成为例进行说明.
湍流现象是种混沌,它普遍存在于行星和地球
大气、海洋与江河、火箭尾流乃至血液流动等自然现
象之中.流体的运动一般用确定性的流体力学方程描
述.
当流体绕过圆柱体流
动时,随着表征流体中外
力与黏性力竞争的雷诺数
的不断增大,当雷诺数达
到某个临界值时,流动中
就出现湍流.当雷诺数Re<1
选择进入下一节 §3-0 教学基本要求 §3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系 §3-4 定轴转动刚体的角动量定律和角动量守恒定 律 §3-5 进动 §3-6 理想流体模型 定常流动 伯努利方程 §3-7 牛顿力学的内在随机性 混沌
感谢下 载
3.线性和非线性物理现象的区分
第一,线性现象一般表现为时空中的平滑运 动,并可用性能良好的函数表示;而非线性现象则表 现为从规则运动向不规则运动的转化和跃变.
第二,线性系统往往表现为对外界的影响成 比例地变化;而非线性系统中参量在一些关节点上的 极微小变化,可引起系统运动形式的决定性改变。
第三,反映在连续介质中的波动上,线性行 为表现为色散引起波包的弥散,导致结构的消失,而 非线性作用却可促使空间规整性结构的形成和维持.
感谢下 载
பைடு நூலகம்
自然界大量存在的相互作用是非线性的,线性 作用只不过是非线性作用在一定条件下的近似.
二、混沌和牛顿力学的内在随机性
1.混沌 由确定性方程描述的简单系统可以出现极为
复杂的貌似随机的无规运动,这就是混沌. 常见的混沌想象
(1)天体力学中的地球上流星的起源问题 太阳系的小行星大部分存在与火星与木星
之间,因此地球上的 流星也只能起源于这个小行星 带。但是这个小行星带离地球很远,只有偏心率达 到57%的小行星的轨道才能与地球轨道相交。
*§3-7 牛顿力学的内在随机性 混沌
一、线性科学和非线性科学
1.线性科学 牛顿建立的经典力学属于线性科学范畴.所
谓线性是指量与量之间成正比关系,用直角坐标形 象地画出来,是一根直线.
在线性系统中,部分之和等于整体,描述线 性系统的方程遵从叠加原理,即方程的不同解相加 仍然是个解.
2.非线性科学 非线性则指整体不等于部分之和,叠加原理失效, 非线性方程两个解之和不再是方程的解.
(3)生理学中的“反”混沌------动态病 传统生理学认为,健康人的心率是规则的,
具有周期性。然而更为精确的测量与研究发现,心 律节奏与时间的变化是极不规则的,即心率在时间 上是混沌的。
并不指混乱不堪无规可循,而是确定性系统的内 在随机性的表现,是一种无周期的有序。
动态病----以异常时间组织结构为特征的疾 病 动态病的出现不在于人体中的“混沌”,而恰恰在 于出现了“周期性”-。-----“反混
考虑非共面效应和木星轨道平面相对于行星带的缓慢 变化,发现混沌运动确实可以使偏心率达到60%。
Wisdom通过具体计算,能够给出与观察一致的流星 轨道与丰度,特别是所谓的“下午效应”(即下午 观察到的流星是上午的两倍)。
(2)地磁场的混沌运动 地球的磁场不断地改换极性,而且每种极
性维持的时间间隔是无规则的,这可能是由于地球 内部物质与电荷的经向与纬向的两种运动耦合产生 的。两个方向的运动及两个方向磁场的相互作用会 产生混沌运动。
,出现图(d)所示的另一次转变,湍流形成了.由边界 层里产生的小涡旋中充满着一条条细带,其流动是紊 乱无规的,这就是湍流状态.在流体力学中就这么一 个没有单位的雷诺数,它的数值的增减竞能引起如此 多样的转折,实在令人惊异不止!如果事情只局限于 流体宏观运动的能量,经过大、中、小、微等等许多 尺度上的旋涡,最后转化成分子尺度上的热运动,那 么统计描述仍可能奏效.问题还在于以紊乱无规的湍 流为背景,流动中还会出现大尺度的、颇为规则的结 构和纹样,出现协调一致的运动,真令人不可思议!
2.内随机性
随机性:在一定条件下,如果系统的某个状态 既可能出现,也可能不出现。
外随机性 系统自身不会出现随机性,随机性来 自系统外部或某些尚不清楚的原因的 干扰作用。
内随机性 看来完全确定的系统(用确定的微 分方程描述)内部产生的随机性。
混沌现象产生的根源在系统自身,而不在外部的影响。
我们把混沌说成是在确定性动力学系统 中出现的一种貌似随机的运动.“确定性”是指 描述动力学系统的微分方程中的系数都是确定的 ,没有概率性因素·对确定的初始值,确定性方 程应给出确定的解,描述着系统确定的行为.但 在某些非线性系统中,这种过程会因初始值极微 小的扰动而产生很大变化.由于系统的这种初值 敏感性,从物理上看,这过程似乎是随机的,但 这种随机性是确定性系统内部所固有的,所以被 叫做内存随机性.具有内在随机性的动力学系统 ,通常兼有规则运动和随机运动的两种不同区域 .随着某种参数变化,随机区域可能逐渐扩大, 甚至吞掉规则运动的区域.
时,流动情形如图 (a)所
示.增大流速,使雷诺数
Re≈20时,可看到圆柱体后
面出现两个对称的涡旋,
如图(b)
所示.当雷诺数达到40左右,又发生另一次突变:一个 涡旋被拉长后摆脱柱体,漂向下游;柱后另一侧的流 体转了一个弯,形成新的涡旋.这些涡旋交替产生、
脱落,向下游移去,如图(c)所示.当雷诺数Re≈104
沌”
正常个体身上各个主要系统中的各种节 律之间有着错综复杂的相互关系,这些节律极少表 现出绝对的周期性。
体内功能的混沌标志着健康, 结论
而周期性行为却可能预示着疾病。 正是由于混沌系统可在范围十分广泛的各种条 件下工作,它们具有高度的适应性和灵活性,可 使系统应付多变环境中出现的种种突变。
若系统表现为周期运动,那么系统就只有很少 的运动模式,无法应付多变的环境中所出现的种 种突变,这会导致系统损伤和功能失调。
