2019-2020学年四川省南充市白塔中学高二文综下学期第三次月考试题
四川省南充市白塔中学2019-2020学年高二下学期第三次月考(文)

1四川省南充市白塔中学2019-2020学年高二下学期第三次月考(文)(满分:150分 时间:120分钟)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.) 1.设i 是虚数单位,复数iiz +=14,则z =( ) A .1BCD .2.设动点M 到A (0,-5)的距离与它到B (0,5)的距离的差等于6,则M 点的轨迹方程是( )A.x 29-y 216=1B.y 29-x 216=1C.y 29-x 216=1(y >0)D.x 29-y 216=1(x >0) 3.函数||ln 2x x y +=的图象大致为 ( ) A . B . C . D .4.等差数列}{n a 中的1a ,4039a 是函数34231)(23---=x x x x f 的极值点,则220202)(log a 的值为( )A.-1B.0C.1D.25.若抛物线24(0)=>y px p 的焦点是双曲线1222=-py p x 的一个焦点,则p =( ) A .2 B .3 C .4 D .86.已知曲线()cos 3f x x x x =+在点()()0,0f 处的切线与直线210ax y ++=平行,则实数a 的值为( ).A .-8B .-4C .12D . 427.若函数f (x )=ax 3-x 2-x -1在(-∞,+∞)上单调递减,则a 的取值范围是( )A .a >13B .a ≥13C .a <-13D .a ≤-138.某公司奖励甲,乙,丙三个团队去A ,B ,C 三个景点游玩,三个团队各去一个不同景点,征求三个团队意见得到:甲团队不去B ;乙团队不去C ;丙团队只去A 或B .公司按征求意见安排,则下列说法一定正确的是( )A.丙团队一定去A 景点B.甲团队一定去C 景点C.乙团队一定去B 景点D.乙团队一定去A 景点9.在平面直角坐标系xOy 中,已知△ABC 顶点A(-2,0)和C(2,0),顶点B 在椭圆13722=+y x 上,则BCA sin sin sin += ( )A.27 B.23 C. 2 D. 21 10.设F 为抛物线x y 42=的焦点,A ,B ,C 为该抛物线上三点,若0=++FC FB FA ,则=++||||||( )A.4B.6C.9D.1211.已知双曲线)0,0(,12222>>=-b a b y a x 的左、右焦点分别为F 1,F 2,过F 2且与渐近线垂直的直线分别与该渐近线和y 轴相交于A ,B 两点,O 为坐标原点,若32=∆∆AOBAOF S S ,则双曲线的离心率为( )A.2B.3C.2D. 5 12.已知f (x )是定义在R 上的可导函数,对于任意实数x ,均有x e x f x f 2)()(=-,当0<x 时,0)()(>'+x f x f ,若)1()12(-≥-a f a f e a ,则实数a 的取值范围是( )A.]32,0[B.]0,32[- C.),0[+∞ D.]0,(-∞二、填空题(本大题共4小题,每小题5分,满分20分)13.若复数z 满足2z +z =1+i ,其中i 为虚数单位,则z =________.314.已知抛物线C :y x 82=的焦点为F ,O 为坐标原点,点P 在抛物线C 上,且OF PF ⊥,则||PF OF -=_______________________ 15.已知F 是双曲线15422=-y x 的左焦点,点A (1,5),P 是双曲线右支上的动点,则|PF |+|PA |的最小值为________.16.已知13)1()(-+=x ex x f ,a x x x g -++=44)(2,若R x R x ∈∃∈∀21,,使得)()(21x g x f ≥成立,则实数a 的取值范围是__________.三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤,第17 ~ 21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.) 17.(本小题满分12分)为考察某种疫苗预防疾病的效果,进行动物试验,得到统计数据如下:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为53.⑴求2×2列联表中的数据x ,y ,A ,B 的值.⑵能否在犯错误的概率不超过0.01的前提下认为疫苗有效?附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),n =a +b +c +d .临界值表:418.(本小题满分12分)某厂家准备在“6.18”举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x (万元)和销售量y (万台)的数据如下:两位);⑵若用y =c +d x 模型拟合y 与x 的关系,可得回归方程x y+=51.1ˆ,经计算线性回归模型和该模型的R 2分别约为0.774和0.888,请用R 2说明选择哪个回归模型更好;⑶已知利润z 与x ,y 的关系为z =200y -x .根据(2)的结果,当广告费x =20时,求销售量及利润的预报值.参考公式:回归直线y ^=a ^+b ^x 的斜率和截距的最小二乘估计分别为b ^=∑∑∑∑====--⋅-=-⋅-ni ii ni ini ini i i x xy y x xx n xyx n yx 1211221)()()(,x b y aˆˆ-=. 参考数据:5≈2.24, ∑==715.275i i i y x , ∑==712708i i x519.(本小题满分12分)在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线θρcos 6:=C ,直线l 的参数方程为:)(221为参数t t y tx ⎩⎨⎧+=+=,直线l 与曲线C分别交于M ,N 两点.⑴写出曲线C 的直角坐标方程和直线l 的普通方程; ⑵若点)2,1(P ,求|||1||1|PN PM -的值.20.(本小题满分12分)设函数ax x x x f -+=221ln 6)(. ⑴当5=a 时,求函数()f x 的单调区间; ⑵当1a =-时,方程221)(x mx x f +=在区间21,e ⎡⎤⎣⎦上有两个实数解,求实数m 的取值范围.21.(本小题满分12分)已知点F 1为椭圆E :12222=+by a x (a >b >0)的左焦点,且两焦点与短轴的一个顶点构成一个等腰直角三角形,直线3+=x y 与椭圆E 有且仅有一个交点M .⑴求椭圆E 的方程;⑵设直线3+=x y 与y 轴交于P ,过点P 的直线l 与椭圆E 交于不同的两点A ,B ,若λ|PM |2=|PA |·|PB |,求实数λ的取值范围.选考题:共10分,请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计6分.22.在以原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为4πθ=,平面直角坐标系xOy 中,曲线C 的参数方程为)(sin 3cos 4为参数ααα⎩⎨⎧==y x . ⑴设直线l 与曲线C 交于M ,N 两点,求|MN|;⑵若点P (x ,y )为曲线C 上任意一点,求|2|-+y x 的取值范围.23.已知函数f (x )=|2x -4|+|x +1|.⑴解不等式f (x )≤5;(2)求函数g (x )=f (x )-3|x +1|的值域M .7参考答案一、选择题(本大题共12小题,每小题5分,共60分.)二、填空题(本大题共4小题,每小题5分,满分20分)13. i+3114. 52 15. 7 16. ),27[5+∞e三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤)17.解:⑴设“从所有试验动物中任取一只,取到‘注射疫苗’动物”为事件M ,由已知得P (M )=10040y +=53,所以y =20 ………3分 则B =60,x =20,A =40. ………6分⑵因为K 2=60404060)20402020(1002⨯⨯⨯⨯-⨯⨯100×(20×10-40×30)260×40×50×50≈2.778<6.635.………11分所以不能在犯错误的概率不超过0.01的前提下认为疫苗有效. …………12分 18.解:⑴∵8=x ,1.4=y , ………………2分∴b ^=18.02609.45877081.4875.2752≈=⨯-⨯⨯-,x b y a ˆˆ-==4.1-0.18×8=2.66,……5分∴y 关于x 的线性回归方程为y ^=0.18x +2.66. ……………6分 ⑵∵0.774<0.888且R 2越大,反映残差平方和越小,模型的拟合效果越好, ∴选用x y+=51.1ˆ更好. ……………8分 ⑶由⑵知,当x =20时,销售量的预报值99.52051.1ˆ≈+=y(万台),…10分 利润的预报值z =200×5.99-20=1178(万元). …………12分819.解:⑴∵θρcos 6=∴θρρcos 62=则x y x 622=+,即9)3(22=+-y x 为曲线C 直角坐标方程. ………3分∵)(221为参数t ty tx ⎩⎨⎧+=+=∴032=+-y x 为直线l 的普通方程.………5分 ⑵直线l 的参数方程化为)(5525521为参数u u y u x ⎪⎪⎩⎪⎪⎨⎧+=+= …………7分 代入x y x 622=+得015542=--u u , 0>∆恒成立,…………8分 设M ,N 对应的参数分别为1u ,2u ,则55421=+u u ,0121<-=u u ………9分 ∴554|||||||||||||||||1||1||||1||1|2112211221=+=-=-=-u u u u u u u u u u PN PM …12分 20.解:⑴依题意,可知()f x 的定义域为(0,)+∞,………1分当5=a 时,ax x x x f -+=221ln 6)(,xx x x x x x x x f )3)(2(6556)(2--=+-=-+=', …………2分 令()0f x '=,解得32==x x 或,当320><<x x 或时,()0f x '>,当32<<x 时,()0f x '<,所以()f x 的单调递增区间为)2,0(,),3(+∞,递减区间为)3,2(.……………5分⑵1a =-时,由221)(x mx x f +=得mx x x =+ln 6,又0x >,所以xxm ln 61+=, 要使方程221)(x mx x f +=在区间21,e ⎡⎤⎣⎦上有两个实数解,只需xx m ln 61+=有两个实数解, 即函数m y =与xxy ln 61+=的图象有两个交点 ……7分 令)1(ln 61)(2e x x x x g ≤≤+=,则2)ln 1(6)(x x x g -=',9由()0g x '>,得1x e ≤<,由()0g x '<,得e x >.∴()g x 在区间[1,e]上是增函数,在区间2,e e ⎡⎤⎣⎦上是减函数. ………9分∴当e x =时,()g x 取得极大值,且为最大值,ee g x g 61)()(max +== ∵(1)1g =,1121)(22>+=e e g ,∴1)1()(min ==g x g ………11分 结合图象可知,实数m 的取值范围为]61,121[2e e++. ………12分21.解:⑴∵221B F F ∆为等腰直角三角形∴a c b 22==,则椭圆E 方程化为:122222=+b y b x …2分由⎪⎩⎪⎨⎧=++=1232222b ybx x y 得021812322=-++b x x )218(341222b -⨯-=∆ ∵直线3+=x y 与椭圆E 有且仅有一个交点M . ∴0=∆,即32=b …4分∴椭圆E 方程化为:13622=+y x …………5分⑵由(1)得M )1,2(-,直线3+=x y 与y 轴交于P )3,0(,22||=PM ………6分 方法一:①当直线l 与x 轴垂直时,|PA |·|PB |=(3×(3)=6, ∴43||||||2=⋅=PM PB PA λ ……………7分②当直线l 与x 轴不垂直时,设直线l 的方程为y =kx +3,A (x 1,y 1),B (x 2,y 2),由⎪⎩⎪⎨⎧=++=136322yx kx y 得01212)21(22=+++kx x k , 0)21(124)12(22>+⨯-=∆k k ,即12>k ,x 1x 2=021122>+k,……8分 ∴|PA |·|PB |=||)1()3()3(212222222122122222121x x k x k x x k x y x y x +=+⋅+=-+⋅-+=λ8216621)1(12222=++=++k k k………10分10∵12>k ∴8216662<++<k ,即886<<λ,则143<<λ………11分 综上所述,λ的取值范围是[43,1). …………12分 方法二:设直线l 的参数方程为)(sin 3cos 为参数t t y t x ⎩⎨⎧+==αα,…………7分代入椭圆E 的方程得012sin 12)sin 1(22=+++ααt t ,0>∆,即21sin 2>α…8分 设A ,B 对应的参数分别为1t ,2t ,则0sin 112221>+=αt t ……………9分 ∴|PA|·|PB|=λα8sin 112||||||2212121=+===⋅t t t t t t …………10分 ∵1sin 212≤<α∴8sin 11262<+≤α,即886<≤λ,则143<≤λ 综上所述,λ的取值范围是[43,1). ……………12分 22.解:⑴直线l :4πθ=的参数直角坐标方程为:y =x ①, ………1分曲线C 的参数方程为)(sin 3cos 4为参数ααα⎩⎨⎧==y x 普通方程为191622=+y x ②.……2分由①②得259162⨯=x ,即512±=x ,∴)512,512(M ,)512,512(--N ,2524||=MN …5分 ⑵点P (x ,y )为曲线C 上任意一点,设)sin 3,cos 4(ααP ,R ∈α …6分 则|2)sin(5||2sin 3cos 4||2|-+=-+=-+ϕαααy x ,其中34tan =α …8分 ∵R ∈α ∴R ∈+ϕα 则1)sin(1≤+≤-ϕα,32)sin(57≤-+≤-ϕα, 即7|2|0≤-+≤y x ,故|2|-+y x 的取值范围为[0,7] ……10分23.解:(1)f (x )=|2x -4|+|x +1|=⎪⎩⎪⎨⎧>-≤<-+--≤+-2,3321,51,33x x x x x x∴f (x )≤5⇔⎩⎨⎧≤+--≤5331x x 或⎩⎨⎧≤+-≤<-5521x x 或⎩⎨⎧≤->5332x x………3分解得38220≤<≤≤x x 或,即380≤≤x11 即原不等式的解集为{x |380≤≤x }.…………5分 ⑵g (x )=f (x )-3|x +1|=|2x -4|-|2x +2|, 6|)22()42(|||22||42||=+--≤+--x x x x (当且仅当1x 20)22)(42(-≤≥≥+-或即x x x 时等号成立) ∴M =[-6,6].……………10分。
四川省南充市白塔中学2019-2020高二下学期第三次月考试题

四川省南充市白塔中学2019-2020学年高二历史下学期第三次月考试题24.春秋初期发生过“周郑交质”,郑庄公姬寤生先把世子(继承人)送到周都城,周平王接着把太子送到了郑国居住,以证明双方互信.这主要反映出A.周王对诸侯的控制力不足B.嫡长子继承制度遭到破坏C.礼乐制度遭到破坏D.周礼规范了贵族阶层道德25.甲骨文的笔画较为简单,入刀出刀处常见锋迹,笔画转折处多方折。
刻者的用刀都是一刀顺下,不加修饰,线条显得流畅、自然、质朴,虽然刀有钝有锐,骨有细硬有疏松,刻出的笔画有粗有细,但整体以瘦硬为主。
这反映出甲骨文A.与占卜活动有关B.具备一定的审美价值C.带有图案的特征D.已经是较成熟的文字26.汉代,蜀地百姓“帅导群妾,咸循蚕蔟。
分茧理丝,女工是敕.”在齐地,平民“织作冰纨绮绣纯丽之物,号为冠带衣履天下.”这反映出当时A.家庭丝织业生产盛行B.生产具有标准化的特征C.丝织业地域分工形成D.丝织业商品化趋势明显27.西汉盛行比武、斗兽、狩猎等危险、激烈的体育娱乐活动,数量众多的社会上层分子和文人也亲身参与。
由此可见,当时A。
军事形势严峻 B。
世风阳刚劲健C。
贵族引领时尚 D。
弃文从武成风28.氾胜之强调坚硬强地黑垆土耕后必须及时“平摩其块",“勿令有块”;土性松散的土壤耕后必须“蔺(镇压)之"“重蔺之"。
“冬雨雪止,辄以蔺之.掩地雪,勿使从风飞去.后雪复蔺之,则立春保泽,冻虫死,来年宜稼.”这反映了中国古代农业A.农作物产量的提高B.生产工具的革新C.对精耕细作的重视D.耕作技术的进步29。
西晋和东晋政权面临着政治上与经济上的双重压力,在长达近一个半世纪的时期内未曾铸造铜钱。
但在民间,汉五铢钱和各种旧钱并行,且盗铸铜钱现象严重。
这表明当时A.庶族掌控铸币实权B.民间力量制约皇权C.抑商观念上下背离D. 商品经济仍具活力30.《旧唐书·桓彦范传》载:时有墨敕授方术人郑普思秘书监,叶净能国子祭酒,彦范(政事堂宰相)苦言其不可.帝曰:“既要用之,无容便止.”彦范又对曰:“陛下自龙飞宝位,遂下制云:‘军国政化,皆依贞观故事。
四川省南充市白塔中学2019-2020学年高二下学期第三次月考文综-地理试题+Word版含答案

下图中甲城的市区人口约290万,是所在国家的第三大城市,是著名的国际金融中心,被誉为摩天大楼的故乡。
甲城因终年多风,被称为风城,当地人自嘲:甲城“一年一场风,从春刮到冬”。
据此完成1~2题。
1.受密歇根湖影响,甲城夏季白天的主导风向应为( )A.偏东风B.偏西风C.偏南风D.偏北风2.与密歇根湖沿岸的其他地区相比,甲城风力更强的主要原因是( )A.地面开阔 B.高楼林立C.距离风源地更近D.距离湖泊更近科皮村地处湘西州永顺县芙蓉镇西南部,是国家连片特困地区武陵山区的贫困村,总面积12.24平方公里,居民1288人,过去主要种植水稻,近年来科皮村创建了貅猴桃种植协会、湘西黑猪养殖协会、水产养殖协会、中药材种植协会、生态禽类养殖协会、油茶种植协会、和谐科皮文艺协会等专业合作社。
2019年建档立卡贫困户人均年纯收入突破8000元。
据此完成3~5题。
3.科皮村种植水稻村民不能致富,主要是因为()A.劳动力缺乏B.产品较单一C.生产规模小D.产品单产低4.科皮村创建的农村专业合作社类型多,主要是基于当地()A.地势起伏较大B.土地连片集中C.村民生活需求D.气候类型多样5.成立专业合作社的目的主要是为了()A.扩大种植面积B.抵御市场风险C.减少运输成本D.增加产品种类银叶树为热带海岸红树林的树种之一,多分布于高潮线附近的海滩内缘,以及大潮或特大洪水才能淹没的滩地,或海岸内陆。
近年来银叶树面积大幅度减少。
下图为某市银叶树分布图。
据此回答6~7题。
6.银叶树的典型特征是( )A.根系发达、耐盐性强B.根系脆弱、耐旱性强C.根系发达、耐寒性强D.根系脆弱、耐碱性强7.和乙区域相比,银叶树对甲区域海岸地区最重要的生态效益是 ( )A.涵养水源B.调节气候C.防风消浪D.保持水土被称为“特硬豆”的优质咖啡豆树种生长在海拔1 500米以上的山坡,并且海拔越高,咖啡豆质量越好。
下图所示区域盛产优质咖啡,圣何塞常年气候宜人,温暖如春。
2019-2020学年四川省南充市白塔中学高二物理月考试卷含解析

2019-2020学年四川省南充市白塔中学高二物理月考试卷含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. (单选)关于静电场,下列说法中正确的是( )A.在电场强度为零的区域电势一定处处为零B.两点间的电势差与零电势的选取有关C.负电荷从电势低的点运动到电势高的点,电势能一定减少D.根据公式U= Ed 知,在匀强电场中两点间的距离越大,电势差就越大参考答案:C2. (单选)如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内()A.重力的冲量为0B.拉力F的冲量为FtC.拉力F的冲量为FtcosθD.物体动量的变化量等于Ft参考答案:B3. (多选)如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中CD )A.导体框中产生的感应电流方向相同B.导体框中产生的焦耳热相同C.导体框ad边两端电势差相同D.通过导体框截面的电量相同参考答案:AD4. (多选)关于振动和波动,下列说法正确的是()A.单摆做简谐运动的周期与摆球的质量有关B.部队过桥不能齐步走而要便步走,是为了避免桥梁发生共振现象C.在波的干涉中,振动加强的点位移不一定始终最大D.各种波均会发生偏振现象参考答案:CB5. (单选)如图2所示a、b、c、d是匀强电场中的四个点,它们正好是一个矩形的四个顶点。
电场线与矩形所在平面平行。
已知a点的电势为20V,b点的电势为24V,d点的电势为4V,由此可知c点的电势为( )A.12V B.24V C.4V D.8 V参考答案:D二、填空题:本题共8小题,每小题2分,共计16分6. 光由空气以45°的入射角射向介质时,折射角是30°,则光由介质射向空气的临界角是。
参考答案:45°7. (4分)在真空中,氢原子从能级A跃迁到能级B时,辐射出波长为λ1的光子;从能级A跃迁到能级C时,辐射出波长为λ2的光子。
四川省南充市白塔中学2019-2020高二下学期第三次月考数学(理)试题(wd无答案)

四川省南充市白塔中学2019-2020高二下学期第三次月考数学(理)试题(wd无答案)一、单选题(★★) 1. 在复平面上,复数的对应点所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限(★★★) 2. 下列求导运算正确的是()A.B.C.D.(★★) 3. 已知随机变量 X服从二项分布.若,,则()A.B.C.D.(★★) 4. 函数的单调减区间为().A.B.C.D.(★★★) 5. 甲、乙二人进行围棋比赛,采取“三局两胜制”,已知甲每局取胜的概率为,则甲获胜的概率为 ( ).A.B.C.D.(★★★) 6. 某医院计划从3名医生,9名护士中选派5人参加湖北新冠肺炎疫情狙击战,要求选派的5人中至少要有2名医生,则不同的选派方法有()A.495种B.288种C.252种D.126种(★★) 7. 若的展开式中的各项系数的和为1,则该展开式中的常数项为()A.672B.-672C.5376D.-5376(★★) 8. 已知变量,之间的线性回归方程为,且变量,之间的一组相关数据如下表所示,则下列说法错误的是()681012632A.可以预测,当时,B.C.变量,之间呈负相关关系D.该回归直线必过点(★★★) 9. 二面角--为60°, A、 B是棱上的两点,、分别在半平面内,,,且,,则的长为()A.B.C.D.(★★) 10. 函数的图象大致是( )A.B.C.D.(★★★) 11. 已知双曲线(,),以点()为圆心,为半径作圆,圆与双曲线的一条渐近线交于,两点,若,则的离心率为()A.B.C.D.(★★) 12. 已知函数,则不等式的解集是()A.B.C.D.二、填空题(★★)13. 已知平面的一个法向量,,,且,则直线与平面所成的角为______.(★★) 14. = .(★) 15. 已知随机变量ξ服从正态分布 N(3,σ 2),且 P(ξ>2)=0.85,则 P(3<ξ<4)=_____.(★★★) 16. 已知展开式中第二项、第三项、第四项的二项式系数成等差数列,将展开式中所有项重新排列,则有理项不相邻的概率为______.三、解答题(★★) 17. 甲、乙两人各射击一次,击中目标的概率分别是和,假设两人射击是否击中目标相互没有影响,每人每次射击是否击中目标相互也没有影响.(1)求甲、乙两人各射击一次均击中目标的概率;(2)若乙在射击中出现连续次未击中目标则会被终止射击,求乙恰好射击次后被终止射击的概率.(★★★) 18. 白塔中学为了解校园爱国卫生系列活动的成效,对全校学生进行了一次卫生意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:等级不合格合格得分频数624(1)求统计表、直方图中的a ,b ,c的值;(2)用分层抽样的方法,从等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为 ,求 的数学期望.(★★★) 19. 已知函数. (1)若函数 在区间上单调递增,求的取值范围;(2)设函数 ,若存在,使不等式 成立,求实数 的取值范围.(★★★) 20. 已知长方形中,,,现将长方形沿对角线折起,使,得到一个四面体,如图所示.(1)试问:在折叠的过程中,异面直线 与 能否垂直?若能垂直,求出相应的 的值;若不垂直,请说明理由; (2)当四面体体积最大时,求二面角的余弦值.(★★★) 21. 已知点,点 P 为平面上的动点,过点 P 作直线 l :的垂线,垂足为Q ,且.Ⅰ 求动点 P 的轨迹 C 的方程;Ⅱ 设点 P 的轨迹 C 与 x 轴交于点 M ,点 A , B 是轨迹 C 上异于点 M 的不同的两点,且满足,求的取值范围.(★★★★) 22. 已知函数与的图象在它们的交点处具有相同的切线.(1)求的解析式;(2)若函数有两个极值点,,且,求的取值范围.。
四川省南充市白塔中学2019-2020学年高二下学期第三次月考数学(理)试题 Word版含答案

南充市白塔中学2019-2020学年下期(2020.06.28)高二数学试题 (理科)一.选择题(每小题5分,共60分.)1.在复平面上,复数(2)z i i =-+的对应点所在象限是( )A .第一象限B .第二象限C .第三象限D .第四象限2.下列求导运算正确的是( ) A .()x x sin cos ='B .()xxxeex 22='C .()e xx3log 33='D .()xx 12ln =' 3.已知随机变量X ~B (n ,p ).若E (X )=2,D (X )=,则p =( )A .B .C .D .4.函数()x xx f ln 5+=的单调减区间为( ) A .(﹣∞,5)B .(0,5)C .(5,+∞)D .(0,+∞)5.甲、乙二人进行围棋比赛,采取“三局两胜制”,已知甲每局取胜的概率为,则甲获胜的概率为( )A .()2+C ()2()1B .()2+C ()2C .()2+C ()2()1D .()2+C ()1()16.南充市中心医院医院计划从3名医生,9名护士中选派5人参加湖北新冠肺炎疫情狙击战,要求选派的5人中至少要有2名医生,则不同的选派方法有( ) A .495种B .288种C .252种D .126种7.若921ax x ⎛⎫- ⎪⎝⎭的展开式中的各项系数的和为1,则该展开式中的常数项为( ) A .672B .-672C .5376D .-53768.已知变量x ,y 之间的线性回归方程为3.107.0ˆ+-=x y,且变量x ,y 之间的一组相关数据如表所示,则下列说法错误的是( )A .可以预测,当x =20时,7.3ˆ-=yB .m =5C .变量x ,y 之间呈负相关关系D .该回归直线必过点(8,5)9.二面角α-l -β为60°,A 、B 是棱l 上的两点,AC 、BD 分别在半平面α、β内,AC ⊥l ,BD ⊥l ,且AB =AC =a ,BD =2a ,则CD 的长为( ) A 3a B .2a C 5a D .2a 10.函数()()22xf x x x e =-的图象大致是( )A B C D11.已知双曲线2222:1x y C a b-=(0a >,0b >),以点P (,0b )为圆心,a 为半径作圆P ,圆P与双曲线C 的一条渐近线交于M ,N 两点,若90MPN ∠=︒,则C 的离心率为( )2B.35 712.已知函数)(,2)(R x x ee xf xx ∈--=-,则不等式01()1(2≥-++)x f x f 的解集是( )x 8 10 12 y 6 m 3 2A .[]2,1-B .[]1,2-C .(][)∞+⋃∞,,21-- D .(][)∞+⋃∞,,12-- 二.填空题(每小题5分,共20分.) 13.已知平面α的一个法向量,A ∈α,P ∉α,且,则直线PA 与平面α所成的角为 .14.1012x dx ⎫=⎪⎭⎰ . 15.已知随机变量ξ~N (3,σ2),且P (ξ>2)=0.85,则P (3<ξ<4)= .16.已知n xx )2(3+展开式中第二项、第三项、第四项的二项式系数成等差数列,将展开式中所有项重新排列,则有理项不相邻的概率为 .三.解答题(共70分.解答应写出文字说明、证明过程或演算步骤。
四川省南充市白塔中学2019_2020学年高二语文12月月考试题扫描版20-含答案

四川省南充市白塔中学2019-2020学年高二语文12月月考试题(扫描版)高二语文月考答案(2019/12/12)1.C A项“被遗忘权和隐私权的提出都是为了对抗大数据”曲解文意,原文第一段表明了“被遗忘权”的出现“意在改变数据主体难以‘被遗忘’的格局,对于数据主体对信息进行自决控制的权利,并且有着更深的调节、修复大数据时代数字化记忆伦理的意义”。
B项将第一段“数字化记忆……比选择性删除所耗费的成本更低”和第四段“大数据技术加速了人的主体身份的‘被数据化’”进行简单拼接,强加因果。
D项曲解文意。
原文最后一段可推知,“数据控制者选择和构建关于我们的数字化记忆”的行为本身属于数字化记忆霸权,而且明确表示“适度的、合理的遗忘,是对这种数字化记忆霸权的抵抗”。
2.D 项混淆时态。
“可能”错误,文章分析的是已然发生的问题。
3.A 项以偏概全。
原文说“不论是个人的遗忘还是社会的遗忘,在某种程度都是一种个人及社会修复和更新的机制”,选项去掉了“在某种程度上”的限制。
4.B 项曲解文意。
从原文看,作者认为用鲧来比晴雯,够古怪,联系后文的“《红楼梦》作者翻‘直’为‘刚直’,仿佛更进了一步”的一句看,这是值得肯定的一比,选项说“荒唐,全无道理”是错误的。
5.A 项以偏概全。
从全文看,文章最终强调“必须把《红接梦》的传统性跟它的独创性合并地看,才能见出真面目”,《红楼梦》是传统性与独创性的统一。
首段只是全文的第一个分论点,选项理解为统摄全篇的中心论点,这是错误的。
故选A。
6.D 项以偏概全。
从全文看,对文学传统的继承,是《红楼梦》成为巅峰之作的必要条件;作者认为要真正领略其要领,“必须把《红接梦》的传统性跟它的独创性合并地看”,说明《红楼梦》成为中国古代小说的巅峰之作,“传统性”和“独创性”缺一不可。
选项“……传统性,决定了《红楼梦》成为中国古代小说巅峰之作的结果”之说错误。
故选D。
7.(B E) B项,并非“直接”,而是含蓄地交代出来。
四川省南充市白塔中学2019_2020学年高二数学下学期第三次月考试题文
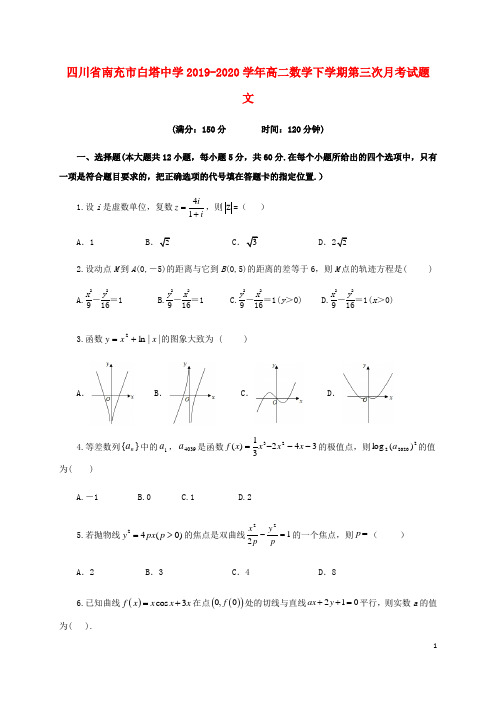
四川省南充市白塔中学2019-2020学年高二数学下学期第三次月考试题文(满分:150分 时间:120分钟)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.)1.设i 是虚数单位,复数iiz +=14,则z =( ) A .1 B .2C .3D .222.设动点M 到A (0,-5)的距离与它到B (0,5)的距离的差等于6,则M 点的轨迹方程是( )A.x 29-y 216=1B.y 29-x 216=1C.y 29-x 216=1(y >0)D.x 29-y 216=1(x >0) 3.函数||ln 2x x y +=的图象大致为 ( )A .B .C .D .4.等差数列}{n a 中的1a ,4039a 是函数34231)(23---=x x x x f 的极值点,则220202)(log a 的值为( )A.-1B.0C.1D.25.若抛物线24(0)=>y px p 的焦点是双曲线1222=-py p x 的一个焦点,则p =( ) A .2 B .3 C .4 D .86.已知曲线()cos 3f x x x x =+在点()()0,0f 处的切线与直线210ax y ++=平行,则实数a 的值为( ).A .-8B .-4C .12D .47.若函数f (x )=ax 3-x 2-x -1在(-∞,+∞)上单调递减,则a 的取值范围是( ) A .a >13 B .a ≥13 C .a <-13 D .a ≤-138.某公司奖励甲,乙,丙三个团队去A ,B ,C 三个景点游玩,三个团队各去一个不同景点,征求三个团队意见得到:甲团队不去B ;乙团队不去C ;丙团队只去A 或B .公司按征求意见安排,则下列说法一定正确的是( )A.丙团队一定去A 景点B.甲团队一定去C 景点C.乙团队一定去B 景点D.乙团队一定去A 景点9.在平面直角坐标系xOy 中,已知△ABC 顶点A(-2,0)和C(2,0),顶点B 在椭圆13722=+y x 上,则BCA sin sin sin += ( )A.27 B.23 C. 2 D. 21 10.设F 为抛物线x y 42=的焦点,A ,B ,C 为该抛物线上三点,若=++,则=++||||||FC FB FA ( )A.4B.6C.9D.1211.已知双曲线)0,0(,12222>>=-b a b y a x 的左、右焦点分别为F 1,F 2,过F 2且与渐近线垂直的直线分别与该渐近线和y 轴相交于A ,B 两点,O 为坐标原点,若32=∆∆AOBAOF S S ,则双曲线的离心率为( ) A.2 B.3 C.2 D. 512.已知f (x )是定义在R 上的可导函数,对于任意实数x ,均有x e x f x f 2)()(=-,当0<x 时,0)()(>'+x f x f ,若)1()12(-≥-a f a f e a ,则实数a 的取值范围是( )A.]32,0[B.]0,32[- C.),0[+∞ D.]0,(-∞二、填空题(本大题共4小题,每小题5分,满分20分)13.若复数z 满足2z +z =1+i ,其中i 为虚数单位,则z =________.14.已知抛物线C :y x 82=的焦点为F ,O 为坐标原点,点P 在抛物线C 上,且OF PF ⊥,则||PF OF -=_______________________15.已知F 是双曲线15422=-y x 的左焦点,点A (1,5),P 是双曲线右支上的动点,则|PF |+|PA |的最小值为________.16.已知13)1()(-+=x ex x f ,a x x x g -++=44)(2,若R x R x ∈∃∈∀21,,使得)()(21x g x f ≥成立,则实数a 的取值范围是__________.三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤,第17 ~ 21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.)17.(本小题满分12分)为考察某种疫苗预防疾病的效果,进行动物试验,得到统计数据如下:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为53.⑴求2×2列联表中的数据x ,y ,A ,B 的值.⑵能否在犯错误的概率不超过0.01的前提下认为疫苗有效?附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),n =a +b +c +d .临界值表:18.(本小题满分12分)某厂家准备在“6.18”举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x (万元)和销售量y (万台)的数据如下:); ⑵若用y =c +d x 模型拟合y 与x 的关系,可得回归方程x y+=51.1ˆ,经计算线性回归模型和该模型的R 2分别约为0.774和0.888,请用R 2说明选择哪个回归模型更好;⑶已知利润z 与x ,y 的关系为z =200y -x .根据(2)的结果,当广告费x =20时,求销售量及利润的预报值.参考公式:回归直线y ^=a ^+b ^x 的斜率和截距的最小二乘估计分别为b ^=∑∑∑∑====--⋅-=-⋅-ni ii ni ini ini i i x xy y x xx n xyx n yx 1211221)()()(,x b y aˆˆ-=. 参考数据:5≈2.24, ∑==715.275i i i y x , ∑==712708i i x19.(本小题满分12分)在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线θρcos 6:=C ,直线l 的参数方程为:)(221为参数t t y tx ⎩⎨⎧+=+=,直线l 与曲线C 分别交于M ,N 两点.⑴写出曲线C 的直角坐标方程和直线l 的普通方程;⑵若点)2,1(P ,求|||1||1|PN PM -的值.20.(本小题满分12分)设函数ax x x x f -+=221ln 6)(. ⑴当5=a 时,求函数()f x 的单调区间; ⑵当1a =-时,方程221)(x mx x f +=在区间21,e ⎡⎤⎣⎦上有两个实数解,求实数m 的取值范围. 21.(本小题满分12分)已知点F 1为椭圆E :12222=+by a x (a >b >0)的左焦点,且两焦点与短轴的一个顶点构成一个等腰直角三角形,直线3+=x y 与椭圆E 有且仅有一个交点M .⑴求椭圆E 的方程;⑵设直线3+=x y 与y 轴交于P ,过点P 的直线l 与椭圆E 交于不同的两点A ,B ,若λ|PM |2=|PA |·|PB |,求实数λ的取值范围.选考题:共10分,请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.在以原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为4πθ=,平面直角坐标系xOy 中,曲线C 的参数方程为)(sin 3cos 4为参数ααα⎩⎨⎧==y x .⑴设直线l 与曲线C 交于M ,N 两点,求|MN|;⑵若点P (x ,y )为曲线C 上任意一点,求|2|-+y x 的取值范围.23.已知函数f (x )=|2x -4|+|x +1|. ⑴解不等式f (x )≤5;(2)求函数g (x )=f (x )-3|x +1|的值域M .高二数学(文科)参考答案(6月)一、选择题(本大题共12小题,每小题5分,共60分.)二、填空题(本大题共4小题,每小题5分,满分20分)13. i+3114. 52 15. 7 16. ),27[5+∞e三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤)17.解:⑴设“从所有试验动物中任取一只,取到‘注射疫苗’动物”为事件M , 由已知得P (M )=10040y +=53,所以y =20 ………………………3分则B =60,x =20,A =40. ………………………6分⑵因为K2=60404060)20402020(1002⨯⨯⨯⨯-⨯⨯100×(20×10-40×30)260×40×50×50≈2.778<6.635. ………………11分所以不能在犯错误的概率不超过0.01的前提下认为疫苗有效. ………………………12分18.解:⑴∵8=x ,1.4=y , ………………………2分∴b ^=18.02609.45877081.4875.2752≈=⨯-⨯⨯-,x b y a ˆˆ-== 4.1-0.18×8=2.66, …………………5分∴y 关于x 的线性回归方程为y^=0.18x +2.66. ………………………6分⑵∵0.774<0.888且R 2越大,反映残差平方和越小,模型的拟合效果越好,∴选用x y+=51.1ˆ更好. ………………………8分⑶由⑵知,当x =20时,销售量的预报值99.52051.1ˆ≈+=y(万台), ………………………10分利润的预报值z =200×5.99-20=1178(万元). ………………………12分19.解:⑴∵θρcos 6=∴θρρcos 62=则x y x 622=+,即9)3(22=+-y x 为曲线C 直角坐标方程. ………………………3分∵)(221为参数t ty tx ⎩⎨⎧+=+=∴032=+-y x 为直线l 的普通方程. ………………………5分 ⑵直线l 的参数方程化为)(5525521为参数u u y u x ⎪⎪⎩⎪⎪⎨⎧+=+= ………………………7分代入x y x 622=+得015542=--u u ,0>∆恒成立, ………………………8分设M ,N 对应的参数分别为1u ,2u ,则55421=+u u ,0121<-=u u ………………………9分∴554|||||||||||||||||1||1||||1||1|2112211221=+=-=-=-u u u u u u u u u u PN PM ………………………12分20.解:⑴依题意,可知()f x 的定义域为(0,)+∞, ………………………1分当5=a 时,ax x x x f -+=221ln 6)(,xx x x x x x x x f )3)(2(6556)(2--=+-=-+=', …………2分令()0f x '=,解得32==x x 或,当320><<x x 或时,()0f x '>,当32<<x 时,()0f x '<,所以()f x 的单调递增区间为)2,0(,),3(+∞,递减区间为)3,2(. ………………………5分⑵1a =-时,由221)(x mx x f +=得mx x x =+ln 6,又0x >,所以xxm ln 61+=, 要使方程221)(x mx x f +=在区间21,e ⎡⎤⎣⎦上有两个实数解,只需xx m ln 61+=有两个实数解, 即函数m y =与xxy ln 61+=的图象有两个交点 ………………………7分令)1(ln 61)(2e x x x x g ≤≤+=,则2)ln 1(6)(x x x g -=', 由()0g x '>,得1x e ≤<,由()0g x '<,得e x >.∴()g x 在区间[1,e]上是增函数,在区间2,e e ⎡⎤⎣⎦上是减函数. (9)分∴当e x =时,()g x 取得极大值,且为最大值,ee g x g 61)()(max +== ∵(1)1g =,1121)(22>+=ee g ,∴1)1()(min ==g x g ………………………11分结合图象可知,实数m 的取值范围为]61,121[2e e ++. ………………………12分21.解:⑴∵221B F F ∆为等腰直角三角形 ∴a c b 22==,则椭圆E 方程化为:122222=+b y b x…2分由⎪⎩⎪⎨⎧=++=1232222b ybx x y 得021812322=-++b x x )218(341222b -⨯-=∆ ∵直线3+=x y 与椭圆E 有且仅有一个交点M . ∴0=∆,即32=b ………………4分∴椭圆E 方程化为:13622=+y x………………………5分⑵由(1)得M )1,2(-,直线3+=x y 与y 轴交于P )3,0(,22||=PM ………………6分方法一:①当直线l 与x 轴垂直时,|PA |·|PB |=(3)=6, ∴43||||||2=⋅=PM PB PA λ ………………………7分②当直线l 与x 轴不垂直时,设直线l 的方程为y =kx +3,A (x 1,y 1),B (x 2,y 2), 由⎪⎩⎪⎨⎧=++=136322y x kx y 得01212)21(22=+++kx x k , 0)21(124)12(22>+⨯-=∆k k ,即12>k ,x 1x 2=021122>+k, ………………………8分∴|PA |·|PB |=||)1()3()3(212222222122122222121x x k x k x x k x y x y x +=+⋅+=-+⋅-+ =λ8216621)1(12222=++=++k k k………………………10分 ∵12>k ∴8216662<++<k ,即886<<λ,则143<<λ………………………11分 综上所述,λ的取值范围是[43,1). ………………………12分方法二:设直线l 的参数方程为)(sin 3cos 为参数t t y t x ⎩⎨⎧+==αα, ………………………7分代入椭圆E 的方程得012sin 12)sin 1(22=+++ααt t ,0>∆,即21sin 2>α ………………8分设A ,B 对应的参数分别为1t ,2t ,则0sin 112221>+=αt t ………………………9分 ∴|PA|·|PB|=λα8sin 112||||||2212121=+===⋅t t t t t t ………………………10分 ∵1sin 212≤<α∴8sin 11262<+≤α,即886<≤λ,则143<≤λ 综上所述,λ的取值范围是[43,1). ………………………12分22.解:⑴直线l :4πθ=的参数直角坐标方程为:y =x①, ………………1分 曲线C 的参数方程为)(sin 3cos 4为参数ααα⎩⎨⎧==y x 普通方程为191622=+y x ②. ………………2分 由①②得259162⨯=x ,即512±=x ,∴)512,512(M ,)512,512(--N ,2524||=MN ………………5分⑵点P (x ,y )为曲线C 上任意一点,设)sin 3,cos 4(ααP ,R ∈α …………………6分则|2)sin(5||2sin 3cos 4||2|-+=-+=-+ϕαααy x ,其中34tan =α ………………8分∵R ∈α ∴R ∈+ϕα 则1)sin(1≤+≤-ϕα,32)sin(57≤-+≤-ϕα,即7|2|0≤-+≤y x ,故|2|-+y x 的取值范围为[0,7] ………………………10分23.解:(1)f (x )=|2x -4|+|x +1|=⎪⎩⎪⎨⎧>-≤<-+--≤+-2,3321,51,33x x x x x x∴f (x )≤5⇔⎩⎨⎧≤+--≤5331x x 或⎩⎨⎧≤+-≤<-5521x x 或⎩⎨⎧≤->5332x x………………………3分 解得38220≤<≤≤x x 或,即380≤≤x 即原不等式的解集为{x |380≤≤x }. ………………………5分 ⑵g (x )=f (x )-3|x +1|=|2x -4|-|2x +2|,6|)22()42(|||22||42||=+--≤+--x x x x (当且仅当1x 20)22)(42(-≤≥≥+-或即x x x 时等号成立)∴M =[-6,6]. ………………………10分。
【精准解析】四川省南充市白塔中学2019-2020学年高二下学期第三次月考数学(文)试题

B. 4
1 C.
2
【解析】
【分析】
利用导数可求得 f 0 ,根据两直线平行可构造斜率相等关系求得结果.
D. 4
【详解】 f x cos x x sin x 3 , f 0 1 3 4 ,
a 4 ,解得: a 8. 2
故选: A .
【点睛】本题考查利用导数的几何意义求解切线斜率、利用两直线平行关系求解参数值的问
【详解】由条件可知 f x 3ax2 2x 1 0 恒成立,
当 a 0 时, f x 2x 1 0 不恒成立,
a 0 当 a 0 时, 4 12a 0
,解得: a 1 . 3
故选:D
【点睛】本题考查导数和函数单调性的应用,意在考查转化与化归的思想,属于基础题型.
8.某公司奖励甲,乙,丙三个团队去 A,B,C 三个景点游玩,三个团队各去一个不同景点,
3 由题意可得 a1 、 a4039 是方程 x2 4x 4 0 的实根,
由韦达定理可得 a1 a4039 4 ,
由等差数列的性质可得 2a2020 a1 a4039 4 ,
解得 a2020 2 ,log2 (a2020 )2 log2 22 2
故选:D.
【点睛】本题考查等差数列的性质和韦达定理,属于基础题.
到所求的轨迹方程.
【详解】 MA MB 6 10 AB , M 点轨迹是焦点在 y 轴上的双曲线的上半支,
-1-
其中 a 3 , c 5 ,b2 c2 a2 4 ,
M 点轨迹方程为: y2 x2 1 y 0 .
9 16 故选: C .
【点睛】本题考查动点轨迹方程的求解问题,解题关键是熟练掌握双曲线的定义;易错点是 忽略动点轨迹为双曲线的半支,从而造成轨迹方程求解错误.
四川省南充市白塔中学2019_2020学年高二化学下学期开学考试试题

四川省南充市白塔中学2019-2020学年高二化学下学期开学考试试题(考试时间90分钟,满分100分)本试卷分为试题卷和答题卡两部分,其中试题卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)组成,共6页;答题卡共2页。
注意事项:1. 答题前,考生务必将自己的学校、班级、姓名用0.5毫米黑色墨水签字笔填写清楚,同时用2B铅笔将考号准确填涂在“考号”栏目内。
2. 选择题使用2B铅笔填涂在答题卡对应题目标号的位置上,如需改动,用橡皮擦擦干净后再选涂其它答案;非选择题用0.5毫米黑色墨水签字笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
可能用到的相对原子质量:H-1 C-12 O-16 Mg-24 Al-27 P-31 S-32 Cu-64第Ⅰ卷(选择题共60分)一、选择题(本题包括20小题,每题3分,共60分,每小题只有一个选项符合题意)1.冠状病毒对热敏感、对有机溶剂和消毒剂敏感,56℃下30分钟,75%乙醇、乙醚、氯仿、甲醛、含氯消毒剂、过氧乙酸和紫外线均可灭活病毒。
下列说法正确的是A.灭活病毒的主要原理是使病毒的蛋白质变性B.高浓度酒精(95%)消毒杀菌效果更好C.口罩主要是避免发生接触传播D.氯仿是一种常见的有机溶剂;可通过甲烷和氯气的加成反应得到2.下列关于有机化合物的说法正确的是A.2甲基丙烷也叫异丁烷B.蛋白质和糖类均为天然高分子化合物C.乙烯和丙烯只能发生加成反应,不能发生取代反应D.苯使溴水褪色的原因是发生加成反应3.如图所示是常见四种有机物的比例模型示意图。
下列说法不正确的是A.甲不能使酸性高锰酸钾溶液褪色B.乙可与溴的四氯化碳溶液发生加成反应使其褪色C.丙中的碳碳键是一种介于碳碳单键和碳碳双键之间的独特的键D.丁可由乙与水发生取代反应生成4.下列除杂方法(括号内为杂质)正确的是A.乙醇(水) 加新制的生石灰,过滤B.乙烷(乙烯) 通过溴的四氯化碳溶液,洗气C.溴苯(苯) 加水,振荡静置后分液D.乙酸乙酯(乙酸) 加饱和Na2CO3溶液,振荡静置后分液5.分枝酸可用于生化研究,其结构简式如下图所示。
【高中数学】四川省南充市白塔中学2019-2020学年高二下学期第三次月考(理)试卷含解析

四川省南充市白塔中学2019-2020学年高二下学期第三次月考(理)一.选择题(每小题5分,共60分.)1.在复平面上,复数(2)z i i =-+的对应点所在象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限2.下列求导运算正确的是( ) A .()x x sin cos ='B .()xxxeex 22='C .()e xx3log 33='D .()xx 12ln =' 3.已知随机变量X ~B (n ,p ).若E (X )=2,D (X )=,则p =( ) A . B .C .D .4.函数()x xx f ln 5+=的单调减区间为( ) A .(﹣∞,5)B .(0,5)C .(5,+∞)D .(0,+∞)5.甲、乙二人进行围棋比赛,采取“三局两胜制”,已知甲每局取胜的概率为,则甲获胜的概率为( )A .()2+C ()2()1B .()2+C ()2 C .()2+C ()2()1D .()2+C ()1()16.南充市中心医院医院计划从3名医生,9名护士中选派5人参加狙击战,要求选派的5人中至少要有2名医生,则不同的选派方法有( ) A .495种B .288种C .252种D .126种7.若921ax x ⎛⎫- ⎪⎝⎭的展开式中的各项系数的和为1,则该展开式中的常数项为( )A .672B .-672C .5376D .-5376 8.已知变量x ,y 之间的线性回归方程为3.107.0ˆ+-=x y,且变量x ,y 之间的一组相关数据如表所示,则下列说法错误的是( )x 8 1012y6m3 2A .可以预测,当x =20时,7.3ˆ-=yB .m =5C .变量x ,y 之间呈负相关关系D .该回归直线必过点(8,5)9.二面角α-l -β为60°,A 、B 是棱l 上的两点,AC 、BD 分别在半平面α、β内,AC ⊥l ,BD ⊥l ,且AB =AC =a ,BD =2a ,则CD 的长为( ) A 3a B .2a C 5a D .2a 10.函数()()22xf x x x e =-的图象大致是( )A B C D11.已知双曲线2222:1x y C a b-=(0a >,0b >),以点P (,0b )为圆心,a 为半径作圆P ,圆P 与双曲线C 的一条渐近线交于M ,N 两点,若90MPN ∠=︒,则C 的离心率为( )2 35D.7212.已知函数)(,2)(R x x e e x f x x ∈--=-,则不等式01()1(2≥-++)x f x f 的解集是( ) A .[]2,1-B .[]1,2-C .(][)∞+⋃∞,,21-- D .(][)∞+⋃∞,,12-- 二.填空题(每小题5分,共20分.) 13.已知平面α的一个法向量,A ∈α,P ∉α,且,则直线P A 与平面α所成的角为 . 14.120112x x dx ⎫-=⎪⎭⎰ .15.已知随机变量ξ~N (3,σ2),且P (ξ>2)=0.85,则P (3<ξ<4)= .16.已知n xx )2(3+展开式中第二项、第三项、第四项的二项式系数成等差数列,将展开式中所有项重新排列,则有理项不相邻的概率为 . 三.解答题(共70分.解答应写出文字说明、证明过程或演算步骤。
