新版上海大学数学考研经验考研真题考研参考书
专业课复习有重点!上海大学数学专业考研经验分享
研途宝考研/zykzl?fromcode=9820楼主是上海大学数学专业的学长，自认为数学基础挺好，暑假7月份才决定的跨考数学专业。
因此楼主在本文中为研苞们提供了参考教材，同时还贴心的为研苞们的专业课划好了重点！考研er们还等什么呢？一、参考教材数学分析第四版教材必不可少，课后习题可能会考成真题，这个历年都有题，可以比对。
还有就是题解精粹，当时学校图书馆有这方面的书。
我借了以下几本：数学分析解题方法；数学分析考研教案；数学分析选讲；高代考研教案，高代钱吉林～习题精粹建议：如果现在开始复习的话先看课本和习题精粹，做笔记，练题目每天必不可少。
等你不知道怎么复习了，也不知道以及在哪方面薄弱，就可以看我以上推荐的书籍，当然图书馆有条件的话。
下面开始说一下我的复习经验。
字数太多只能分开叙述，有时间我会写上高代的复习经验。
数学分析：课本一定要看，着重看华中师范大学的第四版教材，课后习题一定要做，好多历年真题都是课后习题原题，06年之前的真题有数学分析第二版研途宝考研/zykzl?fromcode=9820的课后习题，题解精粹一定要买，上面的题有时候都做，时间不够专门看武汉大学，华中师范大学，天津大学，四川大学这几个学校的相关题目，复习过程中一定要记笔记，课本最少看两遍，书上的定理都要会证明，尽管近几年考试真题都是一个套路，没有考有关定理的证明，比如闭区间套定理，有限覆盖定理，魏尔斯特拉斯定理等等，考前记忆一下就行。
二、专业课重点：第一：数列极限的定义和证明（17年第一题，第二题）。
第二：函数极限的定义和证明。
第三：一致连续概念以及证明特别是几个特殊函数sinx，sinx2等等（17年第三题）。
第四：一致收敛定义以及证明（17年没有考）。
第五：零点存在性定理以及几个微分中值定理都要会运用（17年第6题）～具体题号记不太清。
第六：还有级数的收敛，反常积分的收敛，含参变量积分的收敛（这几个要研途宝考研/zykzl?fromcode=9820学会总结，方法都是一样的，狄利克雷和阿贝尔两个判别法要熟练运用，其他的一些判别法要知道）。
上海大学应用数学专业考研
来源：凯程考研集训营，资料获取、课程辅导咨询凯程老师
第 1 页 共 1 页 上海大学应用数学专业考研
应用数学：本专业以奇异摄动理论与渐近分析、数学建模与工业中的数学反问题、小波分析及其应用、分层理论与非线性偏微分方程、分支理论的应用及数值方法、非光滑分析与变分不等方程理论及应用、连续介质力学中的数学方法和微分方程问题为主要研究方向。
主要从事基础理论研究及其在工程中的应用，为国家重点工程项目特别是上海的经济和社会发展服务。
培养既有坚实的数学理论知识，又能在工程技术应用方面具有研究、开发能力的高级科技人才。
本专业现有教授6名，副教授10余名。
自1980年起招收硕士研究生，已培养了三十余名研究生。
本专业已与国内外学术界建立了广泛联系，先后有10余名国外应用数学专家来访。
上海市应用数学和力学研究所已成为国内外注目的应用数学研究基地之一。
一、研究方向
01.奇异摄动理论与渐近分析
02.数学建模与工业中的数学反问题
03.小波分析及其应用
04.分层理论与非线性偏微分方程
05.分支理论的应用及数值方法
06.偏微分方程的边值问题和反问题
07.非光滑分析与变分不等方程理论及应用
08.连续介质力学中的数学方法和微分方程问题
二、指导教师
刘曾荣教授、朱正佑教授、施惟慧教授、郭兴明教授和10余名副教授。
新版上海交通大学数学考研经验考研真题考研参考书
一年就这样过去了，内心思绪万千。
一年很短，备考的经历历历在目，一年很长，长到由此改变了一个人的轨迹，并且成就一个梦想。
回忆着一年的历程，总想把它记录下来，希望可以给还在考研道路上奋斗的小伙伴们一点帮助。
考研是一个非常需要坚持的过程，需要你不断坚持和努力才能获得成功，所以你必须要想清楚自己为什么要考研，这一点非常重要，因为只有确认好坚定的动机，才能让你在最后冲刺阶段时能够坚持下来。
如果你只是看到自己周围的人都在考研而决定的考研，自己只是随波逐流没有坚定的信心，那么非常容易在中途就放弃掉了，而且现在考研非常火热，这就意味着竞争也会非常激烈，而且调剂的机会都会非常难得，所以备考时的压力也会比较大，所以大家一定要调整好心态，既不能压力太大，也不能懈怠。
既然选择了，就勇敢的走下去吧。
考研整个过程确实很煎熬，像是小火慢炖，但是坚持下来，你就会发现，原来世界真的是美好的。
文章整体字数较多，大家可视自己情况阅读，在文章末尾我也分享了自己备考过程中的资料和真题，大家可自行下载。
上海交通大学数学的初试科目为：(101)思想政治理论(201)英语一(614)数学分析和(828)高等代数参考书目为：1.《数学分析》（第二版）上、下，陈纪修等编，高等教育出版社，20042.《数学分析教程》上、下，常庚哲、史济怀著，高等教育出版社，20033.《高等代数》（第四版），北京大学数学系编，高等教育出版社，20134.《高等代数与解析几何》（第三版）上、下，孟道骥编，科学出版社，2014年先说英语吧。
词汇量曾经是我的一块心病，跟我英语水平差不多的同学，词汇量往往比我高出一大截。
从初中学英语开始就不爱背单词。
在考研阶段，词汇量的重要性胜过四六级，尤其是一些熟词僻义，往往一个单词决定你一道阅读能否做对。
所以，一旦你准备学习考研英语，词汇一定是陪伴你从头至尾的一项工作。
考研到底背多少个单词足够？按照大纲的要求，大概是5500多个。
实际上，核心单词及其熟词僻义才是考研的重点。
上海市考研数学复习资料高等数学重点整理
上海市考研数学复习资料高等数学重点整理一、导数和微分1. 函数的极限和连续性- 函数的极限定义及计算方法- 函数在某点的连续性判断与性质- 闭区间上连续函数的性质2. 导数的定义和计算- 函数在某点的导数定义及几何意义- 常见函数的导数公式及例题- 高阶导数及其应用3. 微分的概念和应用- 微分的定义及计算- 几何应用：切线、法线和曲率- 物理应用：极值与最优化问题二、不定积分和定积分1. 不定积分- 不定积分的定义及计算方法- 常见函数的不定积分公式及例题- 特殊换元法与分部积分法2. 定积分- 定积分的概念及计算方法- 牛顿-莱布尼兹公式- 定积分的几何应用与物理应用3. 反常积分- 反常积分的概念及判敛方法- 常见函数的反常积分计算- 反常积分的应用思想三、级数和幂级数1. 数项级数- 数项级数的概念及性质- 收敛级数的判定方法- 常见收敛级数的计算2. 幂级数- 幂级数的收敛半径和收敛域- 幂级数的性质及运算法则- 幂级数的收敛性判断方法3. 函数展开为幂级数- 方程函数的幂级数解法- 常见函数的幂级数展开- 泰勒级数及其应用四、微分方程1. 微分方程的基本概念- 微分方程的定义及解的分类- 一阶微分方程的解法- 二阶线性常系数齐次微分方程解法2. 高阶线性常系数非齐次微分方程- 常用非齐次项的特解求法- 常系数非齐次方程的解法- 欧拉方程及应用3. 变量分离与常微分方程- 变量分离法解方程的步骤- 可分离变量方程的解法- 常微分方程的应用五、多元函数微分学1. 多元函数的极限与连续性- 多元函数的极限定义及计算方法- 多元函数的连续性判定与性质- 多元函数的偏导数及其几何应用2. 隐函数与参数方程- 隐函数的偏导数公式及计算方法- 参数方程的导数与曲线切线- 参数方程求极限和导数3. 多元函数的微分学- 多元函数的全微分及偏导数运算- 雅可比矩阵与梯度- 多元函数的极值与最优化问题六、多重积分与曲线曲面积分1. 二重积分- 二重积分的定义及几何意义- 二重积分的计算方法- 二重积分的应用2. 三重积分- 三重积分的定义及几何意义- 三重积分的计算方法- 三重积分的应用3. 曲线曲面积分- 一元曲线积分的定义与计算- 二重曲面积分的定义与计算- 曲线曲面积分的应用七、向量代数与空间解析几何1. 向量的基本概念- 向量的定义及基本运算- 向量的共线、共面与线性相关性- 平面与空间向量的内积与外积2. 空间解析几何- 点、直线与平面的位置关系- 直线与平面的相交及距离计算- 圆锥曲线与二次曲线的基本性质综上所述，以上整理的高等数学重点内容涵盖了上海市考研数学复习资料中的主要知识点。
上海大学数学分析历年考研真题
上海大学2000年度研究生入学考试试题数学分析1、 设122(1)n n x x nx y n n +++=+，若lim n n x a →∞=，证明：（1）当a 为有限数时，lim 2n n ay →∞=；（2）当a =+∞时，lim n n y →∞=+∞.2、设()f x 在[]0,1上有二阶导数（端点分别指左、右导数），(0)(1)0f f ==，且[]0,1min ()1f x =-证明：[]0,1max ()8f x ''≥3、 证明：黎曼函数[]1, x= (0,,)()0,10,p q p q q q R x ⎧>⎪=⎨⎪⎩当为互质整数在上可积当x 为无理数. 4、 证明：12210()lim (0),t tf x dx f t x π+-→=+⎰其中()f x 在[]1,1-上连续.5、 设()1ln 11n n p a n ⎛⎫=+- ⎪⎝⎭，讨论级数2n n a +∞=∑的收敛性.6、 设()f x dx +∞⎰收敛且()f x 在[]0,+∞上单调，证明：01lim ()()h n h f nh f x dx ++∞+∞→==∑⎰.7、 计算曲面2222x y z a ++=包含在曲面22221(0)x y b a a b+=<≤内的那部分的面积.8、 将函数()f x x =在[]0,2π上展成Fourier 级数,并计算级数1sin k kk +∞=∑的值. 上海大学2001年度研究生入学考试试题数学分析1、 计算下列极限、导数和积分:(1) 计算极限1lim();xx x +→ (2) 计算2()()x x f t dt ϕ=⎰的导数()x ϕ',其中()f x 2,(1).1,(1)t t t t ≤⎧=⎨+>⎩ (3) 已知)211sin x x '⎤=⎥+⎦,求积分2011sin I dx x π=+⎰. (4) 计算()()22222()0x y z t f t xyz dxdydz t ++≤=>⎰⎰⎰的导数()f t '(只需写出()f t '的积分表达式).2、 设()f x 在[],a b 上连续，在(),a b 上可导，若()()0f a f b >且()02a bf +=，试证明必存在(),a b ξ∈使得()0f ξ'=. 3、 令(),1y F x y y xe =+-(1)、证明:111311,0,,;,0,,.2121221212F x x F x x ⎛⎫⎛⎫⎛⎫⎡⎤<∈->∈- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦(2)、证明:对任意的11,1212x ⎛⎫∈- ⎪⎝⎭,方程(),0F x y >在13,22y ⎛⎫∈ ⎪⎝⎭中存在唯一的解()y x . (3)、计算(0)y '和(0)y ''. 4、一致连续和一致收敛性(1)、函数2()f x x =在[]0,1上是一致连续的,对210ε-=,试确定0δ>,使得当1201x x ≤<≤,且12x x δ-<时有3321210x x --<.(2)、设[]2231(),0,1,1,2,,2n n x f x x n n x+=∈=+证明: ()n f x 在[]0,1上是内闭一致收敛的,但不是一致收敛的.5、曲线积分、格林公式和原函数. (1)计算第二型曲线积分()221,2L xdy ydxI x y π-=+⎰其中L 是逐段光滑的简单闭曲线,原点属于L 围成的内部区域,(L)的定向是逆时针方向.(2) 设(),p x y ,(),q x y 除原点外是连续的,且有连续的偏导数,若<a>()(),,0,0p q x y y x∂∂=≠∂∂ <b>()0,L pdy qdx c +=≠⎰其中(L)的参数方程cos ,(02)sin x tt y tπ=⎧≤≤⎨=⎩ 证明：存在连续可微函数()()(),,,0,0F x y x y ≠，使得()()2222,,,22F c y F c xp x y q x y x x y y x yππ∂∂=+=-∂+∂+. 上海大学2002年度研究生入学考试题数学分析1、 求α和β使得当x →+∞等价于无穷小量x βα.2、 求椭圆2221Ax Bxy Cy ++=所围成的面积S ,其中20,0,,,A AC B A B C >->均为常数.3、 试给出三角级数01(cos sin )2n n n a a nx b nx ∞=++∑中系数的计算公式(不必求出具体值),使得该级数在[]0,1上一致收敛到2x ,并说明理论依据。
上海大学考研真题611数学分析
三、参考书目：
《数学分析》（上、下册） 陈纪修等编 高等教育出版社2004年
考核重点包括
1.数学分析课程的基本概念。
2.实数的基本性质相关的几个公理的等价性以及它们的应用。
3.极限的各种计算方法与理论证明。
4.连续与间断、一致连续以及闭区间上连续函数性质的证明与应用。
5.中值定理包括微分、积分中值定理的理论推导及应用，特别是用来证明各种不等式。
6.微积分基本定理的。
7.级数(各种级数)的收敛性（含绝对、条件以及一致收敛性）判定，函数的幂级数展开和富里埃级数展开以及收敛范围的确定，各种级数的特定求和办法。
8.平面点集的性质，多元函数极限值的计算以及连续性、可微性的讨论。
9.一元函数和多元函数极值的计算及应用。
10.隐函数定理与函数相关性的结论与证明和应用。
11.二重和三重积分以及一些特殊的n重积分的计算和应用。
考试科目：数学分析
适用专业：基础数学、应用数学、计算数学、运筹学与控制论、系统分析与集成
一、复习要求：
要求学生掌握数学分析课程的基本概念、基本结论与算法，能够运用数学分析的理论求解和证明相关命题。
二、主要复习内容：
本课程考核内容包括实数的基本理论与极限、单变量微积分学，级数论，多变量微积分学、广义积分五大部分组成.
实数的基本理论和极限理论部分包括变量与函数，极限与连续，连续函数以及闭区间上的连续函数的性质；单变量微积分包括导数与微分，几个中值定理，微积分学的基本定理及其应用，不定积分，定积分及其应用。级数论中含数项级数，函数项级数（含幂级数、泰勒级数），富里埃级数和富里埃变换。多变量微积分学中含多元函数的极限与连续，偏导数和全微分，极值和条件极值，隐函数定理与函数相关性；多重积分及其应用，曲线积分，曲面积分以及场论初步。广义积分部分包括含参变量的积分和广义积分。
上海大学2021年专业学位硕士研究生初试参考书目
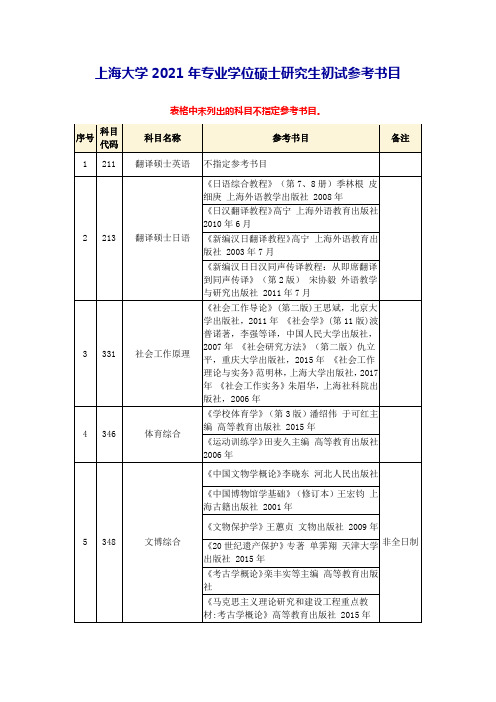
《中国电影史》， 钟大丰 / 舒晓鸣，中国广播电视出版社
《认识电影》， （美）路易斯·贾内梯，世界图书出版公司
37
962
半导体物理（专）
《半导体物理学》（第7版），刘恩科 朱秉升 罗晋生，电子工业出版社，2017年
38
963
材料科学基础（五）（专）
《材料科学基础》 (第三版)，胡赓祥 蔡珣 戎咏华，上海交通大学出版社，2010年
《跨文化交际学概论》（第 1 版）胡文仲 外语教学与研究出版社 1999 年
18
448
汉语写作与百科知识
《汉语写作与百科知识》刘军平 武汉大学出版社 2012年7月
19
714
电影创作基础
《拍电影》，（美）琳恩·格罗斯 /（美）拉里·沃德，世界图书出版公司
《纪录片怎么讲故事》，（美）希拉·柯伦·伯纳德，世界图书出版公司
《新编汉日翻译教程》高宁 上海外语教育出版社 2003年7月
《新编汉日日汉同声传译教程：从即席翻译到同声传译》（第2版） 宋协毅 外语教学与研究出版社 2011年7月
3
331
社会工作原理
《社会工作导论》(第二版)王思斌，北京大学出版社，2011年 《社会学》(第11版)波普诺著，李强等译，中国人民大学出版社，2007年 《社会研究方法》（第二版）仇立平，重庆大学出版社，2015年 《社会工作理论与实务》范明林，上海大学出版社，2017年 《社会工作实务》朱眉华，上海社科院出版社，2006年
31
926
物理化学（专）
《物理化学》（第5版）天津大学物理化学教研室编 北京：高等教育出版社 2009年 《物理化学解题指南》（第2版）冯霞 高正虹 陈丽编 北京:高等教育出版社 2009年
上海大学历年运筹学考研真题及答案、考研大纲汇总
考试科目：运筹学适用专业：管理科学与工程一、复习要求：要求考生熟悉模型的构建及应用，掌握定量化决策和模型化的基本思想和方法，能灵活运用运筹学的方法求解各类问题。
二、主要复习内容：1、线性规划线性规划问题与数学模型、图解法、线性规划单纯形算法、单纯形法的进一步讨论、线性规划的对偶问题、对偶问题的基本性质、影子价格、对偶单纯形法、灵敏度分析、参数线性规划。
重点：构建线性规划的数学模型，单纯形算法的掌握，对偶问题的建立，影子价格的理解，灵敏度分析。
2、运输问题运输问题及其数学模型，用表上作业法求解运输问题，运输问题的进一步讨论，应用问题举例。
重点：运输问题的数学模型，运输问题的求解。
3、整数规划整数规划的数学模型及其解的特点，0－1 规划的数学模型，整数规划求解的方法（分枝定界法、割平面法、纯0－1 规划的求解方法），指派问题。
重点：含0-1 变量的混合整数规划模型的构建，整数规划的求解方法。
4、动态规划多阶段决策问题的最优化，动态规划的基本概念和基本原理，动态规划模型的建立与求解，动态规划在经济管理中的运用。
重点：动态规划模型的建立与求解，动态规划在经济管理中的运用。
5、排队论基本概念，到达间隔的分布和服务时间的分布，M/M/s 等待制排队模型，M/M/s混合制排队模型。
重点：随机服务系统的分析以及各量值的计算。
一、参考书目：《运筹学教程》（第 3 版），胡运权主编，清华大学出版社2007年-------------------------------------------------- ∙2A.F警A<n0)■己■可r?・三.∣¼0)・•••■■力* ι∙ R. <∙∙-.^a.已・■#产•・■■■■■Λ <∣t ♦> ««■•上■«∙xfUI午・穴・・梅—^e∙tft<t∙α・•介韵S∙⅜∙<<4<∙:^■・什片・(B t<∙CW∏∙∙∣Φ ∙t∙ow2nαt <M2«> ^‰ι⅞a^lm ta∙∏9∙M>WR^ttlRt∙id *a⅜4l<∙αΛfW・■ EE H∙■汽∙4F∙∙"♦祝■片■■少一♦. Bt⅜∙⅜44<■口・♦臨EMA ” P»• m ujw∙∙≡>Hf ∙>∙w∙m∙ιxf j ^¼e⅜<∙*>->τ*・(H⅜ Mr lΛτ⅜^aχ≡efl∙AX∙∙∙ F∙MΛ<k f ∙4 "⅜⅝∙M v∙⅛t≤M ■k∙¼1∙X <44 < ■»*■)「⅜. MO⅜m ∙vft■・*・∙・Cl ・■•••■・写*・・代・ Wn>∙∙∙. u ⅜<4∣ tx ∙⅜w≠<Rwκτ・ JIa ^⅞w^t ∙v ∙ ⅜an<<B ⅜⅜R. jκ∙κrv ∙ M 仙0>ixe*w^tmmr. ^Λ∣Mas ∙qa ・**几a><<r ∙wΛ<^*A ΓI2 1t ∙■厂人■・ 1・ 6 ■∙∙・■戻・■Hl ∙Mt>■工 Xe) 心”) WWS, Nr-J - ~Γ~ Λ T F -----f t ~5 44 β 4> R <RLR ≡ 皿<∣>∙■■门∙∙ c. D >a ⅜∙^∣ ∙^∙ a Hiab "尸∙∙∙∙∙τ<∙■ ■鼻y ・∙<∙*L ■戻M w. <∙ta<宣产“■・ ∣χaw2t ∙ 4 « ■的■窃■■・Mt>J>∙H∣f)⅜wr 亠”・ A f ⅜T^≡rAB⅜Jf ⅜∙11t fc Wf &■・∙∙ι ∙∙"∙^∙・・IXlI B≠M <∙ <≡> ⅜' ∙∙ C ∙trsτ^∙. j ∙, ■■辜星■■・∙,∙∙ΛΛ>⅝⅝. CΛ ∙CRXW ・∙ *0∙A ∙∙.七・no»已・・fL∙WM≡ <ιr> aτ.UΛ> M AJflhJT E・«•∙IΛ) W≡m∙ER∙NIM∙W<∙rtr・Λβ (IZ)・∙"∙Hem∙XJH ∙M⅜r・(1/) HMHAMOMftfl* P. *■ Λ-f*,4Γ∙.・ u⅜v ∙1∙∙∙■・上海大学≡ • 年改it 硕士学位研究生入学考试试题a%∙A< 4<MB. ***w ∙∙—[<m∕∙0I. <»•> ••样・・ <ι*> M 41 &>. d≡rcRmeM ∙∙⅜L-e c ∙i ■ K T - I ∙ 1 1-• ∙ . I 1~ * i • . ■ K T" i T" i ∙ 厂 3 *⅜ i 1- ∙ 1M÷∙β.<Ha t ⅜t:・・∙■ ∙⅜∙.・C ∙W ∙<∙∙・■■♦∙ <1> ∙・ Sl ∙≡1t ∙∙∙fHH ⅞<F ・<3) v l ∙t ∙∙α∙∙M ∙ <uκ<» ‰e<Mβ■・∙■・・«> ∙・・♦∙∙∙!Msf r ・ M4∙≠t<aa^∙<・■ ∙««14-« ・<» BbM>∙l rStr l A-ItA X BMfl>∙a<! Mlfr4Rffl∙<≡∙∙<α⅛≡∙∙・X a∙∙∙∙MH 31∖ A ■ C∙ IT A4i ∙J a> ⅜4 i ■K iJ5 ■ X∙∙ ・Ht ∙∙f9⅞ BeKl1≡ fe ⅜A ∙ ・・・・・■ VVMJHl^Wl A. ≡∙S ∙M ∙W9WMMt ∙⅛∙tMMM ∙∙ ∙∙∙・ «<l∣ ∙■”■・∙<1∙ ∙∙AΛ ・♦・∙■∙<>► A9*a<B ∙・«•<» ∙∙4∙∙∙ ⅜< MIHtM ・(S ∙∙∙∙∙MI ∙・<r ■∙■▼・∙ VWM> ∣A. MVMA*a>∙∙∙ ・∙・∙■■■*■ ・・・A rr÷∙tfH∣∙.∙ ■ l ∙∙I 1 ~ > ⅜ W∣4 -I ■ TS■- 和∙ Rr-B~ ■ IM4s ■ KO ¼ IJ - ∣∙ 匸皿 IB ->∙<> ∙> «/ ∙HW ⅜∙⅛⅜∣∙ ac ・∙∙∙∙w 口 一 Wa ∙∙M<4aa ∙ J ⅜∙I >M ‰ ir ・・AMMJ) <≡w ・ — L(»t> "∙er∙> .MA4∙HM ∙X. ,>l ∙ΛH ∙<*^∙∙∙Ra ∙Π≡ →<m ∙4<b ∙.t. (M ∙) 拿•»■■■■■■ I“ te l ∙X*l ∙U 1SII 7⅜-U l <l ⅝<B3∙9.⅜.⅜>■ (I4⅜><l* ■・∙∙<f ⅞∙∙M ∙C ・X ・ <∏> ∙MV ∙MBR ∙1U∣⅜V*・ ttfF *∙cr χr<⅛ ・ <>•-#•«•■■•・ ∙∙∙≡e ∙ αaM ∙aasw ∙M∣⅜. x ∙ ♦■算4上海大学XKtt 年a**±学位研究生入学考试试题r ∙" m ∙g ∙ W-∙ '»*1・・・I. ■ 个・・・■. ■■气負∙∙∙!∙r ∙∙∙∙tf ∙几 C 2・.".∙k ∙・…∙ut3 匕■・■ “•・ MKBl ⅜ ta4trn ⅜MftV. ■ T a< a ∙M4RM n «s.∙D ∙ ΛB>M ⅜<Oβ・・∙∙9∙∙ ∙∙ZJ∣∣M. “■■・■ ∙MUU ■方 IU <WC ∙ ∙∙2∙∙>■•■■・・■ 9•拿(W)M.・・■ ∙∙∙≡i(9J ∙l ■ne 4UΛW<<M∣xfl •・ «也 H ∙G . ∙U ∙J ∙∙∙4∙A ⅜M ∙r ∙κ∙∙. *^⅜vt M ∙Λ< X ・Efl ・ 4M ・f ■■彳・ «<•«>> ^a<s ⅜∙t-^<∙M ∙a. ■M∙1 ■2 B) OM 4■ I ? <2 AiI 9 > ■ n ASS ∙ S ∙ IS W π n ■»<∙> W ∙¼Λ≡Λ Λ∙⅛<∙W ∙⅜∙<» ■片・K ・∙M∣aΛ∙>><» Λ <1)ΦW4l ∙r)R**MM∣aflCU∣R ・・・■・∙.■ —aJs ∙∙3・》M…<n∙, <■.<∕∙ι.・■»<7>■W U∙∣. *”・»At ∙∙r∙∙■■・《—、∙∙⅜∙∙s∙∙r"∙∙∙J⅜p ∙∙.・・■∙>«■■■・・. ∙∙∙∙⅜Q M∙・・<▼+■■∙∙∙«・上■大«200 3 年入学考试试题■■■■■" J tA l ・ <υ*) KJ tΛMW 户 IL 己・ ttAAX4t ««lD 卩M<Z ς∙¼ ÷⅛∙>∙I2I >nΛ9r*ifiM*A<fj ・•□・■ ■值.O «>2) ■出上■■出绘■■台■口・ S*⅛4tttβ<∣tt9^*<t∏toA*■・(,分) n ^BA «tinvTiiwM.ciD «<■朝Jm 褊■更•(5*)4) AXttRΠM*∙n*■・■** e ∙ 5. 10). ■分輪 attιιn ⅞ft. o »> 5> ・ Ka -■■仿∙us ∙ ” 20・■分•■优 *«*«・ <5*> 入(IOlh «b «n «■弭■化刃■冷雇， ÷4∏ ・ 2t ⅞÷S*<⅜l 4»« ・«>♦ 2*ι-*f*∙ 2>»<2∣4≤ 142ι∣< ltj÷ »・ ‰ >2■»10. r>≤0< *>M ・ Ce 北畀勺■・s ∙ <JI *, <U ∙λ∏字・・■■的■从 hMWBVitth∙Λ M ∏ V∏R ∙M*ftt ∙>⅜. I) >#.<l>a ∙<∏7^⅛9⅜^< α>∣ι*≡R ■■篙∙α∙ (3>MSa∏7tl ⅜T4 ■・ HWl «> ∙saπτ≡>!r^w ⅜wH ∙ ID nV ∙Rl>WΛttβW^<・， (糾β<^rτr≡<∙Hi<> ■■・<fl*∙RRΨWβ∙HWWtt 2 *∙(・■宣人11・住・■■ — ・ Mβ∙f ⅜ΨW ・4f ∙Xf ・ I ：人t*4β<W ∙r ■L x∣∙2^*)a∣<2< (■ *t*B)1*∣<2*3→II <M <∙-∏W≡> 山・&・1>£0<» 用•今斤∙α∙*ε∙∙μrW ∙o ⅝f∣∙∙∙∙ ⑸ 2>ΦM <IImlaib e.4∙ ∙»*> ≡it ∙!rτ∙Λ> 个臺∙∙m^ιtβ4nr,**∙ ∙∙<*∙∙∙F ・・・∙ ・F ・・e ∙BWHM. .∙MM ∙∙ UBMffX ∙waβ∙⅜. ιτ⅜∙∙*∙∙≡. ∙1. (U*>crt≡■■・■ FgAt -A**βr ∙tιH∙ι<0.>>AM ∙Xaftll ⅜J > <-s. ■ -n ∙ci) «a*<C) t∣t*Hlt ⅛∙iUl ・ ∙. <20t>(l)己・MfIMMflAMZ-<XU. AX→XXI真•，AZ M Att*a ⅜MIWll ∙M*a*β∣a*HMMBK. W ∙*K<∙・ N ¾^(r∣-I A ・tan ∙MβM<l ∙■・O)已・>■・《1“代・・■忧・■MBZ-CXU AX-⅛XX)KKXR*⅛t*H→14< «St ・■ atC ∙9H ∙∙WhΛ・■■鲜■ *R ∙tt ∙・r KlM2E^√∑∙T 片 ∙M<ftA ⅝a ⅛H ∙*l β∙ftΛ A100 w>122 I MW C ‰20⅜∙ WB 200 IOoo ・ I ∙(ΛΛO MJ4 IJ JJ4 «r K ∙MΛ> B. ♦・ J K ・己■各#戶 *4A ・ B. Cnft■・■啊■車・ #ItBRfXHe ■口!■WWUlA ・忖・勇付・"・■金尸F ∙«M ・M0.∙∣・∙∙ f ∙17 乂∙∙aey ・■・■•∙a∙trW∙•、•∙∙<ιc∙wOMIt—]r⅜>H t∙ WWWem aaα√*e *n4 ∙∙flM∣∙∙∙∙r>2∣M* ¼4∙∙∙V∙・ r⅜fl・∙∙・・■・∙・∙"0”■・■)・■■・■<♦∙»∙"4∏BV⅞HΓ7. Cl ∣∙⅛∙⅜r>n a>∣∙λa∙ *n .∙l∙r>]∙W4∙C∙∙fΦ∙l∙>∙F∙t>∙f∙ n⅜Rm t∙β«051 ¼W(W9 *tt ^e) gκ氨SOoZSI 1> *U *<4 I ・■y% ・iA V■料βf.j9 e.<Ll*nβmr< ∙w, ∙4∙. ♦M 2‰∙U,∙4∙,B •■・•∙aι⅝歼∙∙0∙7 7∙∙•■人M^∙aa∙∙・•♦・•■■ ：• **e-eβA・∙tΛ∙ 2.∙∙M>n∙∙∙■■••••∙∙,∙∙^ ・■—的∙A∙∙iH∙■吋比s∙∙τ ∙r∙^*Rrι∙∙u t»BM2B L.■■■■■•*>. 9Λ<KMMI F AV* ・in α⅜∙<Hirc⅜⅜t^⅛<M>>< ∙∙∙<>> ∙ >* WP ΛC* ♦■!*・••<・λM∙•・・・■•a. ■・■•・. ∙∙a∙. ∙∙w ∙∙<∙w∙—e ・•• M<∙n⅜auNv∙∙*••・<∙< mc2U2SL>tt・∙・ u∙∙"∙■ ∙■■・・・]・*・■■■ T.y上海大学2006 年攻读硕士学位研究生入学考试试题招生专业：管理科学与工程考试科目：运筹学一、判断（2 分*10=20 分）1、单纯刑法计算中，如果不按最小比值法选取换出变量，则在下一个解中至少有一个基变量的值为负。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考研已落下帷幕考研虽然已经结束好长时间，而它对于我来说，就像是昨天刚发生一样，清晰且深刻。
回首考研的这段经历，我收获了很多，也成长了许多。
开始基础复习的时候，是在网上找了一下教程视频，然后跟着教材进行学习，先是对基础知识进行了了解，在5月-7月的时候在基础上加深了理解，对于第二轮的复习，自己还根据课本讲义画了知识构架图，是自己更能一目了然的掌握知识点。
8月以后一直到临近考试的状态，开始认真的刷真题，并且对那些自己不熟悉的知识点反复的加深印象，这也是一个自我提升的过程。
考研一路走来，真的很辛苦，考研帮里学长学姐们分享的宝贵经验不仅能让我打起精神背水一战，还使我的复习有条不紊地进行。
初试成绩出来的这两天，酝酿了一下，我也想为将要参加下一届考研的的学弟学妹们写一篇文章，希望你们从复习的开始就运筹帷幄，明年的这个时候旗开得胜。
文章字数很多，大家有时间可以阅读，文末有真题和资料下载分享，谢谢大家。
上海大学数学的初试科目为：(101)思想政治理论(201)英语一(611)数学分析和(811)高等代数参考书目为：1.《数学分析》(第2版上下册)陈纪修等高等教育出版社2004年2.《高等代数》（第3版）（线性代数及多项式部分）北京大学高等教育出版社2004年先说英语吧。
词汇量曾经是我的一块心病，跟我英语水平差不多的同学，词汇量往往比我高出一大截。
从初中学英语开始就不爱背单词。
在考研阶段，词汇量的重要性胜过四六级，尤其是一些熟词僻义，往往一个单词决定你一道阅读能否做对。
所以，一旦你准备学习考研英语，词汇一定是陪伴你从头至尾的一项工作。
考研到底背多少个单词足够？按照大纲的要求，大概是5500多个。
实际上，核心单词及其熟词僻义才是考研的重点。
单词如何背？在英语复习的前期一定不要着急开始做真题，因为在单词和句子的基础非常薄弱的情况下，做真题的效果是非常差的。
刚开始复习英语的第一个月，背单词的策略是大量接触。
前半月每天两个list，大概150个单词左右，平均速度大概1分钟看1个，2个半小时可以完成一天的内容。
前一个月可以把单词过两遍。
历年的英语真题，单词释义题都是高频考点，这一点在完型中体现的非常突出，不仅是是完型，其实阅读中每年也都有关于单词辨析的题目，掌握了高频单词，对于做题的帮助还是非常大的，英语真题我用的是木糖英语真题手译。
进入第二个月开始刷真题，单词接触的量可以减少，但是对于生疏词应该进行重点的记忆，一天过1个list（75个单词）。
一定记住的有两点：①背单词不需要死记单词的拼写！②多余的方法无用，音标法加上常用的词根词缀就能搞定考研英语的词汇！9月开学后，专业课的学习进入白热化的阶段。
英语学习的重中之重变成了真题阅读。
这个时候单词的学习时长应该逐渐减少（根据自身情况）。
我在9月大概是每天1个半小时左右，内容是标记的生疏单词，每天看两个list的生疏单词。
这样9月可以再过两遍单词。
10月和11月是生理和心理都最累的阶段。
这个阶段英语学习的重点仍旧是真题阅读。
恢复到一天看一个list的状态，我相信到这一阶段看单词的感觉已经大不一样，你会发现你竟然有猜词的能力了。
12月的单词学习转移到拼写上，主要是作文句式以及作文模版所需要使用的单词。
这部分单词需要准确无误的拼写，需要花一些时间来记忆。
以上的日常单词学习是需要单独给出时间来的，实际上，在做阅读的过程中，存在着单词用法的学习，这个需要在理解句子的前提上进行记忆，涉及到做真题阅读的问题。
在第一个月，句子的学习应该同步开始，考研阅读存在着大量的长难句，因而打好句子的基础也十分重要。
做真题阅读的方法是先做一遍，然后进行单词和句子的解读，标注不会的单词，弄懂没有看明白的句子。
之后对选项进行解析，主要是比对各选项和文章中目标句之间的差异，理解出题人设陷阱的点，这些参考书上都会有所涉及。
在做过三套真题后，一定要进行一次总结，反思不足，再继续做下去。
关于具体的阅读方法，大致是读选项——找定位——比对选项和定位句——排除干扰项——联系主旨选出正确项。
具体的方法可以单独成为一篇经验贴，我在后续会补上，不过现在说这些可能也有点早。
形成自己的阅读方法是建立在大量阅读、分析真题的基础之上的。
作文、翻译、完型作文的学习我个人以为无需太早下手，在11月左右开始为时不晚。
考研作文不必四六级作文难，思路也相对比较死板。
因此作文并不是太能拉分。
翻译和完型是我认为无需特别准备的部分，这两个部分设计到你的英语实际水平的高低，花时间在这两个题型上我认为是没有必要的。
在你已经具有一定的单词水平和句子水平后，翻译和完型也差不到哪去。
在复习时间比较有限的前提下（注意我的前提），最后考虑这三个题型，它们的重要度排名是作文>翻译>完型，根据我的经验，这三个题型影响大局的能力很小。
在你的阅读能拿高分的情况下，你的考研英语分数就低不下来了。
(811)高等代数专业课作为最大的拦路虎，必须从一开始就要重视，从第一天复习开始就要开始复习，故其重视程度可见一斑。
个人觉得专业课有以下几点比较重要，首先知识点是核心，例如S是复数集C的一个非空子集,如果对于S中任意两个数a、b来说，a+b,a-b,ab都在S内，那么称S是一个数环，不管你采用什么办法知识点是最最基本的，虽然考研不考知识点，但是知识点是必须记住的，这一点没有条件可以谈。
在这之前我把知识点全部写到卡片上，每张卡片上44个知识点，方便随身携带，只要有空就拿出来识记，因此知识点一定要做到乱熟于心。
我专业课可能没考的理想中那么好，像任何数域都包含有理数域，有理数域是最小的数域，这点是一定要记住的。
除了客观原因外，大题可能是失分主要项。
因为后面对答案的时候，我大题得分很少，这和我平时水平不相符，但是我一直也没时间怎么认真准备，所以可能在这上有点吃亏，希望后来者引以为戒。
不管你看几遍课本，最终目的是要熟悉理解课本，首先你要知道哪些章节要看，哪些章节可以先放一放，哪些是重点，比如实数域上不可约多项式，除一次多项式外，只含非实共轭复数根的二次多项式。
每一个次数大于0的实系数多项式都可以分解为实系数的一次和二次不可约因式的乘积，这些定理一定要牢记。
等到看到真题你知道答案在哪一章是哪方面的内容就可以了。
毕竟不是本校生，不知道答案应该如何回答，所以我是买的上岸学姐的真题和答案（根据自己的情况，不是必须要答案，自己可以的可以不要），学姐整理的比较好，然后在自己做题的时候把自己认为还该补充的东西补充了一下，在这里还想感谢一下那位学姐，给我省了不少时间。
还在某宝上买了研教新版课本配套习题和题库，这些足够了。
有人问真题要做几遍，我认为做三遍挺合理的，既能印象深刻，又增加了熟练度，真题很重要，每年都会有重复，这个重要性不用我再多讲了吧。
除了真题，模拟题也很重要，研教新版练习题解析，不是依照章节，而是依照板块，更适合全面复习检测使用，有利于宏观了解。
它的编排较为条理清晰，一目了然，容纳了重要冲刺知识点，有利于难题型的解答。
这本书都是历年预测真题比较准的，题的质量也都不错，有条件最好都买，买来一定要做，一些重点题必要的要背一背，如下图：除了做模拟题之外，还涉及到要不要报班的问题，专业课个人觉得报不报班都可以，关键要靠自己背，所有的教材无论是哪位老师的，大同小异，资料不在多有一本就行，由于一种依赖和偷懒心理，我报了考研班。
不过，除去最后考点分析还有所收获外，其他一概走马观花。
主要是自己没有好好背，基础知识不牢固，练习没有跟上，所以专业分数不高，这点教训希望能作为前车之鉴。
最后强调一下，专业课就是多背多练多总结。
其实公共课也离不开做题，英语阅读理解所占分值较大，也最能拉开分数，但是阅读理解命题有比较强的命题思维和解题技巧，不熟悉命题思路的人即便能读懂全文，却可能选不对选项，而通过大量真题训练的人，只读懂部分段落，也可得高分。
《木糖英语真题手译》中总结了很多好的解题技巧，其实边做题边揣摩命题人的命题思路，过段时间就会发现，命题人的命题意图大同小异。
政治不能只背诵也要多做题，多看李凡《政治新时器》里的解析，结合解析来做题，认真研究试题的题干及选项，分析正确选项的特点，分析错误选项的陷阱以及常见套路。
做材料题时，要学会如何分析出答题点，要注重材料题问题的本质，分析题眼。
掌握了正确的答题思路和方法，复习定会事半功倍。
说了这么多，有些跑题，我们继续聊专业课。
专业课就得多练习多对比多总结多反思，知识面方面，经常浏览一些相关专业知识文章，其中收录了很多关键知识点。
经常去网上搜索知识必读材料，打印出来，每天翻一翻。
还有就是可以用参考书。
由于知识太杂太多，我平时会把整理好的知识自已录音录下来，在路上反复听反复记。
真题方面，买了历年的真题集锦，单就这还不够，最好自己对照其他院校所有真题中出现过的题材都拿来练一练。
还要多多背诵知识考点，练习答题速度等等。
佛说：一切皆有因果。
世上不会没有无因而结的果，也不会有无果而开的花，决定考研之前先思考清楚为什么要考研。
研究生作为中国高等教育的升华版，其不仅是在专业知识的精进和升华，更是一种逻辑思维能力、语言表达能力、学习分析能力的锻炼，这种能力将是你未来工作的利器.首先要认清自己想要的方向，自己的实力，以及各方面条件，素质。
做选择前，慎重思考。
做好选择了就不要想那么多了。
学校招几个人无所谓，要相信自己就是他们招的为数不多的佼佼者。
多少人报考，哪个学校的学生报考，都与你无关。
总之，你就是在一条单行赛道，尽自己最大的力量奔跑就好。
瞬间已经又写了这么多字，想对大家说的何止这些。
只希望你们首先清楚自己想要什么，至于研友的问题，如果有合适的，互相鼓励最好，如果没有合适的，自己一个人也不错，毕竟考研是一个人的事情，谁都没有办法帮你或者干涉你。
我当初就想着，自己本科院校不好，想有一个更好的平台，另外专业知识也没学扎实，就这样参加工作，丝毫没有信心，而且家人提供不了帮助，以后的道路只能靠自己，我不甘于这样的现状，所以毫不犹豫的选择了考研，并且过程中再艰难也从未动摇。
如果这时候你满脑子装的还是考研一定成功，不许失败，只会让你很有压力。
不如先不考虑那么远，从手头的书本开始，从眼下的复习开始。
每一门科目划分成一个个短时期内要完成的目标，写在纸上，用来时刻提醒自己。
当一步步都完成后，考研成功也就不远了。
在每个小任务完成后可以适当“奖励”自己，比如看一场心仪的电影，吃一顿美味的大餐，让自己的心态逐渐积极起来。
考研是需要你付出百分之百精力的，所以你可能就顾不上学校、朋友的一些事情，过程中可能疏忽了友情，但你要记得，真正的朋友不会因为短暂的疏远就怪罪于你，反而会理解你、鼓励你，希望你能够取的好成绩！如果你们遇到不理解你的人，根本不必在意她的感受，因为眼下你做的才是于你而言最重要的！最后想告诉大家，一定要相信努力的意义，备考的这一年全力以赴，不给自己留下遗憾，那是个很美好的地方，值得我们拼一把！写到这里，已经很多字了，但是想说的还有许多许多。