(完整版)生物数据挖掘-决策树实验报告
数据挖掘实验报告1

实验一 ID3算法实现一、实验目的通过编程实现决策树算法,信息增益的计算、数据子集划分、决策树的构建过程。
加深对相关算法的理解过程。
实验类型:验证计划课间:4学时二、实验内容1、分析决策树算法的实现流程;2、分析信息增益的计算、数据子集划分、决策树的构建过程;3、根据算法描述编程实现算法,调试运行;4、对所给数据集进行验算,得到分析结果。
三、实验方法算法描述:以代表训练样本的单个结点开始建树;若样本都在同一个类,则该结点成为树叶,并用该类标记;否则,算法使用信息增益作为启发信息,选择能够最好地将样本分类的属性;对测试属性的每个已知值,创建一个分支,并据此划分样本;算法使用同样的过程,递归形成每个划分上的样本决策树递归划分步骤,当下列条件之一成立时停止:给定结点的所有样本属于同一类;没有剩余属性可以进一步划分样本,在此情况下,采用多数表决进行四、实验步骤1、算法实现过程中需要使用的数据结构描述:Struct{int Attrib_Col; // 当前节点对应属性int Value; // 对应边值Tree_Node* Left_Node; // 子树Tree_Node* Right_Node // 同层其他节点Boolean IsLeaf; // 是否叶子节点int ClassNo; // 对应分类标号}Tree_Node;2、整体算法流程主程序:InputData();T=Build_ID3(Data,Record_No, Num_Attrib);OutputRule(T);释放内存;3、相关子函数:3.1、 InputData(){输入属性集大小Num_Attrib;输入样本数Num_Record;分配内存Data[Num_Record][Num_Attrib];输入样本数据Data[Num_Record][Num_Attrib];获取类别数C(从最后一列中得到);}3.2、Build_ID3(Data,Record_No, Num_Attrib){Int Class_Distribute[C];If (Record_No==0) { return Null }N=new tree_node();计算Data中各类的分布情况存入Class_Distribute Temp_Num_Attrib=0;For (i=0;i<Num_Attrib;i++)If (Data[0][i]>=0) Temp_Num_Attrib++;If Temp_Num_Attrib==0{N->ClassNo=最多的类;N->IsLeaf=TRUE;N->Left_Node=NULL;N->Right_Node=NULL;Return N;}If Class_Distribute中仅一类的分布大于0{N->ClassNo=该类;N->IsLeaf=TRUE;N->Left_Node=NULL;N->Right_Node=NULL;Return N;}InforGain=0;CurrentCol=-1;For i=0;i<Num_Attrib-1;i++){TempGain=Compute_InforGain(Data,Record_No,I,Num_Attrib); If (InforGain<TempGain){ InforGain=TempGain; CurrentCol=I;}}N->Attrib_Col=CurrentCol;//记录CurrentCol所对应的不同值放入DiferentValue[];I=0;Value_No=-1;While i<Record_No {Flag=false;For (k=0;k<Value_No;k++)if (DiferentValu[k]=Data[i][CurrentCol]) flag=true;if (flag==false){Value_No++;DiferentValue[Value_No]=Data[i][CurrentCol] } I++;}SubData=以Data大小申请内存空间;For (i=0;i<Value_No;i++){k=-1;for (j=0;j<Record_No-1;j++)if (Data[j][CurrentCol]==DiferentValu[i]){k=k++;For(int i1=0;i1<Num_Attrib;i1++)If (i1<>CurrentCol)SubData[k][i1]=Data[j][i1];Else SubData[k][i1]=-1;}N->Attrib_Col=CurrentCol;N->Value=DiferentValu[i];N->Isleaf=false;N->ClassNo=0;N->Left_Node=Build_ID3(SubData,k+1, Num_Attrib);N->Right_Node=new Tree_Node;N=N->Right_Node;}}3.3、计算信息增益Compute_InforGain(Data,Record_No, Col_No, Num_Attrib) {Int DifferentValue[MaxDifferentValue];Int Total_DifferentValue;Int s[ClassNo][MaxDifferentValue];s=0;// 数组清0;Total_DifferentValue=-1;For (i=0;i<Record_No;i++){J=GetPosition(DifferentValue,Total_DifferentValue,Data[i][Col_no]);If (j<0) {Total_DifferentValue++;DifferentValue[Total_DifferentValue]=Data[i][Col_no];J=Total_DifferentValue;}S[Data[i][Num_Attrib-1]][j]++;}Total_I=0;For (i=0;i<ClassNo;i++){Sum=0;For(j=0;j<Record_No;j++) if Data[j][Num_Attrib-1]==i sum++; Total_I=Compute_PI(Sum/Record_No);}EA=0;For (i=0;i<Total_DifferentValue;i++);{ temp=0;sj=0; //sj是数据子集中属于类j的样本个数;For (j=0;j<ClassNO;j++)sj+=s[j][i];For (j=0;j<ClassNO;j++)EA+=sj/Record_No*Compute_PI(s[j][i]/sj);}Return total_I-EA;}3.4、得到某数字在数组中的位置GetPosition(Data, DataSize,Value){For (i=0;i<DataSize;i++) if (Data[i]=value) return I;Return -1;}3.5、计算Pi*LogPiFloat Compute_PI(float pi){If pi<=0 then return 0;If pi>=1 then return 0;Return 0-pi*log2(pi);}五、实验报告要求1、用C语言实现上述相关算法(可选择利用matlab函数实现)2、实验操作步骤和实验结果,实验中出现的问题和解决方法。
(完整版)生物数据挖掘-决策树实验报告

实验四决策树一、实验目的1.了解典型决策树算法2.熟悉决策树算法的思路与步骤3.掌握运用Matlab对数据集做决策树分析的方法二、实验内容1.运用Matlab对数据集做决策树分析三、实验步骤1.写出对决策树算法的理解决策树方法是数据挖掘的重要方法之一,它是利用树形结构的特性来对数据进行分类的一种方法。
决策树学习从一组无规则、无次序的事例中推理出有用的分类规则,是一种实例为基础的归纳学习算法。
决策树首先利用训练数据集合生成一个测试函数,根据不同的权值建立树的分支,即叶子结点,在每个叶子节点下又建立层次结点和分支,如此重利生成决策树,然后对决策树进行剪树处理,最后把决策树转换成规则。
决策树的最大优点是直观,以树状图的形式表现预测结果,而且这个结果可以进行解释。
决策树主要用于聚类和分类方面的应用。
决策树是一树状结构,它的每一个叶子节点对应着一个分类,非叶子节点对应着在某个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集。
构造决策树的核心问题是在每一步如何选择适当的属性对样本进行拆分。
对一个分类问题,从已知类标记的训练样本中学习并构造出决策树是一个自上而下分而治之的过程。
2.启动Matlab,运用Matlab对数据集进行决策树分析,写出算法名称、数据集名称、关键代码,记录实验过程,实验结果,并分析实验结果(1)算法名称: ID3算法ID3算法是最经典的决策树分类算法。
ID3算法基于信息熵来选择最佳的测试属性,它选择当前样本集中具有最大信息增益值的属性作为测试属性;样本集的划分则依据测试属性的取值进行,测试属性有多少个不同的取值就将样本集划分为多少个子样本集,同时决策树上相应于该样本集的节点长出新的叶子节点。
ID3算法根据信息论的理论,采用划分后样本集的不确定性作为衡量划分好坏的标准,用信息增益值度量不确定性:信息增益值越大,不确定性越小。
因此,ID3算法在每个非叶节点选择信息增益最大的属性作为测试属性,这样可以得到当前情况下最纯的划分,从而得到较小的决策树。
实验三决策树算法实验实验报告

实验三决策树算法实验实验报告一、引言决策树算法是一种常用的机器学习算法,它通过构建一个决策树模型来解决分类和回归问题。
在本次实验中,我们将使用决策树算法对一个分类问题进行建模,评估算法的性能,并对实验结果进行分析和总结。
二、实验目的1.学习理解决策树算法的基本原理和建模过程。
2. 掌握使用Python编程实现决策树算法。
3.分析决策树算法在不同数据集上的性能表现。
三、实验过程1.数据集介绍2.决策树算法实现我们使用Python编程语言实现了决策树算法。
首先,我们将数据集随机分为训练集和测试集,其中训练集占70%,测试集占30%。
然后,我们使用训练集来构建决策树模型。
在构建决策树时,我们采用了ID3算法,该算法根据信息增益来选择最优的特征进行分割。
最后,我们使用测试集来评估决策树模型的性能,计算并输出准确率和召回率。
3.实验结果与分析我们对实验结果进行了统计和分析。
在本次实验中,决策树算法在测试集上的准确率为0.95,召回率为0.94、这表明决策树模型对于鸢尾花分类问题具有很好的性能。
通过分析决策树模型,我们发现花瓣长度是最重要的特征,它能够很好地区分不同种类的鸢尾花。
四、实验总结通过本次实验,我们学习了决策树算法的基本原理和建模过程,并使用Python实现了决策树算法。
通过实验结果分析,我们发现决策树算法在鸢尾花分类问题上具有很好的性能。
然而,决策树算法也存在一些不足之处,例如容易过拟合和对数据的敏感性较强等。
在实际应用中,可以使用集成学习方法如随机森林来改进决策树算法的性能。
数据挖掘实验报告结论(3篇)

第1篇一、实验概述本次数据挖掘实验以Apriori算法为核心,通过对GutenBerg和DBLP两个数据集进行关联规则挖掘,旨在探讨数据挖掘技术在知识发现中的应用。
实验过程中,我们遵循数据挖掘的一般流程,包括数据预处理、关联规则挖掘、结果分析和可视化等步骤。
二、实验结果分析1. 数据预处理在实验开始之前,我们对GutenBerg和DBLP数据集进行了预处理,包括数据清洗、数据集成和数据变换等。
通过对数据集的分析,我们发现了以下问题:(1)数据缺失:部分数据集存在缺失值,需要通过插补或删除缺失数据的方法进行处理。
(2)数据不一致:数据集中存在不同格式的数据,需要进行统一处理。
(3)数据噪声:数据集中存在一些异常值,需要通过滤波或聚类等方法进行处理。
2. 关联规则挖掘在数据预处理完成后,我们使用Apriori算法对数据集进行关联规则挖掘。
实验中,我们设置了不同的最小支持度和最小置信度阈值,以挖掘出不同粒度的关联规则。
以下是实验结果分析:(1)GutenBerg数据集在GutenBerg数据集中,我们以句子为篮子粒度,挖掘了林肯演讲集的关联规则。
通过分析挖掘结果,我们发现:- 单词“the”和“of”在句子中频繁出现,表明这两个词在林肯演讲中具有较高的出现频率。
- “and”和“to”等连接词也具有较高的出现频率,说明林肯演讲中句子结构较为复杂。
- 部分单词组合具有较高的置信度,如“war”和“soldier”,表明在林肯演讲中提到“war”时,很可能同时提到“soldier”。
(2)DBLP数据集在DBLP数据集中,我们以作者为单位,挖掘了作者之间的合作关系。
实验结果表明:- 部分作者之间存在较强的合作关系,如同一研究领域内的作者。
- 部分作者在多个研究领域均有合作关系,表明他们在不同领域具有一定的学术影响力。
3. 结果分析和可视化为了更好地展示实验结果,我们对挖掘出的关联规则进行了可视化处理。
通过可视化,我们可以直观地看出以下信息:(1)频繁项集的分布情况:通过柱状图展示频繁项集的分布情况,便于分析不同项集的出现频率。
《数据挖掘实验》---K-means聚类及决策树算法实现预测分析实验报告

实验设计过程及分析:1、通过通信企业数据(USER_INFO_M.csv),使用K-means算法实现运营商客户价值分析,并制定相应的营销策略。
(预处理,构建5个特征后确定K 值,构建模型并评价)代码:setwd("D:\\Mi\\数据挖掘\\")datafile<-read.csv("USER_INFO_M.csv")zscoredFile<- na.omit(datafile)set.seed(123) # 设置随机种子result <- kmeans(zscoredFile[,c(9,10,14,19,20)], 4) # 建立模型,找聚类中心为4round(result$centers, 3) # 查看聚类中心table(result$cluster) # 统计不同类别样本的数目# 画出分析雷达图par(cex=0.8)library(fmsb)max <- apply(result$centers, 2, max)min <- apply(result$centers, 2, min)df <- data.frame(rbind(max, min, result$centers))radarchart(df = df, seg =5, plty = c(1:4), vlcex = 1, plwd = 2)# 给雷达图加图例L <- 1for(i in 1:4){legend(1.3, L, legend = paste("VIP_LVL", i), lty = i, lwd = 3, col = i, bty = "n")L <- L - 0.2}运行结果:2、根据企业在2016.01-2016.03客户的短信、流量、通话、消费的使用情况及客户基本信息的数据,构建决策树模型,实现对流失客户的预测,F1值。
决策树 实验报告
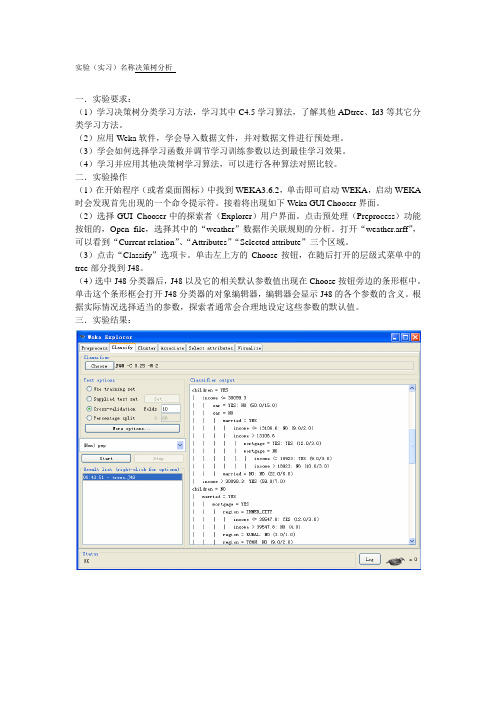
实验(实习)名称决策树分析一.实验要求:(1)学习决策树分类学习方法,学习其中C4.5学习算法,了解其他ADtree、Id3等其它分类学习方法。
(2)应用Weka软件,学会导入数据文件,并对数据文件进行预处理。
(3)学会如何选择学习函数并调节学习训练参数以达到最佳学习效果。
(4)学习并应用其他决策树学习算法,可以进行各种算法对照比较。
二.实验操作(1)在开始程序(或者桌面图标)中找到WEKA3.6.2,单击即可启动WEKA,启动WEKA 时会发现首先出现的一个命令提示符。
接着将出现如下Weka GUI Chooser界面。
(2)选择GUI Chooser中的探索者(Explorer)用户界面。
点击预处理(Preprocess)功能按钮的,Open file,选择其中的“weather”数据作关联规则的分析。
打开“weather.arff”,可以看到“Current relation”、“Attributes”“Selected attribute”三个区域。
(3)点击“Classify”选项卡。
单击左上方的Choose按钮,在随后打开的层级式菜单中的tree部分找到J48。
(4)选中J48分类器后,J48以及它的相关默认参数值出现在Choose按钮旁边的条形框中。
单击这个条形框会打开J48分类器的对象编辑器,编辑器会显示J48的各个参数的含义。
根据实际情况选择适当的参数,探索者通常会合理地设定这些参数的默认值。
三.实验结果:计算正确率可得:(74+132)/(74+30+64+132)=0.69四.实验小结:通过本次试验,我学习了决策树分类方法,以及其中C4.5算法,并了解了其他ADtree、Id3等其它分类方法,应用Weka软件,学会导入数据文件,并对数据文件进行预处理,今后还需努力。
决策树实验报告

决策树实验报告决策树实验报告引言决策树是一种常见的机器学习算法,被广泛应用于数据挖掘和预测分析等领域。
本文将介绍决策树的基本原理、实验过程和结果分析,以及对决策树算法的优化和应用的思考。
一、决策树的基本原理决策树是一种基于树形结构的分类模型,通过一系列的判断和决策来对数据进行分类。
决策树的构建过程中,首先选择一个特征作为根节点,然后根据该特征的取值将数据划分为不同的子集,接着对每个子集递归地构建子树,直到满足停止条件。
构建完成后,通过树的分支路径即可对新的数据进行分类。
二、实验过程1. 数据准备为了验证决策树算法的效果,我们选择了一个包含多个特征的数据集。
数据集中包含了学生的性别、年龄、成绩等特征,以及是否通过考试的标签。
我们将数据集分为训练集和测试集,其中训练集用于构建决策树模型,测试集用于评估模型的准确性。
2. 决策树构建在实验中,我们使用了Python编程语言中的scikit-learn库来构建决策树模型。
首先,我们导入所需的库和数据集,并对数据进行预处理,包括缺失值处理、特征选择等。
然后,我们使用训练集来构建决策树模型,设置合适的参数,如最大深度、最小样本数等。
最后,我们使用测试集对模型进行评估,并计算准确率、召回率等指标。
3. 结果分析通过实验,我们得到了决策树模型在测试集上的准确率为80%。
这意味着模型能够正确分类80%的测试样本。
此外,我们还计算了模型的召回率和F1值等指标,用于评估模型的性能。
通过对结果的分析,我们可以发现模型在某些特征上表现较好,而在其他特征上表现较差。
这可能是由于数据集中某些特征对于分类结果的影响较大,而其他特征的影响较小。
三、决策树算法的优化和应用1. 算法优化决策树算法在实际应用中存在一些问题,如容易过拟合、对噪声敏感等。
为了提高模型的性能,可以采取以下措施进行优化。
首先,可以通过剪枝操作减少决策树的复杂度,防止过拟合。
其次,可以使用集成学习方法,如随机森林和梯度提升树,来进一步提高模型的准确性和鲁棒性。
实验二决策树实验实验报告

实验二决策树实验实验报告
一、实验目的
本实验旨在通过实际操作,加深对决策树算法的理解,并掌握
决策树的基本原理、构建过程以及应用场景。
二、实验原理
决策树是一种常用的机器学习算法,主要用于分类和回归问题。
其基本原理是将问题划分为不同的决策节点和叶节点,通过一系列
的特征测试来进行决策。
决策树的构建过程包括特征选择、划分准
则和剪枝等步骤。
三、实验步骤
1. 数据收集:从开放数据集或自有数据中选择一个适当的数据集,用于构建决策树模型。
2. 数据预处理:对收集到的数据进行缺失值处理、异常值处理
以及特征选择等预处理操作,以提高模型的准确性和可靠性。
3. 特征选择:采用合适的特征选择算法,从所有特征中选择对
分类或回归任务最重要的特征。
4. 构建决策树模型:根据选定的特征选择算法,以及划分准则(如信息增益或基尼系数)进行决策树模型的构建。
5. 模型评估:使用交叉验证等方法对构建的决策树模型进行评估,包括准确率、召回率、F1-score等指标。
6. 模型调优:根据评估结果,对决策树模型进行调优,如调整模型参数、采用剪枝技术等方法。
7. 模型应用:将得到的最优决策树模型应用于实际问题中,进行预测和决策。
四、实验结果及分析
在本次实验中,我们选择了某电商网站的用户购买记录作为数据集,利用决策树算法构建用户购买意愿的预测模型。
经过数据预处理和特征选择,选取了用户地理位置、年龄、性别和购买历史等特征作为输入。
利用信息增益作为划分准则,构建了一棵决策树模型。
实验二-决策树实验-实验报告

决策树实验一、实验原理决策树是一个类似于流程图的树结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一个测试输入,而每个树叶结点代表类或类分布。
数的最顶层结点是根结点。
一棵典型的决策树如图1所示。
它表示概念buys_computer,它预测顾客是否可能购买计算机。
内部结点用矩形表示,而树叶结点用椭圆表示。
为了对未知的样本分类,样本的属性值在决策树上测试。
决策树从根到叶结点的一条路径就对应着一条合取规则,因此决策树容易转化成分类规则。
图1ID3算法:■决策树中每一个非叶结点对应着一个非类别属性,树枝代表这个属性的值。
一个叶结点代表从树根到叶结点之间的路径对应的记录所属的类别属性值。
■每一个非叶结点都将与属性中具有最大信息量的非类别属性相关联。
■采用信息增益来选择能够最好地将样本分类的属性。
信息增益基于信息论中熵的概念。
ID3总是选择具有最高信息增益(或最大熵压缩)的属性作为当前结点的测试属性。
该属性使得对结果划分中的样本分类所需的信息量最小,并反映划分的最小随机性或“不纯性”。
二、算法伪代码算法Decision_Tree(data,AttributeName)输入由离散值属性描述的训练样本集data;候选属性集合AttributeName。
输出一棵决策树。
(1)创建节点N;(2)If samples 都在同一类C中then(3)返回N作为叶节点,以类C标记;(4)If attribute_list为空then(5)返回N作为叶节点,以samples 中最普遍的类标记;//多数表决(6)选择attribute_list 中具有最高信息增益的属性test_attribute;(7)以test_attribute 标记节点N;(8)For each test_attribute 的已知值v //划分samples(9)由节点N分出一个对应test_attribute=v的分支;(10令S v为samples中test_attribute=v 的样本集合;//一个划分块(11)If S v为空then(12)加上一个叶节点,以samples中最普遍的类标记;(13)Else 加入一个由Decision_Tree(Sv,attribute_list-test_attribute)返回节点值。
决策树实验报告

决策树实验报告一、实验背景随着人工智能和机器学习技术的不断发展,决策树作为一种常见的模型学习方法,在数据分析、分类和预测等方面得到越来越广泛的应用。
本次实验旨在通过使用决策树算法解决某一具体问题,掌握决策树模型的构建及优化方法。
二、实验过程1.数据预处理:本次实验使用Kaggle平台上的“泰坦尼克号生存预测”数据集。
首先进行数据清洗,将缺失值和无关数据进行处理,再将字符串转换为数字,使得数据能够被计算机处理。
接着对数据进行切分,将数据集划分成训练集和测试集。
2.模型建立:本次实验使用Python编程语言,在sklearn库中使用决策树算法进行分类预测。
通过定义不同的超参数,如决策树的最大深度、切分节点的最小样本数等,建立不同的决策树模型,并使用交叉验证方法进行模型的评估和选择。
最终,确定最优的决策树模型,并用该模型对测试集进行预测。
3.模型优化:本次实验采用了两种优化方法进行模型的优化。
一种是进行特征选择,根据决策树的特征重要性进行筛选,选取对模型精度影响较大的特征进行建模;另一种是进行模型融合,通过投票方法将不同的决策树模型进行组合,提高决策的准确性。
三、实验结果本次实验的最优模型使用了决策树的最大深度为5,切分节点的最小样本数为10的超参数。
经过交叉验证,模型在训练集上的平均精度达到了79.2%,在测试集上的精度达到了80.2%。
优化后的模型在测试集上的精度进一步提高至81.2%。
四、实验结论本次实验使用了决策树算法,解决了“泰坦尼克号生存预测”问题。
经过数据预处理、模型建立和模型优化三个阶段,最终得到了在测试集上精度为81.2%的最优模型。
决策树模型具有良好的可解释性和易于理解的特点,在分类预测和决策分析中得到越来越广泛的应用。
数据挖掘实例实验报告(3篇)

第1篇一、实验背景随着大数据时代的到来,数据挖掘技术逐渐成为各个行业的重要工具。
数据挖掘是指从大量数据中提取有价值的信息和知识的过程。
本实验旨在通过数据挖掘技术,对某个具体领域的数据进行挖掘,分析数据中的规律和趋势,为相关决策提供支持。
二、实验目标1. 熟悉数据挖掘的基本流程,包括数据预处理、特征选择、模型选择、模型训练和模型评估等步骤。
2. 掌握常用的数据挖掘算法,如决策树、支持向量机、聚类、关联规则等。
3. 应用数据挖掘技术解决实际问题,提高数据分析和处理能力。
4. 实验结束后,提交一份完整的实验报告,包括实验过程、结果分析及总结。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 数据挖掘库:pandas、numpy、scikit-learn、matplotlib四、实验数据本实验选取了某电商平台用户购买行为数据作为实验数据。
数据包括用户ID、商品ID、购买时间、价格、商品类别、用户年龄、性别、职业等。
五、实验步骤1. 数据预处理(1)数据清洗:剔除缺失值、异常值等无效数据。
(2)数据转换:将分类变量转换为数值变量,如年龄、性别等。
(3)数据归一化:将不同特征的范围统一到相同的尺度,便于模型训练。
2. 特征选择(1)相关性分析:计算特征之间的相关系数,剔除冗余特征。
(2)信息增益:根据特征的信息增益选择特征。
3. 模型选择(1)决策树:采用CART决策树算法。
(2)支持向量机:采用线性核函数。
(3)聚类:采用K-Means算法。
(4)关联规则:采用Apriori算法。
4. 模型训练使用训练集对各个模型进行训练。
5. 模型评估使用测试集对各个模型进行评估,比较不同模型的性能。
六、实验结果与分析1. 数据预处理经过数据清洗,剔除缺失值和异常值后,剩余数据量为10000条。
2. 特征选择通过相关性分析和信息增益,选取以下特征:用户ID、商品ID、购买时间、价格、商品类别、用户年龄、性别、职业。
决策树算法应用实验报告

一、实验背景随着大数据时代的到来,数据挖掘技术在各个领域得到了广泛应用。
决策树算法作为一种常用的数据挖掘方法,因其易于理解和实现的特点,在分类和回归任务中具有很高的应用价值。
本实验旨在通过实践操作,深入了解决策树算法的原理、实现过程及其在实际问题中的应用。
二、实验目的1. 理解决策树算法的基本原理和分类方法。
2. 掌握决策树算法的编程实现。
3. 学会使用决策树算法解决实际问题。
4. 分析决策树算法的优缺点和适用场景。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy、Pandas、Scikit-learn四、实验内容1. 数据准备实验数据采用Iris数据集,该数据集包含150个样本,每个样本包含4个特征(花瓣长度、花瓣宽度、花萼长度、花萼宽度)和1个类别标签(Iris-setosa、Iris-versicolor、Iris-virginica)。
2. 决策树算法实现(1)基于ID3算法的决策树实现首先,定义计算信息熵、条件熵和信息增益的函数。
然后,根据信息增益选择最优特征进行节点分裂,递归地构建决策树。
```pythondef calculate_entropy(data):# ...def calculate_condition_entropy(data, feature, value):# ...def calculate_information_gain(data, feature, value):# ...def build_tree(data):# ...```(2)基于CART算法的决策树实现首先,定义计算Gini指数的函数。
然后,根据Gini指数选择最优特征进行节点分裂,递归地构建决策树。
```pythondef calculate_gini_index(data):# ...def build_tree_cart(data):# ...```3. 模型评估使用交叉验证方法评估决策树模型的性能。
数据挖掘6个实验实验报告

中南民族大学计算机科学学院《数据挖掘与知识发现》综合实验报告姓名年级专业软件工程指导教师学号序号实验类型综合型2016年12 月10 日一、使用Weka建立决策树模型1、准备数据:在记事本程序中编制ColdType-training.arff,ColdType-test.arff。
2、加载和预处理数据。
3、建立分类模型。
(选择C4.5决策树算法)4、分类未知实例二、使用Weka进行聚类1、准备数据:使用ColdType.csv文件作为数据集。
2、加载和预处理数据。
3、聚类(用简单K -均值算法)4、解释和评估聚类结果三、完成感冒类型的相关操作及相应处理结果1.加载了ColdType-training.arff文件后的Weka Explorer界面:2.感冒类型诊断分类模型输出结果:Sore-throat = Yes| Cooling-effect = Good: Viral (2.0)4.感冒类型诊断聚类结果:Cluster centroids:Cluster#Attribute Full Data 0 1(10) (5) (5) ================================================= Increased-lym Yes Yes No Leukocytosis Yes No Yes Fever Yes Yes Yes Acute-onset Yes Yes No Sore-throat Yes No Yes Cooling-effect Good Good Notgood Group Yes Yes NoTime taken to build model (full training data) : 0 seconds=== Model and evaluation on training set ===Clustered Instances0 5 ( 50%)1 5 ( 50%)Class attribute: Cold-typeClasses to Clusters:0 1 <-- assigned to cluster5 1 | Viral0 4 | BacterialCluster 0 <-- ViralCluster 1 <-- BacterialIncorrectly clustered instances : 1.010 %分析:由诊断聚类结果图可知,聚类中有两个簇Cluster0和Cluster1,分别对应Viral类和Bacterial类,但有一个实例被聚类到错误的簇,聚类错误率为10%。
决策树分类实验报告

决策树分类实验报告决策树分类实验报告引言:决策树是一种常用的机器学习算法,它通过构建一棵树状的决策模型来进行分类。
在本次实验中,我们将使用决策树算法对一个数据集进行分类,并评估模型的性能和准确率。
数据集介绍:我们选择了一个包含多个特征的数据集,其中每个样本都有一个类别标签。
该数据集包含了不同类型的动物,并根据它们的特征进行分类。
特征包括动物的体重、身高、食性等。
我们的目标是根据这些特征来预测动物的类别。
实验步骤:1. 数据预处理:在进行决策树分类之前,我们首先对数据进行预处理。
这包括处理缺失值、标准化数据等操作。
缺失值的处理可以采用填充平均值或者使用其他样本的特征进行预测。
标准化数据可以使得不同特征之间的数值范围一致,避免某些特征对分类结果的影响过大。
2. 特征选择:在构建决策树模型之前,我们需要选择最具有分类能力的特征。
常用的特征选择方法包括信息增益、信息增益比等。
通过计算每个特征的分类能力指标,我们可以选择最优的特征作为分类依据。
3. 构建决策树模型:在选择了最优特征之后,我们可以开始构建决策树模型。
决策树的构建过程包括选择根节点、划分子节点等步骤。
通过递归地选择最优特征并划分子节点,我们可以构建一棵完整的决策树模型。
4. 模型评估:构建完决策树模型后,我们需要对其进行评估。
常用的评估指标包括准确率、精确率、召回率等。
准确率是指模型分类正确的样本数占总样本数的比例,精确率是指模型预测为正类的样本中真实为正类的比例,召回率是指真实为正类的样本中被模型预测为正类的比例。
实验结果:经过数据预处理、特征选择和模型构建,我们得到了一棵决策树模型。
通过使用测试集对模型进行评估,我们得到了如下结果:准确率:90%精确率:92%召回率:88%结论:本次实验中,我们成功地使用决策树算法对一个数据集进行了分类。
通过对数据进行预处理、特征选择和模型构建,我们得到了一棵准确率为90%的决策树模型。
该模型在分类任务中表现良好,具有较高的精确率和召回率。
决策树算法实验报告

决策树算法实验报告哈尔滨工业大学数据挖掘理论与算法实验报告(2022年度秋季学期)课程编码 S1300019C 授课教师高宏学生姓名赵天意学号 14S101018学院电气工程及自动化学院一、实验内容使用ID3算法设计实现决策树二、实验设计给定特征是离散的1组实例,设计并实现决策树算法,对实例建立决策树,观察决策树是否正确。
三、实验环境及测试数据实验环境:Windows7操作系统,Python2.7 IDLE 测试数据:样本 outlook temperature Humidity 1 sunny hot High 2 sunny hot High 3 overcast hot High4 rainy mild High5 rainy cool normal6 rainy cool normal7 overcast cool normal8 sunny mild High9 sunny cool normal 10 rainy mild normal 11 sunny mild normal 12 overcast mild High 13 overcast hot normal 14 rainy mild high windy FALSE TRUE FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE TRUE TRUE FALSE TRUE play no no yes yes yes no yes no yes yes yes yes yes no 四、实验过程编写决策树程序,输出决策树,输入实例,输出预测类别五、实验结果样本建立的决策树与对所有样本的预测六、遇到的困难及解决方法、心得体会建树过程中用到了递归思想,递归建树。
1/ 1。
数据挖掘决策树实验报告

• 实验背景• 数据集与预处理• 决策树算法实现• 实验结果分析• 实验结论与建议• 参考文献
目录
实验背景
重要性随着大数据时代的到来,数据挖掘在 商业决策、科学研究、医疗保健等领 域发挥着越来越重要的作用,能够帮 助人们更好地理解和分析数据,发现 潜在规律和趋势。
定义数据挖掘是从大量数据中提取有用信 息和知识的过程,这些信息和知识是 隐含的、未知的、有用的。
召回率与精确率召回率反映的是所有正例中被正确预测为正例的比例,精 确率反映的是预测为正例的正例样本数与所有预测为正例 的样本数的比例。通过调整阈值,可以找到最佳的召回率 和精确率。AUC值AUC值是ROC曲线下的面积,用于衡量模型对正负样本的 区分能力。 AUC值越接近1,模型性能越好。
准确率通过对比模型预测结果与实际结果,计算决策树模型的准 确率。准确率越高,模型性能越好。
目标本实验旨在通过数据挖掘决策树算法对给定的数据集进行分类预测,并评估算 法的性能和准确率。
实验目标与意义
数据集与预处理
数据集来源与特性
在数据清洗阶段,我们还对异常值进行了处理,例如,对于极端的开盘价、最高价、最低价和收盘价,我们进行了合理的修正,以避免对模型造成过大影响。
为了使模型更好地进行学习,我们对特征进行了缩放,将所有的特征值缩放到[0,1]之间。
在数据预处理阶段,我们首先对缺失值进行了处理,由于数据集中的缺失值较少,我们选择直接删除含有缺失值的行。
数据清洗与预处理
异常值处理
数据清洗
特征缩放
特征工程在特征工程阶段,我们对原始特征进行了加工,生成了一些新的特征,例如,收盘价与开 盘价的差值、最高价与最低价的差值等,这些新特征能够更ห้องสมุดไป่ตู้地反映股票价格的变动情况。
数据挖掘实验报告(两篇)2024

引言概述:数据挖掘是一项广泛应用于各个行业的技术,通过对大数据的处理和分析,可以发现隐藏在数据中的有价值信息。
本文是数据挖掘实验报告(二),将对具体的数据挖掘实验进行详细的阐述和分析。
本实验主要聚焦于数据预处理、特征选择、模型建立和评估等关键步骤,以增加对实验过程和结果的理解,提高实验的可靠性和准确性。
通过实验结果的分析和总结,可以帮助读者更好地理解数据挖掘的方法和技术,并为实际应用提供参考和指导。
正文内容:1. 数据预处理在进行数据挖掘之前,首先需要对原始数据进行预处理。
数据预处理的目的是清洗数据、处理缺失值和异常值等数据问题,以确保数据的质量和准确性。
在本实验中,我们采用了多种方法对数据进行预处理。
其中包括数据清洗、缺失值处理和异常值检测等。
具体的操作包括了数据去重、数据标准化、缺失值的填补和异常值的处理等。
2. 特征选择特征选择是数据挖掘的关键步骤之一,它的目的是从原始数据中选择出对问题解决有价值的特征。
在本实验中,我们通过使用相关性分析、方差选择和递归特征消除等方法,对原始数据进行特征选择。
通过分析特征与目标变量之间的关系,我们可以得出最有价值的特征,从而减少计算复杂度和提高模型准确性。
3. 模型建立模型建立是数据挖掘实验的核心步骤之一。
在本实验中,我们采用了多种模型进行建立,包括决策树、支持向量机、朴素贝叶斯等。
具体而言,我们使用了ID3决策树算法、支持向量机算法和朴素贝叶斯算法等进行建模,并通过交叉验证和网格搜索等方法选择最佳的模型参数。
4. 模型评估模型评估是对建立的模型进行准确性和可靠性评估的过程。
在本实验中,我们采用了多种评估指标进行模型评估,包括准确率、召回率、F1分数等。
通过对模型的评估,我们可以得出模型的准确性和可靠性,并进一步优化模型以达到更好的效果。
5. 结果分析与总结总结:本文是对数据挖掘实验进行详细阐述和分析的实验报告。
通过对数据预处理、特征选择、模型建立和评估等关键步骤的分析和总结,我们得出了对数据挖掘方法和技术的深入理解。
数据仓库与数据挖掘--决策树实验

实验3 决策树一、实验目的1.了解决策树的基本概念。
2.掌握决策树挖掘分析的操作步骤。
二、实验内容对三国志4 武将数据.xls 中的数据进行决策树分析。
三、实验仪、设备计算机、visual studio 2008、分析用数据、数据库服务四、实验步骤准备工作:三国志4 武将数据.xls 数据导入数据库中。
(1)打开visual studio 2008,新建项目,选择商业智能项目,analysis services项目图1 新建项目(2)在解决方案资源管理器中,右键单击数据源,选择新建数据源图2 数据源向导(3)在该界面中选择新建,进行数据源具体设置图3 新建数据源(4)在服务器名中填写要连接的数据库服务器名称,或者单击服务器名右方下拉按钮进行选择;勾选使用windows身份验证;选择或输入一个数据库名中填写将要分析数据所在的数据库或者单击右方下拉按钮进行选择图4 数据源具体设置(5)确定后配置完的数据源已显示在窗口上,继续下一步图5 完成数据源具体设置(6)勾选使用服务账户,继续下一步图6 模拟信息设置(7)数据源名称保持默认,完成图7 完成数据源设置向导(8)在解决方案资源管理器中,右键单击数据源视图,选择新建数据源视图图8 数据源视图向导(9)下一步图9 选择数据源(10)在可用对象中,将要分析数据所在表添加到包含的对象中,继续下一步图11 选择包含对象(11)默认名称,完成图12 完成数据源视图向导(12)在解决方案资源管理器中,右键单击挖掘结构,选择新建挖掘结构图13 数据挖掘向导(13)勾选从现有关系数据库或数据仓库,继续下一步图14 选择定义方法(14)选择microsoft 决策树,继续下一步图15 创建数据挖掘模型结构(15)下一步图16 选择数据源视图(16)勾选事例,继续下一步图17 指定表类型(17)在键列勾选序号码,在输入列勾选出身、国别、魅力、统御、武力、政治、智慧、忠诚,在可预测列勾选身份,继续下一步图18 指定定型数据(18)下一步图19 指定内容和数据类型(19)勾选允许钻取,完成图21 完成数据挖掘向导(20)单击挖掘模型查看器图22 完成设置(21)询问是否部署项目,是图23 部署项目(22)询问是否继续,是图24 处理模型(23)单击运行图25 运行挖掘项目(24)待处理完成后,关闭图26 处理结果(25)关闭处理窗口后,就可在挖掘模型查看器的决策树中看到系统经过分析得出的结果图27 分类关系图依赖关系网络:图27 分类剖面图(26)在挖掘模型中,右键单击挖掘模型可以设置算法参数图28 算法参数(27)算法参数的意义COMPLEXITY_PENALTY:禁止决策树生长。
机器学习与数据挖掘实验-决策树

实验二决策树一、实验目的本实验课程是计算机、智能、物联网等专业学生的一门专业课程,通过实验,帮助学生更好地掌握数据挖掘相关概念、技术、原理、应用等;通过实验提高学生编写实验报告、总结实验结果的能力;使学生对机器学习算法、数据挖掘实现等有比较深入的认识。
1.掌握机器学习中涉及的相关概念、算法。
2.熟悉数据挖掘中的具体编程方法;3.掌握问题表示、求解及编程实现。
二、基本要求1.实验前,复习《机器学习与数据挖掘》课程中的有关内容。
2.准备好实验数据。
3.编程要独立完成,程序应加适当的注释。
4.完成实验报告。
三、实验软件使用Python语言实现。
四、实验内容:表4.1的西瓜数据集包括17个训练样例,请学习一个决策树,用于预测一个西瓜是不是好瓜。
具体要求如下:(1)在生成决策树的过程中,请分别使用ID3算法、C4.5算法、CART 算法,并对比三个算法结果。
其中,ID3算法在生成决策树的各结点使用信息增益准则进行特征选择;C4.5算法在生成决策树的过程使用信息增益比进行特征选择;CART算法假设决策树是一个二叉树,通过递归地二分每个特征,将特征空间划分为有限个单元,并在这些单元上确定预测的概率分布。
(2)请自己写程序实现决策树的生成过程,不要直接调用决策树算法包。
五、实验具体实现算法理论知识决策树的具体流程:(1)创建数据集(2)计算数据集的信息熵(3)遍历所有的特征,选择信息熵最小的特征,即为最好的分类特征(4)根据上一步得到的分类特征分割数据集,并将该特征从列表中移除(5)使用决策树执行分类,返回分类结果学习的伪代码:I if 每个子项属于同一个类,return 类标签II else(1)寻找划分数据集的最好特征(2)划分数据集(3) 创建分支结点①for 每个划分的子集②调用分支创建函数并增加返回结果到分支结点中(4)返回分支结点ID3算法生成决策树的各结点使用信息增益准则进行特征选择,存在偏向于选择取值较多的特征的问题在生成决策树的过程使用信息增益比进行特征选择;剪枝算法预剪枝:后剪枝:六、代码实现0、辅助画图# coding: utf-8import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签plt.rcParams['axes.unicode_minus'] = False # 这两行需要手动设置# 使用文本注解绘制树结点decisionNode = dict(boxstyle="sawtooth", fc="0.8")leafNode = dict(boxstyle="round4", fc="0.8")arrow_args = dict(arrowstyle="<-")def plotNode(nodeText, centerPt, parentPt, nodeType):createPlot.ax1.annotate(nodeText, xy=parentPt, xycoords='axes fraction', \xytext=centerPt, textcoords='axes fraction', va='center', ha='center', \bbox=nodeType, arrowprops=arrow_args)# 获取叶子节点的数目和树的层数def getNumLeaves(myTree):numLeaves = 0firstStr = list(myTree.keys())[0] # 决策树的第一个键值secondDict = myTree[firstStr] # 字典中第一个key所对应的value,即下面的目录for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict': # 如果是字典类型,则继续递归numLeaves += getNumLeaves(secondDict[key])else: # 如果不是字典类型,则停止递归numLeaves += 1return numLeavesdef getTreeDepth(myTree):maxDepth = 0thisDepth = 0firstStr = list(myTree.keys())[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':thisDepth += getTreeDepth(secondDict[key])else:thisDepth = 1if (thisDepth > maxDepth):maxDepth = thisDepthreturn maxDepth# 预先存储树的信息,方便读取测试def retrieveTree(i):listOfTrees = [{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}]return listOfTrees[i]def plotMidText(centerPt, parentPt, txtStr):xMid = (parentPt[0] + centerPt[0]) / 2.0yMid = (parentPt[1] + centerPt[1]) / 2.0createPlot.ax1.text(xMid, yMid, txtStr)def plotTree(myTree, parentPt, nodeTxt):firstStr = list(myTree.keys())[0]numLeaves = getNumLeaves(myTree)depth = getTreeDepth(myTree)centerPt = (plotTree.xOff + (1.0 + float(numLeaves)) / 2.0 / plotTree.totalW, plotTree.yOff)# centerPt = (0.5, plotTree.yOff)plotMidText(centerPt, parentPt, nodeTxt)plotNode(firstStr, centerPt, parentPt, decisionNode)secondDict = myTree[firstStr]plotTree.yOff -= 1.0 / plotTree.totalD # 由于绘图是自顶向下的,所以y的偏移要递减for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':plotTree(secondDict[key], centerPt, str(key))else:plotTree.xOff += 1.0 / plotTree.totalWplotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), centerPt, leafNode)plotMidText((plotTree.xOff, plotTree.yOff), centerPt, str(key)) plotTree.yOff += 1.0 / plotTree.totalD # 在绘制了所有子节点后,增加y的偏移def createPlot(inTree):fig = plt.figure(1, facecolor='white')fig.clf()axprops = dict(xticks=[], yticks=[])createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)plotTree.totalW = float(getNumLeaves(inTree))plotTree.totalD = float(getTreeDepth(inTree))plotTree.xOff = -0.5 / plotTree.totalWplotTree.yOff = 1.0plotTree(inTree, (0.5, 1.0), '')plt.show()1.1、ID3算法代码:from pandas import read_excelfrom math import log2from copy import deepcopyimport treePlotter# 阶段一:特征选择# 1、创建数据集def createDataSet(filename, sheetName='Sheet1') -> '从excel中获取数据和标签属性': # 本实验调用获取数据案例: df = readFromExcelByPandas(r"watermelon_dataset.xlsx") df = read_excel(filename, sheet_name=sheetName, header=0)labels = df.columns.tolist()[1:-1]dataSet = df.values.tolist()dataSet = [example[1:] for example in dataSet] # 由于本数据集的第一项是编号,对实验结果影响不大,需要删除for data in dataSet:if data[-1] == '否':data[-1] = '坏瓜'else:data[-1] = '好瓜'return dataSet, labels# 2、求数据集D的经验熵H(D)def calcShannon(dataSet) -> '从数据集中计算':# 对类别计算dataSetLen = len(dataSet) # 行数p = {} # 获取{类别:个数}H = 0.0 # 熵值for data in dataSet: # 统计类别和对应出现次数key = data[-1]if key not in p.keys():p[key] = 0p[key] += 1for key in p:px = float(p[key]) / float(dataSetLen)if px > 0:H -= px * log2(px)return H# 3、根据给定的特征和特征值选择子数据集def splitDataSet(dataSet, axis, value) -> '第axis个标签为value的集合': subDataSet = []for feature_vector in dataSet:if feature_vector[axis] == value:reduce_vector = feature_vector[:axis]reduce_vector.extend(feature_vector[axis + 1:]) # 去除原来axis的属性subDataSet.append(reduce_vector)return subDataSet# 4、求特征A对数据集D的经验条件熵H(D|A)和信息增益g(D,A),选择最优的信息增益def chooseBestFeature(dataSet) -> '返回信息增益最大的标签属性序号':FeaturesNum = len(dataSet[0]) - 1 # 选择总特征值baseEntropy = calcShannon(dataSet) # H(D)bestInfoGain = 0.0 # 最佳信息增益,越大越好;初始默认为0bestFeature = -1 # 最佳划分属性dataSetLen = len(dataSet) # 行数for i in range(FeaturesNum): # 遍历每一个特征# 获取该特征的所有值,存入列表featureListfeatureList = [feature[i] for feature in dataSet]uniqueVals = set(featureList)sonEntropy = 0.0 # 经验条件熵H(D|A)for value in uniqueVals: # 遍历特征所有可能取值subDataSet = splitDataSet(dataSet, i, value) # 该特征对应的该值在的子集合prob = float(len(subDataSet)) / float(dataSetLen) # 该特征对应的该值的子集合在全部集合中所占比列sonEntropy += prob * calcShannon(subDataSet)# 计算信息增益g(D,A)InfoGain = baseEntropy - sonEntropyif InfoGain > bestInfoGain:bestInfoGain = InfoGainbestFeature = ireturn bestFeature# 阶段二:决策树生成# 5、没有特征时选择数目最多的类别返回def majorityCnk(classList) -> '返回次数最多的分类':p = {} # 获取{类别:个数}for data in classList: # 统计类别和对应出现次数key = data[-1]if key not in p:p[key] = 0p[key] += 1sortedClassDict = sorted(p.keys(), reverse=True)return sortedClassDict[0]# 6、创建决策树的函数代码def createTree(dataSet, labels) -> '返回决策树T':labelsTmp = deepcopy(labels)classList = [data[-1] for data in dataSet] # 统计dataSet中所有的标签# 结束条件1:若D中所有实例都是属于同一类Ck,则T为单结点树,将Ck作为该节点的类标识if classList.count(classList[0]) == len(classList):return classList[0]# 结束条件2:若特征集为空,则T为单结点树,将Ck作为该节点的类标识if len(labelsTmp) == 0:return majorityCnk(classList)# 否则计算特征集A中各特征对D的信息增益,选择信息增益最大的特征AgbestFeatureIndex = chooseBestFeature(dataSet)myTree = {bestFeature: {}} # 用字典构建树del (labelsTmp[bestFeatureIndex]) # 删除这个最佳划分的特征的标签# 获取当前最优特征所有可能取值featureList = [data[bestFeatureIndex] for data in dataSet]uniqueVals = set(featureList)# 只要还可以划分就继续递归调用for value in uniqueVals:sonTree = splitDataSet(dataSet, bestFeatureIndex, value)myTree[bestFeature][value] = createTree(sonTree, labelsTmp) return myTree# 阶段三:测试分类效果,使用决策树进行分类def classify_ID3(inputTree, labels, testFeature) -> 'feaLabels和testVec都是列表': firstStr = list(inputTree.keys())[0] # 第一个特征secondDict = inputTree[firstStr] # 子树字典featureIndex = labels.index(firstStr) # 将标签字符串转换为输入数据标签的索引下标for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict': # 如果还有节点,则继续递归classLabel = classify_ID3(secondDict[key], labels, testFeature)return classLabelelse: # 如果到达叶子节点,则返回当前节点的分类标签classLabel = secondDict[key]return classLabelreturn "Wrong Classified result.Have not defined this kind of feature."def main():dataSet, labels = createDataSet(r"../watermelon_dataset.xlsx")trees = createTree(dataSet, labels)treePlotter.createPlot(trees)print(classify_ID3(trees, labels, ['浅白', '稍蜷', '浊响', '清晰', '平坦', '软粘']))if __name__ == '__main__':main()1.2、ID3运行结果(截图同书上一样)拿一个这个图中没有的例子测试时,结果是2.1、C4.5算法代码:from pandas import read_excelfrom math import log2from copy import deepcopyimport treePlotter# 阶段一:特征选择# 1、创建数据集def createDataSet(filename, sheetName='Sheet1') -> '从excel中获取数据和标签属性': # 本实验调用获取数据案例: df = readFromExcelByPandas(r"watermelon_dataset.xlsx") df = read_excel(filename, sheet_name=sheetName, header=0)labels = df.columns.tolist()[1:-1]dataSet = df.values.tolist()dataSet = [example[1:] for example in dataSet] # 由于本数据集的第一项是编号,对实验结果影响不大,需要删除# 选择测试for data in dataSet:if data[-1] == '否':data[-1] = '坏瓜'else:data[-1] = '好瓜'return dataSet, labels# 2、求数据集D的经验熵H(D)def calcShannon(dataSet, feat=-1) -> '从数据集中计算':# 对类别计算dataSetLen = len(dataSet) # 行数p = {} # 获取{类别:个数}H = 0.0 # 熵值for data in dataSet: # 统计类别和对应出现次数key = data[feat]if key not in p:p[key] = 0p[key] += 1for key in p:px = float(p[key]) / float(dataSetLen)if px > 0:H -= px * log2(px)return H# 3、根据给定的特征和特征值选择子数据集def splitDataSet(dataSet, axis, value) -> '第axis个标签为value的集合': subDataSet = []for feature_vector in dataSet:if feature_vector[axis] == value:reduce_vector = feature_vector[:axis]reduce_vector.extend(feature_vector[axis + 1:]) # 去除原来axis的属性subDataSet.append(reduce_vector)return subDataSet# 4、求特征A对数据集D的经验条件熵H(D|A)和信息增益g(D,A):g(D,A)=H(D)-H(D|A)# 再求分裂信息H(A),求最优增益率gr(D,A):gr(D,A) = g(D,A)/H(A)def chooseBestFeature(dataSet) -> '返回信息增益率最大的标签属性序号':FeaturesNum = len(dataSet[0]) - 1 # 选择总特征值baseEntropy = calcShannon(dataSet) # H(D)bestInfoGainRate = 0.0 # 最佳信息增益率,越大越好;初始默认为0bestFeature = -1 # 最佳划分属性dataSetLen = len(dataSet) # 行数for i in range(FeaturesNum): # 遍历每一个特征# 获取该特征的所有值,存入列表featureListfeatureList = [feature[i] for feature in dataSet]uniqueVals = set(featureList)sonEntropy = 0.0 # 经验条件熵H(D|A)SplitInfo = 0.0 # 分裂信息H(A)for value in uniqueVals: # 遍历特征所有可能取值subDataSet = splitDataSet(dataSet, i, value) # 该特征对应的该值在的子集合prob = float(len(subDataSet)) / float(dataSetLen) # 该特征对应的该值的子集合在全部集合中所占比列sonEntropy += prob * calcShannon(subDataSet)if prob > 0:SplitInfo -= prob * log2(prob)# SplitInfo = calcShannon(dataSet, i) # 注释的功能和上面功能一样if SplitInfo == 0:continue# 计算信息增益g(D,A)InfoGain = baseEntropy - sonEntropy# 计算增益率InfoGainRate = float(InfoGain) / float(SplitInfo)if InfoGainRate > bestInfoGainRate:bestInfoGainRate = InfoGainRatebestFeature = ireturn bestFeature# 阶段二:决策树生成# 5、没有特征时选择数目最多的类别返回def majorityCnk(classList) -> '返回次数最多的分类':p = {} # 获取{类别:个数}for data in classList: # 统计类别和对应出现次数key = data[-1]if key not in p:p[key] = 1else:p[key] += 1sortedClassDict = sorted(p.keys(), reverse=True)return sortedClassDict[0]# 6、创建决策树的函数代码def createTree(dataSet, labels) -> '返回决策树T':labelsTmp = deepcopy(labels)classList = [data[-1] for data in dataSet] # 统计dataSet中所有的标签# 结束条件1:若D中所有实例都是属于同一类Ck,则T为单结点树,将Ck作为该节点的类标识if classList.count(classList[0]) == len(classList):return classList[0]# 结束条件2:若特征集为空,则T为单结点树,将Ck作为该节点的类标识if len(labelsTmp) == 0:return majorityCnk(classList)# 否则计算特征集A中各特征对D的信息增益,选择信息增益最大的特征AgbestFeatureIndex = chooseBestFeature(dataSet)bestFeature = labelsTmp[bestFeatureIndex]myTree = {bestFeature: {}} # 用字典构建树del (labelsTmp[bestFeatureIndex]) # 删除这个最佳划分的特征的标签# 获取当前最优特征所有可能取值featureList = [data[bestFeatureIndex] for data in dataSet]uniqueVals = set(featureList)# 只要还可以划分就继续递归调用for value in uniqueVals:sonTree = splitDataSet(dataSet, bestFeatureIndex, value)myTree[bestFeature][value] = createTree(sonTree, labelsTmp) return myTree# 阶段三:测试分类效果,使用决策树进行分类def classify_C45(inputTree, labels, testFeature) -> 'feaLabels和testVec都是列表': firstStr = list(inputTree.keys())[0] # 第一个特征secondDict = inputTree[firstStr] # 子树字典featureIndex = labels.index(firstStr) # 将标签字符串转换为输入数据标签的索引下标for key in secondDict.keys():if testFeature[featureIndex] == key:if type(secondDict[key]).__name__ == 'dict': # 如果还有节点,则继续递归classLabel = classify_C45(secondDict[key], labels, testFeature)return classLabelelse: # 如果到达叶子节点,则返回当前节点的分类标签classLabel = secondDict[key]return classLabelreturn "Wrong Classified result.Have not defined this kind of feature."# 阶段四:利用验证集对决策树后剪枝def prune(Tree, labels, testData):"""后剪枝:param inputTree:训练好但未剪枝的树:param testData: 验证集:return:"""if len(testData) == 0:raise Exception('请输入测试集')firstStr = list(Tree.keys())[0] # 第一个特征secondDict = Tree[firstStr] # 子树字典featureIndex = labels.index(firstStr) # 将标签字符串转换为输入数据标签的索引下标if not isTree(secondDict):return secondDictchange = FalsefirstError = 0for key in secondDict.keys():if isTree(secondDict[key]):change = TruesecondDict[key] = prune(secondDict[key], labels, testData)continueelse:tmpList = splitDataSet(testData,featureIndex, key)for lst in tmpList:if lst[-1] != secondDict[key]:firstError += 1if not change:secondError = 0classList = [[example[-1]] for example in testData]# 计划取代的特征值meanValue = majorityCnk(classList)for lst in testData:if lst[-1] != meanValue:secondError += 1if firstError >= secondError:print("merging")return meanValuereturn Treedef isTree(obj):return type(obj).__name__ == 'dict'def main():dataSet, labels = createDataSet(r"../watermelon_dataset.xlsx")# from random import sample# train_list = sample([i for i in range(len(dataSet))], len(dataSet) // 2 + 1) train_list = [1, 2, 3, 6, 7, 10, 14, 15, 16, 17, 4] # 指定测试案例train_list = [i - 1 for i in train_list]test_list = list(set([i for i in range(len(dataSet))]) - set(train_list))dataSet1 = []for i in train_list:dataSet1.append(dataSet[i]) # 训练集trees = createTree(dataSet1, labels)treePlotter.createPlot(trees)print(trees)dataSet2 = [] # 测试集for i in test_list:dataSet2.append(dataSet[i]) # 训练集trees = prune(trees, labels, dataSet2)treePlotter.createPlot(trees)print(trees)p rint(classify_C45(trees, labels, ['浅白', '稍蜷', '浊响', '清晰', '平坦', '软粘']))if __name__ == '__main__':main()2.2、C4.5算法运行结果(截图同书上一样):剪枝前:剪枝后:对于上次ID3算法没有解决的例子,C4..5测试出来的结果是坏瓜3.1、CART算法代码:from pandas import read_excelfrom copy import deepcopyimport treePlotter# 阶段一:特征选择# 1、创建数据集def createDataSet(filename, sheetName='Sheet1') -> '从excel中获取数据和标签属性': # 本实验调用获取数据案例: df = readFromExcelByPandas(r"watermelon_dataset.xlsx") df = read_excel(filename, sheet_name=sheetName, header=0)labels = df.columns.tolist()[1:-1]dataSet = df.values.tolist()dataSet = [example[1:] for example in dataSet] # 由于本数据集的第一项是编号,对实验结果影响不大,需要删除for data in dataSet:if data[-1] == '否':data[-1] = '坏瓜'else:data[-1] = '好瓜'return dataSet, labels# 2、求数据集D的基尼值属Gini(D)def calcGini(dataSet):# 对类别计算dataSetLen = len(dataSet) # 行数p = {} # 获取{类别:个数}G = 1.0 # 训练元组集D的不纯度for data in dataSet: # 统计类别和对应出现次数key = data[-1]if key not in p:p[key] = 0p[key] += 1for key in p:px = float(p[key]) / float(dataSetLen)G -= px * pxreturn G# 3、根据给定的特征和特征值选择子数据集def splitDataSet(dataSet, axis, value) -> '第axis个标签为value的集合':subDataSet = [] # 符合条件的子集otherDataSet = [] # 其他不符合的子集for feature_vector in dataSet:reduce_vector = feature_vector[:axis]reduce_vector.extend(feature_vector[axis + 1:]) # 去除原来axis的属性if feature_vector[axis] == value:subDataSet.append(reduce_vector)else:otherDataSet.append(reduce_vector)return subDataSet, otherDataSet# 4、求特征A对数据集D的最优划分属性min_Gini_value(D,a)的属性a:ax的基尼指数加权值# 返回最好的特征以及二分特征值def chooseBestFeature(dataSet) -> '返回不纯度下降最大的标签属性序号':min_Gini_value = float("inf") # 初始化最小的基尼指数FeaturesNum = len(dataSet[0]) - 1 # 选择总特征值dataSetLen = len(dataSet) # 行数bestFeatureIndex = -1 # 基尼指数最小的属性作为最优划分属性bestValue = Nonefor i in range(FeaturesNum): # 遍历每一个特征# 获取该特征的所有值,存入列表featureListfeatureList = [feature[i] for feature in dataSet]uniqueVals = set(featureList)for value in uniqueVals: # 遍历特征所有可能取值Gini_value = 0 # 基于当前属性的基尼值subDataSet, otherDataSet = splitDataSet(dataSet, i, value) # 该特征对应的该值在的子集合prob = float(len(subDataSet)) / float(dataSetLen) # 该特征对应的该值的子集合在全部集合中所占比列Gini_value += prob * calcGini(subDataSet)prob = float(len(otherDataSet)) / float(dataSetLen) # 该特征对应的该值的子集合在全部集合中所占比列Gini_value += prob * calcGini(otherDataSet)if min_Gini_value >= Gini_value:min_Gini_value = Gini_valuebestFeatureIndex = i # 特征下标bestValue = value # 特征对应值return bestFeatureIndex, bestValue# 阶段二:决策树生成# 5、没有特征时选择数目最多的类别返回def majorityCnk(classList) -> '返回出现次数最多的分类':p = {} # 获取{类别:个数}for data in classList: # 统计类别和对应出现次数key = data[-1]if key not in p:p[key] = 1else:p[key] += 1sortedClassDict = sorted(p.keys(), reverse=True)return sortedClassDict[0]# 6、创建决策树的函数代码def createTree(dataSet, labels) -> '返回决策树T':labelsTmp = deepcopy(labels)classList = [data[-1] for data in dataSet] # 统计dataSet中所有的标签# 结束条件1:若D中所有实例都是属于同一类Ck,则T为单结点树,将Ck作为该节点的类标识if classList.count(classList[0]) == len(classList):return classList[0]# 结束条件2:若特征集为空,则T为单结点树,将Ck作为该节点的类标识# 如果没有继续可以划分的特征,就多数表决决定分支的类别if len(labelsTmp) == 0:return majorityCnk(classList)# 否则计算特征集A中各特征对D的信息增益,选择信息增益最大的特征AgbestFeatureIndex, bestValue = chooseBestFeature(dataSet)bestFeature = labelsTmp[bestFeatureIndex]myTree = {bestFeature: {}} # 用字典构建树del (labelsTmp[bestFeatureIndex]) # 删除这个最佳划分的特征的标签sonTree, otherSonTree = splitDataSet(dataSet, bestFeatureIndex, bestValue)myTree[bestFeature][bestValue] = createTree(sonTree, labelsTmp)myTree[bestFeature]["Not " + bestValue] = createTree(otherSonTree, labelsTmp) return myTree# 阶段三:测试分类效果,使用决策树进行分类def classify_Gini(inputTree, labels, testFeature) -> 'feaLabels和testVec都是列表': firstStr = list(inputTree.keys())[0] # 第一个特征secondDict = inputTree[firstStr] # 子树字典featureIndex = labels.index(firstStr) # 将标签字符串转换为输入数据标签的索引下标ensure_key = list(secondDict.keys())[0]unsure_key = list(secondDict.keys())[1]if ensure_key.startswith('Not'):ensure_key, unsure_key = unsure_key, ensure_keykey = unsure_keyif testFeature[featureIndex] == ensure_key:key = ensure_keyif isTree(secondDict[key]): # 如果还有节点,则继续递归classLabel = classify_Gini(secondDict[key], labels, testFeature)return classLabelelse: # 如果到达叶子节点,则返回当前节点的分类标签classLabel = secondDict[key]return classLabeldef isTree(obj):return type(obj).__name__ == 'dict'# 阶段四:后剪枝def prune(Tree, labels, testData):"""后剪枝:param inputTree:训练好但未剪枝的树:param testData: 验证集:return:"""if len(testData) == 0:raise Exception('请输入测试集')firstStr = list(Tree.keys())[0] # 第一个特征secondDict = Tree[firstStr] # 子树字典featureIndex = labels.index(firstStr) # 将标签字符串转换为输入数据标签的索引下标if not isTree(secondDict):return secondDictensure_key = list(secondDict.keys())[0]unsure_key = list(secondDict.keys())[1]if ensure_key.startswith('Not'):ensure_key, unsure_key = unsure_key, ensure_key# 测试集if isTree(secondDict[ensure_key]):secondDict[ensure_key] = prune(secondDict[ensure_key], labels, testData) if isTree(secondDict[unsure_key]):secondDict[unsure_key] = prune(secondDict[unsure_key], labels, testData) if not isTree(secondDict[ensure_key]) and not isTree(secondDict[unsure_key]): # 比较误差,判断是否需要合并分支为标签lSet, rSet = splitDataSet(testData, featureIndex, ensure_key)firstError = 0for lst in lSet:if lst[-1] != secondDict[ensure_key]:firstError += 1for lst in rSet:if lst[-1] == secondDict[ensure_key]:firstError += 1secondError = 0classList = [[example[-1]] for example in testData]# 计划取代的特征值meanValue = majorityCnk(classList)for lst in testData:if lst[-1] != meanValue:secondError += 1if firstError >= secondError:print("merging")return meanValuereturn Treedef main():dataSet, labels = createDataSet(r"../watermelon_dataset.xlsx")# from random import sample# train_list = sample([i for i in range(len(dataSet))], len(dataSet) // 2 + 1) train_list = [1, 2, 3, 6, 7, 10, 14, 15, 16, 17, 4] # 指定测试案例train_list = [i-1 for i in train_list]test_list = list(set([i for i in range(len(dataSet))]) - set(train_list))dataSet1 = []for i in train_list:dataSet1.append(dataSet[i]) # 训练集trees = createTree(dataSet1, labels)treePlotter.createPlot(trees)print(trees)dataSet2 = [] # 测试集for i in test_list:dataSet2.append(dataSet[i]) # 训练集trees = prune(trees, labels, dataSet2)treePlotter.createPlot(trees)print(trees)print(classify_Gini(trees, labels, ['浅白', '稍蜷', '浊响', '清晰', '平坦', '软粘']))if __name__ == '__main__':main()3.2、CART算法运行结果剪枝前:剪枝后:对ID3测试不了的案例,在这里测试结果为坏瓜,结果和C4.5一样,但是很明显,树的结点都比C4.5的少,这个就是CART算法的一个优势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四决策树一、实验目的1.了解典型决策树算法2.熟悉决策树算法的思路与步骤3.掌握运用Matlab对数据集做决策树分析的方法二、实验内容1.运用Matlab对数据集做决策树分析三、实验步骤1.写出对决策树算法的理解决策树方法是数据挖掘的重要方法之一,它是利用树形结构的特性来对数据进行分类的一种方法。
决策树学习从一组无规则、无次序的事例中推理出有用的分类规则,是一种实例为基础的归纳学习算法。
决策树首先利用训练数据集合生成一个测试函数,根据不同的权值建立树的分支,即叶子结点,在每个叶子节点下又建立层次结点和分支,如此重利生成决策树,然后对决策树进行剪树处理,最后把决策树转换成规则。
决策树的最大优点是直观,以树状图的形式表现预测结果,而且这个结果可以进行解释。
决策树主要用于聚类和分类方面的应用。
决策树是一树状结构,它的每一个叶子节点对应着一个分类,非叶子节点对应着在某个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集。
构造决策树的核心问题是在每一步如何选择适当的属性对样本进行拆分。
对一个分类问题,从已知类标记的训练样本中学习并构造出决策树是一个自上而下分而治之的过程。
2.启动Matlab,运用Matlab对数据集进行决策树分析,写出算法名称、数据集名称、关键代码,记录实验过程,实验结果,并分析实验结果(1)算法名称: ID3算法ID3算法是最经典的决策树分类算法。
ID3算法基于信息熵来选择最佳的测试属性,它选择当前样本集中具有最大信息增益值的属性作为测试属性;样本集的划分则依据测试属性的取值进行,测试属性有多少个不同的取值就将样本集划分为多少个子样本集,同时决策树上相应于该样本集的节点长出新的叶子节点。
ID3算法根据信息论的理论,采用划分后样本集的不确定性作为衡量划分好坏的标准,用信息增益值度量不确定性:信息增益值越大,不确定性越小。
因此,ID3算法在每个非叶节点选择信息增益最大的属性作为测试属性,这样可以得到当前情况下最纯的划分,从而得到较小的决策树。
ID3算法的具体流程如下:1)对当前样本集合,计算所有属性的信息增益;2)选择信息增益最大的属性作为测试属性,把测试属性取值相同的样本划为同一个子样本集;3)若子样本集的类别属性只含有单个属性,则分支为叶子节点,判断其属性值并标上相应的符号,然后返回调用处;否则对子样本集递归调用本算法。
(2)数据集名称:鸢尾花卉Iris数据集选择了部分数据集来区分Iris Setosa(山鸢尾)及Iris Versicolour(杂色鸢尾)两个种类。
(3)实验代码:%% 使用ID3决策树算法预测鸢尾花卉Iris种类clear ;%% 数据预处理disp('正在进行数据预处理...');[matrix,attributes_label,attributes] = id3_preprocess();%% 构造ID3决策树,其中id3()为自定义函数disp('数据预处理完成,正在进行构造树...');tree = id3(matrix,attributes_label,attributes);%% 打印并画决策树[nodeids,nodevalues] = print_tree(tree);tree_plot(nodeids,nodevalues);disp('ID3算法构建决策树完成!');%% 构造函数id3_preprocessfunction [ matrix,attributes,activeAttributes ] = id3_preprocess( )%% ID3算法数据预处理,把字符串转换为0,1编码%% 读取数据txt={ '序号' '花萼大小' '花瓣长度' '花瓣宽度' '类型' '' '小' '长' '长' 'versicolor''' '小' '长' '长' 'versicolor''' '小' '长' '长' 'versicolor''' '小' '短' '长' 'versicolor''' '小' '长' '长' 'versicolor''' '小' '短' '长' 'versicolor''' '小' '长' '短' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '短' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '小' '长' '长' 'setosa''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '短' 'versicolor''' '小' '短' '短' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '短' '短' 'setosa''' '大' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '短' 'setosa''' '大' '短' '短' 'setosa' }attributes=txt(1,2:end);% attributes: 属性和Label;activeAttributes = ones(1,length(attributes)-1);% activeAttributes : 属性向量,全1;data = txt(2:end,2:end);%% 针对每列数据进行转换[rows,cols] = size(data);matrix = zeros(rows,cols);% matrix:转换后的0,1矩阵;for j=1:colsmatrix(:,j) = cellfun(@trans2onezero,data(:,j));endend%%构造函数trans2onezerofunction flag = trans2onezero(data)if strcmp(data,'小')||strcmp(data,'短')...||strcmp(data,'setosa')flag =0;return ;endflag =1;end%%构造函数id3function [ tree ] = id3( examples, attributes, activeAttributes )%% ID3 算法,构建ID3决策树%% 提供的数据为空,则报异常if (isempty(examples));error('必须提供数据!');endnumberAttributes = length(activeAttributes);% activeAttributes: 活跃的属性值;-1,1向量,1表示活跃;numberExamples = length(examples(:,1));% example: 输入0、1矩阵;% 创建树节点tree = struct('value', 'null', 'left', 'null', 'right', 'null');% 如果最后一列全部为1,则返回“versicolor”lastColumnSum = sum(examples(:, numberAttributes + 1));if (lastColumnSum == numberExamples);tree.value = 'versicolor';returnend% 如果最后一列全部为0,则返回“setosa”if (lastColumnSum == 0);tree.value = 'setosa';returnend% 如果活跃的属性为空,则返回label最多的属性值if (sum(activeAttributes) == 0);if (lastColumnSum >= numberExamples / 2);tree.value = 'versicolor';elsetree.value = 'setosa';endreturnend%% 计算当前属性的熵p1 = lastColumnSum / numberExamples;if (p1 == 0);p1_eq = 0;elsep1_eq = -1*p1*log2(p1);endp0 = (numberExamples - lastColumnSum) / numberExamples;if (p0 == 0);p0_eq = 0;elsep0_eq = -1*p0*log2(p0);endcurrentEntropy = p1_eq + p0_eq;%% 寻找最大增益gains = -1*ones(1,numberAttributes); % 初始化增益for i=1:numberAttributes;if (activeAttributes(i)) % 该属性仍处于活跃状态,对其更新s0 = 0; s0_and_true = 0;s1 = 0; s1_and_true = 0;for j=1:numberExamples;if (examples(j,i));s1 = s1 + 1;if (examples(j, numberAttributes + 1));s1_and_true = s1_and_true + 1;endelses0 = s0 + 1;if (examples(j, numberAttributes + 1));s0_and_true = s0_and_true + 1;endendendif (~s1); % 熵S(v=1)p1 = 0;elsep1 = (s1_and_true / s1);endif (p1 == 0);p1_eq = 0;elsep1_eq = -1*(p1)*log2(p1);endif (~s1);p0 = 0;elsep0 = ((s1 - s1_and_true) / s1);endif (p0 == 0);p0_eq = 0;elsep0_eq = -1*(p0)*log2(p0);endentropy_s1 = p1_eq + p0_eq;if (~s0); % 熵S(v=0)p1 = 0;elsep1 = (s0_and_true / s0);endif (p1 == 0);p1_eq = 0;elsep1_eq = -1*(p1)*log2(p1);endif (~s0);p0 = 0;elsep0 = ((s0 - s0_and_true) / s0);endif (p0 == 0);p0_eq = 0;elsep0_eq = -1*(p0)*log2(p0);endentropy_s0 = p1_eq + p0_eq;gains(i)=currentEntropy-((s1/numberExamples)*entropy_s1)-((s0/numberExamples)*entropy_s0);endend% 选出最大增益[~, bestAttribute] = max(gains);% 设置相应值tree.value = attributes{bestAttribute};% 去活跃状态activeAttributes(bestAttribute) = 0;% 根据bestAttribute把数据进行分组examples_0= examples(examples(:,bestAttribute)==0,:);examples_1= examples(examples(:,bestAttribute)==1,:);% 当value = false or 0, 左分支if (isempty(examples_0));leaf = struct('value', 'null', 'left', 'null', 'right', 'null');if (lastColumnSum >= numberExamples / 2); % for matrix examplesleaf.value = 'true';elseleaf.value = 'false';endtree.left = leaf;else% 递归tree.left = id3(examples_0, attributes, activeAttributes);end% 当value = true or 1, 右分支if (isempty(examples_1));leaf = struct('value', 'null', 'left', 'null', 'right', 'null');if (lastColumnSum >= numberExamples / 2);leaf.value = 'true';elseleaf.value = 'false';endtree.right = leaf;else% 递归tree.right = id3(examples_1, attributes, activeAttributes);end% 返回returnend%%构造函数print_treefunction [nodeids_,nodevalue_] = print_tree(tree)%% 打印树,返回树的关系向量global nodeid nodeids nodevalue;nodeids(1)=0; % 根节点的值为0nodeid=0;nodevalue={};if isempty(tree)disp('空树!');return ;endqueue = queue_push([],tree);while ~isempty(queue) % 队列不为空[node,queue] = queue_pop(queue); % 出队列visit(node,queue_curr_size(queue));if ~strcmp(node.left,'null') % 左子树不为空queue = queue_push(queue,node.left); % 进队endif ~strcmp(node.right,'null') % 左子树不为空queue = queue_push(queue,node.right); % 进队endend%% 返回节点关系,用于treeplot画图nodeids_=nodeids;nodevalue_=nodevalue;end%%构造函数visitfunction visit(node,length_)%% 访问node 节点,并把其设置值为nodeid的节点global nodeid nodeids nodevalue;if isleaf(node)nodeid=nodeid+1;fprintf('叶子节点,node: %d\t,属性值: %s\n', ...nodeid, node.value);nodevalue{1,nodeid}=node.value;else % 要么是叶子节点,要么不是%if isleaf(node.left) && ~isleaf(node.right) % 左边为叶子节点,右边不是nodeid=nodeid+1;nodeids(nodeid+length_+1)=nodeid;nodeids(nodeid+length_+2)=nodeid;fprintf('node: %d\t属性值: %s\t,左子树为节点:node%d,右子树为节点:node%d\n', ...nodeid, node.value,nodeid+length_+1,nodeid+length_+2);nodevalue{1,nodeid}=node.value;endend%%构造函数isleaffunction flag = isleaf(node)%% 是否是叶子节点if strcmp(node.left,'null') && strcmp(node.right,'null') % 左右都为空flag =1;elseflag=0;endend%%构造函数tree_plotfunction tree_plot( p ,nodevalues)%% 参考treeplot函数[x,y,h]=treelayout(p);f = find(p~=0);pp = p(f);X = [x(f); x(pp); NaN(size(f))];Y = [y(f); y(pp); NaN(size(f))];X = X(:);Y = Y(:);n = length(p);if n < 500,hold on ;plot (x, y, 'ro', X, Y, 'r-');nodesize = length(x);for i=1:nodesize%text(x(i)+0.01,y(i),['node' num2str(i)]);text(x(i)+0.01,y(i),nodevalues{1,i});endhold off;elseplot (X, Y, 'b-');end;xlabel(['height = ' int2str(h)]);axis([0 1 0 1]);end%%构造函数queue_curr_sizefunction [ length_ ] = queue_curr_size( queue )%% 当前队列长度length_= length(queue);end%%构造函数queue_popfunction [ item,newqueue ] = queue_pop( queue )%% 访问队列if isempty(queue)disp('队列为空,不能访问!');return;enditem = queue(1); % 第一个元素弹出newqueue=queue(2:end); % 往后移动一个元素位置end%%构造函数queue_pushfunction [ newqueue ] = queue_push( queue,item )%% 进队% cols = size(queue);% newqueue =structs(1,cols+1);newqueue=[queue,item];end(4)实验步骤:>> Untitled正在进行数据预处理...txt =35×5 cell 数组'序号' '花萼大小' '花瓣长度' '花瓣宽度' '类型' '' '小' '长' '长' 'versicolor' '' '小' '长' '长' 'versicolor' '' '小' '长' '长' 'versicolor' '' '小' '短' '长' 'versicolor' '' '小' '长' '长' 'versicolor' '' '小' '短' '长' 'versicolor' '' '小' '长' '短' 'versicolor' '' '大' '长' '长' 'versicolor' '' '大' '长' '短' 'versicolor' '' '大' '长' '长' 'versicolor' '' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '小' '长' '长' 'setosa''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '短' 'versicolor''' '小' '短' '短' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '短' '短' 'setosa''' '大' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '短' 'setosa''' '大' '短' '短' 'setosa'数据预处理完成,正在进行构造树...node: 1属性值: 花瓣长度,左子树为节点:node2,右子树为节点:node3 node: 2属性值: 花瓣宽度,左子树为节点:node4,右子树为节点:node5 node: 3属性值: 花萼大小,左子树为节点:node6,右子树为节点:node7 node: 4属性值: 花萼大小,左子树为节点:node8,右子树为节点:node9 node: 5属性值: 花萼大小,左子树为节点:node10,右子树为节点:node11 node: 6属性值: 花瓣宽度,左子树为节点:node12,右子树为节点:node13叶子节点,node: 7,属性值: versicolor叶子节点,node: 8,属性值: setosa叶子节点,node: 9,属性值: setosa叶子节点,node: 10,属性值: setosa叶子节点,node: 11,属性值: versicolor叶子节点,node: 12,属性值: setosa叶子节点,node: 13,属性值: versicolorID3算法构建决策树完成!(4)实验结果。
