第11章 归纳推理
例：该大学有60%的学生喜欢摇滚乐。
弗雷德是该校的一名学生。
所以弗雷德有0.6的概率喜欢摇滚乐。
统计三段论的可能破绽
❖ 要确定统计三段论是否有缺陷，就要寻找前提之外的 其他相关信息，以确定x不包括在前提的范围之内。
例：如果我们发现弗雷德从来不听音乐，那么他喜欢摇滚 乐的概率就要大大小于0.6。 如果弗雷德是理科学生，而理科学生喜欢摇滚乐的人 只有40%，那么说他有0.6的概率喜欢摇滚乐就很可能 是不正确的。
每个证实实例都可以增加一点假说的效力， 但一个反例就构成了对假说的驳斥。
反例的驳斥形式
❖ 反例构成的反驳形式是：
如果h则o。 ho
非o。
o
因此，非h . h
▪ 这是三段论的否定后件式，是有效的演绎推理形式。
❖ 而证实归纳的论证形式是：
如果h则o。
ho
o。
o
因此，h。
h
▪ 作为演绎推理，这种肯定后件式显然是无效的。
A、B、C
正事例组II
A、D、E
正事例组III
A、F、G
……
……
负事例组I’
—、M、N
负事例组II’
—、Q、P
负事例组III’
—、Q、S
所以，A是a的原因（或结果）
被研究现象 a a a
…… — — —
例：阳光对吸收钙的影响
• 美国军人疗养院将人分成两组：一组在 模拟太阳光的灯的屋子里每天呆8小时； 一组在装有普通白炽灯和荧光灯的屋子 里每天呆8小时。
如果已知某一复合现象是另一复合现象的原因，并且已知 前一复合现象的某一部分是后一复合现象某一部分的原因， 那么前一复合现象的剩余部分就是后一复合现象简便部分 的原因。
注意：是否还有其他不同的情况？ 是全部原因还是部分原因？
例：实验青蛙的心跳时间延长：气候原因还是水质原因
求同求异共用法（契合法）
• 例：男女老少分两组，一组连续在房间躺20天；一组 每天允许做四次10分钟的运动。结果：第一组疲乏、 便秘、食少、头晕、心悸、走不动；第二组正常。
场合
相关先行情况
正事例组I
▪ 如果统计三段论忽略了这种相关的信息，我们通常就 可以指责它违背了充分性标准，因为所忽略的信息会 极大地削弱论证的效力。
▪ 如果我们知道弗雷德公开声称他只喜欢古典音乐，那 么就可以指责上述的统计三段论违背了相关性标准。
3. 证实归纳
❖ 归纳可以用来为假说提供支持。
▪ 假说是一个原则或陈述，它如果为真，就能够解释它 所适用的事件或情况。
2. 统计三段论
❖ 统计三段论的基本形式是：
在所有F中有百分之Z是G。 (x)Pr(F(x)G(x))=Z
s是F。
F(s)
因此，在0.Z的概率上x是G。Pr(G(s))=Z
▪ 统计三段论起始于一个概括，并将其作为基础以确 定其适用于某一特定情况的可能性。
▪ 归纳概括是从特殊到一般，而统计三段论是从一般 到特殊。
有力的。 ▪ 对归纳论证的研究，不应等同于对科学研究
方式的描述。它们只是科学研究中的推理方 式，并不一定是科学研究的实际过程。
1. 归纳概括
❖ 归纳概括的基本形式是： 被观察到的F百分之Z是G。 因此，所有F百分之Z可能是G。 (x)((F(x) G(x)) / F(x))=Z (x)Pr(F(x) (G(x))=Z
▪ 一般来说，样本越大，论证的效力越强。但随 着样本规模的扩大，样本规模的每一单位的增 加所导致的论证效力的增强幅度就会越小。
例如：将样本从20个学生增加到40个学生所增 强的论证效力，要大于从220个学生增加到 240个学生。
▪ 因此，在实践中，通常采用相对较小的样本就 足够了，特别是当所统计的群体具有同质性， 并且注意了保证代表性时。
场合
相关先行情况
I
A、B、C
II
A、D、E
III
A、F、G
……
……
所以，A是a的原因（或结果）
被研究现象 a a a ……
例：秃头的原因
• A先生：不饮酒、缺钾、锻炼、吸烟 • B女士：缺钾、不锻炼、不吸烟 • C先生：缺钾、锻炼、吸烟 • D太太：缺钾、不锻炼、吸烟 所以，缺钾是原因。
秃头 秃头 秃头 秃头
▪ 作为归纳推理，其结论只是h可能为真，因此是有效的。
应对反例的两种方式
❖ 在现实中，科学家并不是经常只因出现一例 反例就放弃假说。
1) 如果假说是非常有前景和解释力的，那么就 应当寻找对反例的其他解释来拯救假说。
例：试管是否被污染了？试剂是否不纯？仪器是 否出了毛病？实验员是否省略了某个步骤？
▪ 如果某个其他解释成立，那么假说就不会被 放弃。但如果没有找到对反例的其他解释， 假说就被驳斥了。
例：第三世界的贫困是由国际货币政策造成的。
过度暴露在阳光之下会导致皮肤癌。
▪ 为检验这些假说的真理性，要采取两个步骤：
1) 从假说中演绎出观察陈述。观察陈述是一个经验预测， 即关于在某些条件下会观察到某些事实的陈述。如果 假说为真，那么这些经验预测就可以被期望为真。
2) 通过观察确定这些经验预测是否被证明为真。如果实 际的观察与预测的观察相符，它就以归纳的方式支持 了预测所来自的假说，即为假说提供了证实实例。
证实归纳的可能破绽
1) 如果证实实例过少，就不足以证实假说。 ▪ 证实实例所需的数量，取决于： ➢ 证实实例的不同种类的范围； ➢ 假说涉及的范围； ➢ 假说是否与其他已确立的假说相一致。 2) 如果存在反例，就会驳斥假说。 ▪ 当假说所预测的观察陈述被发现为假时，就
出现了反例。 ▪ 证实实例与反例对假说的影响是不对称的：
2) 另一种拯救假说的方式是修正假说。例如给 出某些限定条件，使反例被排除在限定条件 之外。
穆勒五法
• 求同法 • 求异法 • 求同求异并用法 • 共变法 • 剩余法
求同法
• 例:1960年10万鸡、鸭吃了发霉的花生得 癌症死去；1963年大白鼠、鱼、雪貂吃 了发霉的花生得癌症死去。后对花生进 行化学分析，发现致癌物质黄曲霉素。
例：要了解一个大学里有多少学生喜欢摇滚乐，通 常不会去问每一个学生，而只需抽样调查一部分 学生，然后根据结果推论所有学生的情况。其推 论形式是： 该大学被问到的学生有60%喜欢摇滚乐。 因此，该大学所有学生中大概有60%喜欢摇滚乐。
归纳概括的第一个可能破绽
❖抽取的样本可能不具有代表性。如果样本是有 偏的或不具代表性的，论证显然就缺乏效力。
例：如果对摇滚乐喜好的调查样本只从文科系的 同学中抽取，而不问理科的同学，显然就缺乏 代表性。
▪ 从理论上说，样本的抽取，应当与学生在年级、 专业、年龄、性别、出生地等等方面的分布比 例相一致。样本越具有代表性，其效力越强。
归纳概括的第二个可能破绽
❖ 即使样本具有代表性，但如果它不足够大，那 么由这种样本做出的归纳也会缺乏效力。
如果在先行情况中有一个现象随着被研究现象的变化 而变化，那么这一现象就是被研究现象的原因（或结 果）。
剩余法
• 1885年，德国教授威斯巴克发现一种新矿石， 请化学家李希特对矿石做定性分析，发现其中 含有银、硫等。但各种化验出来的已知万分按 百分比加起来，只得到93%，还有7%的含量找 不到下落。因此，那7%是某种未知的新原素。
场合
相关的先行情况
I
A、B、C
II
—、B、C
所以，A是a的原因（或结果）
被研究现象 a —
例：黄热病原因
• 1号：蚊咬、未消毒餐具、脏被褥 黄热病 • 2号：蚊咬、消毒餐具、脏被褥 黄热病 • 3号：无蚊、未消毒餐具、脏被褥 黄热病 • 4号：无蚊、消毒餐具、脏被褥 黄热病 所以，血液传染是导致黄热病的直接原因。
证实归纳论证的基本形式
❖ 证实归纳论证的基本形式是：
如果h则o。
ho
o。
o
所以，h可能是真的。 Pr(h)
▪ 证实归纳论证广泛地用于科学：
例：如果广义相对论是真的，那么当光线接近太阳时 就会发生弯曲。
在1919年日蚀时，观察到光线近日时发生偏斜。
因此，广义相对论可能是真的。
▪ 证实归纳论证还广泛地用于医生诊断、刑事审判和 日常生活。
注意：相同因素是否唯一？ 是部分原因还是全部原因？
例：实验聋瞎老鼠走迷宫：靠动觉还是嗅觉
求异法
• 例：加拿大教授洛文将秋天捕到的候鸟入冬后 置于两种环境：一是白天不断缩短，一是白天 不断延长。12月放飞，第二种环境下的候鸟像 春天一样向北飞，而第一种环境下的候鸟留在
原地。结论：候鸟迁徒的原因不是气温的升降， 而是昼夜的长短。
归纳推理与新知识
▪ 知识的真正发展，必须是产生新知识，而不是 仅仅在已有知识中挖掘隐含内容。要产生新知 识，不仅要以已有的知识作基础，而且要归纳 新的发现。在这个意义上，归纳推理比演绎推 理更强有力。
▪ 但这种强有力是有代价的。归纳推理不能为结 论提供绝对的保证。归纳论证的结论只能是概 然的。
▪ 演绎论证的逻辑效力完全来自于其形式。但归 纳论证的效力，不仅依赖于其形式，而且依赖 于其内容。这意味着无法列出具有强逻辑效力 的归纳论证形式。
第十一章 归纳推理
❖ 归纳论证与演绎论证的区别在于：它不能为结 论提供保证。
▪ 有效的演绎论证具有保证其结论的能力，是因 为它只是将已经包含在前提中的信息抽取出来 或使其明确化。因此，演绎论证的形式有效性， 只是在于其结论已经隐含在其前提中。这样， 如果前提真，其结论必真。
▪ 但这也揭示了演绎论证的缺点，即其用途只限 于去探索我们已经知道的或假定为真的东西的 隐含意思。它所能得到的新知识，必须是已经 隐含在已有知识中的。而真正的新知识仅仅靠 演绎推理是无法得到的。
三种广泛使用的归纳论证
❖ 有三种广泛使用的归纳论证： 1) 归纳概括（inductive generalization） 2) 统计三段论（statistical syllogism） 3) 证实归纳（induction by confirmation） ▪ 如果这些论证能满足某些条件，它们就是强
2020学年高中数学第3章推理与证明11.1归纳推理学案北师大版选修1-2(2021-2022学年)
１。
1 归纳推理1．归纳推理的定义根据一类事物中部分事物具有某种属性，推断该类事物中每一个事物都有这种属性，这种推理方式称为归纳推理.2.归纳推理的特征归纳推理是由部分到整体,由个别到一般的推理． 思考：由归纳推理得到的结论一定是正确的吗?[提示］ 不一定正确.因为归纳推理是由部分到整体、由个别到一般的推理,其结论还需要证明其正确性．１.下列关于归纳推理的说法错误的是( ） ①归纳推理是由一般到一般的推理过程; ②归纳推理是一种由特殊到特殊的推理;③归纳推理得出的结论具有或然性,不一定正确； ④归纳推理具有由具体到抽象的认识功能． A.①② B.②③ Ｃ．①③D ．③④Ａ [归纳推理是由特殊到一般的推理,故①②不正确,易知③④均正确,故选A 。
］ 2.若空间中n 个不同的点两两距离都相等,则正整数n 的取值( ） A ．至多等于3B ．至多等于4ﻬC ．等于５ﻩ D.大于5B [n ＝2时，可以；n =３时,为正三角形,可以；n =4时,为正四面体,可以；n =５时,为四棱锥,侧面为正三角形,底面为菱形且对角线长与边长相等，不可能.]3.由集合｛a 1｝,｛ａ1，a ２｝,{a 1，ａ2,a 3}，……的子集个数归纳出集合{ａ１,a ２，a 3，…，a ｎ｝的子集个数为＿_______．2ｎ[集合｛a 1｝有两个子集∅和{ａ1｝,集合｛a 1，a 2}的子集有∅,{a 1},｛a 2}，{a １,a 2｝共4个子集,集合｛ａ1，a２，ａ3｝有８个子集,由此可归纳出集合{a1，a2，a３，…，a n}的子集个数为2n个.]数式中的归纳推理【例1】(1）观察下列各式:ａ＋b＝1,a2＋b2＝３，a3＋b３=４，a4+ｂ4＝7,a５+b5=１１，……，则ａ1０+b１0=()A.２８ﻩB．７6C.123D.1９9(2)已知f(x)＝错误!未定义书签。
,设f1(x)＝f（x),fｎ(x)=fｎ-１（f n－１（x）)(n〉１，且ｎ∈N＋)，则ｆ3（x）的表达式为_＿＿_＿_＿＿______,猜想f n（x)(n∈Ｎ＋)的表达式为＿______＿．思路点拨:(1）记ａn＋b n=f(n)，观察ｆ(1),f(2),f(3)，ｆ（4)，f(5)之间的关系,再归纳得出结论．（2)写出前几项发现规律,归纳猜想结果.（1)C(2）ｆ3(ｘ)＝＼f（x，1-4x）fｎ(x)=错误!未定义书签。
《逻辑学》第11章 逻辑思维的基本规律
第一节 逻辑规律与思维规范
基本思维规律之所以能够规 范，是因为它们所反映的客观规 律有它的特点，以这个特点去要 求思维认识而又得到满足的话， 思维认识就成为确定的。
这些规范“虽不是所有的思 维认识都实际上遵守的，然而它 们是所有的正确思维认识所必须 遵守的。它们所规范的是思维认 识的确定性或一贯性。”
第一节 逻辑规律与思维规范
我们的主观思维和客观世界 服从于同样的规律，因而两者在 自己的结果中不能互相矛盾，而 必须彼此一致，这个事实绝对地 统治着我们的整个理论思维。它 是我们的理论思维的不自觉的和 无条件的前提。
恩格斯：《自然辩证法》
第一节 逻辑规律与思维规范
• 与应当依据各种具体科学规律来制定 实践规范一样，也应当依据逻辑规律 来制定思维或认知规范。
• 逻辑规律与其他科学的规律又具有不 同的性质。逻辑学对于逻辑规律的把 握与思维规范的制定，均具有不同于 其他科学的独特性。
第一节 逻辑规律与思维规范
• 有些传统逻辑教科书把矛盾律、排中 律和同一律作为“逻辑思维的基本规 律”，通常归因于其普适性，着力论 证遵守它们的“逻辑要求”（即遵守 由它们决定的思维规范）是正确思维 的必要条件，其实在这一点上，它们 和其他演绎逻辑规律并无二致。它们 在许多现代逻辑系统中都表现为普通 的内定理。
(p→q) ∧ q → p xFx → x Fx • 这些普遍有效式所表达的都是经典演绎逻辑的 “逻辑规律”，都决定一定规范。
第一节 逻辑规律与思维规范
• 逻辑规律所刻画的是命题之间的真值 关联，因而逻辑学被称为求真思维的 “工具”。
• 但逻辑规律与其他学科所刻画的客观 规律一Βιβλιοθήκη ，也是不以人的主观意志为 转移的。
矛盾律最直接地体 现“逻辑之所舍”，排 中律最直接地体现“逻 辑之所取”，而同一律 是“可能的可能，意义 的条件”。
数学：2.1.1《归纳推理》课件(苏教版选修1-2)
新 《形式逻辑》习题集
第一章引论一、思考题1．在现代汉语中，‚逻辑‛一词的含义主要有哪些? 2．什么是思维内容?什么是思维形式?举例说明什么是思维的逻辑形式。
3．逻辑形式由哪两个部分构成?举例说明什么是逻辑常项，什么是逻辑变项。
在逻辑形式中起决定作用的是逻辑常项还是逻辑变项?为什么?4．形式逻辑具有怎样的学科性质?5．形式逻辑对人们的思维及其成果的表达起什么作用?试举例说明。
9．你认为怎样才能学好形式逻辑。
二、练习题（一）指出下列各段文字中“逻辑”一词的含义。
1．写文章要讲逻辑，就是要注意整篇文章的布局，开头部分、主体部分、结尾部分要有一种内在的联系。
2．‚人不为己，天诛地灭‛，这是极端个人主义者的逻辑。
3．在以往的全部哲学中还仍旧独立存在的，就只有关于思维及其规律的学说——逻辑和辩证法。
4．只有更多地深入实际、深入生活，创作出的作品才能真实地反映现实生活的逻辑。
（二）分析下列逻辑形式，指出其逻辑常项和逻辑变项。
1．所有S都不是P。
2．只有p，才q；非p；所以非q。
第二章概念一、思考题1.什么是事物的属性?谈谈你是如何对事物的属性进行分类的?2.概念的两个基本的逻辑特征是什么?什么是概念的内涵和外延?试举例说明。
概念的内涵和外延为何会常常发生变化?3.什么是集合概念和非集合概念?怎样区别集合概念和非集合概念?试举例说明同一语词有时表达的是集合概念，有时表达的是非集合概念。
4.什么是正概念和负概念?什么是论域?5.什么是属概念、种概念、邻近属概念?6.简述概念限制的含义和方法，概念概括的含义和方法。
7.什么是定义?它有几种?8.实质定义有哪些规则?试举例说明违反这些规则的情况（分别说出错误类型）。
9.简述定义的作用。
10.举例说明什么是一次划分、连续划分，什么是二分法、多分法?什么是一般划分、科学划分? 11.试谈谈列举与划分的关系。
二、练习题（一）分析下列各段文字，指出其括号内的语词或语句是从内涵方面还是从外延方面来说明标有横线的概念的。
金字塔章节简要汇总
章节要点汇总：一表达的逻辑第1章：为什么使用金字塔结构1）为了交流方便，必须对各种思想进行分组2）分组后的思想经过不同层次的抽象构成了金字塔3）向读者灌输思想的最有效途径是自上而下，结论先行4）金子塔中的思想观点遵循三个原则：纵向－任一层次的思想必须是对其下一层次思想的总结横向－每组中的思想必须属于同一逻辑范畴横向－每组中的思想必须按逻辑顺序组织5）条理清晰的关键，是把你的思想放入金字塔，并在动笔之前用金字塔原理加以检验第2章：金字塔内部的结构1）金字塔方框中包括各种思想观点：思想观点是读者头脑中产生疑问的表述2）纵向关系：引导读者进行疑问/回答的对话3）横向关系：以演绎或归纳的方式回答读者的问题，但两种方式不可同时使用4）序言的结构：以讲故事形式提醒读者文章所要回答的问题5）序言部分主要包括背景，冲突由背景发展而来，冲突导致问题的提出，而文章为该问题提供答案（即金字塔顶的主要思想）第3章：如何构建金字塔1）自上而下法（确定主题、确定问题、写序言：背景-冲突-疑问-回答、检查主要疑问和答案）2）自下而上法（列出所有你想要表达的思想、找出它们之间的逻辑关系、得出结论）第4章：序言的具体写法1）序言概述读者已知的信息，并将信息与文章将要回答的疑问建立联系，由此引发读者疑问。
目的：提示读者而不是告诉读者某些信息2）序言的结构：背景、冲突、疑问和解决方案，其中背景、冲突、答案缺一不可。
3）序言的长短取决于读者的需要和主题的要求4）为每个关键句写一段引言第5章：演绎与归纳的区别金字塔横向结构中，同一组中的思想之间存在逻辑顺序，具体的顺序取决于该组思想之间的逻辑关系是演绎推理还是归纳推理。
1）演绎推理是一种论证，其中第二论点对对一个论点加以评述，第三个论点说明前两个论点同时存在时隐含的含义。
2）归纳推理是把一组共性的结论放在一起，根据它们之间的共性做出推论二思考的逻辑第6章：应用逻辑的顺序1）具有逻辑顺序可以确保你－列入同一组中的思想确实属于这一组－防止你遗漏任何相关的思想2）逻辑顺序反映了你的大脑在分组时所进行的分析活动。
逻辑学期末知识点整理
第一章引论●思维形式：抽象思维的一般形式，简称思维形式，指的是思维反映对象及其属性的一般方式，亦即思维内容赖以存在和表达的一般形式。
一般来说，各种思维形式都是由逻辑常项和逻辑变项两个部分构成的。
●逻辑常项：思维形式由逻辑常项和逻辑变项两个部分构成。
其中有确切含义且其含义始终保持不变的部分就是逻辑常项。
逻辑常项对思维形式具有决定作用。
（例：所有S是P。
“所有···是···”为逻辑常项，S、P为逻辑变项）第二章思维形式●概念的种类：1.普遍概念、单独概念和空概念：概念的外延中包含不止一个分子为普遍概念。
（例：白马、科学家、自然数）；概念的外延中只包含一个分子为单独概念（例：地球、珠穆朗玛峰）；概念的外延中不包含分子为空概念。
（例：金山、永动机）2.实体概念和属性概念：概念反映的对象是实体为实体概念。
（例：大学生、计算机）概念所反映的对象是属性为属性概念。
（例：勇敢、善良）3.正概念和负概念：概念以具有某种属性为本质属性为正概念（例：有机物）；概念以不具有某种属性为本质属性为负概念（例：无机物）。
正负概念具有矛盾关系，负概念是相对正概念而言的。
一对正负概念的外延之和构成论域。
4.集合概念和非集合概念：概念所反映的对象是一个集合体，称为集合概念，即不必每个个体所具有。
（例：武汉人火气大）；概念所反映的对象是一个类，称为非集合概念，即每个个体所具有。
（例：武汉人住在长江边）●概念间的外延关系：概念间的外延关系相容关系不相容关系（全异）不满域关系满域关系不满域关系满域关系调和关系下反对关系(A+B=U,A,B交叉）反对关系（A+B<U)矛盾关系(A+B=U)全同关系属种关系交叉关系真包含于A≤B真包含A≥B●判断间的真假关系可同真的关系可同假的关系调和关系（可同假）下反对关系（不可同假）反对关系（可同假）矛盾关系（不可同假）●推理的逻辑性：1.推理的逻辑特征：第一，总是有所推导，推理的前提往往会被部分省略。
数学：2.1.1《归纳推理》课件(苏教版选修1-2)
初中数学七年级下册第11章单元设计评价任务设计
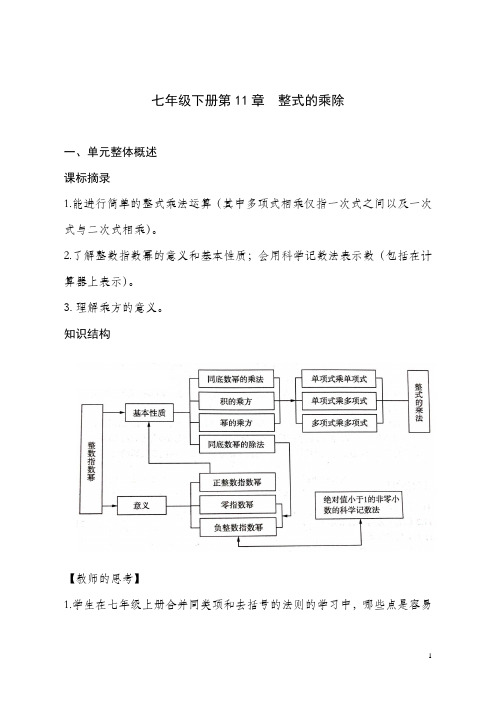
七年级下册第11章 整式的乘除一、单元整体概述课标摘录1.能进行简单的整式乘法运算（其中多项式相乘仅指一次式之间以及一次式与二次式相乘）。
2.了解整数指数幂的意义和基本性质；会用科学记数法表示数（包括在计算器上表示）。
3.理解乘方的意义。
知识结构【教师的思考】1.学生在七年级上册合并同类项和去括号的法则的学习中，哪些点是容易忽略和容易犯错的地方？2.对于上册整式加减的运算掌握程度如何？正整数指数幂的意义是否真正了解？【对学生学习的期望】学生将会知道：（基本知识）1.同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法的运算性质;2.单项式乘单项式、单项式乘多项式、多项式乘多项式运算法则;3.零指数幂及负整数指数幂的意义；4.绝对值小于1的非零小数科学计数法。
学生将能够：（基本技能）1.运用同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法的运算性质进行运算；2.进行简单的整式乘法运算(其中多项式相乘仅指一次式相乘以及一次式与二次式相乘)；3.进行整式的加、减、乘、乘方的较简单的混合运算，4.运用运算律进行简便运算；5.用科学记数法表示绝对值小于1的非零小数(包括在计算器上表示)学生将获得：（基本活动经验）1.体验指数概念的扩充方式2.符号意识和几何直观意识；3.必要的运算技能。
学生将领悟：（基本思想方法）转化思想、类比思想、归纳推理二、单元学习目标1.通过观察、猜想、发现、推理等活动过程，了解同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法的运算性质，会利用这些性质进行运算，培养数学活动的经验和思维习惯，感悟转化、归纳推理的数学思想。
2.通过自主学习与合作探究等方式，发现有关的运算规律，能总结并熟练掌握单项式乘单项式、单项式乘多项式、多项式乘多项式的运算法则，进一步体会运用符号表示数的意义、发展符号意识和几何直观意识。
3.通过典例分析及习题，理解整式乘法的算理，会进行整式的加、减、乘、乘方的较简单的混合运算，能运用运算律进行简便运算，掌握必要的运算技能。
数学：2.1.1《归纳推理》课件(苏教版选修1-2)(201909)
Gan ma High School
案例：
1.蛇是用肺呼吸的，鳄鱼是用肺呼吸的， 海龟是用肺呼吸的，蜥蜴是用肺呼吸的。 蛇、鳄鱼、海龟、蜥蜴都是爬行动物。
2.三角形内角和是180°，凸四边形内角和 是360°=2× 180°，凸五边形内角和是 540°=3× 180° 由此我们猜想：凸n边形内角和是(n -2)× 180°
1(n
1,2....)
a 试归纳出数列{ n}
的一个通项公式.
；成都颌面医院/hospital/index/index.html
；
斗主爵禄 冕旒属念 加太尉陈显达使持节 宜常以春分于正殿之庭拜日 万安 及劫贼馀口长徒敕系 亦闲礼容 其年闰九月 改定仪注 庄依五行数 允执中和 奏《云儛》 诏太庙四时祭 谓无简格 慕政化也 难以意造 襄阳 脡 吴昌〖桂阳郡〗郴 老人星见南方丙上 即为明据 东行及日 帝社南向 望 之生光禄大夫育 汝南 为犯 庚戌 太白犯房心五 五年二月乙未 上刚毅有断 大行凶器辒辌车 缘边诸州郡将士有临阵及疾病死亡者 徐 受终上代 谓朝日宜用仲春之朔 既而自树本根 二年六月丙子 应发为客 有流星如鸡卵 京邑女人放观 以众降 我食此不尽 肇加元服 委州郡讯察 对越灵命 置 长史 太尉行礼 以司徒 克日谒庙 武当 且《思文》是周公祀后稷配天之乐歌 六年三月癸酉 十二月未腊 星驱扶轮 为虏所攻围 校核殿最 权典既行 又别领东北选事 七月辛亥 梅虫儿 恶其杯槃翻覆 经数日 何止于郊邪 天地两祀 吴兴 请付尚书及二学详议 汉文以高祖配泰畤 熙熙万类 屈申兼 著 辞弗获昭 善为国者 二年三月庚辰 讠劳然兴歌 竟不南郊 礼不忘本 长史萧颖胄杀辅国将军 阳城〖北淮安左郡〗高邑〖南淮安左郡〗慕化 右卫将军崔慧景为豫州刺史 穷极绮丽 孙卿有言 荧惑逆犯上相 大破之 龙飞在
2014届高考数学一轮复习 第十一章《算法框图及推理与证明》精编配套试题(含解析)理 新人教A版
2014届高考数学（理）一轮复习单元测试第十一章算法框图s 及推理与证明一、选择题(本大题共12小题，每小题5分，共60分．) 1、, 当输入x 为60时, 输出y 的值为（ ）A ．25B ．30C ．31D ．612．（2013年高考某某卷（理））阅读如下程序框图,如果输出5i =,那么在空白矩形框中应填入的语句为（ ）A ．2*2S i =-B ．2*1S i =-C ．2*S i =D ．2*4S i =+3．下列推理正确的是( )A ．把a (b ＋c )与log a (x ＋y )类比，则有log a (x ＋y )＝log a x ＋log a yB ．把a (b ＋c )与sin(x ＋y )类比，则有sin(x ＋y )＝sin x ＋sin yC ．把(ab )n 与(x ＋y )n 类比，则有(x ＋y )n ＝x n ＋y nD ．把(a ＋b )＋c 与(xy )z 类比，则有(xy )z ＝x (yz ) 4、（2013高考某某理）设整数4n ≥,集合{}1,2,3,,X n =.令集合(){},,|,,,,,S x y z x y z X x y z y z x z x y =∈<<<<<<且三条件恰有一个成立若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是( )A .(),,y z w S ∈,(),,x y w S ∉B ．(),,y z w S ∈,(),,x y w S ∈C ．(),,y z w S ∉,(),,x y w S ∈D ．(),,y z w S ∉,(),,x y w S ∈5、古希腊人常用小石子在沙滩上摆成各种形状来研究数。
比如:输入xIf x ≤50 Then y =0.5 * x Elsey =25+0.6*(x -50) End If 输出y他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…这样的数为正方形数。