第四章综合测试卷

合集下载

八年级科学下册第四章《植物与土壤》综合测试卷 (新版)浙教版-(新版)浙教版初中八年级下册自然科学

第四章《植物与土壤》综合测试卷一、选择题（每小题2分，共40分）1．长期单一使用化肥会破坏土壤结构，下列不属于使用单一化肥引起的是（）A．团粒结构破坏 B．腐殖质得到补充C．土壤容易板结D．土壤容易积水2．有时候，园林工人在移栽较大的绿化树木时，会给绿化树“挂吊瓶”，补充水和无机盐，以提高成活率，“挂吊瓶”的针头应插入到较大绿化树树干（茎）的（）A．树皮B．韧皮部C．木质D．形成层3．一节废电池相当于一颗“炸弹”，一节废电池烂在地里能使1平方米的土地失去利用价值，主要是因为电池中的汞、镉、铅等重金属物质会渗透出来造成( )A．大气污染 B．水污染C．土壤污染 D．生物污染4．水分吸收的主要部分、运输通道、散失的门户依次是（）A．成熟区、气孔、导管B．根毛、叶脉、气孔C．根毛、导管、气孔D．根毛叶脉、保卫细胞5．下列符合壤土类土壤性状的是( )A．通气性能好，保水能力差B．通气性能差，保水能力好C．通气性能好，保水能力好D．通气性能差，保水能力差6．下列有关植物根的叙述不正确的是( )A．植物的根系的分布只与地下水位高低有关B．植物的根有吸收和固定的功能C．主根上生出的根，称之为侧根D．直根系上有明显的主根7．小梅把几滴香水加到小花瓶的水中，瓶内放入几株鲜花，不久从花叶上能闻到此香水的缕缕香气，这主要和植物的哪个功能有关（）A．导管和输导作用B．筛管和输导作用C．蒸腾作用D．呼吸作用8．植物可以进行无土栽培的原因是（）A．植物的根吸收的只是水和无机盐 B．土壤对植物生长没有作用C．植物的根吸收的不是土壤中的无机盐 D．根只吸收水9．根尖的结构包括根冠、分生区、伸长区、成熟区四部分。

下列有关叙述不正确的是（）A．根冠具有保护作用B．分生区能不断分裂产生新细胞C．伸长区细胞体积变大、变长，是细胞分化的结果D．成熟区是吸收水分和无机盐的主要部位10．按下列百分比配置的土壤中加点水，用手一搓，最容易搓成条状体的是( ) A．砂粒20% 粉砂粒40% 黏粒40%B．砂粒10% 粉砂粒40% 黏粒50%C．砂粒10% 粉砂粒30% 黏粒60%D．砂粒20% 粉砂粒50% 黏粒30%11．下列与植物蒸腾作用有关的叙述，不正确的是（）A．蒸腾作用能促进水分和无机盐的运输B．植物的气孔很小，因此通过气孔散失的水分很少C．蒸腾作用散失水分的“门户”是气孔D．上表皮气孔少，可减少水分的散失12．做“茎输导水分和无机盐的实验”，应选用带叶的枝条，才能观察到红墨水在导管内的运输情况，这是因为（）A．叶片进行光合作用需要吸收水分、无机盐B．蒸腾作用是茎运输水分、无机盐的动力C．叶片呼吸作用放出的能量是茎吸收和运输水分、无机盐的动力D．茎细胞生活所需的有机物是由叶片供给的13．俗话说“梨树砍三刀，果枝压弯腰”，在初夏梨树的“坐果”期，有经验的果农会给梨树的茎做半环状剥皮，这样做的目的是（）A．促进有机物更多地输送给果实B．促进水分更多地输送给果实C．促进无机盐更多地输送给果实D．阻止形成层的分裂，促进果实的发育14．某校科学兴趣小组在野外考察时，绘制出下面的树桩年轮特征示意图。

含答-案答案在前湘教版高中地理必修第一册第四章综合测试试卷含答-案答案在前2含答案-答案在前

第四章综合测试答案解析一、1.【答案】A【解析】根据水循环的基本环节可以判断 M 主要为下渗形成的地下水。

2.【答案】A【解析】植树造林有利于涵养水源，增加地表水的下渗，增加地下水量。

3.【答案】D【解析】水循环的能量主要来自太阳辐射能，选 D。

4.【答案】B【解析】“天河工程”是利用三江源区天然水汽输送格局，采用人工影响天气技术，把部分天然落入长江流域的降水截留在或诱导到黄河流域，主要改变了水循环的水汽输送和降水环节，对应图中的②③，选 B。

5.【答案】A【解析】“蓝水”和“绿水”均来自于降水。

“蓝水”是降水中形成地表水和地下水的部分，而“绿水”是降水下渗到土壤中的水，故“蓝水”的数量与“绿水”的数量并不完全相同。

“绿水”是降水下渗到土壤中的水，不包括地表径流，而且土壤水和地下径流也存在显著的差别。

通常所说的水资源包括河流水、淡水湖泊水和浅层地下水，大部分属于“蓝水”。

6.【答案】C【解析】“绿水”是降水下渗到土壤中的水，没有直接参与地表形态的塑造。

海上内循环与陆地各水体关系不大。

“绿水”进入大气后，可以强烈吸收地面辐射（大气中的CO 和水汽能强烈吸收地面长波辐射），进2而增强大气逆辐射，对地面起保温作用。

“绿水”是降水下渗到土壤中的水，受降水量季节变化的影响，“绿水”数量也发生变化。

7.【答案】C【解析】从图中可知云贵高原、黄土高原、内蒙古高原和大、小兴安岭地区是我国少涝区，而多涝区则分布在江汉平原和东南沿海平原地区，充分说明雨涝与地势高低有明显的关系。

8.【答案】B【解析】从图中可知，华北平原干旱频次高，是我国旱灾多发区。

华南沿海和西南地区因受季风影响，旱涝现象非常普遍，因而也是我国的旱灾多发区。

9.【答案】C【解析】读图可知，同纬度水温西低东高，A 错；随纬度增加水温降低，B 错；西部等温线较东部密集，因此西部温差大，东部温差小，C 正确；由南向北，等温线分布疏密不均，因此由南向北递减变化不均匀，D 错。

(苏科版)初中数学七年级上册第4章综合测试试卷01及答案

第四章综合测试一、单选题1.下列判断错误的是（）A .若a b =，则33ac bc -=-B .若a b =，则33a b =--C .若ax bx =，则a b=D .若2x =，则22x x=2.已知3x k =-，2y k =+，则y 与x 的关系是（）A .5x y +=B .1x y +=C .1x y -=D .1y x =-3.下列各式不是方程的是（）A .20x x +=B .0x y +=C .1x x+D .0x =4.将372x x -=变形正确的是（）A .327x x +=B .327x x -=-C .327x x +=-D .327x x -=5.下列等式的变形中，不正确的是（）A .若x y =，则55x y +=+B .若(0)x ya a a=¹，则x y =C .若33x y -=-，则x y=D .若mx my =，则x y=6.有一应用题：“李老师存了一个两年的定期储蓄5 000元，到期后扣除20%的利息税能取5 176元，求这种储蓄的年利率是多少？”四位同学都是设这种储蓄的年利率是x ，可他们列出的方程却不同，下列列出的方程中正确的是（）A .5000(1220%)5176x +´´=B .5000(12)80%5176x +´=C .50005000280%5176x +´´=D .5000500080%5176x +´=7.下列方程为一元一次方程的是（）A .123+=B .423m n m+=C .2223x x+=D .423x x-=8.下列利用等式的性质，错误的是（）A .若a b =，则11a b -=-B .若237a b +=-，则255a b +=-C .若a b =，则22ma mb =D .若ac bc =，则a b=二、填空题9.一件商品按成本价提高20%后标价，又以9折销售，售价为270元.设这件商品的成本价为x 元，则可列方程：________10.若13x --=，则x =________11.一组数：2，1，3，x ，7，9-，…，满足“从第三个数起，前两个数依次为a 、b ，紧随其后的数就是2a b -”，例如这组数中的第三个数“3”是由“221´-”得到的，那么这组数中x 表示的数为________.12.若代数式7y -与21y -的值相等，则y 的值是________.13.已知关于x 的方程231x a -=-的解为1x =-，则a 的值等于________.14.当x =________时，代数式21x +与58x -的值互为相反数.15.当x =________时，式子1x -与式子214x -的值相等.16.写出一个满足下列条件的一元一次方程：①某个未知数的系数是3；②方程的解是2；这样的方程是________.17.已知3x =-是方程(21)40k x +-=的解，则k =________.三、计算题18.解方程：（1）2523163x x x +--=-；（2）2130.20.5x x -+-=.19.解方程：（1）3723x x+=-（2）3(2)(21)x x x -=--（3）12123x x-=+.20.解方程：31112x x -+=+.四、综合题21.已知方程323452x x -=-（1）求方程的解；（2）若上述方程与关于x 的方程383()2a x a a +=+-是同解方程，求a 的值；（3）在（2）的条件下，a 、b 在数轴上对应的点在原点的两侧，且到原点的距离相等，c 是倒数等于本身的数，求2005()a b c ++的值.第四章综合测试答案解析一、1.【答案】C【解析】A .利用等式性质1，两边都减去3，得到33a b -=-，所以A 成立；B .利用等式性质2，两边都除以3-，得到33a b=--，所以B 成立；C .因为x 必须不为0，所以C 不成立；D .利用等式性质2，两边都乘x ，得到22x x =，所以D 成立；故选C .2.【答案】A【解析】3x k =-Q ，2y k =+，325x y k k \+=-++=.故选：A .3.【答案】C【解析】解：A .20x x +=是方程，x 是未知数，式子又是等式，故本选项不符合题意；B .0x y +=是方程，x 、y 是未知数，式子又是等式，故本选项不符合题意；C .1x x+是分式，不是等式，故本选项符合题意；D .0x =是方程，x 是未知数，式子又是等式，故本选项不符合题意；故选：C .4.【答案】D【解析】等式两边都加7得：327x x =+，等式两边都减2x 得：327x x -=.故选D .5.【答案】D【解析】A .若x y =，根据等式的性质1，两边同时加5可得55x y +=+，故正确；B .若(0)x ya a a=¹，根据等式的性质2，两边同时乘以(0)a a ¹可得x y =，故正确；C .若33x y -=-，根据等式的性质2，两边同时除以3-可得x y =，故正确；D .若mx my =，根据等式的性质2，两边同时除以m ，(0)m ¹，才可得x y =，缺少条件，错误.故选D .6.【答案】C【解析】解：设这种储蓄的年利率为x ，由题意得500050002(120%)5176x +´´-=，即50005000280%5176x +´´=.故答案为：C .7.【答案】D【解析】A .不含有未知数，是等式，不是方程，故选项错误；B .是二元一次方程，故选项错误；C .未知数的最高次数是2次，不是一元一次方程，故选项错误；D .符合一元一次方程的定义，故选项正确.故选D .8.【答案】D【解析】当0c =时，0ac bc ==，但a 不一定等于b ，故D 错误.故答案为：D .二、9.【答案】(120%)0.9270x +´=【解析】解：标价为(120%)x ´+，\可列方程为：(120%)0.9270x +´=.10.【答案】4-【解析】解：等式的两边同时加1得，1131x --+=+，即4x -=，等式的两边同时除以1-得，4x =-.故答案为：4-.11.【答案】1-【解析】解：Q 该组数列满足“从第三个数起，前两个数依次为a 、b ，紧随其后的数就是2a b -”，2131x \=´-=-.故答案为：1-.12.【答案】6-【解析】解：Q 代数式7y -与21y -的值相等，7=21y y \--，移项、合并同类项，可得：=6y -.故答案为：6-.13.【答案】13-【解析】解：把1x =-代入方程231x a -=-得：231a --=-，解得：13a =-，故答案为：13-.14.【答案】1【解析】解：根据题意得：21580x x ++-=，移项合并得：77x =，解得：1x =，故答案为：1.15.【答案】32【解析】由式子1x -与式子214x -的值相等，得2114x x --=，去分母得：4421x x -=-解得：32x =.16.【答案】360x -=【解析】解：由题意可知：3a =，2x =.则将a 与x 的值代入0ax b +=中得：320b ´+=，解得：6b =-，所以，该一元一次方程为：360x -=.故答案为：360x -=.17.【答案】76-【解析】解： 3 x =-Q 是方程(21)40k x +-=的解，(2k 1)(3)40\+´--=，解得：76k =-.故答案为：76-.三、18.【答案】（1）解：去分母得：625646x x x --=-+，移项合并得：817x =，解得：178x =.（2）解：方程整理得：510223x x ---=，移项合并得：315x =，解得：5x =.【解析】（1）方程去分母，去括号，移项合并，把未知数系数化为1，即可求出解.（2）方程整理后，去分母，去括号，移项合并，把未知数系数化为1，即可求出解.19.【答案】（1）移项合并得：416x =，解得：4x =.（2）去括号得：3621x x x -=-+，移项合并得：47x =，解得：74x =.（3）去分母得：3(1)46x x -=+，去括号得：3346x x -=+，解得：9x =-.【解析】（1）方程移项合并，把x 系数化为1，即可求出解.（2）方程去括号，移项合并，把x 系数化为1，即可求出解.（3）方程去分母，去括号，移项合并，把x 系数化为1，即可求出解.20.【答案】解：方程两边都乘2得：31222x x -+=+，移项得：32212x x -=+-，合并同类项得：1x =.【解析】按照去分母，移项，合并的计算过程计算即可.四、21.【答案】（1）解：方程两边同时乘以10得：2(32)53410x x -=´-´，去括号得：641540x x -=-，移项得：615440x x -=-，合并同类项得：936x -=-，系数化为1得：4x =.（2）解：4x =Q 是方程383()2a x a a +=+-的解，383(4)2a a a \+=+-，解得：2a =.（3）解：2a =Q ，2b \=-，又c Q 是倒数等于本身的数，1c \=±，当1c =时，20052005()(221)1a b c \++=-+=；当1c =-时，20052005()(221)1a b c \++=--=-；综上所述：2005()a b c ++的值为1±.【解析】（1）根据解一元一次方程的步骤：去分母——去括号——移项——合并同类项——系数化为1.（2）将4x =代入方程383()2a x a a +=+-解得2a =.（3）根据题意可得2a =，2b =-，1c =±，再分情况求得代数式的值即可.。

人教版高中地理必修第一册第四章综合测试试卷含答-案答案在前2

第四章综合测试答案解析一、1.【答案】B【解析】由图中信息可知，该地区发育有大量的喀斯特地貌——溶洞、地下河等，该种地貌景观主要分布在我国的云贵高原地区。

2.【答案】A【解析】溶洞、地下河等是流水侵蚀作用形成的。

3.【答案】D【解析】考查内力和外力的作用顺序。

因为①和②处有缺口，所以该地貌的形成必先内力作用形成松软的岩石层，之后地表流水下渗侵蚀形成了上层洞穴，然后下渗的流水一边继续下蚀到下层洞穴，同时洞穴中开始形成石钟乳和石笋。

所以四者的顺序应该是④①②或者④①③。

故选D 项。

4.【答案】C【解析】考查喀斯特地貌的特征。

喀斯特地貌区石灰岩广布，流水侵蚀作用强烈，水土流失严重，多地下暗河，地表水贫乏。

故选C 项。

5.【答案】D【解祈】本题考查外力作用与地貌。

①风蚀蘑菇——风力侵蚀作用；②冲积扇——流水堆积作用；③沙丘——风力堆积作用；④瀑布——流水侵蚀作用。

6.【答案】C【解析】本题考查外力作用与地貌的分布。

①和③地貌，都是风力作用形成的，多见于我国西北内陆地区，A 项错误。

我国青藏高原海拔高，周边地区多大山，④地貌可见，但③地貌少见，B 项错误。

根据③中新月形沙丘可以判断风向，沙丘的缓坡是迎风坡，C 项正确。

②为冲积扇，颗粒大的先沉积，颗粒小的后沉积，②中沉积物颗粒大小分布有规律性，D 项错误。

7.【答案】C【解析】古代采玉的主要方法之一是在河床拣玉，新疆深居内陆，河水主要是高山的冰雪融水补给，夏季河水流量大，不宜采玉；冬季气温低，易涨高，不利于采玉；春季高山部分积雪融化，河水增加，不利于采玉；秋季，高山冰雪融水减少，河床裸露，是采玉最佳季节。

8.【答案】B【解析】由于古代采玉的主要方法之一是在河水较少时在河床上拣玉，玉石颗粒较大较重，N 河段处于河流出山口地段，流速变缓，有利于玉石沉积；H 和R 河段海拔高，落差大，水流急，多是大块石头，较少见玉；M 河段在河流下游，多是细小泥沙沉积。

9.【答案】A【解析】本题组考查影响聚落选址的因素，考查外力作用及其地貌形态。

湘教版初中地理七年级上册第四章综合测试试卷含答案-答案在前

第四章综合测试答案解析一、1.【答案】（1）D（2）B【解析】（1）日常生活中，我们应根据实际需要选择合适的地图。

游客进入世园会参观，为了更好地游览各个景点，应该选择世园会游览图。

故答案为：D。

（2）读图可知，该日北京的天气状况是中雨转多云，西北风四级，气温日较差29−22 =7 ℃，污染指数大于50 小于100，空气质量良。

故答案为：B。

2.【答案】（1）D（2）C【解析】（1）由图示天气符号可知，40°N 附近的天气状况是西北风六级，有沙尘暴。

依据题意，故答案为：D。

（2）如图可知，30°N 附近是中雨天气，因此生活在30°N 附近的人们，当日出行应带好雨具。

故答案为：C。

3.【答案】A【解析】喜马拉雅山由于海拔高，气温低，山顶终年白雪皑皑。

即最主要的影响因素是地形。

故A 符合题意。

4.【答案】D【解析】读图可知，图中A 是阴天，B 是雷阵雨，C 是多云，D 是沙尘暴。

重庆地处我国西南部，位于我国的湿润地区。

在重庆发生概率较小的天气是沙尘暴，沙尘暴天气是我国西北地区和华北北部地区出现的强灾害性天气。

5.【答案】B【解析】读图可知，该图示4 到9 月降水超过100 mm，降水较多，故A 正确。

该地最低气温在0°C 以上，位于亚热带地区，位于南方地区，故B 错误。

1、2 月份气温在0°C 以上，该地河流冬季无结冰现象；故C正确。

该地气候特点为夏季高温多雨，冬季温和少雨；为亚热带季风气候；故D 正确。

6.【答案】（1）A（2）B【解析】（1）2019 年5 月4 日这一天，地球是运行在A 表示的春分日（即3 月21 日前后）与B 表示的夏至日（即6 月22 日前后）之间，故答案为：A。

（2）春分日这一天，太阳直射在赤道上，故A 错误。

夏至日这一天，太阳直射在北回归线线，是北半球各地白昼时间最长的一天，故B 正确。

秋分日这一天，是我国北方地区秋季的开始，是落叶的季节，故C 错误。

《管理会计》第四章测试试卷及答案

《管理会计》第四章测试试卷及答案一、单选题（共 15 题，每题 2 分）1. 下列各项中，属于生产决策主要方法的是（）。

A. 差量分析法B. 本量利分析法C. 边际贡献分析法D. 以上都是2. 在亏损产品决策中，只要亏损产品提供的（）大于零，就应该继续生产。

A. 边际贡献B. 销售收入C. 固定成本D. 净利润3. 下列决策方法中，能够直接揭示中选的方案比放弃的方案多获得的利润或少发生损失的方法是（）。

A. 单位资源贡献边际分析法B. 贡献边际总额分析法C. 差别损益分析法D. 相关损益分析法4. 剩余生产能力无法转移时，亏损产品满足（）就不应停产。

A. 单价大于单位变动成本B. 单位贡献边际大于零C. 边际贡献大于零D. 以上都对5. 下列关于零部件自制或外购决策的说法中，错误的是（）。

A. 自制零部件的单位变动成本低于外购单价时，应选择自制B. 自制零部件的单位变动成本高于外购单价时，应选择外购C. 如果剩余生产能力可以用于生产其他产品，那么就需要考虑机会成本D. 一般而言，零部件的自制或外购决策与固定成本无关6. 在新产品开发的品种决策中，如果方案涉及到追加专属成本，则下列方法中不宜采用的是（）。

A. 单位资源贡献边际分析法B. 贡献边际总额分析法C. 差别损益分析法D. 相关损益分析法7. 某企业生产 A、B、C 三种产品，其中 C 产品为亏损产品。

C 产品的销售收入为 2000 元，变动成本为 1500 元，固定成本为 600 元。

则 C 产品（）。

A. 边际贡献为 500 元B. 边际贡献为 -100 元C. 应停产D. 不应停产8. 下列各项中，属于是否增产决策的相关成本的是（）。

A. 原有固定成本B. 新增专属成本C. 不可避免成本D. 沉没成本9. 已知某企业有剩余生产能力 2000 小时，生产 A 产品，单位产品耗费工时 4 小时，正常单位售价 20 元，单位变动成本 12 元，现有客户追加订货 500 件，单价 15 元。

浙科版高中生物必修1分子与细胞第四章综合测试试卷含答案-答案在前(2)

第四章综合测试答案解析一、1.【答案】C【解析】糖类分子都是由C、H、O 组成的，A 正确；淀粉、糖原、纤维素的基本单位都是葡萄糖，故是由葡萄糖聚合形成的多糖，B 正确；核糖不能给生物体的生命活动提供能量，C 错误；食物中的糖类主要是淀粉，需在消化道中消化后才能被吸收，D 正确。

2.【答案】C【解析】膜由蛋白质——脂质——蛋白质三层结构组成是膜的静态结构的描述，而不是流动镶嵌模型的描述，A 错误；磷脂双分子层的亲水端朝向外侧，疏水端朝向内侧，B 错误；构成膜的基本骨架是磷脂双分子层，C 正确；蛋白质分子有的镶嵌在磷脂双分子层表面，有的部分或全部嵌入磷脂双分子层中，有的横跨整个磷脂双分子层，D 错误。

3.【答案】B【解析】高尔基体膜不能合成ATP，A 错误；叶绿体类囊体膜、线粒体内膜都能合成ATP，B 正确；叶绿体内膜不能合成ATP，C 错误；溶酶体膜、叶绿体外膜都不能合成ATP，D 错误。

4.【答案】B【解析】细胞外液中甘油进入组织细胞的方式为扩散，其速度取决于组织细胞内外甘油的浓度差，B 正确；细胞外液中甘油进入组织细胞的方式为扩散，不需要能量，也不需要载体蛋白，不能体现细胞膜的选择透过性，ACD 错误。

5.【答案】C【解析】植物长期处于黑暗中时，光合作用无法进行，故②③④⑥均无法进行，A 错误；晴朗上午10 点植物光合作用大于呼吸作用，理论上无①的释放，B 错误；晴朗夏天中午因为气温过高，气孔关闭，因此光合作用会减弱，而呼吸作用不减弱，净光合作用速率会降低，C 正确；两种细胞器都能产生ATP，但叶绿体产生的ATP 不能从叶绿体运出，D 错误。

6.【答案】A【解析】蓝鲸和蜂鸟的同类器官或组织的细胞大小一般无明显差异，二者大小的不同主要取决于构成生物体的细胞的数量的多少。

7.【答案】A【解析】有丝分裂是真核细胞增殖的主要方式，但不是唯一方式，真核细胞还可以通过减数分裂和无丝分裂方式增殖，A 错误；有丝分裂能将亲代细胞的染色体经过复制以后，精确地平均分配到两个子细胞中去，因此可以维持细胞遗传的稳定性，B 正确；有丝分裂能产生新细胞，使生物体生长，C 正确；有丝分裂产生新细胞，替换死亡的细胞，D 正确。

湘教版初中地理七年级上册第四章综合测试试卷含答案-答案在前(1)

第四章综合测试答案解析一、1.【答案】C【解析】本题考查天气和气候的区别。

天气时刻在变化，气候比较稳定，变化不大。

选项C“今天最高气温32℃”符合时刻变化的特点，为描述天气的语句。

2.【答案】D【解析】本题考查天气和气候的区别。

天气指某个地方短时间内的大气状况，特点是多变；气候指一个地方多年的天气平均状况，具有稳定性。

由此可以判断③冬冷夏热④四季如春表示的是气候；①风雨交加②风和日丽表示的是天气。

3.【答案】B【解析】本题考查天气符号和天气变化等内容。

根据题干叙述“16 日夜间到17 日，大部分地区阴有小雪”，首先排除选项C 和D。

小雪的天气符号是一个雪花。

4.【答案】B【解析】本题考查天气对人类的影响。

东汉末年的诸葛亮借助东南风火烧曹营，取得赤壁之战的胜利。

5.【答案】A【解析】本题考查对卫星云图的判读。

卫星云图中，绿色表示陆地。

在天气预报的卫星云图中，长江中下游地区为绿色，说明该地区没有云层覆盖，天气状况应为晴天。

6.【答案】D【解析】本题考查天气与气候方面的知识。

气候是大气物理特征的长期平均状态，比较稳定，A 项、B 项都不正确；天气是多变的，但是短时间内的天气是可以预测的，C 项不正确；为了预防气象灾害，应建立对极端天气的预警和应急防范机制，D 项正确。

7.【答案】D【解析】本题主要考查学生对常见天气符号的识记情况。

选项A 为冰雹，选项B 为阴天，选项C 为多云，选项D 为雷雨。

需要关掉家用电器电源的天气是D。

8.【答案】C初中地理七年级上册1/ 6【解析】本题考查气温的年变化。

由于海陆的热力差异，南半球大陆月平均气温最高值出现在1 月，而南半球海洋月平均气温最高值出现在2 月。

9.【答案】A【解析】本题考查气温的日变化。

“早穿皮袄午穿纱”，说明吐鲁番盆地早晨寒冷，中午炎热，即气温日较差大。

10.【答案】D【解析】本题考查空气污染指数与空气质量的对应关系。

空气污染指数越大，空气质量越差。

人教版高中地理必修第一册第四章综合测试试卷含答-案答案在前1

第四章综合测试答案解析一、1.【答案】D【解析】河流形成的早期，河岸比较平直，此时期的河流侧蚀比较明显。

河流水在侧蚀过程中可能遇到河流两岸岩石软硬不同，较软的一岸侵蚀严重，逐渐形成凹岸，另一岸为凸岸。

此后河流凹岸不断遭侵蚀，河流越来越弯曲（河道向凹岸一侧不断弯曲），河流弯曲到很大的程度后，通过自然裁弯取直或人工裁弯取直，废弃的河道形成牛轭湖。

故选D。

2.【答案】C【解析】根据图示通过人工“裁弯取直”，能加快水流速度，减少泥沙淤积，缩短航运里程。

能够减轻洪涝灾害，但不能避免洪涝灾害。

3.【答案】C4.【答案】C【解析】由图中经纬度与地理信息可知，此处为黄河三角洲，为黄河泥沙在入海口处堆积而成，河口附近陆地面积的增加来自泥沙的不断堆积，由于中、上游植被保护使水土流失减弱，黄河输沙量减少，加之近年来黄河断流等导致三角洲面积增速减慢。

5.【答案】C【解析】图中有沙丘、海滩、海积与河积物、三角洲，都属于堆积地貌，没有侵蚀海岸，排除海蚀崖；风蚀蘑菇主要分布在干旱、半干旱区。

6.【答案】A【解析】海岸沙丘是海滩物质受风力作用形成的风积地貌；三角洲是流水堆积作用形成的。

7.【答案】D【解析】冲积扇和洪积平原发育在山前，多在河流上游；河漫滩平原一般在中下游地区，河流在凸岸堆积，河床宽广。

三角洲一般发育在河流下游入海口处。

本题叙述位于河流中游地区。

故选D。

8.【答案】C【解析】该沙丘位于雅鲁藏布江中游强风口地段，秋末至春末期间劲风如飓，该沙丘前后河床上因枯水期而露头的河沙，经年复一年地吹送、搬运并堆积，便形成了这一特殊的地貌景观。

沙丘形成主要受风力影响，它的迎风面沙粒在顶部附近堆积，背风坡形成较陡峭的滑落面，丘体两坡不对称，迎风坡凸出而平缓，背风坡凹入而较陡。

故选C。

9.【答案】C【解析】京张铁路八达岭段地势陡、坡度大，为了减小坡度，詹天佑设计出用“长度”换“高度”的“人”字形铁路。

10.【答案】B【解析】“人”字形铁路的设计可以将线路的坡度降低，缩短了隧道开挖长度，减少了工程建设费用，降低了施工的强度和难度。

北师大版初中数学七年级上册第四章综合测试试卷-含答案02

第四章综合测试一、选择题（本大题共12小题，共36分，每小题只有一个正确选项）1.下列说法正确的是（）（1）线段AB 与线段BA 是同一条线段；（2）射线OA 与射线AO 是同一条射线；（3）直线AB 与直线BA 是同一条直线；（4）射线AB 与射线BA 是同一条射线.A .（1）（2）（3）（4）B .（1）（2）（3）C .（1）（3）D .（2）（3）2.下列说法，正确的是（）A .过两点有且只有一条直线B .连接两点的线段叫作两点的距离C .两点之间直线最短D .若AB BC =，则B 是AC 的中点3.如图所示，AB CD =，则AC 与BD 的大小关系是（）A .AC BD ＞B .AC BD ＜ C .AC BD = D .不能确定4.学校电影院公园在平面图上对应的点分别是A ，B ，C ，电影院在学校的正东方向，公园在学校的南偏西25︒方向，那么平面图上的CAB ∠=（）A .115︒B .125︒C .25︒D .65︒5.如图，将长方形ABCD 沿AE 折叠，使点D 落在BC 边上的点F 处，若60BAF ∠=︒，则DAE ∠=（）A .15︒B .30︒C .45︒D .60︒6.某一个顶点与和它不相邻的其他各顶点连接，可将多边形分成七个三角形，则这个多边形是（）A .六边形B .七边形C .八边形D .九边形7.如图所示，12∠∠＋＝（）A .60︒B .90︒C .110︒D .180︒8.如图，OB 是AOC ∠的平分线，OD 是COE ∠的平分线，如果50AOB ∠=︒，60COE ∠︒＝，则下列结论错误的是（）A .110AOE ︒∠=B .80BOD ∠=︒C .BOC 50︒∠=D .DOE 30︒∠=9.下列属于正n 边形的特征的有（）①各边相等；②各个内角相等；③各条对角线都相等；④从一个顶点可以引(n 2)-条对角线；⑤从一个顶点引出的对角线将n 边形分成面积相等的(n 2)-个三角形.A .2个B .3个C .4个D .5个10.下列说法，正确的是（）A .若ac bc =，则a b =B .钟表上的时间是9点40分，此时时针与分针所成的夹角是50︒C .一个圆被三条半径分成面积比2:3:4的三个扇形，则最小扇形的圆心角为90︒D .3°°'0.153015=11.如图，90AOB COD ∠=∠=︒，58COB ∠=︒，则DOA ∠的度数是（）A .102︒B .112︒C .122︒D .142︒12.如图，将两块三角尺AOB 与COD 的直角顶点O 重合在一起，若4AOD BOC ∠=∠，OE 为BOC ∠的平分线，则DOE ∠的度数为（）A .36︒B .45︒C .60︒D .72︒二、填空题（本大题共6小题，每题4分，共24分）13.如图，1AB BC CD ===，则图中所有线段长度之和为________.14.已知从十边形的一个顶点出发，可以引m 条对角线，这些对角线可以把这个十边形分成n 个三角形，则m n +=________.15.为了解深圳市民对“垃圾分类知识”的知晓程度，某数学学习兴趣小组对市民进行随机抽样的问卷调查，调查结果分为“A 非常了解”、“B 了解”、“C 基本了解”、“D 不太了解”四个等级进行统计，并将统计结果绘制成了如下的统计图，请根据图中的信息.在图中的扇形统计图中，表示“C 基本了解”所在扇形的圆心角度数为________度；16.如图，C 岛在A 岛的北偏东60°方向，C 岛在B 岛的北偏西50°方向，从C 岛看A ，B 两岛的视角ACB ∠是________度.17.时钟表面3时30分时，时针与分针的夹角的度数是________；8时20分时，时针和分针的夹角的度数是________.18．如图，直线AB ，CD 相交于点O ，且3DOE COE ∠=∠，90EOB ︒∠=，则AOD ∠的度数________.三、解答题（共7小题共60分）19.（6分）按要求作图：如图，在同一平面内有四个点A 、B 、C 、D ①画射线CD ；②画直线AD ；③连结AB ；④直线BD 与直线AC 相交于点O .20.（6分）计算：（1）153********'''''26'︒+︒；（2）903''57''2144'︒︒-；（3）3315'165︒"⨯；21.（8分）如图，76°AOB ∠=，OC 为AOB ∠内部一条射线，OM ，ON 分别平分BOC ∠，AOC ∠，求MON ∠的大小.22.（8分）线段，角，三角形和圆都是几何研究的基本图形，请用这些图形设计表现客观事物的图案，每幅图案可以由一种图形组成，也可以由两种或三种图形组成，但总数不得超过三个，并且为每幅图案命名，命名要求与图案相符，不少于两幅（如图）.23.（8分）王老师到市场买菜，发现如果把10千克的菜放到秤上，指标盘上的指针转了180︒，第二天王老师就给同学们出了两个问题：（1）如果把0.6千克的菜放在秤上，指针转过多少角度？（2）如果指针转712︒'了，这些菜有多少千克？24.（12分）钟面角是指时钟的时针与分针所成的角.如图，在钟面上，点O 为钟面的圆心，图中的圆我们称之为钟面圆.为便于研究，我们规定：钟面圆的半径OA 表示时针，半径OB 表示分针，它们所成的钟面角为AOB ∠；本题中所提到的角都不小于0︒，且不大于180︒，本题中所指的时刻都介于0点整到12点整之间.（1）时针每分钟转动的角度为________°，分针每分钟转动的角度为________°；（2）8点整，钟面角120AOB ∠︒＝，钟面角与此相等的整点还有：________；（3）如图，设半径OC 指向12点方向，在图中画出6点15分时半径OA ，OB 的大概位置，并求出此时AOB ∠的度数.25.（12分）如图，点C 在线段AB 上，8 cm AC =， 6 cm CB =，点M 、N 分别是AC 、BC 的中点.（1）求线段MN 的长；（2）若C 为线段AB 上任一点，满足 cm AC CB a +=，其它条件不变，你能猜想MN 的长度吗？并说明理由；（3）若C 在线段AB 的延长线上，且满足 cm AC BC b -=，M 、N 分别为AC 、BC 的中点，你能猜想MN 的长度吗？请画出图形，写出你的结论，并说明理由；（4）你能用一句简洁的话，描述你发现的结论吗？初中数学七年级上册 1 / 2第四章综合测试答案一、1.【答案】C2.【答案】A3.【答案】C4.【答案】A5.【答案】A6.【答案】D7.【答案】B8.【答案】A9.【答案】A10.【答案】B11.【答案】C12.【答案】D13.【答案】1014.【答案】14.1515.【答案】15.7216.【答案】16.11017.【答案】17.75︒ 130︒18.【答案】18.135︒19.【答案】如图所示：20.【答案】解：（1）18010''︒（2）3238'19''︒（3）16616'20''︒21.【答案】解：因为OM ，ON 分别平分BOC ∠，AOC ∠，所以1MOC BOC 2∠=∠，1NOC AOC 2∠=∠，所以1111MON MOC NOC BOC AOC (BOC AOC)AOB 2222∠=∠+∠=∠+∠=∠+∠=∠答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

(人教版A版)高中数学必修第一册第四章综合测试试卷03及答案

第四章综合测试一、单项选择题1.式子）A B C .D .2.函数()lg 3f x x x =+-的零点所在区间为（）A .(2,3)B .(3,4)C .(1,2)D .(0,1)3.设lg 2a =，lg3b =，则12log 5=（）A .12a a b-+B .12a a b -+C .12a a b++D .12a a b++4. 已知2log 0.1a =，0.12b =，110.2c =，则a ，b ，c 的大小关系是（）A .a b c ＜＜B .b c a＜＜C .c a b＜＜D .a c b＜＜5.函数1()(0,1)x f x a a a a=-¹＞的图象可能是（）A .B .C .D .6.已知函数2,0()21,0x a x f x x x ì-£=í->î，a R Î，若函数()f x 在R 上有两个零点，则a 的取值范围是（）A .(,1)-¥-B .(,1]-¥-C .[1,0)-D .(0,1]7.若()2()lg 21f x x ax a =-++在区间(,1]-¥上单调递减，则a 的取值范围为（）A .[1,2)B .[1,2]C .[1,)+¥D .[2,)+¥8.已知函数()|lg |f x x =。

若0a b ＜＜，且()()f a f b =，则2a b +的取值范围是（）A .)+¥B .)+¥C .(3,)+¥D .[3,)+¥二、多项选择题9.（多选）下列计算正确的是（）A .=B .21log 3223-=C =D .233log (4)4log 2-=10.对于函数()f x 定义域内的任意()1212,x x x x ¹，当()lg f x x =时，下述结论中正确的是（）A .(0)1f =B .()()()1212f x x f x f x +=×C .()()()1212f x x f x f x -=+D .()()1212f x f x x x --E .()()121222f x f x x x f ++æöç÷èø＜11.下列函数中，能用二分法求函数零点的有（）A .() 3 1f x x =-B .2()21f x x x =-+C .4()log f x x=D .()2x f x e =-12.在一次社会实践活动中，某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量y （单位：千克）与时间x （单位：小时）的函数图像，则以下关于该产品生产状况的正确判断是（）A .在前三小时内，每小时的产量逐步增加B .在前三小时内，每小时的产量逐步减少C .最后一小时内的产量与第三小时内的产量相同D .最后两小时内，该车间没有生产该产品三、填空题13.已知函数6()log (1)f x x =+，则(1)(2)f f +=________，()0f x ＞的解集为________。

浙教版数学九年级上册第四章相似三角形综合测试卷(原卷+答案)

第四章综合测试卷相似三角形班级学号得分姓名一、选择题(本大题有10小题，每小题3分，共30分)1.己知 ab =25,则a +b b的值为( )A 25B 35C 75D 232.如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )A.BC DF=12 B.∠A 的度数∠D 的度数=12C.△ABC的面积△def 的面积= 12 D. △ABC 的周长△def 的周长= 123.如图,在直角坐标系中,△OAB 的顶点为O(0,0),A(4,3),B(3,0).以点O 为位似中心,在第三象限内作与△OAB 的位似比 13的位似图形△OCD,则点C 坐标为( )A. (-1,-1)B.(−43,−1)C.(−1,−43) D. (-2,-1)4. 如图，四边形ABCD 是正方形，E 是CD 的中点，P 是BC 边上的一点，下列条件中，不能推出 △ABP 与△ECP 相似的是( )A.∠APB=∠EPCB. ∠APE=90°C. 点 P 是BC 的中点D. BP: BC=2:35.如图,在△ABC 中,点D 在BC 边上,连结AD,点E 在AC 边上,过点E 作EF∥BC,交 AD 于点F,过点E 作EG∥AB,交BC 于点G,则下列式子一定正确的是( ) A.AE EC=EF CDB.EF CD=EG ABC.AFFD=BG GCD.CG BC=AF AD6. 如图，小明为了测量一凉亭的高度AB(顶端A 到水平地面BD 的距离)，在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE(DE=BC=0.5m ，A ，B ，C 三点共线)，把一面镜子水平放置在平台上的点 G 处，测得CG=15m ，然后沿直线CG 后退到点E 处，这时恰好在镜子里看到凉亭的顶端A ，测得 EG=3m ，小明身高EF=1.6m,则凉亭的高度AB 约为( )A. 8.5mB. 9mC. 9.5mD. 10m7. 在如图所示的象棋盘(各个小正方形的边长均相等)中，根据“马走日”的规则，“马”落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )A. ①处B. ②处C. ③处D. ④处8. 如图,在△ABC 中,AD 平分∠BAC,按如下步骤作图:第一步，分别以点A ，D 为圆心，以大 12AD 的长为半径在AD 两侧作弧，交于两点M ，N第二步,连结MN 分别交AB,AC 于点E,F;第三步,连结DE,DF.若BD=6,AF=4,CD=3,则BE 的长是( )A. 2B. 4C. 6D. 89. 如图,在△ABC 中,点 D 为BC 边上的一点,且AD=AB=2,AD⊥AB,过点 D 作DE⊥AD,DE 交AC 于点E,若DE=1,则△ABC 的面积为( )A. 2B. 4C.25D. 810. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分 AC,点 H 为垂足.设AB=x ，AD=y ，则y 关于x 的函数关系用图象大致可以表示为( )二、填空题(本大题有6小题，每小题4分，共24分)11. 如图所示，点 E 是平行四边形ABCD 的边BC 延长线上一点，连结AE ，交 CD 于点F ，连结BF.写出图中任意一对相似三角形： .12. 已知 a6=b5=c4,且a+b-2c=6,则a 的值为 .13. 如图,在平行四边形ABCD 中,AB=10,AD=6,点E 是AD 的中点,在AB 上取一点F,使△CBF∽△CDE,则 BF 的长是 .14. 如图，在一块斜边长为30cm 的直角三角形木板(Rt△ACB)上截取一个正方形CDEF ，点D 在边BC 上，点E 在斜边AB 上，点F 在边AC 上，若AF ：AC=1：3，则这块木板截取正方形 CDEF 后，剩余部分的面积为 .15.如图①，长、宽均为3，高为8的长方体容器，放置在水平桌面上，里面盛有水，水面高为6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图②是此时的示意图，则图②中水面高度为16. 如图所示，在直角坐标系中有两点A(4，0)，B(0，2).如果点C 在x 轴上，且点 C 与点O 及点A 不重合，当点 C 的坐标为时，使得由点B ，O ，C 构成的三角形与△AOB 相似(至少找出两个符合条件的点).三、解答题(本大题有8小题，共66分)17.(6分)如图,在△ABC中，DE‖BC,EF‖AB,求证：△ADEO△EFC.18. (6分)如图，一块材料的形状是锐角三角形 ABC，边BC=120mm,高AD=80mm,把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上，这个正方形零件的边长是多少?19.(6分)如图,点 P 是⊙O的直径AB 延长线上一点,且AB=4,点 M为A AB上一个动点(不与A，B重合)，射线 PM与⊙O交于点 N(不与M重合).(1)当M在什么位置时，△MAB的面积最大? 并求出这个最大值；(2)求证:△PAN∽△PMB.20. (8 分)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.21. (8分)如图,在△ABC中,点 D,E分别在边AB,AC上,且∠ABE=∠ACD,BE,CD交于点G,连结DE.(1)求证:△AEDO△ABC;(2)如果BE平分∠ABC,求证:DE=CE.22.(10分)如图,在 △ABC 中,点D,E,F 分别在AB,BC,AC 边上, DE‖AC,EF‖AB.(1)求证: △BDEO △EFC.(2)设AF FC=12,①若. BC =12,，求线段BE 的长；②若△EFC 的面积是20,求△ABC 的面积.23.(10分)在矩形ABCD 中,AE⊥BD 于点E,点 P 是边AD 上一点.(1)若BP 平分∠ABD,交 AE 于点G,PF⊥BD 于点F,如图①,证明四边形 AGFP 是菱形;(2)如图②,若PE⊥EC,求证:AE·AB=DE·AP;(3)在(2)的条件下,若AB=1,BC=2,求AP 的长.24.(12分)如图,已知 △ABC 是边长为6cm 的等边三角形，动点P ，Q 同时从A ，B 两点出发，分别沿AB,BC 匀速运动,其中点 P 运动的速度是 1cm/s,点 Q 运动的速度是2cm/s,当点 Q 到达点C 时，P ，Q 两点都停止运动.设运动时间为t(s)，解答下列问题：(1) 当 t =2时，判断 △BPQ 的形状，并说明理由；(2)设 △BPQ 的面积为 S (cm²),求S 与t 的函数表达式；(3)如图,作 QR//BA 交AC 于点R,连结PR,当t 为何值时,△APR∽△PRQ?第四章综合测试卷相似三角形1. C2. D3. B4. C5. C6. A7. B8. D9. B 10. D 11. △ADF∽△ECF(答案不唯一)12. 12 13. 1.8 14. 100cm² 15.24516. (-1,0)或(1,0)或(-4,0)(答案不唯一)17. 证明:∵DE∥BC,∴△ADE∽△ABC,∵EF∥AB,∴△EFC∽△ABC,∴△ADE∽△EFC.18. 解：设这个正方形零件的边长为 xmm ，则△AEF 的边EF 上的高AK=(80-x) mm.∵四边形EF-HG是正方形,∴EF∥GH,即 EF∥BC.∴△AEF CABC.∴EF BC=AK AD,即 x 120=80−x 80⋅∴x =48.∴这个正方形零件的边长是48mm.19. (1)解:当点 M 在 AB 的中点处时，△MAB 的面积最大，此时( OM⟂AB,∵OM =12AB =12×4=2,∴S ABM =12AB ⋅OM =12×4×2=4. (2)证明:∵∠PMB=∠PAN,∠P=∠P,∴△PAN∽△PMB.20. 解: ∵BD 为∠ABC 的平分线,∴∠ABD =∠CBD,∵AB∥CD,∴∠D=∠ABD,∴∠D=∠CBD,∴BC=CD.∵BC=4,∴CD=4.∵AB∥ CD,∴ABECDE,∴AB CD=AE CE,∴84=AE CE,∴AE=2CE,∵AC=6=AE+CE,∴AE=4.21. 证明:(1)∵∠ABE=∠ACD,且∠A 是公共角, ∴ABEACD.∴AE AD=AB AC,即AEAB =ADAC ,又∵∠A 是公共角,∴△AED∽△ABC. (2)∵∠ABE=∠ACD,∠BGD=∠CGE,∴△BGD∽ CGE.:DG EG=BG CG,即DG BG=EG CG.又∵∠DGE=∠BGC,∴△DGE∽△BGC.∴∠GBC=∠GDE,∵BE 平分∠ABC,∴∠GBC=∠ABE,∵∠ABE=∠ACD,∴∠GDE=∠ACD.∴DE=CE.22. (1)证明:∵DE∥AC,∴∠BED=∠C.∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.(2)解:①∵EF//AB,∴BE EC=AF FC=12.∵BC = 12,∴BE12−BE =12,∴BE =4.②∵EF∥AB,∴△EFC∽△BAC,∴S△BC= (EC BC)2⋅∴BE EC=12,∴EC BC=23.又∵△EFC 的面积是20, ∴20SABC=(23)2,∴SABC=45,即△ABC 的面积是45.23. (1)证明:∵四边形 ABCD 是矩形,∴∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,∴∠BAE=∠ADE,∵BP 平分∠ABD,∴∠ABG=∠PBD.∵∠AGP=∠BAG+∠ABG,∠APB =∠ADE+∠PBD,∠ABG=∠PBD,∴∠AGP=∠APG,∴AP=AG,∵PA⊥AB,PF⊥BD,BP 平分∠ABD,∴PA=PF,∴PF=AG,∵AE⊥BD,PF⊥BD,∴PF∥AG,∴四边形AGFP 是平行四边形,∵PA=PF,∴四边形AGFP 是菱形.(2)证明:∵AE⊥BD,PE⊥EC,∴∠AED=∠PEC=90°,∴∠AEP=∠DEC,∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,∴∠EAP=∠EDC,∴△AEP∽△DEC,∴DE·AP.(3)解:∵四边形 ABCD 是矩形,∴AD=BC=2,∠BAD=90°,∴BD=√AB²+AD² =5,∵AE ⊥BD,∴S ABD =12⋅BD ⋅AE = 12⋅AB ⋅AD,∴AE =255,∴DE =AD 2−AE 2=455,∵AE ⋅AB =DE ⋅AP,∴ AP =255×1455=12.24. 解:(1)△BPQ 是等边三角形.当t=2时,AP=21 =2( cm),BQ=2×2=4( cm),∴BP=AB-AP=6-2=4( cm),∴BQ=BP,又∵∠B = 60°,∴△BPQ 是等边三角形.(2)如图,过点 Q 作QE⊥AB,垂足为 E,由 QB=2tcm,∠B=60°,∠BEQ=90°,得 QE =3tcm,由AP= tcm,得 PB =(6−t )cm,∴S =12BP ⋅QE = 12×(6−t )×3t =−32t 2+33t.(3)∵QR‖BA,∴∠QRC=∠A=60°,∠RQC=∠B=60°,∴△QRC是等边三角形,∴QR=RC=QC=(6-2t)cm⋅:BE=12BQ=12×2t=t(cm),∴EP=AB−AP−BE=6−t−t=6−2t(cm),∵EP‖QR,EP=QR,∴四边形 EPRQ是平行四边形,∴PR=EQ3tcm.又∵∠PEQ=90°,∴∠APR∠PRQ=90°,∴△APR∽△PRQ,∴∠QPR=∠A=60∘,QRPR=6−2t3t=3,解得t=65.∴当t=65时,△APR∽△PRQ.。

北师大版初中数学七下第四章综合测试试题试卷含答案

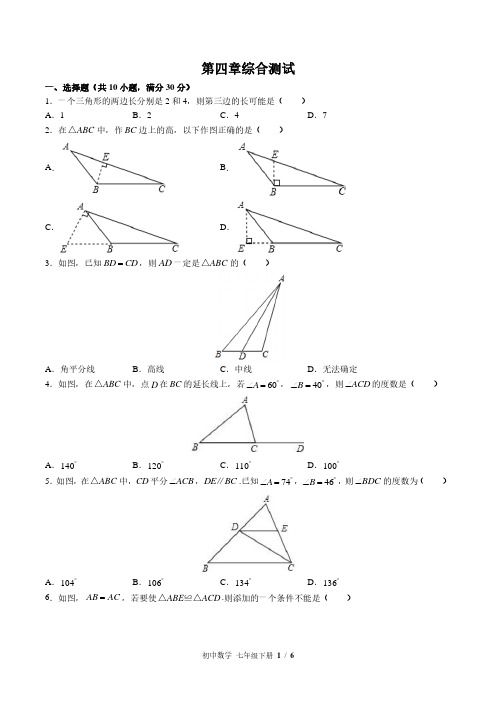
第四章综合测试一、选择题（共10小题，满分30分）1．一个三角形的两边长分别是2和4，则第三边的长可能是（） A ．1B ．2C ．4D ．72．在ABC △中，作BC 边上的高，以下作图正确的是（）A ．B ．C ．D ．3．如图，已知BD CD =，则AD 一定是ABC △的（）A ．角平分线B ．高线C ．中线D ．无法确定4．如图，在ABC △中，点D 在BC 的延长线上，若60A ︒∠=，40B ︒∠=，则ACD ∠的度数是（）A ．140︒B ．120︒C ．110︒D ．100︒5．如图，在ABC △中，CD 平分ACB ∠，DE BC ∥.已知74A ︒∠=，46B ︒∠=，则BDC ∠的度数为（）A ．104︒B ．106︒C ．134︒D ．136︒6．如图，AB AC =，若要使ABE ACD △≌△.则添加的一个条件不能是（）A ．BC ∠=∠ B ．ADC AEB ∠=∠ C ．BD CE = D ．BE CD =7．如图，A B 、两点分别位于一个池塘的两端，小明想用绳子测量A B 、间的距离，如图所示的这种方法，是利用了三角形全等中的（）A ．SSSB ．ASAC ．AASD ．SAS8．小明学习了全等三角形后总结了以下结论： ①全等三角形的形状相同、大小相等； ②全等三角形的对应边相等、对应角相等； ③面积相等的两个三角形是全等图形； ④全等三角形的周长相等. 其中正确的结论个数是（） A ．1B ．2C ．3D ．49．如图，AD 是ABC △的高，BE 是ABC △的角平分线，BE AD ，相交于点F ，已知42BAD ︒∠=，则BFD ∠=（）A ．45︒B ．54︒C ．56︒D ．66︒10．如图，ABC △的三边长均为整数，且周长为22，AM 是边BC 上的中线，ABM △的周长比ACM △的周长大2，则BC 长的可能值有（）个.A ．4B ．5C ．6D ．7二、填空题（共6小题，满分24分）11．下列4个图形中，属于全等的2个图形是________.（填序号）12．如图，某人将一块三角形玻璃打碎成两块，带________块（填序号）能到玻璃店配一块完全一样的玻璃，用到的数学道理是________.13．如图，Rt ABC △中，90C ︒∠=，25B ︒∠=，分别以点A 和点B 为圆心，大于AB 的长为半径作弧，两弧相交于M N 、两点，作直线MN ，交BC 于点D ，连接AD ，则CAD ∠的度数是________.14．如图，在ABC △中，AC BC =，过点A B ，分别作过点C 的直线的垂线AE BF ，.若3AE CF ==，4.5BF =，则EF =________.15．边长为整数、周长为20的三角形的个数为________.16．如图，Rt ABC △中，90BAC ︒∠=，6AB =，3AC =，G 是ABC △重心，则AGC S =△________.三、解答题（共8小题，满分66分）17．如图，在一个三角形的一条边上取四个点，把这些点与这条边所对的顶点连接起来.问图中共有多少个三角形.请你通过与数线段或数角的问题进行类比来思考.18．如图，AB DE =，AC DF =，BE CF =，求证：ABC DEF △≌△.19．王强同学用10块高度都是2cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ︒∠=），点C 在DE 上，点A 和B 分别与木墙的顶端重合. （1）求证：ADC CEB △≌△；（2）求两堵木墙之间的距离.20．如图，已知B D ，在线段AC 上，且AD CB =，BF DE =，90AED CFB ︒∠=∠= 求证：（1）AED CFB △≌△；（2）BE DF ∥.21．如图，已知锐角ABC △，AB BC ＞.（1）尺规作图：求作ABC △的角平分线BD ；（保留作图痕迹，不写作法）（2）点E 在AB 边上，当BE 满足什么条件时？BED C ∠=∠.并说明理由.22．如图，ABC △中，90ACB ︒∠=，D 为AB 上一点，过D 点作AB 垂线，交AC 于E ，交BC 的延长线于F .（1）1∠与B ∠有什么关系？说明理由.（2）若BC BD =，请你探索AB 与FB 的数量关系，并且说明理由.23．如图1，点A B 、分别在射线OM ON 、上运动（不与点O 重合），AC BC 、分别是BAO ∠和ABO ∠的角平分线，BC 延长线交OM 于点G .（1）若60MON ︒∠=，则ACG ∠=________︒；若90MON ︒∠=，则ACG ∠=________︒；（2）若MON n ︒∠=.请求出ACG ∠的度数；（用含n 的代数式表示）（3）如图2，若MON n ︒∠=，过C 作直线与AB 交F .若CF OA ∥时，求BGO ACF ∠−∠的度数.（用含n 的代数式表示）24．如图1所示，在Rt ABC △中，90C ︒∠=，点D 是线段CA 延长线上一点，且AD AB =，点F 是线段AB上一点，连接DF ，以DF 为斜边作等腰Rt DFE △，连接EA ，EA 满足条件EA AB ⊥.（1）若20AEF ︒∠=，50ADE ︒∠=，2BC =，求AB 的长度；（2）求证：AE AF BC =+；（3）如图2，点F 是线段BA 延长线上一点，探究AE AF BC 、、之间的数量关系，并证明你的结论.第四章综合测试答案解析一、 1．【答案】C【解析】解：设第三边的长为x ，由题意得：4242x −+＜＜，26x ＜＜，故选：C. 2．【答案】D【解析】解：BC 边上的高应从点A 向BC 引垂线，只有选项D 符合条件，故选：D. 3．【答案】C【解析】解：由于BD CD =，则点D 是边BC 的中点，所以AD 一定是ABC △的一条中线.故选：C.4．【答案】D【解析】解：ACD ∠是ABC △的一个外角，100ACD A B ︒∴∠=∠+∠=，故选：D. 5．【答案】A【解析】解：74A ︒∠=，46B ︒∠=，60ACB ︒∴∠=，CD 平分ACB ∠，11603022BCD ACD ACB ︒︒∴∠=∠=∠=⨯=，180104BDC B BCD ︒︒∴∠=−∠−∠=，故选：A. 6．【答案】D【解析】解：A 、添加B C ∠=∠可利用ASA 定理判定ABE ACD △≌△，故此选项不合题意；B 、添加ADC AEB ∠=∠可利用AAS 定理判定ABE ACD △≌△，故此选项不合题意；C 、添加BD CE =可得AD AE =，可利用利用SAS 定理判定ABE ACD △≌△，故此选项不合题意；D 、添加BE CD =不能判定ABE ACD △≌△，故此选项符合题意；故选：D.7．【答案】D【解析】解：观察图形发现：AC DC BC BC ACB DCB ==∠=∠，，，所以利用了三角形全等中的SAS ，故选：D. 8．【答案】C【解析】解：①全等三角形的形状相同、大小相等，正确；②全等三角形的对应边相等、对应角相等，正确；③面积相等的两个三角形是全等图形，错误；④全等三角形的周长相等，正确.故选：C. 9．【答案】D 【解析】解：AD 是ABC △的高，90ADB ︒∴∠=，42BAD ︒∠=，18048ABD ADB BAD ︒︒∴∠=−∠−∠=，BE 是ABC △的角平分线， 1242ABF ABD ︒∴∠=∠=，422466BFD BAD ABF ︒︒︒∴∠=∠+∠=+=，故选：D. 10．【答案】A【解析】解：ABC △的周长为22，ABM △的周长比ACM △的周长大2，222BC BC ∴−＜＜，解得211BC ＜＜，又ABC △的三边长均为整数，ABM △的周长比ACM △的周长大2，2222BC AC −−∴=为整数， BC ∴边长为偶数， 46810BC ∴=，，，，故选：A. 二、11．【答案】①③【解析】解：根据全等三角形的判定（SAS ）可知属于全等的2个图形是①③，故答案为：①③. 12．【答案】② ASA【解析】解：第①块只保留了原三角形的一个角和部分边，根据这两块中的任一块不能配一块与原来完全一样的；第②块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA 来配一块一样的玻璃.应带②去.故答案为：②，ASA . 13．【答案】40︒【解析】解：Rt ABC △中，90C ︒∠=，25B ︒∠=，90902565CAB B ︒︒︒︒∴∠=−∠=−=，由作图过程可知：MN 是AB 的垂直平分线，DA DB ∴=， 25DAB B ︒∴∠=∠=，652540CAD CAB DAB ︒︒︒∴∠=∠−∠=−=.答：CAD ∠的度数是40︒. 故答案为：40︒. 14．【答案】7.5【解析】解：过点A B ，分别作过点C 的直线的垂线AE BF ，，90AEC CFB ︒∴∠=∠=，在Rt AEC △和Rt CFB △中，AC BCAE CF =⎧⎨=⎩，Rt Rt AEC CFB HL ∴△≌△（）， 4.5EC BF ∴==，4.537.5EF EC CF ∴=+=+=，故答案为：7.5. 15．【答案】8【解析】解：边长为整数、周长为20的三角形分别是：（9，9，2）（8，8，4）（7，7，6）（6，6，8）（9，6，5）（9，7，4）（9，8，3）（8，7，5），共8个.故答案为：8. 16．【答案】3【解析】解：延长AG 交BC 于E .90BAC ︒∠=，63AB AC ==，，192ABC S AB AC ∴==△， G 是ABC △的重心，2AG GE BE EC ∴==，，19 4.52AEC S ∴=⨯=△，233AGC AEC S S ∴=⨯=△△，故答案为3. 三、17．【答案】解：如图所示，图中三角形的个数有ABC △，ACD △，ADE △，AEF △，AFG △，ABD △，ABE △，ABF △，ABG △ACE △，ACF △，ACG △，ADF △，ADG △，AEG △.18．【答案】解：BE CF =，BE EC CF EC ∴+=+，即BC EF =，在ABC △和DEF △中，AB DE AC DFBC EF =⎧⎪=⎨⎪=⎩（已知）（已知）（已知）， ABC DEF SSS ∴△≌△（）.19．【答案】（1）证明：由题意得：AC BC =，90ACB ︒∠=，AD DE BE DE ⊥⊥，，90ADC CEB ︒∴∠=∠=，9090ACD BCE ACD DAC ︒︒∴∠+∠=∠+∠=，， BCE DAC ∴∠=∠在ADC △和CEB △中ADC CEB DAC BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，ADC CEB AAS ∴△≌△（）；（2）解：由题意得：236cm AD =⨯=，7214cm BE =⨯=，ADC CEB △≌△，6cm EC AD ∴==，14cm DC BE ==， 20cm DE DC CE ∴=+=（），答：两堵木墙之间的距离为20cm .20．【答案】证明（1）90AED CFB ︒∠=∠=，在Rt AED △和Rt CFB △中AD BCDE BF =⎧⎨=⎩， Rt Rt AED CFB HL ∴△≌△（）.（2）AED CFB △≌△，BDE DBF ∴∠=∠，在DBE △和BDF △中DE BFBDE DBF BD DB =⎧⎪∠=∠⎨⎪=⎩，DBE BDF SAS ∴△≌△（），DBE BDF ∴∠=∠， BE DF ∴∥.21．【答案】解：（1）如图，线段BD 即为所求.（2）结论：BE BC =. 理由：BD 平分ABC ∠， EBD CBD ∴∠=∠， BE BC BD BD ==，，BDE BDC SAS ∴△≌△（）， BED C ∴∠=∠.22．【答案】解：（1）1∠与B ∠相等，理由：ABC △中，90ACB ︒∠=，190F ︒∴∠+∠=，FD AB ⊥，90B F ︒∴∠+∠=，1B ∴∠=∠；（2）若BC BD =，AB 与FB 相等，理由：ABC △中，90ACB ︒∠=，DF AB ⊥，90ACB FDB ︒∴∠=∠=，在ACB △和FDB △中，B B ACB FDB BC BD ∠=∠∠=∠=⎧⎪⎨⎪⎩，ACB FDB AAS ∴△≌△（），AB FB ∴=.23．【答案】（1）60 45（2）在AOB △中，180180OBA OAB AOB n ︒︒︒∠+∠=−∠=−，OBA OAB ∠∠、的平分线交于点C ，1118022ABC BAC OBA OAB n ︒︒∴∠+∠=∠+∠=−（）（），即1902ABC BAC n ︒︒∠+∠=−， 11180180909022ACB ABC BAC n n ︒︒︒︒︒︒∴∠=−∠+∠=−−=+（）（）， 1809090ACG n n ︒︒︒︒︒∴∠=−+=−（）；（3）AC BC 、分别是BAO ∠和ABO ∠的角平分线，1122ABC ABO BAC OAC BAO ∴∠=∠∠=∠=∠，， CF AO ∥，ACF CAG ∴∠=∠，BGO BAG ABG ∠=∠+∠，°12902BGO ACF BAG ABG ACF BAC ABG BAC ABG BAC n ︒∴∠−∠=∠+∠−∠=∠+∠−∠=∠+∠=−. 【解析】解：（1）60MON ︒∠=，120OBA OAB ︒∴∠+∠=，OBA OAB ∠∠、的平分线交于点C ，1120602ABC BAC ︒︒∴∠+∠=⨯=， 18060120ACB ︒︒︒∴∠=−=，60ACG ︒∴∠=；90MON ︒∠=，90OBA OAB ︒∴∠+∠=，OBA OAB ∠∠、的平分线交于点C ，195452ABC BAC ︒︒∴∠+∠=⨯=， 18045135ACB ︒︒︒∴∠=−=；45ACG ︒∴∠=；故答案为：60，45.24．【答案】解：（1）在等腰直角三角形DEF 中，°90DEF ∠=， 120︒∠=，2170DEF ︒∴∠∠−∠=＝，23180EDA ︒∠+∠+∠=，360︒∴∠=，EA AB ⊥，°90EAB ∴∠=，3180EAB A ︒∠+∠+∠=，430︒∴∠=，90C ︒∠=，24AB BC ∴==；（2）如图1，过D 作DM AE ⊥于M ，在DEM △中，2590︒∠+∠=， 2190︒∠+∠=，15∴∠=∠，DE FE =，在DEM △与EFA △中，51DME EAF DE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩， DEM EFA ∴△≌△，AF EM ∴=，490B ︒∠+∠=，34180EAB ︒∠+∠+∠=，3490︒∴∠+∠=，3B ∴∠=∠，在DAM △与ABC △中，3B DMA C AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，DAM ABC ∴△≌△，BC AM ∴=，AE EM AM AF BC ∴=+=+；（3）如图2，过D 作DM AE ⊥交AE 的延长线于M ， 90C ︒∠=，190B ︒∴∠+∠=，°°2118090MAB MAB ∠+∠+∠=∠=，，21902B ︒∴∠+∠=∠=∠，，在ADM △与BAC △中，2M CB AD AB∠=∠∠=∠=⎧⎪⎨⎪⎩，ADM BAC ∴△≌△，BC AM ∴=，°90EF DE DEF =∠=，，34180DEF ︒∠+∠+∠=，°3490∴∠+∠=，°3590∠+∠=，45∴∠=∠，在MED △与AFE △中，54M EAFDE EF∠=∠∠=∠=⎧⎪⎨⎪⎩，MED AFE ∴△≌△，ME AF ∴=，AE AF AE ME AM BC ∴+=+==，即AE AF BC +=.。

(北师大版)初中数学八年级上册第四章综合测试试卷02及答案

第四章综合测试一、选择题（每题3分，共30分）1.下列图象中，表示y 是x 的函数的个数有（）A .1个B .2个C .3个D .4个2.若一次函数()21y k x =-+的函数值y 随x 的增大而增大，则（）A .2k ＜B .2k ＞C .0k ＞D .0k ＜3.一次函数2y x =+的图象与y 轴的交点坐标为（）A .()0,2B .()0,2-C .()2,0D .()2,0-4.将直线23y x =-向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为（）A .24y x =-B .24y x =+C .22y x =+D .22y x =-5.小聪在画一次函数的图象时，当他列表后，发现题中一次函数y x =◆＋◆中的k 和b 看不清了，则（）x 03y2A .2k =，3b =B .23k =-，2b =C .3k =，2b =D .1k =，1b =-6.点()111,P x y ，()222,P x y 是一次函数43y x =-+图象上的两个点，且12x x ＜，则1y 与2y 的大小关系是（）A .12y y ＞B .120y y ＞＞C .12y y ＜D .12y y =7.为了建设社会主义新农村，某市积极推进“村村通客车工程”.张村和王村之间的道路需要进行改造，施工队在工作了一段时间后，因暴雨被迫停工几天，不过施工队随后加快了施工进度，按时完成了两村之间道路的改造.下面能反映该工程尚未改造的道路里程y （km ）与时间x （天）的函数关系的大致图象是（）8.一家电信公司提供两种手机的月通话收费方式供用户选择，其中一种有月租费，另一种无月租费.这两种收费方式的通话费用y （元）与通话时间x （min ）之间的函数关系如图所示.小红根据图象得出下列结论：①l1描述的是无月租费的收费方式；②12描述的是有月租费的收费方式；③当每月的通话时间为500min 时，选择有月租费的收费方式省钱.其中，正确结论的个数是（）第8题图A .0B .1C .2D .39.如图，把直线2y x =-向上平移后得到直线AB ，直线AB 经过点(),m n ，且26m n +=，则直线AB 的解析式是（）第9题图A .23y x =--B .26y x =--C .23y x =-+D .26y x =-+10.（天门）甲、乙两车从A 地出发，匀速驶向B 地.甲车以80km/h 的速度行驶1h 后，乙车才沿相同路线行驶.乙车先到达B 地并停留1h 后，再以原速按原路返回，直至与甲车相遇.在此过程中，两车之间的距离y （km ）与乙车行驶时间x （h ）之间的函数关系如图所示.下列说法：①乙车的速度是120km/h ；②160m =；③点H 的坐标是()7,80；④7.5n =.其中说法正确的是（）第10题图A .①②③B .①②④C .①③④D .①②③④二、填空题（每题3分，共24分）11.已知()3221m y m x -=-是一次函数，则m =________.12.直线21y x =+经过点()0,a ，则a =________.13.已知一次函数()12y m x m =-+-，当m ________时，y 随x 的增大而增大.14.已知直线y kx b =+，若5k b +=-，6kb =，那么该直线不经过第________象限.15.直线2y x b =+与x 轴的交点坐标是()2,0，则关于x 的方程20x b +=的解是________.16.一次函数的图象与直线1y x =-+平行，且过点()8,2，那么此一次函数的表达式为________.17.如图，已知点A 和点B 是直线34y x =上的两点，A 点坐标是32,2æöç÷èø.若5AB =，则点B 的坐标是________.18.直线()1110y k x b k =+＞与()2220y k x b k =+＜相交于点()2,0-，且两直线与y 轴围成的三角形面积为4，那么12b b -=________.三、解答题（19题6分，20，21题每题9分，22～24题每题10分，25题12分，共66分）19.已知一次函数y ax b =+.（1）当点(),P a b 在第二象限时，直线y ax b =+经过哪几个象限？（2）如果0ab ＜，且y 随x 的增大而增大，则函数的图象不经过哪些象限？20.一个正比例函数和一个一次函数，它们的图象都经过点()2,2P -，且一次函数的图象与y 轴相交于点()0,4Q .（1）求出这两个函数的表达式；（2）在同一坐标系中，分别画出这两个函数的图象；（3）直接写出一次函数图象在正比例函数图象下方时x 的取值范围.21.如图，直线23y x =+与x 轴相交于点A ，与y 轴相交于点B .（1）求点A ，B 的坐标；（2）求当2x =-时，y 的值，当10y =时，x 的值；（3）过点B 作直线BP 与x 轴相交于点P ，且使2OP OA =，求ABP △的面积.22.某城市居民用水实行阶梯收费，每户每月用水量如果未超过20t ，按每吨1.9元收费.如果超过20t ，未超过的部分按每吨1.9元收费，超过的部分按每吨2.8元收费.设某户每月用水量为t x ，应收水费为y 元.（1）分别写出每月用水量未超过20t 和超过20t 时，y 与x 之间的函数表达式；（2）若该城市某户5月份水费平均每吨为2.2元，求该户5月份用水多少吨？23.某销售公司推销一种产品，设x （件）是推销产品的数量，y （元）是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示，推销员可以任选一种与公司签订合同，看图解答下列问题：（1）求每种付酬方案y 关于x 的函数表达式；（2）当选择方案一所得报酬高于选择方案二所得报酬时，求x 的取值范围.24.一次函数()0y kx b k =+¹的图象由直线3y x =向下平移得到，且过点()1,2A .（1）求一次函数的解析式；（2）求直线y kx b =+与x 轴的交点B 的坐标；（3）设坐标原点为O ，一条直线过点B ，且与两条坐标轴围成的三角形的面积是12，这条直线与y 轴交于点C ，求直线AC 对应的一次函数的解析式.25.甲、乙两车分别从A ，B 两地同时出发相向而行，并以各自的速度匀速行驶，甲车途经C 地时休息一小时，然后按原速度继续前进到达B 地；乙车从B 地直接到达A 地，如图是甲、乙两车和B 地的距离y （km ）与甲车出发时间x （h ）的函数图象.（1）直接写出a ，m ，n 的值；（2）求出甲车与B 地的距离y （km ）与甲车出发时间x （h ）的函数关系式（写出自变量x 的取值范围）；（3）当两车相距120km 时，乙车行驶了多长时间？第四章综合测试答案一、1.【答案】B 2.【答案】B 3.【答案】A 4.【答案】A 5.【答案】B 6.【答案】A 7.【答案】D 8.【答案】D 9.【答案】D【解析】原直线的2k =-，向上平移后得到了新直线，那么新直线的2k =-.∵直线AB 经过点(),m n ，且26m n +=，∴直线AB 经过点(),62m m -.可设新直线的解析式为12y x b =-+，把点(),62m m -代到12y x b =-+中，可得16b =.∴直线AB 的解析式是26y x =-+.10.【答案】A【解析】根据题意，两车距离为函数，由图象可知两车起始距离为80，从而得到乙车速度，根据图象变化规律和两车运动状态，得到相关未知量.解：由图象可知，乙出发时，甲乙相距80km ，2小时后，乙车追上甲.则说明乙每小时比甲快40km ，则乙的速度为120km/h .①正确；由图象第2-6小时，乙由相遇点到达B ，用时4小时，每小时比甲快40km ，则此时甲乙距离440160km ´=，则160m =，②正确；当乙在B 休息1h 时，甲前进80km ，则H 点坐标为()7,80，③正确；乙返回时，甲乙相距80km ，到两车相遇用时()80120800.4¸+=小时，则610.47.4n =++=，④错误.故选A.二、11.【答案】112.【答案】113.【答案】1＜14.【答案】一15.【答案】2x =16.【答案】10y x =-+17.【答案】96,2æöç÷èø或32,2æö--ç÷èø【解析】由题意可得,3,4A B A B =两点的纵坐标之差两点的横坐标之差，再由222,,AB A B A B =+两点的纵坐标之差两点的横坐标之差，求得4,A B =两点的横坐标之差，,3A B =两点的纵坐标之差.再分两种情况讨论求解即可.18.【答案】4【解析】如图，在ABC △中，BC 为底，AO 为高，且高为2，面积为4，故ABC △的底边4224BC =´¸=.因为点B 的坐标为()10,b ，点C 的坐标为()20,b ，所以12b b -即是BC 的长，为4.三、19.【答案】解：（1）因为点(),P a b 在第二象限，所以0,0a b <>.所以直线y ax b =+经过第一、二、四象限.（2）因为y 随x 的增大而增大，所以0a ＞.又因为0ab ＜，所以0b ＜.所以一次函数y ax b =+的图象不经过第二象限.20.【答案】解：（1）设正比例函数的表达式为1y k x =，则()122k =´-，解得11k =-.所以正比例函数的表达式为y x =-.设一次函数的表达式为2y k x b =+，则()222k b =´-+，4b =，解得4b =，21k =，所以一次函数的表达式为4y x =+.（2）图略.（3）2x -＜.21.【答案】解：（1）当0y =时，230x +=，得32x =-，则3,02A æö-ç÷èø.当0x =时，3y =，则()0,3B .（2）当2x =-时，1y =-；当10y =时，72x =.（3）2OP OA =，3,02A æö-ç÷èø，则点P 的位置有两种情况，点P 在x 轴的正半轴上或点P 在x 轴的负半轴上.当点P 在x 轴负半轴上时，()3,0P -，则ABP △的面积为13933224æö´-´=ç÷èø；当点P 在x 轴的正半轴上时，()3,0P ，则ABP △的面积为132733224æö´´+=ç÷èø.22.【答案】解：（1）当20x ≤时， 1.9y x =；当20x ＞时，()1.92020 2.8 2.818y x x =´+-´=-.（2）因为5月份水费平均为每吨2.2元，月用水量如果未超过20t ，按每吨1.9元收费，所以该户5月份用水量超过了20t .由2.818 2.2x x -=，解得30x =.答：该户5月份用水30t .23.【答案】解：（1）设方案一的解析式为y kx =，把()40,1600代入解析式，可得40k =，故解析式为40y x =；设方案二的解析式为y ax b =+，把()40,1400和()0,600代入解析式，可得20a =，600b =，故解析式为20600y x =+；（2）根据两直线相交可得方程4020600x x =+，解得30x =.根据两函数图象可知，当30x ＞时，选择方案一所得报酬高于选择方案二所得报酬.24.【答案】解：（1）根据题意，得3k =，2k b +=，解得1b =-31y x \=-；（2）在31y x =-中，当0y =时，13x =，∴点B 的坐标为1,03æöç÷èø；（3）设直线AC 的解析式为y mx n =+（其中0m ¹），则点C 的坐标为()0,n ，根据题意得111||232BOC S n ´==△，3n \=，3n \=±.当3n =时，2m n +=，解得1m =-，3y x \=-+；当3n =-时，2m n +=，解得5m =，53y x \=-.∴直线AC 的解析式为3y x =-+或53y x =-.25.【答案】解：（1）∵甲车途经C 地时休息一小时，2.51m \-=， 1.5m \=.乙车的速度为1202a m =，即601.5a=，解得90a =.甲车的速度为3003001201 1.5n -=-，解得 3.5n =；（2）设甲车的y 与x 的函数关系式为y kx b =+.①休息前，0 1.5x ≤≤，函数图象经过点()0,300和()1.5,120，所以300b =，1.5120k b +=，所以120k =-，所以120300y x =-+；②休息时，1.5 2.5x ＜＜，120y =；③休息后，2.5 3.5x ≤≤，函数图象经过点()3.5,0，又由题意可知120k =-，故420b =，所以120420y x =-+.综上，y 与x 的函数关系式为 120300(0 1.5),120(1.5 2.5),120420(2.5 3.5);x x y x x x -+ìï=<<íï-+î…………（3）设当两车相距120km 时，乙车行驶了h x .甲车的速度为()()300120 1.5120km/h -¸=，乙车的速度为()120260km/h ¸=.①若相遇前，则12060300120x x +=-，解得1x =；②若相遇后，则()120160300120x x -+=+，解得3x =.答：当两车相距120km 时，乙车行驶了1h 或3h .。

鲁教版(五四制)八年级数学上册第四章综合测试卷含答案

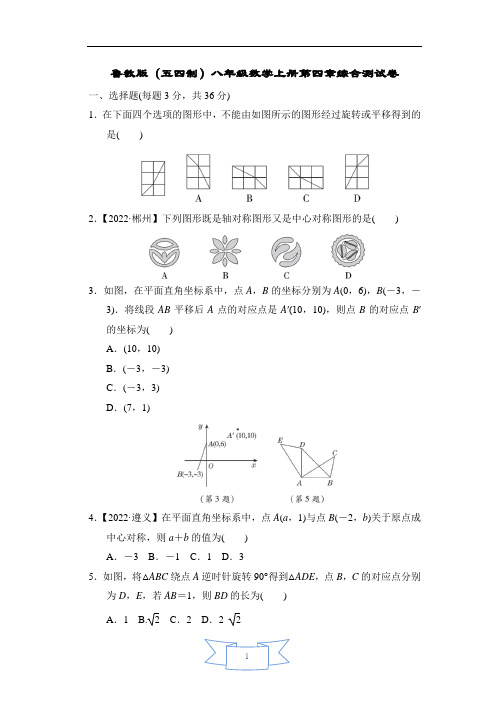
鲁教版（五四制）八年级数学上册第四章综合测试卷一、选择题(每题3分，共36分)1．在下面四个选项的图形中，不能由如图所示的图形经过旋转或平移得到的是()2．【2022·郴州】下列图形既是轴对称图形又是中心对称图形的是()3．如图，在平面直角坐标系中，点A，B的坐标分别为A(0，6)，B(－3，－3)．将线段AB平移后A点的对应点是A′(10，10)，则点B的对应点B′的坐标为()A．(10，10)B．(－3，－3)C．(－3，3)D．(7，1)4．【2022·遵义】在平面直角坐标系中，点A(a，1)与点B(－2，b)关于原点成中心对称，则a＋b的值为()A．－3 B．－1 C．1 D．35．如图，将△ABC绕点A逆时针旋转90°得到△ADE，点B，C的对应点分别为D，E，若AB＝1，则BD的长为()A．1 B. 2 C．2 D．2 26．如图，在平面直角坐标系xOy中，△ABC与△A1B1C1是中心对称图形．则对称中心的坐标是()A．(1，1) B．(1，0) C．(1，－1) D．(1，－2)7．【2023·泰安新泰市月考】如图，△ADE与△CDB关于点D成中心对称，连接AB，以下结论错误的是()A．AD＝CDB．∠C＝∠EC．AE＝CBD．S△ADE＝S△ADB8．如图，△ABC的顶点都在方格线的交点(格点)上，如果将△ABC绕C点按逆时针方向旋转90°，那么点B的对应点B′的坐标是()A．(0，1) B．(0，－1) C．(1，0) D．(－1，0)9. 如图是一块长方形ABCD的场地，长AB＝99 m，宽AD＝41 m，从A，B两处入口的路宽都为1米，两小路汇合处路口宽为2 m，其余部分种植草坪，草坪的面积为()A．3 783 m 2B．3 880 m 2C．3 920 m 2D．4 000 m 210．如图，边长为3的等边三角形ABC沿BC所在直线向右平移，若平移的距离为1，则公共部分△OB′C的面积为()A. 3B.32 3 C．2 3 D．3 311．如图，△ABC是等边三角形，点P在△ABC内，P A＝2，将△P AB绕点A 逆时针旋转得到△P1AC，则P1P的长等于()A．2 B. 3 C.32D．112．【2023·济宁任城区月考】如图，在△ABC中，∠BAC＝120°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD.当点A，D，E在同一条直线上时，下列结论不正确的是()A．∠ADC＝60°B．∠BCE＝60°C．AE平分∠BACD．AE⊥BC二、填空题(每题3分，共18分)13．【母题：教材P98随堂练习T1】如图所示的图案，可以看作是一个四边形(阴影部分)按顺时针方向通过3次旋转得到的，每次旋转的角度是________．14．【2023·德州禹城市期中】如图，在平面直角坐标系中，将点P(2，3)绕原点O顺时针旋转180°得到点P′，则点P′的坐标是________．15．如图，射线AC，BD分别与直线l交于点A，B.现将射线AC沿直线l向右平移过点B，若∠1＝46°，∠2＝72°，则∠3的度数为________．16．如图，射线OM，ON互相垂直，OA＝8，点B位于射线OM的上方，且在线段OA的垂直平分线l上，连接AB，AB＝5.将线段AB绕点O逆时针旋转得到线段A′B′，若点B′恰好落在射线ON上，则点A′到射线ON的距离d＝________．17．如图，在直角坐标系中，点A的坐标是(2，2)，点O的坐标是(0，0)，AO＝AB，将△AOB平移得到△A′O′B′，使得点A′在y轴上．点O′，B′在x 轴上．则点B′的坐标是________．18．一副三角板按如图所示叠放在一起，∠C＝60°，∠OAB＝45°，其中点B，D重合，若固定三角板AOB，将三角板ACD绕着公共顶点A顺时针旋转一周后停止，当旋转角为________时，CD∥AO.三、解答题(23题12分，24题14分，其余每题10分，共66分)19．如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A(－1，4)，B(－3，1)．(1)画出线段AB向右平移4个单位长度后的线段A1B1；(2)画出线段AB绕原点O旋转180°后的线段A2B2.20．【母题：教材P112习题T2】如图，在6×6的网格中已经涂色了三个小正方形，请按下列要求画图．(1)在图①中涂色一个小正方形，使涂色的四个小正方形组成一个轴对称图形．(2)在图②中涂色一个小正方形，使涂色的四个小正方形组成一个中心对称图形．21．如图，△ABC平移后得到△DEF.(1)若∠A＝80°，∠E＝60°，求∠C的度数；(2)若AC＝BC，BC与DF相交于点O，则OD与OB相等吗？说明理由．22．如图，在△ABC中，AF⊥BC于点F.将△ABC绕点A顺时针旋转一定角度得到△ADE，点B的对应点D恰好落在BC边上．(1)若∠B＝50°，求∠DAF的度数；(2)若∠E＝∠CAD，求证：AD＝CD.23．△ABC在平面直角坐标系中如图所示，每个顶点都在格点上．(1)求△ABC的面积；(2)若△ABC中任意一点P(x0，y0)经平移后的对应点为P1(x0＋3，y0＋4)，请画出△ABC平移后得到的△A1B1C1，并写出点A1，B1，C1的坐标；(3)在x轴上是否存在点Q，使以A1，B，Q三点为顶点的三角形的面积为3？若存在，请直接写出点Q的坐标；若不存在，请说明理由．24．已知△ABC是等腰直角三角形，∠ACB＝90°，点D是平面内任意一点，CD绕着点C逆时针旋转90°到CE.(1)如图①，若D为△ABC内一点，求证：AD＝BE；(2)如图②，若D为AB边上一点，AD＝5，BD＝12，求DE的长．答案一、1.A 2.B3．D 【点拨】由点A (0，6)，A ′(10，10)可知平移方式是向右平移10个单位长度，向上平移4个单位长度，∴点B (－3，－3)向右平移10个单位长度，向上平移4个单位长度得到B ′(－3＋10，－3＋4)，即(7，1)． 4．C5．B 【点拨】∵将△ABC 绕点A 逆时针旋转90°得到△ADE ，∴AD ＝AB ，∠BAD ＝90°， ∴△ABD 是等腰直角三角形．由勾股定理，得BD ＝2AB . ∵AB ＝1，∴BD ＝ 2.6．C 【点拨】连接AA 1，CC 1，两线交点即为对称中心． 7．B 【点拨】∵△ADE 与△CDB 关于点D 成中心对称，∴AD ＝CD ，BD ＝ED ，AE ＝CB ，∠E ＝∠CBD ， ∵BD ＝ED ，∴S △ABD ＝S △ADE .8．C 【点拨】如图，可知B ′的坐标为(1，0)．9．B 【点拨】(99－2)×(41－1)＝97×40＝3 880(平方米)，∴种植草坪面积为3 880平方米．10．A 【点拨】如图，过点O 作OH ⊥BC 于点H ，∵△ABC 为等边三角形，∴∠ABC＝∠ACB＝60°，由平移的性质可知BB′＝1，∠A′B′C′＝∠ABC＝60°，∴B′C＝3－1＝2，△OB′C为等边三角形，∴OC＝2，∴OH＝3，∴S△OB′C ＝12×2×3＝ 3.11．A【点拨】∵△ABC是等边三角形，∴AC＝AB，∠CAB＝60°.∵将△P AB绕点A逆时针旋转得到△P1AC，∴AP1＝AP，∠CAP1＝∠BAP，∴∠CAB＝∠CAP＋∠BAP＝∠CAP＋∠CAP1＝60°，即∠P AP1＝60°，∴△APP1是等边三角形，∴P1P＝P A＝2.12．D【点拨】由旋转的性质可知∠EDC＝∠BAC＝120°，∴当点A，D，E在同一条直线上时，∠ADC＝180°－∠EDC＝60°，A正确；由旋转的性质可知△BAC≌△EDC，∴∠BCA＝∠ECD，CA＝CD.又∵∠ADC＝60°，∴△ACD为等边三角形，∴∠ACD＝60°.∵∠BCA＝∠ECD，∴∠BCE＝∠BCD＋∠ECD＝∠BCD＋∠BCA＝∠ACD＝60°，B正确；∵△ACD为等边三角形，∴∠DAC＝60°.∵∠BAC＝120°，∴∠BAE＝∠BAC－∠DAC＝60°，∴∠BAE＝∠DAC，∴AE平分∠BAC，故C正确．二、13.120°【点拨】每次旋转了360°÷3＝120°.14．(－2，－3) 15.62°16.245【点拨】如图，连接OB，过点A作AC⊥OB交OB的延长线于点C.∵l为OA的垂直平分线，∴AD＝12OA＝4，∠ADB＝90°.在Rt△ABD中，BD＝AB2－AD2＝52－42＝3.由旋转可知，点A′到射线ON的距离d＝AC，∵12OB·AC＝12OA·BD，∴AC＝OA·BDOB＝245.17．(2，0)【点拨】∵AO＝AB，点A的横坐标为2，∴OB＝4，点B的坐标为(4，0)，要想让点O′，B′还在x轴上，只能左右平移．∵点A的坐标是(2，2)，移动到y轴上时，坐标变为(0，2)，说明点A向左平移了2个单位长度，即横坐标减2，∴点B也遵循点A的移动规律，则点B′的坐标是(2，0)．18．75°或255°【点拨】如图①，当CD在OA的左侧，CD∥AO时，旋转角为45°＋30°＝75°；如图②，当CD在OA的右侧，CD∥OA时，旋转角为45°＋180°＋30°＝255°.三、19.解：(1)如图，线段A1B1即为所求．(2)如图，线段A2B2即为所求．20．解：(1)如图①所示．(答案不唯一)(2)如图②所示．(答案不唯一)21．解：(1)∵△ABC平移后得到△DEF，∴∠ABC＝∠E＝60°.在△ABC中，∠C＝180°－∠A－∠ABC＝180°－80°－60°＝40°.(2)OD＝OB.理由如下：∵AC＝BC，∴∠A＝∠ABC.由平移的性质得∠A＝∠EDF，∴∠ABC＝∠EDF，∴OD＝OB.22．(1)解：∵将△ABC绕点A顺时针旋转一定角度得到△ADE，∴AD＝AB.∵∠B＝50°，∴∠ADF＝∠B＝50°.∵AF⊥BC，∴在Rt△ADF中，∠DAF＝90°－50°＝40°.(2)证明：∵将△ABC绕点A顺时针旋转一定角度得到△ADE，点B的对应点D恰好落在BC边上．∴∠C＝∠E.又∵∠E＝∠CAD，∴∠C＝∠CAD.∴AD＝CD.23．解：(1)△ABC 的面积＝3×4－12×3×1－12×3×2－12×4×1＝5.5.(2)如图，△A 1B 1C 1即为所作．A 1(2，3)，B 1(5，5)，C 1(1，6)．(3)存在．Q 的坐标为(－1，0)或(5，0)．24．(1)证明：∵△ABC 是等腰直角三角形，∴∠ACB ＝90°，AC ＝BC ，∵CD 绕着点C 逆时针旋转90°到CE ，∴∠DCE ＝90°，CD ＝CE ，∴∠ACB －∠DCB ＝∠DCE －∠DCB ，即∠ACD ＝∠BCE ，在△ACD 和△BCE 中，⎩⎨⎧AC ＝BC ，∠ACD ＝∠BCE ，CD ＝CE ，∴△ACD ≌△BCE (SAS)，∴AD ＝BE .(2)解：∵△ABC 是等腰直角三角形，∴∠A ＝∠ABC ＝45°，∵△ACD ≌△BCE ，∴∠CBE ＝∠A ＝45°，AD ＝BE ，∴∠ABE ＝∠ABC ＋∠CBE ＝90°，在Rt △BDE 中，由勾股定理得BD 2＋BE 2＝DE 2， ∴DE 2＝BD 2＋BE 2＝BD 2＋AD 2＝122＋52＝169， ∴DE ＝13.。

粤沪版物理八年级上册第四章综合测试卷(共27张PPT)

（3）他们同时发现所测得盐水凝固点并不相同，于是对比了双方实验过程，发现烧杯中装水都是200 mL，小明加了1汤匙的盐，而小红加了3汤匙的盐，由此作出猜想：盐水的凝固点与盐水的浓度有关。接着多次实验得出不同浓度盐水的凝固点，数据记录如下表：
盐水浓度 0% 3% 6% 9% 12% 15% 18% 21% 24% 27% 30% 36%
11. 如图4-6是铺在青藏铁路冻土区路基两侧的“热棒”示意图，它能对路基进行主动降温，保持路基冻土不熔化。在热棒内封装有一定量的氨，棒内下端的氨发生的物态变化是____汽__化______（填“汽化”或“液化”），该过程____吸__热______（填“吸热”或“放热”），使路基温度____降__低______，冻土就不会熔化。
（2）图4-8乙中温度计的示数是_____9_7______℃。（3）小敏小组中的两位同学用相同的火力，做了两次实验，绘制成了图4-8丙中a、b两条图线，则a、b图线不同的原因是两次实验所用水的____质__量______不同。（4）分析图4-8丙可知，水沸腾时的特点是_持__续__吸__热__，__温__度__保_。持不变
三、实验题(本大题2小题，共22分) 17. （12分）小华用图4-7甲所示的装置做“探究冰的熔化特点” 的实验。
（1）装有碎冰的烧杯直接放置在空气中，不用酒精灯加热。这样做，不但能使烧杯均匀受热，而且冰的温度升高较___慢____(填 “快”或“慢”)，便于记录各个时刻的温度。为了使烧杯内各部分受热均匀，还需要进行的操作是用__玻__璃__棒__不__断__搅__拌____。
20. （9分）走进气象站，可以看到如图4-11所示的百叶箱，箱内主要的测量仪器有两支湿度计（绝对湿度计和相对湿度计）和两支温度计（测量并记录一天中最高气温的温度计和最低气温的温度计）。