第二讲几何之圆与扇形2精选.

合集下载

冀教版六年级数学上册 (扇形的认识)圆和扇形课件

( 圆心角)的大小有关。
同学们，你了解圆心角了吗？加油！
1.选择题。
（1）圆心角是由两条（ A ）组成的。
A 半径
B 直径
（2）扇形圆心角的度数是（ C ）。
A 大于0° C 大于0°，小于360°
B 大于0°，等于360° D 任意度
同学们，这些题你都明白为什么了吗？
2.判断题。（1）扇形总是比圆小。
5 如图是小红家去年的支出情况统计图。如果小红家去年全年支出10000元，那么教育支出有多少元?
10000×25%=2500（元）
答：教育支出有2500元。
扇形统计图是用整个圆的面积表示总数，用圆
认识
内的扇形面积表示各部分占总数的百分比。
扇
形
统计
扇形统计图的作用：扇形统计图可以清楚地表示出
从图上直接可以了解到哪些情况？
从图上直接可以看出部分占整体的百分比。扇形统计图可以很清楚地表示部分和整体之间的关系。
这样的统计图叫做扇形统计
图。
1 根据统计图（4）回答问题。
篮球（2）如果你是六（1）班的体育委员，班里要组织球类比赛，你打算组织什么比赛？为什么？
篮球，因为喜欢篮球的人数最多。
玉
米
大豆
50
12.5
%
谷%
子
10
%
答：李庄种植大豆50公（3）顷自。己提出问题并解答。
李庄种植谷子多少公顷？
400×10%=40（公顷）
答：李庄种植谷子40公顷。
4 黄豆的成分如下面的统计图所示，自己提出问题并解答。 100千克黄豆中含脂肪多少千克？ 100×16%=16（千克）答：100千克黄豆中含脂肪16千克。

《扇形的认识》圆和扇形PPT课件

扇形是由两条半径和圆上的一段曲线围成的。
左图中，圆上A、B 两点之间的部分叫做弧。读作：弧AB。顶点在圆心，两条半与扇形的大小有什么关系？
（1）画圆心角不同的扇形：在同一个圆中分别画出圆心角是30°、60°、90°和120°的扇形。 B C 60° 90° A 30° ● D 120° ①画一个圆。 ②画30°、60°、 90°120°的圆心角。
冀教版数学六年级上册第一单元
扇形的认识
教学目标
1、在观察、讨论、判断等活动中，经历初步认识扇形的过程。 2、知道扇形，初步了解扇形的特征，能在圆中
画出扇形。
3、体会扇形和圆的关系，知道扇形的各部分名
称。
观察各圆中涂色的部分，说一说它们的形状像什么？
说一说
扇形有什么特征？
扇形都有一个角，角的顶点是圆心。
1、不要做刺猬，能不与人结仇就不与人结仇，谁也不跟谁一辈子，有些事情没必要记在心上。 2、相遇总是猝不及防，而离别多是蓄谋已久，总有一些人会慢慢淡出你的生活，你要学会接受而不是怀念。 3、其实每个人都很清楚自己想要什么，但并不是谁都有勇气表达出来。渐渐才知道，心口如一，是一种何等的强大! 4、有些路看起来很近，可是走下去却很远的，缺少耐心的人永远走不到头。人生，一半是现实，一半是梦想。 5、没什么好抱怨的，今天的每一步，都是在为之前的每一次选择买单。每做一件事，都要想一想，日后打脸的时候疼不疼。 6、过去的事情就让它过去，一定要放下。学会狠心，学会独立，学会微笑，学会丢弃不值得的感情。 7、成功不是让周围的人都羡慕你，称赞你，而是让周围的人都需要你，离不开你。 8、生活本来很不易，不必事事渴求别人的理解和认同，静静的过自己的生活。心若不动，风又奈何。你若不伤，岁月无恙。 9、与其等着别人来爱你，不如自己努力爱自己，对自己好点，因为一辈子不长，对身边的人好点，因为下辈子不一定能够遇见。 10、你迷茫的原因往往只有一个，那就是在本该拼命去努力的年纪，想得太多，做得太少。 11、有一些人的出现，就是来给我们开眼的。所以，你一定要禁得起假话，受得住敷衍，忍得住欺骗，忘得了承诺，放得下一切。 12、不要像个落难者，告诉别人你的不幸。逢人只说三分话，不可全抛一片心。 13、人生的路，靠的是自己一步步去走，真正能保护你的，是你自己的选择。而真正能伤害你的，也是一样，自己的选择。 14、不要那么敏感，也不要那么心软，太敏感和太心软的人，肯定过得不快乐，别人随便的一句话，你都要胡思乱想一整天。 15、不要轻易去依赖一个人，它会成为你的习惯，当分别来临，你失去的不是某个人，而是你精神的支柱;无论何时何地，都要学会独立行走，它会让你走得更坦然些。 16、在不违背原则的情况下，对别人要宽容，能帮就帮，千万不要把人逼绝了，给人留条后路，懂得从内心欣赏别人，虽然这很多时候很难。 17、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭 18、不要太高估自己在集体中的力量，因为当你选择离开时，就会发现即使没有你，太阳照常升起。 19、时间不仅让你看透别人，也让你认清自己。很多时候，就是在跌跌拌拌中，我们学会了生活。 20、命运要你成长的时候，总会安排一些让你不顺心的人或事刺激你。 21、你的假装努力，欺骗的只有你自己，永远不要用战术上的勤奋，来掩饰战略上的懒惰。 22、成长是一场和自己的比赛，不要担心别人会做得比你好，你只需要每天都做得比前一天好就可以了。 23、你没那么多观众，别那么累。做一个简单的人，踏实而务实。不沉溺幻想，更不庸人自扰。 24、奋斗的路上，时间总是过得很快，目前的困难和麻烦是很多，但是只要不忘初心，脚踏实地一步一步的朝着目标前进，最后的结局交给时间来定夺。 25、你心里最崇拜谁，不必变成那个人，而是用那个人的精神和方法，去变成你自己。 26、运气是努力的附属品。没有经过实力的原始积累，给你运气你也抓不住。上天给予每个人的都一样，但每个人的准备却不一样。不要羡慕那些总能撞大运的人，你必须很努力，才能遇上好运气。 27、时间只是过客，自己才是主人，人生的路无需苛求，只要你迈步，路就在你的脚下延伸，只要你扬帆，便会有八面来风，启程了，人的生命才真正开始。 28、每个人身上都有惰性和消极情绪，成功的人都是懂得管理自己的情绪和克服自己的惰性，并像太阳一样照亮身边的人，激励身边的人。 29、最终你相信什么就能成为什么。因为世界上最可怕的二个词，一个叫执着，一个叫认真，认真的人改变自己，执着的人改变命运。只要在路上，就没有到不了的地方。 30、人生，就要活得漂亮，走得铿锵。自己不奋斗，终归是摆设。无论你是谁，宁可做拼搏的失败者，也不要做安于现状的平凡人。 31、不管做什么都不要急于回报，因为播种和收获不在同一个季节，中间隔着的一段时间，我们叫它为坚持。 32、知人者智，自知者明。胜人者有力，自胜者强。——老子

六年级数学圆和扇形知识点总结

六年级数学圆和扇形知识点总结一、圆的认识圆是一种几何图形，由一个动点以一定点为中心，以一定长度为距离旋转一周所形成的封闭曲线。

1、圆的各部分名称圆心：用字母“O”表示，圆中心的一点叫做圆心，它决定了圆的位置。

半径：连接圆心和圆上任意一点的线段叫做半径，用字母“r”表示。

半径决定了圆的大小。

直径：通过圆心并且两端都在圆上的线段叫做直径，用字母“d”表示。

2、圆的特征在同一个圆内，有无数条半径，所有的半径都相等；有无数条直径，所有的直径也都相等。

在同一个圆内，直径的长度是半径的 2 倍，即 d ＝ 2r 或 r ＝ d÷2。

圆是轴对称图形，直径所在的直线是圆的对称轴，圆有无数条对称轴。

3、圆的周长圆的周长是指围成圆的曲线的长度。

圆的周长计算公式：C ＝πd 或 C ＝2πr （其中 C 表示圆的周长，π是圆周率，通常取值 314，d 表示圆的直径，r 表示圆的半径）4、圆的面积圆的面积是指圆所占平面的大小。

圆的面积计算公式：S ＝πr² （其中 S 表示圆的面积）二、扇形的认识扇形是由圆心角的两条半径和圆心角所对的弧围成的图形。

1、扇形的各部分名称圆心角：顶点在圆心的角叫做圆心角。

弧：圆上两点之间的部分叫做弧。

2、扇形的特征扇形是圆的一部分。

扇形的大小与圆心角的大小和半径的长短有关。

圆心角越大，扇形越大；半径越长，扇形越大。

3、扇形的面积扇形的面积公式：S ＝（n÷360）×πr² （其中 S 表示扇形的面积，n 表示圆心角的度数，r 表示扇形所在圆的半径）三、圆和扇形的应用1、计算圆的周长和面积已知圆的半径或直径，直接代入相应的公式计算。

例如：一个圆的半径是 5 厘米，求它的周长和面积。

周长：C ＝2πr ＝ 2×314×5 ＝ 314（厘米）面积：S ＝πr² ＝ 314×5²＝ 785（平方厘米）2、计算扇形的面积已知扇形的圆心角和半径，代入扇形面积公式计算。

第二讲圆和扇形的周长与面积学案及详解[六年级秋]

第二讲图形问题(二)————圆的周长与面积知识导航一、概念。

圆：到定点等于定长的点的集合叫做圆，其中定点叫做圆心，圆心用字母O表示。

圆的半径：从圆心到圆上任意一点之间的线段叫做圆的半径，用字母r表示。

在同一个圆中有无数条半径，所有半径长度都相等。

圆的直径：通过圆心并且两端都在圆上的线段叫做圆的直径，直径用字母d表示。

在同一个圆里有无数条直径，所有直径长度都相等。

圆周率：圆的周长与它的直径的比值叫做圆周率，用字母π表示。

它是一个固定的数，是一个无限不循环小数（即无理数）。

圆的周长：围成圆的曲线的长叫做圆的周长。

圆的面积：圆所占平面的大小叫做圆的面积。

圆是轴对称图形，圆的直径所在的直线就是圆的对称轴，它有无数条对称轴。

二、常用公式。

用字母C、S分别表示圆的周长与面积，计算公式可以表示为：C=πd或C=2πr S=πr²三、解题策略数形结合、代换……精典例题例1：把一个圆切拼成一个宽等于半径的近似长方形后，周长增加12cm，那么这个圆的面积与周长各是多少？(2007年成都七中育才学校东区衔接班招生考试题1)思路点拨想一想：你能画出切拼图吗？并在图上标出切拼图与圆的关系吗？模仿练习把一个圆切拼成一个宽等于半径的近似长方形后，这个长方形的周长是33.12cm，那么这个圆的面积与周长各是多少？例2：在一个面积为20cm²的正方形中画一个最大的圆，这个圆的面积是多少？思路点拨想一想：在一个正方形中画一个最大的圆，这个圆与正方形有什么关系？如果从另一个角度想：要求圆的面积必须知道的最直接的条件是什么？友情提示：所谓的最直接的条件，就是指知道后可以只用一步计算就能回答问题的。

模仿练习在一个正方形中画一个最大的圆，这个最大圆的面积是15.7cm²，那么这个正方形的面积是多少？例3：图中阴影部分的面积是4cm²，环形面积是多少？(2004年成都七中育才东区初中招生考试题)思路点拨想一想：难吧！其实不难，把问题想简单一点儿！什么叫做圆环，圆环的面积怎么计算？想清楚后，你会发现这道题格外的简单！模仿练习如图，阴影部分的面积是60cm²，那么圆环的面积是多少？例4：如图所示，已知正方形的边长是3cm，那么阴影部分的面积是多少？思路点拨想一想，计算阴影部分面积的基本方法是什么？你认为关键是要先求出什么？现在你可以计算了吗？再想一想，还有没有更巧的方法呢？模仿练习已知下图长方形的长宽分别是6cm、4cm，分别以长、宽为半径作了两个直角扇形，计算阴影部分的面积。

2024版《扇形》圆和扇形PPT教学课件[1]

扇形与其他图形的组合
扇形可以与其他图形进行组合，形成更复杂的几何图形，如圆锥、圆柱等。
扇形的变形和拓展
通过对扇形的变形和拓展，可以得到更多有趣的几何图形，如弓形、环形等。
25
思考题与练习题
2024/1/29
思考题
请思考扇形面积和周长的计算公式是如何推导出来的？这些公式在实际应用中有哪些限制？
扇形与相交圆的组合
两个相交圆的交点位于扇形的弧上，通过计算扇形的面积和两个相交圆的面积，可以得到组合图形的总面积。同时，还可以利用相交圆的性质求解一些与扇形相关的几何问题。
22
PART 06
总结回顾与拓展延伸
REPORTING
2024/1/29
23
总结回顾本次课程重点内容
扇形的定义和性质
扇形是由两个半径和一个圆弧所围成的图形，具有特定的面积和周长计算公式。
圆心角和弧度的关系
圆心角的大小决定了扇形的面积和周长，而弧度则是圆心角的度量单位。
扇形的面积和周长计算
通过给定的圆心角和半径，可以计算出扇形的面积和周长。
2024/1/29
24
拓展延伸：探索更多扇形相关的知识领域
2024/1/29
扇形的应用
扇形在日常生活和工业生产中有着广泛的应用，如风扇叶片、汽车轮胎等。
练习题
请计算给定半径和圆心角的扇形的面积和周长，并比较不同半径和圆心角对扇形面积和周长的影响。同时，尝试探索扇形面积和周长与半径和圆心角之间的函数关系。
26
THANKS
感谢观看
REPORTING
2024/1/29
27
扇形面积公式的应用利用扇形面积公式可以计算出任意大小、任意中心角的扇形的面积，为几何学和物理学等领域的研究提供了便利。

《圆和扇形》PPT课件

2．画圆时，圆规两脚间的距离是圆的（半径）。
3．由两条半径和圆上的一段曲线围成的图形叫（扇形）。
4．用圆规画一个半径为 5 厘米的圆，圆规两脚间的距离是（ 5厘米），如果画一个直径为 6 厘米的圆，则圆规两脚间的距离是（ 3厘米）。
二、明辨是非。（判断对错） 1．两端都在圆上的所有线段中，直径最长。（ √ ） 2．在同一个圆内，两条半径就是一条直径。（ × ） 3．通过圆心的线段叫做圆的直径。（ × ） 4．一个圆至少对折3 次，就可以找到圆的圆心。（ × ） 5．在正方形中画一个最大的圆，直径和正方形的边长相等。（√） 6．圆在平面滚动时，圆心在一条直线上运动。（ √ ） 7．圆上任意一点到圆心的距离都相等。（ √ ）
.
6
在日常生活和学习中，我们经常用圆规画圆。
（1）把圆规的两脚分开，定好两脚间的距离（即半径）。
（2）把有针尖的一只脚固定在一点（即圆心）上。
（3）把装有铅笔尖的一只脚旋转一周，就画出一个圆。
欣赏图案。（1）
（2）
（3）
（4）
用圆规和直尺等工具就能设计出这些图案。
右图中，圆上A、B两点之间的部分叫做弧，读作：弧AB。
顶点在圆心，两条半径组成的∠AOB，叫做圆心角。
A
.圆 o心弧
角 B
扇形：扇形是由两条半径和圆上一段曲线围成的。
扇形都有一个角，角的顶点在圆心。
一、精彩补白。（填空） 1．在同一个圆中，可以画（无数）条直径和半径，所有的直径都（相等），所有的半径都（相等），直径等于半径（ 2 ）倍。
圆Байду номын сангаас扇形
.
1
长方形

全国通用六年级下册数学奥数：几何之圆与扇形(解析版)

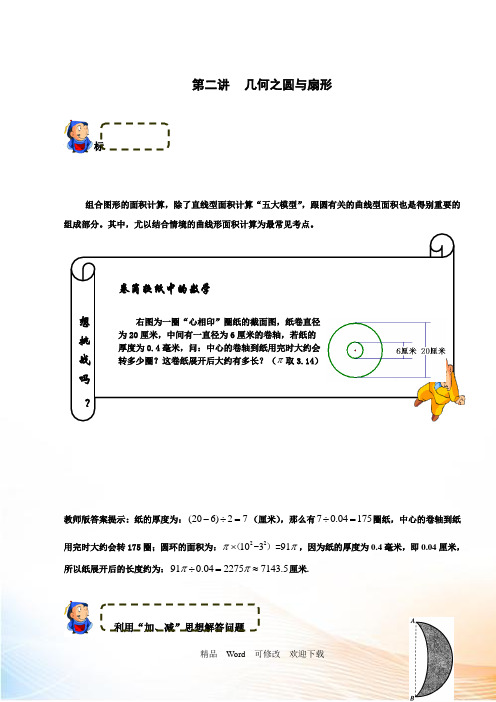
第二讲几何之圆与扇形教学目标组合图形的面积计算，除了直线型面积计算“五大模型”，跟圆有关的曲线型面积也是得别重要的组成部分。

其中，尤以结合情境的曲线形面积计算为最常见考点。

教师版答案提示：纸的厚度为：(206)27-÷=（厘米），那么有70.04175÷=圈纸，中心的卷轴到纸用完时大约会转175圈；圆环的面积为：2210391ππ⨯（-）=，因为纸的厚度为0.4毫米，即0.04厘米，所以纸展开后的长度约为：910.0422757143.5ππ÷=≈厘米.利用“加、减”思想解答问题想挑战吗？卷筒软纸中的数学右图为一圈“心相印”圈纸的截面图，纸卷直径为20厘米，中间有一直径为6厘米的卷轴，若纸的厚度为0.4毫米，问：中心的卷轴到纸用完时大约会转多少圈？这卷纸展开后大约有多长？（π取3.14）【例1】如图，一个“月牙”形屏幕在屏幕上随意平行移动（不许发生转动也不越过屏幕边界），已知线段AB 是月牙外半圆弧的直径，长为2厘米。

初始时，A 、B 两点在矩形屏幕的一条边上。

屏幕的长和宽分别为30厘米和20厘米。

问：屏幕上“月牙”擦不到的部分的面积是多少平方厘米？（π取3）分析：由于“月牙”形屏幕在屏幕上只能平行移动（不许发生转动也不越过屏幕边界），所以它擦不到的地方只是屏幕的右上角和右下角两部分，如右下图中斜线所示区域，其面积为0.5平方厘米。

［前铺］如右图所示，等腰直角三角形ABC 的高AD=4厘米，以AD 为直径作圆分别交AB 、AC 与E 、F ，求阴影部分的面积。

（π取3）分析：连接EF ，那么有BED ABD EOD S S S =-阴影三角形扇形，计算可得阴影部分面积为6平方厘米。

［巩固］一个长方形的长为9，宽为6，一个半径为l 的圆在这个长方形内任意运动，在长方形内这圆无法运动到的部分，面积的和是多少？(π取3)分析：圆无法运动到的部分是右下图中角处的阴影部分面积的4倍，114111π⨯⨯-⨯⨯=［拓展］如右图所示，用一块面积为36平方厘米铝板下料，可裁出七个同样大小的圆铝板。

圆的弧长与扇形面积计算知识点总结

圆的弧长与扇形面积计算知识点总结在几何学中，圆是一个非常重要且常见的图形。

计算圆的弧长和扇形面积是解决与圆相关问题的基础。

本文将对圆的弧长和扇形面积的计算方法进行总结。

一、圆的弧长计算圆的弧长是圆的一部分所对应的弧长，可以通过圆的半径或直径来计算。

假设半径为r、弧度为θ的圆弧的弧长为L，弧长可以通过下面的公式来计算：L = θ * r其中，θ表示角度，它可以用弧度（radian）或度（degree）来表示。

如果θ用弧度表示，则上式中的弧长单位为弧长单位为r；如果θ用度表示，则上式中的弧长单位为π。

例如，如果半径为3的圆弧对应的角度为π/3弧度，则该圆弧的弧长为：L = (π/3) * 3 = π二、扇形面积的计算扇形是由圆心和圆上两个切点连线所围成的区域。

计算扇形的面积需要知道圆的半径以及对应的圆心角。

假设半径为r、对应的圆心角为θ的扇形的面积为S，面积可以通过下面的公式来计算：S = (θ/360) * π * r^2其中，θ表示度数。

公式中的θ/360表示圆心角度数与360度的比值，可以用来表示扇形所占的比例。

面积的单位为平方单位，如平方厘米、平方米等。

例如，如果半径为4的扇形的圆心角为90度，则该扇形的面积为：S = (90/360) * π * 4^2 = (1/4) * π * 16 = 4π三、计算实例下面通过几个实例来演示圆的弧长和扇形面积的计算方法。

实例一：已知半径为5的圆上的圆心角为60度，求圆弧的弧长和扇形的面积。

弧长的计算：L = (60/360) * 2π * 5 = (1/6) * 2π * 5 = 5π/6扇形面积的计算：S = (60/360) * π * 5^2 = (1/6) * π * 25 = 25π/6实例二：已知半径为8的圆上的圆心角为120度，求圆弧的弧长和扇形的面积。

弧长的计算：L = (120/360) * 2π * 8 = (1/3) * 2π * 8 = 16π/3扇形面积的计算：S = (120/360) * π * 8^2 = (1/3) * π * 64 = 64π/3实例三：已知半径为10的圆上的圆心角为270度，求圆弧的弧长和扇形的面积。

第二讲圆与扇形试题及答案

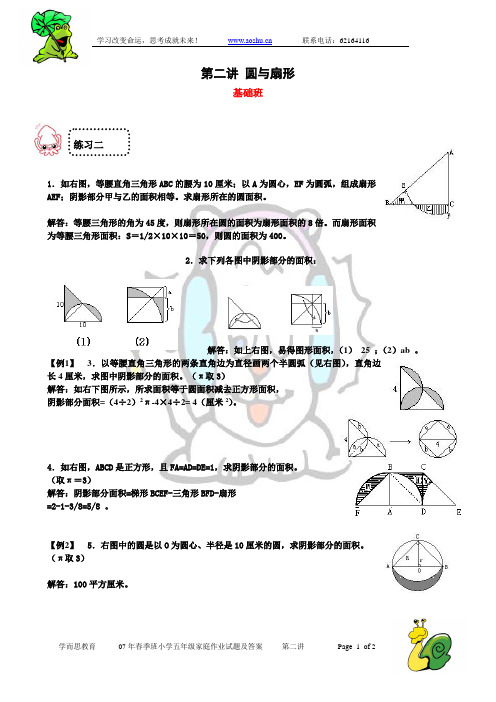
第二讲圆与扇形基础班练习二1．如右图，等腰直角三角形ABC的腰为10厘米；以A为圆心，EF为圆弧，组成扇形AEF；阴影部分甲与乙的面积相等。

求扇形所在的圆面积。

解答：等腰三角形的角为45度，则扇形所在圆的面积为扇形面积的8倍。

而扇形面积为等腰三角形面积：S＝1/2×10×10＝50，则圆的面积为400。

2．求下列各图中阴影部分的面积：解答：如上右图，易得图形面积，（1）25 ；（2）ab 。

【例1】3．以等腰直角三角形的两条直角边为直径画两个半圆弧（见右图），直角边长4厘米，求图中阴影部分的面积。

（π取3）解答：如右下图所示，所求面积等于圆面积减去正方形面积，阴影部分面积=（4÷2）2π-4×4÷2= 4（厘米2）。

4．如右图，ABCD是正方形，且FA=AD=DE=1，求阴影部分的面积。

（取π＝3）解答：阴影部分面积=梯形BCEF-三角形BFD-扇形=2-1-3/8=5/8 。

【例2】5．右图中的圆是以O为圆心、半径是10厘米的圆，求阴影部分的面积。

（π取3）解答：100平方厘米。

提高班练习二1．如右图，等腰直角三角形ABC的腰为10厘米；以A为圆心，EF为圆弧，组成扇形AEF；阴影部分甲与乙的面积相等。

求扇形所在的圆面积。

解答：等腰三角形的角为45度，则扇形所在圆的面积为扇形面积的8倍。

而扇形面积为等腰三角形面积：S＝1/2×10×10＝50，则圆的面积为400。

2．求下列各图中阴影部分的面积：解答：如上右图，易得图形面积，（1）25 ；（2）ab 。

3．以等腰直角三角形的两条直角边为直径画两个半圆弧（见右图），直角边长4厘米，求图中阴影部分的面积。

（π取3）解答：如右下图所示，所求面积等于圆面积减去正方形面积，阴影部分面积=（4÷2）2π-4×4÷2= 4（厘米2）。

4．如右图，ABCD是正方形，且FA=AD=DE=1，求阴影部分的面积。

圆与扇形知识点总结

圆与扇形知识点总结一、圆的基本概念圆是平面几何中的一个重要概念，它是由平面上到一个定点的距离等于定长的所有点的集合。

这个定点称为圆心，定长称为半径，表示为 r。

圆的直径是通过圆心，并且两端都在圆上的线段，它的长度是半径的两倍，表示为 d=2r。

圆的知识点包括：圆的半径、直径；圆心、圆周、圆的面积、周长等。

二、扇形的基本概念扇形是由圆心O、半径OA、圆弧AB、弦AB四部分组成的一个平面图形。

扇形与圆有着密切的联系，它是圆的一部分。

扇形的圆心角是指扇形的两条边所夹的角。

扇形的知识点包括：扇形的圆心角、弧长、扇形的面积等。

三、圆的周长和面积1.圆的周长圆的周长是指圆的边上所有的长度。

圆的周长可以通过直径或半径进行计算。

当知道圆的直径是d时，周长为πd；当知道圆的半径是r时，周长为2πr。

其中，π是圆周率，其值约为3.14。

2.圆的面积圆的面积是指圆所包含的平面区域。

圆的面积可以通过直径或半径进行计算。

当知道圆的直径是d时，面积为π(d/2)²；当知道圆的半径是r时，面积为πr²。

四、扇形的周长和面积1.扇形的周长扇形的周长是指扇形的边上所有的长度。

扇形的周长包括弧长和弦长两部分。

弧长是扇形圆弧的长度，可以通过圆心角和半径进行计算；弦长是扇形的两端点之间的线段，可以通过圆心角和半径进行计算。

2.扇形的面积扇形的面积是指扇形所包含的平面区域。

扇形的面积可以通过圆心角和半径进行计算。

扇形的面积公式为S=(θ/360)πr²，其中θ为扇形的圆心角，r为扇形的半径。

五、相关公式1.圆的周长及面积圆的周长公式为C=2πr圆的面积公式为S=πr²2.扇形的周长及面积扇形的周长公式为 L=r+L扇形的面积公式为S=(θ/360)πr²六、圆与扇形的应用圆与扇形是几何中非常重要的概念，它们的知识点和公式可以应用到各种各样的场景中。

比如，地面上的径向扇形公园，墙壁上的粉刷面积，环形跑道的长度等等。

圆与扇形题型归类

圆与扇形——公式与割补内容提要本讲主要讲解与圆和扇形有关的概念，及周长、面积公式等．下面我们来说说这方面的基础知识．圆是我们在生活中经常见到的图形，它也是最完美的平面图形：有无数条通过圆心的对称轴，绕圆心旋转任何角度还保持原状．而且，所有的平面图形在周长相同的情况下，圆的面积是最大的．我们知道，圆的周长和直径的比值是一个固定不变的数，这正是圆周率，用π表示．另外，一般把直径记作d ，半径记作r ，如图1所示．所以，圆的周长2C d r ππ=⨯=⨯⨯，圆的面积2S r π=⨯．如图3，由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．它是圆的一部分，所以关于扇形的各种计算可以应用圆里面的结论．dr图1n°r图3扇形的圆心角为n °时，它的弧长和面积应该分别是圆周长和圆面积的360n ．我们先来熟悉一下这些公式．练习：1. 半径是2的圆的面积和周长分别是多少？2.3.4. 直径是5的圆的面积和周长分别是多少？5.6.7. 周长是10π的圆的面积是多少？8.9.10. 面积是9π的圆的周长是多少？11.12.例题一、基本公式运用例题1.已知扇形的圆心角为120°，半径为2，则这个扇形的面积和周长各是多少？（圆周率按3.14计算）例题2.已知扇形面积为18.84平方厘米，圆心角为60°，则这个扇形的半径和周长各是多少？（圆周率按3.14计算）60°例题4.随堂练习：1.已知一个扇形的弧长为0.785厘米，圆心角为45，这个扇形的半径和周长各是多少？2.3.4.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是多少？5.6.如图，直角三角形ABC的面积是45，分别以B，C为圆心，3为半径画圆．已知图中阴影部分的面积是35.58．请问：角A是多少度？（π取3.14）AB C7.二、圆中方，方中圆8.如图，左下图和右下图中的正方形边长都是2，那么大圆、小圆的面积分别为________、________．9.10.随堂练习：1.已知外面大圆的半径是4，里面小圆的面积是多少？（答案用π表示）2.二、割补法11.求下列各图中阴影部分的面积（图中长度单位为厘米，圆周率按3.14计算）：2（1）（2）随堂练习：7求下图中阴影部分的面积（图中长度单位为厘米，圆周率按3.14计算）：（1）（2）4求下列各图中阴影部分的面积（图中长度单位为厘米，圆周率按3.14计算）：22（1）（2）（2）（3）（4）（5）（6）（7）（8）（9）（10）12.已知图中正方形的边长为2，分别以其四个顶点为圆心的直角扇形恰好交于正方形中心，那么图中阴影部分的面积为________．（答案用表示）13.14.15.16.根据图中所给数值，求下面图形的外周长和总面积分别是多少？（π取3.14）417.作业：1.半径为4厘米的圆的周长是________厘米，面积是________平方厘米；2.3.半径为4厘米，圆心角为90︒的扇形周长是________厘米，面积是________平方厘米．（π取3.14）4.5.家里来客人了，淘气到超市买了4瓶啤酒，售货员阿姨将4瓶啤酒捆扎在一起（如下图所示），捆4圈至少要用绳子________厘米．（π取3.14，接头处忽略不计）O 7厘米1 16.求下列各图中阴影部分的面积（图中长度单位为厘米，圆周率按3.14计算）：7.（1）（2）10109.10.下列图形中的正方形的边长为2，则下图中各个阴影部分面积的大小分别为______、______．（π取3.14）11.12.用一块面积为36π平方厘米的圆形铝板下料，从中裁出了7个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？O圆与扇形旋转与重叠知识总结：学习如何利用割补法和包含排除的思想计算图形中特定部分的面积；学会分析几何图形的运动过程，并由此得出点的轨迹和图形扫过的区域．例题：一、重叠问题例题1.下图中甲区域比乙区域的面积大57平方厘米，且半圆的半径是10厘米，那么其中直角三角形的另一条直角边的长度是多少？（圆周率?取3.14）例题2.例题3.下图中有一个等腰直角三角形ABC ，一个以AB 为直径的半圆，和一个以BC 为半径的扇形．已知10AB BC ==厘米．图中阴影部分的面积为多少平方厘米？（π取3.14）例题4.随堂练习1. 如图17-13，以AB 为直径做半圆，三角形ABC 是直角三角形，阴影部分①比阴影部分②的面积小28平方厘米，AB 长40厘米．求BC 的长度．（?取3.14．） 2. 3.4.5.6.例题5.如图，直角三角形的两条直角边分别为3和5，分别以三条边做了3个半圆（直角顶点在以斜边为直径的半圆上），那么阴影部分的面积为______．ABB例题6.例题7.例题8.例题9.图1是一个直径是3厘米的半圆，AB是直径．如图2所示，让A点不动，把整个半圆逆时针转60°，此时B点移动到C点．请问：图中阴影部分的面积是多少平方厘米？（π取3.14）图1 AB A B60 图2C例题11.例题12.例题13.二、动态扫面积问题例题14.如图，正方形ABCD边长为1厘米，依次以A、B、C、D为圆心，以AD、BE、CF、DG 为半径画出四个直角扇形，那么阴影部分的面积为________平方厘米．（取3.14）例题15.例题16.例题17.例题18.例题19.例题20.例题21.例题22.例题23.例题24.如图所示，以等边三角形的B、C、A三点分别为圆心，分别以AB、CD、AE为半径画弧，这样形成的曲线ADEF被称为正三角形ABC的渐开线，如果正三角形ABC的边长为3厘米，那么此渐开线的长度为多少厘米，图中I、II、III三部分的面积之和是多少平方厘米？例题例题26.例题27.三、运动圆扫面积例题28.图中正方形的边长是4厘米，而圆环的半径是1厘米．当圆环绕正方形无滑动地滚动一周又回到原来位置时，其扫过的面积有多大？（π取3.14）例题29.例题30.随堂练习1.图中长方形的长是10厘米，宽是4厘米，而圆环的半径是1厘米．当圆环绕正方形无滑动地滚动一周又回到原来位置时，其扫过的面积有多大？（π取3.14）2.例题31.图中等边三角形的边长是3厘米，而圆环的半径是1厘米．当圆环绕等边三角形无滑动地滚动一周又回到原来位置时，其扫过的面积有多大？（π取3.14）例题32.例题33.例题34.例题35.思考题如图所示，一只小狗被拴在一个边长为4米的正五边形的建筑物的一个顶点处，四周都是空地．绳长刚好够小狗走到建筑物外墙边的任一位置．小狗的活动范围是多少平方米？（建筑外墙不可逾越，小狗身长忽略不计，π取3）狗作业：1.图17-14由一个长方形与两个90?角的扇形构成，其中阴影部分的面积是_______平方厘米．（?取3.14．）图17-143.4.图中有一个矩形和两个半径分别为5和2的直角扇形，那么两个阴影部分的面积相差为_______．（π取3.14）6. 如图，直角三角形的两条直角边长分别是10cm 和6cm ，分别以直角边为直径作出两个半圆，这两个半圆的交点恰好落在斜边上，那么阴影部分的面积是_______cm 2．（?取3.14）7. （17??30）8.9. 图1是一个直径是3厘米的半圆，AB 是直径．如图2所示，让A 点不动，把整个半圆逆时针转60°，此时B 点移动到C 点．请问：图中阴影部分的面积是_______平方厘米（π取3.14）10cm6cm图1 AB A BC 40 图2C11.图中正方形的边长是6厘米，而圆环的半径是1厘米．当圆环绕正方形无滑动地滚动一周又回到原来位置时，其扫过的面积有______．（π取3.14）12.13.图中等边三角形的边长是5厘米，圆形的半径是1厘米．当圆形绕等边三角形滚动一周又回到原来位置时，扫过的面积有________．（π取3.14）14.。

九年级圆和扇形的知识点总结归纳

九年级圆和扇形的知识点总结归纳圆和扇形是九年级几何学的重要内容，通过学习和掌握这些知识点，可以帮助我们更好地理解几何学的基本概念和应用。

本文将对九年级圆和扇形的知识点进行总结和归纳，以帮助读者更好地掌握这些知识。

一、圆的定义和特性：圆是由一个平面上与一个确定点的距离恒定的所有点组成的图形。

圆的特性如下：1. 圆心和半径：圆心是确定圆的一个点，通常用字母O表示。

半径是从圆心到圆上任意一点的距离，用字母r表示。

2. 直径和周长：直径是通过圆心并且两端在圆上的一条线段，其长度等于半径的两倍。

周长是圆的边界长度，用字母C表示，公式为C=2πr，其中π≈3.14。

3. 弧和弦：弧是圆上两点之间的一段弧线，弧长是弧的长度。

弦是圆上两个点之间的一条线段。

4. 弧与圆心角：圆心角是以圆心为顶点的角，其对应的弧长等于角度的一半。

二、扇形的定义和特性：扇形是由圆心、半径与边界上的两点所围成的图形。

扇形的特性如下：1. 扇形的面积：扇形的面积是由圆心角所对应的弧所围的部分的面积。

计算公式为：扇形的面积 = 圆的面积 × (圆心角度数 / 360°)。

2. 扇形的弧长：扇形的弧长是扇形边界上的弧的长度。

计算公式为：扇形的弧长 = 圆的周长 × (圆心角度数 / 360°)。

三、圆和扇形的应用：圆和扇形的知识点在日常生活中有广泛的应用，下面列举几个常见的例子：1. 圆形物体的计算：例如，计算一个圆形饼的面积或一个轮胎的周长都需要使用圆的相关知识。

2. 扇形地块的计算：在土地规划和建筑设计中，经常需要计算扇形地块的面积和边界长度，以便合理规划和利用土地。

3. 扇形的角度：在舞台设计和演艺表演中，扇形的角度可以决定演员的出场和表演区域，因此需要准确计算角度。

4. 扇形钟表：钟面上的刻度通常是圆形的，各个时间刻度之间可以看作是扇形，帮助我们读取时间。

综上所述，九年级的圆和扇形知识点是几何学重要的内容，通过学习和掌握这些知识，我们可以更好地理解圆形图形的定义、特性以及其在应用中的使用。

【讲义】5年级下册第02讲_圆与扇形进阶

第二讲圆与扇形进阶- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -自然界中，圆与方是最基本的两种图形．古人认为“天圆地方”，宇宙就像一个圆形的大锅盖在一个方形的棋盘上．中国古代的建筑也会经常采用圆形和正方形的图案．而在面积计算中，圆与正方形也有很大的关系．关于正方形和圆，有以下的面积关系：由此我们可以进一步推断：圆外切正方形面积是内接正方形面积的______倍；正方形外接圆面积是内切圆面积的______倍．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1．（1）左图中正方形的面积是8，那么圆的面积是多少？（π取3.14）（2）右图中正方形的面积是16，那么圆的面积是多少？（π取3.14）分析：利用圆中方和方中圆的比例关系可以轻松求解．练习1．如图，已知正方形的边长是2，求大圆及小圆的面积．（π取3.14）圆的外切正方形与内接正方形正方形的外接圆与内切圆方中圆圆中方例题2．计算下面各图中阴影部分的面积，并比较大小．（π取3.14）分析：利用方中圆的比例关系可以轻松求解．练习2．如图，已知长方形的面积是12，则图中阴影部分的面积是多少？（π取3.14）- - - - - - - - - - - - - -小故事圆与方有一天，圆形和方形碰到了一起，它们一见面就吵了个面红耳赤，不管谁劝都不听．圆形说：“我们圆形就是比你们方形用处大，人们日常生活中用的锅呀、碗呀，体育中的蓝球、排球，水果里的苹果、桔子，大到汽车轮胎、自行车轮胎，都是我的家族．瞧，我们是不是比你们用处大！”圆形得意洋洋地说完．方形“哼”了一声说：“我们方形家族才是无处不在呢，人们用的电器、冰箱、彩电、电脑，就连学生用的课本都是我们方形的哟！”方形也自豪地说．它们谁也无法说服谁，都来到大街上．望着街上的车，方形对着圆形的车轮喊了声：“变！”转眼间车轮变成了方形．正当方形喜笑颜开时，人群出现了混乱，汽车开不了，自行车也只能扛着了，大家都在说：“这是谁干的呀！真是害人呀！”而圆形来到一座刚建好的大楼前，望着由一块块方形红砖盖成的大楼，圆形生气地大声喊了声“变！”呀，方形红砖变成圆形了．圆形还没来及高兴呢，就听“轰”一声大楼倒了下来．看到这个情景，圆形呆住了：“这是怎么回事？”只见混乱的人群里走出了一位老人，他来到方形和圆形面前对它们说：“其实你们都很棒，只是你们分工不同而已，只要你们齐心协力，一定会为人类作更大的贡献．在上一讲中，我们主要使用割补的方法来计算不规则图形的面积．而对于一些比较特殊8的形状，我们可以把它看成是一些基本图形的重叠部分，利用容斥原理计算出它的面积．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3．如图，求下面各图中阴影部分的面积．（π取3.14）分析：阴影部分可以看成是哪些图形的重叠部分？练习3．已知下图中正方形的面积是16，那么阴影部分的面积是多少？（π取3.14）在生活当中，有很多旋转的物体，比如车轮、方向盘等．这些物体在运动的过程中，扫过的图形都是曲线形．这些曲线形的周长和面积应该怎么计算呢？例题4．图中正方形的边长是4厘米，圆形的半径是1厘米．当圆形绕正方形滚动一周又回到原来位置时，扫过的面积有多大？（π取3.14）分析：要求扫过的面积，关键在于弄清扫过的区域；而要弄清扫过的区域，关键在于弄清区域的边界．你能通过合理动态想象，画出边界来吗？练习4．如图，正方形的边长是2厘米，圆形的半径是1厘米．当圆形绕正方形滚动一周又回到原来位置时，扫过的面积有多大？（π取3.14）例题5．如图，求阴影部分的面积．（π取3.14）分析：阴影部分可以看成是四个扇形的重叠部分，但是扇形的半径图中并没有给出，那么应该怎么计算扇形的面积呢？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题6．（1）如图，一只小狗被拴在一个边长为4米的正方形的建筑物的顶点A处，四周都是空地．绳长8米．小狗的活动范围是多少平方米？（2）如果小狗不是被拴在A处，而是在一边的中点B处，那么小狗的活动范围是多少平方米？（建筑外墙不可逾越，小狗身长忽略不计，π取3.14）分析：如果没有建筑物的阻挡，小狗的活动范围应该是一个圆．有建筑物的话，活动范围会受到什么样的影响呢？A含有“圆”字的成语圆首方足：出自《淮南子·精神训》：“头之圆也象天，足之方也象地．”用来代指人类．戴圆履方：出自《淮南子·本经训》：“戴圆履方，抱表怀绳．”履：踩着；圆、方：古人以为天圆地方．头顶着天，脚踩着地．指生活在人间．方枘圆凿：出自战国时楚国宋玉的《九辨》：“圆凿而方枘兮，吾固知其龃龉而难入．”凿：榫眼；枘：榫头．方枘装不进圆凿．比喻格格不入，不能相合．这三个成语之外，还有很多成语中都含有“圆”和“方”这两个字，如圆孔方木、圆颅方趾、外圆内方等．这说明古人对于圆和方的认识非常深刻，已经将其应用到了生活中的很多方面．而我们在圆与扇形的学习中，也要注意圆形与正方形之间的联系．元方，你怎么看？破镜重圆：这个成语故事是由华阴人、隋越国公杨素的一段成人之美的佳话而来的．杨素，字处道，在辅佐隋文帝杨坚结束割据，统一天下，建立隋朝江山方面立下了汗马功劳．他不仅足智多谋，才华横溢，而且文武双全，风流倜傥．在朝野上下都声势显赫，颇著声名．隋开皇九年（公元589年）杨素与文帝杨坚的两个儿子陈后主叔宝的嫔妃、亲戚，其中有陈叔宝的妹妹枣陈太子舍人徐德言之妻，也就是陈国的乐昌公主．由于杨素破陈有功，加之乐昌公主才色绝代，隋文帝就乱点鸳鸯，将乐昌公主送进杨素中，赐为杨素小妾．杨素既仰慕乐昌公主的才华，又贪图乐昌公主的美色，因此就更加宠爱，还为乐昌公主专门营造了宅院．然而乐昌公主却终日郁郁寡欢，默无一语．原来，乐昌公主与丈夫徐德言两心相知，情义深厚．陈国将亡之际，徐德言曾流着泪对妻子说：“国已危如累卵，家安岂能保全，你我分离已成必然．以你这般容貌与才华，国亡后必然会被掠入豪宅之家，我们夫妻长久离散，名居一方，唯有日夜相思，梦中神会．倘若老天有眼，不割断我们今世的这段情缘，你我今后定会有相见之日．所以我们应当有个信物，以求日后相认重逢．”说完，徐德言把一枚铜镜一劈两半，夫妻二人各藏半边．徐德言又说：“如果你真的被掠进富豪人家，就在明年正月十五那天，将你的半片铜镜拿到街市去卖，假若我也幸存人世，那一天就一定会赶到都市，通过铜镜去打问你的消息．”一对恩爱夫妻，在国家山河破碎之时，虽然劫后余生，却受尽了离散之苦．好容易盼到第二年正月十五，徐德言经过千辛万苦，颠沛流离，终于赶到都市大街，果然看见一个老头在叫卖半片铜镜，而且价钱昂贵，令人不敢问津．徐德言一看半片铜镜，知妻子已有下落，禁不住涕泪俱下．他不敢怠慢，忙按老者要的价给了钱，又立即把老者领到自己的住处．吃喝已罢，徐德言向老者讲述一年前破镜的故事，并拿出自己珍藏的另一半铜镜．颤索索两半铜镜还未吻合，徐德言早已泣不成声……卖镜老人被他们的夫妻深情感动得热泪盈眶．他答应徐德言，一定要在他们之间传递消息，让他们夫妻早日团圆．徐德言就着月光题诗一首，托老人带给乐昌公主．诗这样写道：镜与人俱去，镜归人不归．无复嫦娥影，空留明月辉．乐昌公主看到丈夫题诗，想到与丈夫咫尺天涯，难以相见，更是大放悲声，终日容颜凄苦，水米不进．杨素再三盘问，才知道了其中情由，也不由得被他二人的真情深深打动．他立即派人将徐德言召入府中，让他夫妻二人团聚．府中上下都为徐陈二人破镜重圆和越国公杨素的宽宏大度、成人之美而感叹不已．在欢庆的感激之情．宴罢，夫妻二人携手同归江南故里．这段佳话被四处传扬，所以就有了破镜重圆的典故，一直流传至今．作业1. 如图，图中较小圆的面积是3.14，较大圆的面积是多少？作业2. 如图，正方形的面积是8，阴影部分的面积是多少？（π取3.14）作业3. 如图，一头山羊被拴在一个边长为4米的等边三角形的建筑物的一个顶点处，四周都很空旷．绳长刚好够山羊走到三角形建筑物外的任一位置，山羊的活动范围有多少平方米？（建筑外墙不可逾越，山羊身长忽略不计，π取3）作业4. 如图，正方形ABCD 边长为1厘米，依次以A 、B 、C 、D 为圆心，以AD 、BE 、CF 、DG 为半径画出四个直角扇形，那么阴影部分的面积是多少？（π取3.14）作业5. 如图，长方形的长为6厘米，宽为2厘米，圆形的半径是1厘米．当圆形绕长方形滚动一周又回到原来位置时，扫过的面积有多大？（π取3.14）第1题图第2题图第3题图第4题图 AB C D EH F。

第二讲二 1.圆与椭圆的参数方程

第二章参数方程
椭圆的参数方程
Байду номын сангаас
第二章参数方程椭圆的参数方程
x = a cos ϕ x y 1 .参数方程 y = b sin ϕ 是椭圆 2 + 2 = 1 a b 的参数方程. 的参数方程.
2 2
2 .在椭圆的参数方程中，常数a、b分别在椭圆的参数方程中，是椭圆的长半轴长和短半轴长. 是椭圆的长半轴长和短半轴长. a>b
y
x2 y2 椭圆的标准方程: 椭圆的标准方程: 2 + 2 =1 a b x = acosφ 椭圆的参数方程: (φ为参数 ) 椭圆的参数方程: y = bsinφ
椭圆的参数方程中参数φ的几何意义: 椭圆的参数方程中参数φ的几何意义: 不是∠ 是∠AOX=φ,不是∠MOX=φ. 不是圆的标准方程: 圆的标准方程: x2+y2=r2
故 x = 2 2 cos ϕ = −
8 1 8 1 y = sin ϕ = ，点 P (− , ) 即为所求. 即为所求. ， 3 3 3 3
第二章参数方程参数方程与普通方程的互化
x + y =r
2 2
2
2
x = r cos θ y = r sin θ
2 2
(x − a) + (y −b) = r
x = a +r cosθ y = b+r sinθ
注：1、参数方程的特点是没有直接体现曲线上点的横、参数方程的特点是没有直接体现曲线上点的横、纵坐标之间的关系，而是分别体现了点的横、纵坐标之间的关系，而是分别体现了点的横、纵坐标与参数之间的关系。与参数之间的关系。参数方程的应用往往是在x 2、参数方程的应用往往是在x与y直接关系很难或不可能体现时，通过参数建立间接的联系。或不可能体现时，通过参数建立间接的联系。

几何画板(2)-----绘制圆弧和扇形(选内部、内部着色)

(二) 画∠DEF的表示角度的弧线
在角边ED上取一点A，以角的顶点E为圆心，顶点E到点A的长为半径画圆，交另一边于一点B，在圆上取一点C，将点C置于角内部弧AB上，依次选定点A、C、B，以这三点画弧，隐藏圆(选定圆，右键→隐藏圆)及点A、C、B(选定点，右键→隐藏圆)即可。

练习：从木板的三个角处割取扇形，使这三个扇形能构成一个半圆。

(1)先构造最短边的中点先点选最短边的一个端点，再点选中点，
构造→以圆心和圆周上的点作圆，构造圆形
(2)点选圆和另一条边，构造→交点，得到另一边上的点
(3)隐藏圆，依次点选圆心和圆上两点(与两边的交点，其中一个
即为前述中点)，构造→圆弧。

(4)选中弧线，构造→弧内部→扇形内部，可以画出扇形并着色
(5)然后选中扇形内部，显示→颜色，修改扇形颜色
(6)蓝色的扇形：利用绿色扇形画一半径线段(连接圆心和圆弧上
一点)，先点选蓝色扇形对应的圆心，再点选作出的半径线段，构造→以圆心和半径作圆，剩余步骤同上。

圆的弧长与扇形面积

圆的弧长与扇形面积圆是几何学中最简单的形状之一，它具有许多特性和属性。

其中，圆的弧长和扇形面积是我们经常研究和计算的两个重要方面。

本文将就圆的弧长和扇形面积进行详细的解析和计算。

1. 圆的弧长：圆的弧长是指任意两个点在圆上的弧所对应的弧长。

在计算弧长时，需要知道圆的半径和所对应的圆心角。

弧长的计算公式如下：弧长 = 半径 ×圆心角（弧度制）根据这个公式，我们可以计算出任意圆的弧长。

下面通过一个示例进行计算。

示例1：假设一个圆的半径为5cm，圆心角为60°，我们来计算这个圆的弧长。

解：首先需要将圆心角转换为弧度制。

1° = π/180，因此60°转换为弧度为60° × π/180 = π/3。

弧长= 5cm × π/3 ≈ 5.24cm因此，这个圆的弧长约为5.24cm。

2. 扇形的面积：扇形是由圆心和圆上的两个点所构成的区域。

在计算扇形的面积时，需要知道扇形的圆心角和圆的半径。

扇形的面积计算公式如下：面积 = 1/2 ×半径² ×圆心角（弧度制）下面通过一个示例来计算扇形的面积。

示例2：假设一个扇形的半径为8cm，圆心角为45°，我们来计算这个扇形的面积。

解：首先需要将圆心角转换为弧度制。

1° = π/180，因此45°转换为弧度为45° × π/180 = π/4。

面积= 1/2 × 8cm² × π/4 ≈ 12.57cm²因此，这个扇形的面积约为12.57cm²。

通过以上的计算示例，我们可以看出，圆的弧长和扇形面积的计算都与圆心角息息相关。

圆心角的大小决定了弧长和扇形面积的大小。

需要注意的是，在计算圆的弧长和扇形面积时，弧度制是常用的单位制。

对于给定的角度，可以使用以下公式进行转换：弧度 = 角度× π/180综上所述，通过掌握圆的弧长和扇形面积的计算方法，我们可以更好地理解和应用圆的特性，为解决实际问题提供便利。

圆形和扇形的关系

圆形和扇形的关系在数学中，圆形和扇形是两个常见的概念，它们之间有着紧密的联系和关系。

本文就来探讨一下圆形和扇形的关系。

一、什么是圆形和扇形圆形是指所有点到圆心距离相等的图形，可以看作是一个角度为360度的扇形所围成的图形。

圆形是几何学中最基本的图形之一，也是应用最广泛的图形之一。

而扇形是指一个圆形的一部分，它是由圆心、圆周上的两个端点和它们之间的弧所围成的一个图形。

扇形可以根据所包含的弧度大小来进行分类，比如弧度为180度的扇形就是半圆形。

1.圆形是由无数个扇形组成的我们可以想象一下，将一个圆形分割成许多小块的扇形，这些扇形相互贴合可以组成整个圆形。

此外，当我们将扇形的弧长不断缩小，最后它被缩成一点时，就得到了圆形的定义。

2.扇形是圆形的一部分3.由扇形得到圆的公式我们可以通过扇形所围成的面积来得到圆的面积，假设扇形的半径为r，弧度为θ，则扇形面积为：S=1/2r²θ而圆形的面积就是扇形所围成的圆的面积，即：将扇形面积带入上式中得到：化简后得到：θ=2π即圆的周长为2πr。

这个公式就是扇形面积可以通过圆的面积来计算的证明。

4.扇形的周长和面积扇形的周长等于圆形的周长乘以扇形所包含的角度除以360度，即：C=2πrθ/360°=πrθ/180°最后，需要注意的是，当θ=360°时，扇形就是圆形，其面积和周长与圆形相同。

三、小结综上所述，圆形和扇形的关系是紧密的，圆形是由无数个扇形组成的，而扇形则是圆形的一部分。

我们可以根据扇形的面积公式来得到圆的面积公式，也可以根据扇形的周长公式来得到圆的周长公式。

同时，我们也可以通过扇形的计算方法来推导出圆形的性质，这些都是数学中十分重要的知识点。

高斯小学奥数五年级下册含答案第02讲_圆与扇形进阶

第二讲圆与扇形进阶- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -自然界中，圆与方是最基本的两种图形．古人认为“天圆地方”，宇宙就像一个圆形的大锅盖在一个方形的棋盘上．中国古代的建筑也会经常采用圆形和正方形的图案．而在面积计算中，圆与正方形也有很大的关系．关于正方形和圆，有以下的面积关系：由此我们可以进一步推断：圆外切正方形面积是内接正方形面积的______倍；正方形外接圆面积是内切圆面积的______倍．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1．（1）左图中正方形的面积是8，那么圆的面积是多少？（π取3.14）（2）右图中正方形的面积是16，那么圆的面积是多少？（π取3.14）分析：利用圆中方和方中圆的比例关系可以轻松求解．练习1．如图，已知正方形的边长是2，求大圆及小圆的面积．（π取3.14）圆的外切正方形与内接正方形正方形的外接圆与内切圆方中圆圆中方例题2．计算下面各图中阴影部分的面积，并比较大小．（π取3.14）分析：利用方中圆的比例关系可以轻松求解．练习2．如图，已知长方形的面积是12，则图中阴影部分的面积是多少？（π取3.14）- - - - - - - - - - - - - -小故事圆与方有一天，圆形和方形碰到了一起，它们一见面就吵了个面红耳赤，不管谁劝都不听．圆形说：“我们圆形就是比你们方形用处大，人们日常生活中用的锅呀、碗呀，体育中的蓝球、排球，水果里的苹果、桔子，大到汽车轮胎、自行车轮胎，都是我的家族．瞧，我们是不是比你们用处大！”圆形得意洋洋地说完．方形“哼”了一声说：“我们方形家族才是无处不在呢，人们用的电器、冰箱、彩电、电脑，就连学生用的课本都是我们方形的哟！”方形也自豪地说．它们谁也无法说服谁，都来到大街上．望着街上的车，方形对着圆形的车轮喊了声：“变！”转眼间车轮变成了方形．正当方形喜笑颜开时，人群出现了混乱，汽车开不了，自行车也只能扛着了，大家都在说：“这是谁干的呀！真是害人呀！”而圆形来到一座刚建好的大楼前，望着由一块块方形红砖盖成的大楼，圆形生气地大声喊了声“变！”呀，方形红砖变成圆形了．圆形还没来及高兴呢，就听“轰”一声大楼倒了下来．看到这个情景，圆形呆住了：“这是怎么回事？” 只见混乱的人群里走出了一位老人，他来到方形和圆形面前对它们说：“其实你们都很棒，只是你们分工不同而已，只要你们齐心协力，一定会为人类作更大的贡献．在上一讲中，我们主要使用割补的方法来计算不规则图形的面积．而对于一些比较特殊8的形状，我们可以把它看成是一些基本图形的重叠部分，利用容斥原理计算出它的面积．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3．如图，求下面各图中阴影部分的面积．（π取3.14）分析：阴影部分可以看成是哪些图形的重叠部分？练习3．已知下图中正方形的面积是16，那么阴影部分的面积是多少？（π取3.14）在生活当中，有很多旋转的物体，比如车轮、方向盘等．这些物体在运动的过程中，扫过的图形都是曲线形．这些曲线形的周长和面积应该怎么计算呢？例题4．图中正方形的边长是4厘米，圆形的半径是1厘米．当圆形绕正方形滚动一周又回到原来位置时，扫过的面积有多大？（π取3.14）分析：要求扫过的面积，关键在于弄清扫过的区域；而要弄清扫过的区域，关键在于弄清区域的边界．你能通过合理动态想象，画出边界来吗？练习4．如图，正方形的边长是2厘米，圆形的半径是1厘米．当圆形绕正方形滚动一周又回到原来位置时，扫过的面积有多大？（π取3.14）例题5．如图，求阴影部分的面积．（π取3.14）分析：阴影部分可以看成是四个扇形的重叠部分，但是扇形的半径图中并没有给出，那么应该怎么计算扇形的面积呢？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题6．（1）如图，一只小狗被拴在一个边长为4米的正方形的建筑物的顶点A处，四周都是空地．绳长8米．小狗的活动范围是多少平方米？（2）如果小狗不是被拴在A处，而是在一边的中点B处，那么小狗的活动范围是多少平方米？（建筑外墙不可逾越，小狗身长忽略不计，π取3.14）分析：如果没有建筑物的阻挡，小狗的活动范围应该是一个圆．有建筑物的话，活动范围会受到什么样的影响呢？A含有“圆”字的成语圆首方足：出自《淮南子·精神训》：“头之圆也象天，足之方也象地．”用来代指人类．戴圆履方：出自《淮南子·本经训》：“戴圆履方，抱表怀绳．”履：踩着；圆、方：古人以为天圆地方．头顶着天，脚踩着地．指生活在人间．方枘圆凿：出自战国时楚国宋玉的《九辨》：“圆凿而方枘兮，吾固知其龃龉而难入．”凿：榫眼；枘：榫头．方枘装不进圆凿．比喻格格不入，不能相合．这三个成语之外，还有很多成语中都含有“圆”和“方”这两个字，如圆孔方木、圆颅方趾、外圆内方等．这说明古人对于圆和方的认识非常深刻，已经将其应用到了生活中的很多方面．而我们在圆与扇形的学习中，也要注意圆形与正方形之间的联系．元方，你怎么看？破镜重圆：这个成语故事是由华阴人、隋越国公杨素的一段成人之美的佳话而来的．杨素，字处道，在辅佐隋文帝杨坚结束割据，统一天下，建立隋朝江山方面立下了汗马功劳．他不仅足智多谋，才华横溢，而且文武双全，风流倜傥．在朝野上下都声势显赫，颇著声名．隋开皇九年（公元589年）杨素与文帝杨坚的两个儿子陈后主叔宝的嫔妃、亲戚，其中有陈叔宝的妹妹枣陈太子舍人徐德言之妻，也就是陈国的乐昌公主．由于杨素破陈有功，加之乐昌公主才色绝代，隋文帝就乱点鸳鸯，将乐昌公主送进杨素中，赐为杨素小妾．杨素既仰慕乐昌公主的才华，又贪图乐昌公主的美色，因此就更加宠爱，还为乐昌公主专门营造了宅院．然而乐昌公主却终日郁郁寡欢，默无一语．原来，乐昌公主与丈夫徐德言两心相知，情义深厚．陈国将亡之际，徐德言曾流着泪对妻子说：“国已危如累卵，家安岂能保全，你我分离已成必然．以你这般容貌与才华，国亡后必然会被掠入豪宅之家，我们夫妻长久离散，名居一方，唯有日夜相思，梦中神会．倘若老天有眼，不割断我们今世的这段情缘，你我今后定会有相见之日．所以我们应当有个信物，以求日后相认重逢．”说完，徐德言把一枚铜镜一劈两半，夫妻二人各藏半边．徐德言又说：“如果你真的被掠进富豪人家，就在明年正月十五那天，将你的半片铜镜拿到街市去卖，假若我也幸存人世，那一天就一定会赶到都市，通过铜镜去打问你的消息．”一对恩爱夫妻，在国家山河破碎之时，虽然劫后余生，却受尽了离散之苦．好容易盼到第二年正月十五，徐德言经过千辛万苦，颠沛流离，终于赶到都市大街，果然看见一个老头在叫卖半片铜镜，而且价钱昂贵，令人不敢问津．徐德言一看半片铜镜，知妻子已有下落，禁不住涕泪俱下．他不敢怠慢，忙按老者要的价给了钱，又立即把老者领到自己的住处．吃喝已罢，徐德言向老者讲述一年前破镜的故事，并拿出自己珍藏的另一半铜镜．颤索索两半铜镜还未吻合，徐德言早已泣不成声……卖镜老人被他们的夫妻深情感动得热泪盈眶．他答应徐德言，一定要在他们之间传递消息，让他们夫妻早日团圆．徐德言就着月光题诗一首，托老人带给乐昌公主．诗这样写道：镜与人俱去，镜归人不归．无复嫦娥影，空留明月辉．乐昌公主看到丈夫题诗，想到与丈夫咫尺天涯，难以相见，更是大放悲声，终日容颜凄苦，水米不进．杨素再三盘问，才知道了其中情由，也不由得被他二人的真情深深打动．他立即派人将徐德言召入府中，让他夫妻二人团聚．府中上下都为徐陈二人破镜重圆和越国公杨素的宽宏大度、成人之美而感叹不已．在欢庆的感激之情．宴罢，夫妻二人携手同归江南故里．这段佳话被四处传扬，所以就有了破镜重圆的典故，一直流传至今．作业1. 如图，图中较小圆的面积是3.14，较大圆的面积是多少？作业2. 如图，正方形的面积是8，阴影部分的面积是多少？（π取3.14）作业3. 如图，一头山羊被拴在一个边长为4米的等边三角形的建筑物的一个顶点处，四周都很空旷．绳长刚好够山羊走到三角形建筑物外的任一位置，山羊的活动范围有多少平方米？（建筑外墙不可逾越，山羊身长忽略不计，π取3）作业4. 如图，正方形ABCD 边长为1厘米，依次以A 、B 、C 、D 为圆心，以AD 、BE 、CF 、DG 为半径画出四个直角扇形，那么阴影部分的面积是多少？（π取3.14）作业5. 如图，长方形的长为6厘米，宽为2厘米，圆形的半径是1厘米．当圆形绕长方形滚动一周又回到原来位置时，扫过的面积有多大？（π取3.14）第1题图第2题图第3题图第4题图ABCD E HF第二讲圆与扇形进阶例题1.答案：（1）6.28；（2）25.12详解：（1）方中圆，方与圆的比为4:π，可求出圆的面积是6.28；（2）圆中方，圆与方的面积之比是π:2，可求出圆的面积是25.12．例题2.答案：面积都是12.56详解：左图中阴影部分的面积为24π112.56⨯⨯=，右图中阴影部分的面积为2π212.56⨯=．例题3.答案：（1）2.28；（2）2.28详解：（1）可利用重叠求出阴影部分面积，阴影面积等于两个圆心角为90°、半径为2的扇形面积减去边长为2的正方形面积．即212222 2.284S π=⨯⨯⨯-⨯=；（2）将四个半径为1厘米的半圆叠加起来，恰好将每块阴影各算了两遍，每块空白各算了一遍．所以阴影部分面积等于4个半径为1厘米的半圆面积之和减去边长为2厘米的正方形面积，即21412224 2.282ππ⨯⨯⨯-⨯=-=平方厘米．例题4.答案：44.56详解：扫过的区域如图中阴影所示，由两类图形组成：4个长为4厘米、宽为2厘米的长方形，4块半径为2厘米、圆心角为90度的扇形（恰好拼成一个圆）．所以扫过的面积是2424π244.56⨯⨯+⨯=平方厘米．例题5.答案：2.28详解：阴影部分面积等于四块扇形面积减去正方形面积，而四块扇形恰好构成一个整圆．圆的直径等于正方形的对角线．设正方形对角线为l ，圆的直径为d ，则242l =，28l =，28d =，圆的面积为22 6.284d S ππ===．=6.284=2.28S -．例题6.答案：（1）175.84平方米；（2）163.28平方米详解：（1）如下左图，小狗的活动范围为圆心角为270°、半径为8米的扇形，和两个圆心角为90°、半径为4米的扇形．总大小为223184256175.8444πππ⨯⨯+⨯⨯⨯==平方米．（2）如下右图，小狗的活动范围为半径是8米的半圆，和两个圆心角为90°、半径为6米的扇形，以及两个圆心角为90°、半径为2米的扇形．总大小为2221118622252163.28244ππππ⨯⨯+⨯⨯⨯+⨯⨯⨯==平方米．练习1.答案：6.28，3.14简答：方中圆，方和圆的面积比为4:π，可求出小圆的面积是3.14．大圆的面积是小圆面积的2倍，是6.28．练习2.答案：2.58简答：长方形可以分成两个面积相等的正方形，面积都是6．方中圆，方和圆的面积比为4:π，可求出小圆的面积是1.5π．那么阴影部分的面积是12 1.5π2 2.58-⨯=．练习3.答案：9.12简答：21π42169.124⨯⨯⨯-=．练习4.答案：28.56简答：扫过的区域如图所示．正方形的边长是2厘米，四个正方形的面积之和是16平方厘米．四个扇形正好可以拼成一个半径为2厘米的圆，圆的面积是12.56平方厘米．最后的结果是28.56平方厘米．作业1.答案：6.28简答：较大圆、正方形和较小圆之间的比是2π：4：π，即较大圆的面积是较小圆的2倍．作业2. 答案：4.56简答：四个半圆的面积之和减去正方形的面积就是阴影部分的面积．四个半圆可以拼成两个相同的圆．而这个圆和正方形正好是方中圆的关系，由此可求出圆的面积是6.28．那么阴影部分的面积就是6.2828 4.56⨯-=．作业3.答案：98简答：山羊的活动范围如图所示，绳长为6米，面积为2230012098ππ62π2983603603⨯⨯+⨯⨯⨯==平方米．作业4. 答案：23.55 简答：阴影部分的面积是2221113.141 3.142 3.143444⨯⨯+⨯⨯+⨯⨯ 213.14423.554+⨯⨯=平方厘米．作业5. 答案：44.56简答：扫过的区域如图所示，面积为2226222π244.56⨯⨯+⨯⨯+⨯=平方厘米．。

圆和扇形知识点归纳

圆和扇形知识点归纳圆和扇形是几何学中的基本图形，广泛应用于建筑、工程、地理测量等领域。

它们具有一些重要的特性和性质，下面将对圆和扇形的知识点进行归纳。

一、圆的基本概念：1.圆的定义：由平面上所有与给定点（圆心）的距离等于常数（半径）的点的集合所组成的图形叫做圆。

2.圆心和半径：圆心是圆上任意两点的连线的中点，圆半径是圆心到圆上任意一点的距离。

3.圆的重要性质：(1)圆上任意两点与圆心的距离相等；(2)圆的直径是圆的一条由圆心到圆上的点的线段，它的长度等于半径的两倍；(3)圆的弦是圆上的两点间的线段，弦的长度小于等于直径；(4)圆的弧是圆上的一段弦；(5)圆的面积公式为S=πr²，其中S是圆的面积，r是圆的半径。

二、扇形的基本概念：1.扇形的定义：由圆心和圆上一条弧段所组成的图形叫做扇形。

2.扇形的重要性质：(1)扇形的弧长是扇形弧的长度，可以通过圆的周长与圆心角的比例得到；(2)扇形的面积是扇形所占圆的面积的比例，可以通过圆的面积与圆心角的比例得到；(3)扇形弧的度数是指扇形所对的圆心角的度数，单位为度或弧度；(4)扇形所对的圆心角的度数等于其所包含的弧长与半径的比例。

三、圆和扇形之间的关系：1.扇形是圆的一部分，是圆的一个划分区域。

2.扇形的度数与其所对的圆心角的度数相等。

3.扇形的面积是圆的面积的一部分，可以通过圆的面积与圆心角的比例计算得到。

4.扇形的弧长是圆的周长的一部分，可以通过圆的周长与圆心角的比例计算得到。

四、圆和扇形的应用：1.圆和扇形在建筑领域中用于设计圆形建筑物、广场等。

2.圆和扇形在地理测量中用于计算球面上的角度和弧长。

3.圆和扇形在制图中用于画圆形或弧形的路径。

4.圆和扇形在机械工程中用于设计齿轮、曲柄等圆形传动装置。

5.圆和扇形在电子学中用于设计电路板上的圆形路径。

综上所述，圆和扇形是几何学中的基本图形，具有一些重要的特性和性质。

它们的应用广泛，涉及到建筑、工程、地理测量等多个领域。

扇形的魅力：启蒙性的《圆之认识扇形》教案设计

扇形是几何图形中的一种，具有独特的魅力。

它的美丽和神秘性吸引了许多数学爱好者。

在数学教育中，扇形是一个相对容易理解和学习的几何图形之一。

今天，我们将介绍一种启蒙性的教学方法——《圆之认识扇形》教案设计，来探索扇形的魅力。

1.教学目的通过此教案，学生能够：1）学习关于扇形的定义和基本性质；2）了解扇形在实际中的应用；3）提高学生的几何思维能力。

2.教学内容1）扇形的定义和性质：扇形是由一条弧和两条半径所围成的区域。

其中，弧所对的圆心角为扇形的中心角，两条半径为直径的线段互相垂直，同时也是扇形的边界线段。

扇形具有以下基本性质：①扇形的面积= (π×r2×θ)/360° （其中，r为半径，θ为扇形圆心角的度数）；②扇形的周长= r×(θ/180°)π+2r 。

2）扇形的应用：扇形在生活中有着广泛的应用，比如可以用来计算圆形的面积和周长，还可以用来计算圆形的弧长和圆心角。

此外，扇形在风扇、电扇等电气设备中也有很广泛的应用。

3.教学过程1）引入问题：老师可以利用一个有趣的问题来引入扇形的学习，例如：如果你喜欢吃披萨，你能否算一算当你吃掉一个披萨切成的扇形时，这个扇形的面积是多少？2）讲解扇形定义和性质：老师可以使用幻灯片等形式来讲解扇形的定义和基本性质，并引导学生进行互动讨论和思考。

让学生通过观察、推理等方式，深入理解扇形的知识点。

3）扇形应用实例：让学生通过实例来理解扇形的应用，比如计算圆的面积和周长，如何测量圆柱的侧面积等等。

这样可以帮助学生增强对扇形的实际应用的认识和理解。

4）巩固和拓展训练：老师可以设计一些巩固和拓展训练，让学生进行个人或小组测验，测试他们对扇形知识的掌握程度，并运用和运用扇形的数学技能，通过创新、探索与发现，突破常规，以展现更有创意、有趣和有挑战性的多种复杂问题的解决能力。

4.教学评估教师主要可以从以下几个方面对学生进行评估：1）学生是否掌握扇形的定义和性质；2）能否熟练计算扇形的面积和周长，并能使用扇形计算实际问题；3）思维和创新能力是否得到提高。