重庆备战中考数学压轴题专题锐角三角函数的经典综合题
备战中考数学锐角三角函数-经典压轴题附详细答案

备战中考数学锐角三角函数-经典压轴题附详细答案一、锐角三角函数1.小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.(1)求∠CAO'的度数.(2)显示屏的顶部B'比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.【解析】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×=12,由C、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,∴sin∠CAO′=,∴∠CAO′=30°;(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×=12,∵O′C⊥OA,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,∴O′B′+O′C﹣BD=24+12﹣12=36﹣12,∴显示屏的顶部B′比原来升高了(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,理由:∵显示屏O′B与水平线的夹角仍保持120°,∴∠EO′F=120°,∴∠FO′A=∠CAO′=30°,∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.2.如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.(1) 试判断BE与FH的数量关系,并说明理由;(2) 求证:∠ACF=90°;(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求的长.图1 图2【答案】(1)BE="FH" ;理由见解析(2)证明见解析(3)=2π【解析】试题分析:(1)由△ABE≌△EHF(SAS)即可得到BE=FH(2)由(1)可知AB=EH,而BC=AB,FH=EB,从而可知△FHC是等腰直角三角形,∠FCH 为45°,而∠ACB也为45°,从而可证明(3)由已知可知∠EAC=30°,AF是直径,设圆心为O,连接EO,过点E作EN⊥AC于点N,则可得△ECN为等腰直角三角形,从而可得EN的长,进而可得AE的长,得到半径,得到所对圆心角的度数,从而求得弧长试题解析:(1)BE=FH.理由如下:∵四边形ABCD是正方形∴∠B=90°,∵FH⊥BC ∴∠FHE=90°又∵∠AEF=90°∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°∴∠HEF=∠BAE ∴∠AEB=∠EFH 又∵AE=EF∴△ABE≌△EHF(SAS)∴BE=FH(2)∵△ABE≌△EHF∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE="CH"∴CH=FH∴∠FCH=45°,∴∠FCM=45°∵AC是正方形对角线,∴∠ACD=45°∴∠ACF=∠FCM +∠ACD =90°(3)∵AE=EF,∴△AEF是等腰直角三角形△AEF外接圆的圆心在斜边AF的中点上.设该中点为O.连结EO得∠AOE=90°过E作EN⊥AC于点NRt△ENC中,EC=4,∠ECA=45°,∴EN=NC=Rt△ENA中,EN =又∵∠EAF=45°∠CAF=∠CEF=15°(等弧对等角)∴∠EAC=30°∴AE=Rt△AFE中,AE== EF,∴AF=8AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°=2π·4·(90°÷360°)=2π考点:1、正方形;2、等腰直角三角形;3、圆周角定理;4、三角函数3.在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P 作PF∥BC,交对角线BD于点F.(1)如图1,将△PDF 沿对角线BD 翻折得到△QDF ,QF 交AD 于点E .求证:△DEF 是等腰三角形;(2)如图2,将△PDF 绕点D 逆时针方向旋转得到△P'DF',连接P'C ,F'B .设旋转角为α(0°<α<180°).①若0°<α<∠BDC ,即DF'在∠BDC 的内部时,求证:△DP'C ∽△DF'B . ②如图3,若点P 是CD 的中点,△DF'B 能否为直角三角形?如果能,试求出此时tan ∠DBF'的值,如果不能,请说明理由.【答案】(1)证明见解析;(2)①证明见解析;②12或33. 【解析】【分析】(1)根据翻折的性质以及平行线的性质可知∠DFQ=∠ADF ,所以△DEF 是等腰三角形;(2)①由于PF ∥BC ,所以△DPF ∽△DCB ,从而易证△DP′F′∽△DCB ;②由于△DF'B 是直角三角形,但不知道哪个的角是直角,故需要对该三角形的内角进行分类讨论.【详解】(1)由翻折可知:∠DFP=∠DFQ , ∵PF ∥BC , ∴∠DFP=∠ADF , ∴∠DFQ=∠ADF , ∴△DEF 是等腰三角形;(2)①若0°<α<∠BDC ,即DF'在∠BDC 的内部时, ∵∠P′DF′=∠PDF ,∴∠P′DF′﹣∠F′DC=∠PDF ﹣∠F′DC , ∴∠P′DC=∠F′DB ,由旋转的性质可知:△DP′F′≌△DPF , ∵PF ∥BC , ∴△DPF ∽△DCB , ∴△DP′F′∽△DCB ∴''DC DP DB DF , ∴△DP'C ∽△DF'B ;②当∠F′DB=90°时,如图所示,∵DF′=DF=12BD , ∴'12DF BD =, ∴tan ∠DBF′='12DF BD =;当∠DBF′=90°,此时DF′是斜边,即DF′>DB ,不符合题意; 当∠DF′B=90°时,如图所示,∵DF′=DF=12BD , ∴∠DBF′=30°,∴tan ∠DBF′=3.【点睛】本题考查了相似三角形的综合问题,涉及旋转的性质,锐角三角函数的定义,相似三角形的性质以及判定等知识,综合性较强,有一定的难度,熟练掌握相关的性质与定理、运用分类思想进行讨论是解题的关键.4.已知:如图,在Rt △ABC 中,∠ACB=90°,点M 是斜边AB 的中点,MD ∥BC ,且MD=CM ,DE ⊥AB 于点E ,连结AD 、CD . (1)求证:△MED ∽△BCA ; (2)求证:△AMD ≌△CMD ;(3)设△MDE 的面积为S 1,四边形BCMD 的面积为S 2,当S 2=175S 1时,求cos ∠ABC 的值.【答案】(1)证明见解析;(2)证明见解析;(3)cos ∠ABC=57. 【解析】 【分析】(1)易证∠DME=∠CBA ,∠ACB=∠MED=90°,从而可证明△MED ∽△BCA ; (2)由∠ACB=90°,点M 是斜边AB 的中点,可知MB=MC=AM ,从而可证明∠AMD=∠CMD ,从而可利用全等三角形的判定证明△AMD ≌△CMD ; (3)易证MD=2AB ,由(1)可知:△MED ∽△BCA ,所以2114ACB S MD S AB ⎛⎫== ⎪⎝⎭V ,所以S △MCB =12S △ACB =2S 1,从而可求出S △EBD =S 2﹣S △MCB ﹣S 1=25S 1,由于1EBD S ME S EB =V ,从而可知52ME EB =,设ME=5x ,EB=2x ,从而可求出AB=14x ,BC=72,最后根据锐角三角函数的定义即可求出答案. 【详解】(1)∵MD ∥BC , ∴∠DME=∠CBA , ∵∠ACB=∠MED=90°, ∴△MED ∽△BCA ;(2)∵∠ACB=90°,点M 是斜边AB 的中点, ∴MB=MC=AM , ∴∠MCB=∠MBC , ∵∠DMB=∠MBC ,∴∠MCB=∠DMB=∠MBC , ∵∠AMD=180°﹣∠DMB ,∠CMD=180°﹣∠MCB ﹣∠MBC+∠DMB=180°﹣∠MBC , ∴∠AMD=∠CMD , 在△AMD 与△CMD 中,MD MD AMD CMD AM CM =⎧⎪∠=∠⎨⎪=⎩, ∴△AMD ≌△CMD (SAS ); (3)∵MD=CM ,∴AM=MC=MD=MB , ∴MD=2AB ,由(1)可知:△MED ∽△BCA , ∴2114ACB S MD S AB ⎛⎫== ⎪⎝⎭V , ∴S △ACB =4S 1, ∵CM 是△ACB 的中线, ∴S △MCB =12S △ACB =2S 1, ∴S △EBD =S 2﹣S △MCB ﹣S 1=25S 1, ∵1EBDS MES EB=V , ∴1125S MEEB S =,∴52ME EB =, 设ME=5x ,EB=2x , ∴MB=7x , ∴AB=2MB=14x ,∵12MD ME AB BC ==, ∴BC=10x ,∴cos ∠ABC=105147BC x AB x ==. 【点睛】本题考查相似三角形的综合问题,涉及直角三角形斜边中线的性质,全等三角形的性质与判定,相似三角形的判定与性质,三角形面积的面积比,锐角三角函数的定义等知识,综合程度较高,熟练掌握和灵活运用相关的性质及定理进行解题是关键.5.如图,AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于切点为G ,连接AG 交CD 于K . (1)求证:KE=GE ;(2)若KG 2=KD•GE ,试判断AC 与EF 的位置关系,并说明理由; (3)在(2)的条件下,若sinE=,AK=,求FG 的长.【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= .【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KD•GE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.试题解析:(1)如图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.(2)AC∥EF,理由为连接GD,如图2所示.∵KG2=KD•GE,即,∴,又∵∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∵∠C=∠AGD,∴∠E=∠C,∴AC∥EF;(3)连接OG,OC,如图3所示,∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.∵sinE=sin∠ACH=,设AH=3t,则AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK-CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即(3t)2+t2=(2)2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即(r-3t)2+(4t)2=r2,解得r= t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH=,∴FG=【点睛】此题考查了切线的性质,相似三角形的判定与性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握定理及性质是解本题的关键.6.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.7.如图,已知点从出发,以1个单位长度/秒的速度沿轴向正方向运动,以为顶点作菱形,使点在第一象限内,且;以为圆心,为半径作圆.设点运动了秒,求:(1)点的坐标(用含的代数式表示);(2)当点在运动过程中,所有使与菱形的边所在直线相切的的值.【答案】解:(1)过作轴于,,,,,点的坐标为.(2)①当与相切时(如图1),切点为,此时,,,.②当与,即与轴相切时(如图2),则切点为,,过作于,则,,.③当与所在直线相切时(如图3),设切点为,交于,则,,.过作轴于,则,,化简,得,解得,,.所求的值是,和.【解析】(1)过作轴于,利用三角函数求得OD、DC的长,从而求得点的坐标⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=oc/op,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.8.如图,已知正方形在直角坐标系中,点分别在轴、轴的正半轴上,点在坐标原点.等腰直角三角板的直角顶点在原点,分别在上,且将三角板绕点逆时针旋转至的位置,连结(1)求证:(2)若三角板绕点逆时针旋转一周,是否存在某一位置,使得若存在,请求出此时点的坐标;若不存在,请说明理由.【答案】(1)证明见解析(2)存在,或【解析】(1)证明:∵四边形为正方形,∴∵三角板是等腰直角三角形,∴又三角板绕点逆时针旋转至的位置时,∴···························· 3分(2)存在.································· 4分∵∴过点与平行的直线有且只有一条,并与垂直,又当三角板绕点逆时针旋转一周时,则点在以为圆心,以为半径的圆上,························ 5分∴过点与垂直的直线必是圆的切线,又点是圆外一点,过点与圆相切的直线有且只有2条,不妨设为和此时,点分别在点和点,满足·························· 7分当切点在第二象限时,点在第一象限,在直角三角形中,∴∴∴点的横坐标为:点的纵坐标为:∴点的坐标为··························· 9分当切点在第一象限时,点在第四象限,同理可求:点的坐标为综上所述,三角板绕点逆时针旋转一周,存在两个位置,使得此时点的坐标为或································ 11分(1)根据旋转的性质找到相等的线段,根据SAS定理证明;(2)由于△OEF是等腰Rt△,若OE∥CF,那么CF必与OF垂直;在旋转过程中,E、F的轨迹是以O为圆心,OE(或OF)长为半径的圆,若CF⊥OF,那么CF必为⊙O的切线,且切点为F;可过C作⊙O的切线,那么这两个切点都符合F点的要求,因此对应的E点也有两个;在Rt△OFC中,OF=2,OC=OA=4,可证得∠FCO=30°,即∠EOC=30°,已知了OE 的长,通过解直角三角形,不难得到E点的坐标,由此得解.9.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.【答案】故大坝的截面的周长是(345)米,面积是1470平方米.【解析】试题分析:先根据两个坡比求出AE和BF的长,然后利用勾股定理求出AD和BC,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC,梯形的面积公式可得出答案.试题解析:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,∴AE=18米,在RT△ADE中,22+34DE AE∵背水坡坡比为1:2,∴BF=60米,在RT△BCF中,22+5CF BF∴周长345(345)米,面积=(10+18+10+60)×30÷2=1470(平方米).故大坝的截面的周长是(345)米,面积是1470平方米.10.阅读下面材料:观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,过A 作AD ⊥BC 于D (如图),则sin B =AD c ,sin C =ADb,即AD =c sin B ,AD =b sin C ,于是c sin B =b sin C ,即sin sin b c B C = .同理有:sin sin c aC A=,sin sin a b A B=,所以sin sin sin a b cA B C ==. 即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.(1)如图,△ABC 中,∠B =75°,∠C =45°,BC =60,则AB = ;(2)如图,一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B 处,此时又测得灯塔A 在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A 的距离AB . (3)在(2)的条件下,试求75°的正弦值.(结果保留根号)【答案】(1)6;(2)6海里;(36+2【解析】 【分析】(1)根据材料:在一个三角形中,各边和它所对角的正弦的比相等,写出比例关系,代入数值即可求得AB 的值.(2)此题可先由速度和时间求出BC 的距离,再由各方向角得出∠A 的角度,过B 作BM ⊥AC 于M ,求出∠MBC=30°,求出MC ,由勾股定理求出BM ,求出AM 、BM 的长,由勾股定理求出AB 即可;(3)在三角形ABC 中,∠A=45,∠ABC=75,∠ACB=60,过点C 作AC 的垂线BD ,构造直角三角形ABD ,BCD ,在直角三角形ABD 中可求出AD 的长,进而可求出sin75°的值. 【详解】解:(1)在△ABC 中,∠B=75°,∠C=45°,BC=60,则∠A=60°,∵ABsinC =sinBCA,∴45ABsin o=60sin60o,即22=32,解得:AB=206.(2)如图,依题意:BC=60×0.5=30(海里)∵CD∥BE,∴∠DCB+∠CBE=180°∵∠DCB=30°,∴∠CBE=150°∵∠ABE=75°.∴∠ABC=75°,∴∠A=45°,在△ABC中,sinABACB∠=BCsin A∠即60?ABsin=3045?sin,解之得:6.答:货轮距灯塔的距离6海里.(3)过点B作AC的垂线BM,垂足为M.在直角三角形ABM中,∠A=45°,AB=156,所以AM=153,在直角三角形BDC中,∠BCM=60°,BC=30°,可求得CM=15,所以AC=153+15,由题意得,15315+=156,sin75°=6+2.【点睛】本题考查方向角的含义,三角形的内角和定理,含30度角的直角三角形,等腰三角形的性质和判定等知识点,解题关键是熟练掌握解直角三角形方法.11.3米/秒 =65.88千米/小时>60千米/小时.∴此车超过限制速度.…4分12.如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D(1)求证:PC是⊙O的切线;(2)求证:PA AD PC CD=;(3)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P=35,CF=5,求BE的长.【答案】(1)见解析;(2)BE=12.【解析】【分析】(1)连接OC,由PC切⊙O于点C,得到OC⊥PC,于是得到∠PCA+∠OCA=90°,由AB为⊙O的直径,得到∠ABC+∠OAC=90°,由于OC=OA,证得∠OCA=∠OAC,于是得到结论;(2)由AE∥PC,得到∠PCA=∠CAF根据垂径定理得到弧AC=弧AG,于是得到∠ACF=∠ABC,由于∠PCA=∠ABC,推出∠ACF=∠CAF,根据等腰三角形的性质得到CF=AF,在R t△AFD中,AF=5,sin∠FAD=35,求得FD=3,AD=4,CD=8,在R t△OCD中,设OC=r,根据勾股定理得到方程r2=(r-4)2+82,解得r=10,得到AB=2r=20,由于AB为⊙O的直径,得到∠AEB=90°,在R t△ABE中,由sin∠EAD=35,得到BEAB=35,于是求得结论.【详解】(1)证明:连接OC,∵PC切⊙O于点C,∴OC⊥PC,∴∠PCO=90°,∴∠PCA+∠OCA=90°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ABC+∠OAC=90°,∵OC=OA,∴∠OCA=∠OAC,∴∠PCA=∠ABC;(2)解:∵AE∥PC,∴∠PCA=∠CAF,∵AB⊥CG,∴弧AC=弧AG,∴∠ACF=∠ABC,∵∠PCA=∠ABC,∴∠ACF=∠CAF,∴CF=AF,∵CF=5,∴AF=5,∵AE∥PC,∴∠FAD=∠P,∵sin∠P=35,∴sin∠FAD=35,在R t△AFD中,AF=5,sin∠FAD=35,∴FD=3,AD=4,∴CD=8,在R t△OCD中,设OC=r,∴r2=(r﹣4)2+82,∴r=10,∴AB=2r=20,∵AB为⊙O的直径,∴∠AEB=90°,在R t△ABE中,∵sin∠EAD=35,∴35BEAB,∵AB=20,∴BE=12.【点睛】本题考查切线的性质,锐角三角函数,圆周角定理,等腰三角形的性质,解题关键是连接OC构造直角三角形.13.已知Rt△ABC,∠BAC=90°,点D是BC中点,AD=AC,BC=43,过A,D两点作⊙O,交AB于点E,(1)求弦AD的长;(2)如图1,当圆心O在AB上且点M是⊙O上一动点,连接DM交AB于点N,求当ON 等于多少时,三点D、E、M组成的三角形是等腰三角形?(3)如图2,当圆心O不在AB上且动圆⊙O与DB相交于点Q时,过D作DH⊥AB(垂足为H)并交⊙O于点P,问:当⊙O变动时DP﹣DQ的值变不变?若不变,请求出其值;若变化,请说明理由.【答案】(1)23(2)当ON 等于1﹣1时,三点D 、E 、M 组成的三角形是等腰三角形(3)不变,理由见解析【解析】【分析】(1)根据直角三角形斜边上的中线等于斜边的一半即可得到AD 的长;(2)连DE 、ME ,易得当ED 和EM 为等腰三角形EDM 的两腰,根据垂径定理得推论得OE ⊥DM ,易得到△ADC 为等边三角形,得∠CAD=60°,则∠DAO=30°,∠DON=60°,然后根据含30°的直角三角形三边的关系得DN=12;当MD=ME ,DE 为底边,作DH ⊥AE ,由于∠DAE=30°,得到,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,又∠M=∠DAE=30°,MD=ME ,得到∠MDE=75°,则∠ADM=90°-75°=15°,可得到∠DNO=45°,根据等腰直角三角形的性质得到;(3)连AP 、AQ ,DP ⊥AB ,得AC ∥DP ,则∠PDB=∠C=60°,再根据圆周角定理得∠PAQ=∠PDB ,∠AQC=∠P ,则∠PAQ=60°,∠CAQ=∠PAD ,易证得△AQC ≌△APD ,得到DP=CQ ,则DP-DQ=CQ-DQ=CD ,而△ADC 为等边三角形,DP-DQ 的值.【详解】解:(1)∵∠BAC =90°,点D 是BC 中点,BC =∴AD=12BC = (2)连DE 、ME ,如图,∵DM >DE ,当ED 和EM 为等腰三角形EDM 的两腰,∴OE ⊥DM ,又∵AD =AC ,∴△ADC 为等边三角形,∴∠CAD =60°,∴∠DAO =30°,∴∠DON =60°,在Rt △ADN 中,DN =12AD ,在Rt △ODN 中,ON DN =1, ∴当ON 等于1时,三点D 、E 、M 组成的三角形是等腰三角形;当MD =ME ,DE 为底边,如图3,作DH ⊥AE ,∵AD =∠DAE =30°,∴DH ∠DEA =60°,DE =2,∴△ODE为等边三角形,∴OE=DE=2,OH=1,∵∠M=∠DAE=30°,而MD=ME,∴∠MDE=75°,∴∠ADM=90°﹣75°=15°,∴∠DNO=45°,∴△NDH为等腰直角三角形,∴NH=DH=3,∴ON=3﹣1;综上所述,当ON等于1或3﹣1时,三点D、E、M组成的三角形是等腰三角形;(3)当⊙O变动时DP﹣DQ的值不变,DP﹣DQ=23.理由如下:连AP、AQ,如图2,∵∠C=∠CAD=60°,而DP⊥AB,∴AC∥DP,∴∠PDB=∠C=60°,又∵∠PAQ=∠PDB,∴∠PAQ=60°,∴∠CAQ=∠PAD,∵AC=AD,∠AQC=∠P,∴△AQC≌△APD,∴DP=CQ,∴DP﹣DQ=CQ﹣DQ=CD=23.【点睛】本题考查了垂径定理和圆周角定理:平分弧的直径垂直弧所对的弦;在同圆和等圆中,相等的弧所对的圆周角相等.也考查了等腰三角形的性质以及含30°的直角三角形三边的关系.14.如图,正方形ABCD2+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,(1)求证:△ABF∽△ACE;(2)求tan∠BAE的值;(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x =1,在Rt △ABE 中,∵∠ABE =90°,∴tan ∠EAB =221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC 22AB BC +2,∴OA =OC =OB =12AC 22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =222+ •2﹣1)=22, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH 2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=22+.. ∴PE+PF 22+【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.15.如图,某次中俄“海上联合”反潜演习中,我军舰A 测得潜艇C 的俯角为30°.位于军舰A 正上方1000米的反潜直升机B 侧得潜艇C 的俯角为68°.试根据以上数据求出潜艇C 离开海平面的下潜深度.(结果保留整数.参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,3)【答案】潜艇C离开海平面的下潜深度约为308米【解析】试题分析:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,用锐角三角函数分别在Rt△ACD中表示出CD和在Rt△BCD中表示出BD,利用BD=AD+AB二者之间的关系列出方程求解.试题解析:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,根据题意得:∠ACD=30°,∠BCD=68°,设AD=x,则BD=BA+AD=1000+x,在Rt△ACD中,CD=tan AD ACD=tan30x= 3x在Rt△BCD中,BD=CD•tan68°,∴325+x=3x•tan68°解得:x≈100米,∴潜艇C离开海平面的下潜深度为100米.点睛:本题考查了解直角三角形的应用,解题的关键是作出辅助线,从题目中找出直角三角形并选择合适的边角关系求解.视频。
中考数学真题精选之《锐角三角函数》综合解答题

中考数学真题精选之《锐角三角函数》综合解答题1.如图所示是消防员攀爬云梯到小明家的场景.已知AE⊥BE,BC⊥BE,CD∥BE,AC=10.4m,BC=1.26m,点A关于点C的仰角为70°,则楼AE的高度为多少m?(结果保留整数.参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)2.贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC为50m.索道AB与AF的夹角为15°,CD与水平线夹角为45°,A、B两处的水平距离AE为576m,DF⊥AF,垂足为点F.(图中所有点都在同一平面内,点A、E、F在同一水平线上)(1)求索道AB的长(结果精确到1m);(2)求水平距离AF的长(结果精确到1m).(参考数据:sin15°≈0.25,cos15°≈0.96,tan15°≈0.26,√2≈1.41)3.徐州电视塔为我市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点C 处,用测角仪测得塔顶A的仰角∠AFE=36°,他在平地上沿正对电视塔的方向后退至点D处,测得塔顶A的仰角∠AGE=30°.若测角仪距地面的高度FC=GD=1.6m,CD =70m,求电视塔的高度AB(精确到0.1m).(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin30°≈0.50,cos30°≈0.87,tan30°≈0.58)4.问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.问题设置:把筒车抽象为一个半径为r的⊙O.如图②,OM始终垂直于水平面,设筒车半径为2米.当t=0时,某盛水筒恰好位于水面A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处.问题解决:(1)求该盛水筒从A处逆时针旋转到B处时,∠BOM的度数;(2)求该盛水筒旋转至B处时,它到水面的距离.(结果精确到0.1米)(参考数据√2≈1.414,√3≈1.732)5.今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形ABCD 是平行四边形,座板CD与地面MN平行,△EBC是等腰三角形且BC=CE,∠FBA=114.2°,靠背FC=57cm,支架AN=43cm,扶手的一部分BE=16.4cm.这时她问小余同学,你能算出靠背顶端F点距地面(MN)的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:sin65.8°=0.91,cos65.8°=0.41,tan65.8°=2.23)6.暑假期间,小明与小亮相约到某旅游风景区登山.需要登顶600m高的山峰,由山底A 处先步行300m到达B处,再由B处乘坐登山缆车到达山顶D处.已知点A,B,D,E,F在同一平面内,山坡AB的坡角为30°,缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计).(1)求登山缆车上升的高度DE;(2)若步行速度为30m/min,登山缆车的速度为60m/min,求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1min).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)7.如图,一艘海轮位于灯塔P的北偏东72°方向,距离灯塔100nmile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东40°方向上的B处.这时,B处距离灯塔P有多远(结果取整数)?(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)8.为了增强学生体质、锤炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为B点和C点,行进路线为A→B→C→A.B点在A 点的南偏东25°方向3√2km处,C点在A点的北偏东80°方向,行进路线AB和BC所在直线的夹角∠ABC为45°.(1)求行进路线BC和CA所在直线的夹角∠BCA的度数;(2)求检查点B和C之间的距离(结果保留根号).9.为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD长度为20米,∠C=18°,求斜坡AB的长.(结果精确到0.1米)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)10.2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达A点时,从位于地面C处的雷达站测得AC 的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°.(1)求点A离地面的高度AO;(2)求飞船从A处到B处的平均速度.(结果精确到0.1km/s,参考数据:√3≈1.73)11.“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼AB的高度,测量方案如图:先将无人机垂直上升至距水平地面225m的P点,测得奇楼顶端A的俯角为15°,再将无人机沿水平方向飞行200m到达点Q,测得奇楼底端B的俯角为45°,求奇楼AB的高度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)12.无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度BC,无人机在空中点P处,测得点P距地面上A点80米,点A处的俯角为60°,楼顶C点处的俯角为30°,已知点A与大楼的距离AB为70米(点A,B,C,P在同一平面内),求大楼的高度BC(结果保留根号).13.图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度OA=160cm,识别的最远水平距离OB=150cm.(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处,请问小杜最少需要下蹲多少厘米才能被识别?(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)14.鄂州市莲花山是国家4A级风景区,元明塔造型独特,是莲花山风景区的核心景点,深受全国各地旅游爱好者的青睐.今年端午节,景区将举行大型包粽子等节日庆祝活动.如图2,景区工作人员小明准备从元明塔的点G处挂一条大型竖直条幅到点E处,挂好后,小明进行实地测量,从元明塔底部F点沿水平方向步行30米到达自动扶梯底端A点,在A点用仪器测得条幅下端E的仰角为30°;接着他沿自动扶梯AD到达扶梯顶端D点,测得点A和点D的水平距离为15米,且tan∠DAB=43;然后他从D点又沿水平方向行走了45米到达C点,在C点测得条幅上端G的仰角为45°.(图上各点均在同一个平面内,且G,C,B共线,F,A,B共线,G、E、F共线,CD∥AB,GF⊥FB).(1)求自动扶梯AD的长度;(2)求大型条幅GE的长度.(结果保留根号)15.综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪ABCD为正方形,AB=30cm,顶点A处挂了一个铅锤M.如图是测量树高的示意图,测高仪上的点D,A 与树顶E在一条直线上,铅垂线AM交BC于点H.经测量,点A距地面1.8m,到树EG 的距离AF=11m,BH=20cm.求树EG的高度(结果精确到0.1m).16.如图,直线MN和EF为河的两岸,且MN∥EF,为了测量河两岸之间的距离,某同学在河岸FE的B点测得∠CBE=30°,从B点沿河岸FE的方向走40米到达D点,测得∠CDE=45°.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D点继续沿DE的方向走(12√3+12)米到达P点.求tan∠CPE的值.17.如图1是我国第一个以“龙”为主题的主题公园——“兰州龙源”、“兰州龙源”的“龙”字主题雕塑以紫铜铸造,如巨龙腾空,气势如虹,屹立在黄河北岸、某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动,具体过程如下,如图2,“龙”字雕塑CD 位于垂直地面的基座BC上,在平行于水平地面的A处测得∠BAC=38°,∠BAD=53°,AB=18m.求“龙”字雕塑CD的高度,(B,C,D三点共线,BD⊥AB,结果精确到0.1m)(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78,sin53°=080,cos53°=0.60,tan53°=1.33)18.2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站.如图中的照片展示了中国空间站上机械臂的一种工作状态.当两臂AC=BC=10m,两臂夹角∠ACB=100°时,求A,B两点间的距离.(结果精确到0.1m,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)19.东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示,城门楼B在角楼A的正东方向520m处,南关桥C在城门楼B的正南方向1200m 处.在明珠大剧院P测得角楼A在北偏东68.2°方向,南关桥C在南偏东56.31°方向(点A,B,C,P四点在同一平面内),求明珠大剧院到龙堤BC的距离(结果精确到1m)(参考数据:sin68,2°≈0.928,cos68.2°≈0.371,tan68.2°≈2.50,sin56.31°≈0.832,cos56.31°≈0.555,tan56.31°≈1.50)20.某次军事演习中,一艘船以40km/h的速度向正东航行,在出发地A测得小岛C在它的北偏东60°方向,2小时后到达B处,浏得小岛C在它的北偏西45°方向,求该船在航行过程中与小岛C的最近距离(参考数据:√2≈1.41,√3≈1.73.结果精确到0.1km).21.我国航天事业捷报频传,2023年5月30日,被誉为“神箭”的长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹,中国空间站应用与发展阶段首次载人发射任务取得圆满成功.如图,有一枚运载火箭从地面O处发射,当火箭到达P处时,地面A处的雷达站测得AP距离是5000m,仰角为23°,9s后,火箭直线到达Q处,此时地面A处雷达站测得Q处的仰角为45°,求火箭从P到Q处的平均速度(结果精确到1m/s).(参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42)22.根据背景素材,探索解决问题.测算发射塔的高度背景素材某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN(如图1),他们通过自制的测倾仪(如图2)在A,B,C三个位置观测,测倾仪上的示数如图3所示.经讨论,只需选择其中两个合适的位置,通过测量、换算就能计算发射塔的高度问题解决任务1分析规划选择两个观测位置:点和点.获取数据写出所选位置观测角的正切值,并量出观测点之间的图上距离.任务2推理计算计算发射塔的图上高度MN.任务3换算高度楼房实际宽度DE为12米,请通过测量换算发射塔的实际高度.注:测量时,以答题纸上的图上距离为准,并精确到1mm.23.“一缕清风银叶转”,某市20台风机依次矗立在云遮雾绕的山脊之上,风叶转动,风能就能转换成电能,造福千家万户.某中学初三数学兴趣小组,为测量风叶的长度进行了实地测量.如图,三片风叶两两所成的角为120°,当其中一片风叶OB与塔干OD叠合时,在与塔底D水平距离为60米的E处,测得塔顶部O的仰角∠OED=45°,风叶OA 的视角∠OEA=30°.(1)已知α,β两角和的余弦公式为:cos(α+β)=cosαcosβ﹣sinαsinβ,请利用公式计算cos75°;(2)求风叶OA的长度.24.图1是某款篮球架,图2是其示意图,立柱OA垂直地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行地面OB,篮筐EF与支架DE在同一直线上,OA=2.5米,AD=0.8米.∠AGC=32°.(1)求∠GAC的度数;(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗?请通过计算说明理由.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)25.某校学生开展综合实践活动,测量某建筑物的高度AB,在建筑物附近有一斜坡,坡长CD=10米,坡角α=30°,小华在C处测得建筑物顶端A的仰角为60°,在D处测得建筑物顶端A的仰角为30°.(已知点A,B,C,D在同一平面内,B,C在同一水平线上)(1)求点D到地面BC的距离;(2)求该建筑物的高度AB.。
备战中考数学综合题专题复习【锐角三角函数】专题解析附答案解析

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B港口之间的距离CB的长为海里.考点:解直角三角形的应用-方向角问题.2.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定3.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(215-+;(3758+【解析】试题分析:(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠CBD=36°, ∵∠CBD=∠A=36°,∠C=∠C , ∴△ABC ∽△BCD ; (2)∵∠A=∠ABD=36°, ∴AD=BD , ∵BD=BC , ∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1, ∵△ABC ∽△BCD ,∴AB BC BD CD =,即111x x +=, 整理得:x 2+x-1=0,解得:x 1=15-+,x 2=15--(负值,舍去),则x=15-+; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=154-+, 在Rt △ABE 中,cosA=cos36°=151514151AE AB -+++==-++ 在Rt △BCE 中,cosC=cos72°=1515414EC BC -+-+==, 则cos36°-cos72°=51+=15-+=12. 【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.4.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.5.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为 cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.【答案】(1);(2)12cm;(3)cm.【解析】试题分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案:∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm.∵∠ACD=30°,∠DAC=90°,AC=12cm,∴(cm).∵点E为CD边上的中点,∴AE=DC=cm.(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,根据轴对称的性质,此时DP+EP值为最小,进而得出答案.(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.试题解析:解:(1).(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE.∴△ADE为等边三角形.∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°.∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′.∴点E,D′关于直线AC对称.如答图1,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′.∵△ADE是等边三角形,AD=AE=,∴,即DP+EP最小值为12cm.(3)如答图2,连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=.在△ABD′和△CBD′中,∵,∴△ABD′≌△CBD′(SSS).∴∠D′BG=∠D′BC=45°.∴D′G=GB.设D′G长为xcm,则CG长为cm,在Rt△GD′C中,由勾股定理得,解得:(不合题意舍去).∴点D′到BC边的距离为cm.考点:1.翻折和单动点问题;2.勾股定理;3.直角三角形斜边上的中线性质;4.等边三角形三角形的判定和性质;5.轴对称的应用(最短线路问题);6.全等三角形的判定和性质;7.方程思想的应用.6.在正方形ABCD中,AC是一条对角线,点E是边BC上的一点(不与点C重合),连接AE,将△ABE沿BC方向平移,使点B与点C重合,得到△DCF,过点E作EG⊥AC于点G,连接DG,FG.(1)如图,①依题意补全图;②判断线段FG与DG之间的数量关系与位置关系,并证明;(2)已知正方形的边长为6,当∠AGD=60°时,求BE的长.BE【答案】(1)①见解析,②FG=DG,FG⊥DG,见解析;(2)3【解析】【分析】(1)①补全图形即可,②连接BG,由SAS证明△BEG≌△GCF得出BG=GF,由正方形的对称性质得出BG=DG,得出FG=DG,在证出∠DGF=90°,得出FG⊥DG即可,(2)过点D作DH⊥AC,交AC于点H.由等腰直角三角形的性质得出DH=AH=2FG=DG=2GH=6,得出DF2DG=3Rt△DCF中,由勾股定理得出CF=3得出结果.【详解】解:(1)①补全图形如图1所示,②FG=DG,FG⊥DG,理由如下,连接BG,如图2所示,∵四边形ABCD是正方形,∴∠ACB=45°,∵EG⊥AC,∴∠EGC =90°,∴△CEG 是等腰直角三角形,EG =GC , ∴∠GEC =∠GCE =45°, ∴∠BEG =∠GCF =135°, 由平移的性质得:BE =CF ,在△BEG 和△GCF 中,BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩,∴△BEG ≌△GCF (SAS ), ∴BG =GF ,∵G 在正方形ABCD 对角线上, ∴BG =DG , ∴FG =DG ,∵∠CGF =∠BGE ,∠BGE+∠AGB =90°, ∴∠CGF+∠AGB =90°, ∴∠AGD+∠CGF =90°, ∴∠DGF =90°, ∴FG ⊥DG.(2)过点D 作DH ⊥AC ,交AC 于点H .如图3所示, 在Rt △ADG 中, ∵∠DAC =45°, ∴DH =AH =2在Rt △DHG 中,∵∠AGD =60°, ∴GH 33236,∴DG =2GH =6, ∴DF 2DG =3 在Rt △DCF 中,CF ()22436-3∴BE =CF =3.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识;本题综合性强,证明三角形全等是解题的关键.7.在Rt△ABC中,∠ACB=90°,AB=7,AC=2,过点B作直线m∥AC,将△ABC绕点C 顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分別交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在C A′,CB′的延长线上时,试探究四边形PA'B′Q的面积是否存在最小值.若存在,求出四边形PA′B′Q的最小面积;若不存在,请说明理由.【答案】(1)60°;(2)PQ=72;(3)存在,S四边形PA'B′Q=33【解析】【分析】(1)由旋转可得:AC=A'C=2,进而得到BC3=∠A'BC=90°,可得cos∠A'CB3'BCA C==∠A'CB=30°,∠ACA'=60°;(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB3=32=,依据tan∠Q=tan∠A32=BQ=BC3=2,进而得出PQ=PB+BQ72=;(3)依据S四边形PA'B'Q=S△PCQ﹣S△A'CB'=S△PCQ3-S四边形PA'B'Q最小,即S△PCQ最小,而S△PCQ12=PQ×BC3=,利用几何法即可得到S△PCQ的最小值=3,即可得到结论.【详解】(1)由旋转可得:AC =A 'C =2.∵∠ACB =90°,AB 7=,AC =2,∴BC 3=. ∵∠ACB =90°,m ∥AC ,∴∠A 'BC =90°,∴cos ∠A 'CB 3'BC A C ==,∴∠A 'CB =30°,∴∠ACA '=60°;(2)∵M 为A 'B '的中点,∴∠A 'CM =∠MA 'C ,由旋转可得:∠MA 'C =∠A ,∴∠A =∠A 'CM ,∴tan ∠PCB =tan ∠A 3=,∴PB 3=BC 32=. ∵∠BQC =∠BCP =∠A ,∴tan ∠BQC =tan ∠A 3=,∴BQ =BC 3⨯=2,∴PQ =PB +BQ 72=; (3)∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ 3-,∴S 四边形PA 'B 'Q 最小,即S △PCQ 最小,∴S △PCQ 12=PQ ×BC 3=PQ , 取PQ 的中点G . ∵∠PCQ =90°,∴CG 12=PQ ,即PQ =2CG ,当CG 最小时,PQ 最小,∴CG ⊥PQ ,即CG 与CB 重合时,CG 最小,∴CG min 3=,PQ min =23,∴S △PCQ 的最小值=3,S 四边形PA 'B 'Q =33-;【点睛】本题属于几何变换综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.8.在Rt △ABC 中,∠ACB =90°,CD 是AB 边的中线,DE ⊥BC 于E ,连结CD ,点P 在射线CB 上(与B ,C 不重合)(1)如果∠A =30°,①如图1,∠DCB 等于多少度;②如图2,点P 在线段CB 上,连结DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连结BF ,补全图2猜想CP 、BF 之间的数量关系,并证明你的结论;(2)如图3,若点P 在线段CB 的延长线上,且∠A =α(0°<α<90°),连结DP ,将线段DP绕点逆时针旋转2α得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系(不需证明)【答案】(1)①∠DCB=60°.②结论:CP=BF.理由见解析;(2)结论:BF﹣BP=2DE•tanα.理由见解析.【解析】【分析】(1)①根据直角三角形斜边中线的性质,结合∠A=30°,只要证明△CDB是等边三角形即可;②根据全等三角形的判定推出△DCP≌△DBF,根据全等的性质得出CP=BF,(2)求出DC=DB=AD,DE∥AC,求出∠FDB=∠CDP=2α+∠PDB,DP=DF,根据全等三角形的判定得出△DCP≌△DBF,求出CP=BF,推出BF﹣BP=BC,解直角三角形求出CE=DEtanα即可.【详解】(1)①∵∠A=30°,∠ACB=90°,∴∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠DCB=60°.②如图1,结论:CP=BF.理由如下:∵∠ACB=90°,D是AB的中点,DE⊥BC,∠DCB=60°,∴△CDB为等边三角形.∴∠CDB=60°∵线段DP绕点D逆时针旋转60°得到线段DF,∵∠PDF=60°,DP=DF,∴∠FDB=∠CDP,在△DCP和△DBF中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF.(2)结论:BF ﹣BP =2DEtanα.理由:∵∠ACB =90°,D 是AB 的中点,DE ⊥BC ,∠A =α,∴DC =DB =AD ,DE ∥AC ,∴∠A =∠ACD =α,∠EDB =∠A =α,BC =2CE ,∴∠BDC =∠A+∠ACD =2α,∵∠PDF =2α,∴∠FDB =∠CDP =2α+∠PDB ,∵线段DP 绕点D 逆时针旋转2α得到线段DF ,∴DP =DF ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF ,而 CP =BC+BP ,∴BF ﹣BP =BC ,在Rt △CDE 中,∠DEC =90°,∴tan ∠CDE =CE DE, ∴CE =DEtanα, ∴BC =2CE =2DEtanα,即BF ﹣BP =2DEtanα.【点睛】本题考查了三角形外角性质,等边三角形的判定和性质,全等三角形的性质和判定,直角三角形的性质,旋转的性质的应用,能推出△DCP ≌△DBF 是解此题的关键,综合性比较强,证明过程类似.9.如图,正方形ABCD+1,对角线AC 、BD 相交于点O ,AE 平分∠BAC 分别交BC 、BD 于E 、F ,(1)求证:△ABF ∽△ACE ;(2)求tan ∠BAE 的值;(3)在线段AC 上找一点P ,使得PE+PF 最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x=1,在Rt△ABE中,∵∠ABE=90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC =22AB BC +=2+2,∴OA =OC =OB =12AC =22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =222+ •(2﹣1)=22, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+..【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.10.小明坐于堤边垂钓,如图①,河堤AC 的坡角为30°,AC 长米,钓竿AO 的倾斜角是60°,其长为3米,若AO 与钓鱼线OB 的夹角为60°,求浮漂B 与河堤下端C 之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
中考数学锐角三角函数-经典压轴题附答案

一、锐角三角函数
1.如图,从地面上的点 A 看一山坡上的电线杆 PQ,测得杆顶端点 P 的仰角是 45°,向前 走 6m 到达 B 点,测得杆顶端点 P 和杆底端点 Q 的仰角分别是 60°和 30°.
(1)求∠ BPQ 的度数;
(2)求该电线杆 PQ 的高度(结果精确到 1m).备用数据:
1cm )?
【答案】
【解析】
过 A 作 AF CD 于 F ,根据锐角三角函数的定义用 θ1、θ2 表示出 DF、EF 的值,又可证 四边形 ABCE 为平行四边形,故有 EC=AB=25cm,再再根据 DC=DE+EC 进行解答即可.
3.如图,在平行四边形 ABCD 中, 平分
, 与 交于点 ,连接 , .
则 BE=(3 3 +3)米. 在直角△ BEQ 中,QE= 3 BE= 3 (3 3 +3)=(3+ 3 )米.
33 ∴ PQ=PE-QE=9+3 3 -(3+ 3 )=6+2 3 ≈9(米).
答:电线杆 PQ 的高度约 9 米. 考点:解直角三角形的应用-仰角俯角问题.
2.如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太
,
【答案】(1)∠ BPQ=30°; (2)该电线杆 PQ 的高度约为 9m. 【解析】
试题分析:(1)延长 PQ 交直线 AB 于点 E,根据直角三角形两锐角互余求得即可; (2)设 PE=x 米,在直角△ APE 和直角△ BPE 中,根据三角函数利用 x 表示出 AE 和 BE,根 据 AB=AE-BE 即可列出方程求得 x 的值,再在直角△ BQE 中利用三角函数求得 QE 的长,则 PQ 的长度即可求解. 试题解析:延长 PQ 交直线 AB 于点 E,
中考数学锐角三角函数综合经典题含答案

中考数学锐角三角函数综合经典题含答案一、锐角三角函数1.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG =FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.【答案】553【解析】【分析】如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可.【详解】解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.∵AM⊥CD,∴∠QMP=∠MPO=∠OQM=90°,∴四边形OQMP是矩形,∴QM=OP,∵OC=OD=10,∠COD=60°,∴△COD是等边三角形,∵OP⊥CD,∠COD=30°,∴∠COP=12∴QM=OP=OC•cos30°=3∵∠AOC=∠QOP=90°,∴∠AOQ=∠COP=30°,∴AQ=1OA=5(分米),2∴AM=AQ+MQ=5+3∵OB∥CD,∴∠BOD=∠ODC=60°在Rt△OFK中,KO=OF•cos60°=2(分米),FK=OF•sin60°=23(分米),在Rt△PKE中,EK=22-=26(分米),EF FK∴BE=10−2−26=(8−26)(分米),在Rt△OFJ中,OJ=OF•cos60°=2(分米),FJ=23(分米),在Rt△FJE′中,E′J=22-(2)=26,63∴B′E′=10−(26−2)=12−26,∴B′E′−BE=4.故答案为:5+53,4.【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.2.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt △ACD 中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B 港口之间的距离CB 的长为海里.考点:解直角三角形的应用-方向角问题.3.如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB 和CD (均与水平面垂直),再将集热板安装在AD 上.为使集热板吸热率更高,公司规定:AD 与水平面夹角为1θ,且在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ,并已知1tan 1.082θ=,2tan 0.412θ=.如果安装工人确定支架AB 高为25cm ,求支架CD 的高(结果精确到1cm )?【答案】【解析】过A 作AF CD ⊥于F ,根据锐角三角函数的定义用θ1、θ2表示出DF 、EF 的值,又可证四边形ABCE为平行四边形,故有EC=AB=25cm,再再根据DC=DE+EC进行解答即可.4.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定5.如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;(2)若AB=5,,求PD的长;(3)在点P运动过程中,设=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)【答案】(1)证明见解析;(2);(3).【解析】试题分析:(1)应用圆周角定理证明∠APD=∠FPC,得到∠APC=∠FPD,又由∠PAC=∠PDC,即可证明结论.(2)由AC=2BC,设,应用勾股定理即可求得BC,AC的长,则由AC=2BC得,由△ACE∽△ABC可求得AE,CE的长,由可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得,即可求得PD的长.(3)连接BP,BD,AD,根据圆的对称性,可得,由角的转换可得,由△AGP∽△DGB可得,由△AGD∽△PGB可得,两式相乘可得结果.试题解析:(1)由APCB内接于圆O,得∠FPC=∠B,又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,∴∠APD=∠FPC.∴∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD.又∵∠PAC=∠PDC,∴△PAC∽△PDF.(2)连接BP,设,∵∠ACB=90°,AB=5,∴.∴.∵△ACE∽△ABC,∴,即. ∴.∵AB⊥CD,∴.如图,连接BP,∵,∴△APB是等腰直角三角形. ∴∠PAB=45°,.∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.由(1)△PAC∽△PDF得,即.∴PD的长为.(3)如图,连接BP,BD,AD,∵AC=2BC,∴根据圆的对称性,得AD=2DB,即.∵AB⊥CD,BP⊥AE,∴∠ABP=∠AFD.∵,∴.∵△AGP∽△DGB,∴.∵△AGD∽△PGB,∴.∴,即.∵,∴.∴与之间的函数关系式为.考点:1.单动点问题;2.圆周角定理;3.相似三角形的判定和性质;4.勾股定理;5.等腰直角三角形的判定和性质;6.垂径定理;7.锐角三角函数定义;8.由实际问题列函数关系式.6.如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.(1)求tan∠DBC的值;(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.【答案】(1)tan∠DBC=;(2)P(﹣,).【解析】试题分析:(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4,BE=BC﹣DE=.由此可知tan∠DBC=;(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知=,通过解方程求得点P的坐标为(﹣,).试题解析:(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,解得 x1=﹣1,x2=4.∴A(﹣1,0),B(4,0).当x=3时,y=﹣32+3×3+4=4,∴D(3,4).如图,连接CD,过点D作DE⊥BC于点E.∵C(0,4),∴CD//AB,∴∠BCD=∠ABC=45°.在直角△OBC中,∵OC=OB=4,∴BC=4.在直角△CDE中,CD=3.∴CE=ED=,∴BE=BC﹣DE=.∴tan∠DBC=;(2)过点P作PF⊥x轴于点F.∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,∴tan∠PBF=.设P(x,﹣x2+3x+4),则=,解得 x1=﹣,x2=4(舍去),∴P(﹣,).考点:1、二次函数;2、勾股定理;3、三角函数7.如图,已知点从出发,以1个单位长度/秒的速度沿轴向正方向运动,以为顶点作菱形,使点在第一象限内,且;以为圆心,为半径作圆.设点运动了秒,求:(1)点的坐标(用含的代数式表示);(2)当点在运动过程中,所有使与菱形的边所在直线相切的的值.【答案】解:(1)过作轴于,,,,,点的坐标为.(2)①当与相切时(如图1),切点为,此时,,,.②当与,即与轴相切时(如图2),则切点为,,过作于,则,,.③当与所在直线相切时(如图3),设切点为,交于,则,,.过作轴于,则,,化简,得,解得,,.所求的值是,和.【解析】(1)过作轴于,利用三角函数求得OD、DC的长,从而求得点的坐标⊙P 与菱形OABC 的边所在直线相切,则可与OC 相切;或与OA 相切;或与AB 相切,应分三种情况探讨:①当圆P 与OC 相切时,如图1所示,由切线的性质得到PC 垂直于OC ,再由OA=+t ,根据菱形的边长相等得到OC=1+t ,由∠AOC 的度数求出∠POC 为30°,在直角三角形POC 中,利用锐角三角函数定义表示出cos30°=oc/op ,表示出OC ,等于1+t 列出关于t 的方程,求出方程的解即可得到t 的值;②当圆P 与OA ,即与x 轴相切时,过P 作PE 垂直于OC ,又PC=PO ,利用三线合一得到E 为OC 的中点,OE 为OC 的一半,而OE=OPcos30°,列出关于t 的方程,求出方程的解即可得到t 的值;③当圆P 与AB 所在的直线相切时,设切点为F ,PF 与OC 交于点G ,由切线的性质得到PF 垂直于AB ,则PF 垂直于OC ,由CD=FG ,在直角三角形OCD 中,利用锐角三角函数定义由OC 表示出CD ,即为FG ,在直角三角形OPG 中,利用OP 表示出PG ,用PG+GF 表示出PF ,根据PF=PC ,表示出PC ,过C 作CH 垂直于y 轴,在直角三角形PHC 中,利用勾股定理列出关于t 的方程,求出方程的解即可得到t 的值,综上,得到所有满足题意的t 的值.8.在平面直角坐标系中,四边形OABC 是矩形,点()0,0O ,点()3,0A ,点()0,4C ,连接OB ,以点A 为中心,顺时针旋转矩形AOCB ,旋转角为()0360αα︒<<︒,得到矩形ADEF ,点,,O C B 的对应点分别为,,D E F .(Ⅰ)如图,当点D 落在对角线OB 上时,求点D 的坐标;(Ⅱ)在(Ⅰ)的情况下,AB 与DE 交于点H .①求证BDE DBA ∆≅∆;②求点H 的坐标.(Ⅲ)α为何值时,FB FA =.(直接写出结果即可).【答案】(Ⅰ)点D 的坐标为5472(,)2525;(Ⅱ)①证明见解析;②点H 的坐标为(3,258);(Ⅲ)60α=︒或300︒.【解析】【分析】 (Ⅰ) 过A D 、分别作,AM OB DN OA ⊥⊥,根据点A 、点C 的坐标可得出OA 、OC 的长,根据矩形的性质可得AB 、OB 的长,在Rt △OAM 中,利用∠BOA 的余弦求出OM 的长,由旋转的性质可得OA=AD ,利用等腰三角形的性质可得OD=2OM ,在Rt △ODN 中,利用∠BOA 的正弦和余弦可求出DN 和ON 的长,即可得答案;(Ⅱ)①由等腰三角形性质可得∠DOA=∠ODA ,根据锐角互余的关系可得ABD BDE ∠∠=,利用SAS 即可证明△DBA ≌△BDE ;②根据△DBA ≌△BDE 可得∠BEH=∠DAH ,BE=AD ,即可证明△BHE ≌△DHA ,可得DH=BH ,设AH=x ,在Rt △ADH 中,利用勾股定理求出x 的值即可得答案;(Ⅲ)如图,过F 作FO ⊥AB ,由性质性质可得∠BAF=α,分别讨论0<α≤180°时和180°<α<360°时两种情况,根据FB=FA 可得OA=OB ,利用勾股定理求出FO 的长,由余弦的定义即可求出∠BAF 的度数.【详解】(Ⅰ)∵点()30A ,,点()04C ,, ∴3,4OA OC ==.∵四边形OABC 是矩形,∴AB=OC=4,∵矩形DAFE 是由矩形AOBC 旋转得到的∴3AD AO ==.在Rt OAB ∆中,225OB OA AB =+=, 过A D 、分别作B,DN OA AM O ⊥⊥在Rt ΔOAM 中,OM OA 3cos BOA OA OB 5∠===, ∴9OM 5= ∵AD=OA ,AM ⊥OB , ∴18OD 2OM 5==. 在Rt ΔODN 中:DN 4sin BOA OD 5∠==,cos ∠BOA=ON OD =35, ∴72DN 25=,54ON 25=. ∴点D 的坐标为5472,2525⎛⎫⎪⎝⎭.(Ⅱ)①∵矩形DAFE 是由矩形AOBC 旋转得到的,∴OA AD 3,ADE 90,DE AB 4∠===︒==.∴OD AD =.∴DOA ODA ∠∠=.又∵DOA OBA 90∠∠+=︒,BDH ADO 90∠∠+=︒∴ABD BDE ∠∠=. 又∵BD BD =,∴ΔBDE ΔDBA ≅.②由ΔBDE ΔDBA ≅,得BEH DAH ∠∠=,BE AD 3==,又∵BHE DHA ∠∠=,∴ΔBHE ΔDHA ≅.∴DH=BH ,设AH x =,则DH BH 4x ==-,在Rt ΔADH 中,222AH AD DH =+,即()222x 34x =+-,得25x 8=, ∴25AH 8=. ∴点H 的坐标为253,8⎛⎫ ⎪⎝⎭. (Ⅲ)如图,过F 作FO ⊥AB ,当0<α≤180°时,∵点B 与点F 是对应点,A 为旋转中心,∴∠BAF 为旋转角,即∠BAF=α,AB=AF=4,∵FA=FB ,FO ⊥AB ,∴OA=12AB=2, ∴cos ∠BAF=OA AF =12, ∴∠BAF=60°,即α=60°,当180°<α<360°时, 同理解得:∠BAF′=60°,∴旋转角α=360°-60°=300°.综上所述:α60=︒或300︒.【点睛】本题考查矩形的性质、旋转变换、全等三角形的判定与性质、锐角三角函数的定义等知识,正确找出对应边与旋转角并熟记特殊角的三角函数值是解题关键.9.如图,在⊙O 的内接三角形ABC 中,∠ACB =90°,AC =2BC ,过C 作AB 的垂线l 交⊙O 于另一点D ,垂足为E .设P 是»AC 上异于A ,C 的一个动点,射线AP 交l 于点F ,连接PC 与PD ,PD 交AB 于点G .(1)求证:△PAC ∽△PDF ;(2)若AB =5,¼¼AP BP=,求PD 的长.【答案】(1)证明见解析;(2310 【解析】【分析】 (1)根据AB ⊥CD ,AB 是⊙O 的直径,得到¶¶ADAC =,∠ACD =∠B ,由∠FPC =∠B ,得到∠ACD =∠FPC ,可得结论;(2)连接OP ,由¶¶APBP =,得到OP ⊥AB ,∠OPG =∠PDC ,根据AB 是⊙O 的直径,得到∠ACB =90°,由于AC =2BC ,于是得到tan ∠CAB =tan ∠DCB =BC AC ,得到12CE BE AE CE ==,求得AE =4BE ,通过△OPG ∽△EDG ,得到OG OP GE ED=,然后根据勾股定理即可得到结果.【详解】(1)证明:连接AD,∵AB⊥CD,AB是⊙O的直径,∴¶¶AD AC=,∴∠ACD=∠B=∠ADC,∵∠FPC=∠B,∴∠ACD=∠FPC,∴∠APC=∠ACF,∵∠FAC=∠CAF,∴△PAC∽△CAF;(2)连接OP,则OA=OB=OP=15 22 AB=,∵¶¶AP BP=,∴OP⊥AB,∠OPG=∠PDC,∵AB是⊙O的直径,∴∠ACB=90°,∵AC=2BC,∴tan∠CAB=tan∠DCB=BCAC,∴12 CE BEAE CE==,∴AE=4BE,∵AE+BE=AB=5,∴AE=4,BE=1,CE=2,∴OE=OB﹣BE=2.5﹣1=1.5,∵∠OPG=∠PDC,∠OGP=∠DGE,∴△OPG∽△EDG,∴OG OP GE ED=,∴2.52 OE GE OPGE CE-==,∴GE=23,OG=56,∴PG5 6 =,GD23 =,∴PD=PG+GD【点睛】本题考查了相似三角形的判定和性质,垂径定理,勾股定理,圆周角定理,证得△OPG ∽△EDG 是解题的关键.10.阅读下面材料:观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,过A 作AD ⊥BC 于D (如图),则sin B =AD c ,sin C =AD b ,即AD =c sin B ,AD =b sin C ,于是c sin B =b sin C ,即sin sin b c B C = .同理有:sin sin c a C A =,sin sin a b A B=,所以sin sin sin a b c A B C ==. 即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.(1)如图,△ABC 中,∠B =75°,∠C =45°,BC =60,则AB = ;(2)如图,一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B 处,此时又测得灯塔A 在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A 的距离AB .(3)在(2)的条件下,试求75°的正弦值.(结果保留根号)【答案】(1)6;(2)6海里;(36+2 【解析】【分析】(1)根据材料:在一个三角形中,各边和它所对角的正弦的比相等,写出比例关系,代入数值即可求得AB的值.(2)此题可先由速度和时间求出BC的距离,再由各方向角得出∠A的角度,过B作BM⊥AC于M,求出∠MBC=30°,求出MC,由勾股定理求出BM,求出AM、BM的长,由勾股定理求出AB即可;(3)在三角形ABC中,∠A=45,∠ABC=75,∠ACB=60,过点C作AC的垂线BD,构造直角三角形ABD,BCD,在直角三角形ABD中可求出AD的长,进而可求出sin75°的值.【详解】解:(1)在△ABC中,∠B=75°,∠C=45°,BC=60,则∠A=60°,∵ABsinC =sinBCA,∴45ABsin o=60sin60o,即2 =3,解得:AB=206.(2)如图,依题意:BC=60×0.5=30(海里)∵CD∥BE,∴∠DCB+∠CBE=180°∵∠DCB=30°,∴∠CBE=150°∵∠ABE=75°.∴∠ABC=75°,∴∠A=45°,在△ABC中,sin AB ACB∠=BCsin A∠即60?ABsin=3045?sin,解之得:AB=156.答:货轮距灯塔的距离AB=156海里.(3)过点B作AC的垂线BM,垂足为M.在直角三角形ABM中,∠A=45°,6,所以3BDC中,∠BCM=60°,BC=30°,可求得CM=15,所以3,15315+156sin75°6+2.【点睛】本题考查方向角的含义,三角形的内角和定理,含30度角的直角三角形,等腰三角形的性质和判定等知识点,解题关键是熟练掌握解直角三角形方法.11.如图,A(0,2),B(6,2),C(0,c)(c>0),以A为圆心AB长为半径的¶BD 交y轴正半轴于点D,¶BD与BC有交点时,交点为E,P为¶BD上一点.(1)若c=3,①BC=,¶DE的长为;②当CP=2时,判断CP与⊙A的位置关系,井加以证明;(2)若c=10,求点P与BC距离的最大值;(3)分别直接写出当c=1,c=6,c=9,c=11时,点P与BC的最大距离(结果无需化简)【答案】(1)①12,π;②详见解析;(2)①65;②65(3)答案见详解 【解析】【分析】 (1)①先求出AB ,AC ,进而求出BC 和∠ABC ,最后用弧长公式即可得出结论;②判断出△APC 是直角三角形,即可得出结论;(2)分两种情况,利用三角形的面积或锐角三角函数即可得出结论;(3)画图图形,同(2)的方法即可得出结论.【详解】 (1)①如图1,∵c =3+2,∴OC =3,∴AC =3﹣2=3∵AB =6,在Rt △BAC 中,根据勾股定理得,BC =12,tan ∠ABC =AC AB3 ∴∠ABC =60°,∵AE =AB ,∴△ABE 是等边三角形,∴∠BAE =60°,∴∠DAE =30°, ∴»DE的长为306180π⨯=π, 故答案为12,π;②CP 与⊙A 相切.证明:∵AP =AB =6,AC =OC ﹣OA =63, ∴AP 2+CP 2=108,又AC 2=(63)2=108,∴AP 2+PC 2=AC 2.∴∠APC =90°,即:CP ⊥AP .而AP 是半径,∴CP 与⊙A 相切.(2)若c =10,即AC =10﹣2=8,则BC =10.①若点P 在»BE上,AP ⊥BE 时,点P 与BC 的距离最大,设垂足为F , 则PF 的长就是最大距离,如图2,S △ABC =12AB ×AC =12BC ×AF , ∴AF =AB AC BC ⋅=245, ∴PF =AP ﹣AF =65; ②如图3,若点P 在»DE 上,作PG ⊥BC 于点G ,当点P 与点D 重合时,PG 最大.此时,sin ∠ACB =PG AB CP BC =, 即PG =AB CP BC ⋅=65∴若c =10,点P 与BC 距离的最大值是65; (3)当c =1时,如图4,过点P 作PM ⊥BC ,sin ∠BCP =AB PMBC CD= ∴PM =67423737AB CD BC ⋅⨯===423737; 当c =6时,如图5,同c =10的①情况,PF =6﹣1213=1213613-,当c =9时,如图6,同c =10的①情况,PF =4285685-,当c =11时,如图7,点P 和点D 重合时,点P 到BC 的距离最大,同c =10时②情况,DG 18117. 【点睛】此题是圆的综合题,主要考查了弧长公式,勾股定理和逆定理,三角形的面积公式,锐角三角函数,熟练掌握锐角三角函数是解本题的关键.12.如图,AB 为O e 的直径,C 、D 为O e 上异于A 、B 的两点,连接CD ,过点C作CE DB ⊥,交CD 的延长线于点E ,垂足为点E ,直径AB 与CE 的延长线相交于点F .(1)连接AC 、AD ,求证:180DAC ACF ∠+∠=︒. (2)若2ABD BDC ∠=∠. ①求证:CF 是O e 的切线. ②当6BD =,3tan 4F =时,求CF 的长. 【答案】(1)详见解析;(2)①详见解析;② 203CF =. 【解析】 【分析】(1)根据圆周角定理证得∠ADB=90°,即AD ⊥BD ,由CE ⊥DB 证得AD ∥CF ,根据平行线的性质即可证得结论;(2)①连接OC .先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC ∥DB ,再由CE ⊥DB ,得到OC ⊥CF ,根据切线的判定即可证明CF 为⊙O 的切线;②由CF ∥AD ,证出∠BAD=∠F ,得出tan ∠BAD=tan ∠F=BD AD =34,求出AD=43BD=8,利用勾股定理求得AB=10,得出OB=OC=,5,再由tanF=OC CF =34,即可求出CF . 【详解】解:(1)AB 是O e 的直径,且D 为O e 上一点,90ADB ∴∠=︒, CE DB ⊥Q , 90DEC ∴∠=︒, //CF AD ∴,180DAC ACF ∴∠+∠=︒. (2)①如图,连接OC . OA OC =Q ,12∴∠=∠. 312∠=∠+∠Q , 321∴∠=∠.42BDC Q ∠=∠,1BDC ∠=∠, 421∴∠=∠, 43∴∠=∠,//OC DB ∴. CE DB ⊥Q , OC CF ∴⊥.又OC Q 为O e 的半径, CF ∴为O e 的切线.②由(1)知//CF AD ,BAD F ∴∠=∠,3tan tan 4BAD F ∴∠==, 34BD AD ∴=. 6BD =Q483AD BD ∴==, 226810AB ∴=+=,5OB OC ==. OC CF Q ⊥, 90OCF ∴∠=︒,3tan 4OC F CF ∴==,解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果.13.如图,在平面直角坐标系xOy 中,抛物线y =﹣14x 2+bx +c 与直线y =12x ﹣3分别交x 轴、y 轴上的B 、C 两点,设该抛物线与x 轴的另一个交点为点A ,顶点为点D ,连接CD 交x 轴于点E .(1)求该抛物线的表达式及点D 的坐标; (2)求∠DCB 的正切值;(3)如果点F 在y 轴上,且∠FBC =∠DBA +∠DCB ,求点F 的坐标.【答案】(1)21y 234x x =-+-,D (4,1);(2)13;(3)点F 坐标为(0,1)或(0,﹣18). 【解析】 【分析】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3,求出点B 、C 的坐标,将点B 、C 坐标代入抛物线y =﹣14x 2+bx+c ,即可求解; (2)求出则点E (3,0),EH =EB•sin ∠OBC =5,CE =32,则CH =5,即可求解;(3)分点F 在y 轴负半轴和在y 轴正半轴两种情况,分别求解即可. 【详解】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3, 则点B 、C 的坐标分别为(6,0)、(0,﹣3),则c =﹣3, 将点B 坐标代入抛物线y =﹣14x 2+bx ﹣3得:0=﹣14×36+6b ﹣3,解得:b =2, 故抛物线的表达式为:y =﹣14x 2+2x ﹣3,令y =0,则x =6或2, 即点A (2,0),则点D (4,1); (2)过点E 作EH ⊥BC 交于点H ,C 、D 的坐标分别为:(0,﹣3)、(4,1), 直线CD 的表达式为:y =x ﹣3,则点E (3,0), tan ∠OBC =3162OC OB ==,则sin ∠OBC 5,则EH=EB•sin∠OBC=5,CE=32,则CH=5,则tan∠DCB=13 EHCH=;(3)点A、B、C、D、E的坐标分别为(2,0)、(6,0)、(0,﹣3)、(4,1)、(3,0),则BC=35,∵OE=OC,∴∠AEC=45°,tan∠DBE=164-=12,故:∠DBE=∠OBC,则∠FBC=∠DBA+∠DCB=∠AEC=45°,①当点F在y轴负半轴时,过点F作FG⊥BG交BC的延长线与点G,则∠GFC=∠OBC=α,设:GF=2m,则CG=GFtanα=m,∵∠CBF=45°,∴BG=GF,即:5=2m,解得:m=5CF22GF CG+5=15,故点F(0,﹣18);②当点F在y轴正半轴时,同理可得:点F(0,1);故:点F坐标为(0,1)或(0,﹣18).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形等相关知识,其中(3),确定∠FBC =∠DBA+∠DCB =∠AEC =45°,是本题的突破口.14.如图,在ABC △中,10AC BC ==,3cos5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P e 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P e 与边BC 相切时,求P e 的半径;()2联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;()3在()2的条件下,当以PE 长为直径的Q e 与P e 相交于AC 边上的点G 时,求相交所得的公共弦的长.【答案】(1)409;(2))25880010x x x y x -+=<<;(3)105- 【解析】 【分析】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=45,sinC=HP CP =R 10R -=45,即可求解; (2)PD ∥BE ,则EB PD =BFPF,即:2248805x x x y xy--+=,即可求解;(3)证明四边形PDBE 为平行四边形,则AG=GP=BD ,即:5求解. 【详解】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=35, sinC=HP CP =R 10R -=45,解得:R=409; (2)在△ABC 中,AC=BC=10,cosC=35, 设AP=PD=x ,∠A=∠ABC=β,过点B 作BH ⊥AC ,则BH=ACsinC=8, 同理可得:CH=6,HA=4,AB=45,则:tan ∠CAB=2BP=()2284x +-=2880x x -+, DA=25x ,则BD=45-25x ,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β,tanβ=2,则cosβ=5,sinβ=5,EB=BDcosβ=(45-25x)×5=4-25x,∴PD∥BE,∴EBPD=BFPF,即:2248805x x x yx y--+-=,整理得:y=()25x x8x800x10-+<<;(3)以EP为直径作圆Q如下图所示,两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,GD为相交所得的公共弦,∵点Q时弧GD的中点,∴DG⊥EP,∵AG是圆P的直径,∴∠GDA=90°,∴EP∥BD,由(2)知,PD∥BC,∴四边形PDBE为平行四边形,∴AG=EP=BD,∴5设圆的半径为r,在△ADG中,55AG=2r,5551+,则:55相交所得的公共弦的长为5【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.15.已知AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K . (1)如图1,求证:KE =GE ; (2)如图2,连接CABG ,若∠FGB =12∠ACH ,求证:CA ∥FE ; (3)如图3,在(2)的条件下,连接CG 交AB 于点N ,若sin E =35,AK =10,求CN 的长.【答案】(1)证明见解析;(2)△EAD 是等腰三角形.证明见解析;(3201013【解析】 试题分析:(1)连接OG ,则由已知易得∠OGE=∠AHK=90°,由OG=OA 可得∠AGO=∠OAG ,从而可得∠KGE=∠AKH=∠EKG ,这样即可得到KE=GE ;(2)设∠FGB=α,由AB 是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE 可得∠EKG=90°-α,这样在△GKE 中可得∠E=2α,由∠FGB=12∠ACH 可得∠ACH=2α,这样可得∠E=∠ACH ,由此即可得到CA ∥EF ; (3)如下图2,作NP ⊥AC 于P ,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,10a ,结合10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G , ∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α,∵∠FGB=12∠ACH , ∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a , 则224AC CH a -=,tan ∠CAH=43CH AH =, ∵CA ∥FE ,∴∠CAK=∠AGE,∵∠AGE=∠AKH,∴∠CAK=∠AKH,∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=AHHK =3,AK=2210AH HK a+=,∵AK=10,∴1010a=,∴a=1.AC=5,∵∠BHD=∠AGB=90°,∴∠BHD+∠AGB=180°,在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG,∵∠ACN=∠ABG,∴∠AKH=∠ACN,∴tan∠AKH=tan∠ACN=3,∵NP⊥AC于P,∴∠APN=∠CPN=90°,在Rt△APN中,tan∠CAH=43PNAP=,设PN=12b,则AP=9b,在Rt△CPN中,tan∠ACN=PNCP=3,∴CP=4b,∴AC=AP+CP=13b,∵AC=5,∴13b=5,∴b=513,∴CN=22PN CP+=410b⋅=2010 13.。
备战中考数学——锐角三角函数的综合压轴题专题复习及详细答案

备战中考数学一一锐角三角函数的综合压轴题专题复习及详细答案—、锐角三角函数1•图1是一种折叠式晾衣架•晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚0C= 0D= 10分米,展开角 / COD= 60°晾衣臂0A= OB= 10分米,晾衣臂支架HG=FE= 6分米,且H0= F0= 4分米.当/ AOC= 90°时,点A离地面的距离AM为______________ 分米;当OB从水平状态旋转到OB (在CO延长线上)时,点E绕点F随之旋转至OB上【解析】【分析】如图,作OP丄CD于P, OQ丄AM于Q, FK丄OB于K, FJL OC于J.解直角三角形求出MQ , AQ 即可求出AM,再分别求出BE, B'即可.【详解】解:如图,作OP丄CD于P, OQ丄AM于Q, FK丄OB于K, FJ丄OC于J.•/ AM 丄CD,••• / QMP= / MPO = / OQM = 90 °•••四边形OQMP是矩形,•- QM = OP,•/ OC= OD= 10, / COD= 60;•△ COD是等边三角形,T OP 丄CD,1•/ COP= / COD= 30 ;2• QM = OP= OC?cos30 =°、、3 (分米),•/ / AOC= / QOP= 90 ;•/ AOQ= / COP= 30 :1• AQ= — OA= 5 (分米),2• AM = AQ + MQ = 5+ 5 ■::.•「OB// CD,•/ BOD= / ODC= 60 °在Rt A OFK中,KO= OF?cos60= 2 (分米),FK= OF?sin60°= 2 3 (分米),在Rt A PKE中,EK= EF2―FK2 = 2、百(分米),BE= 10-2-2,6 =( 8-2 6 )(分米),在Rt A OFJ中,OJ= OF?cos60= 2 (分米),FJ= 2 3 (分米),在Rt A FJE中,E J62(2后=2晶,••• B' =10- (2 .6 -2)= 12-2 6 ,• B' E'=4Er故答案为:5 + 5 3 , 4.M <?圏2 °水平地面【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.2. 已知:如图,在四边形ABCD中,AB// CD, / ACB =90;AB=10cm, BC=8cm, OD 垂直平分A C.点P从点B出发,沿BA方向匀速运动,速度为1cm/s ;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE± AB,交BC于点E,过点Q作QF// AC,分别交AD, OD于点F, G.连接OP, EG.设运动时间为t ( s ) (0v t v 5),解答下列问题:(1 )当t为何值时,点E在BAC的平分线上?(2)设四边形PEGO的面积为S^m2),求S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)连接OE, OQ,在运动过程中,是否存在某一时刻t,使OE! OQ?若存在,求出t【解析】【分析】(1) 当点E 在/BAC 的平分线上时,因为 即可解决问题.(2) 根据S 四边形 OPEG=S\OEG +S^OPE =S^OEG +(3 )利用二次函数的性质解决问题即可. EC GQ(4)证明/ EOC=Z QOG ,可得tan / EOC=tan/ QOG ,推出——— 由此构建方程即 OC OG可解决问题.【详解】(1 )在 RtAABC 中,•/ / ACB=90 , AB=10cm , BC=8cm,二 AC =、. 102 82 =6 (cm ),•/ OD 垂直平分线段 AC ,••• OC=OA=3 (cm ), / DOC=90 °•••CD // AB ,• / BAC=/ DCO,•/ / DOC=/ ACB,•••△ DOC^A BCA,• AC AB BC"OC CD OD ,• 6 10 8"3 CD OD ,• CD=5 (cm ) , OD=4 ( cm ),•/ PB=t , PE 丄 AB ,35 易知:PE=— t , BE=— t ,4 4 当点E 在/ BAC 的平分线上时,•/ EP 丄 AB , EC 丄 AC,• PE=EC35 • — t=8- t ,4 4 • t=4.•••当t 为4秒时,点E 在/BAC 的平分线上.(2) 如图,连接OE , PC.【答案】(1) t=4s ;( 2) S 四边形 PEGO 8t 2 15 5 ’6 , (0 t 5) ;(3) t -时, 四边形PEGO 取得最大值;(4) t时, 5 OE OQ .EP 丄AB , EC 丄AC,可得PE=EC 由此构建方程 (Sx OPC +S X PCE -S A OE ©构建函数关系式即可.(3) 存在. S 8 5 2 68 t (0 t 5), 3 2 3 t= 5四边形 OPEG 的面积最大,最大值为 68 2 3 (4) 存在. 如图, 连接 OQ. •••OE 丄 OQ , ••• / EOC+/ QOC=90 ,° •/ / QOC+/ QOG=9O ° • / EOC=/ QOG, • tan / EOC=tanZ QOG, • EC GQ "OC OG ° 本题属于四边形综合题,考查了解直角三角形,相似三角形的判定和性质,锐角三角函 数,多边形的面积等知识,解题的关键是学会利用参数构建方程解决问题 • 1 4 1 4 1 c 5 -4 -t 3 —38 -t 8 t 2 5 2 5 2 4 8 2 15 t 2 t 16(t 5). 5t 8 5t 3t 3 4 4t 5 整理得:5t 2-66t+160=0 , 解得t 16或10 (舍弃)5 •当t 16 , 秒时,OE 丄OQ 5【点睛】S 四边形 OPEG =S\OEG +S A OPE =S X OEG + ( S AOPC +S^ ) 3 33. 如图(1),在平面直角坐标系中,点A (0,- 6),点B (6° 0). Rt A CDE中, / CDE=90 , CD=4, DE=4 .直角边CD在y轴上,且点C与点A重合.Rt A CDE沿y轴正方向平行移动,当点C运动到点0时停止运动.解答下列问题:(1)如图(2),当Rt A CDE运动到点D与点0重合时,设CE交AB于点M,求/ BME 的度数.(2)如图(3),在Rt A CDE的运动过程中,当CE经过点B时,求BC的长.(3)在Rt A CDE的运动过程中,设AC=h, △ OAB与厶CDE的重叠部分的面积为S,请写出【答案】(1) Z BME=15 ;(2BC=4J ;(3)hW2时,S=- ’h2+4h+8,4当h>2时,S=18- 3h.【解析】试题分析:(1)如图2,由对顶角的定义知,Z BME=Z CMA,要求Z BME的度数,需先求出Z CMA的度数•根据三角形外角的定理进行解答即可;(2)如图3,由已知可知Z OBC=Z DEC=30,又0B=6,通过解直角△ BOC就可求出BC的长度;(3 )需要分类讨论:①h<2时,如图4,作MN丄y轴交y轴于点N,作MF丄DE交DE于点F, S=S\EDC-S A EFM;② 当h时,如图3, S=S\OBC.试题解析:解:(1)如图2,•••在平面直角坐标系中,点A ( 0,- 6),点B (6, 0)•••OA=OB,••• Z OAB=45 ,°•/ Z CDE=90,° CD=4, DE=4 J ,•Z OCE=60 ,°二Z CMA=Z OCE- Z OAB=60 - 45 =15 ,•Z BME=Z CMA=15 ;郅•••/ CDE=90,° CD=4, DE=4「,••• / OBC=Z DEC=30 ,°•/ OB=6,• BC=4J ;(3)①h W2时,如图4,作MN 丄y 轴交y 轴于点N ,作MF 丄DE 交DE 于点F , V * d IB x——0D 0 F ?二N C AZ ME 34•/ CD=4, DE=4「, AC=h, AN=NM ,• CN=4 - FM , AN=MN=4+h - FM ,•/△ CMN s^ CEDCNc5_4-W/• S=S\EDC — S A EFM =— X 4X4 -— (4如4 - h ) X (4 -: ) = - h 2+4h+8,二 22 4 ②如图3,当h 》2时, 11 S=S OB C = _ OC X OB= (6 - h ) X 6=1 &3h .考点:1、三角形的外角定理;2、相似;3、解直角三角形 4.已知Rt A ABC 中,AB 是O O 的弦,斜边 AC 交O O 于点D,且AD=DC,延长CB 交O O 于点E.如图3,解得FM=4 - ^—L 空(1 )图1的A、B、C D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作O O的切线,交AC的延长线于点F.①若CF=CD时,求sin / CAB的值;②若CF=aCD(a>0)时,试猜想sin/ CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1) AE=CE (2)①汗;②口+2 .【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得 / ADE=Z ABE=90 ,由于AD=DC,根据垂直平分线的性质可得AE=CE(2)连接AE、ED,如图2,由/ ABE=9 0可得AE是O O的直径,根据切线的性质可得/ AEF=90 ,°从而可证到△ ADE^A AEF,然后运用相似三角形的性质可得=AD?AF.①当CF=CD时,可得I - - - U丨,从而有EC=AE申CD,在Rt A DEC中运用三角函数可得DCsin / CED』'’*,根据圆周角定理可得 / CAB=Z DEC即可求出sin/CAB的值;②当CF=aCD( a> 0)时,同① 即可解决问题.试题解析:(1) AE=CE理由:连接AE、DE,如图 1 , •/ / ABC=90 , /• / ABE=90, /• / ADE=/ ABE=90 , •/ AD=DC••• AE=CE(2)连接AE、ED,如图2, •/ / ABE=90 , • AE是O O的直径,•/ EF是O 00的切线,AE AD•/ AEF=90 , ° • / ADE=/ AEF=90 ,。
中考数学锐角三角函数-经典压轴题含详细答案

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)【答案】2.5m.【解析】试题分析:设DF=x,在Rt△DFC中,可得CF=DF=x,则BF=4-x,根据线段的和差可得AN=5-x,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,利用∠EAB的正切值解得x的值.试题解析:解:设DF=,在Rt△DFC中,∠CDF=,∴CF=tan·DF=,又∵CB=4,∴BF=4-,∵AB=6,DE=1,BM= DF=,∴AN=5-,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,EN=4-,AN=5-,tan==0.60,解得=2.5,答:DM和BC的水平距离BM为2.5米.考点:解直角三角形.2.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G,连接AG交CD于K.(1)求证:KE=GE;(2)若KG2=KD•GE,试判断AC与EF的位置关系,并说明理由;(3)在(2)的条件下,若sinE=,AK=,求FG的长.【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= .【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KD•GE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.试题解析:(1)如图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.(2)AC∥EF,理由为连接GD,如图2所示.∵KG2=KD•GE,即,∴,又∵∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∵∠C=∠AGD,∴∠E=∠C,∴AC∥EF;(3)连接OG,OC,如图3所示,∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.∵sinE=sin∠ACH=,设AH=3t,则AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK-CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即(3t)2+t2=(2)2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即(r-3t)2+(4t)2=r2,解得r= t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH=,∴FG=【点睛】此题考查了切线的性质,相似三角形的判定与性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握定理及性质是解本题的关键.3.如图13,矩形的对角线,相交于点,关于的对称图形为.(1)求证:四边形是菱形;(2)连接,若,.①求的值;②若点为线段上一动点(不与点重合),连接,一动点从点出发,以的速度沿线段匀速运动到点,再以的速度沿线段匀速运动到点,到达点后停止运动.当点沿上述路线运动到点所需要的时间最短时,求的长和点走完全程所需的时间.【答案】(1)详见解析;(2)①②和走完全程所需时间为【解析】试题分析:(1)利用四边相等的四边形是菱形;(2)①构造直角三角形求;②先确定点沿上述路线运动到点所需要的时间最短时的位置,再计算运到的时间.试题解析:解:(1)证明:四边形是矩形.与交于点O,且关于对称四边形是菱形.(2)①连接,直线分别交于点,交于点关于的对称图形为在矩形中,为的中点,且O为AC的中点为的中位线同理可得:为的中点,②过点P作交于点由运动到所需的时间为3s由①可得,点O以的速度从P到A所需的时间等于以从M运动到A即:由O运动到P所需的时间就是OP+MA和最小.如下图,当P运动到,即时,所用时间最短.在中,设解得:和走完全程所需时间为考点:菱形的判定方法;构造直角三角形求三角函数值;确定极值时动点的特殊位置4.如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,2 1.4142.【答案】塔高AB约为32.99米.【解析】【分析】过点D作DH⊥AB,垂足为点H,设AB=x,则AH=x﹣3,解直角三角形即可得到结论.【详解】解:过点D作DH⊥AB,垂足为点H.由题意,得HB = CD = 3,EC = 15,HD = BC,∠ABC =∠AHD = 90°,∠ADH = 32°.设AB = x ,则 AH = x – 3.在Rt △ABE 中,由 ∠AEB = 45°,得 tan tan451ABAEB EB∠=︒==. ∴ EB = AB = x .∴ HD = BC = BE + EC = x + 15. 在Rt △AHD 中,由 ∠AHD = 90°,得 tan AHADH HD∠=. 即得 3tan3215x x -︒=+. 解得 15tan32332.991tan32x ⋅︒+=≈-︒.∴ 塔高AB 约为32.99米. 【点睛】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.5.如图,在平面直角坐标系xOy 中,点P 是⊙C 外一点,连接CP 交⊙C 于点Q ,点P 关于点Q 的对称点为P ′,当点P ′在线段CQ 上时,称点P 为⊙C “友好点”.已知A (1,0),B (0,2),C (3,3) (1)当⊙O 的半径为1时,①点A ,B ,C 中是⊙O “友好点”的是 ; ②已知点M 在直线y =﹣33x +2 上,且点M 是⊙O “友好点”,求点M 的横坐标m 的取值范围;(2)已知点D (23,0),连接BC ,BD ,CD ,⊙T 的圆心为T (t ,﹣1),半径为1,若在△BCD 上存在一点N ,使点N 是⊙T “友好点”,求圆心T 的横坐标t 的取值范围.【答案】(1)①B ;②0≤m 3(2)﹣3t <3 【解析】 【分析】(1))①根据“友好点”的定义,OB =<2r =2,所以点B 是⊙O “友好点”;②设M(m,﹣33m+2 ),根据“友好点”的定义,OM=223222m m⎛⎫+-+≤⎪⎪⎝⎭,由此求解即可;(2)B(0,2),C(3,3),D(23,0),⊙T的圆心为T(t,﹣1),点N是⊙T“友好点”,NT≤2r=2,所以点N只能在线段BD上运动,过点T作TN⊥BD于N,作TH∥y轴,与BD交于点H.易知∠BDO=30°,∠OBD=60°,NT=32HT,直线BD:y=﹣33x+2,可知H(t,﹣3 3t+2),继而可得NT=﹣12t+332,由此可得关于t的不等式,解出t的范围即可.【详解】(1)①∵r=1,∴根据“友好点”的定义,OB=<2r=2,∴点B是⊙O“友好点”,∵OC=2233+=32>2r=2,∴点C不是⊙O“友好点”,A(1,0)在⊙O上,不是⊙O“友好点”,故答案为B;②如图,设M(m 3+2 ),根据“友好点”的定义,∴OM223222m m⎛⎫+-+≤⎪⎪⎝⎭,整理,得2m2﹣3≤0,解得0≤m3∴点M的横坐标m的取值范围:0≤m3;(2)∵B(0,2),C(3,3),D30),⊙T的圆心为T(t,﹣1),点N是⊙T“友好点”,∴NT≤2r=2,∴点N 只能在线段BD 上运动,过点T 作TN ⊥BD 于N ,作TH ∥y 轴,与BD 交于点H .∵tan ∠BDO =3323OB OD ==∴∠BDO=30°, ∴∠OBD =60°, ∴∠THN=∠OBD=60°, ∴NT =HT•sin ∠3, ∵B (0,2),D 30), ∴直线BD :y 3+2, ∵H 点BD 上, ∵H (t 3+2), ∴HT 3+2﹣(﹣1)3+3, ∴NT =32HT =32(﹣33t +3)=﹣12t +332,∴﹣12t +332≤2, ∴t ≥﹣3当H 与点D 重合时,点T 的横坐标等于点D 的横坐标,即t =3, 此时点N 不是“友好点”, ∴t <3故圆心T 的横坐标t 的取值范围:﹣3t <3 【点睛】本题是圆的综合题,正确理解“友好点”的意义,熟练运用相似三角形的性质与特殊三角函数是解题的关键.6.如图,已知二次函数212y x bx c =++的图象经过点A (-3,6),并与x 轴交于点B (-1,0)和点C ,顶点为点P . (1)求这个二次函数解析式;(2)设D 为x 轴上一点,满足∠DPC =∠BAC ,求点D 的坐标;(3)作直线AP ,在抛物线的对称轴上是否存在一点M ,在直线AP 上是否存在点N ,使AM +MN 的值最小?若存在,求出M 、N 的坐标:若不存在,请说明理由.【答案】(1)点C 坐标为(3,0),点P (1,-2);(2)点P (7,0);(3)点N (-75,145). 【解析】 【分析】(1)将点A 、B 坐标代入二次函数表达式,即可求解; (2)利用S △ABC = 12×AC×BH= 12×BC×y A ,求出sinα= 222105BH AB ==,则tanα= 12,在△PMD 中,tanα=MDPM 1222x =+,即可求解; (3)作点A 关于对称轴的对称点A′(5,6),过点A′作A′N ⊥AP 分别交对称轴与点M 、交AP 于点N ,此时AM+MN 最小,即可求解. 【详解】(1)将点A 、B 坐标代入二次函数表达式得:96332102b b c ⎧=-+⎪⎪⎨⎪=--+⎪⎩,解得:132b c =-⎧⎪⎨=-⎪⎩,故:抛物线的表达式为:y =12x 2-x -32, 令y =0,则x =-1或3,令x =0,则y =-32, 故点C 坐标为(3,0),点P (1,-2);(2)过点B作BH⊥AC交于点H,过点P作PG⊥x轴交于点G,设:∠DPC=∠BAC=α,由题意得:AB=210,AC=62,BC=4,PC=22,S△ABC=12×AC×BH=12×BC×y A,解得:BH=22,sinα=BHAB=22210=15,则tanα=12,由题意得:GC=2=PG,故∠PCB=45°,延长PC,过点D作DM⊥PC交于点M,则MD=MC=x,在△PMD中,tanα=MDPM=22xx+=12,解得:x=22,则CD=2x=4,故点P(7,0);(3)作点A关于对称轴的对称点A′(5,6),过点A′作A′N⊥AP分别交对称轴与点M、交AP于点N,此时AM+MN最小,直线AP表达式中的k值为:84-=-2,则直线A′N表达式中的k值为12,设直线A′N的表达式为:y=12x+b,将点A′坐标代入上式并求解得:b=72,故直线A′N的表达式为:y=12x+72…①,当x=1时,y=4,故点M(1,4),同理直线AP的表达式为:y=-2x…②,联立①②两个方程并求解得:x=-75,故点N(-75,145).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形等知识,其中(3),利用对称点求解最小值,是此类题目的一般方法.7.已知抛物线y=﹣16x2﹣23x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.(1)求直线AC的解析式;(2)如图,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP 面积最大时,求|PM﹣OM|的值.(3)如图,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.【答案】(1) y=13x+2;(2) 点M坐标为(﹣2,53)时,四边形AOCP的面积最大,此时|PM﹣OM|61 (3)存在,D′坐标为:(0,4)或(﹣6,2)或(35,195).【解析】【分析】(1)令x=0,则y=2,令y=0,则x=2或﹣6,求出点A、B、C坐标,即可求解;(2)连接OP交对称轴于点M,此时,|PM﹣OM|有最大值,即可求解;(3)存在;分①A′D′⊥A′E;②A′D′⊥ED′;③ED′⊥A′E三种情况利用勾股定理列方程求解即可.【详解】(1)令x=0,则y=2,令y=0,则x=2或﹣6,∴A(﹣6,0)、B(2,0)、C(0,2),函数对称轴为:x=﹣2,顶点坐标为(﹣2,83),C点坐标为(0,2),则过点C的直线表达式为:y=kx+2,将点A坐标代入上式,解得:k13=,则:直线AC的表达式为:y13=x+2;(2)如图,过点P作x轴的垂线交AC于点H.四边形AOCP面积=△AOC的面积+△ACP的面积,四边形AOCP面积最大时,只需要△ACP的面积最大即可,设点P坐标为(m,16-m223-m+2),则点G坐标为(m,13m+2),S△ACP12=PG•OA12=•(16-m223-m+213-m﹣2)•612=-m2﹣3m,当m=﹣3时,上式取得最大值,则点P坐标为(﹣3,52).连接OP交对称轴于点M,此时,|PM﹣OM|有最大值,直线OP的表达式为:y56=-x,当x=﹣2时,y53=,即:点M坐标为(﹣2,5 3),|PM﹣OM|的最大值为:2222555(32)()2()233-++--+=616.(3)存在.∵AE=CD,∠AEC=∠ADC=90°,∠EMA=∠DMC,∴△EAM≌△DCM(AAS),∴EM=DM,AM=MC,设:EM=a,则:MC=6﹣a.在Rt△DCM中,由勾股定理得:MC2=DC2+MD2,即:(6﹣a)2=22+a2,解得:a83=,则:MC103=,过点D作x轴的垂线交x轴于点N ,交EC 于点H .在Rt △DMC 中,12DH •MC 12=MD •DC ,即:DH 10833⨯=⨯2,则:DH 85=,HC 65==,即:点D 的坐标为(61855-,); 设:△ACD 沿着直线AC 平移了m 个单位,则:点A ′坐标(﹣6D ′坐标为(61855,-++),而点E 坐标为(﹣6,2),则2''A D =22618(6)()55-++=36,2'A E =222)+=24m +,2'ED =22248((55+=21285m +.若△A ′ED ′为直角三角形,分三种情况讨论:①当2''A D +2'A E =2'ED 时,36+24m -=21285m +,解得:m ,此时D ′(61855,-++)为(0,4); ②当2''A D +2'ED =2'A E 时,36+21285m +=24m +,解得:m =D ′(61855,-)为(-6,2);③当2'A E +2'ED =2''A D 时,24m +21285m +=36,解得:m =或m =5,此时D ′(61855,-+)为(-6,2)或(35,195). 综上所述:D 坐标为:(0,4)或(﹣6,2)或(35,195). 【点睛】本题考查了二次函数知识综合运用,涉及到一次函数、图形平移、解直角三角形等知识,其中(3)中图形是本题难点,其核心是确定平移后A ′、D ′的坐标,本题难度较大.8.已知:在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,BE :AB=3:5,若 ,cos ∠ACD= 45,求tan ∠AEC 的值及CD 的长.【答案】tan ∠AEC=3, CD=12125 【解析】 解:在RT △ACD 与RT △ABC 中∵∠ABC+∠CAD=90°, ∠ACD+∠CAD=90°∴∠ABC=∠ACD, ∴cos ∠ABC=cos ∠ACD=45 在RT △ABC 中,45BC AB = 令BC=4k,AB=5k 则AC=3k 由35BE AB = ,BE=3k 则CE=k,且CE=2 则k=2,AC=32 ∴RT △ACE 中,tan ∠AEC=AC EC =3 ∵RT △ACD 中cos ∠ACD=45CD AC = ,,CD=12125.9.在等腰△ABC 中,∠B=90°,AM 是△ABC 的角平分线,过点M 作MN ⊥AC 于点N ,∠EMF=135°.将∠EMF 绕点M 旋转,使∠EMF 的两边交直线AB 于点E ,交直线AC 于点F ,请解答下列问题:(1)当∠EMF 绕点M 旋转到如图①的位置时,求证:BE+CF=BM ;(2)当∠EMF 绕点M 旋转到如图②,图③的位置时,请分别写出线段BE ,CF ,BM 之间的数量关系,不需要证明;(3)在(1)和(2)的条件下,tan ∠BEM=,AN=+1,则BM= ,CF= .【答案】(1)证明见解析(2)见解析(3)1,1+或1﹣【解析】【分析】(1)由等腰△ABC中,∠B=90°,AM是△ABC的角平分线,过点M作MN⊥AC于点N,可得BM=MN,∠BMN=135°,又∠EMF=135°,可证明的△BME≌△NMF,可得BE=NF,NC=NM=BM进而得出结论;(2)①如图②时,同(1)可证△BME≌△NMF,可得BE﹣CF=BM,②如图③时,同(1)可证△BME≌△NMF,可得CF﹣BE=BM;(3) 在Rt△ABM和Rt△ANM中,,可得Rt△ABM≌Rt△ANM,后分别求出AB、 AC、 CN 、BM、 BE的长,结合(1)(2)的结论对图①②③进行讨论可得CF的长.【详解】(1)证明:∵△ABC是等腰直角三角形,∴∠BAC=∠C=45°,∵AM是∠BAC的平分线,MN⊥AC,∴BM=MN,在四边形ABMN中,∠,BMN=360°﹣90°﹣90°﹣45°=135°,∵∠ENF=135°,,∴∠BME=∠NMF,∴△BME≌△NMF,∴BE=NF,∵MN⊥AC,∠C=45°,∴∠CMN=∠C=45°,∴NC=NM=BM,∵CN=CF+NF,∴BE+CF=BM;(2)针对图2,同(1)的方法得,△BME≌△NMF,∴BE=NF,∵MN⊥AC,∠C=45°,∴∠CMN=∠C=45°,∴NC=NM=BM,∵NC=NF﹣CF,∴BE﹣CF=BM;针对图3,同(1)的方法得,△BME≌△NMF,∴BE=NF,∵MN⊥AC,∠C=45°,∴∠CMN=∠C=45°,∴NC=NM=BM,∵NC=CF﹣NF,∴CF﹣BE=BM;(3)在Rt△ABM和Rt△ANM中,,∴Rt△ABM≌Rt△ANM(HL),∴AB=AN=+1,在Rt△ABC中,AC=AB=+1,∴AC=AB=2+,∴CN=AC﹣AN=2+﹣(+1)=1,在Rt△CMN中,CM=CN=,∴BM=BC﹣CM=+1﹣=1,在Rt△BME中,tan∠BEM===,∴BE=,∴①由(1)知,如图1,BE+CF=BM,∴CF=BM﹣BE=1﹣②由(2)知,如图2,由tan∠BEM=,∴此种情况不成立;③由(2)知,如图3,CF﹣BE=BM,∴CF=BM+BE=1+,故答案为1,1+或1﹣.【点睛】本题考查三角函数与旋转与三角形全等的综合,难度较大,需综合运用所学知识求解.10.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD 交圆的切线BE于点E(1)判断直线PD是否为⊙O的切线,并说明理由;(2)如果∠BED=60°,PD=3,求PA的长;(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.【答案】(1)证明见解析;(2)1;(3)证明见解析.【解析】【分析】(1)连接OD,由AB是圆O的直径可得∠ADB=90°,进而求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;(2)根据BE是⊙O的切线,则∠EBA=90°,即可求得∠P=30°,再由PD为⊙O的切线,得∠PDO=90°,根据三角函数的定义求得OD,由勾股定理得OP,即可得出PA;(3)根据题意可证得∠ADF=∠PDA=∠PBD=∠ABF,由AB是圆O的直径,得∠ADB=90°,设∠PBD=x°,则可表示出∠DAF=∠PAD=90°+x°,∠DBF=2x°,由圆内接四边形的性质得出x 的值,可得出△BDE是等边三角形.进而证出四边形DFBE为菱形.【详解】(1)直线PD为⊙O的切线,理由如下:如图1,连接OD,∵AB是圆O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°,又∵DO=BO,∴∠BDO=∠PBD,∵∠PDA=∠PBD,∴∠BDO=∠PDA,∴∠ADO+∠PDA=90°,即PD⊥OD,∵点D在⊙O上,∴直线PD为⊙O的切线;(2)∵BE是⊙O的切线,∴∠EBA=90°,∵∠BED=60°,∴∠P=30°,∵PD为⊙O的切线,∴∠PDO=90°,在Rt△PDO中,∠P=30°,3∴0 tan30ODPD,解得OD=1,∴22=+=2,PO PD OD∴PA=PO﹣AO=2﹣1=1;(3)如图2,依题意得:∠ADF=∠PDA,∠PAD=∠DAF,∵∠PDA=∠PBD∠ADF=∠ABF,∴∠ADF=∠PDA=∠PBD=∠ABF,∵AB是圆O的直径,∴∠ADB=90°,设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°,∵四边形AFBD内接于⊙O,∴∠DAF+∠DBF=180°,即90°+x+2x=180°,解得x=30°,∴∠ADF=∠PDA=∠PBD=∠ABF=30°,∵BE、ED是⊙O的切线,∴DE=BE,∠EBA=90°,∴∠DBE=60°,∴△BDE是等边三角形,∴BD=DE=BE,又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°,∴△BDF是等边三角形,∴BD=DF=BF,∴DE=BE=DF=BF,∴四边形DFBE为菱形.【点睛】本题是一道综合性的题目,考查了切线的判定和性质,圆周角定理和菱形的性质,是中档题,难度较大.。
中考数学锐角三角函数-经典压轴题含详细答案

中考数学锐角三角函数-经典压轴题含详细答案一、锐角三角函数1.如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.(1) 试判断BE与FH的数量关系,并说明理由;(2) 求证:∠ACF=90°;(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求的长.图1 图2【答案】(1)BE="FH" ;理由见解析(2)证明见解析(3)=2π【解析】试题分析:(1)由△ABE≌△EHF(SAS)即可得到BE=FH(2)由(1)可知AB=EH,而BC=AB,FH=EB,从而可知△FHC是等腰直角三角形,∠FCH 为45°,而∠ACB也为45°,从而可证明(3)由已知可知∠EAC=30°,AF是直径,设圆心为O,连接EO,过点E作EN⊥AC于点N,则可得△ECN为等腰直角三角形,从而可得EN的长,进而可得AE的长,得到半径,得到所对圆心角的度数,从而求得弧长试题解析:(1)BE=FH.理由如下:∵四边形ABCD是正方形∴∠B=90°,∵FH⊥BC ∴∠FHE=90°又∵∠AEF=90°∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°∴∠HEF=∠BAE ∴∠AEB=∠EFH 又∵AE=EF∴△ABE≌△EHF(SAS)∴BE=FH(2)∵△ABE≌△EHF∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE="CH"∴CH=FH∴∠FCH=45°,∴∠FCM=45°∵AC是正方形对角线,∴∠ACD=45°∴∠ACF=∠FCM +∠ACD =90°(3)∵AE=EF,∴△AEF是等腰直角三角形△AEF外接圆的圆心在斜边AF的中点上.设该中点为O.连结EO得∠AOE=90°过E作EN⊥AC于点NRt△ENC中,EC=4,∠ECA=45°,∴EN=NC=Rt△ENA中,EN =又∵∠EAF=45°∠CAF=∠CEF=15°(等弧对等角)∴∠EAC=30°∴AE=Rt△AFE中,AE== EF,∴AF=8AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°=2π·4·(90°÷360°)=2π考点:1、正方形;2、等腰直角三角形;3、圆周角定理;4、三角函数2.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O 于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC•3DC=,∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED===;②当CF=aCD(a>0)时,sin∠CAB=.∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC•(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.3.在等腰△ABC中,∠B=90°,AM是△ABC的角平分线,过点M作MN⊥AC于点N,∠EMF=135°.将∠EMF绕点M旋转,使∠EMF的两边交直线AB于点E,交直线AC于点F,请解答下列问题:(1)当∠EMF绕点M旋转到如图①的位置时,求证:BE+CF=BM;(2)当∠EMF绕点M旋转到如图②,图③的位置时,请分别写出线段BE,CF,BM之间的数量关系,不需要证明;(3)在(1)和(2)的条件下,tan∠BEM=,AN=+1,则BM=,CF=.【答案】(1)证明见解析(2)见解析(3)1,1+或1﹣【解析】【分析】(1)由等腰△ABC中,∠B=90°,AM是△ABC的角平分线,过点M作MN⊥AC于点N,可得BM=MN,∠BMN=135°,又∠EMF=135°,可证明的△BME≌△NMF,可得BE=NF,NC=NM=BM进而得出结论;(2)①如图②时,同(1)可证△BME≌△NMF,可得BE﹣CF=BM,②如图③时,同(1)可证△BME≌△NMF,可得CF﹣BE=BM;(3) 在Rt△ABM和Rt△ANM中,,可得Rt△ABM≌Rt△ANM,后分别求出AB、 AC、 CN 、BM、 BE的长,结合(1)(2)的结论对图①②③进行讨论可得CF的长.【详解】(1)证明:∵△ABC是等腰直角三角形,∴∠BAC=∠C=45°,∵AM是∠BAC的平分线,MN⊥AC,∴BM=MN,在四边形ABMN中,∠,BMN=360°﹣90°﹣90°﹣45°=135°,∵∠ENF=135°,,∴∠BME=∠NMF,∴△BME≌△NMF,∴BE=NF,∵MN⊥AC,∠C=45°,∴∠CMN=∠C=45°,∴NC=NM=BM,∵CN=CF+NF,∴BE+CF=BM;(2)针对图2,同(1)的方法得,△BME≌△NMF,∴BE=NF,∵MN⊥AC,∠C=45°,∴∠CMN=∠C=45°,∴NC=NM=BM,∵NC=NF﹣CF,∴BE﹣CF=BM;针对图3,同(1)的方法得,△BME≌△NMF,∴BE=NF,∵MN⊥AC,∠C=45°,∴∠CMN=∠C=45°,∴NC=NM=BM,∵NC=CF﹣NF,∴CF﹣BE=BM;(3)在Rt△ABM和Rt△ANM中,,∴Rt△ABM≌Rt△ANM(HL),∴AB=AN=+1,在Rt△ABC中,AC=AB=+1,∴AC=AB=2+,∴CN=AC﹣AN=2+﹣(+1)=1,在Rt△CMN中,CM=CN=,∴BM=BC﹣CM=+1﹣=1,在Rt△BME中,tan∠BEM===,∴BE=,∴①由(1)知,如图1,BE+CF=BM,∴CF=BM﹣BE=1﹣②由(2)知,如图2,由tan∠BEM=,∴此种情况不成立;③由(2)知,如图3,CF﹣BE=BM,∴CF=BM+BE=1+,故答案为1,1+或1﹣.【点睛】本题考查三角函数与旋转与三角形全等的综合,难度较大,需综合运用所学知识求解.4.如图,等腰△ABC 中,AB=AC ,∠BAC=36°,BC=1,点D 在边AC 上且BD 平分∠ABC ,设CD=x .(1)求证:△ABC ∽△BCD ; (2)求x 的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(2)152-+;(3)5816.【解析】试题分析:(1)由等腰三角形ABC 中,顶角的度数求出两底角度数,再由BD 为角平分线求出∠DBC 的度数,得到∠DBC=∠A ,再由∠C 为公共角,利用两对角相等的三角形相似得到三角形ABC 与三角形BCD 相似;(2)根据(1)结论得到AD=BD=BC ,根据AD+DC 表示出AC ,由(1)两三角形相似得比例求出x 的值即可;(3)过B 作BE 垂直于AC ,交AC 于点E ,在直角三角形ABE 和直角三角形BCE 中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果. 试题解析:(1)∵等腰△ABC 中,AB=AC ,∠BAC=36°, ∴∠ABC=∠C=72°, ∵BD 平分∠ABC , ∴∠ABD=∠CBD=36°, ∵∠CBD=∠A=36°,∠C=∠C , ∴△ABC ∽△BCD ; (2)∵∠A=∠ABD=36°, ∴AD=BD , ∵BD=BC , ∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1, ∵△ABC ∽△BCD ,∴AB BC BD CD =,即111x x +=, 整理得:x 2+x-1=0,解得:x 1=152-+,x 2=152--(负值,舍去),则x=152-+; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=154-+, 在Rt △ABE 中,cosA=cos36°=15151441512AE AB -+++==-++, 在Rt △BCE 中,cosC=cos72°=1515414EC BC -+-+==, 则cos36°-cos72°=514+=-154-+=12. 【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.5.如图,抛物线C 1:y=(x+m )2(m 为常数,m >0),平移抛物线y=﹣x 2,使其顶点D 在抛物线C 1位于y 轴右侧的图象上,得到抛物线C 2.抛物线C 2交x 轴于A ,B 两点(点A 在点B 的左侧),交y 轴于点C ,设点D 的横坐标为a .(1)如图1,若m=.①当OC=2时,求抛物线C2的解析式;②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;(2)如图2,当OB=2﹣m(0<m<)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).【答案】(1) ①y=﹣x2+x+2.②.(2)P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【解析】试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C (0,2)在C2上,求出抛物线C2的解析式;②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;(2)解题要点有3个:i)判定△ABD为等边三角形;ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.试题解析:(1)当m=时,抛物线C1:y=(x+)2.∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+)2).∴抛物线C2:y=﹣(x﹣a)2+(a+)2(I).①∵OC=2,∴C(0,2).∵点C在抛物线C2上,∴﹣(0﹣a)2+(a+)2=2,解得:a=,代入(I)式,得抛物线C2的解析式为:y=﹣x2+x+2.②在(I)式中,令y=0,即:﹣(x﹣a)2+(a+)2=0,解得x=2a+或x=﹣,∴B(2a+,0);令x=0,得:y=a+,∴C(0,a+).设直线BC的解析式为y=kx+b,则有:,解得,∴直线BC的解析式为:y=﹣x+(a+).假设存在满足条件的a值.∵AP=BP,∴点P在AB的垂直平分线上,即点P在C2的对称轴上;∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,∴OP⊥BC.如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,则OP⊥BC,OE=a.∵点P在直线BC上,∴P(a,a+),PE=a+.∵tan∠EOP=tan∠BCO=,∴,解得:a=.∴存在a=,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP"(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+m)2).∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).∵OB=2﹣m,∴2a+m=2﹣m,∴a=﹣m.∴D(﹣m,3).AB=OB+OA=2﹣m+m=2.如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=,OE=OB﹣BE=﹣m.∵tan∠ABD=,∴∠ABD=60°.又∵AD=BD,∴△ABD为等边三角形.作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°=×=1,∴P1(﹣m,1);在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.在Rt△BEP2中,P2E=BE•tan60°=•=3,∴P2(﹣m,﹣3);易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2,且P3P4∥x轴.∴P3(﹣﹣m,3)、P4(3﹣m,3).综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,其坐标为:P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【考点】二次函数综合题.6.我市在创建全国文明城市的过程中,某社区在甲楼的A处与E处之间悬挂了一副宣传条幅,在乙楼顶部C点测得条幅顶端A点的仰角为45°,条幅底端E点的俯角为30°,若甲、乙两楼之间的水平距离BD 为12米,求条幅AE 的长度.(结果保留根号)【答案】AE 的长为(123)+【解析】【分析】在Rt ACF 中求AF 的长, 在Rt CEF 中求EF 的长,即可求解.【详解】过点C 作CF AB ⊥于点F由题知:四边形CDBF 为矩形12CF DB ∴==在Rt ACF 中,45ACF ∠=︒tan 1AF ACF CF∴∠== 12AF ∴=在Rt CEF 中,30ECF ∠=︒tan EF ECF CF∴∠= 312EF ∴= 43EF ∴=1243AE AF EF ∴=+=+∴求得AE 的长为(1243+【点睛】本题考查了三角函数的实际应用,中等难度,作辅助线构造直角三角形是解题关键.7.如图,某校数学兴趣小组为测量校园主教学楼AB 的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点C ,用测角器测得主教学楼顶端A 的仰角为30°,再向主教学楼的方向前进24米,到达点E 处(C ,E ,B 三点在同一直线上),又测得主教学楼顶端A 的仰角为60°,已知测角器CD 的高度为1.6米,请计算主教学楼AB 的高3,结果精确到0.1米)【答案】22.4m【解析】【分析】首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造等量关系,进而求解.【详解】解:在Rt △AFG 中,tan ∠AFG =3, ∴FG =tan 3AG AG AFG =∠, 在Rt △ACG 中,tan ∠ACG =AG CG , ∴CG =tan AG ACG∠=3AG . 又∵CG ﹣FG =24m ,即3AG ﹣3AG =24m , ∴AG =123m ,∴AB =123+1.6≈22.4m .8.如图①,抛物线y =ax 2+bx+c 经过点A (﹣2,0)、B (4,0)、C (0,3)三点.(1)试求抛物线的解析式;(2)点P 是y 轴上的一个动点,连接PA ,试求5PA+4PC 的最小值;(3)如图②,若直线l 经过点T (﹣4,0),Q 为直线l 上的动点,当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时,试求直线l 的解析式.【答案】(1)233384y x x =-++;(2)5PA+4PC 的最小值为18;(3)直线l 的解析式为334y x =+或334y x =--. 【解析】【分析】(1)设出交点式,代入C 点计算即可 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ,易证△CDP ∽△COB ,得到比例式PC PD BC OB =,得到PD=45PC ,所以5PA+4PC =5(PA+45PC )=5(PA+PD ),当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小,利用等面积法求出AE=185,即最小值为18 (3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆, 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90°,即∠AQB =90°时,只有一个满足条件的点Q ,∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个;此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ,利用cos ∠QFT 求出QG ,分出情况Q 在x 轴上方和x 轴下方时,分别代入直接l 得到解析式即可【详解】解:(1)∵抛物线与x 轴交点为A (﹣2,0)、B (4,0)∴y =a (x+2)(x ﹣4)把点C (0,3)代入得:﹣8a =3∴a =﹣38∴抛物线解析式为y =﹣38(x+2)(x ﹣4)=﹣38x 2+34x+3 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D∴∠CDP =∠COB =90°∵∠DCP =∠OCB∴△CDP ∽△COB ∴PC PD BC OB= ∵B (4,0),C (0,3)∴OB=4,OC =3,BC∴PD =45PC ∴5PA+4PC =5(PA+45PC )=5(PA+PD ) ∴当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小∵A (﹣2,0),OC ⊥AB ,AE ⊥BC∴S △ABC =12AB•OC =12BC•AE ∴AE =631855AB OC BC ⨯== ∴5AE =18∴5PA+4PC 的最小值为18.(3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90° ∴∠AQB =90°时,只有一个满足条件的点Q∵当Q 在⊙F 上运动时(不与A 、B 重合),∠AQB =90°∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个此时,连接FQ ,过点Q 作QG ⊥x 轴于点G∴∠FQT =90°∵F 为A (﹣2,0)、B (4,0)的中点∴F (1,0),FQ =FA =3∵T (﹣4,0)∴TF =5,cos ∠QFT =35FQ TF = ∵Rt △FGQ 中,cos ∠QFT =35FG FQ = ∴FG =35FQ =95∴x Q =1﹣9455=-,QG 125== ①若点Q 在x 轴上方,则Q (41255-,)设直线l 解析式为:y =kx+b ∴4041255k b k b -+=⎧⎪⎨-+=⎪⎩ 解得:343k b ⎧=⎪⎨⎪=⎩ ∴直线l :334y x =+ ②若点Q 在x 轴下方,则Q (41255--,) ∴直线l :334y x =-- 综上所述,直线l 的解析式为334y x =+或334y x =--【点睛】本题是二次函数与圆的综合题,同时涉及到三角函数、勾股定理等知识点,综合度比较高,需要很强的综合能力,第三问能够找到满足条件的Q 点是关键,同时不要忘记需要分情况讨论9. 兰州银滩黄河大桥北起安宁营门滩,南至七里河马滩,是黄河上游的第一座大型现代化斜拉式大桥如图,小明站在桥上测得拉索AB 与水平桥面的夹角是31°,拉索AB 的长为152米,主塔处桥面距地面7.9米(CD 的长),试求出主塔BD 的高.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)【答案】主塔BD的高约为86.9米.【解析】【分析】根据直角三角形中由三角函数得出BC相应长度,再由BD=BC+CD可得出.【详解】在Rt△ABC中,∠ACB=90°,sin BCAAB=.∴sin152sin311520.5279.04BC AB A︒=⨯=⨯=⨯=.79.047.986.9486.9BD BC CD=+=+=≈(米)答:主塔BD的高约为86.9米.【点睛】本题考察了直角三角形与三角函数的结合,熟悉掌握是解决本题的关键.10.如图,在▱ABCD中,AC与BD交于点O,AC⊥BC于点C,将△ABC沿AC翻折得到△AEC,连接DE.(1)求证:四边形ACED是矩形;(2)若AC=4,BC=3,求sin∠ABD的值.【答案】(1)证明见解析(2)13 65【解析】【分析】(1)根据▱ABCD中,AC⊥BC,而△ABC≌△AEC,不难证明;(2)依据已知条件,在△ABD或△AOC作垂线AF或OF,求出相应边的长度,即可求出∠ABD的正弦值.【详解】(1)证明:∵将△ABC 沿AC 翻折得到△AEC ,∴BC =CE ,AC ⊥CE ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴AD =CE ,AD ∥CE , ∴四边形ACED 是平行四边形,∵AC ⊥CE ,∴四边形ACED 是矩形.(2)解:方法一、如图1所示,过点A 作AF ⊥BD 于点F ,∵BE =2BC =2×3=6,DE =AC =4,∴在Rt △BDE 中, 2222BD BE DE 64213=+=+=∵S △BDE =12×DE •AD =12AF•BD , ∴AF =4361313213⨯=, ∵Rt △ABC 中,AB =2234+=5,∴Rt △ABF 中,sin ∠ABF =sin ∠ABD =61361313655AF AB ==.方法二、如图2所示,过点O 作OF ⊥AB 于点F ,同理可得,OB =1132BD =, ∵S △AOB =11OF AB OA BC 22⋅=⋅, ∴OF =23655⨯=, ∵在Rt △BOF 中,sin ∠FBO =0661365513F OB ==, ∴sin ∠ABD =61365.【点睛】本题考查直角三角形翻折变化后所得图形的性质,矩形的判定和性质,平行四边形的性质和解直角三角形求线段的长度,关键是正确添加辅助线和三角形面积的计算公式求出sin ∠ABD .11.如图,在平面直角坐标系中,菱形ABCD 的边AB 在x 轴上,点B 坐标(﹣6,0),点C 在y 轴正半轴上,且cos B =35,动点P 从点C 出发,以每秒一个单位长度的速度向D 点移动(P 点到达D 点时停止运动),移动时间为t 秒,过点P 作平行于y 轴的直线l 与菱形的其它边交于点Q .(1)求点D 坐标;(2)求△OPQ 的面积S 关于t 的函数关系式,并求出S 的最大值; (3)在直线l 移动过程中,是否存在t 值,使S =320ABCD S 菱形?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)点D 的坐标为(10,8).(2)S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩,S 的最大值为503.(3)3或7. 【解析】【分析】(1)在Rt △BOC 中,求BC,OC,根据菱形性质再求D 的坐标;(2)分两种情况分析:①当0≤t ≤4时和②当4<t ≤10时,根据面积公式列出解析式,再求函数的最值;(3)分两种情况分析:当0≤t ≤4时,4t =12,;当4<t ≤10时,22201233t t -+=【详解】解:(1)在Rt △BOC 中,∠BOC =90°,OB =6,cos B =35, 10cos OB BC B∴==8OC ∴==∵四边形ABCD 为菱形,CD ∥x 轴,∴点D 的坐标为(10,8).(2)∵AB =BC =10,点B 的坐标为(﹣6,0),∴点A 的坐标为(4,0).分两种情况考虑,如图1所示.①当0≤t ≤4时,PQ =OC =8,OQ =t ,∴S =12PQ •OQ =4t , ∵4>0,∴当t =4时,S 取得最大值,最大值为16;②当4<t ≤10时,设直线AD 的解析式为y =kx +b (k ≠0),将A (4,0),D (10,8)代入y =kx +b ,得:4k b 010k b 8+=⎧⎨+=⎩,解得:4k 316b 3⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线AD 的解析式为41633y x =-. 当x =t 时,41633y t =-, 41648(10)333PQ t t ⎛⎫∴=--=- ⎪⎝⎭ 21220233S PQ OP t t ∴=⋅=-+ 22202502(5),033333S t t t =-+=--+-<∴当t =5时,S 取得最大值,最大值为503. 综上所述:S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩,S 的最大值为503. (3)S 菱形ABCD =AB •OC =80.当0≤t ≤4时,4t =12,解得:t =3;当4<t ≤10时,222033t t -+=12, 解得:t 1=5﹣7(舍去),t 2=5+ 7. 综上所述:在直线l 移动过程中,存在t 值,使S =320ABCD S 菱形,t 的值为3或5+7.【点睛】考核知识点:一次函数和二次函数的最值问题.数形结合,分类讨论是关键.12.抛物线y=ax²+bx+4(a≠0)过点A(1, ﹣1),B(5, ﹣1),与y 轴交于点C .(1)求抛物线表达式;(2)如图1,连接CB ,以CB 为边作▱CBPQ ,若点P 在直线BC 下方的抛物线上,Q 为坐标平面内的一点,且▱CBPQ 的面积为30,①求点P 坐标;②过此二点的直线交y 轴于F, 此直线上一动点G,当GB+2GF 2最小时,求点G 坐标. (3)如图2,⊙O1过点A 、B 、C 三点,AE 为直径,点M 为 上的一动点(不与点A ,E 重合),∠MBN 为直角,边BN 与ME 的延长线交于N ,求线段BN 长度的最大值【答案】(1)y=x²﹣6x+4(2)①P(2, -4)或P(3, -5) ②G(0, -2)(3)313【解析】【分析】(1)把点A (1,-1),B (5,-1)代入抛物线y=ax 2+bx+4解析式,即可得出抛物线的表达式;(2)①如图,连接PC ,过点P 作y 轴的平行线交直线BC 于R ,可求得直线BC 的解析式为:y=-x+4,设点P(t,t2-6t+4),R(t,-t+4),因为▱CBPQ的面积为30,所以S△PBC=1 2×(−t+4−t2+6t−4)×5=15,解得t的值,即可得出点P的坐标;②当点P为(2,-4)时,求得直线QP的解析式为:y=-x-2,得F(0,-2),∠GOR=45°,因为GB+2 2GF=GB+GR,所以当G于F重合时,GB+GR最小,即可得出点G的坐标;当点P为(3,-5)时,同理可求;(3)先用面积法求出sin∠ACB=21313,tan∠ACB=23,在Rt△ABE中,求得圆的直径,因为MB⊥NB,可得∠N=∠AEB=∠ACB,因为tanN=MBBN=23,所以BN=32MB,当MB为直径时,BN的长度最大.【详解】(1) 解:(1)∵抛物线y=ax2+bx+4(a≠0)过点A(1,-1),B(5,-1),∴1412554a ba b-++⎧⎨-++⎩=,=解得16ab⎧⎨-⎩=,=∴抛物线表达式为y=x²﹣6x+4.(2)①如图,连接PC,过点P作y轴的平行线交直线BC于R,设直线BC的解析式为y=kx+m,∵B(5,-1),C(0,4),∴154k mm-+⎧⎨⎩==,解得14km=,=-⎧⎨⎩∴直线BC的解析式为:y=-x+4,设点P(t,t2-6t+4),R(t,-t+4),∵▱CBPQ的面积为30,∴S△PBC=12×(−t+4−t2+6t−4)×5=15,解得t=2或t=3,当t=2时,y=-4当t=3时,y=-5,∴点P坐标为(2,-4)或(3,-5);②当点P为(2,-4)时,∵直线BC解析式为:y=-x+4, QP∥BC,设直线QP的解析式为:y=-x+n,将点P代入,得-4=-2+n,n=-2,∴直线QP的解析式为:y=-x-2,∴F(0,-2),∠GOR=45°,∴GB+22GF=GB+GR当G于F重合时,GB+GR最小,此时点G的坐标为(0,-2),同理,当点P为(3,-5)时,直线QP的解析式为:y=-x-2,同理可得点G的坐标为(0,-2),(3) )∵A(1,-1),B(5,-1)C(0,4),∴AC=26,BC=52,∵S△ABC=12AC×BCsin∠ACB=12AB×5,∴sin∠ACB=21313,tan∠ACB=23,∵AE为直径,AB=4,∴∠ABE=90°,∵sin∠AEB=sin∠ACB=21313=4AE,∴AE=213,∵MB⊥NB,∠NMB=∠EAB,∴∠N=∠AEB=∠ACB,∴tanN=MBBN =23,∴BN=32MB,当MB为直径时,BN的长度最大,为313.【点睛】题考查用到待定系数法求二次函数解析式和一次函数解析式,圆周角定理,锐角三角函数定义,平行四边形性质.解决(3)问的关键是找到BN与BM之间的数量关系.13.如图,正方形ABCD的边长为2+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,(1)求证:△ABF∽△ACE;(2)求tan∠BAE的值;(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE =∠HEC =45°,∴HC =EH ,∴BE =EH =HC ,设BE =HE =HC =x ,则EC =2x , ∵BC =2+1,∴x+x =2+1,∴x =1,在Rt △ABE 中,∵∠ABE =90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC 22AB BC +2,∴OA =OC =OB =12AC 22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB 22+ •2﹣12 ∴HM =OH+OM =222+, 在Rt △EHM 中,EH 2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=22+.. ∴PE+PF 22+【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.14.如图,半圆O 的直径AB =20,弦CD ∥AB ,动点M 在半径OD 上,射线BM 与弦CD 相交于点E (点E 与点C 、D 不重合),设OM =m .(1)求DE 的长(用含m 的代数式表示);(2)令弦CD 所对的圆心角为α,且sin 4=25α. ①若△DEM 的面积为S ,求S 关于m 的函数关系式,并求出m 的取值范围;②若动点N 在CD 上,且CN =OM ,射线BM 与射线ON 相交于点F ,当∠OMF =90° 时,求DE 的长.【答案】(1)DE =10010m m -;(2)①S =2360300m m m-+,(5013<m <10),②DE =52. 【解析】【分析】 (1)由CD ∥AB 知△DEM ∽△OBM ,可得DE DM OB OM=,据此可得; (2)①连接OC 、作OP ⊥CD 、MQ ⊥CD ,由OC =OD 、OP ⊥CD 知∠DOP =12∠COD ,据此可得sin ∠DOP =sin ∠DMQ =45、sin ∠ODP =35,继而由OM =m 、OD =10得QM =DM sin ∠ODP =35(10﹣m ),根据三角形的面积公式即可得;如图2,先求得PD =8、CD =16,证△CDM ∽△BOM 得CD DM BO OM =,求得OM =5013,据此可得m 的取值范围; ②如图3,由BM =OB sin ∠BOM =10×35=6,可得OM =8,根据(1)所求结果可得答案.【详解】(1)∵CD ∥AB ,∴△DEM ∽△OBM ,∴DE DM OB OM =,即1010DE m m-=, ∴DE =10010m m-; (2)①如图1,连接OC 、作OP ⊥CD 于点P ,作MQ ⊥CD 于点Q ,∵OC =OD 、OP ⊥CD ,∴∠DOP =12∠COD , ∵sin 2α=45, ∴sin ∠DOP =sin ∠DMQ =45,sin ∠ODP =35, ∵OM =m 、OD =10, ∴DM =10﹣m , ∴QM =DM sin ∠ODP =35(10﹣m ), 则S △DEM =12DE •MQ =12×10010m m -×35(10﹣m )=2360300m m m-+, 如图2,∵PD =OD sin ∠DOP =10×45=8, ∴CD =16,∵CD ∥AB ,∴△CDM ∽△BOM ,∴CD DM BO OM =,即1610=10OM OM-, 解得:OM =5013, ∴5013<m <10, ∴S =2360300m m m-+,(5013<m <10).②当∠OMF =90°时,如图3,则∠BMO =90°,在Rt △BOM 中,BM =OB sin ∠BOM =10×35=6, 则OM =8,由(1)得DE =100108582-⨯=. 【点睛】本题主要考查圆的综合题,解题的关键是熟练掌握圆的有关性质、相似三角形的判定与性质及解直角三角形的能力.15.如图所示,一堤坝的坡角62ABC ∠=︒,坡面长度25AB =米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角50ADB ∠=︒,则此时应将坝底向外拓宽多少米?(结果保留到0.01 米)(参考数据:sin620.88︒≈,cos620.47︒≈,tan50 1.20︒≈)【答案】6.58米【解析】试题分析:过A 点作AE ⊥CD 于E .在Rt △ABE 中,根据三角函数可得AE ,BE ,在Rt △ADE 中,根据三角函数可得DE ,再根据DB=DE ﹣BE 即可求解.试题解析:过A 点作AE ⊥CD 于E . 在Rt △ABE 中,∠ABE=62°. ∴AE=AB•sin62°=25×0.88=22米,BE=AB•cos62°=25×0.47=11.75米, 在Rt △ADE 中,∠ADB=50°, ∴DE==18米,∴DB=DE ﹣BE≈6.58米. 故此时应将坝底向外拓宽大约6.58米.考点:解直角三角形的应用-坡度坡角问题.。
中考数学专题复习之锐角三角函数(共20题)

中考数学专题复习之锐角三角函数(共20题)一.选择题(共10小题)1.如图,一个长方体木箱沿斜面滑至如图位置时,AB=2m,木箱高BE=1m,斜面坡角为α,则木箱端点E距地面AC的高度表示为()m.A.+2sinαB.2cosα+sinαC.cosα+2sinαD.tanα+2sinα2.为了疫情防控工作的需要,某学校在学校门口的大门上方安装了一个人体体外测温摄像头,学校大门高ME=7.5米,学生身高BD=1.5米,当学生准备进入识别区域时,在点B时测得摄像头M的仰角为30°,当学生刚好离开识别区域时,在点A时测得摄像头M 的仰角为60°,则体温监测有效识别区域AB的长()A.米B.米C.5米D.6米3.某网红地惊现震撼的裸眼3D超清LED巨幕,成功吸引了广大游客前来打卡.小丽想了解该LED屏AB的高度,进行了实地测量,她从大楼底部C点沿水平直线步行30米到达台阶底端D点,在D点测得屏幕下端点B的仰角为27°,然后她再沿着i=4:3长度为35米的自动扶梯到达扶梯顶端E点,又沿水平直线行走了45米到达F点,在F点测得屏幕上端点A的仰角为50°(A,B,C,D,E,F,G在同一个平面内,且E、F和C、D、G分别在同一水平线上),则该LED屏AB的高度约为()(结果精确到0.1,参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin50°≈0.77,tan50°≈1.19)A.86.2米B.114.2米C.126.9米D.142.2米4.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E,在此测得旗杆顶端点A的仰角为39°,则旗杆的高度AB约为()米.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)A.12.9B.22.2C.24.9D.63.15.我校小伟同学酷爱健身,一天去爬山锻炼,在出发点C处测得山顶部A的仰角为30度,在爬山过程中,每一段平路(CD、EF、GH)与水平线平行,每一段上坡路(DE、FG、HA)与水平线的夹角都是45度,在山的另一边有一点B(B、C、D同一水平线上),斜坡AB的坡度为2:1,且AB长为900,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为()(图中所有点在同一平面内≈1.41,≈1.73)A.60分钟B.70分钟C.80分钟D.90分钟6.李白笔下“孤帆一片日边来”描述了在喷薄而出的红日映衬下,远远望见一叶帆船驶来的壮美河山之境.聪明的小芬同学利用几何图形,构造出了此意境!如图,半径为5的⊙O在线段AB上方,且圆心O在线段AB的中垂线上,到AB的距离为,AB=20,线段PQ在边AB上(AP<AQ),PQ=6,以PQ中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=,设AP=m,当边DE与⊙O有交点时,m的取值范围是()A.B.C.D.7.勾股定理有着悠久的历史,它曾引起很多人的兴趣.英国佩里加(H.Perigal,1801﹣1898)用“水车翼轮法”(图1)证明了勾股定理.该证法是用线段QX,ST,将正方形BIJC分割成四个全等的四边形,再将这四个四边形和正方形ACYZ拼成大正方形AEFB (图2).若AD=,tan∠AON=,则正方形MNUV的周长为()A.B.18C.16D.8.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为()A.B.C.D.9.已知α,β均为锐角,若tanα=,tanβ=,则α+β=()A.45°B.30°C.60°D.90°10.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是()A.B.C.D.二.填空题(共5小题)11.如图1是一张双挡位可调节靠背椅,挡位调节示意图如图2.两脚AB,AC以及靠背DE,座位FG,其中D,F分别为AC,DE上固定连接点,GF在点A上移动实现靠背的调节,DC=4AD,EF=4DF,已知AB=AC=DE=50分米,tan∠ABC=2.(1)当GF∥BC时,点E离水平地面BC的高度为分米.(2)当靠背DE′⊥AC时,有G′E′∥BC,则GF的长为分米.12.如图1为温州乐园的游乐设施一摩天轮与飞天梭.当摩天轮一座舱A与飞天梭高度相同时(如图2),另一座舱B恰好位于摩天轮最低点;当座舱A顺时针旋转至与飞天梭相同高度的A′点时,座舱B旋转至点B'.此时地面某观测点P与点A',圆心O恰好在同一条直线上,且sin∠A'PC=,已知摩天轮的半径为32米,则点B,B'间的距离为米;现又测得∠APC=∠B'PC,则点B'距离地面的高度为米.13.如图,已知A、B两点的坐标分别为(﹣8,0)、(0,8),点C、F分别是直线x=5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE的面积取得最小值时,tan∠BAD=.14.如图是一款利用杠杆原理设计的平衡灯,灯管AB与支架AD,砝码杆AC均成120°角,且AB=40cm,AC=18cm,AD=6cm,底座是半径为2cm的圆柱体,点P是杠杆的支点.如图1,若砝码E在端点C时,当杠杆平衡时,支架AD垂直于桌面,则此时垂直光线照射到最远点M到支点P的距离PM为cm.由于特殊设计,灯管的重力集中在端点B,砝码杆重力集中在砝码E上,支架AD的重力忽略不计,由杠杆原理可知,平衡时重力保持垂直水平桌面向下,且G1•h2=G2•h1,如图2.为了使得平衡时砝码杆与桌面平行,则砝码E到离A点的距离为cm.15.小君家购入如图1的划船机一台,如图2是划船机的部分示意图.阻尼轮⊙O由支架AD和AC支撑,点A处于点O的正下方,AD与⊙O相切,脚踏板点E和圆心O在连杆CE上,CD部分隐藏在阻尼轮内部,测量发现点E到地面的高度EF为35cm,E、A两点间的水平距离AF为72cm,tan∠DAC=,则CD的长为cm.三.解答题(共5小题)16.某海域有一小岛P,在以P为圆心,半径r为10(3+)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.(1)求A,P之间的距离AP;(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?17.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.18.脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,为了测量房屋的高度,在地面上C点测得屋顶A的仰角为35°,此时地面上C点、屋檐上E 点、屋顶上A点三点恰好共线,继续向房屋方向走8m到达点D时,又测得屋檐E点的仰角为60°,房屋的顶层横梁EF=12m,EF∥CB,AB交EF于点G(点C,D,B在同一水平线上).(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)(1)求屋顶到横梁的距离AG;(2)求房屋的高AB(结果精确到1m).19.【材料阅读】2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上立一个觇标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300m时,还要考虑球气差,球气差计算公式为f=(其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.【问题解决】某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图,点A,B的水平距离d=800m,测量仪AC=1.5m,觇标DE=2m,点E,D,B在垂直于地面的一条直线上,在测量点A处用测量仪测得山顶觇标顶端E的仰角为37°,测量点A处的海拔高度为1800m.(1)数据6400000用科学记数法表示为;(2)请你计算该山的海拔高度.(要计算球气差,结果精确到0.01m)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)20.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为3m的筒车⊙O按逆时针方向每分钟转圈,筒车与水面分别交于点A、B,筒车的轴心O距离水面的高度OC长为2.2m,筒车上均匀分布着若干个盛水筒.若以某个盛水筒P刚浮出水面时开始计算时间.(1)经过多长时间,盛水筒P首次到达最高点?(2)浮出水面3.4秒后,盛水筒P距离水面多高?(3)若接水槽MN所在直线是⊙O的切线,且与直线AB交于点M,MO=8m.求盛水筒P从最高点开始,至少经过多长时间恰好在直线MN上.(参考数据:cos43°=sin47°≈,sin16°=cos74°≈,sin22°=cos68°≈)。
中考数学—锐角三角函数的综合压轴题专题复习及详细答案

中考数学—锐角三角函数的综合压轴题专题复习及详细答案一、锐角三角函数1.如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;(2)求证:BC2=2CD•OE;(3)若314cos,53BAD BE∠==,求OE的长.【答案】(1)DE为⊙O的切线,理由见解析;(2)证明见解析;(3)OE =356.【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.试题解析:(1)DE为⊙O的切线,理由如下:连接OD,BD,∵AB为⊙O的直径,∴∠ADB=90°,在Rt△BDC中,E为斜边BC的中点,∴CE=DE=BE=BC,∴∠C=∠CDE ,∵OA=OD ,∴∠A=∠ADO ,∵∠ABC=90°,∴∠C+∠A=90°,∴∠ADO+∠CDE=90°,∴∠ODE=90°,∴DE ⊥OD ,又OD 为圆的半径,∴DE 为⊙O 的切线;(2)∵E 是BC 的中点,O 点是AB 的中点,∴OE 是△ABC 的中位线,∴AC=2OE ,∵∠C=∠C ,∠ABC=∠BDC ,∴△ABC ∽△BDC , ∴,即BC 2=AC•CD .∴BC 2=2CD•OE ;(3)解:∵cos ∠BAD=, ∴sin ∠BAC=, 又∵BE=,E 是BC 的中点,即BC=, ∴AC=.又∵AC=2OE ,∴OE=AC=.考点:1、切线的判定;2、相似三角形的判定与性质;3、三角函数2.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)已知:如图,AB 是半圆O 的直径,弦//CD AB ,动点P 、Q 分别在线段OC 、CD 上,且DQ OP =,AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F (点F 与点C 、D 不重合),20AB =,4cos 5AOC ∠=.设OP x =,CPF ∆的面积为y .(1)求证:AP OQ =;(2)求y 关于x 的函数关系式,并写出它的定义域;(3)当OPE ∆是直角三角形时,求线段OP 的长.【答案】(1)证明见解析;(2)236030050(10)13x x y x x -+=<<;(3)8OP = 【解析】【分析】(1)证明线段相等的方法之一是证明三角形全等,通过分析已知条件,OP DQ =,联结OD 后还有OA DO =,再结合要证明的结论AP OQ =,则可肯定需证明三角形全等,寻找已知对应边的夹角,即POA QDO ∠=∠即可;(2)根据PFC ∆∽PAO ∆,将面积转化为相似三角形对应边之比的平方来求;(3)分成三种情况讨论,充分利用已知条件4cos 5AOC ∠=、以及(1)(2)中已证的结论,注意要对不符合(2)中定义域的答案舍去.【详解】(1)联结OD ,∵OC OD =,∴OCD ODC ∠=∠,∵//CD AB ,∴OCD COA ∠=∠,∴POA QDO ∠=∠.在AOP ∆和ODQ ∆中, {OP DQPOA QDO OA DO=∠=∠=,∴AOP ∆≌ODQ ∆,∴AP OQ =;(2)作PH OA ⊥,交OA 于H , ∵4cos 5AOC ∠=, ∴4455OH OP x ==,35PH x =,∴132AOP S AO PH x ∆=⋅=. ∵//CD AB ,∴PFC ∆∽PAO ∆, ∴2210()()AOP yCP x S OP x∆-==, ∴2360300x x y x-+=,当F 与点D 重合时, ∵42cos 210165CD OC OCD =⋅∠=⨯⨯=, ∴101016x x =-,解得5013x =, ∴2360300x x y x-+=50(10)13x <<; (3)①当90OPE ∠=o 时,90OPA ∠=o , ∴4cos 1085OP OA AOC =⋅∠=⨯=; ②当90POE ∠=o 时,1010254cos cos 25OC CQ QCO AOC ====∠∠, ∴252OP DQ CD CQ CD ==-=-2571622=-=, ∵501013OP <<, ∴72OP =(舍去); ③当90PEO ∠=o 时,∵//CD AB ,∴AOQ DQO ∠=∠,∵AOP ∆≌ODQ ∆,∴DQO APO ∠=∠,∴AOQ APO ∠=∠,∴90AEO AOP ∠=∠=o ,此时弦CD 不存在,故这种情况不符合题意,舍去; 综上,线段OP 的长为8.3.如图,在Rt △ABC 中,∠BAC=90°,∠B=60°,BC=16cm ,AD 是斜边BC 上的高,垂足为D ,BE=1cm .点M 从点B 出发沿BC 方向以1cm/s 的速度运动,点N 从点E 出发,与点M 同时同方向以相同的速度运动,以MN 为边在BC 的上方作正方形MNGH .点M 到达点D 时停止运动,点N 到达点C 时停止运动.设运动时间为t (s ).(1)当t为何值时,点G刚好落在线段AD上?(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?【答案】(1)3;(2);(3)t=9s或t=(15﹣6)s.【解析】试题分析:(1)求出ED的距离即可求出相对应的时间t.(2)先求出t的取值范围,分为H在AB上时,此时BM的距离,进而求出相应的时间.同样当G在AC上时,求出MN的长度,继而算出EN的长度即可求出时间,再通过正方形的面积公式求出正方形的面积.(3)分DP=PC和DC=PC两种情况,分别由EN的长度便可求出t的值.试题解析:∵∠BAC=90°,∠B=60°,BC=16cm∴AB=8cm,BD=4cm,AC=8cm,DC=12cm,AD=4cm.(1)∵当G刚好落在线段AD上时,ED=BD﹣BE=3cm∴t=s=3s.(2)∵当MH没有到达AD时,此时正方形MNGH是边长为1的正方形,令H点在AB 上,则∠HMB=90°,∠B=60°,MH=1∴BM=cm.∴t=s.当MH到达AD时,那么此时的正方形MNGH的边长随着N点的继续运动而增大,令G点在AC上,设MN=xcm,则GH=DH=x,AH=x,∵AD=AH+DH=x+x=x=4,∴x=3.当≤t≤4时,S MNGN=1cm2.当4<t≤6时,S MNGH=(t﹣3)2cm2∴S关于t的函数关系式为:.(3)分两种情况:①∵当DP=PC时,易知此时N点为DC的中点,∴MN=6cm∴EN=3cm+6cm=9cm.∴t=9s故当t=9s的时候,△CPD为等腰三角形;②当DC=PC时,DC=PC=12cm∴NC=6cm∴EN=16cm﹣1cm﹣6cm=(15﹣6)cm∴t=(15﹣6)s故当t=(15﹣6)s时,△CPD为等腰三角形.综上所述,当t=9s或t=(15﹣6)s时,△CPD为等腰三角形.考点:1.双动点问题;2.锐角三角函数定义;3.特殊角的三角函数值;4.正方形的性质;5.由实际问题列函数关系式;6.等腰三角形的性质;7.分类思想的应用.4.如图,已知点从出发,以1个单位长度/秒的速度沿轴向正方向运动,以为顶点作菱形,使点在第一象限内,且;以为圆心,为半径作圆.设点运动了秒,求:(1)点的坐标(用含的代数式表示);(2)当点在运动过程中,所有使与菱形的边所在直线相切的的值.【答案】解:(1)过作轴于,,,,,点的坐标为.(2)①当与相切时(如图1),切点为,此时,,,.②当与,即与轴相切时(如图2),则切点为,,过作于,则,,.③当与所在直线相切时(如图3),设切点为,交于,则,,.过作轴于,则,,化简,得,解得,,.所求的值是,和.【解析】(1)过作轴于,利用三角函数求得OD、DC的长,从而求得点的坐标⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=oc/op,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.5.如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点F.(1)求证:DF⊥AC;(2)若∠ABC=30°,求tan∠BCO的值.3【答案】(1)证明见解析; (2) tan∠【解析】试题分析:(1)连接OD,根据三角形的中位线定理可求出OD∥AC,根据切线的性质可证明DE⊥OD,进而得证.(2)过O作OF⊥BD,根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长,根据三角函数的定义求解.试题解析:证明:连接OD∵DE为⊙O的切线, ∴OD⊥DE∵O为AB中点, D为BC的中点∴OD‖AC∴DE⊥AC(2)过O作OF⊥BD,则BF=FD 在Rt△BFO中,∠ABC=30°∴OF=12OB, BF=32OB∵BD=DC, BF=FD,∴FC=3BF=332OB在Rt△OFC中,tan∠BCO=13233OBOFFCOB==.点睛:此题主要考查了三角形中位线定理及切线的性质与判定、三角函数的定义等知识点,有一定的综合性,根据已知得出OF=12OB,BF=3OB,FC=3BF=33OB是解题关键.6.如图,某校数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点C,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(C,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(3≈1.73,结果精确到0.1米)【答案】22.4m【解析】【分析】首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造等量关系,进而求解.【详解】解:在Rt△AFG中,tan∠AFG3,∴FG=tan3AGAFG=∠,在Rt△ACG中,tan∠ACG=AGCG,∴CG =tan AG ACG ∠=3AG . 又∵CG ﹣FG =24m , 即3AG ﹣3=24m , ∴AG =123m ,∴AB =123+1.6≈22.4m .7.许昌芙蓉湖位于许昌市水系建设总体规划中部,上游接纳清泥河来水,下游为鹿鸣湖等水系供水,承担着承上启下的重要作用,是利用有限的水资源、形成良好的水生态环境打造生态宜居城市的重要部分.某校课外兴趣小组想测量位于芙蓉湖两端的A ,B 两点之间的距离他沿着与直线AB 平行的道路EF 行走,走到点C 处,测得∠ACF=45°,再向前走300米到点D 处,测得∠BDF=60°.若直线AB 与EF 之间的距离为200米,求A ,B 两点之间的距离(结果保留一位小数)【答案】215.6米.【解析】【分析】过A 点做EF 的垂线,交EF 于M 点,过B 点做EF 的垂线,交EF 于N 点,根据Rt △ACM 和三角函数tan BDF ∠求出CM 、DN ,然后根据MN MD DN AB =+=即可求出A 、B 两点间的距离.【详解】解:过A 点做EF 的垂线,交EF 于M 点,过B 点做EF 的垂线,交EF 于N 点在Rt △ACM 中,∵45ACF ∠=︒,∴AM=CM=200米,又∵CD=300米,所以100MD CD CM =-=米,在Rt △BDN 中,∠BDF=60°,BN=200米∴115.6tan 60BN DN =≈o米, ∴215.6MN MD DN AB =+=≈米即A ,B 两点之间的距离约为215.6米.【点睛】本题主要考查三角函数,正确做辅助线是解题的关键.8.如图,AB 是⊙O 的直径,E 是⊙O 上一点,C 在AB 的延长线上,AD ⊥CE 交CE 的延长线于点D ,且AE 平分∠DAC .(1)求证:CD 是⊙O 的切线;(2)若AB =6,∠ABE =60°,求AD 的长.【答案】(1)详见解析;(2)92【解析】【分析】 (1)利用角平分线的性质得到∠OAE =∠DAE ,再利用半径相等得∠AEO =∠OAE ,等量代换即可推出OE ∥AD ,即可解题,(2)根据30°的三角函数值分别在Rt △ABE 中,AE =AB·cos30°, 在Rt △ADE 中,AD=cos30°×AE 即可解题.【详解】证明:如图,连接OE ,∵AE 平分∠DAC ,∴∠OAE =∠DAE .∵OA =OE ,∴∠AEO =∠OAE .∴∠AEO =∠DAE .∴OE ∥AD .∵DC ⊥AC ,∴OE ⊥DC .∴CD 是⊙O 的切线.(2)解:∵AB 是直径,∴∠AEB =90°,∠ABE =60°.∴∠EAB =30°,在Rt △ABE 中,AE =AB·cos30°=6×3=33, 在Rt △ADE 中,∠DAE =∠BAE =30°,∴AD=cos30°×AE=32×33=92. 【点睛】 本题考查了特殊的三角函数值的应用,切线的证明,中等难度,利用特殊的三角函数表示出所求线段是解题关键.9.如图①,抛物线y =ax 2+bx+c 经过点A (﹣2,0)、B (4,0)、C (0,3)三点.(1)试求抛物线的解析式;(2)点P 是y 轴上的一个动点,连接PA ,试求5PA+4PC 的最小值;(3)如图②,若直线l 经过点T (﹣4,0),Q 为直线l 上的动点,当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时,试求直线l 的解析式.【答案】(1)233384y x x =-++;(2)5PA+4PC 的最小值为18;(3)直线l 的解析式为334y x =+或334y x =--. 【解析】【分析】(1)设出交点式,代入C 点计算即可 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ,易证△CDP ∽△COB ,得到比例式PC PD BC OB =,得到PD=45PC ,所以5PA+4PC =5(PA+45PC )=5(PA+PD ),当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小,利用等面积法求出AE=185,即最小值为18 (3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆, 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90°,即∠AQB =90°时,只有一个满足条件的点Q ,∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个;此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ,利用cos ∠QFT 求出QG ,分出情况Q 在x 轴上方和x 轴下方时,分别代入直接l 得到解析式即可【详解】解:(1)∵抛物线与x 轴交点为A (﹣2,0)、B (4,0)∴y =a (x+2)(x ﹣4)把点C (0,3)代入得:﹣8a =3∴a =﹣38∴抛物线解析式为y =﹣38(x+2)(x ﹣4)=﹣38x 2+34x+3 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D∴∠CDP =∠COB =90°∵∠DCP =∠OCB∴△CDP ∽△COB ∴PC PD BC OB= ∵B (4,0),C (0,3)∴OB =4,OC =3,BC∴PD =45PC ∴5PA+4PC =5(PA+45PC )=5(PA+PD ) ∴当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小∵A (﹣2,0),OC ⊥AB ,AE ⊥BC∴S △ABC =12AB•OC =12BC•AE ∴AE =631855AB OC BC ⨯==n ∴5AE =18∴5PA+4PC 的最小值为18.(3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90° ∴∠AQB =90°时,只有一个满足条件的点Q∵当Q 在⊙F 上运动时(不与A 、B 重合),∠AQB =90°∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个此时,连接FQ ,过点Q 作QG ⊥x 轴于点G∴∠FQT =90°∵F 为A (﹣2,0)、B (4,0)的中点∴F (1,0),FQ =FA =3∵T (﹣4,0)∴TF =5,cos ∠QFT =35FQ TF = ∵Rt △FGQ 中,cos ∠QFT =35FG FQ =∴FG =35FQ =95∴x Q =1﹣9455=-,QG =2222912FQ 355FG ⎛⎫-=-= ⎪⎝⎭①若点Q 在x 轴上方,则Q (41255-,)设直线l 解析式为:y =kx+b ∴4041255k b k b -+=⎧⎪⎨-+=⎪⎩ 解得:343k b ⎧=⎪⎨⎪=⎩ ∴直线l :334y x =+ ②若点Q 在x 轴下方,则Q (41255--,) ∴直线l :334y x =-- 综上所述,直线l 的解析式为334y x =+或334y x =--【点睛】本题是二次函数与圆的综合题,同时涉及到三角函数、勾股定理等知识点,综合度比较高,需要很强的综合能力,第三问能够找到满足条件的Q点是关键,同时不要忘记需要分情况讨论10.在正方形ABCD中,AC是一条对角线,点E是边BC上的一点(不与点C重合),连接AE,将△ABE沿BC方向平移,使点B与点C重合,得到△DCF,过点E作EG⊥AC于点G,连接DG,FG.(1)如图,①依题意补全图;②判断线段FG与DG之间的数量关系与位置关系,并证明;(2)已知正方形的边长为6,当∠AGD=60°时,求BE的长.BE【答案】(1)①见解析,②FG=DG,FG⊥DG,见解析;(2)3【解析】【分析】(1)①补全图形即可,②连接BG,由SAS证明△BEG≌△GCF得出BG=GF,由正方形的对称性质得出BG=DG,得出FG=DG,在证出∠DGF=90°,得出FG⊥DG即可,(2)过点D作DH⊥AC,交AC于点H.由等腰直角三角形的性质得出DH=AH=2FG=DG=2GH=6,得出DF2DG=3Rt△DCF中,由勾股定理得出CF=3得出结果.【详解】解:(1)①补全图形如图1所示,②FG=DG,FG⊥DG,理由如下,连接BG,如图2所示,∵四边形ABCD是正方形,∴∠ACB =45°,∵EG ⊥AC ,∴∠EGC =90°,∴△CEG 是等腰直角三角形,EG =GC ,∴∠GEC =∠GCE =45°,∴∠BEG =∠GCF =135°,由平移的性质得:BE =CF ,在△BEG 和△GCF 中,BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩,∴△BEG ≌△GCF (SAS ),∴BG =GF ,∵G 在正方形ABCD 对角线上,∴BG =DG ,∴FG =DG ,∵∠CGF =∠BGE ,∠BGE+∠AGB =90°,∴∠CGF+∠AGB =90°,∴∠AGD+∠CGF =90°,∴∠DGF =90°,∴FG ⊥DG.(2)过点D 作DH ⊥AC ,交AC 于点H .如图3所示,在Rt △ADG 中,∵∠DAC =45°,∴DH =AH =2在Rt △DHG 中,∵∠AGD =60°,∴GH 33236,∴DG =2GH =6,∴DF 2DG =3在Rt △DCF 中,CF ()22436-3∴BE =CF =23.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识;本题综合性强,证明三角形全等是解题的关键.11.如图所示的是一个地球仪及它的平面图,在平面图中,点A 、B 分别为地球仪的南、北极点,直线AB 与放置地球仪的平面交于点D ,所夹的角度约为67°,半径OC 所在的直线与放置它的平面垂直,垂足为点E ,DE =15cm ,AD =14cm .(1)求半径OA 的长(结果精确到0.1cm ,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)(2)求扇形BOC 的面积(π取3.14,结果精确到1cm )【答案】(1)半径OA 的长约为24.5cm ;(2)扇形BOC 的面积约为2822cm .【解析】【分析】(1)在Rt △ODE 中,DE=15,∠ODE=67°,根据∠ODE 的余弦值,即可求得OD 长,减去AD 即为OA .(2)用扇形面积公式即可求得.【详解】(1)在Rt △ODE 中,15cm DE =,67ODE ∠=︒.∵cos DE ODE DO ∠=, ∴150.39OD ≈, ∴()384614245cm OA OD AD =-≈-≈.., 答:半径OA 的长约为24.5cm .(2)∵67ODE ∠=︒,∴157BOC ∠=︒, ∴2360BOC n r S π=扇形 2157 3.1424.52360⨯⨯≈ ()2822cm ≈.答:扇形BOC 的面积约为2822cm .【点睛】此题主要考查了解直角三角形的应用,本题把实际问题转化成数学问题,利用三角函数中余弦定义来解题是解题关键.12.如图,AB 为O e 的直径,C 、D 为O e 上异于A 、B 的两点,连接CD ,过点C 作CE DB ⊥,交CD 的延长线于点E ,垂足为点E ,直径AB 与CE 的延长线相交于点F .(1)连接AC 、AD ,求证:180DAC ACF ∠+∠=︒.(2)若2ABD BDC ∠=∠.①求证:CF 是O e 的切线.②当6BD =,3tan 4F =时,求CF 的长. 【答案】(1)详见解析;(2)①详见解析;② 203CF =. 【解析】【分析】 (1)根据圆周角定理证得∠ADB=90°,即AD ⊥BD ,由CE ⊥DB 证得AD ∥CF ,根据平行线的性质即可证得结论;(2)①连接OC .先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC ∥DB ,再由CE ⊥DB ,得到OC ⊥CF ,根据切线的判定即可证明CF 为⊙O 的切线;②由CF ∥AD ,证出∠BAD=∠F ,得出tan ∠BAD=tan ∠F=BD AD =34,求出AD=43BD=8,利用勾股定理求得AB=10,得出OB=OC=,5,再由tanF=OC CF =34,即可求出CF . 【详解】解:(1)AB 是O e 的直径,且D 为O e 上一点,90ADB ∴∠=︒,CE DB ⊥Q ,90DEC ∴∠=︒,//CF AD ∴,180DAC ACF ∴∠+∠=︒.(2)①如图,连接OC .OA OC =Q ,12∴∠=∠.312∠=∠+∠Q ,321∴∠=∠.42BDC Q ∠=∠,1BDC ∠=∠,421∴∠=∠,43∴∠=∠,//OC DB ∴.CE DB ⊥Q ,OC CF ∴⊥.又OC Q 为O e 的半径,CF ∴为O e 的切线.②由(1)知//CF AD ,BAD F ∴∠=∠,3tan tan 4BAD F ∴∠==, 34BD AD ∴=. 6BD =Q483AD BD ∴==, 226810AB ∴=+=,5OB OC ==.OC CF Q ⊥,90OCF ∴∠=︒,3tan 4OC F CF ∴==, 解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果.13.如图,在Rt △ABC 中,∠C =90°,∠A =30°,AB =4,动点P 从点A 出发,沿AB 以每秒2个单位长度的速度向终点B 运动.过点P 作PD ⊥AC 于点D (点P 不与点A ,B 重合),作∠DPQ =60°,边PQ 交射线DC 于点Q .设点P 的运动时间为t 秒.(1)用含t 的代数式表示线段DC 的长:_________________; (2)当t =__________时,点Q 与点C 重合时; (3)当线段PQ 的垂直平分线经过△ABC 一边中点时,求出t 的值.【答案】(1);(2)1;(3)t 的值为或或. 【解析】 【分析】(1)先求出AC ,用三角函数求出AD ,即可得出结论;(2)利用AQ=AC ,即可得出结论;(3)分三种情况,利用锐角三角函数,即可得出结论.【详解】(1)∵AP= , AB=4,∠A =30°∴AC=, AD= ∴CD=; (2)AQ=2AD=当AQ=AC 时,Q 与C 重合 即=∴t=1;(3)①如图,当PQ 的垂直平分线过AB 的中点F 时,∴∠PGF =90°,PG =PQ =AP =t ,AF =AB =2.∵∠A=∠AQP=30°,∴∠FPG=60°,∴∠PFG=30°,∴PF=2PG=2t,∴AP+PF=2t+2t=2,∴t=②如图,当PQ的垂直平分线过AC的中点N时,∴∠QMN=90°,AN=AC=,QM=PQ=AP=t.在Rt△NMQ中,∵AN+NQ=AQ,∴③如图,当PQ的垂直平分线过BC的中点F时,∴BF=BC=1,PE=PQ=t,∠H=30°.∵∠ABC=60°,∴∠BFH=30°=∠H,∴BH=BF=1.在Rt△PEH中,PH=2PE=2t.∵AH=AP+PH=AB+BH,∴2t+2t=5,∴t=.即当线段PQ的垂直平分线经过△ABC一边中点时,t的值为或或.【点睛】此题是三角形综合题,主要考查了等腰三角形的判定和性质,锐角三角函数,垂直平分线的性质,正确作出图形是解本题的关键.14.如图,正方形ABCD2+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,(1)求证:△ABF∽△ACE;(2)求tan∠BAE的值;(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x=1,在Rt△ABE中,∵∠ABE=90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC =22AB BC +=2+2,∴OA =OC =OB =12AC =22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =222+ •(2﹣1)=22, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+..【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.15.小明坐于堤边垂钓,如图①,河堤AC 的坡角为30°,AC 长米,钓竿AO 的倾斜角是60°,其长为3米,若AO 与钓鱼线OB 的夹角为60°,求浮漂B 与河堤下端C 之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
2020-2021中考数学压轴题专题锐角三角函数的经典综合题含答案解析

2020-2021中考数学压轴题专题锐角三角函数的经典综合题含答案解析一、锐角三角函数1.如图,△ABC 内接于⊙O ,2,BC AB AC ==,点D 为»AC 上的动点,且10cos B =. (1)求AB 的长度;(2)在点D 运动的过程中,弦AD 的延长线交BC 的延长线于点E ,问AD•AE 的值是否变化?若不变,请求出AD•AE 的值;若变化,请说明理由.(3)在点D 的运动过程中,过A 点作AH ⊥BD ,求证:BH CD DH =+.【答案】(1) 10AB (2) 10AD AE ⋅=;(3)证明见解析.【解析】【分析】(1)过A 作AF ⊥BC ,垂足为F ,交⊙O 于G ,由垂径定理可得BF=1,再根据已知结合RtΔAFB 即可求得AB 长;(2)连接DG ,则可得AG 为⊙O 的直径,继而可证明△DAG ∽△FAE ,根据相似三角形的性质可得AD•AE=AF•AG ,连接BG ,求得AF=3,FG=13,继而即可求得AD•AE 的值; (3)连接CD ,延长BD 至点N ,使DN=CD ,连接AN ,通过证明△ADC ≌△ADN ,可得AC=AN ,继而可得AB=AN ,再根据AH ⊥BN ,即可证得BH=HD+CD. 【详解】(1)过A 作AF ⊥BC ,垂足为F ,交⊙O 于G ,∵AB=AC ,AF ⊥BC ,∴BF=CF=12BC=1, 在RtΔAFB 中,BF=1,∴AB=10cos 10BF B == (2)连接DG ,∵AF ⊥BC ,BF=CF ,∴AG 为⊙O 的直径,∴∠ADG=∠AFE=90°,又∵∠DAG=∠FAE ,∴△DAG ∽△FAE , ∴AD :AF=AG :AE ,∴AD•AE=AF•AG ,连接BG ,则∠ABG=90°,∵BF ⊥AG ,∴BF 2=AF•FG ,∵22AB BF -=3, ∴FG=13,∴AD•AE=AF•AG=AF•(AF+FG )=3×103=10; (3)连接CD ,延长BD 至点N ,使DN=CD ,连接AN ,∵∠ADB=∠ACB=∠ABC ,∠ADC+∠ABC=180°,∠ADN+∠ADB=180°,∴∠ADC=∠ADN ,∵AD=AD ,CD=ND ,∴△ADC ≌△ADN ,∴AC=AN ,∵AB=AC ,∴AB=AN ,∵AH ⊥BN ,∴BH=HN=HD+CD.【点睛】本题考查了垂径定理、三角函数、相似三角形的判定与性质、全等三角形的判定与性质等,综合性较强,正确添加辅助线是解题的关键.2.如图,某无人机于空中A 处探测到目标B D 、的俯角分别是30、60︒︒,此时无人机的飞行高度AC 为60m ,随后无人机从A 处继续水平飞行303m 到达'A 处.(1)求之间的距离(2)求从无人机'A 上看目标的俯角的正切值.【答案】(1)120米;(223. 【解析】【分析】(1)解直角三角形即可得到结论;(2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D ,于是得到'60A E AC ==, '30CE AA ==3Rt △ABC 中,求得DC=333,然后根据三角函数的定义即可得到结论.【详解】解:(1)由题意得:∠ABD=30°,∠ADC=60°,在Rt △ABC 中,AC=60m ,∴AB=sin 30AC ︒=6012=120(m ) (2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D ,则'60A E AC ==, '30CE AA ==3,在Rt △ABC 中, AC=60m ,∠ADC=60°, ∴DC=33AC=203 ∴DE=503∴tan ∠A 'A D= tan ∠'A DC='A E DE =503=235答:从无人机'A 上看目标D 的俯角的正切值是235.【点睛】本题考查了解直角三角形的应用,添加辅助线建立直角三角形是解题的关键.3.如图,AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于切点为G ,连接AG 交CD 于K .(1)求证:KE=GE ;(2)若KG 2=KD•GE ,试判断AC 与EF 的位置关系,并说明理由;(3)在(2)的条件下,若sinE=,AK=,求FG 的长.【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= .【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KD•GE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.试题解析:(1)如图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.(2)AC∥EF,理由为连接GD,如图2所示.∵KG2=KD•GE,即,∴,又∵∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∵∠C=∠AGD,∴∠E=∠C,∴AC∥EF;(3)连接OG,OC,如图3所示,∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.∵sinE=sin∠ACH=,设AH=3t,则AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK-CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即(3t)2+t2=(2)2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即(r-3t)2+(4t)2=r2,解得r= t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH=,∴FG=【点睛】此题考查了切线的性质,相似三角形的判定与性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握定理及性质是解本题的关键.4.在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH、PH.(1)若点P在线CD上,如图1,①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)【答案】(1)①如图;②AH=PH,AH⊥PH.证明见解析(2)或【解析】试题分析:(1)①如图(1);②(1)法一:轴对称作法,判断:AH=PH,AH⊥PH.连接CH,根据正方形的每条对角线平分一组对角得:△DHQ等腰Rt△,根据平移的性质得DP=CQ,证得△HDP≌△△HQC,全等三角形的对应边相等得PH=CH,等边对等角得∠HPC=∠HCP,再结合BD是正方形的对称轴得出∠AHP=180°-∠ADP=90°,∴AH=PH且AH⊥PH.四点共圆作法,同上得:∠HPC=∠DAH,∴A、D、P、H共向,∴∠AHP=90°,∠APH=∠ADH=45°,∴△APH等腰Rt△.(2)轴对称作法同(1)作HR⊥PC于R,∵∠AHQ=152°,∴∠AHB=62°,∴∠DAH=17°∴∠DCH=17°.设DP=x,则.由代入HR,CR解方程即可得出x的值. 四点共圆作法,A、H、D、P共向,∴∠APD=∠AHB=62°,∴.试题解析:(1)①法一:轴对称作法,判断:AH=PH,AH⊥PH证:连接CH ,得:△DHQ 等腰Rt △,又∵DP =CQ ,∴△HDP ≌△△HQC ,∴PH =CH ,∠HPC =∠HCPBD 为正方形ABCD 对称轴,∴AH =CH ,∠DAH =∠HCP ,∴AH =PH ,∠DAH =∠HPC ,∴∠AHP =180°-∠ADP =90°,∴AH =PH 且AH ⊥PH .法二:四点共圆作法,同上得:∠HPC =∠DAH ,∴A 、D 、P 、H 共向,∴∠AHP =90°,∠APH =∠ADH =45°,∴△APH 等腰Rt △.(2)法一:轴对称作法考虑△DHQ 等腰Rt △,PD =CQ ,作HR ⊥PC 于R ,∵∠AHQ =152°,∴∠AHB =62°,∴∠DAH =17°∴∠DCH =17°.设DP =x ,则. 由得:,∴.即PD=法二:四点共向作法,A 、H 、D 、P 共向,∴∠APD =∠AHB =62°,∴.考点:全等三角形的判定;解直角三角形;正方形的性质;死电脑共圆5.如图,在平面直角坐标系中,点O 为坐标原点,直线4y kx =+交x 轴、y 轴分别于点A 、点B ,且ABO ∆的面积为8.(1)求k 的值;(2)如图,点P 是第一象限直线AB 上的一个动点,连接PO ,将线段OP 绕点O 顺时针旋转90°至线段OC ,设点P 的横坐标为t ,点C 的横坐标为m ,求m 与t 之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,过点B 作直线BM OP ⊥,交x 轴于点M ,垂足为点N ,点K 在线段MB 的延长线上,连接PK ,且0PK KB P +=,2PMB KPB ∠=∠,连接MC ,求四边形BOCM 的面积.【答案】(1)1k =;(2)4m t =+;(3)32BOCM S =Y .【解析】【分析】(1)先求出A 的坐标,然后利用待定系数法求出k 的值;(2) 过点P 作PD x ⊥轴,垂足为D ,过点C 作CE x ⊥轴,垂足为E ,证POD OCE ∆≅∆可得OE PD =,进一步得出m 与t 的函数关系式;(3)过点O 作直线OT AB ⊥,交直线BM 于点Q ,垂足为点T ,连接QP ,先证出QTB PTO ∆≅∆;再证出KPB BPN ∠=∠;设KPB x ∠=︒,通过计算证出PO PM =;再过点P 作PD x ⊥轴,垂足为点D ,根据tan tan OPD BMO ∠=∠得到OD BO PD MO =,列式可求得t=4;所以OM=8进一步得出四边形BOCM 是平行四边形,最后可得其面积为32.【详解】解:(1)把0x =代入4y kx =+,4y =,∴4BO =,又∵4ABO S ∆=, ∴142AO BO ⋅=,4AO =, ∴(4,0)A -,把4x =-,0y =代入4y kx =+,得044k =-+,解得1k =.故答案为1;(2)解:把x t =代入4y x =+,4y t =+, ∴(,4)P t t +如图,过点P 作PD x ⊥轴,垂足为D ,过点C 作CE x ⊥轴,垂足为E ,∴90PDO CEO ∠=∠=︒,∴90POD OPD ∠+∠=︒,∵线段OP 绕点O 顺时针旋转90°至线段OC ,∴90POC ∠=︒,OP OC =,∴90POD EOC ∠+∠=︒,∴OPD EOC ∠=∠,∴POD OCE ∆≅∆,∴OE PD =,4m t =+.故答案为4m t =+.(3)解:如图,过点O 作直线OT AB ⊥,交直线BM 于点Q ,垂足为点T ,连接QP ,由(1)知,4AO BO ==,90BOA ∠=︒,∴ABO ∆为等腰直角三角形,∴45ABO BAO ∠=∠=︒,9045BOT ABO ABO ∠=︒-∠=︒=∠, ∴BT TO =,∵90BTO ∠=︒,∴90TPO TOP ∠+∠=︒,∵PO BM ⊥,∴90BNO ∠=︒,∴BQT TPO ∠=∠,∴QTB PTO ∆≅∆,∴QT TP =,PO BQ =,∴PQT QPT ∠=∠,∵PO PK KB =+,∴QB PK KB =+,QK KP =, ∴KQP KPQ ∠=∠,∴PQT KQP QPT KPQ ∠-∠=∠-∠,TQB TPK ∠=∠, ∴KPB BPN ∠=∠,设KPB x ∠=︒,∴BPN x ∠=︒,∵2PMB KPB ∠=∠,∴2PMB x ∠=︒,45POM PAO APO x ∠=∠+∠=︒+︒,9045NMO POM x ∠=︒-∠=︒-︒, ∴45PMO PMB NMO x POM ∠=∠+∠=︒+︒=∠, ∴PO PM =,过点P 作PD x ⊥轴,垂足为点D , ∴22OM OD t ==,9045OPD POD x BMO ∠=︒-∠=︒-︒=∠, tan tan OPD BMO ∠=∠,OD BO PD MO =,442t t t=+, 14t =,22t =-(舍)∴8OM =,由(2)知,48m t OM =+==, ∴CM y P 轴,∵90PNM POC ∠=∠=︒,∴BM OC P ,∴四边形BOCM 是平行四边形, ∴4832BOCM S BO OM =⨯=⨯=Y . 故答案为32.【点睛】本题考查了一次函数和几何的综合题,全等三角形的判定和性质,解直角三角形,添加适当的辅助线构造全等三角形是本题的关键.6.2018年12月10日,郑州市城乡规划局网站挂出《郑州都市区主城区停车场专项规划》,将停车纳入城市综合交通体系,计划到2030年,在主城区新建停车泊位33.04万个,2019年初,某小区拟修建地下停车库,如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度为1:3,DE =3米,点C在DE上,CD=0.5米,CD是限高标志屏的高度(标志牌上写有:限高米),如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据2≈1.41,3≈1.73)【答案】该停车库限高约为2.2米.【解析】【分析】据题意得出3tan B=,即可得出tan A,在Rt△ADE中,根据勾股定理可求得DE,即可得出∠1的正切值,再在Rt△CEF中,设EF=x,即可求出x,从而得出CF3的长.【详解】解:由题意得,3 tan3B=∵MN∥AD,∴∠A=∠B,∴tan A3,∵DE⊥AD,∴在Rt△ADE中,tan A=DEAD,∵DE=3,又∵DC=0.5,∴CE=2.5,∵CF⊥AB,∴∠FCE+∠CEF=90°,∵DE⊥AD,∴∠A+∠CEF=90°,∴∠A=∠FCE,∴tan∠FCE=3.在Rt△CEF中,设EF=x,CF=3x(x>0),CE=2.5,代入得(52)2=x2+3x2,解得x=1.25,∴CF=3x≈2.2,∴该停车库限高约为2.2米.【点睛】本题考查了解直角三角形的应用,坡面坡角问题和勾股定理,解题的关键是坡度等于坡角的正切值.7.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD 交圆的切线BE于点E(1)判断直线PD是否为⊙O的切线,并说明理由;(2)如果∠BED=60°,PD=3,求PA的长;(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.【答案】(1)证明见解析;(2)1;(3)证明见解析.【解析】【分析】(1)连接OD,由AB是圆O的直径可得∠ADB=90°,进而求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;(2)根据BE是⊙O的切线,则∠EBA=90°,即可求得∠P=30°,再由PD为⊙O的切线,得∠PDO=90°,根据三角函数的定义求得OD,由勾股定理得OP,即可得出PA;(3)根据题意可证得∠ADF=∠PDA=∠PBD=∠ABF,由AB是圆O的直径,得∠ADB=90°,设∠PBD=x°,则可表示出∠DAF=∠PAD=90°+x°,∠DBF=2x°,由圆内接四边形的性质得出x 的值,可得出△BDE是等边三角形.进而证出四边形DFBE为菱形.【详解】(1)直线PD为⊙O的切线,理由如下:如图1,连接OD,∵AB是圆O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°,又∵DO=BO,∴∠BDO=∠PBD,∵∠PDA=∠PBD,∴∠BDO=∠PDA,∴∠ADO+∠PDA=90°,即PD⊥OD,∵点D在⊙O上,∴直线PD为⊙O的切线;(2)∵BE是⊙O的切线,∴∠EBA=90°,∵∠BED=60°,∴∠P=30°,∵PD为⊙O的切线,∴∠PDO=90°,在Rt△PDO中,∠P=30°,3∴0 tan30ODPD=,解得OD=1,∴22PO PD OD+,∴PA=PO﹣AO=2﹣1=1;(3)如图2,依题意得:∠ADF=∠PDA,∠PAD=∠DAF,∵∠PDA=∠PBD∠ADF=∠ABF,∴∠ADF=∠PDA=∠PBD=∠ABF,∵AB是圆O的直径,∴∠ADB=90°,设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°,∵四边形AFBD内接于⊙O,∴∠DAF+∠DBF=180°,即90°+x+2x=180°,解得x=30°,∴∠ADF=∠PDA=∠PBD=∠ABF=30°,∵BE、ED是⊙O的切线,∴DE=BE,∠EBA=90°,∴∠DBE=60°,∴△BDE是等边三角形,∴BD=DE=BE,又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°,∴△BDF是等边三角形,∴BD=DF=BF,∴DE=BE=DF=BF,∴四边形DFBE为菱形.【点睛】本题是一道综合性的题目,考查了切线的判定和性质,圆周角定理和菱形的性质,是中档题,难度较大.8.如图,在平面直角坐标系中,直线DE交x轴于点E(30,0),交y轴于点D(0,40),直线AB:y=13x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.(1)求边EF的长;(2)将正方形EFGH沿射线FB10个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).①当点F1移动到点B时,求t的值;②当G1,H1两点中有一点移动到直线DE上时,请直接写出此时正方形E1F1G1H1与△APE 重叠部分的面积.【答案】(1)EF=15;(2)①10;②120;【解析】【分析】(1)根据已知点E(30,0),点D(0,40),求出直线DE的直线解析式y=-43x+40,可求出P点坐标,进而求出F点坐标即可;(2)①易求B(0,5),当点F1移动到点B时,1010=10;②F点移动到F'10t,F垂直x轴方向移动的距离是t,当点H运动到直线DE上时,在Rt△F'NF中,NFNF'=13,EM=NG'=15-F'N=15-3t,在Rt△DMH'中,43MHEM'=,t=4,S=12×(12+454)×11=10238;当点G运动到直线DE上时,在Rt△F'PK中,PKF K'=13,PK=t-3,F'K=3t-9,在Rt△PKG'中,PKKG'=31539tt--+=43,t=7,S=15×(15-7)=120.【详解】(1)设直线DE的直线解析式y=kx+b,将点E(30,0),点D(0,40),∴30040k bb+=⎧⎨=⎩,∴4340kb⎧=-⎪⎨⎪=⎩,∴y=﹣43x+40,直线AB与直线DE的交点P(21,12),由题意知F(30,15),∴EF=15;(2)①易求B(0,5),∴BF=10,∴当点F1移动到点B时,t=1010=10;②当点H 运动到直线DE 上时,F 点移动到F'的距离是10t , 在Rt △F'NF 中,NF NF '=13, ∴FN =t ,F'N =3t , ∵MH'=FN =t ,EM =NG'=15﹣F'N =15﹣3t , 在Rt △DMH'中,43MH EM '=, ∴41533t t =-, ∴t =4,∴EM =3,MH'=4,∴S =1451023(12)11248⨯+⨯=; 当点G 运动到直线DE 上时,F 点移动到F'10, ∵PF =10 ∴PF'10t ﹣10, 在Rt △F'PK 中,13PK F K =',∴PK =t ﹣3,F'K =3t ﹣9, 在Rt △PKG'中,PK KG '=31539t t --+=43, ∴t =7,∴S =15×(15﹣7)=120. 【点睛】本题考查一次函数图象及性质,正方形的性质;掌握待定系数法求函数解析式,利用三角形的正切值求边的关系,利用勾股定理在直角三角形中建立边之间的联系,准确确定阴影部分的面积是解题的关键.9.阅读下面材料:观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,过A 作AD ⊥BC 于D (如图),则sin B =AD c ,sin C =ADb,即AD =c sin B ,AD =b sin C ,于是c sin B =b sin C ,即sin sin b c B C = .同理有:sin sin c aC A=,sin sin a b A B=,所以sin sin sin a b cA B C ==. 即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.(1)如图,△ABC 中,∠B =75°,∠C =45°,BC =60,则AB = ;(2)如图,一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B 处,此时又测得灯塔A 在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A 的距离AB . (3)在(2)的条件下,试求75°的正弦值.(结果保留根号)【答案】(1)6;(2)6海里;(36+2【解析】 【分析】(1)根据材料:在一个三角形中,各边和它所对角的正弦的比相等,写出比例关系,代入数值即可求得AB的值.(2)此题可先由速度和时间求出BC的距离,再由各方向角得出∠A的角度,过B作BM⊥AC于M,求出∠MBC=30°,求出MC,由勾股定理求出BM,求出AM、BM的长,由勾股定理求出AB即可;(3)在三角形ABC中,∠A=45,∠ABC=75,∠ACB=60,过点C作AC的垂线BD,构造直角三角形ABD,BCD,在直角三角形ABD中可求出AD的长,进而可求出sin75°的值.【详解】解:(1)在△ABC中,∠B=75°,∠C=45°,BC=60,则∠A=60°,∵ABsinC =sinBCA,∴45ABsin o=60sin60o,即22=3,解得:AB=206.(2)如图,依题意:BC=60×0.5=30(海里)∵CD∥BE,∴∠DCB+∠CBE=180°∵∠DCB=30°,∴∠CBE=150°∵∠ABE=75°.∴∠ABC=75°,∴∠A=45°,在△ABC中,sinABACB∠=BCsin A∠即60?ABsin=3045?sin,解之得:6.答:货轮距灯塔的距离AB=156海里.(3)过点B作AC的垂线BM,垂足为M.在直角三角形ABM中,∠A=45°,6,所以3BDC中,∠BCM=60°,BC=30°,可求得CM=15,所以3,由题意得,1531575sin o=660sin o,sin75°=6+24.【点睛】本题考查方向角的含义,三角形的内角和定理,含30度角的直角三角形,等腰三角形的性质和判定等知识点,解题关键是熟练掌握解直角三角形方法.10.3米/秒 =65.88千米/小时>60千米/小时.∴此车超过限制速度.…4分11.已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.(1)如图1,求证:KE=GE;(2)如图2,连接CABG,若∠FGB=12∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sin E=35,AK10CN的长.【答案】(1)证明见解析;(2)△EAD 是等腰三角形.证明见解析;(3)201013. 【解析】 试题分析:(1)连接OG ,则由已知易得∠OGE=∠AHK=90°,由OG=OA 可得∠AGO=∠OAG ,从而可得∠KGE=∠AKH=∠EKG ,这样即可得到KE=GE ;(2)设∠FGB=α,由AB 是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE 可得∠EKG=90°-α,这样在△GKE 中可得∠E=2α,由∠FGB=12∠ACH 可得∠ACH=2α,这样可得∠E=∠ACH ,由此即可得到CA ∥EF ; (3)如下图2,作NP ⊥AC 于P ,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,AK=10a ,结合AK=10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G ,∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α,∵∠FGB=12∠ACH , ∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a , 则224AC CH a -=,tan ∠CAH=43CH AH =, ∵CA ∥FE , ∴∠CAK=∠AGE , ∵∠AGE=∠AKH , ∴∠CAK=∠AKH ,∴AC=CK=5a ,HK=CK ﹣CH=4a ,tan ∠AKH=AHHK=3,2210AH HK a +=, ∵10 ∴1010a =∴a=1.AC=5, ∵∠BHD=∠AGB=90°, ∴∠BHD+∠AGB=180°,在四边形BGKH 中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG,∵∠ACN=∠ABG,∴∠AKH=∠ACN,∴tan∠AKH=tan∠ACN=3,∵NP⊥AC于P,∴∠APN=∠CPN=90°,在Rt△APN中,tan∠CAH=43PNAP=,设PN=12b,则AP=9b,在Rt△CPN中,tan∠ACN=PNCP=3,∴CP=4b,∴AC=AP+CP=13b,∵AC=5,∴13b=5,∴b=513,∴CN=22PN CP+=410b⋅=2010 13.12.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).【答案】拦截点D处到公路的距离是(500+500)米.【解析】试题分析:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=BC=×1000=500米;解Rt△CDF,求出CF=CD=500米,则DA=BE+CF=(500+500)米.试题解析:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.在Rt△BCE中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE=BC=×1000=500米;在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF=CD=500米,∴DA=BE+CF=(500+500)米,故拦截点D处到公路的距离是(500+500)米.考点:解直角三角形的应用-方向角问题.13.如图,直线与轴交于点,与轴交于点,抛物线经过点,.点为轴上一动点,过点且垂直于轴的直线分别交直线及抛物线于点,.(1)填空:点的坐标为,抛物线的解析式为;(2)当点在线段上运动时(不与点,重合),①当为何值时,线段最大值,并求出的最大值;②求出使为直角三角形时的值;(3)若抛物线上有且只有三个点到直线的距离是,请直接写出此时由点,,,构成的四边形的面积.【答案】(1),;(2)①当时,有最大值是3;②使为直角三角形时的值为3或;(3)点,,,构成的四边形的面积为:6或或.【解析】【分析】(1)把点A坐标代入直线表达式y=,求出a=−3,把点A、B的坐标代入二次函数表达式,即可求解;(2)①设:点P(m,),N(m,)求出PN值的表达式,即可求解;②分∠BNP=90°、∠NBP=90°、∠BPN=90°三种情况,求解即可;(3)若抛物线上有且只有三个点N到直线AB的距离是h,则只能出现:在AB直线下方抛物线与过点N的直线与抛物线有一个交点N,在直线AB上方的交点有两个,分别求解即可.【详解】解:(1)把点坐标代入直线表达式,解得:,则:直线表达式为:,令,则:,则点坐标为,将点的坐标代入二次函数表达式得:,把点的坐标代入二次函数表达式得:,解得:,故:抛物线的解析式为:,故:答案为:,;(2)①∵在线段上,且轴,∴点,,∴,∵,∴抛物线开口向下,∴当时,有最大值是3,②当时,点的纵坐标为-3,把代入抛物线的表达式得:,解得:或0(舍去),∴;当时,∵,两直线垂直,其值相乘为-1,设:直线的表达式为:,把点的坐标代入上式,解得:,则:直线的表达式为:,将上式与抛物线的表达式联立并解得:或0(舍去),当时,不合题意舍去,故:使为直角三角形时的值为3或;(3)∵,,在中,,则:,,∵轴,∴,若抛物线上有且只有三个点到直线的距离是,则只能出现:在直线下方抛物线与过点的直线与抛物线有一个交点,在直线上方的交点有两个.当过点的直线与抛物线有一个交点,点的坐标为,设:点坐标为:,则:,过点作的平行线,则点所在的直线表达式为:,将点坐标代入,解得:过点直线表达式为:,将拋物线的表达式与上式联立并整理得:,,将代入上式并整理得:,解得:,则点的坐标为,则:点坐标为,则:,∵,,∴四边形为平行四边形,则点到直线的距离等于点到直线的距离,即:过点与平行的直线与抛物线的交点为另外两个点,即:、,直线的表达式为:,将该表达式与二次函数表达式联立并整理得:,解得:,则点、的横坐标分别为,,作交直线于点,则,作轴,交轴于点,则:,,,则:,同理:,故:点,,,构成的四边形的面积为:6或或.【点睛】本题考查的是二次函数知识的综合运用,涉及到一次函数、解直角三角形等相关知识,其中(3)中确定点N的位置是本题的难点,核心是通过△=0,确定图中N点的坐标.14.如图,某次中俄“海上联合”反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为68°.试根据以上数据求出潜艇C 离开海平面的下潜深度.(结果保留整数.参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,3)【答案】潜艇C离开海平面的下潜深度约为308米【解析】试题分析:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,用锐角三角函数分别在Rt△ACD中表示出CD和在Rt△BCD中表示出BD,利用BD=AD+AB二者之间的关系列出方程求解.试题解析:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,根据题意得:∠ACD=30°,∠BCD=68°,设AD=x,则BD=BA+AD=1000+x,在Rt△ACD中,CD=tan AD ACD=tan30x= 3x在Rt△BCD中,BD=CD•tan68°,∴325+x=3x•tan68°解得:x≈100米,∴潜艇C离开海平面的下潜深度为100米.点睛:本题考查了解直角三角形的应用,解题的关键是作出辅助线,从题目中找出直角三角形并选择合适的边角关系求解.视频15.已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若2,cos∠ACD= 45,求tan∠AEC的值及CD的长.【答案】tan ∠AEC=3, CD=12125【解析】解:在RT △ACD 与RT △ABC 中∵∠ABC+∠CAD=90°, ∠ACD+∠CAD=90°∴∠ABC=∠ACD, ∴cos ∠ABC=cos ∠ACD=45在RT △ABC 中,45BC AB = 令BC=4k,AB=5k 则AC=3k 由35BE AB = ,BE=3k 则CE=k,且2 则2,2 ∴RT △ACE 中,tan ∠AEC=ACEC=3 ∵RT △ACD 中cos ∠ACD=45CD AC = ,,12125。
中考数学——锐角三角函数的综合压轴题专题复习含答案

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O 于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD 时,AD=DC=CF ,AF=3DC ,∴=DC•3DC=,∴AE=DC ,∵EC=AE ,∴EC=DC ,∴sin ∠CAB=sin ∠CED===;②当CF=aCD (a >0)时,sin ∠CAB=.∵CF=aCD ,AD=DC ,∴AF=AD+DC+CF=(a+2)CD ,∴=DC•(a+2)DC=(a+2),∴AE=DC ,∵EC=AE ,∴EC=DC ,∴sin ∠CAB=sin ∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.2.如图,反比例函数() 0k y k x=≠ 的图象与正比例函数 2y x = 的图象相交于A (1,a ),B 两点,点C 在第四象限,CA ∥y 轴,90ABC ∠=︒. (1)求k 的值及点B 的坐标; (2)求tanC 的值.【答案】(1)2k =,()1,2B --;(2)2. 【解析】【分析】(1)先根据点A 在直线y=2x 上,求得点A 的坐标,再根据点A 在反比例函数()0ky k x=≠ 的图象上,利用待定系数法求得k 的值,再根据点A 、B 关于原点对称即可求得点B 的坐标;(2)作BH ⊥AC 于H ,设AC 交x 轴于点D ,根据90ABC ∠=︒ , 90BHC ∠=︒ ,可得C ABH ∠∠=,再由已知可得AOD ABH ∠∠=,从而得C AOD ∠∠=,求出Ctan 即可.【详解】(1)∵点A (1,a )在2y x =上, ∴a =2,∴A (1,2),把A (1,2)代入 ky x= 得2k =, ∵反比例函数()0ky k x=≠ 的图象与正比例函数 2y x = 的图象交于A ,B 两点, ∴A B 、 两点关于原点O 中心对称,∴()12B --, ; (2)作BH ⊥AC 于H ,设AC 交x 轴于点D ,∵90ABC ∠=︒ , 90BHC ∠=︒ ,∴C ABH ∠∠=,∵CA ∥y 轴,∴BH ∥x 轴,∴AOD ABH ∠∠=,∴C AOD ∠∠=,∴AD 22OD 1tanC tan AOD =∠===.【点睛】本题考查了反比例与一次函数综合问题,涉及到待定系数法、中心对称、三角函数等知识,熟练掌握和应用相关知识是解题的关键,(2)小题求出∠C=∠AOD 是关键.3.如图,矩形OABC 中,A(6,0)、C(0,3、D(0,3),射线l 过点D 且与x 轴平行,点P 、Q 分别是l 和x 轴的正半轴上的动点,满足∠PQO =60º.(1)点B的坐标是,∠CAO= º,当点Q与点A重合时,点P的坐标为;(2)设点P的横坐标为x,△OPQ与矩形OABC重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.【答案】(1)(6,23). 30.(3,33)(2)()()()()243x430x3331333x x3x5S{23x1235x93543x9+≤≤-+-<≤=-+<≤>【解析】解:(1)(6,23). 30.(3,33).(2)当0≤x≤3时,如图1,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;由题意可知直线l∥BC∥OA,可得EF PE DC31==OQ PO DO333==,∴EF=13(3+x),此时重叠部分是梯形,其面积为:EFQO14343S S EF OQ OC 3x x 43233==+⋅=+=+梯形()()当3<x≤5时,如图2,()HAQ EFQO EFQO 221S S S S AH AQ243331333 x 43x 3=x x 32232∆=-=-⋅⋅=+---+-梯形梯形。
锐角三角函数中考复习(重庆)

(1)求BC的距离;(结果保留整数)
(2)解:与小岛C最近的D处,即CD⊥BE,在B处沿北偏东75°方向继续航行,则∠CBD= ∠BCD= 45°,在小岛C加油后,再沿南偏东75°方向航行,则∠ECF= 75°,∴ ∠ECD= 30°+ 75°-45°=60°,∠CED= 90°-60°=30°由(1)得BC的距离为164海里,在 中, ,在 中,∠CED=30°, ∴∴渔船所用时间为:
牛刀小试
(1)求火车站A与小区C之间的距离(精确到1米);
解:根据题意,得∴过点B作BD⊥AC于点D,∴∴CD=BD∴AB=400m∴AD=200m,∴
(2)解:受到影响,理由如下:过点B作BM⊥l于点M,∴∠MAB=∠MBA=45°,∵AB=400m,∴∴所以小区B受到影响,以300米为腰长,以BM为高构造等腰三角形 ,根据勾股定理计算∴ ,根据三线合一性质∴
牛刀小试
(1)求BC的距离;(结果保留整数)
解:过点作CF⊥AB,由题意得AB=1×60=60 (海里),在A处测得小岛C在北偏东45°方向,则∠CAF=45°,在B处测得小岛C在北偏东30°方向,则∠CBF=60°,设 海里,在 中, ,则 , ,则在 中, ,则 ,
(1)求步道DE的长度(精确到个位);(2)点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?(参考数据: , )
(1)求步道DE的长度(精确到个位);(参考数据: , )
解:作GH⊥AC交AC的延长线于点H,交BF于点M,连接AG,设DM=x, ∵∠GDF=45° ∴DM=DM=x,DG=√x ∴GH=8+x∵DB=2.8 ∴AH=AC+BD+DM=19.2+2.8+x=22+x
中考数学专项复习《锐角三角函数》练习题(附答案)

中考数学专项复习《锐角三角函数》练习题(附答案)一、单选题1.如图,在△ABC中CA=CB=4,cosC=14,则sinB的值为()A.√102B.√153C.√64D.√1042.在Rt△ABC中,△C=90°,cosA=35,那么tanB=()A.35B.45C.43D.34 3.如图,在Rt△ABC中∠ACB=90°,BC=1,AB=2则下列结论正确的是()A.sinA=√32B.tanA=12C.cosB=√32 D.tanB=√34.如图,已知△ABC内接于△O,△BAC=120°,AB=AC,BD为△O的直径,AD=6,则BC的长为()A.2√3B.6C.2√6D.3√3 5.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是()A.2海里B.2sin55°海里C.2cos55°海里D.2tan55°海里6.在矩形ABCD中AD=2,AB=1,G为AD的中点,一块足够大的三角板的直角顶点与点G重合,将三角板绕点G旋转,三角板的两直角边分别交AB、BC(或它们的延长线)于点E、F设∠AGE=α(0°<α<90°),下列四个结论:①AE= CF;②∠AEG=∠BFG;③AE+CF=1;④S△GEF=1cos2α,正确的个数是()A.1B.2C.3D.4 7.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得△PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为()A.11−sinαB.11+sinαC.11−cosαD.11+cosα8.如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,下列结论:①△ABC的形状是等腰三角形;②△ABC的周长是2√10+√2;③点C到AB边的距离是38√10;④tan∠ACB的值为2,正确的个数为()A .0个B .1个C .2个D .3个9.在Rt△ABC 中△ACB=90°,BC=1,AB=2,则下列结论正确的是( )A .sinA=√32B .cosA=√32C .tanA=12D .cotA=√3310.已知:如图,正方形网格中∠AOB 如图放置,则cos∠AOB 的值为( )A .2√55B .2C .12D .√5511.如图,菱形ABCD 的周长为20cm ,DE△AB ,垂足为E ,cosA=45,则下列结论中正确的个数为( )①DE=3cm ;②EB=1cm ;③S 菱形ABCD =15cm 2A .3个B .2个C .1个D .0个12.如图,在Rt △ABC 中 ∠ABC =90°,以其三边为边向外作正方形,连接EH ,交AC 于点P ,过点P 作PR ⊥FG 于点R.若tan∠AHE =12,EH =8√5,则PR 的值为( )A.10B.11C.4√5D.5√5二、填空题13.如图,在RtΔABC中∠B=90°,AB=3 ,BC=4 ,点M、N分别在AC、AB两边上,将ΔAMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当ΔDCM是直角三角形时,则tan∠AMN的值为.14.如图,在△ABC中∠ABC=60°,AB=6,BC=10将△ABC绕点B顺时针旋转得到△A1BC1(点A的对应点是点A1,点C的对应点是点C1,A1落在边BC上,连接AC1,则AC1的长为.15.如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C 的仰角为45°,点P到建筑物的距离为PD=20米,则BC=米.16.如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是.17.如图,某高为60米的大楼AB旁边的山坡上有一个“5G”基站DE,从大楼顶端A 测得基站顶端E的俯角为45°,山坡坡长CD=10米,坡度i=1:√3,大楼底端B 到山坡底端C的距离BC=30米,则该基站的高度DE=米.18.在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1,2号楼进行测高实践,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,则2号楼的高度为(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)三、综合题19.(1)已知Rt△ABC中△C=90°,△A=30°,BC= √3,解直角三角形.(2)已知△ABC中△A=45°,AB=4,BC=3,求AC的长.20.如图1,已知∠PAQ=60°.请阅读下列作图过程,并解答所提出的问题.△如图2,以点A为圆心,任意长为半径画弧,分别与AP,AQ交于B,C两点;△如图3,分别以B,C两点为圆心,以大于12BC的长为半径画弧,两弧交于点D;△如图4,作射线AD,连接BC,与AD交于点E.问题:(1)∠ABC的度数为.(2)若AB=4,求AE的长.21.如图,在△ABC中△C=60°,△O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.(1)求证:PA是△O的切线;(2)若AB=2 √3,求图中阴影部分的面积.(结果保留π和根号)22.如图,物理教师为同学们演示单摆运动,单摆左右摆动中在OA的位置时俯角△EOA=30°,在OB的位置时俯角△FOB=60°,若OC△EF,点A比点B高7cm.求:(1)单摆的长度(√3≈1.7);(2)从点A摆动到点B经过的路径长(π≈3.1).23.已知:如图,AB是△O的直径,C是△O上一点,OD△BC于点D,过点C作△O 的切线,交OD的延长线于点E,连接BE.(1)求证:BE与△O相切;(2)连接AD并延长交BE于点F,若OB=9,sin△ABC= 23,求BF的长.24.如图,AB是△O的直径,OE垂直于弦BC,垂足为F,OE交△O于点D,且△CBE=2△C.(1)求证:BE与△O相切;(2)若DF=9,tanC= 34,求直径AB的长.参考答案1.【答案】D2.【答案】D3.【答案】D4.【答案】B5.【答案】C6.【答案】A7.【答案】A8.【答案】C9.【答案】B10.【答案】D11.【答案】A12.【答案】B13.【答案】1或214.【答案】1415.【答案】(20√3−20)16.【答案】√31817.【答案】(25﹣5 √3)18.【答案】45.8米19.【答案】(1)解:在Rt△ABC中△C=90°,△A=30°∴△B=90°-△A=60°,AB=2BC=2 √3∴AC= √AB2−BC2=√(2√3)2−(√3)2=3;(2)解:如图,过点B作BD△AC于D∵△A=45°∴△ABD=△A=45°∴AD=BD∵AB=4,AD2+BD2=AB2∴AD=BD= 2√2在Rt△BCD中BC=3∴CD=√BC2−BD2=1∴AC=AD+CD= 2√2+1.20.【答案】(1)60°(2)由作图可知AB=AC,AD平分∠PAQ∴AE⊥BC.∵∠PAQ=60°∴∠BAE=30°.在Rt△ABC中AE=AB⋅cos30°=4×√32=2√3.答:AE的长为2√3.21.【答案】(1)解:如图,连接OA;∵△C=60°∴△AOB=120°;而OA=OB∴△OAB=△OBA=30°;而AB=AP∴△P=△ABO=30°;∵△AOB=△OAP+△P∴△OAP=120°﹣30°=90°∴PA是△O的切线.(2)解:如图,过点O作OM△AB,则AM=BM= √3∵tan30°= OMAM sin30°=OMAO∴OM=1,OA=2;∴S△AOB=12·AB·OM= 12× 2√3×1= √3S扇形OAB =120π⋅22360= 4π3∴图中阴影部分的面积= 4π3−√3.22.【答案】(1)解:如图,过点A作AP△OC于点P,过点B作BQ△OC于点Q∵△EOA=30°、△FOB=60°,且OC△EF∴△AOP=60°、△BOQ=30°设OA=OB=x则在Rt△AOP中OP=OAcos△AOP= 1 2x在Rt△BOQ中OQ=OBcos△BOQ= √32x由PQ=OQ﹣OP可得√32x﹣12x=7解得:x=7+7 √3≈18.9(cm)答:单摆的长度约为18.9cm(2)解:由(1)知,△AOP=60°、△BOQ=30°,且OA=OB=7+7 √3∴△AOB=90°则从点A摆动到点B经过的路径长为90⋅π⋅(7+7√3)180≈29.295答:从点A摆动到点B经过的路径长为29.295cm 23.【答案】(1)证明:连接OC∵OD△BC∴△COE=△BOE在△OCE和△OBE中∵{OC=OB∠COE=∠BOEOE=OE∴△OCE△△OBE∴△OBE=△OCE=90°,即OB△BE∵OB 是△O 半径∴BE 与△O 相切.(2)解:过点D 作DH△AB ,连接AD 并延长交BE 于点F∵△DOH=△BOD ,△DHO=△BDO=90°∴△ODH△△OBD∴OD OB =OH OD =DH BD又∵sin△ABC= 23,OB=9 ∴OD=6易得△ABC=△ODH∴sin△ODH= 23 ,即 OH OD = 23∴OH=4∴DH= √OD 2−OH 2 =2 √5又∵△ADH△△AFB∴AH AB = DH FB 1318 = 2√5FB∴FB= 36√51324.【答案】(1)证明:∵OE 垂直于弦BC∴△BOE+△OBF=90°∵△CBE=2△C , △BOE=2△C∴△CBE=△BOE∴△CBE+△OBF=90°∴△OBE=90°∴BE 与△O 相切;(2)解:∵OE 垂直于弦BC∴△CFD=△BFO=90°,CF=BF.∵DF=9,tanC= 34∴CF=BF=12.设半径长是x,则OF=x-9在Rt△BOF中∵x2=(x-9)2+122∴x= 25 2∴直径AB=25.。
中考数学锐角三角函数-经典压轴题及答案解析

中考数学锐角三角函数-经典压轴题及答案解析一、锐角三角函数1.如图,海上观察哨所B 位于观察哨所A 正北方向,距离为25海里.在某时刻,哨所A 与哨所B 同时发现一走私船,其位置C 位于哨所A 北偏东53°的方向上,位于哨所B 南偏东37°的方向上.(1)求观察哨所A 与走私船所在的位置C 的距离;(2)若观察哨所A 发现走私船从C 处以16海里/小时的速度向正东方向逃窜,并立即派缉私艇沿北偏东76°的方向前去拦截.求缉私艇的速度为多少时,恰好在D 处成功拦截.(结果保留根号)(参考数据:sin37°=cos53°≈,cos37 =sin53°≈去,tan37°≈2,tan76°≈)【答案】(1)观察哨所A 与走私船所在的位置C 的距离为15海里;(2)当缉私艇以每小时617D 处成功拦截. 【解析】 【分析】(1)先根据三角形内角和定理求出∠ACB =90°,再解Rt △ABC ,利用正弦函数定义得出AC 即可;(2)过点C 作CM ⊥AB 于点M ,易知,D 、C 、M 在一条直线上.解Rt △AMC ,求出CM 、AM .解Rt △AMD 中,求出DM 、AD ,得出CD .设缉私艇的速度为x 海里/小时,根据走私船行驶CD 所用的时间等于缉私艇行驶AD 所用的时间列出方程,解方程即可. 【详解】(1)在ABC △中,180180375390ACB B BAC ︒︒︒︒︒∠=-∠-∠=--=. 在Rt ABC V 中,sin AC B AB =,所以3sin 3725155AC AB ︒=⋅=⨯=(海里). 答:观察哨所A 与走私船所在的位置C 的距离为15海里.(2)过点C 作CM AB ⊥,垂足为M ,由题意易知,D C M 、、在一条直线上. 在Rt ACM V 中,4sin 15125CM AC CAM =⋅∠=⨯=,3cos 1595AM AC CAM =⋅∠=⨯=.在Rt ADM △中,tan MDDAM AM∠=,所以tan 7636MD AM ︒=⋅=. 所以222293691724AD AM MD CD MD MC =+=+==-=,.设缉私艇的速度为v海里/小时,则有2491716=,解得617v=.经检验,617v=是原方程的解.答:当缉私艇以每小时617海里的速度行驶时,恰好在D处成功拦截.【点睛】此题考查了解直角三角形的应用﹣方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.2.小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.(1)求∠CAO'的度数.(2)显示屏的顶部B'比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.【解析】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×=12,由C、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C ⊥OA 于C ,OA=OB=24cm , ∴sin ∠CAO′=,∴∠CAO′=30°;(2)过点B 作BD ⊥AO 交AO 的延长线于D ,∵sin ∠BOD=,∴BD=OBsin ∠BOD ,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin ∠BOD=24×=12,∵O′C ⊥OA ,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°, ∴O′B′+O′C ﹣BD=24+12﹣12=36﹣12, ∴显示屏的顶部B′比原来升高了(36﹣12)cm ;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°, 理由:∵显示屏O′B 与水平线的夹角仍保持120°, ∴∠EO′F=120°, ∴∠FO′A=∠CAO′=30°, ∵∠AO′B′=120°, ∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.3.如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB 和CD (均与水平面垂直),再将集热板安装在AD 上.为使集热板吸热率更高,公司规定:AD 与水平面夹角为1θ,且在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ,并已知1tan 1.082θ=,2tan 0.412θ=.如果安装工人确定支架AB 高为25cm ,求支架CD 的高(结果精确到1cm)?【答案】【解析】于F,根据锐角三角函数的定义用θ1、θ2表示出DF、EF的值,又可证过A作AF CD四边形ABCE为平行四边形,故有EC=AB=25cm,再再根据DC=DE+EC进行解答即可.4.如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(3=1.7).【答案】32.4米.【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.试题解析:如图,过点B作BE⊥CD于点E,根据题意,∠DBE=45°,∠CBE=30°.∵AB⊥AC,CD⊥AC,∴四边形ABEC为矩形,∴CE=AB=12m,在Rt△CBE中,cot∠CBE=BE CE,∴BE=CE•cot30°=12×3=123,在Rt△BDE中,由∠DBE=45°,得DE=BE=123.∴CD=CE+DE=12(3+1)≈32.4.答:楼房CD的高度约为32.4m.考点:解直角三角形的应用——仰角俯角问题.5.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G,连接AG交CD于K.(1)求证:KE=GE;(2)若KG2=KD•GE,试判断AC与EF的位置关系,并说明理由;(3)在(2)的条件下,若sinE=,AK=,求FG的长.【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= .【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KD•GE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.试题解析:(1)如图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.(2)AC∥EF,理由为连接GD,如图2所示.∵KG2=KD•GE,即,∴,又∵∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∵∠C=∠AGD,∴∠E=∠C,∴AC∥EF;(3)连接OG,OC,如图3所示,∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.∵sinE=sin∠ACH=,设AH=3t,则AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK-CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即(3t)2+t2=(2)2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即(r-3t)2+(4t)2=r2,解得r= t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH=,∴FG=【点睛】此题考查了切线的性质,相似三角形的判定与性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握定理及性质是解本题的关键.6.在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH、PH.(1)若点P在线CD上,如图1,①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)【答案】(1)①如图;②AH=PH,AH⊥PH.证明见解析(2)或【解析】试题分析:(1)①如图(1);②(1)法一:轴对称作法,判断:AH=PH,AH⊥PH.连接CH,根据正方形的每条对角线平分一组对角得:△DHQ等腰Rt△,根据平移的性质得DP=CQ,证得△HDP≌△△HQC,全等三角形的对应边相等得PH=CH,等边对等角得∠HPC=∠HCP,再结合BD是正方形的对称轴得出∠AHP=180°-∠ADP=90°,∴AH=PH且AH⊥PH.四点共圆作法,同上得:∠HPC=∠DAH,∴A、D、P、H共向,∴∠AHP=90°,∠APH=∠ADH=45°,∴△APH等腰Rt△.(2)轴对称作法同(1)作HR⊥PC于R,∵∠AHQ=152°,∴∠AHB=62°,∴∠DAH=17°∴∠DCH=17°.设DP=x,则.由代入HR,CR解方程即可得出x的值. 四点共圆作法,A、H、D、P共向,∴∠APD=∠AHB=62°,∴.试题解析:(1)①法一:轴对称作法,判断:AH=PH,AH⊥PH证:连接CH,得:△DHQ等腰Rt△,又∵DP=CQ,∴△HDP≌△△HQC,∴PH=CH,∠HPC=∠HCPBD为正方形ABCD对称轴,∴AH=CH,∠DAH=∠HCP,∴AH=PH,∠DAH=∠HPC,∴∠AHP=180°-∠ADP=90°,∴AH=PH且AH⊥PH.法二:四点共圆作法,同上得:∠HPC=∠DAH,∴A、D、P、H共向,∴∠AHP=90°,∠APH=∠ADH=45°,∴△APH等腰Rt△.(2)法一:轴对称作法考虑△DHQ等腰Rt△,PD=CQ,作HR⊥PC于R,∵∠AHQ=152°,∴∠AHB=62°,∴∠DAH=17°∴∠DCH=17°.设DP=x,则.由得:,∴.即PD=法二:四点共向作法,A、H、D、P共向,∴∠APD=∠AHB=62°,∴.考点:全等三角形的判定;解直角三角形;正方形的性质;死电脑共圆7.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为 cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.【答案】(1);(2)12cm;(3)cm.【解析】试题分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案:∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm.∵∠ACD=30°,∠DAC=90°,AC=12cm,∴(cm).∵点E为CD边上的中点,∴AE=DC=cm.(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,根据轴对称的性质,此时DP+EP值为最小,进而得出答案.(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.试题解析:解:(1).(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE.∴△ADE为等边三角形.∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°.∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′.∴点E,D′关于直线AC对称.如答图1,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′.∵△ADE是等边三角形,AD=AE=,∴,即DP+EP最小值为12cm.(3)如答图2,连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=.在△ABD′和△CBD′中,∵,∴△ABD′≌△CBD′(SSS).∴∠D′BG=∠D′BC=45°.∴D′G=GB.设D′G长为xcm,则CG长为cm,在Rt△GD′C中,由勾股定理得,解得:(不合题意舍去).∴点D′到BC边的距离为cm.考点:1.翻折和单动点问题;2.勾股定理;3.直角三角形斜边上的中线性质;4.等边三角形三角形的判定和性质;5.轴对称的应用(最短线路问题);6.全等三角形的判定和性质;7.方程思想的应用.8.如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.(1)求菱形ABCD的周长;(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.【答案】解:(1)在菱形ABCD中,∵AC⊥BD,AC=80,BD=60,∴。
备战中考数学压轴题专题锐角三角函数的经典综合题含答案

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.如图,山坡上有一棵树AB ,树底部B 点到山脚C 点的距离BC 为63米,山坡的坡角为30°.小宁在山脚的平地F 处测量这棵树的高,点C 到测角仪EF 的水平距离CF=1米,从E 处测得树顶部A 的仰角为45°,树底部B 的仰角为20°,求树AB 的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)【答案】6.4米 【解析】解:∵底部B 点到山脚C 点的距离BC 为6 3 米,山坡的坡角为30°. ∴DC=BC•cos30°=36392==米, ∵CF=1米, ∴DC=9+1=10米, ∴GE=10米, ∵∠AEG=45°, ∴AG=EG=10米, 在直角三角形BGF 中, BG=GF•tan20°=10×0.36=3.6米, ∴AB=AG-BG=10-3.6=6.4米, 答:树高约为6.4米首先在直角三角形BDC 中求得DC 的长,然后求得DF 的长,进而求得GF 的长,然后在直角三角形BGF 中即可求得BG 的长,从而求得树高2.如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB 和CD (均与水平面垂直),再将集热板安装在AD 上.为使集热板吸热率更高,公司规定:AD 与水平面夹角为1θ,且在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ,并已知1tan 1.082θ=,2tan 0.412θ=.如果安装工人确定支架AB 高为25cm ,求支架CD 的高(结果精确到1cm)?【答案】【解析】于F,根据锐角三角函数的定义用θ1、θ2表示出DF、EF的值,又可证过A作AF CD四边形ABCE为平行四边形,故有EC=AB=25cm,再再根据DC=DE+EC进行解答即可.3.已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:(1)如图1,若k=1,则∠APE的度数为;(2)如图2,若k=3,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)如图3,若k=3,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.【答案】(1)45°;(2)(1)中结论不成立,理由见解析;(3)(2)中结论成立,理由见解析.【解析】分析:(1)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE≌△ACD,得出EF=AD=BF,再判断出∠EFB=90°,即可得出结论;(2)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE∽△ACD,再判断出∠EFB=90°,即可得出结论;(3)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△ACD∽△HEA,再判断出∠EFB=90°,即可得出结论;详解:(1)如图1,过点A作AF∥CB,过点B作BF∥AD相交于F,连接EF,∴∠FBE=∠APE,∠FAC=∠C=90°,四边形ADBF是平行四边形,∴BD=AF,BF=AD.∵AC=BD,CD=AE,∴AF=AC.∵∠FAC=∠C=90°,∴△FAE≌△ACD,∴EF=AD=BF,∠FEA=∠ADC.∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EHD.∵AD∥BF,∴∠EFB=90°.∵EF=BF,∴∠FBE=45°,∴∠APE=45°.(2)(1)中结论不成立,理由如下:如图2,过点A作AF∥CB,过点B作BF∥AD相交于F,连接EF,∴∠FBE=∠APE,∠FAC=∠C=90°,四边形ADBF是平行四边形,∴BD=AF,BF=AD.∵3BD,3AE,∴3AC CDBD AE ==. ∵BD=AF ,∴3AC CDAF AE==. ∵∠FAC=∠C=90°, ∴△FAE ∽△ACD ,∴3AC AD BFAF EF EF ===,∠FEA=∠ADC . ∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EMD . ∵AD ∥BF , ∴∠EFB=90°.在Rt △EFB 中,tan ∠FBE=3EF BF =, ∴∠FBE=30°, ∴∠APE=30°,(3)(2)中结论成立,如图3,作EH ∥CD ,DH ∥BE ,EH ,DH 相交于H ,连接AH ,∴∠APE=∠ADH ,∠HEC=∠C=90°,四边形EBDH 是平行四边形, ∴BE=DH ,EH=BD . ∵3BD ,3AE ,∴3AC CDBD AE==. ∵∠HEA=∠C=90°, ∴△ACD ∽△HEA ,∴3AD ACAH EH==∠ADC=∠HAE . ∵∠CAD+∠ADC=90°, ∴∠HAE+∠CAD=90°, ∴∠HAD=90°.在Rt △DAH 中,tan ∠ADH=3AHAD=∴∠ADH=30°,∴∠APE=30°.点睛:此题是三角形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的判定和性质,构造全等三角形和相似三角形的判定和性质.4.如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;(2)若AB=5,,求PD的长;(3)在点P运动过程中,设=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)【答案】(1)证明见解析;(2);(3).【解析】试题分析:(1)应用圆周角定理证明∠APD=∠FPC,得到∠APC=∠FPD,又由∠PAC=∠PDC,即可证明结论.(2)由AC=2BC,设,应用勾股定理即可求得BC,AC的长,则由AC=2BC得,由△ACE∽△ABC可求得AE,CE的长,由可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得,即可求得PD的长.(3)连接BP,BD,AD,根据圆的对称性,可得,由角的转换可得,由△AGP∽△DGB可得,由△AGD∽△PGB可得,两式相乘可得结果.试题解析:(1)由APCB内接于圆O,得∠FPC=∠B,又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,∴∠APD=∠FPC.∴∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD.又∵∠PAC=∠PDC,∴△PAC∽△PDF.(2)连接BP,设,∵∠ACB=90°,AB=5,∴.∴.∵△ACE∽△ABC,∴,即. ∴.∵AB⊥CD,∴.如图,连接BP,∵,∴△APB是等腰直角三角形. ∴∠PAB=45°,.∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.由(1)△PAC∽△PDF得,即.∴PD的长为.(3)如图,连接BP,BD,AD,∵AC=2BC,∴根据圆的对称性,得AD=2DB,即.∵AB⊥CD,BP⊥AE,∴∠ABP=∠AFD.∵,∴.∵△AGP∽△DGB,∴.∵△AGD∽△PGB,∴.∴,即.∵,∴.∴与之间的函数关系式为.考点:1.单动点问题;2.圆周角定理;3.相似三角形的判定和性质;4.勾股定理;5.等腰直角三角形的判定和性质;6.垂径定理;7.锐角三角函数定义;8.由实际问题列函数关系式.5.如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.(1)求tan∠DBC的值;(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.【答案】(1)tan∠DBC=;(2)P(﹣,).【解析】试题分析:(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4,BE=BC﹣DE=.由此可知tan∠DBC=;(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知=,通过解方程求得点P的坐标为(﹣,).试题解析:(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,解得 x1=﹣1,x2=4.∴A(﹣1,0),B(4,0).当x=3时,y=﹣32+3×3+4=4,∴D(3,4).如图,连接CD,过点D作DE⊥BC于点E.∵C(0,4),∴CD//AB,∴∠BCD=∠ABC=45°.在直角△OBC中,∵OC=OB=4,∴BC=4.在直角△CDE中,CD=3.∴CE=ED=,∴BE=BC﹣DE=.∴tan∠DBC=;(2)过点P作PF⊥x轴于点F.∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,∴tan∠PBF=.设P(x,﹣x2+3x+4),则=,解得 x1=﹣,x2=4(舍去),∴P(﹣,).考点:1、二次函数;2、勾股定理;3、三角函数6.如图,已知点从出发,以1个单位长度/秒的速度沿轴向正方向运动,以为顶点作菱形,使点在第一象限内,且;以为圆心,为半径作圆.设点运动了秒,求:(1)点的坐标(用含的代数式表示);(2)当点在运动过程中,所有使与菱形的边所在直线相切的的值.【答案】解:(1)过作轴于,,,,,点的坐标为.(2)①当与相切时(如图1),切点为,此时,,,.②当与,即与轴相切时(如图2),则切点为,,过作于,则,,.③当与所在直线相切时(如图3),设切点为,交于,则,,.过作轴于,则,,化简,得,解得,,.所求的值是,和.【解析】(1)过作轴于,利用三角函数求得OD、DC的长,从而求得点的坐标⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=oc/op,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P 作PE 垂直于OC ,又PC=PO ,利用三线合一得到E 为OC 的中点,OE 为OC 的一半,而OE=OPcos30°,列出关于t 的方程,求出方程的解即可得到t 的值;③当圆P 与AB 所在的直线相切时,设切点为F ,PF 与OC 交于点G ,由切线的性质得到PF 垂直于AB ,则PF 垂直于OC ,由CD=FG ,在直角三角形OCD 中,利用锐角三角函数定义由OC 表示出CD ,即为FG ,在直角三角形OPG 中,利用OP 表示出PG ,用PG+GF 表示出PF ,根据PF=PC ,表示出PC ,过C 作CH 垂直于y 轴,在直角三角形PHC 中,利用勾股定理列出关于t 的方程,求出方程的解即可得到t 的值,综上,得到所有满足题意的t 的值.7.如图,在平面直角坐标系中,菱形ABCD 的边AB 在x 轴上,点B 坐标(﹣6,0),点C 在y 轴正半轴上,且cos B =35,动点P 从点C 出发,以每秒一个单位长度的速度向D 点移动(P 点到达D 点时停止运动),移动时间为t 秒,过点P 作平行于y 轴的直线l 与菱形的其它边交于点Q . (1)求点D 坐标;(2)求△OPQ 的面积S 关于t 的函数关系式,并求出S 的最大值; (3)在直线l 移动过程中,是否存在t 值,使S =320ABCD S 菱形?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)点D 的坐标为(10,8).(2)S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩,S 的最大值为503.(3)3或7. 【解析】 【分析】(1)在Rt △BOC 中,求BC,OC,根据菱形性质再求D 的坐标;(2)分两种情况分析:①当0≤t ≤4时和②当4<t ≤10时,根据面积公式列出解析式,再求函数的最值;(3)分两种情况分析:当0≤t ≤4时,4t =12,;当4<t ≤10时,22201233t t -+= 【详解】解:(1)在Rt △BOC 中,∠BOC =90°,OB =6,cos B =35,10cos OBBC B∴==8OC ∴==∵四边形ABCD 为菱形,CD ∥x 轴,∴点D 的坐标为(10,8).(2)∵AB =BC =10,点B 的坐标为(﹣6,0), ∴点A 的坐标为(4,0). 分两种情况考虑,如图1所示. ①当0≤t ≤4时,PQ =OC =8,OQ =t ,∴S =12PQ •OQ =4t , ∵4>0,∴当t =4时,S 取得最大值,最大值为16;②当4<t ≤10时,设直线AD 的解析式为y =kx +b (k ≠0), 将A (4,0),D (10,8)代入y =kx +b ,得:4k b 010k b 8+=⎧⎨+=⎩,解得:4k 316b 3⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线AD 的解析式为41633y x =-. 当x =t 时,41633y t =-, 41648(10)333PQ t t ⎛⎫∴=--=- ⎪⎝⎭21220233S PQ OP t t ∴=⋅=-+ 22202502(5),033333S t t t =-+=--+-<∴当t =5时,S 取得最大值,最大值为503. 综上所述:S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩,S 的最大值为503.(3)S 菱形ABCD =AB •OC =80. 当0≤t ≤4时,4t =12, 解得:t =3; 当4<t ≤10时,222033t t -+=12,解得:t 1=5﹣7(舍去),t2=5+ 7. 综上所述:在直线l 移动过程中,存在t 值,使S =320ABCD S 菱形,t 的值为3或5+7.【点睛】考核知识点:一次函数和二次函数的最值问题.数形结合,分类讨论是关键.8.如图,在ABC △中,10AC BC ==,3cos 5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P 与边BC 相切时,求P 的半径;()2联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;()3在()2的条件下,当以PE 长为直径的Q 与P 相交于AC 边上的点G 时,求相交所得的公共弦的长.【答案】(1)409;(2))25880010x x x y x -+=<<;(3)105- 【解析】 【分析】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=45,sinC=HP CP =R 10R -=45,即可求解; (2)PD ∥BE ,则EB PD =BFPF,即:2248805x x x y x--+-=,即可求解;(3)证明四边形PDBE 为平行四边形,则AG=GP=BD ,即:AB=DB+AD=AG+AD=45,即可求解. 【详解】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=35, sinC=HP CP =R 10R -=45,解得:R=409; (2)在△ABC 中,AC=BC=10,cosC=35, 设AP=PD=x ,∠A=∠ABC=β,过点B 作BH ⊥AC ,则BH=ACsinC=8, 同理可得:CH=6,HA=4,5tan ∠()2284x +-2880x x -+ 25,则525,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β, tanβ=2,则cosβ=5,sinβ=5, EB=BDcosβ=(45-25x )×5=4-25x ,∴PD ∥BE ,∴EB PD =BFPF,即:2248805x x x y x--+-=,整理得:y=()25x x 8x 800x 103x 20-+<<+;(3)以EP 为直径作圆Q 如下图所示,两个圆交于点G ,则PG=PQ ,即两个圆的半径相等,则两圆另外一个交点为D ,GD 为相交所得的公共弦, ∵点Q 时弧GD 的中点, ∴DG ⊥EP , ∵AG 是圆P 的直径, ∴∠GDA=90°, ∴EP ∥BD ,由(2)知,PD ∥BC ,∴四边形PDBE 为平行四边形, ∴AG=EP=BD ,∴5设圆的半径为r,在△ADG中,AD=2rcosβ=5,DG=5,AG=2r,5+2r=45,解得:2r=51,则:DG=5=10-25,相交所得的公共弦的长为10-25.【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.9.关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ①cos(α+β)=cosαcosβ﹣sinαsinβ②tan(α+β)=③利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:tan105°=tan(45°+60°)==﹣(2+).根据上面的知识,你可以选择适当的公式解决下面的实际问题:如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.【答案】建筑物CD的高为84米.【解析】分析:如图,过点D作DE⊥AB于点E,由题意易得∠ACB=75°,∠ABC=90°,DE=BC=42m,∠ADE=60°,这样在Rt△ABC和在Rt△ADE中,结合题中所给关系式分别求出AB和AE的长,即可由CD=BE=AB-AE求得结果了.详解:如图,过点D作DE⊥AB于点E,由题意可得∠ACB=75°,∠ABC=90°,DE=BC=42m,CD=BE,∠ADE=60°,∴在Rt△ABC和Rt△ADEAB=BC•tan75°=42tan75°=,AE=,∴CD=AB﹣AE=(米).答:建筑物CD的高为84米.睛:读懂题意,把已知量和未知量转化到Rt△ABC和Rt△ADE中,这样利用直角三角形中边角间的关系结合题目中所给的“两角和的三角形函数公式”即可使问题得到解决.10.小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)
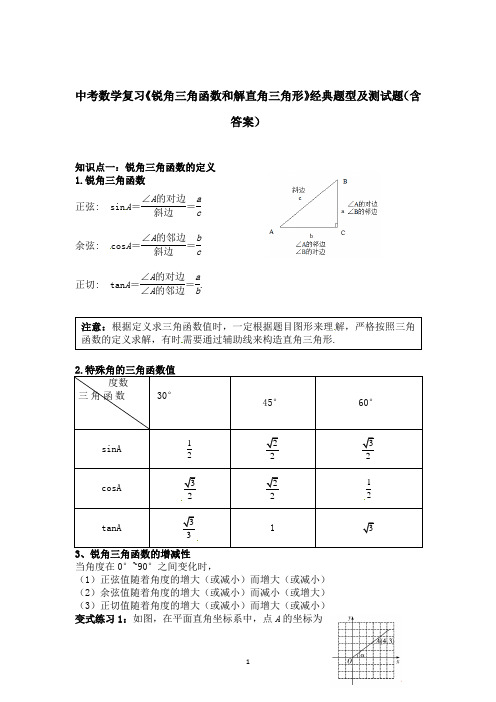
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)知识点一:锐角三角函数的定义 1.锐角三角函数 正弦: sin A =∠A 的对边斜边=ac余弦: cos A =∠A 的邻边斜边=bc正切: tan A =∠A 的对边∠A 的邻边=ab.来源:学&科&网]2.特殊角的三角函数值[来 度数三角函数[来源:Z 。
xx 。
]30°[来源:学#科#网] 45° 60°sinA1222 32 cosA32 2212tanA 331 33、锐角三角函数的增减性当角度在0°~90°之间变化时,(1)正弦值随着角度的增大(或减小)而增大(或减小) (2)余弦值随着角度的增大(或减小)而减小(或增大) (3)正切值随着角度的增大(或减小)而增大(或减小) 变式练习1:如图,在平面直角坐标系中,点A 的坐标为注意:根据定义求三角函数值时,一定根据题目图形来理解,严格按照三角函数的定义求解,有时需要通过辅助线来构造直角三角形.[(4,3),那么cos α的值是( ) A. 34 B. 43 C. 35 D. 45【解析】D 如解图,过点A 作AB ⊥x 轴于点B ,∵A (4,3),∴OB =4,AB =3,∴OA =32+42=5,∴cos α=OB OA =45.变式练习2:在Rt △ABC 中,∠ABC =90°,AB =3,BC =4,则sinA =________. 【解析】∵在Rt △ABC 中,由勾股定理得AC =22AB BC +=32+42=5,∴sin A =BC AC =45. 变式练习3:在Rt △ABC 中,∠C =90°,sin A =35,BC =6,则AB =( D )A .4B .6C .8D .10变式练习4:如图,若点A 的坐标为(1,3),则sin ∠1=__32__. ,知识点二 :解直角三角形 1.解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形. 2.解直角三角形的常用关系在Rt △ABC 中,∠C=90°,∠A ,∠B ,∠C 所对的边分别为a ,b ,c (1)三边之间的关系:a 2+b 2=c 2;(2)锐角之间的关系:∠A +∠B =90°; (3)边角之间的关系:,tan ,cos ,sin ;,tan ,cos ,sin abB c a B c b B b a A c b A c a A ======(sinA==cosB=ac,c osA=sinB=bc,tanA=ab.)变式练习1:在Rt△ABC中,已知a=5,sinA=30°,则c=10,b=5.变式练习2:如图,Rt△ACB中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D.以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI =90°.若AC=a,求CI的长.解:在Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB,∴∠A=60°,∵AC=a,∴CD=AC·sin60°=32a,依此类推CH=(32)3a=338a,在Rt△CHI中,∵∠CHI=60°,∴CI=CH·tan60°=338a×3=98a.变式练习3:如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )A.433B.4 C.8 3 D.4 3,灵活选择解直角三角形的方法顺口溜:已知斜边求直边,正弦、余弦很方便;已知直边求直边,理所当然用正切;已知两边求一边,勾股定理最方便;已知两边求一角,函数关系要记牢;已知锐角求锐角,互余关系不能少;已知直边求斜边,用除还需正余弦.变式练习4:如图,一山坡的坡度为i=1∶3,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了__100__米., ,变式练习5:一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为___40+4033___海里/小时.知识点三:解直角三角形的应用1.仰角、俯角、坡度、坡角和方向角(1)仰、俯角:视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角.(如图①)(2)坡度:坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比),用字母i表示.坡角:坡面与水平面的夹角叫做坡角,用α表示,则有i=tanα.(如图②)(3)方向角:平面上,通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向),则从点O出发的视线与水平线或铅垂线所夹的角,叫做观测的方向角.(如图③)2.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;(3)选择合适的边角关系式,使运算简便、准确;(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.注意:解直角三角形中“双直角三角形”的基本模型:(1)叠合式(2)背靠式解题方法:这两种模型种都有一条公共的直角边,解题时,往往通过这条边为中介在两个三角形中依次求边,或通过公共边相等,列方程求解变式练习1:如图,某数学兴趣小组想测量一棵树CD 的高度,他们先在点A 处测得树顶C 的仰角为30°,然后沿AD 方向前行10 m ,到达B 点,点B 处测得树顶C 的仰角为60°(A 、B 、D 三点在同一直线上).请你根据他们的测量数据计算这棵树CD 的高度(结果精确到0.1 m).(参考数据:2≈1.414,3≈ 1.732)解:如解图,由题意可知∠CAB =30°,∠CBD =60°,AB =10 m ,∵∠CBD =∠CAB +∠BCA ,∴∠BCA =∠CBD -∠CAB =60°-30°=30°=∠CAB , ∴BC =AB =10 m . 在Rt △BCD 中,∵sin ∠CBD =CDBC,∴CD =BC ·sin ∠CBD =10×sin60°=10×32=53≈5×1.732≈8.7 m . 答:这棵树CD 的高度大约是8.7 m .变式练习2:如图,小山岗的斜坡AC 的坡度是tan α=34,在与山脚C 距离200米的D 处,测得山顶A 的仰角为26.6°,求小山岗的高AB (结果取整数;参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50).解:设AB =x 米,在Rt △ABD 中,∠D =26.6°,∴BD =tan 26.6x≈2x ,在Rt △ABC 中,tan α=AB BC =34,∴BC =43x ,∵BD -BC =CD ,CD =200,∴2x-43x=200,解得x=300.答:小山岗的高AB约为300米.变式练习3:如图,小明所在教学楼的每层高度为3.5 m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B 处测得M的仰角为30°,已知每层楼的窗台离该层的地面高度均为1 m,求旗杆MN的高度(结果精确到0.1 m).(参考数据:2≈1.414,3≈1.732)解:如解图,过点M的水平线交直线AB于点H,由题意,得∠AMH=∠MAH=45°,∠BMH=30°,AB=3.5 m,设MH=x m,则AH=x m,BH=x·tan30°=33x≈0.58x m,∴AB=AH-BH=x-0.58x=0.42x=3.5 m,解得x≈8.3,则MN=x+1=9.3 m.答:旗杆MN的高度约为9.3 m.变式练习4:小明去爬山,如图,在山脚看山顶的角度为30°,小明在坡比为5∶12的山坡上走了1300米,此时小明看山顶的角度为60°,则山高为( )A. (600-2505)米B. (6003-250)米C. (350+3503)米D. 500 3 米【解析】B如解图,∵BE∶AE=5∶12,∴设BE=5k,AE=12k,∴AB=2()5K+(12k)2=13k,∴BE∶AE∶AB=5∶12∶13,∵AB=1300米,∴AE=1200米,BE =500米,设EC=FB=x米,∵∠DBF=60°,∴DF=3x米,则DC=(3x+500)米,又∵∠DAC=30°,∴AC=3CD,即1200+x=3(3x+500),解得x=600-2503,∴DF=3x=(6003-750)米,∴CD=DF+CF=(6003-250)米,即山高CD为(6003-250)米.变式练习5:某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)解:如解图,过点A作AD⊥BC交BC于点D,过点B作BH⊥水平线交水平线于点H,由题意∠ACH=75°,∠BCH=30°,AB∥CH,∴∠ABC=30°,∠ACB=45°,∵AB=4×8=32米,∴CD=AD=AB·sin30°=16米,BD=AB·cos30°=32×32=163米,∴BC=CD+BD=(16+163)米,∴BH=BC·sin30°=(16+163)×12=(8+83)米.答:这架无人飞机的飞行高度为(8+83)米.变式练习6:如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中3≈1.732) 解:∵CD∥BE,∴∠EBC+∠DCB=180°.∵∠ABE=60°,∠DCB=30°,∴∠ABC=90°.…………(4分)由题知,BC=80×12=40(海里),∠ACB=60°.在Rt△ABC中,AB=BC·tan60°=403≈40×1.732≈69.3(海里).答:此时渔政船距钓鱼岛A的距离AB的长约为69.3海里.。
中考数学复习《锐角三角函数》专题训练-附带有答案

中考数学复习《锐角三角函数》专题训练-附带有答案一、选择题1.已知α是锐角,若sinα= 12,则α的度数是()A.30°B.45°C.60°D.75°2.如图,在Rt△ABC中,BC=3,斜边AC=5,则下列等式正确的是()A.sinC=35B.cosC=43C.tanA=34D.sinA=453.在Rt△ABC中,∠C=90°,sinA= 513,则tanB的值为()A.1213B.512C.1312D.1254.如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=4m,则坡面AB的长度是()mA.8 B.16 C.4√5D.4√35.如图,在正方形网格中.每个小正方形的边长都是1,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正切值是()A.√55B.15C.2√55D.126.如图,河堤的横断面迎水坡AB的坡比是1:√2,堤高BC=6m,则坡面AB的长度是()A.10m B.12√2m C.6√3m D.6√2m7.如图,在菱形ABCD中,延长AB于E并且CE⊥AE,AC=2CE,则∠CBE的度数为()A.50°B.40°C.30°D.60°8.如图,在▱ABCD中AB=8,∠ABC=60°,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的长为()A.6 B.4 C.4√3D.2√6二、填空题9.计算:2sin30°−tan45°=.10.如图,在平面直角坐标系内有一点P(5,12),那么OP与x轴正半轴的夹角α的正弦值.11.如图,Rt△ABC中,∠C=90°,BC=15,tanA= 15,则AB= .812.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面20√3米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC之间的水平距离为80米,教学楼BC的高度米.(注:点A、B、C、D都在同一平面上,参考数据:√3≈1.7结果保留整数).13.如图,在△ABC中AB=AC,D是△ABC外一点,连接BD和DC,BD=AB,∠BDC+12∠BAC=180°,DC=1,tan∠ABC=2√33则线段BC的长为.三、解答题14.计算:2sin45°+tan30°·cos30°−√2.15.已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,4sin5B=求:(1)线段DC的长;(2)tan∠EDC的值.16.小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15︒方向上,他沿西北方向前进D,此时测得点A在他的东北方向上,端点B在他的北偏西60︒方向上,(点A、B、C、D在同一平面内)(1)求点D与点A的距离;(2)求隧道AB的长度.(结果保留根号)17.如图1,在等腰三角形ABC中AB=AC,O为底边BC的中点,AB切⊙O于点D,连接OD,⊙O交BC于点M,N.(1)求证:AC是⊙O的切线;(2)∠B=42°,①若OD=4,求劣弧DM的长;②如图2,连接DM,若DM=4,直接写出OD的长.(参考数据:sin24°取0.4,cos24°取0.9,tan24°取0.45)18.如图,在边长为9的正方形ABCD中,等腰Rt△CEF的直角顶点与正方形ABCD的顶点C重合,斜边EF与正方形ABCD的对角线交于点E,射线FE与AD交于点P,与BC交于点Q且BQCQ =45.(1)求证:△CDE≌△CBF;(2)求CF的长;(3)求tan∠BCF的值.参考答案1.A2.C3.D4.C5.D6.C7.D8.C9.010.121311.1712.1413.2√314.解:原式=2×√22+√33×√32-√2 =√2+12-√2=1215.(1)解:在△ABC 中,∵AD 是边BC 上的高∴AD ⊥BC .∴sin B =45AD AB =. ∵AD =12 ∴5154AB AD ==. 在Rt △ABD 中,∵222215129BD AB AD --∴CD =BC ﹣BD =14﹣9=5.(2)解:在Rt △ADC 中,E 是AC 的中点∴DE =EC∴∠EDC =∠C .∴tan EDC ∠=tan C ∠=125AD CD =.16.(1)由题意可知:154560ACD ∠=︒+︒=︒ 180454590ADC ∠=︒-︒-︒=︒ 在Rt ADC 中 ∴tan 1003tan 6010033300AD DC ACD =⨯∠=︒==(米)答:点D 与点A 的距离为300米.(2)过点D 作DE AB ⊥于点E .∵AB 是东西走向∴45,60ADE BDE ∠=︒∠=︒在Rt ADE △中 ∴2sin 300sin 453001502DE AE AD ADE ==⨯∠=⨯︒==在Rt BDE 中 ∴tan 1502tan 60231506BE DE BDE =⨯∠=︒==∴26AB AE BE =+=答:隧道AB 的长为(15021506)米17.(1)证明:过点 O 作 OE ⊥AC 于点 E ,连接 OA ,如图∵AB =AC , O 为底边 BC 的中点∴AO 为 ∠BAC 的平分线∵OD ⊥AB∴OD =OE∵OD 为 ⊙O 的半径∴OE为⊙O的半径∴直线AC到圆心O的距离等于圆的半径∴AC是⊙O的切线(2)解:①∵AB切⊙O于点D∴∠ODB=90°∵∠B=42°∴∠BOD=48°∵OD=4∴劣弧DM的长为48×π×4180=16π15;②过点O作OF⊥DM于点F,如图∵OF⊥DM∴DF=MF=12DM=2∵OD=OM∴OF为∠DOM的平分线∴∠DOF=12∠BOD=24° .在Rt△ODF中∵sin∠DOF=DFOD∴sin24°=2OD∴OD=2sin24°≈20.4=5 .18.(1)证明:∵四边形ABCD是正方形,△CEF是等腰直角三角形∴∠BCD=∠ECF=90°,CD=CB,CE=CF∴∠DCE=∠BCF在△CDE与△CBF中∵{CD=CB∠DCE=∠BCFCE=CF∴△CDE≌△CBF;(2)解:∵∠CEQ=∠CBE=45°,∠ECQ=∠BCE∴△CEQ∽△CBE∴CECB=CQCE∵BQCQ=45,BC=9∴BQ=4,CQ=5∴CE=3√5∵CF=CE∴CF=3√5;(3)解:过点F作FR⊥BC于R∵△CDE≌△CBF∴∠FBR=∠EDC=45°∴△BRF是等腰直角三角形∴RF=RB在Rt△CRF中∵CF2=CR2+FR2∴(3√5)2=RF2+(9−RF)2∴RF=3∴BR=3∴CR=6∴tan∠BCF=RFCR =12.。
中考数学压轴题专题锐角三角函数的经典综合题及答案

中考数学压轴题专题锐角三角函数的经典综合题及答案一、锐角三角函数1.如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为63米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)【答案】6.4米【解析】解:∵底部B点到山脚C点的距离BC为6 3 米,山坡的坡角为30°.∴DC=BC•cos30°=3==米,639∵CF=1米,∴DC=9+1=10米,∴GE=10米,∵∠AEG=45°,∴AG=EG=10米,在直角三角形BGF中,BG=GF•tan20°=10×0.36=3.6米,∴AB=AG-BG=10-3.6=6.4米,答:树高约为6.4米首先在直角三角形BDC中求得DC的长,然后求得DF的长,进而求得GF的长,然后在直角三角形BGF中即可求得BG的长,从而求得树高2.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O 于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC•3DC=,∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED===;②当CF=aCD(a>0)时,sin∠CAB=.∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC•(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.3.已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:(1)如图1,若k=1,则∠APE的度数为;(2)如图2,若k=3,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)如图3,若k=3,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.【答案】(1)45°;(2)(1)中结论不成立,理由见解析;(3)(2)中结论成立,理由见解析.【解析】分析:(1)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE≌△ACD,得出EF=AD=BF,再判断出∠EFB=90°,即可得出结论;(2)先判断出四边形ADBF 是平行四边形,得出BD=AF ,BF=AD ,进而判断出△FAE ∽△ACD ,再判断出∠EFB=90°,即可得出结论;(3)先判断出四边形ADBF 是平行四边形,得出BD=AF ,BF=AD ,进而判断出△ACD ∽△HEA ,再判断出∠EFB=90°,即可得出结论;详解:(1)如图1,过点A 作AF ∥CB ,过点B 作BF ∥AD 相交于F ,连接EF ,∴∠FBE=∠APE ,∠FAC=∠C=90°,四边形ADBF 是平行四边形, ∴BD=AF ,BF=AD . ∵AC=BD ,CD=AE , ∴AF=AC . ∵∠FAC=∠C=90°, ∴△FAE ≌△ACD ,∴EF=AD=BF ,∠FEA=∠ADC . ∵∠ADC+∠CAD=90°, ∴∠FEA+∠CAD=90°=∠EHD . ∵AD ∥BF , ∴∠EFB=90°. ∵EF=BF , ∴∠FBE=45°, ∴∠APE=45°.(2)(1)中结论不成立,理由如下:如图2,过点A 作AF ∥CB ,过点B 作BF ∥AD 相交于F ,连接EF ,∴∠FBE=∠APE ,∠FAC=∠C=90°,四边形ADBF 是平行四边形, ∴BD=AF ,BF=AD . ∵3BD ,3AE , ∴3AC CDBD AE==.∵BD=AF ,∴3AC CDAF AE==. ∵∠FAC=∠C=90°, ∴△FAE ∽△ACD ,∴3AC AD BFAF EF EF ===,∠FEA=∠ADC . ∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EMD . ∵AD ∥BF , ∴∠EFB=90°.在Rt △EFB 中,tan ∠FBE=3EF BF =, ∴∠FBE=30°, ∴∠APE=30°,(3)(2)中结论成立,如图3,作EH ∥CD ,DH ∥BE ,EH ,DH 相交于H ,连接AH ,∴∠APE=∠ADH ,∠HEC=∠C=90°,四边形EBDH 是平行四边形, ∴BE=DH ,EH=BD . ∵3BD ,3AE ,∴3AC CDBD AE==. ∵∠HEA=∠C=90°, ∴△ACD ∽△HEA ,∴3AD ACAH EH==∠ADC=∠HAE . ∵∠CAD+∠ADC=90°, ∴∠HAE+∠CAD=90°, ∴∠HAD=90°.在Rt △DAH 中,tan ∠ADH=3AHAD= ∴∠ADH=30°, ∴∠APE=30°.点睛:此题是三角形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的判定和性质,构造全等三角形和相似三角形的判定和性质.4.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.5.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.【答案】故大坝的截面的周长是(345)米,面积是1470平方米.【解析】试题分析:先根据两个坡比求出AE和BF的长,然后利用勾股定理求出AD和BC,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC,梯形的面积公式可得出答案.试题解析:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,∴AE=18米,在RT△ADE中,22+34DE AE∵背水坡坡比为1:2,∴BF=60米,在RT△BCF中,22CF BF+5∴周长345(345)米,面积=(10+18+10+60)×30÷2=1470(平方米).故大坝的截面的周长是(634+305+98)米,面积是1470平方米.6.如图,AB是⊙O的直径,E是⊙O上一点,C在AB的延长线上,AD⊥CE交CE的延长线于点D,且AE平分∠DAC.(1)求证:CD是⊙O的切线;(2)若AB=6,∠ABE=60°,求AD的长.【答案】(1)详见解析;(2)9 2【解析】【分析】(1)利用角平分线的性质得到∠OAE=∠DAE,再利用半径相等得∠AEO=∠OAE,等量代换即可推出OE∥AD,即可解题,(2)根据30°的三角函数值分别在Rt△ABE中,AE=AB·cos30°,在Rt△ADE中,AD=cos30°×AE即可解题.【详解】证明:如图,连接OE,∵AE平分∠DAC,∴∠OAE=∠DAE.∵OA=OE,∴∠AEO=∠OAE.∴∠AEO=∠DAE.∴OE∥AD.∵DC⊥AC,∴OE⊥DC.∴CD是⊙O的切线.(2)解:∵AB是直径,∴∠AEB=90°,∠ABE=60°.∴∠EAB=30°,在Rt△ABE中,AE=AB·cos30°=6×32=33,在Rt△ADE中,∠DAE=∠BAE=30°,∴AD=cos30°×AE=3×33=9 2 .【点睛】本题考查了特殊的三角函数值的应用,切线的证明,中等难度,利用特殊的三角函数表示出所求线段是解题关键.7.在△ABC中,∠B=45°,∠C=30°,点D是边BC上一点,连接AD,将线段AD绕点A 逆时针旋转90°,得到线段AE,连接DE.(1)如图①,当点E落在边BA的延长线上时,∠EDC=度(直接填空);(2)如图②,当点E落在边AC上时,求证:BD=12 EC;(3)当AB=22,且点E到AC的距离等于3﹣1时,直接写出tan∠CAE的值.【答案】(1)90;(2)详见解析;(3)633 tan EAC-∠=【解析】【分析】(1)利用三角形的外角的性质即可解决问题;(2)如图2中,作PA⊥AB交BC于P,连接PE.只要证明△BAD≌△PAE(SAS),提出BD=PE,再证明EC=2PE即可;(3)如图3,作EF⊥AC于F,延长FE交BC于H,作AG⊥BC于G,PA⊥AB交BC于P,连接PE.设PH=x,在Rt△EPH中,可得EP3,EH=2PH=2x,由此FH=31,CF=33,由△BAD≌△PAE,得BD=EP3x,AE=AD,在Rt△ABG中, AG=GB=2,在Rt△AGC中,AC=2AG=4,故AE2=AD2=AF2+EF2,由勾股定理得AF=3tan∠EAF=23tan∠EAC=6-33【详解】(1)如图1中,∵∠EDC=∠B+∠BED,∠B=∠BED=45°,∴∠EDC=90°,故答案为90;(2)如图2中,作PA⊥AB交BC于P,连接PE.∵∠DAE=∠BAP=90°,∴∠BAD=∠PAE,∵∠B=45°,∴∠B=∠APB=45°,∴AB=AP,∵AD=AE,∴△BAD≌△PAE(SAS),∴BD=PE,∠APE=∠B=45°,∴∠EPD=∠EPC=90°,∵∠C=30°,∴EC=2PE=2BD;(3)如图3,作EF⊥AC于F,延长FE交BC于H,作AG⊥BC于G,PA⊥AB交BC于P,连接PE.设PH=x,在Rt△EPH中,∵∠EPH=90°,∠EHP=60°,∴EP3,EH=2PH=2x,∴FH=31,CF3FH=33∵△BAD≌△PAE,∴BD=EP3,AE=AD,在Rt△ABG中,∵AB=2∴AG=GB=2,在Rt△AGC中,AC=2AG=4,∵AE2=AD2=AF2+EF2,∴22+(23)231)2+(4﹣3﹣32,整理得:9x2﹣12x=0,解得x=43(舍弃)或0∴PH=0,此时E,P,H共点,∴AF=3∴tan∠EAF=EFAF 331+=23根据对称性可知当点E在AC的上方时,同法可得tan∠EAC 6-33.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.8.如图,在▱ABCD中,AC与BD交于点O,AC⊥BC于点C,将△ABC沿AC翻折得到△AEC,连接DE.(1)求证:四边形ACED是矩形;(2)若AC=4,BC=3,求sin∠ABD的值.【答案】(1)证明见解析(2)613 【解析】【分析】 (1)根据▱ABCD 中,AC ⊥BC ,而△ABC ≌△AEC ,不难证明;(2)依据已知条件,在△ABD 或△AOC 作垂线AF 或OF ,求出相应边的长度,即可求出∠ABD 的正弦值.【详解】(1)证明:∵将△ABC 沿AC 翻折得到△AEC ,∴BC =CE ,AC ⊥CE ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴AD =CE ,AD ∥CE , ∴四边形ACED 是平行四边形,∵AC ⊥CE ,∴四边形ACED 是矩形.(2)解:方法一、如图1所示,过点A 作AF ⊥BD 于点F ,∵BE =2BC =2×3=6,DE =AC =4,∴在Rt △BDE 中,2222BD BE DE 64213=+=+=∵S △BDE =12×DE•AD =12AF•BD , ∴AF 61313213=, ∵Rt △ABC 中,AB 2234+5,∴Rt △ABF 中,sin ∠ABF =sin ∠ABD =6136135AF AB ==方法二、如图2所示,过点O 作OF ⊥AB 于点F ,同理可得,OB =1132BD = ∵S △AOB =11OF AB OA BC 22⋅=⋅,∴OF =23655⨯=, ∵在Rt △BOF 中, sin ∠FBO =0661365513F OB ==, ∴sin ∠ABD =61365.【点睛】本题考查直角三角形翻折变化后所得图形的性质,矩形的判定和性质,平行四边形的性质和解直角三角形求线段的长度,关键是正确添加辅助线和三角形面积的计算公式求出sin ∠ABD .9.在Rt △ABC 中,∠ACB=90°,AB=7,AC=2,过点B 作直线m ∥AC ,将△ABC 绕点C 顺时针旋转得到△A′B′C(点A ,B 的对应点分别为A',B′),射线CA′,CB′分別交直线m 于点P ,Q .(1)如图1,当P 与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC 的交点为M ,当M 为A′B′的中点时,求线段PQ 的长;(3)在旋转过程中,当点P ,Q 分别在CA′,CB′的延长线上时,试探究四边形PA'B′Q 的面积是否存在最小值.若存在,求出四边形PA′B′Q 的最小面积;若不存在,请说明理由.【答案】(1)60°;(2)PQ =72;(3)存在,S 四边形PA 'B ′Q =3【解析】【分析】(1)由旋转可得:AC =A 'C =2,进而得到BC =∠A 'BC =90°,可得cos ∠A 'CB 'BC A C ==∠A 'CB =30°,∠ACA '=60°;(2)根据M 为A 'B '的中点,即可得出∠A =∠A 'CM ,进而得到PB =32=,依据tan ∠Q =tan ∠A2=BQ =BC =2,进而得出PQ =PB +BQ 72=;(3)依据S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ S 四边形PA 'B 'Q 最小,即S △PCQ 最小,而S △PCQ 12=PQ ×BC =,利用几何法即可得到S △PCQ 的最小值=3,即可得到结论.【详解】(1)由旋转可得:AC =A 'C =2.∵∠ACB =90°,AB=AC =2,∴BC =∵∠ACB =90°,m ∥AC ,∴∠A 'BC =90°,∴cos ∠A 'CB 'BC A C ==∴∠A 'CB =30°,∴∠ACA '=60°;(2)∵M 为A 'B '的中点,∴∠A 'CM =∠MA 'C ,由旋转可得:∠MA 'C =∠A ,∴∠A =∠A 'CM ,∴tan ∠PCB =tan ∠A =∴PB =32=.∵∠BQC =∠BCP =∠A ,∴tan ∠BQC =tan ∠A2=,∴BQ =BC =2,∴PQ =PB +BQ 72=;(3)∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ ∴S 四边形PA 'B 'Q 最小,即S △PCQ 最小,∴S △PCQ 12=PQ ×BC =, 取PQ 的中点G . ∵∠PCQ =90°,∴CG 12=PQ ,即PQ =2CG ,当CG 最小时,PQ 最小,∴CG ⊥PQ ,即CG 与CB 重合时,CG 最小,∴CG min =PQ min ∴S △PCQ 的最小值=3,S 四边形PA 'B 'Q =3;【点睛】本题属于几何变换综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.10.已知:如图,直线y=-x+12分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.(1)求AE的长及sin∠BEC的值;(2)求△CDE的面积.【答案】(1)2,sin∠BEC=35;(2)754【解析】【分析】(1)如图,作CF⊥BE于F点,由函数解析式可得点B,点A坐标,继而可得∠A=∠B=45°,再根据中点的定义以及等腰直角三角形的性质可得OC=BC=6,2,设AE=CE=x,则222-x,在Rt△CEF中,利用勾股定理求出x 的值即可求得答案;(2)如图,过点E作EM⊥OA于点M,根据三角形面积公式则可得S△CDE=S△AED=2,设AD=y,则CD=y,OD=12-y,在Rt△OCD中,利用勾股定理求出y,继而可求得答案.【详解】(1)如图,作CF⊥BE于F点,由函数解析式可得点B(0,12),点A(12,0),∠A=∠B=45°,又∵点C是OB中点,∴OC=BC=6,CF=BF=32,设AE=CE=x,则EF=AB-BF-AE=122-32-x=92-x,在Rt△CEF中,CE2=CF2+EF2,即x2=(92-x)2+(32)2,解得:x=52,故可得sin∠BEC=35CFCE,AE=52;(2)如图,过点E作EM⊥OA于点M,则S△CDE=S△AED=12AD•EM=12AD×AEsin∠EAM=12AD•AE×sin45°=24AD×AE,设AD=y,则CD=y,OD=12-y,在Rt△OCD中,OC2+OD2=CD2,即62+(12-y)2=y2,解得:y=152,即AD=152,故S△CDE=S△AED=24AD×AE=754.【点睛】本题考查了解直角三角形的应用,涉及了勾股定理、折叠的性质、三角形面积、一次函数的性质等知识,综合性较强,正确添加辅助线、熟练应用相关知识是解题的关键.11.在Rt△ABC中,∠ACB=90°,CD是AB边的中线,DE⊥BC于E,连结CD,点P在射线CB上(与B,C不重合)(1)如果∠A=30°,①如图1,∠DCB等于多少度;②如图2,点P在线段CB上,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,补全图2猜想CP、BF之间的数量关系,并证明你的结论;(2)如图3,若点P在线段CB 的延长线上,且∠A=α(0°<α<90°),连结DP,将线段DP绕点逆时针旋转2α得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系(不需证明)【答案】(1)①∠DCB=60°.②结论:CP=BF.理由见解析;(2)结论:BF﹣BP=2DE•tanα.理由见解析.【解析】【分析】(1)①根据直角三角形斜边中线的性质,结合∠A=30°,只要证明△CDB是等边三角形即可;②根据全等三角形的判定推出△DCP≌△DBF,根据全等的性质得出CP=BF,(2)求出DC=DB=AD,DE∥AC,求出∠FDB=∠CDP=2α+∠PDB,DP=DF,根据全等三角形的判定得出△DCP≌△DBF,求出CP=BF,推出BF﹣BP=BC,解直角三角形求出CE=DEtanα即可.【详解】(1)①∵∠A=30°,∠ACB=90°,∴∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠DCB=60°.②如图1,结论:CP=BF.理由如下:∵∠ACB=90°,D是AB的中点,DE⊥BC,∠DCB=60°,∴△CDB为等边三角形.∴∠CDB=60°∵线段DP绕点D逆时针旋转60°得到线段DF,∵∠PDF=60°,DP=DF,∴∠FDB =∠CDP ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF.(2)结论:BF ﹣BP =2DEtanα.理由:∵∠ACB =90°,D 是AB 的中点,DE ⊥BC ,∠A =α,∴DC =DB =AD ,DE ∥AC ,∴∠A =∠ACD =α,∠EDB =∠A =α,BC =2CE ,∴∠BDC =∠A+∠ACD =2α,∵∠PDF =2α,∴∠FDB =∠CDP =2α+∠PDB ,∵线段DP 绕点D 逆时针旋转2α得到线段DF ,∴DP =DF ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF ,而 CP =BC+BP ,∴BF ﹣BP =BC ,在Rt △CDE 中,∠DEC =90°,∴tan ∠CDE =CE DE, ∴CE =DEtanα, ∴BC =2CE =2DEtanα,即BF ﹣BP =2DEtanα.【点睛】本题考查了三角形外角性质,等边三角形的判定和性质,全等三角形的性质和判定,直角三角形的性质,旋转的性质的应用,能推出△DCP ≌△DBF 是解此题的关键,综合性比较强,证明过程类似.12.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).【答案】拦截点D处到公路的距离是(500+500)米.【解析】试题分析:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=BC=×1000=500米;解Rt△CDF,求出CF=CD=500米,则DA=BE+CF=(500+500)米.试题解析:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.在Rt△BCE中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE=BC=×1000=500米;在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF=CD=500米,∴DA=BE+CF=(500+500)米,故拦截点D处到公路的距离是(500+500)米.考点:解直角三角形的应用-方向角问题.13.如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P 处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)(测倾器的高度忽略不计,参考数据:tan53°≈43,tan63.4°≈2)【答案】(1)此人所在P的铅直高度约为14.3米;(2)从P到点B的路程约为127.1米【解析】分析:(1)过P作PF⊥BD于F,作PE⊥AB于E,设PF=5x,在Rt△ABC中求出AB,用含x 的式子表示出AE,EP,由tan∠APE,求得x即可;(2)在Rt△CPF中,求出CP的长.详解:过P作PF⊥BD于F,作PE⊥AB于E,∵斜坡的坡度i=5:12,设PF=5x,CF=12x,∵四边形BFPE为矩形,∴BF=PEPF=BE.在RT△ABC中,BC=90,tan∠ACB=AB BC,∴AB=tan63.4°×BC≈2×90=180,∴AE=AB-BE=AB-PF=180-5x,EP=BC+CF≈90+120x.在RT△AEP中,tan∠APE=1805490123 AE xEP x-≈=+,∴x=207,∴PF=5x=10014.37≈.答:此人所在P的铅直高度约为14.3米.由(1)得CP=13x,∴CP=13×207≈37.1,BC+CP=90+37.1=127.1.答:从P到点B的路程约为127.1米.点睛:本题考查了解直角三角形的应用,关键是正确的画出与实际问题相符合的几何图形,找出图形中的相关线段或角的实际意义及所要解决的问题,构造直角三角形,用勾股定理或三角函数求相应的线段长.14.如图,半圆O的直径AB=20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD 相交于点E(点E与点C、D不重合),设OM=m.(1)求DE的长(用含m的代数式表示);(2)令弦CD所对的圆心角为α,且sin4 =25α.①若△DEM的面积为S,求S关于m的函数关系式,并求出m的取值范围;②若动点N在CD上,且CN=OM,射线BM与射线ON相交于点F,当∠OMF=90°时,求DE的长.【答案】(1)DE=10010mm-;(2)①S=2360300m mm-+,(5013<m<10),②DE=5 2 .【解析】【分析】(1)由CD∥AB知△DEM∽△OBM,可得DE DMOB OM=,据此可得;(2)①连接OC 、作OP ⊥CD 、MQ ⊥CD ,由OC =OD 、OP ⊥CD 知∠DOP =12∠COD ,据此可得sin ∠DOP =sin ∠DMQ =45、sin ∠ODP =35,继而由OM =m 、OD =10得QM =DM sin ∠ODP =35(10﹣m ),根据三角形的面积公式即可得;如图2,先求得PD =8、CD =16,证△CDM ∽△BOM 得CD DM BO OM =,求得OM =5013,据此可得m 的取值范围; ②如图3,由BM =OB sin ∠BOM =10×35=6,可得OM =8,根据(1)所求结果可得答案. 【详解】(1)∵CD ∥AB , ∴△DEM ∽△OBM ,∴DE DM OB OM =,即1010DE m m-=, ∴DE =10010m m -; (2)①如图1,连接OC 、作OP ⊥CD 于点P ,作MQ ⊥CD 于点Q ,∵OC =OD 、OP ⊥CD ,∴∠DOP =12∠COD , ∵sin 2α=45, ∴sin ∠DOP =sin ∠DMQ =45,sin ∠ODP =35, ∵OM =m 、OD =10,∴DM =10﹣m ,∴QM =DM sin ∠ODP =35(10﹣m ), 则S △DEM =12DE •MQ =12×10010m m -×35(10﹣m )=2360300m m m-+, 如图2,∵PD =OD sin ∠DOP =10×45=8, ∴CD =16,∵CD ∥AB ,∴△CDM ∽△BOM ,∴CD DM BO OM =,即1610=10OM OM-, 解得:OM =5013, ∴5013<m <10, ∴S =2360300m m m-+,(5013<m <10). ②当∠OMF =90°时,如图3,则∠BMO =90°,在Rt △BOM 中,BM =OB sin ∠BOM =10×35=6, 则OM =8,由(1)得DE =100108582-⨯=. 【点睛】本题主要考查圆的综合题,解题的关键是熟练掌握圆的有关性质、相似三角形的判定与性质及解直角三角形的能力.15.小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.已知:如图,在四边形 ABCD 中, AB ∥CD , ∠ACB =90°, AB=10cm , BC=8cm , OD 垂直平分 A C .点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s ;同时,点 Q 从点 D 出发,沿 DC 方向匀速运动,速度为 1cm/s ;当一个点停止运动,另一个点也停止运动.过点 P 作 PE ⊥AB ,交 BC 于点 E ,过点 Q 作 QF ∥AC ,分别交 AD , OD 于点 F , G .连接 OP ,EG .设运动时间为 t ( s )(0<t <5) ,解答下列问题: (1)当 t 为何值时,点 E 在BAC 的平分线上?(2)设四边形 PEGO 的面积为 S(cm 2) ,求 S 与 t 的函数关系式;(3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;(4)连接 OE , OQ ,在运动过程中,是否存在某一时刻 t ,使 OE ⊥OQ ?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)4s t =;(2)PEGO S 四边形2315688t t =-++ ,(05)t <<;(3)52t =时,PEGO S 四边形取得最大值;(4)165t =时,OE OQ ⊥. 【解析】 【分析】(1)当点E 在∠BAC 的平分线上时,因为EP ⊥AB ,EC ⊥AC ,可得PE=EC ,由此构建方程即可解决问题.(2)根据S 四边形OPEG =S △OEG +S △OPE =S △OEG +(S △OPC +S △PCE -S △OEC )构建函数关系式即可. (3)利用二次函数的性质解决问题即可.(4)证明∠EOC=∠QOG ,可得tan ∠EOC=tan ∠QOG ,推出EC GQOC OG=,由此构建方程即可解决问题. 【详解】(1)在Rt △ABC 中,∵∠ACB=90°,AB=10cm ,BC=8cm , ∴22108-=6(cm ), ∵OD 垂直平分线段AC , ∴OC=OA=3(cm ),∠DOC=90°, ∵CD ∥AB ,∴∠BAC=∠DCO , ∵∠DOC=∠ACB , ∴△DOC ∽△BCA , ∴AC AB BCOC CD OD ==, ∴61083CD OD==, ∴CD=5(cm ),OD=4(cm ), ∵PB=t ,PE ⊥AB , 易知:PE=34t ,BE=54t ,当点E 在∠BAC 的平分线上时, ∵EP ⊥AB ,EC ⊥AC , ∴PE=EC ,∴34t=8-54t ,∴t=4.∴当t 为4秒时,点E 在∠BAC 的平分线上. (2)如图,连接OE ,PC .S 四边形OPEG =S △OEG +S △OPE =S △OEG +(S △OPC +S △PCE -S △OEC ) =1414153154338838252524524t t t t t ⎡⎛⎫⎛⎫⎛⎫⎛⎫⨯-⨯+⨯⨯-+⨯-⨯-⨯⨯- ⎪ ⎪ ⎪ ⎪⎢⎝⎭⎝⎭⎝⎭⎝⎭⎣ =281516(05)33t t t -++<<. (3)存在.∵28568(05)323S t t ⎛⎫=--+<< ⎪⎝⎭,∴t=52时,四边形OPEG 的面积最大,最大值为683.(4)存在.如图,连接OQ . ∵OE ⊥OQ ,∴∠EOC+∠QOC=90°,∵∠QOC+∠QOG=90°,∴∠EOC=∠QOG,∴tan∠EOC=tan∠QOG,∴EC GQOC OG=,∴358544345ttt -=-,整理得:5t2-66t+160=0,解得165t=或10(舍弃)∴当165t=秒时,OE⊥OQ.【点睛】本题属于四边形综合题,考查了解直角三角形,相似三角形的判定和性质,锐角三角函数,多边形的面积等知识,解题的关键是学会利用参数构建方程解决问题.2.如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=4,直角边CD在y轴上,且点C与点A重合.Rt △CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME 的度数.(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.【答案】(1)∠BME=15°;(2BC=4;(3)h≤2时,S=﹣h2+4h+8,当h≥2时,S=18﹣3h.【解析】试题分析:(1)如图2,由对顶角的定义知,∠BME=∠CMA,要求∠BME的度数,需先求出∠CMA的度数.根据三角形外角的定理进行解答即可;(2)如图3,由已知可知∠OBC=∠DEC=30°,又OB=6,通过解直角△BOC就可求出BC的长度;(3)需要分类讨论:①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,S=S△EDC﹣S△EFM;②当h≥2时,如图3,S=S△OBC.试题解析:解:(1)如图2,∵在平面直角坐标系中,点A(0,﹣6),点B(6,0).∴OA=OB,∴∠OAB=45°,∵∠CDE=90°,CD=4,DE=4,∴∠OCE=60°,∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°,∴∠BME=∠CMA=15°;如图3,∵∠CDE=90°,CD=4,DE=4,∴∠OBC=∠DEC=30°,∵OB=6,∴BC=4;(3)①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,∵CD=4,DE=4,AC=h,AN=NM,∴CN=4﹣FM,AN=MN=4+h﹣FM,∵△CMN∽△CED,∴,∴,解得FM=4﹣,∴S=S△EDC﹣S△EFM=×4×4﹣(44﹣h)×(4﹣)=﹣h2+4h+8,②如图3,当h≥2时,S=S△OBC=OC×OB=(6﹣h)×6=18﹣3h.考点:1、三角形的外角定理;2、相似;3、解直角三角形3.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.4.(2013年四川攀枝花12分)如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB=22.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.(1)点A的坐标为,直线l的解析式为;(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围;(3)试求(2)中当t为何值时,S的值最大,并求出S的最大值;(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.【答案】解:(1)(﹣4,0);y=x+4.(2)在点P、Q运动的过程中:①当0<t≤1时,如图1,过点C作CF⊥x轴于点F,则CF=4,BF=3,由勾股定理得BC=5.过点Q作QE⊥x轴于点E,则BE=BQ•cos∠CBF=5t•35=3t.∴PE=PB﹣BE=(14﹣2t)﹣3t=14﹣5t,S=12PM•PE=12×2t×(14﹣5t)=﹣5t2+14t.②当1<t≤2时,如图2,过点C、Q分别作x轴的垂线,垂足分别为F,E,则CQ=5t﹣5,PE=AF﹣AP﹣EF=11﹣2t﹣(5t﹣5)=16﹣7t.S=1 2PM•PE=12×2t×(16﹣7t)=﹣7t2+16t.③当点M与点Q相遇时,DM+CQ=CD=7,即(2t﹣4)+(5t﹣5)=7,解得t=167.当2<t<167时,如图3,MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t,S=12PM•MQ=12×4×(16﹣7t)=﹣14t+32.综上所述,点Q与点M相遇前S与t的函数关系式为()()225t14t0<t1S{7t16t1<t21614t322<t<7-+≤=-+≤⎛⎫-+ ⎪⎝⎭.(3)①当0<t≤1时,22749S5t14t5t55⎛⎫=-+=--+⎪⎝⎭,∵a=﹣5<0,抛物线开口向下,对称轴为直线t=75,∴当0<t≤1时,S随t的增大而增大.∴当t=1时,S有最大值,最大值为9.②当1<t≤2时,22864S7t16t7t77⎛⎫=-+=--+⎪⎝⎭,∵a=﹣7<0,抛物线开口向下,对称轴为直线t=87,∴当t=87时,S有最大值,最大值为647.③当2<t<167时,S=﹣14t+32∵k=﹣14<0,∴S随t的增大而减小.又∵当t=2时,S=4;当t=167时,S=0,∴0<S<4.综上所述,当t=87时,S有最大值,最大值为647.(4)t=209或t=125时,△QMN为等腰三角形.【解析】(1)利用梯形性质确定点D的坐标,由sin∠DAB=22,利用特殊三角函数值,得到△AOD为等腰直角三角形,从而得到点A的坐标;由点A、点D的坐标,利用待定系数法求出直线l的解析式:∵C(7,4),AB∥CD,∴D(0,4).∵sin∠DAB=2,∴∠DAB=45°.∴OA=OD=4.∴A(﹣4,0).设直线l的解析式为:y=kx+b,则有4k b0{b4-+==,解得:k1{b4==.∴y=x+4.∴点A坐标为(﹣4,0),直线l的解析式为:y=x+4.(2)弄清动点的运动过程分别求解:①当0<t≤1时,如图1;②当1<t≤2时,如图2;③当2<t<167时,如图3.(3)根据(2)中求出的S表达式与取值范围,逐一讨论计算,最终确定S的最大值.(4)△QMN为等腰三角形的情形有两种,需要分类讨论:①如图4,点M在线段CD上,MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t,MN=DM=2t﹣4,由MN=MQ,得16﹣7t=2t﹣4,解得t=209.②如图5,当点M运动到C点,同时当Q刚好运动至终点D,此时△QMN为等腰三角形,t=125.∴当t=209或t=125时,△QMN为等腰三角形.考点:一次函数综合题,双动点问题,梯形的性质,锐角三角函数定义,特殊角的三角函数值,由实际问题列函数关系式,一次函数和二次函数的性质,等腰三角形的性质,分类思想的应用.5.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.【答案】故大坝的截面的周长是(345)米,面积是1470平方米.【解析】试题分析:先根据两个坡比求出AE和BF的长,然后利用勾股定理求出AD和BC,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC,梯形的面积公式可得出答案.试题解析:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,∴AE=18米,在RT△ADE中,22DE AE+34∵背水坡坡比为1:2,∴BF=60米,在RT△BCF中,22CF BF+5∴周长345(345)米,面积=(10+18+10+60)×30÷2=1470(平方米).故大坝的截面的周长是(634+305+98)米,面积是1470平方米.6.如图(1),已知正方形ABCD 在直线MN 的上方BC 在直线MN 上,E 是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)连接GD ,求证:△ADG ≌△ABE ;(2)连接FC ,观察并直接写出∠FCN 的度数(不要写出解答过程)(3)如图(2),将图中正方形ABCD 改为矩形ABCD ,AB =6,BC =8,E 是线段BC 上一动点(不含端点B 、C ),以AE 为边在直线MN 的上方作矩形AEFG ,使顶点G 恰好落在射线CD 上.判断当点E 由B 向C 运动时,∠FCN 的大小是否总保持不变,若∠FCN 的大小不变,请求出tan ∠FCN 的值.若∠FCN 的大小发生改变,请举例说明.【答案】(1)见解析;(2)∠FCN =45°,理由见解析;(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =43.理由见解析. 【解析】【分析】(1)根据三角形判定方法进行证明即可.(2)作FH ⊥MN 于H .先证△ABE ≌△EHF ,得到对应边相等,从而推出△CHF 是等腰直角三角形,∠FCH 的度数就可以求得了.(3)解法同(2),结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE ,得出EH=AD=BC=8,由三角函数定义即可得出结论.【详解】(1)证明:∵四边形ABCD 和四边形AEFG 是正方形,∴AB =AD ,AE =AG =EF ,∠BAD =∠EAG =∠ADC =90°,∴∠BAE +∠EAD =∠DAG +∠EAD ,∠ADG =90°=∠ABE ,∴∠BAE =∠DAG ,在△ADG 和△ABE 中, ADG ABE DAG BAE AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADG ≌△ABE (AAS ).(2)解:∠FCN =45°,理由如下:作FH ⊥MN 于H ,如图1所示:则∠EHF =90°=∠ABE ,∵∠AEF =∠ABE =90°,∴∠BAE +∠AEB =90°,∠FEH +∠AEB =90°,∴∠FEH =∠BAE ,在△EFH 和△ABE 中,EHF ABE FEH BAE AE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EFH ≌△ABE (AAS ),∴FH =BE ,EH =AB =BC ,∴CH =BE =FH ,∵∠FHC =90°,∴∠FCN =45°.(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,理由如下:作FH ⊥MN 于H ,如图2所示:由已知可得∠EAG =∠BAD =∠AEF =90°,结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE ,∴EH =AD =BC =8,∴CH =BE , ∴EH FH FH AB BE CH==; 在Rt △FEH 中,tan ∠FCN =8463FH EH CH AB ===, ∴当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =43. 【点睛】本题是四边形综合题目,考查了正方形,矩形的判定及全等三角形的判定方法等知识点的综合运用,其重点是通过证三角形全等或相似来得出线段的相等或成比例.7.如图,正方形OABC 的顶点O 与原点重合,点A ,C 分别在x 轴与y 轴的正半轴上,点A 的坐标为(4,0),点D 在边AB 上,且tan ∠AOD =12,点E 是射线OB 上一动点,EF ⊥x 轴于点F ,交射线OD 于点G ,过点G 作GH ∥x 轴交AE 于点H .(1)求B ,D 两点的坐标;(2)当点E 在线段OB 上运动时,求∠HDA 的大小; (3)以点G 为圆心,GH 的长为半径画⊙G .是否存在点E 使⊙G 与正方形OABC 的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E 的坐标.【答案】(1)B (4,4),D (4,2);(2)45°;(3)存在,符合条件的点为(8﹣2,8﹣2)或(2,2)或42164216++⎝⎭或16421642,77⎛-- ⎝⎭,理由见解析 【解析】【分析】(1)由正方形性质知AB=OA=4,∠OAB=90°,据此得B (4,4),再由tan ∠AOD= 12得AD=12OA=2,据此可得点D 坐标; (2)由1tan 2GF GOF OF ∠==知GF=12OF ,再由∠AOB=∠ABO=45°知OF=EF ,即GF=12EF ,根据GH ∥x 轴知H 为AE 的中点,结合D 为AB 的中点知DH 是△ABE 的中位线,即HD ∥BE ,据此可得答案;(3)分⊙G 与对角线OB 和对角线AC 相切两种情况,设PG=x ,结合题意建立关于x 的方程求解可得.【详解】解:(1)∵A (4,0),∴OA=4,∵四边形OABC为正方形,∴AB=OA=4,∠OAB=90°,∴B(4,4),在Rt△OAD中,∠OAD=90°,∵tan∠AOD=12,∴AD=12OA=12×4=2,∴D(4,2);(2)如图1,在Rt△OFG中,∠OFG=90°∴tan∠GOF=GFOF =12,即GF=12OF,∵四边形OABC为正方形,∴∠AOB=∠ABO=45°,∴OF=EF,∴GF=12EF,∴G为EF的中点,∵GH∥x轴交AE于H,∴H为AE的中点,∵B(4,4),D(4,2),∴D为AB的中点,∴DH是△ABE的中位线,∴HD∥BE,∴∠HDA=∠ABO=45°.(3)①若⊙G与对角线OB相切,如图2,当点E在线段OB上时,过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG=2x,OF=EF=22x,∵OA=4,∴AF=4﹣22x,∵G为EF的中点,H为AE的中点,∴GH为△AFE的中位线,∴GH=12AF=12×(4﹣22x)=2﹣2x,则x=2﹣2x,解得:x=22﹣2,∴E(8﹣42,8﹣42),如图3,当点E在线段OB的延长线上时,x2x﹣2,解得:x=2∴E(2,2②若⊙G与对角线AC相切,如图4,当点E在线段BM上时,对角线AC,OB相交于点M,过点G 作GP ⊥OB 于点P ,设PG =x ,可得PE =x ,EG =FG =2x , OF =EF =22x ,∵OA =4, ∴AF =4﹣22x ,∵G 为EF 的中点,H 为AE 的中点,∴GH 为△AFE 的中位线,∴GH =12AF =12×(4﹣22x )=2﹣2x , 过点G 作GQ ⊥AC 于点Q ,则GQ =PM =3x ﹣22,∴3x ﹣22=2﹣2x ,∴4227x +=, ∴42164216,E ⎛⎫++ ⎪ ⎪⎝⎭; 如图5,当点E 在线段OM 上时,GQ =PM =23x ,则23x =22,解得4227x =,∴16421642,77E ⎛⎫-- ⎪ ⎪⎝⎭; 如图6,当点E 在线段OB 的延长线上时,3x ﹣22=2x ﹣2,解得:4227x -=(舍去); 综上所述,符合条件的点为(8﹣42,8﹣42)或(8+42,8+42)或42164216,77⎛⎫++ ⎪ ⎪⎝⎭或16421642,77⎛⎫-- ⎪ ⎪⎝⎭. 【点睛】本题是圆的综合问题,解题的关键是掌握正方形和直角三角形的性质、正切函数的定义、三角形中位线定理及分类讨论思想的运用.8.现有一个“Z “型的工件(工件厚度忽略不计),如图所示,其中AB 为20cm ,BC 为60cm ,∠ABC =90,∠BCD =60°,求该工件如图摆放时的高度(即A 到CD 的距离).(结果精确到0.1m ,参考数据:≈1.73)【答案】工件如图摆放时的高度约为61.9cm .【解析】【分析】过点A 作AP ⊥CD 于点P ,交BC 于点Q ,由∠CQP =∠AQB 、∠CPQ =∠B =90°知∠A =∠C =60°,在△ABQ 中求得分别求得AQ 、BQ 的长,结合BC 知CQ 的长,在△CPQ 中可得PQ ,根据AP =AQ +PQ 得出答案.【详解】解:如图,过点A作AP⊥CD于点P,交BC于点Q,∵∠CQP=∠AQB,∠CPQ=∠B=90°,∴∠A=∠C=60°,在△ABQ中,∵AQ=(cm),BQ=AB tan A=20tan60°=20(cm),∴CQ=BC﹣BQ=60﹣20(cm),在△CPQ中,∵PQ=CQ sin C=(60﹣20)sin60°=30(﹣1)cm,∴AP=AQ+PQ=40+30(﹣1)≈61.9(cm),答:工件如图摆放时的高度约为61.9cm.【点睛】本题主要考查解直角三角形的应用,熟练掌握三角函数的定义求得相关线段的长度是解题的关键.9.如图,△ABC中,AC=BC=10,cosC=35,点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点D作DE⊥CB于点E.(1)当⊙P与边BC相切时,求⊙P的半径.(2)连接BP交DE于点F,设AP的长为x,PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围.(3)在(2)的条件下,当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时,求相交所得的公共弦的长.【答案】(1)409R=;(2)25880320xy x xx=-++;(3)50105-.【解析】【分析】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,即可求解;(2)首先证明PD∥BE,则EB BFPD PF=,即:2024588x yxxxy-+--=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=EP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,解得:R=409;(2)在△ABC中,AC=BC=10,cosC=35,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH =ACsinC =8,同理可得:CH =6,HA =4,AB =45,则:tan ∠CAB =2, BP =228+(4)x -=2880x x -+, DA =25x ,则BD =45﹣25x , 如下图所示,PA =PD ,∴∠PAD =∠CAB =∠CBA =β,tanβ=2,则cosβ5,sin β5, EB =BDcosβ=(525x )5=4﹣25x , ∴PD ∥BE , ∴EB BF PD PF =,即:2024588x y x xx -+--=, 整理得:y 25x x 8x 803x 20-++ (3)以EP 为直径作圆Q 如下图所示,两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,GD为相交所得的公共弦,∵点Q是弧GD的中点,∴DG⊥EP,∵AG是圆P的直径,∴∠GDA=90°,∴EP∥BD,由(2)知,PD∥BC,∴四边形PDBE为平行四边形,∴AG=EP=BD,∴AB=DB+AD=AG+AD=5设圆的半径为r,在△ADG中,AD=2rcosβ5DG5AG=2r,5=52r51,则:DG550﹣5相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.10.如图,A(0,2),B(6,2),C(0,c)(c>0),以A为圆心AB长为半径的BD 交y轴正半轴于点D,BD与BC有交点时,交点为E,P为BD上一点.(1)若c=3,①BC=,DE的长为;②当CP=2时,判断CP与⊙A的位置关系,井加以证明;(2)若c=10,求点P与BC距离的最大值;(3)分别直接写出当c=1,c=6,c=9,c=11时,点P与BC的最大距离(结果无需化简)【答案】(1)①12,π;②详见解析;(2)①65;②65(3)答案见详解 【解析】【分析】 (1)①先求出AB ,AC ,进而求出BC 和∠ABC ,最后用弧长公式即可得出结论;②判断出△APC 是直角三角形,即可得出结论;(2)分两种情况,利用三角形的面积或锐角三角函数即可得出结论;(3)画图图形,同(2)的方法即可得出结论.【详解】 (1)①如图1,∵c =3+2,∴OC =3,∴AC =3﹣2=3∵AB =6,在Rt △BAC 中,根据勾股定理得,BC =12,tan ∠ABC =AC AB 3 ∴∠ABC =60°,∵AE =AB ,∴△ABE 是等边三角形,∴∠BAE =60°,∴∠DAE =30°,∴DE 的长为306180π⨯=π,故答案为12,π;②CP 与⊙A 相切.证明:∵AP =AB =6,AC =OC ﹣OA =63, ∴AP 2+CP 2=108,又AC 2=(63)2=108,∴AP 2+PC 2=AC 2.∴∠APC =90°,即:CP ⊥AP .而AP 是半径,∴CP 与⊙A 相切.(2)若c =10,即AC =10﹣2=8,则BC =10.①若点P 在BE 上,AP ⊥BE 时,点P 与BC 的距离最大,设垂足为F ,则PF 的长就是最大距离,如图2,S △ABC =12AB ×AC =12BC ×AF , ∴AF =AB AC BC ⋅=245, ∴PF =AP ﹣AF =65; ②如图3,若点P 在DE 上,作PG ⊥BC 于点G ,当点P 与点D 重合时,PG 最大.此时,sin ∠ACB =PG AB CP BC =, 即PG =AB CP BC ⋅=65∴若c =10,点P 与BC 距离的最大值是65; (3)当c =1时,如图4,过点P作PM⊥BC,sin∠BCP=AB PM BC CD=∴PM=67423737AB CDBC⋅⨯===423737;当c=6时,如图5,同c=10的①情况,PF=6﹣1213=1213613-,当c=9时,如图6,同c=10的①情况,PF=4285685 -,当c=11时,如图7,点P和点D重合时,点P到BC的距离最大,同c=10时②情况,DG 18117.【点睛】此题是圆的综合题,主要考查了弧长公式,勾股定理和逆定理,三角形的面积公式,锐角三角函数,熟练掌握锐角三角函数是解本题的关键.。
