60种折纸方法
第18章数学活动:折纸做60°、30°、15°的角

第十八章数学活动:折纸做60°,30°,15°的角教材分析:本课之前,学生已通过折角平分线、折平行线、折纸研究轴对称等活动获得了较为丰富的折纸经验,为本节课奠定了基础。
本节课是在此基础上折出特殊度数的角。
折纸不仅是培养学生动手能力的一种游戏,折纸中还蕴含着许多数学知识,它还是开发学生智力的一种有效手段。
本节活动课的目的是让学生在动手操作中学会运用数学知识,发展学生的想象力、创造力。
学情分析:学生已学习了平移、旋转、轴对称等基本图形变换,角平分线、平行与垂直、三角形的全等、四边形等知识,教材选取学生熟知的、生活化的折纸游戏作为研究和学习的内容,让学生倍感亲切,能激发学生积极参与数学活动的兴趣。
教学目标:知识与技能:通过折叠,加深对轴对称、全等图形性质的认识;探索并能折出60°,30°,15°的角;初步体会研究几何问题的方法.过程与方法:学生经历折出60°,30°,15°角的折纸过程,培养学生观察、思考、抽象、动手的能力,领悟数学活动是个充满着探索与创造的过程.情感态度与价值观:通过折纸活动,让学生体会生活与数学是紧密联系的,感受数学中的美;在探索过程中养成学生与他人合作交流的习惯,获得成功的体验,提高克服困难的勇气和信心.教学重点:通过探究折60°,30°,15°的角,培养学生的动手能力和推理能力.教学难点:折出60°,30°,15°角的方法的探究和证明.教学准备:教师:课件;矩形纸片学生:矩形纸片;折纸教学方法:合作探究教学过程:1.创设情境,引入新课:导语:同学们,你们玩过折纸吗?都会折什么?在折纸的过程中,蕴含着许多数学知识,例如图形的全等、轴对称。
这节课,我们一起折60°,30°,15°的角.师生活动:学生欣赏折纸,教师引导.折纸是一门艺术形式,动物、花、船和人等都是折纸的创作题材,在折的过程中要用到很多的数学知识,比如:轴对称、全等、特殊的角度等等,这就需要我们通过数学知识来解决这些问题,今天我们就一起学习如何通过折纸,折出特殊的角度.设计意图:通过观察生活中的实例,点出课题,激起学生的学习兴趣.2.提出问题,深度思考:问题1:在一张矩形纸片上,你怎么折出一个正方形?师生活动:学生在小组内动手折,教师指导,及时调整.追问:正方形的对角线与每一边的夹角是多少度?师生活动:学生观察所折图形,思考教师提出的问题,口述理论依据.设计意图:从学生最熟悉的正方形为知识生长点,折出本节课第一个特殊角.问题2:用一张矩形纸片你还能折出哪些度数的角?师生活动:通过折叠,师生共同归纳对折可以平分一个角,可以把一个角平均分成2n份,还可以利用角的和差得出相关度数的角.设计意图:从简单的折纸游戏出发,提高学生课堂参与度,经过学生的互相补充得出22.5°,67.5°,112.5°等度数的角,由此引导学生发现上面的结论.此过程也让学生感受折纸可以得到角的和差倍分关系.问题3:动手试试,你能否折出30°的角呢?怎样折?师生活动:学生动手尝试,最终会把矩形纸片的90°角折叠的接近三等分.设计意图:这个问题的提出是为了增强学生对新旧知识的联系,突出所学知识的整体性、联系性,是螺旋上升的关系.3.动手操作,实验探究:追问:你能精确的折出30°的角吗?师生活动:学生动手尝试.设计意图:问题层层深入,学生在折叠过程中出现困难,为以下问题做铺垫.问题4:我们学过哪些和30°角有关的知识?师生活动:教师引导学生思考:如果折一个直角三角形,使斜边是直角边的2倍,问题就可以解决,怎样得到满足条件的三角形呢?为突破重难点,教师做以下铺垫:(1)矩形对折,寻找边长的二倍关系(2)FAB FEM NQ PBE=2ME学生探究如何折出满足条件的线段.(小组交流,展示图片)设计意图:让学生体会轴对称变换的性质,为学生更加容易的去构造存在30°角的直角三角形打基础,分散难点.视学生情况,第二种折法也可由教师折叠后与学生分享。
五瓣花球折纸手工制作方法

五瓣花球折纸手工制作方法(三) 五瓣花球折法一:
五瓣花球折纸成品图欣赏
这款花球需要60张正方形纸
元件的折法如下:
如图12,一个元件完成了。
粘贴方法:
组合方法:
蓝线位置为粘贴位置
将12个五瓣花粘在一起
如果想挂起来,先将6个五瓣花粘在一起,然后在其背面粘一根彩绳将剩余的六个五瓣花也粘好,一个花球完成了。
五瓣花球折法二:
五瓣花球折纸成品图欣赏
这款(需要60张正方形纸)是在五瓣花球--传统折法的两种变化基础上变化的,两种元件折好后(未粘贴),继续下面的步骤:
组合方法同五瓣花球--传统折法。
折纸玫瑰花束的制作方法
发布时间:2011-04-26 来源:未知
关键词:折纸玫瑰花制作方法
教过大家很多折玫瑰的做法了,今天这款色卡纸折玫瑰花非常简单,而且效果绝不亚于复杂玫瑰的折纸教程,下面就请看纸折玫瑰花图解吧。
手工纸制作小篮子:实用的纸篮子的折法
发布时间:2011-04-26 来源:
关键词:手工纸制篮子篮子折法折纸
折纸花篮和纸篮子折法难度不高又非常实用,用折纸篮子来盛放小东西非常方便、环保,在郊外游玩的时候,看到漂亮的小花小草,就可以马上折一个折纸花篮出来用了,如果用有花纹的纸来折的话,会更加的漂亮!
手工纸制作小篮子折纸的效果
纸做的篮子详细图解
用彩纸条做的挂饰装点你的创意生活
发布时间:2011-04-26 来源:
关键词:手工挂饰折纸
一组用彩纸条做的挂饰的教学方法图解,非常实用哦!
用纸制作的挂饰图解
第二款折纸挂饰、彩纸挂饰
用彩色纸条制作家居挂饰图解。
报纸的100种玩法

报纸的100种玩法报纸是我们日常生活中常见的媒体之一,除了用来获取新闻信息和读取文章,其实还有许多有趣的玩法可以尝试。
以下是一百种有趣的报纸玩法,希望能给你带来乐趣和灵感:1. 折纸艺术:利用报纸折叠各种花样的 Origami。
2. 剪纸:利用报纸剪出各种创意的图案和造型。
3. DIY封面:将报纸封面用彩色颜料重新设计一番,让它焕然一新。
4. 纸板人:利用报纸固定和塑造纸板成人物形象,可以玩成人偶剧场。
5. 风筝:利用报纸制作风筝,感受风的力量。
6. 纸帽子:用报纸制作自己的帽子,可以展示个性。
7. 纸浆手工:将废报纸浸泡在水中,搅拌后制成纸浆,可以用来制作各种手工制品。
8. 摄影背景:将报纸作为摄影背景,增添独特的纹理效果。
9. 装饰灯笼:将报纸卷起来,制作成漂亮的灯笼。
10. 隔热垫:将报纸剪成适合大小的隔热垫,可以放在桌面或餐桌上使用。
11. 书籍封面:用报纸制作书籍封面,让书籍更加特别。
12. 模型制作:利用报纸制作各种模型,如飞机、汽车等。
13. 墙面装饰:用报纸剪成不同形状贴在墙上,增添居家装饰元素。
14. 宠物玩具:用报纸卷成球状,给宠物作为玩具。
15. 纸板画布:利用报纸的质地,用颜料在上面作画。
16. 手工节日礼物:用报纸制作创意手工礼物送给朋友和家人。
17. 纸偶剧场:利用报纸制作剧场和纸偶,上演自己的小剧场。
18. DIY面具:用报纸创作各种形状的面具,举办化妆舞会。
19. 纸质相框:用报纸制作相框,框住珍贵的回忆照片。
20. 纸艺手链:用报纸制作时尚的纸艺手链。
21. 报纸炭画:用炭笔在报纸上绘制画作,营造独特的艺术效果。
22. 废纸编织:将报纸切成细条,编织成各种饰品,如篮子、手提包等。
23. 写作练习:用报纸上的文章作为写作素材,进行写作练习。
24. 寻宝游戏:利用报纸做藏宝图,玩寻宝游戏。
25. 玩剪纸人:将报纸剪成人形,玩弹跳游戏。
26. 纸质折扇:利用报纸折叠成漂亮的折扇,可以用来降温。
八年级初二数学 图形的对称-翻折变换(折叠问题) 含答案
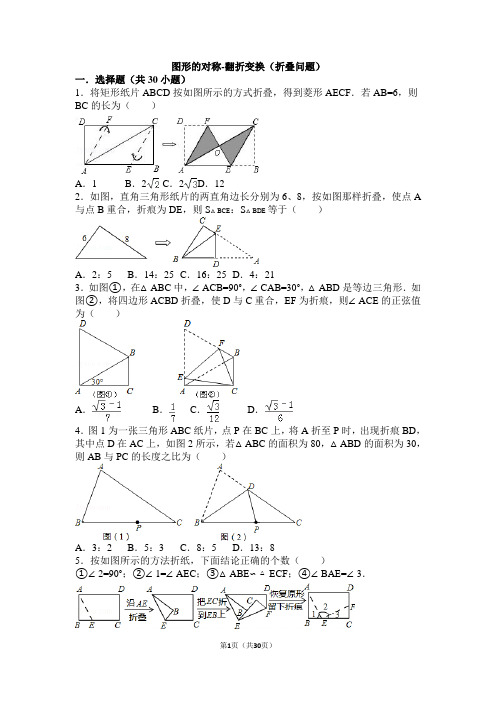
图形的对称-翻折变换(折叠问题)一.选择题(共30小题)1.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为()A.1 B.2 C.2D.122.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B重合,折痕为DE,则S△BCE:S△BDE等于()A.2:5 B.14:25 C.16:25 D.4:213.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.4.图1为一张三角形ABC纸片,点P在BC上,将A折至P时,出现折痕BD,其中点D在AC上,如图2所示,若△ABC的面积为80,△ABD的面积为30,则AB与PC的长度之比为()A.3:2 B.5:3 C.8:5 D.13:85.按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1个B.2个C.3个D.4个6.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于()A.70°B.65°C.80°D.35°7.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长()A.3 B.4 C.3.5 D.68.如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B 落在点E处,AE交CD于点F.连接DE,则DF的长是()A.B.C.D.9.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM 即为所求,对于两人的作法,下列判断正确的是()A.小平的作法正确,张萌的作法不正确B.两人的作法都不正确C.张萌的作法正确,小平的作法不正确D.两人的作法都正确10.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.2411.如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE 沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为()A.B.C.D.12.如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD 沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为()A.cm B.cm C.2cm D.cm13.如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB 沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为()A.y=﹣B.y=﹣x+C.y=﹣D.y=﹣2x+14.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为()A.y=x+5 B.y=x+5 C.y=x+5 D.y=x+515.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为()A.3 B.4 C.5 D.616.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是()A.AF=B.四边形ACDE是矩形C.图中与△ABC全等的三角形有4个D.图中有4个等腰三角形17.如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为()A.16 B.17 C.18 D.1918.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是()A.B.C.D.19.如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为()A.5 B.4 C.3 D.220.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)21.如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC 边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是()A.24cm B.26cm C.28cm D.30cm22.如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=,则AD的长为()A.3 B.4 C.5 D.623.如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为()A.B.2C.2D.24.如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm25.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.1226.如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6 B.8 C.10 D.1227.如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.B.C.1 D.28.如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为()A.1 B.2 C.3 D.1.529.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=.其中所有正确结论的个数是()A.4 B.3 C.2 D.130.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为()A.B.C.2 D.1图形的对称-翻折变换(折叠问题)参考答案与试题解析一.选择题(共30小题)1.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为()A.1 B.2C.2D.12【考点】翻折变换(折叠问题);勾股定理的应用;菱形的性质;矩形的性质.【分析】根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求解.【解答】解:∵菱形AECF,AB=6,∴假设BE=x,∴AE=6﹣x,∴CE=6﹣x,∵四边形AECF是菱形,∴∠FCO=∠ECO,∵∠ECO=∠ECB,∴∠ECO=∠ECB=∠FCO=30°,2BE=CE,∴CE=2x,∴2x=6﹣x,解得:x=2,∴CE=4,利用勾股定理得出:BC2+BE2=EC2,BC===2,故选:C.【点评】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.2.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B重合,折痕为DE,则S△BCE:S△BDE等于()A.2:5 B.14:25 C.16:25 D.4:21【考点】翻折变换(折叠问题).【分析】在Rt△BEC中利用勾股定理计算出AB=10,根据折叠的性质得到AD=BD=5,EA=EB,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中根据勾股定理计算出x=,则EC=8﹣=,利用三角形面积公式计算出S△BCE=BC•CE=×6×=,在Rt△BED中利用勾股定理计算出ED==,利用三角形面积公式计算出S△BDE=BD•DE=×5×=,然后求出两面积的比.【解答】解:在Rt△BAC中,BC=6,AC=8,∴AB==10,∵把△ABC沿DE使A与B重合,∴AD=BD,EA=EB,∴BD=AB=5,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中,∵BE2=EC2+BC2,即x2=(8﹣x)2+62,∴x=,∴EC=8﹣x=8﹣=,∴S△BCE=BC•CE=×6×=,在Rt△BED中,∵BE2=ED2+BD2,∴ED==,∴S△BDE=BD•DE=×5×=,∴S△BCE:S△BDE=:=14:25.故选B.【点评】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了勾股定理.3.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.【考点】翻折变换(折叠问题).【分析】在Rt△ABC中,设AB=2a,已知∠ACB=90°,∠CAB=30°,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可求∠ACE 的正弦值.【解答】解:∵△ABC中,∠ACB=90°,∠BAC=30°,设AB=2a,∴AC=a,BC=a;∵△ABD是等边三角形,∴AD=AB=2a;设DE=EC=x,则AE=2a﹣x;在Rt△AEC中,由勾股定理,得:(2a﹣x)2+3a2=x2,解得x=;∴AE=,EC=,∴sin∠ACE==.故选:B.【点评】本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.4.图1为一张三角形ABC纸片,点P在BC上,将A折至P时,出现折痕BD,其中点D在AC上,如图2所示,若△ABC的面积为80,△ABD的面积为30,则AB与PC的长度之比为()A.3:2 B.5:3 C.8:5 D.13:8【考点】翻折变换(折叠问题).【分析】如图,作辅助线;首先求出△BDP的面积,进而求出△DPC的面积;借助三角形的面积公式求出的值;由旋转变换的性质得到AB=PB,即可解决问题.【解答】解:如图,过点D作DE⊥BC于点E;由题意得:S△ABD=S△PBD=30,∴S△DPC=80﹣30﹣30=20,∴=,由题意得:AB=BP,∴AB:PC=3:2,故选A.【点评】该题主要考查了翻折变换的性质及其应用问题;解题的方法是作高线,表示出三角形的面积;解题的关键是灵活运用翻折变换的性质来分析、判断、推理或解答.5.按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1个B.2个C.3个D.4个【考点】翻折变换(折叠问题);相似三角形的判定与性质.【分析】根据翻折变换的性质、相似三角形的判定定理解答即可.【解答】解:由翻折变换的性质可知,∠AEB+∠FEC=×180°=90°,则∠AEF=90°,即∠2=90°,①正确;由图形可知,∠1<∠AEC,②错误;∵∠2=90°,∴∠1+∠3=90°,又∠1+∠BAE=90°,∴∠BAE=∠3,④正确;∵∠BAE=∠3,∠B=∠C=90°,∴△ABE∽△ECF,③正确.故选:C.【点评】本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.6.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于()A.70°B.65°C.80°D.35°【考点】翻折变换(折叠问题).【分析】根据平角的知识可求出∠DED′的度数,再由折叠的性质可得出∠D′EF=∠DEF=∠DED′,从而根据平行线的性质可得出∠EFB的度数.【解答】解:∵∠AED′=40°,∴∠DED′=180°﹣40°=140°,又由折叠的性质可得,∠D′EF=∠DEF=∠DED′,∴∠DEF=70°,又∵AD∥BC,∴∠EFB=70°.故选:A.【点评】此题考查了翻折变换的知识,解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=∠DED′,难度一般.7.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长()A.3 B.4 C.3.5 D.6【考点】翻折变换(折叠问题).【分析】由矩形的性质得到∠1=∠CFE=60°,由折叠可得∠2=60°,从而求得∠4的度数,得到AE=EC,在Rt△CDE中利用勾股定理可求得EC的长度,即可得到答案.【解答】解:∵矩形ABCD,∴BC∥AD,∴∠1=∠CFE=60°,∵EF为折痕,∴∠2=∠1=60°,AE=EC,∴∠3=180°﹣60°﹣60°=60°,Rt△CDE中,∠4=90°﹣60°=30°,∴EC=2×DE=2×1=2,∴BC=AE+ED=EC+ED=2+1=3.故选:A.【点评】本题考查了翻折问题;由折叠得到角相等,得到AE=EC利用勾股定理求解是正确解答本题的关键.8.如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B 落在点E处,AE交CD于点F.连接DE,则DF的长是()A.B.C.D.【考点】翻折变换(折叠问题).【分析】由四边形ABCD是矩形与△AEC由△ABC翻折得到,AD=CE,∠ADF=∠CEF,由AAS证得△ADF≌△CEF,的长FA=FC,设DF=x,则FA=4﹣x,由勾股定理得:DA2+DF2=AF2,即可求出DF的长.【解答】解:∵四边形ABCD是矩形,∴AD=BC,AB=DC=4,∠ADF=90°,∵△AEC由△ABC翻折得到,∴BC=EC,∠CEF=∠ABC=90°,∴AD=CE,∠ADF=∠CEF,在△ADF与△CEF中,,∴△ADF≌△CEF(AAS),∴FA=FC,设DF=x,则FA=FC=DC﹣DF=4﹣x,在Rt△DFA中,由勾股定理得:DA2+DF2=AF2,即32+x2=(4﹣x)2,解得:x=,即DF的长是.故选C.【点评】本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握折叠的性质,得到相等的线段与角是解决问题的关键.9.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM 即为所求,对于两人的作法,下列判断正确的是()A.小平的作法正确,张萌的作法不正确B.两人的作法都不正确C.张萌的作法正确,小平的作法不正确D.两人的作法都正确【考点】翻折变换(折叠问题).【分析】在图1中,由BM=2BF推出∠BMF=30°,所以∠MBF=60°,再根据等边三角形的判定方法即可证明.在图2中,证明方法类似.【解答】解:图1中,∵四边形ABCD是正方形,∴AB=AD=BC∵AE=ED=BF=FC,AB=BM,∴BM=2BF,∵∠MFB=90°,∴∠BMF=30°,∴∠MBF=90°﹣∠BMF=60°,∵MB=MC,∴△MBC是等边三角形,∴张萌的作法正确.在图2中,∵BM=BC=2BF,∠MFB=90°,∴∠BMF=30°,∴∠MBF=90°﹣∠BMF=60°,∵MB=MC∴△MBC是等边三角形,∴小平的作法正确.故选D.【点评】本题考查正方形的性质、翻折不变性、直角三角形的性质,解题的关键是在一个直角三角形中如果斜边是直角边的两倍那么这条直角边所对的锐角是30度.10.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.24【考点】翻折变换(折叠问题).【分析】先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC ﹣BF=4,易得△CEF的周长.【解答】解:∵四边形ABCD为矩形,∴AD=BC=10,AB=CD=8,∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,∴AF=AD=10,EF=DE,在Rt△ABF中,∵BF==6,∴CF=BC﹣BF=10﹣6=4,∴△CEF的周长为:CE+EF+CF=CE+DE+CF=CD+CF=8+4=12.故选A.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理,利用勾股定理得CF的长是解答此题的关键.11.如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE 沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为()A.B.C.D.【考点】翻折变换(折叠问题).【分析】设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF中根据勾股定理列出关于x的方程,即可解决问题.【解答】解:设CE=x.∵四边形ABCD是矩形,∴AD=BC=5,CD=AB=3,∠A=∠D=90°.∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,∴BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中,由勾股定理得:AF2=52﹣32=16,∴AF=4,DF=5﹣4=1.在Rt△DEF中,由勾股定理得:EF2=DE2+DF2,即x2=(3﹣x)2+12,解得:x=.故选B.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理、矩形的性质、方程思想等知识,关键是熟练掌握勾股定理,找准对应边.12.如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD 沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为()A.cm B.cm C.2cm D.cm【考点】翻折变换(折叠问题).【分析】首先由勾股定理求出BC,由折叠的性质可得∠BED=∠C=90°,BE=BC=3cm,得出AE=AB﹣BE=2cm,设DC=xcm,则DE=xcm,AD=(4﹣x)cm,由勾股定理得出方程,解方程即可.【解答】解:∵∠C=90°,AB=5cm,AC=4cm,∴BC==3cm,∵将△BCD沿着直线BD翻折,使点C落在斜边AB上的点E处,∴△BED≌△BCD,∴∠BED=∠C=90°,BE=BC=3cm,∴AE=AB﹣BE=2cm,设DC=xcm,则DE=xcm,AD=(4﹣x)cm,由勾股定理得:AE2+DE2=AD2,即22+x2=(4﹣x)2,解得:x=.故选:B.【点评】本题主要考查翻折变换的性质,全等三角形的性质,勾股定理;熟练掌握翻折变换的性质,由勾股定理得出方程是解决问题的关键.13.如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB 沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为()A.y=﹣B.y=﹣x+C.y=﹣D.y=﹣2x+【考点】翻折变换(折叠问题);待定系数法求一次函数解析式.【分析】由点A(0,4)、B(3,0),可求得AB的长,然后由折叠的性质,求得OA′的长,且△A′OC∽△AOB,再由相似三角形的性质,求得OC的长,继而利用待定系数法求得直线BC的解析式.【解答】解:∵点A(0,4)、B(3,0),∴OA=4,OB=3,∴AB==5,由折叠的性质可得:A′B=AB=5,∠OA′C=∠OAB,∴OA′=A′B﹣OB=2,∵∠A′OC=∠AOB=90°,∴△A′OC∽△AOB,∴,即,解得:OC=,∴点C的坐标为:(0,),设直线BC的解析式为:y=kx+b,则,解得:,∴直线BC的解析式为:y=﹣x+.故选C.【点评】此题考查了折叠的性质、勾股定理、相似三角形的判定与性质以及待定系数法求一次函数的解析式.注意求得点C的坐标是解此题的关键.14.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为()A.y=x+5 B.y=x+5 C.y=x+5 D.y=x+5【考点】翻折变换(折叠问题);待定系数法求一次函数解析式.【分析】首先在RT△ABE中,求出EB,再在RT△CDE中利用勾股定理即可解决问题.【解答】解:∵△ADE是由△ADO翻折,∴DE=DO,AO=AE=10,∵四边形OABC是矩形,∴OC=AB=8,AO=BC=10,∠B=∠BCO=∠BAO=90°,在RT△ABE中,∵AE=10,AB=8,∴EB===6,∴EC=4,设DO=DE=x,在RT△DCE中,∵CD2+CE2=DE2,∴(8﹣a)2+42=a2,∴a=5,∴点D(0,5),点E(4,8),设直线DE为y=kx+b,∴解得,∴直线DE为:y=+5.故选A.【点评】本题考查翻折变换、待定系数法确定一次函数的解析式,解题的关键是巧妙利用勾股定理,用方程的思想去思考问题,属于中考常考题型.15.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为()A.3 B.4 C.5 D.6【考点】翻折变换(折叠问题).【分析】首先由DE∥BC与折叠的性质,可证得DE是△ABC的中位线,继而求得答案.【解答】解:∵DE∥BC,∴∠ADE=∠B,∠EDF=∠BFD,由折叠的性质可得:∠ADE=∠EDF,AD=DF,∴∠B=∠BFD,∴BD=DF,∴AD=BD,同理:AE=EC,∴DE=BC,即BC=2DE=4.故选B.【点评】此题考查了折叠的性质以及三角形中位线的性质.注意证得DE是△ABC的中位线是关键.16.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是()A.AF=B.四边形ACDE是矩形C.图中与△ABC全等的三角形有4个D.图中有4个等腰三角形【考点】翻折变换(折叠问题);平行四边形的性质.【分析】由四边形ABCD是平行四边形,得到AB=CD,AB∥CD,AD=BC,由折叠的性质得到AB=AE,BC=CE,等量代换得到AE=CD,AD=CE,推出四边形ACDE是平行四边形,于是得到AF=BC,四边形ACDE是矩形,故A,B 正确;根据平行四边形和矩形的性质得到△ACD≌△ACE≌△CDE≌△ADE≌△ABC,于是得到图中与△ABC全等的三角形有4个,故C正确;推出△BCE是等腰三角形,△AEF,△ACF,△CDF,△DEF是等腰三角形,于是得到图中有5个等腰三角形,故D错误.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,AD=BC,由折叠的性质得到AB=AE,BC=CE,∴AE=CD,AD=CE,∵点B、A、E在同一条直线上,∴AE∥CD,∴四边形ACDE是平行四边形,∴AF=BC,四边形ACDE是矩形,故A,B正确;∵四边形ABCD是平行四边形,四边形ACDE是矩形,∴△ACD≌△ACE≌△CDE≌△ADE≌△ABC,∴图中与△ABC全等的三角形有4个,故C正确;∵BC=CE,∴△BCE是等腰三角形,∵四边形ACDE是矩形,∴AF=EF=CF=DF,∴△AEF,△ACF,△CDF,△DEF是等腰三角形,∴图中有5个等腰三角形,故D错误;故选D.【点评】本题考查了平行四边形的性质、折叠的性质以及等腰三角形的判定和性质,解题的关键是熟记等腰三角形和矩形的判定方法.17.如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为()A.16 B.17 C.18 D.19【考点】翻折变换(折叠问题).【分析】根据勾股定理得到BC=8,由折叠的性质得到BD=CD=BC=4,DE⊥BC,根据三角形的中位线的性质得到DE=AB=3,AE=AC=5,于是得到结论.【解答】解:∵AB=6,AC=10,∠ABC=90°,∴BC=8,∵将该直角三角形纸片沿DE折叠,使点C与点B重合,∴BD=CD=BC=4,DE⊥BC,∵∠ABC=90°,∴DE∥AB,∴DE=AB=3,AE=AC=5,∴四边形ABDE的周长=AB+AE+DE+BD=6+5+3+4=18,故选C.【点评】此题考查了折叠的性质,勾股定理,三角形的中位线的性质,注意掌握折叠前后图形的对应关系.18.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是()A.B.C.D.【考点】翻折变换(折叠问题).【分析】根据对称的性质得到△BFE≌△DFE,得到DE=BE.根据已知条件得到∠DEB=90°,设AD=1,BC=4,过A作AG⊥BC于G,根据矩形的性质得到GE=AD=1,根据全等三角形的性质得到BG=EC=1.5,根据勾股定理得到AB=CD==5,通过△BDC∽△DEF,得到,求出BF=,于是得到结论.【解答】解:∵EF是点B、D的对称轴,∴△BFE≌△DFE,∴DE=BE.∵在△BDE中,DE=BE,∠DBE=45°,∴∠BDE=∠DBE=45°.∴∠DEB=90°,∴DE⊥BC.在等腰梯形ABCD中,∵,∴设AD=1,BC=4,过A作AG⊥BC于G,∴四边形AGED是矩形.∴GE=AD=1,∵Rt△ABG≌Rt△DCE,∴BG=EC=1.5,∴AG=DE=BE=2.5∴AB=CD==5,∵∠ABC=∠C=∠FDE,∵∠CDE+∠C=90°,∴∠FDE+∠CDE=90°∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,∴∠BDC=∠DFE,∵∠DEF=∠DBC=45°,∴△BDC∽△DEF,∴,∴DF=,∴BF=,∴AF=AB﹣BF=,∴=.故选B.【点评】此题考查等腰梯形的性质,翻折的性质,三角形全等的判定与性质,等腰直角三角形的性质,相似三角形的判定和性质等知识,注意结合图形,作出常用辅助线解决问题.19.如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为()A.5 B.4 C.3 D.2【考点】翻折变换(折叠问题).【分析】利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;利用勾股定理得出GE2=CG2+CE2,进而求出BG 即可;【解答】解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,在Rt△ABG和Rt△AFG中,,∴Rt△ABG≌Rt△AFG(HL),∴BG=GF,∵E是边CD的中点,∴DE=CE=6,设BG=x,则CG=12﹣x,GE=x+6,∵GE2=CG2+CE2∴(x+6)2=(12﹣x)2+62,解得x=4∴BG=4.故选B.【点评】此题主要考查了全等三角形的判定和性质,勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.20.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)【考点】翻折变换(折叠问题);坐标与图形性质.【分析】根据关于y轴对称的点的特点找到B',结合直角坐标系可得出点B′的坐标.【解答】解:∵将△ABC沿y轴翻折得到△A′B′C′,∴点B与点B′关于y轴对称,∴B′(2,3),故选B.【点评】本题考查了翻折变换﹣折叠问题,坐标与图形的关系,熟记关于y轴对称的点的特点是解答本题的关键.21.如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC 边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是()A.24cm B.26cm C.28cm D.30cm【考点】翻折变换(折叠问题).【分析】根据翻折变换的性质可得AE=EC,AD=CD,然后求出△ABD的周长=AB+BC,代入数据计算即可得解.【解答】解:∵△ABC的边AC对折顶点C和点A重合,∴AE=EC,AD=CD,∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,∵AE=6cm,∴AC=AE+EC=6+6=12,∵△ABC的周长为36cm,∴AB+BC=36﹣12=24cm,∴△ABD的周长是24cm.故选A.【点评】本题考查了翻折变换的性质,熟记翻折前后的两个图形能够完全重合得到相等的边是解题的关键.22.如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=,则AD的长为()A.3 B.4 C.5 D.6【考点】翻折变换(折叠问题).【分析】根据平行线的性质和翻转变换的性质得到FD=FE,FA=FC,根据勾股定理计算即可.【解答】解:∵DC∥AB,∴∠FCA=∠CAB,又∠FAC=∠CAB,∴∠FAC=∠FCA,∴FA=FC=,∴FD=FE,∵DC=AB=8,AF=,∴FD=FE=8﹣=,∴AD=BC=EC==6,故选:D.【点评】本题考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.23.如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为()A.B.2C.2D.【考点】翻折变换(折叠问题).【分析】根据直角三角形两锐角互余求出∠ABC=60°,翻折前后两个图形能够互相重合可得∠BDC=∠BDC′,∠CBD=∠ABD=30°,∠ADE=∠A′DE,然后求出∠BDE=90°,再解直角三角形求出BD,然后求出DE即可.【解答】解:∵△ABC是直角三角形,∠A=30°,∴∠ABC=90°﹣30°=60°,∵将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,∴∠BDC=∠BDC′,∠CBD=∠ABD=∠ABC=30°,∵沿DE折叠点A落在DC′的延长线上的点A′处,∴∠ADE=∠A′DE,∴∠BDE=∠ABD+∠A′DE=×180°=90°,在Rt△BCD中,BD=BC÷cos30°=5÷=cm,在Rt△BDE中,DE=BD•tan30°=×=cm.故选:D.【点评】本题考查了翻折变换的性质,解直角三角形,熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键.24.如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm【考点】翻折变换(折叠问题).【分析】首先根据题意得到:△AED≌△ACD;进而得到AE=AC=6,DE=CD;根据勾股定理求出AB=10;再次利用勾股定理列出关于线段CD的方程,问题即可解决.【解答】解:由勾股定理得:==10,由题意得:△AED≌△ACD,∴AE=AC=6,DE=CD(设为x);∠AED=∠C=90°,∴BE=10﹣6=4,BD=8﹣x;由勾股定理得:(8﹣x)2=42+x2,解得:x=3(cm),故选B.【点评】该命题主要考查了翻折变换及其应用问题;解题的关键是借助翻折变换的性质,灵活运用勾股定理、全等三角形的性质等几何知识来分析、判断、推理或解答.25.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】因为BC为AF边上的高,要求△AFC的面积,求得AF即可,求证△AFD′≌△CFB,得BF=D′F,设D′F=x,则在Rt△AFD′中,根据勾股定理求x,于是得到AF=AB﹣BF,即可得到结果.【解答】解:易证△AFD′≌△CFB,∴D′F=BF,设D′F=x,则AF=8﹣x,在Rt△AFD′中,(8﹣x)2=x2+42,解之得:x=3,∴AF=AB﹣FB=8﹣3=5,∴S△AFC=•AF•BC=10.故选C.【点评】本题考查了翻折变换﹣折叠问题,勾股定理的正确运用,本题中设D′F=x,根据直角三角形AFD′中运用勾股定理求x是解题的关键.26.如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】根据折叠的条件可得:BE=DE,在直角△ABE中,利用勾股定理就可以求解.【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=AE+DE=AE+BE=9.∴BE=9﹣AE,根据勾股定理可知AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选:A.【点评】本题考查了利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.27.如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.B.C.1 D.【考点】翻折变换(折叠问题).【分析】由有一块直角三角形纸片,∠C=90°,AC=2,BC=,利用勾股定理即可求得AB的长,然后由折叠的性质,求得AE的长,继而求得答案.【解答】解:∵∠C=90°,AC=2,BC=,∴AB==,由折叠的性质可得:AE=AB=,∴CE=AE﹣AC=.故选A.【点评】此题考查了折叠的性质以及勾股定理.注意掌握折叠前后图形的对应关系是解此题的关键.28.如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为()A.1 B.2 C.3 D.1.5【考点】翻折变换(折叠问题).【分析】利用平行四边形的对边相等得到AD=BC=4,DC=AB=6,再由折叠的性质得到DE=AD,由DC﹣DE求出EC的长即可.【解答】解:由折叠及平行四边形的性质得:AE=AD=BC=4,DC=AB=6,则EC=DC﹣DE=6﹣4=2,故选B.【点评】此题考查了翻折变换(折叠问题),以及平行四边形的性质,熟练掌握折叠的性质是解本题的关键.29.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:。
正方形纸的100种折法

正方形纸的100种折法折方形纸的折法有很多种,以下是其中的100种常见折法:1. 三折:将正方形纸对角线上的两个顶点对齐,然后将两侧的边向内折叠。
2. 四折:将正方形纸沿中心线对折,然后再次对折成四分之一大小。
3. 六折:将正方形纸按照对角线对折,然后再次对折成六分之一大小。
4. 八折:将正方形纸沿着中心线和对角线分别对折两次,最终得到八分之一大小。
5. 十折:将正方形纸按照对角线对折,然后再次对折成十分之一大小。
6. 十二折:将正方形纸沿中心线和对角线分别对折三次,最终得到十二分之一大小。
7. 十六折:将正方形纸沿着中心线和对角线分别对折四次,最终得到十六分之一大小。
8. 菱形折法:将正方形纸对角线上的两个顶点对折,然后将两侧的边向内折叠,形成一个菱形。
9. 风车折法:将正方形纸按照对角线对折,然后将四个角向内折叠,形成一个风车状的折纸。
10. 长方体折法:将正方形纸沿中心线对折,然后将两侧的边向内折叠,最终形成一个长方体模型。
11. 立方体折法:将正方形纸沿中心线和对角线分别对折两次,然后将两侧的边向内折叠,最终形成一个立方体模型。
12. 蝴蝶结折法:将正方形纸按照对角线对折,然后将四个角向内折叠,形成一个蝴蝶结状的折纸。
13. 纸飞机折法:将正方形纸对角线上的两个顶点对齐,然后将两侧的边向内折叠,形成一个纸飞机的形状。
14. 花朵折法:将正方形纸沿中心线对折,然后将四个角向内折叠,再次对折成八分之一大小,形成一个花朵的形状。
15. 箱子折法:将正方形纸沿着中心线和对角线分别对折两次,然后将两侧的边向内折叠,形成一个盒子的模型。
16. 裙子折法:将正方形纸按照对角线对折,然后将四个角向内折叠,再次对折成八分之一大小,形成一个裙子的形状。
17. 兔子折法:将正方形纸沿着中心线和对角线分别对折两次,然后将两侧的边向内折叠,形成一个兔子的模型。
18. 鱼折法:将正方形纸对角线上的两个顶点对齐,然后将两侧的边向内折叠,形成一个鱼的形状。
T字之谜(四巧板)505种问题图+答案

431
432
马步
六角
433
434
双头虫
435
帐篷
射灯 3
436
437
438
439
440
老头帽
上下相同
短柄刀
海轮
鹅
441
花瓣
442
443
444
445
双面斧
犀牛
曲柄铲
修鞋刀 2
446
447
448
449
450
马桶 2
钩子
钩刀
躺椅
三腿锅
9
451
452
二阶梯
支架
453
健身房
454
V管
455
天鹅 1
456
457
458
459
460
庭石
猫头鹰
飞去来器
钻石
元宝盆
461
462
463
464
木偶腿
变形弹簧 3
搭桥
465
包裹
折叠凳
466
467
468
469
470
花瓶
小鸟
楔子
井口 1
空心波浪
471
472
473
斗量
海锚 1
字母 Z
474
475
多米诺骨牌
徽章
476
477
478
字母 H
手风琴
海锚 2
479
480
两边向下会合
折纸
481
206
207
树干 1
镰刀
208
战舰
209
210
小燕子
修鞋锤
211
a4纸的一百种用法

a4纸的一百种用法A4纸是我们日常生活中不可缺少的物品,除了打印、复印、写作业外,还有很多别的用处。
这里列出了一百种A4纸的用途,其中你或许会发现一些新鲜的想法。
1. 手写信件或明信片,送给亲友;2. 制作生日贺卡、父母节礼物等;3. 制作家庭日历并放在客厅;4. 折纸艺,例如折千纸鹤;5. 贴在墙上,用作便签或提醒事项;6. 制作小巧的纸盒、纸袋等;7. 做成小礼品盒,装上心爱的小物件送给亲友;8. 制作折纸风车、喜鹊、蝴蝶等;9. 用于DIY手工艺品中;10. 制作摆放于桌面的信件架、手机支架等;11. 用于收集积攒的纸屑;12. 制作名片、订房卡等;13. 用来收纳杂物,如餐巾纸;14. 充当写字板,记录重要的事项和备忘录;15. 在笔记本上粘贴标签;16. 挂在门口用做“请勿打扰”的牌子;17. 制作可储存的笔袋,保存手写笔等文具;18. 制作小型书籍、书签等;19. 折成三角形,用于所有者的标识;20. 做成大小皆宜的纸笼、围栏等小型动物原型;21. 制作餐桌饰品、植物住所等;22. 制作家庭照片相册;23. 贴在家中窗户上,用作季节性装饰;24. 制作闹钟、计时器、计数器等;25. 制作“我爱你“纸牌或挂饰;26. 制作课本封面、桌面封面等;27. 制作年度计划书;28. 制作照片集合出版物,例如家庭纪念册;29. 用于信件封面或邮票的印刷;30. 制作手工智能游戏、填字游戏;31. 制作虎头燕尾、红烛、金鱼、花灯等;32. 制作人物和动物面具;33. 研究折纸技巧,吸纸和禅和Washi 折纸的雕塑技巧;34. 制作小型鬼脸和怪物脸;35. 做成清新小花坛用于家居装饰;36. 进行Uchiyama手工艺;37. 制作小型餐厅装饰、咖啡店装饰和吊饰;38. 制作书架、盘子、水杯等小型家具;39. 制作文具盒;40. 用于随身携带的文件夹内;41. 在桌上随意拣起做原稿用;42. 制作黑板用于宣传、教学、公告;43. 针对高精度需求的手工艺;44. 制作家庭和社交娱乐活动的券票等;45. 制作超现实主义作品;46. 拆开做成记分卡;47. 制作巨大的拼图;48. 进行猜猜谜、日语汉字等知识性游戏;49. 做成五彩纸风车,用于展示和装饰;50. 制作小幅绘画和手绘图案;51. 制作“只属于我的物品”的标签;52. 制作家庭防护、安全咨询指南;53. 制作可包含被个性化的小糖果、巧克力盒;54. 制作在特定场景和活动中使用的可分享图片;55. 期末考之前制作替身木乃伊;56. 做成造型各异、充满趣味的纸假面具;57. 制作明信片游戏,选择一张结合排列在一起制造有趣寓意的画面;58. 在桌面上铺成饼干被子;59. 制作年历、日历卡等;60. 制作带有福利影响的“路标”;61. 在日常生活中发挥装饰和教育作用,制作日常环保提示、菜谱、单词等;62. 制作个性化的垃圾桶的标签;63. 制作节日派对装饰、卡片和装饰品;64. 制作银行UI设计;65. 制作长桌的边角植物网格;66. 制作充满创意的家居装饰品;67. 制作并放在桌子上的调料罐标签;68. 制作地图和建筑图样来帮助指导和学习;69. 制作家庭遥控器盒装订文件;70. 制作友好的提醒框;71. 制作额外的小型日记本;72. 在桌面上散播小型纸鹤的设计;73. 制作能多次使用的活页夹;74. 制作个性化的沟通卡;75. 制作流程图和带批注的工作书;76. 制作超大号的黑板;77. 制作手工抽屉;78. 制作性别友好的日程管理表;79. 制作带有便签、标签和提示的工具手册;80. 当做任务卡和进度管理记录;81. 制作可重复使用的声音音色表;82. 制作宝藏地图;83. 制作户外游戏及教育游戏所需的物品;84. 制作任务常规、怀孕、瑜伽等指南;85. 在特定场合制作互动凭证,例如任职资格证书;86. 制作奖品决策播报统计表;87. 制作活动当场的视觉报告;88. 制作宣传品及手册;89. 制作提高能力的日程、播客、教程;90. 制作促销活动的传单、海报和活动表格等;91. 制作职业规划和提升能力方面的笔记;92. 制作家庭教育子女笔记;93. 制作个人故事书并励志分享;94. 制作活动和家庭白板;95. 制作可移动的场景布景;96. 制作雷达图和星形图;97. 制作无聊的调皮磁片;98. 做成心情日记簿,记录生活经验;99. 制作个人花边等;100. 可以随身携带的祈祷册。
手工纸灯笼教案6篇

手工纸灯笼教案6篇(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作计划、工作报告、军训心得、学习心得、培训心得、条据文书、读后感、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as work plans, work reports, military training experiences, learning experiences, training experiences, doctrinal documents, post reading feedback, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please stay tuned!手工纸灯笼教案6篇设计生动活泼的教案能够增加学生的学习动力,我们写的教案要考虑到学生的学习能力和背景,制定合适的教学计划,下面是本店铺为您分享的手工纸灯笼教案6篇,感谢您的参阅。
浙教版初中数学八年级上册 2.1 图形的轴对称-折纸问题探究课 教案

趣味翻折,折出精彩——折纸问题探究课一、背景分析本课是浙教版数学八年级上册第二章《特殊三角形》的一个拓展性课程.折纸,一个看似简单的操作,对八年级学生来说是一个不易征服的数学领域.按纸的形状可分为:折长方形、折正方形、折三角形、折圆等,按次数可分为:折一次、折两次或者折n次.爱因斯坦曾经说过:“兴趣是最好的老师”,兴趣是调动学生积极思维、探求知识的内在动力.有力兴趣,学习不是负担,而是一种享受.因此,本堂课的学习可以增添数学学习的乐趣,帮助大家更好地明白折纸问题的数学本质.二、学情分析根据学生平时的作业情况了解到,孩子们对折纸问题既陌生又害怕,有些时候折出图形也不一定能完成接下去的思考,折纸问题较抽象,具有一定的难度,学生不易理解.三、教学目标基础知识:通过“折鸭子”的过程,让学生理解折纸的本质是一种轴对称变换,轴对称变换产生的全等图形中有许多的角相等、边相等.基本技能:探究“折红勾”的过程,不同夹角90°、60°、70°所产生的变与不变.基本思想:运用转化思想将折纸问题转化成轴对称变换,运用类比的思想探究角度变化的问题,运动数形结合的思想解决抽象的图形,运用方程思想解决折纸中求线段长度的问题.基本活动经验:感受折纸的过程,能够将图形进行还原,能够将实物抽象成几何图形.四、重点难点重点:折纸的本质是轴对称变换.难点:活动四(4)中,将实物抽象成几何图形,并探究线段长度,重叠部分面积的过程,是本堂课的难点.五、教学用具教师:长方形红纸条4张、正方形纸片1张、磁石贴16个、三角尺.学生:长方形红纸条4张、正方形纸片1张.六、教学流程师:同学们,你们喜欢折纸吗?会折哪些东西呢?活动一:作品观赏纸除了能折这些小玩意外,还能折一些大家伙呢!比如说纸做的船,可以载人入水,同学们见过吗?活动二:视频欣赏如果你认为纸只能做这些东西的话,那就大错特错啦,接下来让我们一起来欣赏一个视频!看了这个视频后,相信同学们肯定手痒痒了,接下来陈老师带大家一起来折一个小作品,同学们一边折一边猜,我们折的是什么.活动三:动手实践第一步:将正方形纸片沿着它的斜对角线对折,然后打开.同学们仔细观察一下,这个正方形被中间这条折痕分成了两个什么图形?中间这条折痕可以看作是一条什么呢?对折的过程是在做一个什么变换呢?生:两个等腰直角三角形;对称轴;轴对称变换.师:接下来请同学们按照这个步骤继续往下折,这是一个什么作品呢?生:鸭子.(请同学将作品贴到黑板上展示)师:同学们,你们知道鸭子的嘴巴是多少度吗?请大家来猜猜看.生:15°、25°、12.5°、11.25°.师:同学们产生了这么多不同的意见,那大家都是怎么得到答案的呢?生:量角器.师:可见这个时候量角器已经帮不上忙了,那同学们想想,这个鸭子的嘴在刚刚的折纸过程中,可以体现在哪里呢?生:直角的对折,再对折,再对折.师:是的,其实折纸的问题就是轴对称变换,同学们能够得到图形的全等,从而得到相等的角、相等的边.活动四:重点探究师:同学们都喜欢老师在题目上打上“√”,对不同的老师来说,打“√”的角度是不一样的呢!接下来让我们拿起手上的红纸条,折出一个“√”.(1)若红勾所成的夹角是90°,则重叠部分是一个什么图形呢?请说明理由.生:等腰直角三角形.因为对顶角相等,所以∠BAC =90°、AB 、AC 是纸条的宽度,长方形纸条宽度处处相等,所以△ABC 是等腰直角三角形.(2)若红勾所成的夹角是60°,则重叠部分是一个什么图形呢?请说明理由.生1:等边三角形.因为对顶角相等,所以∠BAC=60°、AB 、AC 是纸条的宽度,长方形纸条宽度处处相等,所以△ABC 是等边三角形.生2:此时AB 、AC 也正好是长方形纸条的宽度吗?生1:好像不是.师:那同学们觉得,可以怎么来验证它是一个等边三角形呢?生:把图形进行还原.师:请同学们在导学案上画出还原之后的图形.你有什么发现?生:∵AE //DB∴∠DBA =60°∵翻折∴∠ABC =∠GBC =︒=︒-︒60260180 ∵∠BAC =60°(对顶角相等)∴△ABC 是等边三角形(有两个角是60°的三角形是等边三角形).师:除了用“有两个角是60°的三角形是等边三角形”外,还有哪些判定等边三角形的方法呢?生:一个角是60°的等腰三角形是等边三角形.师:虽然此时的AB 和AC 不是纸条的宽度,但是他们肯定是相等的,已知∠ABC =60°,你能通过证明AB =AC ,来证明△ABC 是等边三角形吗?请同学们以小组形式展开讨论.生:∵BC 平分∠ABG∴∠GBC =∠ABC∵AF //BG∴∠ACB =∠GBC∴∠ABC =∠ACB∴AB =AC∵∠BAC =60°∴△ABC 是等边三角形(一个角是60°的等腰三角形是等边三角形).师:本题中,我们可以看到:BC 是一条角平分线,BD //AC ,因此得到等腰三角形. 角平分线+平行线 等腰三角形.(3)接下来,让我们类比..着90°、60°的情况,来探究一下70°的时候,重叠部分会是一个什么图形?生:等腰三角形.(4)沿着EF 将长方形纸条进行折叠,使点D 与点B 重合,你能画出折叠后的图形吗?(5)若长方形纸条长为9cm ,宽为3cm ,你能求出AE 的长度吗?师:要求AE 的长度,我们需要怎么做?生:将图形进行还原.师:在这个翻折过程中,有哪些线段是不变的呢?生:BE =DE .师:这里有没有特殊的三角形呢?生:△ABE 是直角三角形,△BEF 是等腰三角形.解:设AE =x ,则BE =DE =9-x .运用勾股定理求得x =4cm .(6)你能求出重叠部分△BEF 的面积吗?请以小组形式展开探究.组1:过点E 作EG ⊥BF ,EG =AB =3cm ,.5.75321212cm BF EG S BEF =⨯⨯=⋅=∆ 组2:∵未重叠部分两个三角形面积相同,重叠部分两个三角形面积相同,∴64321=⨯⨯==∆∆CDF ABE S S ,().5.71293212cm S BEF =-⨯=∆ 七、课堂小结通过今天这一堂课的学习,同学们对折纸问题有了哪些新的认识呢?希望今天课上学习到的数学方法及数学思想能帮助你轻松克服折纸问题,让折纸问题不再害怕!八、板书设计画图区:九、课后习题 1.如图,把长方形纸片ABCD 沿EF ,GH 同时折叠,B ,C 两点恰好落在AD 边的点P 处,若︒=∠90FPH ,8=PF ,6=PH ,则长方形ABCD 的面积为___________.2.如图1是长方形纸带,将纸带沿EF 折叠成图2,再沿BF 折叠成图3,(1)若DEF ∠=20°,则图3中CFE ∠度数是多少?(2)若DEF ∠=α,把图3中CFE ∠用α表示。
手工玩具的100个制作方法

手工玩具的100个制作方法玩具是孩子们最爱的东西,而手工玩具则有着更为珍贵的意义,让他们在手工制作的过程中锻炼动手能力和创造力。
在这篇文章中,我将为大家分享100个手工玩具的制作方法,并帮助你们打造出具有特色的玩具。
1. 纸板飞机:利用纸板和剪刀制作,可以根据喜好进行各种花式飞行试验。
2. 纸袋家:将纸袋切成适当的大小,然后将其转化为可用的复杂套房和家具。
3. 纸杯造型:在纸杯上剪出不同的形状,制作出各种有趣的角色,比如动物、汽车、机器人等。
4. 遥控车道:使用彩色胶带设计车道并制作车辆,再用遥控器控制车辆上下左右的运动。
5. 素描书:将事物分解成有趣的素描形状,帮助孩子理解和发展一系列的认知和创造力。
6. 塑料泡沫动物:使用塑料泡沫将动物的轮廓割开,然后用颜料加工干净,制作出各种有趣的动物造型。
7. 塑料袋球:用塑料袋堆积成一个球,然后利用颜料和装饰制作出适合孩子们的玩具。
8. 纸板制作汽车:利用纸板制作出各种有趣的汽车模型,让孩子们可以在娱乐中学到制造的知识。
9. 木头玩具:由于木制玩具的强度和稳定性远高于塑料玩具,孩子们可以在安全的环境中玩耍。
10. 玩具箱:由各种颜色和材料制作的玩具箱能够让孩子们更好地组织自己的玩具和物品。
11. 石膏制作娃娃:将石膏和水混合起来,然后按照喜好的形状和大小制作出逐渐成型的娃娃。
12. DIY玩具车:用工具制作出真正的玩具车,可以是套装、人像、凌驾器、机器人等。
13. 编织小物件:如手链、钥匙链、毛线小裙子等,可以装饰你的生活空间。
14. 糖纸花和糖果:糖纸可以制作成比较真实的花朵,糖果也可以根据需要进行造型。
15. 纸制品:折纸、补漏、贴紙、剪贴,可以让孩子们在生动中学习道理和理解事物。
16. 自制DIY遥控车:在模块和电子元件的帮助下,制作出充满动力和创造力的遥控车。
17. 用布料或毛毡制作布艺玩具:一些有趣的小鼠、青蛙、马、熊等,都能让孩子们喜欢。
18. 玩具建筑材料:使用不同的材料创造各种建筑物和场景,并将它们组合在一起,制作一个具有趣味性的世界。
曲别针的1000种用法

曲别针的1000种用法全文共四篇示例,供读者参考第一篇示例:1. 将曲别针穿过绳子两端,制作简易的手链或项链。
2. 用曲别针将钥匙串在一起,不易丢失。
3. 在曲别针上穿上珠子或小饰品,制作个性化的耳环或胸针。
4. 利用曲别针的弯曲性,将其制作成各种形状的手工艺品。
5. 将曲别针划分成不同长度,做成简易的尺吉他弦。
6. 用曲别针卡住打火机的按钮,省去按压的步骤。
7. 利用曲别针的尖头挖土,种植小型植物。
8. 用曲别针穿起线,缝补破损的衣物。
9. 将曲别针弯曲成“S”形,挂起小挂件或装饰物。
10. 用曲别针代替拉链拉头,方便拉链使用。
11. 用曲别针勾住拉链,防止拉链滑落。
12. 将曲别针穿过衣架,挂起多层衬衣或外套。
13. 用曲别针将两张纸固定在一起,制作临时的笔记本。
14. 用曲别针将书页固定在一起,方便翻阅和整理。
15. 用曲别针挑坏质地的瓦片,处理瓦片边缘。
16. 将曲别针固定在木棍头部,制作简易的拨浪鼓。
17. 用曲别针夹住线端,方便在穿眼针时使用。
18. 用曲别针连接两个类似物品,制作简易的链条。
19. 用曲别针固定标签和纸牌,方便分类和整理。
20. 用曲别针挑断电线绝缘层,检测电线是否正常。
21. 用曲别针勾住信纸,不易飘落。
22. 用曲别针固定电话线,防止杂乱。
23. 将曲别针固定在指导线上,标识距离或位置。
24. 用曲别针固定卡片和照片,制作简易展示版。
25. 用曲别针串起颜色不同的羽毛,制作简易挂饰。
26. 利用曲别针长直的形状,作为直尺使用。
27. 用曲别针固定绳索的末端,不易散开。
28. 用曲别针固定门帘,减少风吹开的情况。
29. 用曲别针固定窗帘,防止窗帘飘动。
30. 将曲别针连成一串,制作简易的连接链。
31. 用曲别针固定书签,方便翻阅。
32. 将曲别针穿过香烟盒孔,起到固定作用。
33. 用曲别针挂住钥匙,不易遗失。
34. 将曲别针挂在墙上,挂吊饰或小物品。
35. 用曲别针固定帆布,不易松脱。
折纸幼儿园中班教案10篇word版

幼儿园是孩子接触学校启蒙教育的最早阶段,教育内容的趣味性非常重要,既要有趣又要能够传达一些道理,培养孩子的各项基础能力。
幼儿园阶段最常用的资料是幼儿园教案,一般包括活动目标、活动准备过程、提问互动环节、活动反思等内容,帮助幼儿园教师梳理安排好每次的课堂环节。
好的教案设计能让孩子们积极参与,掌握知识技能。
为大家整理了幼儿园一些优质的教案案例,方便大家使用学习。
《折纸中班教案10篇》这是优秀的中班主题教案文章,希望可以对您的学习工作中带来帮助!折纸中班教案第1篇活动目标:1、教幼儿学习折纸的技能(边、角对齐、压平)。
2、学习单张纸的简单折叠技能和简单的变化方法。
3、培养幼儿对这纸的.兴趣。
活动准备:折叠用纸若干、变形金刚一只。
活动过程:1、出示玩具变形金刚,作几次变化。
2、出示正方形的纸一张,教幼儿将这张纸变成一件有趣的玩具。
(1)将正方形的纸对折成长方形(2)将对折后的长方形想旁边对折成小正方形(方法同上)(3)将对折后的正方形拉开,在其两边向中间各对折一次,形成两扇门(4)将小门的上端啦出两个三角形(难点,重点演示)(5)将三角形的下端往上折一下,即成一架钢琴(在讲解、演示的同时出示折纸的图示,要求幼儿边听老师讲解、边看图示)(6)将上述过程编成一个顺口溜:一个正方形,变成长方形,在变成一个正方形。
关上两扇小门。
拉出两只三角形,鼻子往上翘一翘,变成一架小钢琴。
3、将钢琴变一变师:我是变形金刚,我会把钢琴变成另外一件玩具(教师将钢琴变成畚箕。
教幼儿将钢琴变成畚箕(教幼儿将钢琴的上部用手一捏,即成畚箕)4、将畚箕变一变教师说:我在来变一变。
变成一顶济公帽教幼儿将畚箕变成济公帽。
教师用顺口溜的形式进行:放下一个鼻子,把它翻个身子,关上两扇窗子,叠好两床被子,拉开来就是一顶帽子。
5、结束:幼儿带上济公帽,听听音乐、唱唱、走走、玩玩。
折纸中班教案第2篇教案是教师为顺利而有效地开展教学活动,根据教学大纲和教科书要求及学生的实际情况,以课时或课题为单位,对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书。
《数学活动——折纸做60°,30°,15°的角》

问题3:根据等腰三角形和矩形的对称性,你能利用矩形纸片ABCD折出以AB为底的等腰三角形吗?
师生活动:学生独立尝试通过动手操作,利用图形的轴对称性,折出等腰三角形。
【设计意图】直接折出等边三角形是ห้องสมุดไป่ตู้个难点,利用学生的最近发展区,让学生先动手尝试折叠等腰三角形,再折叠等边三角形,降低难度。
问题4:你能折出等边三角形吗?(以小组为单位进行讨论),并说明理由.
师生活动:学生以小组为单位进行讨论,教师针对每组的讨论引导学生观察、分析、思考,然后请学生代表上台展示说明操作过程,板书证明过程。
【设计意图】在折纸的过程中让学生体会轴对称变换的性质,为学生更容易构造腰和底相等的等边三角形打下基础,分散难点。
师生活动:学生推理论证三个角都相等并且都等于30°。
【设计意图】学生了解折纸可以得到角的倍分关系。
问题6:通过折纸,构造等边三角形,我们已经能够折出60°和30°的角,你还有其它的折法吗?
师生活动:不同学生进行展示,
【设计意图】学生经历动手操作、实验度量、大胆猜想、推理论证后最终解决问题,培养学生的动手操作能力、逻辑推理能力、空间观念,同时通过一个问题多种解决方法,培养学生的发散思维能力。
2.复习巩固知识链接
1.如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相,这个图形就叫做.
2.等腰三角形、等边三角形,矩形都是对称图形.
3.轴对称图形的对称轴是任何一对对应点所连线段的.
4.线段垂直平分线上的点与这条线段的两个端点的距离.
【设计意图】复习是一座架设在学生新、旧知识之间的桥梁,加强了对旧知识的巩固,也为接下来的内容做好铺垫。
折纸大师罗伯特朗(robert j. lang)折纸心得关于用纸 及罗伯特朗作品下载╭★肉丁

折纸大师罗伯特·朗(Robert J. Lang)折纸心得——关于用纸及罗伯特·朗作品下载╭★肉丁...折纸大师罗伯特·朗(Robert J. Lang)作品全集下载:[用eMule、迅雷等软件下载] [ng.-.折纸教程大全]ng.-.Origami.Constructions.pdf (1.75 MB) [ng.-.折纸教程大全]ng.-.Origami.Design.Secr.r.an.Ancient.Art.p df (113.66 MB)[ng.-.折纸教程大全]ng.-.Origami.Diagramming.Conventions.pdf (166.82 KB)[ng.-.折纸教程大全]ng.-.Origami.in.Action.pdf (11.79 MB) [ng.-.折纸教程大全]ng.-.Origami.Insects.and.Their.Kin.pdf (40.09 MB)[ng.-.折纸教程大全]ng.-.Origami.Insects.Vol.2.(NC).pdf (74.64 MB)[ng.-.折纸教程大全]ng.&.John.Montroll.-.mi.Sea.Life.(NC).pdf(25.33 MB)[ng.-.折纸教程大全]ng.-.Origami.Insects.(Vol.2).zip (73.46 MB)折纸大师罗伯特·朗(Robert J. Lang)折纸心得——关于用纸:纸我总是被问及用什么纸适合折纸。
这个问题取决于你折的模型,可以有很多方案。
我就来和大家谈一下最常用的折纸用纸和我个人的一些经验。
找纸孩童时代折纸最吸引我的事情之一就是它所需要的工具无处不在;我所要的只是我的双手和一张纸,而纸更是唾手可得!好多年间,我都使用父亲的旧商务用纸。
等同于现在的影印纸。
它们都需要被切成正方,然后你就可以开始折了!对于简单的折纸,影印纸非常好用。
深度解析以折纸为背景的中考题

深度解析以折纸为背景的中考题冯志贤(江苏省常熟市白茆中学ꎬ江苏常熟215532)摘㊀要:中考题经常考查以折纸为背景的试题ꎬ考查考生的动手能力和直观想象能力.文章从折叠方法解析和问题解答的角度来深度剖析几道经典的中考题.关键词:中考题ꎻ折纸ꎻ折叠ꎻ操作ꎻ解析中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)35-0086-03收稿日期:2023-09-15作者简介:冯志贤(1981.10-)ꎬ男ꎬ江苏省常熟人ꎬ本科ꎬ中学一级教师ꎬ从事初中数学教学研究.㊀㊀折纸是我国的传统文化ꎬ也是一门艺术.以折纸为背景的中考题ꎬ因其高度抽象而成为难点.笔者以几道经典的中考题为例ꎬ给出折叠方法解析㊁操作过程分析和试题解答.例1㊀已知矩形纸片ABCDꎬAB=2ꎬAD=1ꎬ将纸片折叠ꎬ使顶点A与边CD上的点E重合.(1)如果折痕FG分别与AD㊁AB交于点F㊁GꎬAF=23ꎬ求DE的长ꎻ(2)如果折痕FG分别与CD㊁AB交于点F㊁GꎬAED的外接圆与直线BC相切ꎬ求折痕FG的长ꎬ如图1[1].图1㊀例1题图折叠方法解析㊀本题的折纸操作方法可以用以下4个步骤描述:操作1㊀将AD与BC重合对折ꎬ折痕为MNꎬ如图2所示ꎻ图2㊀操作1图操作2㊀将AD与MN重合对折ꎬ折痕为RSꎬ如图3所示ꎻ图3㊀操作2图操作3㊀过S㊁M两点折叠ꎬ折痕为MSꎬ折叠以后BS与AD的交点为Fꎬ如图4所示ꎻ图4㊀操作3图操作4㊀过点F将点A折到CD上ꎬ折痕为FGꎬ点A的对应点为Eꎬ如图5所示.68图5㊀操作4图问题解答㊀(1)从操作1到操作3ꎬ可知点F为AD的三等分点.因为A关于折痕FG的对应点为Eꎬ所以AF=EFꎬEF=23ꎬDF=13ꎬ所以DE=33.(2)折叠的关键是要确定点E的位置ꎬ我们先假设已经折出来了ꎬ如图6所示ꎬ然后再计算CE的长度ꎬ从而确定点E的位置.图6㊀确定E的位置记AE与FG的交点为Pꎬ过点P作PQʅBC于Qꎬ由于BC与三角形ADE的外接圆相切ꎬ所以PQ=AP=EPꎬ且øAQE=90ʎꎬCQ=BQꎬ因此øCQE+øAQB=90ʎꎬ有øCQE=øQABꎬ所以әCEQʐәABQꎬCECQ=BQABꎬ由此可解得CE=18.因为线段的18是容易折叠的ꎬ所以问题(2)可以由下列操作来完成折叠过程.操作5㊀将长方形ABCD的边BC与MN重合对折ꎬ折痕为M1N1ꎬ再将BC与M1N1重合对折ꎬ折痕为M2N2ꎬ继续将BC与M2N2重合对折ꎬ即可得到CE=18ꎬ如图7所示.图7㊀操作5图操作6㊀将A㊁E两点重合对折ꎬ折痕为FGꎬ如图8所示.求折痕FG的长度.图8㊀操作6图在图8中ꎬ由操作6知GFʅAEꎬ所以øAGP+øGAP=90ʎꎬ而øGAP+øDAE=90ʎꎬ所以øAGP=øDAE.如图9所示ꎬ过点F折AB的垂线FHꎬ因为øAGP=øDAEꎬ则әFHG~әADEꎬ由HGFH=ADDEꎬ得HG=ADˑFHDE=AD2CD-CE=12-18=815ꎬ又由于FH2+HG2=FG2ꎬ所以FG=28915=1715.图9㊀计算FG的长例2㊀如图10ꎬ在梯形ABCD中ꎬADʊBCꎬAB=DC=3ꎬ沿对角线BD翻折梯形ABCDꎬ若点A恰好落在下底BC的中点E处ꎬ则梯形的周长为.图10㊀例2题图折叠方法解析㊀ 沿对角线BD翻折梯形AB ̄CD ꎬ实际上是过B㊁D两点折叠ꎻ 若点A恰好落在BC的中点E处 这必须是非常特殊的梯形才能办到.那么这是怎样的一个梯形呢?如图11所示ꎬ因为点A关于折痕BD的对应点为Eꎬ所以әABD≅әBDEꎬ即AB=BEꎬAD=DEꎬøADB=øEDB.因为ADʊBCꎬ有øADB=øDBEꎬ所以øDBE=øEDBꎬ即BE=DEꎬ因此四边形A ̄78BED是菱形.又因为E是BC的中点ꎬ而AB=CDꎬ所以әCDE是等边三角形.图11㊀折叠解析问题解答㊀由上述讨论可知ꎬ梯形ABCD是底角为60ʎ的等腰梯形ꎬ周长等于5倍腰的长度ꎬ即等于15.例3㊀矩形纸片ABCD的边长AB=4ꎬAD=2ꎬ将矩形纸片沿EF折叠ꎬ点A与点C重合ꎬ折叠后在其一面着色(如图12)ꎬ则着色部分的面积为(㊀㊀)[2].A.8㊀㊀㊀B.112㊀㊀㊀C.4㊀㊀㊀D.52折叠方法解析㊀ 将矩形纸片沿EF折叠ꎬ点A与点C重合 ꎬ实际上ꎬ将两点重合对折的折痕是唯一的ꎬ所以先给出折痕ꎬ然后再将两点重合对折这种描述方式不够严谨ꎬ本题的操作过程可以描述为:将矩形ABCD的两顶点A与C重合对折ꎬ折痕为EFꎬ点D的对应点为Gꎬ如图13所示.图12㊀折叠解析问题解答㊀求梯形CEFG的面积.因为点A关于折痕EF的对称点为Cꎬ点D关于折痕EF的对应点为Gꎬ所以四边形ADFE与四边形CEFG全等ꎬ所以AD=CGꎬ又因为折痕垂直平分两对应点的连线ꎬ即EF垂直平分ACꎬ有CF=CEꎬ所以梯形CEFG的上底FG加下底CE正好等于CDꎬ于是梯形CEFG的面积等于4.例4㊀如图14ꎬ矩形ABCD沿AE折叠ꎬ使点D落在边BC上的点F处ꎬ如果øBAF=60ʎꎬ那么øDAE=(㊀㊀)[3].A.15ʎ㊀㊀B.30ʎ㊀㊀C.45ʎ㊀㊀D.60ʎ图13㊀例3题图折叠方法解析㊀可以将 矩形ABCD沿AE折叠ꎬ使点D落在边BC上的点F处 描述:过点A将点D折到BC上ꎬ折痕为AEꎬD的对应点为Fꎬ如图14所示.图14㊀折叠解析问题解答㊀从条件øBAF=60ʎ可知ꎬ且øDAE=øFAEꎬ即øDAE=15ʎ.纵观以上的考题ꎬ我们发现很多的中考题都是以折纸为背景来考查的ꎬ这就要求一线教师在日常教学中要渗透折纸艺术㊁关注学生的动手操作能力.同时ꎬ也在教学中启示了一线教师:折纸可以进入中小学数学课堂ꎬ通过折纸操作活动ꎬ引导学生观察折痕所形成的边角关系ꎬ帮助学生建立折纸操作与数学内容的联系ꎬ培养其动手能力㊁观察能力㊁想象能力和创造性思维能力.还要注意科学性与操作性相结合㊁趣味性与严谨性相结合㊁启发性与示范性相结合的原则.参考文献:[1]陈厚嵩.中考图形折叠问题[J].中学教与学ꎬ2007(07):16-18.[2]黄燕苹ꎬ张辉蓉.中考折纸问题解析[J].数学教学ꎬ2009(11):42-45.[3]王彦秋.有关折纸的中考题几例[J].中学生数学ꎬ2011(12):45-47.[责任编辑:李㊀璟]88。
100种简单折纸方法

100种简单折纸方法100种简单折纸方法折纸是一种古老而有趣的手工艺术,可以通过简单的折叠就能创造出各种形状和动物。
以下是100个简单的折纸方法,让你快速入门并享受折纸的乐趣。
动物系列1. 简单的兔子2. 简单的狗3. 简单的猫头鹰4. 简单的鸟儿5. 简单的鱼6. 简单的蝴蝶7. 简单的青蛙8. 简单的小象9. 简单的熊10. 简单的猪食品系列11. 简单的盘子12. 简单的杯子13. 简单的甜甜圈14. 简单的冰淇淋16. 简单的披萨17. 简单的热狗18. 简单的香蕉19. 简单的草莓20. 简单的苹果花系列21. 简单的莲花22. 简单的玫瑰23. 简单的康乃馨24. 简单的太阳花25. 简单的樱花26. 简单的郁金香27. 简单的牵牛花28. 简单的菊花29. 简单的水仙30. 简单的玉兰花车辆系列31. 简单的飞机32. 简单的汽车33. 简单的火车34. 简单的轮船36. 简单的直升机37. 简单的潜艇38. 简单的自行车39. 简单的摩托车40. 简单的警车装饰系列41. 简单的圣诞树42. 简单的星星43. 简单的纸条44. 简单的雪花45. 简单的彩色气球46. 简单的纸鹞47. 简单的爱心48. 简单的礼物盒49. 简单的网球50. 简单的风车人物系列51. 简单的天使52. 简单的人物头像53. 简单的小丑54. 简单的跳跳虎55. 简单的人物剪影56. 简单的小孩子57. 简单的嘴巴眼睛58. 简单的小人儿童59. 简单的不倒翁60. 简单的玛丽娃娃生物系列61. 简单的恐龙62. 简单的人鱼63. 简单的鲸鱼64. 简单的海豚65. 简单的章鱼66. 简单的海星67. 简单的蜜蜂68. 简单的蜗牛69. 简单的蝉70. 简单的蝴蝶结建筑系列71. 简单的房子72. 简单的桥73. 简单的城堡74. 简单的教堂76. 简单的大楼77. 简单的电视塔78. 简单的威尼斯水城79. 简单的摩天大楼80. 简单的金字塔科技系列81. 简单的机器人82. 简单的太空船83. 简单的卫星84. 简单的火箭85. 简单的电视机86. 简单的电脑87. 简单的电话88. 简单的相机89. 简单的电扇90. 简单的键盘乐器系列91. 简单的吉他92. 简单的小提琴93. 简单的手风琴94. 简单的鼓96. 简单的口琴97. 简单的竖琴98. 简单的萨克斯99. 简单的长笛100. 简单的喇叭以上是100个简单的折纸方法,希望这些方法能够激发你的创造力,让你尽情享受折纸的乐趣。
气球的100种手工做法

气球的100种手工做法1.基础动物造型:如小狗、长颈鹿、小猫等,通过扭曲和连接不同颜色的气球,做出逼真的动物形象。
2.气球花朵:将多个小气球打结后串在一起,制作成五彩斑斓的气球花束或单个立体气球花。
3.气球动物帽饰:利用长条形气球制作成马头、兔耳朵等形状,固定在儿童帽子上,增添派对气氛。
4.气球人偶:用多个气球组合成完整的人形或卡通人物,包括四肢、头部和身体部分。
5.气球编织手链:将细长的小气球拧扭成环状,然后串联起来,制成彩色的手链或项链。
6.气球装饰挂件:填充氦气的气球可以制作成五彩缤纷的气球挂饰,用于派对、婚礼现场布置。
7.气球画笔:将颜料装入气球内,捏爆气球时即可在纸上形成独特的艺术效果。
8.气球火箭模型:模拟火箭外形,用气球作为主体部分,配合纸筒或其他材料制作尾翼和喷嘴。
9.气球鞭炮装饰:一连串小型气球并排串起,模拟鞭炮的样子,可用于新年或其他喜庆场合装饰。
10.气球魔术表演道具:魔术师可利用气球快速变换出各种形状,进行互动式表演。
11.气球立体字母/数字:根据字母或数字的轮廓,用不同颜色的气球塑造出来,适用于生日派对场景。
12.气球浮水玩具:在气球中加入适量水,扎紧口子,成为水上乐园中的简易浮水玩具。
13.气球编织篮子:使用特殊技术将多根气球编织成篮子形状,可用作盛放糖果或礼品。
14.气球动物手指套:制作微型气球动物,并将其套在手指上,形成有趣的亲子互动游戏道具。
15.气球编织家具模型:对于大型活动,可以用气球编织成椅子、桌子等家居模型作为艺术装置。
16.气球圣诞树:利用绿色气球制作成树叶形状,一层层堆叠出圣诞树的形态。
17.气球编织爱心:两个心形气球相互交叉缠绕,表达爱意,适合作为礼物赠送。
18.气球编织灯罩:透明气球内部放入LED灯泡,外层再包裹彩色气球,做成别致的夜灯装饰。
19.气球彩绘创作:在充气后的气球表面进行绘画创作,制作独一无二的艺术品。
20.气球拼图游戏:预先做好不同形状的气球,让孩子通过拼接来完成一个完整的图案。
100种折飞镖的方法

100种折飞镖的方法折飞镖是一项古老的手工艺活动,有很多不同的方法可以用来折飞镖。
以下是一百种折飞镖的方法:1. 传统三角形折法。
2. 简单直线折法。
3. 飞镖形状折法。
4. 对称折法。
5. 螺旋折法。
6. 菱形折法。
7. 立体立方体折法。
8. 蝴蝶折法。
9. 快速折法。
10. 长方形折法。
11. 花式折法。
12. 折纸飞镖折法。
13. 对角线折法。
14. 旋转折法。
15. 螺旋折法。
16. 对称镜像折法。
17. 立体折法。
18. 立体对称折法。
19. 立体螺旋折法。
20. 旋转对称折法。
21. 立体蝴蝶折法。
22. 复杂折法。
23. 多边形折法。
24. 立体多边形折法。
25. 多层次折法。
26. 对角线多层次折法。
27. 多层次螺旋折法。
28. 多层次对称折法。
29. 多层次蝴蝶折法。
30. 多层次立体折法。
32. 多层次立体螺旋折法。
33. 多层次旋转对称折法。
34. 多层次立体蝴蝶折法。
35. 多层次复杂折法。
36. 多层次多边形折法。
37. 多层次立体多边形折法。
38. 立体多层次折法。
39. 立体对角线多层次折法。
40. 立体多层次螺旋折法。
41. 立体多层次对称折法。
43. 立体多层次复杂折法。
44. 立体多层次多边形折法。
45. 立体多层次立体多边形折法。
46. 复杂多层次折法。
47. 复杂对角线多层次折法。
48. 复杂多层次螺旋折法。
49. 复杂多层次对称折法。
50. 复杂多层次蝴蝶折法。
51. 复杂多层次立体折法。
52. 复杂多层次立体对称折法。
53. 复杂多层次立体螺旋折法。
54. 复杂多层次旋转对称折法。
55. 复杂多层次立体蝴蝶折法。
56. 复杂多层次复杂折法。
57. 复杂多层次多边形折法。
58. 复杂多层次立体多边形折法。
59. 多重对角线折法。
60. 多重螺旋折法。
61. 多重对称折法。
62. 多重蝴蝶折法。
63. 多重立体折法。
65. 多重立体螺旋折法。
66. 多重旋转对称折法。
我拼的几种折法

我拼的几种折法
- 对边折:将正方形或长方形纸两边相对折叠,成为两个长方形。
- 对角折:用正方形纸,将两角相对折叠,而成为两个直角三角形。
- 集中一角折:在正方形纸的对角线上,将相邻的两边相对着折叠。
- 集中一边折:在正方形或长方形的中线上,将相邻的两边相对着折叠。
- 四角向心折:将正方形纸先折两条对角形,找出中心点,然后将四个角向中心点折。
- 双正方折:用正方形纸,先对边折,再根据中线一边向前,一边向后折,从中间撑开,压平。
- 双三角折:用正方形纸,先对角折,再根据分角线一边向前,一边向后折,从中间撑开,压平。
你可以根据自己的喜好和创意,选择适合的折法进行尝试。
在折纸的过程中,需要耐心和细心,慢慢地将纸张折叠成各种形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、无篷小船
3、风轮
4、气球
5、有篷小船
6、十字飞镖
7、东南西北
8、帆船
9、千纸鹤
10、尖头飞机
11、平头飞机
12、信封
13、爱心
14、五角星
15、各种花的折法 (1).
(2).Байду номын сангаас
(3).
16、船
17、带蓬的船
57.背着的猴子 58.抱着的猴子
59.河马
60.长颈鹿
30.狐狸
31.蜻蜓
32.蝎子
33.螳螂
34.野猪
35.鳄鱼
36.鹈鹕
37.蛇
38.瓢虫
39.蜥蜴
40.甲虫
41.蝗虫
42.蝉
43.蝴蝶
44.飞蝴蝶
45.天鹅
46.纸鹤
47.乌鸦
48.海鸥
49.燕子
50.小象
51.狮子
52.雄狮
53.骆驼
54.鸵鸟
55.猴子
56.猴子家族
18、小鬼
19、巫婆
20、站立的公鸡
21、蹲着的公鸡
会跳的青蛙
无篷小船
风轮
气球
有篷小船
十字飞镖
东南西北
帆船
千纸鹤
尖头飞机
平头飞机
信封
爱心
五角星
各种花的折法 1.
2.
3.
4.船
5.带蓬的船
6.小鬼
7.巫婆
8.站立的公鸡
9.蹲着的公鸡
10.小猪
11.小猫
12.白胡子黑猫
13.竖起耳朵的小兔子
14.兔子盒子
15.小猫钓鱼
16.斑点狗
17.腊肠狗
18.绵羊
19.小老鼠
20.卷曲的小老鼠
21.鹦鹉
22.奶牛
23.马
24.仓鼠
25.松鼠
26.鼹鼠
27.小鸟
28.鸽子
微信最大知识百库微信号:zsbk88
29.考拉
