直线和圆的位置关系(第二课时)PPT教学课件
合集下载
人教版九年级数学上册《点和圆、直线和圆的位置关系(第2课时)》示范教学课件

练习 请作出锐角三角形、直角三角形、钝角三角形的外接圆.这些
外接圆的圆心在什么位置?
外心在三角形的内部 外心是斜边的中点 外心在三角形的外部
归纳 (1)锐角三角形的外心在三角形的内部;直角三角形的外心是
斜边的中点;钝角三角形的外心在三角形的外部.因此可由外心的 位置判断三角形的形状.
(2)三角形外心到三个顶点的距离相等,等于其外接圆的半径.
因此,经过一个点 A 作圆,只
要以点 A 以外任意一点为圆心,以
这一点与点 A 的距离为半径就可以
A
作出,这样的圆有_无__数__个.
经过两个已知点 A,B 能不能作圆?如果能,圆心分布有什么 特点?
经过两点 A,B 作圆,因为圆心到 A, B 的距离__相__等____,所以圆心应在线段 AB 的__垂__直__平__分__线__上.
探究 过任意三点都不在同一直线上的四点能作一个圆吗?也就是说
过任意一个四边形的四个顶点能作一个圆吗?
分析:要想过四点作圆,应先作出经过不在同一条直线上的三 点的圆,若第四个点到圆心的距离等于半径,则第四个点在圆上, 否则不在圆上.
探究 过下列四边形的四个顶点能作一个圆吗?
O
O
O
探究 分别测量上面各四边形的内角,你发现四边形的哪些元素决
定了过它的四个顶点可以作一个圆?能再找几个四边形验证吗?
过对角互补的四边形的四个顶点可以作一个圆.
不在同一条直线上的 三个点确定一个圆
确定圆的条件
三角形的外接圆
线段 AB 的垂直平分线上有_无__数_____个
A
B
点,所以这样的圆心有__无__数____个,这样的
圆也可以作出___无__数___个.
2.5.1 直线与圆位置关系 课件(共23张PPT)

2
(
3
)
4 1 2= 1 > 0
因为
所以,直线 l 与圆相交,有两个公共点.
由 2 − 3 + 2 = 0 ,解得1 = 2, 2 = 1.
把 1 = 2代入方程①,得 1 = 0 ;
把 2 = 1代入方程① ,得 2 = 3.
所以,直线 l 与圆的两个交点是:
(2,0),(1,3)
【分析】如图,点(2,1)位于圆: 2 + 2 = 1外,经过圆外一点有两条直线与这个圆相切.我们设切线方
程为 − 1 = ( − 2), k为斜率.由直线与圆相切可求出k的值.
y
解法1:设切线的斜率为,则切线的方程为 − 1= − 2 ,
P.
即kx-y+1-2k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
【分析】思路一 判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解;
思路二 可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系.
解法一:由直线 l 与圆的方程,得:
3x y 6 0,
2
2
x
y
2 y 4 0.
消去y,得 x 2 3x 2 0
①当切线l的斜率存在时, 即 − + 2 − = 0,
由圆心(0,0)到切线l的距离等于圆的半径1,得
|2 − |
2
+1
= 1, 解得
3
=4 ,
y
.
P
此时,切线l的方程为3 − 4 + 5 = 0.
②当切线l的斜率不存在时,此时直线x=1也符合题意.
(
3
)
4 1 2= 1 > 0
因为
所以,直线 l 与圆相交,有两个公共点.
由 2 − 3 + 2 = 0 ,解得1 = 2, 2 = 1.
把 1 = 2代入方程①,得 1 = 0 ;
把 2 = 1代入方程① ,得 2 = 3.
所以,直线 l 与圆的两个交点是:
(2,0),(1,3)
【分析】如图,点(2,1)位于圆: 2 + 2 = 1外,经过圆外一点有两条直线与这个圆相切.我们设切线方
程为 − 1 = ( − 2), k为斜率.由直线与圆相切可求出k的值.
y
解法1:设切线的斜率为,则切线的方程为 − 1= − 2 ,
P.
即kx-y+1-2k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
【分析】思路一 判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解;
思路二 可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系.
解法一:由直线 l 与圆的方程,得:
3x y 6 0,
2
2
x
y
2 y 4 0.
消去y,得 x 2 3x 2 0
①当切线l的斜率存在时, 即 − + 2 − = 0,
由圆心(0,0)到切线l的距离等于圆的半径1,得
|2 − |
2
+1
= 1, 解得
3
=4 ,
y
.
P
此时,切线l的方程为3 − 4 + 5 = 0.
②当切线l的斜率不存在时,此时直线x=1也符合题意.
《直线与圆的位置关系》课件——第2课时

青岛版初中数学九年级上册
第三单元
第4课
导入新课
1.直线与圆的位置关系?
当直线l与⊙O有两个公共点时,叫做直线l与⊙O 相
交。直线l叫做⊙O的割线,两个公共点叫做交点。
当直线l与⊙O有唯一的公共点时,叫做直线l与⊙O相
切。直线l叫做⊙O的切线,唯一的公共点叫做切点。 当直线l与⊙O没有公共点时,叫做直线 l 与⊙O 相 离。
新课学习
(1)过⊙O 的半径OA的外端点A作与半径OA垂直的直 线l(图 3-38),你发现直线l与⊙O有怎样的位置关 系?为什么?
新课学习
切线的判定定理 过半径的外端并且垂直于半径的直线是圆的切线.
新课学习
(2)利用上面的定理,过⊙O上任意一点,你会用三
角尺画⊙O的切线吗?试一试.
新课学习
例2:如图3-39,以△ABC的边AB为直径作⊙O,如果
⊙O经过AC的中点D,然后过D作DE⊥BC,垂足为点E .
DE是⊙O的切线吗?说明理由
新课学习
解:DE是⊙O的切线. 理由如下:连接 OD .
∵AB是⊙O的直径,∴AO=OB .
又∵AD=DC,
∴OD是△ABC的中位线,
从而OD∥BC .
∵DE⊥BC,∴DE⊥OD, ∴DE是⊙O 的切线
课堂练习
2.如图,点D是∠AOB的平分线OC上任意一点,过D作 DE⊥O并证明你的结论
A C D
O
E
B
作业布置
课本P.94第1、2题
板书设计
3.4直线与圆的位置关系
第二课时
1.切线的判定定理:
例2
新课学习
挑战自我 已知⊙O和圆上一点P,你会用尺规过点P作⊙O的切线 吗?说出你的作法和作图的道理。
第三单元
第4课
导入新课
1.直线与圆的位置关系?
当直线l与⊙O有两个公共点时,叫做直线l与⊙O 相
交。直线l叫做⊙O的割线,两个公共点叫做交点。
当直线l与⊙O有唯一的公共点时,叫做直线l与⊙O相
切。直线l叫做⊙O的切线,唯一的公共点叫做切点。 当直线l与⊙O没有公共点时,叫做直线 l 与⊙O 相 离。
新课学习
(1)过⊙O 的半径OA的外端点A作与半径OA垂直的直 线l(图 3-38),你发现直线l与⊙O有怎样的位置关 系?为什么?
新课学习
切线的判定定理 过半径的外端并且垂直于半径的直线是圆的切线.
新课学习
(2)利用上面的定理,过⊙O上任意一点,你会用三
角尺画⊙O的切线吗?试一试.
新课学习
例2:如图3-39,以△ABC的边AB为直径作⊙O,如果
⊙O经过AC的中点D,然后过D作DE⊥BC,垂足为点E .
DE是⊙O的切线吗?说明理由
新课学习
解:DE是⊙O的切线. 理由如下:连接 OD .
∵AB是⊙O的直径,∴AO=OB .
又∵AD=DC,
∴OD是△ABC的中位线,
从而OD∥BC .
∵DE⊥BC,∴DE⊥OD, ∴DE是⊙O 的切线
课堂练习
2.如图,点D是∠AOB的平分线OC上任意一点,过D作 DE⊥O并证明你的结论
A C D
O
E
B
作业布置
课本P.94第1、2题
板书设计
3.4直线与圆的位置关系
第二课时
1.切线的判定定理:
例2
新课学习
挑战自我 已知⊙O和圆上一点P,你会用尺规过点P作⊙O的切线 吗?说出你的作法和作图的道理。
直线和圆的位置关系(第2课时)同步课件

∵O__A_⊥__A_B__,__O_A 是⊙O的半径
∴_A_B_是__⊙__O_的__切_线__
,
,
∴_A__B_⊥__O_A___. .
∴A__B_是_⊙__O_的__切__线_.
有切线,圆心连 切点,得垂直
证切线,圆心连 准切点,证垂直
作垂直,证半径
自主合作,探究新知
核心知识点二: 三角形的内切圆及内心
②三角形的内心是三个角平分线的交点;
③三角形的外心到三边的距离相等;
④三角形的外心是三边中垂线的交点.
A.①②③④
B.①②③
C.①②④
D.②③④
随堂练习
2.下列说法错误的是( C ) A.三角形的内切圆与三角形的三边都相切 B.一个三角形一定有唯一一个内切圆 C.一个圆一定有唯一一个外切三角形 D.等边三角形的内切圆与外接圆是同心圆
r
●O
┐d
l
相交
r ●O
d
┐
l
相切
r ●O d
┐l
相离
d< r
d= r
d> r
创设情境,引入新知
问题:一辆急速行驶的火车的车轮与铁轨之间存在 着什么样的位置关系?
车轮可以看成什么图形?铁轨可以看成什么图形? 你有没有判定两者位置关系的方法?
自主合作,探究新知
核心知识点一: 圆的切线的判定
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则 圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
随堂练习
3.如图,AB是⊙O的直径,线段BC与⊙O的交点D是
BC的中点,DE⊥AC于点E,连接AD,则下列结论中
正确的个数是( D )
《直线与圆的位置关系》第二课时

台风路 经范围 如图所 示
D A P B C
经过半径的外端并且垂直这条半径的 直线是圆的切线。 符号语言: ∵ OA是半径, l ⊥ OA于A ∴ l是⊙O的切线。
O
l
A
问题:定理中的两个条件缺少一个行不行?
判 断
1. 过半径的外端的直线是圆的切线(× ) 2. 与半径垂直的的直线是圆的切线( × ) 3. 过半径的端点与半径垂直的直线是圆的切线( × )
求证:AT是⊙O的切线.
B
O
T
A
l1
AB是⊙O的直径,直线l1与l2是 ⊙O的切线,A,B是切点, l1 与l2有怎样的位置关系? A
O
l2
B
思考:如果直线l是⊙O的切线,切 点为A,那么半径OA与直线l是不 是一定垂直?
切线的性质定理: 圆的切线垂直于过 切点的半径 l M A
O
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB 于D,以O为圆心,OD为半径作⊙O。 求证:⊙O与AC相切。 A 证明:过O作OE⊥AC于E。 ∵ AO平分∠BAC,OD⊥AB ∴ OE=OD 即圆心O到AC的距离 d = r ∴ AC是⊙O切线。
三种方法有联系吗?
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB, CA=CB。
求证:直线AB是⊙O的切线。 分析:由于AB过⊙O上的点C,所以连 接OC,只要证明AB⊥OC即可。 证明:连结OC(如图)。 ∵ OAB中, OA=OB ,CA=CB, ∴ AB⊥OC。 ∵ OC是⊙O的半径 ∴ AB是⊙O的切线。
A
O
C
B
练习
1 判断下列命题是否正确. (1)经过半径外端的直线是圆的切线. (2)垂直于半径的直线是圆的切线. (3)过直径的外端并且垂直于这条直径的直线 是圆的切线. (4)和圆有一个公共点的直线是圆的切线. (5)以等腰三角形的顶点为圆心,底边上的高 为半径的圆与底边相切.
直线与圆的位置关系ppt课件

x 2 y 2 Dx Ey F 0
( D 2 +E 2 4 F 0)
代数方法
几何
图形性质究过程,如何通过代数方法,
研究直线与圆的位置关系?
联立两直线方程
两直线的位置关系
方程组解的情况
直线与圆的位置关系
联立直线与圆方程
方程组解的情况
求直线被圆截得的弦长.
(法1) 圆心为C (1, 2), 半径为r 2,
圆心C到直线l的距离d
| 2 2+2 |
2 5 2 8 5
2 2 5
2
弦长为2 (2) (
)
.
=
2
5
5
5
5
22 12
x2 y 2 2x 4 y 1 0
(法2)解 : 联立
2.5.1直线与圆的位置关系
春
来
江
水
绿
如
蓝
日
出
江
花
红
胜
火
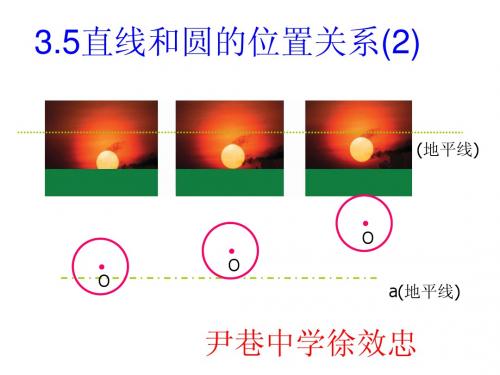
问题1:把太阳看作一个圆,海天交线看作一条直线,那么在日出的过程中,
体现了直线和圆的哪些位置关系?
相交
相切
相离
探究交流
问题2:如何判断直线与圆的位置关系?
d
d
d
r
r
r
地平线
直线与圆相切
直线与圆相交
1.通过直线与圆的公共点个数判断
直线与圆有两个公共点
2.弦心距:圆心到弦所在直线的距离;
弦心距
A
O
l
C
O
3.垂径定理:垂直于弦的直径平分这条弦,且平分弦所对的两条弧。
4.求弦长:
①两点距离:联立直线与圆的方程求两交点A,B的坐标
直线和圆的位置关系(第2课时)(课件)-2022-2023学年九年级数学下册同步精品课件(北师大版)

∴BO,CO分别是∠ABC和∠ACB的平分线
O C
即∠ OBC= 1 ∠ABC ∠OCB=1 ∠ACB
2
2
∴∠ BOC=180°-(∠ OBC+∠OCB)
=180°- 1 ( ∠ABC +∠ACB)== 125°.
2
1.下列说法错误的是( ) A.三角形的内切圆与三角形的三边都相切 B.一个三角形一定有唯一一个内切圆 C.一个圆一定有唯一一个外切三角形 D.等边三角形的内切圆与外接圆是同心圆
探索&交流
如图,AB 是 ⊙O 的直径,直线 l 与 AB 的夹角为∠Biblioteka . 当l 绕点 A 旋转时,
B
(1)随着∠α的变化,点 O 到 l 的距 l 离 d 如何变化?直线 l 与 ⊙O 的位置 关系如何变化?
Od α
A
l l
∠α从90°变小到0°,再由0°变大 到90°,点 O 到 l 的距离 d 先由 r 变小到0,再由0变大到 r.
练习&巩固
练习&巩固
2.如图,点C 是⊙ O上的一点,AB 是⊙ O的直径,∠CAB=∠DCB,
那么CD 与⊙ O 的位置关系是( )
A. 相交
B. 相离
C. 相切
D. 相交或相切
练习&巩固
3.如图,☉O内切于△ABC,切点D、E、F分别在BC、AB、AC上.已
知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF等于
第三章 圆
6.2 直线和圆的位置关系
北师大版九年级数学下册
学习&目标
1.理解并掌握圆的切线的判定定理及运用.(重点) 2.三角形的内切圆和内心的概念及性质.(难点)
O C
即∠ OBC= 1 ∠ABC ∠OCB=1 ∠ACB
2
2
∴∠ BOC=180°-(∠ OBC+∠OCB)
=180°- 1 ( ∠ABC +∠ACB)== 125°.
2
1.下列说法错误的是( ) A.三角形的内切圆与三角形的三边都相切 B.一个三角形一定有唯一一个内切圆 C.一个圆一定有唯一一个外切三角形 D.等边三角形的内切圆与外接圆是同心圆
探索&交流
如图,AB 是 ⊙O 的直径,直线 l 与 AB 的夹角为∠Biblioteka . 当l 绕点 A 旋转时,
B
(1)随着∠α的变化,点 O 到 l 的距 l 离 d 如何变化?直线 l 与 ⊙O 的位置 关系如何变化?
Od α
A
l l
∠α从90°变小到0°,再由0°变大 到90°,点 O 到 l 的距离 d 先由 r 变小到0,再由0变大到 r.
练习&巩固
练习&巩固
2.如图,点C 是⊙ O上的一点,AB 是⊙ O的直径,∠CAB=∠DCB,
那么CD 与⊙ O 的位置关系是( )
A. 相交
B. 相离
C. 相切
D. 相交或相切
练习&巩固
3.如图,☉O内切于△ABC,切点D、E、F分别在BC、AB、AC上.已
知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF等于
第三章 圆
6.2 直线和圆的位置关系
北师大版九年级数学下册
学习&目标
1.理解并掌握圆的切线的判定定理及运用.(重点) 2.三角形的内切圆和内心的概念及性质.(难点)
2.5.1 直线与圆的位置关系(第2课时)高二数学课件(人教A版2019选择性必修第一册)

x
圆的最值
1
解:(1)x 和 y 满足以(-1,0)为圆心,以 为半径的圆
2
(x-2)2+(y-3)2表示圆上的点(x,y)到点 M(2,3)的距离,
1
1
因为|CM|=3 2,因此最大值为 3 2+ ,最小值为 3 2- .
2
2
y
(2) 可认为是圆上的点与坐标原点连线的斜率,由图形知当过原点的直线与圆
因为 > 0,所以 =
2
2
= 14.52
+ + 10.5
2
= 14.52 .
14.52 − (−2)2 − 10.5 ≈ 14.36 − 10.5 = 3.86(m).
直线与圆的位置关系应用
例2.一个小岛的周围有环岛暗礁, 暗礁分布在以小岛中心为圆心, 半径为20km的圆形区域内. 已知
小岛中心位于轮船正西40km处, 港口位于小岛中心正北30km处. 如果轮船沿直线返港, 那么它是
离为 1 即可.设圆心(0,0)到直线 12x-5y+c=0 的距离为 d,则 r-d>1,所以
|c|
d<r-1=1.即 <1,解得-13<c<13.
13
圆的最值
总结
当直线与圆相交时,设圆心到直线的距离为 d(d>0),圆的半径为 r,则圆上
的点到直线的最大距离为 r+d,劣弧上的点到直线的最大距离为 r-d.
人教A版2019选修第一册
第 二 章 直线和圆的方程
2.5.1 直线与圆的位置关系
学习目标
1.能正确理解直线与圆的方程,培养数学抽象的核心素养;
2.能用直线和圆的方程解决一些简单的数学问题与实际问题,培养数学运算、逻辑推
圆的最值
1
解:(1)x 和 y 满足以(-1,0)为圆心,以 为半径的圆
2
(x-2)2+(y-3)2表示圆上的点(x,y)到点 M(2,3)的距离,
1
1
因为|CM|=3 2,因此最大值为 3 2+ ,最小值为 3 2- .
2
2
y
(2) 可认为是圆上的点与坐标原点连线的斜率,由图形知当过原点的直线与圆
因为 > 0,所以 =
2
2
= 14.52
+ + 10.5
2
= 14.52 .
14.52 − (−2)2 − 10.5 ≈ 14.36 − 10.5 = 3.86(m).
直线与圆的位置关系应用
例2.一个小岛的周围有环岛暗礁, 暗礁分布在以小岛中心为圆心, 半径为20km的圆形区域内. 已知
小岛中心位于轮船正西40km处, 港口位于小岛中心正北30km处. 如果轮船沿直线返港, 那么它是
离为 1 即可.设圆心(0,0)到直线 12x-5y+c=0 的距离为 d,则 r-d>1,所以
|c|
d<r-1=1.即 <1,解得-13<c<13.
13
圆的最值
总结
当直线与圆相交时,设圆心到直线的距离为 d(d>0),圆的半径为 r,则圆上
的点到直线的最大距离为 r+d,劣弧上的点到直线的最大距离为 r-d.
人教A版2019选修第一册
第 二 章 直线和圆的方程
2.5.1 直线与圆的位置关系
学习目标
1.能正确理解直线与圆的方程,培养数学抽象的核心素养;
2.能用直线和圆的方程解决一些简单的数学问题与实际问题,培养数学运算、逻辑推
2.5.1 直线与圆的位置关系(共27张PPT)

(1)求直线l的方程;
(2)若圆C的圆心为点(3,0),直线l被该圆所截得的弦长为2
2
,求圆C的标准方程.
解:(1)由已知得:
2x-y-3 = 0,
x = 2,
解得
y = 1,
4x-3y-5 = 0,
∴两直线交点为(2,1).
设直线l的斜率为k1,∵l与x+y-2=0垂直,
∴k1=1,
∵l过点(2,1),∴l的方程为y-1=x-2,即x-y-1=0;
|2-1--1|
心(2,1)到直线 mx-y-m-1=0 的距离 d=
当
当
当
1+2
=
|-2|
1+2
.
4
d<2,即 m>0 或 m<- 时,直线与圆相交,即直线与圆有两个公共点;
3
4
d=2,即 m=0 或 m=-3时,直线与圆相切,即直线与圆只有一个公共点;
4
d>2,即- <m<0 时,直线与圆相离,即直线与圆没有公共点.
轴,建立直角坐标系,设圆心为 C,水面所在弦的端点为 A、
B,则由已知得 A(6,-2).
设圆的半径为 r,则 C(0,-r),即圆的方程为
x2+(y+r)2=r2.①
将点 A 的坐标为(6,-2)代入方程①,解得 r=10.
∴ 圆的方程为 x2+(y+10)2=100.②
当水面下降 1 米后,可设点 A′的坐标为(x0,-3)(x0>3),
当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点?
思路分析:可联立方程组,由方程组解的个数判断,也可求出圆心到直线
直线与圆的位置关系PPT教学课件

点,⊙P与BC相切.求证: 切.
⊙P与AB相
C
E
oP
B
A
F
证明:设⊙P的半径为r,点P到BC,AB的距离分别为d1,d2.
} 点P在∠ABC的平分线上d1=d2 ⊙P与BC相切d1= r
d2= r
⊙P与AB相切
例题2
在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,为半径的圆 与AB有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm (3)r=3cm。
A1
设直线l与l1的夹角为θ,则
52
sin 2 2
52
B1
故θ=450
由直线l1:x+y+1=0的倾斜角为1350,
知直线l的倾斜角为00或900,
又由直线l过点P(3,1),故所求l的方程为x=3或y=1。
例2、已知直线l经过点P(3,1),且被两平行
直线l1:x+y+1=0和l2:x+y+6=0截得的
大家想象一下海上升明月的情景, 是一个怎样的过程?如果把海 平面 抽象 为一条直线,把圆月抽象为一 个圆,我们用数学语言怎么来描绘 呢?
1、直线 与圆的位置关系
相离 相切
相交
这时直线叫圆的割线 。
o
r d
l
d>r
o
rd
d=r
o
r
d
l
l A DB
d<r
直线L和O相离 直线L和O相切 直线L和O相交
l2:A2x+B2y+C2=0
①l1∥l2 A1B2-A2B1=0 且 B1C2-B2C1≠0
②l1⊥l2 A1A2+B1B2=0
3.5直线和圆的位置关系(第2课时)课件_北师大版
(1)①解:E的坐标是:(1,12),故答案为: (1,12);②证明:∵矩形OABC,∴CE=AE, BC∥OA,∴∠HCE=∠EAG,∵在△CHE和 △AGE中∠HCE=∠EAGCE=AE∠HEC=∠GEA, ∴△CHE≌△AGE,∴AG=CH.
(2)解:如图2,连接DE并延长DE交CB于M, 连接AC,∵DO=OC=1=1/2OA,∴D是OA的中 点,∵BC∥OA,∴∠MCE=∠DAE,∵在 △CME和△ADE中 ∠MCE=∠DAECE=AE∠MEC=∠DEA, ∴△CME≌△ADE,∴CM=AD=2-1=1, ∵BC∥OA,∠COD=90°,∴四边形CMDO是 矩形,∴MD⊥OD,MD⊥CB,∴MD切⊙O于D, ∵HG切⊙O于F,E(1,1/2),
A M
I ●
●
B
┓
上右图就是三角形的内切圆作法:
C
B
┓ D
C
(1)作∠ABC、∠ACB的平分线BM和CN,交点为I. (2)过点I作ID⊥BC,垂足为D. (3)以I为圆心,ID为半径作⊙I, ⊙I就是所求
• 这样的圆可以作出几个呢?为什么?. ∵直线BE和CF只有一个交点I, 并且点I到△ABC三边的距离相 等(为什么?), 因此和△ABC三边都相切的 圆可以作出一个,并且只能 B 作一个.
1.解:连接DF、OE,过点D作DG⊥AC于点 G.∵∠C=∠CGD=∠CFD=90°,∴四边 形CGDF是矩形,∴DG=CF=y;∵OE∥DG, ∴△AOE∽△ADG,∴OE:AO=DG:AD,即 1:(x+1)=y:x,化简可得y=x:(1+x).
3.(1)①根据矩形的性质和边长即可求出E的坐标;②推出 CE=AE,BC∥OA,推出∠HCE=∠EAG,证出△CHE≌△AGE 即可;
人教版数学九年级上册24.直线和圆的位置关系(第2课时)课件

O.
图1
图2
猜猜看:图2中直线l与⊙O由怎样的位置关系?
相切的语言把这一结论总结出来吗?
切线的判定定理:经过半径的外端并且垂直于这条半径的直
线是圆的切线
符号表示: ∵OA是⊙O半径,l⊥OA于点A, ∴l是的⊙O切线.
及时练
问题:定理中的两个条件缺少一个行不行?
1. 过半径的外端的直线是圆的切线( × ) 2. 与半径垂直的的直线是圆的切线( ×) 3. 过半径的端点与半径垂直的直线是圆的切线( ×)
03
练习
例1
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与 ⊙O相切于点D. 求证:AC是⊙O的切线.
分析:根据切线的判定定理,要证明AC是 ⊙O的切线,只要证明由点O向AC所作的垂 线段OE是⊙O的半径就可以了,而OD是的 半径,因此需要证明OE=OD.
例1
证明:如图,过点 O 作 OE⊥AC,垂足为 E,连接 OD,OA. ∵⊙O 与 AB 相切于点 D, ∴OD⊥AB. 又为等腰三角形,O 是底边 BC 的中点, ∴AO 是∠BAC 的平分线. ∴OE=OD,即 OE 是⊙O 的半径. 这样,AC 经过⊙O 的半径 OE 的外端 E,并且垂直于半径 OE,所以 AC 与⊙O 相切.
1.要解决此问题用什么方法? 切线的判定定理 2.AB要具备哪些条件? 经过半径的外端并且垂直于这条半径 3.连接OB就使AB过半径的外端,只需证明 OB⊥AB即可,如何证明呢?
例
常用证两条 线段(或直 线)垂直的 方法
例
证法1:连接OB ∵OB=OC,CA=OC ∴BC= 1 OA
2
∴ ∠OBA=90º, 即AB⊥OB ∴AB是⊙O的切线
反证法:假设AB与OC不垂直, 则过点O作OM⊥AB,垂足为M, 根据垂线段最短,得OM<OC, 即圆心O到直线AB的距离d<R ∴直线AB与⊙O相交, 这与已知“AB是⊙O的切线”矛盾 ∴假设不成立,即AB⊥OC.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O AC B
DB
A
O
E C
(1)有交点,连半径,证垂直. (2)无交点, 作垂直,证半径.
2020/12/11
13
2、如图,△ABC中,AB=AC,AO⊥BC于O,
OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证:AB是⊙O的切线.
A
F
E
B
O
C
2020/12/11
14
3、如图,AB是⊙O的直径,点D在AB的延长 线上,BD=OB,点C在⊙O上, ∠CAB=30°.
课前5分钟
如图,将长方形ABCD沿直线BD折叠,使C点落 在C′处,BC′交AD于E. (1)求证:BE=DE; (2)若AD=8,AB=4,求△BED的面积.
2020/12/11
1
切线的判定定理
2020/12/11
2
直线和圆的位置关系.
r o
d
l
r o
d
l
r
o d l
(1)直线 l 和⊙O相离
d>r
(2)直线 l 和⊙O相
d=r
切(3)直线 l 和⊙O相交
d<r
图中直线l满足什么
条件时是⊙O的切线?
O
l
方法1:直线与圆有唯一公共点
方法2:直线到圆心的距离等于半径
2020/12/11
4
请在⊙O上任意取一点A,连接OA,过 点A作直线l⊥OA.思考:
(1)圆心O到直线l的距离和
圆的半径有什么数量关系?
注:已知切线、切点, 则连接半径,应用切线 的性质定理得到垂直关 系,从而应用勾股定理 计算。
2020/12/11
B OA P
20
2、如图,AB、AC分别切⊙O于B、C,若 ∠A=600,点P是圆上异于B、C的一动点,
则∠BPC的度数是( )
A、600
B、1200
B
C、600或1200
O
D、1400或600 P
求证:DC是⊙O的切线.
C
A OBD
2020/12/11
15
4、如图,在△ABC中,AB=AC,以AB为直径 的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
A
O
E
B
C P
2020/12/11
16
如图,如果直线l是⊙O的切线,切点为A, 那么半径OA与直线l是不是一定垂直呢?
∵ l是⊙O的切线,切点为A O
∴ l ⊥OA
2020/12/11
l
A
17
切线的性质定理:圆的切 线垂直于过切点的半径。
O
2020/12/11
l
A
18
切线判定定理:
①过半径外端; ②垂直于这条半径.
切线性质定理:
①圆的切线; ②过切点的半径.
2020/12/11
O
切线
l
A
切线垂直于半径
19
1、如图, ⊙O切PB于点B,PB=4,PA=2,则 ⊙O的半径多少?
端;②垂直于这条半径.
2020/12/11
7
定理的几何语言:
∵ OA是半径, l ⊥OA于点A
∴ l是⊙O的切线
O
r l
A
2020/12/11
8
1、判断:
(1)过半径的外端的直线是圆的切线( ×) (2)与半径垂直的的直线是圆的切线( ×)
(3)过半径的端点与半径垂直的直线是圆的
切线(×)
O l
求证:直线AB是⊙O的切线。
O
A CB 分析:由于AB过⊙O上的点C,所以连接OC, 只要证明AB⊥OC即可。
2020/12/11
11
例2 如图,已知:O为∠BAC平分线上一
点,OD⊥AB于D,以O为圆心,OD为半径
作
⊙O。
求证:⊙O与AC相切。
A
DB O
EC
2020/12/11
12
例1与例2的证法有何不同?
A
C
2020/12/11
21
PPT教学课件
谢谢观看
Thank You For Watching
2020/12/11
22
r
2020/12/11 A
O r
l
A
O l
r
A
9
1、定义法:和圆有且只有一个公共点的直线是 圆的切线.
2、数量法(d=r):和圆心距离等于半径的直 线是圆的切线.
3、判定定理:经过半径外端且垂直于这条半径 的直线是圆的切线.
例1 如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
(2)直线 l 和⊙O有什么位置
关系?
l
2020/12/11
O
A
5
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A. 则:直线l与⊙O相切
O l
A
2020/12/11
6
切线的判定定理:
经过半径的外端并且垂直这条半径
的直线是圆的切线。
对定理的理解:
O l
A
切线必须同时满足两条:①经过半径外
