简易方程整理和复习1
人教版五年级上册数学第五单元 简易方程整理与复习

第五单元简易方程一、知识梳理1.用字母表示数。
(1)用字母表示数。
①字母与数字相乘,可以省略乘号,数字要写在字母的前面。
如x×6=6x;如果1与字母相乘,可以省略1与乘号,如m×1=m。
②字母与字母相乘,字母中间的乘号可以记作“•”,也可以省略不写。
③含有加减关系的代数式,后面有单位时,代数式必须用括号括起来。
如(3a-2b)米,而5n米就不用加括号了。
④a2与2a的区别:a2表示2个a相乘,是a×a;2a表示2个a相加,是a+a。
(2)用字母表示运算定律。
加法交换律:a+b=b+a;加法结合律:(a+b)+c=a+(b+c);乘法交换律:ab=ba;乘法结合律:(ab)c=a(bc);乘法分配律:(a+b)c=ac+bc。
(3)用字母表示计算公式。
长方形的面积公式:s=ab;长方形的周长公式:c=2(a+b);正方形的面积公式:s=a2;正方形的周长公式:c=4a。
(4)用字母表示常见的数量关系。
如路程、速度和时间之间的关系可以表示为s=vt。
(5)求含有字母的式子的值。
用含有字母的式子表示指定的数量,再把字母的取值代入式子中求值。
(6)字母的取值范围。
在含有字母的式子里,字母的取值范围是由实际情况决定的。
2.方程的意义。
(1)方程的意义。
含有未知数..就是方程。
...的等式(2)等式的性质。
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
3.解方程。
(1)方程的解与解方程。
使方程左右两边相等的未知数的值,叫做方程的解;求方程的解的过程叫做解方程。
(2)解形如x±a=b、ax=b、ax±b=c和a(x±b)=c的方程。
依据等式的性质来解此类方程。
(3)检验。
把求得的未知数的值代入原方程,看方程左边的值是否等于右边的值。
如果相等,所求的未知数的值就是原方程的解,否则就不是。
简易方程整理和复习

0.5(x+2)=3
3x+1.5=13.5
四、实际问题与方程
列方程解决问题的一般步骤: (1)弄清题意,找出未知数,用x表示; (2)分析、找出数量之间的相等关系,列
方程; (3)解方程; (4)检验,写出答案。
列方程解决问题
图书室科技书的本数比文艺书的3倍少75本, 科技书有495本。文艺书有多少本?
4、在自然数中,与数a相邻的两个数是 ( a-1 )和( a+1 )它们三个数的和是 ( 3a )。
二、方程的意义
含有未知数的等式叫做方程。 比如,X-12=30, y+12=42,
6X=30,60+25=85,X÷4=1.8 等等都是方程。方程一定是等式,等 式不一定是方程。
解方程的意义Байду номын сангаас
北京和上海相距1320km。甲乙两列火车同 时从北京和上海相对开出,6小时后两车相 遇,甲车每小时行120千米,乙车每小时行 多少千米?
三、总结
我们一起整理复习了简易方程,相信大家的 收获非常大,学会了整理一个单元的知识要 点和应用知识去解决问题。
谢谢! 再见!
简易方程整理与复习
襄阳市襄州区伙牌镇中心小学 周彦兵
温故而知新,可以为师矣 !
今天我来跟大家一起整理复 习简易方程。
一、用字母表示数
苹果有a个,梨有b个,a+b表示 (苹果和梨一共的个数 ),苹果比梨多(a- )个; 爸爸x岁,妈妈y岁,x-y=3表示(b爸爸比妈妈大3)岁 ; a×b=b×a;长方形的面积s=ab; 正方形的周长c=4a 。
1、什么叫方程的解?使方程左右两边相等的未知 数的值,叫做方程的解
人教新课标五年级数学上册《 5 简易方程——整理与复习 》教案(1)

人教新课标五年级数学上册《 5 简易方程——整理与复习》教案(1)一. 教材分析本节课是人教新课标五年级数学上册《简易方程——整理与复习》的内容。
通过本节课的学习,学生将复习和巩固之前学过的简易方程的知识,提高解题能力,培养逻辑思维能力。
教材内容主要包括简易方程的定义、特点、解法以及应用。
二. 学情分析五年级的学生已经掌握了简易方程的基本知识,具备了一定的解题能力。
但在解题过程中,部分学生对方程的化简、移项等操作还不够熟练,容易出错。
此外,部分学生在应用方程解决实际问题时,缺乏思路和方法。
三. 教学目标1.知识与技能:巩固简易方程的基本知识,提高解题能力。
2.过程与方法:通过复习和练习,培养学生运用方程解决实际问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作精神。
四. 教学重难点1.重点:简易方程的解法及应用。
2.难点:方程的化简、移项以及在实际问题中的运用。
五. 教学方法采用讲练结合、分组合作、启发式教学等方法,引导学生主动参与课堂,提高学生的动手操作能力和思维能力。
六. 教学准备1.课件:制作相关教学课件,展示和解题步骤。
2.练习题:准备一定数量的练习题,用于巩固和拓展学生的知识。
七. 教学过程1.导入(5分钟)利用课件引入本节课的主题,简要回顾简易方程的定义和特点,激发学生的学习兴趣。
2.呈现(10分钟)展示一些典型的简易方程题目,引导学生观察和分析题目的特点,总结解题方法。
3.操练(10分钟)让学生分组合作,共同完成一些简易方程的练习题。
教师在这个过程中给予适当的指导,帮助学生掌握解题方法。
4.巩固(10分钟)针对学生练习过程中出现的问题,进行讲解和巩固,确保学生掌握简易方程的解法。
5.拓展(10分钟)引导学生运用简易方程解决实际问题,培养学生的应用能力。
可以让学生分组讨论,分享解题思路和方法。
6.小结(5分钟)对本节课的内容进行总结,强调简易方程的解法和应用。
五年级简易方程整理与复习

含有未知数的等式叫做方程 含有未知数的等式叫做方程 使方程左右两边相等的未知 数的值,叫做方程的解 数的值,叫做方程的解 求方程的解的过程叫做解方程 求方程的解的过程叫做解方程
五年级简易方程复习
一、用字母表示数
用字母表示运算定律
加法运算定律 乘法运算定律
表示面积和周长
长方形面积: 长方形面积:S=ab 周长: 周长:C=2(a+b)或C=2a+2b ( ) 正方形面积: 正方形面积:S=a 周长: 周长:( 3C+A ) 的 倍与 的和是( 倍与A的和是 三个连续自然数,中间的数是n, 三个连续自然数,中间的数是 ,另 外的两个数分别是( 外的两个数分别是( n-1 )和 ( n+1 )。 一条路长a米 小雪每分钟走x米 一条路长 米,小雪每分钟走 米, 走了6分钟后 还剩( 分钟后, 走了 分钟后,还剩( a-6x )米。 一本故事书有m页 小明已经读了 天 一本故事书有 页,小明已经读了7天, 平均每天读n页 小明读了( 平均每天读 页,小明读了( 7n )页。
用字母公式计算
比如:
S表示路程,V表示速度,t表示 表示路程, 表示速度 表示 表示速度, 表示路程 时间。 时间。三者之间的关系和字母公式 根据这个公式,假如客车3小时行了 根据这个公式,假如客车 小时行了 204千米,客车每小时行多少千米? 千米, 千米 客车每小时行多少千米?
简易方程 X+7.8=20.2 5X=20.5 5.6 X-8.6=19.4 - 3.2 X-1.5 X=0.51 - (4.5+X)×2=13 + × x-6=12.5 x÷6=18.6 ÷ 2 X+1.2×5=7 ×
人教版数学五年级上册教案-五《简易方程》整理和复习

人教版数学五年级上册教案-五《简易方程》整理和复习一、课时安排•本节课所需时间:1课时•教学内容:简易方程的整理和复习•教学目标:能够熟练应用简易方程解决相关问题•教学重点:理解简易方程的概念,熟练应用简易方程进行计算•教学难点:巩固简易方程的解题方法二、教学内容1. 复习简易方程的基本概念•简易方程的定义:一元一次方程,通常表示形式为a*x + b = c•解决简易方程的步骤:去括号、去分母、合并同类项、移项求解•简易方程的解的含义:求出使等式成立的未知数的值2. 简易方程的练习1.已知方程 a*x + b = c,其中a=2,b=3,c=9,求x的值。
2.如果一个数等于它的三分之一再加上5,求这个数是多少?3. 拓展练习1.若一个数等于它的三倍再加上10,求这个数是多少?2.我们班共有40名同学,男生人数是女生人数的2倍,求男生和女生的人数各是多少?三、教学方法•教师讲解与示范•学生练习与讨论•小组合作解决问题•师生互动,激发学生思维四、教学过程1.引入:通过提出实际问题引导学生认识简易方程的应用价值。
2.复习:让学生回顾简易方程的基本概念,并解释解题步骤。
3.练习:让学生尝试解决简易方程的练习题,巩固知识。
4.拓展:提出拓展练习,鼓励学生思考,激发学生解决问题的兴趣。
5.总结:帮助学生总结本节课的教学要点,强化知识记忆。
五、教学反思本节课设计了复习简易方程的内容,并通过练习和拓展练习的方式帮助学生巩固和拓展知识。
教学过程中,学生表现积极,能够熟练运用简易方程解决问题,但在拓展练习中仍存在一定挑战。
在今后的教学中,需要更加重视拓展练习的设计,培养学生解决问题的能力。
以上为本节课的教案内容,希望能够帮助大家更好地理解和应用简易方程的知识。
人教版数学五年级上册第5单元《简易方程 整理和复习 第1课时》教案

人教版数学五年级上册第5单元《简易方程整理和复习第1课时》教案一. 教材分析人教版数学五年级上册第5单元《简易方程整理和复习第1课时》主要让学生通过整理和复习,掌握简易方程的解法和应用。
教材中包含了简易方程的定义、解法以及实际应用案例。
本节课的内容是学生进一步学习方程解决实际问题的基础,对于提高学生的数学思维能力和解决问题的能力具有重要意义。
二. 学情分析五年级的学生已经掌握了整数、小数和分数的基本知识,对于方程的概念和解法也有一定的了解。
但是,学生在解决实际问题时,还存在着对方程的理解不够深入、解题方法不够灵活等问题。
因此,在教学过程中,教师需要针对学生的实际情况,引导学生深入理解方程的内涵,提高解题的灵活性。
三. 教学目标1.知识与技能:使学生掌握简易方程的解法,能够运用简易方程解决实际问题。
2.过程与方法:通过整理和复习,提高学生解决问题的能力,培养学生的数学思维。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.重点:简易方程的解法及其应用。
2.难点:如何引导学生灵活运用简易方程解决实际问题。
五. 教学方法采用讲解法、引导法、实践法、讨论法等教学方法,以学生为主体,教师为指导,充分发挥学生的主动性和积极性。
六. 教学准备1.教师准备:熟悉教材内容,了解学生学情,设计教学过程。
2.学生准备:预习相关知识,了解简易方程的概念和解法。
七. 教学过程1.导入(5分钟)教师通过一个简单的实际问题,引出简易方程的概念,激发学生的学习兴趣。
2.呈现(10分钟)教师通过PPT或黑板,呈现教材中的简易方程及其解法,引导学生回顾已学知识。
3.操练(10分钟)教师设计一些练习题,让学生独立完成,检查学生对简易方程解法的掌握情况。
4.巩固(10分钟)教师学生进行小组讨论,共同探讨如何运用简易方程解决实际问题,巩固所学知识。
5.拓展(10分钟)教师提出一些拓展问题,引导学生运用所学知识进行思考,提高学生的解决问题的能力。
简易方程-整理和复习(一)

哈,93kg!这两 个月我坚持锻炼, 体重减少了3kg。
两个月前,他的体 重是多少千克?
解:设两个月前他的体重为x kg。 x-3=93 x=96
(1)a²>2a (2)含有未知数的式子就是方程。
(×) (×)
(3)5x+5=5(x+1)。 (4)x=6是方程3x-6=12的解。
(√) (√ )
四、巩固提高
三、解方程
x÷8=0.4 解:x÷8×8=0.4×8
x=3.2
6x+18=48 解:6x+18-18=48-18
6x=30
x=5
用方程解决问题有哪些步骤?验算时要注意什么?
这些知识点中有哪些容易出 错或应该注意的地方?
1. 平方。 2. 省略乘号。 3. 数字写在字母前面,乘1时1可省略。 4. 应用等式的性质解方程时,方程两边要同加同减
同乘同除以相同的数,乘上和除以的数不能是0。 5. 解方程后别忘了检验。 6. 要从题目的关键句中找等量关系,再列出方程。
一、填空题
答:两个月前他的体重是96kg。
五、重点回顾
知识点2:用形如ax=b的方程解决实际问题。
这条街一共有多少盏路灯?
解:设这条街一共有x盏路灯. 5x=140
5x÷5=140÷5 x=28
答:这条街一共有28盏路灯。
五、重点回顾
知识点3:形如ax+ab=c的方程的解法和画图解 决问题。
小明和小红在校门口分手,7分钟后 他们同时到家。小明平均每分钟走45 m, 小红平均每分钟走多少米?
简易方程整理与复习教案

简易方程第一讲一、创设情景,导入复习谈话:你现在有几本书,加上图书柜里的书一共有多少本?(不要去数图书柜里的书)(可以随便举实例引入新课)根据学生的反应情况,逐步引导学生回想起可以用一个字母来表示未知的数,也可以用一个含有字母的式子表示数量,引入课题。
二、回忆梳理,理清脉络。
(复习目标一:自己喜欢的方式整理有关简易方程的知识内容)1、想一想,我们学了哪些知识?下面请同学们用自己喜欢的方式整理有关简易方程的知识。
(学生自主整理,教师巡视并对个别学生给予指导和点拨).2.交流矫正,优化再建1、用字母表示数2、用字母表示运算定律用字母表示数3、用字母表示计算公式4、用字母表示数量关系1、方程的意义简易方程2、等式的基本性质解方程3、方程的解4、解方程解简易方程稍复杂的方程今天我们先复习“用字母表示数”(复习目标二:1、进一步明确用字母表示数的意义和作用。
2、会用字母表示运算定律、计算公式以及常见的数量关系。
3、会求含有字母的式子的值。
)(1)举例说明用字母怎么表示数?(2)你能用字母表示运算定律和计算公式吗?加法交换律:加法结合律:乘法交换律:乘法结合律:乘法分配律:(3)你能用字母表示计算公式吗?正方形的面积:长方形的面积:正方形的周长:长方形的周长:(4)你知道哪些常用的数量关系,你能用字母表示出来吗?路程=速度*时间工作总量=工作效率×工作时间总价=单价*数量总产量=单产量×数量(5)提问:不管是用字母表示数还是表示运算定律。
有什么意义?(简明易记,便于应用)二、重点复习,强化提高。
(复习目标三:通过强化练习,使我们对已学的基础知识得到进一步巩固。
)巩固练习一、填空:1、学校有图书4000本,又买来a本,现在一共有()本。
2、学校有学生a人,其中男生b人,女生有()人。
3、李师傅每小时生产x个零件,10小时生产()个。
4、食堂买来大米400千克,每天吃a千克,吃了几天后还剩b千克,已吃了()天。
简易方程整理和复习

简易方程整理和复习一、基本练习解方程。
(1) x-4.8=7.2 (2)y+12=45 (3)2.5x=14 (4)x÷5=30 (5)4x+30=94 (6) 2x -7.5=7.5列方程解x+b=c应用题一、铺垫孕伏商店原有一些饺子粉,卖出35千克以后,还剩40千克。
这个商店原来有饺子粉多少千克?二、探究新知商店原来有一些饺子粉,每袋5千克,卖出7袋后,还剩40千克。
这个商店原来有多少千克饺子粉?等量关系式:_____的重量-_____的重量=_______的重量解:设原来有___千克饺子粉。
答:原来有_____千克饺子粉。
三、总结列方程解应用题的一般步骤1、弄清题意,找出未知数,并用x表示;2、找出应用题中数量间的相等关系;3、解方程;4、检验,写出答案。
四、练习1、图书小组原来有一些故事书,借给3个班,每班18本,还剩35本。
原来有故事书多少本?2、四年级做了3种颜色的花,每种25朵,布置教室用去一些以后还剩28朵。
布置教室用去多少朵?列方程解ax+b=c 的应用题一、铺垫孕伏写出下面各题的式子(1)比x的3倍多15 (2)比x的4倍少2(3)2个x与34的和(4)5个x与0.6的3倍的差二、探究新知(一)少年宫合唱队有84人,合唱队的人数比舞蹈队的3倍多15人。
舞蹈队有多少人?等量关系式:解:设舞蹈队有__人。
答:舞蹈队有___人。
(二)变式练习:少年宫唱队有84人,合唱队的人数比舞蹈队的人数的4倍少8人,舞蹈队有多少人?三、小结四、练习1、等腰三角形的周长是86厘米,底是38厘米。
腰是多少厘米?2、学校饲养小组今年养兔25只,比去年养的只数的3倍少8只。
去年养兔多少只?列方程ax+ab=c解决问题一、铺垫孕伏1、用含有字母的式子表示。
(1)每筐梨重x千克,5筐梨重()千克,10筐梨重()千克;(2)每支钢笔x元,3支钢笔()元,8支钢笔()元;(3)一列火车每时行x千米,4时行()千米,12时行()千米;(4)修路队每天修路x米.10天修路()米,20天修路()米。
人教版五年级上册数学 简易方程(整理和复习)

第四单元:简易方程整理和复习(一)一、填空.1、果园里有苹果树和梨树共45棵,其中梨树有a棵,苹果树比梨树多( )棵.2、2a表示( )或者( ),a2表示( )3、一个正方形周长是m米,这个正方形的边长是( )这个正方形的面积是( )4、某工厂每月用水a吨,全年用水( )吨5、三角形在面积公式用字母表示是( ),当a=3.6厘米,h=4厘米时,s=( )二、判断(对的打”√”,错的打”×”)1、a2>2a ( )2、2x+3=11的解是x=4. ( )3、4x+5>10是方程( )4、当a=3,b=5时,2a+3b=21 ( )5、42+3=2x,不是方程是等式.( )三、解下列方程.4x-18×2=20 2.5x-0.5x=0.4×8 x-4.5+10=17.8四、列方程解文字题.1、一个数的5倍加上这个数的8倍等于169,求这个数?2、9个0.6比x的2倍多2.7,求x?整理和复习(二)一、选择合适的方法解下列应用题.1、一个三角形面积是24.8平方米,底是12.4米高是多少米?2、小青家今年养了50只鸡,比鹅的3倍还多5只,小青家今年养鹅多少只?3、甲乙两辆汽车分别从相距800千米的两城相向开出,8小时相遇,已知甲车每小时行驶45千米, 乙车每小时会驶多少千米?4、香蕉每千克4.50元,梨每千克4元,小红的妈妈买了4千克香蕉,给了营业员30元,剩下的钱去买梨,能买梨多少千克?5、小红和小军一共储蓄了235元,已知小红储蓄的是小军的1.5倍,小红和小军各储蓄多少元?6、三个数的平均数是120,甲数是乙数的2倍,丙数比甲数多5,甲, 乙,丙三个数各是多少?第四单元测试题(A卷)一、填空.1、平行四边形底长a米,高是底的1.8倍,面积是( )2、货车每小时行S千米,客车每小时行m千米,客车3小时后和货车5小时一共行驶了( )千米.3、食堂买来200千克煤,已烧了a天,还剩b千克,平均每天烧了( )千克.4、每个足球x元,买4个足球,付出200元,应找回( )元.5、三个连续自然数,已知中间一个数是m,那么前一个数是( ),后一个数是( ),三数之和是( )6、当x=5时,x2=( ),2x+8=( )7、用字母表示梯形面积公式是( )8、一种商品降价a元后是80元,原价是( )元.二、判断.(对的打”√”,错的打”×”)(1)、方程一定是等式,等式不一定是方程.( )(2)、小明今年a岁,哥哥比他大b岁,c年后,哥哥比他大b+c岁.( )(3)、x的3倍与3x相等. ( )(4)、3x+4x=7x, 3a+4b=7ab ( )(5)、含有x的等式叫方程. ( )三、选择题.(填序号)(1)、下列式子中是方程的是( )①、4a=0.8 ②、0.17x+2.5 ③、3x+7>15 ④、3.5x-1.7x<8(2)、47除一个数所得的商是6余5,求这个数的方程是( )①、6x+5=47 ②、6x-5=47 ③、47÷6-5=x(3)、当a=8,b=6时,2a+3b等于( )①、36 ②、34 ③、240(4)、甲数是a,是乙数的3倍, 乙数是( )①、3a ②、a÷3 ③、2a(5)、一个正方形边长是8米,若边长增加2米,面积增加( )①、4平方米②、16平方米③、36平方米④、100平方米四、解下列方程.5.5x+6.7=7.8 28-x+3.6=20 3.5x-0.8x=11.348x-27.54÷2.7=1.8 6.2x-x=41.6 9x-14×5.5=58五、列式计算.1、20.3被2.9除的商去乘0.67与1.33的和,积是多少?2、15个8比一个数的4倍多10,求这个数.(列方程解答)3、甲数是x,乙数是甲数的3倍少0.2, 乙数是5.8,甲数是多少?(列方程解答)六、看图列方程.X本文艺术X本X本16本91本故事书七、应用题.1、汽车站有480箱货物,一辆货车运了5次,还剩30箱,平均每次运多少箱?(列方程解答)2、A,B两城相距150千米,甲乙两人同时骑自行车从两地相对出发,甲每小时行16千米,4小时后,两人还相距30千米, 乙每小时行多少千米?3、果园里有桃树和杏树一共1080棵,已知杏树经桃树的棵数多180棵,杏树和桃树各有多少棵?4、一个长方形操场周长是348米,宽是69米,它的面积是多少平方米?5、龟兔赛跑,全程200米,龟每分钟跑2.5米,兔每分钟跑32米,兔自以为是,在途中睡了一觉,当龟到达终点时,兔子离终点还有40米,兔子在途中睡了几分钟?第四单元测试(B 卷)一、 填空.1、长方形周长计算公式用字母表示是( )2、李师傅每天做m 个零件,比张师傅多做8个,两人一天共做( )3、每本练习本x,买了6本,付出10元,应找回( )元.4、甲数是乙数的a 倍,甲数比乙数多( )倍.5、( )叫方程.6、甲乙两数之差是14,两数之和是108,甲数是( ), 乙数是( ).7、a ×(7+b),当a =5时,b=( )才能使a ×(7+b) =52.58、一个正方形周长是a 厘米,用字母表示它面积的式子是( ),当a =24时,正方形面积应是( )平方厘米.二、把左右两边意义相等的用直线连起来.a 与a 相乘 a +2ba 与相加 a 2a 的2倍 2a +3aa 的二分之一 2a比a 的2倍多3的数 a +aa 与b 的和的2倍 21a a 与b 的2倍的和 (a +b)×2三、判断(对的打”√”,错的打”×”)(1)、等式就是方程. ( )(2)、42=4×2 ( )(3)、4x -20=4与50-5x =20的解是相同的. ( )(4)、光明商店上午卖出a 台冰箱,下午卖出b 台冰箱,这天一共卖了ab 台.( )(5)、2.5a +b =2.5ab ( )(6)、2b ×(b +c)=2b 2+2c ( )四、选择(填序号)1、a 除150的商再减去20的差,列式为( )①、a÷150-20 ②、150÷a-20③、a÷(150-20) ④、150÷(a -20)2、下列式子里是方程的有( )①、x+3 ②、3+15=18 ③、4a+27=78 ④、4x-15<203、0.75x-4×1.8=0.3的解是( )①、x=8 ②、x=10 ③、x=1004、根据8x-6=50,可推得3x+7的值是( )①、50 ②、28 ③、215、m是三个连续自然数中间一个数,三个数之和是( )①、3m+2 ②、3m ③、3m+1 ④、3m-1五、当a=4,b=5,c=6时,求下列各式的值.a+3b-2c abc÷12 bc÷a-b六、列方程并求出方程的解.1、5x减去3.2与9的积差是2.7.2、一个数的7.5倍与这个数的4.5倍多24,这个数是多少?七、应用题.1、同学们植树,一班比二班多植63棵,一班42人,平均每人植8棵,二班39人,平均每人植多少棵?(用方程解答)2、买3张桌子和4把椅子一共用了308元,每把椅子32元,每张桌子多少元?(用方程解答)3、一个长方形周长和一个正方形周长相等,已知长方形长24厘米,宽16厘米,求正方形面积?4、两辆汽车从相距400千米的两地同时相对开出,3小时后还相距10千米,已知一辆汽车每小时行驶55千米,求另一辆汽车速度?(用两种方法解答)1、鸡兔同笼,共有35个头,94条腿,求鸡兔各有几只?总复习(一)一、直接写出得数.8-0.72=0.72×2.5×4=7.2÷0.8=0.64÷1.6=8.7÷2.9×2.9= 4.2÷0.1=7.2+6.5+2.8= 1.5×0.75+1.5×0.25=二、用自己喜欢的方法计算下列各题.12.7-(8.65+2.7) 92.5×0.25×4 6.7×0.9+6.7×0.18.25×9.9+0.825 3.4×8.7+34×0.13 6.5×1.1三、笔算下列各题.7.89×4.27 28.56÷5.1 102.6÷3.8四、列式计算.1、8.5与4.2的积比17.8的一半多多少?2、26.34比3.4与4.6的积多多少?总复习(二)一、填空.1、0.78+0.78+0.78+0.78改写成简便算式是( ),这个算式表示的意义是( ),也表示( ).2、5小时24分=( )小时 2.3小时=( )小时( )分3、12.53里面有( )个0.01 125个0.1是( )4、8.789保留整数是( ),保留一位小数是( ),精确到百分位是( )5、20÷6的商是一个( )小数,写成简便记法是( )6、求6.25的十分之三是多少?列式是( )7、在3.6262,3.62,3.62,3.626中,是有限小数的( );是无限小数的有( );纯循环小数是( ),混循环小数是( ).二、判断(1)、8.25×4.7与82.5×0.47的积相等. ( )(2)、无限小数一定比有限小数大. ( )(3)、两个小相等,积一定比其中任何一个因数大.( )(4)、循环小数一定是无限小数.( )(5)、一个数除以小数,商一定比被除数小.( )(6)、3.26的循环节是26.( )三、计算下面各题(得数保留两位小数)3.03÷(0.25×68) 16.06÷5.7×1.74.65×5.73÷3.9总复习(三)一、填空.1、加法、减法叫做( )运算, 乘法,除法叫做( )运算2、只含同一级运算的要( )计算,含有两级运算的要先算( )运算,再算( )运算.3、8.2+4.5×0.3÷1.5这道算式含有( )级运算,要先算( )法,再算( )法,最后算( )法,如果把这道算式改写成先算加,再算除,最后算乘法,列式为( )二、按顺序计算,然后列成综合算式.列综合算式:______________ 列综合算式:______________三、列式计算.1、5.2与3.5的差去除10.5,所得商再加上20.9,和是多少?2、1.28减去1.54与0.31的差,所得的差再乘9.4,积是多少?总复习(四)一、 填空.1、7.2公顷=( )平方米 3.04平方米=( )平方米( )方分米2、两个完全一样的( )梯形可拼成一个长方形,这个拼成的长方形面积是每个梯形面积的( )倍.3、一个三角形与一个平行四边形等底等高,这个三角形面积一定是这个平行四边形面积的( )4、一个平行四边形的面积是63平方米,现在底缩小3倍,高不变,面积是( )平方米.二、计算下面每个图形的面积(单位:厘米)5.2 5.8 4.7 3.4 4.2 4.5 4.8 5.5 3.2三、应用题.1、有一块三角形小麦地,高30米,比底长18米,这块地面积是多少平方米?2、有一个平行四边形底是15分米,高8分米,它和另一个三角形的面积,底相等,这个三角形的高是多少分米?3、如右图,用篱笆围一块菜地,利用了一面墙.篱笆全长40米,这块菜地面积是多少平方米?9米总复习(五)一、填空.1、一个三角形,它的底是a米,高是2米,它的面积是( )2、a+b比a大( ),a-s比a小( )3、a+a+a+a+a=( ) a×a×a=( )4、a、b、c 三数的平均数是( )5、甲数比乙数大5,如果乙数是m,那么甲数是( ),如果甲数是m,那么乙数是( )6、当x=5时,2x-1.7×4的值是( )二、判断题.(对的打”√”,错的打”×”.)1、等式一定是方程.( )2、只含有未知数x的等式才是方程.( )3、a×b×2=2ab,a×2b=2ab. ( )4、2×2=4,22=4,所以a2=a×2. ( )三、解下列方程1.8×2-0.3x=2.4 15x-8x+30=135 8x+0.4×1.2=1.2四、列方程并求出方程的解.1、12.5减去一个数的2.5倍,等于这个数的3.5倍,求这个数?2、3.5除17.5的商比一个数的4倍多0.2,求这个数?总复习(六)应用题.1、梯形上底是a米,下底是b米,高是h米,(1)用字母表示出梯形的面积S.(2)当a=2.5,b=4.8,h=2.4时这个梯形面积是多少?2、一枝钢笔的价钱是一枝圆珠笔的2.5倍,现各买2支,一共用了10.5元,每支钢笔和圆珠笔各是多少元?3、AB两城相距720千米,一列客车从A城开往B城,行2小时后,另一辆货车从B城开往A城,4小时后与客车相遇,已知客车每小时行80千米,货车平均每小时行多少千米?4、一根绳子长13.4米,第一次剪去3.2米,第二次剪去多少米才能使剩下的长度刚好是第一次剪去的2倍?5、甲乙丙三数之和是183,甲数比乙数的2倍多7,丙数比乙数的3倍少4,求甲乙丙三数各是多少?。
人教新课标五年级数学上册《5简易方程——整理与复习》教学设计(1)

人教新课标五年级数学上册《 5 简易方程——整理与复习》教学设计(1)一. 教材分析《5简易方程——整理与复习》这一课是人教新课标五年级数学上册的一部分,主要目的是让学生回顾和巩固之前学习的简易方程知识。
教材通过不同的练习题,让学生在实际操作中理解和掌握简易方程的解法和应用。
二. 学情分析五年级的学生已经学习了一定数量的数学知识,对简易方程有一定的理解。
但在解题过程中,可能会遇到一些困难和混淆。
因此,在教学过程中,教师需要针对学生的实际情况,进行有针对性的指导和讲解。
三. 教学目标1.让学生回顾和巩固简易方程的知识点。
2.提高学生解题的准确性和速度。
3.培养学生独立思考和解决问题的能力。
四. 教学重难点1.重难点:简易方程的解法和应用。
2.难点:在解题过程中,如何快速准确地找到关键信息,并运用所学的简易方程知识。
五. 教学方法采用讲解法、练习法、讨论法等多种教学方法,引导学生主动参与课堂,提高学生的学习兴趣和效果。
六. 教学准备1.准备相关的教学PPT或黑板。
2.准备一些练习题,用于课堂练习和巩固。
七. 教学过程1.导入(5分钟)教师通过简单的讲解,引导学生回顾简易方程的知识点,为新课的学习做好铺垫。
2.呈现(15分钟)教师通过PPT或黑板,展示一些典型的例题,让学生观察和分析。
引导学生运用已学的简易方程知识,解决问题。
3.操练(20分钟)教师给出一些练习题,让学生独立完成。
在学生解题过程中,教师进行巡回指导,帮助学生解决遇到的问题。
4.巩固(15分钟)教师选取一些学生的作业,进行讲解和分析,让学生进一步理解和巩固简易方程的知识。
5.拓展(10分钟)教师给出一些有一定难度的练习题,让学生进行挑战。
通过讨论和讲解,引导学生深入理解简易方程的解法和应用。
6.小结(5分钟)教师引导学生回顾本节课所学的内容,总结简易方程的解法和应用。
7.家庭作业(5分钟)教师布置一些练习题,让学生回家后进行巩固和练习。
简易方程整理和复习

复习三:果园里一共种了340棵桃树和杏树,其 中桃树的棵数比杏数的3倍多20棵。两种树各种 X 了多少棵?
杏树的棵数:
桃树的棵数: X+3X+20=340 想:这道题要求两个未 3X+20 4X+20-20=340-20 知数。我们可以先设其中一 4X=320 个未知数为X,根据题意列方 4X÷4=320÷4 程解答,然后再求出另一个 X=80 未知数。 3X+20=3×80+20 =260 解:设杏树有X棵。那 X X X 多20
解:设第二个书架有x本书,那么第一个书架有1.5x本书。 第一个书架书的本数-第二个书架书的本数=相差的本数 1.5x-x= 50×2 不写单位 0.5x= 100 0.5x÷0.5= 100÷0.5 x= 200 第一个书架:1.5x=1.5×200=300 答:第一个书架是300本,第二个书架是200本。
如: x + 3.2=8、 11x=363、x÷7.6=11.4等都是方程。 3x+1>5 、 x-12.5﹤5 3+6.5=9.5等不是方程。
(3)方程与等式的关系: 等式的范围比方程的范围大。
方程都是等式,但等式不一定是方程。
如:35 ÷7=5、2x=0、 3.5x=4、11.2-x=11.14等都是等式, 但 35÷ 7=5 不是方程。
(4)花金鱼比黑金鱼的1.2倍还多8条。
B. 列方程解决问题。 (1)桔树有150棵,比梨树多30棵,梨树有几棵?
解:设梨树有X棵。 梨树棵数+30棵=桔树棵数 x+30=150 (2)桔树有150棵,是梨树的3倍,梨树有几棵? 解:设梨树有X棵。 梨树棵数×3=桔树棵数 3X=150 (3)桔树有150棵,比梨树的3倍还多30棵,梨树有几棵? 解:设梨树有X棵。 梨树棵数×3+30=桔树棵数 3X+30=150 (4)果园运来25捆桔树和梨树,共150棵,已知每捆桔树 4棵,每捆梨树有几棵? 解:设梨树有X棵。 桔树棵数+梨树棵数=150棵 25×4+25X=150 (5)桔树和梨树共有150棵,桔树棵数是梨树的2倍, 桔树和梨树各有几棵? 解:设梨树有X棵,那么桔树有2X棵。 桔树棵数+梨树棵数=150 2X+X=150
简易方程(整理与复习)

借助线段图理清题意 (借)
找等量关系
(找)
设未知数 列方程
(设) (列)
解方程 检验 写答
(解) (检) (答)
2.小红和小丽去买一种奥运纪念邮票,小红买了10张,小丽买
了8张,小红比小丽多用了6元,每张邮票多少元?(先写出等
量关系式,再列方程解答)
10χ元
小红 :
χ元
8χ元
小丽 :
6元
小红买10张花的钱数-小丽买8张花的钱数=多花的钱数
1. 方程的解与解方程的意义相同。( )
2. 方程4x-6=10的解是( x=4 )。
解: 4x-6=10 4x-6+6=10+6 4x=16 4x÷4=16÷4 x=4
二:解方程的依据是什么?
①等式的两边同时加上或减去相同的数, 等式的基本
等式不变。(同加同减)。
性质1
②等式的两边同时乘或除以相同的数(0 等式的基本
除外),等式不变。(同乘同除)
性质2
注意:在解方程时一定要写上解字。
三、解方程的类型有哪些?如何解方程?
第一类 第二类
第三类
第四类
x±a=b ax=b
ax±b=c
ax±bx=c
方程的两 边同时减 (加)a
方程的两边 先将方程的两 先将含有x的 同时除以 边同时减(加)项合并,然后 a(0除外) b,然后方程 再将方程的两
简易方程(整理与复习)
一:区分概念
1.什么叫做方程? 含有未知数的等式叫做方程。 2.什么叫做方程的解? 使方程左右两边相等的未知数的值,叫做方程 的解。
3.什么叫做解方程? 求方程的解的过程叫做解方程。
1. 在式子6+32=38,5n=75,x+y<z中,方 程 有( 1 )个,等式有( 2 )个。
简易方程整理和复习
利用加数、加数、 利用加数、加数、 和,三者之间的关 系解方程
利用等式的性质( 利用等式的性质(等式 的两边同时减去相等的 数,等式不变 ) 解方程 例一:例一:x+3.2=4.6
例一:x+3.2=4.6 解:x=4.6-3.2 x=1.4
X+2.4x=5.1 3.4x=5.1 X=5.1÷3.4 ÷ X=1.5
利用被除数、除数、 利用等式的性质, 利用被除数、除数、 利用等式的性质,等式 商,三者之间的关 的两边同时乘相等的数, 系解方程 等式不变。解方程 等式不变 解方程 例四: ÷ 0 3 例四:x÷7=0.3 例四:x÷7=0.3 解:x=0.3×7 x=2.1 解:x÷7×7=0.3×7 ÷ × × x=2.1
利用被乘数、乘数、 利用等式的性质, 利用被乘数、乘数、 利用等式的性质,等式 积,三者之间的关 的两边同时除以相等的 系解方程 除外),等式不变。 ),等式不变 数(0除外),等式不变。 解方程 例三:1.6x=6.4 解:x=6.4÷1.6 x=4 例三: 例三: 1.6x=6.4 解:1.6x=6.4 6 1.6x÷1.6=6.4÷1.6 ÷ ÷ x=4
解:x+3.2-3.2=4.6-3.2 x=1.4
利用被减数、减数、 利用等式的性质( 利用被减数、减数、 利用等式的性质(等式 差,三者之间的关 的两边同时加上相等的 系解方程 数,等式不变 ) 解方程 例二:x-1.8=4 解:x=4+1.8 x=5.8 例二:x-1.8=4 例二: 解:x-1.8+1.8=4+1.8 x=5.8
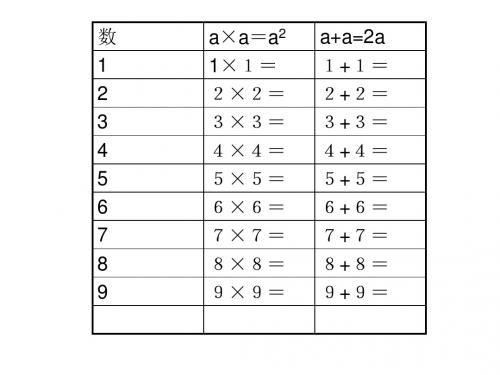
数 1 2 3 4 5 6 7 8 9
a×a=a2 1×1= 2×2= 3×3= 4×4= 5×5= 6×6= 7×7= 8×8= 9×9=
五年级上册简易方程整理与复习课件

列方程解题
2.什么数的3倍正好是5.4的一半?
解:设这个数为x。 3x=5.4÷2 3x=2.7
3x÷3=2.7÷3 x=0.9
答:这个数是0.9。
解决问题
四、常用数量关系
路程=速度×时间 速度=路程÷时间
时间=路程÷速度
总价=单价×数量 单价=总价÷数量
数量 =总价÷单价
总产量=单产量×数量 单产量=总产量÷数量 数量=总产量÷单产量
程左右两边相等的未知数的值。 解方程: 求方程的解的过程。
三、解方程依据
1、等式性质:
等式两边同时加、减、乘、除以相同的数(0除外), 等式依然成立。
三、解方程依据
2、数量关系:
加法:和=加数+加数 一个加数=和-另一个加数 减法:差=被减数-减数 被减数=减数+差
工作总量=工作效率×时间 工作效率=工作总量÷时间
时间=工作总量÷工作效率
算术法与方程对比
1.小明今年9岁,妈妈比小明的4倍少1岁,妈妈今年 几岁? 4×9-1=35(岁) 标准量已知,可用算术法
答:妈妈今年35岁。
2.妈妈今年34岁,比小红的4倍大2岁,小红今年几岁?
解:设小红今年x岁。 4x+2=34
解方程(“ax+bx=c”型):
5x=3x+18 解:5x-3x=3x+18-3x
2x=18 2x÷2=18÷2
x=9
30.6x-5.8x=1.24 解: 24.8x=1.24
x=1.24÷24.8 x=0.05
易错方程
解方程(“ax+b=c”型):
6.5÷x=5.2 解:6.5÷x×x=5.2×x
简易方程整理与复习01

遇呢?
解: 设两车X小时后相遇。 80 X 60 X 840
( 80 60 ) X 840
关键词:
140 X :两车6小时后相遇。
A、B两地相离540千米,红、黄两车分别从 A、B两地同时相向而行、5小时后相遇了。 如果红车比黄车每小时快12Km。那么,这两 车每小时分别各行驶多少千米?
解: 设红车每小时行驶X 千米。
X 5 (X-12) 5 540
5X 5X - 60 540 10X - 60 + 60 540 + 60
X 600 10 X 60 答:红车每小时行驶60 千米。黄车每小时行驶48千米。
例:如图,红车与黄车相距560米,黄 车每秒能行驶15米,这个红车速度为 25m/s。问:红车几秒后能追上黄车?
如图:有两辆长度相同的动车组列车,正同向而行。红车 的速度是180Km/h,蓝车的速度是144Km/h,红车从追上 蓝车到超过蓝车用了27秒的时间。问:这动车组列车的长 度是多少?
你的体会:
1。如何审题,即:注意哪些方面呢? 2。建立方程的关键是什么? 3。建立方程解题的步骤是什么?
解:设第3次重逢时,红点移动的时间为X秒 A 7X 3 X 5 3
4 X 15 E
B
X 15 4
3 1X45
45 4
11.25 D
答:在BC边上
C
拓展题:
相遇分离: 如图:有两辆长度相同的动车组列车,正相向而行。红车 的速度是180Km/h,蓝车的速度是144Km/h,这两车从相 遇到分离只用了2秒的时间。问:这动车组列车的长度是多 少? 追及分离:
学习目的: 1。复习巩固有关“相遇运动”
和“追及运动”的应用问题。 2。通过探究学习,体会把动
简易方程整理与复习

(二)选择。 1.下面的式子中,有( )个是方程。 ①2.5x+7 ②15-3=12 ③6x+y=8.2 ④4x+7<9 ⑤ a+b=b+a A、 1 B、2 C 、3 D 、4 2、下列正确的是( )。 A、5x+2=20,则5x÷5+2=20÷5 B、3.5-x=0.7,则3.5x+x=0.7+x C、x÷3.1=6.2,则x=2 D、6x-0.9=4.5,则6x0.9+0.9=4.5-0.9 3、爸爸今年a岁,比女儿年龄的3倍还大5岁。女儿今年( ) 岁。 A、3a+5 B、3(a+5) C、(a+5)÷3 D、(a-5)÷3 4、甲、乙两车从相距480千米的两地同时出发,相对开出,3小时 后还相距15千米。甲车每小时行75千米,乙车每小时行多少 千米? 解:设乙车每小时行x千米。不正确的方程是( ) A、75×3+3x=480 B、75×3+3x+15=480 C、3(75+x)=480-15 D、3(75+x)+15=480
1.用字母可以表示哪些内容?在含 有字母的式子里,乘号怎样简写、 略写? 2.什么叫做等式?什么叫做方程? 它们有什么关系? 3.什么是方程的解?什么是解方程? 它们之间有什么关系? 4.解方程的依据是什么?
(一)判断对错。
1.x=0既是方程,也是方程的解。( ) 2.方程3÷x=1.5的解是2.( ) 3.只有在x=2时,2x与x2才相等。( ) 4.小明今年m岁,小强今年(m-3)岁,所以 小强比小明小3岁。( )
小结:
利用方程我们可以轻松的解决较复杂 的实际问题。方程是一种很重要的数 学思想方法,我们应该学好它。
作业:关于简易方程这部分内容,你 还有什么没解决的问题,请记录 下来,与同学老师交流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
含有未知数的等式叫方程。
方程一定是等式,但等式不 一定是方程。
使方程左右两边相 等的未知数的值,叫 做方程的解。同一个数,等 式仍然成立。这是等式的 基本性质。 等式两边同时乘(除 以)同一个数(0除外), 等式仍然成立。
两个未知数怎么办? 可以选择其中一个 设为x,用含有x的式子 表示出另一个未知数。 等列方程解出x后,再求 出另一个未知数的值。
两条已知信息怎么用? 可以把其中一条信 息用来写含有x的式子, 表示出另一个未知数, 另一条信息用来作相等 关系列出方程。
(1)填一填 某修路队6小时修路a千米。照这样计算, 1小时可修路( )千米。 小明买了x本笔记本,每本2.5元。付出 40元,应找回( )元。 已知x=4是方程ax-18=6的解,则a的值 是( ) 在自然数中,与数a(a﹥0)相邻的两 个数是( )和( ),这三个数的和 是( )。
(2)火眼金睛辩对错。 方程一定是等式,等式也 一定是方程。( ) 由方程3x+3=3,解得x=0, 所以这个方程没有解。( ) a+b×2可简写成ab2。( )
(3)解决问题: 小红和小明共有 126张邮票,小红的有 票数是小明的2倍。小 红和小明各有多少张 邮票?
(4)解决问题: 甲乙两车从相距272 千米的两地同时相对而行, 3小时后两车相距17千米。 甲每小时行45千米,乙小 时行多少千米?
