典型习题和题例分析与解答
材料力学典型例题及解析 12.冲击问题典型习题解析

击构件瞬间的速度为 υ
,只须将前面(a)式右端改为
1 2
⋅
Pυ2 g
= Vε
,即可导出 kd
=
υ2 。 g∆st
(4)、前面推导过程中,冲击物的势能取为 Ep = P(h + ∆d ) ,一般情况下 ∆d << h ,可将其忽
略,取 Ep = Ph ,读者可仿照上面推导一下,并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为: kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论:(1)、在线弹性范围内,载荷、变形、应变、应力之间都是线性关系,也就是说,当
外载荷被放大 kd 倍,则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解:设小球离开木拍瞬间速度为υ ,则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ;而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ,其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形,
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ,于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数,则有
Fd P
=
∆d ∆st
= σd σ st
五年级简易方程典型练习题

五年级简易方程典型练习题知识分析】大家在课堂上已经学了简单的解方程,现在我们学习比较复杂的解方程。
首先,我们要对方程进行观察,将能够先计算的部分先计算或合并,使其化简,然后求出X 的值。
【例题解读】例 1 解方程:6X+9X-13=17【分析】方程左边的6X与9X可以合并为15X,因此,可以将原方程转化成15X-13=17从而顺利地求出方程的解。
解:6X+9X-13=17,15X-13=1715X=30X=2 。
例2 解方程:10X-7=4.5X+20.5【分析】方程的两边都有X运用等式的性质,我们先将方程的两边同时减去4.5X然后再在两边同时加上7,最后求出X.解:10X-7-4.5X=4.5X+20.5-4.5X, 5.5X-7=20.5 5.5X-7+7=20.5+75.5X=27.5,X=5.【经典题型练习】解方程:7.5X-4.1X+1.8=12解方程:13X+4X-19.5=40解方程:5X+0.7X-3X=10-1.9解方程练习课【巩固练习】1、解方程:7(2X-6)=842、解方程5(X-8)=3X3、解方程4X+8=6X-44、解方程7.4X-3.9=4.8X+11.7列方程解应用题知识分析】大家在三四年级的时候一定学过“年龄问题”吧!记得那时候思考这样的问题挺麻烦的,现在可好啦!我们学习了列方程解应用题, 就可以轻松地解决类似于这样的应用题。
【例题解读】例题 1 今年王老师的年龄是陈强的 3 倍,王老师6 年前的年龄和陈强10 年后的年龄相等,陈强和王老师今年各是多少岁?【分析】要求陈强和王老师两个人的年龄,我们不妨设今年陈强的年龄是X岁王老师的年龄是3X岁,然后根据“王老师在6年前的年龄和陈强10 年后的年龄相等”这个数量关系式,列出方程。
解:设今年陈强的年龄是X岁,王老师的年龄是3X岁,可列方程:3X-6=X+10,2X=16,X=83X=3X 8=24答:陈强今年8 岁,王老师今年24岁。
小学五年级数学易错题库练习题分析及解答

小学五年级数学易错题库练习题分析及解答1.题例:做一种奶油蛋糕,每个要7.5克奶油,50克奶油最多可以做成多少个这样的蛋糕?50÷0.75=66.666…≈67(个)2.错误原因分析:该题在求蛋糕个数取近似值时,许多同学往往根据四舍五入法,取近似值,而不考虑实际生活情况,得67个蛋糕。
而实际生活中在做完66个整蛋糕后,剩下的50克奶油并不够做一个完整的蛋糕。
3.解题思路点拨:该题在解题时应考虑实际生活情况,每个蛋糕要7.5克奶油,50克奶油能做50÷0.75=66(个)……50(克),剩下的50克奶油并不够做一个完整的蛋糕,应该舍去,用去尾法解决该题。
4.解题过程:50÷0.75≈66(个)答:50克奶油最多可以做成66个这样的蛋糕。
5.变式矫正:(1)每套衣服用布2.2米,50米布最多可以做多少套这样的衣服?(2)每个足球45元,汪叔叔用300元最多可以买多少个这样的足球?(3)每个油壶可装3千克油,装40千克油需准备多少个这样的油壶?(4)一堆货物13.6吨,如果用载重量4吨的卡车装运,至少要几次才能运完?(5)幼儿园买了50个蛋糕,每8个装一盒,至少要用多少个这样的盒子?02小学五年级数学下册易错题填空类(一)1.把5米长的绳子平均剪成4段,每段长()米,每段是全长的()。
2.把3kg水果平均分给4个小朋友,每个小朋友分得这3kg 水果的(),每个小朋友分到()kg。
3.王师傅8分钟制作了5个零件,他每分钟能制作()个零件,制作一个零件要()分钟4.把5米长的绳子剪去米,还剩下()米。
5米长的绳子剪去它的,还剩下()米。
5、的分子加上9,分母加()分数的大小才不会变。
6.同时是2、3倍数的最小三位数是(),同时是2、3、5倍数的最小三位数是(),同时是2、3倍数的最大两位数是(),同时是3、5倍数的最大两位数是(),同时是2、3、5倍数的最大两位数是(),100以内最大的质数是(),50以内最大的质数是()。
材料力学典型例题与详解(经典题目)
= 3.64
2、按挤压强度条件确定铆钉数:挤压面面积 A = δ d ,铆钉挤压强度条件为
σ bs
=
Fb Abs
=
F nδ d
≤ [σ
bs]
得
n
≥
δ
d
F [σ
bs
]
=
10
× 10 −3
m
×
160 ×103 20 ×10−3 m
N × 320
× 10 6
N/m 2
= 2.5
两者取大值,最后确定铆钉数 n = 4。
衡条件得 F 作用截面上侧轴力为
FNB +
=
L a2ρ 2
=
4 m × (0.2 m)2 2
× 20 × 103
N/m 3
= 1.6 × 103 N = 1.6 kN
然后将杆沿 F 作用截面(B-B)下侧截开,设截面上轴力为压力 FNB− ,研究上半部分
杆段。这时杆段受本身重量作用和集中力 F 作用,所以由静力平衡条件得 F 作用截面下侧 轴力为
FNB−
=
L a2ρ 2
+
F
=
4 m × (0.2 m)2 2
× 20 ×103
N/m 3
+ 10 ×103
N = 11.6 ×103 N = 11.6 kN
4、计算 A-A 截面轴力:从 A-A 截面将杆截开,设截面上轴力为压力 FNA ,则 FNA 应与该杆
上所有外力平衡。杆所受外力为杆的自重和集中力 F ,杆段自重为 La 2 ρ ,方向向下。于是
2 图示石柱桥墩,压力 F = 1000 kN,石料密度 ρ = 25 kN / m3 ,许用应力 [σ ] =1 MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱;(2)三段等长度的阶梯石柱;(3)等 强度石柱(柱的每个截面的应力都等于许用应力 [σ ] )。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥墩顶截面只 有压力 F 作用,轴力最小;在桥墩底截面,除压力 F 外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱
典型例题解析(化学分析部分)

分析化学典型例题解析(化学分析部分)例 1. 分析某药物的含氮量,测定数据如下:37.45%,37.20%,37.50%,37.30%,37.25%。
计算平均值、平均偏差、相对平均偏差、标准偏差和相对标准偏差,如果真实含量为37.38%,求其绝对误差和相对误差。
[解题分析]该题的主要目的是练习掌握有关误差的基本概念及计算 [解题演示]5%25.37%30.37%50.37%20.37%45.37++++=∑=n x x i 每一次测定值与平均值之差 D 1=x 1-x =37.45%-37.34%=+0.11% 相同的计算方法得d 2= -0.14% d 3=+0.16% d 4= -0.04% d 5=-0.09% 平均偏差 5%09.0%04.0%16.0%14.0%11.0++++=∑=nd d i =0.11%相对平均偏差%29.0%100%34.37%11.0%100=⨯=⨯=x d r d 标准偏差15%)09.0(%)04.0(%)16.0()14.0(%)11.0(1222222--+-++-+=-∑=n d s i 相对标准偏差 %35.0%100%34.37%13.0%100=⨯=⨯=x s s r 绝对误差 %04.0%38.37%34.37=-=-=真实T x E a 相对误差%1.0%100%38.37%04.0%100=⨯=⨯=真实T E a [解题评注] 计算此类习题,误差的基本概念和公式,特别是它们之间的区别与联系要清楚。
该类型的习题是加深理解误差基本概念的较好的题型。
例2 某试样甲乙二人的分析结果分别为甲:40.15%,40.15%,40.14%,40.16% 乙:40.25%,40.01%,40.01%,40.26%问:谁的结果可靠,为什么?[解题分析] 该题目的目的是比较甲、乙两个人的分析结果的可靠性,由于题目并未知试题的真实值,故该题目只能从精密度的角度来考核结果。
(完整版)等差数列典型例题及分析

第四章 数列[例1]已知数列1,4,7,10,…,3n+7,其中后一项比前一项大3.(1)指出这个数列的通项公式;(2)指出1+4+…+(3n -5)是该数列的前几项之和.正解:(1)a n =3n -2;(2) 1+4+…+(3n -5)是该数列的前n -1项的和.[例2] 已知数列{}n a 的前n 项之和为① n n S n -=22 ② 12++=n n S n求数列{}n a 的通项公式。
正解: ①当1=n 时,111==S a 当2≥n 时,34)1()1(2222-=-+---=n n n n n a n 经检验 1=n 时 11=a 也适合,∴34-=n a n ②当1=n 时,311==S a 当2≥n 时,nn n n n a n 21)1()1(122=-----++= ∴ ⎩⎨⎧=n a n 23)2()1(≥=n n [例3] 已知等差数列{}n a 的前n 项之和记为S n ,S 10=10 ,S 30=70,则S 40等于 。
正解:由题意:⎪⎪⎩⎪⎪⎨⎧=⨯+=⨯+7022930301029101011d a d a 得152,521==d a 代入得S 40 =1204023940401=⨯⨯+d a 。
[例5]已知一个等差数列{}n a 的通项公式a n =25-5n ,求数列{}||n a 的前n 项和;正解: ⎪⎪⎩⎪⎪⎨⎧≥+--≤-6,502)5)(520(5,2)545(n n n n n n[例6]已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n 项和的公式吗?[例7]已知:nn a -+=12lg 1024 (3010.02lg =)+∈N n (1) 问前多少项之和为最 大?(2)前多少项之和的绝对值最小? 解:(1) ⎩⎨⎧<-=≥-+=+02lg 102402lg )1(10241n a n a n n 3403340112lg 10242lg 1024<<⇒+≤<⇒n n∴3402=n (2) 0)2lg (2)1(1024=--+=n n n S n 当n n S S 或0=近于0时其和绝对值最小 令:0=n S 即 1024+0)2lg (2)1(=--n n 得:99.680412lg 2048≈+=n ∵ +∈N n ∴6805=n [例8]项数是n 2的等差数列,中间两项为1+n n a a 和是方程02=+-q px x 的两根,求证此数列的和n S 2是方程 0)lg (lg lg )lg (lg lg 2222=+++-p n x p n x 的根。
材料力学典型例题及解析7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁,某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体,并求出各点的主应力。
b = 60 mm ,h = 100 mm 。
解题分析:从图中可分析1、4点是单向应力状态,2点在中性轴上为纯剪切应力状态,31取平行和垂直与梁横截面的六个平面,构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解:、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==)bh I z 1点处弯曲正应力(压应力)MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态,所以021==σσ,MPa 1003−=σ2点为纯剪切应力状态,MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ(向下)容易得到,MPa 301=σ,02=σ,MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ,02=σ,MPa 6.83−=σ4点为单向拉伸应力状态,拉伸正应力的大小与1点相等。
小学四年级奥数巧算年龄例题及练习题-精华版

小学四年级奥数巧算年龄例题及练习题【篇一】例题:爸爸今年43岁,儿子今年11岁。
几年后爸爸的年龄是儿子的3倍?分析与解答:儿子出生后,无论在哪一年,爸爸和儿子的年龄差总是不变的,这个年龄差是43-11=32岁。
所以,当爸爸的年龄是儿子3倍时,儿子是32÷(3-1)=16岁,因此16-11=5年后,爸爸的年龄是儿子的3倍。
练习题:1、妈妈今年36岁,儿子今年12岁。
几年后妈妈年龄是儿子的2倍?2、小强今年15岁,小亮今年9岁。
几年前小强的年龄是小亮的3倍?3、爷爷今年60岁,孙子今年6岁。
再过多少年爷爷的年龄比孙子大2倍?【篇二】例题:甜甜的爸爸今年28岁,妈妈今年26岁。
再过多少年,她的爸爸和妈妈的年龄和为80岁?分析与解答:两人的年龄和每年增加2岁,先求今年爸爸和妈妈的年龄和:28+26=54岁,再求80比54多80-54=26岁。
26里面包含多少个2,就是经过的年数。
所以,再过26÷2=13年爸爸和妈妈的年龄和为80岁。
练习题:1、蜜蜜的爸爸今年27岁,她的妈妈今年26岁。
再过多少年,她爸爸和妈妈的年龄和为73岁?2、林星今年8岁,爸爸今年34岁。
当他们的年龄和为72岁时,爸爸和林星各多少岁?3、今年爸爸56岁,儿子30岁。
当父子的年龄和为46岁时,爸爸和儿子各是多少岁?【篇三】例题:妈妈今年的年龄是女儿的4倍,3年前,妈妈和女儿的年龄和是39岁。
妈妈和女儿今年各多少岁?分析与解答:从3年前到今年,妈妈和女儿都长了3岁,她们今年的年龄和是:39+3×2=45岁。
于是,这个问题可转化为和倍问题来解决。
所以,今年女儿的年龄是45÷(1+4)=9岁,妈妈今年是9×4=36岁。
练习题:1、今年爸爸的年龄是儿子的4倍,3年前,爸爸和儿子的年龄和是44岁。
爸爸和儿子今年各是多少岁?2、今年小丽和她爸爸的年龄和是41岁,4年前爸爸的年龄恰好是小丽的10倍。
第二章习题解答.doc

8第二章 高频小信号放大器典型例题分析与计算例2-1 图2-18所示电路为一等效电路,其中L =0.8uH,Q 0=100,C =5pF,C 1 =20pF,C 2 =20pF,R =10k Ω,R L =5k Ω,试计算回路的谐振频率、谐振电阻。
题意分析 此题是基本等效电路的计算,其中L 为有损电感,应考虑损耗电阻0R (或电导0g )。
解由图2-18可画出图2-19所示的等效电路。
图2-18 等效电路 图2-19 等效电路(1)回路的谐振频率0f由等效电路可知L =0.8H μ,回路总电容C ∑为12122020515(pF)2020C C C C C C ∑⨯=+=+=++则0f ==45.97(MHz)=(2)R L 折合到回路两端时的接入系数p 为211212121112C C p C C C C C C ωω===++则9()2233110.50.0510s 510L P R -=⨯=⨯⨯ 电感L 的损耗电导0g 为0660011245.97100.810100g LQ ωπ-==⨯⨯⨯⨯⨯ ()643.3010s -=⨯总电导 23-3031110.0433100.05101010L g g P R R ∑-=++=+⨯+⨯⨯ ()30.193310s -=⨯谐振电阻 ()P 1 5.17k R g ∑==Ω例2-2 有一个RLC 并联谐振电路如图2-20所示,已知谐振频率f 0=10MHz,L =4μH ,Q 0=100,R =4k Ω。
试求(1)通频带20.7f ∆;(2)若要增大通频带为原来的2倍,还应并联一个多大电阻?题意分析 此题是一个RLC 并联谐振电路的基本计算,了解通频带的变化与回路电阻的关系。
解 (1)计算通频带电感L 的损耗电导0g 为 图2-20 RLC 并联谐振回路066001121010410100g LQ ωπ-==⨯⨯⨯⨯⨯()639.810s -=⨯回路总电导6031139.810410g g R ∑-=+=+⨯⨯ ()6289.810s -=⨯10回路的有载品质因数L Q 为666011g 21010410289.810L Q L ∑ωπ--==⨯⨯⨯⨯⨯⨯13.74=回路通频带()()6600.7101020.72810Hz 0.728MHz 13.74L f f Q ∆⨯===⨯= (2)若通带增大一倍,即20.71.456MHz f ∆=,计算应再并多大电阻R '根据题意要求通频带增大一倍,则回路的有载品质因数应减小一倍,即16.872LL Q Q '== 对应的'g ∑应该增大一倍,即 ()6'2579.610s g g ∑∑-==⨯ 因为0'11g g R R∑=++' 所以0''11g g g g R R ∑∑∑⎛⎫=-+=- ⎪'⎝⎭()6289.810s -=⨯则 3.45k R '=Ω图2-21 单调谐放大电路11例2-3 单调谐放大器如图2-21所示。
材料力学典型例题及解析 1.拉伸应力典型习题解析

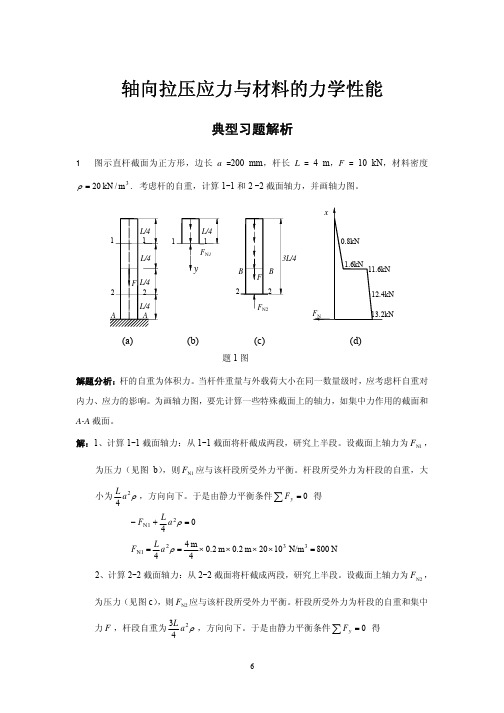
轴向拉压应力与材料的力学性能典型习题解析1 图示直杆截面为正方形,边长a =200 mm ,杆长L = 4 m ,F = 10 kN ,材料密度3m /kN 20=ρ. 考虑杆的自重,计算1-1和2 -2截面轴力,并画轴力图。
解题分析:杆的自重为体积力。
当杆件重量与外载荷大小在同一数量级时,应考虑杆自重对内力、应力的影响。
为画轴力图,要先计算一些特殊截面上的轴力,如集中力作用的截面和A-A 截面。
解:1、计算1-1截面轴力:从1-1截面将杆截成两段,研究上半段。
设截面上轴力为1N F ,为压力(见图b ),则1N F 应与该杆段所受外力平衡。
杆段所受外力为杆段的自重,大小为ρ24a L ,方向向下。
于是由静力平衡条件∑=0y F 得 042N1=+−ρa L F N 800N/m 1020m 2.0m 2.04m 44332N1=××××==ρa L F 2、计算2-2截面轴力:从2-2截面将杆截成两段,研究上半段。
设截面上轴力为N2F ,为压力(见图c ),则N2F 应与该杆段所受外力平衡。
杆段所受外力为杆段的自重和集中力F ,杆段自重为ρ243a L ,方向向下。
于是由静力平衡条件∑=0y F 得(c)(a) (b)题1图(d)kN 12.4N 104.12N/m 1020m 2.0m 2.04m43N 10104333332N2=×=×××××+×=+=ρa L F F 3、计算集中力F 作用截面上的轴力:首先将杆沿力F 作用截面(B-B )上侧截开,设截面上轴力为压力+B F N ,研究上半部分杆段。
由于只受本身重量作用,所以由静力平衡条件得F 作用截面上侧轴力为kN 1.6N 106.1N/m 1020)m 2.0(2m 4233322N =×=×××==+ρa L F B 然后将杆沿F 作用截面(B-B )下侧截开,设截面上轴力为压力−B F N ,研究上半部分杆段。
物质的量专题[整理]:典型例题+习题(含答案)
![物质的量专题[整理]:典型例题+习题(含答案)](https://img.taocdn.com/s3/m/9885ccaedd3383c4bb4cd2e2.png)
一. 知识分析:1. 考查学生的记忆能力,如MCES90第3题:在国际单位制中,物质的量的基本单位是( )A. 千克B. 摩尔C. 立方米D. 克/摩分析:本题考查了学生的记忆能力。
“物质的量”是1971年国际计量大会规定的第七个物理量,表示物质所含微粒数的多少,国际计量大会上规定的七个物理量分别是:质量、长度、热力学温度、时间、电流、光强度、物质的量,它们的单位分别是:千克、米、开尔文、秒、安培、坎德拉、摩尔。
即摩尔是物质的量的基本单位,阿伏加德罗常数个微粒为1摩尔。
对物质的量和摩尔这两个概念的学习,不能单纯靠机械识记,因为它们极具丰富的实践性和内涵,具有很丰实的理解内容,如能掌握它们的真谛,变抽象的概念为具体的模型,就会使记忆准确而持久。
虽说现在高考中单纯考识记的题目所占的比分很小,但很多题目中都包括有记忆的知识。
如果平时不注意记忆、积累,解题一定不会熟练、快捷。
因此,不可忽视记忆的作用。
2. 考查学生的应用能力,如MCEN92第31题:在某温度时,一定量的元素A 的氢化物3AH ,在一定体积的密闭容器中可以完全分解成两种气态物质,此时压强增加了75%,则A 单质的一个分子中有 个A 原子,3AH 分解的化学方程式是 。
分析:本题考查了学生应用阿伏德罗定律解题的能力。
阿伏加德罗定律指出:在相同的温度和压强下,相同体积的任何气体都含有相同的分子。
在温度和体积都不变的条件下,气态物质的压强与其物质的量成正比。
由于反应前后气体的压强之比为75.1:1,则反应前后气态物质的物质的量的和之比也为75.1:1,即7:4,则)(6)()(423g H g A g AH x +=,4=x ,A 单质分子里有4个A 原子,该反应的化学方程式是:24364H A AH +=。
也可以先写出反应的化学方程式为:2323H x A xAH x +=,根据阿伏加德罗定律推出,在体积一定时压强增加75%,即是物质的量增加75%,则%)751(231+=+x x ,4=x 。
带电粒子在电场运动规律经典例题及典型习题(附答案)

带电粒子在电场运动规律透析一、带电粒子在电场中的加速1运动状态的分析:带电粒子沿与电场线平行的方向进入匀强电场,受到的电场力与运动方向在同一直线上,做加(减)速直线运动。
2用功能观点分析:电场力对带电粒子动能的增量。
2022121mv mv qU -= 说明:①此法不仅适用于匀强电场,也适用于非匀强电场。
②对匀强电场,也可直接应用运动学公式和牛顿第二定律典型例题例1:1:如图所示,两平行金属板竖直放置,如图所示,两平行金属板竖直放置,左极板接地,中间有小孔。
右极板电势随时间变化的规律如图所示。
电子原来静止在左极板小孔处。
(不计重力作用)下列说法中正确的是法中正确的是A.A.从从t=0时刻释放电子,电子将始终向右运动,直到打到右极板上B.B.从从t=0时刻释放电子,电子可能在两板间振动C.C.从从t=T /4时刻释放电子,电子可能在两板间振动,也可能打到右极板上D.D.从从t=3T /8时刻释放电子,电子必将打到左极板上解析:从t=0时刻释放电子,如果两板间距离足够大,电子将向右先匀加速T /2,接着匀减速T /2,速度减小到零后,又开始向右匀加速T /2,接着匀减速T /2直到打在右极板上。
……直到打在右极板上。
电子不可能向左运动;电子不可能向左运动;电子不可能向左运动;如果两板间距离不够大,电子如果两板间距离不够大,电子也始终向右运动,直到打到右极板上。
从t=T /4时刻释放电子,如果两板间距离足够大,电子将向右先匀加速T /4,接着匀减速T /4,速度减小到零后,改为向左先匀加速T /4,接着匀减速T /4。
即在两板间振动;如果两板间距离不够大,则电子在第一次向右运动过程中就有可能打在右极板上。
子在第一次向右运动过程中就有可能打在右极板上。
从从t=3T /8时刻释放电子,时刻释放电子,如如果两板间距离不够大,电子将在第一次向右运动过程中就打在右极板上;如果第一次向右运动没有打在右极板上,那就一定会在第一次向左运动过程中打在左极板上。
计算机系统结构第一章课后题答案

1.3 典型习题和题例分析与解答题1.1 有一个经解释实现的计算机,可以按功能划分成4级。
每一级为了执行一条指令需要下一级的N 条指令解释。
若执行第1级的一条指令要K ns 时间,那么执行第2、第3、第4级的一条指令各需要用多少时间?[分析] 计算机按功能分成级时,最底层是第l 级,向上依次为第2、第3和第4级;解释方式的执行是在低级机器级上用它的一串语句或指令来仿真高一级机器级上的一条语 句或指令的功能,而且是通过对高级机器级程序中的每条语句或指令逐条加以解释来实现的。
[解答] 执行第2、第3、第4级的一条指令各需KN ns 、KN 2 ns 、KN 3 ns 的时间。
题1.2 操作系统机器级的某些指令就用传统机器级的指令,这些指令可以用微程序直接实现,而不必由操作系绕自己来实现。
你认为这样做有哪些好处?[解答] 这样做,可以加快操作系统中操作命令解释的速度,同时也节省了存放解释操作命令这部分解释程序所占的存贮空间,简化了操作系统机器级的设计,也有利于减少传统机器级的指令条数。
题1.3 有一个计算机系统可按功能分成4级,各级的指令都不相同,每一级的指令都比其下一级的指令在效能上强M 倍,即第i 级的一条指令能完成第i-1级的M 条指令的计算量。
现若需第i 级的N 条指令解释第i+l 级的一条指令,而有一段第l 级的程序需要运行的时间为K s ,问在第2、3和4级上一段等效的程序各需要运行多长时间?[分析] 因为从功能意义上讲,第i 级的一条指令能完成第i-1级的M 条指令的计算量,但第i 级的一条指令的执行,都是靠第i-1级的N 条指令的执行来解释完成。
已知,第1级的一段程序运行时间为K s 。
第2级的一段程序从功能等效上讲,所需的指令条数应当是第1级上指令数的1/M 。
而由第1级解释时又需要执行N 条指令,所以,第2级一段等效程序的运行就需要K ·s M N 的时间。
第3、4级则可依次类推。
五年级简易方程典型练习题

简易方程【知识分析】大家在课堂上已经学了简单的解方程,现在我们学习比较复杂的解方程。
首先,我们要对方程进行观察,将能够先计算的部分先计算或合并,使其化简,然后求出X的值。
【例题解读】例1解方程:6X+9X-13=17【分析】方程左边的6X与9X可以合并为15X,因此,可以将原方程转化成15X-13=17,从而顺利地求出方程的解。
解:6X+9X-13=17,15X-13=1715X=30X=2。
例2解方程:10X-7=4.5X+20.5【分析】方程的两边都有X,运用等式的性质,我们先将方程的两边同时减去4.5X,然后再在两边同时加上7,最后求出X.解:10X-7-4.5X=4.5X+20.5-4.5X,5.5X-7=20.55.5X-7+7=20.5+75.5X=27.5,X=5.【经典题型练习】解方程:7.5X-4.1X+1.8=12解方程:13X+4X-19.5=40解方程:5X+0.7X-3X=10-1.9解方程练习课【巩固练习】1、解方程:7(2X-6)=842、解方程5(X-8)=3X3、解方程4X+8=6X-44、解方程7.4X-3.9=4.8X+11.7列方程解应用题【知识分析】大家在三四年级的时候一定学过“年龄问题”吧!记得那时候思考这样的问题挺麻烦的,现在可好啦!我们学习了列方程解应用题,就可以轻松地解决类似于这样的应用题。
【例题解读】例题1 今年王老师的年龄是陈强的3倍,王老师6年前的年龄和陈强10年后的年龄相等,陈强和王老师今年各是多少岁?【分析】要求陈强和王老师两个人的年龄,我们不妨设今年陈强的年龄是X岁,王老师的年龄是3X岁,然后根据“王老师在6年前的年龄和陈强10年后的年龄相等”这个数量关系式,列出方程。
解:设今年陈强的年龄是X岁,王老师的年龄是3X岁,可列方程:3X-6=X+10,2X=16,X=83X=3×8=24答:陈强今年8岁,王老师今年24岁。
例题2 今年哥哥的年龄比弟弟年龄的3倍多1岁,弟弟5年后的年龄比3年前哥哥的年龄大1岁,兄弟俩现在各多少岁?【分析】先表示出哥哥和弟弟今年的年龄,然后运用弟弟5年后,哥哥3年前的年龄作为等量关系。
分析化学部分 习题及典型例题分析三

第六章习题和典型例题分析第六章 色谱法典型例题解析例1.在1m 长的填充色谱柱上,某镇静药物A 及其异构体B 的保留时间分别为5.80min和6.60min,峰底宽度分别为0.78min 及0.82min,空气通过色谱柱需1.10min 。
计算(1)组分B 的分配比(2)A 及B 的分离度(3)该色谱柱的平均有效理论塔板数和塔板高度(4)分离度为1.5时,所需的柱长解:(1) 00.510.110.160.6)('=-=-==M M R M R t t t t t k (2) 00.182.078.0)80.560.6(2)(221)1()2(=+-=+-=Y Y t t R R R (3) 2'16)(有效Y t n R = 581)78.010.180.5(162=-=A n720)82.010.160.6(162=-=B n 6502720581=+=平均n (4) 有效有效有效)(H r r R n H L ⨯-=⨯=21,21,22116 =m 56.215.0)17.45.57.45.5(5.1162=⨯-⨯ 例2.采用内标法分析燕麦敌1号试样中燕麦敌的含量时,以正十八烷为内标,称取燕麦敌试样8.12 g,加入正十八烷 1.88g,经色谱分析测得峰面积20.68mm A =燕麦敌, 20.87mm A =正十八烷。
已知燕麦敌以正十八烷为标准的定量校正因子40.2=i f ,计算试样中燕麦敌的百分含量。
解:此法为内标法%4.43%10012.810.8788.140.20.68%100%100%=⨯⨯⨯⨯⨯=⨯=⨯=m f A m f A m m c S S S i i i i例3.采用氢火焰离子化检测器对C 8芳烃异构体样品进行气相色谱分析时,所得实验数据如下:组份 乙苯 对二甲苯 间二甲苯 邻二甲苯A/mm 2 120 75 140 105 'i f 0.97 1.00 0.96 0.98计算各组份的百分含量。
小学行程问题汇总(含典型例题和习题)

小学行程问题汇总(含典型例题和习题)我们把研究路程、速度、时间这三者之间关系的问题称为行程问题。
行程问题主要包括相遇问题、相背问题和追及问题。
这一周我们来学习一些常用的、基本的行程问题。
解答行程问题时,要理清路程、速度和时间之间的关系,紧扣基本数关系“路程=速度×时间”来思考,对具体问题要作仔细分析,弄清出发地点、时间和运动结果。
知道三个量中的两个量,就能求出第三个量。
它大致分为以下三种情况:(1)相向而行:相遇时间=距离÷速度和(2)相背而行:相背距离=速度和×时间。
(3)同向而行:速度慢的在前,快的在后。
追及时间=追及距离÷速度差在环形跑道上,速度快的在前,慢的在后。
追及距离=速度差×时间。
解决行程问题时,要注意充分利用图示把题中的情节形象地表示出来,有助于分析数量关系,有助于迅速地找到解题思路。
在行程问题中,与环行有关的行程问题的解决方法与一般的行程问题的方法类似,但有两点值得注意:一是两人同地背向运动,从第一次相遇到下次相遇共行一个全程;二是同地、同向运动时,甲追上乙时,甲比乙多行了一个全程。
结合分数、百分数知识相关的较为复杂抽象的行程问题。
要注意:出发的时间、地点和行驶方向、速度的变化等,常常需画线段图来帮助理解题意。
例1:甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
两人几小时后相遇?分析与解答:这是一道相遇问题。
所谓相遇问题就是指两个运动物体以不同的地点作为出发地作相向运动的问题。
根据题意,出发时甲乙两人相距20千米,以后两人的距离每小时缩短6+4=10千米,这也是两人的速度和。
所以,求两人几小时相遇,就是求20千米里面有几个10千米。
因此,两人20÷(6+4)=2小时后相遇。
练习 11、甲乙两艘轮船分别从A、B两港同时出发相向而行,甲船每小时行驶18千米,乙船每小时行驶15千米,经过6小时两船在途中相遇。
初中化学经典例题及讲解(50道题)

解析:准确理解分子的含义。 答案:A 1 [例 3] 1 下列说法中,错误的是( ) A. 质子数相同的粒子,可能分别是同一种元素的原子和离子,也可能分别是 同一种元素的两种离子 B. 只含有一种元素的物质一定不是化合物,可能是混合物 C. 由不同元素组成的物质一定是化合物 D. 任何离子中所带的质子总数与电子总数一定不相等 解析:对元素中各种粒子的相互关系应准确掌握。
应是交叉关系,但有很多化合反应不属于氧化反应;在 D 中,有许多还原反应不是
置换反应。 答案:B
[例 3] 表中 1~5 组的物质分类正确的是( )
1
2
3
4
5
酸 硝酸 硫酸 盐酸 酸式硫 氢硫酸
第 2 页 共 42 页
酸钠
碱 烧碱
碱式碳
纯碱 苛性钠
消石灰
酸铜
盐 大理石 胆矾 纯碱 蓝矾 石灰石
A. ①③④ B. ②③⑤ C. ④⑤ D. ①③⑤
③ 与碱作用
CO2 Ca(OH )2 CaCO3 H2O
: ②
还原性:
④氧化性: C CO2 高温 2CO
3CO Fe2O3 高温
是酸性氧化物。
2Fe 3CO2 CO CuO Cu CO2
是不成盐氧化物。
制 ① 工业制法:煅烧石灰石 ① 工业制法:碳不充
法
CaCO3 高温 CaO CO2
别和联系。对纯净物和混合物、化合反应和分解反应等,则可采取辩证的方法。有
第 3 页 共 42 页
些易混淆的概念,可以运用综合练习的习题复习法。
行测逻辑推理题库(例题及试题解析)

行测逻辑推理题库(例题及试题解析)一、利用分析矛盾解析考试中有这样的试题:试题1:某仓库失窃,四个保管员因涉嫌而被传讯。
四人的供述如下:甲:我们四人都没作案;乙:我们中有人作案;丙:乙和丁至少有一人没作案;丁:我没作案。
如果四人中有两人说的是真话,有两人说的是假话,则以下哪项断定成立?()A.说真话的是甲和丁B.说真话的是乙和丙C.说真话的是甲和丙D.说真话的是乙和丁这是典型的利用分析矛盾解析的试题。
历年至今,在全国各地考试中屡见鲜见。
解析这类试题,关键要找到条件之间的逻辑矛盾,然后真假自明。
什么是逻辑矛盾?简明地说,两个不同的断定,必有一个真,一个假。
比如:“这马是白的”和“这马不是白的”就构成了逻辑矛盾。
两者不能同真也不能同假。
而“这马是白的”和“这马是黄的”就不是逻辑矛盾。
虽然它们不能同真,但有可能都是假的一一如果它是一匹红色的马呢?了解了这些常识,可以利用分析矛盾的方法,解答上题。
[解析](1)四人中,两人诚实,两人说谎。
(2)甲和乙的话有矛盾!甲:我们四人都没作案;乙:我们中有人作案;可断定:甲和乙两人一个诚实一个撒谎。
剩余丙、丁两人中也必然是一个诚实一个撒谎。
(3)假设:丁说的是真话,那么,可推出丙说的话也真!丙:乙和丁至少有一人没作案;丁:我没作案。
显然,丁说真话不成立,于是推出:丁说假话,丙说真话。
(4)断定了丁说假话,就推出甲说的也是假话,乙说真话。
答案B。
即:说真话的是乙和丙。
试题2:军训最后一天,一班学生进行实弹射击。
几位教官谈论一班的射击成绩。
张教官说:“这次军训时间太短,这个班没有人射击成绩会是优秀。
”孙教官说:“不会吧,有几个人以前训练过,他们的射击成绩会是优秀。
”周教官说:“我看班长或是体育委员能打出优秀成绩。
”结果发现三位教官中只有一人说对了。
由此可以推出以下哪一项肯定为真?()A.全班所有人的射击成绩都不是优秀B.班里所有人的射击成绩都是优秀C.班长的射击成绩是优秀D.体育委员的射击成绩不是优秀[解析](1)三人中只有一个说的对。
光合作用和呼吸作用典型例题和练习题

光合作用典型例题例1在“绿叶在光下制造淀粉”的实验中,先将天竺葵放在黑暗处一昼夜,其目的是()A.使叶片内原有的淀粉消耗掉。
B.使叶内的淀粉储存在叶绿体中。
C.停止光合作用,使淀粉储存在叶肉细胞中。
D.储备养料,准备进行光合作用。
【答案】A。
【分析】本题考察的是学生能否理解实验设计中对“淀粉”这一因素的处理和控制。
本实验要证明淀粉是在光照下合成的,首先应使叶片中处于无淀粉的状态,即在黑暗处消耗掉原有的储存的淀粉,然后在有无光照的差别下再检验有无淀粉的形成。
例2在做“绿叶在光下制造淀粉”的实验时,用黑纸片把叶的一部分把两面遮盖起来,移到阳光下几小时后,摘下叶片,去掉黑纸片时()A.被遮盖的部分颜色变浅。
B.被遮盖的部分没有变蓝,而其他部分变成蓝色。
C.叶片无明显的颜色差别。
D.遮盖部分绿色深,其他部分绿色浅。
【答案】C。
【分析】本题一方面考察学生在实验中是否有细致的观察,另一方面考察学生对淀粉的检验方法是否理解。
例3把叶片放入酒精隔水加热的目的是()A.溶解叶片中的淀粉,避免将叶片烫死B.将淀粉煮熟,避免将叶片烫死C.溶解叶片中的叶绿体,避免酒精过度挥发D.溶解叶片中的叶绿素,避免酒精燃烧起来【答案】D。
【分析】这也是对实验中包含的科学道理的理解问题,要求学生知道实验的设计原理:一是为什么要去掉色素,怎样去掉;二是为什么要隔水加热。
1.下列哪一组生物都能够进行光合作用()A.苔藓和蘑菇B.蕨类和种子植物C.草履虫和酵母菌D.细菌和病毒2.植物能够进行光合作用的部位是()A.整个植物体B.绿色的叶片C.所有绿色的部分D.只有茎和叶3.下列关于光合作用意义的叙述不正确的一项是()A.为动物和人类提供能量B.为植物体自己制造有机物C.吸收氧气,释放二氧化碳D.吸收二氧化碳,释放氧气4.人们常在清晨和下午到草地或树林中锻炼身体。
你认为在哪一个环境中植物光合作用产生的氧气更多()A.清晨的草地B.下午的草地C.清晨的树林D.下午的树林5.填空题①植物光合作用需要的能量来源于。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.3 典型习题和题例分析与解答题5.1 假设指令的解释分取指、分析和执行3步,每步的时间相应地为t取指、t分析、t执行,(1)分别计算下列几种情况下,执行完100条指令所需时间的一般关系式;i.顺序方式;ii.仅“执行x”与“取指x剩”重叠,iii.仅“执行x”、“分析r+:”,“取指。
+:”重叠.(2)分别在t取指=t分析=2,t执行=l及t取指=t执行=5,t分析 =2两种情况下,计算出上述各结果。
[分析] 可先按指令间所要求的时间关系画出指令间的时间重叠关系图,由图就可以列出各种情况下,计算100条指令所需时间的一般关系式。
再将给出的时间值代入,实际完成100条指令所需的时间就可以求得。
*顺序方式工作的时间关系如图5.1所示。
取指k分析k执行k取指k+1分析k+1执行k+1取指k+2分析k+2执行k+2图顺序方式工作的时间关系图仅“执行k”与“取指k+1”、重叠方式工作的时间关系如图5.2所示.取指k分析k执行k取指k+1分析k+1执行k+1'取指k+2分析k+2执行k+2图5.2 仅“执行k”,与“取指k+1”重叠方式工作的时间关系图仅“执行k”、“分析k+1”、“取指k+2”重叠方式工作的时间关系如图5.3所示.取指k分析k执行k取指k+1分析k+1执行k+1^取指k+2分析k+2执行k+2图5.3 仅“执行k”、“分析k+1”、“取指k+2”重叠方式工作的时间关系图[解答] (1)计算执行完100条指令所需要的时间:(i)顺序方式工作时为100(t t t⨯++取指分析执行)(ii)仅“执行k”,与“取指k+1”重叠方式工作时为—{}10099maxt t t t t++⨯+取指分析取指执行执行,(iii)仅“执行k”、“分析k+1”、“取指k+2”重叠方式工作时为{}{}{} max98max max,t t t t t t t t t ++⨯++取指分析取指取指分析执行执行分析执行,,,(2)当t取指=t分析=2、t执行=l时,代入上面的各式,可求得100条指令执行所需要的时间是:顺序方式工作时为500。
仅“执行k”,与“取指k+1”重叠方式工作时为401。
仅“执行k ”、“分析k+1”、“取指k+2”重叠方式工作时为203。
【当 t 取指=t 执行=5,t分析 =2,代入上面的各式,可求得100条指令执行所需要的时间是:顺序方式工作时为1200。
仅“执行k”,与“取指k+1”重叠方式工作时为705。
仅“执行k ”、“分析k+1”、“取指k+2”重叠方式工作时为510。
题5.2 流水线由4个功能部件组成,每个功能部件的延迟时间为△t 。
当输。
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ① ②图5.4 题5. 2的流水时空图所以,按周期性工作时的流水线平均吞吐宰为: 《 105147p T t t==∆∆题5.3 有一个浮点乘流水线如图5.5(a)所示,其乘积可直接返回输入端或暂存于相应缓冲寄存器中,画出实现A*B*C*D 的时空图以及精入端的变化,并求出该流水线的吞吐率和效率;当流水线改为图5.5(b)形式实现同一计算时,求该流水线的效率及吞吐率。
[分析] 为了减少运算过程中的操作数相关,A*B*C*D 应改为采用((A*B) * (C*D))的算法步骤进行运算。
[解答] 按图5.5(a)组织.实现A*B*C ,D 的时空关系如图5.6所示。
-吞吐率 313p T t =∆效率 35531313t t η⨯∆==⨯∆流水按图(b )组织时,实现A*B*C*D 的时空关系如图所示。
吞吐率 311p T t =∆效率 35531111t t η⨯∆==⨯∆题5.4 一个4段的双输入端规格化浮点加法流水线,每段经过时间10ns ,输出可直接返回输入或将结果暂存于相应缓冲器中,问最少需经多少时间能求出10∑ii=1A,并画出时空图。
[分析] 为了避免流水线的先写后读相关,使流水线性能尽可能高,需将10∑i i=1A调整成$((((1A +2A )+(3A 十4A ))十(j t 9A +10A ))+((5A +6A )+(7A +8A ))) 的算法步骤来进行。
[解答] 按((((1A +2A )+(3A 十4A ))十(8A 9A +10A ))+((5A +6A )+(7A +8A ))) 流水的时空图如图5.8所示.由图5.8之时空图可知,求10∑i i=1A 所需要的最少时间为170ns 。
题 为提高流水线的效率可用哪两种主要途径来克服速度瓶颈现有3段流水线各段经过的时间依次为△t 、3△t 、△t 。
|(1)分别计算在连续输入3条指令时和30条指令时的吞吐率和效率。
(2)按两种逾径之一改进,画出你的流水线结构示意图.同时计算连续输入3条指令和30条指令时的吞吐率和效率。
(3)通过对(1)、(2)两小题的计算比较可得出什么结论[分析] 根据题意可以看出,原3段的流水线工作起来仍可看成是一条线性流水线只是其中经过时间为3△t 的段是瓶颈段,所以可以按1(1)p miji nT t n t==∆+-∆∑及 11(1)mii mi j i n t m t n t η==•∆=⎡⎤∆+-∆⎢⎥⎣⎦∑∑来求得p T 和η.其中,n 为连续输入的指令数,m 为3个段,,△1t =△t ,2t =3△t ,△3t =△t, △j t 为瓶颈段经过时间,本题的△j t 为3△t 。
在改进流水性能时,无论是将瓶颈段2段细分成3个时间分别为△t 的子段,还是用3个瓶颈段2段并联,计算吞吐率、效率时,只需将公式中的m 由3改成5,△j t 改成,△i t 即可。
…[解答] 提高流水线效率,消除速度瓶颈主要有将瓶颈段再细分以及重复设置多个颈段并联工作,给其轮流分配任务的两种途径。
(1)在3段流水线,各段经过时间依次为△t 、3△t 、△t 的情况下,连续流入3条指令时,将n=3,m =3,△1t =△t ,2t =3△t ,△3t =△t, △j t =3△t 代入,可得吞吐率p T ,和效率η为13352311(1)p miji nT t t tt n t====∆+⨯∆∆∆+-∆∑1135531111(1)mii m i j i n t t t m t n t η==•∆⨯∆===⨯∆⎡⎤∆+-∆⎢⎥⎣⎦∑∑而连续流入30条指令时,只需将上式之n 改为30,其它参数不变,得 31303015529346(301)p iji T t t tt t====∆+⨯∆∆∆+-∆∑3052539246t t η⨯∆==⨯∆ 。
(2)若采取将2段细分成3个子段,每个子段均为△t ,构成的流水线结构如图5.92所示。
连续流入3条指令时,将n =3,m =5,△i t =△j t =△t 代入,得 51333527(31)p iii T t t tt t====∆+∆∆∆+-∆∑5133515575717ii t t tt tη=•∆⨯∆===⨯∆⨯∆∆∑连续流入30条指令时,将n=30代入,其它参数不变,有 5130301552917(301)p iii T t t tt t====∆+∆∆∆+-∆∑"3051553417t t η⨯∆==⨯∆若采取将3个2段并联构成的流水线,其构成如图5.10所示。
连续流入3条指令及流入30条指令时的吞吐率p T ,和效率η所计算的结果分别与子过程细分的相同。
(3)将(1)题的计算结果进行比较可以看出,只有当连续流入流水线的联指令越多时,流水线的实际吞吐率和效率才会提高。
将(1)、(2)题的计算结果进行比较,同样可以看出,无论采用瓶颈子过程再细分,还是将多个瓶颈子过程并联来消除流水线瓶颈,都只有在连续流入流水线的指令数越多时才能使实际吞吐率和效率得到显著的提高。
若连续流入流水线的指令数太少,消除流水线瓶颈虽可以提高流水线的实际吞吐率p T ,而效率η却可能下降。
题 有一个双输入端的加一乘双功能静态流水线,由经过时间为△t 、2△t 、2△t 、△t 的l 、2、3、4四个子过程构成.加按1—2—4连接,乘按1—3—4连接,流水线,S 出设有数据缓冲器,也可将数据直接返回输入.现要执行A*(B+C*(D+E*F ))+G*H的运算,请调整计算顺序,画出能获得吞吐率尽量高的流水时空图,标出流水线入,出端数据的变化情况,求出完成全部运算的时间及此期间流水线的效率.如对流水线瓶颈子过程再细分,最少只需多少时间可完成全部运算若子过程3不能再细分,只能用并联方法改进,问流水线的效率为多少 )[分析] 因为是加一乘双功能静态流水线,为了能有高的吞吐率,应减少流水线的功能切换次数。
因此,宜将算法调整成先一连串的乘,然后再切换成一连串的加.这样,将计算式展开成 :A*B+A*C*D+A*C*E*F+G*H对于该表达式的计算,自然应先进行乘法流水.为了减少因先写后读相关而等待的时间,应尽量安排对计算式子项数量多的乘法先进行操作.此外,由于流水线中瓶颈子过程为 2△t ,所以,流水输入端最快也只能每隔2△t 输入一组数据。
[解答] 根据题意,对算法经调整后,能使流水吞吐宰尽量高的流水时空图如图所示。
图中已标出了流水线入、出端的数据变化情况.根据图5.11的流水时空图,可以看出,完成全部运算的时间为2△t 。
在此期间的流水线效率1122334455667788)))))))a b a b a b a b a b a b a b a b •+•+•+•+•+•+•+•(((((((如果现在将瓶颈子过程2和3均细分成两个子过程.则时空图如图5.12所示。
…图5.12 子过程细分后的沈水线时空图由田5.12可见,完成全部运算最少需要18△t 的时间即可。
现在若干过程3不能再细分了,只能用2个子过程3通过并联来改进,则其时空图如图5.13所示。
完成全部运算时的流水线效率241216183t t t η∆+∆==⨯∆题 现在长度为8的向量A 和B ,请分别画出在下列4种结构的处理器上求点积A •B 的时空图,并求完成全部结果的最少时钟拍数。
设处理器中每个部件的输出均可直接送到任何部件的输入端或存入缓冲器,其间的传送延时不计,指令和源操作数均能连续提供。
(1)… (2) 处理器有一个乘法部件和一个加法部件,不能同时工作,部件内也只能顺序方式工作,完成一次加法或乘法均只需5拍;(3) 与(1)基本相同,只是乘法部件和加法部件可并行;(4) 处理器有一个乘、加功能静态流水线,乘、加均由5个部件流水段构成,各段经过时间要1拍;(5) 处理器有乘、加两条流水线,可同时工作,各由5段构成,每段经过时间为1拍。
[分析] 长度为8的向量A 和B 的点积为811223344556677881i i i A B a b a b a b a b a b a b a b a b a b =•=•=+++++++∑共需做8次乘法和7次加法。
