2017第34届全国中学生物理竞赛决赛真题几答案解析
最新第34届全国中学生物理竞赛复赛理论考试试题和答案

第34届全国中学生物理竞赛复赛理论考试试题解答2017年9月16日一、(40分)一个半径为r 、质量为m 的均质实心小圆柱被置于一个半径为R 、质量为M 的薄圆筒中,圆筒和小圆柱的中心轴均水平,横截面如图所示。
重力加速度大小为g 。
试在下述两种情形下,求小圆柱质心在其平衡位置附近做微振动的频率: (1)圆筒固定,小圆柱在圆筒内底部附近作无滑滚动; (2)圆筒可绕其固定的光滑中心细轴转动,小圆柱仍在圆筒内底部附近作无滑滚动。
解: (1)如图,θ为在某时刻小圆柱质心在其横截面上到圆筒中心轴的垂线与竖直方向的夹角。
小圆柱受三个力作用:重力,圆筒对小圆柱的支持力和静摩擦力。
设圆筒对小圆柱的静摩擦力大小为F ,方向沿两圆柱切点的切线方向(向右为正)。
考虑小圆柱质心的运动,由质心运动定理得sin F mg ma θ-= ①式中,a 是小圆柱质心运动的加速度。
由于小圆柱与圆筒间作无滑滚动,小圆柱绕其中心轴转过的角度1θ(规定小圆柱在最低点时10θ=)与θ之间的关系为1()R r θθθ=+ ②由②式得,a 与θ的关系为22122()d d a r R r dt dtθθ==- ③考虑小圆柱绕其自身轴的转动,由转动定理得212d rF I dtθ-= ④式中,I 是小圆柱绕其自身轴的转动惯量212I mr = ⑤由①②③④⑤式及小角近似sin θθ≈ ⑥ 得22203()θθ+=-d gdt R r ⑦由⑦式知,小圆柱质心在其平衡位置附近的微振动是简谐振动,其振动频率为f =⑧(2)用F 表示小圆柱与圆筒之间的静摩擦力的大小,1θ和2θ分别为小圆柱与圆筒转过的角度(规定小圆柱相对于大圆筒向右运动为正方向,开始时小圆柱处于最低点位置120θθ==)。
对于小圆柱,由转动定理得221212θ⎛⎫-= ⎪⎝⎭d Fr mr dt⑨对于圆筒,同理有2222()θ=d FR MR dt ⑩由⑨⑩式得22122221θθ⎛⎫-+=- ⎪⎝⎭d d F r R m M dt dt ⑪设在圆柱横截面上小圆柱质心到圆筒中心轴的垂线与竖直方向的夹角θ,由于小圆柱与圆筒间做无滑滚动,有12()θθθθ=+-R r R ⑫ 由⑫式得22212222()θθθ-=-d d d R r r R dt dt dt⑬设小圆柱质心沿运动轨迹切线方向的加速度为a ,由质心运动定理得 sin F mg ma θ-= ⑭ 由⑫式得22()θ=-d a R r dt⑮由⑪⑬⑭⑮式及小角近似sin θθ≈,得22203d M m gdt M m R rθθ++=+- ⑯由⑯式可知,小圆柱质心在其平衡位置附近的微振动是简谐振动,其振动频率为f =⑰评分参考:第(1)问20分,①②式各3分,③式2分,④式3分,⑤⑥式各2分,⑦式3分,⑧式2分;第(2)问20分,⑨⑩⑪式各2分,⑫式3分,⑬⑭⑮式各2分,⑯式3分,⑰式2分。
2017年初中物理竞赛试题参考答案和评分标准

2017年初中物理竞赛试题参考答案和评分标准一、单项选择题(每小题3分,共18分)1.B2.C3.D4.A5.A6.A二、填空题(第7-8题每题3分,第9题4分,第10题3分,共13分)7.保持F竖直向上8.6N9. 0 1010.红绿蓝白反射红光三、实验设计题(每题6分,共18分)11.器材:篮球、带阀门(夹子)的胶管、打气筒、天平、量筒、水、水槽操作步骤:(1)取一球胆(篮球)接一根带阀门(夹子)的胶管,用打气筒向球内打足气后,用天平称出其质量m1.(2)如图所示,用排水集气法在量筒中收集气体,集气完毕后,拧紧夹子,上下移动量筒,使其内外水平面一样高,以保证内外气体压强相等,然后由量筒刻度读出气体体积V.(3)再用天平称出放出气体后篮球的质量m2,篮球体积不变,避免篮球浮力对测量的影响。
则量筒内气体的质量为m1-m2.(4)空气的密度注:实验要考虑到压强和浮力对实验的影响,否则最多得3分12.如图(有错不给分) 13.如图(有错不给分)四、计算题(共27分)14.开关S 闭合,L 1和L 2并联后与L 3串联。
L 3为“6V 、 1W ”,它的电阻为:R 3=U 2/P 3=36Ω。
(1分)L 1和L 2为“6V 10W ”,电阻均为R=U 2/P=3.6Ω。
总电阻R 总=R 3+R/2=37.8Ω(1分) 通过L 3的电流I 3=U /R 总=0.16A (1分)L 3的功率P 3=I 2R=0.92W ,与L 3的额定功率(1W)相差不多,L 3能发光.(2分) L 1和L 2并联,通过每只灯泡的电流I 1=I 2=I 3/2=0.08A ,L 1的实际功率为P 1=I 2R=0.023W ,比它的额定功率10W 小得多,L 1不能发光。
同理,L 2也不能发光。
(2分)15.解:(1)F 浮=ρ水gV 排 =1×103kg/m 3×10N/kg ×4×10-2m 3=400N (2分) (2)P =Fυ P 1= F 1υ绳=2 F 1υ P 2= F 2υ绳 =2 F 2υ21F F =21P P =1516 ① (2分) (3)在匀速提升水中物体M 的过程中,以动滑轮A 和物体M 为研究对象,受力分析如图3甲所示;在匀速提升水中物体M 的过程中,以动滑轮B 和物体M 为研究对象,受力分析如图图32F 1 F 浮 G 1G 甲 2F 2F 浮G 2G 乙3乙所示。
2017第34届全国重点中学生物理竞赛复赛理论考试试题和参考答案

第34届全国中学生物理竞赛复赛理论考试试题解答2017年9月16日由⑦式知,小圆柱质心在其平衡位置附近的微振动是简谐振动,其振动频率为 f =(2)用F 表示小圆柱与圆筒之间的静摩擦力的大小,1θ和2θ分别为小圆柱与圆筒转过的角度(规定小圆柱相对于大圆筒向右运动为正方向,开始时小圆柱处于最低点位置120θθ==)。
对于小圆柱,由转动定理得221212θ⎛⎫-= ⎪⎝⎭d Fr mr dt⑨对于圆筒,同理有2222()θ=d FR MR dt⑩由⑨⑩式得22122221θθ⎛⎫-+=- ⎪⎝⎭d d F r R m M dt dt ?设在圆柱横截面上小圆柱质心到圆筒中心轴的垂线与竖直方向的夹角θ,由于小圆柱与圆筒间做无滑滚动,有12()θθθθ=+-R r R ? 由?式得22212222()θθθ-=-d d d R r r R dt dt dt?设小圆柱质心沿运动轨迹切线方向的加速度为a ,由质心运动定理得道半径的三分之一,不考虑地球和彗星之间的相互影响。
求彗星 (1)先后两次穿过地球轨道所用的时间; (2)经过C 、D 两点时速度的大小。
已知积分公式()()3/21/2223x a a x a C =+-++,式中C 是任意常数。
解:(1)由题设,彗星的运动轨道为抛物线,故 1, 0E ε==①彗星绕太阳运动的轨道方程为:1cos kr θ=+②彗星绕太阳运动过程中,机械能守恒()2221022L mr V r E mr ++==&③ 式中()MmV r Gr=-④⑥式得2T t =∆=⑩将题给数据代入⑩式得66.4010s T ≈⨯?(2)彗星在运动过程中机械能守恒2102GMm m E r-==v ? 式中v 是彗星离太阳的距离为r 时的运行速度的大小。
由?式有=v 当彗星经过C 、D 处时C D E r r R ==?由??式得,彗星经过C 、D 两点处的速度的大小为C D =v v ? 由?式和题给数据得 4C D 4.2210m/s ==⨯v v ?评分参考:第(1)问28分,①式4分,②式2分,③式4分,④式2分,⑤式4分,⑥⑦⑧⑨⑩?式各2分;第(2)问12分,?式4分,????式各2分。
第34届全国中学生物理竞赛决赛试题
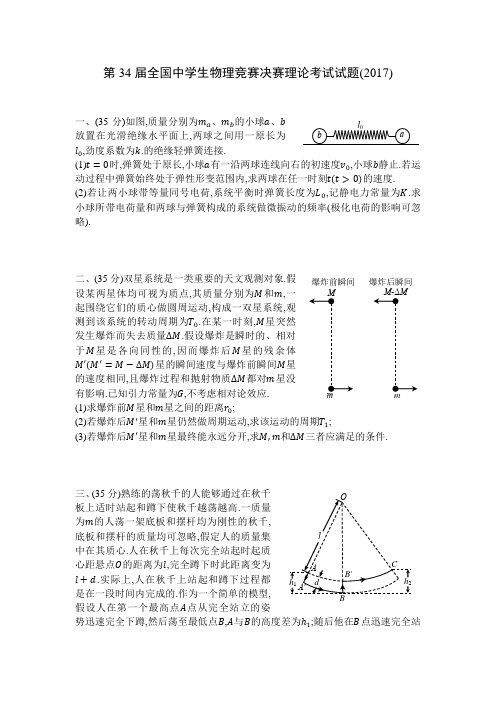
第34届全国中学生物理竞赛决赛理论考试试题(2017)一、(35分)如图,质量分别为 、 的小球 、 放置在光滑绝缘水平面上,两球之间用一原长为 ,劲度系数为 .的绝缘轻弹簧连接.(1) 时,弹簧处于原长,小球 有一沿两球连线向右的初速度 ,小球 静止.若运动过程中弹簧始终处于弹性形变范围内,求两球在任一时刻 的速度.(2)若让两小球带等量同号电荷,系统平衡时弹簧长度为 ,记静电力常量为 .求小球所带电荷量和两球与弹簧构成的系统做微振动的频率(极化电荷的影响可忽略).二、(35分)双星系统是一类重要的天文观测对象.假设某两星体均可视为质点,其质量分别为 和 ,一起围绕它们的质心做圆周运动,构成一双星系统,观测到该系统的转动周期为 .在某一时刻, 星突然发生爆炸而失去质量 .假设爆炸是瞬时的、相对于 星是各向同性的,因而爆炸后 星的残余体星的瞬间速度与爆炸前瞬间 星的速度相同,且爆炸过程和抛射物质 都对 星没有影响.已知引力常量为 ,不考虑相对论效应. (1)求爆炸前 星和 星之间的距离 ;(2)若爆炸后 星和 星仍然做周期运动,求该运动的周期 ;(3)若爆炸后 星和 星最终能永远分开,求 和 三者应满足的条件.三、(35分)熟练的荡秋千的人能够通过在秋千板上适时站起和蹲下使秋千越荡越高.一质量为 的人荡一架底板和摆杆均为刚性的秋千,底板和摆杆的质量均可忽略,假定人的质量集中在其质心.人在秋千上每次完全站起时起质心距悬点 的距离为 ,完全蹲下时此距离变为 .实际上,人在秋千上站起和蹲下过程都是在一段时间内完成的.作为一个简单的模型,假设人在第一个最高点 点从完全站立的姿势迅速完全下蹲,然后荡至最低点 , 与 的高度差为 ;随后他在 点迅速完全站l 0a b 爆炸前瞬间爆炸后瞬间起(且最终径向速度为零),继而随秋千荡至第二个最高点 ,这一过程中该人质心运动的轨迹如图所示.此后人以同样的方式回荡,重复前述过程,荡向第3、4等最高点.假设人站起和蹲下的过程中,人与秋千的相互作用力始终与摆杆平行.以最低点 为重力势能零点.(1)假定在始终完全蹲下和始终完全站立过程中没有机械能损失,求该人质心在 各个阶段的机械能及其变化;(2)假定在始终完全蹲下和始终完全站立过程中的机械能损失 与过程前后高度差的绝对值 的关系分别为,始终完全蹲下,始终完全站立这里, 、 、 和 是常量, 是重力加速度的大小.求(i)相对于 点,第 个最高点的高度 与第 个最高点的高度 之间的关系; (ii) 与 之间的关系式和 与 之间的关系式.四、(35分)如图,在磁感应强度大小为 、方向竖直向上的匀强磁场中.有一均质刚性导电的正方形线框abcd,线框质量为 ,边长为 ,总电阻为 .线框可绕通过ad 边和 边中点的光滑轴 转动. 、 点是线框引线的两端, 轴和 轴位于同一水平面内,且相互重直,不考虑线框自感.(1)求线框绕 轴的转动惯量 ;(2) 时,线框静止,其所在平面与 轴有一很小的夹角 ,此时给线框通以大小为 的恒定直流电流,方向沿 ,求此后线框所在平面与 轴的夹角 、线框转动的角速度 和角加速度 随时间变化的关系式;(3) 时,线框平面恰好逆时针转至水平,此时断开 、 与外电路的连接.此后线框如何运动?求 、 间电压 随时间变化的关系式;(4)线框做上述运动一段时间后,当其所在平面与 轴夹角为 时,将 、 短路,线框再转一小角度 后停止,求 与 的关系式和 的最小值五、(35分)如图,某圆形薄片材料置于 水平面上,圆心位于坐标原点 平面上方存在大小为 、沿 轴负向的匀强电场,以该圆形材料为底的圆柱体区域内存在大小为 、沿 轴正向的匀强磁场,圆柱体区域外无磁场.从原点 向 平面上方的各方向均匀发射电荷量为 、质量为 、速度大小为 的带正电荷的粒子.粒子所受重力的影响可忽略,不考虑粒子间的相互作用.(1)若粒子每次与材料表面的碰撞为弹性碰撞,且被该电场和磁场束缚在上述圆柱体内的粒子占发射粒子总数的百分比为 ,求该薄片材料的圆半径 .(2)若在粒子每次与材料表面碰撞后的瞬间,速度竖直分量反向,水平分量方向不变,竖直方向的速度大小和水平方向的速度大小均按同比例减小,以至于动能减小10%.(i)求在粒子射出直至它第一次与材料表面发生碰撞的过程中,粒子在 平面上的投影点走过路程的最大值;(ii)对(i)问中投影点走过路程最大的粒子,求该粒子从发射直至最终动能耗尽而沉积于材料表面的过程中走过的路程.已知 为积分常数.六、(35分)有一根长为 、内外半径分别为 和 的玻璃毛细管.(1)毛细管竖直悬空固定放置,注入水后,在管的下端中央形成一悬挂的水滴,管中水柱表面中心相对于水滴底部的高度为 ,求水滴底部表面的曲率半径 ;(2)若将该毛细管长度的三分之一竖直浸入水中,问需要多大向上的力才能使该毛细管保持不动?已知玻璃的密度是水的2倍,水的密度是 ,水的表面张力系数为 ,水与玻璃的接触角 可视为零,重力加速度取 .七、(35分)(1)爱因斯坦等效原理可表述为:在有引力作用的情况下的物理规律和没有引力但有适当加速度的参考系中的物理规律是相同的.作为一个例子,考察下面两种情况:(i)当一束光从引力势比较低的地方传播到引力势比较高的地方时,其波长变长,这个现象称为引力红移.如果在某质量分布均匀的球形星体表面附近的 处竖直向上发射波长为 的光,在 处竖直上方高度为 的 处放置一固定接收器,求 处接收器接收到的光的波长 .已知该星体质量为 ,半径为 ;引力场满足弱场条件,可应用牛顿引力理论;真空中的光速为 ,引力常量为 .(ii)如图,假设在没有引力的情况下,有一个长度为 的箱子,在箱子上、下面的 两处分别放置激光接收器和激光发射器.在 时刻,箱子从初速度为零开始,沿 方向做加速度为 的匀加速运动 ,同时从 处发出一束波长为 的激光.a根据狭义相对论,求 处接收器接收到的激光波长 .(iii)根据等效原理,试比较(i)和(ii)的结果,要使物理规律在(i)和(ii)中的情况下相同,则(ii)中的 应为多大?(2)引力红移现象的第一个实验验证是在地球表面附近利用穆斯堡尔探测器完成的,穆斯堡尔探测器能以极高的精度分辨伽马光子的能量.按第(1)(i)问,在地球表面附近,A 处放置一个静止的伽马辐射源,辐射的伽马光子的频率为 处放置一个穆斯堡尔探测器,假设该探测器在相对于自身静止的参考系中仅能探测到频率为 的伽马光子.为了探测到从 处发射的伽马光子,该穆斯堡尔探测器需要某一竖直向下的运动速度.1960-1964年期间,庞德、雷布卡和斯奈德利用美国哈佛大学杰弗逊物理实验室的高塔多次做了这个实验,实验中 .试问: 处发射的伽马光子被探测到时,该穆斯堡尔探测器的运动速度为多大?已知地球表面重力加速度 ,真空中的光速 .八、(35分)用薄膜制备技术在某均质硅基片上沉积一层均匀等厚氮化镓薄膜,制备出一个硅基氮化镓样品,如图1所示.(1)当用波长范围为 的光垂直均匀照射该样品氮化镓表面,观察到其反射光谱仅有两种波长的光获得最大相干加强,其中之一波长为 ;氮化镓的折射率 与入射光在真空中波长 (单位 )之间的关系(色散关系)为硅的折射率随波长在 范围内变化.只考虑氮化镓表面和氮化镓-硅基片界面的反射,求氮化镓薄膜的厚度 和另一种获得最大相干加强光的波长. (2)在该样品硅基片的另一面左、右对称的两个半面上分别均匀沉积一光谱选择性材料涂层,如图2所示;对某种特定波长的光,左半面涂层全吸收,右半面全反射.用两根长均为 的轻细线竖直悬挂该样品,样品长为 、宽为 ,可绕过其中心的光滑竖直固定轴 转动,也可上下移动,如图3所示.开始时,样品静止,用上述特定波长的强激光持续均匀垂直照射该样品涂层表面.此后保持激光方向始终不变,样品绕 轴转动直至稳定.涂层表面始终被激光完全照射.不计激光对样品侧面的照射.设硅基片厚度为 、密度为 ,氮化镓薄膜的厚度为 、密度为 ,涂层质量可忽略,图2真空的介电常量,重力加速度为.若样品稳定后相对于光照前原位形的转角为,求所用强激光的电场强度有效值.(3)取,求的值.。
2017年第34届全国中学生物理竞赛决赛真题及答案(高清pdf版)

f 1 2π
3L0 L0
2l0
k0
1
2π
3L0 L0
2l0
ma mb ma mb
k0
⑳
最后一步利用了②式。 评分参考:第(1)问 24 分,①②③④⑤⑥⑦⑧⑨⑩⑪⑫式各 2 分;第(2)问 11 分,⑬⑭⑮式各 2 分,⑰式 1 分,⑲⑳式各 2 分。
二、(35 分) 参考解答: (1)两体系统的相对运动相当于质量为 Mm 的质点在固定力场中的运动,其运动方程是
人在 A 处完全下蹲,在 A A 过程中系统重力势能减少,(因受到摆底板的限制)动能仍然为零。人
在 A 处时系统的机械能为 U A' K A VA 0 mg(d l)(1 cos A )
②
mg
l
l
d
(h1
d
)
人在 B 仍处位于完全下蹲状态,在 A B 过程中系统机械能守恒。人在 B 处的动能为
0 为平衡位置、圆频率
6BI 、周期 T 2π m
m 6BI
、振幅为0 的简谐运动。
(3)线框在做上述运动的过程中,当逆时针转至 ab 边与 X 轴正向重合时,
0 ,且0 0
6BI , m
⑨
此时 P 、 Q 形成断路,线框内没有了电流,不再受到安培力的力矩。由于没有阻力,线框将保持作角
三、(35 分)参考解答:
(1)假定在始终完全蹲下和始终完全站立过程中没 有机械能损失。将人和秋千作为一个系统。人在 A
处位于完全站立状态,此时系统的机械能为
U A K A VA 0 mg[l(1 cos A ) d ] mgh1 ① 式中,K A 0 和VA mgh1 分别是人在 A 处时系统的动 能和重力势能, A 是秋千与竖直方向的夹角(以 下使用类似记号)如图所示。
(完整word版)2017第34届全国中学生物理竞赛复赛理论考试题和答案

第34届全国中学生物理竞赛复赛理论考试试题解答2017年9月16日一、(40分)一个半径为r 、质量为m 的均质实心小圆柱被置于一个半径为R 、质量为M 的薄圆筒中,圆筒和小圆柱的中心轴均水平,横截面如图所示。
重力加速度大小为g 。
试在下述两种情形下,求小圆柱质心在其平衡位置附近做微振动的频率: (1)圆筒固定,小圆柱在圆筒内底部附近作无滑滚动;(2)圆筒可绕其固定的光滑中心细轴转动,小圆柱仍在圆筒内底部附近作无滑滚动。
解:(1)如图,θ为在某时刻小圆柱质心在其横截面上到圆筒中心轴的垂线与竖直方向的夹角。
小圆柱受三个力作用:重力,圆筒对小圆柱的支持力和静摩擦力.设圆筒对小圆柱的静摩擦力大小为F ,方向沿两圆柱切点的切线方向(向右为正).考虑小圆柱质心的运动,由质心运动定理得sin F mg ma θ-= ①式中,a 是小圆柱质心运动的加速度。
由于小圆柱与圆筒间作无滑滚动,小圆柱绕其中心轴转过的角度1θ(规定小圆柱在最低点时10θ=)与θ之间的关系为1()R r θθθ=+ ② 由②式得,a 与θ的关系为22122()d d a r R r dtdtθθ==- ③考虑小圆柱绕其自身轴的转动,由转动定理得212d rF I dtθ-= ④式中,I 是小圆柱绕其自身轴的转动惯量212I mr = ⑤ 由①②③④⑤式及小角近似sin θθ≈ ⑥ 得22203()θθ+=-d gdt R r ⑦由⑦式知,小圆柱质心在其平衡位置附近的微振动是简谐振动,其振动频率为f =⑧(2)用F 表示小圆柱与圆筒之间的静摩擦力的大小,1θ和2θ分别为小圆柱与圆筒转过的角度(规定小圆柱相对于大圆筒向右运动为正方向,开始时小圆柱处于最低点位置120θθ==)。
对于小圆柱,由转动定理得221212θ⎛⎫-= ⎪⎝⎭d Fr mr dt⑨对于圆筒,同理有2222()θ=d FR MR dt⑩由⑨⑩式得22122221θθ⎛⎫-+=- ⎪⎝⎭d d F r R m M dt dt ⑪设在圆柱横截面上小圆柱质心到圆筒中心轴的垂线与竖直方向的夹角θ,由于小圆柱与圆筒间做无滑滚动,有12()θθθθ=+-R r R ⑫ 由⑫式得22212222()θθθ-=-d d d R r r R dt dt dt⑬设小圆柱质心沿运动轨迹切线方向的加速度为a ,由质心运动定理得 sin F mg ma θ-= ⑭ 由⑫式得22()θ=-d a R r dt⑮由⑪⑬⑭⑮式及小角近似sin θθ≈,得22203d M m gdtM m R rθθ++=+- ⑯由⑯式可知,小圆柱质心在其平衡位置附近的微振动是简谐振动,其振动频率为f =⑰评分参考:第(1)问20分,①②式各3分,③式2分,④式3分,⑤⑥式各2分,⑦式3分,⑧式2分;第(2)问20分,⑨⑩⑪式各2分,⑫式3分,⑬⑭⑮式各2分,⑯式3分,⑰式2分。
2017第34届全国中学生物理竞赛决赛真题几答案解析

专业知识--整理分享1 k 0 2π μ 2π m m 1 m a + m b k0 a b第34 届全国中学生物理竞赛决赛试题与参考解答一、(35 分)如图,质量分别为m a 、m b 的小球a 、b 放置在光滑绝缘水平面上,两球之间用一原长为l 0 、劲度系数为k 0 的绝缘轻弹簧连接。
(1) t = 0 时,弹簧处于原长,小球 a 有一沿两球连线向右的初速度v 0 ,小球b 静止。
若运动过程中弹簧始终处于弹性形变范围内,求两球在任一时刻t (t > 0) 的速度。
(2)若让两小球带等量同号电荷,系统平衡时弹簧长度为 L 0 ,记静电力常量为 K 。
求小球所带电荷量 和两球与弹簧构成的系统做微振动的频率(极化电荷的影响可忽略)。
参考解答:(1)如图, t 时刻弹簧的伸长量为u = l - l 0有d 2uμ dt 2式中μ = = -k 0u ①m a m b②m a + m b为两小球的约化质量。
由①②式知,弹簧的伸长量u 服从简谐振动的动力学方程,振动频率为f = ω 2π = = ③最后一步利用了②式。
t 时刻弹簧的伸长量u 的表达式为u = A sin ωt + B cos ωt④式中 A 、B 为待定常量。
t = 0 时,弹簧处于原长,即 u (0) = B = 0 将 B = 0 代入④式得a 相对于b 的速度为u = A sin ωt⑤v ' =dr a - dr b = du= A ω cos ωt ⑥adt dt dtt = 0 时有k0 (L -l )K 0 0L=-va'(0) =v- 0 =Aω⑦由⑥⑦式得va'=vcosωt⑧系统在运动过程中动量守恒小球a 相对于地面的速度为mav=mava+mbvb⑨va=va'+vb⑩由③⑧⑨⑩式可得,t 时刻小球a 和小球b 的速度分别为⎡m ⎛ (m +m )k ⎫⎤mv =⎢1 +b cosa b 0 t ⎪⎥a v ⑪⎢m m m ⎥m +m 0⎣ a ⎝ a b⎡⎛(m +m )k ⎫⎤⎭⎦ a bmv =⎢1 - cosa b 0 t ⎪⎪⎥ a v ⑫⎢m m ⎥m +m 0⎣⎝ a b ⎭⎦ a b(2)若两球带等量同号电荷,电荷量为q ,系统平衡时有q2K2k(Ll) ⑬由⑬式得设t时刻弹簧的长度为L (见图II),有q =L⑭d 2 L q2μdt2=-k(L -l) +KL2⑮图II令x =L -L为t 时刻弹簧相对平衡时弹簧长度L的伸长量,⑮式可改写为d 2 x q2 ⎛x ⎫-2μ dt2=-kx -k(L-l) +KL21+L⎪⑯系统做微振动时有0 ⎝0 ⎭x因而⎛x ⎫-2x ⎡⎛x ⎫2 ⎤1 +L⎪ = 1 - 2L+O ⎢L⎪⎥⑰⎝0 ⎭ 0 ⎣⎢⎝ 0 ⎭⎦⎥baL⎛ 1 2π3L - 2l 00 ⎫ ⎝ 0 ⎭ μ L ⎪ 0 k 1 ⎛ 3L - 2l ⎫ ⎛ m + m ⎫ 2π 0 0 ⎪ a b⎪ k ⎝ 0 ⎭ ⎝ a b L m m 0⎭L 30 L 0利用上式,⑯式可写为d 2x ⎡q 2⎤ ⎛q 2⎫ ⎡⎛ x ⎫2 ⎤ μ dt 2 = ⎢-k 0 (L 0 - l 0 ) + K L 2 ⎥ - k 0 + 2K L 3 ⎪ x + O ⎢ L⎪ ⎥⑱⎡⎛ x ⎫2 ⎤⎣ 0 ⎦ ⎝ 0 ⎭ ⎢⎣⎝ 0 ⎭ ⎥⎦略去O ⎢ L ⎪ ⎥ ,并利用⑬或⑭式,⑱式可写为⎢⎣⎝ 0 ⎭ ⎥⎦d 2 x ⎛q 2 ⎫3L - 2l μ = - k + 2K ⎪ x = - 0 0 k x⑲dt 2⎝⎭由⑲式知, 3L 0 - 2l 0 > 0 ,系统的微振动服从简谐振动的动力学方程,振动频率为f = = ⑳最后一步利用了②式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12π2π第34 届全国中学生物理竞赛决赛试题与参考解答一、(35 分)如图,质量分别为ma、m b 的小球a 、b 放置在光滑绝缘水平面上,两球之间用一原长为l0 、劲度系数为k的绝缘轻弹簧连接。
(1)t 时,弹簧处于原长,小球a 有一沿两球连线向右的初速度v,小球b 静止。
若运动过程中弹簧始终处于弹性形变范围内,求两球在任一时刻t(t ) 的速度。
(2)若让两小球带等量同号电荷,系统平衡时弹簧长度为L,记静电力常量为K 。
求小球所带电荷量和两球与弹簧构成的系统做微振动的频率(极化电荷的影响可忽略)。
参考解答:(1)如图,t 时刻弹簧的伸长量为ul l有d 2udt2式中ku ①mamb ②mamb为两小球的约化质量。
由①②式知,弹簧的伸长量u 服从简谐振动的动力学方程,振动频率为f2π③最后一步利用了②式。
t 时刻弹簧的伸长量u 的表达式为u A sin t B cos t ④式中A 、B 为待定常量。
t 时,弹簧处于原长,即u B将 B 代入④式得a 相对于b 的速度为u A sin t ⑤vdradrbduA cos t ⑥a dt dt dtt 时有专业知识--整理分享kL = - va (0) v 0 0 A⑦由⑥⑦式得v a v 0 cost⑧系统在运动过程中动量守恒小球 a 相对于地面的速度为m a v 0m av am b vb⑨v a v av b⑩由③⑧⑨⑩式可得, t 时刻小球a 和小球b 的速度分别为m (m m ) mvbcosa b 0t a vmm m 0 a (m m )a bmvaa⑫m 0a bab(2)若两球带等量同号电荷,电荷量为 q ,系统平衡时有q 2K 2k 0 (L 0 l 0 ) ⑬由⑬式得设t 时刻弹簧的长度为 L (见图 II ),有q L 0 ⑭d 2 L q 2dt 2k 0 (L l 0 ) K L 2⑮图 II令 xLL 0 为t 时刻弹簧相对平衡时弹簧长度 L 0的伸长量,⑮式可改写为d 2x q 2xdt 2 k 0 x k 0 (L 0 l 0 ) KL2L⑯系统做微振动时有x因而xxx 2LLOL⑰b a L 0WORD格式-可编辑专业知识--整理分享WORD格式-可编辑12π2πL3L利用上式,⑯式可写为d 2x q2q2x 2dt2k0 (L0 l0 ) K L2k2KL3x OL⑱x20 0 0略去OL,并利用⑬或⑭式,⑱式可写为d 2 x q2 3L 2lk 2K x 0 0 kx ⑲dt2 0由⑲式知,3Ll,系统的微振动服从简谐振动的动力学方程,振动频率为f ⑳最后一步利用了②式。
评分参考:第(1)问 24 分,①②③④⑤⑥⑦⑧⑨⑩⑪⑫式各 2 分;第(2)问 11 分,⑬⑭⑮式各2分,⑰式 1 分,⑲⑳式各 2 分。
二、(35 分)双星系统是一类重要的天文观测对象。
假设某两星体均可视为质点,其质量分别为M 和m ,一起围绕它们的质心做圆周运动,构成一双星系统,观测到该系统的转动周期为T。
在某一时刻,M 星突然发生爆炸而失去质量M 。
假设爆炸是瞬时的、相对于M 星是各向同性的,因而爆炸后M星的残余体M (M M M ) 星的瞬间速度与爆炸前瞬间M 星的速度相同,且爆炸过程和抛射物质M 都对m 星没有影响。
已知引力常量为G ,不考虑相对论效应。
(1)求爆炸前M 星和m 星之间的距离r;(2)若爆炸后M 星和m 星仍然做周期运动,求该运动的周期T1;(3)若爆炸后M 星和m 星最终能永远分开,求M 、m 和M 三者应满足的条件。
参考解答:WORD 格式-可编辑专业知识--整理分享(1)两体系统的相对运动相当于质量为Mm Mm的质点在固定力场中的运动,其运动方程是⎛ 2GM ⎝ 0 r - v 2 ⎪ GM ⎫-1 ⎛ 0 ⎭ + G 2M 2-⎛ 2GM ⎝⎝r - v 2 ⎪ r 2v 2⎪ ⎫ ⎫0 0 0⎪- 2 22 2 MmrGMmr①其中 r 是两星体间的相对位矢。
①式可化为M mr 3rG (M m )r②r 3由②式可知,双星系统的相对运动可视为质点在质量为 M m 的固定等效引力源的引力场中的运动。
爆炸前为圆周运动,其运动方程是G (M m ) 2π 2r 2Tr 0③由③式解得G (Mm )T 21/3r0 ④(2)爆炸前, m 星相对于 M 星的速度大小是4π2v2πr 02π G (M m )T 2 1/30 2πG (M m )1/3⑤TT 4π2T 00 0方向与两星体连线垂直。
爆炸后,等效引力源的质量变为M M m M m M⑥相对运动轨道从圆变成了椭圆、抛物线或双曲线。
由爆炸刚刚完成时(取为初始时刻)两星体的位置和运动状态可知,两星体初始距离为r 0 ,初始相对速度的大小为v 0 ,其方向与两星体连线垂直,所以初始位置必定是椭圆、抛物线或双曲线的顶点。
对于椭圆轨道,它是长轴的一个端点。
设椭圆轨道长轴的另一个端点与等效引力源的距离为 r 1 ,在 r 1 处的速度(最小速度)为v min (理由见⑪式),由角动量守恒和机械能守恒得r 1v 1 r 0v 0⑦和v 2GM v 2GM 1⑧2r 12r 0由⑦⑧式得 r 1 满足方程2GMv r 2GM rr v 0 ⑨由⑨式解得r 0 0 1 10 0r 1⑩GMG ( 2r r v 2(GM r v 2 GM) 0 0r 2GM r v 22GM r v 2 00 00 0另一解r 0 可在⑩式右端根号前取减号得到。
由⑩式可知r 1 r 0⑪利用方程⑨和韦达定理(或由⑩式),椭圆的半长轴是rr GM G (M m )T 21/3Mm M a 01 2 2GMrv 2r 04π ⑫M mM要使运行轨道为椭圆,应有由⑫⑬式得0 0a⑬据开普勒第三定律得M m M 0⑭T 12π⑮将⑥⑫式代入⑮式得⑯[解法(二)爆炸前,设 M 星与m 星之间的相对运动的速度为v 相对0 ,有v 相对0⑤爆炸后瞬间, m 星的速度没有改变, M M 星与爆炸前的速度相等,设 M M 星与m 星之间的相对运动的速度为v 相对 ,有v 相对 v 相对0⑥爆炸后质心系的总动能为E 1 (MM )m v 2⑦质心系总能量为k2 Mm M 相对EEG (M M )m⑧r 0对于椭圆轨道运动有EG (M M )m⑨2 A式中T 1 0kGG由开普勒第三定律有 AMmMr⑩MmM 0T2π⑪由⑩⑪式有T 12π⑫有(M m )(MmM )2 1/ 2T 1(M m M )3 T 0⑬](3)根据⑫式,当M ≥ (M m )/2 的时候,⑬式不再成立,轨道不再是椭圆。
所以若 M星和m星最终能永远分开,须满足M ≥ (M m )/2⑰由题意知联立⑰⑱式知,还须满足⑯⑲式即为所求的条件。
MM ⑱Mm⑲评分参考:第(1)问 8 分,①②③④式各 2 分; 第(2)问 23 分,⑤⑥⑦⑧⑨⑩⑪⑫式各 2 分,⑬式 1 分,⑭⑮⑯式各 2 分;解法(二)⑤⑥式各 2分;⑦⑧⑨式各 3 分;⑩式 2 分,⑪式 3 分,⑫式 2 分,⑬式 3 分; 第(3)问 4 分,⑰⑲式各 2 分。
三、(35 分)熟练的荡秋千的人能够通过在秋千板上适时站起和蹲下使秋千越荡越高。
一质量为m 的人荡一架底板和摆杆均为刚性的秋千,底板和摆杆的质量均可忽略,假定人的质量集中在其质心。
人在秋千上每次完全站起时起质心距悬点O 的距离为l ,完全蹲下时此距离变为l d 。
实际上,人在秋千上站起和蹲下过程都是在一段时间内完成的。
作为一个简单的模型,假设人在第一个最高点 A 点从完全站立的姿势迅速完全下蹲,然后荡至最低点 B ,A 与 B 的高度差为h 1 ;随后他在 B 点迅速完全站起(且最终径向速度为零),继而随秋千荡至第二个最高点C ,这一过程中该人质心运动的轨迹如图所示。
此后人以同样的方式回荡,重复前述过程,荡向第 3、4 等最高点。
假设人站起和蹲下的过程中,人与秋千的相互作用力始终与摆杆平行。
以最低点 B 为重力势能零点。
( 1 ) 假 定 在 始 终 完 全 蹲 下 和 始 终 完 全 站 立 过 程 中 没 有 机 械 能 损 失 , 求 该 人 质 心 在 A A B B C 各个阶段的机械能及其变化; (2)假定在始终完全蹲下和始终完全站立过程中的机械能损失E 与过程前后高度差的绝对值h 的关系分别为 Ek 1mg (h 0h ) ,k 1,始终完全蹲下Ek2 mg (h 0h ) ,0 k 21 ,始终完全站立这里, k 1 、k 2 、h 0 和h 0是常量, g 是重力加速度的大小。
求(i )相对于 B 点,第 n 个最高点的高度h n 与第n个最高点的高度h n之间的关系;(ii ) h n 与h 1 之间的关系式和h n h n 与h 1 之间的关系式。
参考解答:(1)假定在始终完全蹲下和始终完全站立过程中没有机械能损失。
将人和秋千作为一个系统。
人在 A 处位于完全站立状态,此时系统的机械能为UA K AV A0 mg [l cosA ) d ] mgh 1①式中,K A 和V A mgh 1 分别是人在 A 处时系统的动能和重力势能,A是秋千与竖直方向的夹角(以下使用类似记号)如图所示。
人在 A 处完全下蹲,在 A A 过程中系统重力势能减少,(因受到摆底板的限制)动能仍然为零。
人在 A 处时系统的机械能为U A 'K A VA0 mg ( dl )(1 cos A )②mg l d(h d )l1人在 B 仍处位于完全下蹲状态,在AB 过程中系统机械能守恒。
人在 B 处的动能为 K1mv 2U③式中下标 1 表示秋千第一次到 B 处。
B 12B 1A人在 B处突然站立,人做功,机械能增加。
设人站立前后体系的角动量分别为 L B 1 和 L B1,在 B B过程中系统角动量守恒L B 1mv B 1 (l d m (K B 1 / mm (ld④L B1mlv B1由此得人在 B 处的机械能为v B1U1mv 2mgd⑤B 12B 11l d 32 m 2 lg (h 1 dmgd⑥人在C 仍处于完全站立状态,在 BC 过程中系统机械能守恒。
人在C 处时系统的机械能为 U Cmgh 2(ld )3由⑥⑦式得mg l3 (h 1d ) mgdU B 1⑦l d3h 2dl (h 1d )于是l d3U C U Amgl(h 1 d )⑧(2)(1)假定在始终完全蹲下和始终完全站立过程中有机械能损失。
按题给模型,人第n 第在 B 处时系统的动能为1mv 2 mgh k (mgh mgh )WORD格式-可编辑专业知识--整理分享2Bn n 1 0 nWORD 格式-可编辑专业知识--整理分享(1 k 1 )mgh nk 1mgh 0⑨k )mgld(hdk mgh1l n1即v 2 2(1 k )gl d(hd ) 2k gh⑨Bn1ln1按题给模型,人第 n 次在 B处时系统的动能为1mv 2 mg (h d ) k[mgh mg (hd )]2B nn 2 0n(1k 2 )mg (h n1d ) k 2mgh 0⑩即v2k )g (hd )k gh⑩B n2在第 n 次 B B过程中,系统角动量守恒,有n2(ld )mv Bn lmv Bn⑪由⑨⑩⑪式得k )l 2 g (hd ) 2k l 2 gh2n 22(1 k )(l d )2gl d(h d ) 2k (ld )2gh⑫由⑫式得1ln1kld3kld2kh n1d1(h nd )1h2h 0k 2lk 2lk 2k l d3k l d2k1(h n d )1h2h⑬ k2l1k2 lk2(h nd式中kld31⑭k2lWORD 格式-可编辑专业知识--整理分享k ld 2k1h 02h 0 ⑮k2l1 k 2(ii )由⑬⑭⑮式有h nd (h nd[(h ndWORD 格式-可编辑专业知识--整理分享n -111-λ12 (hd )) ⑯n(hdn即nn(h 1dnh n于是(h 1 d ) d⑰h n- h nn[(h d ) ] ⑱评分参考:第(1)问 17 分。
