图形的折叠问题试卷
苏科八上精选专题《轴对称图形》:翻折变换(折叠问题)精选题31道

翻折变换(折叠问题)精选题31道一.选择题(共12小题)1.如图,矩形ABCD中,E是AD的中点,将ABE∆沿直线BE折叠后得到GBE∆,延长BG 交CD于点F.若6AB=,46BC=,则FD的长为()A.2B.4C.6D.232.如图,在ABC∆中,D是AC边上的中点,连结BD,把BDC∆沿BD翻折,得到BDC'∆,DC'与AB交于点E,连结AC',若2AD AC='=,3BD=,则点D到BC'的距离为( )A.33B.321C.7D.133.如图,ABC∆中,90BAC∠=︒,3AB=,4AC=,点D是BC的中点,将ABD∆沿AD 翻折得到AED∆,连CE,则线段CE的长等于()A.2B.54C.53D.754.如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为()A .2B .3C .2D .15.如图,已知正方形ABCD 的边长为12,BE EC =,将正方形边CD 沿DE 折叠到DF ,延长EF 交AB 于G ,连接DG ,现在有如下4个结论:①ADG FDG ∆≅∆;②2GB AG =;③GDE BEF ∆∆∽;④725BEF S ∆=.在以上4个结论中,正确的有( )A .1B .2C .3D .46.如图,把一张矩形纸片ABCD 沿EF 折叠后,点A 落在CD 边上的点A '处,点B 落在点B '处,若240∠=︒,则图中1∠的度数为( )A .115︒B .120︒C .130︒D .140︒7.如图,在矩形ABCD 中,点E ,F 分别在边AB ,BC 上,且13AE AB =,将矩形沿直线EF 折叠,点B 恰好落在AD 边上的点P 处,连接BP 交EF 于点Q ,对于下列结论:①2EF BE =;②2PF PE =;③4FQ EQ =;④PBF ∆是等边三角形.其中正确的是( )A .①②B .②③C .①③D .①④8.如图,Rt ABC ∆中,9AB =,6BC =,90B ∠=︒,将ABC ∆折叠,使A 点与BC 的中点D 重合,折痕为MN ,则线段BN 的长为( )A .53B .52C .4D .59.如图,在矩形ABCD 中,8AB =,4BC =,将矩形沿AC 折叠,点D 落在点D '处,则重叠部分AFC ∆的面积为( )A .6B .8C .10D .1210.如图,在ABC ∆中.90ACB ∠=︒,4AC =,2BC =,点D 在AB 上,将ACD ∆沿CD 折叠,点A 落在点1A 处,1A C 与AB 相交于点E ,若1//A D BC ,则1A E 的长为( )A .22B .83C .52D .324- 11.如图,点O 是矩形ABCD 的中心,E 是AB 上的点,沿CE 折叠后,点B 恰好与点O 重合,若3BC =,则折痕CE 的长为( )A .23B .332C .3D .612.如图,矩形纸片ABCD ,4AB =,3BC =,点P 在BC 边上,将CDP ∆沿DP 折叠,点C 落在点E 处,PE 、DE 分别交AB 于点O 、F ,且OP OF =,则cos ADF ∠的值为( )A .1113B .1315C .1517D .1719二.填空题(共12小题)13.如图,正方形ABCD 的边长是16,点E 在边AB 上,3AE =,点F 是边BC 上不与点B ,C 重合的一个动点,把EBF ∆沿EF 折叠,点B 落在B '处.若CDB ∆'恰为等腰三角形,则DB '的长为 .14.如图,矩形ABCD 中,3AB =,4BC =,点E 是BC 边上一点,连接AE ,把B ∠沿AE 折叠,使点B 落在点B '处.当CEB ∆'为直角三角形时,BE 的长为 .15.如图矩形ABCD 中,5AD =,7AB =,点E 为DC 上一个动点,把ADE ∆沿AE 折叠,当点D 的对应点D '落在ABC ∠的角平分线上时,DE 的长为 .16.如图,在Rt ABC ∆中,90A ∠=︒,AB AC =,21BC =+,点M ,N 分别是边BC ,AB上的动点,沿MN 所在的直线折叠B ∠,使点B 的对应点B '始终落在边AC 上,若△MB C '为直角三角形,则BM 的长为 .17.如图,矩形ABCD 中,8AB =,6BC =,P 为AD 上一点,将ABP ∆沿BP 翻折至EBP ∆,PE 与CD 相交于点O ,BE 与CD 相交于点G ,且OE OD =,则AP 的长为 .18.如图,在Rt ABC ∆中,90C ∠=︒,6AC =,8BC =,点F 在边AC 上,并且2CF =,点E 为边BC 上的动点,将CEF ∆沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是 .19.如图,正方形纸片ABCD 的边长为12,E 是边CD 上一点,连接AE 、折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上,若5DE =,则GE 的长为 .20.折叠矩形纸片ABCD 时,发现可以进行如下操作:①把ADE ∆翻折,点A 落在DC 边上的点F 处,折痕为DE ,点E 在AB 边上;②把纸片展开并铺平;③把CDG ∆翻折,点C 落在线段AE 上的点H 处,折痕为DG ,点G 在BC 边上,若2AB AD =+,1EH =,则AD = .21.如图,把某矩形纸片ABCD 沿EF ,GH 折叠(点E ,H 在AD 边上,点F ,G 在BC 边上),使点B 和点C 落在AD 边上同一点P 处,A 点的对称点为A '点,D 点的对称点为D '点,若90FPG ∠=︒,△A EP '的面积为4,△D PH '的面积为1,则矩形ABCD 的面积等于 .22.如图,将正方形纸片ABCD 沿MN 折叠,使点D 落在边AB 上,对应点为D ',点C 落在C '处.若6AB =,2AD '=,则折痕MN 的长为 .23.如图,在矩形纸片ABCD 中,将AB 沿BM 翻折,使点A 落在BC 上的点N 处,BM 为折痕,连接MN ;再将CD 沿CE 翻折,使点D 恰好落在MN 上的点F 处,CE 为折痕,连接EF 并延长交BM 于点P ,若8AD =,5AB =,则线段PE 的长等于 .24.如图,在Rt ABC ∆中,90C ∠=︒,23BC =,2AC =,点D 是BC 的中点,点E 是边AB 上一动点,沿DE 所在直线把BDE ∆翻折到△B DE '的位置,B D '交AB 于点F .若△AB F '为直角三角形,则AE 的长为 .三.解答题(共7小题)25.阅读理解如图1,ABC ∆中,沿BAC ∠的平分线1AB 折叠,剪掉重复部分;将余下部分沿11B A C ∠的平分线12A B 折叠,剪掉重复部分;⋯;将余下部分沿n n B A C ∠的平分线1n n A B +折叠,点n B 与点C 重合,无论折叠多少次,只要最后一次恰好重合,BAC ∠是ABC ∆的好角. 小丽展示了确定BAC ∠是ABC ∆的好角的两种情形.情形一:如图2,沿等腰三角形ABC 顶角BAC ∠的平分线1AB 折叠,点B 与点C 重合;情形二:如图3,沿BAC ∠的平分线1AB 折叠,剪掉重复部分;将余下部分沿11B A C ∠的平分线12A B 折叠,此时点1B 与点C 重合. 探究发现(1)ABC ∆中,2B C ∠=∠,经过两次折叠,BAC ∠是不是ABC ∆的好角? (填“是”或“不是” ).(2)小丽经过三次折叠发现了BAC ∠是ABC ∆的好角,请探究B ∠与C ∠(不妨设)B C ∠>∠之间的等量关系.根据以上内容猜想:若经过n 次折叠BAC ∠是ABC ∆的好角,则B ∠与C∠(不妨设)∠>∠之间的等量关系为.B C应用提升(3)小丽找到一个三角形,三个角分别为15︒、60︒、105︒,发现60︒和105︒的两个角都是此三角形的好角.请你完成,如果一个三角形的最小角是4︒,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.26.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:APB BPH∠=∠;(2)当点P在边AD上移动时,PDH∆的周长是否发生变化?并证明你的结论;(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.27.如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A'处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B 恰好落在DE上的点H处.如图2.(1)求证:EG CH=;(2)已知2AF=,求AD和AB的长.28.如图,AEF∆,∆中,45∆沿AE折叠得到AEB∠=︒,AG EF⊥于点G,现将AEGEAF将AFG∆,延长BE和DF相交于点C.∆沿AF折叠得到AFD(1)求证:四边形ABCD是正方形;(2)连接BD分别交AE、AF于点M、N,将ABM∆绕点A逆时针旋转,使AB与AD重合,得到ADH∆,试判断线段MN、ND、DH之间的数量关系,并说明理由.(3)若4BM=,求AG、MN的长.GF=,32EG=,629.如图1,一张矩形纸片ABCD,其中8=,先沿对角线BD对折,点CAB cmAD cm=,6落在点C'的位置,BC'交AD于点G.(1)求证:AG C G=';(2)如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.30.如图1,在ABO∠=︒,8∆外OB=.以OB为一边,在OABAOB∠=︒,30∆中,90OAB作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.(1)求点B的坐标;(2)求证:四边形ABCE是平行四边形;(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.31.如图,矩形ABCD中,点E在边CD上,将BCE∆沿BE折叠,点C落在AD边上的点F 处,过点F作//FG CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若6AD=,求四边形CEFG的面积.AB=,10翻折变换(折叠问题)精选题31道参考答案与试题解析一.选择题(共12小题)1.如图,矩形ABCD 中,E 是AD 的中点,将ABE ∆沿直线BE 折叠后得到GBE ∆,延长BG 交CD 于点F .若6AB =,46BC =,则FD 的长为( )A .2B .4C 6D .23【分析】根据点E 是AD 的中点以及翻折的性质可以求出AE DE EG ==,然后利用“HL ”证明EDF ∆和EGF ∆全等,根据全等三角形对应边相等可证得DF GF =;设FD x =,表示出FC 、BF ,然后在Rt BCF ∆中,利用勾股定理列式进行计算即可得解.【解答】解:E 是AD 的中点,AE DE ∴=,ABE ∆沿BE 折叠后得到GBE ∆,AE EG ∴=,AB BG =,ED EG ∴=,在矩形ABCD 中,90A D ∴∠=∠=︒,90EGF ∴∠=︒,在Rt EDF ∆和Rt EGF ∆中,ED EG EF EF =⎧⎨=⎩, Rt EDF Rt EGF(HL)∴∆≅∆,DF FG ∴=,设DF x =,则6BF x =+,6CF x =-,在Rt BCF ∆中,222(46)(6)(6)x x +-=+,解得4x =.故选:B .【点评】本题考查了矩形的性质,全等三角形的判定与性质,勾股定理的应用,翻折的性质,熟记性质,找出三角形全等的条件ED EG =是解题的关键.2.如图,在ABC ∆中,D 是AC 边上的中点,连结BD ,把BDC ∆沿BD 翻折,得到BDC '∆,DC '与AB 交于点E ,连结AC ',若2AD AC ='=,3BD =,则点D 到BC '的距离为( )A 33B 321C 7D 13【分析】连接CC ',交BD 于点M ,过点D 作DH BC '⊥于点H ,由翻折知,BDC BDC '∆≅∆,BD 垂直平分CC ',证ADC '∆为等边三角形,利用解直角三角形求出1DM =,33C M DM '==2BM =,在Rt BMC '∆中,利用勾股定理求出BC '的长,在BDC '∆中利用面积法求出DH 的长.【解答】解:如图,连接CC ',交BD 于点M ,过点D 作DH BC '⊥于点H ,2AD AC ='=,D 是AC 边上的中点,2DC AD ∴==,由翻折知,BDC BDC '∆≅∆,BD 垂直平分CC ',2DC DC '∴==,BC BC '=,CM C M '=,2AD AC DC '∴='==,ADC '∴∆为等边三角形,60ADC AC D C AC '''∴∠=∠=∠=︒,DC DC '=,160302DCC DC C ''∴∠=∠=⨯︒=︒, 在Rt △C DM '中,30DC C '∠=︒,2DC '=,1DM ∴=,33C M DM '==,312BM BD DM ∴=-=-=, 在Rt BMC '∆中,22222(3)7BC BM C M ''=+=+=,1122BDC S BC DH BD CM '∆'==, ∴733DH =⨯,3217DH ∴=, 故选:B .【点评】本题考查了轴对称的性质,解直角三角形,勾股定理等,解题关键是会通过面积法求线段的长度.3.如图,ABC ∆中,90BAC ∠=︒,3AB =,4AC =,点D 是BC 的中点,将ABD ∆沿AD 翻折得到AED ∆,连CE ,则线段CE 的长等于( )A .2B .54C .53D .75【分析】如图连接BE 交AD 于O ,作AH BC ⊥于H .首先证明AD 垂直平分线段BE ,BCE ∆是直角三角形,求出BC 、BE ,在Rt BCE ∆中,利用勾股定理即可解决问题.【解答】解:如图连接BE 交AD 于O ,作AH BC ⊥于H .在Rt ABC ∆中,4AC =,3AB =, 22345BC ∴=+=, CD DB =,52ED DC DB ∴===, 1122BC AH AB AC =, 125AH ∴=, AE AB =,∴点A 在BE 的垂直平分线上.DE DB DC ==,∴点D 在BE 的垂直平分线上,BCE ∆是直角三角形,AD ∴垂直平分线段BE ,1122AD BO BD AH =, 125OB ∴=, 2425BE OB ∴==, 在Rt BCE ∆中,22222475()55EC BC BE =-=-=, 故选:D .【点评】本题考查翻折变换、直角三角形的斜边中线的性质、勾股定理等知识,解题的关键是学会利用面积法求高,属于中考常考题型.4.如图,把正方形纸片ABCD 沿对边中点所在的直线对折后展开,折痕为MN ,再过点B 折叠纸片,使点A 落在MN 上的点F 处,折痕为BE .若AB 的长为2,则FM 的长为( )A .2B .3C .2D .1【分析】根据翻折不变性,2AB FB ==,1BM =,在Rt BFM ∆中,可利用勾股定理求出FM 的值.【解答】解:四边形ABCD 为正方形,2AB =,过点B 折叠纸片,使点A 落在MN 上的点F 处,2FB AB ∴==,1BM =,则在Rt BMF ∆中,2222213FM BF BM =-=-=,故选:B .【点评】此题考查了翻折变换的性质,适时利用勾股定理是解答此类问题的关键.5.如图,已知正方形ABCD 的边长为12,BE EC =,将正方形边CD 沿DE 折叠到DF ,延长EF 交AB 于G ,连接DG ,现在有如下4个结论:①ADG FDG ∆≅∆;②2GB AG =;③GDE BEF ∆∆∽;④725BEF S ∆=.在以上4个结论中,正确的有( )A .1B .2C .3D .4【分析】根据正方形的性质和折叠的性质可得AD DF =,90A GFD ∠=∠=︒,于是根据“HL ”判定ADG FDG ∆≅∆,再由12GF GB GA GB +=+=,EB EF =,BGE ∆为直角三角形,可通过勾股定理列方程求出4AG =,8BG =,进而求出BEF ∆的面积,再抓住BEF ∆是等腰三角形,而GED ∆显然不是等腰三角形,判断③是错误的.【解答】解:由折叠可知,DF DC DA ==,90DFE C ∠=∠=︒,90DFG A ∴∠=∠=︒,ADG FDG ∴∆≅∆,①正确;正方形边长是12,6BE EC EF ∴===,设AG FG x ==,则6EG x =+,12BG x =-,由勾股定理得:222EG BE BG =+,即:222(6)6(12)x x +=+-,解得:4x =4AG GF ∴==,8BG =,2BG AG =,②正确;6BE EF ==,BEF ∆是等腰三角形,易知GED ∆不是等腰三角形,③错误; 168242S GBE ∆=⨯⨯=,67224105EF S BEF S GBE EG ∆=∆==,④正确. 故选:C .【点评】本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算,有一定的难度.6.如图,把一张矩形纸片ABCD 沿EF 折叠后,点A 落在CD 边上的点A '处,点B 落在点B '处,若240∠=︒,则图中1∠的度数为( )A .115︒B .120︒C .130︒D .140︒【分析】根据折叠的性质和矩形的性质得出BFE EFB '∠=∠,90B B '∠=∠=︒,根据三角形内角和定理求出50CFB '∠=︒,进而解答即可.【解答】解:把一张矩形纸片ABCD 沿EF 折叠后,点A 落在CD 边上的点A '处,点B 落在点B '处,BFE EFB '∴∠=∠,90B B '∠=∠=︒,240∠=︒,50CFB '∴∠=︒,1180EFB CFB ''∴∠+∠-∠=︒,即1150180∠+∠-︒=︒,解得:1115∠=︒,故选:A .【点评】本题考查了矩形的性质,折叠的性质,三角形的内角和定理的应用,能综合运用性质进行推理和计算是解此题的关键,注意:折叠后的两个图形全等.7.如图,在矩形ABCD 中,点E ,F 分别在边AB ,BC 上,且13AE AB =,将矩形沿直线EF 折叠,点B 恰好落在AD 边上的点P 处,连接BP 交EF 于点Q ,对于下列结论:①2EF BE =;②2PF PE =;③4FQ EQ =;④PBF ∆是等边三角形.其中正确的是( )A .①②B .②③C .①③D .①④【分析】求出2BE AE =,根据翻折的性质可得PE BE =,再根据直角三角形30︒角所对的直角边等于斜边的一半求出30APE ∠=︒,然后求出60AEP ∠=︒,再根据翻折的性质求出60BEF ∠=︒,根据直角三角形两锐角互余求出30EFB ∠=︒,然后根据直角三角形30︒角所对的直角边等于斜边的一半可得2EF BE =,判断出①正确;利用30︒角的正切值求出3PF PE ,判断出②错误;求出2BE EQ =,2EF BE =,然后求出3FQ EQ =,判断出③错误;求出60PBF PFB ∠=∠=︒,然后得到PBF ∆是等边三角形,判断出④正确.【解答】解:13AE AB =, 2BE AE ∴=,由翻折的性质得,PE BE =,30APE ∴∠=︒,903060AEP ∴∠=︒-︒=︒,11(180)(18060)6022BEF AEP ∴∠=︒-∠=︒-︒=︒,906030∴∠=︒-︒=︒,EFB∴=,故①正确;2EF BE=,BE PE2∴=,EF PE>,EF PF∴<,故②错误;2PF PE由翻折可知EF PB⊥,EBQ EFB∴∠=∠=︒,30BE EQ∴=,22=,EF BEFQ EQ∴=,故③错误;3由翻折的性质,30∠=∠=︒,EFB EFPBFP∴∠=︒+︒=︒,303060PBF EBQ∠=︒-∠=︒-︒=︒,90903060∴∠=∠=︒,60PBF PFB∴∆是等边三角形,故④正确;PBF综上所述,结论正确的是①④.故选:D.【点评】本题考查了翻折变换的性质,直角三角形30︒角所对的直角边等于斜边的一半的性质,直角三角形两锐角互余的性质,等边三角形的判定,熟记各性质并准确识图是解题的关键.8.如图,Rt ABC∠=︒,将ABC∆折叠,使A点与BC的中点∆中,9BBC=,90AB=,6D重合,折痕为MN,则线段BN的长为()A .53B .52C .4D .5【分析】设BN x =,则由折叠的性质可得9DN AN x ==-,根据中点的定义可得3BD =,在Rt BDN ∆中,根据勾股定理可得关于x 的方程,解方程即可求解.【解答】解:设BN x =,由折叠的性质可得9DN AN x ==-,D 是BC 的中点,3BD ∴=,在Rt BDN ∆中,2223(9)x x +=-,解得4x =.故线段BN 的长为4.故选:C .【点评】考查了翻折变换(折叠问题),涉及折叠的性质,勾股定理,中点的定义以及方程思想,综合性较强,但是难度不大.9.如图,在矩形ABCD 中,8AB =,4BC =,将矩形沿AC 折叠,点D 落在点D '处,则重叠部分AFC ∆的面积为( )A .6B .8C .10D .12【分析】因为BC 为AF 边上的高,要求AFC ∆的面积,求得AF 即可,求证AFD CFB ∆'≅∆,得BF D F =',设D F x '=,则在Rt AFD ∆'中,根据勾股定理求x ,于是得到AF AB BF =-,即可得到结果.【解答】解:易证AFD CFB ∆'≅∆,D F BF ∴'=,设D F x '=,则8AF x =-,在Rt AFD ∆'中,222(8)4x x -=+,解之得:3x =,835AF AB FB ∴=-=-=,1102AFC S AF BC ∆∴==. 故选:C .【点评】本题考查了翻折变换-折叠问题,勾股定理的正确运用,本题中设D F x '=,根据直角三角形AFD '中运用勾股定理求x 是解题的关键.10.如图,在ABC ∆中.90ACB ∠=︒,4AC =,2BC =,点D 在AB 上,将ACD ∆沿CD 折叠,点A 落在点1A 处,1A C 与AB 相交于点E ,若1//A D BC ,则1A E 的长为( )A .22B .83C 52D .324-【分析】利用平行线的性质以及折叠的性质,即可得到1190A A DB ∠+∠=︒,即AB CE ⊥,再根据勾股定理可得2232AB BC AC =+,最后利用面积法得出1122AB CE BC AC ⨯=⨯,可得43BC AC CE AB ⨯==,进而依据14AC AC ==,即可得到183A E =. 【解答】解:1//A D BC ,1B A DB ∴∠=∠,由折叠可得,1A A ∠=∠,又90A B ∠+∠=︒,1190A A DB ∴∠+∠=︒,AB CE ∴⊥,90ACB ∠=︒,4AC =,2BC ,2232AB BC AC ∴=+1122AB CE BC AC ⨯=⨯,43BC AC CE AB ⨯∴==, 又14AC AC ==, 148433A E ∴=-=, 故选:B .【点评】本题主要考查了折叠问题以及勾股定理的运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决问题的关键是得到CE AB ⊥以及面积法的运用.11.如图,点O 是矩形ABCD 的中心,E 是AB 上的点,沿CE 折叠后,点B 恰好与点O 重合,若3BC =,则折痕CE 的长为( )A .23B 332C 3D .6【分析】先根据图形翻折变换的性质得出BC OC =,BE OE =,90B COE ∠=∠=︒,BCE ACE ∠=∠,求出2AC BC =,求出30BAC ∠=︒,求出30BCE ∠=︒,解直角三角形求出CE 即可.【解答】解:CEO ∆是CEB ∆翻折而成,BC OC ∴=,BE OE =,90B COE ∠=∠=︒,BCE ACE ∠=∠,EO AC ∴⊥,O 是矩形ABCD 的中心,OE ∴是AC 的垂直平分线,2236AC BC ==⨯=,30CAB ∴∠=︒,60BCA ∴∠=︒,30BCE ACE ∴∠=∠=︒,在Rt BCE ∆中,23cos303BC CE ===︒, 故选:A . 【点评】本题考查了翻折变换,矩形的性质,直角三角形的性质,解直角三角形等知识点,能求出30BAC ∠=︒是解此题的关键.12.如图,矩形纸片ABCD ,4AB =,3BC =,点P 在BC 边上,将CDP ∆沿DP 折叠,点C 落在点E 处,PE 、DE 分别交AB 于点O 、F ,且OP OF =,则cos ADF ∠的值为( )A .1113B .1315C .1517D .1719【分析】根据折叠的性质可得出DC DE =、CP EP =,由EOF BOP ∠=∠、B E ∠=∠、OP OF =可得出()OEF OBP AAS ∆≅∆,根据全等三角形的性质可得出OE OB =、EF BP =,设EF x =,则BP x =、4DF x =-、3BF PC x ==-,进而可得出1AF x =+,在Rt DAF ∆中,利用勾股定理可求出x 的值,再利用余弦的定义即可求出cos ADF ∠的值.【解答】解:根据折叠,可知:DCP DEP ∆≅∆,4DC DE ∴==,CP EP =.在OEF ∆和OBP ∆中,90EOF BOP B E OP OF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,()OEF OBP AAS ∴∆≅∆,OE OB ∴=,EF BP =.设EF x =,则BP x =,4DF DE EF x =-=-,又BF OB OF OE OP PE PC =+=+==,3PC BC BP x =-=-,1AF AB BF x ∴=-=+.在Rt DAF ∆中,222AF AD DF +=,即222(1)3(4)x x ++=-, 解得:35x =, 1745DF x ∴=-=, 15cos 17AD ADF DF ∴∠==. 故选:C .【点评】本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形,利用勾股定理结合1AF x =+,求出AF 的长度是解题的关键.二.填空题(共12小题) 13.如图,正方形ABCD 的边长是16,点E 在边AB 上,3AE =,点F 是边BC 上不与点B ,C 重合的一个动点,把EBF ∆沿EF 折叠,点B 落在B '处.若CDB ∆'恰为等腰三角形,则DB '的长为 16或45 .【分析】根据翻折的性质,可得B E '的长,根据勾股定理,可得CE 的长,根据等腰三角形的判定,可得答案.【解答】解:()i 当B D B C '='时,过B '点作//GH AD ,则90B GE ∠'=︒,当B C B D '='时,182AG DH DC ===, 由3AE =,16AB =,得13BE =.由翻折的性质,得13B E BE '==.835EG AG AE∴=-=-=,222213512B G B E EG∴'='-=-=,16124B H GH B G∴'=-'=-=,22224845DB B H DH∴'='+=+=()ii当DB CD'=时,则16DB'=(易知点F在BC上且不与点C、B重合).()iii当CB CD'=时,则CB CB=',由翻折的性质,得EB EB=',∴点E、C在BB'的垂直平分线上,EC∴垂直平分BB',由折叠,得EF也是线段BB'的垂直平分线,∴点F与点C 重合,这与已知“点F是边BC上不与点B,C重合的一个动点”不符,故此种情况不存在,应舍去.综上所述,DB'的长为16或45.故答案为:16或45.【点评】本题考查了翻折变换,利用了翻折的性质,勾股定理,等腰三角形的判定.14.如图,矩形ABCD中,3AB=,4BC=,点E是BC边上一点,连接AE,把B∠沿AE折叠,使点B落在点B'处.当CEB∆'为直角三角形时,BE的长为32或3.【分析】当CEB∆'为直角三角形时,有两种情况:①当点B'落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出5∠'=∠=︒,而当AB E BAC=,根据折叠的性质得90∠沿AE折∠'=︒,所以点A、B'、C共线,即BEB C∆'为直角三角形时,只能得到90CEB叠,使点B落在对角线AC上的点B'处,则EB EB=',3AB ABCB'=,='=,可计算出2设BE xCE x∆'中运用勾股定理可计算出x.=-,然后在Rt CEB'=,4=,则EB x②当点B'落在AD边上时,如答图2所示.此时ABEB'为正方形.【解答】解:当CEB∆'为直角三角形时,有两种情况:①当点B'落在矩形内部时,如答图1所示.连结AC,在Rt ABC∆中,3BC=,AB=,422AC∴=+,435∠沿AE折叠,使点B落在点B'处,B∴∠'=∠=︒,90AB E B当CEB∠'=︒,EB C∆'为直角三角形时,只能得到90∠沿AE折叠,使点B落在对角线AC上的点B'处,∴点A、B'、C共线,即B∴=',3EB EBAB AB='=,∴'=-=,532CB设BE x=-,CE x=,则EB x'=,4在Rt CEB ∆'中,222EB CB CE '+'=,2222(4)x x ∴+=-,解得32x =, 32BE ∴=; ②当点B '落在AD 边上时,如答图2所示.此时ABEB '为正方形,3BE AB ∴==.综上所述,BE 的长为32或3. 故答案为:32或3. 【点评】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题有两种情况,需要分类讨论,避免漏解.15.如图矩形ABCD 中,5AD =,7AB =,点E 为DC 上一个动点,把ADE ∆沿AE 折叠,当点D 的对应点D '落在ABC ∠的角平分线上时,DE 的长为 52或53 .【分析】连接BD ',过D '作MN AB ⊥,交AB 于点M ,CD 于点N ,作D P BC '⊥交BC 于点P ,先利用勾股定理求出MD ',再分两种情况利用勾股定理求出DE .【解答】解:如图,连接BD ',过D '作MN AB ⊥,交AB 于点M ,CD 于点N ,作D P BC'⊥交BC 于点P点D 的对应点D '落在ABC ∠的角平分线上,M D PD ∴'=',设MD x '=,则PD BM x '==,7AM AB BM x ∴=-=-,又折叠图形可得5AD AD ='=,22(7)25x x ∴+-=,解得3x =或4,即3MD '=或4.在Rt END ∆'中,设ED a '=,①当3MD '=时,734AM =-=,532D N '=-=,4EN a =-,2222(4)a a ∴=+-, 解得52a =,即52DE =, ②当4MD '=时,743AM =-=,541D N '=-=,3EN a =-,2221(3)a a ∴=+-,解得53a =,即53DE =. 故答案为:52或53. 【点评】本题主要考查了折叠问题,解题的关键是明确掌握折叠以后有哪些线段是对应相等的.16.如图,在Rt ABC ∆中,90A ∠=︒,AB AC =,21BC =+,点M ,N 分别是边BC ,AB上的动点,沿MN 所在的直线折叠B ∠,使点B 的对应点B '始终落在边AC 上,若△MB C '为直角三角形,则BM 的长为 11222+或1 .【分析】①如图1,当90B MC ∠'=︒,B '与A 重合,M 是BC 的中点,于是得到结论;②如图2,当90MB C ∠'=︒,推出CMB ∆'是等腰直角三角形,得到2CM MB ',列方程即可得到结论.【解答】解:①如图1,当90B MC ∠'=︒,B '与A 重合,M 是BC 的中点,1112222BM BC ∴=;②如图2,当90MB C ∠'=︒,90A ∠=︒,AB AC =,45C ∴∠=︒,CMB ∴∆'是等腰直角三角形, 2CM MB ∴=', 沿MN 所在的直线折叠B ∠,使点B 的对应点B ',BM B M ∴=',2CM BM ∴=,21BC =,221CM BM BM BM ∴+=+=+,1BM ∴=,综上所述,若△MB C '为直角三角形,则BM 的长为11222+或1, 故答案为:11222+或1.【点评】本题考查了翻折变换-折叠问题,等腰直角三角形的性质,正确的作出图形是解题的关键.17.如图,矩形ABCD 中,8AB =,6BC =,P 为AD 上一点,将ABP ∆沿BP 翻折至EBP ∆,PE 与CD 相交于点O ,BE 与CD 相交于点G ,且OE OD =,则AP 的长为 4.8 .【分析】由折叠的性质得出EP AP =,90E A ∠=∠=︒,8BE AB ==,由ASA 证明ODP OEG ∆≅∆,得出OP OG =,PD GE =,设AP EP x ==,则6PD GE x ==-,DG x =,求出CG 、BG ,根据勾股定理得出方程,解方程即可.【解答】解:如图所示:四边形ABCD 是矩形,90D A C ∴∠=∠=∠=︒,6AD BC ==,8CD AB ==,根据题意得:ABP EBP ∆≅∆,EP AP ∴=,90E A ∠=∠=︒,8BE AB ==,在ODP ∆和OEG ∆中,D E OD OEDOP EOG ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ODP OEG ASA ∴∆≅∆,OP OG ∴=,PD GE =,DG EP ∴=,设AP EP x ==,则6PD GE x ==-,DG x =,8CG x ∴=-,8(6)2BG x x =--=+,根据勾股定理得:222BC CG BG +=,即2226(8)(2)x x +-=+,解得: 4.8x =,4.8AP ∴=;故答案为:4.8.【点评】本题考查了矩形的性质、折叠的性质、全等三角形的判定与性质、勾股定理;熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.18.如图,在Rt ABC ∆中,90C ∠=︒,6AC =,8BC =,点F 在边AC 上,并且2CF =,点E 为边BC 上的动点,将CEF ∆沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是 1.2 .【分析】如图,延长FP 交AB 于M ,当FP AB ⊥时,点P 到AB 的距离最小,利用AFM ABC ∆∆∽,得到AF FM AB BC=求出FM 即可解决问题. 【解答】解:如图,延长FP 交AB 于M ,当FP AB ⊥时,点P 到AB 的距离最小.(点P 在以F 为圆心CF 为半径的圆上,当FP AB ⊥时,点P 到AB 的距离最小)A A ∠=∠,90AMF C ∠=∠=︒,AFM ABC ∴∆∆∽,∴AF FM AB BC=, 2CF =,6AC =,8BC =,4AF ∴=,2210AB AC BC +=,∴4108FM =, 3.2FM ∴=,2PF CF ==,1.2PM ∴=∴点P 到边AB 距离的最小值是1.2.故答案为1.2.【点评】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理.垂线段最短等知识,解题的关键是正确找到点P 位置,属于中考常考题型.19.如图,正方形纸片ABCD 的边长为12,E 是边CD 上一点,连接AE 、折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上,若5DE =,则GE 的长为4913.【分析】由折叠及轴对称的性质可知,ABF GBF ∆≅∆,BF 垂直平分AG ,先证ABF DAE ∆≅∆,推出AF 的长,再利用勾股定理求出BF 的长,最后在Rt ADF ∆中利用面积法可求出AH 的长,可进一步求出AG 的长,GE 的长. 【解答】解:四边形ABCD 为正方形,12AB AD ∴==,90BAD D ∠=∠=︒,由折叠及轴对称的性质可知,ABF GBF ∆≅∆,BF 垂直平分AG ,BF AE ∴⊥,AH GH =,90BAH ABH ∴∠+∠=︒,又90FAH BAH ∠+∠=︒,ABH FAH ∴∠=∠,()ABF DAE ASA ∴∆≅∆, 5AF DE ∴==,在Rt ABF ∆中,222212513BF AB AF =++, 1122ABF S AB AF BF AH ∆==, 12513AH ∴⨯=, 6013AH ∴=, 120213AG AH ∴==, 13AE BF ==,12049131313GE AE AG ∴=-=-=, 故答案为:4913.【点评】本题考查了正方形的性质,轴对称的性质,全等三角形的判定与性质,勾股定理,面积法求线段的长度等,解题关键是能够灵活运用正方形的性质和轴对称的性质. 20.折叠矩形纸片ABCD 时,发现可以进行如下操作:①把ADE ∆翻折,点A 落在DC 边上的点F 处,折痕为DE ,点E 在AB 边上;②把纸片展开并铺平;③把CDG ∆翻折,点C 落在线段AE 上的点H 处,折痕为DG ,点G 在BC 边上,若2AB AD =+,1EH =,则AD = 323+ .【分析】设AD x =,则2AB x =+,利用折叠的性质得DF AD =,EA EF =,90DFE A ∠=∠=︒,则可判断四边形AEFD 为正方形,所以AE AD x ==,再根据折叠的性质得2DH DC x ==+,当1AH AE HE x =-=-,然后根据勾股定理得到222(1)(2)x x x +-=+,再解方程求出x 即可. 【解答】解:设AD x =,则2AB x =+, 把ADE ∆翻折,点A 落在DC 边上的点F 处,DF AD ∴=,EA EF =,90DFE A ∠=∠=︒,∴四边形AEFD 为正方形,AE AD x ∴==,把CDG ∆翻折,点C 落在直线AE 上的点H 处,折痕为DG ,点G 在BC 边上, 2DH DC x ∴==+,1HE =,当1AH AE HE x =-=-, 在Rt ADH ∆中,222AD AH DH +=,222(1)(2)x x x ∴+-=+,整理得2630x x --=,解得1323x =+,2323x =-(舍去), 即AD 的长为323+. 故答案为:323+.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理. 21.如图,把某矩形纸片ABCD 沿EF ,GH 折叠(点E ,H 在AD 边上,点F ,G 在BC 边上),使点B 和点C 落在AD 边上同一点P 处,A 点的对称点为A '点,D 点的对称点为D '点,若90FPG ∠=︒,△A EP '的面积为4,△D PH '的面积为1,则矩形ABCD 的面积等于 1065+ .【分析】设AB CD x ==,由翻折可知:PA AB x '==,PD CD x '==,因为△A EP '的面积为4,△D PH '的面积为1,推出12D H x '=,由11122x x =,可得2x =(负根已经舍弃),即可解决问题.【解答】解:四边形ABC 是矩形, AB CD ∴=,AD BC =,设AB CD x ==,由翻折可知:PA AB x '==,PD CD x '==,△A EP '的面积为4,△D PH '的面积为1, 又△A EP '∽△D PH ', :2A P D H ∴''=,PA x '=, 12D H x ∴'=, 11122x x =, 2x ∴=(负根已经舍弃), 2AB CD ∴==,222425PE =+=,22125PH =+=, 42551535AD ∴=+++=+,∴矩形ABCD 的面积2(535)1065=+=+.故答案为1065+【点评】本题考查翻折变换,矩形的性质,勾股定理,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.22.如图,将正方形纸片ABCD 沿MN 折叠,使点D 落在边AB 上,对应点为D ',点C 落在C '处.若6AB =,2AD '=,则折痕MN 的长为 210 .【分析】作NF AD ⊥,垂足为F ,连接DD ',根据图形折叠的性质得出DD MN '⊥,先证明DAD DEM ∆'∆∽,再证明NFM DAD ∆≅∆',然后利用勾股定理的知识求出MN 的长. 【解答】解:作NF AD ⊥,垂足为F ,连接DD ',将正方形纸片ABCD 折叠,使得点D 落在边AB 上的D '点,折痕为MN , DD MN ∴'⊥,90A DEM ∠=∠=︒,ADD EDM ∠'=∠,DAD DEM ∴∆'∆∽, DD A DME ∴∠'=∠,在NFM ∆和DAD ∆'中 DD A NMF A NFMNF DA ∠'=∠⎧⎪∠=∠⎨⎪=⎩, ()NFM DAD AAS ∴∆≅∆',2FM AD ∴='=,又在Rt MNF ∆中,6FN =,∴根据勾股定理得:222262210MN FN FM =+=+=.故答案为:210.【点评】此题主要考查了图形的翻折变换,根据图形折叠前后图形不发生大小变化得出三角形的全等是解决问题的关键,难度一般.23.如图,在矩形纸片ABCD 中,将AB 沿BM 翻折,使点A 落在BC 上的点N 处,BM 为折痕,连接MN ;再将CD 沿CE 翻折,使点D 恰好落在MN 上的点F 处,CE 为折痕,连接EF 并延长交BM 于点P ,若8AD =,5AB =,则线段PE 的长等于203.【分析】根据折叠可得ABNM 是正方形,5CD CF ==,90D CFE ∠=∠=︒,ED EF =,可求出三角形FNC 的三边为3,4,5,在Rt MEF ∆中,由勾股定理可以求出三边的长,通过作辅助线,可证FNC PGF ∆∆∽,三边占比为3:4:5,设未知数,通过PG HN =,列方程求出待定系数,进而求出PF 的长,然后求PE 的长.【解答】解:过点P 作PG FN ⊥,PH BN ⊥,垂足为G 、H , 由折叠得:ABNM 是正方形,5AB BN NM MA ====, 5CD CF ==,90D CFE ∠=∠=︒,ED EF =, 853NC MD ∴==-=,在Rt FNC ∆中,22534FN =-=, 541MF ∴=-=,在Rt MEF ∆中,设EF x =,则3ME x =-,由勾股定理得,2221(3)x x +-=, 解得:53x =, 90CFN PFG ∠+∠=︒,90PFG FPG ∠+∠=︒, CFN FPG ∴∠=∠,又90FGP CNF ∠=∠=︒ FNC PGF ∴∆∆∽,::::3:4:5FG PG PF NC FN FC ∴==,设3FG m =,则4PG m =,5PF m =,43GN PH BH m ∴===-,5(43)134HN m m PG m =--=+==,解得:1m =, 55PF m ∴==, 520533PE PF FE ∴=+=+=,故答案为:203.【点评】考查折叠轴对称的性质,矩形、正方形的性质,直角三角形的性质等知识,知识的综合性较强,是有一定难度的题目.24.如图,在Rt ABC ∆中,90C ∠=︒,23BC =,2AC =,点D 是BC 的中点,点E 是边AB 上一动点,沿DE 所在直线把BDE ∆翻折到△B DE '的位置,B D '交AB 于点F .若△AB F '为直角三角形,则AE 的长为 3或145.【分析】利用三角函数的定义得到30B ∠=︒,4AB =,再利用折叠的性质得3DB DC ==EB EB '=,30DB E B ∠'=∠=︒,设AE x =,则4BE x =-,4EB x '=-,讨论:当90AFB ∠'=︒时,则332BF ∴︒=,则35(4)22EF x x =--=-,于是在Rt △B EF '中利用2EB EF '=得到542()2x x -=-,解方程求出x 得到此时AE 的长;若B '不落在C 点处,作EH AB ⊥'于H ,连接AD ,如图,证明Rt ADB Rt ADC ∆'≅∆得到2AB AC '==,再计算出60EB H ∠'=︒,则1(4)2B H x '=-,3)EH x -,接着利用勾股定理得到22231(4)[(4)2]42x x x -+-+=,方程求出x 得到此时AE 的长. 【解答】解:90C ∠=︒,23BC =,2AC =,3tan 23AC B BC ∴===, 30B ∴∠=︒,24AB AC ∴==,点D 是BC 的中点,沿DE 所在直线把BDE ∆翻折到△B DE '的位置,B D '交AB 于点F 3DB DC ∴==,EB EB '=,30DB E B ∠'=∠=︒,设AE x =,则4BE x =-,4EB x '=-, 当90AFB ∠'=︒时, 在Rt BDF ∆中,cos BFB BD=, 33cos302BF ∴=︒=, 35(4)22EF x x ∴=--=-, 在Rt △B EF '中,30EB F ∠'=︒,2EB EF ∴'=,即542()2x x -=-,解得3x =,此时AE 为3;若B '不落在C 点处,作EH AB ⊥'于H ,连接AD ,如图, DC DB =',AD AD =, Rt ADB Rt ADC ∴∆'≅∆, 2AB AC ∴'==,9030120AB E AB F EB F ∠'=∠'+∠'=︒+︒=︒, 60EB H ∴∠'=︒,在Rt EHB ∆'中,11(4)22B H B E x '='=-,33(4)EH B H x ='=-, 在Rt AEH ∆中,222EH AH AE +=,∴22231(4)[(4)2]42x x x -+-+=,解得145x =,此时AE 为145.综上所述,AE 的长为3或145. 故答案为3或145.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形。
七年级数学下专题——折叠问题

七年级数学下专题——折叠问题1、将一张等宽的纸条按照图示方式折叠,如果∠1=50°,那么∠2的角度是多少?2、在矩形ABCD中(AD>AB),点M在CD上,如果沿着AM折叠,那么点N会恰好落在BC上。
求∠ANB+∠MNC的度数。
3、将长方形纸片ABCD沿着EF折叠,使得ED与BC相交于点G,点D和C分别在M和N的位置上。
如果∠EFG=55°,那么∠1和∠2的角度分别是多少?4、将一个正方形折叠三次,然后沿着虚线剪下,得到的图形是()。
如果将EB延长线与AD或其延长线相交于F,则△EAF是()。
5、将矩形ABCD沿着折痕MN对折,然后将点B叠在折痕上。
6、将标号为A、B、C、D的正方形沿着虚线剪开,得到标号为P、Q、M、N的四个图形。
按照“哪个正方形剪开后得到哪个图形”的对应关系填空:A与______对应,B与______对应,C与______对应,D与______对应。
7、将一张正方形纸片对折两次,并剪出一个菱形小洞,然后展开铺平。
得到的图形是()。
8、将一块正方形纸片沿着对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是()。
9、将一圆形纸片对折两次,然后沿着图中的虚线剪开,得到两部分。
其中一部分展开后的平面图形是()。
10、将ABC沿着DE折叠后,点A落在BC边上的A 处,如果点D是AB边的中点,且B50,那么BDA的度数是多少?11、将一块长方形布料ABCD沿着AE折叠,使得D点落在BC边的F处。
如果∠BAF=60º,那么∠DAE的度数是多少?12、将正方形ABCD沿着折痕EF对折。
将这个正方形展平后,再分别将A、B对折,使点A、点B都与折痕EF上的点G重合。
这时,我们可以发现,线段DE与线段FG重合,线段EF与线段DG重合,因此三角形DEF与三角形GDE完全重合,它们的所有角度都相等。
所以∠1的度数为90度。
2020年九年级数学中考专题:图形折叠的问题

2020年九年级数学中考专题:图形折叠的问题专题图形的折叠问题⼀.选择题1. 如图,在矩形ABCD 中,AB =4,BC =6,点E 为BC 的中点,连接AE ,将△ABE 沿AE 折叠,使得点B 落在点B ′处,则点B ′到线段BC 的距离为( ).A.2572 B.1336 C. 4 D.4357 2. 如图,将矩形ABCD 沿直线AC 折叠,点B 落在点E 处,连接DE ,BE ,若△ABE 为等边三⾓形,且S △CDE =3,则CD 的长为().A.√3B. 2√3C. 3D. 23. 如图,将矩形纸⽚ABCD 沿AE 折叠,使点B 落在对⾓线AC 上的点F 处,再沿EG 折叠,使点C 落在矩形内的点H 处,且E 、F 、H 在同⼀直线上,若AB =6,BC =8,则CG 的长是( ).A. 3B.2C. 2.5D.4.54. 如图,在菱形ABCD 中,BD =211,AC =10,点P 在对⾓线AC 上,过点P 作EF ⊥AC 交AD 于点E ,交AB 于点F ,将△AEF 折叠,使点A 落在点A ′处,A ′C =A ′D ,则AP 的长为( ).A.25 B.21 C. 3 D.43 ⼆.填空题5. 如图,四边形ABCD 是矩形,点E 是BC 上⼀点,连接AE ,将△DEC 沿DE 所在的直线对折,使得点C 落在AE 上的点F 处,连接BF ,若EF =13AE ,AB =1,则AF =________.6. 如图,边长为4的菱形纸⽚ABCD 中,∠A =60°,折叠菱形纸⽚ABCD ,使点C 落在DP (P 为AB 的中点)所在直线上的C ′处,得到经过点D 的折痕DE ,则CE =________.7. 如图,将?ABCD 沿EF 对折,使点A 落在点C 处,若∠A =60°,AD =4,AB =8,则AE 的长为________.8. 将矩形ABCD 按如图所⽰的⽅式折叠,BE ,EG ,FG 为折痕,且顶点A ,C ,D 都落在点O 处,且点B ,O ,G 在同⼀条直线上,同时点E ,F ,O 在另⼀条直线上,若AB =2,则AD 的长为 .9.如图,在矩形ABCD中,点E为AB边上的点,将△ADE沿直线DE翻折,使得点A与BC边上的点G重合,连接AG交DE于点F,若AD=6,EF=1,则AB的长为.10.如图,正⽅形ABCD,E为BC边的中点,连接AE,点P是边CD上⼀点,沿AP折叠使D点落在AE上的H处,延长PH交BC于F点,若EF=1,则AB的长为.三.解答题11.如图,矩形ABCD中,△BCD沿BD折叠,使点C落到点E处,BE与AD相交于点F,点O是BD的中点,连接FO并延长交BC于点G,若AB=6,AD=8,(1)求证:四边形BFDG是平⾏四边形(2)求FG的长。
专题03 折叠问题压轴题(学生版)
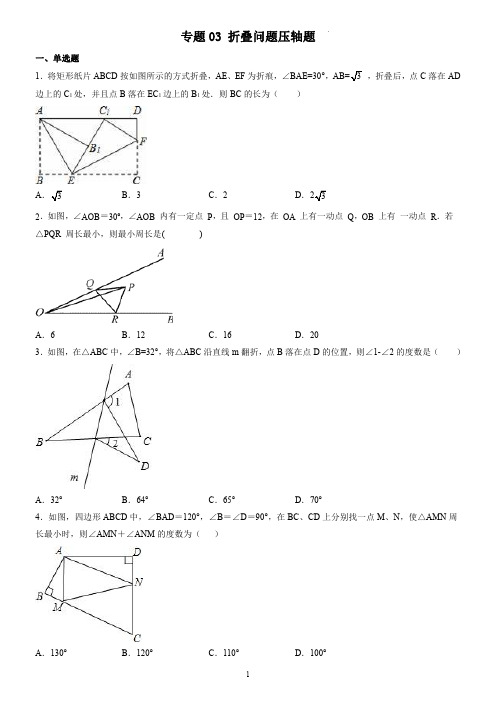
专题03折叠问题压轴题一、单选题,折叠后,点C落在AD1.将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,边上的C1处,并且点B落在EC1边上的B1处.则BC的长为()B.3C.2D.A2.如图,∠AOB=30º,∠AOB内有一定点P,且OP=12,在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是()A.6B.12C.16D.203.如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是()A.32°B.64°C.65°D.70°4.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为()A.130°B.120°C.110°D.100°5.如图,∠AOB =30°,OC 为∠AOB 内部一条射线,点P 为射线OC 上一点,OP =6,点M 、N 分别为OA 、OB 边上动点,则△MNP 周长的最小值为()A .3B .6C .D .6.如图,△ABC 中,∠A =20°,沿BE 将此三角形对折,又沿BA′再一次对折,点C 落在BE 上的C′处,此时∠C′DB =74°,则原三角形的∠C 的度数为()A .27°B .59°C .69°D .79°7.如图,将ABC ∆沿DE EF 、翻折,使其顶点A B 、均落在点O 处,若72CDO CFO ∠+∠=,则C ∠的度数为()A .36oB .54oC .64D .728.如图,在锐角△ABC 中,∠ACB =50°;边AB 上有一定点P ,M 、N 分别是AC 和BC 边上的动点,当△PMN 的周长最小时,∠MPN 的度数是()A .50°B .60°C .70°D .80°9.如图,在ABC 中,AB AC >,AD 平分BAC ∠,交BC 于点D .若7BC =,2DC =,则AB AC -的值可能是()A .7BC .3D10.折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着EF 进行第一次折叠,使得C ,D 两点落在1C 、1D 的位置,再将纸条沿着GF 折叠(GF 与BC 在同一直线上),使得1C 、1D 分别落在2C 、2D 的位置.若23EFB EFC ∠=∠,则GEF ∠的度数为()A .30°B .36︒C .45︒D .60︒11.如图,Rt △ABC 中,∠C=90°,AC=3,BC=4,D ,E ,F 分别是AB ,BC ,AC 边上的动点,则△DEF 的周长的最小值是()A .2.5B .3.5C .4.8D .6二、填空题12.在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有__种.13.如图,在边长为2的菱形ABCD 中,∠D=60°,点E 、F 分别在边AB 、BC 上.将△BEF 沿着直线EF 翻折,点B 恰好与边AD 的中点G 重合,则BE 的长等于_____.14.在平行四边形ABCD 中,AB 2=,AD 3=,点E 为BC 中点,连结AE ,将ABE 沿AE 折叠到△AB´E 的位置,若BAE 45∠=,则点B´到直线BC 的距离为______.15.如图1,在长方形纸片ABCD 中,E 点在边AD 上,F 、G 分别在边AB 、CD 上,分别以EF 、EG 为折痕进行折叠并压平,点A 、D 的对应点分别是点A′和点D′,若ED′平分∠FEG ,且'ED 在A EF ∠'内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n 的代数式表示).16.如图,将长方形纸片进行折叠,, ED EF 为折痕,A 与'A B 、与'B C 、与'C 重合,若25AED ∠=︒,则BEF ∠的度数为____________17.如图,△ABC 中,AB =AC ,∠BAC =62°,∠BAC 的平分线与AB 的垂直平分线交于点O ,将∠C 沿EF (E 在BC 上,F 在AC 上)折叠,点C 与点O 恰好重合,则∠OEC 为_____度.18.图1是一张足够长的纸条,其中//PN QM ,点A 、B 分别在PN ,QM 上,记()090ABM αα∠=︒<≤︒.如图2,将纸条折叠,使BM 与BA 重合,得折痕1BR ;如图3,将纸条展开后再折叠,使BM 与1BR 重合,得折痕2BR :将纸条展开后继续折叠,使BM 与2BR 重合,得折痕3BR ;...依此类推,第n 次折叠后,n AR N ∠=_______(用含α和n 的代数式表示).19.如图(1)是由两块形状相同的三角板拼成,已知90BAC ADC ∠=∠=︒,30B ACD ∠=∠=︒,点E 是边BC 上的动点,连结AE ,将三角形ACD 沿直线AE 翻折,点C ,D 的对应点分别为N ,M ,则:(1)如图(2),当点N 恰好落在AB 边上时,AEC ∠的度数是___________;(2)当MN 与三角形ABC 的一边平行时,AEC ∠的度数为________.三、解答题20.如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.⑴若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为.⑵若∠PEF=75°,∠CFQ=∠PFC,求∠EFP的度数.21.如图所示的“钻石”型网格是由边长都为1个单位长度的等边三角组成.(1)若在网格中任取一点,求该点落在阴影部分的概率是多少?(2)请在作图区所给的图中,将一个空白小三角形涂上阴影,使它与原阴影部分组成的图形是轴对称图形.的图中.(画出所有可能的结果,所给的图未必全用).22.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠AEN的度数.(提示,长方形的四个角都是90°)23.如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β|=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)(1)若∠A=80°,则∠A的半余角的度数为;(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.24.(1)填空①把一张长方形的纸片按如图①所示的方式折叠,EM ,FM 为折痕,折叠后的C 点落在1B M 或1B M 的延长线上,那么EMF ∠的度数是________;②把一张长方形的纸片按如图②所示的方式折叠,B 点与M 点重合,EM ,FM 为折痕,折叠后的C 点落在1A M 或1A M 的延长线上,那么EMF ∠的度数是_______.(2)解答:①把一张长方形的纸片按如图③所示的方式折叠,EM ,FM 为折痕,折叠后的C 点落在1B M 或1B M 的延长线上左侧,且80EMF ∠=︒,求11C MB ∠的度数;②把一张长方形的纸片按如图④所示的方式折叠,B 点与M 点重合,EM ,FM 为折痕,折叠后的C 点落在1A M 或1A M 的延长线右侧,且60EMF ∠=︒,求11C MA ∠的度数.(3)探究:把一张四边形的纸片按如图⑤所示的方式折叠,EB ,FB 为折痕,设ABC α∠=︒,EBF β∠=︒,11A BC γ∠=︒,求α,β,γ之间的数量关系.25.直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F 向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.26.在平面直角坐标系xOy 中,点P (x ,y )经过变换τ得到点P′(x′,y′),该变换记作τ(x ,y )=(x′,y′),其中x ax by y ax by =+⎧⎨=-''⎩(a ,b 为常数).例如,当a =1,且b =1时,τ(﹣2,3)=(1,﹣5).(1)当a =﹣1,且b =2时,τ(0,1)=;(2)若τ(1,2)=(﹣2,0),则a =,b =;(3)设点P (x ,﹣2x ),点P 经过变换τ得到点P′(x′,y′).若点P′与点P 关于x 轴对称,求a 和b 的值.27.如图1,三角形ABC 中,64A ∠=︒,90B ∠=︒,26C ∠=︒.点D 是AC 边上的定点,点E 在BC 边上运动,沿DE 折叠三角形CDE ,点C 落在点G 处.(1)如图2,若//DE AB ,求ADG ∠的度数.(2)如图3,若//EG AB ,求ADG ∠的度数.(3)当三角形DEG 的三边与三角形ABC 的三边有一组边平行时,直接写出其他所有情况下ADG ∠的度数.28.已知:M、N分别是∠AOB的边OA、OB上的定点.(1)如图1,若∠O=∠OMN,过M作射线MD//OB(如图),点C是射线MD上一动点,∠MNC的平分线NE 交射线OA于E点.试探究∠MEN与∠MCN的数量关系;(2)如图2,若P是线段ON上一动点,Q是射线MA上一动点.∠AOB=20 ,当MP+PQ+QN取得最小值时,求∠OPM+∠OQN的值.11。
四年级数学上册第八单元:折叠图形中的角度问题专项练习(原卷版)苏教版

2022-2023学年四年级数学上册典型例题系列之第八单元:折叠图形中的角度问题专项练习(原卷版)一、填空题。
1.一张长方形纸如图那样折起,已知130∠=︒,那么2∠=( )︒。
2.把长方形纸折叠后(如图),∠2=75°,则∠1等于( )°。
3.下图长方形的每个角的度数都是( )。
如果将这个长方形从一条边上的点A折叠,出现两个角(如下图),已知∠1=110°,那么∠2=( )°。
4.下图是一张长方形纸折起一个角。
已知130,23∠∠∠∠=( )==,2度。
5.如图,一张长方形纸折起一个角,已知∠1=52°,那么∠2=( )°。
6.如图是一张长方形纸折起来形成的图形,∠1=40°,那么∠2=( )°。
7.如图,一个长方形和一个正方形如图叠放,∠1=( )°。
8.一个长方形和一个正方形如图叠放,∠1=∠2,则∠1=( )°。
9.如图,∠1+∠2+∠3=110°,∠l=( )°,∠3=( )°。
10.如图是一张长方形纸折起来以后的图形,已知∠2是65°,∠1是( )度。
二、解答题。
11.下图是一张长方形纸折起来以后得到的图形。
如果∠1=36°,那么∠2是多少度?如果∠2=36°,那么∠1是多少度?12.如图,把一张长方形的一个角折过来,已知∠1=70°,求∠2。
13.将一张长方形的纸按如图所示的方法折叠.∠1是多少度?14.将一张长方形的纸按如图所示的方法折叠.∠1是多少度?15.下图表示一张长方形纸折起一个角。
已知∠2=60°,∠1是多少度?请你写出计算过程。
折叠问题专题练

A B C D M N PQ 折叠问题1.将一张长方形纸片按如图所示的方式折叠,BC 、BD 为折痕,则∠CBD 的度数为_____ 2.如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于______3、如图,把矩形ABCD 沿EF 对折后使两部分重合,若150∠=°,则AEF ∠=( )A .110° B.115° C.120° D.130°4、如图,梯形ABCD 中,AD∥BC,DC⊥BC,将梯形沿对角线BD 折叠,点A 恰好落在DC 边上的点A´处,若∠A´BC=20°,则∠A´BD 的度数为( ) A .15° B.20° C.25° D.30°5、如图,将纸片△ABC 沿DE 折叠,点A 落在点A′处,已知∠1+∠2=100°,则∠A 的大小等于____________度.6 、点E 是矩形ABCD 的边CD 上的点,沿着AE 折叠矩形ABCD ,使D 落在BC 边上的F 点处,如果∠BAF =60°,则∠DEA =____________.7.如图,已知正方形纸片ABCD ,M ,N 分别是AD 、BC 的中点,把BC 边向上翻折,使点C 恰好落在MN 上的P 点处,BQ 为折痕,则∠PBQ = 度.1 A EDCBF8. 如图,在平行四边形ABCD中,∠A=70°,将平行四边形折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于_____________。
9.如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C’,D’处,C’E交AF于点G.若∠CEF=70°,则∠GFD’=_____。
10、将矩形纸片ABCD折叠,使点D与点B重合,点C落在点c'处,折痕为EF,若∠ABE=20°,那么∠EFC'的度数为_________。
初二数学能力测试题(折纸问题)

初二数学能力测试题(折纸问题)一、填空题:1、把边长为1的正方形对折n次后,所得图形的面积是。
2、将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕MN上(如图1上点B),若AB=3,则折痕AE的长是,△AEF是三角形。
3、如图2,矩形纸片ABCD沿对角线BD折叠,设点D落在D1处,BC1交AD于E,= 。
=6cm,BC=8cm,则S阴4、如图3,折叠矩形纸片ABCD的一边AD,点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EC= 。
5、如图4,把矩形纸片折叠,使点落在AD边的中点C1处,设折痕为EF,AB=3,BC=4,则CE:BE= ,CF:FD 。
6、如图5,把矩形ABCD纸片折叠,使点D与点B重合,则四边形BEDF是形;若AB=6,BC=8,则折痕EF= 。
7、如图6,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在C1的位置,则BC1与BC之间的数量关系是。
8、如图7、把一张长方形ABCD的纸片,沿着EF折叠后,ED和BC的交点为G,点D、C分别落在D1、C1的位置上,若∠EFG=55°,则∠1= 度。
9、如图8,将△ABC折叠成图8,则折出两条定理,这两条定理是:①;②。
10、如图9,在△ABC中,周长为22,AB=AC,BC=6,现把线段AB对折,设折痕为DE,则△BEC的周长是。
11、如图10,折叠矩形ABCD,先折出折痕(对角线)BD,再折叠AD,使AD边落在折痕BD上,得折痕DG,若AB=2,BC=1,则AG= 。
12、如图11,把边长为a的等边△ABC折叠,使点A落在BC边的点D,且BD:DC=2:3,设折痕为MN,则AM:AN的值是。
13、如图12,一边长为250cm的正方形ABCD纸片,AD上有一点P,且AP= ,折这纸片使点B落在点P上,则折痕EF的长是 cm。
14、如图13,EF 为正方形纸ABCD 的对折线,将∠A 沿DK 折叠,使它的的顶点A 落在EF 上的G 点,则∠DKG 的度数是 。
中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案

中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一 单选题1.如图 在矩形纸片ABCD 中 将BCD △沿BD 折叠 C 点落在C '处 则图中共有全等三角形( )A .2对B .3对C .4对D .5对2.如图 对折矩形纸片ABCD 使AB 与DC 重合得到折痕EF 将纸片展平 再一次折叠 使点D 落到EF 上点G 处 并使折痕经过点A 展平纸片后DAG ∠的大小为( )A .40︒B .60︒C .55︒D .75︒3.如图 在矩形ABCD 中 5AB = 8BC = 点E 和F 是边BC 上的两点 连结AE DF 、 将ABE 和CDF 沿AE DF 、折叠后 点B 和点C 重合于点M 则EF 的长是( )A .2.5B .3C .1.5D .44.如图 在矩形纸片ABCD 中 已知8AD = 折叠纸片使AB 边与对角线AC 重合 点B 落在点F 处 折痕为AE 且3EF = 则ABE 的面积为( )A .10B .9C .8D .75.如图 在矩形OABC 中 9OA = 15AB = E 是BC 上一点 沿AE 折叠 使点B 恰好落在x 轴的点D 处.E 点坐标是( )A .()5,15B .()3,15C .()15,2D .()15,4 6.如图 在矩形ABCD 中 点E 是边CD 的中点 将ADE 沿AE 折叠后得到AFE △ 且点F 在矩形ABCD 的内部 将AF 延长后交边BC 于点G 且45CG GB = 则AB AD 的值为( )A .43B .56C .1D .77.如图 把矩形纸片ABCD 沿对角线BD 折叠 设重叠部分为EBD △ 则下列结论不一定成立的是( )A .AB CD = B .BAE DCE ≌△△C .EB ED = D .30ABE ∠=︒ 8.如图 在一张菱形纸片ABCD 中 2AB = 30B ∠=︒ 点E 在BC 边上(不与B C 重合)将ABE 沿直线AE 折叠得到AFE △ 连接BF EF DF 有以下四个结论:AE EF =① 105BFD ∠=︒② ③当AE BC ⊥时 FD AC = ④当FE 平分AFB ∠时 则23FD = 其中正确的结论个数是( )A .1B .2C .3D .4二 填空题9.如图 正方形纸片ABCD 的边长为12 E 是边CD 上一点 连接AE 折叠该纸片 使点A 落在AE 上的点G 并使折痕经过点B 得到折痕BF 点F 在AD 上.若5DE = 则GE 的长为 .10.将一张长方形纸片ABCD 按如图所示方式折叠 AE AF 为折痕 点B D 折叠后的对应点分别为B' 'D 若''4B AD ∠=︒ 则EAF ∠的度数为 .11.如图 在长方形ABCD 中 3AD = 2AB = 点F 是AB 上一点 1AF = 点E 是BC 上一动点 连接EF 将BEF △沿EF 折叠 记点B 的对应点为点B ' 连接DB ' 则FB DB '+'的最小值是 .12.如图 在矩形ABCD 中 5AB = 8AD = 边AD 上有一动点P 连结BP 把ABP沿BP 折叠当点A 的对应点A '刚好落在BC 的垂直平分线上时 点A '到AD 的距离为 .13.如图所示 在完全重合放置的两张矩形纸片ABCD 中 8AB = 16BC = 将上面的矩形纸片折叠 使点C 与点A 重合 折痕为EF 点D 的对应点为点G 连接DG 则图中阴影部分的面积为 .三 解答题14.如图 正方形纸片ABCD 的边长12AB = E 是DC 上一点 5CE = 折叠正方形纸片 使点B 和点E 重合 折痕为FG 试求FG 的长.15.如图 把一张长方形纸片ABCD 折叠起来 使其对角顶点A 与C 重合 D 与G 重合 若长方形的长BC 为8 宽AB 为4(1)求DE 的长(2)求阴影部分的面积.16.如图1 将矩形纸片()ABCD AD AB >折叠 使点C 刚好落在线段AD 上 且折痕分别与边BC AD 相交 设折叠后点C D 的对应点分别为点G H 折痕分别与边BC AD 相交于点E F .(1)求证:四边形CEGF 是菱形(2)如图2 若3AB = 9BC = 当点G 与点A 重合时 求折痕EF 的长.17.如图 在四边形纸片ABCD 中 AD BC ∥ AD CD > 将纸片沿过点D 的直线折叠 使点C 落在AD 上的点C '处 折痕DE 交BC 于点E 连接C E '.(1)请确定四边形CDC E '的形状 并说明理由(2)若30BCD ∠=︒ 2CE = 过点C '作C F BC '⊥于F 连接CC '交DE 于点M 连接FM : ①四边形CDC E '的面积为①2FM = .18.已知矩形ABCD 中 4AB = 6AD = 点P 是边AD 的中点.(1)如图1 连接BP 并延长 与CD 的延长线交干点F 问:线段CF 上是否存在点Q 使得PFQ △是以PF 为腰的等腰三角形 若存在 请直接写出DQ 的长 若不存在 请说明理由.(2)①如图2 把矩形ABCD 沿直线MN 折叠 使点B 落在点D 上 直线MN 与AD BD BC 、、的交点分别为M H N 求折痕MN 的长.①如图3:在①的条件下 以点A 为原点 分别以矩形ABCD 的两条边AD AB 、所在的直线为x 轴和y 轴建立平面直角坐标系 若点R 在x 轴上 在平面内是否存在点S 使以R M N S 为顶点的四边形是菱形?若存在 请求出点S 的坐标 若不存在 请说明理由.(3)如图4:若点E 为CD 边上的一个动点 连结PE 以PE 为边向下方作等边PEG △ 连结AG 则AG 的最小值是______.(请直接写出答案)参考答案:1.C2.B3.B4.B5.D6.A7.D8.B9.491310.43︒111012.213.72514.解:如图 过点F 作FM BC ⊥ 垂足为M 连接BE .①四边形ABCD 为正方形①AB BC CD AD === 90A ABC C D ∠=∠=∠=∠=︒①90A ABC BMF ===︒∠∠∠①四边形ABMF 为矩形①12MF AB BC ===①将正方形纸片ABCD 折叠 使点B 落在边CD 上的点E 折痕为FG ①90C FMG ∠=∠=︒ BE FG ⊥①90BNG C ∠=∠=︒①90MGF CBE BEC CBE ∠+∠=∠+∠=︒ ①MGF CEB ∠=∠在FMG 和BCE 中 MGF CEB FMG C FM BC ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS FMG BCE ≌①MG CE =.又①5CE =①5MG =.在Rt MFG 中 根据勾股定理得13FG == 即FG 的长是13.15.(1)设DE EG x == 则8AE x =- 在Rt AEG △中 222AG EG AE +=所以()22168x x +=-解得:3x =即3DE =(2)过点G 作GM AD ⊥于M 则1122AG GE AE GM ⨯=⨯4AG AB == 5AE = 3GE = 所以1143522GM ⨯⨯=⨯⨯所以125GM = 所以11825CED S GM DE =⨯=△. 16.解:(1)证明:①四边形ABCD 是矩形 ①AD ①BC①①GFE =①FEC①图形翻折后点G 与点C 重合 EF 为折线 ①①GEF =①FEC FG =FC EG =EC ①①GFE =①FEG①GF =GE①GE =EC =CF =FG①四边形CEGF 为菱形(2)当G 与A 重合时 由折叠的性质得AE =CE ①①B =90° AB =3 BC =9 BE =9-CE ①Rt ①ABE 中 AE 2=AB 2+BE 2即CE 2=32+(9-CE )2解得 CE =5.AC 222239310AB BC ++=由(1)知四边形CEGF 为菱形 ①12CEGF S EF AC CE AB =⨯=⨯菱形 ①10310EF == 17.(1)解:四边形CDC E '是菱形 理由如下: 根据折叠的性质可得:CD C D C DE CDE '∠=∠ CE C E '= ①AD BC ∥①C DE CED '∠=∠①CDE CED ∠=∠①CD CE =①CD C D C E CE ''===①四边形CDC E '为菱形(2)①①四边形CDC E '是菱形 ①2C E CE '== C E CD '∥ CM C M '= ①30C EF DCB '∠=∠=︒ ①C F BE '⊥ ①112C F C E ''== EF F '=①四边形CDC E '的面积212CE C F '=⨯=⨯= 故答案为:2①①EF = 2CE =①2CF =①(2222218C C C F CF ''=+=+=+①C F BC CM C M ''⊥=, ①12FM C C '=①22124FM C C '==故答案为:2 18.(1)解:存在 理由如下: 四边形ABCD 是矩形 90A ADC ∴∠=∠=︒ AB CD = 90FDP ∴∠=︒点P 是边AD 的中点 AP DP ∴=又APB DPF ∠=∠ ()ASA ABP DFP ∴△≌△ PF PB ∴= AB DF = 4,6AB AD ==4DF AB ∴== 132AP PD AD === 90A ∠=︒在Rt ABP 中:2222345PB AB AP +=+=5PF ∴=PFQ △为等腰三角形 以PF 为腰的等腰三角形分为两种情形: ①当PF PQ =时 此时点Q 与点C 重合 故4DQ DC == ①当FP FQ =时 如图:5PF = 5FQ = FD =4541DQ FQ FD =-=-=综合①① DQ 的长为:4或1(2)解:①如图:连接BM DN根据题意可知:MN 垂直平分BD ,MN BD BH DH ∴⊥= ,NB ND MB MD == 四边形ABCD 是矩形AD BN ∴MDH HBN ∴∠=∠ 又MHD NHB ∠=∠MHD NHB ∴△≌△MH HN ∴= MD NB =∴四边形MBND 是菱形设AM b = 则6MD MB b ==-在Rt AMB △中222BM AM AB =+即:222(6)4b b -=+ 解得:53b = 5513,6333AM BM ∴==-= 在Rt △ABD 中BD 12BH BD ∴=MH BD ⊥∴在Rt MHB △中MH ==2MN MH ∴== ①建立平面直角坐标系如图:由①知:53AM = 133BN MD MB ===4AB = MN = ①5130433M N ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,,, R M N S 为顶点的四边形是菱形 点R 在x 轴上当MR 为对角线时 MR NS ⊥,M R 都在x 轴上 ∴,N S 关于x 轴对称 1343S ⎛⎫∴ ⎪⎝⎭, 当MN 为对角线时 MN RS ⊥ 由(2)知 四边形MBND 是菱形 则S 与点B 重合 ∴此时(0,4)S -当MS 为对角线时 则MR SN ∥ MR SN =MN = 13(,4)3N -①1343S ⎛⎫- ⎪ ⎪⎝⎭综上可知 存在点S 使得以R M N S 为顶点的四边形是菱形 点S 坐标为:134134⎫--⎪⎪⎝⎭ 134134⎫+-⎪⎪⎝⎭ 13,43⎛⎫⎪⎝⎭ (0,4)- (3)解:如图:分别以PD PC 为边向下方作等边,PDF PCH △△ 过点F 作FI AD ⊥垂足为I 连接AF HF P 为AD 中点 ∴132AP PD AD ===PDF △为等边三角形1322PI PD ∴== 60DPF ∠=︒ PD PF =PA PF = 60DPF ∠=︒30PAF PFA ∴∠=∠=︒120APF ∴∠=︒92AI AP PI ∴=+=点E 为CD 边上的一个动点 以PE 为边向下方作等边PEG △ 当点E 与点D 重合时 点G 与点F 重合 当点E 与点C 重合时 点G 与点H 重合 ∴点G 在线段FH 上运动 当AG HF ⊥时 AG 最小 PEG △为等边三角形60EPG ∴∠=︒ PE PG =60 FPG FPE FPE EPD∴∠+∠=∠+∠=︒FPG DPE∴∠=∠∴FPG DPE△≌△PDE PFG∴∠=∠90PDE∠=︒∴90PFG∠=︒PF FH∴⊥当AG HF⊥时AG PF120,30APF PAF∠=︒∠=︒18012060PAG∴∠=︒-︒=︒603030 FAG PAG PAF∠=∠-∠=︒-︒=︒IAF GAF∴∠=∠FI AD⊥90AIF∴=︒在AFI和AFI中AIF AGFAF AFFAG FAI∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASAAFI AFI≌AG AI∴=∴当AG HF⊥时92AG AI==故答案为:92.。
中考数学专题训练:图形的折叠问题(附参考答案)

中考数学专题训练:图形的折叠问题(附参考答案)1.如图,在平面直角坐标系中,矩形ABCD的边AD=5,OA∶OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1处,则点E的坐标是( )A.(1,2) B.(-1,2)C.(√5-1,2) D.(1-√5,2)2.如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=30°,则∠α的度数是( )A.30°B.45°C.74°D.75°3.如图,在矩形ABCD中,AB=2,BC=2√5,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos ∠ECF的值为( )A.23B.√104C.√53D.2√554.把一张矩形纸片ABCD按如图所示方法进行两次折叠,得到等腰直角三角形BEF.若BC=1,则AB的长度为( )A.√2B.√2+12C.√5+12D.435.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别在AB,AC 上,连接DE,将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上.若FD平分∠EFB,则AD的长为( )A.259B.258C.157D.2076.如图,在Rt△ABC中,∠C=90°,CA=CB=3,点D在边BC上.将△ACD沿AD折叠,使点C落在点C′处,连接BC′,则BC′的最小值为__________.7.如图,在Rt△ABC纸片中,∠ACB=90°,CD是边AB上的中线,将△ACD沿CD折叠,当点A落在点A′处时,恰好CA′⊥AB.若BC=2,则CA′=_______.8.如图,点E在矩形ABCD的边CD上,将△ADE沿AE折叠,点D恰好落在边BC 上的点F处.若BC=10,sin ∠AFB=45,则DE=_____.9.如图,在扇形AOB中,点C,D在AB⏜上,将CD⏜沿弦CD折叠后恰好与OA,OB 相切于点E,F.已知∠AOB=120°,OA=6,则EF⏜的度数为________;折痕CD 的长为_______.10.如图,在矩形ABCD中,AB=5,AD=4,M是边AB上一动点(不含端点),将△ADM沿直线DM对折,得到△NDM.当射线CN交线段AB于点P时,连接DP,则△CDP的面积为______;DP的最大值为_______.11.如图,在矩形ABCD中,AB=2,AD=√7,动点P在矩形的边上沿B→C→D →A运动.当点P不与点A,B重合时,将△ABP沿AP对折,得到△AB′P,连接CB′,则在点P的运动过程中,线段CB′的最小值为_________.12.如图,DE平分等边三角形ABC的面积,折叠△BDE得到△FDE,AC分别与DF,EF相交于G,H两点.若DG=m,EH=n,用含m,n的式子表示GH的长是______.13.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E,将△DEC沿DE折叠得到△DEF,DF交AC于点G.若AGGE =73,则tan A=______.14.如图,在等边三角形ABC中,过点C作射线CD⊥BC,点M,N分别在边AB,BC上,将△ABC沿MN折叠,使点B落在射线CD上的点B′处,连接AB′,已知AB=2.给出下列四个结论:①CN+NB′为定值;②当BN=2NC时,四边形BMB′N为菱形;③当点N与C重合时,∠AB′M=18°;④当AB′最短时,MN=7√21.20其中正确的结论是__________.(填序号)15.将一个矩形纸片OABC放置在平面直角坐标系中,点O(0,0),点A(3,0),点C(0,6),点P在边OC上(点P不与点O,C重合),折叠该纸片,使折痕所在的直线经过点P,并与x轴的正半轴相交于点Q,且∠OPQ=30°,点O的对应点O′落在第一象限.设OQ=t.(1)如图1,当t=1时,求∠O′QA的大小和点O′的坐标;(2)如图2,若折叠后重合部分为四边形,O′Q,O′P分别与边AB相交于点E,F,试用含有t的式子表示O′E的长,并直接写出t的取值范围;(3)若折叠后重合部分的面积为3√3,则t的值可以是__________________________________________.(请直接写出两个不同....的值即可)16.如图,已知△ABC,AB=AC,BC=16,AD⊥BC,∠ABC的平分线交AD于点E,且DE=4.将∠C沿GM折叠使点C与点E恰好重合.下列结论正确的有________.(填序号)①BD=8;②点E到AC的距离为3;③EM=103;④EM∥AC.17.综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动,有一位同学操作过程如下:操作一:对折正方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;操作二:在AD上选一点P,沿BP折叠,使点A落在正方形内部点M处,把纸片展平,连接PM,BM,延长PM交CD于点Q,连接BQ.(1)如图1,当点M在EF上时,∠EMB=________;(填度数)(2)改变点P在AD上的位置(点P不与点A,D重合)如图2,判断∠MBQ与∠CBQ 的数量关系,并说明理由.参考答案1.D 2.D 3.C 4.A 5.D6. 3√2-3 7.2√3 8.5 9.60°4√6 10.10 2√511.-2 12.√m2+n2 13.3√7714.①②④15.(1)∠O′QA=60°点O′的坐标为(32,√32)(2)O′E=3t-6,其中t的取值范围是2<t<3 (3)3或103(答案不唯一,满足3≤t<2√3即可) 16.①④17.(1)30°(2)∠MBQ=∠CBQ,理由略。
2019年八年级数学——图形的对称-翻折变换(折叠问题)
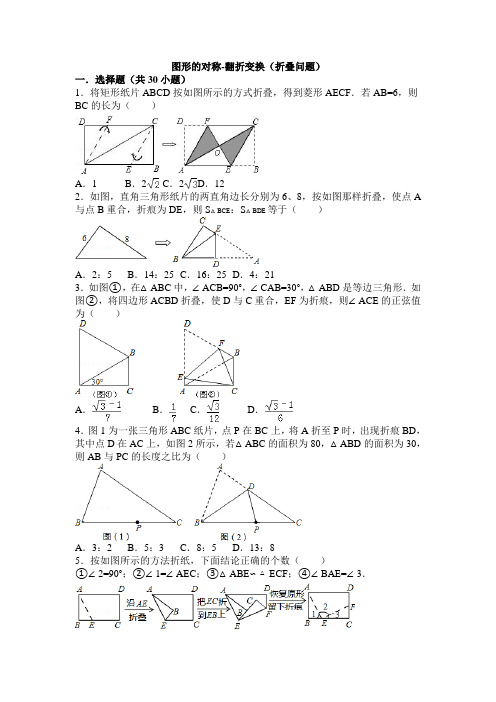
图形的对称-翻折变换(折叠问题)一.选择题(共30小题)1.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为()A.1 B.2 C.2D.122.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B重合,折痕为DE,则S△BCE:S△BDE等于()A.2:5 B.14:25 C.16:25 D.4:213.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.4.图1为一张三角形ABC纸片,点P在BC上,将A折至P时,出现折痕BD,其中点D在AC上,如图2所示,若△ABC的面积为80,△ABD的面积为30,则AB与PC的长度之比为()A.3:2 B.5:3 C.8:5 D.13:85.按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1个B.2个C.3个D.4个6.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于()A.70°B.65°C.80°D.35°7.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长()A.3 B.4 C.3.5 D.68.如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B 落在点E处,AE交CD于点F.连接DE,则DF的长是()A.B.C.D.9.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM 即为所求,对于两人的作法,下列判断正确的是()A.小平的作法正确,张萌的作法不正确B.两人的作法都不正确C.张萌的作法正确,小平的作法不正确D.两人的作法都正确10.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.2411.如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE 沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为()A.B.C.D.12.如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD 沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为()A.cm B.cm C.2cm D.cm13.如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB 沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为()A.y=﹣B.y=﹣x+C.y=﹣D.y=﹣2x+14.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为()A.y=x+5 B.y=x+5 C.y=x+5 D.y=x+515.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为()A.3 B.4 C.5 D.616.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是()A.AF=B.四边形ACDE是矩形C.图中与△ABC全等的三角形有4个D.图中有4个等腰三角形17.如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为()A.16 B.17 C.18 D.1918.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是()A.B.C.D.19.如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为()A.5 B.4 C.3 D.220.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)21.如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC 边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是()A.24cm B.26cm C.28cm D.30cm22.如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=,则AD的长为()A.3 B.4 C.5 D.623.如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为()A.B.2C.2D.24.如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm25.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.1226.如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6 B.8 C.10 D.1227.如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.B.C.1 D.28.如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为()A.1 B.2 C.3 D.1.529.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=.其中所有正确结论的个数是()A.4 B.3 C.2 D.130.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为()A.B.C.2 D.1图形的对称-翻折变换(折叠问题)参考答案与试题解析一.选择题(共30小题)1.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为()A.1 B.2C.2D.12【考点】翻折变换(折叠问题);勾股定理的应用;菱形的性质;矩形的性质.【分析】根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求解.【解答】解:∵菱形AECF,AB=6,∴假设BE=x,∴AE=6﹣x,∴CE=6﹣x,∵四边形AECF是菱形,∴∠FCO=∠ECO,∵∠ECO=∠ECB,∴∠ECO=∠ECB=∠FCO=30°,2BE=CE,∴CE=2x,∴2x=6﹣x,解得:x=2,∴CE=4,利用勾股定理得出:BC2+BE2=EC2,BC===2,故选:C.【点评】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.2.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B重合,折痕为DE,则S△BCE:S△BDE等于()A.2:5 B.14:25 C.16:25 D.4:21【考点】翻折变换(折叠问题).【分析】在Rt△BEC中利用勾股定理计算出AB=10,根据折叠的性质得到AD=BD=5,EA=EB,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中根据勾股定理计算出x=,则EC=8﹣=,利用三角形面积公式计算出S△BCE=BC•CE=×6×=,在Rt△BED中利用勾股定理计算出ED==,利用三角形面积公式计算出S△BDE=BD•DE=×5×=,然后求出两面积的比.【解答】解:在Rt△BAC中,BC=6,AC=8,∴AB==10,∵把△ABC沿DE使A与B重合,∴AD=BD,EA=EB,∴BD=AB=5,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中,∵BE2=EC2+BC2,即x2=(8﹣x)2+62,∴x=,∴EC=8﹣x=8﹣=,∴S△BCE=BC•CE=×6×=,在Rt△BED中,∵BE2=ED2+BD2,∴ED==,∴S△BDE=BD•DE=×5×=,∴S△BCE:S△BDE=:=14:25.故选B.【点评】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了勾股定理.3.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.【考点】翻折变换(折叠问题).【分析】在Rt△ABC中,设AB=2a,已知∠ACB=90°,∠CAB=30°,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可求∠ACE 的正弦值.【解答】解:∵△ABC中,∠ACB=90°,∠BAC=30°,设AB=2a,∴AC=a,BC=a;∵△ABD是等边三角形,∴AD=AB=2a;设DE=EC=x,则AE=2a﹣x;在Rt△AEC中,由勾股定理,得:(2a﹣x)2+3a2=x2,解得x=;∴AE=,EC=,∴sin∠ACE==.故选:B.【点评】本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.4.图1为一张三角形ABC纸片,点P在BC上,将A折至P时,出现折痕BD,其中点D在AC上,如图2所示,若△ABC的面积为80,△ABD的面积为30,则AB与PC的长度之比为()A.3:2 B.5:3 C.8:5 D.13:8【考点】翻折变换(折叠问题).【分析】如图,作辅助线;首先求出△BDP的面积,进而求出△DPC的面积;借助三角形的面积公式求出的值;由旋转变换的性质得到AB=PB,即可解决问题.【解答】解:如图,过点D作DE⊥BC于点E;由题意得:S△ABD=S△PBD=30,∴S△DPC=80﹣30﹣30=20,∴=,由题意得:AB=BP,∴AB:PC=3:2,故选A.【点评】该题主要考查了翻折变换的性质及其应用问题;解题的方法是作高线,表示出三角形的面积;解题的关键是灵活运用翻折变换的性质来分析、判断、推理或解答.5.按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1个B.2个C.3个D.4个【考点】翻折变换(折叠问题);相似三角形的判定与性质.【分析】根据翻折变换的性质、相似三角形的判定定理解答即可.【解答】解:由翻折变换的性质可知,∠AEB+∠FEC=×180°=90°,则∠AEF=90°,即∠2=90°,①正确;由图形可知,∠1<∠AEC,②错误;∵∠2=90°,∴∠1+∠3=90°,又∠1+∠BAE=90°,∴∠BAE=∠3,④正确;∵∠BAE=∠3,∠B=∠C=90°,∴△ABE∽△ECF,③正确.故选:C.【点评】本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.6.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于()A.70°B.65°C.80°D.35°【考点】翻折变换(折叠问题).【分析】根据平角的知识可求出∠DED′的度数,再由折叠的性质可得出∠D′EF=∠DEF=∠DED′,从而根据平行线的性质可得出∠EFB的度数.【解答】解:∵∠AED′=40°,∴∠DED′=180°﹣40°=140°,又由折叠的性质可得,∠D′EF=∠DEF=∠DED′,∴∠DEF=70°,又∵AD∥BC,∴∠EFB=70°.故选:A.【点评】此题考查了翻折变换的知识,解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=∠DED′,难度一般.7.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长()A.3 B.4 C.3.5 D.6【考点】翻折变换(折叠问题).【分析】由矩形的性质得到∠1=∠CFE=60°,由折叠可得∠2=60°,从而求得∠4的度数,得到AE=EC,在Rt△CDE中利用勾股定理可求得EC的长度,即可得到答案.【解答】解:∵矩形ABCD,∴BC∥AD,∴∠1=∠CFE=60°,∵EF为折痕,∴∠2=∠1=60°,AE=EC,∴∠3=180°﹣60°﹣60°=60°,Rt△CDE中,∠4=90°﹣60°=30°,∴EC=2×DE=2×1=2,∴BC=AE+ED=EC+ED=2+1=3.故选:A.【点评】本题考查了翻折问题;由折叠得到角相等,得到AE=EC利用勾股定理求解是正确解答本题的关键.8.如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B 落在点E处,AE交CD于点F.连接DE,则DF的长是()A.B.C.D.【考点】翻折变换(折叠问题).【分析】由四边形ABCD是矩形与△AEC由△ABC翻折得到,AD=CE,∠ADF=∠CEF,由AAS证得△ADF≌△CEF,的长FA=FC,设DF=x,则FA=4﹣x,由勾股定理得:DA2+DF2=AF2,即可求出DF的长.【解答】解:∵四边形ABCD是矩形,∴AD=BC,AB=DC=4,∠ADF=90°,∵△AEC由△ABC翻折得到,∴BC=EC,∠CEF=∠ABC=90°,∴AD=CE,∠ADF=∠CEF,在△ADF与△CEF中,,∴△ADF≌△CEF(AAS),∴FA=FC,设DF=x,则FA=FC=DC﹣DF=4﹣x,在Rt△DFA中,由勾股定理得:DA2+DF2=AF2,即32+x2=(4﹣x)2,解得:x=,即DF的长是.故选C.【点评】本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握折叠的性质,得到相等的线段与角是解决问题的关键.9.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM 即为所求,对于两人的作法,下列判断正确的是()A.小平的作法正确,张萌的作法不正确B.两人的作法都不正确C.张萌的作法正确,小平的作法不正确D.两人的作法都正确【考点】翻折变换(折叠问题).【分析】在图1中,由BM=2BF推出∠BMF=30°,所以∠MBF=60°,再根据等边三角形的判定方法即可证明.在图2中,证明方法类似.【解答】解:图1中,∵四边形ABCD是正方形,∴AB=AD=BC∵AE=ED=BF=FC,AB=BM,∴BM=2BF,∵∠MFB=90°,∴∠BMF=30°,∴∠MBF=90°﹣∠BMF=60°,∵MB=MC,∴△MBC是等边三角形,∴张萌的作法正确.在图2中,∵BM=BC=2BF,∠MFB=90°,∴∠BMF=30°,∴∠MBF=90°﹣∠BMF=60°,∵MB=MC∴△MBC是等边三角形,∴小平的作法正确.故选D.【点评】本题考查正方形的性质、翻折不变性、直角三角形的性质,解题的关键是在一个直角三角形中如果斜边是直角边的两倍那么这条直角边所对的锐角是30度.10.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.24【考点】翻折变换(折叠问题).【分析】先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC ﹣BF=4,易得△CEF的周长.【解答】解:∵四边形ABCD为矩形,∴AD=BC=10,AB=CD=8,∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,∴AF=AD=10,EF=DE,在Rt△ABF中,∵BF==6,∴CF=BC﹣BF=10﹣6=4,∴△CEF的周长为:CE+EF+CF=CE+DE+CF=CD+CF=8+4=12.故选A.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理,利用勾股定理得CF的长是解答此题的关键.11.如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE 沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为()A.B.C.D.【考点】翻折变换(折叠问题).【分析】设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF中根据勾股定理列出关于x的方程,即可解决问题.【解答】解:设CE=x.∵四边形ABCD是矩形,∴AD=BC=5,CD=AB=3,∠A=∠D=90°.∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,∴BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中,由勾股定理得:AF2=52﹣32=16,∴AF=4,DF=5﹣4=1.在Rt△DEF中,由勾股定理得:EF2=DE2+DF2,即x2=(3﹣x)2+12,解得:x=.故选B.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理、矩形的性质、方程思想等知识,关键是熟练掌握勾股定理,找准对应边.12.如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD 沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为()A.cm B.cm C.2cm D.cm【考点】翻折变换(折叠问题).【分析】首先由勾股定理求出BC,由折叠的性质可得∠BED=∠C=90°,BE=BC=3cm,得出AE=AB﹣BE=2cm,设DC=xcm,则DE=xcm,AD=(4﹣x)cm,由勾股定理得出方程,解方程即可.【解答】解:∵∠C=90°,AB=5cm,AC=4cm,∴BC==3cm,∵将△BCD沿着直线BD翻折,使点C落在斜边AB上的点E处,∴△BED≌△BCD,∴∠BED=∠C=90°,BE=BC=3cm,∴AE=AB﹣BE=2cm,设DC=xcm,则DE=xcm,AD=(4﹣x)cm,由勾股定理得:AE2+DE2=AD2,即22+x2=(4﹣x)2,解得:x=.故选:B.【点评】本题主要考查翻折变换的性质,全等三角形的性质,勾股定理;熟练掌握翻折变换的性质,由勾股定理得出方程是解决问题的关键.13.如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB 沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为()A.y=﹣B.y=﹣x+C.y=﹣D.y=﹣2x+【考点】翻折变换(折叠问题);待定系数法求一次函数解析式.【分析】由点A(0,4)、B(3,0),可求得AB的长,然后由折叠的性质,求得OA′的长,且△A′OC∽△AOB,再由相似三角形的性质,求得OC的长,继而利用待定系数法求得直线BC的解析式.【解答】解:∵点A(0,4)、B(3,0),∴OA=4,OB=3,∴AB==5,由折叠的性质可得:A′B=AB=5,∠OA′C=∠OAB,∴OA′=A′B﹣OB=2,∵∠A′OC=∠AOB=90°,∴△A′OC∽△AOB,∴,即,解得:OC=,∴点C的坐标为:(0,),设直线BC的解析式为:y=kx+b,则,解得:,∴直线BC的解析式为:y=﹣x+.故选C.【点评】此题考查了折叠的性质、勾股定理、相似三角形的判定与性质以及待定系数法求一次函数的解析式.注意求得点C的坐标是解此题的关键.14.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为()A.y=x+5 B.y=x+5 C.y=x+5 D.y=x+5【考点】翻折变换(折叠问题);待定系数法求一次函数解析式.【分析】首先在RT△ABE中,求出EB,再在RT△CDE中利用勾股定理即可解决问题.【解答】解:∵△ADE是由△ADO翻折,∴DE=DO,AO=AE=10,∵四边形OABC是矩形,∴OC=AB=8,AO=BC=10,∠B=∠BCO=∠BAO=90°,在RT△ABE中,∵AE=10,AB=8,∴EB===6,∴EC=4,设DO=DE=x,在RT△DCE中,∵CD2+CE2=DE2,∴(8﹣a)2+42=a2,∴a=5,∴点D(0,5),点E(4,8),设直线DE为y=kx+b,∴解得,∴直线DE为:y=+5.故选A.【点评】本题考查翻折变换、待定系数法确定一次函数的解析式,解题的关键是巧妙利用勾股定理,用方程的思想去思考问题,属于中考常考题型.15.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为()A.3 B.4 C.5 D.6【考点】翻折变换(折叠问题).【分析】首先由DE∥BC与折叠的性质,可证得DE是△ABC的中位线,继而求得答案.【解答】解:∵DE∥BC,∴∠ADE=∠B,∠EDF=∠BFD,由折叠的性质可得:∠ADE=∠EDF,AD=DF,∴∠B=∠BFD,∴BD=DF,∴AD=BD,同理:AE=EC,∴DE=BC,即BC=2DE=4.故选B.【点评】此题考查了折叠的性质以及三角形中位线的性质.注意证得DE是△ABC的中位线是关键.16.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是()A.AF=B.四边形ACDE是矩形C.图中与△ABC全等的三角形有4个D.图中有4个等腰三角形【考点】翻折变换(折叠问题);平行四边形的性质.【分析】由四边形ABCD是平行四边形,得到AB=CD,AB∥CD,AD=BC,由折叠的性质得到AB=AE,BC=CE,等量代换得到AE=CD,AD=CE,推出四边形ACDE是平行四边形,于是得到AF=BC,四边形ACDE是矩形,故A,B 正确;根据平行四边形和矩形的性质得到△ACD≌△ACE≌△CDE≌△ADE≌△ABC,于是得到图中与△ABC全等的三角形有4个,故C正确;推出△BCE是等腰三角形,△AEF,△ACF,△CDF,△DEF是等腰三角形,于是得到图中有5个等腰三角形,故D错误.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,AD=BC,由折叠的性质得到AB=AE,BC=CE,∴AE=CD,AD=CE,∵点B、A、E在同一条直线上,∴AE∥CD,∴四边形ACDE是平行四边形,∴AF=BC,四边形ACDE是矩形,故A,B正确;∵四边形ABCD是平行四边形,四边形ACDE是矩形,∴△ACD≌△ACE≌△CDE≌△ADE≌△ABC,∴图中与△ABC全等的三角形有4个,故C正确;∵BC=CE,∴△BCE是等腰三角形,∵四边形ACDE是矩形,∴AF=EF=CF=DF,∴△AEF,△ACF,△CDF,△DEF是等腰三角形,∴图中有5个等腰三角形,故D错误;故选D.【点评】本题考查了平行四边形的性质、折叠的性质以及等腰三角形的判定和性质,解题的关键是熟记等腰三角形和矩形的判定方法.17.如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为()A.16 B.17 C.18 D.19【考点】翻折变换(折叠问题).【分析】根据勾股定理得到BC=8,由折叠的性质得到BD=CD=BC=4,DE⊥BC,根据三角形的中位线的性质得到DE=AB=3,AE=AC=5,于是得到结论.【解答】解:∵AB=6,AC=10,∠ABC=90°,∴BC=8,∵将该直角三角形纸片沿DE折叠,使点C与点B重合,∴BD=CD=BC=4,DE⊥BC,∵∠ABC=90°,∴DE∥AB,∴DE=AB=3,AE=AC=5,∴四边形ABDE的周长=AB+AE+DE+BD=6+5+3+4=18,故选C.【点评】此题考查了折叠的性质,勾股定理,三角形的中位线的性质,注意掌握折叠前后图形的对应关系.18.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是()A.B.C.D.【考点】翻折变换(折叠问题).【分析】根据对称的性质得到△BFE≌△DFE,得到DE=BE.根据已知条件得到∠DEB=90°,设AD=1,BC=4,过A作AG⊥BC于G,根据矩形的性质得到GE=AD=1,根据全等三角形的性质得到BG=EC=1.5,根据勾股定理得到AB=CD==5,通过△BDC∽△DEF,得到,求出BF=,于是得到结论.【解答】解:∵EF是点B、D的对称轴,∴△BFE≌△DFE,∴DE=BE.∵在△BDE中,DE=BE,∠DBE=45°,∴∠BDE=∠DBE=45°.∴∠DEB=90°,∴DE⊥BC.在等腰梯形ABCD中,∵,∴设AD=1,BC=4,过A作AG⊥BC于G,∴四边形AGED是矩形.∴GE=AD=1,∵Rt△ABG≌Rt△DCE,∴BG=EC=1.5,∴AG=DE=BE=2.5∴AB=CD==5,∵∠ABC=∠C=∠FDE,∵∠CDE+∠C=90°,∴∠FDE+∠CDE=90°∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,∴∠BDC=∠DFE,∵∠DEF=∠DBC=45°,∴△BDC∽△DEF,∴,∴DF=,∴BF=,∴AF=AB﹣BF=,∴=.故选B.【点评】此题考查等腰梯形的性质,翻折的性质,三角形全等的判定与性质,等腰直角三角形的性质,相似三角形的判定和性质等知识,注意结合图形,作出常用辅助线解决问题.19.如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为()A.5 B.4 C.3 D.2【考点】翻折变换(折叠问题).【分析】利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;利用勾股定理得出GE2=CG2+CE2,进而求出BG 即可;【解答】解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,在Rt△ABG和Rt△AFG中,,∴Rt△ABG≌Rt△AFG(HL),∴BG=GF,∵E是边CD的中点,∴DE=CE=6,设BG=x,则CG=12﹣x,GE=x+6,∵GE2=CG2+CE2∴(x+6)2=(12﹣x)2+62,解得x=4∴BG=4.故选B.【点评】此题主要考查了全等三角形的判定和性质,勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.20.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)【考点】翻折变换(折叠问题);坐标与图形性质.【分析】根据关于y轴对称的点的特点找到B',结合直角坐标系可得出点B′的坐标.【解答】解:∵将△ABC沿y轴翻折得到△A′B′C′,∴点B与点B′关于y轴对称,∴B′(2,3),故选B.【点评】本题考查了翻折变换﹣折叠问题,坐标与图形的关系,熟记关于y轴对称的点的特点是解答本题的关键.21.如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC 边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是()A.24cm B.26cm C.28cm D.30cm【考点】翻折变换(折叠问题).【分析】根据翻折变换的性质可得AE=EC,AD=CD,然后求出△ABD的周长=AB+BC,代入数据计算即可得解.【解答】解:∵△ABC的边AC对折顶点C和点A重合,∴AE=EC,AD=CD,∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,∵AE=6cm,∴AC=AE+EC=6+6=12,∵△ABC的周长为36cm,∴AB+BC=36﹣12=24cm,∴△ABD的周长是24cm.故选A.【点评】本题考查了翻折变换的性质,熟记翻折前后的两个图形能够完全重合得到相等的边是解题的关键.22.如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=,则AD的长为()A.3 B.4 C.5 D.6【考点】翻折变换(折叠问题).【分析】根据平行线的性质和翻转变换的性质得到FD=FE,FA=FC,根据勾股定理计算即可.【解答】解:∵DC∥AB,∴∠FCA=∠CAB,又∠FAC=∠CAB,∴∠FAC=∠FCA,∴FA=FC=,∴FD=FE,∵DC=AB=8,AF=,∴FD=FE=8﹣=,∴AD=BC=EC==6,故选:D.【点评】本题考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.23.如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为()A.B.2C.2D.【考点】翻折变换(折叠问题).【分析】根据直角三角形两锐角互余求出∠ABC=60°,翻折前后两个图形能够互相重合可得∠BDC=∠BDC′,∠CBD=∠ABD=30°,∠ADE=∠A′DE,然后求出∠BDE=90°,再解直角三角形求出BD,然后求出DE即可.【解答】解:∵△ABC是直角三角形,∠A=30°,∴∠ABC=90°﹣30°=60°,∵将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,∴∠BDC=∠BDC′,∠CBD=∠ABD=∠ABC=30°,∵沿DE折叠点A落在DC′的延长线上的点A′处,∴∠ADE=∠A′DE,∴∠BDE=∠ABD+∠A′DE=×180°=90°,在Rt△BCD中,BD=BC÷cos30°=5÷=cm,在Rt△BDE中,DE=BD•tan30°=×=cm.故选:D.【点评】本题考查了翻折变换的性质,解直角三角形,熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键.24.如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm【考点】翻折变换(折叠问题).【分析】首先根据题意得到:△AED≌△ACD;进而得到AE=AC=6,DE=CD;根据勾股定理求出AB=10;再次利用勾股定理列出关于线段CD的方程,问题即可解决.【解答】解:由勾股定理得:==10,由题意得:△AED≌△ACD,∴AE=AC=6,DE=CD(设为x);∠AED=∠C=90°,∴BE=10﹣6=4,BD=8﹣x;由勾股定理得:(8﹣x)2=42+x2,解得:x=3(cm),故选B.【点评】该命题主要考查了翻折变换及其应用问题;解题的关键是借助翻折变换的性质,灵活运用勾股定理、全等三角形的性质等几何知识来分析、判断、推理或解答.25.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】因为BC为AF边上的高,要求△AFC的面积,求得AF即可,求证△AFD′≌△CFB,得BF=D′F,设D′F=x,则在Rt△AFD′中,根据勾股定理求x,于是得到AF=AB﹣BF,即可得到结果.【解答】解:易证△AFD′≌△CFB,∴D′F=BF,设D′F=x,则AF=8﹣x,在Rt△AFD′中,(8﹣x)2=x2+42,解之得:x=3,∴AF=AB﹣FB=8﹣3=5,∴S△AFC=•AF•BC=10.故选C.【点评】本题考查了翻折变换﹣折叠问题,勾股定理的正确运用,本题中设D′F=x,根据直角三角形AFD′中运用勾股定理求x是解题的关键.26.如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】根据折叠的条件可得:BE=DE,在直角△ABE中,利用勾股定理就可以求解.【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=AE+DE=AE+BE=9.∴BE=9﹣AE,根据勾股定理可知AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选:A.【点评】本题考查了利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.27.如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.B.C.1 D.【考点】翻折变换(折叠问题).【分析】由有一块直角三角形纸片,∠C=90°,AC=2,BC=,利用勾股定理即可求得AB的长,然后由折叠的性质,求得AE的长,继而求得答案.【解答】解:∵∠C=90°,AC=2,BC=,∴AB==,由折叠的性质可得:AE=AB=,∴CE=AE﹣AC=.故选A.【点评】此题考查了折叠的性质以及勾股定理.注意掌握折叠前后图形的对应关系是解此题的关键.28.如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为()A.1 B.2 C.3 D.1.5【考点】翻折变换(折叠问题).【分析】利用平行四边形的对边相等得到AD=BC=4,DC=AB=6,再由折叠的性质得到DE=AD,由DC﹣DE求出EC的长即可.【解答】解:由折叠及平行四边形的性质得:AE=AD=BC=4,DC=AB=6,则EC=DC﹣DE=6﹣4=2,故选B.【点评】此题考查了翻折变换(折叠问题),以及平行四边形的性质,熟练掌握折叠的性质是解本题的关键.29.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:。
八年级数学下册《图形的折叠问题》练习题与答案(人教版)

八年级数学下册《图形的折叠问题》练习题与答案(人教版)一、选择题1.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )A.20°B.30°C.35°D.55°2.如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )A.4cmB.6cmC.8cmD.10cm3.如图,将▱ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )A.2B.3C.4D.54.在△ABC中,AB=10,AC=12,BC=9,AD是BC边上的高,将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( )A.9.5B.10.5C.11D.15.55.如图,将三角形纸片ABC沿直线DE折叠后,使得点B与点A重合,折痕分别交BC,AB于点D,E.如果AC=5cm,△ADC的周长为17cm,那么BC的长为( )A.7cmB.10cmC.12cmD.22cm6.如果将长为6 cm,宽为5 cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )A.8 cmB.5 2 cmC.5.5 cmD.1 cm二、填空题7.如图,在▱ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为.8.如图,将菱形ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长为2 cm,∠BAD=120°,则EF的长为 .9.如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC 上的点F处.若点D的坐标为(10,8),则点E的坐标为10.把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.若AB=6cm,BC=8cm,则线段FG的长为11.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF面积为________.12.把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为______.三、解答题13.如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.14.如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F 处.(1)求EF的长;(2)求四边形ABCE的面积.15.如图①,将矩形ABCD沿DE折叠使点A落在A′处,然后将矩形展平,如图②沿EF折叠使点A落在折痕DE上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.(1)求证:EG=CH;(2)已知AF=2,求AD和AB的长.16.如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.(1)当m=3时,点B的坐标为_________,点E的坐标为_________;(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.17.如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.(1)求证:四边形AFHG为正方形;(2)若BD=6,CD=4,求AB的长.18.如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若AB=6,AD=10,求四边形CEFG的面积.19.在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.(1)如图1,求证:AE⊥BF;(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4求QF的值.20.如图1,在△OAB中,∠OAB=90º,∠AOB=30º,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.(1)求点B的坐标;(2)求证:四边形ABCE是平行四边形;(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.21.如图1,在矩形纸片ABCD中,AB=12 cm,AD=20 cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动;①当点Q与点C重合时(如图2),求菱形BFEP的边长;②若限定P,Q分别在边BA,BC上移动,求出点E在边AD上移动的最大距离.图1 图2参考答案1.A.2.A3.B.4.D.5.C.6.A7.答案为:36°.8.答案为:3(cm).10.答案为:3cm.11.答案为:2.12.答案为:28.8.13.解:∵四边形ABCD是矩形∴AD=BC=40cm,DC=AB=32cm;∠B=90°由题意得:AF=AD=40cm;DE=EF(设为x),EC=40﹣x;由勾股定理得:BF2=402﹣322=576∴BF=24,CF=40﹣24=16;由勾股定理得:x2=162+(40﹣x)2,解得:x=23.2∴EC=32﹣23.2=8.8.14.解:(1)设EF=x依题意知:△CDE≌△CFE∴DE=EF=x,CF=CD=6.∵在Rt△ACD中,AC=10∴AF=AC﹣CF=4,AE=AD﹣DE=8﹣x.在Rt△AEF中,有AE2=AF2+EF2即(8﹣x)2=42+x2解得x=3,即:EF=3.(2)由(1)知:AE=8﹣3=5∴S梯形ABCE=(5+8)×6÷2=39.15.解:(1)证明:由折叠知△AEF≌△GEF,△BCE≌△HCE∵AE=A′E=BC,∠AEF=∠BCE∴△AEF≌△BCE∴△GEF≌△HCE∴EG=CH;(2)∵AF=FG=2,∠FDG=45°∴FD=2,AD=2+2;∵AF=FG=HE=EB=2,AE=AD=2+ 2∴AB=AE+EB=2+2+2=2+2 2.16.解:(1)(3,4);(0,1)(2)点E能恰好落在x轴上.理由如下:∵四边形OABC为长方形∴BC=OA=4,∠AOC=∠DCE=90°由折叠的性质可得DE=BD=BC﹣CD=4﹣1=3,AE=AB=OC=m.如图,假设点E恰好落在x轴上.在Rt△CDE中,由勾股定理可得EC=22,则有OE=OC﹣CE=m﹣2 2.在Rt△AOE中,OA2+OE2=AE2,即42+(m﹣22)2=m2,解得m=3 2.17.证明:(1)∵AD⊥BC∴∠ADB=∠ADC=90°;由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°∠BAG=∠BAD,∠CAF=∠CAD∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°;∴∠GAF=∠BAG+∠CAF+∠BAC=90°;∴四边形AFHG是正方形解:(2)∵四边形AFHG是正方形∴∠BHC=90°又GH=HF=AD,GB=BD=6,CF=CD=4;设AD的长为x则BH=GH﹣GB=x﹣6,CH=HF﹣CF=x﹣4.在Rt△BCH中,BH2+CH2=BC2∴(x﹣6)2+(x﹣4)2=102,解得x1=12,x2=﹣2(不合题意,舍去) ∴AD=12∴AB=6 5.18.证明:(1)由题意可得,△BCE≌△BFE∴∠BEC=∠BEF,FE=CE∵FG∥CE∴∠FGE=∠CEB∴∠FGE=∠FEG∴FG=FE∴FG=EC∴四边形CEFG是平行四边形又∵CE=FE∴四边形CEFG是菱形;(2)∵矩形ABCD中,AB=6,AD=10,BC=BF∴∠BAF=90°,AD=BC=BF=10∴AF=8∴DF=2设EF=x,则CE=x,DE=6﹣x∵∠FDE=90°∴22+(6﹣x)2=x 2,解得,x =103 ∴CE =103∴四边形CEFG 的面积是:CE •DF =103×2=203. 19.证明:(1)∵E ,F 分别是正方形ABCD 边BC ,CD 的中点 ∴CF =BE在△ABE 和△BCF 中∴Rt △ABE ≌Rt △BCF(SAS)∴∠BAE =∠CBF又∵∠BAE +∠BEA =90°∴∠CBF +∠BEA =90°∴∠BGE =90°∴AE ⊥BF ;(2)解:∵将△BCF 沿BF 折叠,得到△BPF∴FP =FC ,∠PFB =∠BFC ,∠FPB =90°∵CD ∥AB∴∠CFB =∠ABF∴∠ABF =∠PFB∴QF =QB设QF =x ,PB =BC =AB =4,CF =PF =2∴QB =x ,PQ =x ﹣2在Rt △BPQ 中∴x 2=(x ﹣2)2+42解得:x =5,即QF =5.20.解:(1)∵在△OAB 中,∠OAB =90º,∠AOB =30º,OB =8 ∴OA =43,AB =4.∴点B 的坐标为(43,4).(2)∵∠OAB =90º∴AB ⊥x 轴∴AB ∥EC.又∵△OBC 是等边三角形∴OC =OB =8.又∵D 是OB 的中点,即AD 是Rt △OAB 斜边上的中线∴AD =OD∴∠OAD =∠AOD =30º∴OE =4.∴EC =OC -OE =4.∴AB =EC.∴四边形ABCE 是平行四边形.(3)设OG =x ,则由折叠对称的性质,得GA =GC =8-x. 在Rt △OAG 中,由勾股定理,得GA 2=OA 2+OG2 即,解得,x =1. ∴OG 的长为1.21. (1)证明:∵折叠纸片使B 点落在边AD 上的E 处,折痕为PQ ∴点B 与点E 关于PQ 对称∴PB =PE ,BF =EF ,∠BPF =∠EPF.又∵EF ∥AB∴∠BPF =∠EFP ,∴∠EPF =∠EFP∴EP =EF ,∴BP =BF =EF =EP ∴四边形BFEP 为菱形.(2)解:①∵四边形ABCD 是矩形∴BC =AD =20,CD =AB =12,∠A =∠D =90°.∵点B 与点E 关于PQ 对称∴CE =BC =20.在Rt △CDE 中,DE =CE 2-CD 2=16∴AE =AD -DE =20-16=4.在Rt △APE 中,AE =4,AP =12-PB =12-PE∴EP 2=42+(12-EP)2.解得EP =203∴菱形BFEP 的边长为203cm. ②当点Q 与点C 重合时,点E 离点A 最近,由①知,此时AE =4. 当点P 与点A 重合时,如图点E离点A最远,此时四边形ABQE为正方形,AE=AB=12 ∴点E在边AD上移动的最大距离为8 cm.。
折叠几何综合专题---16道题目(含答案)

折叠几何综合专题---16道题目(含答案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN01如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E 处,过点E作EG∥CD交AF于点G,连接DG.(1)求证:四边形EFDG是菱形;(2)探究线段EG,GF,AF之间的数量关系,并说明理由;(3)若AG=6,EG=25,求BE的长.(1)证明:由折叠性质可得,EF =FD ,∠AEF =∠ADF =90°,∠EFA =∠DFA ,EG =GD ,∵EG ∥DC ,∴∠DFA =∠EGF , ∴∠EFA =∠EGF ,∴EF =EG =FD =GD ,∴四边形EFDG 是菱形;(2)解:EG 2=12GF ·AF .理由如下: 如解图,连接ED ,交AF 于点H ,∵四边形EFDG 是菱形,∴DE ⊥AF ,FH =GH =12GF ,EH =DH =12DE , ∵∠FEH =90°-∠EFA =∠FAE ,∠FHE =∠AEF =90°, ∴Rt △FEH ∽Rt △FAE ,∴EFAF =FHEF ,即EF 2=FH ·AF ,又∵FH =12GF ,EG =EF ,∴EG 2=12GF ·AF ;(3)解:∵AG =6,EG =25,EG 2=12AF ·GF ,∴(25)2=12(6+GF )·GF ,解得GF =4或GF =-10(舍),∴GF =4,∴AF =10.∵DF =EG =25,∴AD =BC =AF 2-DF 2=45,DE =2EH =2EG 2-(12GF )2=8,∵∠CDE +∠DFA =90°,∠DAF +∠DFA =90°,∴∠CDE =∠DAF ,∵∠DCE =∠ADF =90°,∴Rt △DCE ∽Rt △ADF ,∴EC DF =DE AF ,即EC 25=810,∴EC =855,∴BE =BC -EC =1255.02如图,将矩形ABCD 沿对角线BD 对折,点C 落在E 处,BE 与AD 相交于点F ,若DE =4,BD =8.(1)求证:AF =EF ;(2)求证:BF 平分∠ABD .证明:(1)在矩形ABCD 中,AB =CD ,∠A =∠C =90°, ∵△BED 是△BCD 对折得到的,∴ED =CD ,∠E =∠C ,∴ED =AB ,∠E =∠A ,(2分)又∵∠AFB =∠EFD ,∴△ABF ≌△EDF (AAS),∴AF =EF ;(4分)(2)在Rt △BCD 中,∵DC =DE =4,BD =8,∴sin ∠CBD =DC BD =12, ∴∠CBD =30°,(5分)∴∠EBD =∠CBD =30°,∴∠ABF=90°-30°×2=30°,(7分)∴∠ABF=∠EBD,∴BF平分∠ABD.(8分)03把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F 重合(E、F两点均在BD上),折痕分别为BH、DG。
图形的折叠问题试卷

图形的折叠问题试卷文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]翻折组卷一.选择题(共9小题)1.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则的值是()A .1 B.C.D.2.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则的值是()A .1 B.C.D.3.如图,将矩形纸片ABCD沿DE折叠,使DC落在DA上,点C的落点记为F,已知AD=10 cm,BE=4cm,则CD等于()A .3cm B.4cm C.5cm D.6cm4.如图,有一矩形纸片ABCD,且AB:BC=3:2,先将纸片折叠,使AD落在AB 边上,折痕为AE;再将△AED以DE为折痕向右折叠,AE交BC于F.那么DB:BA等于()A .3:2 B.2:3 C.1:1 D.2:15.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使点D落在AB边上的D′处,折痕为AE,再将△AD′E以D′E为折痕向右折叠,使点A落在点A′处,设A′E与BC交于点F(如图),则A′F的长为()A .B.C.D.6.如图,在矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF 的面积为()A .1 B.2 C.4 D.87.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为()A .1B.1 C.D.8.小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为()A .B.C.D.9.如图,矩形纸片ABCD中,AD=10 cm,将纸片沿DE折叠,使点C落在边AD上(与点F重合),若BE=6 cm,则CD等于()A .4cm B.6cm C.8cm D.10cm二.填空题(共16小题)10.如图,一张宽为6cm的矩形纸片,按图示加以折叠,使得一角顶点落在AB 边上,则折痕DF= ______cm.11.如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=_________ °.12.如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为_________ .13.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,已知∠EFG=50°,那么∠BEG的度数为_________ .14.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB 边交于点N.若∠MPC=75°,则∠NPB′=_________ °.15.把矩形纸片ABCD折叠,使B、C两点恰好落在AD边上的点P处(如图),若∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的宽为_________ cm,面积为_________ cm2.16.把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为_________ .17.把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为_________cm2.18.如图,将长为4cm宽为2cm的矩形纸片ABCD折叠,使点B落在CD边上的中点E处,压平后得到折痕MN,则线段AM的长度为_________ cm.19.如图,有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为_________ .20.如图,把一张矩形纸片ABCD沿EF折叠后,点C﹑D分别落在点C′、D′的位置上,EC′交AD于点G.已知∠EFG=55°,那么∠BEG=_________ 度.21.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,若∠ABE=40°,则∠ADB=_________ .22.如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,EC′交AD于点G,已知∠EFG=53°,那么∠BEG=_________ °.23.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为_________ .24.现将矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,且,那么AD=_________ .25.如图,折叠一张矩形纸片,使它的一个顶点落在长边上,已知:β=110°,求α=_________ 度.三.解答题(共5小题)26.课本中,把长与宽之比为的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸请说明理由.(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,问第5次对开后所得标准纸的周长是多少探索直接写出第2012次对开后所得标准纸的周长.…27.把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,求矩形纸片ABCD的面积.28.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,试判断重叠部分的三角形BED的形状,并证明你的结论.29.如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.(1)求证:平行四边形ABCD是矩形;(2)求BF的长;(3)求折痕AF长.30.如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G.(1)求证:△CEG是等边三角形;(2)若矩形的一边AD=3,求另一边AB的长.初中数学组卷参考答案与试题解析一.选择题(共9小题)1.(2010赤峰)如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则的值是()A .1 B.C.D.考点:翻折变换(折叠问题);矩形的性质;相似三角形的判定与性质.专题:压轴题.分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.解答:解:由题意知:AB=BE=6,BD=AD﹣AB=2,AD=AB﹣BD=4;∵CE∥AB,∴△ECF∽△ADF,得=,即DF=2CF,所以CF:CD=1:3;故选C.点评:此题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度不大.2.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则的值是()A .1 B.C.D.考点:翻折变换(折叠问题).专题:应用题.分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.解答:解:由题意知:AB=BE=6,BD=AD﹣AB=2,AD=AB﹣BD=4;∵CE∥AB,∴△ECF∽△ADF,得=,即DF=2CF,所以CF:CD=1:3;故选C.点评:本题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度适中.3.(2010白下区二模)如图,将矩形纸片ABCD沿DE折叠,使DC落在DA上,点C的落点记为F,已知AD=10 cm,BE=4cm,则CD等于()A .3cm B.4cm C.5cm D.6cm考点:翻折变换(折叠问题);矩形的性质.专题:计算题.分析:根据折叠的性质和正方形的判定方法,得四边形CDFE是正方形,四边形ABEF 是矩形;根据矩形的性质,得AF=BE=4,则DF=6,则CD=DF=6(cm).解答:解:根据一组邻边相等的矩形是正方形,得四边形CDFE是正方形,则四边形ABEF是矩形.∴BE=AF=4.∴DF=AD﹣AF=6.∴CD=DF=6(cm).故选D.点评:此题考查了折叠问题,要能够根据折叠的方法发现正方形.4.(2004广安)如图,有一矩形纸片ABCD,且AB:BC=3:2,先将纸片折叠,使AD落在AB边上,折痕为AE;再将△AED以DE为折痕向右折叠,AE交BC于F.那么DB:BA等于()A .3:2 B.2:3 C.1:1 D.2:1考点:翻折变换(折叠问题).专题:压轴题.分析:由矩形纸片ABCD中,AB:BC=3:2,可设AB=3x,BC=2x,即可得BD=x,继而求得AB的值,则可求得答案.解答:解:∵矩形纸片ABCD中,AB:BC=3:2,∴设AB=3x,BC=2x,则AD=BC=2x,∴BD=AB﹣AD=3x﹣2x=x,如图3:AB=AD﹣BD=2x﹣x=x,∴DB:BA=x:x=1:1.故选C.点评:此题考查了折叠的性质以及矩形的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.5.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使点D落在AB边上的D′处,折痕为AE,再将△AD′E以D′E为折痕向右折叠,使点A落在点A′处,设A′E与BC交于点F(如图),则A′F的长为()A .B.C.D.考点:翻折变换(折叠问题).分析:利用折叠的性质,即可求得AD=AD′=A′D′=、BD′=AB﹣AD=﹣,A′E=AE=AD=2,又由相似三角形的对应边成比例,即可求得EF:A′F=EC:A′B,从而求得A′F的长度.解答:解:根据折叠的性质知,AD=AD′=A′D′=、CE=CD﹣DE=﹣,.∵CE∥A′B,∴△ECF∽△A′BF,∴CE:BA′=EF:A′F(相似三角形的对应边成比例);又∵CE=CD﹣DE=﹣,BA′=AD﹣CE=2﹣,∴=;而A′E=AE=AD=2,∴A′F=4﹣.故选D.点评:本题考查了翻折变换及正方形的性质,利用了折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等及正方形的性质,平行线的性质,有一定的难度.6.如图,在矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF 的面积为()A .1 B.2 C.4 D.8考点:翻折变换(折叠问题).分析:根据折叠易得BD,AB长,利用相似可得BF长,也就求得了CF的长度,△CEF的面积=CFCE.解答:解:由折叠的性质知,第二个图中BD=AB﹣AD=2,第三个图中AB=AD﹣BD=6,∵BC∥DE,∴BF:DE=AB:AD,∴BF=4,CF=BC﹣BF=2,∴△CEF的面积=CFCE=4.故选C.点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②矩形的性质,平行线的性质,三角形的面积公式等知识点.7.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为()A .1B.1 C.D.考点:翻折变换(折叠问题).专题:几何图形问题;压轴题;数形结合.分析:利用折叠的性质,即可求得BD的长与图3中AB的长,又由相似三角形的对应边成比例,即可求得BF的长,则由CF=BC﹣BF即可求得答案.解答:解:如图2,根据题意得:BD=AB﹣AD=﹣=1,如图3,AB=AD﹣BD=﹣1=,∵BC∥DE,∴△ABF∽△ADE,∴,即,∴BF=,∴CF=BC﹣BF=﹣=1.故选B.点评:此题考查了折叠的性质与相似三角形的判定与性质.题目难度不大,注意数形结合思想的应用.8.(2012历下区二模)小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为()A .B.C.D.考点:翻折变换(折叠问题);锐角三角函数的定义.专题:数形结合.分析:根据折叠的性质可得出CF=CB,在RT△CDF中利用勾股定理可求出DF的长度,继而可求出cos∠DFC的值.解答:解:由折叠的性质得,CB=CF,设AB=4x,则BC=5x,在RT△DFC中,DF==3x,∴cos∠DFC==.故选B.点评:此题考查了翻折变换及勾股定理的知识,解答本题的关键是根据折叠的性质得出CF的长度,在RT△CDF中求出DF的长度,难度一般.9.如图,矩形纸片ABCD中,AD=10 cm,将纸片沿DE折叠,使点C落在边AD上(与点F重合),若BE=6 cm,则CD等于()A .4cm B.6cm C.8cm D.10cm考点:轴对称的性质.分析:根据对称的性质和AD=10,BE=6可得出CD的长度.解答:解:根据轴对称的性质可得可得出CD=DF=AD﹣AF=AD﹣BE,∴CD=4cm故选A.点评:本题考查轴对称的性质,关键在于根据图形判断出CD=DF.二.填空题(共16小题)10.如图,一张宽为6cm的矩形纸片,按图示加以折叠,使得一角顶点落在AB边上,则折痕DF= 8 cm.考点:翻折变换(折叠问题).分析:根据折叠的性质可得∠EDF=30°,从而求出∠ADE=30°,在Rt△ADE中求出DE,在Rt△DEF中可求出DF.解答:解:由折叠的性质可得:∠EDF=∠CDF=30°,则∠ADE=90°﹣30°﹣30°=30°,在Rt△ADE中,AD=6cm,∠ADE=30°,∴AE=ADtan∠ADE=2cm,DE=2AE=4cm,在Rt△DEF中,∠EDF=30°,DE=4cm,∴DF==8cm.故答案为:8.点评:本题考查了翻折变换的知识,注意掌握翻折前后对应边相等,对应角相等.11.(2012宿迁)如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=40 °.考点:平行线的性质;翻折变换(折叠问题).分析:根据两直线平行,内错角相等求出∠EFG,再根据平角的定义求出∠EFD,然后根据折叠的性质可得∠EFD′=∠EFD,再根据图形,∠GFD′=∠EFD′﹣∠EFG,代入数据计算即可得解.解答:解:矩形纸片ABCD中,AD∥BC,∵∠CEF=70°,∴∠EFG=∠CEF=70°,∴∠EFD=180°﹣70°=110°,根据折叠的性质,∠EFD′=∠EFD=110°,∴∠GFD′=∠EFD′﹣∠EFG,=110°﹣70°,=40°.故答案为:40.点评:本题考查了平行线的性质,以及折叠变换,根据两直线平行,内错角相等求出∠EFG是解题的关键,另外,根据折叠前后的两个角相等也很重要.12.(2013日照)如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为(3π﹣)cm2.考点:切线的性质;矩形的性质;扇形面积的计算;翻折变换(折叠问题).专题:压轴题.分析:如图,露在外面部分的面积可用扇形ODK与△ODK的面积差来求得,在Rt△A'DC中,可根据AD即圆的直径和CD即圆的半径长,求出∠DA'C的度数,进而得出∠ODH和∠DOK的度数,即可求得△ODK和扇形ODK的面积,由此可求得阴影部分的面积.解答:解:作OH⊥DK于H,连接OK,∵以AD为直径的半圆,正好与对边BC相切,∴AD=2CD,∴A'D=2CD,∵∠C=90°,∴∠DA'C=30°,∴∠ODH=30°,∴∠DOH=60°,∴∠DOK=120°,∴扇形ODK的面积为=3πcm2,∵∠ODH=∠OKH=30°,OD=3cm,∴OH=cm,DH=cm;∴DK=3cm,∴△ODK的面积为cm2,∴半圆还露在外面的部分(阴影部分)的面积是:(3π﹣)cm2.故答案为:(3π﹣)cm2.点评:此题考查了折叠问题,解题时要注意找到对应的等量关系;还考查了圆的切线的性质,垂直于过切点的半径;还考查了直角三角形的性质,直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度.13.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,已知∠EFG=50°,那么∠BEG的度数为80°.考点:翻折变换(折叠问题).专题:探究型.分析:先根据正方形的性质得出AD∥BC,由∠EFG=50°可求出∠1的度数,再根据图形翻折变换的性质得出∠1=∠2=50°,由平角的性质即可得出∠BEG的度数.解答:解:∵四边形ABCD是矩形,∴AD∥BC,∵∠EFG=50°,∴∠1=∠EFG=50°,∵四边形EFD′C′是四边形EFDC翻折而成,∴∠1=∠2=50°,∴∠BEG=180°﹣∠1﹣∠2=180°﹣50°﹣50°=80°.故答案为:80°.点评:本题考查的是图形翻折变换的性质、矩形的性质及平行线的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.14.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=15 °.考点:翻折变换(折叠问题).分析:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,再利用平角为180°,即可求出∠NPB′的度数.解答:解:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,∴∠NPM=2×75°=150°,∴∠C′PB=30°,由折叠的性质可知:∠C′PN=∠BPN,∴∠NPB′=15°.故答案为:15.点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.15.把矩形纸片ABCD折叠,使B、C两点恰好落在AD边上的点P处(如图),若∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的宽为cm,面积为cm2.考点:翻折变换(折叠问题).分析:根据勾股定理,得MN=10;根据直角三角形的面积公式,得AB=;根据折叠,知BC=6+8+10=24,进而求得矩形的面积.解答:解:过点P作PE⊥MN,∵∠MPN=90°,PM=6cm,PN=8cm,∴MN==10(cm),∴S△PMN=PMPN=MNPE,∴PMPN=MNPE,即PE==(cm),即矩形纸片ABCD的宽为:;∵BC=PM+MN+PN=6+10+8=24(cm),∴S矩形ABCD=×24=(cm2).故答案为:,.点评:此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.16.(2005遂宁)把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为.考点:翻折变换(折叠问题).专题:压轴题.分析:利用折叠的性质和勾股定理可知.解答:解:由勾股定理得,MN=5,设Rt△PMN的斜边上的高为h,由矩形的宽AB也为h,根据直角三角形的面积公式得,h=PMPN÷MN=,由折叠的性质知,BC=PM+MN+PN=12,∴矩形的面积=ABBC=.点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②勾股定理,直角三角形和矩形的面积公式求解.17.(2010徐汇区二模)把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为cm2.考点:翻折变换(折叠问题).分析:根据勾股定理,得MN=10;根据直角三角形的面积公式,得AB=;根据折叠,知BC=6+8+10=24,进而求得矩形的面积.解答:解:∵∠MPN=90°,PM=6cm,PN=8cm,∴MN=10,BC=10+6+8=24.根据直角三角形的面积公式,得AB==.则矩形的面积=×24=(cm2).点评:此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法.18.如图,将长为4cm宽为2cm的矩形纸片ABCD折叠,使点B落在CD边上的中点E处,压平后得到折痕MN,则线段AM的长度为cm.考点:翻折变换(折叠问题);勾股定理.专题:计算题;探究型.分析:连接BM,EM,BE,由折叠的性质可知,四边形ABNM和四边形FENM关于直线MN对称,由垂直平分线的性质可知BM=EM,再由点E是CD的中点,可求出DE的长,由勾股定理即可求出AM的长.解答:解:如图,连接BM,EM,BE,由折叠的性质可知,四边形ABNM和四边形FENM关于直线MN对称.∴MN垂直平分BE,∴BM=EM,∵点E是CD的中点,DE=1,∴在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,∴AM2+AB2=DM2+DE2.设AM=x,则DM=4﹣x,∴x2+22=(4﹣x)2+12.解得,即cm.故答案为:.点评:本题考查的是图形折叠的性质及勾股定理,解答此类问题时,首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.19.如图,有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为 1 .考点:翻折变换(折叠问题).专题:数形结合.分析:利用折叠的性质,即可求得BD的长与图3中AB的长,又由相似三角形的对应边成比例,即可求得BF的长,则由CF=BC﹣BF即可求得答案.解答:解:如图2,根据题意得:BD=AB﹣AD=﹣=1,如图3,AB=AD﹣BD=﹣1=,∵BC∥DE,∴△ABF∽△ADE,∴=,即=,∴BF=,∴CF=BC﹣BF=﹣=1.故答案为:1.点评:本题考查了翻折变换及正方形的性质,利用了折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等及正方形的性质,平行线的性质,有一定的难度.20.如图,把一张矩形纸片ABCD沿EF折叠后,点C﹑D分别落在点C′、D′的位置上,EC′交AD于点G.已知∠EFG=55°,那么∠BEG=70 度.考点:翻折变换(折叠问题).专题:计算题.分析:由矩形的性质可知AD∥BC,可得∠CEF=∠EFG=55°,由折叠的性质可知∠GEF=∠CEF,再由邻补角的性质求∠BEG.解答:解:∵AD∥BC,∴∠CEF=∠EFG=55°,由折叠的性质,得∠GEF=∠CEF=55°,∴∠BEG=180°﹣∠GEF﹣∠CEF=70°.故答案为:70.点评:本题考查了翻折变换(折叠问题).关键是明确折叠前后,对应角相等,两直线平行,内错角相等的性质.21.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,若∠ABE=40°,则∠ADB=25°.考点:翻折变换(折叠问题).分析:首先根据矩形的性质可得∠ABC=90°,AD∥BC,进而可以计算出∠EBC,再根据折叠可得∠EBD=∠CBD=∠EBC,然后再根据平行线的性质可以计算出∠ADB的度数.解答:解:∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC,∵∠ABE=40°,∴∠EBC=90°﹣40°=50°,根据折叠可得∠EBD=∠CBD,∴∠CBD=25°,∵AD∥BC,∴∠ADB=∠DBC=25°,故答案为:25°.点评:此题主要考查了图形的折叠,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.22.如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,EC′交AD于点G,已知∠EFG=53°,那么∠BEG=64 °.考点:翻折变换(折叠问题).专题:几何图形问题.分析:由矩形的性质可知AD∥BC,可得∠CEF=∠EFG=53°,由折叠的性质可知∠GEF=∠CEF,再由邻补角的性质求∠BEG.解答:解:∵AD∥BC,∴∠CEF=∠EFG=53°,由折叠的性质,得∠GEF=∠CEF=53°,∴∠BEG=180°﹣∠GEF﹣∠CEF=64°.故答案为:64.点评:本题考查了翻折变换(折叠问题).关键是明确折叠前后,对应角相等,以及两直线平行,内错角相等的性质.23.(2010盐城)小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为:1 .考点:翻折变换(折叠问题).专题:压轴题.分析:连DE,由翻折的性质知,四边形ABEF为正方形,∠EAD=45°,而M点正好在∠NDG的平分线上,则DE平分∠GDC,易证RT△DGE≌Rt△DCE,得到DC=DG,而△AGD为等腰直角三角形,得到AD=DG=CD.解答:解:连DE,如图,∵沿过A点的直线折叠,使得B点落在AD边上的点F处,∴四边形ABEF为正方形,∴∠EAD=45°,由第二次折叠知,M点正好在∠NDG的平分线上,∴DE平分∠GDC,∴RT△DGE≌Rt△DCE,∴DC=DG,又∵△AGD为等腰直角三角形,∴AD=DG=CD,∴矩形ABCD长与宽的比值为:1.故答案为::1.点评:本题考查了翻折的性质:翻折前后的两个图形全等.也考查了正方形、角的平分线的性质以及等腰直角三角形的性质.24.(2011桐乡市一模)现将矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,且,那么AD= 2 .考点:翻折变换(折叠问题).专题:计算题.分析:连DE,由矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②),根据折叠的性质得到∠EAF=∠EAB=45°,又沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③),再次根据折叠的性质得到∠NDG=∠CDG=45°,∠MDG=∠EDG,DN=DC=,则△AGD为等腰直角三角形,而M点正好在∠NDG的平分线上,得到∴∠NDM=∠GDM,易证Rt△NMD≌Rt△GMD,得到DG=DN=,根据AD=DG即可求出AD.解答:解:∵矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B 点落在AD边上的点F处,折痕为AE(如图②),∴∠EAF=∠EAB=45°,又∵沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).连DE,∴∠NDG=∠CDG=45°,∠MDG=∠EDG,DN=DC=,∴△AGD为等腰直角三角形,即∠MGD=90°,又∵第二次折叠后,M点正好在∠NDG的平分线上,∴∠NDM=∠GDM,∴Rt△NMD≌Rt△GMD,∴DG=DN=,∴AD=DG=2.故答案为2.点评:本题考查了折叠的性质:折叠后两重合的图形全等.也考查了三角形全等的判定与性质以及等腰直角三角形三边的关系.25.(2013南昌模拟)如图,折叠一张矩形纸片,使它的一个顶点落在长边上,已知:β=110°,求α=20 度.考点:平行线的性质;翻折变换(折叠问题).专题:计算题.分析:由折叠及矩形的性质得到∠AFE为直角,利用平角的定义得到一对角互余,再由AB与DC平行,利用两直线平行同旁内角互补得到一对角互补,求出∠AFC的度数,即可确定出α的度数.解答:解:由折叠的性质得:∠AFE=90°,∴α+∠AFC=90°,∵AB∥CD,∴∠β+∠AFC=180°,∵∠β=110°,∴∠AFC=70°,则α=20°.故答案为:20点评:此题考查了平行线的性质,以及翻折变换,熟练掌握平行线的性质是解本题的关键.三.解答题(共5小题)26.(2012衢州)课本中,把长与宽之比为的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸请说明理由.(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,问第5次对开后所得标准纸的周长是多少探索直接写出第2012次对开后所得标准纸的周长.…考点:翻折变换(折叠问题);全等三角形的判定与性质;勾股定理;等腰直角三角形;矩形的性质;图形的剪拼.专题:几何综合题;压轴题.分析:(1)根据==2==,得出矩形纸片ABEF也是标准纸;(2)利用已知得出△ADG是等腰直角三角形,得出==,即可得出答案;(3)分别求出每一次对折后的周长,进而得出变化规律求出即可.解答:解:(1)是标准纸,理由如下:∵矩形纸片ABCD是标准纸,∴=,由对开的含义知:AF=BC,∴==2==,∴矩形纸片ABEF也是标准纸.(2)是标准纸,理由如下:设AB=CD=a,由图形折叠可知:DN=CD=DG=a,DG⊥EM,由图形折叠可知:△ABE≌△AFE,∴∠DAE=∠BAD=45°,∴△ADG是等腰直角三角形,∴在Rt△ADG中,AD==a,∴==,∴矩形纸片ABCD是一张标准纸;。
2020年九年级数学中考专题:图形折叠的问题

专题 图形的折叠问题一.选择题1. 如图,在矩形ABCD 中,AB =4,BC =6,点E 为BC 的中点,连接AE ,将△ABE 沿AE 折叠,使得点B 落在点B ′处,则点B ′到线段BC 的距离为( ).A.2572 B.1336 C. 4 D.4357 2. 如图,将矩形ABCD 沿直线AC 折叠,点B 落在点E 处,连接DE ,BE ,若△ABE 为等边三角形,且S △CDE =3,则CD 的长为( ).A.√3B. 2√3C. 3D. 23. 如图,将矩形纸片ABCD 沿AE 折叠,使点B 落在对角线AC 上的点F 处,再沿EG 折叠,使点C 落在矩形内的点H 处,且E 、F 、H 在同一直线上,若AB =6,BC =8,则CG 的长是( ).A. 3B.2C. 2.5D.4.54. 如图,在菱形ABCD 中,BD =211,AC =10,点P 在对角线AC 上,过点P 作EF ⊥AC 交AD 于点E ,交AB 于点F ,将△AEF 折叠,使点A 落在点A ′处,A ′C =A ′D ,则AP 的长为( ).A.25 B.21 C. 3 D.43 二.填空题5. 如图,四边形ABCD 是矩形,点E 是BC 上一点,连接AE ,将△DEC 沿DE 所在的直线对折,使得点C 落在AE 上的点F 处,连接BF ,若EF =13AE ,AB =1,则AF =________.6. 如图,边长为4的菱形纸片ABCD 中,∠A =60°,折叠菱形纸片ABCD ,使点C 落在DP (P 为AB 的中点)所在直线上的C ′处,得到经过点D 的折痕DE ,则CE =________.7. 如图,将▱ABCD 沿EF 对折,使点A 落在点C 处,若∠A =60°,AD =4,AB =8,则AE 的长为________.8. 将矩形ABCD 按如图所示的方式折叠,BE ,EG ,FG 为折痕,且顶点A ,C ,D 都落在点O 处,且点B ,O ,G 在同一条直线上,同时点E ,F ,O 在另一条直线上,若AB =2,则AD 的长为 .9.如图,在矩形ABCD中,点E为AB边上的点,将△ADE沿直线DE翻折,使得点A与BC边上的点G重合,连接AG交DE于点F,若AD=6,EF=1,则AB的长为.10.如图,正方形ABCD,E为BC边的中点,连接AE,点P是边CD上一点,沿AP折叠使D点落在AE上的H处,延长PH交BC于F点,若EF=1,则AB的长为.三.解答题11.如图,矩形ABCD中,△BCD沿BD折叠,使点C落到点E处,BE与AD相交于点F,点O是BD的中点,连接FO并延长交BC于点G,若AB=6,AD=8,(1)求证:四边形BFDG是平行四边形(2)求FG的长。
图形的折叠问题 小学数学 习题集

一、选择题1. 一个正方形对折以后,可以得到2个相同的(),还可以得到2个相同的()。
A.长方形;三角形B.正方形;圆C.平行四边形;三角形D.圆;平行四边形2. 把一张长方形纸对折四次,其中一份是这张纸的()。
A.B.C.D.3. 将一张正方形的纸连续对折两次(有不同的折法),并在折后的纸中央打一个圆孔,再将纸展开,得到下面不同的图形。
请为下面的折法选择展开后的图形:展开后是()。
A.B.C.D.4. 笑笑用一张圆形纸片对折后剪下一个图案(如下图),展开后的样子是()。
A.B.C.5. 一根绳子连续对折2次,每小段是全长的()A.B.C.二、填空题6. 兰兰用一张长方形纸对折后做一张生日贺卡,对折后的长方形长是15厘米,宽是12厘米,对折前长方形纸的长是( )厘米,宽是( )厘米,周长是( )厘米。
7. 一个圆的直径是d,连续对折2次后(不打开),周长是( )。
8. 把一张长方形纸连续对折3次,这张纸被平均分成了()份,每份是这张纸的。
9. 小明将一张长方形纸沿对角线对折,如图,那么涂色部分的周长是( )。
10. 将一个正方形纸用不同的方法对折,得到的图形可以是一个( ),也可以是一个( )。
三、解答题11. 把一条长32dm的彩带连续对折2次,这时每段彩带长多少分米?如果要使每段彩带长1dm,那么应该将这条彩带连续对折几次?12. 把一张长方形纸折起来后的图形如下,∠1=80°,求∠2的度数。
13. 下面是一张长方形折起来以后形成的图形,求∠2的度数,写出解题步骤。
已知:∠1=31°14. 把下边的大正方形对折两次,不可能折成什么图形?。
图形的折叠问题 小学数学 测试题
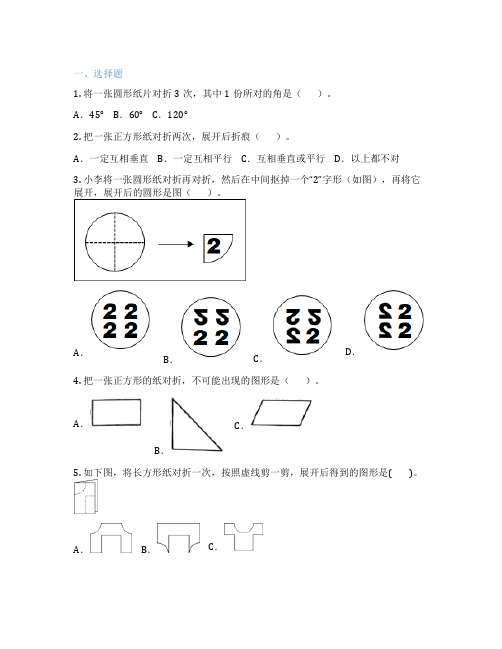
一、选择题1. 将一张圆形纸片对折3次,其中1份所对的角是()。
A.45°B.60°C.120°2. 把一张正方形纸对折两次,展开后折痕()。
A.一定互相垂直B.一定互相平行C.互相垂直或平行D.以上都不对3. 小李将一张圆形纸对折再对折,然后在中间抠掉一个“2”字形(如图),再将它展开,展开后的圆形是图()。
D.A.B.C.4. 把一张正方形的纸对折,不可能出现的图形是()。
A.C.B.5. 如下图,将长方形纸对折一次,按照虚线剪一剪,展开后得到的图形是( )。
A.B.C.二、填空题6. 把一根绳子对折2次,这根绳子被平均分成了( )份,每份是它( )。
7. 把一根彩带对折2次后的长度占全长的( )。
8. 把一张长方形纸对折后,每份是这张长方形纸的( ),把这张长方形纸再对折两次后,每份是这张长方形纸的( )。
9. 一张纸的厚度大约是0.1毫米。
小亮把这样的一张纸对折……一共对折3次。
那么对折后的这叠纸厚( )毫米。
10. 将一张圆形纸片对折2次,所得到的是( )角,是( )度。
三、解答题11. 用一张圆形的纸折45°的角,最少需要对折几次?12. 把一根绳子对折,对折,再对折,这时每段绳子长5米,这根绳子原来长多少米?13. 一张正方形纸片边长是12厘米,现将这张正方形纸,对折再对折,展开后得到如下图形。
每一个小长方形的周长是多少厘米?14. 文文制作了一份对折的“新年贺卡”,对折后的贺卡正好是一个周长48厘米的正方形。
这张贺卡打开后的周长是多少?。
图形的折叠问题 小学数学 测试卷

一、选择题1. 如图,将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,最后沿虚线剪下一个角。
将这张纸片展开后,得到的图形是()。
A.B.C.D.2. 把一张边长是6厘米的正方形纸,对折成两个长方形,其中每个长方形的周长为()。
A.12厘米B.18厘米C.24厘米3. 在手工课上,小明把一张长8厘米、宽4厘米的长方形对折两次,折痕之间的关系是()。
A.互相平行B.互相垂直C.可能平行,也可能垂直D.既不互相垂直也不互相平行4. 把一张长方形的纸对折三次,折痕间的关系是()。
A.互相平行B.互相垂直C.可能互相平行,也可能互相垂直5. 一张长方形纸对折两次后展开,两条折痕()。
A.互相平行B.互相垂直C.可能互相平行,可能互相垂直D.不确定二、填空题6. 把一张长方形的纸沿着同一方向对折两次,打开后折痕互相( )。
7. 一个面积为16cm2的正方形纸,对折3次后,把其中一份涂上绿色,绿色部分占正方形的。
8. 下面哪些图形通过一次对折即可从折痕处用剪刀剪出来?在下面的()里画“√”。
9. 将一张圆形纸片连续对折两次,得到的角是( )度,共有( )个这样的角。
10. 在中,,( ).三、解答题11. 一根绳子对折再对折后长1米,这根绳子全长多少米?12. 淘气在对折好的纸上剪了两个洞,打开后会是哪一个?想一想,做一做。
13. 诚诚制作了一份对折的“新年贺卡”对折后的贺卡正好是一个周长为68厘米的正方形。
这张贺卡打开后的周长是多少?14. 把下边的大正方形对折两次,不可能折成什么图形?。
图形的折叠问题 小学数学 随堂作业

一、选择题1. 观察下图:已知∠1=25°,那么∠2=()。
A.25°B.40°C.65°2. 如图所示,阴影部分面积占大三角形的,占小三角形的,小三角形是大三角形面积的()。
A.B.C.D.3. 把一张圆形纸片对折两次后所形成的角是()。
A.锐角B.直角C.钝角D.平角4. 请问A图形如何变换得到B()。
A.向右折叠B.向下折叠C.向左折叠5. 一个长方形的一个角折叠后如图:已知∠2=42°,∠1=()。
A.45°B.30°C.24°二、填空题6. 将一张圆形纸对折3次可以得到一个( )角,这个角的度数是( )。
7. 一根绳子对折再对折后长20米,这根绳子长( )米。
8. 一根绳子长12米,小明把这根绳子对折,再对折后,每一段长( )米。
9. 把一张长方形纸对、再对折……数一数每对折后平均分成的份数,填在下表里,并说说每份占这张纸的几分之几。
对折的次数 1 2 3 ( ) ( ) ( )平均分成的份数 2 ( ) ( ) ( ) ( ) ( )每份占这张纸的几分之几( ) ( ) ( ) ( ) ( ) ( )10. 一张长方形纸对折2次,这张纸被平均分成了()份,每份是这张纸的的,其中的3份是这张纸的。
三、解答题11. 淘气在对折好的纸上剪了两个洞,打开后会是哪一个?想一想,做一做。
12. 取一张长方形纸片,折出它的,你有几种不同的折法,折一折,再画一画。
13. 把一张边长是6厘米的正方形纸,对折成两个长方形,其中一个长方形的周长是多少厘米?宁宁是这样想的:4×6÷2=12(厘米)你觉得宁宁的想法对吗?如果不对,请帮他改正。
14. 下面是一张长方形纸折起来以后形成的图形,已知:∠1和一个145°的角正好可拼成一个平角,求∠1和∠2的度数。
专题 简单的轴对称图形:折叠问题(巩固篇)

专题07简单的轴对称图形:折叠问题(巩固篇)一、单选题1.如图,一张长方形纸片ABCD,它的四个内角都是直角,将其沿BD折叠后,点C落在点E处,BE交AD于点F,再将DEF沿DF折叠后,点E落在点G处,若DG刚好平分ADB∠,那么DBF∠的度数是()A.18°B.20°C.36°D.45°∥的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,2.如图1是AD BC若图3中∠CFE=18°,则图2中∠AEF的度数为()A.108°B.114°C.116°D.120°3.将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是()A.菱形B.直角三角形C.矩形D.等腰三角形4.如图,在Rt ACB ∆中,90ACB ︒∠=,25A ︒∠=,D 是AB 上一点,将Rt ABC ∆沿CD 折叠,使B 点落在AC 边上的E 处,则ADE ∠等于()A .25︒B .30︒C .35︒D .40︒5.如图,在Rt △ABC 中,C ∠=90°,沿着过点B 的一条直线BE 折叠△ABC ,使点C 恰好落在AB 的中点D 处,则A ∠的度数为()A .30°B .45°C .60°D .75°6.如图,将三角形纸片ABC 沿DE 折叠,使B 与C 重合,CD ,AE 相交于F ,已知BD =4AD ,设△ABC 的面积为S ,△CEF 的面积为S 1,△ADF 的面积为S 2,则12S S S -的值为()A .110B .15C .310D .257.如图,把△ABC 纸片沿DE 折叠,当点C 落在四边形ABDE 的外部时,测得∠1=108°,∠C =35°,则∠2的度数为()A .35°B .36°C .37°D .38°8.如图,将长方形纸片ABCD 沿AE 向上折叠,使点B 落在DC 边上的点F 处.若∠FEC =28°,则∠EAB 度数的值为()A .12°B .14°C .16°D .18°9.如图在四边形ABEC 中,BEC ∠和BAC ∠都是直角,且AB AC =.现将BEC ∆沿BC 翻折,点E 的对应点为E ',BE '与AC 边相交于D 点,恰好BE '是ABC ∠的角平分线,若1CE =,则BD 的长为()A .1.5B .1.6C .2D .310.如图,已知长方形纸片ABCD ,点E 、H 在AD 边上,点F ,G 在BC 边上,分别沿EF ,GH 折叠,使点B 和点C 都落在点P 处,若+=116EFB HGC ∠∠︒,则∠IPK 的度数为()A .129°B .128°C .127°D .126°11.如图,将长方形ABCD 沿直线BD 折叠,使点C 落在点E 处,BE 交AD 于F ,连接CE ,交AD 于点G ,连接CF 交BD 于点H .下列结论①FB FD =;②BD 平分FBC ∠;③DEC FBH ∠=∠;④HC DH =中正确的是()A .①②B .①②③C .②③④D .①②③④12.如图1是//AD BC 的一张纸条,按图1→图2→图3,把这一纸条先沿EF 折叠并压平,再沿BF 折叠并压平,若图3中18,CFE ∠=︒则图2中AEF ∠的度数为()A .126oB .114C .112oD .12013.如图,在△ABC 中,∠ACB =90°,D 是AC 上一点,连接BD ,将△BDA 沿BD 对折得到△BDE ,若BE 恰好经过点C ,则下列结论错误的是()A .DA =DEB .∠CDE =2∠ABDC .∠BDE ﹣∠ABD =90°D .S △ABD :S △CDE =BC :CE14.如图,图1是一个四边形纸条ABCD ,其中//AB CD ,E ,F 分别为边,AB CD 上的两个点,将纸条ABCD 沿EF 折叠得到图2,再将图2沿DF 折叠得到图3,若在图3中,25FEM ∠=︒,则EFC ∠的度数为()A .75︒B .105︒C .100︒D .80︒二、填空题15.如图,将△ABC 沿着过BC 的中点D 的直线折叠,使点B 落在AC 边上的1B 处,称为第一次操作,折痕DE 到AC 的距离为1h ;还原纸片后,再将△BDE 沿着过BD 的中点1D 的直线折叠,使点B 落在DE 边上的2B 处,称为第二次操作,折痕11D E 到AC 的距离记为2h ;按上述方法不断操作下去…经过第n 次操作后得到折痕11n n D E --到AC 的距离记为n h ,若11h =,则n h 的值为______.16.如图,正方形纸片ABCD 的四个角都为90︒,若该纸片沿AC 折叠,则点D 会与点B 重合,已知点E 为正方形ABCD 的边CD 上一点,连接AE ,将三角形ADE 沿AE 折叠,点D 落在点D ¢处,作AF 平分BAD '∠.若12CAD BAF ∠=∠',则'CAD ∠的度数为____________︒17.如图,长方形纸片ABCD ,点E 为边AB 上一点,连接CE 、DE .将∠AED 沿ED 对折,点A 落在点A′处;将∠BEC 沿EC 对折,点B 落在点B′处.若∠A′EB′=α.下列结论:①若∠AED =48°,∠BEC =58°,则∠CED =72°;②∠AED+∠BEC ﹣∠CED =α;③若∠CEA′=2∠DEB′=α,则∠DEB′=15°;④若A′E 平分∠CEB′,则∠DEB′=90°﹣32α.其中一定正确的有_____(填序号即可).18.如图,ABC 是等腰直角三角形,90ABC ∠=︒,将ABC 沿着一条直线折叠,使顶点A 的对应点A '刚好落在边BC 上,这条折痕分别交AB ,AC 于点D ,E .ABC ∠的平分线交A D '于点F ,连接EF ,若CE A B '=,则A EF '∠=______︒.19.如图,已知长方形纸带ABCD ,AB ∥CD ,AD ∥BC ,将纸带沿EF 折叠后,点B ,C 分别落在H 、G 的位置,再沿GF 折叠成图2,点A 、D 分别落在Q 、M 的位置,已知2∠QMG =4∠GFM ﹣108°,则∠EFC =______.20.如图,在△ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边BC 上E 处,折痕为CD ,则∠EDB =_____.21.如图,在Rt △ABC 中,90ACB ∠=︒,点D 为斜边AB 上的一点,连接CD ,将BCD ∆沿CD 翻折,使点B 落在点E 处,点F 为直角边AC 上一点,连接DF ,将ADF ∆沿DF 翻折,点A 恰好与点E 重合,则∠CEF 的度数为________.22.如图所示,将三角形纸片沿DE 折叠,使点C 落在点C′处,若EC′恰好与BC 平行,且∠C =80°,则∠BDE =_____.23.如图,将笔记本活页一角折过去,使角的顶点A 落在A '处,BC 为折痕,再将另一角EDB ∠斜折过去,使BD 边落在A BC '∠内部,折痕为BE ,点D 的对应点为D ¢,设35,63∠︒=︒∠=ABC EBD ,则∠''A BD 的大小为________︒.24.如图,在ABC 中,4AB =,5BC =,6AC =,将ABD △沿AD 折叠,使得点B 恰好落在AC 边上的点E 处,折痕为AD ,若点F 为AD 上一动点,则EFC △的周长最小值为___________.25.有长方形纸片,E ,F 分别是AD ,BC 上一点∠DEF =x (0°<x <45°),将纸片沿EF 折叠成图1,再沿GF 折叠成图2.(1)如图1,当x =32°时,FGD ∠'=_____度;(2)如图2,作∠MGF 的平分线GP 交直线EF 于点P ,则∠GPE =_____(用x 的式子表示).26.如图,将长方形纸片ABCD 沿折痕EF 折叠,点D ,C 的对应点分别为点D ¢,C ',C D ''交BC 于点G ,再把三角形GC F '沿GF 折叠,点C '的对应点为点H ,若104D GH '∠=︒,则DED ∠'的大小是______.27.如图,点E ,F 分别为长方形纸片ABCD 的边AB ,CD 上的点,将纸片沿EF 翻折,点B ,C 分别落在点B ',C '处.下列结论一定正确..的有________(填序号即可).①AEF EFC '∠=∠;②90DFC AEB ''∠+∠=︒;③BEF AEF DFC '∠-∠=∠;④若BEF ∠的度数比DFC '∠的2倍还多9︒,则BEF ∠的度数为118︒.28.如图,点F ,G 是长方形ABCD 边AD 上两点,点H 是边CD 上的点,连接BF ,GH ,分别将△ABF ,△GDH 沿BF ,GH 翻折,点A ,D 恰好都与对角线上的点E 重合,若∠ABF =25°,则∠EHC =___.29.将一张长为12.6cm ,宽为acm 的长方形纸片按图折叠出一个正方形并剪下,称为第一次操作;将余下的长方形纸片再次折叠出一个正方形并剪下,称为第二次操作…如此操作下去,若每一次剪下后的长方形纸片只能折出一个正方形,当第五次操作后,剩下图形的长与宽之比为2:1,则a 的值为____.30.在Rt△ABC中,∠ACB=90°,将三角形折叠,使得点B与线段BC延长线上的点E重合,折痕分别与AB 边交于点D,与BC边交于点F,连接DE交AC边于点G,若AC=3CG且GE=1,则AB边的长度为____________.三、解答题31.如图,一条长方形纸带ABCD中,//AD BC.现将它沿着线段EF折叠,点C,D分别落在C',D¢上,C E'HG FE,交线段BE于点G.交AD于点H,过点H作//(1)12∠=∠吗?请说明理由;∠的度数;(2)若3∠=50°,求AHG∠,并说明理由.(3)判断HG是否平分AHE32.同学们,我们已经学习了角的平分线的定义,请你用它解决下列问题:(1)如图1,已知∠AOC,若将∠AOC沿着射线OC翻折,射线OA落在OB处,则射线OC一定平分∠AOB.理由如下:因为∠BOC是由∠AOC翻折而成,而翻折不改变图形的形状和大小,所以∠BOC=______,所以射线______是∠AOB的平分线;(2)如图2,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕.①若EA′恰好平分∠FEB,求出∠FEB的度数;②过点E再将长方形的另一角∠B做折叠,使点B落在∠FEB的内部B′处(B′不在射线EA′上),EH为折痕,H为EH与射线BC的交点.请猜想∠A′EF,∠B′EH与∠A′EB′三者的数量关系,并说明理由.33.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是;(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为;(直接填写答案)②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.34.如图,长方形纸片ABCD,点E,F,C分别在边AD,AB,CD上.将∠AEF沿折痕EF翻折,点A落在点A'处;将∠DEG沿折痕EG翻折,点D落在点D'处.(1)如图1,若∠AEF=40°,∠DEG=35°,求∠A'ED'的度数;(2)如图1,若∠A'ED'=α,求∠FEG的度数(用含α的式子表示);(3)如图2,若∠A'ED'=α,求∠FEG的度数(用含α的式子表示)35.ABCD是长方形纸片的四个顶点,点E、F、H分别边AD、BC、AD上的三点,连接EF、FH.(1)将长方形纸片的ABCD按如图①所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′,点B′在FC′上,则∠EFH的度数为;(2)将长方形纸片的ABCD按如图②所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D'(B′、C′的位置如图所示),若∠B'FC′=16°,求∠EFH的度数;(3)将长方形纸片的ABCD按如图③所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′,D′(B′、C′的位置如图所示).若∠EFH=n°,则∠B′FC′的度数为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
翻折组卷一.选择题(共9小题)1.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB 落在AD边上,折痕为AE,再将△ABE 以BE为折痕向右折叠,AE与CD交于点F,则的值是()A.1 B.C.D.2.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB 落在AD边上,折痕为AE ,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则的值是()A.1 B.C.D.3.如图,将矩形纸片ABCD沿DE折叠,使DC落在DA上,点C的落点记为F,已知AD=10 cm,BE=4cm,则CD等于()A.3cm B.4cm C.5cm D.6cm4.如图,有一矩形纸片ABCD,且AB:BC=3:2,先将纸片折叠,使AD落在AB边上,折痕为AE;再将△AED以DE为折痕向右折叠,AE交BC于F.那么DB:BA等于()A .3:2 B.2:3 C.1:1 D.2:15.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使点D落在AB边上的D′处,折痕为AE,再将△AD′E以D′E为折痕向右折叠,使点A落在点A′处,设A′E与BC交于点F(如图),则A′F的长为()A .B.C.D.6.如图,在矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为()A .1 B.2 C.4 D.87.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为()A 1B 1C D....8.小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为()A.B.C.D.9.如图,矩形纸片ABCD中,AD=10 cm,将纸片沿DE折叠,使点C落在边AD上(与点F重合),若BE=6 cm,则CD等于()A.4cm B.6cm C.8cm D.10cm二.填空题(共16小题)10.如图,一张宽为6cm的矩形纸片,按图示加以折叠,使得一角顶点落在AB边上,则折痕DF= ______cm.11.如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E 交AF于点G,若∠CEF=70°,则∠GFD′=_________ °.12.如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为_________ .13.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,已知∠EFG=50°,那么∠BEG的度数为_________ .14.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P 的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=_________ °.15.把矩形纸片ABCD折叠,使B、C两点恰好落在AD边上的点P处(如图),若∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的宽为_________ cm,面积为_________ cm2.16.把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为_________ .17.把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为_________ cm2.18.如图,将长为4cm宽为2cm的矩形纸片ABCD折叠,使点B落在CD边上的中点E 处,压平后得到折痕MN,则线段AM的长度为_________ cm.19.如图,有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为_________ .20.如图,把一张矩形纸片ABCD沿EF折叠后,点C﹑D分别落在点C′、D′的位置上,EC′交AD于点G.已知∠EFG=55°,那么∠BEG=_________ 度.21.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,若∠ABE=40°,则∠ADB=_________ .22.如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,EC′交AD于点G,已知∠EFG=53°,那么∠BEG=_________ °.23.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为_________ .24.现将矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD 边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M 点正好在∠NDG的平分线上,且,那么AD= _________ .25.如图,折叠一张矩形纸片,使它的一个顶点落在长边上,已知:β=110°,求α= _________ 度.三.解答题(共5小题)26.课本中,把长与宽之比为的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.…27.把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,求矩形纸片ABCD的面积.28.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,试判断重叠部分的三角形BED的形状,并证明你的结论.29.如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.(1)求证:平行四边形ABCD是矩形;(2)求BF的长;(3)求折痕AF长.30.如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G.(1)求证:△CEG是等边三角形;(2)若矩形的一边AD=3,求另一边AB的长.初中数学组卷参考答案与试题解析一.选择题(共9小题)1.(2010•赤峰)如图,有一矩形纸片ABCD ,AB=6,AD=8,将纸片折叠使AB落在AD 边上,折痕为AE ,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则的值是()A.1 B.C.D.考点:翻折变换(折叠问题);矩形的性质;相似三角形的判定与性质.专题:压轴题.分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.解答:解:由题意知:AB=BE=6,BD=AD﹣AB=2,AD=AB﹣BD=4;∵CE∥AB,∴△ECF∽△ADF,得=,即DF=2CF,所以CF:CD=1:3;故选C.点评:此题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度不大.2.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则的值是()A.1 B.C.D.考点:翻折变换(折叠问题).专题:应用题.分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.解答:解:由题意知:AB=BE=6,BD=AD﹣AB=2,AD=AB﹣BD=4;∵CE∥AB,∴△ECF∽△ADF,得=,即DF=2CF,所以CF:CD=1:3;故选C.点评:本题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度适中.3.(2010•白下区二模)如图,将矩形纸片ABCD沿DE折叠,使DC落在DA上,点C的落点记为F,已知AD=10 cm,BE=4cm,则CD等于()A .3cm B.4cm C.5cm D.6cm考点:翻折变换(折叠问题);矩形的性质.专题:计算题.分析:根据折叠的性质和正方形的判定方法,得四边形CDFE是正方形,四边形ABEF是矩形;根据矩形的性质,得AF=BE=4,则DF=6,则CD=DF=6(cm).解答:解:根据一组邻边相等的矩形是正方形,得四边形CDFE是正方形,则四边形ABEF是矩形.∴BE=AF=4.∴DF=AD﹣AF=6.∴CD=DF=6(cm).故选D.点评:此题考查了折叠问题,要能够根据折叠的方法发现正方形.4.(2004•广安)如图,有一矩形纸片ABCD,且AB:BC=3:2,先将纸片折叠,使AD 落在AB边上,折痕为AE;再将△AED以DE为折痕向右折叠,AE交BC于F.那么DB:BA等于()A.3:2 B.2:3 C.1:1 D.2:1考点:翻折变换(折叠问题).专题:压轴题.分析:由矩形纸片ABCD中,AB:BC=3:2,可设AB=3x,BC=2x,即可得BD=x,继而求得AB的值,则可求得答案.解答:解:∵矩形纸片ABCD中,AB:BC=3:2,∴设AB=3x,BC=2x,则AD=BC=2x,∴BD=AB﹣AD=3x﹣2x=x,如图3:AB=AD﹣BD=2x﹣x=x,∴DB:BA=x:x=1:1.故选C.点评:此题考查了折叠的性质以及矩形的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.5.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使点D 落在AB边上的D′处,折痕为AE,再将△AD′E以D′E为折痕向右折叠,使点A落在点A′处,设A′E与BC交于点F(如图),则A′F的长为()A .B.C.D.考点:翻折变换(折叠问题).分析:利用折叠的性质,即可求得AD=AD′=A′D′=、BD′=AB﹣AD=﹣,A′E=AE=AD=2,又由相似三角形的对应边成比例,即可求得EF :A′F=EC:A′B,从而求得A′F 的长度.解答:解:根据折叠的性质知,AD=AD′=A′D′=、CE=CD﹣DE=﹣,.∵CE∥A′B,∴△ECF∽△A′BF,∴CE:BA′=EF:A′F(相似三角形的对应边成比例);又∵CE=CD﹣DE=﹣,BA′=AD﹣CE=2﹣,∴=;而A′E=AE=AD=2,点评:本题考查了翻折变换及正方形的性质,利用了折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等及正方形的性质,平行线的性质,有一定的难度.6.如图,在矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为()A .1 B.2 C.4 D.8考点:翻折变换(折叠问题).分析:根据折叠易得BD,AB长,利用相似可得BF长,也就求得了CF的长度,△CEF的面积=CF•CE.解答:解:由折叠的性质知,第二个图中BD=AB﹣AD=2,第三个图中AB=AD﹣BD=6,∵BC∥DE,∴BF:DE=AB:AD,∴BF=4,CF=BC﹣BF=2,点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②矩形的性质,平行线的性质,三角形的面积公式等知识点.7.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为()A.1B.1 C.D.考点:翻折变换(折叠问题).专题:几何图形问题;压轴题;数形结合.分析:利用折叠的性质,即可求得BD的长与图3中AB的长,又由相似三角形的对应边成比例,即可求得BF的长,则由CF=BC﹣BF即可求得答案.解答:解:如图2,根据题意得:BD=AB﹣AD=2.5﹣1.5=1,如图3,AB=AD﹣BD=1.5﹣1=0.5,∵BC∥DE,∴△ABF∽△ADE,∴,∴BF=0.5,∴CF=BC﹣BF=1.5﹣0.5=1.故选B.点评:此题考查了折叠的性质与相似三角形的判定与性质.题目难度不大,注意数形结合思想的应用.8.(2012•历下区二模)小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为()A.B.C.D.考点:翻折变换(折叠问题);锐角三角函数的定义.专题:数形结合.分析:根据折叠的性质可得出CF=CB,在RT△CDF中利用勾股定理可求出DF 的长度,继而可求出cos∠DFC的值.解答:解:由折叠的性质得,CB=CF,设AB=4x,则BC=5x,在RT△DFC中,DF==3x,∴cos∠DFC==.故选B.点评:此题考查了翻折变换及勾股定理的知识,解答本题的关键是根据折叠的性质得出CF的长度,在RT△CDF中求出DF的长度,难度一般.9.如图,矩形纸片ABCD中,AD=10 cm,将纸片沿DE折叠,使点C落在边AD上(与点F重合),若BE=6 cm,则CD等于()A.4cm B.6cm C.8cm D.10cm考点:轴对称的性质.分析:根据对称的性质和AD=10,BE=6可得出CD的长度.解答:解:根据轴对称的性质可得可得出CD=DF=AD﹣AF=AD﹣BE,∴CD=4cm故选A.点评:本题考查轴对称的性质,关键在于根据图形判断出CD=DF.二.填空题(共16小题)10.如图,一张宽为6cm的矩形纸片,按图示加以折叠,使得一角顶点落在AB边上,则折痕DF= 8 cm.考点:翻折变换(折叠问题).分析:根据折叠的性质可得∠EDF=30°,从而求出∠ADE=30°,在Rt△ADE中求出DE,在Rt△DEF中可求出DF.解答:解:由折叠的性质可得:∠EDF=∠CDF=30°,则∠ADE=90°﹣30°﹣30°=30°,在Rt△ADE中,AD=6cm,∠ADE=30°,∴AE=ADtan∠ADE=2cm,DE=2AE=4cm,在Rt△DEF中,∠EDF=30°,DE=4cm,∴DF==8cm.故答案为:8.点评:本题考查了翻折变换的知识,注意掌握翻折前后对应边相等,对应角相等.11.(2012•宿迁)如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=40 °.考点:平行线的性质;翻折变换(折叠问题).分析:根据两直线平行,内错角相等求出∠EFG,再根据平角的定义求出∠EFD,然后根据折叠的性质可得∠EFD′=∠EFD,再根据图形,∠GFD′=∠EFD′﹣∠EFG,代入数据计算即可得解.解答:解:矩形纸片ABCD中,AD∥BC,∵∠CEF=70°,∴∠EFG=∠CEF=70°,∴∠EFD=180°﹣70°=110°,根据折叠的性质,∠EFD′=∠EFD=110°,∴∠GFD′=∠EFD′﹣∠EFG,=110°﹣70°,=40°.故答案为:40.点评:本题考查了平行线的性质,以及折叠变换,根据两直线平行,内错角相等求出∠EFG是解题的关键,另外,根据折叠前后的两个角相等也很重要.12.(2013•日照)如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为(3π﹣)cm2.考点:切线的性质;矩形的性质;扇形面积的计算;翻折变换(折叠问题).专题:压轴题.分析:如图,露在外面部分的面积可用扇形ODK与△ODK的面积差来求得,在Rt△A'DC中,可根据AD即圆的直径和CD即圆的半径长,求出∠DA'C的度数,进而得出∠ODH和∠DOK的度数,即可求得△ODK和扇形ODK的面积,由此可求得阴影部分的面积.解答:解:作OH⊥DK于H,连接OK,∵以AD为直径的半圆,正好与对边BC相切,∴AD=2CD,∴A'D=2CD,∵∠C=90°,∴∠DA'C=30°,∴∠ODH=30°,∴∠DOH=60°,∴∠DOK=120°,∴扇形ODK的面积为=3πcm2,∵∠ODH=∠OKH=30°,OD=3cm,∴OH=cm,DH=cm;∴DK=3cm,∴△ODK的面积为cm2,∴半圆还露在外面的部分(阴影部分)的面积是:(3π﹣)cm2.故答案为:(3π﹣)cm2.点评:此题考查了折叠问题,解题时要注意找到对应的等量关系;还考查了圆的切线的性质,垂直于过切点的半径;还考查了直角三角形的性质,直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度.13.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,已知∠EFG=50°,那么∠BEG的度数为80°.考点:翻折变换(折叠问题).专题:探究型.分析:先根据正方形的性质得出AD∥BC,由∠EFG=50°可求出∠1的度数,再根据图形翻折变换的性质得出∠1=∠2=50°,由平角的性质即可得出∠B EG的度数.解答:解:∵四边形ABCD是矩形,∴AD∥BC,∵∠EFG=50°,∴∠1=∠EFG=50°,∵四边形EFD′C′是四边形EFDC翻折而成,∴∠1=∠2=50°,∴∠BEG=180°﹣∠1﹣∠2=180°﹣50°﹣50°=80°.故答案为:80°.点评:本题考查的是图形翻折变换的性质、矩形的性质及平行线的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.14.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P 的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=15 °.考点:翻折变换(折叠问题).分析:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,再利用平角为180°,即可求出∠NPB′的度数.解答:解:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,∴∠NPM=2×75°=150°,∴∠C′PB=30°,由折叠的性质可知:∠C′PN=∠BPN,∴∠NPB′=15°.故答案为:15.点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.15.把矩形纸片ABCD折叠,使B、C两点恰好落在AD边上的点P处(如图),若∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的宽为 4.8 cm,面积为115.2 cm2.考点:翻折变换(折叠问题).分析:根据勾股定理,得MN=10;根据直角三角形的面积公式,得AB=4.8;根据折叠,知BC=6+8+10=24,进而求得矩形的面积.解答:解:过点P作PE⊥MN,∵∠MPN=90°,PM=6cm,PN=8cm,∴MN==10(cm),∴S△PMN=PM•PN=MN•PE,∴PM•PN=MN•PE,即PE==4.8(cm),即矩形纸片ABCD的宽为:4.8cm;∵BC=PM+MN+PN=6+10+8=24(cm),∴S矩形ABCD=4.8×24=115.2(cm2).故答案为:4.8,115.2.点评:此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.16.(2005•遂宁)把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为.考点:翻折变换(折叠问题).专题:压轴题.分析:利用折叠的性质和勾股定理可知.解答:解:由勾股定理得,MN=5,设Rt△PMN的斜边上的高为h,由矩形的宽AB也为h,根据直角三角形的面积公式得,h=PM•PN÷MN=,由折叠的性质知,BC=PM+MN+PN=12,∴矩形的面积=AB•BC=.点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②勾股定理,直角三角形和矩形的面积公式求解.17.(2010•徐汇区二模)把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为115.2 cm2.考点:翻折变换(折叠问题).分析:根据勾股定理,得MN=10;根据直角三角形的面积公式,得AB=4.8;根据折叠,知BC=6+8+10=24,进而求得矩形的面积.解答:解:∵∠MPN=90°,PM=6cm,PN=8cm,∴MN=10,BC=10+6+8=24.根据直角三角形的面积公式,得AB==4.8.则矩形的面积=4.8×24=115.2(cm2).点评:此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法.18.如图,将长为4cm宽为2cm的矩形纸片ABCD折叠,使点B落在CD边上的中点E 处,压平后得到折痕MN,则线段AM的长度为cm.考点:翻折变换(折叠问题);勾股定理.专题:计算题;探究型.分析:连接BM,EM,BE,由折叠的性质可知,四边形ABNM和四边形FENM 关于直线MN对称,由垂直平分线的性质可知BM=EM,再由点E是CD的中点,可求出DE的长,由勾股定理即可求出AM的长.解答:解:如图,连接BM,EM,BE,由折叠的性质可知,四边形ABNM和四边形FENM关于直线MN对称.∴MN垂直平分BE,∴BM=EM,∵点E是CD的中点,DE=1,∴在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,∴AM2+AB2=DM2+DE2.设AM=x,则DM=4﹣x,∴x2+22=(4﹣x)2+12.解得,即cm.故答案为:.点评:本题考查的是图形折叠的性质及勾股定理,解答此类问题时,首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.19.如图,有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为 1 .考点:翻折变换(折叠问题).专题:数形结合.分析:利用折叠的性质,即可求得BD的长与图3中AB的长,又由相似三角形的对应边成比例,即可求得BF的长,则由CF=BC﹣BF即可求得答案.解答:解:如图2,根据题意得:BD=AB﹣AD=2.5﹣1.5=1,如图3,AB=AD﹣BD=1.5﹣1=0.5,∵BC∥DE,∴△ABF∽△ADE,∴=,即=,∴BF=0.5,∴CF=BC﹣BF=1.5﹣0.5=1.故答案为:1.点评:本题考查了翻折变换及正方形的性质,利用了折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等及正方形的性质,平行线的性质,有一定的难度.20.如图,把一张矩形纸片ABCD沿EF折叠后,点C﹑D分别落在点C′、D′的位置上,EC′交AD于点G.已知∠EFG=55°,那么∠BEG=70 度.考点:翻折变换(折叠问题).专题:计算题.分析:由矩形的性质可知AD∥BC,可得∠CEF=∠EFG=55°,由折叠的性质可知∠GEF=∠CEF,再由邻补角的性质求∠BEG.解答:解:∵AD∥BC,∴∠CEF=∠EFG=55°,由折叠的性质,得∠GEF=∠CEF=55°,∴∠BEG=180°﹣∠GEF﹣∠CEF=70°.故答案为:70.点评:本题考查了翻折变换(折叠问题).关键是明确折叠前后,对应角相等,两直线平行,内错角相等的性质.21.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,若∠ABE=40°,则∠ADB=25°.考点:翻折变换(折叠问题).分析:首先根据矩形的性质可得∠ABC=90°,AD∥BC,进而可以计算出∠EBC,再根据折叠可得∠EBD=∠CBD=∠EBC,然后再根据平行线的性质可以计算出∠ADB的度数.解答:解:∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC,∵∠ABE=40°,∴∠EBC=90°﹣40°=50°,根据折叠可得∠EBD=∠CBD,∴∠CBD=25°,∵AD∥BC,∴∠ADB=∠DBC=25°,故答案为:25°.点评:此题主要考查了图形的折叠,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.22.如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,EC′交AD于点G,已知∠EFG=53°,那么∠BEG=64 °.考点:翻折变换(折叠问题).专题:几何图形问题.分析:由矩形的性质可知AD∥BC,可得∠CEF=∠EFG=53°,由折叠的性质可知∠GEF=∠CEF,再由邻补角的性质求∠BEG.解答:解:∵AD∥BC,∴∠CEF=∠EFG=53°,由折叠的性质,得∠GEF=∠CEF=53°,∴∠BEG=180°﹣∠GEF﹣∠CEF=64°.故答案为:64.点评:本题考查了翻折变换(折叠问题).关键是明确折叠前后,对应角相等,以及两直线平行,内错角相等的性质.23.(2010•盐城)小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为:1 .考点:翻折变换(折叠问题).专题:压轴题.分析:连DE,由翻折的性质知,四边形ABEF为正方形,∠EAD=45°,而M点正好在∠NDG的平分线上,则DE平分∠GDC,易证RT△DGE≌Rt△DCE,得到DC=DG,而△AGD为等腰直角三角形,得到AD=DG=CD.解答:解:连DE,如图,∵沿过A点的直线折叠,使得B点落在AD边上的点F处,∴四边形ABEF为正方形,∴∠EAD=45°,由第二次折叠知,M点正好在∠NDG的平分线上,∴DE平分∠GDC,∴DC=DG,又∵△AGD为等腰直角三角形,∴AD=DG=CD,∴矩形ABCD长与宽的比值为:1.故答案为::1.点评:本题考查了翻折的性质:翻折前后的两个图形全等.也考查了正方形、角的平分线的性质以及等腰直角三角形的性质.24.(2011•桐乡市一模)现将矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,且,那么AD= 2 .考点:翻折变换(折叠问题).专题:计算题.分析:连DE,由矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②),根据折叠的性质得到∠EAF=∠EAB=45°,又沿过D点的直线折叠,使得C点落在DA次根据折叠的性质得到∠NDG=∠CDG=45°,∠MDG=∠EDG,DN=DC=,则△AGD为等腰直角三角形,而M点正好在∠NDG的平分线上,得到∴∠NDM=∠GDM,易证Rt△NMD≌Rt△GMD,得到DG=DN=,根据AD=DG即可求出AD.解答:解:∵矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②),∴∠EAF=∠EAB=45°,又∵沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).连DE,∴∠NDG=∠CDG=45°,∠MDG=∠EDG,DN=DC=,∴△AGD为等腰直角三角形,即∠MGD=90°,又∵第二次折叠后,M点正好在∠NDG的平分线上,∴∠NDM=∠GDM,∴Rt△NMD≌Rt△GMD,∴DG=DN=,∴AD=DG=2.故答案为2.点评:本题考查了折叠的性质:折叠后两重合的图形全等.也考查了三角形全等的判定与性质以及等腰直角三角形三边的关系.25.(2013•南昌模拟)如图,折叠一张矩形纸片,使它的一个顶点落在长边上,已知:考点:平行线的性质;翻折变换(折叠问题).专题:计算题.分析:由折叠及矩形的性质得到∠AFE为直角,利用平角的定义得到一对角互余,再由AB与DC平行,利用两直线平行同旁内角互补得到一对角互补,求出∠AFC的度数,即可确定出α的度数.解答:解:由折叠的性质得:∠AFE=90°,∴α+∠AFC=90°,∵AB∥CD,∴∠β+∠AFC=180°,∵∠β=110°,∴∠AFC=70°,则α=20°.故答案为:20点评:此题考查了平行线的性质,以及翻折变换,熟练掌握平行线的性质是解本题的关键.三.解答题(共5小题)26.(2012•衢州)课本中,把长与宽之比为的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.…考点:翻折变换(折叠问题);全等三角形的判定与性质;勾股定理;等腰直角三角形;矩形的性质;图形的剪拼.专题:几何综合题;压轴题.分析:(1)根据==2•==,得出矩形纸片ABEF也是标准纸;(2)利用已知得出△ADG是等腰直角三角形,得出==,即可得出答案;(3)分别求出每一次对折后的周长,进而得出变化规律求出即可.解答:解:(1)是标准纸,理由如下:∵矩形纸片ABCD是标准纸,∴=,由对开的含义知:AF=BC,∴==2•==,∴矩形纸片ABEF也是标准纸.(2)是标准纸,理由如下:设AB=CD=a,由图形折叠可知:DN=CD=DG=a,DG⊥EM,由图形折叠可知:△ABE≌△AFE,∴∠DAE=∠BAD=45°,∴△ADG是等腰直角三角形,∴在R t△ADG中,AD==a,∴==,∴矩形纸片ABCD是一张标准纸;。
