【精选】八年级全等三角形中考真题汇编[解析版]

合集下载

八年级全等三角形专题练习(解析版)

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,：在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为：在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用：如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解：(1)证实：BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下：: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下：由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实：PC=PE；〔2〕求N CPE的度数：〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论：⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案；(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE；⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>：⑶、AP = CE理由是：在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点：三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£＞为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系：②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由；〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析：②成立,理由见解析：〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可：〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解：〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD：②成立,理由如下：如图2：VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD：(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证：△.所为等腰直角三角形：〔2〕假设△ABC的面积为7,求四边形AEDF•的面积：〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析；〔2〕 3.5：〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形；〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可；〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解：〔1〕证实：如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又；Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn；AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又；Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又：Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空：AABC的面积等于—；(2)连接CE,求证：CE是NAC3的平分线；(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—：〔2〕证实见解析：〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得：〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实：〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解：〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为：—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=；(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为：50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm ：(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等？假设存在,请求出v的值：假设不存在,请说明理由.【答案】(1) (12-2/)； (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长：(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得；(3)先分两种情况：当BP=CQ, AB=PC 时,△ABPgZ\PCQ：或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解：(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin：.PC = BC-BP = (n-2i)cm故答案为：(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下：①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item：.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.：在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证：MN = CN — BM ；(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析：(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM： (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实：・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由：•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA：.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现：如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证：△BADgZkCAE；(2)在(1)的条件下,求N8EC的度数：拓广探索：(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析：(2) 70°； (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实：如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,：.Z EAC=A DAB,AE=AD. AC=AB9：.△ BAD^ & CAE (SAS).(2)解：如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解：如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,：AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是；②设NBA尸=a,用.表示NBCF的大小；〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE；②NBCF=.：(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案；②由釉对称性,得：AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解：(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,：.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下：作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证：CF = EG ；〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证：CD = CE+CF；〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解；〔2〕证实见详解：〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论：(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论；(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, ：.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即：ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),：.CF = EG ；(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、：.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即：ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下：过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即：NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。

八年级上册数学全等三角形中考真题汇编[解析版]

八年级上册数学全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，在菱形ABCD中，∠ABC=120°，AB=10cm，点P是这个菱形内部或边上的一点．若以P，B，C为顶点的三角形是等腰三角形，则P，A（P，A两点不重合）两点间的最短距离为______cm．-【答案】10310【解析】解：连接BD，在菱形ABCD中，∵∠ABC=120°，AB=BC=AD=CD=10，∴∠A=∠C=60°，∴△ABD，△BCD都是等边三角形，分三种情况讨论：①若以边BC为底，则BC垂直平分线上（在菱形的边及其内部）的点满足题意，此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”，即当点P与点D重合时，PA最小，最小值PA=10；②若以边PB为底，∠PCB为顶角时，以点C为圆心，BC长为半径作圆，与AC相交于一点，则弧BD（除点B外）上的所有点都满足△PBC是等腰三角形，当点P在AC上时，AP-；最小，最小值为10310③若以边PC为底，∠PBC为顶角，以点B为圆心，BC为半径作圆，则弧AC上的点A与点D均满足△PBC为等腰三角形，当点P与点A重合时，PA最小，显然不满足题意，故此种情况不存在；-（cm）．综上所述，PA的最小值为10310-．故答案为：10310点睛：本题考查菱形的性质、等边三角形的性质，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．∥，2．如图所示，ABC为等边三角形，P是ABC内任一点，PD AB，PE BCPF AC ∥，若ABC 的周长为12cm ，则PD PE PF ++=____cm ．【答案】4【解析】【分析】先说明四边形HBDP 是平行四边形，△AHE 和△AHE 是等边三角形，然后得到一系列长度相等的线段,最后求替换求和即可．【详解】解：∵PD AB ，PE BC ∥∴四边形HBDP 是平行四边形∴PD=HB∵ABC 为等边三角形,周长为12cm∴∠B=∠A=60°,AB=4∵PE BC ∥∴∠AHE=∠B=60°∴∠AHE=∠A=60°∴△AHE 是等边三角形∴HE=AH∵∠HFP=∠A=60°∴∠HFP=∠AHE=60°∴△AHE 是等边三角形，∴FP=PH∴PD+PE+PF=BH+(HP+PE)=BH+HE=BH+AH=AB=4cm故答案为4cm ．【点睛】本题考查了平行四边形的判定和性质以及等边三角形的性质，掌握等边三角形的性质是解答本题的关键．3．如图，已知等边ABC ∆的边长为8，E 是中线AD 上一点，以CE 为一边在CE 下方作等边CEF ∆，连接BF 并延长至点,N M 为BN 上一点，且5CM CN ==，则MN 的长为_________．【答案】6【解析】【分析】作CG⊥MN于G，证△ACE≌△BCF，求出∠CBF=∠CAE=30°，则可以得出124CG BC==，在Rt△CMG中，由勾股定理求出MG，即可得到MN的长．【详解】解：如图示：作CG⊥MN于G，∵△ABC和△CEF是等边三角形，∴AC=BC，CE=CF，∠ACB=∠ECF=60°，∴∠ACB-∠BCE=∠ECF-∠BCE，即∠ACE=∠BCF，在△ACE与△BCF中AC BCACE BCFCE CF=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△BCF（SAS），又∵AD是三角形△ABC的中线∴∠CBF=∠CAE=30°，∴124CG BC==，在Rt△CMG中，2222543MG CM CG=-=-，∴MN=2MG=6，故答案为：6．【点睛】本题考查了勾股定理，等边三角形的性质，全等三角形的性质和判定的应用，解此题的关键是推出△ACF≌△BCF．4．在平面直角坐标系中，点A在x轴的正半轴上，点B在y轴的正半轴上，36ABO∠=︒，在x轴或y轴上取点C，使得ABC∆为等腰三角形，符合条件的C点有__________个．【答案】8【解析】【分析】观察数轴，按照等腰三角形成立的条件分析可得答案．【详解】解：如下图所示，若以点A为圆心，以AB为半径画弧，与x轴和y轴各有两个交点，但其中一个会与点B重合，故此时符合条件的点有3个；若以点B为圆心，以AB为半径画弧，同样与x轴和y轴各有两个交点，但其中一个与点A重合，故此时符合条件的点有3个；线段AB的垂直平分线与x轴和y轴各有一个交点，此时符合条件的点有2个．∴符合条件的点总共有：3＋3＋2=8个．故答案为：8．【点睛】本题考查了等腰三角形的判定，可以观察图形，得出答案．5．如图，△ABC中，AB=AC，∠A=30°，点D在边AB上，∠ACD=15°，则ADBC____．【答案】2．【解析】【分析】根据题意作CE ⊥AB 于E ，作DF ⊥AC 于F ，在CF 上截取一点H ，使得CH ＝DH ，连接DH ，并设AD ＝2x ，解直角三角形求出BC （用x 表示）即可解决问题．【详解】解：作CE ⊥AB 于E ，作DF ⊥AC 于F ，在CF 上截取一点H ，使得CH=DH ，连接DH ．设AD=2x ，∵AB=AC ，∠A=30°，∴∠ABC=∠ACB=75°，DF 12=AD=x ，AF 3=， ∵∠ACD=15°，HD=HC ，∴∠HDC=∠HCD=15°，∴∠FHD=∠HDC+∠HCD=30°，∴DH=HC=2x ，FH 3=，∴3x ，在Rt △ACE 中，EC 12=AC=x 3+，AE 3=3=， ∴BE=AB ﹣AE 3=﹣x ，在Rt △BCE 中，BC 22BE EC =+=2x ， ∴222AD BC x ==．故答案为：22．【点睛】本题考查的等腰三角形的性质和解直角三角形以及直角三角形30度角的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．6．如图，在直角坐标系中，点()8,8B -，点()2,0C -，若动点P 从坐标原点出发，沿y 轴正方向匀速运动，运动速度为1/cm s ，设点P 运动时间为t 秒，当BCP ∆是以BC 为腰的等腰三角形时，直接写出t 的所有值__________________．【答案】2秒或46秒或14秒【解析】【分析】分两种情况：PC 为腰或BP 为腰.分别作出符合条件的图形，计算出OP 的长度，即可求出t 的值．【详解】解：如图所示，过点B 作BD ⊥x 轴于点D ，作BE ⊥y 轴于点E ，分别以点B 和点C 为圆心，以BC 长为半径画弧交y 轴正半轴于点F ，点H 和点G∵点B （-8，8），点C （-2，0），∴DC=6cm ，BD=8cm ，由勾股定理得：BC=10cm∴在直角三角形COG 中，OC=2cm ，CG=BC=10cm ，∴2210246(cm)-=，当点P 运动到点F 或点H 时，BE=8cm ，BH=BF=10cm ，∴EF=EH=6cm∴OP=OF=8-6=2（cm ）或OP=OH=8+6=14（cm ），故答案为：2秒，6秒或14秒．【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用，通过作图找出要求的点的位置，利用勾股定理来求解是本题的关键．7．△ABC中，最小内角∠B＝24°，若△ABC被一直线分割成两个等腰三角形，如图为其中一种分割法，此时△ABC中的最大内角为90°，那么其它分割法中，△ABC中的最大内角度数为_____．【答案】117°或108°或84°．【解析】【分析】根据等腰三角形的性质进行分割，写出△ABC中的最大内角的所有可能值.【详解】①∠BAD＝∠BDA＝12（180°﹣24°）＝78°，∠DAC＝∠DCA＝12∠BDA＝39°，如图1所示：∴∠BAC＝78°+39°＝117°；②∠DBA＝∠DAB＝24°，∠ADC＝∠ACD＝2∠DBA＝48°，如图2所示：∴∠DAC＝180°﹣2×48°＝84°，∴∠BAC＝24°+84°＝108°；③∠DBA＝∠DAB＝24°，∠ADC＝∠DAC＝2∠DBA＝48°，如图3所示：∴∠BAC＝24°+48°＝72°，∠C＝180°﹣2×48°＝84°；∴其它分割法中，△ABC中的最大内角度数为117°或108°或84°，故答案为：117°或108°或84°．【点睛】本题考查了等腰三角形的性质，解题的关键是根据等腰三角形的性质进行分割找出所有情况.8．如图，△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点，如果点P在线段BC 上以v厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动。

八年级全册全套试卷中考真题汇编[解析版]

八年级全册全套试卷中考真题汇编[解析版]一、八年级数学三角形填空题（难）1．一个等腰三角形的两边长分别为4cm和9cm，则它的周长为__cm．【答案】22【解析】【分析】底边可能是4，也可能是9，分类讨论，去掉不合条件的，然后可求周长.【详解】试题解析：①当腰是4cm，底边是9cm时：不满足三角形的三边关系，因此舍去．②当底边是4cm，腰长是9cm时，能构成三角形，则其周长=4+9+9=22cm．故填22．【点睛】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答.2．三角形的三个内角度数比为1：2：3，则三个外角的度数比为_____．【答案】5:4:3【解析】试题解析：设此三角形三个内角的比为x，2x，3x，则x+2x+3x=180，6x=180，x=30，∴三个内角分别为30°、60°、90°，相应的三个外角分别为150°、120°、90°，则三个外角的度数比为：150°：120°：90°=5：4：3，故答案为5：4：3．3．如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内时，∠A与∠1＋∠2之间有始终不变的关系是__________．【答案】2∠A＝∠1＋∠2【解析】【分析】根据∠1与∠AED的2倍和∠2与∠ADE的2倍都组成平角，结合△AED的内角和为180°可求出答案．【详解】∵△ABC纸片沿DE折叠，∴∠1＋2∠AED＝180°，∠2＋2∠ADE＝180°，∴∠AED＝12（180°−∠1），∠ADE＝12（180°−∠2），∴∠AED＋∠ADE＝12（180°−∠1）＋12（180°−∠2）＝180°−12（∠1＋∠2）∴△ADE中，∠A＝180°−（∠AED＋∠ADE）＝180°−[180°−12（∠1＋∠2）]＝12（∠1＋∠2），即2∠A＝∠1＋∠2．故答案为：2∠A＝∠1＋∠2．【点睛】本题考查的是三角形内角和定理，熟知三角形的内角和等于180°及图形翻折变换的性质是解答此题的关键．4．如果一个n边形的内角和是1440°，那么n=__．【答案】10【解析】∵n边形的内角和是1440°，∴(n−2)×180°=1440°，解得：n=10.故答案为：10.5．如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是_____．【答案】85°．【解析】【分析】根据三角形内角和得出∠C=60°，再利用角平分线得出∠DBC=35°，进而利用三角形内角和得出∠BDC的度数．【详解】∵在△ABC中，∠A=50°，∠ABC=70°，∴∠C=60°，∵BD平分∠ABC，∴∠DBC=35°，∴∠BDC=180°﹣60°﹣35°=85°．故答案为85°．6．如图，Rt△ABC中，∠ACB＝90°，∠A＝50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB的度数为_____．【答案】10°【解析】【分析】根据直角三角形两锐角互余求出∠B，根据翻折变换的性质可得∠CA′D=∠A，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【详解】∵∠ACB＝90°，∠A＝50°，∴∠B＝90°﹣50°＝40°，∵折叠后点A落在边CB上A′处，∴∠CA′D＝∠A＝50°，由三角形的外角性质得，∠A′DB＝∠CA′D﹣∠B＝50°﹣40°＝10°．故答案为：10°．【点睛】本题考查了翻折变换，直角三角形两锐角互余，三角形的一个外角等于与它不相邻的两个内角的和的性质，翻折前后对应边相等，对应角相等．二、八年级数学三角形选择题（难）7．若△ABC内有一个点P1，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）A．n·180°B．（n+2）·180°C．（2n-1）·180°D．（2n+1）·180°【答案】D【解析】当△ABC内的点的个数是1时，三角形内互不重叠的小三角形的个数是3；当△ABC内的点的个数是2时，三角形内互不重叠的小三角形的个数是5；依此类推得到当△ABC内的点的个数是3时，三角形内互不重叠的小三角形的个数是7；当△ABC内的点的个数是n 时，三角形内互不重叠的小三角形的个数2n+1，所以这些小三角形的内角和为（2n+1）·180°【详解】】解：图1中，当△ABC内只有1个点时，可分割成3个互不重叠的小三角形；图2中，当△ABC内只有2个点时，可分割成5个互不重叠的小三角形；图3中，当△ABC内只有3个点时，可分割成7个互不重叠的小三角形；根据以上规律，当△ABC内有n个点（P1，P2，…，P n）时，可以把△ABC分割成S=2n+1个互不重叠的三角形，所以这些小三角形的内角和为（2n+1）·180°.【点睛】此题考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键．8．马小虎在计算一个多边形的内角和时，由于粗心少算了2个内角，其和等于830，则该多边形的边数是( )A．7B．8C．7或8D．无法确定【答案】C【解析】【分析】n边形的内角和是（n-2）•180°，即为180°的（n-2）倍，多边形的内角一定大于0度，小于180度，因而多边形中，除去2个内角外，其余内角和与180度的商加上2，以后所得的数值，比这个数值大1或2的整数就是多边形的边数．【详解】设少加的2个内角和为x度，边数为n．则（n-2）×180=830+x，即（n-2）×180=4×180+110+x，因此x=70，n=7或x=250，n=8．故该多边形的边数是7或8．故选C．【点睛】本题考查了多边形的内角和定理，正确理解多边形内角的大小的特点，以及多边形的内角和定理是解决本题的关键．9．能够铺满地面的正多边形组合是（）A．正三角形和正五边形B．正方形和正六边形C．正方形和正五边形D．正五边形和正十边形【解析】【分析】正多边形的组合能否铺满地面，关键是要看位于同一顶点处的几个角之和能否为360°．若能，则说明能铺满；反之，则说明不能铺满．【详解】解：A、正五边形和正三边形内角分别为108°、60°，由于60m+108n=360，得m=6-95 n，显然n取任何正整数时，m不能得正整数，故不能铺满，故此选项错误；B、正方形、正六边形内角分别为90°、120°，不能构成360°的周角，故不能铺满，故此选项错误；C、正方形、正五边形内角分别为90°、108°，当90n+108m=360，显然n取任何正整数时，m不能得正整数，故不能铺满，故此选项错误；D、正五边形和正十边形内角分别为108、144，两个正五边形与一个正十边形能铺满地面，故此选项正确．故选：D．【点睛】此题主要考查了平面镶嵌，两种或两种以上几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．需注意正多边形内角度数=180°-360°÷边数．10．一个三角形的两边长分别为5和7，设第三边上的中线长为x，则x的取值范围是（）A．x>5 B．x<7 C．2<x<12 D．1<x<6【答案】D【解析】如图所示:AB=5，AC=7，设BC=2a，AD=x，延长AD至E，使AD=DE，在△BDE与△CDA中，∵AD=DE，BD=CD，∠ADC=∠BDE，∴△BDE≌△CDA，∴AE=2x，BE=AC=7，在△ABE中，BE-AB＜AE＜AB+BE，即7-5＜2x＜7+5，∴1＜x＜6．故选D．11．如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（）A．4cm B．2cm C．4cm或2cm D．小于或等于4cm，且大于或等于2cm【答案】D【解析】试题分析：①当A，B，C三点在一条直线上时，分点B在A、C之间和点C在A、B之间两种情况讨论；②当A，B，C三点不在一条直线上时，根据三角形三边关系讨论.解：当点A、B、C在同一条直线上时，①点B在A、C之间时：AC=AB+BC=3+1=4；②点C 在A、B之间时：AC=AB-BC=3-1=2，当点A、B、C不在同一条直线上时，A、B、C三点组成三角形，根据三角形的三边关系AB-BC＜AC＜AB+BC，即2＜AC＜4，综上所述，选D.故选D.点睛：本题主要考查点与线段的位置关系..利用分类思想得出所有情况的图形是解题的关键，12．如图，七边形ABCDEFG中，AB，ED的延长线交于点O，若∠1，∠2，∠3，∠4的外角和等于215°，则∠BOD的度数为()A．20°B．35°C．40°D．45°【答案】B【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE的内角和，则可求得∠BOD．【详解】解：∵∠1、∠2、∠3、∠4的外角的角度和为215°，∴∠1+∠2+∠3+∠4+215°=4×180°，∴∠1+∠2+∠3+∠4=505°，∵五边形OAGFE内角和=（5-2）×180°=540°，∴∠1+∠2+∠3+∠4+∠BOD=540°，∴∠BOD=540°-505°=35°，故选：B．【点睛】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．三、八年级数学全等三角形填空题（难）13．如图，ABE△，BCD均为等边三角形，点A，B，C在同一条直线上，连接AD，EC，AD与EB相交于点M，BD与EC相交于点N，连接OB，下列结论正确的有_________．①AD EC=；②BM BN=；③MN AC；④EM MB=；⑤OB平分AOC∠【答案】①②③⑤.【解析】【分析】由题意根据全等三角形的判定和性质以及等边三角形的性质和角平分线的性质，对题干结论依次进行分析即可.【详解】解：∵△ABE，△BCD均为等边三角形，∴AB=BE，BC=BD，∠ABE=∠CBD=60°，∴∠ABD=∠EBC，在△ABD和△EBC中，AB BEABD EBCBD BC⎧⎪∠∠⎨⎪⎩＝＝＝∴△ABD≌△EBC（SAS），∴AD=EC，故①正确；∴∠DAB=∠BEC，又由上可知∠ABE=∠CBD=60°，∴∠EBD=60°，在△ABM 和△EBN 中，MAB NEB AB BEABE EBN ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ∴△ABM ≌△EBN （ASA ），∴BM=BN ，故②正确；∴△BMN 为等边三角形，∴∠NMB=∠ABM=60°，∴MN ∥AC ，故③正确；若EM=MB ，则AM 平分∠EAB ，则∠DAB=30°，而由条件无法得出这一条件，故④不正确；如图作,,BG AD BH EC ⊥⊥∵由上可知△ABD ≌△EBC ，∴两个三角形对应边的高相等即BG BH =，∴OB 是AOC ∠的角平分线，即有OB 平分AOC ∠，故⑤正确.综上可知：①②③⑤正确.故答案为：①②③⑤.【点睛】本题考查全等三角形的判定和性质，熟练掌握全等三角形的判定和性质以及等边三角形的性质和角平分线的性质与平行线的判定是解题的关键.14．如图，∠ACB ＝90°，AC ＝BC ，点C(1，2)、A(－2，0)，则点B 的坐标是__________.【答案】(3，－1)【解析】分析：过C和B分别作CD⊥OD于D，BE⊥CD于E，利用已知条件可证明△ADC≌△CEB，再由全等三角形的性质和已知数据即可求出B点的坐标．详解：过C和B分别作CD⊥OD于D，BE⊥CD于E，∵∠ACB=90°，∴∠ACD+∠CAD=90°,∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ADC和△CEB中，∠ADC=∠CEB=90°；∠CAD=∠BCE，AC=BC，∴△ADC≌△CEB(AAS)，∴DC=BE，AD=CE，∵点C的坐标为(1,2),点A的坐标为(−2,0)，∴AD=CE=3，OD=1，BE=CD=2，∴则B点的坐标是(3,−1).故答案为(3,−1).点睛：本题主要考查了全等三角形的判定与性质，解题关键在于结合坐标、图形性质和已经条件.15．如图，直角三角形ABC与直角三角形BDE中，点B,C,D在同一条直线上，已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F，连DF,EF,分别交AB、BC于M、N，已知点F到△ABC三边距离为3，则△BMN的周长为____________.【答案】6【解析】【分析】由角平分线和三角形的内角和定理可得∠AFC=135°，由△AFC≌△DFC可得∠DFC=∠AFC=135°，可得∠AFD=90°．同理可得∠CFE=90°，可求得∠MFN=45°，过点F作FP⊥AB于点P，FQ⊥BC于点Q，由正方形的半角模型可得MN=MP+NQ，由此即可得出答案．【详解】解：过点F作FP⊥AB于点P，FQ⊥BC于点Q，过点F作FG⊥FM，交BC于点G．∵点F是∠BAC和∠BCA的角平分线交点，∴FP=FQ=3，∵∠ABC=90°，∴四边形BPFQ是正方形，∴BP=BQ=3．在Rt△ABC中，∠BAC+∠BCA=90°，∵AF、CF是角平分线，∴∠FAC+∠FCA=45°，∴∠AFC=180°-45°=135°．易证△AFC≌△DFC（SAS），∴∠AFC=∠DFC=135°，∴∠ADF=90°，同理可得∠EFC=90°，∴∠MFN=360°-90°-90°-135°=45°．∵∠PFM+∠MFN=90°，∠MFN+∠QFG=90°，∴∠PMF=∠QFG，∵∠FPM=∠FQG=90°，FP=FQ，∴△FPM≌△FQG（ASA），∴PM=QG，FM=FG．在△FMN和△FGN中45FM FGMFN GFNFN FN=⎧⎪∠=∠=⎨⎪=⎩∴△FMN≌△FGN（SAS），∴MN=NG，∴MN=NG=NQ+QG=PM+QN，∴△BMN的周长为：BM+BN+MN= BM+BN+ PM+QN=BP+BQ=3+3=6．故答案为：6．【点睛】本题是一道全等三角形的综合题，主要考查了全等三角形的判定和性质的应用，角平分线的性质，以及全等三角形常用辅助线的作法，作出辅助线，准确的找出全等三角形是解决此题的关键．16．如图，Rt△ABC中，∠C=90°．E为AB中点，D为AC上一点，BF∥AC交DE的延长线于点F．AC=6，BC=5．则四边形FBCD周长的最小值是______．【答案】16【解析】四边形FBCD周长=BC+AC+DF；当DF BC⊥时，四边形FBCD周长最小为5+6+5=1617．如图，在△A BD中，∠BAD＝80°，C为BD延长线上一点，∠BAC＝130°，△ABD的角平分线BE与AC交于点E，连接DE，则∠DEB＝_____．【答案】40°【解析】【分析】做辅助线，构建角平分线的距离，根据角平分线的性质和逆定理可得：EF=EG=EH，设∠DEG=y，∠GEB=x，根据三角形内角和定理可得：∠GEA=∠FEA=40°，∠FEB=∠HEB，列方程为2y+x=80-x,y+x=40,可得结论：∠DEB＝40°.【详解】如图，过E作EF⊥AB于F，EG⊥AD于G，EH⊥BC于H，∵BE平分∠ABD∴EH=EF∵∠BAC＝130°，∠BAD＝80°∴∠FAE=∠CAD=50°∴EF=EG∴EG=EH∴ED平分∠CDG∴∠HED=∠DEG设∠DEG=y，∠GEB=x，∵∠EFA=∠EGA=90°∴∠GEA=∠FEA=40°∵∠EFB=∠EHB=90°，∠EBH=∠EBF∴∠FEB=∠HEB∴2y+x=80-x,2y+2x=80y+x=40即∠DEB＝40°.故答案为：40°.【点睛】本题考查三角形内角和定理和角平分线的性质，正确作辅助线是解题的关键.18．如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，P、Q是边AC、BC上的两个动点，PD⊥AB于点D， QE⊥AB于点E．设点P、Q运动的时间是t秒（t＞0）．若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回到点C停止运动；点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动，到达点C后停止运动，当t= 时，△APD和△QBE全等．【答案】2或4．【解析】试题分析：①0≤t＜83时，点P从C到A运动，则AP=AC=CP=8﹣3t，BQ=t，当△ADP≌△QBE时，则AP=BQ，即8﹣3t=t，解得：t=2；②t≥83时，点P从A到C运动，则AP=3t﹣8，BQ=t，当△ADP≌△QBE时，则AP=BQ，即3t﹣8=t，解得：t=4；综上所述：当t=2s或4s时，△ADP≌△QBE．考点：1．全等三角形的判定；2．动点型；3．分类讨论．四、八年级数学全等三角形选择题（难）19．如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下五个结论：①△PFA≌△PEB，②EF=AP，③△PEF是等腰直角三角形，④当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），S四边形AEPF=12S△ABC，上述结论中始终正确有（）A．1个B．2个C．3个D．4个【答案】C【解析】∵AB=AC，∠BAC=90°，P是BC中点，∴AP⊥BC，AP=PB，∠B=∠CAP=45°，∵∠APF+∠FPA=90°，∠ APF+∠BPE=90°，∴∠APF=∠BPE，在△BPE和△APF中，∠B=∠CAP， BP=AP，∠BPE =∠APF，∴△PFA≌△PEB；故①正确；∵△ABC是等腰直角三角形点P是BC的中点，∴AP=12 BC，又∵EF不一定是△ABC的中位线，∴EF≠AP，故结论②错误；∵△PFA≌△PEB，∴PE=PF，又∵∠EPF=90°，∴△PEF是等腰直角三角形，故③正确；∵△PFA≌△PEB，∴S△PFA =S△PEB，∴S四边形AEPF=S△APE+S△APF=S△APE+S△BPE=S△APB=12S△ABC，故结论④正确；综上，当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），始终正确的有3个结论.故选：C.点睛：本题意旋转为背景考查了全等三角形的判定和性质，解题时需要运用等腰直角三角形的判定和性质，综合性较强，根据题意得出△PFA≌△PEB是解答此题的关键.20．下列命题中的假命题是（）A．等边三角形的一个内角的平分线把这个等边三角形分成的两个三角形全等B．等腰三角形底边上的中线把这个等腰三角形分成的两个三角形全等C．等腰直角三角形底边上的高把这个等腰直角三角形分成的两个三角形全等D．直角三角形斜边上的中线把这个直角三角形分成的两个三角形全等【答案】D【解析】【分析】根据等边三角形、等腰三角形、直角三角形的性质和全等三角形的判定进行判定即可.【详解】解：A、等边三角形的一个内角的平分线把这个等边三角形分成的两个三角形全等，正确，是真命题；B、等腰三角形底边上的中线把这个等腰三角形分成的两个三角形全等，正确，是真命题；C、等腰直角三角形底边上的高把这个等腰直角三角形分成的两个三角形全等，正确，是真命题；D、直角三角形斜边上的中线把这个直角三角形分成的两个三角形全等，错误，是假命题，故答案为D．【点睛】本题考查了等边三角形、等腰三角形、直角三角形的性质和全等三角形的判定，其中灵活应用所学知识是解答本题的关键.21．如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作等边三角形ABC 和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD＝BE；②AP＝BQ；③PQ∥AE；④DE＝DP；⑤∠AOE＝120°；其中正确结论的个数为（）A．2个B．3个C．4个D．5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形，可知AC=BC，CD=CE，∠ACB=∠DCE=60°，从而证出△ACD≌△BCE，可推知AD=BE，故①正确；②由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△ACP≌△BCQ （ASA），所以AP=BQ；故②正确；③根据②△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知③正确；④根据∠QCP=60°，∠DPC=∠BCA+∠PAC＞60°，可知PD≠CD，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，由平角的性质可得∠AOE=120°，可知⑤正确；【详解】①∵△ABC和△CDE为等边三角形∴AC＝BC，CD＝CE，∠BCA＝∠DCB＝60°∴∠ACD＝∠BCE∴△ACD≌△BCE（SAS）∴AD＝BE，故①正确；由（1）中的全等得∠CBE＝∠DAC，且BC＝AC，∠ACB＝∠BCQ＝60°∴△CQB≌△CPA（ASA），∴AP＝BQ，故②正确；∵△CQB≌△CPA，∴PC＝PQ，且∠PCQ＝60°∴△PCQ为等边三角形，∴∠PQC＝∠DCE＝60°，∴PQ∥AE，故③正确，∵∠QCP＝60°，∠DPC＝∠BCA+∠PAC＞60°，∴PD≠CD，∴DE≠DP，故④DE＝DP错误；∵BC∥DE，∴∠CBE＝∠BED，∵∠CBE＝∠DAE，∴∠AOB＝∠OAE+∠AEO＝60°，∴∠AOE＝120°，故⑤正确，故选C．【点睛】本题考查了全等三角形的判定与性质，利用了等边三角形的判定与性质，全等三角形的判定与性质，平行线的判定与性质，综合性较强，题目难度较大．22．如图，等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上的一点，当PA=CQ时，连接PQ交AC于点D，下列结论中不一定正确的是（）A．PD=DQ B．DE=12AC C．AE=12CQ D．PQ⊥AB【答案】D【解析】过P作PF∥CQ交AC于F，∴∠FPD=∠Q，∵△ABC是等边三角形，∴∠A=∠ACB=60°，∴∠A=∠AFP=60°，∴AP=PF，∵PA=CQ，∴PF=CQ，在△PFD与△DCQ 中，FPD QPDE CDQPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PFD≌△QCD，∴PD=DQ，DF=CD，∴A选项正确，∵AE=EF，∴DE=12AC，∴B选项正确，∵PE⊥AC，∠A=60°，∴AE=12AP=12CQ，∴C选项正确，故选D．23．已知OD平分∠MON，点A、B、C分别在OM、OD、ON上(点A、B、C都不与点O重合)，且AB=BC, 则∠OAB与∠BCO的数量关系为（）A．∠OAB+∠BCO=180°B．∠OAB=∠BCOC．∠OAB+∠BCO=180°或∠OAB=∠BCO D．无法确定【答案】C【解析】根据题意画图，可知当C处在C1的位置时，两三角形全等，可知∠OAB=∠BCO；当点C处在C2的位置时，根据等腰三角形的性质和三角形的外角的性质，∠OAB+∠BCO=180°.故选C.24．如图所示，在Rt ABC∆中，E为斜边AB的中点，ED AB⊥，且:1:7CAD BAD∠∠=，则BAC∠=( )A．70B．45C．60D．48【答案】D【解析】根据线段的垂直平分线，可知∠B=∠BAD，然后根据直角三角形的两锐角互余，可得∠BAC+∠B=90°，设∠CAD=x，则∠BAD=7x，则x+7x+7x=90°，解得x=6°，因此可知∠BAC=∠CDA+∠BAD=6°+42°=48°.故选：D.点睛：此题主要考查了线段垂直平分线的性质，利用线段垂直平分线的性质和直角三角形的性质求角的关系，根据比例关系设出未知数，然后根据角的关系列方程求解是解题关键.五、八年级数学轴对称三角形填空题（难）25．如图，点P是AOB∠内任意一点，OP=5 cm，点M和点N分别是射线OA和射线OB上的动点，PN PM MN++的最小值是5 cm，则AOB∠的度数是__________．【答案】30°【解析】试题解析：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示：∵点P关于OA的对称点为D，关于OB的对称点为C，∴PM=DM，OP=OD，∠DOA=∠POA；∵点P关于OB的对称点为C，∴PN=CN，OP=OC，∠COB=∠POB，∴OC=OP=OD，∠AOB=12∠COD，∵PN+PM+MN的最小值是5cm，∴PM+PN+MN=5，∴DM+CN+MN=5，即CD=5=OP，∴OC=OD=CD，即△OCD是等边三角形，∴∠COD=60°，∴∠AOB=30°．26．如图，在ABC中，AB AC>，按以下步骤作图：分别以点B和点C为圆心，大于BC 一半长为半径作画弧，两弧相交于点M 和点N ，过点M N 、作直线交AB 于点D ，连接CD ，若10AB =，6AC =，则ADC 的周长为_____________________．【答案】16【解析】【分析】利用基本作图可以判定MN 垂直平分BC ，则DC=DB ，然后利用等线段代换得到ACD ∆的周长=AB+AC ，再把10AB =，6AC =代入计算即可．【详解】解：由作法得MN 垂直平分BC ，则DC=DB ，10616ACD C CD AC AD DB AD AC AB AC ∆=++=++=+=+=故答案为：16．【点睛】本题考查了基本作图和线段垂直平分线的性质，熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）是本题的关键．27．如图，∠MON ＝30°，点A 1、A 2、A 3…在射线ON 上，点B 1、B 2，B 3…在射线OM 上，△A 1B 1A 2，△A 2B 2A 3，△A 3B 3A 4…均为等边三角形，从左起第1个等边三角形的边长记a 1，第2个等边三角形的边长记为a 2，以此类推，若OA 1＝3，则a 2=_______，a 2019=_______.【答案】6； 3×22018.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A 1B 1∥A 2B 2∥A 3B 3，以及a 2=2a 1=6，得出a 3=4a 1，a 4=8a 1，a 5=16a 1…进而得出答案．【详解】解：如图，∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°，∵∠MON=30°，∴∠1=180°-120°-30°=30°，又∵∠3=60°，∴∠5=180°-60°-30°=90°，∵∠MON=∠1=30°，∴OA1=A1B1=3，∴A2B1=3，∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°，∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴a2=2a1=6，a3=4a1，a4=8a1，a5=16a1，以此类推：a2019=22018a1=3×22018故答案是：6；3×22018．【点睛】此题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出a2=2a1=6，a3=4a1，a4=8a1，a5=16a1…进而发现规律是解题关键．28．如图,A,B,C三点在同一直线上,分别以AB,BC（AB>BC）为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论：①AE=DC，②MN//AB，③BD⊥AE，④∠DPM=60°，⑤ΔBMN是等边三角形.其中正确的是__________（把所有正确的序号都填上）.【答案】①②④⑤【解析】【分析】①由三角形ABD与三角形BCE都为等边三角形，利用等边三角形的性质得到两条边对应相等，两个角相等都为60°，利用SAS即可得到三角形ABE与三角形DBC全等即可得结论；②由①中三角形ABE与三角形DBC全等，利用全等三角形的对应角相等得到一对角相等，再由∠ABD=∠EBC=60°，利用平角的定义得到∠MBE=∠NBC=60°，再由EB=CB，利用ASA 可得出三角形EMB与三角形CNB全等，利用全等三角形的对应边相等得到MB=NB，再由∠MBE=60°，利用有一个角为60°的等腰三角形为等边三角形可得出三角形BMN为等边三角形；可得∠BMN=60°，进行可得∠BMN=∠ABD，故MN//AB，从而可判断②，⑤正确；③无法证明PM=PN，因此不能得到BD⊥AE；④由①得∠EAB=∠CDB，根据三角形内角和和外角的性质可证得结论.【详解】①∵等边△ABD和等边△BCE，∴AB=DB，BE=BC，∠ABD=∠EBC=60°，∴∠ABE=∠DBC=120°，在△ABE和△DBC中，∵AB DBABE DBC BE BC⎪∠⎪⎩∠⎧⎨＝＝＝，∴△ABE≌△DBC（SAS），∴AE=DC，故①正确；∵△ABE≌△DBC，∴∠AEB=∠DCB，又∠ABD=∠EBC=60°，∴∠MBE=180°-60°-60°=60°，即∠MBE=∠NBC=60°，在△MBE和△NBC中，∵AEB DCB EB CBMBE NBC ∠∠∠⎧⎪⎪⎩∠⎨＝＝＝，∴△MBE≌△NBC（ASA），∴BM=BN，∠MBE=60°，则△BMN为等边三角形，故⑤正确；∵△BMN为等边三角形，∴∠BMN=60°,∵∠ABD=60°,∴∠BMN=∠ABD，∴MN//AB，故②正确；③无法证明PM=PN，因此不能得到BD⊥AE；④由①得∠EAB=∠CDB，∠APC+∠PAC+∠PCA=180°，∴∠PAC+∠PCA=∠PDB+∠PCB=∠DBA=60°，∵∠DPM =∠PAC+∠PCA∴∠DPM =60°，故④正确，故答案为：①②④⑤.【点睛】此题考查了等边三角形的判定与性质，以及全等三角形的判定与性质，熟练掌握判定与性质是解本题的关键．29．如图，在△ABC中，AB＝AC，点D、E在BC的延长线上，G是AC上一点，且CG＝CD，F是GD上一点，且DF＝DE．若∠A＝100°，则∠E的大小为_____度．【答案】10【解析】【分析】由DF=DE，CG=CD可得∠E=∠DFE，∠CDG=∠CGD，再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E，∠ACB=∠CDG+∠CGD=2∠CD G，进而可得∠ACB=4∠E，最后代入数据即可解答.【详解】解：∵DF＝DE，CG＝CD，∴∠E＝∠DFE，∠CDG＝∠CGD，∵GDC＝∠E+∠DFE，∠ACB＝∠CDG+∠CGD，∴GDC＝2∠E，∠ACB＝2∠CDG，∴∠ACB＝4∠E，∵△ABC中，AB＝AC，∠A＝100°，∴∠ACB＝40°，∴∠E＝40°÷4＝10°．故答案为10．【点睛】本题考查等腰三角形的性质以及三角形外角的定义，解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.30．如图，△ABC中，AC＝DC＝3，BD垂直∠BAC的角平分线于D，E为AC的中点，则图中两个阴影部分面积之差的最大值为________．【答案】9 2【解析】【分析】首先证明两个阴影部分面积之差＝S△ADC，当CD⊥AC时，△ACD的面积最大．【详解】延长BD交AC于点H．设AD交BE于点O．∵AD⊥BH，∴∠ADB＝∠ADH＝90°，∴∠ABD＋∠BAD＝90°，∠H＋∠HAD＝90°，∵∠BAD＝∠HAD，∴∠ABD＝∠H，∴AB＝AH，∵AD⊥BH，∴BD＝DH，∵DC＝CA，∴∠CDA ＝∠CAD ，∵∠CAD ＋∠H ＝90°，∠CDA ＋∠CDH ＝90°，∴∠CDH ＝∠H ，∴CD ＝CH ＝AC ，∵AE ＝EC ，∴S △ABE ＝14S △ABH ，S △CDH ＝14S △ABH ， ∵S △OBD −S △AOE ＝S △ADB −S △ABE ＝S △ADH −S △CDH ＝S △ACD ，∵AC ＝CD ＝3，∴当DC ⊥AC 时，△ACD 的面积最大，最大面积为12×3×3＝92．故填：92．【点睛】本题考查等腰三角形的判定和性质，三角形中线的性质等知识，解题的关键是学会用转化的思想思考问题．六、八年级数学轴对称三角形选择题（难）31．在Rt ABC ∆中，90ACB ∠=︒，以ABC ∆的一边为边画等腰三角形，使得它的第三个顶点在ABC ∆的其他边上，则可以画出的不同的等腰三角形的个数最多可画几个？（）A ．9个B ．7个C ．6个D ．5个【答案】B【解析】【分析】先以Rt ABC ∆三个顶点分别为圆心，再以每个顶点所在的较短边为半径画弧，即可确定等腰三角形的第三个顶点；也可以作三边的垂直平分线确定等腰三角形的第三个顶点即得．【详解】解：①如图1，以B 为圆心，BC 长为半径画弧，交AB 于点D ，则∆BCD 就是等腰三角形；②如图2，以A 为圆心，AC 长为半径画弧，交AB 于点E ，则∆ACE 就是等腰三角形； ③如图3，以C 为圆心，BC 长为半径画弧，交AB 于M ，交AC 于点F ，则∆BCM 、∆BCF 是等腰三角形；④如图4，作AC 的垂直平分线交AB 于点H ，则∆ACH 就是等腰三角形；⑤如图5，作AB 的垂直平分线交AC 于点G ，则∆AGB 就是等腰三角形；⑥如图6，作BC 的垂直平分线交AB 于I ，则∆BCI 就是等腰三角形．故选：B ．【点睛】本题考查等腰三角形的判定的应用，通过作垂直平分线或者画弧的方法确定相等的边是解题关键．32．如图，已知：30MON ∠=︒，点1A 、2A 、3A …在射线ON 上，点1B 、2B 、3B …在射线OM 上，112A B A △、223A B A △、334A B A △…均为等边三角形，若112OA =，则667A B A 的边长为( )A ．6B ．12C ．16D ．32【答案】C【解析】【分析】先根据等边三角形的各边相等且各角为60°得：∠B 1A 1A 2=60°，A 1B 1=A 1A 2，再利用外角定理求∠OB 1A 1=30°，则∠MON=∠OB 1A 1，由等角对等边得：B 1A 1=OA 1=12，得出△A 1B 1A 2的边长为12，再依次同理得出：△A 2B 2A 3的边长为1，△A 3B 3A 4的边长为2，△A 4B 4A 5的边长为：22=4，△A 5B 5A 6的边长为：23=8，则△A 6B 6A 7的边长为：24=16．【详解】解：∵△A 1B 1A 2为等边三角形，∴∠B 1A 1A 2=60°，A 1B 1=A 1A 2，∵∠MON=30°，∴∠OB 1A 1=60°-30°=30°，∴∠MON=∠OB 1A 1，∴B 1A 1=OA 1=12， ∴△A 1B 1A 2的边长为12，同理得：∠OB 2A 2=30°， ∴OA 2=A 2B 2=OA 1+A 1A 2=12+12=1， ∴△A 2B 2A 3的边长为1，同理可得：△A 3B 3A 4的边长为2，△A 4B 4A 5的边长为：22=4，△A 5B 5A 6的边长为：23=8，则△A 6B 6A 7的边长为：24=16．故选：C ．【点睛】本题考查等边三角形的性质和外角定理，运用类比的思想，依次求出各等边三角形的边长，解题关键是总结规律，得出结论．33．如图，AOB α∠=，点P 是AOB ∠内的一定点，点,M N 分别在OA OB 、上移动，当PMN ∆的周长最小时，MPN ∠的值为（）A ．90α+B ．1902α+C ．180α-D ．1802α-【答案】D【解析】【分析】过P 点作角的两边的对称点，在连接两个对称点，此时线段与角两边的交点，构成的三角形周长最小.再根据角的关系求解.【详解】解：过P 点作OB 的对称点1P ，过P 作OA 的对称点2P ,连接12PP ，交点为M,N ，则此时PMN 的周长最小，且△1P NP 和△2PMP 为等腰三角形.此时∠12P PP =180°-α；设∠NPM=x°，则180°-x°=2（∠12P PP -x°）所以 x°=180°-2α 【点睛】求出M,N 在什么位子△PMN 周长最小是解此题的关键.34．在一个33 的正方形网格中，A ，B 是如图所示的两个格点，如果C 也是格点，且ABC 是等腰三角形，则符合条件的C 点的个数是（）A ．6B ．7C ．8D ．9【答案】C【解析】【分析】根据题意、结合图形，画出图形即可确定答案.【详解】解：根据题意，画出图形如图：共8个.故答案为C.【点睛】本题主要考查了等腰三角形的判定，根据题意、画出符合实际条件的图形是解答本题的关键.35．如图，已知AD为ABC∆的高线，AD BC=，以AB为底边作等腰Rt ABE∆，连接ED，EC，延长CE交AD于F点，下列结论：①DAE CBE∠=∠；②CE DE⊥；③BD AF=；④AED∆为等腰三角形；⑤BDE ACES S∆∆=，其中正确的有( )A．①③B．①②④C．①③④D．①②③⑤【答案】D【解析】【分析】①根据等腰直角三角形的性质即可证明∠CBE＝∠DAE，再得到△ADE≌△BCE；②根据①结论可得∠AEC＝∠DEB，即可求得∠AED＝∠BEG，即可解题；③证明△AEF≌△BED即可；④根据△AEF≌△BED得到DE=EF, 又DE⊥CF，故可判断；⑤易证△FDC是等腰直角三角形，则CE＝EF，S△AEF＝S△ACE，由△AEF≌△BED，可知S△BDE ＝S△ACE，所以S△BDE＝S△ACE．【详解】①∵AD为△ABC的高线，∴CBE＋∠ABE＋∠BAD＝90°，∵Rt△ABE是等腰直角三角形，∴∠ABE＝∠BAE＝∠BAD＋∠DAE＝45°，AE＝BE，∴∠CBE＋∠BAD＝45°，∴∠DAE＝∠CBE，故①正确；在△DAE和△CBE中，AE BEDAE CBEAD BC⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADE≌△BCE（SAS）；②∵△ADE≌△BCE，∴∠EDA＝∠ECB，∵∠ADE＋∠EDC＝90°，∴∠EDC＋∠ECB＝90°，∴∠DEC＝90°，∴CE⊥DE；故②正确；③∵∠BDE＝∠ADB＋∠ADE，∠AFE＝∠ADC＋∠ECD，∴∠BDE＝∠AFE，∵∠BED＋∠BEF＝∠AEF＋∠BEF＝90°，∴∠BED＝∠AEF，在△AEF和△BED中，BDE AFEBED AEFAE BE∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△AEF≌△BED（AAS），∴BD＝AF故③正确；∵△AEF≌△BED∴DE=EF, 又DE⊥CF，∴△DEF为等腰直角三角形，故④错误；④∵AD＝BC，BD＝AF，∴CD＝DF，∵AD⊥BC，∴△FDC是等腰直角三角形，∵DE⊥CE，∴EF＝CE，∴S△AEF＝S△ACE，∵△AEF≌△BED，∴S△AEF＝S△BED，∴S△BDE＝S△ACE．故④正确；故选：D．【点睛】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△BFE≌△CDE是解题的关键．36．如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，D为AB的中点，E为线段AD上一点，过E点的线段FG交CD的延长线于G点，交AC于F点，且EG＝AE，分别延长CE，。

八年级数学全册全套试卷中考真题汇编[解析版]

八年级数学全册全套试卷中考真题汇编[解析版]一、八年级数学三角形填空题（难）1．如图，已知四边形ABCD中，对角线BD平分∠ABC，∠BAC=64°，∠BCD+∠DCA=180°，那么∠BDC为_________度.【答案】32【解析】【分析】过C点作∠ACE=∠CBD，根据三角形内角和为180°，以及等量关系可得∠ECD=∠BDC，根据角平分线的定义可得∠ABD=∠CBD，再根据三角形内角和为180°，以及等量关系可得∠BDC的度数．【详解】过C点作∠ACE=∠CBD，∵∠BCD+∠DCA=180°，∠BCD+∠CBD+∠BDC=180°，∴∠ECD=∠BDC，∵对角线BD平分∠ABC，∴∠ABD=∠CBD，∴∠ABD=∠ACE，∴∠BAC=∠CEB=64°，∴∠BDC=12∠CEB=32°．故答案为：32．【点睛】此题考查了三角形内角与外角，三角形内角和为180°，三角形的一个外角等于和它不相邻的两个外角的和．2．等腰三角形的三边长分别为：x+1，2x+3，9，则x=________.【答案】3【解析】①当x+1=2x+3时，解得x=−2(不合题意,舍去)；②当x+1=9时，解得x=8，则等腰三角形的三边为:9、19、9，因为9+9=18<19，不能构成三角形，故舍去；③当2x+3=9时，解得x=3，则等腰三角形的三边为:4、9、9，能构成三角形。

所以x的值是3.故填3.3．若（a﹣4）2+|b﹣9|=0，则以a、b为边长的等腰三角形的周长为_______．【答案】22【解析】【分析】先根据非负数的性质列式求出a、b再根据等腰三角形和三角形三边关系分情况讨论求解即可．【详解】解：根据题意得，a-4=0，b-9=0，解得a=4，b=9，①若a=4是腰长，则底边为9，三角形的三边分别为4、4、9，不能组成三角形，②若b=9是腰长，则底边为4，三角形的三边分别为9、9、4，能组成三角形，周长=9+9+4=22．【点睛】本题主要考查了等腰三角形的性质，非负数的性质，以及三角形的三边关系，解决本题的关键是要熟练掌握非负数的非负性质和三角形三边关系.4．如图，△ABC中，∠A = 40°，∠B = 72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF =_________度.【答案】74°【解析】【分析】【详解】试题分析：首先根据三角形的内角和定理求得∠ACB的度数，以及∠BCD的度数，根据角平分线的定义求得∠BCE的度数，则∠ECD可以求解，然后在△CDF中，利用内角和定理即可求得∠CDF的度数．∵∠A=40°，∠B=70°，∴∠ACB=180°﹣∠A﹣∠B=70°．∵CE平分∠ACB，∠ACB=35°．∵CD⊥AB于D，∴∠CDA=90°，∠ACD=180°﹣∠A﹣∴∠ACE=12∠CDA=50°．∴∠ECD=∠ACD﹣∠ACE=15°．∵DF⊥CE，∴∠CFD=90°，∴∠CDF=180°﹣∠CFD﹣∠DCF=75°．考点：三角形内角和定理．5．如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠A=100°，则∠1+∠2+∠3+∠4= ．【答案】280°【解析】试题分析：先根据邻补角的定义得出与∠EAB相邻的外角∠5的度数，再根据多边形的外角和定理即可求解．解：如图，∵∠EAB+∠5=180°，∠EAB=100°，∴∠5=80°．∵∠1+∠2+∠3+∠4+∠5=360°，∴∠1+∠2+∠3+∠4=360﹣80°=280°故答案为280°．考点：多边形内角与外角．∠__________．6．如图，五边形ABCDE的每一个内角都相等，则外角CBF=【答案】72︒【解析】【分析】多边形的外角和等于360度，依此列出算式计算即可求解．【详解】360°÷5=72°．故外角∠CBF等于72°．故答案为：72 ．【点睛】此题考查了多边形内角与外角，关键是熟悉多边形的外角和等于360度的知识点．二、八年级数学三角形选择题（难）7．在多边形内角和公式的探究过程中，主要运用的数学思想是（）A．化归思想B．分类讨论C．方程思想D．数形结合思想【答案】A【解析】【分析】根据多边形内角和定理：（n-2）·180（n≥3）且n为整数）的推导过程即可解答．【详解】解：多边形内角和定理：（n-2）·180（n≥3）且n为整数），该公式推导的基本方法是从n 边形的一个顶点出发引出（n-3）条对角线，将n边形分割为（n-2）个三角形，这（n-2）个三角形的所有内角之和正好是n边形的内角和，体现了化归思想．故答案为A．【点睛】本题主要考查了在数学的学习过程应用的数学思想，弄清推导过程是解答此题的关键.8．如图，已知AE是ΔABC的角平分线，AD是BC边上的高．若∠ABC=34°，∠ACB=64°，则∠DAE的大小是（）A．5°B．13°C．15°D．20°【答案】C【解析】【分析】由三角形的内角和定理，可求∠BAC=82°，又由AE是∠BAC的平分线，可求∠BAE=41°，再由AD是BC边上的高，可知∠ADB=90°，可求∠BAD=56°，所以∠DAE=∠BAD-∠BAE，问题得解．【详解】在△ABC中，∵∠ABC=34°，∠ACB=64°,∴∠BAC=180°−∠B−∠C=82°，∵AE 是∠BAC 的平分线，∴∠BAE=∠CAE=41°.又∵AD 是BC 边上的高，∴∠ADB=90°，∵在△ABD 中∠BAD=90°−∠B=56°，∴∠DAE=∠BAD −∠BAE =15°. 【点睛】在本题中，我们需要注意到已知条件中已经告诉三角形的两个角，所以利用内角和定理可以求出第三个角，再有已知条件中提到角平分线和高线，所以我们可以利用角平分线和高线的性质计算出相关角，从而利用角的和差求解，在做几何证明题时需注意已知条件衍生的结论.9．如图,△ABC 中,E 是 AC 的中点,延长 BC 至 D ,使 BC ：CD =3:2,以 CE ,CD 为邻边做▱CDFE ，连接 AF,BE,BF ，若△ABC 的面积为 9，则阴影部分面积是（）A ．6B ．4C ．3D ．2【答案】A【解析】【分析】根据三角形中位线性质结合三角形面积去解答.【详解】解：在ABC 中，E 是 AC 的中点,S ABC 9=, BC ：CD =3:2▱CDFE 中，CD=EF1S BCE 4.52S ABC ∴== 设BCE 的高为1h , ABC 的高为2.h11S BCE 4.52BC h ∴=⨯⨯= 13h =12:1:2h h =26h ∴=S AEF S EFB s ∴=+阴()2111122EF h h EF h =⨯⨯-+⨯⨯ 212EF h =⨯⨯1262=⨯⨯6.=【点睛】此题重点考察学生对三角形中位线和面积的理解，熟练掌握三角形面积计算方法是解题的关键.10．已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为( )A．B．C．D．不能确定【答案】B【解析】如图，∵等边三角形的边长为3，∴高线AH=3×333 =S△ABC=1111••••2222BC AH AB PD BC PE AC PF ==+∴1111 3?3?3?3? 2222AH PD PE PF ⨯=⨯+⨯+⨯∴PD+PE+PF=AH=33 2即点P到三角形三边距离之和为33 2.故选B.11．一个多边形的内角和是1260°，这个多边形的边数是（）A．6 B．7 C．8 D．9【答案】D【解析】试题解析：设这个多边形的边数为n，由题意可得：（n-2）×180°=1260°，解得n=9，∴这个多边形的边数为9，故选D．12．如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（）A．110︒B．115︒C．120︒D．125︒【答案】A【解析】【分析】根据三角形外角的性质三角形的一个外角等于和它不相邻的两个内角的和可得∠AEB=∠A+∠C=65°，∠DFE=∠B+∠AEC，进而可得答案．【详解】解：∵∠A=27°，∠C=38°，∴∠AEB=∠A+∠C=65°，∵∠B=45°，∴∠DFE=65°+45°=110°，故选：A．【点睛】此题主要考查了三角形外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．三、八年级数学全等三角形填空题（难）13．如图，平面直角坐标系中，A（0，3），B（4，0），BC∥y轴，且BC＜OA，第一象限内有一点P（a，2a-3），若使△ACP是以AC斜边的等腰直角三角形，则点P的坐标为_______________．33【解析】【详解】解：∵点P的坐标为（a，2a-3），∴点P在直线y=2x-3上，如图所示，当点P在AC的上方时，过P作y轴的垂线，垂足为D，交BC的延长线于E，则∠E=∠ADP=90°，∵△ACP是以AC为斜边的等腰直角三角形，∴AP=PC，∠APD=∠PCE，∴△APD≌△PCE，∴PE=AD，又∵OD=2a-3，AO=3，∴AD=2a-6=PE，∵DE=OB=4，DP=a，又∵DP+PE=DE，∴a+（2a-6）=4，解得a=10 3∴2a-3=11 3，∴P（103，113）；当点P在AC下方时，过P作y轴的垂线，垂足为D，交BC于E，a=2，此时，CE=2，BE=2，即BC=2+2=4＞AO，不合题意；综上所述，点P的坐标为P（103，113）3314．如图，在△ABC中，AC=AB，∠BAC=90°，D是AC边上一点，连接BD，AF⊥BD于点F，点E在BF上，连接AE，∠EAF=45°，连接CE，AK⊥CE于点K，交DE于点H，∠DEC=30°，HF=32，则EC=______【答案】6【解析】【分析】延长AF交CE于P，证得△ABH≌△APC得出AH=CP，证得△AHF≌△EPF得出AH=EP，得出EC=2AH，解30°的直角三角形AFH求得AH，即可求得EC的长．【详解】如图，延长AF交CE于P，∵∠ABH+∠ADB=90°，∠PAC+∠ADB=90°，∴∠ABH=∠PAC，∵AK⊥CE，AF⊥BD，∠EHK=∠AHF，∴∠HEK=∠FAH，∵∠FAH+∠AHF=90°，∠HEK+∠EPF=90°，∴∠AHF=∠EPF，∴∠AHB=∠APC，在△ABH与△APC中，ABE PACAB ACAHB APC∠∠⎧⎪⎨⎪∠∠⎩＝＝＝，∴△ABH≌△APC（ASA），∴AH=CP，在△AHF与△EPF中，90AHF EPFAFH EFPAF EF∠∠⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△AHF≌△EPF（AAS），∴AH=EP，∠CED=∠HAF，∴EC=2AH，∵∠DEC=30°，∴∠HAF=30°，∴AH=2FH=2×32=3，∴EC=2AH=6．【点睛】本题考查了三角形全等的判定和性质，等腰直角三角形的判定和性质，作出辅助线根据全等三角形是解题的关键．15．如图，点E是等边△ABC内一点，且EA＝EB，△ABC外一点D满足BD＝AC，且BE平分∠DBC，则∠D＝__________.【答案】30°【解析】试题解析：（1）连接CE，∵△ABC是等边三角形，∴AC=BC，在△BCE与△ACE中，{AC BCAE BECE CE＝＝＝∴△BCE≌△ACE（SSS）∴∠BCE=∠ACE=30°∵BE平分∠DBC，∴∠DBE=∠CBE，在△BDE与△BCE中，{BD BCDBE CBEBE BE∠∠＝＝＝∴△BDE≌△BCE（SAS），∴∠BDE=∠BCE=30°．16．如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，P、Q是边AC、BC上的两个动点，PD⊥AB于点D， QE⊥AB于点E．设点P、Q运动的时间是t秒（t＞0）．若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回到点C停止运动；点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动，到达点C后停止运动，当t= 时，△APD和△QBE全等．【答案】2或4．【解析】试题分析：①0≤t＜83时，点P从C到A运动，则AP=AC=CP=8﹣3t，BQ=t，当△ADP≌△QBE时，则AP=BQ，即8﹣3t=t，解得：t=2；②t≥83时，点P从A到C运动，则AP=3t﹣8，BQ=t，当△ADP≌△QBE时，则AP=BQ，即3t﹣8=t，解得：t=4；综上所述：当t=2s或4s时，△ADP≌△QBE．考点：1．全等三角形的判定；2．动点型；3．分类讨论．17．把两个三角板如图甲放置，其中90ACB DEC∠=∠=︒，45A∠=︒，30D∠=︒，斜边12AB =，14CD =，把三角板DCE 绕着点C 顺时针旋转15︒得到△11D CE （如图乙），此时AB 与1CD 交于点O ，则线段1AD 的长度为_________．【答案】10【解析】试题分析：如图所示，∠3=15°，∠1E =90°， ∴∠1=∠2=75°，又∵∠B=45°， ∴∠OF 1E =∠B+∠1=45°+75°=120° ∴∠1D FO=60° ∵∠C 11D E =30°，∴∠5=∠4=90°，又∵AC=BC ，AB=12， ∴OA=OB=6 ∵∠ACB=90°，∴CO=12AB=6，又∵C 1D =CD=14， ∴O 1D =C 1D -OC=14-6=8，在Rt △A 1D O 中，222211A 6810D OA OD =+=+=点睛：本题主要考查的就是旋转的性质、三角形的外角性质、直角三角形的性质及判定以及勾股定理的应用.解决这个问题的关键就是首先根据三角形外角的性质以及旋转图形的性质得出△AO 1D 为直角三角形，然后根据直角三角形的性质得出AO 和O 1D 的长度，最后根据直角三角形的勾股定理得出答案.18．如图：△ABC 中，∠ACB=90°，∠CAD=30°，AC=BC=AD ，CE ⊥CD ，且CE=CD ，连接BD ，DE ，BE ，则下列结论：①∠ECA=165°，②BE=BC ；③AD ⊥BE ；其中正确的是_________【答案】①②③【解析】如图，（1）∵AC=AD ，∠CAD=30°，∴∠ACD=∠ADC=18030752-=，∵CE⊥DC，∴∠DCE=90°，∴∠ACE=∠ACD+∠DCE=165°.故①正确；（2）由（1）可知：∠ACB=∠DCE=90°，∴∠ACE-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE，在△ACD和△BCE中，AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△BCE，∴BE=AD=BC.故②正确；（3）延长AD交BE于点F，∵△ACD≌△BCE，∴∠2=∠CAD=30°，∵AC=BC，∠ACB=90°，∴∠CAB=∠3=45°，∴∠1=∠CAB-∠CAD=15°，∴∠AFB=180°-∠1-∠2-∠3=90°，∴AD⊥BE.故③正确；综上所述：正确的结论是①②③.四、八年级数学全等三角形选择题（难）19．如图，ABC∆中，45ABC∠=，CD AB⊥于D，BE平分ABC∠，且BE AC⊥于E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G，下列结论正确的有( )个①BF AC=；②12AE BF=；③67.5A∠=；④DGF∆是等腰三角形；⑤ADGE GHCES S=四边形四边形.A．5个B．4个C．3个D．2个【答案】B【解析】【分析】只要证明△BDF ≌△CDA ，△BAC 是等腰三角形，∠DGF ＝∠DFG ＝67.5°，即可判断①②③④正确，作GM ⊥BD 于M ，只要证明GH ＜DG 即可判断⑤错误．【详解】∵CD ⊥AB ，BE ⊥AC ，∴∠BDC ＝∠ADC ＝∠AEB ＝90°，∴∠A ＋∠ABE ＝90°，∠ABE ＋∠DFB ＝90°，∴∠A ＝∠DFB ，∵∠ABC ＝45°，∠BDC ＝90°，∴∠DCB ＝90°−45°＝45°＝∠DBC ，∴BD ＝DC ，在△BDF 和△CDA 中BDF CDA A DFBBD CD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△BDF ≌△CDA （AAS ），∴BF ＝AC ，故①正确．∵∠ABE ＝∠EBC ＝22.5°，BE ⊥AC ，∴∠A ＝∠BCA ＝67.5°，故③正确，∴BA ＝BC ，∵BE ⊥AC ，∴AE ＝EC ＝12AC ＝12BF ，故②正确， ∵BE 平分∠ABC ，∠ABC ＝45°，∴∠ABE ＝∠CBE ＝22.5°，∵∠BDF ＝∠BHG ＝90°，∴∠BGH ＝∠BFD ＝67.5°，∴∠DGF ＝∠DFG ＝67.5°，∴DG ＝DF ，故④正确．作GM ⊥AB 于M ．∵∠GBM ＝∠GBH ，GH ⊥BC ，∴GH ＝GM ＜DG ，∴S △DGB ＞S △GHB ，∵S △ABE ＝S △BCE ，∴S 四边形ADGE ＜S 四边形GHCE ．故⑤错误，∴①②③④正确，故选：B ．【点睛】此题是三角形综合题，考查了等腰三角形的性质，直角三角形的性质，全等三角形的性质和判定，三角形的面积等知识点的综合运用，第五个问题难度比较大，添加辅助线是解题关键，属于中考选择题中的压轴题．20．如图，点B，F，C，E在同一条直线上，点A，D在直线BE的两侧，AB∥DE，BF＝CE，添加一个适当的条件后，仍不能使得△ABC≌△DEF（）A．AC＝DF B．AC∥DF C．∠A＝∠D D．AB＝DE【答案】A【解析】【分析】根据AB∥DE证得∠B＝∠E，又已知BF＝CE证得BC＝EF，即已具备两个条件：一边一角，再依次添加选项中的条件即可判断.【详解】∵AB∥DE，∴∠B＝∠E，∵BF＝CE，∴BF+FC＝CE+FC，∴BC＝EF，若添加AC＝DF，则不能判定△ABC≌△DEF，故选项A符合题意；若添加AC∥DF，则∠ACB＝∠DFE，可以判断△ABC≌△DEF（ASA），故选项B不符合题意；若添加∠A＝∠D，可以判断△ABC≌△DEF（AAS），故选项C不符合题意；若添加AB＝DE，可以判断△ABC≌△DEF（SAS），故选项D不符合题意；故选：A．【点睛】此题考查三角形全等的判定定理，熟练掌握定理，并能通过定理去判断条件是否符合全等是解决此题的关键.21．下列两个三角形中,一定全等的是( )A．两个等边三角形B．有一个角是40︒,腰相等的两个等腰三角形C．有一条边相等,有一个内角相等的两个等腰三角形D．有一个角是100︒,底相等的两个等腰三角形【答案】D【解析】【分析】根据全等三角形的判定方法及等腰三角形的性质对各个选项进行分析,从而得到答案．【详解】解：A、当两个等边三角形的对应边不相等时,这两个等边三角形也不会全等，故本选项错误；B、当该角不是对应角时,这两个等腰三角形也不会全等，故本选项错误；C、当两个等腰三角形的对应边与对应角不相等时,这两个等腰三角形也不会全等，故本选项错误；D、等腰三角形的100°角只能是顶角,则两个底角是40°,它们对应相等，所以由全等三角形的判定定理ASA或AAS证得它们全等，故本选项正确；故选D．【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角．22．如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作等边三角形ABC 和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD＝BE；②AP＝BQ；③PQ∥AE；④DE＝DP；⑤∠AOE＝120°；其中正确结论的个数为（）A．2个B．3个C．4个D．5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形，可知AC=BC，CD=CE，∠ACB=∠DCE=60°，从而证出△ACD≌△BCE，可推知AD=BE，故①正确；②由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△ACP≌△BCQ （ASA），所以AP=BQ；故②正确；③根据②△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知③正确；④根据∠QCP=60°，∠DPC=∠BCA+∠PAC＞60°，可知PD≠CD，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，由平角的性质可得∠AOE=120°，可知⑤正确；【详解】①∵△ABC和△CDE为等边三角形∴AC＝BC，CD＝CE，∠BCA＝∠DCB＝60°∴∠ACD＝∠BCE∴△ACD≌△BCE（SAS）∴AD＝BE，故①正确；由（1）中的全等得∠CBE＝∠DAC，且BC＝AC，∠ACB＝∠BCQ＝60°∴△CQB≌△CPA（ASA），∴AP＝BQ，故②正确；∵△CQB≌△CPA，∴PC＝PQ，且∠PCQ＝60°∴△PCQ为等边三角形，∴∠PQC＝∠DCE＝60°，∴PQ∥AE，故③正确，∵∠QCP＝60°，∠DPC＝∠BCA+∠PAC＞60°，∴PD≠CD，∴DE≠DP，故④DE＝DP错误；∵BC∥DE，∴∠CBE＝∠BED，∵∠CBE＝∠DAE，∴∠AOB＝∠OAE+∠AEO＝60°，故选C．【点睛】本题考查了全等三角形的判定与性质，利用了等边三角形的判定与性质，全等三角形的判定与性质，平行线的判定与性质，综合性较强，题目难度较大．23．如图，，，，点D、E为BC边上的两点，且，连接EF、BF则下列结论：≌；≌；；，其中正确的有( )个．A．1B．2C．3D．4【答案】D【解析】【分析】根据∠DAF=90°，∠DAE=45°，得出∠FAE=45°，利用SAS证明△AED≌△AEF，判定①正确；由△AED≌△AEF得AF=AD,由，得∠FAB=∠CAD，又AB=AC, 利用SAS证明≌,判定②正确；先由∠BAC=∠DAF=90°，得出∠CAD=∠BAF，再利用SAS证明△ACD≌△ABF，得出CD=BF，又①知DE=EF，那么在△BEF中根据三角形两边之和大于第三边可得BE+BF＞EF，等量代换后判定③正确；先由△ACD≌△ABF，得出∠C=∠ABF=45°，进而得出∠EBF=90°，判定④正确．【详解】‚解：①∵∠DAF=90°，∠DAE=45°，∴∠FAE=∠DAF-∠DAE=45°．在△AED与△AEF中，，∴△AED≌△AEF（SAS），①正确；②∵△AED≌△AEF,∴AF=AD,∵,∴∠FAB=∠CAD,∵AB=AC，③∵∠BAC=∠DAF=90°，∴∠BAC-∠BAD=∠DAF-∠BAD，即∠CAD=∠BAF．在△ACD与△ABF中，，∴△ACD≌△ABF（SAS），∴CD=BF，由①知△AED≌△AEF，∴DE=EF．在△BEF中，∵BE+BF＞EF，∴BE+DC＞DE，③正确；④由③知△ACD≌△ABF，∴∠C=∠ABF=45°，∵∠ABE=45°，∴∠EBF=∠ABE+∠ABF=90°．④正确．故答案为D．【点睛】本题考查了勾股定理，全等三角形的判定与性质，等腰直角直角三角形的性质，三角形三边关系定理，相似三角形的判定，此题涉及的知识面比较广，解题时要注意仔细分析，有一定难度．24．如图，点 D 是等腰直角△ABC 腰 BC 上的中点，点B 、B′ 关于 AD 对称，且BB′ 交AD 于 F，交 AC 于 E，连接 FC 、 AB′，下列说法：① ∠BAD=30°；② ∠BFC=135°；③ AF=2B′ C；正确的个数是（）A．1 B．2 C．3 D．4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点，可得tan∠BAD=12，即可得到∠BAD≠30°；连接B'D，即可得到∠BB'C=∠BB'D+∠DB'C=90°，进而得出△ABF≌△BCB'，判定△FCB'是等腰直角三角形，即可得到∠CFB'=45°，即∠BFC=135°；由△ABF≌△BCB'，可得AF=BB'=2BF=2B'C；依据△AEF与△CEB'不全等，即可得到S△AFE≠S△FCE．【详解】∵点D是等腰直角△ABC腰BC上的中点，∴BD=12BC=12AB，∴tan∠BAD=12，∴∠BAD≠30°，故①错误；如图，连接B'D，∵B、B′关于AD对称，∴AD垂直平分BB'，∴∠AFB=90°，BD=B'D=CD，∴∠DBB'=∠BB'D，∠DCB'=∠DB'C，∴∠BB'C=∠BB'D+∠DB'C=90°，∴∠AFB=∠BB'C，又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF，∴∠BAF=∠CBB'，∴△ABF≌△BCB'，∴BF=CB'=B'F，∴△FCB'是等腰直角三角形，∴∠CFB'=45°，即∠BFC=135°，故②正确；由△ABF≌△BCB'，可得AF=BB'=2BF=2B'C，故③正确；∵AF＞BF=B'C，∴△AEF与△CEB'不全等，∴AE≠CE，∴S△AFE≠S△FCE，故④错误；故选B．【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．五、八年级数学轴对称三角形填空题（难）25．如图，已知△ABC和△ADE都是正三角形，连接CE、BD、AF，BF=4,CF=7,求AF的长_________ .【答案】3【解析】【分析】过点A作AF⊥CE交于I，AG⊥BD交于J,证明CAE≅BAD，再证明CAI≅BAJ，求出°7830∠=∠=，然后求出12IF FJ AF==，，通过设FJ x=求出x，即可求出AF的长.【详解】解：过点A作AF⊥CE交于I，AG⊥BD交于J在CAE和BAD中AC ABCAE BADAE AD=⎧⎪∠=∠⎨⎪=⎩∴CAE≅BAD∴ICA ABJ∠=∠∴BFE CAB∠=∠（8字形）∴°120CFD∠=在CAI 和BAJ 中°90ICA ABJ CAI BJA CA BA ∠=∠⎧⎪∠=∠=⎨⎪=⎩∴CAI ≅BAJ ,AI AJ CI BJ ==∴°60CFA AFJ ∠=∠=∴°30FAI FAE ∠=∠=在RtAIF 和RtAJF 中°30FAI FAE ∠=∠=∴12IF FJ AF ==设FJ x = 7,4CF BF ==则47x x +=-32x ∴=2AF FJ =AF ∴=3【点睛】此题主要考查了通过做辅助线证明三角形全等，得出相关的边相等，学会合理添加辅助线求解是解决本题的重点.26．如图，在01A BA △中，20B ∠=︒，01A B A B =，在1A B 上取点C ，延长01A A 到2A ，使得121A A AC =；在2A C 上取一点D ，延长12A A 到3A ，使得232A A A D =；…，按此做法进行下去，第n 个等腰三角形的底角n A ∠的度数为__________．【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律即可得出第n 个等腰三角形的底角∠A n 的度数．【详解】解：∵在△A 0BA 1中，∠B=20°，A 0B=A 1B ， ∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°， ∵A 1A 2=A 1C ，∠BA 1 A 0是△A 1A 2C 的外角，∴∠CA 2A 1= 108022BA A ︒∠= =40°；同理可得，∠DA 3A 2=20°，∠EA 4A 3=10°，∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律是解答此题的关键．27．如图，点P 是∠AOB 内任意一点，OP ＝5，M ，N 分别是射线OA 和OB 上的动点，若△PMN 周长的最小值为5，则∠AOB 的度数为_____．【答案】30°．【解析】【分析】如图：分别作点P 关于OB 、AO 的对称点P'、P''，分别连OP'、O P''、P' P''交OB 、OA 于M 、N ，则可证明此时△PMN 周长的最小，由轴对称性，可证明△P'O P''为等边三角形，∠AOB=12∠P'O P''=30°. 【详解】解：如图：分别作点P 关于OB 、AO 的对称点P'、P''，分别连OP'、O 、P' 交OB 、OA 于M 、N ，由轴对称△PMN 周长等于PN+NM+MP=P'N+NM+MP"=P'P"∴由两点之间线段最短可知，此时△PMN 周长的最小∴P'P"=5由对称OP=OP'=OP"=5∴△P'OP"为等边三角形∴∠P'OP"=60∵∠P'OB=∠POB ，∠P"OA=∠POA∴∠AOB=12∠P'O P''=30°. 故答案为30°.【点睛】本题是动点问题的几何探究题，考查最短路径问题，应用了轴对称图形性质和等边三角形性质.28．如图，在等腰直角三角形ABC 中，90ACB ∠=︒，4AC BC ==，D 为BC 中点，E 为AC 边上一动点，连接DE ，以DE 为边并在DE 的右侧作等边DEF ∆，连接BF ，则BF 的最小值为______.【答案】3【解析】【分析】由60°联想旋转全等，转换动长为定点到定线的长，构建等边三角形BDG ，利用△BDF ≌△GDE ，转换BF=GE ，然后即可求得其最小值.【详解】以BD 为边作等边三角形BDG ，连接GE ，如图所示：∵等边三角形BDG ，等边三角形DEF∴∠BDG=∠EDF=60°，BD=GD=BG ，DE=DF=EF∴∠BDG+∠GFD=∠EDF+∠GFD ，即∠BDF=∠GDE∴△BDF ≌△GDE （SAS ）∴BF=GE当GE ⊥AC 时，GE 有最小值，如图所示GE′，作DH ⊥GE′∴BF=GE= CD+12DG=2+1=3 故答案为：3.【点睛】此题主要考查等边三角形的性质以及全等三角形的判定与性质，解题关键是由60°联想旋转全等，转换动长为定点到定线的长.29．如图，ABC ∆中，AB AC =，点D 是ABC ∆内部一点，DB DC =，点E 是边AB 上一点，若CD 平分ACE ∠，100AEC =∠，则BDC ∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD，再根据角的和差关系得到∠ECB =∠ACB－2∠ACD，然后利用外角定理得到∠ABC+∠ECB=100°，代换化简得出∠ACB－∠ACD=50°，即∠DCB=50°，从而求出∠BDC即可.【详解】∵CD平分∠ACE，∴∠ACE=2∠ACD=2∠ECD，∴∠ECB=∠ACB－∠ACE=∠ACB－2∠ACD，∵∠AEC=100°，∴∠ABC+∠ECB=100°，∴∠ABC+∠ACB－2∠ACD=100°，∵AB=AC，∴∠ABC=∠ACB,∴2∠ACB－2∠ACD=100°，∴∠ACB－∠ACD=50°，即∠DCB=50°，∵DB=DC，∴∠DBC=∠DCB，∴∠BDC=180°－2∠DCB=180°－2×50°=80°.【点睛】本题考查了角平分线，三角形内角和，外角定理，及等边对等角的性质等知识，熟练掌握基本知识，找出角与角之间的关系是解题的关键.30．如图，在△ABC中，AB=AC，AB边的垂直平分线DE交AC于点D．已知△BDC的周长为14，BC=6，则AB=___．【答案】8【解析】试题分析：根据线段垂直平分线的性质，可知AD=BD，然后根据△BDC的周长为BC+CD+BD=14，可得AC+BC=14，再由BC=6可得AC=8，即AB=8.故答案为8.点睛：此题主要考查了线段的垂直平分线的性质，解题时，先利用线段的垂直平分线求出BD=AD，然后根据三角形的周长互相代换，即可其解.六、八年级数学轴对称三角形选择题（难）31．如图，△ABC的周长为32，点D、E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝12，则PQ的长为（）A．3 B．4 C．5 D．6【答案】B【解析】【分析】首先判断△BAE、△CAD是等腰三角形，从而得出BA＝BE，CA＝CD，由△ABC的周长为32以及BC＝12，可得DE＝8，利用中位线定理可求出PQ．【详解】∵BQ平分∠ABC，BQ⊥AE，∴∠ABQ＝∠EBQ，∵∠ABQ+∠BAQ＝90°，∠EBQ+∠BEQ＝90°，∴∠BAQ＝∠BEQ，∴AB＝BE，同理：CA＝CD，∴点Q是AE中点，点P是AD中点（三线合一），∴PQ是△ADE的中位线，∵BE+CD＝AB+AC＝32﹣BC＝32﹣12＝20，∴DE＝BE+CD﹣BC＝8，∴PQ＝12DE＝4．故选：B．【点睛】本题考查了三角形的中位线定理和等腰三角形的性质和判定，解答本题的关键是判断出△BAE、△CAD是等腰三角形，利用等腰三角形的性质确定PQ是△ADE的中位线．32．如图，∠AOB=60°，点P是∠AOB内的定点且3，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（）A．362B．332C．6 D．3【答案】D【解析】分析：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，利用轴对称的性质得MP=MC，NP=ND，OP=OD=OC=3，∠BOP=∠BOD，∠AOP=∠AOC，所以∠COD=2∠AOB=120°，利用两点之间线段最短判断此时△PMN周长最小，作OH⊥CD于H，则CH=DH，然后利用含30度的直角三角形三边的关系计算出CD即可．详解：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，OP=OD=OC=3，∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+MC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=12OC=3，CH=3OH=3 2 ,∴CD=2CH=3．故选D．点睛：本题考查了轴对称﹣最短路线问题：熟练掌握轴对称的性质，会利用两点之间线段最短解决路径最短问题．33．如图，△ABC中，AB＝AC，且∠ABC＝60°，D为△ABC内一点，且DA＝DB，E 为△ABC 外一点，BE＝AB，且∠EBD＝∠CBD，连DE，CE. 下列结论：①∠DAC＝∠DBC；②BE⊥AC ；③∠DEB＝30°. 其中正确的是（）A．①... B．①③... C．② ... D．①②③【答案】B【解析】【分析】连接DC,证ACD BCD DAC DBC∠∠≅=得出①，再证BED BCD≅，得出BED BCD30∠∠==︒;其它两个条件运用假设成立推出答案即可.【详解】解：证明：连接DC，∵△ABC是等边三角形，∴AB=BC=AC，∠ACB=60°，∵DB=DA，DC=DC，在△ACD与△BCD中，AB BCDB DADC DC=⎧⎪=⎨⎪=⎩,∴△ACD≌△BCD （SSS），由此得出结论①正确；∴∠BCD=∠ACD=1302ACB∠=︒∵BE=AB，∴BE=BC，∵∠DBE=∠DBC，BD=BD，在△BED与△BCD中，BE BCDBE DBCBD BD=⎧⎪∠=∠⎨⎪=⎩,∴△BED ≌△BCD （SAS ），∴∠DEB=∠BCD=30°．由此得出结论③正确；∵EC ∥AD ，∴∠DAC=∠ECA ，∵∠DBE=∠DBC ，∠DAC=∠DBC ，∴设∠ECA=∠DBC=∠DBE=∠1，∵BE=BA ，∴BE=BC ，∴∠BCE=∠BEC=60°+∠1，在△BCE 中三角和为180°，∴2∠1+2（60°+∠1）=180°∴∠1=15°，∴∠CBE=30，这时BE 是AC 边上的中垂线，结论②才正确．因此若要结论②正确，需要添加条件EC ∥AD.故答案为：B.【点睛】本题考查的知识点主要是全等三角形的判定与性质以及等边三角形的性质，通过已知条件作出恰当的辅助线是解题的关键点.34．如图，Rt ACB ∆中，90ACB ∠=︒，ABC ∠的平分线BE 和BAC ∠的外角平分线AD 相交于点P ，分别交AC 和BC 的延长线于E ，D .过P 作PF AD ⊥交AC 的延长线于点H ，交BC 的延长线于点F ，连接AF 交DH 于点G .下列结论：①45APB ∠=︒；②PB 垂直平分AF ；③BD AH AB -=；④2DG PA GH =+；其中正确的结论有（）A ．4个B ．3个C ．2个D ．1个【答案】A【解析】【分析】①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP ，再根据角平分线的定义∠ABP ＝12∠ABC ，然后利用三角形的内角和定理整理即可得解；②先求出∠APB ＝∠FPB ，再利用“角边角”证明△ABP 和△FBP 全等，根据全等三角形对应边相等得到AB ＝BF ，AP ＝PF ；③根据直角的关系求出∠AHP ＝∠FDP ，然后利用“角角边”证明△AHP 与△FDP 全等，根据全等三角形对应边相等可得DF ＝AH ；④求出∠ADG ＝∠DAG ＝45°，再根据等角对等边可得DG ＝AG ，再根据等腰直角三角形两腰相等可得GH ＝GF ，然后根据即可得到DG GH =+. 【详解】解：①∵∠ABC 的角平分线BE 和∠BAC 的外角平分线，∴∠ABP ＝12∠ABC ， ∠CAP ＝12（90°＋∠ABC ）＝45°＋12∠ABC ，在△ABP 中，∠APB ＝180°−∠BAP−∠ABP ，＝180°−（45°＋12∠ABC ＋90°−∠ABC ）−12∠ABC ，＝180°−45°−12∠ABC−90°＋∠ABC−12∠ABC ，＝45°，故本小题正确；②∵PF ⊥AD ，∠APB ＝45°（已证），∴∠APB ＝∠FPB ＝45°，∵∵PB 为∠ABC 的角平分线，∴∠ABP ＝∠FBP ，在△ABP 和△FBP 中，APB FPB PB PBABP FBP ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△ABP ≌△FBP （ASA ），∴AB ＝BF ，AP ＝PF ；∴PB 垂直平分AF ，故②正确；③∵∠ACB ＝90°，PF ⊥AD ，∴∠FDP ＋∠HAP ＝90°，∠AHP ＋∠HAP ＝90°，∴∠AHP ＝∠FDP ，∵PF ⊥AD ，∴∠APH ＝∠FPD ＝90°，在△AHP 与△FDP 中，90AHP FDP APH FPD AP PF ∠∠⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△AHP ≌△FDP （AAS ），∴DF ＝AH ，∵BD ＝DF ＋BF ，∴BD ＝AH ＋AB ，∴BD−AH ＝AB ，故③小题正确；④∵AP ＝PF ，PF ⊥AD ，∴∠PAF ＝45°，∴∠ADG ＝∠DAG ＝45°，∴DG ＝AG ，∵∠PAF ＝45°，AG ⊥DH ，∴△ADG 与△FGH 都是等腰直角三角形，∴DG ＝AG ，GH ＝GF ，∴DG ＝GH ＋AF ，∴FG=GH,AF=2PA故2DG PA GH =+.综上所述①②③④正确．故选：A ．【点睛】本题考查了直角三角形的性质，全等三角形的判定，以及等腰直角三角形的判定与性质，等角对等边，等边对等角的性质，综合性较强，难度较大，做题时要分清角的关系与边的关系．35．如图，ABC △，AB AC =，56BAC ︒∠=，BAC ∠的平分线与AB 的垂直平分线交于O ，将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与O 点恰好重合，则∠OEC 的度数为（）A ．132︒B ．130︒C ．112︒D ．110︒【答案】C【解析】【分析】连接OB 、OC ，根据角平分线的定义求出∠BAO ，根据等腰三角形两底角相等求出∠ABC ，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB ，根据等边对等角可得∠ABO=∠BAO ，再求出∠OBC ，然后判断出点O 是△ABC 的外心，根据三角形外心的性质可得OB=OC ，再根据等边对等角求出∠OCB=∠OBC ，根据翻折的性质可得OE=CE ，然后根据等边对等角求出∠COE ，再利用三角形内角和定理列式计算即可得出答案.【详解】如图，连接OB 、OC ，∵56BAC ︒∠=，AO 为BAC ∠的平分线∴11562822BAO BAC ︒︒∠=∠=⨯= 又∵AB AC =，∴()()11180180566222ABC BAC ︒︒︒︒∠=-∠=-= ∵DO 是AB 的垂直平分线， ∴OA OB =．∴28ABO BAO ︒∠=∠=，∴622834OBC ABC ABO ︒︒︒∠=∠-∠=-=∵DO 是AB 的垂直平分线，AO 为BAC ∠的平分线∴点О是ABC △的外心，∴OB OC =，∴34OCB OBC ︒∠=∠=，∵将C ∠沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合∴OE CE =，∴34COE OCB ︒∠=∠=，在OCE △中，1801803434112OEC COE OCB ︒︒︒︒︒∠=-∠-∠=--=【点睛】本题主要考查了线段垂直平分线上的点到线段两端点距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，以及翻折变换的性质，综合性较强，难度较大，做辅助线构造出等腰三角形是解决本题的关键.36．如图，ABC △是等边三角形，ABD △是等腰直角三角形，∠BAD =90°，AE ⊥BD 于点E ．连CD 分别交AE ，AB 于点F ，G ，过点A 做AH ⊥CD 交BD 于点H ，则下列结论：①∠ADC=15°；②AF=AG；③AH=DF；④△ADF≌△BAH；⑤DF=2EH.其中正确结论的个数为（）A．5 B．4 C．3 D．2【答案】B【解析】【分析】①根据△ABC为等边三角形，△ABD为等腰直角三角形，可以得出各角的度数以及DA=AC，即可作出判断；②分别求出∠AFG和∠AGD的度数，即可作出判断；④根据三角形内角和定理求出∠HAB的度数，求证EHG DFA∠=∠，利用AAS即可证出两个三角形全等；③根据④证出的全等即可作出判断；⑤证明∠EAH=30°，即可得到AH=2EH，又由③可知AH DF=，即可作出判断.【详解】①正确：∵ABC△是等边三角形，∴60BAC︒∠=，∴CA AB=．∵ABD△是等腰直角三角形，∴DA AB=．又∵90BAD︒∠=，∴150CAD BAD BAC︒∠=∠+∠=，∴DA CA=，∴()1180150152ADC ACD︒︒︒∠=∠=-=；②错误：∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③，④正确，由题意可得45DAF ABH︒∠=∠=，DA AB=，∵AE BD⊥，AH CD⊥．∴180EHG EFG︒∠+∠=．又∵180?DFA EFG∠+∠=，∴EHG DFA∠=∠，在DAF△和ABH中()AFD BHADAF ABH AASDA AB∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF△≌ABH．∴DF AH=．⑤正确：∵150CAD︒∠=，AH CD⊥，。

八年级数学全等三角形中考真题汇编[解析版]

八年级数学全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，在锐角△ABC中，AB=5，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是______．【答案】5【解析】【分析】作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN为所求的最小值，再根据AD是∠BAC的平分线可知MH=MN，再由等腰直角三角形的性质即可得出结论．【详解】如图，作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN 为所求的最小值．∵AD是∠BAC的平分线，∴MH=MN，∴BH是点B到直线AC的最短距离（垂线段最短）．∵AB=5，∠BAC=45°，∴BH==5．∵BM+MN的最小值是BM+MN=BM+MH=BH=5．故答案为5．【点睛】本题考查了轴对称﹣最短路线问题，解答此类问题时要从已知条件结合图形认真思考，通过角平分线性质，垂线段最短，确定线段和的最小值．2．如图，已知正六边形 ABCDEF 的边长是 5，点 P 是 AD 上的一动点，则 PE+PF 的最小值是_____．【答案】10【解析】利用正多边形的性质，可得点B关于AD对称的点为点E，连接BE交AD于P点，那么有PB=PF，PE+PF=BE最小，根据正六边形的性质可知三角形APB是等边三角形，因此可知BE 的长为10，即PE+PF的最小值为10.故答案为10.3．在平面直角坐标系中，点A在x轴的正半轴上，点B在y轴的正半轴上，∠=︒，在x轴或y轴上取点C，使得ABC∆为等腰三角形，符合条件的C点有ABO36__________个．【答案】8【解析】【分析】观察数轴，按照等腰三角形成立的条件分析可得答案．【详解】解：如下图所示，若以点A为圆心，以AB为半径画弧，与x轴和y轴各有两个交点，但其中一个会与点B重合，故此时符合条件的点有3个；若以点B为圆心，以AB为半径画弧，同样与x轴和y轴各有两个交点，但其中一个与点A 重合，故此时符合条件的点有3个；线段AB 的垂直平分线与x 轴和y 轴各有一个交点，此时符合条件的点有2个．∴符合条件的点总共有：3＋3＋2=8个．故答案为：8．【点睛】本题考查了等腰三角形的判定，可以观察图形，得出答案．4．如图，在ABC ∆中，点D 是BC 的中点，点E 是AD 上一点，BE AC =．若70C ∠=︒，50DAC ∠=︒ 则EBD ∠的度数为______．【答案】10︒【解析】【分析】延长AD 到F 使DF AD =，连接BF ，通过ACD FDB ≅，根据全等三角形的性质得到CAD BFD ∠=∠，AC BF =，等量代换得BF BE =，由等腰三角形的性质得到F BEF ∠=∠，即可得到BEF CAD ∠=∠，进而利用三角形的内角和解答即可得．【详解】如图，延长AD 到F ，使DF AD =，连接BF ：∵D 是BC 的中点∴BD CD =又∵ADC FDB ∠=∠，AD DF =∴ACD FDB ≅∴AC BF =， CAD F ∠=∠，C DBF ∠=∠∵AC BE =， 70C ︒∠=， 50CAD ︒∠=∴BE BF =， 70DBF ︒∠=∴50BEF F ︒∠=∠=∴180180505080EBF F BEF ︒︒︒︒︒∠=-∠-∠=--=∴807010EBD EBF DBF ︒︒︒∠=∠-∠=-=故答案为：10︒【点睛】本题主要考查的知识点有全等三角形的判定及性质、等腰三角形的性质及三角形的内角和定理，解题的关键在于通过倍长中线法构造全等三角形．5．如图，已知△ABC 中，AB=AC ，∠BAC=90°，直角∠EPF 的顶点P 是BC 中点，两边PE 、PF 分别交AB 、AC 于点E 、F ，给出下列四个结论：①AE=CF ；②△EPF 是等腰直角三角形；③EF=AB ；④12ABC AEPF S S ∆=四边形，当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A 、B 重合)，上述结论中始终正确的有________(把你认为正确的结论的序号都填上).【答案】①②④【解析】试题分析：∵∠APE 、∠CPF 都是∠APF 的余角，∴∠APE=∠CPF ，∵AB=AC ，∠BAC=90°，P 是BC 中点，∴AP=CP ，∴∠PAE=∠PCF，在△APE与△CPF中，{?PAE PCFAP CPEPA FPC∠=∠=∠=∠，∴△APE≌△CPF（ASA），同理可证△APF≌△BPE，∴AE=CF，△EPF是等腰直角三角形，S四边形AEPF=12S△ABC，①②④正确；而AP=12BC，当EF不是△ABC的中位线时，则EF不等于BC的一半，EF=AP，∴故③不成立．故始终正确的是①②④．故选D．考点：1．全等三角形的判定与性质；2．等腰直角三角形．6．如图，在△ABC中，AB的中垂线交BC于D，AC的中垂线交BC于E，若∠BAC=126°，则∠EAD=_____°.【答案】72°【解析】【分析】根据AB的中垂线可得BAD∠，再根据AC的中垂线可得EAC∠，再结合∠BAC=126°即可计算出∠EAD.【详解】根据AB的中垂线可得BAD∠=B根据AC的中垂线可得EAC∠=C∠18012654B C︒︒︒∠+∠=-=又126BAD DAE EAC BAC︒∠+∠+∠=∠=+C+126B DAE︒∴∠∠∠=72DAE︒∴∠=【点睛】本题主要考查中垂线的性质，重点在于等量替换表示角度.7．如图，在等腰直角三角形ABC 中，90ACB ∠=︒，4AC BC ==，D 为BC 中点，E 为AC 边上一动点，连接DE ，以DE 为边并在DE 的右侧作等边DEF ∆，连接BF ，则BF 的最小值为______.【答案】3【解析】【分析】由60°联想旋转全等，转换动长为定点到定线的长，构建等边三角形BDG ，利用△BDF ≌△GDE ，转换BF=GE ，然后即可求得其最小值.【详解】以BD 为边作等边三角形BDG ，连接GE ，如图所示：∵等边三角形BDG ，等边三角形DEF∴∠BDG=∠EDF=60°，BD=GD=BG ，DE=DF=EF∴∠BDG+∠GFD=∠EDF+∠GFD ，即∠BDF=∠GDE∴△BDF ≌△GDE （SAS ）∴BF=GE当GE ⊥AC 时，GE 有最小值，如图所示GE′，作DH ⊥GE′∴BF=GE= CD+12DG=2+1=3故答案为：3.【点睛】此题主要考查等边三角形的性质以及全等三角形的判定与性质，解题关键是由60°联想旋转全等，转换动长为定点到定线的长.8．如图，已知每个小方格的边长为1，A、B两点都在小方格的格点（顶点）上，请在图中找一个格点C，使△ABC是等腰三角形，这样的格点C有________个。

天津市自立中学数学全等三角形中考真题汇编[解析版]

天津市自立中学数学全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P有_____个．【答案】4【解析】【分析】由A点坐标可得OA=22，∠AOP＝45°，分别讨论OA为腰和底边，求出点P在x轴正半轴和负半轴时，△APO是等腰三角形的P点坐标即可.【详解】（1）当点P在x轴正半轴上，①如图，以OA为腰时，∵A的坐标是（2，2），∴∠AOP＝45°，OA＝22，当∠AOP为顶角时，OA=OP=22，当∠OAP为顶角时，AO=AP，∴OPA=∠AOP=45°，∴∠OAP=90°，∴OP=2OA=4，∴P的坐标是（4，0）或（22，0）.②以OA为底边时，∵点A的坐标是（2，2），∴∠AOP=45°，∵AP=OP，∴∠OAP=∠AOP=45°，∴∠OPA=90°，∴OP=2， ∴P 点坐标为（2，0）.（2）当点P 在x 轴负半轴上，③以OA 为腰时，∵A 的坐标是（2，2），∴OA ＝22，∴OA ＝OP ＝22，∴P 的坐标是（﹣22，0）．综上所述：P 的坐标是（2，0）或（4，0）或（22，0）或（﹣22，0）．故答案为：4．【点睛】此题主要考查等腰三角形的判定及坐标与图形性质的综合运用，注意分类讨论思想的运用是解题关键．2．如图，ABC ∆中，90BAC ∠=︒，AD BC ⊥，ABC ∠的平分线BE 交AD 于点F ，AG 平分DAC ∠．给出下列结论：①BAD C ∠=∠；②EBC C ∠=∠；③AE AF =；④//FG AC ；⑤EF FG =．其中正确的结论是______．【答案】①③④【解析】【分析】①根据等角的余角相等即可得到结果，故①正确；②如果∠EBC=∠C ，则∠C=12∠ABC ，由于∠BAC=90°，那么∠C=30°，但∠C 不一定等于30°，故②错误；③由BE 、AG 分别是∠ABC 、∠DAC 的平分线，得到∠ABF=∠EBD ．由于∠AFE=∠BAD+∠FBA ，∠AEB=∠C+∠EBD ，得到∠AFE=∠AEB ，可得③正确；④连接EG ，先证明△ABN ≌△GBN ，得到AN=GN ，证出△ANE ≌△GNF ，得∠NAE=∠NGF ，进而得到GF ∥AE ，故④正确；⑤由AE=AF ，AE=FG ，而△AEF 不一定是等边三角形，得到EF 不一定等于AE ，于是EF 不一定等于FG ，故⑤错误．【详解】∵∠BAC=90°，AD ⊥BC ，∴∠C+∠ABC=90°，∠C+∠DAC=90°，∠ABC+∠BAD=90°，∴∠ABC=∠DAC ，∠BAD=∠C ，故①正确；若∠EBC=∠C ，则∠C=12∠ABC ， ∵∠BAC=90°，那么∠C=30°，但∠C 不一定等于30°，故②错误；∵BE 、AG 分别是∠ABC 、∠DAC 的平分线，∴∠ABF=∠EBD ，∵∠AFE=∠BAD+∠ABF ，∠AEB=∠C+∠EBD ，又∵∠BAD=∠C ，∴∠AFE=∠AEF ，∴AF=AE ，故③正确；∵AG 是∠DAC 的平分线，AF=AE ，∴AN ⊥BE ，FN=EN ，在△ABN 与△GBN 中， ∵90ABN GBN BN BN ANB GNB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，∴△ABN ≌△GBN （ASA ），∴AN=GN ，又∵FN=EN ，∠ANE=∠GNF ，∴△ANE ≌△GNF （SAS ），∴∠NAE=∠NGF ，∴GF ∥AE ，即GF ∥AC ，故④正确；∵AE=AF ，AE=FG ，而△AEF 不一定是等边三角形，∴EF 不一定等于AE ，∴EF 不一定等于FG ，故⑤错误．故答案为：①③④．【点睛】本题主要考查等腰三角形的判定和性质定理，全等三角形的判定和性质定理，直角三角形的性质定理，掌握掌握上述定理，是解题的关键．3．如图，ABC 中，ABC=45∠︒，CD AB ⊥于D ，BE 平分ABC ∠，且BE AC ⊥于E ，与CD 相交于点F ，H 是BC 边的中点，连接DH 与BE 相交于点G ，下列结论：BF=AC ①；A=67.5∠︒②；DG=DF ③；ADGE GHCE S S =四边形四边形④，其中正确的有__________（填序号）．【答案】①②③【解析】【分析】只要证明△BDF ≌△CDA ，△BAC 是等腰三角形，∠DGF=∠DFG=67.5°，即可判断①②③正确，作GM ⊥BD 于M ，只要证明GH ＜DG 即可判断④错误．【详解】解：∵CD ⊥AB ，BE ⊥AC ，∴∠BDC=∠ADC=∠AEB=90°，∴∠A ＋∠ABE=90°，∠ABE ＋∠DFB=90°，∴∠A=∠DFB ，∵∠ABC=45°，∠BDC=90°，∴∠DCB=90°−45°=45°=∠DBC ，∴BD=DC ，在△BDF 和△CDA 中，∠BDF=∠CDA ，∠A=∠DFB ，BD=CD ，∴△BDF ≌△CDA （AAS ），∴BF=AC ，故①正确．∵∠ABE=∠EBC=22.5°，BE ⊥AC ，∴∠A=∠BCA=67.5°，故②正确，∵BE 平分∠ABC ，∠ABC=45°，∴∠ABE=∠CBE=22.5°，∵∠BDF=∠BHG=90°，∴∠BGH=∠BFD=67.5°，∴∠DGF=∠DFG=67.5°，∴DG=DF，故③正确．作GM⊥AB于M．如图所示：∵∠GBM=∠GBH，GH⊥BC，∴GH=GM＜DG，∴S△DGB＞S△GHB，∵S△ABE=S△BCE，∴S四边形ADGE＜S四边形GHCE．故④错误，故答案为：①②③．【点睛】此题是三角形综合题，考查了等腰三角形的性质，直角三角形的性质，全等三角形的性质和判定，三角形的面积等知识点的综合运用，第五个问题难度比较大，添加辅助线是解题关键，属于中考选择题中的压轴题．4．在平面直角坐标系中，点A在x轴的正半轴上，点B在y轴的正半轴上，∆为等腰三角形，符合条件的C点有∠=︒，在x轴或y轴上取点C，使得ABCABO36__________个．【答案】8【解析】【分析】观察数轴，按照等腰三角形成立的条件分析可得答案．【详解】解：如下图所示，若以点A为圆心，以AB为半径画弧，与x轴和y轴各有两个交点，但其中一个会与点B重合，故此时符合条件的点有3个；若以点B为圆心，以AB为半径画弧，同样与x轴和y轴各有两个交点，但其中一个与点A重合，故此时符合条件的点有3个；线段AB的垂直平分线与x轴和y轴各有一个交点，此时符合条件的点有2个．∴符合条件的点总共有：3＋3＋2=8个．故答案为：8．【点睛】本题考查了等腰三角形的判定，可以观察图形，得出答案．5．如图,A,B,C三点在同一直线上,分别以AB,BC（AB>BC）为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论：①AE=DC，②MN//AB，③BD⊥AE，④∠DPM=60°，⑤ΔBMN是等边三角形.其中正确的是__________（把所有正确的序号都填上）.【答案】①②④⑤【解析】【分析】①由三角形ABD与三角形BCE都为等边三角形，利用等边三角形的性质得到两条边对应相等，两个角相等都为60°，利用SAS即可得到三角形ABE与三角形DBC全等即可得结论；②由①中三角形ABE与三角形DBC全等，利用全等三角形的对应角相等得到一对角相等，再由∠ABD=∠EBC=60°，利用平角的定义得到∠MBE=∠NBC=60°，再由EB=CB，利用ASA 可得出三角形EMB与三角形CNB全等，利用全等三角形的对应边相等得到MB=NB，再由∠MBE=60°，利用有一个角为60°的等腰三角形为等边三角形可得出三角形BMN为等边三角形；可得∠BMN=60°，进行可得∠BMN=∠ABD，故MN//AB，从而可判断②，⑤正确；③无法证明PM=PN，因此不能得到BD⊥AE；④由①得∠EAB=∠CDB，根据三角形内角和和外角的性质可证得结论.【详解】①∵等边△ABD和等边△BCE，∴AB=DB，BE=BC，∠ABD=∠EBC=60°，∴∠ABE=∠DBC=120°，在△ABE和△DBC中，∵AB DBABE DBC BE BC⎪∠⎪⎩∠⎧⎨＝＝＝，∴△ABE≌△DBC（SAS），∴AE=DC，故①正确；∵△ABE≌△DBC，∴∠AEB=∠DCB，又∠ABD=∠EBC=60°，∴∠MBE=180°-60°-60°=60°，即∠MBE=∠NBC=60°，在△MBE和△NBC中，∵AEB DCB EB CBMBE NBC ∠∠∠⎧⎪⎪⎩∠⎨＝＝＝，∴△MBE≌△NBC（ASA），∴BM=BN，∠MBE=60°，则△BMN为等边三角形，故⑤正确；∵△BMN为等边三角形，∴∠BMN=60°,∵∠ABD=60°,∴∠BMN=∠ABD，∴MN//AB，故②正确；③无法证明PM=PN，因此不能得到BD⊥AE；④由①得∠EAB=∠CDB，∠APC+∠PAC+∠PCA=180°，∴∠PAC+∠PCA=∠PDB+∠PCB=∠DBA=60°，∵∠DPM =∠PAC+∠PCA∴∠DPM =60°，故④正确，故答案为：①②④⑤.【点睛】此题考查了等边三角形的判定与性质，以及全等三角形的判定与性质，熟练掌握判定与性质是解本题的关键．6．如图，已知每个小方格的边长为1，A 、B 两点都在小方格的格点（顶点）上，请在图中找一个格点C ，使△ABC 是等腰三角形，这样的格点C 有________个。

初二数学三角形全等中考真题含解析

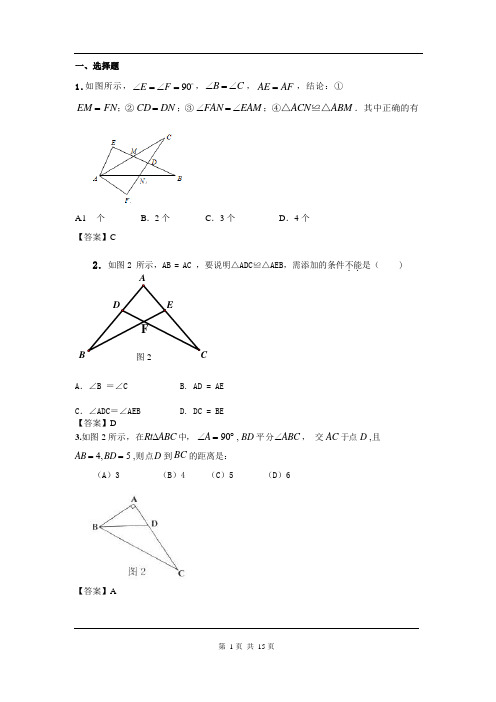
DEF一、选择题1．如图所示， ∠E = ∠F = 90，∠B = ∠C ， AE = AF ，结论：① EM = FN ；② CD = DN ；③ ∠FAN = ∠EAM ；④△ACN ≌△ABM ．其中正确的有A.1 个 B ．2 个 C ．3 个 D ．4 个【答案】C2．如图 2 所示，AB = AC ，要说明△ADC≌△AEB，需添加的条件不．能．是（ )BCA ．∠B ＝∠CB. AD = AEC ．∠ADC＝∠AEBD. DC = BE【答案】D3.如图 2 所示，在Rt ∆ABC 中， ∠A = 90︒ , BD 平分∠ABC ，交 AC 于点 D ,且AB = 4, BD = 5 ,则点D 到 BC 的距离是：（A ）3（B ）4（C ）5（D ）6【答案】A4．如图3，Rt△ABC 中，∠C=90°，∠ABC 的平分线BD交AC 于D，若CD=3cm，则点D 到AB 的距离DE 是A．5cm B．4cm C．3cm D．2cm【答案】C5．如图，△A BC≌△D E F，BE=4，A E=1，则DE的长是（）A．5 B．4 C．3 D．2【答案】A二、填空题1．如图，已知AC=FE，BC=DE，点A、D、B、F 在一条直线上，要使△ ABC ≌△ FDE ，还需添加一．个．条件，这个条件可以是．ADCB EF第（13）题【答案】∠C=∠E（答案不惟一，也可以是AB=FD或AD=FB）2．（2010 广西钦州市）如图，在△ABC 和△BAD 中，BC = AD，请你再补充一个条件，使△ABC≌△BAD．你补充的条件是_ ▲ _（只填一个）．C DA B第8 题【答案】AC =BD 或∠CBA＝∠DAB三、解答题CF1．如图，C 是线段 AB 的中点，CD 平分∠ACE ，CE 平分 ∠BCD ，CD=CE ．(1) 求证：△ ACD ≌△ BCE ；(2)若∠D=50°，求∠B 的度数．【答案】2．如图，已知：点 B 、F 、C 、E 在一条直线上，FB =CE ，AC =DF ．能否由上面的已知条件证明 AB ∥ED ？如果能，请给出证明；如果不能，请从下列三个条件中选择一．个．合．适．的．条．件．，添加到已知条件中，使 AB ∥ED 成立，并给出证明．供选择的三个条件（请从其中选择一个）：①AB =ED ； ②BC =EF ； ③∠ACB =∠DFE ．ABED（第 25 题）FDE ( 第 18 题⎨⎩【答案】解：由上面两条件不能证明AB//ED.有两种添加方法.第一种：FB=CE，AC=DF 添加①AB=ED证明：因为FB=CE，所以BC=EF，又AC=EF，AB=ED，所以ABC≅DEF所以∠ABC=∠DEF 所以AB//ED第二种：FB=CE，AC=DF 添加③∠ACB=∠DFE证明：因为FB=CE，所以BC=EF，又∠ACB=∠DFE AC=EF，所以ABC ≅DEF 所以∠ABC=∠DEF 所以AB//ED3．如图，在△ABC 中，D是BC 边上的点（不与B，C 重合），F，E 分别是AD及其延长线上的点，CF∥BE. 请你添加一个条件，使△B D E≌△C A D F (不再添加其它线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是：▲； B C（2）证明：【答案】解：（1）BD=DC(或点D是线段BC 的中点)，FD=ED，CF=BE中任选一个即可﹒（2）以BD =DC 为例进行证明：∵CF∥BE，∴∠FCD﹦∠EBD．又∵ BD =DC ，∠FDC﹦∠EDB，∴△BDE≌△CDF．4．（1）如图，点B、E、C、F 在一条直线上，BC＝EF，AB∥DE，∠A＝∠D．求证：△ABC≌△DEF．(第 17(1)题)【答案】证明：∵ AB∥DE．∴ ∠B＝∠DEF．在△ABC 和△DEF 中，⎧∠B =∠DEF，⎪∠A =∠D，⎪BC =EF．∴ △ABC ≌△DEF ．5．如图，分别过点 C 、B 作△ABC 的 BC 边上的中线 AD 及其延长线的垂线，垂足分别为 E 、F ．求证：BF =CE ．【答案】∵CE ⊥AF ，FB ⊥AF ，∴∠DEC ＝∠DFB ＝90°又∵AD 为 BC 边上的中线，∴BD ＝CD ，且∠EDC ＝∠FDB （对顶角相等） ∴所以△BFD ≌△C D E （AAS ），∴BF =CE ． 6．如图，已知 AD 是△A BC 的角平分线，在不添加任何辅助线的前提下，要使△AE D≌△AFD ，需添加一个条件是：，并给予证明.ABD C【答案】解法一：添加条件：AE ＝AF ，证明：在△AED 与△AFD 中，∵AE＝AF ，∠EAD＝∠FAD，AD ＝AD ，∴△AED≌△AFD（SAS ）.解法二：添加条件：∠EDA＝∠FDA，证明：在△AED 与△AFD 中，∵∠EAD＝∠FAD，AD ＝AD ，∠EDA＝∠FDA ∴△AED≌△AFD（ASA ）.EF⎨⎩7．如图，B，F，C，E 在同一条直线上，点A，D在直线BE 的两侧，AB∥DE，AC∥DF，BF=CE．求证：AC=DF【答案】证明：∵AB∥DE，∴∠ABC=∠DEF∵AC∥DF，∴∠ABC=∠DEF∵BF=CE，∴BC=EF∴△ABC≌△DEF∴AC=DF8．已知：如图，点C 是线段 AB 的中点，CE=CD，∠ACD=∠BCE,求证：AE=BD．【答案】证明：∵点 C 是线段 AB 的中点，∴AC=BC，∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD,题 20 图⎧AC =BC在△ACE 和△BCD 中，⎪∠ACE =∠BCD ，⎪CE∴△A CE≌△BCD（SAS），∴AE=BD.=CD9．已知：如图，点A、B、C、D在同一条直线上，EA⊥AD，FD⊥AD，AE=DF，AB=DC．求证：∠ACE=∠DBF．⎨⎩EBCD⎨ ⎩【答案】证明：∵AB =DC∴AC =DB∵EA ⊥AD ，FD ⊥AD ∴∠A =∠D =90° 在△EAC 与△FDB 中⎧EA = FD ⎪∠A = ∠D ⎪AC = DB ∴△EAC ≌△FDB ∴∠ACE =∠DBF ．10．如图，点 A 、E 、B 、D 在同一条直线上，AE ＝DB ，AC ＝DF ，AC ∥DF .请探索 BC 与 EF 有怎样的位置关系？并说明理由．FAD【答案】解：BC ∥EF ．理由如下：∵AE ＝DB ，∴AE ＋BE ＝DB ＋BE ，∴AD ＝DE .∵AC ∥DF ， ∴∠A ＝∠D ，∵AC ＝DF ， ∴△ACB ≌△DFE ，∴∠FED ＝∠CBA ，∴BC ∥EF ． 11．如图，点 B 、D 、C 、F 在一条直线上，且 BC = FD ，A B = E F .（1）请你只添加一个条件（不再加辅助线），使△A BC ≌△E FD ，你添加的条件是；（2）添加了条件后，证明△ABC ≌△EFD.ABFE【答案】（1）∠B = ∠F 或 AB ∥EF 或 AC = ED .（2）证明：当∠B = ∠F 时在△ABC 和△EFD 中⎧A B = E⎪∠B = ∠F ⎪BC = FD求证：⑴ △ABC ≌△DEF ；⑵ BE ＝CF ．∴△ABC ≌△EFD (SAS)12．如图 4，已知 AC ∥DF ，且 BE =CF . （1）请你只添加一．个．条件，使△ ABC ≌△D EF ，你添加的条件是；（2）添加条件后，证明△ ABC ≌△DEF.【答案】（１）添加的条件是 AC ＝DF （或 AB ∥D E 、∠B ＝∠D E F 、∠A ＝∠D ）（有一个即可）（２）证明：∵AC ∥DF ，∴∠ACB ＝∠F ，∵BE=CF ，∴BC ＝EF ，在△ ABC 和△ DEF 中，⎧BC = EF ⎪⎨∠ACB = ∠F ⎪⎩AC = DF ，∴△ABC ≌△DEF. 13．如图， ∠BAC = ∠ABD .（1）要使OC = OD ，可以添加的条件为：或；（写出 2 个符合题意的条件即可）（2）请选择(1)中你所添加的一个条件，证明OC = OD .CD【答案】解：（1）答案不唯一. 如∠C = ∠D ，或∠ABC = ∠BAD ，或∠OAD = ∠OBC ，或 AC = BD . ……4 分说明：2 空全填对者，给 4 分；只填 1 空且对者，给 2 分. （2）答案不唯一. 如选 AC = BD 证明 OC=OD.证明: ∵ ∠BAC = ∠ABD ，∴ OA=OB. ……………………6 分 DC又 AC = BD ， O∴ AC-OA=BD-OB ，或 AO+OC=BO+OD. AB∴ OC = OD......................................................... 8 分14．已知：点B 、E 、C 、F 在同一直线上，AB ＝DE ，∠A ＝∠D ，AC ∥ DF ．O AB⎨⎩【答案】证明：(1)∵AC ∥DF∴∠ACB ＝∠F ...................................................................................................... 2 分在△ABC 与△DEF 中⎧∠ACB = ∠F ⎪∠A = ∠D ⎪ AB = DE ∴△ABC≌△DEF ................................................... 6 分(2) ∵△ABC≌△DEF∴BC=EF ∴BC–EC=EF –EC即 BE=CF ......................................................... 10 分 15．如图，已知点E ，C 在线段 BF 上， BE = CF ，请在下列四个等式中，①AB ＝DE ，②∠ACB ＝∠F ，③∠A ＝∠D ，④AC ＝DF ．选出两．个．作为条件，推出 △ABC ≌△DEF ．并予以证明．（写出一种即可）已知：，．求证： △ABC≌△DEF ．证明：A DBECF【答案】解：已知：①④（或②③、或②④） .........3 分AD证明：若选①④ ∵ BE = CFB EC C ∴ BE + EC = CF + EC ,即BC = EF ． .............................. 5 分在△ABC 和△DEF 中AB ＝DE ，BC ＝EF ，AC ＝DF ． ..................... 8 分∴ △ABC ≌△DEF ． .......................... 9 分 16．八（1）班同学上数学活动课，利用角尺平分一个角（如图）.设计了如下方案：⎨⎩（Ⅰ）∠AOB 是一个任意角，将角尺的直角顶点 P 介于射线 OA 、OB 之间，移动角尺使角尺两边相同的刻度与 M 、N 重合，即 PM=PN ，过角尺顶点 P 的射线 OP 就是∠AOB 的平分线. （Ⅱ）∠AOB 是一个任意角，在边 OA 、OB 上分别取 OM=ON ，将角尺的直角顶点 P 介于射线 OA 、OB 之间，移动角尺使角尺两边相同的刻度与 M 、N 重合，即 PM=PN ，过角尺顶点 P 的射线 OP 就是∠AOB 的平分线.（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由. （2）在方案（Ⅰ）PM=PN 的情况下，继续移动角尺，同时使 PM⊥OA，PN⊥OB.此方案是否可行？请说明理由.【答案】解：（1）方案（Ⅰ）不可行.缺少证明三角形全等的条件. …………………………… 2 分（2）方案（Ⅱ）可行 ...................... 3 分证明：在△OPM 和△OPN 中⎧OM = OP ⎪PM = PN ⎪ OP = OP ∴△OPM≌△OPN(SSS)∴∠AOP=∠BOP(全等三角形对应角相等) ............................................. 5 分（3）当∠AOB 是直角时，此方案可行 ...................... 6 分∵四边形内角和为 360°，又若 PM⊥OA,PN⊥OB, ∠OMP=∠ONP=90°, ∠MPN=90°,∴∠AOB=90° ∵若 PM⊥OA,PN⊥OB, 且 PM=PN∴OP 为∠AOB 的平分线.(到角两边距离相等的点在这个角的角平分线上) 当∠AOB 不为直角时，此方案不可行 .......... 8 分 17．如图，AB 是∠D AC 的平分线，且 AD =AC 。

人教版数学八年级上册全册全套试卷中考真题汇编[解析版]

人教版数学八年级上册全册全套试卷中考真题汇编[解析版]一、八年级数学三角形填空题（难）1．已知三角形的两边的长分别为2cm和8cm，设第三边中线的长为x cm，则x的取值范围是_______【答案】3＜x＜5【解析】【分析】延长AD至M使DM=AD，连接CM，先说明△ABD≌△CDM，得到CM=AB=8，再求出2AD的范围，最后求出AD的范围.【详解】解：如图：AB=8，AC=2，延长AD至M使DM=AD，连接CM在△ABD和△CDM中，AD MDADB MDCBD CD=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△MCD（SAS），∴CM=AB=8．在△ACM中：8-2＜2x＜8+2，解得：3＜x＜5．故答案为：3＜x＜5．【点睛】本题考查了三角形的三边关系，解答的关键在于画出图形，数形结合完成解答.2．如图，1BA和1CA分别是ABC∆的内角平分线和外角平分线，2BA是1A BD∠的角平分线，2CA是1A CD∠的角平分线，3BA是2A BD∠的角平分线，3CA是2A CD∠的角平分线，若1Aα∠=，则2018A∠=_____________【答案】20172α【解析】【分析】根据角平分线的定义可得∠A 1BC=12∠ABC ，∠A 1CD=12∠ACD ，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC ，∠A 1CD=∠A 1BC+∠A 1，整理即可得解，同理求出∠A 2，可以发现后一个角等于前一个角的12，根据此规律即可得解．【详解】∵A 1B 是∠ABC 的平分线，A 1C 是∠ACD 的平分线，∴∠A 1BC=12∠ABC ，∠A 1CD=12∠ACD ，又∵∠ACD=∠A+∠ABC，∠A 1CD=∠A 1BC+∠A 1，∴12（∠A+∠ABC ）=12∠ABC+∠A 1， ∴∠A 1=12∠A ， ∵∠A 1=α．同理理可得∠A 2=12∠A 1=12α，∠A 3=12∠A 2=212α， ……， ∴∠A 2018=20172α，故答案为20172α．【点睛】本题主要考查的是三角形内角和定理，熟知三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义是解题的关键．3．一个正多边形的每个外角为60°，那么这个正多边形的内角和是_____．【答案】720°．【解析】【分析】先利用多边形的外角和为360°计算出这个正多边形的边数，然后再根据内角和公式进行求解即可．【详解】这个正多边形的边数为36060︒︒=6，所以这个正多边形的内角和=（6﹣2）×180°=720°，故答案为720°．【点睛】本题考查了多边形内角与外角：内角和定理：（n﹣2）•180 （n≥3）且n为整数）；多边形的外角和等于360度．4．一机器人以0.3m/s的速度在平地上按下图中的步骤行走，那么该机器人从开始到停止所需时间为__s．【答案】160.【解析】试题分析：该机器人所经过的路径是一个正多边形，利用360°除以45°，即可求得正多边形的边数，即可求得周长，利用周长除以速度即可求得所需时间．试题解析：360÷45=8，则所走的路程是：6×8=48m，则所用时间是：48÷0.3=160s．考点：多边形内角与外角．5．如图，将一张三角形纸片 ABC 的一角折叠，使点 A 落在△ABC 外的 A'处，折痕为DE．如果∠A＝α，∠CEA′＝β，∠BDA'＝γ，那么α，β，γ 三个角的数量关系是__________ ．【答案】γ=2α+β．【解析】【分析】根据三角形的外角得：∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，代入已知可得结论．【详解】由折叠得：∠A=∠A'，∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，∵∠A=α，∠CEA′=β，∠BDA'=γ，∴∠BDA'=γ=α+α+β=2α+β，故答案为：γ=2α+β．【点睛】此题考查三角形外角的性质，熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键．6．如图，小新从A点出发，沿直线前进50米后向左转30°，再沿直线前进50米，又向左转30°，…照这样下去，小新第一次回到出发地A点时，一共走了__米．【答案】600【解析】【分析】【详解】解：根据题意可知：小新从A点出发，沿直线前进50米后向左转30º，再沿直线前进50米，又向左转30º，……照这样下去,小新第一次回到出发地A点时,小新走的路线围成一个正多边形,且这个多边形的外角等于30º，所以这个正多边形的边数是12，小新一共走了12×50=600米，故答案为：600．二、八年级数学三角形选择题（难）7．如图，∠ABC =∠ACB ，BD 、CD 分别平分△ABC 的内角∠ABC 、外角∠ACP ，BE平分外角∠MBC 交 DC 的延长线于点 E ，以下结论：①∠BDE =12∠BAC ；② DB⊥BE ；③∠BDC +∠ACB= 90︒；④∠BAC + 2∠BEC = 180︒ .其中正确的结论有（）A．1 个B．2 个C．3 个D．4 个【答案】D【解析】【分析】根据角平分线的定义、三角形的内角和定理、三角形的外角的性质、判断即可．【详解】① ∵BD、CD分别平分△ABC的内角∠ABC、外角∠ACP，∴∠ACP=2∠DCP，∠ABC=2∠DBC，又∵∠ACP=∠BAC+∠ABC，∠DCP=∠DBC+∠BDC，∴∠BAC=2∠BDE，∴∠BDE =12∠BAC∴①正确；②∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC，∴∠DBE=∠DBC+∠EBC=12∠ABC+12∠MBC=12×180°=90°，∴EB⊥DB，故②正确，③∵∠DCP=∠BDC+∠CBD，2∠DCP=∠BAC+2∠DBC，∴2(∠BDC+∠CBD)=∠BAC+2∠DBC，∴∠BDC=12∠BAC，∵∠BAC+2∠ACB=180°，∴12∠BAC+∠ACB=90°，∴∠BDC+∠ACB=90°，故③正确，④∵∠BEC=180°−12(∠MBC+∠NCB)=180°−12(∠BAC+∠ACB+∠BAC+∠ABC)=180°−12(180°+∠BAC)∴∠BEC=90°−12∠BAC，∴∠BAC+2∠BEC=180°，故④正确，即正确的有4个，故选D【点睛】此题考查三角形的外角性质，平行线的判定与性质，三角形内角和定理，解题关键在于掌握各性质定理8．已知三角形的三边长分别为2，a－1，4，则化简|a－3|＋|a－7|的结果为（）A．2a－10B．10－2aC．4D．－4【答案】C【解析】试题分析：已知三角形的三边长分别为2，a－1，4，则根据三角形的三边关系：可得：a-1>4-2，a-1<2+4即a>3，a<7.所以a－3>0，a-7<0. |a－3|＋|a－7|=a-3+（7-a）=4.故选C点睛：本题主要考查考生三角形的三边关系：两边之和大于第三边，两边之差小于第三边。

八年级数学上册全等三角形中考真题汇编[解析版]

八年级数学上册全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，已知等边ABC∆的边长为8，E是中线AD上一点，以CE为一边在CE下方作等边CEF∆，连接BF并延长至点,N M为BN上一点，且5CM CN==，则MN的长为_________．【答案】6【解析】【分析】作CG⊥MN于G，证△ACE≌△BCF，求出∠CBF=∠CAE=30°，则可以得出124CG BC==，在Rt△CMG中，由勾股定理求出MG，即可得到MN的长．【详解】解：如图示：作CG⊥MN于G，∵△ABC和△CEF是等边三角形，∴AC=BC，CE=CF，∠ACB=∠ECF=60°，∴∠ACB-∠BCE=∠ECF-∠BCE，即∠ACE=∠BCF，在△ACE与△BCF中AC BCACE BCFCE CF=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△BCF（SAS），又∵AD是三角形△ABC的中线∴∠CBF=∠CAE=30°，∴124CG BC==，在Rt△CMG中，2222543MG CM CG=-=-，∴MN=2MG=6，故答案为：6．【点睛】本题考查了勾股定理，等边三角形的性质，全等三角形的性质和判定的应用，解此题的关键是推出△ACF ≌△BCF ．2．如图，在△ABC 中，AB 的中垂线交BC 于D ，AC 的中垂线交BC 于E ，若∠BAC=126°，则∠EAD=_____°.【答案】72° 【解析】【分析】根据AB 的中垂线可得BAD ∠，再根据AC 的中垂线可得EAC ∠，再结合∠BAC=126°即可计算出∠EAD .【详解】根据AB 的中垂线可得BAD ∠=B根据AC 的中垂线可得EAC ∠=C ∠18012654B C ︒︒︒∠+∠=-=又 126BAD DAE EAC BAC ︒∠+∠+∠=∠=+C+126B DAE ︒∴∠∠∠=72DAE ︒∴∠=【点睛】本题主要考查中垂线的性质，重点在于等量替换表示角度.3．如图，将ABC ∆沿着过AB 中点D 的直线折叠，使点A 落在BC 边上的1A 处，称为第1次操作，折痕DE 到BC 的距离记为1h ，还原纸片后，再将ADE ∆沿着过AD 中点1D 的直线折叠，使点A 落在DE 边上的2A 处，称为第2次操作，折痕11D E 到BC 的距离记为2h ，按上述方法不断操作下去…经过第2020次操作后得到的折痕20192019D E 到BC 的距离记为2020h ，若11h =，则2020h 的值为______．【答案】2019122-【解析】【分析】根据中点的性质及折叠的性质可得DA=DA ₁=DB,从而可得∠ADA ₁=2∠B,结合折叠的性质可得.，∠ADA ₁=2∠ADE,可得∠ADE=∠B,继而判断DE// BC,得出DE 是△ABC 的中位线，证得AA ₁⊥BC,AA ₁=2，由此发现规律：012122h =-=-₁同理21122h =-3211122222h =-⨯=-…于是经过第n 次操作后得到的折痕Dn-1 En-1到BC 的距离1122n n h -=-，据此求得2020h 的值．【详解】解：如图连接AA ₁,由折叠的性质可得：AA ₁⊥DE, DA= DA ₁ ,A ₂、A ₃…均在AA ₁上又∵ D 是AB 中点，∴DA= DB ,∵DB= DA ₁ ,∴∠BA ₁D=∠B ,∴∠ADA ₁=∠B +∠BA ₁D=2∠B,又∵∠ADA ₁ =2∠ADE ,∴∠ADE=∠B∵DE//BC,∴AA ₁⊥BC ,∵h ₁=1∴AA ₁ =2,∴01 2122h =-=-₁ 同理：21122h =-； 3211122222h =-⨯=-； …∴经过n 次操作后得到的折痕D n-1E n-1到BC 的距离1122n n h -=-∴20202019122h =-【点睛】本题考查了中点性质和折叠的性质，本题难度较大，要从每次折叠发现规律，求得规律的过程是难点．4．如图，在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ，过点O 作//EF BC 交AB 于E ，交AC 于F ，过点O 作OD AC ⊥于D 下列结论：①EF BE CF =+；②点O 到ABC ∆各边的距离相等；③1902BOC A ∠=+∠；④设OD m =，AE AF n +=，则AEF S mn ∆=；⑤1()2AD AB AC BC =+-.其中正确的结论是.__________．【答案】①②③⑤【解析】【分析】由在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，根据角平分线的定义与三角形内角和定理，即可求得③∠BOC =90°+12∠A 正确；由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF =BE +CF 故①正确；由角平分线的性质得出点O 到△ABC 各边的距离相等，故②正确；由角平分线定理与三角形面积的求解方法，即可求得④设OD =m ，AE +AF =n ，则S △AEF =12mn ，故④错误，根据HL 证明△AMO ≌△ADO 得到AM =AD ，同理可证BM =BN ，CD =CN ，变形即可得到⑤正确．【详解】∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC =12∠ABC ，∠OCB =12∠ACB ，∠A +∠ABC +∠ACB =180°，∴∠OBC +∠OCB =90°﹣12∠A ，∴∠BOC =180°﹣（∠OBC +∠OCB ）=90°+12∠A ；故③正确； ∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC =∠OBE ，∠OCB =∠OCF ． ∵EF ∥BC ，∴∠OBC =∠EOB ，∠OCB =∠FOC ，∴∠EOB =∠OBE ，∠FOC =∠OCF ，∴BE =OE ，CF =OF ，∴EF =OE +OF =BE +CF ，故①正确；过点O 作OM ⊥AB 于M ，作ON ⊥BC 于N ，连接OA ．∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴ON =OD =OM =m ，∴S △AEF =S △AOE +S △AOF =12AE •OM +12AF •OD =12OD •（AE +AF ）=12mn ；故④错误； ∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴点O 到△ABC 各边的距离相等，故②正确；∵AO =AO ，MO =DO ，∴△AMO ≌△ADO （HL ），∴AM =AD ；同理可证：BM =BN ，CD =CN ．∵AM +BM =AB ，AD +CD =AC ，BN +CN =BC ，∴AD =12（AB +AC ﹣BC ）故⑤正确．故答案为：①②③⑤．【点睛】本题考查了角平分线的定义与性质，等腰三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用．5．如图，已知，点E 是线段AB 的中点，点C 在线段BD 上，8BD =，2DC =，线段AC 交线段DE 于点F ，若AF BD =，则AC =__________.【答案】10.【解析】【分析】延长DE 至G ，使EG=DE ，连接AG ，证明BDE AGE ∆≅∆，而后证明AFG ∆、CDF ∆是等腰三角形，即可求出CF 的长，于是可求AC 的长.【详解】解：如图，延长DE 至G ，使EG=DE ，连接AG，∵点E 是线段AB 的中点，∴AE=BE,∴在BDE ∆和AGE ∆中，BE AE BED AEGDE EG =⎧⎪∠=∠⎨⎪=⎩, ∴BDE AGE ∆≅∆,∴AG=BD, BDE AGE ∠=∠,∵AF=BD=8,∴AG=AF,∴AFG AGE ∠=∠∵AFG DFC ∠=∠,∴BDE DFC ∠=∠,∴FC=DC,∴FC=2,∴AC=AF+FC=8+2=10. 【点睛】本题考查了等腰三角形的性质与判定以及全等三角形的判定与性质，能利用中点条件作辅助线构造全等三角形是解题的关键.6．如图，在第一个△A 1BC 中，∠B ＝30°，A 1B ＝CB ，在边A 1B 上任取一D ，延长CA 2到A 2，使A 1A 2＝A 1D ，得到第2个△A 1A 2D ，在边A 2B 上任取一点E ，延长A 1A 2到A 3，使A 2A 3＝A 2E ，得到第三个△A 2A 3E ，…按此做法继续下去，第n 个等腰三角形的底角的度数是_____度．【答案】1752n - 【解析】【分析】先根据∠B ＝30°，AB ＝A 1B 求出∠BA 1C 的度数，在由A 1A 2＝A 1D 根据内角和外角的关系求出∠DA 2A 1的度数，同理求出∠EA 3A 2＝754，∠FA 4A 3＝758,即可得到第n 个等腰三角形的底角的度数＝1752n ．【详解】 ∵在△ABA 1中，∠B ＝30°，AB ＝A 1B ， ∴∠BA 1C ＝1802B ︒-∠＝75°， ∵A 1A 2＝A 1D ，∠BA 1C 是△A 1A 2D 的外角， ∴∠DA 2A 1＝12∠BA 1C ＝12×75°＝37.5°；同理可得，∠EA 3A 2＝754，∠FA 4A 3＝758, ∴第n 个等腰三角形的底角的度数＝1752n ．故答案为1752n -．【点睛】此题考查等腰三角形的性质，利用等边对等角求出等腰三角形底角的度数.7．如图，在四边形ABCD中，∠A+∠C＝180°，E、F分别在BC、CD上，且AB＝BE，AD ＝DF，M为EF的中点，DM＝3，BM＝4，则五边形ABEFD的面积是_____．【答案】12【解析】【分析】延长BM至G，使MG＝BM，连接FG、DG，证明△BME≌△GMF（SAS），得出FG＝BE，∠MBE＝∠MGF，证出AB＝FG，证明△DAB≌△DFG（SAS），得出DB＝DG，由等腰三角形的性质即可得DM⊥BM，由五边形ABEFD的面积＝△DBG的面积，可求解．【详解】延长BM至G，使MG＝BM＝4，连接FG、DG，如图所示：∵M为EF中点，∴ME＝MF，在△BME和△GMF中，BM MGBME GMFME MF=⎧⎪∠=∠⎨⎪=⎩，∴△BME≌△GMF（SAS），∴FG＝BE，∠MBE＝∠MGF，S△BEM＝S△GFM，∴FG∥BE，∴∠C＝∠GFC，∵∠A +∠C ＝180°，∠DFG +∠GFC ＝180°，∴∠A ＝∠DFG ，∵AB ＝BE ，∴AB ＝FG ，在△DAB 和△DFG 中， AB FG A DFGAD DF =⎧⎪∠=∠⎨⎪=⎩， ∴△DAB ≌△DFG （SAS ），∴DB ＝DG ，S △DAB ＝S △DFG ，∵MG ＝BM ，∴DM ⊥BM ，∴五边形ABEFD 的面积＝△DBG 的面积＝12×BG ×DM ＝12×8×3＝12，故答案为：12．【点睛】本题考查了全等三角形的判定与性质、平行线的性质、等腰三角形的判定与性质等知识；熟练掌握等腰三角形的判定由性质，证明三角形全等是解题的关键．8．如图：在ABC ∆中，D ，E 为边AB 上的两个点，且BD BC =，AE AC =，若108ACB ∠=︒，则DCE ∠的大小为______.【答案】036【解析】【分析】根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ，用∠A 表示∠AEC,用∠B 表示∠BDC，然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080，∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC,∴01(180)2AEC A ∠=-∠01902A =-∠01(180)2BDC B ∠=-∠ =01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800，∴0180DCE CDE CED ∠=-∠-∠= 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质，注意两条等边所在三角形，依此判断对应的两个底角相等.9．如图，在四边形ABCD 中，∠A=60°， ∠ADC=∠ABC=90°，在AB 、AD 上分别找一点F 、E ，连接CE 、EF 、CF ，当△CEF 的周长最小时，则∠ECF 的度数为______．【答案】60°【解析】【分析】此题需分三步：第一步是作出△CEF 的周长最小时E 、F 的位置（用对称即可）；第二步是证明此时的△CEF 的周长最小（利用两点之间线段最短）；第三步是利用对称性求此时∠ECF 的值.【详解】分别作出C 关于AD 、AB 的对称点分别为C 1、C 2，连接C 1C 2，分别交AD ，AB 于点E 、F 再连接CE 、CF 此时△CEF 的周长最小，理由如下：在AD、AB上任意取E1、F1两点根据对称性：∴CE=C1E，CE1=C1E1，CF=C2F，CF1=C2F1∴△CEF的周长= CE＋EF＋CF= C1E＋EF＋C2F= C1C2而△CE1F1的周长= CE1＋E1F1＋CF1= C1E1＋E1F1＋C2F1根据两点之间线段最短，故C1E1＋E1F1＋C2F1＞C1C2∴△CEF的周长的最小为：C1C2.∵∠A=60°，∠ADC=∠ABC=90°∴∠DCB=360°－∠A－∠ADC－∠ABC=120°∴∠C C1C2＋∠C C2C1=180°－∠DCB=60°根据对称性：∠C C1C2=∠E CD，∠C C2C1=∠F CB∴∠E CD＋∠F CB=∠C C1C2＋∠C C2C1=60°∴∠ECF=∠DCB－（∠E CD＋∠F CB）=60°故答案为：60°【点睛】此题考查的是周长最小值的作图方法（对称点），及周长最小值的证法：两点之间线段最短，掌握周长最小值的作图方法是解决此题的关键.10．已知，∠MON=30°，点A1、A2、A3在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A7B7A8的边长为______．【答案】64a【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，根据30°角所对直角边等于斜边的一半得到A2B2=2B1A2，进而得出A3B3=4B1A2=4a，A4B4=8B1A2=8a，A5B5=16B1A2…从而得到答案．【详解】∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°．∵∠MON=30°，∴∠1=180°﹣120°﹣30°=30°．又∵∠3=60°，∴∠5=180°﹣60°﹣30°=90°．∵∠MON=∠1=30°，∴OA1=A1B1=a，∴A2B1=a．∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°．∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴A2B2=2B1A2，B3A3=2B2A3，∴A3B3=4B1A2=4a，A4B4=8B1A2=8a，A5B5=16B1A2=16a，以此类推：A7B7=64B1A2=64a．故答案为：64a．【点睛】本题考查了等边三角形的性质、等腰三角形的性质以及含30°角的直角三角形的性质，根据已知得出A3B3=4B1A2，A4B4=8B1A2，A5B5=16B1A2进而发现规律是解题的关键．二、八年级数学轴对称三角形选择题（难）11．如图，在等边△ABC中，AD是BC边上的高，∠BDE=∠CDF=30°，在下列结论中：①△ABD≌△ACD；②2DE=2DF=AD；③△ADE≌△ADF；④4BE=4CF=AB．正确的个数是（）A．1 B．2 C．3 D．4【答案】D【解析】【分析】由等边三角形的性质可得BD=DC，AB=AC，∠B=∠C=60°，利用SAS可证明△ABD≌△ACD，从而可判断①正确；利用ASA可证明△ADE≌△ADF，从而可判断③正确；在Rt△ADE与Rt△ADF中，∠EAD=∠FAD=30°，根据30度角所对的直角边等于斜边的一半可得2DE=2DF=AD ，从而可判断②正确；同理可得2BE=2CF=BD ，继而可得4BE=4CF=AB ，从而可判断④正确，由此即可得答案.【详解】∵等边△ABC 中，AD 是BC 边上的高，∴BD=DC ，AB=AC ，∠B=∠C=60°，在△ABD 与△ACD 中90AD AD ADB ADC DB DC =⎧⎪∠=∠=︒⎨⎪=⎩， ∴△ABD ≌△ACD ，故①正确；在△ADE 与△ADF 中60EAD FAD AD ADEDA FDA ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△ADE ≌△ADF ，故③正确；∵在Rt △ADE 与Rt △ADF 中，∠EAD=∠FAD=30°，∴2DE=2DF=AD ，故②正确；同理2BE=2CF=BD ，∵AB=2BD ，∴4BE=4CF=AB ，故④正确，故选D ．【点睛】本题考查了等边三角形的性质、含30度的直角三角形的性质、全等三角形的判定等，熟练掌握相关性质与定理是解题的关键.12．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）A ．511a 32⨯（）B ．511a 23⨯（）C ．611a 32⨯（）D ．611a 23⨯（）【答案】A【解析】连接AD 、DB 、DF ，求出∠AFD=∠ABD=90°，根据HL 证两三角形全等得出∠FAD=60°，求出AD ∥EF ∥GI ，过F 作FZ ⊥GI ，过E 作EN ⊥GI 于N ，得出平行四边形FZNE 得出EF=ZN=13a ，求出GI 的长，求出第一个正六边形的边长是13a ，是等边三角形QKM 的边长的13；同理第二个正六边形的边长是等边三角形GHI 的边长的13；求出第五个等边三角形的边长，乘以13即可得出第六个正六边形的边长．连接AD 、DF 、DB ．∵六边形ABCDEF 是正六边形， ∴∠ABC=∠BAF=∠AFE ，AB=AF ，∠E=∠C=120°，EF=DE=BC=CD ，∴∠EFD=∠EDF=∠CBD=∠BDC=30°，∵∠AFE=∠ABC=120°，∴∠AFD=∠ABD=90°，在Rt △ABD 和RtAFD 中AF=AB {AD=AD∴Rt △ABD ≌Rt △AFD （HL ），∴∠BAD=∠FAD=12×120°=60°， ∴∠FAD+∠AFE=60°+120°=180°，∴AD ∥EF ，∵G 、I 分别为AF 、DE 中点，∴GI ∥EF ∥AD ，∴∠FGI=∠FAD=60°，∵六边形ABCDEF 是正六边形，△QKM 是等边三角形，∴∠EDM=60°=∠M ，∴ED=EM ，同理AF=QF，即AF=QF=EF=EM，∵等边三角形QKM的边长是a，∴第一个正六边形ABCDEF的边长是13a，即等边三角形QKM的边长的13，过F作FZ⊥GI于Z，过E作EN⊥GI于N，则FZ∥EN，∵EF∥GI，∴四边形FZNE是平行四边形，∴EF=ZN=13a，∵GF=12AF=12×13a=16a，∠FGI=60°（已证），∴∠GFZ=30°，∴GZ=12GF=112a，同理IN=112a，∴GI=112a+13a+112a=12a，即第二个等边三角形的边长是12a，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是13×12a；同理第第三个等边三角形的边长是12×12a，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是13×12×12a；同理第四个等边三角形的边长是12×12×12a，第四个正六边形的边长是13×12×12×12a；第五个等边三角形的边长是12×12×12×12a，第五个正六边形的边长是1 3×12×12×12×12a；第六个等边三角形的边长是12×12×12×12×12a，第六个正六边形的边长是1 3×12×12×12×12×12a，即第六个正六边形的边长是13×512（）a，故选A．13．如图，坐标平面内一点A(2，－1)，O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为( )A．2 B．3 C．4 D．5【答案】C【解析】以O点为圆心，OA为半径作圆与x轴有两交点，这两点显然符合题意．以A点为圆心，OA为半径作圆与x轴交与两点（O点除外）．以OA中点为圆心OA长一半为半径作圆与x 轴有一交点．共4个点符合，14．如图，已知△ABC中，AB=AC，AD=AE，∠BAE=30°，则∠DEC等于（）A．7.5°B．10°C．15°D．18°【答案】C【解析】根据等腰三角形性质求出∠C=∠B，根据三角形的外角性质求出∠B=∠C=∠AED+α﹣30°，根据AE=AD，可得∠AED=∠ADE=∠C+α，得出等式∠AED=∠AED+α﹣30°+α，求出α=15°，即得到∠DEC=α=15°，故选C.点睛：本题考查了等腰三角形的性质，三角形的内角和定理，三角形的外角性质等知识点的应用，主要考查学生运用定理进行推理的能力，本题有一点难度，但题型不错．15．如图，在△ABC 中，分别以点A 和点B 为圆心，大于12AB 的长为半径画弧，两弧相交于点M 、N ，作直线MN ，交BC 于点D ，连接AD ，若△ADC 的周长为14，BC=8，则AC 的长为A ．5B ．6C ．7D ．8【答案】A【解析】【分析】根据题意可得MN 是直线AB 的中点，所以可得AD=BD ，BC=BD+CD ，而△ADC 为AC+CD+AD=14，即AC+CD+BD=14，因此可得AC+BC=14，已知BC 即可求出AC .【详解】根据题意可得MN 是直线AB 的中点AD BD ∴=ADC 的周长为14AC CD AD ++=14AC CD BD ++=∴BC BD CD =+14AC BC =∴+已知8BD =6AC ∴= ，故选B【点睛】本题主要考查几何中的等量替换，关键在于MN 是直线AB 的中点，这样所有的问题就解决了.16．如图，AOB α∠=，点P 是AOB ∠内的一定点，点,M N 分别在OA OB 、上移动，当PMN ∆的周长最小时，MPN ∠的值为（）A ．90α+B ．1902α+C ．180α-D ．1802α-【答案】D【解析】【分析】过P 点作角的两边的对称点，在连接两个对称点，此时线段与角两边的交点，构成的三角形周长最小.再根据角的关系求解.【详解】解：过P 点作OB 的对称点1P ，过P 作OA 的对称点2P ,连接12PP ，交点为M,N ，则此时PMN 的周长最小，且△1P NP 和△2PMP 为等腰三角形.此时∠12P PP =180°-α；设∠NPM=x°，则180°-x°=2（∠12P PP -x°）所以 x°=180°-2α 【点睛】求出M,N 在什么位子△PMN 周长最小是解此题的关键.17．如图，ABC ∆中，60BAC ∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ，DE AB ⊥交AB 的延长线于点E ，DF AC ⊥于点F ，现有下列结论：①DE DF =；②DE DF AD +=；③DM 平分EDF ∠；④2AB AC AE +=，其中正确的是（）A ．①②B ．①②③C ．①②④D ．①②③④【答案】C【解析】【分析】 ①由角平分线的性质可知①正确；②由题意可知∠EAD=∠FAD=30°，故此可知ED=12AD，DF=12AD，从而可证明②正确；③若DM平分∠EDF，则∠EDM=90°，从而得到∠ABC为直角三角形，条件不足，不能确定，故③错误；④连接BD、DC，然后证明△EBD≌△DFC，从而得到BE=FC，从而可证明④．【详解】解：如图所示：连接BD、DC．①∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴ED=DF．∴①正确．②∵∠EAC=60°，AD平分∠BAC，∴∠EAD=∠FAD=30°．∵DE⊥AB，∴∠AED=90°．∵∠AED=90°，∠EAD=30°，∴ED=12 AD．同理：DF=12 AD．∴DE+DF=AD．∴②正确．③由题意可知：∠EDA=∠ADF=60°．假设MD平分∠EDF，则∠ADM=30°．则∠EDM=90°，又∵∠E=∠BMD=90°，∴∠EBM=90°．∴∠ABC=90°．∵∠ABC是否等于90°不知道，∴不能判定MD平分∠EDF，故③错误．④∵DM是BC的垂直平分线，∴DB=DC．在Rt△BED和Rt△CFD中DE DFBD DC⎧⎨⎩＝＝，∴Rt△BED≌Rt△CFD．∴BE=FC．∴AB+AC=AE-BE+AF+FC又∵AE=AF，BE=FC，∴AB+AC=2AE．故④正确．综上所述，①②④正确，故选：C．【点睛】本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质，掌握本题的辅助线的作法是解题的关键．18．如图，∠AOB=60°，点P是∠AOB内的定点且OP=3，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（）A36B33C．6 D．3【答案】D【解析】分析：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，利用轴对称的性质得MP=MC，NP=ND，3∠BOP=∠BOD，∠AOP=∠AOC，所以∠COD=2∠AOB=120°，利用两点之间线段最短判断此时△PMN周长最小，作OH⊥CD于H，则CH=DH，然后利用含30度的直角三角形三边的关系计算出CD即可．详解：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，3∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+MC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=12OC=32，CH=3OH=3 2 ,∴CD=2CH=3．故选D．点睛：本题考查了轴对称﹣最短路线问题：熟练掌握轴对称的性质，会利用两点之间线段最短解决路径最短问题．19．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，在直线AC上取一点P，使得△PAB为等腰三角形，则符合条件的点P共有()A．6个B．5个C．4个D．3个【答案】C【解析】【分析】根据等腰三角形的判定定理即可得到结论．【详解】解：根据题意，∵△PAB为等腰三角形，∴可分为：PA=PB，PA=AB，PB=AB三种情况，如图所示：∴符合条件的点P共有4个；故选择：C.本题考查了等腰三角形的判定来解决实际问题，其关键是根据等腰三角形的判定定理解答．20．如果三角形有一个内角为120°，且过某一顶点的直线能将该三角形分成两个等腰三角形，那么这个三角形最小的内角度数是( )A．15°B．40 C．15°或20°D．15°或40°【答案】C【解析】【分析】依据三角形的一个内角的度数为120°，且过某一顶点能将该三角形分成两个等腰三角形，运用分类思想和三角形内角和定理，即可得到该三角形其余两个内角的度数．【详解】如图1，当∠A=120°，AD=AC，DB=DC时，∠ADC=∠ACD=30°，∠DBC=∠DCB=15°，所以，∠DBC=15°，∠ACB=30°+15°=45°；故∠ABC=60°，∠C=80°；如图2，当∠BAC=120°，可以以A为顶点作∠BAD=20°，则∠DAC=100°，∵△APB，△APC都是等腰三角形；∴∠ABD=20°，∠ADC=∠ACD=40°，如图3，当∠BAC=120°，以A为顶点作∠BAD=80°，则∠DAC=40°，∵△APB，△APC都是等腰三角形，∴∠ABD=20°，∠ADC=100°，∠ACD=40°．故选C．本题主要考查了三角形内角和定理以及等腰三角形的性质的运用，解决问题的关键是掌握等腰三角形的性质以及三角形内角和定理．。

八年级上册数学【几何模型三角形轴对称】试卷中考真题汇编[解析版]

八年级上册数学【几何模型三角形轴对称】试卷中考真题汇编[解析版]一、八年级数学全等三角形解答题压轴题（难）1．如图，已知△ABC中，AB＝AC＝20cm，BC＝16cm，点D为AB的中点．（1）如果点P在线段BC上以6cm/s的速度由B点向C点运动，同时点Q在线段CA上由C向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？【答案】（1）①△BPD≌△CQP，理由见解析；②V7.5Q（厘米/秒）；（2）点P、Q在AB边上相遇，即经过了803秒，点P与点Q第一次在AB边上相遇．【解析】【分析】（1）①先求出t=1时BP=BQ=6，再求出PC=10=BD，再根据∠B＝∠C证得△BPD≌△CQP；②根据V P≠V Q，使△BPD与△CQP全等，所以CQ＝BD＝10，再利用点P的时间即可得到点Q的运动速度；（2）根据V Q＞V P，只能是点Q追上点P，即点Q比点P多走AB+AC的路程，设运动x秒，即可列出方程1562202x x，解方程即可得到结果.【详解】（1）①因为t＝1（秒），所以BP＝CQ＝6（厘米）∵AB＝20，D为AB中点，∴BD＝10（厘米）又∵PC＝BC﹣BP＝16﹣6＝10（厘米）∴PC＝BD∵AB＝AC，∴∠B＝∠C，在△BPD与△CQP中，BP CQ B C PC BD =⎧⎪∠=∠⎨⎪=⎩, ∴△BPD ≌△CQP （SAS ），②因为V P ≠V Q ，所以BP ≠CQ ，又因为∠B ＝∠C ，要使△BPD 与△CQP 全等，只能BP ＝CP ＝8，即△BPD ≌△CPQ ，故CQ ＝BD ＝10．所以点P 、Q 的运动时间84663BP t （秒），此时107.543Q CQ V t （厘米/秒）．（2）因为V Q ＞V P ，只能是点Q 追上点P ，即点Q 比点P 多走AB +AC 的路程设经过x 秒后P 与Q 第一次相遇，依题意得1562202x x ，解得x=803(秒) 此时P 运动了8061603（厘米）又因为△ABC 的周长为56厘米，160＝56×2+48，所以点P 、Q 在AB 边上相遇，即经过了803秒，点P 与点Q 第一次在AB 边上相遇．【点睛】此题考查三角形全等的证明，三角形与动点相结合的解题方法，再证明三角形全等时注意顶点的对应关系是证明的关键.2．(1)如图1：在四边形ABCD 中，AB =AD ，∠BAD =120°，∠B =∠ADC =90°．E ，F 分别是BC ，CD 上的点．且∠EAF =60°．探究图中线段EF ，BE ，FD 之间的数量关系．小明同学探究的方法是：延长FD 到点G ．使DG =BE ．连结AG ，先证明△ABE ≌△ADG ，再证明△AEF ≌△AGF ，可得出结论，他的结论是（直接写结论，不需证明）；(2)如图2，若在四边形ABCD 中，AB =AD ，∠B +∠D =180°，E 、F 分别是BC ，CD 上的点，且∠EAF 是∠BAD 的二分之一，上述结论是否仍然成立，并说明理由．(3)如图3，四边形ABCD 是边长为5的正方形，∠EBF =45°，直接写出三角形DEF 的周长．【答案】（1）EF=BE+DF．（2）成立，理由见解析；（3）10.【解析】【分析】（1）如图1，延长FD到G，使得DG=DC,先证△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，进一步根据题意得∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.(2)如图2，延长FD到点G．使DG=BE．连结AG，证得△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，再结合题意得到∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.（3）如图3，延长DC到点G，截取CG=AE，连接BG，先证△AEB≌△CGB，得到BE=BG，∠ABE=∠CBG，结合已知条件得∴∠CBF+∠CBG=45°，再证明△EBF≌△GBF，得到EF=FG，最后求三角形的周长即可.【详解】解答：（1）解：如图1，延长FD到G，使得DG=DC在△ABE和△ADG中，∵DC DGB ADG AB AD=⎧⎪∠=∠⎨⎪=⎩∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵EAF GAFAF AF⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；故答案为：EF=BE+DF．（2）解：结论EF=BE+DF仍然成立；理由：如图2，延长FD到点G．使DG=BE．连结AG在△ABE和△ADG中，∵DG BEB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩，∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵AE AGEAF GAFAF AF=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；（3）解：如图3，延长DC到点G，截取CG=AE，连接BG，在△AEB与△CGB中，∵A BOG AF BF ⎪∠=∠⎨⎪=⎩，∴△AEB ≌△CGB （SAS ），∴BE =BG ，∠ABE =∠CBG ．∵∠EBF =45°，∠ABC =90°，∴∠ABE +∠CBF =45°，∴∠CBF +∠CBG =45°．在△EBF 与△GBF 中，∵BE BG EBF GBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△EBF ≌△GBF （SAS ），∴EF =GF ，∴△DEF 的周长=EF +ED +CF =AE +CF +DE +DF =AD +CD =10．【点睛】本题主要考查了三角形全等的判定和性质，灵活运用全等三角形的性质和判定是解答本题的关键.但本题分为三问，难度不断增加，对提升思维能力大有好处.3．（1）已知△ABC 是等腰三角形，其底边是BC,点D 在线段AB 上，E 是直线BC 上一点，且∠DEC=∠DCE,若∠A 等于60°（如图①）.求证：EB=AD ；（2）若将（1）中的“点D 在线段AB 上”改为“点D 在线段AB 的延长线上”，其他条件不变（如图②），（1）的结论是否成立，并说明理由．【答案】（1）证明见解析（2）证明见解析【解析】试题分析：（1）作DF∥BC 交AC 于F ，由平行线的性质得出∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，证明△ABC 是等边三角形，得出∠ABC=∠ACB=60°，证出△ADF 是等边三角形，∠DFC=120°，得出AD=DF ，由已知条件得出∠FDC=∠DEC，ED=CD ，由AAS 证明△DBE≌△CFD，得出EB=DF ，即可得出结论；（2）作DF∥BC 交AC 的延长线于F ，同（1）证出△DBE≌△CFD，得出EB=DF ，即可得出结论.试题解析：（1）证明：如图，作DF ∥BC 交AC 于F ，则△ADF 为等边三角形∴AD=DF ，又∵ ∠DEC=∠DCB ，∠DEC+∠EDB=60°，∠DCB+∠DCF=60° ，∴ ∠EDB=∠DCA ，DE=CD ，在△DEB 和△CDF 中，120EBD DFC EDB DCF DE CD ，，∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△DEB ≌△CDF ，∴BD=DF ，∴BE=AD .(2). EB=AD 成立；理由如下：作DF ∥BC 交AC 的延长线于F ，如图所示：同（1）得：AD=DF ，∠FDC=∠ECD ，∠FDC=∠DEC ，ED=CD ，又∵∠DBE=∠DFC=60°，∴△DBE ≌△CFD （AAS ），∴EB=DF ，∴EB=AD.点睛：此题主要考查了三角形的综合，考查等边三角形的判定与性质，全等三角形的判定与性质，等腰三角形的判定与性质，等腰直角三角形的判定与性质，平行线的性质等知识，综合性强，有一定的难度，证明三角形全等是解决问题的关键.4．（1）如图1，在Rt△ABC 中，AB AC=，D 、E是斜边BC上两动点，且∠DAE=45°，将△ABE绕点A逆时针旋转90后，得到△AFC，连接DF.（1）试说明：△AED≌△AFD；（2）当BE=3,CE=9时，求∠BCF的度数和DE的长；（3）如图2，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，D是斜边BC所在直线上一点，BD=3，BC=8，求DE2的长.【答案】（1）略（2）∠BCF=90° DE=5 （3）34或130【解析】试题分析：()1由ABE AFC≌，得到AE AF=，BAE CAF∠=∠，45,EAD∠=45,BAE CAD∴∠+∠=45,CAF CAD∴∠+∠=即45.DAF∠=EAD DAF∠=∠，从而得到.AED AFD≌()2由△AED AFD≌得到ED FD=，再证明90DCF∠=︒，利用勾股定理即可得出结论.()3过点A作AH BC⊥于H,根据等腰三角形三线合一得，14.2AH BH BC===1DH BH BD=-=或7,DH BH BD=+=求出AD的长，即可求得2DE.试题解析：()1ABE AFC≌，AE AF=，BAE CAF∠=∠，45,EAD∠=90,BAC∠=45,BAE CAD∴∠+∠=45,CAF CAD∴∠+∠=即45.DAF∠=在AED和AFD中，{AF AEEAF DAEAD AD，=∠=∠=.AED AFD∴≌()2AED AFD≌，ED FD∴=，,90.AB AC BAC =∠=︒45B ACB ∴∠=∠=︒，45ACF ，∠=︒ 90.BCF ∴∠=︒设.DE x =,9.DF DE x CD x ===- 3.FC BE ==222,FC DC DF +=()22239.x x ∴+-=解得： 5.x =故 5.DE = ()3过点A 作AH BC ⊥于H ,根据等腰三角形三线合一得，1 4.2AH BH BC === 1DH BH BD =-=或7,DH BH BD =+= 22217AD AH DH =+=或65.22234DE AD ==或130.点睛：D 是斜边BC 所在直线上一点,注意分类讨论.5．如图，△ABC 中，D 是BC 的中点，过D 点的直线GF 交AC 于F ，交AC 的平行线BG 于G 点，DE ⊥DF ，交AB 于点E ，连结EG 、EF ．（1）求证：BG ＝CF ；（2）请你判断BE +CF 与EF 的大小关系，并说明理由．【答案】（1）详见解析；（2）BE +CF ＞EF ，证明详见解析【解析】【分析】（1）先利用ASA 判定△BGD ≅CFD ，从而得出BG=CF ；（2）利用全等的性质可得GD=FD ，再有DE ⊥GF ，从而得到EG=EF ，两边之和大于第三边从而得出BE+CF ＞EF ．【详解】解：（1）∵BG ∥AC ，∴∠DBG ＝∠DCF ．∵D 为BC 的中点，∴BD ＝CD又∵∠BDG ＝∠CDF ，在△BGD 与△CFD 中，∵DBG DCF BD CD BDG CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BGD ≌△CFD （ASA ）．∴BG ＝CF ．（2）BE +CF ＞EF ．∵△BGD ≌△CFD ，∴GD ＝FD ，BG ＝CF ．又∵DE ⊥FG ，∴EG ＝EF （垂直平分线到线段端点的距离相等）．∴在△EBG 中，BE +BG ＞EG ，即BE +CF ＞EF ．【点睛】本题考查了三角形全等的判定和性质，要注意判定三角形全等的一般方法有：SSS 、SAS 、AAS 、ASA 、HL ．6．如图①，在ABC 中，90BAC ∠=︒，AB AC =，AE 是过A 点的一条直线，且B 、C 在AE 的异侧，BD AE ⊥于D ，CE AE ⊥于E .（1）求证：BD DE CE =+.（2）若将直线AE 绕点A 旋转到图②的位置时（BD CE <），其余条件不变，问BD 与DE 、CE 的关系如何？请予以证明.【答案】（1）见解析；（2）BD=DE-CE ，理由见解析.【解析】【分析】（1）根据已知利用AAS 判定△ABD ≌△CAE 从而得到BD=AE ，AD=CE ，因为AE=AD+DE ，所以BD=DE+CE ；（2）根据已知利用AAS 判定△ABD ≌△CAE 从而得到BD=AE ，AD=CE ，因为AD+AE=BD+CE ，所以BD=DE-CE ．【详解】解：（1）∵∠BAC=90°，BD ⊥AE ，CE ⊥AE ，∴∠BDA=∠AEC=90°，∵∠ABD+∠BAE=90°，∠CAE+∠BAE=90°∴∠ABD=∠CAE ，∵AB=AC ，在△ABD 和△CAE 中，BDA AEC ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△CAE （AAS ），∴BD=AE ，AD=CE ，∵AE=AD+DE ，∴BD=DE+CE ；（2）BD 与DE 、CE 的数量关系是BD=DE-CE ，理由如下：∵∠BAC=90°，BD ⊥AE ，CE ⊥AE ，∴∠BDA=∠AEC=90°，∴∠ABD+∠DAB=∠DAB+∠CAE ，∴∠ABD=∠CAE ，∵AB=AC ，在△ABD 和△CAE 中，BDA AEC ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△CAE （AAS ），∴BD=AE ，AD=CE ，∴AD+AE=BD+CE ，∵DE=BD+CE ，∴BD=DE-CE ．【点睛】此题主要考查全等三角形的判定和性质，常用的判定方法有SSS ，SAS ，AAS ，HL 等．这种类型的题目经常考到，要注意掌握．7．如图1，在长方形ABCD 中，AB=CD=5 cm ， BC=12 cm ，点P 从点B 出发，以2cm/s 的速度沿BC 向点C 运动，设点P 的运动时间为ts ．（1）PC=___cm ；(用含t 的式子表示)（2）当t 为何值时，△ABP ≌△DCP ？．（3）如图2，当点P 从点B 开始运动，此时点Q 从点C 出发，以vcm/s 的速度沿CD 向点D 运动，是否存在这样的v 值，使得某时刻△ABP 与以P ，Q ，C 为顶点的直角三角形全等？若存在，请求出v 的值；若不存在，请说明理由．【答案】（1）()122t -；（2）3t =；（3）存在，2v =或53v =【解析】【分析】（1）根据P 点的运动速度可得BP 的长，再利用BC 的长减去BP 的长即可得到PC 的长；（2）先根据三角形全等的条件得出当BP=CP ，列方程求解即得；（3）先分两种情况：当BP=CQ ，AB=PC 时，△ABP ≌△PCQ ；或当BA=CQ ，PB=PC 时，△ABP ≌△QCP ，然后分别列方程计算出t 的值，进而计算出v 的值．【详解】解：（1）当点P 以2cm/s 的速度沿BC 向点C 运动时间为ts 时2BP tcm =∵12BC cm =∴()122PC BC BP t cm =-=-故答案为：()122t -（2）∵ABP DCP ∆≅∆∴BP CP =∴2122t t =-解得3t =．（3）存在，理由如下：①当BP=CQ ，AB=PC 时，△ABP ≌△PCQ ，∴PC=AB=5∴BP=BC-PC=12-5=7∵2BP tcm =∴2t=7解得t=3.5∴CQ=BP=7，则3.5v=7解得2v =．②当BA CQ =，PB PC =时，ABP QCP ∆≅∆∵12BC cm = ∴162BP CP BC cm === ∵2BP tcm =∴26t =解得3t =∴3CQ vcm = ∵5AB CQ cm ==∴35v = 解得53v =．综上所述，当2v =或53v =时，ABP ∆与以P ，Q ，C 为顶点的直角三角形全等．【点睛】本题考查全等三角形的判定及性质和矩形的性质，解题关键是将动态情况化为某一状态情况，并以这一状态为等量关系建立方程求解．8．如图1，Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D 是BC 边的中点连接AD ，则易证AD ＝BD ＝CD ，即AD ＝12BC ；如图2，若将题中AB ＝AC 这个条件删去，此时AD 仍然等于12BC ．理由如下：延长AD 到H ，使得AH ＝2AD ，连接CH ，先证得△ABD ≌△CHD ，此时若能证得△ABC ≌△CHA ，即可证得AH ＝BC ，此时AD ＝12BC ，由此可见倍长过中点的线段是我们三角形证明中常用的方法．（1）请你先证明△ABC ≌△CHA ，并用一句话总结题中的结论；（2）现将图1中△ABC 折叠（如图3），点A 与点D 重合，折痕为EF ，此时不难看出△BDE 和△CDF 都是等腰直角三角形．BE ＝DE ，CF ＝DF ．由勾股定理可知DE 2+DF 2＝EF 2，因此BE 2+CF 2＝EF 2，若图2中△ABC 也进行这样的折叠（如图4），此时线段BE 、CF 、EF 还有这样的关系式吗？若有，请证明；若没有，请举反例．（3）在（2）的条件下，将图3中的△DEF 绕着点D 旋转（如图5），射线DE 、DF 分别交AB 、AC 于点E 、F ，此时（2）中结论还成立吗？请说明理由．图4中的△DEF 也这样旋转（如图6），直接写出上面的关系式是否成立．【答案】（1）详见解析；（2）有这样分关系式；（3）EF2＝BE2+CF2.【解析】【分析】（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可．（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB≌△HD （SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．（3）图5，图6中，上面的关系式仍然成立．【详解】（1）证明：如图2中，∵BD＝DC，∠ADB＝∠HDC，AD＝HD，∴△ADB≌△HDC（SAS），∴∠B＝∠HCD，AB＝CH，∴AB∥CH，∴∠BAC+∠ACH＝180°，∵∠BAC＝90°，∴∠ACH＝∠BAC＝90°，∵AC＝CA，∴△BAC≌△HCA（SAS），∴AH＝BC，∴AD＝DH＝BD＝DC，∴AD＝12 BC．结论：直角三角形斜边上的中线等于斜边的一半．（2）解：有这样分关系式．理由：如图4中，延长ED 到H 山顶DH ＝DE ．∵ED ＝DH ，∠EDB ＝∠HDC ，DB ＝DC ，∴△EDB ≌△HDC （SAS ），∴∠B ＝∠HCD ，BE ＝CH ，∵∠B +∠ACB ＝90°，∴∠ACB +∠HCD ＝90°，∴∠FCH ＝90°，∴FH 2＝CF 2+CH 2，∵DF ⊥EH ，ED ＝DH ，∴EF ＝FH ，∴EF 2＝BE 2+CF 2．（3）图5，图6中，上面的关系式仍然成立．结论：EF 2＝BE 2+CF 2．证明方法类似（2）．【点睛】本题属于几何变换综合题，考查了旋转变换，翻折变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．9．在等边ABC 中，点D 是边BC 上一点.作射线AD ，点B 关于射线AD 的对称点为点E .连接CE 并延长，交射线AD 于点F .（1）如图，连接AE ，①AE 与AC 的数量关系是__________；②设BAF α∠=，用α表示BCF ∠的大小；（2）如图，用等式表示线段AF ，CF ，EF 之间的数量关系，并证明.【答案】(1)①AB=AE；②∠BCF=α；(2) AF-EF=CF，理由见详解.【解析】【分析】（1）①根据轴对称性，即可得到答案；②由轴对称性，得：AE=AB，∠BAF=∠EAF=α，由ABC是等边三角形，得AB=AC，∠BAC=∠ACB=60°，再根据等腰三角形的性质和三角形内角和等于180°，即可求解；（2）作∠FCG=60°交AD于点G，连接BF，易证∆FCG是等边三角形，得GF=FC，再证∆ACG≅∆BCF(SAS)，从而得AG=BF，进而可得到结论.【详解】（1）①∵点B关于射线AD的对称点为点E，∴AB和AE关于射线AD的对称，∴AB=AE.故答案是：AB=AE；②∵点B关于射线AD的对称点为点E，∴AE=AB，∠BAF=∠EAF=α，∵ABC是等边三角形，∴AB=AC，∠BAC=∠ACB=60°，∴∠EAC=60°-2α，AE=AC，∴∠ACE=1180(602)602αα⎡⎤--=+⎣⎦，∴∠BCF=∠ACE-∠ACB=60α+-60°=α.（2）AF-EF=CF，理由如下：作∠FCG=60°交AD于点G，连接BF，∵∠BAF=∠BCF=α，∠ADB=∠CDF，∴∠ABC=∠AFC=60°，∴∆FCG是等边三角形，∴GF=FC，∵ABC是等边三角形，∴BC=AC，∠ACB=60°，∴∠ACG=∠BCF=α.在∆ACG和∆BCF中，∵CA CBACG BCFCG CF=⎧⎪∠=∠⎨⎪=⎩，∴∆ACG≅∆BCF(SAS)，∴AG=BF，∵点B关于射线AD的对称点为点E，∴AG=BF=EF，∵AF-AG=GF，∴AF-EF=CF.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理，添加辅助线，构造全等三角形，是解题的关键.10．已知：4590ABC A ACB∆∠=∠=，，，点D是AC延长线上一点，且22AD=+，，M是线段CD上一个动点，连接BM，延长MB到H，使得HB MB=，以点B为中心，将线段BH逆时针旋转45，得到线段BQ，连接AQ．（1）依题意补全图形；（2）求证：ABQ AMB∠=∠；（3）点N是射线AC上一点，且点N是点M关于点D的对称点，连接BN，如果QA BN=，求线段AB的长．【答案】（1）见解析；（2）证明见解析；（3）22AB=【解析】【分析】（1）根据题意可以补全图形；（2）根据三角形外角的性质即可证明；（3）作QE ⊥AB ，根据AAS 证得QEB BCM ≅，根据HL 证得Rt QEA Rt BCN ≅，设法证得2AB CD =，设AC BC x ==，则2AB x =，2CD x =，结合已知22AD =+，构建方程即可求解. 【详解】（1）补全图形如下图所示：（2）解：∵∠ABH 是ABM 的一个外角，∴ ABH BAM AMB ∠=∠+∠∵ABH HBQ ABQ ∠=∠+∠ 又∵45HBQ BAM ∠=∠=︒∴ ABQ AMB ∠=∠（3）过Q 作QE ⊥AB ，垂足为E ，如下图：∵⊥QE AB∴90QEB BCM ∠=∠=︒，在QEB 和BCM 中，QEB BCM QBE BMC QB BM ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ QEB BCM ≅(AAS)∴EB CM =，QE BC =，在Rt QEA 和Rt BCN 中∵QE BC =，Q A BN = ∴Rt QEA Rt BCN ≅ (HL)∴AE CN CM MD DN ==++∵点N 是点M 关于点D 的对称点，∴MD DN =∴22AE CM MD EB MD =+=+∴ ()2222AB AE EB EB MD EB MD CD =+=+=+=设AC BC x ==，则AB =，CD x =，又∵2AD =， 2AD AC CD x x =+=+∴22x x += 解得：2x =∴ AB =【点睛】本题主要考查了全等三角形的判定与性质、三角形外角定理、等腰直角三角形的判定与性质等知识点．熟悉全等三角形的判定方法以及正确作出辅助线、构建方程是解答的关键．。

八年级全等三角形中考真题汇编[解析版]

八年级全等三角形中考真题汇编[解析版] 一、八年级数学轴对称三角形填空题（难） 1．在直角坐标系中，O 为坐标原点，已知点 A （1，2），点 P 是 y 轴正半轴上的一点，且△AOP 为等腰三角形，则点 P 的坐标为_____________．【答案】5(0,5),(0,4),0,4⎛⎫ ⎪⎝⎭【解析】【分析】有三种情况：①以O 为圆心，以OA 为半径画弧交y 轴于D ，求出OA 即可；②以A 为圆心，以OA 为半径画弧交y 轴于P ，求出OP 即可；③作OA 的垂直平分线交y 轴于C ，则AC ＝OC ，根据勾股定理求出OC 即可．【详解】有三种情况：①以O 为圆心，以OA 为半径画弧交y 轴于D ，则OA ＝OD ＝22125+=；∴D （0，5）；②以A 为圆心，以OA 为半径画弧交y 轴于P ，OP ＝2×y A =4，∴P （0，4）；③作OA 的垂直平分线交y 轴于C ，则AC ＝OC ，由勾股定理得：OC ＝AC ＝()2212OC +-，∴OC ＝54， ∴C （0，54）；故答案为：5(0,5),(0,4),0,4⎛⎫ ⎪⎝⎭．【点睛】本题主要考查对线段的垂直平分线，等腰三角形的性质和判定，勾股定理，坐标与图形性质等知识点的理解和掌握，能求出符合条件的所有情况是解此题的关键．2．如图，在ABC 中，点A 的坐标为()0,1，点B 的坐标为()0,4，点C 的坐标为()4,3，点D 在第二象限，且ABD 与ABC 全等，点D 的坐标是______．【答案】(－4，2)或(－4，3)【解析】【分析】【详解】把点C 向下平移1个单位得到点D （4，2），这时△ABD 与△ABC 全等，分别作点C ，D 关于y 轴的对称点（-4，3）和（-4，2），所得到的△ABD 与△ABC 全等.故答案为(－4，2)或(－4，3).3．如图，P 为∠AOB 内一定点，M ，N 分别是射线OA ，OB 上一点，当△PMN 周长最小时，∠OPM ＝50°，则∠AOB ＝___________．【答案】40°【解析】【分析】作P 关于OA ，OB 的对称点P 1，P 2．连接OP 1，OP 2．则当M ，N 是P 1P 2与OA ，OB 的交点时，△PMN 的周长最短，根据对称的性质可以证得：∠OP 1M=∠OPM=50°，OP 1=OP 2=OP ，根据等腰三角形的性质即可求解．【详解】如图：作P 关于OA ，OB 的对称点P 1，P 2．连接OP 1，OP 2．则当M ，N 是P 1P 2与OA 、OB 的交点时，△PMN 的周长最短，连接P 1O 、P 2O ，∵PP 1关于OA 对称，∴∠P 1OP=2∠MOP ，OP1=OP ，P 1M=PM ，∠OP 1M=∠OPM=50°同理，∠P 2OP=2∠NOP ，OP=OP 2，∴∠P 1OP 2=∠P 1OP+∠P 2OP=2（∠MOP+∠NOP ）=2∠AOB ，OP 1=OP 2=OP ，∴△P 1OP 2是等腰三角形．∴∠OP 2N=∠OP 1M=50°，∴∠P 1OP 2=180°-2×50°=80°，∴∠AOB=40°，故答案为：40°【点睛】本题考查了对称的性质，正确作出图形，证得△P 1OP 2是等腰三角形是解题的关键．4．如图，在ABC ∆中，点D 是BC 的中点，点E 是AD 上一点，BE AC =．若70C ∠=︒，50DAC ∠=︒ 则EBD ∠的度数为______．【答案】10︒【解析】【分析】延长AD 到F 使DF AD =，连接BF ，通过ACD FDB ≅，根据全等三角形的性质得到CAD BFD ∠=∠，AC BF =，等量代换得BF BE =，由等腰三角形的性质得到F BEF ∠=∠，即可得到BEF CAD ∠=∠，进而利用三角形的内角和解答即可得．【详解】如图，延长AD 到F ，使DF AD =，连接BF ：∵D 是BC 的中点∴BD CD =又∵ADC FDB ∠=∠，AD DF =∴ACD FDB ≅∴AC BF =， CAD F ∠=∠，C DBF ∠=∠∵AC BE =， 70C ︒∠=， 50CAD ︒∠=∴BE BF =， 70DBF ︒∠=∴50BEF F ︒∠=∠=∴180180505080EBF F BEF ︒︒︒︒︒∠=-∠-∠=--=∴807010EBD EBF DBF ︒︒︒∠=∠-∠=-=故答案为：10︒【点睛】本题主要考查的知识点有全等三角形的判定及性质、等腰三角形的性质及三角形的内角和定理，解题的关键在于通过倍长中线法构造全等三角形．5．如图，已知每个小方格的边长为1，A 、B 两点都在小方格的格点（顶点）上，请在图中找一个格点C ，使△ABC 是等腰三角形，这样的格点C 有________个。

全等三角形中考真题汇编[解析版]

全等三角形中考真题汇编［解析版］—s八年级数学轴对称三角形填空题(难)2•如图所示ABC为等边三角形，P是M49C内任一点，PDWAB? PE//BC.PF//AC若厶 43C的周长为12cm，则PD+PE+PF二C航.【答案】4【解析】【分析】先说明四边形HBDP是平行四边形，AAHE和AAHE是等边三角形，然后得到一系列长度相等的线段•最后求替换求和即可.【详解】解：・.• PD I I 4B, PE〃BC•・.四边形HBDP是平行四边形APD-HB• • • MBC为等边三角形周长为12CmAZ B二ZA 二60。

应二4…• PE//BCAZAHE=ZB=60°AZAHE=ZA=60°.• .AAHE是等边三角形AHE二AH•・・ ZHFP 二ZA二60°••・ ZHFP二ZAHE二60。

.・・AAHE是等边三角形，AFP 二PH/\PD 十PE 十PF 二BH 十(HP+PE)二BH 十HE 二BH 十AH 二AB 二4cm故答案为4cm •5 cm时，ZA OB的度数是度.【点睛】本题考查了平行四边形的判定和性质以及等边三角形的性质，掌握等边三角形的性质是解答本题的关键.2•如图，点P是AoB内任意一点，OP二5加,点P与点C关于射线QA对称，点P与点D关于射线OB对称，连接CD交OA于点匕交OB于点F,当的周长是D【答案】30【解析】【分析】根据轴对称得岀OA为PC的垂直平分线’OB是PD的垂直平分线，根据线段垂宜平分线性质得出ZCOA ZAOP:LZCOPfZPoB/DOB IZPOD、PE二CE, OP二OC二5cm2 2PF二FD, OP二OD二5crr\求岀ZkCOD是等边三角形，即可得岀答案.【详解】解：如图示：连接0C.0D,〕点P与点C关于射线OA对称，点P与点D关于射线OB对称•/ .0A为PC的垂直平分线，OB是PD的垂直平分线，VOP 二5cm,：• ZCOA 二ZAOP 二LZCoP, ZPoB 二ZDOB 二LZPOD. PE二CEt OP二OC二5cm, PF二FD, 2 2 OP 二OD 二5cm,VA PEF的周长是5cm,.・・ PE十EF十PF二CE十EF十FD二CD二5cm,CD 二OD 二OD 二5cm»AA OCD是等边三角形，/\Z8D 二60、5 cm时，ZA OB的度数是度.：• ZAoB二AAOP 十ZBoP二丄AC OP + 丄ADOP二IZCoD 二30° ,2 2 2故答案为：30.【点睛】本题考查了线段垂直平分线性质，轴对称性质和等边三角形的性质和判左，能求出ACOD是等边三角形是解此题的关键.3•如图，点P是ZAOB内任意一点，0P二5cm,点M和点N分別是射线0A和射线0B上的动点，PN + PM+MN的最小值是5cm,则ZAOB的度数是__________________________________________ .【答案】30°【解析】试题解析：分别作点P关于OA、OB的对称点C、D旌接CD,分别交OA、OB于点M、N,连接OC、ODxPMxPNsMN,如图所示…点P关于OA的对称点为D,关于OB的对称点为C ,APM-DM r OP^OD , ZDOA=ZPOA ；T点P关于OB的对称点为C,APN-CN , OP二OC r ZCOB二ZPOB .AOC二OP二OD , ZAOB二- ZcOD fVPN十PM十MN的最小值是5cm/\PM+PN十MN二5 ,ADM 十CN + MN二5, 即CD二S二OPjAOC二OD二CD r即AOCD是等边三角形. ・・・ZCOD二60°zZAOB二30。

八年级数学上册全册全套试卷中考真题汇编[解析版]

八年级数学上册全册全套试卷中考真题汇编[解析版]一、八年级数学全等三角形解答题压轴题（难）1．如图，已知△ABC中，AB＝AC＝20cm，BC＝16cm，点D为AB的中点．（1）如果点P在线段BC上以6cm/s的速度由B点向C点运动，同时点Q在线段CA上由C向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？【答案】（1）①△BPD≌△CQP，理由见解析；②V7.5Q（厘米/秒）；（2）点P、Q在AB边上相遇，即经过了803秒，点P与点Q第一次在AB边上相遇．【解析】【分析】（1）①先求出t=1时BP=BQ=6，再求出PC=10=BD，再根据∠B＝∠C证得△BPD≌△CQP；②根据V P≠V Q，使△BPD与△CQP全等，所以CQ＝BD＝10，再利用点P的时间即可得到点Q的运动速度；（2）根据V Q＞V P，只能是点Q追上点P，即点Q比点P多走AB+AC的路程，设运动x秒，即可列出方程1562202x x，解方程即可得到结果.【详解】（1）①因为t＝1（秒），所以BP＝CQ＝6（厘米）∵AB＝20，D为AB中点，∴BD＝10（厘米）又∵PC＝BC﹣BP＝16﹣6＝10（厘米）∴PC＝BD∵AB＝AC，∴∠B＝∠C，在△BPD与△CQP中，BP CQ B C PC BD =⎧⎪∠=∠⎨⎪=⎩, ∴△BPD ≌△CQP （SAS ），②因为V P ≠V Q ，所以BP ≠CQ ，又因为∠B ＝∠C ，要使△BPD 与△CQP 全等，只能BP ＝CP ＝8，即△BPD ≌△CPQ ，故CQ ＝BD ＝10．所以点P 、Q 的运动时间84663BP t （秒），此时107.543Q CQ V t （厘米/秒）．（2）因为V Q ＞V P ，只能是点Q 追上点P ，即点Q 比点P 多走AB +AC 的路程设经过x 秒后P 与Q 第一次相遇，依题意得1562202x x ，解得x=803(秒) 此时P 运动了8061603（厘米）又因为△ABC 的周长为56厘米，160＝56×2+48，所以点P 、Q 在AB 边上相遇，即经过了803秒，点P 与点Q 第一次在AB 边上相遇．【点睛】此题考查三角形全等的证明，三角形与动点相结合的解题方法，再证明三角形全等时注意顶点的对应关系是证明的关键.2．如图，在△ABC 中，∠ABC 为锐角，点D 为直线BC 上一动点，以AD 为直角边且在AD 的右侧作等腰直角三角形ADE ，∠DAE ＝90°，AD ＝AE ．（1）如果AB ＝AC ，∠BAC ＝90°．①当点D 在线段BC 上时，如图1，线段CE 、BD 的位置关系为___________，数量关系为___________②当点D 在线段BC 的延长线上时，如图2，①中的结论是否仍然成立，请说明理由．（2）如图3，如果AB ≠AC ，∠BAC ≠90°，点D 在线段BC 上运动．探究：当∠ACB 多少度时，CE ⊥BC ？请说明理由．【答案】（1）①垂直，相等．②都成立，理由见解析；（2）45°，理由见解析【解析】【分析】（1）①根据∠BAD=∠CAE ，BA=CA ，AD=AE ，运用“SAS ”证明△ABD ≌△ACE ，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE 、BD 之间的关系；②先根据“SAS ”证明△ABD ≌△ACE ，再根据全等三角形性质得出对应边相等，对应角相等，即可得到①中的结论仍然成立；（2）先过点A 作AG ⊥AC 交BC 于点G ，画出符合要求的图形，再结合图形判定△GAD ≌△CAE ，得出对应角相等，即可得出结论．【详解】（1）：（1）CE 与BD 位置关系是CE ⊥BD ，数量关系是CE=BD ．理由：如图1，∵∠BAD=90°-∠DAC ，∠CAE=90°-∠DAC ，∴∠BAD=∠CAE ．又 BA=CA ，AD=AE ，∴△ABD ≌△ACE （SAS ）∴∠ACE=∠B=45°且 CE=BD ．∵∠ACB=∠B=45°，∴∠ECB=45°+45°=90°，即 CE ⊥BD ．故答案为垂直，相等；②都成立，理由如下：∵∠BAC ＝∠DAE ＝90°，∴∠BAC ＋∠DAC ＝∠DAE ＋∠DAC ，∴∠BAD ＝∠CAE ，在△DAB 与△EAC 中，AD AE BAD CAE AB AC ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△DAB ≌△EAC ，∴CE ＝BD ，∠B ＝∠ACE ，∴∠ACB ＋∠ACE ＝90°，即CE ⊥BD ；（2）当∠ACB＝45°时，CE⊥BD（如图）．理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC＝90°﹣45°＝45°，∴∠ACB＝∠AGC＝45°，∴AC＝AG，在△GAD与△CAE中，AC AGDAG EACAD AE⎧⎪∠∠⎨⎪⎩＝＝＝∴△GAD≌△CAE，∴∠ACE＝∠AGC＝45°，∠BCE＝∠ACB＋∠ACE＝45°＋45°＝90°，即CE⊥B C．3．在ABC中，AB AC=，点D在BC边上，且60,ADB E∠=︒是射线DA上一动点(不与点D重合，且DA DB≠)，在射线DB上截取DF DE=，连接EF．()1当点E在线段AD上时，①若点E与点A重合时，请说明线段BF DC=；②如图2，若点E不与点A重合，请说明BF DC AE=+；()2当点E在线段DA的延长线上()DE DB>时，用等式表示线段,,AE BF CD之间的数量关系(直接写出结果，不需要证明)．【答案】（1）①证明见解析；②证明见解析；（2）BF＝AE-CD【解析】【分析】（1）①根据等边对等角，求到B C∠=∠，再由含有60°角的等腰三角形是等边三角形得到ADF∆是等边三角形，之后根据等边三角形的性质以及邻补角的性质得到120AFB ADC∠=∠=︒，推出ABF ACD∆∆≌，根据全等三角形的性质即可得出结论；②过点A做AG∥EF交BC于点G，由△DEF为等边三角形得到DA＝DG，再推出AE＝GF，根据线段的和差即可整理出结论；（2）根据题意画出图形，作出AG，由（1）可知，AE=GF，DC=BG，再由线段的和差和等量代换即可得到结论．【详解】（1）①证明：AB AC=B C∴∠=∠,60DF DE ADB=∠=︒，且E与A重合，ADF∴∆是等边三角形60ADF AFD∴∠=∠=︒120AFB ADC∴∠=∠=︒在ABF∆和ACD∆中AFB ADCB CAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩ABF ACD∴∆∆≌BF DC∴=②如图2，过点A做AG∥EF交BC于点G，∵∠ADB＝60°DE＝DF∴△DEF为等边三角形∵AG∥EF∴∠DAG＝∠DEF＝60°，∠AGD＝∠EFD＝60°∴∠DAG＝∠AGD∴DA＝DG∴DA－DE＝DG－DF，即AE＝GF由①易证△AGB≌△ADC∴BG＝CD∴BF＝BG＋GF＝CD＋AE（2）如图3，和（1）中②相同，过点A做AG∥EF交BC于点G，由（1）可知，AE=GF，DC=BG，∴+=+==BF CD BF BG GF AE=-．故BF AE CD【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．4．探究与发现：如图（1）所示的图形，像我们常见的学习用品一圆规，我们，不妨把这样图形叫做“规形图（1）观察“规形图（1）”，试探究∠BDC与∠A、∠B、∠C之间的数量关系，并说明理由；（2）请你直接利用以上结论，解决以下问题：①如图（2），把一块三角尺XYZ放置在△ABC上使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝40°，则∠ABX+∠ACX＝°．②如图（3），DC平分∠ADB，EC平分∠AEB，若∠DAE＝40°，∠DBE＝130°，求∠DCE 的度数．【答案】（1）∠BDC＝∠BAC+∠B+∠C，理由见解析；（2）①50；②∠DCE＝85°．【解析】【分析】（1）首先连接AD并延长至点F，然后根据外角的性质，即可判断出∠BDC＝∠BAC+∠B+∠C；（2）①由（1）可得∠A+∠ABX+∠ACX＝∠X，然后根据∠A＝40°，∠X＝90°，即可求解；（3）②由∠A＝40°，∠DBE＝130°，求出∠ADE+∠AEB的值，然后根据∠DCE＝∠A+∠ADC+∠AEC，求出∠DCE的度数即可.【详解】（1）如图，∠BDC＝∠BAC+∠B+∠C，理由是：过点A、D作射线AF，∵∠FDC＝∠DAC+∠C，∠BDF＝∠B+∠BAD，∴∠FDC+∠BDF＝∠DAC+∠BAD+∠C+∠B，即∠BDC＝∠BAC+∠B+∠C；（2）①如图（2），∵∠X＝90°，由（1）知：∠A+∠ABX+∠ACX＝∠X＝90°，∵∠A＝40°，∴∠ABX+∠ACX＝50°，故答案为：50；②如图（3），∵∠A＝40°，∠DBE＝130°，∴∠ADE+∠AEB＝130°﹣40°＝90°，∵DC平分∠ADB，EC平分∠AEB，∴∠ADC＝12∠ADB，∠AEC＝12∠AEB，∴∠ADC+∠AEC＝1(ADB AEB)2∠+∠＝45°，∴∠DCE＝∠A+∠ADC+∠AEC＝40°+45°＝85°．【点睛】本题主要考查了三角形外角性质以及角平分线的定义的运用，熟知三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.5．如图，在边长为 4 的等边△ABC 中，点 D 从点A 开始在射线 AB 上运动，速度为 1 个单位/秒，点F 同时从 C 出发，以相同的速度沿射线 BC 方向运动，过点D 作 DE⊥AC，连结DF 交射线 AC 于点 G(1)当 DF⊥AB 时，求 t 的值；(2)当点 D 在线段 AB 上运动时，是否始终有 DG=GF?若成立，请说明理由。

全等三角形中考真题汇编[解析版]

故答案为：4．
【点睛】
此题主要考查等腰三角形的判定及坐标与图形性质的综合运用，注意分类讨论思想的运用是解题关键．
2．在直角坐标系中，O为坐标原点，已知点A（1，2），点P是y轴正半轴上的一点，且△AOP为等腰三角形，则点P的坐标为_____________．
【答案】
【解析】
【分析】
有三种情况：①以O为圆心，以OA为半径画弧交y轴于D，求出OA即可；②以A为圆心，以OA为半径画弧交y轴于P，求出OP即可；③作OA的垂直平分线交y轴于C，则AC＝OC，根据勾股定理求出OC即可．
全等三角形中考真题汇编[解析版]
一、八年级数学轴对称三角形填空题（难）
1．如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P有_____个．
【答案】4
【解析】
【分析】
由A点坐标可得OA=2 ，∠AOP＝45°，分别讨论OA为腰和底边，求出点P在x轴正半轴和负半轴时，△APO是等腰三角形的P点坐标即可.
∵点∵AP=OP，
∴∠OAP=∠AOP=45°，
∴∠OPA=90°，
∴OP=2，
∴P点坐标为（2，0）.
（2）当点P在x轴负半轴上，
③以OA为腰时，
∵A的坐标是（2，2），
∴OA＝2 ，
∴OA＝OP＝2 ，
∴P的坐标是（﹣2 ，0）．
综上所述：P的坐标是（2，0）或（4，0）或（2 ，0）或（﹣2 ，0）．
【解析】
【分析】
先求出∠DAO=50°，分三种情况讨论：①AO=AD，则∠AOD=∠ADO，②OA=OD，则∠OAD=∠ADO，③OD=AD，则∠OAD=∠AOD，分别求出α的角度即可.
【详解】
解：∵设∠CBO=∠CAD=a，∠ABO=b，∠BAO=c，∠CAO=d，

数学八年级上册全等三角形中考真题汇编[解析版]

数学八年级上册全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）∥，1．如图所示，ABC为等边三角形，P是ABC内任一点，PD AB，PE BC++=____cm．∥，若ABC的周长为12cm，则PD PE PFPF AC【答案】4【解析】【分析】先说明四边形HBDP是平行四边形，△AHE和△AHE是等边三角形，然后得到一系列长度相等的线段,最后求替换求和即可．【详解】∥解：∵PD AB，PE BC∴四边形HBDP是平行四边形∴PD=HB∵ABC为等边三角形,周长为12cm∴∠B=∠A=60°,AB=4∥∵PE BC∴∠AHE=∠B=60°∴∠AHE=∠A=60°∴△AHE是等边三角形∴HE=AH∵∠HFP=∠A=60°∴∠HFP=∠AHE=60°∴△AHE是等边三角形，∴FP=PH∴PD+PE+PF=BH+(HP+PE)=BH+HE=BH+AH=AB=4cm故答案为4cm．【点睛】本题考查了平行四边形的判定和性质以及等边三角形的性质，掌握等边三角形的性质是解答本题的关键．∆中取点P使得PA，PB，PC的长分别为3， 4， 5，则2．如图，在等边ABCAPC APB S S ∆∆+=_________．【答案】936 【解析】【分析】把线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS 证得△ADB ≌△APC ，连接PD ，根据旋转的性质知△APD 是等边三角形，利用勾股定理的逆定理可得△PBD 为直角三角形，∠BPD ＝90︒，由△ADB ≌△APC 得S △ADB ＝S △APC ，则有S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ，根据等边3S △ADP ＋S △BPD ＝332＋12×3×4＝936+．【详解】将线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，连接PD∴AD ＝AP ，∠DAP ＝60︒，又∵△ABC 为等边三角形，∴∠BAC ＝60︒，AB ＝AC ，∴∠DAB ＋∠BAP ＝∠PAC ＋∠BAP ，∴∠DAB ＝∠PAC ，又AB=AC,AD=AP∴△ADB ≌△APC∵DA ＝PA ，∠DAP ＝60︒，∴△ADP 为等边三角形，在△PBD 中，PB ＝4，PD ＝3，BD ＝PC ＝5，∵32＋42＝52，即PD 2＋PB 2＝BD 2，∴△PBD 为直角三角形，∠BPD ＝90︒，∵△ADB ≌△APC ，∴S △ADB ＝S △APC ，∴S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ＝34×32＋12×3×4＝9364+．故答案为：9364 ．【点睛】本题考查了等边三角形的性质与判定，解题的关键是熟知旋转的性质作出辅助线进行求解．3．如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD，当△AOD是等腰三角形时，求α的角度为______【答案】110°、125°、140°【解析】【分析】先求出∠DAO=50°，分三种情况讨论：①AO=AD，则∠AOD=∠ADO，②OA=OD，则∠OAD=∠ADO，③OD=AD，则∠OAD=∠AOD，分别求出α的角度即可.【详解】解：∵设∠CBO=∠CAD=a，∠ABO=b，∠BAO=c，∠CAO=d，则a+b=60°，b+c=180°﹣110°=70°，c+d=60°，∴b﹣d=10°，∴（60°﹣a）﹣d=10°，∴a+d=50°，即∠DAO=50°，分三种情况讨论：①AO=AD，则∠AOD=∠ADO，∴190°﹣α=α﹣60°，∴α=125°；②OA=OD，则∠OAD=∠ADO，∴α﹣60°=50°，∴α=110°；③OD=AD，则∠OAD=∠AOD，∴190°﹣α=50°，∴α=140°；所以当α为110°、125°、140°时，三角形AOD是等腰三角形，故答案为：110°、125°、140°.【点睛】本题是对等边三角形的考查，熟练掌握等边三角形的性质定理及分类讨论是解决本题的关键.4．如图，点P是AOB∠内任意一点，OP=5 cm，点M和点N分别是射线OA和射线OB上的动点，PN PM MN++的最小值是5 cm，则AOB∠的度数是__________．【答案】30°【解析】试题解析：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示：∵点P关于OA的对称点为D，关于OB的对称点为C，∴PM=DM，OP=OD，∠DOA=∠POA；∵点P关于OB的对称点为C，∴PN=CN，OP=OC，∠COB=∠POB，∴OC=OP=OD，∠AOB=12∠COD，∵PN+PM+MN的最小值是5cm，∴PM+PN+MN=5，∴DM+CN+MN=5，即CD=5=OP，∴OC=OD=CD，即△OCD是等边三角形，∴∠COD=60°，∴∠AOB=30°．5．如图，线段AB，DE的垂直平分线交于点C，且72ABC EDC∠=∠=︒，92AEB∠=︒，则EBD∠的度数为 ________ ．【答案】128︒【解析】【分析】连接CE，由线段AB，DE的垂直平分线交于点C，得CA=CB，CE=CD，ACB=∠ECD=36°，进而得∠ACE=∠BCD，易证∆ACE≅∆BCD，设∠AEC=∠BDC=x，得则∠BDE=72°-x，∠CEB=92°-x，BDE中，∠EBD=128°，根据三角形内角和定理，即可得到答案．【详解】连接CE，∵线段AB，DE的垂直平分线交于点C，∴CA=CB，CE=CD，∵72ABC EDC∠=∠=︒=∠DEC，∴∠ACB=∠ECD=36°，∴∠ACE=∠BCD，在∆ACE与∆BCD中，∵CA CBACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩，∴∆ACE≅∆BCD（SAS），∴∠AEC=∠BDC，设∠AEC=∠BDC=x，则∠BDE=72°-x，∠CEB=92°-x，∴∠BED=∠DEC-∠CEB=72°-（92°-x）=x-20°，∴在∆BDE中，∠EBD=180°-（72°-x）-（x-20°）=128°．故答案是：128︒．【点睛】本题主要考查中垂线的性质，三角形全等的判定和性质定理以及三角形内角和定理，添加辅助线，构造全等三角形，是解题的关键．6．等腰三角形顶角为30°，腰长是4cm，则三角形的面积为__________【答案】4【解析】如图，根据30°角所对直角边等于斜边的一半的性质，可由等腰三角形的顶角为30°，腰长是4cm，可求得BD=12AB =4×12=2，因此此三角形的面积为：S=12AC•BD=12×4×2=8×12=4（cm2）．故答案是：4．7．如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法：①AD是∠BAC的平分线；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△DAC：S△ABC＝1：3.其中正确的是__________________．(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP，MP，根据SSS定理可得△ANP≌△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30°，根据直角三角形的性质可知∠ADC=60°；③根据∠1=∠B可知AD=BD，故可得出结论；④先根据直角三角形的性质得出∠2=30°，CD=12AD，再由三角形的面积公式即可得出结论．【详解】①连接NP，MP．在△ANP与△AMP中，∵AN AMNP MPAP AP=⎧⎪=⎨⎪=⎩，∴△ANP≌△AMP，则∠CAD=∠BAD，故AD是∠BAC的平分线，故此选项正确；②∵在△ABC中，∠C=90°，∠B=30°，∴∠CAB=60°．∵AD是∠BAC的平分线，∴∠1=∠2=12∠CAB=30°，∴∠3=90°﹣∠2=60°，∴∠ADC=60°，故此选项正确；③∵∠1=∠B=30°，∴AD=BD，∴点D在AB的中垂线上，故此选项正确；④∵在Rt△ACD中，∠2=30°，∴CD=12AD，∴BC=BD+CD=AD+12AD=32AD，S△DAC=12AC•CD=14AC•AD，∴S △ABC=12AC•BC=12AC•32AD=34AC•AD，∴S△DAC：S△ABC=1：3，故此选项正确．故答案为①②③④．【点睛】本题考查的是作图﹣基本作图，熟知角平分线的作法是解答此题的关键．8．在△ABC 中，∠ACB＝90º，D、E 分别在 AC、AB 边上，把△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，若△CFD 与△BFE 都是等腰三角形，则∠BAC 的度数为_________．【答案】45°或60°【解析】【分析】根据题意画出图形，设∠BAC的度数为x，则∠B=90°-x，∠EFB =135°-x，∠BEF=2x-45°，当△BFE 都是等腰三角形，分三种情况讨论，即可求解.【详解】∵∠ACB＝90º，△CFD是等腰三角形，∴∠CDF=∠CFD=45°，设∠BAC的度数为x，∴∠B=90°-x，∵△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，∴∠DFE=∠BAC=x，∴∠EFB=180°-45°-x=135°-x，∵∠ADE=∠FDE，∴∠ADE=（180°-45°）÷2=67.5°，∴∠AED=180°-∠ADE-∠BAC=180°-67.5° -x=112.5°-x，∴∠DEF=∠AED=112.5°-x，∴∠BEF=180°-∠AED-∠DEF=180°-（112.5°-x）-（112.5°-x）=2x-45°，∵△BFE 都是等腰三角形，分三种情况讨论：①当FE=FB时，如图1，则∠BEF=∠B，∴90-x=2x-45，解得：x=45；②当BF=BE时，则∠EFB=∠BEF，∴135-x=2x-45，解得：x=60，③当EB=EF时，如图2，则∠B=∠EFB，∴135-x=90-x，无解，∴这种情况不存在.综上所述：∠BAC 的度数为：45°或60°.故答案是：45°或60°.图1 图2【点睛】本题主要考查等腰三角形的性质定理，用代数式表示角度，并进行分类讨论，是解题的关键.9．如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，则BC=_____cm．【答案】8cm.【解析】【详解】解：如图，延长ED交BC于M，延长AD交BC于N，作DF∥BC，∵AB=AC，AD平分∠BAC，∴AN⊥BC，BN=CN，∵∠EBC=∠E=60°，∴△BEM为等边三角形，∴△EFD为等边三角形，∵BE=6cm，DE=2cm，∴DM=4，∵△BEM为等边三角形，∴∠EMB=60°，∵AN⊥BC，∴∠DNM=90°，∴∠NDM=36°，∴NM=2，∴BN=4，∴BC=8．10．如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB 以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P、Q同时出发，用t(s)表示移动的时间，当t=_____s时，△POQ是等腰三角形.【答案】103或10【解析】【分析】根据△POQ是等腰三角形，分两种情况进行讨论：点P在AO上，点P在BO上，分别计算，即可得解.【详解】当PO=QO 时，△POQ 是等腰三角形，如图1所示当点P 在AO 上时，∵PO=AO-AP=10-2t ，OQ=t当PO=QO 时，102t t -=解得103t =当PO=QO 时，△POQ 是等腰三角形，如图2所示当点P 在BO 上时∵PO=AP-AO=2t-10，OQ=t当PO=QO 时，210t t -=解得10t =故答案为：103或10 【点睛】本题考查等腰三角形的性质及动点问题，熟练掌握等腰三角形的性质以及分类讨论思想是解题关键.二、八年级数学轴对称三角形选择题（难）11．如图，120AOB ∠=︒，OP 平分AOB ∠，且2OP =，若点M N 、分别在OA OB 、上，且PMN ∆为等边三角形，则满足上述条件的PMN ∆有（）A ．1个B ．2个C ．3个D ．无数个【答案】D【解析】【分析】根据题意在OA 、OB 上截取OE=OF=OP ，作∠MPN=60°，只要证明△PEM ≌△PON 即可反推出△PMN 是等边三角形满足条件，以此进行分析即可得出结论.【详解】解：如图在OA 、OB 上截取OE=OF=OP ，作∠MPN=60°．∵OP 平分∠AOB ，120AOB ∠=︒，∴∠EOP=∠POF=60°，∵OE=OF=OP ，∴△OPE ，△OPF 是等边三角形，∴EP=OP ，∠EPO=∠OEP=∠PON=∠MPN=60°，∴∠EPM=∠OPN ，在△PEM 和△PON 中，PEM PON PE POEPM OPN ∠⎪∠⎧⎩∠⎪∠⎨＝＝＝ ∴△PEM ≌△PON （ASA ）．∴PM=PN ，∵∠MPN=60°，∴△PNM 是等边三角形，∴只要∠MPN=60°，△PMN 就是等边三角形，故这样的三角形有无数个．故选：D ．【点睛】本题考查等边三角形的判定和性质、全等三角形的判定和性质、角平分线的定义等知识，解题的关键是正确添加辅助线并构造全等三角形.12．如图所示，△ABP 与△CDP 是两个全等的等边三角形，且PA ⊥PD ，有下列四个结论：①∠PBC ＝15°，②AD ∥BC ，③PC ⊥AB ，④四边形ABCD 是轴对称图形，其中正确的个数为（）A ．1个B ．2个C ．3个D ．4个【答案】D【解析】【分析】根据周角的定义先求出∠BPC 的度数，再根据对称性得到△BPC 为等腰三角形，∠PBC 即可求出；根据题意：有△APD 是等腰直角三角形；△PBC 是等腰三角形；结合轴对称图形的定义与判定，可得四边形ABCD 是轴对称图形，进而可得②③④正确．【详解】根据题意，BPC 36060290150∠=-⨯-= ， BP PC =，()PBC 180150215∠∴=-÷=，①正确；根据题意可得四边形ABCD 是轴对称图形，④正确；∵∠DAB+∠ABC=45°+60°+60°+15°=180°，∴AD//BC ，②正确；∵∠ABC+∠BCP=60°+15°+15°=90°，∴PC ⊥AB ，③正确，所以四个命题都正确，故选D ．【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、等腰三角形的判定与性质、轴对称图形的定义与判定等，熟练掌握各相关性质与定理是解题的关键.13．如图，在平面直角坐标系中，A （a ，0），B （0，a ），等腰直角三角形ODC 的斜边经过点B ，OE ⊥AC ，交AC 于E ，若OE ＝2，则△BOD 与△AOE 的面积之差为（）A．2 B．3 C．4 D．5【答案】A【解析】【分析】首先证明△DOB≌△COA（SAS），推出S△DOB﹣S△AOE=S△EOC，再证明△OEC是等腰直角三角形即可解决问题．【详解】∵A（a，0），B（0，a），∴OA=OB．∵△ODC是等腰直角三角形，∴OD=OC，∠D=∠DCO=45°．∵∠DOC=∠BOA=90°，∴∠DOB=∠COA．在△DOB和△COA中，∵OD=OC，∠DOB=∠COA，OB=OA，∴△DOB≌△COA（SAS），∴∠D=∠OCA=45°，S△DOB﹣S△AOE=S△EOC．∵OE⊥AC，∴∠OEC=90°，∴△CEO是等腰直角三角形，∴OE=EC=2，∴S△DOB﹣S△AOE=S△EOC12=⨯2×2=2．故选A．【点睛】本题考查了等腰直角三角形的性质和判定，全等三角形的判定和性质等知识，解题的关键是证明△OEC是等腰直角三角形．14．如图，△ABC是等边三角形，AQ＝PQ，PR⊥AB于点R，PS⊥AC于点S，PR＝PS，则下列结论：①AP⊥BC；②AS＝AR；③QP∥AR；④△BRP≌△QSP.正确的有( )A．1个B．2个C．3个D．4个【答案】D【解析】【分析】根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC，根据等腰三角形“三线合一”的性质判断出①正确；根据HL证明Rt△APR≌Rt△APS，即可判断②正确；根据等边对等角的性质可得∠APQ=∠PAQ，根据三角形外角的性质得到然后得到∠PQC=2∠PAC=60°=∠BAC，然后根据同位角相等两直线平行可得QP∥AB，从而判断出③正确，④由③易证△QPC是等边三角形，得到PQ=PC，等量代换得到BP=PQ，用HL证明Rt△BRP≌Rt△QSP，即可得到④正确．【详解】∵△ABC是等边三角形，PR⊥AB，PS⊥AC，且PR=PS，∴P在∠A的平分线上．∵AB=AC，∴AP⊥BC，故①正确；∵PA=PA，PR=PS，∴Rt△APR≌Rt△APS，∴AS=AR，故②正确；∵AQ=PQ，∴∠APQ=∠PAQ，∴∠PQC=2∠PAC=60°=∠BAC，∴PQ∥AR，故③正确；由③得：△PQC是等边三角形，∴△PQS≌△PCS，∴PQ=PC．又∵AB=AC，AP⊥BC，∴BP=PC，∴BP=PQ．∵PR=PS，∴Rt△BRP≌Rt△QSP，故④也正确．∵①②③④都正确．故选D．【点睛】本题考查了等腰三角形的性质、全等三角形的判定与性质以及等边三角形的判定与性质，准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键．15．如图所示，在等边△ABC中，E是AC边的中点，AD是BC边上的中线，P是AD上的动点，若AD=3，则EP＋CP的最小值为（）A．2 B．3 C．4 D．5【答案】B【解析】由等边三角形的性质得，点B，C关于AD对称，连接BE交AD于点P，则EP+CP=BE最小，又BE=AD，所以EP+CP的最小值是3.故选B.点睛：本题主要考查了等边三角形的性质和轴对称的性质，求一条定直线上的一个动点到定直线的同旁的两个定点的距离的最小值，常用的方法是，①确定两个定点中的一个关于定直线的对称点；②连接另一个定点与对称点，与定直线的交点就是两线段和的值最小时，动点的位置.16．如图，四边形ABCD中，∠C=，∠B=∠D=，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF的度数为（）．A．B．C．D．【答案】D【解析】【分析】【详解】作点A关于直线BC和直线CD的对称点G和H，连接GH，交BC、CD于点E、F，连接AE、AF，则此时△AEF的周长最小，由四边形的内角和为360°可知，∠BAD=360°-90°-90°-50°=130°，即∠1+∠2+∠3=130°①，由作图可知，∠1=∠G，∠3=∠H，△AGH的内角和为180°，则2（∠1+∠3）+ ∠2=180°②，又①②联立方程组，解得∠2=80°．故选D．考点：轴对称的应用；路径最短问题．17．如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且速度都为1cm/s，连接AQ、CP交于点M，下面四个结论:①BP＝CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第43秒或第83秒时，△PBQ为直角三角形，正确的有几个 ( )A．1 B．2 C．3 D．4【答案】C【解析】【分析】①等边三角形ABC中，AB=BC，而AP=BQ，所以BP=CQ．②根据等边三角形的性质，利用SAS证明△ABQ≌△CAP；③由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP，从而得到∠CMQ=60°；④设时间为t秒，则AP=BQ=tcm，PB=（4-t）cm，当∠PQB=90°时，因为∠B=60°，所以PB=2BQ，即4-t=2t故可得出t的值，当∠BPQ=90°时，同理可得BQ=2BP，即t=2（4-t），由此两种情况即可得出结论．【详解】①在等边△ABC中，AB=BC．∵点P、Q的速度都为1cm/s，∴AP=BQ，∴BP=CQ．只有当CM=CQ时，BP=CM．故①错误；②∵△ABC是等边三角形∴∠ABQ=∠CAP，AB=CA，又∵点P、Q运动速度相同，∴AP=BQ，在△ABQ与△CAP中，∵AB CAABQ CAP AP BQ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABQ≌△CAP（SAS）．故②正确；③点P、Q在运动的过程中，∠QMC不变．理由：∵△ABQ≌△CAP，∴∠BAQ=∠ACP，∵∠QMC=∠ACP+∠MAC，∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°．故③正确；④设时间为t秒，则AP=BQ=tcm，PB=（4-t）cm，当∠PQB=90°时，∵∠B=60°，∴PB=2BQ，即4-t=2t，t=43，当∠BPQ=90°时，∵∠B=60°，∴BQ=2BP，得t=2（4-t），t=83，∴当第43秒或第83秒时，△PBQ 为直角三角形．故④正确．正确的是②③④，故选C ．【点睛】此题是一个综合性题目，主要考查等边三角形的性质、全等三角形的判定与性质等知识．熟知等边三角形的三个内角都是60°是解答此题的关键．18．如图，ABC △是等边三角形，ABD △是等腰直角三角形，∠BAD =90°，AE ⊥BD 于点E ．连CD 分别交AE ，AB 于点F ，G ，过点A 做AH ⊥CD 交BD 于点H ，则下列结论：①∠ADC =15°；②AF =AG ；③AH =DF ；④△ADF ≌△BAH ；⑤DF =2EH .其中正确结论的个数为（）A ．5B ．4C ．3D ．2【答案】B【解析】【分析】 ①根据△ABC 为等边三角形，△ABD 为等腰直角三角形，可以得出各角的度数以及DA=AC ，即可作出判断；②分别求出∠AFG 和∠AGD 的度数，即可作出判断；④根据三角形内角和定理求出∠HAB 的度数，求证EHG DFA ∠=∠，利用AAS 即可证出两个三角形全等；③根据④证出的全等即可作出判断；⑤证明∠EAH=30°，即可得到AH=2EH ，又由③可知AH DF =，即可作出判断.【详解】①正确：∵ABC △是等边三角形，∴60BAC ︒∠=，∴CA AB =．∵ABD △是等腰直角三角形，∴DA AB =．又∵90BAD ︒∠=，∴150CAD BAD BAC ︒∠=∠+∠=，∴DA CA =，∴()1180150152ADC ACD ︒︒︒∠=∠=-=； ②错误：∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③，④正确，由题意可得45DAF ABH︒∠=∠=，DA AB=，∵AE BD⊥，AH CD⊥．∴180EHG EFG︒∠+∠=．又∵180?DFA EFG∠+∠=，∴EHG DFA∠=∠，在DAF△和ABH中()AFD BHADAF ABH AASDA AB∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF△≌ABH．∴DF AH=．⑤正确：∵150CAD︒∠=，AH CD⊥，∴75DAH︒∠=，又∵45DAF︒∠=，∴754530EAH︒︒︒∠=-=又∵AE DB⊥，∴2AH EH=，又∵=AH DF，∴2DF EH=【点睛】本题考查了等边三角形的性质，等腰三角形的性质，三角形的内角和定理，三角形外角的性质，全等三角形的判定与性质，综合性较强，属于较难题目.19．如图，平面直角坐标系中，已知A(2，2)、B(4，0)，若在x轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是( )A．1 B．2 C．3 D．4【答案】D【解析】【分析】由点A、B的坐标可得到2，然后分类讨论：若AC=AB；若BC=AB；若CA=CB，确定C点的个数．【详解】∵点A、B的坐标分别为(2，2)、B(4，0)．∴2，如图，①若AC=AB，以A为圆心，AB为半径画弧与x轴有2个交点(含B点)，即(0，0)、(4，0)，∴满足△ABC是等腰三角形的C点有1个；②若BC=AB，以B为圆心，BA为半径画弧与x轴有2个交点，即满足△ABC是等腰三角形的C 点有2个；③若CA=CB ，作AB 的垂直平分线与x 轴有1个交点，即满足△ABC 是等腰三角形的C 点有1个；综上所述：点C 在x 轴上，△ABC 是等腰三角形，符合条件的点C 共有4个．故选D ．【点睛】本题主考查了等腰三角形的判定以及分类讨论思想的运用，分三种情况分别讨论，注意等腰三角形顶角的顶点在底边的垂直平分线上．20．如图，在ABC △中，2B C ∠=∠，AH BC ⊥，AE 平分BAC ∠，M 是 BC 中点，则下列结论正确的个数为（）（1）AB BE AC += （2）2AB BH BC += （3）2AB HM = （4）CH EH AC +=A ．1B ．2C ．3D ．4【答案】D【解析】【分析】（1）延长AB 取BD=BE ，连接DE ，由∠D=∠BED ，2ABC C ∠=∠，得到∠D=∠C ，在△ADE 和△ACE 中，利用AAS 证明ADE ACE ≌，可得AC=AD=AB+BE ；（2）在HC 上截取HF=BH,连接AF ，可知△ABF 为等腰三角形，再根据2ABC AFB C ∠=∠=∠，可得出△AFC 为等腰三角形，所以FC+BH+HF=AB+2BH=BC ；（3）HM=BM-BH ，所以2HM=2BM-2BH=BC-2BH ，再结合（2）中结论，可得2AB HM =；（4）结合（1）（2）的结论，BC 2BH BE BC BH BE BH CH EH AC AB BE =+=-+=-+-=+.【详解】解：①延长AB 取BD=BE ，连接DE ，∴∠D=∠BED ，∠ABC=∠D+∠BED=2∠D,∵2ABC C ∠=∠，∴∠D=∠C ，在△ADE 和△ACE 中，DAE CAE D C AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADE ACE ≌∴AC=AD=AB+BE ，故（1）正确；②在HC 上截取HF=BH,连接AF ，∵AH BC ⊥，∴△ABF 为等腰三角形，∴AB=AF ，∠ABF=∠AFB ，∵2ABC C ∠=∠，∴∠AFB=2∠C=∠C+∠CAF ，∴FC=AF=AB ，∴FC+BH+HF=AB+2BH=BC ，故（2）正确；③∵HM=BM-BH ，∴2HM=2BM-2BH=BC-2BH ，由②可知BC-2BH=AB ，∴2AB HM =④根据①②结论，可得:BC 2BH BE BC BH BE BH CH EH AC AB BE =+=-+=-+-=+，故（4）正确；故选D.【点睛】本题主要考查了等腰三角形的判定和性质、三角形的外角以及全等三角形的判定和性质，结合实际问题作出合适辅助线是解题关键.。

八年级全等三角形中考真题汇编[解析版]

八年级全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P有_____个．【答案】4【解析】【分析】由A点坐标可得OA=22，∠AOP＝45°，分别讨论OA为腰和底边，求出点P在x轴正半轴和负半轴时，△APO是等腰三角形的P点坐标即可.【详解】（1）当点P在x轴正半轴上，①如图，以OA为腰时，∵A的坐标是（2，2），∴∠AOP＝45°，OA＝22，当∠AOP为顶角时，OA=OP=22，当∠OAP为顶角时，AO=AP，∴OPA=∠AOP=45°，∴∠OAP=90°，∴OP=2OA=4，∴P的坐标是（4，0）或（22，0）.②以OA为底边时，∵点A的坐标是（2，2），∴∠AOP=45°，∵AP=OP，∴∠OAP=∠AOP=45°，∴∠OPA=90°，∴OP=2， ∴P 点坐标为（2，0）.（2）当点P 在x 轴负半轴上，③以OA 为腰时，∵A 的坐标是（2，2），∴OA ＝22，∴OA ＝OP ＝22，∴P 的坐标是（﹣22，0）．综上所述：P 的坐标是（2，0）或（4，0）或（22，0）或（﹣22，0）．故答案为：4．【点睛】此题主要考查等腰三角形的判定及坐标与图形性质的综合运用，注意分类讨论思想的运用是解题关键．2．在Rt △ABC 中，∠ABC=90°，AB=3，BC=4，点E ，F 分别在边AB ，AC 上，将△AEF 沿直线EF 翻折，点A 落在点P 处，且点P 在直线BC 上．则线段CP 长的取值范围是____.【答案】15CP ≤≤【解析】【分析】根据点E 、F 在边AB 、AC 上，可知当点E 与点B 重合时，CP 有最小值，当点F 与点C 重合时CP 有最大值，根据分析画出符合条件的图形即可得.【详解】如图，当点E与点B重合时，CP的值最小，此时BP=AB=3，所以PC=BC-BP=4-3=1，如图，当点F与点C重合时，CP的值最大，此时CP=AC，Rt△ABC中，∠ABC=90°，AB=3，BC=4，根据勾股定理可得AC=5，所以CP的最大值为5，所以线段CP长的取值范围是1≤CP≤5，故答案为1≤CP≤5.【点睛】本题考查了折叠问题，能根据点E、F分别在线段AB、AC上，点P在直线BC上确定出点E、F位于什么位置时PC有最大（小）值是解题的关键.3．如图，已知正六边形 ABCDEF 的边长是 5，点 P 是 AD 上的一动点，则 PE+PF 的最小值是_____．【答案】10【解析】利用正多边形的性质，可得点B关于AD对称的点为点E，连接BE交AD于P点，那么有PB=PF，PE+PF=BE最小，根据正六边形的性质可知三角形APB是等边三角形，因此可知BE 的长为10，即PE+PF的最小值为10.故答案为10.4．如图，∠MON＝30°，点A1、A2、A3…在射线ON上，点B1、B2，B3…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4…均为等边三角形，从左起第1个等边三角形的边长记a1，第2个等边三角形的边长记为a2，以此类推，若OA1＝3，则a2=_______，a2019=_______.【答案】6； 3×22018.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及a2=2a1=6，得出a3=4a1，a4=8a1，a5=16a1…进而得出答案．【详解】解：如图，∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°，∵∠MON=30°，∴∠1=180°-120°-30°=30°，又∵∠3=60°，∴∠5=180°-60°-30°=90°，∵∠MON=∠1=30°，∴OA1=A1B1=3，∴A2B1=3，∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°，∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴a2=2a1=6，a3=4a1，a4=8a1，a5=16a1，以此类推：a2019=22018a1=3×22018故答案是：6；3×22018．【点睛】此题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出a2=2a1=6，a3=4a1，a4=8a1，a5=16a1…进而发现规律是解题关键．5．如图，点A,B,C在同一直线上,△ABD和△BCE都是等边三角形，AE,CD分别与BD,BE交于点F,G，连接FG，有如下结论：①AE=CD ②∠BFG= 60°；③EF=CG；④AD⊥CD⑤FG ∥AC 其中，正确的结论有__________________. (填序号)【答案】①②③⑤【解析】【分析】易证△ABE≌△DBC，则有∠BAE＝∠BDC，AE＝CD，从而可证到△ABF≌△DBG，则有AF＝DG，BF＝BG，由∠FBG＝60°可得△BFG是等边三角形，证得∠BFG＝∠DBA＝60°，则有FG∥AC，由∠CDB≠30°，可判断AD与CD的位置关系．【详解】∵△ABD和△BCE都是等边三角形，∴BD＝BA＝AD，BE＝BC＝EC，∠ABD＝∠CBE＝60°．∵点A、B、C在同一直线上，∴∠DBE＝180°﹣60°﹣60°＝60°，∴∠ABE＝∠DBC＝120°．在△ABE和△DBC中，∵BD BAABE DBCBE BC∠∠=⎧⎪=⎨⎪=⎩，∴△ABE≌△DBC，∴∠BAE＝∠BDC，∴AE＝CD ，∴①正确；在△ABF和△DBG中，60BAF BDGAB DBABF DBG∠∠∠∠=⎧⎪=⎨⎪==︒⎩，∴△ABF≌△DBG，∴AF＝DG，BF＝BG．∵∠FBG＝180°﹣60°﹣60°＝60°，∴△BFG是等边三角形，∴∠BFG=60°，∴②正确；∵AE＝CD，AF＝DG，∴EF=CG；∴③正确；∵∠ADB＝60°，而∠CDB=∠EAB≠30°，∴AD与CD不一定垂直，∴④错误．∵△BFG是等边三角形，∴∠BFG=60°，∴∠GFB＝∠DBA＝60°，∴FG∥AB，∴⑤正确．故答案为①②③⑤．【点睛】本题考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、平行线的判定和性质，证得△ABE≌△DBC是解题的关键．6．如图，在Rt ABC△中，AC BC=，D是线段AB上一个动点，把ACD沿直线CD折叠，点A落在同一平面内的A'处，当A D'平行于Rt ABC△的直角边时，ADC∠的大小为________．【答案】112.5︒或67.5︒【解析】【分析】当A D'平行于Rt ABC△的直角边时，有两种情况，一是当A D BC'时，二是当A D AC'时，两种情况根据折叠的性质及等腰三角形的性质进行角度的计算即可．【详解】如图1，当点D在线段AB上，且A D BC'时，45A DB B'∠=∠=︒，45180ADC A DC'∴∠+∠-=︒︒，解得112.5A DC ADC'∠=∠=︒.图1如图2，当A D AC '时，45A DB A '∠=∠=︒，45180ADC A DC '∴∠+∠+=︒︒，解得67.5A DC ADC '∠=∠=︒.图2【点睛】本题考查了翻折变换的性质，等腰直角三角形的性质，掌握折叠的性质是解题关键．7．如图,在ABC 中, 90,ACB ABD ︒∠=是ABC 的轴对称图形,点E 在AD 上,点F 在AC 的延长线上.若点B 恰好在EF 的垂直平分线上,并且5AE =,13AF =,则DE =______．【答案】4．【解析】【分析】连接BE ，BF ，根据轴对称的性质可得△ABD ≌△ACB ，进而可得DB=CB ，AD=AC ，∠D=∠BCA=90°，再利用线段垂直平分线的性质可得BE=BF ，然后证明Rt △DBE ≌Rt △CBF 可得DE=CF ，然后可得ED 长．【详解】解：连接BE ，BF ，∵△ABD 是△ABC 的轴对称图形，∴△ABD ≌△ACB ，∴DB=CB ，AD=AC ，∠D=∠BCA=90°，∴∠BCF=90°，∵点B 恰好在EF 的垂直平分线上，∴BE=BF ，在Rt △DBE 和Rt △CBF 中BD BC EB FB =⎧⎨=⎩，∴Rt △DBE ≌Rt △CBF （HL ），∴DE=CF ，设DE=x ，则CF=x ，∵AE=5，AF=13，∴AC=AD=5+x ，∴AF=5+2x ，∴5+2x=13，∴x=4，∴DE=4，故答案为：4．【点睛】此题主要考查了轴对称和线段垂直平分线的性质，关键是掌握成轴对称的两个图形全等．8．如图，在△ABC 中，AB ＝AC ，点D 、E 在BC 的延长线上，G 是AC 上一点，且CG ＝CD ，F 是GD 上一点，且DF ＝DE ．若∠A ＝100°，则∠E 的大小为_____度．【答案】10【解析】【分析】由DF=DE ，CG=CD 可得∠E=∠DFE ，∠CDG=∠CGD ，再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E ，∠ACB=∠CDG+∠CGD=2∠CD G ，进而可得∠ACB=4∠E ，最后代入数据即可解答.【详解】解：∵DF ＝DE ，CG ＝CD ，∴∠E ＝∠DFE ，∠CDG ＝∠CGD ，∵GDC ＝∠E +∠DFE ，∠ACB ＝∠CDG +∠CGD ，∴GDC ＝2∠E ，∠ACB ＝2∠CDG ，∴∠ACB ＝4∠E ，∵△ABC 中，AB ＝AC ，∠A ＝100°，∴∠ACB ＝40°，∴∠E ＝40°÷4＝10°．故答案为10．【点睛】本题考查等腰三角形的性质以及三角形外角的定义，解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.9．如图，已知AB AC =，AD 平分BAC ∠，60DEB EBC ∠=∠=︒，若3BE =，3DE =，则BC =____________．【答案】33+【解析】【分析】延长ED 交BC 于点M ，延长AD 交BC 于点N ，作DF ∥BC 于点F.由已知条件推出△BEM 是等边三角形，△FDE 是等边三角形，在△DNM 中求出NM 的长度，即可求出BC 的长度.【详解】如图，延长ED 交BC 于点M ，延长AD 交BC 于点N ，作DF ∥BC 于点F ，∵AB AC =，AD 平分BAC ∠，∴AN ⊥BC ，BN=CN ，∵60DEB EBC ∠=∠=︒，∴△BEM 是等边三角形，∴△FDE 是等边三角形，∵3BE =，3DE =33DM =-∵△BEM 是等边三角形，∴∠EMB=60°，∵AN ⊥BC ，∴∠DNM=90°，∴∠NDM=30°，∴1322NM DM ==，∴3BN BM NM =-=-=∴23BC BN ==+【点睛】本题考查了等边三角形的性质，解题的关键是作出辅助线构造等边三角形.10．在下列结论中：①有三个角是60︒的三角形是等边三角形；②有一个外角是120︒的等腰三角形是等边三角形；③有一个角是60︒，且是轴对称的三角形是等边三角形；④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形．其中正确的是__________.【答案】①②③④【解析】【分析】依据等边三角形的定义，含有一个600角的等腰三角形是等边三角形判断即可.【详解】有三个角是600的三角形是等边三角形，故①正确；外角是1200时，邻补角为600，即有一个内角是600的等腰三角形是等边三角形，故②正确；轴对称的三角形是等腰三角形，且含有一个600角，因此是等边三角形，故③正确；一腰上的高也是中线，故底边等于腰长，所以此三角形是等边三角形，故④正确.故此题正确的是①②③④.【点睛】此题考查等边三角形的判定方法，熟记方法才能熟练运用.二、八年级数学轴对称三角形选择题（难）11．已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为( )A B C ．32 D ．不能确定【答案】B【解析】已知，如图，P 为等边三角形内任意一点，PD 、PE 、PF 分别是点P 到边AB 、BC 、AC 的距离，连接AP 、BP 、CP ，过点A 作AH ⊥BC 于点H ，已知等边三角形的边长为3，可求得高线AH S △ABC =12BC •AH =12AB •PD+12BC•PE +12AC •PF ，所以12×3×AH =12×3×PD +12×3×PE +12×3×PF ，即可得PD +PE +PF =AH =332，即点P 到三角形三边距离之和为332．故选B.点睛：本题考查了等边三角形的性质，根据三角形的面积求点P 到三边的距离之和等于等边三角形的高是解题的关键，作出图形更形象直观．12．如图，坐标平面内一点A(2，－1)，O 为原点，P 是x 轴上的一个动点，如果以点P 、O 、A 为顶点的三角形是等腰三角形，那么符合条件的动点P 的个数为( )A ．2B ．3C ．4D ．5【答案】C【解析】以O 点为圆心，OA 为半径作圆与x 轴有两交点，这两点显然符合题意．以A 点为圆心，OA 为半径作圆与x 轴交与两点（O 点除外）．以OA 中点为圆心OA 长一半为半径作圆与x 轴有一交点．共4个点符合，13．在Rt ABC ∆中，90ACB ∠=︒，点D E 、是AB 边上两点，且CE 垂直平分,AD CD 平分,6BCE AC cm ∠=，则BD 的长为（）A ．6cmB ．7cmC ．8cmD ．9cm【答案】A【解析】【分析】根据CE 垂直平分AD ，得AC=CD ，再根据等腰在三角形的三线合一，得ACE ECD∠=∠，结合角平分线定义和90ACB︒∠=，得30ACE ECD DCB︒∠=∠=∠=，则BD CD AC==．【详解】∵CE垂直平分AD∴AC=CD＝6cm，ACE ECD∠=∠∵CD平分BCE∠∴BCD ECD∠=∠∴30ACE ECD DCB︒∠=∠=∠=∴60A︒∠=∴30B BCD︒∠==∠∴6CD BD AC cm===故选：A【点睛】本题考查的知识点主要是等腰三角形的性质的“三线合一”性质定理及判定“等角对等边”，熟记并能熟练运用这些定理是解题的关键．14．如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC 于F，AD交CE于G．则下列结论中错误的是( )A．AD＝BE B．BE⊥ACC．△CFG为等边三角形D．FG∥BC【答案】B【解析】试题解析：A.ABC和CDE△均为等边三角形，60AC BC EC DC ACB ECD∴==∠=∠=︒，，，在ACD与BCE中，{AC BCACD BCECD CF=∠=∠=，ACD BCE∴≌，AD BE∴=，正确.B.据已知不能推出F是AC中点，即AC和BF不垂直，所以AC BE⊥错误，故本选项符合题意.C.CFG是等边三角形，理由如下：180606060ACG BCA∠=︒-︒-︒=︒=∠，ACD BCE≌，CBE CAD∴∠=∠，在ACG和BCF中，{CAG CBFAC BCBCF ACG∠=∠=∠=∠，ACG BCF∴≌，CG CH∴=，又∵∠ACG=60°CFG∴是等边三角形，正确.D.CFG是等边三角形，60CFG ACB∴∠︒=∠﹦，.FG BC∴正确.故选B.15．如图，在平面直角坐标系中，A（a，0），B（0，a），等腰直角三角形ODC的斜边经过点B，OE⊥AC，交AC于E，若OE＝2，则△BOD与△AOE的面积之差为（）A．2 B．3 C．4 D．5【答案】A【解析】【分析】首先证明△DOB≌△COA（SAS），推出S△DOB﹣S△AOE=S△EOC，再证明△OEC是等腰直角三角形即可解决问题．【详解】∵A（a，0），B（0，a），∴OA=OB．∵△ODC是等腰直角三角形，∴OD=OC，∠D=∠DCO=45°．∵∠DOC=∠BOA=90°，∴∠DOB=∠COA．在△DOB和△COA中，∵OD=OC，∠DOB=∠COA，OB=OA，∴△DOB≌△COA（SAS），∴∠D=∠OCA=45°，S△DOB﹣S△AOE=S△EOC．∵OE⊥AC，∴∠OEC=90°，∴△CEO是等腰直角三角形，∴OE=EC=2，∴S△DOB﹣S△AOE=S△EOC12=⨯2×2=2．故选A．【点睛】本题考查了等腰直角三角形的性质和判定，全等三角形的判定和性质等知识，解题的关键是证明△OEC是等腰直角三角形．16．如图，△ABC、△CDE都是等腰三角形，且CA＝CB, CD＝CE,∠ACB＝∠DCE＝α,AD,BE相交于点O，点M,N分别是线段AD,BE的中点，以下4个结论:①AD＝BE;②∠DOB＝180°－α;③△CMN是等边三角形；④连OC,则OC平分∠AOE.正确的是（）A．①②③B．①②④C．①③④D．①②③④【答案】B【解析】【分析】①根据全等三角形的判定定理得到△ACD≌△BCE（SAS），由全等三角形的性质得到AD=BE；故①正确；②设CD与BE交于F，根据全等三角形的性质得到∠ADC=∠BEC，得到∠DOE=∠DCE=α，根据平角的定义得到∠BOD=180°-∠DOE=180°-α，故②正确；③根据全等三角形的性质得到∠CAD=∠CBE，AD=BE，AC=BC根据线段的中点的定义得到AM=BN，根据全等三角形的性质得到CM=CN，∠ACM=∠BCN，得到∠MCN=α，推出△MNC不一定是等边三角形，故③不符合题意；④过C作CG⊥BE于G，CH⊥AD于H，根据全等三角形的性质得到CH=CG，根据角平分线的判定定理即可得到OC平分∠AOE，故④正确．【详解】解：①∵CA=CB，CD=CE，∠ACB=∠DCE=α，∴∠ACB+∠BCD=∠DCE+∠BCD，∴∠ACD=∠BCE，在△ACD和△BCE中AC BCACD BCECD CE⎪∠⎪⎩∠⎧⎨＝＝＝∴△ACD≌△BCE（SAS），∴AD=BE；故①正确；②设CD与BE交于F，∵△ACD≌△BCE，∴∠ADC=∠BEC，∵∠CFE=∠DFO，∴∠DOE=∠DCE=α，∴∠BOD=180°-∠DOE=180°-α，故②正确；③∵△ACD≌△BCE，∴∠CAD=∠CBE，AD=BE，AC=BC又∵点M、N分别是线段AD、BE的中点，∴AM=12AD，BN=12BE，∴AM=BN，在△ACM和△BCN中AC BCCAM CBNAM BN⎪∠⎪⎩∠⎧⎨＝＝＝∴△ACM≌△BCN（SAS），∴CM=CN，∠ACM=∠BCN，又∠ACB=α，∴∠ACM+∠MCB=α，∴∠BCN+∠MCB=α，∴∠MCN=α，∴△MNC不一定是等边三角形，故③不符合题意；④过C作CG⊥BE于G，CH⊥AD于H，∴∠CHD=∠ECG=90°，∵∠CEG=∠CDH，CE=CD，∴△CGE≌△CHD（AAS），∴CH=CG，∴OC平分∠AOE，故④正确，故选：B．【点睛】本题综合考查了全等三角形的性质和判定，三角形的内角和定理，等边三角形的性质和判定等知识点的应用，解此题的关键是根据性质进行推理，此题综合性比较强，有一定的代表性．17．如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，D为AB的中点，E为线段AD上一点，过E点的线段FG交CD的延长线于G点，交AC于F点，且EG＝AE，分别延长CE，BG交于点H，若EH平分∠AEG，HD平分∠CHG则下列说法：①∠GDH＝45°；②GD＝ED；③EF＝2DM；④CG＝2DE+AE，正确的是（）A．①②③B．①②④C．②③④D．①②③④【答案】B【解析】【分析】首先证明△AEC≌△GEC（SAS），推出CA=CG，∠A=∠CGE=45°，推出DE=DG，故②正确；再证明△EDC≌△GDB，推出∠CED=∠BGD，ED=GD，由三角形外角的性质得出∠HDG=∠HDE，进而得出∠GDH=∠EDH=45°，即可判断①正确；通过证明△EDC和△EMD是等腰直角三角形，得到ED2MD，再通过证明△EFC≌△EDC，得到EF=ED，从而可判断③错误；由CG=CD+DG，CD=AD，ED=GD，变形即可判断④正确．【详解】∵AC=BC，∠ACB=90°，AD=DB，∴CD⊥AB，CD=AD=DB，∠A=∠CBD=45°．∵EH平分∠AEG，∴∠AEH=∠GEH．∵∠AEH+∠AEC=180°，∠GEH+∠CEG=180°，∴∠AEC=∠CEG．∵AE=GE，EC=EC，∴△AEC≌△GEC（SAS），∴CA=CG，∠A=∠CGE=45°．∵∠EDG=90°，∴∠DEG=∠DGE=45°，∴DE=DG，∠AEF=∠DEG=∠A=45°，故②正确；∵DE=DG，∠CDE=∠BDG=90°，DC=DB，∴△EDC≌△GDB（SAS），∴∠CED=∠BGD，ED=GD．∵HD平分∠CHG，∴∠GHD=∠EHD．∵∠CED=∠EHD+∠HDE，∠BGD=∠GHD+∠HDG，∴∠HDG=∠HDE．∵∠EDG=∠ADC=90°，∴∠GDH=∠EDH=45°，故①正确；∵∠EDC=90°，ED=GD，∴△EDC是等腰直角三角形，∴∠DEG=45°．∵∠GDH=45°，∴∠EDH=45°，∴△EMD是等腰直角三角形，∴ED=2MD．∵∠AEF=∠DEG=∠A=45°，∴∠AFE=∠CFG=90°．∵∠EDC=90°，∴∠EFC=∠EDC=90°．∵EH平分∠AEG，∴∠AEH=∠GEH．∵∠FEC=∠GEH，∠DEC=∠AEH，∴∠FEC=∠DEC．∵EC=EC，∴△EFC≌△EDC，∴EF=ED，∴EF=2MD．故③错误；∵CG=CD+DG=AD+ED=AE+ED+ED，∴CG=2DE+AE，故④正确．故选B．【点睛】本题考查了等腰直角三角形的性质和判定，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考选择题中的压轴题．18．如图，已知，点A（0，0）、B（43，0）、C（0，4），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第2017个等边三角形的边长等于（）A．3B．3C．3D．3【答案】A【解析】【分析】【详解】根据锐角三函数的性质，由OB=43，OC=1，可得∠OCB=90°，然后根据等边三角形的性质，可知∠A1AB=60°，进而可得∠CAA1=30°，∠CA1O=90°，因此可推导出∠A2A1B=30°，同理得到∠CA2B1=∠CA3B2=∠CA4B3=90°，∠A2A1B=∠A3A2B2=∠A4A3B3=30°，故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半，即OA1=OCcos∠CAA1=23，B1A2=1232⨯，以此类推，可知第2017个等边三角形的边长为：201713()432⨯=.故选A.【点睛】此题主要考查了等边三角形的性质，属于规律型题目，解题关键是仔细审图，得出：后一个等边三角形的边长等于前一个等边三角形的边长的一半.19．如图，在△ABC中，AB=AC=8，BC=5，AB的垂直平分线交AC于D，则△BCD的周长为（）A．13B．15C．18D．21【答案】A【解析】根据线段垂直平分线的性质，可由AB=AC=8，BC=5，AB的垂直平分线交AC于D，得到AD=BD，进而得出△BCD的周长为：CD+BD+BC=AC+BC=8+5=13．故选A．点睛：此题主要考查了线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等．20．如图，在平面直角坐标系中，A(1，2)，B(3，2)，连接AB ，点P 是x 轴上的一个动点，连接AP 、BP ，当△ABP 的周长最小时，对应的点P 的坐标和△ABP 的最小周长分别为( )A ．(1，0)，224+B ．(3，0)，224+C ．(2,0), 25D ．(2,0),252+【答案】D【解析】作A 关于x 轴的对称点N （1，-2），连接BN 与x 轴的交点即为点P 的位置，此时△ABP 的周长最小.设直线BN 的解析式为y kx b =+，∵N (1，-2)，B (3，2)，∴232k b k b +=-⎧⎨+=⎩ ，解得24k b =⎧⎨=-⎩， ∴24y x =-，当0y =时，240x -=，解得，2x =，∴点P 的坐标为（2，0）；∵A (1，2)，B (3，2)，∴AB //x 轴，∵AN ⊥x 轴，∴AB ⊥x 轴，在Rt △ABC 中，AB ＝2，AN ＝4，由勾股定理得，BN==∵AP=NP,∴△ABP的周长最小值为：AB+BP+AP=AB+BP+PN=AB+BN故选D.点睛：本题考查最短路径问题.利用轴对称作出点P的位置是解题的关键.。

八年级全等三角形中考真题汇编[解析版]

八年级全等三角形中考真题汇编[解析版] 一、八年级数学轴对称三角形填空题（难）1．在等腰△ABC中，AD⊥BC交直线BC于点D，若AD=12BC，则△ABC的顶角的度数为_____．【答案】30°或150°或90°【解析】试题分析：分两种情况；①BC为腰，②BC为底，根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°，然后分AD在△ABC内部和外部两种情况求解即可．解：①BC为腰，∵AD⊥BC于点D，AD=12 BC，∴∠ACD=30°，如图1，AD在△ABC内部时，顶角∠C=30°，如图2，AD在△ABC外部时，顶角∠ACB=180°﹣30°=150°，②BC为底，如图3，∵AD⊥BC于点D，AD=12 BC，∴AD =BD =CD ， ∴∠B =∠BAD ，∠C =∠CAD ，∴∠BAD +∠CAD =12×180°=90°， ∴顶角∠BAC =90°，综上所述，等腰三角形ABC 的顶角度数为30°或150°或90°．故答案为30°或150°或90°．点睛：本题考查了含30°交点直角三角形的性质，等腰三角形的性质，分类讨论是解题的关键．2．如图，在等边ABC ∆中取点P 使得PA ，PB ，PC 的长分别为3， 4， 5，则APC APB S S ∆∆+=_________．【答案】9364+【解析】【分析】把线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS 证得△ADB ≌△APC ，连接PD ，根据旋转的性质知△APD 是等边三角形，利用勾股定理的逆定理可得△PBD 为直角三角形，∠BPD ＝90︒，由△ADB ≌△APC 得S △ADB ＝S △APC ，则有S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ，根据等边3S △ADP ＋S △BPD ＝34×32＋12×3×4＝364+．【详解】将线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，连接PD∴AD ＝AP ，∠DAP ＝60︒，又∵△ABC 为等边三角形，∴∠BAC ＝60︒，AB ＝AC ，∴∠DAB ＋∠BAP ＝∠PAC ＋∠BAP ，∴∠DAB ＝∠PAC ，又AB=AC,AD=AP∴△ADB ≌△APC∵DA ＝PA ，∠DAP ＝60︒，∴△ADP 为等边三角形，在△PBD 中，PB ＝4，PD ＝3，BD ＝PC ＝5，∵32＋42＝52，即PD 2＋PB 2＝BD 2，∴△PBD 为直角三角形，∠BPD ＝90︒，∵△ADB ≌△APC ，∴S △ADB ＝S △APC ，∴S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ＝3×32＋12×3×4＝936+．故答案为：9364+．【点睛】本题考查了等边三角形的性质与判定，解题的关键是熟知旋转的性质作出辅助线进行求解．3．在ABC ∆中，边AB 、AC 的垂直平分线分别交边BC 于点D 、点E ，20DAE ∠=︒，则BAC ∠=______°.【答案】80或100【解析】【分析】根据题意，点D 和点E 的位置不确定，需分析谁靠近B 点，则有如下图（图见解析）两种情况：（1）图1中，点E 距离点B 近，根据垂直平分线性质可知，,BD AD AE CE ==，从而有1,2B DAE C DAE ∠=∠+∠∠=∠+∠，再根据三角形的内角和定理可得180B C BAC ∠+∠+∠=︒，联立即可求得；（2）图2中，点D 距离点B 近，根据垂直平分线性质可知，,BD AD AE CE ==，从而有3,4B C ∠=∠∠=∠，由三角形的内角和定理得180B C BAC ∠+∠+∠=︒，联立即可求得.【详解】由题意可分如下两种情况：（1）图1中，根据垂直平分线性质可知，,BD AD AE CE ==，1,2B DAE C DAE ∴∠=∠+∠∠=∠+∠（等边对等角），两式相加得12B C DAE DAE ∠+∠=∠+∠+∠+∠，又12DAE BAC ∠+∠+∠=∠20B C BAC DAE BAC ∴∠+∠=∠+∠=∠+︒，由三角形内角和定理得180B C BAC ∠+∠+∠=︒，20180BAC BAC ∴∠+︒+∠=︒，80BAC ∴∠=︒；（2）图2中，根据垂直平分线性质可知，,BD AD AE CE ==，3,4B C ∴∠=∠∠=∠（等边对等角），两式相加得34B C ∠+∠=∠+∠，又34DAE BAC ∠+∠+∠=∠，3420BAC DAE BAC ∴∠+∠=∠-∠=∠-︒，20B C BAC ∴∠+∠=∠-︒由三角形内角和定理得180B C BAC ∠+∠+∠=︒，20180BAC BAC ∴∠-︒+∠=︒，100BAC ∴∠=︒.故答案为80或100.【点睛】本题考查了垂直平分线的性质（垂直平分线上的点到线段两端点的距离相等）、等腰三角形的定义和性质（等边对等角）、以及三角形内角和定理，本题的难点在于容易漏掉第二种情况，出现漏解.4．如图，在ABC 中，AB AC >，按以下步骤作图：分别以点B 和点C 为圆心，大于BC 一半长为半径作画弧，两弧相交于点M 和点N ，过点M N 、作直线交AB 于点D ，连接CD ，若10AB =，6AC =，则ADC 的周长为_____________________．【答案】16【解析】【分析】利用基本作图可以判定MN 垂直平分BC ，则DC=DB ，然后利用等线段代换得到ACD ∆的周长=AB+AC ，再把10AB =，6AC =代入计算即可．【详解】解：由作法得MN 垂直平分BC ，则DC=DB ，10616ACD C CD AC AD DB AD AC AB AC ∆=++=++=+=+=故答案为：16．【点睛】本题考查了基本作图和线段垂直平分线的性质，熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）是本题的关键．5．如图，己知30MON ∠=︒，点1A ，2A ，3A ，…在射线ON 上，点1B ，2B ，3B ，…在射线OM 上，112A B A ∆，223A B A ∆，334A B A ∆，…均为等边三角形，若12OA =，则556A B A ∆的边长为________.【答案】32【解析】【分析】根据底边三角形的性质求出130∠=︒以及平行线的性质得出112233////A B A B A B ，以及22122A B B A =，得出332212244A B A B B A ===，441288A B B A ==，551216A B B A =⋯进而得出答案．【详解】解：△112A B A 是等边三角形，1121A B A B ∴=，341260∠=∠=∠=︒，2120∴∠=︒，30MON ∠=︒，11801203030∴∠=︒-︒-︒=︒，又360∠=︒，5180603090∴∠=︒-︒-︒=︒，130MON ∠=∠=︒，1112OA A B ∴==，212A B ∴=，△223A B A 、△334A B A 是等边三角形，111060∴∠=∠=︒，1360∠=︒，41260∠=∠=︒，112233////A B A B A B ∴，1223//B A B A ，16730∴∠=∠=∠=︒，5890∠=∠=︒，22122242A B B A =∴==，33232B A B A =，33312428A B B A ∴===，同理可得:444128216A B B A ===，⋯∴△1n n n A B A +的边长为2n ，∴△556A B A 的边长为5232=．故答案为：32．【点睛】本题考查了等边三角形的性质以及30°直角三角形的性质，根据已知得出33124A B B A =，44128A B B A =，551216A B B A =进而发现规律是解题关键．6．如图，在△ABC 中，∠C ＝90°，∠B ＝30°，以点A 为圆心，任意长为半径画弧分别交AB ，AC 于点M 和N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ，则下列说法：①AD 是∠BAC 的平分线；②∠ADC ＝60°；③点D 在AB 的垂直平分线上；④S △DAC ：S △ABC ＝1：3.其中正确的是__________________．(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP，MP，根据SSS定理可得△ANP≌△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30°，根据直角三角形的性质可知∠ADC=60°；③根据∠1=∠B可知AD=BD，故可得出结论；④先根据直角三角形的性质得出∠2=30°，CD=12AD，再由三角形的面积公式即可得出结论．【详解】①连接NP，MP．在△ANP与△AMP中，∵AN AMNP MPAP AP=⎧⎪=⎨⎪=⎩，∴△ANP≌△AMP，则∠CAD=∠BAD，故AD是∠BAC的平分线，故此选项正确；②∵在△ABC中，∠C=90°，∠B=30°，∴∠CAB=60°．∵AD是∠BAC的平分线，∴∠1=∠2=12∠CAB=30°，∴∠3=90°﹣∠2=60°，∴∠ADC=60°，故此选项正确；③∵∠1=∠B=30°，∴AD=BD，∴点D在AB的中垂线上，故此选项正确；④∵在Rt△ACD中，∠2=30°，∴CD=12AD，∴BC=BD+CD=AD+12AD=32AD，S△DAC=12AC•CD=14AC•AD，∴S △ABC=12AC•BC=12AC•32AD=34AC•AD，∴S△DAC：S△ABC=1：3，故此选项正确．故答案为①②③④．【点睛】本题考查的是作图﹣基本作图，熟知角平分线的作法是解答此题的关键．7．如图，在ABC ∆和DBC ∆中，40A ∠=，2AB AC ==，140BDC ∠=，BD CD =，以点D 为顶点作70MDN ∠=，两边分别交,AB AC 于点,M N ，连接MN ，则AMN ∆的周长为_______.【答案】4【解析】【分析】延长AB 至F ，使BF =CN ，连接DF ，通过证明△BDF ≌△CDN ，及△DMN ≌△DMF ，从而得出MN =MF ，△AMN 的周长等于AB +AC 的长．【详解】延长AB 至F ，使BF =CN ，连接DF ．∵BD =CD ，且∠BDC =140°，∴∠BCD =∠DBC =20°．∵∠A =40°，AB =AC =2，∴∠ABC =∠ACB =70°，∴∠DBA =∠DCA =90°．在Rt △BDF 和Rt △CND 中，∵BF =CN ，∠DBA =∠DCA ，DB =DC ，∴△BDF ≌△CDN ，∴∠BDF =∠CDN ，DF =DN ．∵∠MDN =70°，∴∠BDM +∠CDN =70°，∴∠BDM +∠BDF =70°，∴∠FDM =70°=∠MDN ．∵DF =DN ，∠FDM =∠MDN ，DM =DM ，∴△DMN ≌△DMF ，∴MN =MF ，∴△AMN 的周长是：AM +AN +MN =AM +MB +BF +AN =AB +AC =4．故答案为：4．【点睛】本题主要利用等腰三角形的性质来证明三角形全等，构造全等三角形是解答本题的关键．8．如图，已知，点E 是线段AB 的中点，点C 在线段BD 上，8BD =，2DC =，线段AC 交线段DE 于点F ，若AF BD =，则AC =__________.【答案】10.【解析】【分析】延长DE 至G ，使EG=DE ，连接AG ，证明BDE AGE ∆≅∆，而后证明AFG ∆、CDF ∆是等腰三角形，即可求出CF 的长，于是可求AC 的长.【详解】解：如图，延长DE 至G ，使EG=DE ，连接AG ，∵点E 是线段AB 的中点，∴AE=BE,∴在BDE ∆和AGE ∆中，BE AE BED AEGDE EG =⎧⎪∠=∠⎨⎪=⎩, ∴BDE AGE ∆≅∆,∴AG=BD, BDE AGE ∠=∠,∵AF=BD=8,∴AG=AF,∴AFG AGE ∠=∠∵AFG DFC ∠=∠,∴BDE DFC ∠=∠,∴FC=DC,∴FC=2,∴AC=AF+FC=8+2=10.【点睛】本题考查了等腰三角形的性质与判定以及全等三角形的判定与性质，能利用中点条件作辅助线构造全等三角形是解题的关键.9．如图，在△ABC 中，AB ＝AC ，点D 、E 在BC 的延长线上，G 是AC 上一点，且CG ＝CD ，F 是GD 上一点，且DF ＝DE ．若∠A ＝100°，则∠E 的大小为_____度．【答案】10【解析】【分析】由DF=DE，CG=CD可得∠E=∠DFE，∠CDG=∠CGD，再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E，∠ACB=∠CDG+∠CGD=2∠CD G，进而可得∠ACB=4∠E，最后代入数据即可解答.【详解】解：∵DF＝DE，CG＝CD，∴∠E＝∠DFE，∠CDG＝∠CGD，∵GDC＝∠E+∠DFE，∠ACB＝∠CDG+∠CGD，∴GDC＝2∠E，∠ACB＝2∠CDG，∴∠ACB＝4∠E，∵△ABC中，AB＝AC，∠A＝100°，∴∠ACB＝40°，∴∠E＝40°÷4＝10°．故答案为10．【点睛】本题考查等腰三角形的性质以及三角形外角的定义，解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.10．在△ABC 中，∠ACB＝90º，D、E 分别在 AC、AB 边上，把△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，若△CFD 与△BFE 都是等腰三角形，则∠BAC 的度数为_________．【答案】45°或60°【解析】【分析】根据题意画出图形，设∠BAC的度数为x，则∠B=90°-x，∠EFB =135°-x，∠BEF=2x-45°，当△BFE 都是等腰三角形，分三种情况讨论，即可求解.【详解】∵∠ACB＝90º，△CFD是等腰三角形，∴∠CDF=∠CFD=45°，设∠BAC的度数为x，∴∠B=90°-x，∵△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，∴∠DFE=∠BAC=x，∴∠EFB=180°-45°-x=135°-x，∵∠ADE=∠FDE，∴∠ADE=（180°-45°）÷2=67.5°，∴∠AED=180°-∠ADE-∠BAC=180°-67.5° -x=112.5°-x，∴∠DEF=∠AED=112.5°-x，∴∠BEF=180°-∠AED-∠DEF=180°-（112.5°-x）-（112.5°-x）=2x-45°，∵△BFE 都是等腰三角形，分三种情况讨论：①当FE=FB时，如图1，则∠BEF=∠B，∴90-x=2x-45，解得：x=45；②当BF=BE时，则∠EFB=∠BEF，∴135-x=2x-45，解得：x=60，③当EB=EF时，如图2，则∠B=∠EFB，∴135-x=90-x，无解，∴这种情况不存在.综上所述：∠BAC 的度数为：45°或60°.故答案是：45°或60°.图1 图2【点睛】本题主要考查等腰三角形的性质定理，用代数式表示角度，并进行分类讨论，是解题的关键.二、八年级数学轴对称三角形选择题（难）11．如图，平面直角坐标系中存在点A（3，2），点B（1,0），以线段AB为边作等腰三角形ABP，使得点P在坐标轴上.则这样的P点有（）A ．4个B ．5个C ．6个D ．7个【答案】D【解析】【分析】本题是开放性试题，由题意知A 、B 是定点，P 是动点，所以要分情况讨论：以AP 、AB 为腰、以AP 、BP 为腰或以BP 、AB 为腰．则满足条件的点P 可求．【详解】由题意可知：以AP 、AB 为腰的三角形有3个；以AP 、BP 为腰的三角形有2个；以BP 、AB 为腰的三角形有2个．所以，这样的点P 共有7个.故选D ．【点睛】本题考查了等腰三角形的判定及坐标与图形的性质；分类别寻找是正确解答本题的关键．12．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）A ．511a 32⨯（） B ．511a 23⨯（） C ．611a 32⨯（） D ．611a 23⨯（）【答案】A【解析】连接AD 、DB 、DF ，求出∠AFD=∠ABD=90°，根据HL 证两三角形全等得出∠FAD=60°，求出AD ∥EF ∥GI ，过F 作FZ ⊥GI ，过E 作EN ⊥GI 于N ，得出平行四边形FZNE 得出EF=ZN=13a，求出GI的长，求出第一个正六边形的边长是13a，是等边三角形QKM的边长的13；同理第二个正六边形的边长是等边三角形GHI的边长的13；求出第五个等边三角形的边长，乘以13即可得出第六个正六边形的边长．连接AD、DF、DB．∵六边形ABCDEF是正六边形，∴∠ABC=∠BAF=∠AFE，AB=AF，∠E=∠C=120°，EF=DE=BC=CD，∴∠EFD=∠EDF=∠CBD=∠BDC=30°，∵∠AFE=∠ABC=120°，∴∠AFD=∠ABD=90°，在Rt△ABD和RtAFD中AF=AB{AD=AD∴Rt△ABD≌Rt△AFD（HL），∴∠BAD=∠FAD=12×120°=60°，∴∠FAD+∠AFE=60°+120°=180°，∴AD∥EF，∵G、I分别为AF、DE中点，∴GI∥EF∥AD，∴∠FGI=∠FAD=60°，∵六边形ABCDEF是正六边形，△QKM是等边三角形，∴∠EDM=60°=∠M，∴ED=EM，同理AF=QF，即AF=QF=EF=EM，∵等边三角形QKM的边长是a，∴第一个正六边形ABCDEF的边长是13a，即等边三角形QKM的边长的13，过F作FZ⊥GI于Z，过E作EN⊥GI于N，则FZ∥EN，∵EF∥GI，∴四边形FZNE是平行四边形，∴EF=ZN=13a，∵GF=12AF=12×13a=16a，∠FGI=60°（已证），∴∠GFZ=30°，∴GZ=12GF=112a，同理IN=112a，∴GI=112a+13a+112a=12a，即第二个等边三角形的边长是12a，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是13×12a；同理第第三个等边三角形的边长是12×12a，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是13×12×12a；同理第四个等边三角形的边长是12×12×12a，第四个正六边形的边长是13×12×12×12a；第五个等边三角形的边长是12×12×12×12a，第五个正六边形的边长是1 3×12×12×12×12a；第六个等边三角形的边长是12×12×12×12×12a，第六个正六边形的边长是1 3×12×12×12×12×12a，即第六个正六边形的边长是13×512（）a，故选A．13．已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为( ) A ．32 B ．332 C ．32 D ．不能确定【答案】B【解析】已知，如图，P 为等边三角形内任意一点，PD 、PE 、PF 分别是点P 到边AB 、BC 、AC 的距离，连接AP 、BP 、CP ，过点A 作AH ⊥BC 于点H ，已知等边三角形的边长为3，可求得高线AH =332，因S △ABC =12BC •AH =12AB •PD+12BC•PE +12AC •PF ，所以12×3×AH =12×3×PD +12×3×PE +12×3×PF ，即可得PD +PE +PF =AH =332，即点P 到三角形三边距离之和为332．故选B.点睛：本题考查了等边三角形的性质，根据三角形的面积求点P 到三边的距离之和等于等边三角形的高是解题的关键，作出图形更形象直观．14．如图，坐标平面内一点A(2，－1)，O 为原点，P 是x 轴上的一个动点，如果以点P 、O 、A 为顶点的三角形是等腰三角形，那么符合条件的动点P 的个数为( )A ．2B ．3C ．4D ．5【答案】C【解析】以O 点为圆心，OA 为半径作圆与x 轴有两交点，这两点显然符合题意．以A 点为圆心，OA 为半径作圆与x 轴交与两点（O 点除外）．以OA 中点为圆心OA 长一半为半径作圆与x 轴有一交点．共4个点符合，15．在Rt ABC ∆中，90ACB ∠=︒，点D E 、是AB 边上两点，且CE 垂直平分,AD CD 平分,6BCE AC cm ∠=，则BD 的长为（）A ．6cmB ．7cmC ．8cmD ．9cm【答案】A【解析】【分析】根据CE 垂直平分AD ，得AC=CD ，再根据等腰在三角形的三线合一，得ACE ECD ∠=∠，结合角平分线定义和90ACB ︒∠=，得30ACE ECD DCB ︒∠=∠=∠=，则BD CD AC ==．【详解】∵CE 垂直平分AD∴AC=CD ＝6cm ，ACE ECD ∠=∠∵CD 平分BCE ∠∴BCD ECD ∠=∠∴30ACE ECD DCB ︒∠=∠=∠=∴60A ︒∠=∴30B BCD ︒∠==∠∴6CD BD AC cm ===故选：A【点睛】本题考查的知识点主要是等腰三角形的性质的“三线合一”性质定理及判定“等角对等边”，熟记并能熟练运用这些定理是解题的关键．16．如图，30MON ∠=︒．点1A ，2A ，3A ，⋯，在射线ON 上，点1B ，2B ，3B ，⋯，在射线OM 上，112A B A ∆，223A B A ∆，334A B A ∆，⋯均为等边三角形，若11OA =，则201920192020A B A ∆的边长为（）A ．20172B ．20182C ．20192D ．20202【答案】B【解析】【分析】根据等边三角形的性质和30MON ∠=︒，可求得1130∠=︒OB A ，进而证得11OA B ∆是等腰三角形，可求得2OA 的长，同理可得22OA B ∆是等腰三角形，可得222=A B OA ，同理得规律333、、=⋅⋅⋅=n n n A B OA A B OA ，即可求得结果．【详解】解：∵30MON ∠=︒，112A B A ∆是等边三角形，∴11260∠=︒B A A ，1112A B A A =∴1111230∠=∠-∠=︒OB A B A A MON ，∴11∠=∠OB A MON ，则11OA B ∆是等腰三角形，∴111=A B OA ，∵11OA =，∴11121==A B A A OA =1，21122=+=OA OA A A ，同理可得22OA B ∆是等腰三角形，可得222=A B OA =2，同理得23342==A B 、34482==A B ，根据以上规律可得：2018201920192=A B ，即201920192020A B A ∆的边长为20182，故选：B ．【点睛】本题属于探索规律题，主要考查了等边三角形的性质、等腰三角形的判定与性质，掌握等边三角形的三个内角都是60°、等角对等边和探索规律并归纳公式是解题的关键．17．如图，已知等边△ABC 的边长为4，面积为43，点D 为AC 的中点，点E 为BC 的中点，点P 为BD 上一动点，则PE+PC 的最小值为（）A ．3B ．2C ．3D ．3【答案】C【解析】【分析】由题意可知点A 、点C 关于BD 对称，连接AE 交BD 于点P ，由对称的性质可得，PA=PC ，故PE+PC=AE ，由两点之间线段最短可知，AE 即为PE+PC 的最小值．【详解】解：∵△ABC 是等边三角形，点D 为AC 的中点，点E 为BC 的中点，∴BD⊥AC，EC＝2，连接AE，线段AE的长即为PE+PC最小值，∵点E是边BC的中点，∴AE⊥BC，∴PE+PC的最小值是22-=．4223-＝22AC E C故选C．【点睛】本题考查的是轴对称-最短路线问题，熟知等边三角形的性质是解答此题的关键．18．如图，已知正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1）．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换，如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（）A．（-2012，2）B．（-2012，-2）C．（-2013，-2）D．（-2013，2）【答案】A【解析】试题分析：首先由正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1），然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标，即可得规律：第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2），继而求得把正方形ABCD连续经过2014次这样的变换得到正方形ABCD的对角线交点M的坐标．试题解析：∵正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1）．∴对角线交点M的坐标为（2，2），根据题意得：第1次变换后的点M的对应点的坐标为（2-1，-2），即（1，-2），第2次变换后的点M的对应点的坐标为：（2-2，2），即（0，2），第3次变换后的点M的对应点的坐标为（2-3，-2），即（-1，-2），第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2），∴连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（-2012，2）．故选A ．考点：1．翻折变换（折叠问题）；2．正方形的性质；3．坐标与图形变化-平移．19．如图，等腰三角形ABC 的底边BC 长为4，腰AC 的垂直平分线EF 分别交AC ，AB 边于E ，F 点．若点D 为BC 边的中点，点M 为线段EF 上一动点，若△CDM 周长的最小值为8，则△ABC 的面积为（）A ．12B ．16C ．24D ．32 【答案】A【解析】【分析】连接AD ，由于△ABC 是等腰三角形，点D 是BC 边的中点，故AD ⊥BC ，再根据EF 是线段AC 的垂直平分线可知，点C 关于直线EF 的对称点为点A ，故AD 的长为CM+MD 的最小值，再根据三角形的周长求出AD 的长，由此即可得出结论．【详解】连接AD ，∵△ABC 是等腰三角形，点D 是BC 边的中点，∴AD ⊥BC ，∵EF 是线段AC 的垂直平分线，∴点C 关于直线EF 的对称点为点A ，∴AD 的长为CM+MD 的最小值，∵△CDM 周长的最小值为8，∴AD=8-12BC=8-2=6 ∴S △ABC =12BC•AD=12×4×6=12，故选A ．【点睛】本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．20．如图，在ABC △中，2B C ∠=∠，AH BC ⊥，AE 平分BAC ∠，M 是 BC 中点，则下列结论正确的个数为（）（1）AB BE AC += （2）2AB BH BC += （3）2AB HM = （4）CH EH AC +=A ．1B ．2C ．3D ．4【答案】D【解析】【分析】（1）延长AB 取BD=BE ，连接DE ，由∠D=∠BED ，2ABC C ∠=∠，得到∠D=∠C ，在△ADE 和△ACE 中，利用AAS 证明ADE ACE ≌，可得AC=AD=AB+BE ；（2）在HC 上截取HF=BH,连接AF ，可知△ABF 为等腰三角形，再根据2ABC AFB C ∠=∠=∠，可得出△AFC 为等腰三角形，所以FC+BH+HF=AB+2BH=BC ；（3）HM=BM-BH ，所以2HM=2BM-2BH=BC-2BH ，再结合（2）中结论，可得2AB HM =；（4）结合（1）（2）的结论，BC 2BH BE BC BH BE BH CH EH AC AB BE =+=-+=-+-=+.【详解】解：①延长AB 取BD=BE ，连接DE ，∴∠D=∠BED ，∠ABC=∠D+∠BED=2∠D,∵2ABC C ∠=∠，∴∠D=∠C ，在△ADE 和△ACE 中，DAE CAE D C AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADE ACE ≌∴AC=AD=AB+BE ，故（1）正确；②在HC 上截取HF=BH,连接AF ，∵AH BC ⊥，∴△ABF 为等腰三角形，∴AB=AF ，∠ABF=∠AFB ，∵2ABC C ∠=∠，∴∠AFB=2∠C=∠C+∠CAF ，∴FC=AF=AB ，∴FC+BH+HF=AB+2BH=BC ，故（2）正确；③∵HM=BM-BH ，∴2HM=2BM-2BH=BC-2BH ，由②可知BC-2BH=AB ，∴2AB HM =④根据①②结论，可得:BC 2BH BE BC BH BE BH CH EH AC AB BE =+=-+=-+-=+，故（4）正确；故选D.【点睛】本题主要考查了等腰三角形的判定和性质、三角形的外角以及全等三角形的判定和性质，结合实际问题作出合适辅助线是解题关键.。

贵阳清华中学数学全等三角形中考真题汇编[解析版]

贵阳清华中学数学全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P有_____个．【答案】4【解析】【分析】由A点坐标可得OA=22，∠AOP＝45°，分别讨论OA为腰和底边，求出点P在x轴正半轴和负半轴时，△APO是等腰三角形的P点坐标即可.【详解】（1）当点P在x轴正半轴上，①如图，以OA为腰时，∵A的坐标是（2，2），∴∠AOP＝45°，OA＝22，当∠AOP为顶角时，OA=OP=22，当∠OAP为顶角时，AO=AP，∴OPA=∠AOP=45°，∴∠OAP=90°，∴OP=2OA=4，∴P的坐标是（4，0）或（22，0）.②以OA为底边时，∵点A的坐标是（2，2），∴∠AOP=45°，∵AP=OP，∴∠OAP=∠AOP=45°，∴∠OPA=90°，∴OP=2， ∴P 点坐标为（2，0）.（2）当点P 在x 轴负半轴上，③以OA 为腰时，∵A 的坐标是（2，2），∴OA ＝22，∴OA ＝OP ＝22，∴P 的坐标是（﹣22，0）．综上所述：P 的坐标是（2，0）或（4，0）或（22，0）或（﹣22，0）．故答案为：4．【点睛】此题主要考查等腰三角形的判定及坐标与图形性质的综合运用，注意分类讨论思想的运用是解题关键．2．如图，ABC ∆中，90BAC ∠=︒，AD BC ⊥，ABC ∠的平分线BE 交AD 于点F ，AG 平分DAC ∠．给出下列结论：①BAD C ∠=∠；②EBC C ∠=∠；③AE AF =；④//FG AC ；⑤EF FG =．其中正确的结论是______．【答案】①③④【解析】【分析】①根据等角的余角相等即可得到结果，故①正确；②如果∠EBC=∠C ，则∠C=12∠ABC ，由于∠BAC=90°，那么∠C=30°，但∠C 不一定等于30°，故②错误；③由BE 、AG 分别是∠ABC 、∠DAC 的平分线，得到∠ABF=∠EBD ．由于∠AFE=∠BAD+∠FBA ，∠AEB=∠C+∠EBD ，得到∠AFE=∠AEB ，可得③正确；④连接EG ，先证明△ABN ≌△GBN ，得到AN=GN ，证出△ANE ≌△GNF ，得∠NAE=∠NGF ，进而得到GF ∥AE ，故④正确；⑤由AE=AF ，AE=FG ，而△AEF 不一定是等边三角形，得到EF 不一定等于AE ，于是EF 不一定等于FG ，故⑤错误．【详解】∵∠BAC=90°，AD ⊥BC ，∴∠C+∠ABC=90°，∠C+∠DAC=90°，∠ABC+∠BAD=90°，∴∠ABC=∠DAC ，∠BAD=∠C ，故①正确；若∠EBC=∠C ，则∠C=12∠ABC ， ∵∠BAC=90°，那么∠C=30°，但∠C 不一定等于30°，故②错误；∵BE 、AG 分别是∠ABC 、∠DAC 的平分线，∴∠ABF=∠EBD ，∵∠AFE=∠BAD+∠ABF ，∠AEB=∠C+∠EBD ，又∵∠BAD=∠C ，∴∠AFE=∠AEF ，∴AF=AE ，故③正确；∵AG 是∠DAC 的平分线，AF=AE ，∴AN ⊥BE ，FN=EN ，在△ABN 与△GBN 中， ∵90ABN GBN BN BN ANB GNB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，∴△ABN ≌△GBN （ASA ），∴AN=GN ，又∵FN=EN ，∠ANE=∠GNF ，∴△ANE ≌△GNF （SAS ），∴∠NAE=∠NGF ，∴GF ∥AE ，即GF ∥AC ，故④正确；∵AE=AF ，AE=FG ，而△AEF 不一定是等边三角形，∴EF 不一定等于AE ，∴EF 不一定等于FG ，故⑤错误．故答案为：①③④．【点睛】本题主要考查等腰三角形的判定和性质定理，全等三角形的判定和性质定理，直角三角形的性质定理，掌握掌握上述定理，是解题的关键．3．如图，在ABC 中，点A 的坐标为()0,1，点B 的坐标为()0,4，点C 的坐标为()4,3，点D 在第二象限，且ABD 与ABC 全等，点D 的坐标是______．【答案】(－4，2)或(－4，3)【解析】【分析】【详解】把点C 向下平移1个单位得到点D （4，2），这时△ABD 与△ABC 全等，分别作点C ，D 关于y 轴的对称点（-4，3）和（-4，2），所得到的△ABD 与△ABC 全等.故答案为(－4，2)或(－4，3).4．如图，在01A BA △中，20B ∠=︒，01A B A B =，在1A B 上取点C ，延长01A A 到2A ，使得121A A AC =；在2A C 上取一点D ，延长12A A 到3A ，使得232A A A D =；…，按此做法进行下去，第n 个等腰三角形的底角n A ∠的度数为__________．【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律即可得出第n 个等腰三角形的底角∠A n 的度数．【详解】解：∵在△A 0BA 1中，∠B=20°，A 0B=A 1B ，∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°， ∵A 1A 2=A 1C ，∠BA 1 A 0是△A 1A 2C 的外角，∴∠CA 2A 1= 108022BA A ︒∠= =40°；同理可得，∠DA 3A 2=20°，∠EA 4A 3=10°，∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律是解答此题的关键．5．如图，点A,B,C 在同一直线上,△ABD 和△BCE 都是等边三角形，AE,CD 分别与BD,BE 交于点F,G ，连接FG ，有如下结论：①AE=CD ②∠BFG= 60°；③EF=CG ；④AD ⊥CD⑤FG ∥AC 其中，正确的结论有__________________. (填序号)【答案】①②③⑤【解析】【分析】易证△ABE ≌△DBC ，则有∠BAE ＝∠BDC ，AE ＝CD ，从而可证到△ABF ≌△DBG ，则有AF ＝DG ，BF ＝BG ，由∠FBG ＝60°可得△BFG 是等边三角形，证得∠BFG ＝∠DBA ＝60°，则有FG ∥AC ，由∠CDB ≠30°，可判断AD 与CD 的位置关系．【详解】∵△ABD 和△BCE 都是等边三角形，∴BD ＝BA ＝AD ，BE ＝BC ＝EC ，∠ABD ＝∠CBE ＝60°． ∵点A 、B 、C 在同一直线上，∴∠DBE ＝180°﹣60°﹣60°＝60°，∴∠ABE ＝∠DBC ＝120°．在△ABE 和△DBC 中，∵BD BAABE DBCBE BC∠∠=⎧⎪=⎨⎪=⎩，∴△ABE≌△DBC，∴∠BAE＝∠BDC，∴AE＝CD，∴①正确；在△ABF和△DBG中，60BAF BDGAB DBABF DBG∠∠∠∠=⎧⎪=⎨⎪==︒⎩，∴△ABF≌△DBG，∴AF＝DG，BF＝BG．∵∠FBG＝180°﹣60°﹣60°＝60°，∴△BFG是等边三角形，∴∠BFG=60°，∴②正确；∵AE＝CD，AF＝DG，∴EF=CG；∴③正确；∵∠ADB＝60°，而∠CDB=∠EAB≠30°，∴AD与CD不一定垂直，∴④错误．∵△BFG是等边三角形，∴∠BFG=60°，∴∠GFB＝∠DBA＝60°，∴FG∥AB，∴⑤正确．故答案为①②③⑤．【点睛】本题考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、平行线的判定和性质，证得△ABE≌△DBC是解题的关键．6．如图，ABC∆中，AB AC=，点D是ABC∆内部一点，DB DC=，点E是边AB 上一点，若CD平分ACE∠，100AEC=∠，则BDC∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD，再根据角的和差关系得到∠ECB =∠ACB－2∠ACD，然后利用外角定理得到∠ABC+∠ECB=100°，代换化简得出∠ACB－∠ACD=50°，即∠DCB=50°，从而求出∠BDC即可.【详解】∵CD平分∠ACE，∴∠ACE=2∠ACD=2∠ECD，∴∠ECB=∠ACB－∠ACE=∠ACB－2∠ACD，∵∠AEC=100°，∴∠ABC+∠ECB=100°，∴∠ABC+∠ACB－2∠ACD=100°，∵AB=AC，∴∠ABC=∠ACB,∴2∠ACB－2∠ACD=100°，∴∠ACB－∠ACD=50°，即∠DCB=50°，∵DB=DC，∴∠DBC=∠DCB，∴∠BDC=180°－2∠DCB=180°－2×50°=80°.【点睛】本题考查了角平分线，三角形内角和，外角定理，及等边对等角的性质等知识，熟练掌握基本知识，找出角与角之间的关系是解题的关键.7．如图，在3×3的正方形网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中的△ABC为格点三角形，在图中最多能画出_____个格点三角形与△ABC成轴对称．【答案】6【解析】【分析】根据网格结构分别确定出不同的对称轴，然后作出轴对称三角形即可得解．【详解】如图，最多能画出6个格点三角形与△ABC成轴对称．故答案为：6．【点睛】本题考查了利用轴对称变换作图，熟练掌握网格结构并准确找出对应点的位置是解题的关键，本题难点在于确定出不同的对称轴．8．如图，已知30AOB ∠=︒，点P 在边OA 上，14OD DP ==，点E ，F 在边OB 上，PE PF =.若6EF =，则OF 的长为____.【答案】18【解析】【分析】由30°角我们经常想到作垂线，那么我们可以作DM 垂直于OA 于M ，作PN 垂直于OB 于点N ，证明△PMD ≌△PND ，进而求出DF 长度，从而求出OF 的长度.【详解】如图所示，作DM 垂直于OA 于M ，作PN 垂直于OB 于点N.∵∠AOB=30°，∠DMO=90°，PD=DO=14，∴DM=7，∠NPO=60°，∠DPO=30°，∴∠NPD=∠DPO=30°，∵DP=DP ，∠PND=∠PMD=90°，∴△PND ≌△PMD ，∴ND=7，∵EF=6，∴DF=ND-NF=7-3=4，∴OF=DF+OD=14+4=18.【点睛】本题考查了全等三角形的判定及性质定理，作辅助线构造全等三角形是解题的关键.9．如图：在ABC ∆中，D ，E 为边AB 上的两个点，且BD BC =，AE AC =，若108ACB ∠=︒，则DCE ∠的大小为______.【答案】036【解析】【分析】根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ，用∠A 表示∠AEC,用∠B 表示∠BDC，然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080，∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC, ∴01(180)2AEC A ∠=-∠01902A =-∠ 01(180)2BDCB ∠=-∠=01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800，∴0180DCE CDE CED ∠=-∠-∠= 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质，注意两条等边所在三角形，依此判断对应的两个底角相等.10．如图，在四边形ABCD 中，∠A=60°， ∠ADC=∠ABC=90°，在AB 、AD 上分别找一点F 、E ，连接CE 、EF 、CF ，当△CEF 的周长最小时，则∠ECF 的度数为______．【答案】60°【解析】【分析】此题需分三步：第一步是作出△CEF 的周长最小时E 、F 的位置（用对称即可）；第二步是证明此时的△CEF 的周长最小（利用两点之间线段最短）；第三步是利用对称性求此时∠ECF 的值.【详解】分别作出C 关于AD 、AB 的对称点分别为C 1、C 2，连接C 1C 2，分别交AD ，AB 于点E 、F 再连接CE 、CF 此时△CEF 的周长最小，理由如下：在AD、AB上任意取E1、F1两点根据对称性：∴CE=C1E，CE1=C1E1，CF=C2F，CF1=C2F1∴△CEF的周长= CE＋EF＋CF= C1E＋EF＋C2F= C1C2而△CE1F1的周长= CE1＋E1F1＋CF1= C1E1＋E1F1＋C2F1根据两点之间线段最短，故C1E1＋E1F1＋C2F1＞C1C2∴△CEF的周长的最小为：C1C2.∵∠A=60°，∠ADC=∠ABC=90°∴∠DCB=360°－∠A－∠ADC－∠ABC=120°∴∠C C1C2＋∠C C2C1=180°－∠DCB=60°根据对称性：∠C C1C2=∠E CD，∠C C2C1=∠F CB∴∠E CD＋∠F CB=∠C C1C2＋∠C C2C1=60°∴∠ECF=∠DCB－（∠E CD＋∠F CB）=60°故答案为：60°【点睛】此题考查的是周长最小值的作图方法（对称点），及周长最小值的证法：两点之间线段最短，掌握周长最小值的作图方法是解决此题的关键.二、八年级数学轴对称三角形选择题（难）11．如图，在等边△ABC中，AD是BC边上的高，∠BDE=∠CDF=30°，在下列结论中：①△ABD≌△ACD；②2DE=2DF=AD；③△ADE≌△ADF；④4BE=4CF=AB．正确的个数是（）A．1 B．2 C．3 D．4【答案】D【解析】由等边三角形的性质可得BD=DC ，AB=AC ，∠B=∠C=60°，利用SAS 可证明△ABD ≌△ACD ，从而可判断①正确；利用ASA 可证明△ADE ≌△ADF ，从而可判断③正确；在Rt △ADE 与Rt △ADF 中，∠EAD=∠FAD=30°，根据30度角所对的直角边等于斜边的一半可得2DE=2DF=AD ，从而可判断②正确；同理可得2BE=2CF=BD ，继而可得4BE=4CF=AB ，从而可判断④正确，由此即可得答案.【详解】∵等边△ABC 中，AD 是BC 边上的高，∴BD=DC ，AB=AC ，∠B=∠C=60°，在△ABD 与△ACD 中90AD AD ADB ADC DB DC =⎧⎪∠=∠=︒⎨⎪=⎩， ∴△ABD ≌△ACD ，故①正确；在△ADE 与△ADF 中60EAD FAD AD ADEDA FDA ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△ADE ≌△ADF ，故③正确；∵在Rt △ADE 与Rt △ADF 中，∠EAD=∠FAD=30°，∴2DE=2DF=AD ，故②正确；同理2BE=2CF=BD ，∵AB=2BD ，∴4BE=4CF=AB ，故④正确，故选D ．【点睛】本题考查了等边三角形的性质、含30度的直角三角形的性质、全等三角形的判定等，熟练掌握相关性质与定理是解题的关键.12．在Rt ABC ∆中，90ACB ∠=︒，点D E 、是AB 边上两点，且CE 垂直平分,AD CD 平分,6BCE AC cm ∠=，则BD 的长为（）A ．6cmB ．7cmC ．8cmD ．9cm【解析】【分析】根据CE 垂直平分AD ，得AC=CD ，再根据等腰在三角形的三线合一，得ACE ECD ∠=∠，结合角平分线定义和90ACB ︒∠=，得30ACE ECD DCB ︒∠=∠=∠=，则BD CD AC ==．【详解】∵CE 垂直平分AD∴AC=CD ＝6cm ，ACE ECD ∠=∠∵CD 平分BCE ∠∴BCD ECD ∠=∠∴30ACE ECD DCB ︒∠=∠=∠=∴60A ︒∠=∴30B BCD ︒∠==∠∴6CD BD AC cm ===故选：A【点睛】本题考查的知识点主要是等腰三角形的性质的“三线合一”性质定理及判定“等角对等边”，熟记并能熟练运用这些定理是解题的关键．13．如图所示，把多块大小不同的30角三角板，摆放在平面直角坐标系中，第一块三角板AOB 的一条直角边与x 轴重合且点A 的坐标为()2,0，30ABO ∠=︒，第二块三角板的斜边1BB 与第一块三角板的斜边AB 垂直且交x 轴于点1B ，第三块三角板的斜边12B B 与第二块三角板的斜边1BB 垂直且交y 轴于点2B ，第四块三角板斜边23B B 与第三块三角板的斜边12B B 垂直且交x 轴于点3B ，按此规律继续下去，则点2018B 的坐标为（）A ．()20182(3),0-⨯ B ．()20180,2(3)-⨯ C ．()20192(3),0⨯ D ．()20190,2(3)-⨯ 【答案】D【解析】【分析】计算出OB 、OB 1、 OB 2的长度，根据题意和图象可以发现题目中的变化规律，从而可以求得点B 2018的坐标．解：由题意可得， OB = 2242-= 23，OB 1= 3 OB= 233⨯ = 22(3)⨯，OB 2= 3 OB 1= 32(3)⨯，…∵2018÷4=504…2，∴点B 2018在y 轴的负半轴上，∴点B 2018的坐标为()20190,2(3)-⨯．故答案为：D ．【点睛】本题考查规律型：点的坐标规律及含30度角的直角三角形的性质，解答本题的关键是明确题意，找出题目中坐标的变化规律，求出相应的点的坐标．14．如图，Rt ACB ∆中，90ACB ∠=︒，ABC ∠的平分线BE 和BAC ∠的外角平分线AD 相交于点P ，分别交AC 和BC 的延长线于E ，D .过P 作PF AD ⊥交AC 的延长线于点H ，交BC 的延长线于点F ，连接AF 交DH 于点G .下列结论：①45APB ∠=︒；②PB 垂直平分AF ；③BD AH AB -=；④2DG PA GH =+；其中正确的结论有（）A ．4个B ．3个C ．2个D ．1个【答案】A【解析】【分析】 ①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP ，再根据角平分线的定义∠ABP ＝12∠ABC ，然后利用三角形的内角和定理整理即可得解；②先求出∠APB ＝∠FPB ，再利用“角边角”证明△ABP 和△FBP 全等，根据全等三角形对应边相等得到AB ＝BF ，AP ＝PF ；③根据直角的关系求出∠AHP ＝∠FDP ，然后利用“角角边”证明△AHP 与△FDP 全等，根据全等三角形对应边相等可得DF ＝AH ；④求出∠ADG ＝∠DAG ＝45°，再根据等角对等边可得DG ＝AG ，再根据等腰直角三角形两腰相等可得GH ＝GF ，然后根据即可得到DG GH =+. 【详解】解：①∵∠ABC 的角平分线BE 和∠BAC 的外角平分线，∴∠ABP ＝12∠ABC ， ∠CAP ＝12（90°＋∠ABC ）＝45°＋12∠ABC ，在△ABP 中，∠APB ＝180°−∠BAP−∠ABP ，＝180°−（45°＋12∠ABC ＋90°−∠ABC ）−12∠ABC ，＝180°−45°−12∠ABC−90°＋∠ABC−12∠ABC ，＝45°，故本小题正确；②∵PF ⊥AD ，∠APB ＝45°（已证），∴∠APB ＝∠FPB ＝45°，∵∵PB 为∠ABC 的角平分线，∴∠ABP ＝∠FBP ，在△ABP 和△FBP 中，APB FPB PB PBABP FBP ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△ABP ≌△FBP （ASA ），∴AB ＝BF ，AP ＝PF ；∴PB 垂直平分AF ，故②正确；③∵∠ACB ＝90°，PF ⊥AD ，∴∠FDP ＋∠HAP ＝90°，∠AHP ＋∠HAP ＝90°，∴∠AHP ＝∠FDP ，∵PF ⊥AD ，∴∠APH ＝∠FPD ＝90°，在△AHP 与△FDP 中，90AHP FDP APH FPD AP PF ∠∠⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△AHP ≌△FDP （AAS ），∴DF ＝AH ，∵BD ＝DF ＋BF ，∴BD ＝AH ＋AB ，∴BD−AH ＝AB ，故③小题正确；④∵AP ＝PF ，PF ⊥AD ，∴∠PAF ＝45°，∴∠ADG ＝∠DAG ＝45°，∴DG ＝AG ，∵∠PAF ＝45°，AG ⊥DH ，∴△ADG 与△FGH 都是等腰直角三角形，∴DG ＝AG ，GH ＝GF ，∴DG ＝GH ＋AF ，∴FG=GH,AF=2PA故2DG PA GH =+.综上所述①②③④正确．故选：A ．【点睛】本题考查了直角三角形的性质，全等三角形的判定，以及等腰直角三角形的判定与性质，等角对等边，等边对等角的性质，综合性较强，难度较大，做题时要分清角的关系与边的关系．15．如图，ABC △，AB AC =，56BAC ︒∠=，BAC ∠的平分线与AB 的垂直平分线交于O ，将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与O 点恰好重合，则∠OEC 的度数为（）A ．132︒B ．130︒C ．112︒D ．110︒【答案】C【解析】【分析】连接OB 、OC ，根据角平分线的定义求出∠BAO ，根据等腰三角形两底角相等求出∠ABC ，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB ，根据等边对等角可得∠ABO=∠BAO ，再求出∠OBC ，然后判断出点O 是△ABC 的外心，根据三角形外心的性质可得OB=OC ，再根据等边对等角求出∠OCB=∠OBC ，根据翻折的性质可得OE=CE ，然后根据等边对等角求出∠COE ，再利用三角形内角和定理列式计算即可得出答案.【详解】如图，连接OB 、OC ，∵56BAC ︒∠=，AO 为BAC ∠的平分线∴11562822BAO BAC ︒︒∠=∠=⨯= 又∵AB AC =，∴()()11180180566222ABC BAC ︒︒︒︒∠=-∠=-= ∵DO 是AB 的垂直平分线，∴OA OB =．∴28ABO BAO ︒∠=∠=，∴622834OBC ABC ABO ︒︒︒∠=∠-∠=-=∵DO 是AB 的垂直平分线，AO 为BAC ∠的平分线∴点О是ABC △的外心，∴OB OC =，∴34OCB OBC ︒∠=∠=，∵将C ∠沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合∴OE CE =，∴34COE OCB ︒∠=∠=，在OCE △中，1801803434112OEC COE OCB ︒︒︒︒︒∠=-∠-∠=--=【点睛】本题主要考查了线段垂直平分线上的点到线段两端点距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，以及翻折变换的性质，综合性较强，难度较大，做辅助线构造出等腰三角形是解决本题的关键.16．如图，ABC △是等边三角形，ABD △是等腰直角三角形，∠BAD =90°，AE ⊥BD 于点E ．连CD 分别交AE ，AB 于点F ，G ，过点A 做AH ⊥CD 交BD 于点H ，则下列结论：①∠ADC =15°；②AF =AG ；③AH =DF ；④△ADF ≌△BAH ；⑤DF =2EH .其中正确结论的个数为（）A ．5B ．4C ．3D ．2【答案】B【解析】【分析】 ①根据△ABC 为等边三角形，△ABD 为等腰直角三角形，可以得出各角的度数以及DA=AC ，即可作出判断；②分别求出∠AFG 和∠AGD 的度数，即可作出判断；④根据三角形内角和定理求出∠HAB 的度数，求证EHG DFA ∠=∠，利用AAS 即可证出两个三角形全等；③根据④证出的全等即可作出判断；⑤证明∠EAH=30°，即可得到AH=2EH ，又由③可知AH DF =，即可作出判断.【详解】①正确：∵ABC △是等边三角形，∴60BAC ︒∠=，∴CA AB =．∵ABD △是等腰直角三角形，∴DA AB =．又∵90BAD ︒∠=，∴150CAD BAD BAC ︒∠=∠+∠=，∴DA CA =，∴()1180150152ADC ACD ︒︒︒∠=∠=-=； ②错误：∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③，④正确，由题意可得45DAF ABH ︒∠=∠=，DA AB =，∵AE BD ⊥，AH CD ⊥．∴180EHG EFG ︒∠+∠=．又∵180?DFA EFG ∠+∠=，∴EHG DFA ∠=∠，在DAF △和ABH 中 ()AFD BHA DAF ABHAAS DA AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF △≌ABH ．∴DF AH =．⑤正确：∵150CAD ︒∠=，AH CD ⊥，∴75DAH ︒∠=，又∵45DAF ︒∠=，∴754530EAH ︒︒︒∠=-=又∵AE DB ⊥，∴2AH EH =，又∵=AH DF ，∴2DF EH =【点睛】本题考查了等边三角形的性质，等腰三角形的性质，三角形的内角和定理，三角形外角的性质，全等三角形的判定与性质，综合性较强，属于较难题目.17．已知等边△ABC中，在射线BA上有一点D，连接CD，并以CD为边向上作等边△CDE，连接BE和AE，试判断下列结论：①AE=BD；②AE与AB所夹锐夹角为60°；③当D在线段AB或BA延长线上时，总有∠BDE-∠AED=2∠BDC；④∠BCD=90°时，CE2+AD2=AC2+DE2，正确的序号有（）A．①②B．①②③C．①②④D．①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°，∠ACE=∠ACD+60°可得∠BCD=∠ACE，利用SAS可证明△BCD≌△ACE，可得AE=BD，①正确；∠CBD=∠CAE=60°，进而可得∠EAD=60°，②正确，当∠BCD=90°时，可得∠ACD=∠ADC=30°，可得AD=AC，即可得CE2+AD2=AC2+DE2，④正确；当D点在BA延长线上时，∠BDE-∠BDC=60°，根据△BCD≌△ACE可得∠AEC=∠BDC，进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，即可证明∠BDE-∠BDC=∠BDC+∠AED，即∠BDE-∠AED=2∠BDC，当点D在AB上时可证明∠BDE-∠AED=120°，③错误，综上即可得答案.【详解】∵∠BCA=∠DCE=60°，∴∠BCA+∠ACD=∠DCE+∠ACD，∴∠BCD=∠ACE，又∵AC=BC，CE=CD，∴△BCD≌△ACE，∴AE=BD，∠CBA=∠CAE=60°，∠AEC=∠BDC，①正确，∴∠BAE=120°，∴∠EAD=60°，②正确，∵∠BCD=90°，∠BCA=60°，∴∠ACD=∠ADC=30°，∴AC=AD，∵CE=DE，∴CE2+AD2=AC2+DE2，④正确，当D点在BA延长线上时，∠BDE-∠BDC=60°，∵∠AEC=∠BDC，∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC，如图，当点D在AB上时，∵△BCD≌△∠ACE，∴∠CAE=∠CBD=60°，∴∠DAE=∠BAC+∠CAE=120°，∴∠BDE-∠AED=∠DAE=120°，③错误故正确的结论有①②④，故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握18．如图，在△ABC中，AB=AC=8，BC=5，AB的垂直平分线交AC于D，则△BCD的周长为（）A．13B．15C．18D．21【答案】A【解析】根据线段垂直平分线的性质，可由AB=AC=8，BC=5，AB的垂直平分线交AC于D，得到AD=BD，进而得出△BCD的周长为：CD+BD+BC=AC+BC=8+5=13．故选A．点睛：此题主要考查了线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等．19．如图，等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上的一点，当PA=CQ时，连接PQ交AC于点D，下列结论中不一定正确的是（）A．PD=DQ B．DE=12AC C．AE=12CQ D．PQ⊥AB【答案】D【解析】过P作PF∥CQ交AC于F，∴∠FPD=∠Q，∵△ABC是等边三角形，∴∠A=∠ACB=60°，∴∠A=∠AFP=60°，∴AP=PF，∵PA=CQ，∴PF=CQ，在△PFD与△DCQ 中，FPD QPDE CDQPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PFD≌△QCD，∴PD=DQ，DF=CD，∴A选项正确，∵AE=EF，∴DE=12AC，∴B选项正确，∵PE⊥AC，∠A=60°，∴AE=12AP=12CQ，∴C选项正确，故选D．20．如图所示，在四边ABCD中，∠BAD=120°，∠B=∠D=90°，若在BC和CD上分别找一点M，使得△AMN的周长最小，则此时∠AMN+∠ANM的度数为（）A．110°B．120°C．140°D．150°【答案】B【解析】【分析】根据要使△AMN的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠AA′M+∠A″=60°，进而得出∠AMN+∠ANM=2（∠AA′M+∠A″）即可得出答案．【详解】作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值．∵∠DAB=120°，∴∠AA′M+∠A″=180°-120°=60°，∵∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2（∠AA′M+∠A″）=2×60°=120°，故选B．【点睛】此题主要考查了平面内最短路线问题求法，以及三角形的外角的性质和垂直平分线的性质等知识的综合应用，根据轴对称的性质，得出M，N的位置是解题的关键．。

八年级数学全等三角形中考真题汇编[解析版]

八年级数学全等三角形中考真题汇编[解析版]一、八年级数学轴对称三角形填空题（难）1．如图，在等边ABC ∆中取点P 使得PA ，PB ，PC 的长分别为3， 4， 5，则APC APB S S ∆∆+=_________．【答案】936 【解析】【分析】把线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS 证得△ADB ≌△APC ，连接PD ，根据旋转的性质知△APD 是等边三角形，利用勾股定理的逆定理可得△PBD 为直角三角形，∠BPD ＝90︒，由△ADB ≌△APC 得S △ADB ＝S △APC ，则有S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ，根据等边3S △ADP ＋S △BPD ＝332＋12×3×4＝936+．【详解】将线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，连接PD∴AD ＝AP ，∠DAP ＝60︒，又∵△ABC 为等边三角形，∴∠BAC ＝60︒，AB ＝AC ，∴∠DAB ＋∠BAP ＝∠PAC ＋∠BAP ，∴∠DAB ＝∠PAC ，又AB=AC,AD=AP∴△ADB ≌△APC∵DA ＝PA ，∠DAP ＝60︒，∴△ADP 为等边三角形，在△PBD 中，PB ＝4，PD ＝3，BD ＝PC ＝5，∵32＋42＝52，即PD 2＋PB 2＝BD 2，∴△PBD 为直角三角形，∠BPD ＝90︒，∵△ADB ≌△APC ，∴S △ADB ＝S △APC ，∴S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ＝34×32＋12×3×4＝9364+．故答案为：9364+．【点睛】本题考查了等边三角形的性质与判定，解题的关键是熟知旋转的性质作出辅助线进行求解．2．如图，ABC 中，ABC=45∠︒，CD AB ⊥于D ，BE 平分ABC ∠，且BE AC ⊥于E ，与CD 相交于点F ，H 是BC 边的中点，连接DH 与BE 相交于点G ，下列结论：BF=AC ①；A=67.5∠︒②；DG=DF ③；ADGE GHCE S S =四边形四边形④，其中正确的有__________（填序号）．【答案】①②③【解析】【分析】只要证明△BDF ≌△CDA ，△BAC 是等腰三角形，∠DGF=∠DFG=67.5°，即可判断①②③正确，作GM ⊥BD 于M ，只要证明GH ＜DG 即可判断④错误．【详解】解：∵CD ⊥AB ，BE ⊥AC ，∴∠BDC=∠ADC=∠AEB=90°，∴∠A ＋∠ABE=90°，∠ABE ＋∠DFB=90°，∴∠A=∠DFB ，∵∠ABC=45°，∠BDC=90°，∴∠DCB=90°−45°=45°=∠DBC ，∴BD=DC ，在△BDF和△CDA中，∠BDF=∠CDA，∠A=∠DFB，BD=CD，∴△BDF≌△CDA（AAS），∴BF=AC，故①正确．∵∠ABE=∠EBC=22.5°，BE⊥AC，∴∠A=∠BCA=67.5°，故②正确，∵BE平分∠ABC，∠ABC=45°，∴∠ABE=∠CBE=22.5°，∵∠BDF=∠BHG=90°，∴∠BGH=∠BFD=67.5°，∴∠DGF=∠DFG=67.5°，∴DG=DF，故③正确．作GM⊥AB于M．如图所示：∵∠GBM=∠GBH，GH⊥BC，∴GH=GM＜DG，∴S△DGB＞S△GHB，∵S△ABE=S△BCE，∴S四边形ADGE＜S四边形GHCE．故④错误，故答案为：①②③．【点睛】此题是三角形综合题，考查了等腰三角形的性质，直角三角形的性质，全等三角形的性质和判定，三角形的面积等知识点的综合运用，第五个问题难度比较大，添加辅助线是解题关键，属于中考选择题中的压轴题．3．如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法：①AD是∠BAC的平分线；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△DAC：S△ABC＝1：3.其中正确的是__________________．(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP ，MP ，根据SSS 定理可得△ANP ≌△AMP ，故可得出结论；②先根据三角形内角和定理求出∠CAB 的度数，再由AD 是∠BAC 的平分线得出∠1=∠2=30°，根据直角三角形的性质可知∠ADC =60°；③根据∠1=∠B 可知AD =BD ，故可得出结论；④先根据直角三角形的性质得出∠2=30°，CD =12AD ，再由三角形的面积公式即可得出结论．【详解】 ①连接NP ，MP ．在△ANP 与△AMP 中，∵AN AM NP MP AP AP =⎧⎪=⎨⎪=⎩，∴△ANP ≌△AMP ，则∠CAD =∠BAD ，故AD 是∠BAC 的平分线，故此选项正确；②∵在△ABC 中，∠C =90°，∠B =30°，∴∠CAB =60°．∵AD 是∠BAC 的平分线，∴∠1=∠2=12∠CAB =30°，∴∠3=90°﹣∠2=60°，∴∠ADC =60°，故此选项正确；③∵∠1=∠B =30°，∴AD =BD ，∴点D 在AB 的中垂线上，故此选项正确；④∵在Rt △ACD中，∠2=30°，∴CD =12AD ，∴BC =BD +CD =AD +12AD =32AD ，S △DAC =12AC •CD =14AC •AD ，∴S △ABC=12AC •BC =12AC •32AD =34AC •AD ，∴S △DAC ：S △ABC =1：3，故此选项正确．故答案为①②③④．【点睛】本题考查的是作图﹣基本作图，熟知角平分线的作法是解答此题的关键．4．如图，已知∠MON ＝30°，点A 1，A 2，A 3，…在射线ON 上，点B 1，B 2，B 3，…在射线OM 上，△A 1B 1A 2，△A 2B 2A 3，△A 3B 3A 4，…均为等边三角形，若OA 2＝4，则△A n B n A n +1的边长为_____．【答案】2n ．【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A 1B 1∥A 2B 2∥A 3B 3，以及A 2B 2＝2B 1A 2，得出A 3B 3＝4B 1A 2＝8，A 4B 4＝8B 1A 2＝16，A 5B 5＝16B 1A 2…进而得出答案．【详解】解：∵△A 1B 1A 2是等边三角形，∴A 1B 1＝A 2B 1，∵∠MON ＝30°，∵OA 2＝4，∴OA 1＝A 1B 1＝2，∴A 2B 1＝2，∵△A 2B 2A 3、△A 3B 3A 4是等边三角形，∴A 1B 1∥A 2B 2∥A 3B 3，B 1A 2∥B 2A 3，∴A 2B 2＝2B 1A 2，B 3A 3＝2B 2A 3，∴A 3B 3＝4B 1A 2＝8，A 4B 4＝8B 1A 2＝16，A 5B 5＝16B 1A 2＝32，以此类推△A n B n A n +1的边长为 2n ．故答案为：2n ．【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质，由条件得到OA 5=2OA 4=4OA 3=8OA 2=16OA 1是解题的关键．5．如图，ABC ∆中，AB AC =，点D 是ABC ∆内部一点，DB DC =，点E 是边AB 上一点，若CD 平分ACE ∠，100AEC =∠，则BDC ∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD，再根据角的和差关系得到∠ECB =∠ACB－2∠ACD，然后利用外角定理得到∠ABC+∠ECB=100°，代换化简得出∠ACB－∠ACD=50°，即∠DCB=50°，从而求出∠BDC即可.【详解】∵CD平分∠ACE，∴∠ACE=2∠ACD=2∠ECD，∴∠ECB=∠ACB－∠ACE=∠ACB－2∠ACD，∵∠AEC=100°，∴∠ABC+∠ECB=100°，∴∠ABC+∠ACB－2∠ACD=100°，∵AB=AC，∴∠ABC=∠ACB,∴2∠ACB－2∠ACD=100°，∴∠ACB－∠ACD=50°，即∠DCB=50°，∵DB=DC，∴∠DBC=∠DCB，∴∠BDC=180°－2∠DCB=180°－2×50°=80°.【点睛】本题考查了角平分线，三角形内角和，外角定理，及等边对等角的性质等知识，熟练掌握基本知识，找出角与角之间的关系是解题的关键.6．如图，∠AOB＝45°，点M、点C在射线OA上，点P、点D在射线OB上，且OD＝2，则CP+PM+DM的最小值是_____．【答案】34．【解析】【分析】如图，作点C关于OB的对称点C′，作点D关于OA的对称点D′，连接OC′，PC′，D′M，OD′，C′D′，根据轴对称的性质得到OC′＝OC＝2，OD′＝OD＝32，CP＝C′P，DM＝D′M，∠C′OD＝′COD＝∠COD′＝45°，于是得到CP+PM+MD＝C′+PM+D′M≥C′D′，当仅当C′，P，M，D′三点共线时，CP+PM+MD最小为C′D′，作C′T⊥D′O于点T，于是得到结论．【详解】解：如图，作点C关于OB的对称点C′，作点D关于OA的对称点D′，连接OC′，PC′，D′M，OD′，C′D′，则OC′＝OC＝2，OD′＝OD＝32，CP＝C′P，DM＝D′M，∠C′OD＝′COD＝∠COD′＝45°，∴CP+PM+MD＝C′+PM+D′M≥C′D′，当仅当C′，P，M，D′三点共线时，CP+PM+MD最小为C′D′，作C′T⊥D′O于点T，则C′T＝OT＝2，∴D′T＝42，∴C′D′＝34，∴CP+PM+DM的最小值是34．故答案为：34．【点睛】本题考查了最短路径问题，掌握作轴对称点是解题的关键.7．如图，过边长为1的等边三角形ABC的边AB上一点P，作PE⊥AC于点E，Q为BC延长线上一点，当AP＝CQ时，PQ交AC于D，则DE的长为______．【答案】1 2【解析】过点Q作AD的延长线的垂线于点F.因为△ABC是等边三角形，所以∠A=∠ACB=60°.因为∠ACB=∠QCF，所以∠QCF=60°.因为PE⊥AC，QF⊥AC，所以∠AEP=∠CFQ=90°，又因为AP=CQ，所以△AEP≌△CFQ，所以AE=CF，PE=QC.同理可证，△DEP≌△DFQ，所以DE=DF.所以AC=AE+DE+CD=DE+CD+CF=DE+DF=2DE，所以DE=12AC=12.故答案为1 2 .8．如图，△ABC中，AC＝DC＝3，BD垂直∠BAC的角平分线于D，E为AC的中点，则图中两个阴影部分面积之差的最大值为________．【答案】9 2【解析】【分析】首先证明两个阴影部分面积之差＝S△ADC，当CD⊥AC时，△ACD的面积最大．【详解】延长BD交AC于点H．设AD交BE于点O．∵AD⊥BH，∴∠ADB＝∠ADH＝90°，∴∠ABD＋∠BAD＝90°，∠H＋∠HAD＝90°，∵∠BAD＝∠HAD，∴∠ABD＝∠H，∴AB＝AH，∵AD⊥BH，∴BD＝DH，∵DC＝CA，∴∠CDA＝∠CAD，∵∠CAD＋∠H＝90°，∠CDA＋∠CDH＝90°，∴∠CDH＝∠H，∴CD＝CH＝AC，∵AE＝EC，∴S△ABE＝14S△ABH，S△CDH＝14S△ABH，∵S△OBD−S△AOE＝S△ADB−S△ABE＝S△ADH−S△CDH＝S△ACD，∵AC＝CD＝3，∴当DC⊥AC时，△ACD的面积最大，最大面积为12×3×3＝92．故填：92．【点睛】本题考查等腰三角形的判定和性质，三角形中线的性质等知识，解题的关键是学会用转化的思想思考问题．9．如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB 以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P、Q同时出发，用t(s)表示移动的时间，当t=_____s时，△POQ是等腰三角形.【答案】103或10【解析】【分析】根据△POQ是等腰三角形，分两种情况进行讨论：点P在AO上，点P在BO上，分别计算，即可得解.【详解】当PO=QO时，△POQ是等腰三角形，如图1所示当点P在AO上时，∵PO=AO-AP=10-2t，OQ=t当PO=QO时，102t t-=解得103 t=当PO=QO 时，△POQ 是等腰三角形，如图2所示当点P 在BO 上时∵PO=AP-AO=2t-10，OQ=t当PO=QO 时，210t t -=解得10t = 故答案为：103或10 【点睛】本题考查等腰三角形的性质及动点问题，熟练掌握等腰三角形的性质以及分类讨论思想是解题关键.10．如图：在ABC ∆中，D ，E 为边AB 上的两个点，且BD BC =，AE AC =，若108ACB ∠=︒，则DCE ∠的大小为______.【答案】036【解析】【分析】根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ，用∠A 表示∠AEC,用∠B 表示∠BDC，然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080，∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC,∴01(180)2AEC A ∠=-∠01902A =-∠ 01(180)2BDCB ∠=-∠ =01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800，∴0180DCE CDE CED ∠=-∠-∠ = 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质，注意两条等边所在三角形，依此判断对应的两个底角相等.二、八年级数学轴对称三角形选择题（难）11．已知∠AOB =30°，点P 在∠AOB 内部，P 1与P 关于OB 对称，P 2与P 关于OA 对称，则P 1，O ，P 2三点构成的三角形是（）A ．直角三角形B ．钝角三角形C ．等边三角形D ．等腰三角形【答案】C【解析】【分析】根据题意，作出相应的图形，然后对相应的角进行标记；本题先证明P 1，O ，P 2三点构成的三角形中1260POP ∠=︒，然后证边12OP OP OP ==，得到P 1，O ，P 2三点构成的三角形为等腰三角形，又因为该等腰三角形有一个角为60︒，故得证P 1，O ，P 2三点构成的三角形是等边三角形。

八年级数学全册全套试卷中考真题汇编[解析版]

八年级数学全册全套试卷中考真题汇编[解析版]一、八年级数学三角形填空题（难）1．如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H．下列结论：①∠DBE＝∠F；②2∠BEF＝∠BAF＋∠C；③∠F＝∠BAC－∠C；④∠BGH＝∠ABE＋∠C．其中正确个数是( )A．4个B．3个C．2个D．1个【答案】B【解析】解：①∵BD⊥FD，∴∠FGD+∠F=90°，∵FH⊥BE，∴∠BGH+∠DBE=90°，∵∠FGD=∠BGH，∴∠DBE=∠F，①正确；②∵BE平分∠ABC，∴∠ABE=∠CBE，∠BEF=∠CBE+∠C，∴2∠BEF=∠ABC+2∠C，∠BAF=∠ABC+∠C，∴2∠BEF=∠BAF+∠C，②正确；③∠ABD=90°﹣∠BAC，∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC，∵∠CBD=90°﹣∠C，∴∠DBE=∠BAC﹣∠C﹣∠DBE，由①得，∠DBE=∠F，∴∠F=∠BAC﹣∠C﹣∠DBE，③错误；④∵∠AEB=∠EBC+∠C，∵∠ABE=∠CBE，∴∠AEB=∠ABE+∠C，∵BD⊥FC，FH⊥BE，∴∠FGD=∠FEB，∴∠BGH=∠ABE+∠C，④正确．故答案为①②④．点睛：本题考查的是三角形内角和定理，正确运用三角形的高、中线和角平分线的概念以及三角形外角的性质是解题的关键．2．某多边形内角和与外角和共1080°，则这个多边形的边数是__________．【答案】6【解析】∵多边形内角和与外角和共1080°，∴多边形内角和=1080°−360°=720°，设多边形的边数是n，∴(n−2)×180°=720°，解得n=6.故答案为6.点睛：先根据多边形的外角和为360°求出其内角和，再根据多边形内角和定理即可求出多边形的边数．3．有公共顶点A，B的正五边形和正六边形按如图所示位置摆放，连接AC交正六边形于点D，则∠ADE的度数为（）A．144°B．84°C．74°D．54°【答案】B【解析】正五边形的内角是∠ABC=()521805-⨯=108°，∵AB=BC，∴∠CAB=36°，正六边形的内角是∠ABE=∠E=()621806-⨯=120°，∵∠ADE+∠E+∠ABE+∠CAB=360°，∴∠ADE=360°–120°–120°–36°=84°，故选B．4．一个多边形的内角和是外角和的72倍，那么这个多边形的边数为_______.【答案】9【解析】【分析】根据多边形的内角和公式（n-2）•180°与外角和定理列出方程，然后求解即可．【详解】解：设这个多边形是n边形，根据题意得，（n-2）•180°=72×360°，解得：n=9．故答案为：9．【点睛】本题考查了多边形的内角和公式与外角和定理，多边形的外角和与边数无关，任何多边形的外角和都是360°．5．已知一个多边形的内角和与外角和的差是1260°，则这个多边形边数是．【答案】12【解析】试题解析：根据题意，得（n-2）•180-360=1260，解得：n=11．那么这个多边形是十一边形．考点：多边形内角与外角．6．等腰三角形一边长是10cm ，一边长是6cm ，则它的周长是_____cm 或_____cm ．【答案】22cm, 26cm【解析】【分析】题目给出等腰三角形有两条边长为10cm 和6cm ，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】（1）当腰是6cm 时，周长＝6+6+10＝22cm ；（2）当腰长为10cm 时，周长＝10+10+6＝26cm ，所以其周长是22cm 或26cm ．故答案为：22，26．【点睛】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．二、八年级数学三角形选择题（难）7．如图，ABC ∆中，100ABC ∠=︒，且AEF AFE ∠=∠，CFD CDF ∠=∠，则EFD ∠ 的度数为( )A ．80°B ．60°C ．40°D ．20°【答案】C【解析】【分析】连接FB ，根据三角形内角和和外角知识，进行角度计算即可．【详解】解：如图连接FB ，∵AEF AFE ∠=∠，CFD CDF ∠=∠，∴AEF AFE EFB EBF ∠=∠=∠+∠，CFD CDF BFD FBD ∠=∠=∠+∠∴AFE CFD EFB EBF BFD FBD ∠+∠=∠+∠+∠+∠，即AFE CFD EFD EBD ∠+∠=∠+∠，又∵180AFE EFD DFC ∠+∠+∠=︒，∴2180EFD EBD ∠+∠=︒，∵100ABC ∠=︒，∴180100=402EFD ︒-︒∠=︒，故选：C ．【点睛】此题考查三角形内角和和外角定义，掌握三角形内角和为180°，三角形一个外角等于不相邻两内角之和是解题关键．8．如图，ABC 的面积为1．分别倍长（延长一倍）AB ，BC ，CA 得到111A B C ．再分别倍长A 1B 1，B 1C 1，C 1A 1得到222A B C ．…… 按此规律，倍长2018次后得到的201820182018A B C 的面积为（）A ．20176B ．20186C ．20187D ．20188【答案】C【解析】分析：根据等底等高的三角形的面积相等可得三角形的中线把三角形分成两个面积相等的三角形，然后求出第一次倍长后△A 1B 1C 1的面积是△ABC 的面积的7倍，依此类推写出即可．详解：连接AB 1、BC 1、CA 1，根据等底等高的三角形面积相等，△A 1BC 、△A 1B 1C 、△AB 1C 、△AB 1C 1、△ABC 1、△A 1BC 1、△ABC 的面积都相等，所以，S △A 1B 1C 1=7S △ABC ，同理S △A 2B 2C 2=7S △A 1B 1C 1=72S △ABC ，依此类推，S △AnBnCn =7n S △ABC ．∵△ABC的面积为1，∴S △AnBnCn =7n ，∴S △A 2018B 2018C 2018=72018．故选C ．点睛：本题考查了三角形的面积，根据等底等高的三角形的面积相等求出一次倍长后所得的三角形的面积等于原三角形的面积的7倍是解题的关键．9．如图，把△ABC 纸片沿DE 折叠，当点A 在四边形BCDE 的外部时，记∠AEB 为∠1，∠ADC 为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（）A ．∠1＝∠2＋∠AB ．∠1＝2∠A＋∠2C ．∠1＝2∠2＋2∠AD ．2∠1＝∠2＋∠A【答案】B【解析】试题分析：如图在∆ABC 中，∠A+∠B+∠C=180°，折叠之后在∆ADF 中，∠A+∠2+∠3=180°，∴∠B+∠C=∠2+∠3，∠3=180°-∠A -∠2，又在四边形BCFE 中∠B+∠C+∠1+∠3=360°，∴∠2+∠3+∠1+∠3=360°∴∠2+∠1+2∠3=∠2+∠1+2（180°-∠A -∠2）=360°，∴∠2+∠1-2∠A -2∠2=0，∴∠1＝2∠A＋∠2.故选B点睛：本题主要考查考生对三角形内角和，四边形内角和以及三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角和的理解及掌握。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、八年级数学全等三角形解答题压轴题（难）1．如图1，在平面直角坐标系中，点D（m，m+8）在第二象限，点B（0，n）在y轴正半轴上，作DA⊥x轴，垂足为A，已知OA比OB的值大2，四边形AOBD的面积为12．（1）求m和n的值．（2）如图2，C为AO的中点，DC与AB相交于点E，AF⊥BD，垂足为F，求证：AF＝DE．（3）如图3，点G在射线AD上，且GA＝GB，H为GB延长线上一点，作∠HAN交y轴于点N，且∠HAN＝∠HBO，求NB﹣HB的值．【答案】（1）42mn=-⎧⎨=⎩（2）详见解析；（3）NB﹣FB＝4（是定值），即当点H在GB的延长线上运动时，NB﹣HB的值不会发生变化．【解析】【分析】（1）由点D，点B的坐标和四边形AOBD的面积为12，可列方程组，解方程组即可；（2）由（1）可知，AD＝OA＝4，OB＝2，并可求出AB＝BD＝25，利用SAS可证△DAC≌△AOB，并可得∠AEC＝90°，利用三角形面积公式即可求证；（3）取OC＝OB，连接AC，根据对称性可得∠ABC＝∠ACB，AB＝AC，证明△ABH≌△CAN，即可得到结论.【详解】解：（1）由题意()()218122m nn m m--=⎧⎪⎨++-=⎪⎩解得42mn=-⎧⎨=⎩；（2）如图2中，由（1）可知，A（﹣4，0），B（0，2），D（﹣4，4），∴AD＝OA ＝4，OB ＝2，∴由勾股定理可得：AB ＝BD ＝25，∵AC ＝OC ＝2，∴AC ＝OB ，∵∠DAC ＝∠AOB ＝90°，AD ＝OA ，∴△DAC ≌△AOB （SAS ），∴∠ADC ＝∠BAO ，∵∠ADC +∠ACD ＝90°，∴∠EAC +∠ACE ＝90°，∴∠AEC ＝90°，∵AF ⊥BD ，DE ⊥AB ，∴S △ADB ＝12•AB •AE ＝12•BD •AF ， ∵AB ＝BD ，∴DE ＝AF ．（3）解：如图，取OC ＝OB ，连接AC ，根据对称性可得∠ABC ＝∠ACB ，AB ＝AC ，∵AG ＝BG ，∴∠GAB ＝∠GBA ，∵G 为射线AD 上的一点，∴AG ∥y 轴，∴∠GAB ＝∠ABC ，∴∠ACB ＝∠EBA ，∴180°﹣∠GBA ＝180°﹣∠ACB ，即∠ABG ＝∠ACN ，∵∠GAN ＝∠GBO ，∴∠AGB ＝∠ANC ，在△ABG 与△ACN 中，ABH ACN AHB ANC AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ABH ≌△ACN （AAS ），∴BF ＝CN ，∴NB ﹣HB ＝NB ﹣CN ＝BC ＝2OB ，∵OB＝2∴NB﹣FB＝2×2＝4（是定值），即当点H在GB的延长线上运动时，NB﹣HB的值不会发生变化．【点睛】本题属于三角形综合题，全等三角形的判定和性质，解题的关键是相结合添加常用辅助线，构造图形解决问题，学会利用参数构建方程解决问题．2．在平面直角坐标系中，直线AB分别交x轴，y轴于A（a，0），B（0，b），且满足a2+b2+4a﹣8b+20＝0．（1）求a，b的值；（2）点P在直线AB的右侧；且∠APB＝45°，①若点P在x轴上（图1），则点P的坐标为；②若△ABP为直角三角形，求P点的坐标．【答案】（1）a＝﹣2，b＝4；（2）①（4，0）；②P点坐标为（4，2），（2，﹣2）．【解析】【分析】（1）利用非负数的性质解决问题即可．（2）①根据等腰直角三角形的性质即可解决问题．②分两种情形：如图2中，若∠ABP=90°，过点P作PC⊥OB，垂足为C．如图3中，若∠BAP=90°，过点P作PD⊥OA，垂足为D．分别利用全等三角形的性质解决问题即可．【详解】（1）∵a2+4a+4+b2﹣8b+16＝0∴（a+2）2+（b﹣4）2＝0∴a＝﹣2，b＝4．（2）①如图1中，∵∠APB＝45°，∠POB＝90°，∴OP＝OB＝4，∴P（4，0）．故答案为（4，0）．②∵a＝﹣2，b＝4∴OA＝2OB＝4又∵△ABP为直角三角形，∠APB＝45°∴只有两种情况，∠ABP＝90°或∠BAP＝90°①如图2中，若∠ABP＝90°，过点P作PC⊥OB，垂足为C．∴∠PCB＝∠BOA＝90°，又∵∠APB＝45°，∴∠BAP＝∠APB＝45°，∴BA＝BP，又∵∠ABO+∠OBP＝∠OBP+∠BPC＝90°，∴∠ABO＝∠BPC，∴△ABO≌△BPC（AAS），∴PC＝OB＝4，BC＝OA＝2，∴OC＝OB﹣BC＝4﹣2＝2，∴P（4，2）．②如图3中，若∠BAP＝90°，过点P作PD⊥OA，垂足为D．∴∠PDA＝∠AOB＝90°，又∵∠APB＝45°，∴∠ABP＝∠APB＝45°，∴AP＝AB，又∵∠BAD+∠DAP＝90°，∠DPA+∠DAP＝90°，∴∠BAD＝∠DPA，∴△BAO≌△APP（AAS），∴PD＝OA＝2，AD＝OB＝4，∴OD＝AD﹣0A＝4﹣2＝2，∴P （2，﹣2）．综上述，P 点坐标为（4，2），（2，﹣2）．【点睛】本题属于三角形综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题．3．已知,如图A 在x 轴负半轴上，B （0，-4），点E （-6,4）在射线BA 上，(1) 求证：点A 为BE 的中点(2) 在y 轴正半轴上有一点F, 使 ∠FEA=45°，求点F 的坐标.(3) 如图，点M 、N 分别在x 轴正半轴、y 轴正半轴上，MN=NB=MA ，点I 为△MON 的内角平分线的交点，AI 、BI 分别交y 轴正半轴、x 轴正半轴于P 、Q 两点, IH⊥ON 于H, 记△POQ 的周长为C△POQ.求证：C△POQ=2 HI.【答案】（1）证明见解析；（2）22(0,)7F ；（3）证明见解析. 【解析】试题分析：（1）过E 点作EG ⊥x 轴于G ，根据B 、E 点的坐标，可证明△AEG ≌△ABO ，从而根据全等三角形的性质得证；（2）过A 作AD⊥AE 交EF 延长线于D ，过D 作DK ⊥x 轴于K ，然后根据全等三角形的判定得到△AEG ≌△DAK ，进而求出D 点的坐标，然后设F 坐标为（0，y ），根据S 梯形EGKD =S 梯形EGOF +S 梯形FOKD 可求出F 的坐标；（3）连接MI 、NI ，根据全等三角形的判定SAS 证得△MIN ≌△MIA ，从而得到∠MIN=∠MIA 和∠MIN=∠NIB ，由角平分线的性质，求得∠AIB=135°×3-360°=45°再连接OI ，作IS⊥OM 于S, 再次证明△HIP ≌△SIC 和△QIP ≌△QIC ，得到C △POQ 周长.试题解析：（1）过E 点作EG⊥x 轴于G ，∵B （0，-4），E （-6,4），∴OB=EG=4，在△AEG 和△ABO 中，∵90EGA BOA EAG BAO EG BO ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△AEG ≌△ABO （AAS ），∴AE=AB∴A 为BE 中点（2）过A 作AD⊥AE 交EF 延长线于D ，过D 作DK⊥x 轴于K ，∵∠FEA=45°，∴AE=AD ，∴可证△AEG≌△DAK，∴D（1,3），设F （0，y ），∵S 梯形EGKD =S 梯形EGOF +S 梯形FOKD ，∴()()()111347463222y y +⨯=+⨯++ ∴227y = ∴220,7F ⎛⎫ ⎪⎝⎭（3）连接MI、NI∵I为△MON内角平分线交点，∴NI平分∠MNO，MI平分∠OMN，在△MIN和△MIA中，∵MN MANMI AMIMI MI=⎧⎪∠=∠⎨⎪=⎩∴△MIN≌△MIA（SAS），∴∠MIN=∠MIA，同理可得∠MIN=∠NIB，∵NI平分∠MNO，MI平分∠OMN，∠MON=90°，∴∠MIN=135°∴∠MIN=∠MIA =∠NIB=135°，∴∠AIB=135°×3-360°=45°，连接OI，作IS⊥OM于S, ∵IH⊥ON，OI平分∠MON，∴IH=IS=OH=OS，∠HIS=90°，∠HIP+∠QIS=45°，在SM上截取SC=HP，可证△HIP≌△SIC，∴IP=IC，∠HIP=∠SIC，∴∠QIC=45°，可证△QIP≌△QIC，∴PQ=QC=QS+HP，∴C△POQ=OP+PQ+OQ=OP+PH+OQ+OS=OH+OS=2HI.4．如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F（1）证明：PC=PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．【答案】（1）证明见解析（2）90°（3）AP=CE【解析】【分析】(1)、根据正方形得出AB=BC ，∠ABP=∠CBP=45°，结合PB=PB 得出△ABP ≌△CBP ，从而得出结论；(2)、根据全等得出∠BAP=∠BCP ，∠DAP=∠DCP ，根据PA=PE 得出∠DAP=∠E ，即∠DCP=∠E ，易得答案；(3)、首先证明△ABP 和△CBP 全等，然后得出PA=PC ，∠BAP=∠BCP ，然后得出∠DCP=∠E ，从而得出∠CPF=∠EDF=60°，然后得出△EPC 是等边三角形，从而得出AP=CE.【详解】(1)、在正方形ABCD 中，AB=BC ，∠ABP=∠CBP=45°，在△ABP 和△CBP 中，又∵ PB=PB ∴△ABP ≌△CBP （SAS ）， ∴PA=PC ，∵PA=PE ，∴PC=PE ；(2)、由（1）知，△ABP ≌△CBP ，∴∠BAP=∠BCP ，∴∠DAP=∠DCP ，∵PA=PE ， ∴∠DAP=∠E ， ∴∠DCP=∠E ， ∵∠CFP=∠EFD （对顶角相等），∴180°﹣∠PFC ﹣∠PCF=180°﹣∠DFE ﹣∠E ，即∠CPF=∠EDF=90°；(3)、AP ＝CE理由是：在菱形ABCD 中，AB=BC ，∠ABP=∠CBP ，在△ABP 和△CBP 中，又∵ PB=PB ∴△ABP ≌△CBP （SAS ），∴PA=PC ，∠BAP=∠DCP ，∵PA=PE ，∴PC=PE ，∴∠DAP=∠DCP ， ∵PA=PC ∴∠DAP=∠E ， ∴∠DCP=∠E∵∠CFP=∠EFD （对顶角相等）， ∴180°﹣∠PFC ﹣∠PCF=180°﹣∠DFE ﹣∠E ，即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°， ∴△EPC 是等边三角形，∴PC=CE ，∴AP=CE考点：三角形全等的证明5．如图，在ABC ∆中，ACB ∠为锐角，点D 为射线BC 上一动点，连接AD .以AD 为直角边且在AD 的上方作等腰直角三角形ADF .（1）若AB AC =，90BAC ∠=︒①当点D 在线段BC 上时（与点B 不重合），试探讨CF 与BD 的数量关系和位置关系； ②当点D 在线段C 的延长线上时，①中的结论是否仍然成立，请在图2中面出相应的图形并说明理由；（2）如图3，若AB AC ≠，90BAC ∠≠︒，45BCA ∠=︒，点D 在线段BC 上运动，试探究CF 与BD 的位置关系.【答案】（1）①CF ⊥BD ，证明见解析；②成立，理由见解析；（2）CF ⊥BD ，证明见解析.【解析】【分析】（1）①根据同角的余角相等求出∠CAF=∠BAD ，然后利用“边角边”证明△ACF 和△ABD 全等，②先求出∠CAF=∠BAD ，然后与①的思路相同求解即可；（2）过点A 作AE ⊥AC 交BC 于E ，可得△ACE 是等腰直角三角形，根据等腰直角三角形的性质可得AC=AE ，∠AED=45°，再根据同角的余角相等求出∠CAF=∠EAD ，然后利用“边角边”证明△ACF 和△AED 全等，根据全等三角形对应角相等可得∠ACF=∠AED ，然后求出∠BCF=90°，从而得到CF ⊥BD ．【详解】解：（1）①∵∠BAC=90°，△ADF 是等腰直角三角形，∴∠CAF+∠CAD=90°，∠BAD+∠ACD=90°，∴∠CAF=∠BAD ，在△ACF 和△ABD 中，∵AB=AC ，∠CAF=∠BAD ，AD=AF ，∴△ACF ≌△ABD(SAS)，∴CF=BD ，∠ACF=∠ABD=45°，∵∠ACB=45°，∴∠FCB=90°，∴CF ⊥BD ；②成立，理由如下：如图2：∵∠CAB=∠DAF=90°，∴∠CAB+∠CAD=∠DAF+∠CAD，即∠CAF=∠BAD，在△ACF和△ABD中，∵AB=AC，∠CAF=∠BAD，AD=AF，∴△ACF≌△ABD(SAS)，∴CF=BD，∠ACF=∠B，∵AB=AC，∠BAC=90°，∴∠B=∠ACB=45°，∴∠BCF=∠ACF+∠ACB=45°+45°=90°，∴CF⊥BD；（2）如图3，过点A作AE⊥AC交BC于E，∵∠BCA=45°，∴△ACE是等腰直角三角形，∴AC=AE，∠AED=45°，∵∠CAF+∠CAD=90°，∠EAD+∠CAD=90°，∴∠CAF=∠EAD，在△ACF和△AED中，∵AC=AE，∠CAF=∠EAD，AD=AF，∴△ACF≌△AED(SAS)，∴∠ACF=∠AED=45°，∴∠BCF=∠ACF+∠BCA=45°+45°=90°，∴CF⊥BD．【点睛】本题考查全等三角形的动点问题，综合性较强，有一定难度，需要熟练掌握全等三角形的判定和性质进行综合运用.6．如图1，在ABC ∆中，ACB ∠是直角，60B ∠=︒，AD 、CE 分别是BAC ∠、BCA ∠的平分线，AD 、CE 相交于点F ．（1）求出AFC ∠的度数；（2）判断FE 与FD 之间的数量关系并说明理由．（提示：在AC 上截取CG CD =，连接FG ．）（3）如图2，在△ABC ∆中，如果ACB ∠不是直角，而（1）中的其它条件不变，试判断线段AE 、CD 与AC 之间的数量关系并说明理由．【答案】（1）∠AFC ＝120°；（2）FE 与FD 之间的数量关系为：DF ＝EF ．理由见解析；（3）AC ＝AE+CD ．理由见解析．【解析】【分析】（1）根据三角形的内角和性质只要求出∠FAC ，∠ACF 即可解决问题;（2）根据在图2的 AC 上截取CG=CD ，证得△CFG ≌△CFD (SAS),得出DF= GF ；再根据ASA 证明△AFG ≌△AFE ，得EF=FG ，故得出EF=FD ；（3）根据(2) 的证明方法，在图3的AC 上截取AG=AE ，证得△EAF ≌△GAF (SAS)得出∠EFA=∠GFA ；再根据ASA 证明△FDC ≌△FGC ，得CD=CG 即可解决问题．【详解】（1）解：∵∠ACB ＝90°，∠B ＝60°，∴∠BAC ＝90°﹣60°＝30°，∵AD 、CE 分别是∠BAC 、∠BCA 的平分线，∴∠FAC ＝15°，∠FCA ＝45°，∴∠AFC ＝180°﹣（∠FAC+∠ACF ）＝120°（2）解：FE 与FD 之间的数量关系为：DF ＝EF ．理由：如图2，在AC 上截取CG ＝CD ，∵CE 是∠BCA 的平分线，∴∠DCF ＝∠GCF ，在△CFG 和△CFD 中，CG CD DCF GCF CF CF =⎧⎪∠=∠⎨⎪=⎩，∴△CFG ≌△CFD （SAS ），∴DF ＝GF ．∠CFD ＝∠CFG由（1）∠AFC ＝120°得，∴∠CFD ＝∠CFG ＝∠AFE ＝60°，∴∠AFG ＝60°，又∵∠AFE ＝∠CFD ＝60°，∴∠AFE ＝∠AFG ，在△AFG 和△AFE 中，AFE AFG AF AFEAF GAF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AFG ≌△AFE （ASA ），∴EF ＝GF ，∴DF ＝EF ；（3）结论：AC ＝AE+CD ．理由：如图3，在AC 上截取AG ＝AE ，同（2）可得，△EAF ≌△GAF （SAS ），∴∠EFA ＝∠GFA ，AG ＝AE∵∠BAC+∠BCA=180°-∠B=180°-60°=120°∴∠AFC ＝180°﹣(∠FAC+∠FCA)＝180°-12(∠BAC+∠BCA)=180°-12×120°=120°， ∴∠EFA ＝∠GFA ＝180°﹣120°＝60°＝∠DFC ，∴∠CFG ＝∠CFD ＝60°，同（2）可得，△FDC ≌△FGC （ASA ），∴CD ＝CG ，∴AC ＝AG+CG ＝AE+CD ．【点睛】本题考查了全等三角形的判定和性质的运用，全等三角形的判定和性质是证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造全等三角形．7．如图1，在等边△ABC 中，E 、D 两点分别在边AB 、BC 上，BE =CD ，AD 、CE 相交于点F ．（1）求∠AFE 的度数；（2）过点A 作AH ⊥CE 于H ，求证：2FH +FD =CE ；（3）如图2，延长CE 至点P ，连接BP ，∠BPC =30°，且CF =29CP ，求PF AF的值．（提示：可以过点A 作∠KAF =60°，AK 交PC 于点K ，连接KB ）【答案】（1）∠AFE =60°；（2）见解析；（3）75【解析】【分析】（1）通过证明 BCE CAD ≌ 得到对应角相等，等量代换推导出60AFE ∠=︒；（2）由（1）得到60AFE ∠=︒，CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半，等量代换可得；（3）通过在PF 上取一点K 使得KF =AF ，作辅助线证明ABK 和ACF 全等，利用对应边相等，等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】（1）解：如图1中．∵ABC为等边三角形，∴AC=BC，∠BAC=∠ABC=∠ACB=60°，在BCE和CAD中，60BE CDCBE ACDBC CA=⎧⎪∠=∠=︒⎨⎪=⎩，∴BCE CAD≌（SAS），∴∠BCE=∠DAC，∵∠BCE+∠ACE=60°，∴∠DAC+∠ACE=60°，∴∠AFE=60°．（2）证明：如图1中，∵AH⊥EC，∴∠AHF=90°，在Rt△AFH中，∵∠AFH=60°，∴∠FAH=30°，∴AF=2FH，∵EBC DCA≌，∴EC=AD，∵AD=AF+DF=2FH+DF，∴2FH+DF=EC．（3）解：在PF上取一点K使得KF=AF，连接AK、BK，∵∠AFK=60°，AF=KF，∴△AFK为等边三角形，∴∠KAF=60°，∴∠KAB=∠FAC，在ABK和ACF中，AB ACKAB ACFAK AF=⎧⎪∠=∠⎨⎪=⎩，∴ABK ACF≌(SAS)，BK CF=∴∠AKB=∠AFC=120°，∴∠BKE=120°﹣60°=60°，∵∠BPC=30°，∴∠PBK=30°，∴29BK CF PK CP===，∴79PF CP CF CP=-=，∵45()99AF KF CP CF PK CP CP CP==-+=-=∴779559CPPFAF CP== .【点睛】掌握等边三角形、直角三角形的性质，及三角形全等的判定通过一定等量代换为本题的关键.8．如图，在平面直角坐标系中，A、B坐标为()6,0、()0,6，P为线段AB上的一点．（1）如图1，若P为AB的中点，点M、N分别是OA、OB边上的动点，且保持AM ON=，则在点M、N运动的过程中，探究线段PM、PN之间的位置关系与数量关系，并说明理由．（2）如图2，若P为线段AB上异于A、B的任意一点，过B点作BD OP⊥，交OP、OA分别于F、D两点，E为OA上一点，且PEA BDO=∠∠，试判断线段OD与AE的数量关系，并说明理由．【答案】（1）PM=PN，PM⊥PN，理由见解析；（2）OD=AE，理由见解析【解析】【分析】（1）连接OP．只要证明△PON≌△PAM即可解决问题；（2）作AG⊥x轴交OP的延长线于G．由△DBO≌△GOA，推出OD=AG，∠BDO=∠G，再证明△PAE≌△PAG即可解决问题；【详解】（1）结论：PM=PN ，PM ⊥PN ．理由如下：如图1中，连接OP ．∵A 、B 坐标为（6，0）、（0，6），∴OB=OA=6，∠AOB=90°，∵P 为AB 的中点，∴OP=12AB=PB=PA ，OP ⊥AB ，∠PON=∠PAM=45°， ∴∠OPA=90°，在△PON 和△PAM 中， ON AM PON PAM OP AP =⎧⎪∠=∠⎨⎪=⎩，∴△PON ≌△PAM （SAS ），∴PN=PM ，∠OPN=∠APM ，∴∠NPM=∠OPA=90°，∴PM ⊥PN ，PM=PN ．（2）结论：OD=AE ．理由如下：如图2中，作AG ⊥x 轴交OP 的延长线于G ．∵BD ⊥OP ，∴∠OAG=∠BOD=∠OFD=90°，∴∠ODF+∠AOG=90°，∠ODF+∠OBD=90°，∴∠AOG=∠DBO ，∵OB=OA ，∴△DBO ≌△GOA ，∴OD=AG ，∠BDO=∠G ，∵∠BDO=∠PEA ，∴∠G=∠AEP ，在△PAE 和△PAG 中，AEP G PAE PAG AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PAE ≌△PAG （AAS ），∴AE=AG ，∴OD=AE ．【点睛】考查了等腰直角三角形的性质、全等三角形的判定和性质、坐标与图形性质、直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．9．如图1，Rt△ABC中，∠A＝90°，AB＝AC，点D是BC边的中点连接AD，则易证AD＝BD＝CD，即AD＝12BC；如图2，若将题中AB＝AC这个条件删去，此时AD仍然等于12BC．理由如下：延长AD到H，使得AH＝2AD，连接CH，先证得△ABD≌△CHD，此时若能证得△ABC≌△CHA，即可证得AH＝BC，此时AD＝12BC，由此可见倍长过中点的线段是我们三角形证明中常用的方法．（1）请你先证明△ABC≌△CHA，并用一句话总结题中的结论；（2）现将图1中△ABC折叠（如图3），点A与点D重合，折痕为EF，此时不难看出△BDE和△CDF都是等腰直角三角形．BE＝DE，CF＝DF．由勾股定理可知DE2+DF2＝EF2，因此BE2+CF2＝EF2，若图2中△ABC也进行这样的折叠（如图4），此时线段BE、CF、EF还有这样的关系式吗？若有，请证明；若没有，请举反例．（3）在（2）的条件下，将图3中的△DEF绕着点D旋转（如图5），射线DE、DF分别交AB、AC于点E、F，此时（2）中结论还成立吗？请说明理由．图4中的△DEF也这样旋转（如图6），直接写出上面的关系式是否成立．【答案】（1）详见解析；（2）有这样分关系式；（3）EF2＝BE2+CF2.【解析】【分析】（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可．（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB≌△HD （SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．（3）图5，图6中，上面的关系式仍然成立．【详解】（1）证明：如图2中，∵BD＝DC，∠ADB＝∠HDC，AD＝HD，∴△ADB≌△HDC（SAS），∴∠B＝∠HCD，AB＝CH，∴AB∥CH，∴∠BAC+∠ACH＝180°，∵∠BAC＝90°，∴∠ACH＝∠BAC＝90°，∵AC＝CA，∴△BAC≌△HCA（SAS），∴AH＝BC，∴AD＝DH＝BD＝DC，∴AD＝12 BC．结论：直角三角形斜边上的中线等于斜边的一半．（2）解：有这样分关系式．理由：如图4中，延长ED到H山顶DH＝DE．∵ED＝DH，∠EDB＝∠HDC，DB＝DC，∴△EDB≌△HDC（SAS），∴∠B ＝∠HCD ，BE ＝CH ，∵∠B +∠ACB ＝90°，∴∠ACB +∠HCD ＝90°，∴∠FCH ＝90°，∴FH 2＝CF 2+CH 2，∵DF ⊥EH ，ED ＝DH ，∴EF ＝FH ，∴EF 2＝BE 2+CF 2．（3）图5，图6中，上面的关系式仍然成立．结论：EF 2＝BE 2+CF 2．证明方法类似（2）．【点睛】本题属于几何变换综合题，考查了旋转变换，翻折变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．10．如图，ABC ∆是等腰直角三角形，090BAC ∠=，点D 是直线BC 上的一个动点（点D 与点B C 、不重合），以AD 为腰作等腰直角ADE ∆，连接CE .（1）如图①，当点D 在线段BC 上时，直接写出,BC CE 的位置关系，线段,BC CD ，CE 之间的数量关系；（2）如图②，当点D 在线段BC 的延长线上时，试判断线段BC ，CE 的位置关系，线段,,BC CD CE 之间的数量关系，并说明理由；（3）如图③，当点D 在线段CB 的延长线上时，试判断线段,BC CE 的位置关系，线段,,BC CD CE 之间的数量关系，并说明理由.【答案】（1）见解析；（2）BC CE ⊥，CE BC CD =+，理由见解析；（3）,BC CE CD BC CE ⊥=+，理由见解析【解析】【分析】（1）根据条件AB=AC ，∠BAC=90°，AD=AE ，∠DAE=90°，判定△ABD ≌△ACE （SAS ），利用两角的和即可得出BC CE ⊥；利用线段的和差即可得出BC CE CD =+；（2）同（1）的方法根据SAS 证明△ABD ≌△ACE ，得出BD=CE ，∠ACE=∠ABD ，从而得出结论；（3）先根据SAS 证明△ABD ≌△ACE ，得出ADB AEC ∠=∠，BD CE =，从而得出结论．【详解】（1）∵△ABC 、△ADE 是等腰直角三角形，∴AB＝AC ，AE ＝AD ，在△△ABD 和△ACE 中90AB AC BAC DAE AD AE ⎧⎪∠∠=︒⎨⎪⎩＝＝＝， ∴△ABD ≌△ACE （SAS ），∴∠B ＝∠ACE ，BD=CE,又∵△ABC 是等腰直角三角形，∴∠B+∠ACB=90︒,∴∠ACE +∠ACB=90︒,即BC CE ⊥，∵BC=BD+CD, BD=CE ，∴BC CE CD =+；（2）BC CE ⊥，CE BC CD =+，理由如下：∵ABC ∆、ADE ∆是等腰直角三角形，∴0,,90AB AC AD AE BAC DAE ==∠=∠=，∴BAC DAC DAE DAC ∠+∠=∠+∠即BAD CAE ∠=∠,在ABD ∆和ACE ∆中 AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩＝＝ ∴()ABD ACE SAS ∆≅∆∴BD CE =∵BD BC CD =+∴CE BC CD =+，∴ABD ACE ∠=∠，∵090ABD ACE ∠+∠=∴090ACE ACB ∠+∠=∴BC CE ⊥.（3）,BC CE CD BC CE ⊥=+，理由如下：∵ABC ADE ∆∆、是等腰直角三角形，∴0,,90AB AC AD AE BAC DAE ==∠=∠=，∴BAC BAE DAE BAE ∠-∠=∠-∠，即BAD CAE ∠=∠，在ABD ∆和ACE ∆中AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩＝＝ ∴()ABD ACE SAS ∆≅∆，∴ADB AEC ∠=∠，BD CE =，∵CD BD BC =+，∴CD CE BC =+，∵090ADE AED ∠+∠=，即090ADB CDE AED ∠+∠+∠=∴090AEC CDE AED ∠+∠+∠=，∴090DCE ∠=，即BC CE ⊥.【点睛】考查了全等三角形的判定与性质以及等腰直角三角形的性质的运用，解题关键是根据利用两边及其夹角分别对应相等的两个三角形全等判定三角形全等．。

【精选】八年级全等三角形中考真题汇编[解析版]

八年级全等三角形专题练习(解析版)

八年级上册数学 全等三角形中考真题汇编[解析版]

八年级全册全套试卷中考真题汇编[解析版]

八年级数学全册全套试卷中考真题汇编[解析版]

八年级数学全等三角形中考真题汇编[解析版]

天津市自立中学数学全等三角形中考真题汇编[解析版]

初二数学 三角形全等中考真题含解析

人教版数学八年级上册 全册全套试卷中考真题汇编[解析版]

八年级数学上册 全等三角形中考真题汇编[解析版]

八年级上册数学 【几何模型三角形轴对称】试卷中考真题汇编[解析版]

八年级全等三角形中考真题汇编[解析版]

全等三角形中考真题汇编[解析版]

八年级数学上册全册全套试卷中考真题汇编[解析版]

全等三角形中考真题汇编[解析版]

数学八年级上册 全等三角形中考真题汇编[解析版]

八年级全等三角形中考真题汇编[解析版]

八年级全等三角形中考真题汇编[解析版]

贵阳清华中学数学全等三角形中考真题汇编[解析版]

八年级数学全等三角形中考真题汇编[解析版]

八年级数学全册全套试卷中考真题汇编[解析版]

八年级上册数学全等三角形中考真题汇编[解析版]

初二数学三角形全等中考真题含解析

人教版数学八年级上册全册全套试卷中考真题汇编[解析版]

八年级数学上册全等三角形中考真题汇编[解析版]

八年级上册数学【几何模型三角形轴对称】试卷中考真题汇编[解析版]

数学八年级上册全等三角形中考真题汇编[解析版]