2010日本高考数学试题
（完整）2010年全国高考数学试题及答案-全国2卷,推荐文档
（完整）2010年全国高考数学试题及答案-全国2卷,推荐文档绝密★启用前2010年普通高等学校招生全国统一考试（全国Ⅱ卷）文科数学第Ⅰ卷（选择题）本卷共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
参考公式：如果事件A 、B 互斥，那么球的表面积公式(+)()+()P A B P A P B = S=4πR 2如果事件A 、B 相互独立，那么其中R 表示球的半径()()()P A B P A P B ?=? 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么34V R 3π= n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径P ()(1)(0,1,2,,)k k n k n n k C p p k n -=-=L一、选择题（1）设全集{}*U 6x N x =∈<，集合{}{}A 1,3B 3,5==，,则U ()A B =U e（）（Ａ）{}1,4 （Ｂ）{}1,5 （Ｃ）{}2,4 （Ｄ）{}2,5（２）不等式302x x -<+的解集为（）（Ａ）{}23x x -<< （Ｂ）{}2x x <-（Ｃ）{}23x x x <->或（Ｄ）{}3x x >（3）已知2sin 3α=，则cos(2)πα-= (A) 53- (B) 19- (C) 19(D) 53 （4）函数1ln(1)(1)y x x =+->的反函数是(A) 11(0)x y ex +=-> (B) 11(0)x y e x -=+> (C) 11(R)x y e x +=-∈ (D) 11(R)x y e x -=+∈ (5) 若变量,x y 满足约束条件1325x y x x y ≥-??≥??+≤?，则2z x y =+的最大值为(A) 1 (B) 2 (C) 3 (D)4（6）如果等差数列{}n a 中，3a +4a +5a =12，那么1a +2a +…+7a =(A) 14 (B) 21 (C) 28 (D)35（7）若曲线2y x ax b =++在点(0,)b 处的切线方程式10x y -+=，则（A ）1,1a b == （B ）1,1a b =-=（C ）1,1a b ==- （D ）1,1a b =-=-（8）已知三棱锥S ABC -中，底面ABC 为边长等于2的等边三角形，SA 垂直于底面ABC ，SA=3，那么直线AB 与平面SBC 所成角的正弦值为（A ）3 （B ）5 （C ）7 （D ） 34（9）将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1,2的卡片放入同一信封，则不同的放法共有（A ）12种（B ）18种（C ）36种（D ）54种（10）△ABC 中，点D 在边AB 上，CD 平分∠ACB ，若CB a =，CA b =，1,2a b ==，则CD =（A ）1233a b + （B ）2233a b + （C ）3455a b + （D ）4355a b + （11）与正方体1111ABCD A B C D -的三条棱AB 、1CC 、11A D 所在直线的距离相等的点（A ）有且只有1个（B ）有且只有2个（C ）有且只有3个（D ）有无数个（12）已知椭圆C ：22x a +22by =1(0)a b >>的离心率为23，过右焦点F 且斜率为k （k ＞0）的直线与C 相交于A 、B 两点，若AF =3FB ，则k = （A ）1（B ）2 （C ）3 （D ）2第Ⅱ卷（非选择题）二.填空题：本大题共4小题，每小题5分，共20分。
2010年重庆高考日语试题及答案
会考基础回归（必修1）专项训练一、选择题1、糖类、脂肪、蛋白质、核酸共有的元素是（）A．C、H、O、N、P B．C、H、O、N C．C、H、O D．O、H2、在正常人的血浆中，NaHCO3的含量约为H2CO3含量的20倍．当血浆中的NaHCO3含量减少时，会形成酸中毒；当血浆中H2CO3含量减少时，则形成碱中毒。
这个事实表明，某些无机盐的作用是（）A．调节酸碱度B．调节渗透压C．影响细胞形态D．影响生物膜透性3、通过对一小块生物组织进行化学分析，其成分包括蛋白质、核酸、脂质、水、无机盐、纤维素等物质，此组织最可能来自（）A．病毒B．芹菜C．细菌D．家兔4、下图所示是植物细胞部分膜结构示意图，它们分别属于哪一部分，按①②③④顺序依次是（）A．细胞膜、高尔基膜、线粒体膜、核膜B．细胞膜、叶绿体膜、线粒体膜、内质网膜C．线粒体膜、核膜、内质网膜、高尔基体膜D．叶绿体膜、细胞膜、线粒体膜、核膜5、人的胰岛素是由胰岛B细胞分泌的一种调节人体血糖的蛋白质。
在胰岛素合成和分泌过程中，参与的细胞器有（）A．线粒体、中心体、高尔基体、内质网B．线粒体、核糖体、高尔基体、内质网C．核糖体、中心体、高尔基体、内质网D．核糖体、叶绿体、高尔基体、内质网6、线粒体和叶绿体都是进行能量转换的细胞器。
下列相关叙述错误的是（）A．两者都能产生ATP，但最初的能量来源不同B．需氧型生物的细胞均有线粒体，植物细胞都有叶绿体C．两者都含有磷脂、DNA和多种酶，叶绿体中还含有色素D．两者都有内膜和外膜，叶绿体基质中一般还有基粒7、萤火虫发光发生了能量的转化，下列属于该转化的是（）A．动能转变为势能B．热能转变为光能C．化学能转变为电能D．化学能转变为光能8、假设三个细胞液浓度不同的细胞，放在某浓度的蔗糖溶液中出现如图所示状态，你认为这三个细胞在未发生上述情况之前，其细胞液浓度依次是（）A．A＞B＞C B．A＜B＜CC．B＞A＞C D．B＜A＜C9、用显微镜的一个目镜分别与4个不同倍数的物镜组合来观察洋葱根尖细胞装片。
2010年12月日语能力考试N3真题解析(转载新世界外语)
2010年12月新世界日语名师解析N3文字词汇部分 (1)2010年12月名师解析12月能力考N3文法 (5)2010年12月新世界日语名师解析N3读解部分 (7)2010年12月新世界日语名师解析N3听解部分 (11)2010年12月新世界日语名师解析N3文字词汇部分作者：赵芳芳老师新能力考文字词汇出题倾向分析N3是在之前的三级和二级之间增设一个级别，此次乃第二次N3考试。
从这次的考试内容及难度上来看，的确是介于二者之间。
文字部分考了35道题，语法部分考了13道题，排序部分考了5道题，完形填空五道题。
整体而言，这次文字词汇还算比较简单。
要说难也就这次的排序问题稍微难一点。
问题一的8道题目，考的都是最基础的词汇并且也是比较实用的词汇，这也是整个文字词汇部分最简单的一题。
问题二的6道题不难但是迷惑性很强，因为单从中文发音来看几乎都是一样的，稍一不留神就很容易选错，这道题需要小心谨慎，如果是平时马马虎虎的性格，就算题目再简单也极其容易选错。
所以学习N3的学生切记平时要仔细认真，切忌心浮气躁。
问题三的11道题目，综合性很强。
（复合）名词，（复合）动词，外来语，副词，拟声拟态词样样都考。
还好这次出现的词没什么刁钻之处。
只要冷静应试这道题至少可以做对8道。
问题四共五道题目，这题主要考的是近义词，有些词可以找到一模一样的对应的词，但有些词在四个选项中找不到完全一模一样的同义词，此时只能去找意思最为接近的一个选项，所以这题切忌“一根筋”，要懂得随机应变。
问题五共五道题目，这题是整体文字词汇部分最难的一题，中国学生做这题最痛苦，因为大家都认识汉字，岂不知中日文的汉字，有些字面意思和实际意思是一模一样，然而有些汉字字面意思和实际意思完全没有任何联系。
做这题可以用排除法，如果四个选项中有两个选项甚至三个选项用的都是同一个意思，那这两个或者三个肯定都是错的。
另外，大家平时学习时，就应该养成这样的一个好习惯，遇到字面意思和实际意思不同的单词时，一定多留个心眼，勤动动手，把它们归类整理一下。
2010年高考试题文科数学(全国卷I)及答案解析
A
1 1 + x2
=
，
O
P
��� � ��� � ��� � ��� � PA • PB =| PA| ⋅ | PB| cos 2α
2 2 4 2
x 2 (1 − 2 sin2 α )
= B
��� � ��� � x ( x − 1) x − x x4 − x2 = ，令 PA • PB = y ，则 y = ， x2 + 1 x2 + 1 x2 + 1
| PF1 |i| PF2 | =
(A)2 (B)4 (C) 6 (D) 8 8.B【命题意图】本小题主要考查双曲线定义、几何性质、余弦定理，考查转化的数学思想， 通过本题可以有效地考查考生的综合运用能力及运算能力. 【解析 1】.由余弦定理得 cos ∠ F1 P F2 =
| PF1 |2 + | PF2 |2 − | F1 F2 |2 2 | PF1 || PF2 |
D1 A1 D A O B1
C1
C B
面 AC D1 所 成 角 相 等 , 设 DO ⊥ 平 面 AC D1 ， 由 等 体 积 法 得 VD − ACD1 = VD1− ACD , 即
1 1 S ∆ACD1 ⋅ DO = S∆ACD ⋅ DD1 .设 DD1=a, 3 3
则 S∆ ACD1 =
7.C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域，考生在做本 小题时极易忽视 a 的取值范围，而利用均值不等式求得 a+b= a + 题者的用苦良心之处. 【解析 1】因为 f(a)=f(b), 所以|lga|=|lgb|, 所以 a=b(舍去) ，或 b =
1 ≥ 2 , 从而错选 D,这也是命 a
教育考试院2010年高考测试样卷数学文145114
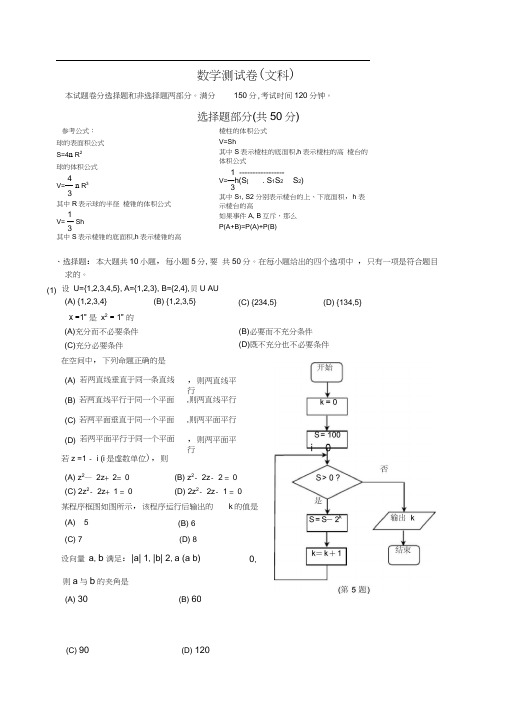
(C) 90 (D) 120数学测试卷(文科)本试题卷分选择题和非选择题两部分。
满分150分,考试时间120分钟。
选择题部分(共50分)参考公式： 球的表面积公式 S=4n R 2 球的体积公式4V=— n R 33其中R 表示球的半径 棱锥的体积公式 1 V= — Sh3其中S 表示棱锥的底面积,h 表示棱锥的高棱柱的体积公式V=Sh其中S 表示棱柱的底面积,h 表示棱柱的高 棱台的体积公式1 ----------------- V=—h(S [ . S 1S2 S 2) 3其中S 1, S2分别表示棱台的上、下底面积，h 表示棱台的高如果事件A, B 互斥，那么 P(A+B)=P(A)+P(B)(B)必要而不充分条件 (D)既不充分也不必要条件(A) 30(1) 、选择题：本大题共10小题，每小题5分, 要求的。
设 U={1,2,3,4,5}, A={1,2,3}, B={2,4},贝U AU (A) {1,2,3,4} (B) {1,2,3,5} x =1” 是 x 2 = 1” 的共50分。
在每小题给出的四个选项中 ，只有一项是符合题目(C) {234,5} (D) {134,5}在空间中，下列命题正确的是 (A) 若两直线垂直于同一条直线 ，则两直线平行(B) 若两直线平行于同一个平面 ,则两直线平行 (C) 若两平面垂直于同一个平面 ,则两平面平行(D) 若两平面平行于同一个平面 ，则两平面平行若z =1 - i (i 是虚数单位)，则 (A) z 2— 2z + 2= 0 (B) z 2- 2z - 2 = 0 (C) 2z 2- 2z + 1 = 0(D) 2z 2- 2z - 1 = 0某程序框图如图所示，该程序运行后输出的 k 的值是(A) 5 (B) 6 (C) 7(D) 8设向量 a , b 满足：|a| 1, |b| 2, a (a b) 0,则a 与b 的夹角是 (A)充分而不必要条件 (C)充分必要条件(B) 60⑺ 在Rt △ ABC 中,/ A = 90，/ B = 60 , AB=1,若圆0的圆心在直角边 AC 上,且与AB 和BC 所在的直交y 轴于点P.若M 为线段FP 的中点，则双曲线的离心率是非选择题部分(共100分)二、填空题：本大题共7小题，每小题4分，共28分。
日本国立公立大学高考(数学)试题介绍
B:
,
的 顶 点坐 标 是
0
2
则在 记号
(f 二犷
、 . ` 了
,
二
,
鲁
)
(臀
,
粤
。 ,
)
则数
号
“
十三
十二 这 一 行 中将 ①涂没 这 一 行 中将⑤ 涂 没
在记
十 二 ③ 曰 @ . ②③④ ⑤⑥ ⑦⑧ ⑨ @ ⑥④ ⑧
B
〔 六〕
〔 〔/ 又 〕 七〕
,
十 三 0 0 @ ① ②③ ④ . ⑥ ⑦⑧ ⑧ @ ⑥ ⑧函 的 面 积为 S
“一
,
在 记号
”
十二
”
行 中涂 去 @
(表 5 )
.
,
在 记 号
皿
H K
=
十三
行 中涂 去 ⑧
(誓 % ( )
一
4 一
一
劲
15
解 答表
:
九 十
0 0 口 ① ②③ ④幼 ⑥⑦ ⑧⑨ @ ⑥⑧ ④ 0 0 匀 ① ②③ ④ ⑤⑥ ⑦⑧ ⑨ @ ⑥ ⑥ 移
.
将所 得结 果
为 顶点 的 三 角 形 O A B
设A
、
O
:
,
B 分别 是
: 3 内分
所 对 应 的符 号 涂 没 二
三
将 三 角形 O
的点
, , , :
A 召的 边 O 刃
Z ,
AB B
l :
,
BO
以2
:
0 0 ⑧ ① ②③④ ⑤⑥ ⑦⑧⑨ @ ⑥ ⑥④ 。 ④ ③ ① ②③④⑤ ⑥ ⑦⑧⑨ @ ⑥⑧ 霉 0 0 ③ ① ②③④ ⑤⑥ ⑦⑧⑨ @ ⑥⑧ ④
2010年高考日语_真题
2010年普通高等学校招生全国日语统一考试第一部分：日语汉字的读音与书写（共分两部分，满分15分）第一节——从A、B、C、D4个选项中选出划底线的日语汉字的正确读音。
（共8小题；每小题1分，满分8分）1.その手紙は間遠って配達されました。
[A]はいたつ[B]はいたち[C]はいだつ[D]はいだち2.昼食の支度をお願いするわ。
[A]しど [B]たび [C]したく [D]つど3.苦いくすりは飲みにくい。
[A]くるしい [B]にが [C]にく [D]わか4.熱が出たので頭を氷冷やす。
[A]すず [B]つめ [C]さめ [D]ひ5.あの喫茶店のコーヒーはとてもおいしいてす。
[A]きさってん [B]きっさでん [C]きさてん [D]きっさてん6.大きい布団を作ってもらったから,今夜からゆっくり寝られる。
[A]ふどん [B]ふとん [C]ぶとん [D]ふだん7.田中さんは試験がよくできたので朗らかな顔をしている。
[A]あき [B]ろう [C]ほか [D]ほが8.名所旧跡の多い町は歴史が長い。
[A]めいしょうきゅうせき [B]めいじょきゅうせき[C]めいしょきゅうせき [D]めいしょきゅうぜき第二节——从A、B、C、D 4个选项中选出划底线的平假名相对应的日语汉字。
（共7小题：每小题1分，满分7分）9.必要などうぐがないと,自転車を直すことができますせん。
[A]器具 [B]道具 [C]工具 [D]用具10.バソコンでこの図に色をつけて,この字をくろくしてください。
[A]黒 [B]濃 [C]暗 [D]重11.えいようをとって,体をじょうぶにする。
[A]荣养 [B]荣養 [C]栄养 [D]栄養12.庭で洗ったシャツをほしている。
[A]干[B]幹[C]晒 [D]晾13.５年ぶりになつかしい故郷に帰った。
[A]恋[B]懐[C]優[D]親14.美しい富士山写真にうつす。
[A]映[B]写[C]照[D]移15.首相が記者たちの前に姿をあらわしたのは深夜だった。
2010年日语高考
2010年普通高等学校招生全国统一考试(含听力)日语(含听力)第一部分：听力（共两节，满分30分）第一节――听下面７段录音，每段录音后有１道小题，从ＡＢＣ三个选项中选出最佳选项。
（共7小题：每小题2分，满分14分）例：男の人はどのぐらい日本語を勉強しましたか。
Ａ６ヶ月Ｂ９ヶ月Ｃ12ヶ月１．明日、誰が中国に来るか。
Ａ山田Ｂ佐藤Ｃ鈴木２．明日、二人はどこで会うか。
Ａ駅の出口Ｂ駅の中Ｃ駅前にある本屋３．良子さんは今どこにいるか。
Ａ外出している。
Ｂ小山さんの家にいる。
Ｃ良子さんの部屋にいる。
４．男の人はどうして引っ越したのか。
Ａ家族が増えたから。
Ｂ前のアパートが遠かったから。
Ｃ前のアパートがにぎやかだったから。
５．女の人はコーヒーに何を入れるか。
Ａ砂糖Ｂ牛乳Ｃ砂糖と牛乳６．女の人が言っているのは何か。
Ａ飛行機Ｂ船Ｃ電車７．大学生のいちばん好きなスポーツはどれか。
ＡサッカーＢジョギングＣ野球第二节――听下面４段录音，每段录音后有２道小题，从ＡＢＣ三个选项中选出最佳选项。
（共8小题：每小题2分，满分16分）８．だれとだれが話し合っているか。
Ａ店の人と学生Ｂ先生と学生Ｃ医者と学生９．男の人はどうして女の人に頼んだのか。
Ａ男の人が病気になったから。
Ｂ女の人が病気になったから。
Ｃ店員の１人が病気になったから。
10．会議は何曜日に変わったのか。
Ａ月曜日Ｂ火曜日Ｃ木曜日11．会議に欠席する人はだれか。
Ａ鈴木Ｂ山下Ｃ松田12．今晩、どんなパーティーがあるか。
Ａ新入生を迎えるパーティーＢ新入生の誕生日を祝うパーティ－Ｃ新しく来た先生を迎えるパーティー13．女の人は、今晩のパーティーはどうするか。
Ａアルバイトがあるので、行かない。
Ｂアルバイトがあるので、遅れていく。
Ｃ発表の準備があるので、遅れていく。
14．男の人は先週どんなスポーツをしたか。
Ａ卓球Ｂ水泳Ｃバスケットボール15．２人は来週の何曜日にスポーツセンターへ行くか。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2010 日本高考试题
[文理科共同]
1. 函数满足下列(A), (B)两个条件
(A) .
(B) 对任意的实数，都有恒成立.
当时，请回答下列问题.
(1) 证明:
(2) 请用表示.
(3) 或者至少有一个成立.
2. 已知三个整数满足，求
的所有解
3. 直角三角形中，设从点C到边的垂线为.为垂足。
从往边作垂线，垂足为. 且与的交点为.
(1) 请用将表示出来
(2) 请用将的面积表示出来.
4. 已知为正实数，平面上有两个点. 点为直线上的动点, 求两线
的最小值.
段长度之积AP BP
5. 次函数有极大值和极小值时，请回答下列问题其中为常数)
(1) 求的取值范围.
(2) 在处的极值为, 求和的值(其中)
(3) 上面(2)成立时，请求出另一个极值.
6. 中将边以内分的点，记为, 将边以内分的点，记为，设线段
与线段的交点为.
(1) 请用和表示出.
(2) ，且边在直线上, 边在直线上. 若的外接圆与相切时，求内
的值.
积OA OB
7. 数列满足下列条件
(1) 请用数学归纳法证明是偶数.
(2) 证明是的倍数.
8. 从记号分别为的张卡片中任意抽取张卡片后在放回去称为一次试验，设在次试验中记有数字的卡片被抽取的次数为奇数的概率为，请将用表示出来.
<答案>
1. (1) 略(2) (3) 略
2.
3. (1) (2)
4.
5. (1) (2) (3)
6. (1) (2)
7. 略
8.。