全状态反馈系统极点配置的数字仿真(终)
状态反馈极点配置基本理论与方法

状态反馈极点配置基本理论与方法IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】第2章 状态反馈极点配置设计基本理论引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数,然后反馈到输入端与参考输入相加形成的控制规律,作为被控系统的控制输入。
图是一个多输入多输出线性时不变系统状态反馈的基本结构:图 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为:x Ax Buy Cx=+=由图可知,加入状态反馈后,受控系统的输入为:u Fx v =+其中v 为参考输入,F 为状态反馈增益阵,因此可以得到状态反馈闭环系统的状态空间表达式:()x A BF x Bv y Cx=++=闭环系统的传递函数矩阵:()()1s W s C sI A BF B -=-+⎡⎤⎣⎦由此可见,引入状态反馈后,通过F 的选择,可以改变闭环系统的特征值,是系统获得所要求的性能。
极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置,一般有四种方法: (1) 传统方法—将系统转化为一个或多个单输入单输出系统。
(2) 直接法—使用稳定的酉矩阵,将这种系统转化为标准型。
(3)矩阵方程法—对矩阵F ,直接解方程AX X BG -Λ=FX G =(4)特征向量法—先找到特征向量x j (等式中矩阵X 的列向量),然后利用等式求解F 。
方法(1)一般难以应用或者数值不稳定。
方法(3)需要解方程,并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法(2)和方法(4)。
其中方法(4)通过使用一系列的迭代算法找到最优解,所以比较复杂。
对于方法(2),当系统的输入多于一个信号输入时,不能确定系统的鲁棒性。
本文结合以上方法提出了一种新的设计方法:首先通过酉变换将状态方程化为一种控制规范形,然后利用最小二乘法解方程的得到最佳的状态反馈矩阵。
状态反馈和极点配置

为了根据期望的闭环极点位置来设计输出反馈矩阵h的参数,只需将期望的 系统特征多项式与该输出反馈系统特征多项式 hC) 相比较即可。
15
输出反馈到参考输入
设被控对象的状态方程为 x Ax Bu
y Cx
输出量反馈到参考输入时, u=r-hy,则该输出反馈系统的动态
方程为 x (A BhC)x Bv
为
0 0 1
Q [ B AB A2 B ] 0
1
6
1
6 31
得出detQ = -1。因此,rankQ = 3。因而该系统是状态完全可控的,可任意
配置极点。
下面用两种方法求解。
11
极点配置 例1
方法1:利用刚才介绍的求解步骤,计算系统矩阵A的特征多项式,求特征值。
7
极点配置定理_充分性
a0 k0 a0 a1 k1 a1
an1
kn1
a n1
求解上述方程组,得到 ki 的值,则
K KP1 [k0 k1
kn 1 ]P 1
[ a0 a0 a1 a1
an1 an1 ] P1
如果系统是状态完全可控的,则通过对应于上式所选取的矩阵K,可任意 配置所有的特征值。
充分性得证。
8
极点配置定理_必要性
即已知闭环系统可任意配置极点,证明被控系统状态完全可控。 现利用反证法证明。 先证明如下命题:如果系统不是状态完全可控的,则矩阵A-BK 的特征值不可能由线性状态反馈来控制。 假设原线性系统 x Ax Bu 状态不可控,则其可控性矩阵的 秩小于n,即
rank[ B AB An1B ] q n
◆考察系统的可控性条件。如果系统是状态完全可控的,则可按下列步骤继续。
状态反馈的极点配置

东南大学自动化学院实验报告课程名称:自动控制基础实验名称:控制系统极点的任意配置院(系):自动化学院专业:自动化姓名:吴静学号:08008419实验室:实验组别:同组人员:实验时间:2011年4月29日评定成绩:审阅教师:一、实验目的1. 掌握用状态反馈的设计方法实现控制系统极点的任意配置;2. 用电路模拟的方法,研究参数的变化对系统性二、实验原理内容用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予予以实现; 理论证明,通过状态反馈的系统,其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为bu Ax x+= cx y =图6-1为其状态变量图。
图6-1 状态变量图令Kx r u -=,其中]...[21n k k k K =,r 为系统的给定量,x 为1⨯n 系统状态变量,u 为11⨯控制量。
则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 相应的特征多项式为)](det[bK A SI --,调节状态反馈阵K 的元素]...[21n k k k ,就能实现闭环系统极点的任意配置。
图6-2为引入状态反馈后系统的方框图。
图6-2 引入状态变量后系统的方框图实验时,二阶系统方框图如6-3所示。
图6-3 二阶系统的方框图引入状态反馈后系统的方框图如图6-4所示。
根据状态反馈后的性能指标:20.0≤p δ,s 5.0T p ≤,试确定状态反馈系数K1和K2图6-4 引入状态反馈后的二阶系统方框图三、实验步骤1.引入状态反馈前根据图6-3二阶系统的方框图,设计并组建该系统相应的模拟电路,如图6-9所示。
图6-9 引入状态反馈前的二阶系统模拟电路图在系统输入端加单位阶跃信号,用上位机软件观测c(t)输出点并记录相应的实验曲线,测量其超调量和过渡时间。
2.引入状态反馈后请预先根据前面给出的指标计算出状态反馈系数K1、K2。
根据图6-4引入状态反馈后的二阶系统的方框图,设计并组建该系统相应的模拟电路,如图6-10所示。
极点配置法设计状态反馈控制器——自动控制原理理论篇

设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
y(t) 2 1x(t)
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
举例----求解过程
解: 0
B 1
0 1 0 1 AB 6 51 5
rankS
rankB
AB
0 1
1 5
2
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设: F f1 f2
s sI A BF
6 f1
SI系统,所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
极点配置法设计状态反馈控制器
——《自动控制原理-理论篇》第8.8节
7.4 状态反馈和极点配置

可配置条件_极点配置定理
考虑线性定常系统
x Ax Bu
假设控制输入u的幅值是无约束的。如果选取控制规律为
u r Kx
式中K为线性状态反馈矩阵。
定理 (极点配置定理) 线性定常系统可通过线性状态反馈任意地 配置其全部极点的充要条件是,此被控系统状态完全可控。
该定理对多变量系统也成立。
证明 (对单输入单输出系统) 1、充分性 2、必要性
kn 1 ]
由于 u r Kx r KPx ,此时该系统的状态方程为 x ( Ac Bc K ) x Bcr
相应的特征方程为 sI Ac BcK 0
因为非奇异线性变换不改变系统的特征值,当利用 u=r-Kx作为控制输 入时,相应的特征方程与上式相同,均有如下结果。
s
1
0
0
s
0
sI Ac BcK
◆确定将系统状态方程变换为可控标准形的变换矩阵P。若给定的状态方程已是 可控标准形,则P = I。此时无需再写出系统的可控标准形状态方程。非奇异线 性变换矩阵P=QW。
◆利用给定的期望闭环极点,可写出期望的特征多项式为
(s 1() s 2 ) (s n ) sn an1sn1 a1s a0
从而确定出a1* , a2 *,… an *的值。
◆最后得到状态反馈增益矩阵K为
K [ a0 a0 a1 a1
a n1
an1
]
P 1
10
极点配置 例1
【例】 考虑如下线性定常系统
0
1
0
0
x Ax Bu A 0
0
1 , B 0
1 5 6
1
利用状态反馈控制,希望该系统的闭环极点为s = -2±j4和s = -10。试确定状
极点配置法设计状态反馈控制器——自动控制原理理论篇

——《自动控制原理-理论篇》第8.8节
自动化工程学院自动控制原理课程组制 2015年11月
主要内容
状态反馈控制系统 状态反馈控制器设计条件 用极点配置法设计状态反馈控制器 举例
主要内容
状态反馈控制系统 状态反馈控制器设计条件 用极点配置法设计状态反馈控制器 举例
SI系统,所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
rankB
AB
0 1
1 5
2
系统能控。
举例求解过程
期望闭环系统特征多项式为:
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设: F f1 f2
s sI A BF
6 f1
1x(t)
F 7 1
线性系统的状态反馈及极点配置

现代控制理论实验(一)线性系统的状态反馈及极点配置——09级自动化本科一.实验目的1.了解和掌握状态反馈及极点配置的原理。
2.了解和掌握利用矩阵法及传递函数法计算状态反馈及极点配置的原理与方法。
3.掌握在被控系统中如何进行状态反馈及极点配置,构建一个性能满足指标要求的新系统的方法。
二.实验原理及说明一个控制系统的性能是否满足要求,要通过解的特征来评价,也就是说,当传递函数是有理函数时,它的全部信息几乎都集中表现为它的极点、零点及传递函数。
因此若被控系统完全能控,则可以通过状态反馈任意配置极点,使被控系统达到期望的时域性能指标。
若有被控系统如图3-3-61所示,它是一个Ⅰ型二阶闭环系统。
图3-3-61 被控系统如图3-3-61所示的被控系统的传递函数为:12021S 11)1(1)(a S a S b T TS T TS S T S i i i ++=++=++=φ (3-3-51) 采用零极点表达式为:))(()(210λλφ--=S S b S (3-3-52)进行状态反馈后,如图3-3-62所示,图中“输入增益阵”L 是用来满足静态要求。
图3-3-62 状态反馈后被控系统设状态反馈后零极点表达式为:))(()(21**--=λλφS S b S (3-3-53)1.矩阵法计算状态反馈及极点配置1)被控系统被控系统状态系统变量图见图3-3-63。
图3-3-63 被控系统状态系统变量状态反馈后的被控系统状态系统变量图见图3-3-64。
图3-3-64 状态反馈后的被控系统状态系统变量图图3-3-61的被控系统的状态方程和输出方程为:状态方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-=+-=••1i 1i 2211X Y u T 1X T 1X X T 1X T 1X (3-3-54)⎪⎩⎪⎨⎧=+==•∑CxY u Ax X B C B A 0),,(式中[]01,T 10B 0T 1T 1T 1A ,i i 21=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=C x x x , 被控系统的特征多项式和传递函数分别为:12010a a b S b )(+++=S S S φB A)C(SI 1--=)(A -SI det a a )(f 0120=++=S S S 可通过如下变换(设P 为能控标准型变换矩阵): —x P X =将∑0C B A ),,(化为能控标准型 ),,(————C B A ∑,即: ⎪⎩⎪⎨⎧=+=•——————x C Y u x A B X 式中 ⎥⎦⎤⎢⎣⎡-==-101a -a 10AP P A — , ⎥⎦⎤⎢⎣⎡==-10B P B 1— , []10b b CP C ==— 2)被控系统针对能控标准型),,(————C B A ∑引入状态反馈:⎥⎦⎤⎢⎣⎡=-=—————式中10k k k xk u ν (3-3-55)可求得对—x 的闭环系统),,—————C B k B A (-∑的状态空间表达式: 仍为能控标准型,即: ⎪⎩⎪⎨⎧=+-=•————————)(x C Y u x B k B A X 式中 ⎥⎦⎤⎢⎣⎡+-+-=-)()(—————1100k a k a 10k B A则闭环系统),,(——————C B k B A -∑的特征多项式和传递函数分别为: )()(—————00112k k a k a k)B (A SI det )(f ++++=⎥⎦⎤⎢⎣⎡--=S S S )k a (k a b S b B )k B A (SI C )(00112011k ———————)(+++++=⎥⎦⎤⎢⎣⎡--=-S S S φ3)被控系统如图3-3-61所示:其中:05.01==T T i则其被控系统的状态方程和输出方程为:[]XY uX X 0110012020=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=期望性能指标为:超调量M P ≤20%;峰值时间t P ≤0.5秒。
综合性实验 极点配置全状态反馈控制指导书

综合性实验 极点配置全状态反馈控制一、实验目的1.学习并掌握用极点配置方法设计全状态反馈控制系统的方法。
2.用电路模拟与软件仿真方法研究参数对系统性能的影响。
二、实验内容1.设计典型二阶系统的极点配置全状态反馈控制系统,并进行电路模拟与软件仿真研究。
2.设计典型三阶系统的极点配置全状态反馈控制系统,并进行电路模拟与软件仿真研究。
三、实验前准备工作1 推导图1的数学模型(状态空间表达式),分析系统的能控性。
2 若系统期望的性能指标为:超调量25%p M ≤,峰值时间0.5p t ≤,求出期望的极点值。
根据以上性能指标要求设计出状态反馈控制器。
3 推导图2的数学模型(传递函数),求出其单位阶跃响应的动态性能指标(超调量、调节时间、静态速度误差系数)。
4 推导图4的数学模型(状态空间表达式),分析系统的能控性。
5考虑系统稳定性等要求,选择理想极点为:S 1=-9,S 2 =-2+j2,S 3=-2-j2, 根据以上性能指标要求思考如何设计状态反馈控制器。
6 推导图7的数学模型(传递函数)。
四、实验步骤1.典型二阶系统(1)对一已知二阶系统(见图1)用极点配置方法设计全状态反馈系数。
(2)见图2和图3,利用实验箱上的电路单元U9、U11、U12和U8,按设计参数设计并连接成系统模拟电路,测取阶跃响应,并与软件仿真结果比较。
(3)改变系统模拟电路接线,使系统恢复到图1所示情况,测取阶跃响应,并与软件仿真结果比较。
(4)对实验结果进行比较、分析,并完成实验报告。
2.典型三阶系统(1)对一已知三阶系统(见图4)用极点配置方法设计全状态反馈系数。
(2)见图5和图7,利用实验箱上的电路单元U9、U11、U12、U15和U8,按设计参数设计并连接成系统模拟电路,测取阶跃响应,并与软件仿真结果比较。
(3)改变系统模拟电路接线,使系统恢复到图5所示情况,测取阶跃响应,并与软件仿真结果比较。
软件仿真直接在MATLAB 中实现。
状态反馈极点配置基本理论与方法

第2章 状态反馈极点配置设计基本理论2.1引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数,然后反馈到输入端与参考输入相加形成的控制规律,作为被控系统的控制输入。
图2.1是一个多输入多输出线性时不变系统状态反馈的基本结构:图2.1 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为:x Ax Buy Cx=+= (2.1)由图2.1可知,加入状态反馈后,受控系统的输入为:u Fx v =+ (2.2)其中v 为参考输入,F 为状态反馈增益阵,因此可以得到状态反馈闭环系统的状态空间表达式:()x A BF x Bv y Cx=++= (2.3)闭环系统的传递函数矩阵:()()1s W s C sI A BF B -=-+⎡⎤⎣⎦ (2.4)由此可见,引入状态反馈后,通过F 的选择,可以改变闭环系统的特征值,是系统获得所要求的性能。
2.2极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置,一般有四种方法: (1) 传统方法—将系统转化为一个或多个单输入单输出系统。
(2) 直接法—使用稳定的酉矩阵,将这种系统转化为标准型。
(3) 矩阵方程法—对矩阵F ,直接解方程AX X BG -Λ= (2.5a)FX G = (2.5b)(4) 特征向量法—先找到特征向量x j (等式(2.5)中矩阵X 的列向量),然后利用等式(2.5b)求解F 。
方法(1)一般难以应用或者数值不稳定。
方法(3)需要解(2.5a)方程,并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法(2)和方法(4)。
其中方法(4)通过使用一系列的迭代算法找到最优解,所以比较复杂。
对于方法(2),当系统的输入多于一个信号输入时,不能确定系统的鲁棒性。
线性系统状态反馈与极点配置

实验报告课程名称:现代控制理论实验名称:线性系统状态反馈与极点配置、实验目的1. 学习并掌握利用MATLAB编程平台进行控制系统设计与仿真的方法。
2. 通过仿真实验,研究并总结线性定常系统状态反馈对系统控制性能影响的规律。
3. 通过仿真实验,研究并总结状态反馈对状态不完全能控系统控制性能影响的规律。
二、实验内容(一)实验任务:1. 自行选择一个状态完全能控型SISO 系统模型及参数,并设定系统控制性能指标,根据性能指标要求计算期望的极点并进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;2. 自行选择一个状态不完全能控型SISO 系统模型及参数,并设定系统控制性能指标,根据性能指标要求进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;根据实验结果,总结各自的规律。
三、实验设计1. 实验条件1. 利用本学期所学的现代控制理论的知识为基础。
2. 笔记本电脑,matlab四、实验过程1. 设计状态完全能控型SISO 系统模型及参数:a)首先判断系统的能控性= ,是Rack([B AB]) = 2,因此此系统为可控的系统。
可以进行任意极点配置。
则期望极点配置二重根1b ) 再求状态反馈阵 :c ) 根据给定的极点,得到期望特征多项式:d )比较和 各对应项系数,可解得:e )即状态反馈控制器:u=-K*x状态反馈闭环系统空间表达式 x=A-B*K*xA1 = A -B*K = [0 1 ; 1 -2]2. 设计状态不完全能控型 SISO 系统模型及参数:a )首先判断系统的能控性, Rank ([B AB]) = 1,因此系统是不完全能控的,b )再求状态反馈阵c )将期望极点配置二重根 1,则:d )比较 和 各对应项系数,可解得:任意值e )即状态反馈控制器:u=-K*x 状态反馈闭环系统空间表达式 x=A-B*K*xA1 = A -B*K = [01; 1 1]五、实验结果(曲线、数据等)1 •状态完全能控型SISO 系统模型:a )配置极点前的波形: A=[0 1; 0 1]不能进行任意极点配 设)b)配置极点后的波形: A1 = A -B*K = [01; 1-2]3. 状态不完全能控型SISO 系统模型a )配置极点前的波形:A=[1 01]■* l-lgu-'E 1 fit E占Jl 血血JWEfllulk 氐*lap ffilndort 也 b□X Fi1J j dk %鵲 、七禺v 插-<2 D £ ■ dM IP 2*S4«|> R :吐parish13ID ・■-霊■・4卜2-1J ftTO2D3) 4D 也Ihrme liucondy.)*a)配置极点后的波形:六、实验结果分析与讨论1•状态完全能控型SISO系统模型通过配置极点后动态性能变好,但是稳态误差不能消除。
自动控制原理学生实验:线性系统的状态反馈及极点配置
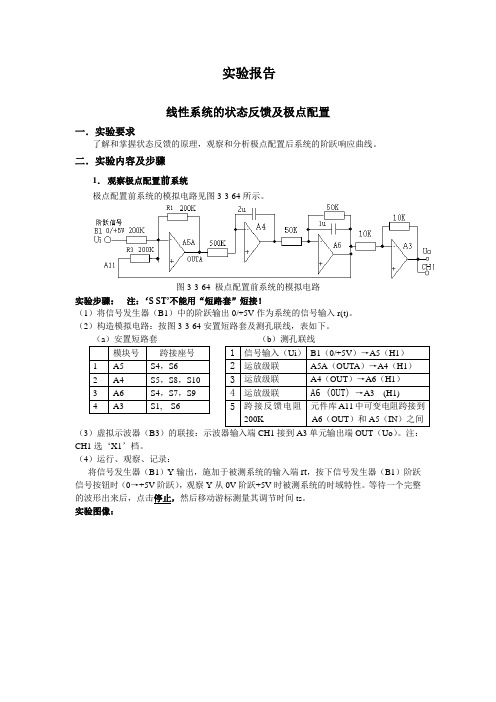
实验报告线性系统的状态反馈及极点配置一.实验要求了解和掌握状态反馈的原理,观察和分析极点配置后系统的阶跃响应曲线。
二.实验内容及步骤1.观察极点配置前系统极点配置前系统的模拟电路见图3-3-64所示。
图3-3-64 极点配置前系统的模拟电路实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入r(t)。
(2)构造模拟电路:按图3-3-64安置短路套及测孔联线,表如下。
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A3单元输出端OUT(Uo)。
注:CH1选‘X1’档。
(4)运行、观察、记录:将信号发生器(B1)Y输出,施加于被测系统的输入端rt,按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),观察Y从0V阶跃+5V时被测系统的时域特性。
等待一个完整的波形出来后,点击停止,然后移动游标测量其调节时间ts。
实验图像:由图得ts=3.880s 2.观察极点配置后系统 极点的计算:受控系统如图所示,若受控系统完全可控,则通过状态反馈可以任意配置极点。
受控系统设期望性能指标为:超调量M P ≤5%;峰值时间t P ≤0.5秒。
由1095.01t 707.0%5eM n n 2n p 1/p 2=≥⇒≤-==⇒≤=--ωωζωπζζζπ取因此,根据性能指标确定系统希望极点为:⎪⎩⎪⎨⎧--=+-=07.707.707.707.7*2*1j j λλ受控系统的状态方程和输出方程为:⎪⎩⎪⎨⎧=+=-----⋅-xC y b x A x μ式中][01,10,020120,21=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=----C b A x x x系统的传递函数为:202020a S a S βS β)(2012010++=+++=S S S G受控制系统的可控规范形为:[][]020T C C b T b a a T A T A X T X X C Y U b X A X K K i o K K KK k K K K ===⎥⎦⎤⎢⎣⎡==⎥⎦⎤-⎢⎣⎡-=⎥⎦⎤-⎢⎣⎡-===⎩⎨⎧=+=---10111,1020120010T ββ为变换阵),(式中当引入状态反馈阵K K =[K 0K 1]后,闭环系统()K K K K K C b K b A ,,-的传递函数为:()()()01201120120)20(20)(K S K S K a S K a S S S G o ++++=+++++=ββ而希望的闭环系统特征多项为:1001.14))(()(2*2*1**12*++=--=++=S S S S a S a S S f oλλ 令G K (S)的分母等于F #(S),则得到K K 为:[][]9.58010-==K K K k最后确定原受控系统的状态反馈阵K :由于 1-=T K K k求得和===---111,T C b T b T A T A K k K求得 ⎥⎥⎦⎤⎢⎢⎣⎡-=-1102011T所以状态反馈阵为: [][]9.59.91102019.580-=⎥⎥⎦⎤⎢⎢⎣⎡--=K极点配置系统如图所示:极点配置后系统根据极点配置后系统设计的模拟电路见下图所示。
极点配置法设计状态反馈控制器——自动控制原理

这两个多项式的系数相等,可得出:
0 0
1
1
n n1
i中含F阵系数fij
当F阵为1 n时
n个方程可解n个系数 fi
(i 1,2,...,n)
设计算法--适用于用能控标准形表示的SI系统的算法
设系统期望的闭环极点为s1、s2、sn ,则其
闭环特征式为s s1 s s2 s s3 s sn
SI系统,所以设 F f1 f2 fn
ห้องสมุดไป่ตู้
设计算法--适用于用能控标准形表示的SI系统的算法
s
1
0
0
0
0
s
1
0
0
0
0
0
s
1
a0 f1 a1 f2 a2 f3 an2 fn1 an1 fn s
sn (an1 fn )sn1 a1 f2 s a0 f1
设计算法--适用于用能控标准形表示的SI系统的算法
解:
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
设: F f1 f2
F 7 1
w
u+
x2 ∫
--
++ -5
x2 x1
∫ x1
-
F 7 1
1
+
2
+
y
-6 1
7
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
线性系统的状态反馈及极点配置

线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟,线性系统的状态反馈控制在控制理论中得到了广泛的应用,并成为了控制领域中重要的一种控制方法。
状态反馈控制能够将系统的状态进行反馈,并利用反馈得到的信息对系统进行控制,从而达到使系统达到预期控制目标的目的。
本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。
2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。
状态反馈控制的基本思想是在系统中引入反馈环节,设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,以期望控制系统按照预期的运动轨迹运行。
因此,状态反馈控制要实现以下两个步骤:- 系统状态量的测量:首先要在系统中安装测量传感器,实时地测量系统状态量,使得状态量可以被反馈到控制器中。
- 反馈控制器的设计:设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,实现对系统的精确控制。
因此,状态反馈控制的基本原理就是将系统状态量反馈到控制器中,以期望控制系统按照预期的运动轨迹运行。
2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。
状态空间模型是一种方便描述线性系统动态行为和控制器的模型。
对于线性时不变系统,我们可以用如下的状态变量描述:x(t) = [x1(t),x2(t),...,xn(t)]T其中,x(t) 是系统在时刻 t 的状态量,n 是状态量的数量,x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。
状态空间模型可以用一组线性常微分方程描述:dx/dt = Ax + Bu其中,A 是系统的状态方程矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接耦合矩阵。
系统的状态反馈控制可以表示为:u(t) = -Kx(t)其中,K 是状态反馈矩阵。
将状态反馈控制引入到状态空间模型中,可以得到控制器的状态空间模型为:y = Cx上述控制器的状态空间模型就是一个闭环系统,通过反馈控制器将系统状态返回到系统,形成了一个反馈环。
状态反馈与闭环极点配置

则 A + BK 的特征值为α1 , α 2 ,"α n . 故 K 存在。 定理结论得证。
12
§3.2-2 单输入系统的极点配置 定理3.2的意义: 1. 单输入能控系统可通过状态反馈任意配置闭环系统的极点. 2. 给出了单输入极点配置问题的算法。 算法: (1) 求 A 的特征多项式, 即(3.2.6); (2) 计算α ( s ), 即(3.2.10); ˆ; (3) 由(3.2.13)计算 K (4) 由(3.2.4)计算变换矩阵 T , 并求出 T −1 ; (5) 由(3.2.14)计算状态反馈矩阵 K.
[sI − A − BK
B ] = [ sI − A
⎡ I B ]⎢ ⎣− K
0⎤ I⎥ ⎦
rank [ sI − A − BK
B ] = rank [ sI − A B ] , ∀s ∈ ^
由PBH判据知定理结论成立。
5
§3.2
闭环极点配置问题
§3.2-1 问题的描述 线性定常系统
(3.2.1) = Ax + Bu x A, B 分别是 x 为 n 维状态向量, u 为p 维控制向量, n × n, n × p 阶常阵。 给定
13
§3.2-2 单输入系统的极点配置 例1 给定单输入线性定常系统为
0 ⎤ ⎡1⎤ ⎡0 0 ⎥ ⎢ ⎥ ⎢ x = ⎢1 − 6 0 ⎥ x + ⎢0⎥u ⎢ ⎢ ⎦ ⎣0 ⎥ ⎦ ⎣0 1 − 12⎥
闭环特征值为
α1 = −2, α 2,3 = −1 ± j
求状态反馈矩阵 K.
14
§3.2-2 单输入系统的极点配置 解:经判断系统为能控。计算系统的特征多项式 求得
全状态反馈系统极点配置的数字仿真(终)

实验一全状态反馈系统极点配置的数字仿真一、实验目的1掌握全状态反馈系统的极点配置方法;2研究不同极点配置对系统特性的影响。
二、实验原理闭环系统性能与闭环极点(特征值)密切相关,在状态空间的分析和综合中,除了利用输出反馈以外,主要利用状态反馈来配置极点,它能提供更多的校正信息。
利用状态反馈任意配置闭环极点的充要条件是:受控系统可控。
设SIMO(Single Input-Multi Output)受控系统的动态方程为,状态向量通过状态反馈矩阵,负反馈至系统参考输入,于是有这样便构成了状态反馈系统,其结构图如图1-1所示图1-1 SIMO状态反馈系统结构图状态反馈系统动态方程为,(1-1)闭环系统特征多项式为(1-2)设闭环系统的期望极点为,,…,,则系统的期望特征多项式为(1-3)欲使闭环系统的极点取期望值,只需令式(1-2)和式(1-3)相等,即(1-4)利用式(1-4)左右两边对应的同次项系数相等,可以求出状态反馈矩阵例如SISO(Single Input-Single Output)受控系统的开环传递函数为若采用输出单位反馈构成闭环系统,则该系统显然是不稳定的,若按指定的极点配置,采用全状态反馈构成闭环系统,则可以满足给定的性能要求。
原系统可控标准形形式的状态方程和输出方程为由于本系统是完全可控的,能够通过反馈向量的选择,使闭环系统的极点置于所希望的位置上,以满足系统的性能指标要求。
若根据系统的性能指标,希望配置的极点为,,则采用状态反馈后系统的特征多项式为希望的系统特征多项式为比较上述两个多项式得系统状态反馈向量为因此,加入状态反馈后,闭环系统的状态方程为其结构图如图1-2所示图1-2 状态反馈系统结构图三、实验内容及步骤实验通过MATLAB软件实现。
1.双击MATLAB图标或单击开始菜单,依次指向“程序”、“MATLAB”,单击MATLAB,进入MATLAB命令窗口。
单击MATLAB工具条上的Simulink图标,运行后出现Simulink模块库浏览器,并单击其工具条左边的图标,弹出新建模型窗口。
状态反馈与闭环极点配置极点配置条件

u B
x
x
y
∫
C
A
H
-
B
∫
C
实际系统基于准确模型,且
A
没有考虑扰动
代入 ye C xe
25
附1:存在扰动时的状态误差
u B
x
x
dy
∫
C
A
H
-
B
∫
C
A
代入 ye C xe d
存在扰动时,不能使状态误差→0
26
附2:存在模型失配时的状态误差
u B'
x
x
y
∫
C'
A'
H
-
B
∫
C
A
存在模型失配时,不能使状态误差→0
2
一、状态反馈与输出反馈
1. 状态反馈
u B -
x
xy
∫
C
A
闭环传函?状态
K
方程?
加入状态反馈后的系统结构图
3
综合的手段:改变 K 阵的参数 综合的目的:改变系统矩阵,从而改变系统的特性
注:状态反馈通常只用系数阵即可满足要求, 一般不需要采用动态环节
4
2. 输出反馈
u B -
x
xy
∫
35
闭环传递函数的不变性
闭环传递函数等同于直接状态反馈的情况; 观测器的引入不影响闭环传递函数
注:分离性原理和传函的不变性都基于精确模型 36
仿真例: 系统的状态空间表达式同前面例
(1)要求状态观测器的特征值为 (2)通过状态反馈将系统的闭环极点配置为
(3)仿真验证观测状态对实际状态的跟踪情况,
27
状态观测器的等价结构
状态空间极点配置控制实验课件

选择控制信号为:
u = −KX
图 1 状态反馈闭环控制原理图
求解上式,得到 x(t) = (A − BK)x(t)
方程的解为: x(t) = e( A−BK )t x(0)
可以看出,如果系统状态完全可控,K 选适当,对于任意的初 始状态,当t趋于无穷时,都可以使x(t)趋于0。
极点配置的设计步骤: 1) 检验系统的可控性条件。
把计算得到的 K 值输入上面的窗口。 运行仿真,得到以下结果:
图 4 直线一级倒立摆状态空间极点配置MATLAB Simulink 仿真结果
ቤተ መጻሕፍቲ ባይዱ
可以看出,在存在干扰的情况下,系统在3 秒内基本上 可以恢复到新的平衡位置,
读者可以修改期望的性能指标,进行新的极点配置, 在“Controller2”模块中设置新的控制参数,并点击 “Manual Switch”把控制信号切换到“Controller2”
3、 极点配置控制实验
❖ 实验步骤如下
1) 进 入 MATLAB Simulink 中“ \\matlab6p5\toolbox\GoogolTech\
InvertedPendulum \ Linear Inverted Pendulum, ”目录,打 开直线一级倒立摆状态空间极点配置控制程序如下:
Googol Linear 1 stage Inverted Pendulum Poles Placement Method1 %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clear; A=[ 0 1 0 0; 0 0 0 0; 0 0 0 1; 0 0 29.4 0]; B=[ 0 1 0 3]'; C=[ 1 0 0 0; 0 0 1 0]; D=[ 0 0 ]'; J=[ -10 0 0 0; 0 -10 0 0; 0 0 -2-2*sqrt(3)*i 0;
极点配置状态反馈控制器设计方法

极点配置状态反馈控制器设计方法
嘿,朋友们!今天咱来聊聊极点配置状态反馈控制器设计方法。
这玩意儿啊,就像是给一个系统装上了精准的导航仪,能让它乖乖地按照咱的想法走。
你看啊,一个系统就好比是一辆汽车,而极点配置状态反馈控制器就是那个掌握方向盘的司机。
咱得通过巧妙的设计,让这个司机能精准地操控汽车,该加速的时候加速,该转弯的时候转弯,不能有一点儿含糊。
设计这个控制器就像是搭积木,一块一块地拼凑起来。
咱得先了解系统的特性,就像了解汽车的性能一样。
然后呢,根据这些特性来选择合适的参数,这可不能马虎,得仔细琢磨。
比如说,要是参数没选好,那可就糟糕啦!就像司机开车老是开歪一样,系统也会变得不稳定,那可不行!咱得让系统稳稳当当的,该干啥干啥。
这其中的学问可大着呢!就好像做菜一样,各种调料得搭配得恰到好处,才能做出美味的菜肴。
极点配置状态反馈控制器的设计也是如此,每个环节都得精心处理。
而且哦,这个设计方法可不是一成不变的。
不同的系统就像不同口味的人,得用不同的方法去对待。
有时候得灵活一点,不能太死板啦。
想想看,如果所有系统都用一种方法去设计控制器,那多无趣啊!就像所有人都穿一样的衣服,那还有啥意思呢?咱得根据实际情况来调整,找到最适合的方案。
在实际应用中,这可真是帮了大忙啦!它能让那些复杂的系统乖乖听话,按照我们的要求运行。
这多厉害呀!难道不是吗?
所以啊,极点配置状态反馈控制器设计方法可真是个宝贝!咱可得好好研究,好好利用。
让它为我们的各种系统服务,让它们变得更智能、更高效。
怎么样,是不是觉得很有意思呢?别犹豫啦,赶紧去试试吧!。
基于状态反馈的线性系统D稳定极点配置仿真研究

l f z ) = 2 a + z + z 。 对于反馈 系统 ,我们希望寻求一个状态反馈控 制 ( f ) = 一 ^ ( ( 2 ) 将 闭环系统 的极点配 置在 区域 D 内 ,由引理 2不难得 出如下推论 : 定理 1反馈系统在状态反馈控制下 ,其 闭环 系统所有极 点在复平 面区域 内,若存 在正定对称 矩阵 X > 0 及任意矩 阵 Q,当且仅当如下 L MI 成立
, n ㈨2 ( z ) = d i a g O C a 1 ( z ) , 2 ) 。 进一 步讲 ,任意有 限个 L MI 区域 的交集仍 为 L MI 区域 。 因此 ,关 于实 轴对称的任一 凸区域都可 以用一个 L MI 区域来 近似 。 定义 2矩阵 A称 为 D 一稳定 的 ,当且 仅当 A的特征 U为 P维 状态 向量 ; A和 为相应维数 的常数 阵。 保 证 状 态 响 应 具 有 稳 定 裕 度 a的 左 半 平 面 D = { z∈ C : R ( Z ) ≤一 a , a > 0 } 是 一个 L M I 区域 ,其特 征 函数为
2 a P - + ( . 4 - B K ) P - + P‘ ’ 一 B l 0
( 4 )
( 5)
D= t z ∈ C: f o ( z ) = R l l + R l 2 z + l + R 2 2 < 0 ( 1 )
其 中 ,R. . , : 是 对称 矩 阵 ,R : = L L 是 半正 定矩 阵 ,z 是 z的共轭 复数 。当 L = 0时 ,则 区域 D称 为一个 L M I区域 , 这些 L M I 区域 都可以用一个线性矩 阵不等式来刻 画。D区域 是关 于实轴 对称 的 区域 ,厂 力 ( z ) =Rl 十R 1 2 z + +R 2 2 称 为 区域 D的特 征 函数 。通常 ,特征 函数 . 厂 D ( z ) 是 He r mi t e矩 阵 , , D < O 表示矩 阵 ( z ) 是负定 的。 许 多常 见的 区域 ,例 如圆盘 ,半平 面 ,椭 圆形 ,扇形 , 抛物形等 区域均是 L MI 区域 。 引 理 1对 于 任 意 两 个 给 定 的 L MI区 域 n 和 Q , 其 交 集 n。n n 仍为L MI 区 域 ,其 特 征 函 数 为
自动控制理论实验课程6.3.1 极点配置仿真实验

极点配置(一)实验原理给定一个连续时间系统的状态空间模型:Bu Ax x += (1)其中:x 是系统的n 维状态向量,u 是m 维控制输入,A 和B 分别是适当维数的已知常数矩阵。
在状态反馈Kx -=u (2)作用下,闭环系统的状态方程是x BK A x )(-= (3)由线性时不变系统的稳定性分析可知,闭环系统(3)的稳定性由闭环系统矩阵A-BK 的特征值决定,即闭环系统(3)渐近稳定的充分必要条件是矩阵A-BK 的所有特征值都具有负实部。
而由经典控制理论知道,矩阵A-BK 的特征值也将影响诸如衰减速度、振荡、超调等过渡过程特性。
因此,若能找到一个适当的矩阵K ,使得矩阵A-BK 的特征值位于复平面上预先给定的特定位置,则以矩阵K 为增益矩阵的状态反馈控制器(2)就能保证闭环系统(3)是渐近稳定的,且具有所期望的动态响应特性。
这种通过寻找适当的状态反馈增益矩阵K ,使得闭环系统极点(即矩阵A-BK 的特征值)位于预先给定位置的状态反馈控制器设计问题称为是状态反馈极点配置问题,简称为极点配置问题。
对给定的线性定常系统(1)和一组给定的期望闭环极点},,{n 2,1λλλ =Ω,按以下步骤可以设计出使得闭环系统(3)具有给定极点},,{n 2,1λλλ =Ω的状态反馈控制器(2)。
第1步:检验系统的能控性。
如果系统是能控的,则继续第2步。
第2步:利用系统矩A 阵的特征多项式0111)det(a a a A I n n n +++=---λλλλ (4)确定的110,,,-n a a a 值。
第3步:确定将系统状态方程变换为能控标准形的变换矩阵T 。
若给定的状态方程已是能控标准形,那么T=I 。
非奇异线性变换矩阵T 可按如下方式确定:可控性矩阵:],b ,[1b A A b U n -= (5)计算1-U ,并记最后一行为h给出变换阵:112],,,h [--=n hA hA hA T (6)第4步:利用给定的期望闭环极点,可得期望的闭环特征多项式为011121)())((b b b n n n n +++=-----λλλλλλλλλ (7)并确定110,,,b -n b b 的值第5步:确定极点配置状态反馈增益矩阵K :T a b a b a b a b K n n n n ],,,[11221100--------= (8)也可以通过待定系数的方法来确定极点配置状态反馈增益矩阵K 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 全状态反馈系统极点配置的数字仿真
一、实验目的
1掌握全状态反馈系统的极点配置方法;
2研究不同极点配置对系统特性的影响。
二、实验原理
闭环系统性能与闭环极点(特征值)密切相关,在状态空间的分析和综合中,除了利用输出反馈以外,主要利用状态反馈来配置极点,它能提供更多的校正信息。
利用状态反馈任意配置闭环极点的充要条件是:受控系统可控。
设SIMO (Single Input-Multi Output )受控系统的动态方程为
u A b x x
+= ,x y C = 状态向量x 通过状态反馈矩阵k ,负反馈至系统参考输入v ,于是有
u v kx =+
这样便构成了状态反馈系统,其结构图如图1-1所示
图1-1 SIMO 状态反馈系统结构图
状态反馈系统动态方程为 x ()A bk x bv =++,x y C = (1-1)
闭环系统特征多项式为
()()f I A bk λλ=-+ (1-2)
设闭环系统的期望极点为1λ,2λ,…,n λ,则系统的期望特征多项式为
)())(()(21*n f λλλλλλλ---= (1-3)
欲使闭环系统的极点取期望值,只需令式(1-2)和式(1-3)相等,即
)()(*λλf f = (1-4)
利用式(1-4)左右两边对应λ的同次项系数相等,可以求出状态反馈矩阵
[]n k k k 21=k
例如SISO (Single Input-Single Output )受控系统的开环传递函数为
3
1)(s s G = 若采用输出单位反馈构成闭环系统,则该系统显然是不稳定的,若按指定的极点配置,采用
全状态反馈构成闭环系统,则可以满足给定的性能要求。
原系统可控标准形形式的状态方程和输出方程为
u x x x u A ⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+=100000100010321b x x []⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡==321001x x x C y x 由于本系统是完全可控的,能够通过反馈向量k 的选择,使闭环系统的极点置于所希望的位置上,以满足系统的性能指标要求。
若根据系统的性能指标,希望配置的极点为31-=p ,2j 23,2±-=p ,则采用状态反馈后系统的特征多项式为
32321()det[I ()]f A bk k k k λλλλλ=-+=---
希望的系统特征多项式为
*32()(3)(2j2)(2j2)72024f λλλλλλλ=++-++=+++
比较上述两个多项式得系统状态反馈向量为
[][]123k 24207k k k ==---
因此,加入状态反馈后,闭环系统的状态方程为
u x x x u A ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=+=10072024100010321b x x 其结构图如图1-2所示
图1-2 状态反馈系统结构图
三、实验内容及步骤
实验通过MATLAB 软件实现。
1. 双击MATLAB 图标或单击开始菜单,依次指向“程序”、“MATLAB ”,单击MATLAB ,进入MATLAB 命令窗口。
单击MATLAB 工具条上的Simulink 图标
,运行后出现Simulink 模块库浏览器,并单击其工具条左边的图标,弹出新建模型窗口。
2.在模块库浏览器窗口中的Simulink 下的输入源模块(Sources)、数学运算模块(Math)、连续系统模块(Continuous)、接收模块(Sinks)库中,分别选择阶跃信号(Step)、求和(Sum)、常量增益(Gain)、积分环节(Integrator)、示波器(Scope)模块,建立如图1-3 所示的仿真图。
图1-3 MATLAB 下状态反馈系统仿真图
3.用鼠标左键双击阶跃信号和各比例环节的模型,设置好参数;选择Simulation 菜单中parameters 选项,设置好仿真参数;选择Simulation 菜单中的start 选项,开始仿真;观察并记录下系统的输出。
4.通过状态反馈,将控制系统的闭环极点设置为110p =-,1j 13,2±-=p ,重复3、4步骤。
此时[][]123k 8106k k k ==---
5.通过状态反馈,将控制系统的闭环极点设置为130p =-,2,33j3p =-±,重复3、4步骤。
此时[][]1
23k 6116k k k ==--- 四、实验报告内容
1.理论计算希望配置的极点为41-=p ,1j 13,2±-=p 和11-=p ,22-=p ,33-=p 时的反馈向量[]321k k k =k ;
2.屏幕拷贝下三组极点配置下的系统响应曲线;并根据响应曲线确定s t 、p t 和%σ。
五、实验思考题
1.在状态反馈系统中,极点任意配置的充要条件是什么?2.试比较状态反馈系统与经典控制理论中的输出反馈系统。
3.。
