2017-2018学年第一学期期末考试一年级数学试卷

合集下载

高一数学期末(A卷)-答案

2分
(2)a2-a1=-6,a3-a2=-4,…………………………………………………………… 2分
由a2-a1≠a3-a2 知,数列{an}不是等差数列.………………………………………… 2分
30.(本题满分 14 分 )
解:(1)f(5)=195,f(35)=135,…………………………………………………………… 2分
浙江省高职考试研究联合体
中等职业学校2017~2018学年第一学期期末考试高一数学试卷(A 卷)参考答案
一、单项选择题(本大题共 15 小题 ,每小题 3 分 ,共 45 分)
1.C 2.C 3.A 4.D 5.A 6.D 7.C 8.D 9.D 10.C 11.C 12.B 13.C 14.B
解
:由图
像
知 ,图
像过
点 (-2,0),(0,5),对称
轴方
程
为x=
3, 2
…………………………
2分
ìï4a-2b+c=0,
则 íïï-2ba=32,
………………………………………………………………………… 2分
îïc=5,
高一数学期末试卷(A 卷)参考答案第1页(共3页)
ìïïa=
-
1, 2
∵B⊆A,∴B=⌀或{2}或{-3}, ………………………………………………………… 1分
∴当 B=⌀时,m =0;当 B={2}时,m
1 =2
;当
B=
{-3}时
,m
=-
1 3
.… …
……
…
……
3分
∴实数 m 的所有可能取值为0,1 2,-1 3.………………………………………………… 1分

人教版小学一年级上册数学期末测试卷精品(历年真题)

人教版小学一年级上册数学期末测试卷一.选择题(共8题，共16分)1.三位同学玩猜数游戏，答案是13的是（）。

A. B.C.2.和16相邻的两个数是（）。

A.16和18B.17和19C.15和173.小明邀请他的好朋友们来家里做客，他拿出8个桃子来招待小客人，每人1个，最后还差3个桃子，小明来了（）名小客人。

A.11B.8C.54.用天平可比较物品的（）。

A.大小B.长短C.轻重5.下面的水果中，最重的是哪个？（）A. B. C.6.小猫的后面是小兔，小兔在小象的前面，( ) 在最前面。

A.小兔B.小象C.小猫7.选择合适的时间：（）。

A.晚9时B.上午10时C.下午3时8.比多（）个。

A.1B.2C.3二.判断题(共8题，共16分)1.比3大比10小的数一共有(7)个。

它们是(3，4，5，6，7，8，9)。

（）2.分针从一个数字走到下个数字，经过的时间是1分。

（）3.2个苹果和第二个苹果一多样。

( )4.16的个位是1，十位是6。

（）5.12时整时，时针和分针都指向12。

（）6.○○○○○○○△△还需要画5个△就和○一样多。

（）7.排队时小华排第6，小明排第10，小华和小明之间有4人。

（）8.20前面的第3个数是18。

（）三.填空题(共8题，共40分)1.动物们排队，小马排第1，小羊前面有( ) 只动物，小兔后面有( ) 只动物。

2.算一算，填一填。

3.下图中，时针指向( )，分针指向( )、接近( )时，所以是快到( )时了，还可以说成大约( )时。

4.按要求凑数。

凑4：1和________ ________和2 3和________凑5：1和________ 2和________ 3和________ 4和________5.数一数，写一写。

________ ________ ________6.从1到20，一共是（）个数，其中比15大的数有（）个，与18相邻的两个数是（）和（）。

7.8和（）合成10，计算8+6=□，把6分成（）和（），先算（），再算（）。

【5套打包】济宁市小学一年级数学上期末考试单元测试卷(含答案)(1)

人教版一年级数学上册期末试卷及答案一、填空题（共10题；共55分）1.按顺序填数：________，14，________ 16，________，________。

2.18由________个十和________个一组成。

3.9前面的第一个数是________，9后面的第一个数是________。

4.1个十和4个一组成的数是________。

5.A A A A A A AM M M M字母A的个数是________，字母M的个数是________，字母A的个数比M的个数多________个6.在“好”的左边画“+”，在“好"右边画“○"，在“好"上面画“﹁”，在“好”下面打“△"。

________7.填“<”、“>"、“=”。

7________9 18________8 9________11 17-7________17-718-6________8 16________8+8 19-7________7+0 15-4________7+48.找规律填数。

9.口算8+3=________ 15+5=________6+7= ________18-8=________17-4=________0+17=________11+2=________16+4=________14+4=________9-6= ________16-0=________13+6=________8+8=________9+9=________19-2=________16-5=________12+8=________13+3=________13+7=________17-7=________15+3=________ 8+9=________11+4=________7+7=________二、解答题1.从左数圆柱排在第________，从右数排在第________。

2017--2018学年度第一学期期末测评小学一年级数学试卷

2017--2018 学年度第一学期期末测评一年级数学试卷4、一个两位数从右边起，第一位是（）位，第二位是（）位。

5、最小的两位数是（），最大的一位数是（），它们的和是（），它们的 O.....题号 ■ 一-二二-三四五六七总计得分时间：90分钟满分：120分6、在O 里填> 、 V 或 =04+7 (7+4 9 18-6 (7^-2 0O 10+7（小1：616+3 20 (75' 14-1 O 5+9 ( 6+87+5 6+7<1220-10O）。

一、我会算。

（共28分）1、直接写出得数（每式 1 分, 共12分）8+7= 9-4= 6+10= 8-8= 19-6= 2+8=9+9= 11-10=0+4= 4+5= 3-0= 5+8=2、按顺序计算（每式2分，共16分）7、被减数是10，减数是8，差是（。

&看图填数。

O....■£9+3+5=6+7-2= 14-4-6=10-1+8=4+5+5=9+8+1=18-2-0= 8+7-2=、我会填。

（第2题每式2分，共6分；第8题每式1分，共4分；其余每空1分，共40分） 102+D = D】f}_2 =||i °-D=n 9、乐乐看一本书，从第3页看到第7页，他一共看了（。

页。

10、妈妈买来一些苹果，小红吃了 2个，还剩9个，妈妈原来买了（。

个苹果O ... :里1、看图写数2、在□里填上合适的数。

9 4- 6 =A□3、找规律填数|1叩引 |15|2 48!211、鼓号队的小朋友排成一列，从前往后数，小丽排在第 10个，小明排在第15 个，小丽和小明之间有（。

个小朋友。

12、 10个一是1个（），2个十是（）。

13、个位上是2，十位上是1，这个数是（）。

三、我会辨。

（正确的在括号里打“V”，错误的打“X”，每题1分，共10分） 1、 12的前一个数是11,后一个数是13。

2017-2018学年度第一学期期中质量检测一年级数学试卷及答案

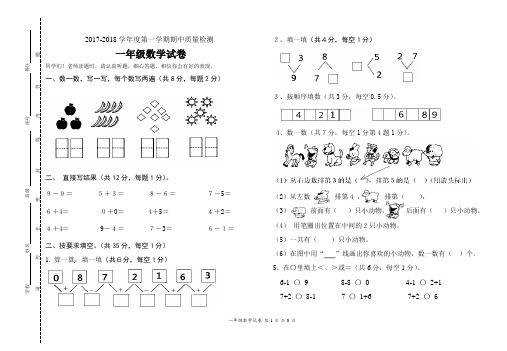
一年级数学试卷第 1 页共 3 页2017-2018学年度第一学期期中质量检测一年级数学试卷同学们！老师读题时，请认真听题，细心答题，相信你会有好的表现。

一、数一数，写一写，每个数写两遍（共8分，每题2分）二、直接写结果（共12分，每题1分）。

９－０＝５＋３＝８－６＝７－5＝６＋4＝０＋0＝ 4＋5＝４＋2＝４＋4＝ 9－４＝７－3＝６－１＝二、按要求填空。

（共35分，每空１分） 1. 算一算，填一填（共６分，每空１分）２、填一填（共４分，每空１分）３、按顺序填数（共3分，每空0.5分）。

4、数一数（共７分，每空1分第4题1分）。

（2）从左数排第4 ，排第（），（3）前面有（）只小动物，后面有（）只小动物。

（4）用笔圈出位置在中间的２只小动物。

（5）一共有（）只小动物。

（6）在图中用“ ”线画出你喜欢的小动物，数一数有（）个。

5、在〇里填上＜、＞或＝（共6分，每空1分）。

6-1 〇 9 8-8 〇 0 4-1 〇 2+1 7+2 〇 8-1 7 〇 1+6 7+2 〇 6学校姓名班级座号得分请勿在密封线内答题6、把卡片上的数或算式结果从大到小的顺序排一排（共6分，每空1分）。

（）＞（）＞（）＞（）＞（）＞（）三、比一比，画一画。

（每题3分，共6分）（1）画，比多3个。

（2）画，比少2个四、连线(8分，每题1分)。

五、看图填空，数一数（共8分，每空2分）。

六、在中填上“+”或“-”（共8分每题2分）七、在中填上适当的数字（共8分，每题2分）八、解决问题(每题2分，共10分)4、一本故事书，我昨天看了5页，今天看了4页，两天共看了多少页？□○□=□（页）5、小明家原来有6只小羊，卖了2只，现在还有多少只？□○□=□（只）请勿在密封线内答题一年级数学试卷第2 页共 3 页参考答案一、数一数，写一写，每个数写两遍（共8分，每题2分）略二、直接写结果（共12分，每题1分）略。

河南省新乡市一中 2017-2018学年上期初一年级第一次月考数学试卷无答案

2017--2018学年上期初一年级第一次月考数学试卷时间：120分钟，总分：120分一、选择题(30分)1.–5的绝对值是 ( )A.5B.–5C.51D.51- 2.下列数据中，准确数是 ( )A.王浩体重为45.8kgB.光明中学七年级有322名女生C.珠穆朗玛峰高出海平面8844. 43mD.中国约有14亿人口3.在–2，+3.5，0，32-，–0.7，11中，负分数有 ( ) A.l 个 B.2个 C.3个 D.4个4.下列各组数中，互为相反数的是 ( )A.2与12B.(–1)2与1C.–1与(–1)2D.2与│–2│ 5.下列各组数中，相等的是 ( )A.–1与(–4)+(–3)B.2)4(-与–16 C.432与169 D.│–3│与–(–3) 6. 我国年可利用的淡水资源总量为27 500亿米3，人均占有淡水资源量居全世界第110位，因此我们要节约用水. 27 500亿这个数用科学记数法表示为 ( )A. 2.75×1010B.2.75×1011C. 2.75×1012D. 2.8×10127. 下列运算结果是负数的是 ( )A. –3–2×(+4)B. (–3)2÷3C.│–3│÷6D.(–3)×(–2)8.有理数a ，b 在数轴上的位置如图所示，下列各式不正确的是 ( )A. a +b <0B.a –b <0C.ab <0D.ba <0 9.下列说法正确的有 ( ) ①最大的负整数是–1； ②1.32×104是精确到百分位；③(–2)4与–24结果相等； ④a +6一定比a 大；⑤数轴上表示–3和3的点到原点的距离相等．A.0个B.1个C.2个D.3个10.已知8.62=73.96，若x 2=0.7396，则x 的值等于 ( )A.86B.0.86C.±0.86D. ±86二、填空题（15分）11.21的相反数等于 . 12.计算：=-+-20182017)1()1( .13.若数轴上的点A 表示数–2，则与点A 相距3个单位长度的点所表示的数为 .14.黄山主峰一天早晨气温为–1℃，中午上升了8℃，夜间又下降了10℃，那么这天夜间黄山主峰的气温是 .15.将卡片正面的数由大到小排列，然后将卡片翻转，卡片上的字母组成的单词是 .三、解答题：（本大题共9小题，共75分）.16.(8分)计算：(1) )3()7()5()3(0-----++-； (2) )41(436-⨯÷；17.(8分)计算：(1) )8()48()32(48-÷---⨯； (2) []22)3(331)5.01(1--⨯⨯---．18.(9分)某一出租车一天下午以鼓楼为出发地在东西方向营运，向东为正，向西为负，行车里程（单位：km ）依先后次序记录如下：+9，–3，–5，+6，–8，+6，–3，–6，–4，+10.(1)将最后一名乘客送到目的地，出租车离鼓楼出发点多远?在鼓楼的什么方向?(2)若每千米的价格为2.4元，司机一个下午的营业额是多少?19.(9分)已知三个有理数a ，b ，c ，其积是负数，其和是正数，当c c b b a a x ++=时，求代数式222017+-x x的值．20.(9分)已知a ，b 互为相反数，c ，d 互为倒数，m 是绝对值等于3的数，求代数式 20172)()(cd m b a cd m +⨯+++的值．21.(10分)请先阅读下列一组内容，然后解答问题：因为：所以： 10910111019141313121211)10191()4131()3121()211(1091431321211=-=-++-+-+-=-++-+-+-=⨯++⨯+⨯+⨯ 111111111111,,12223233434910910=-=-=-⋯=-⨯⨯⨯⨯计算：(1)；820172011431321211⨯++⨯+⨯+⨯(2)22.(10分)规定运算*为：若a >b ，则a *b =a +b ；若a =b ，则a *b =a –b +1；若a <b ，则a *b =ab ．(1)计算6*4和4*6，并比较它们的大小；(2)计算(2*3)–(4*4)–(7*5)．23.(12分)(1)在数轴上标出数–4.5，–2，1，3.5所对应的点A ，B ，C ，D ；(2)C ，D 两点间距离= ；B ，C 两点间距离= ；(3)数轴上有两点M ，N ，点M 对应的数为a ，点N 对应的数为b ，那么M ，N 两点之间的距离= ；(4)若动点P ，Q 分别从点B ，C 同时出发，沿数轴负方向运动；已知点P 的速度是每秒1个单位长度，点Q 的速度是每秒2个单位长度，问①t 为何值时P ，Q 两点重合? ②t 为何值时P ，Q 两点之间的距离为1?201720151751531311⨯++⨯+⨯+⨯。

复旦大学《线性代数I》2017-2018学年第一学期期末考试试卷A卷

2有惟一解，无解，
x1 x2 x3 1
无穷多解？并求其通解 .
解：
1 x 3 1 2 y
1 2 0
2
x
2 2 y
0 2 3
x y3
即得
3
x
16
2
y
4 7
解：
B
Ab
1
1
1 1
0 1 2
r1 r3
r2 r1 r3 r1
1 0
1 1
1
1 1 1
0 0 0 0 0 0
得基础解系
1
0
1
=
1
,2
0
0
1
1
2
0
.1
,
2
已正交，单位化得
p1 =
1 2
0
,
p2
0
1
2
当
3
=
1 时，
A
E
2
0
2 2 0
0 1
03
0 0
1 0 0
0
1 0
,
x1 x3
x2 0
0
1
1
2
得基础解系
3
=
1
，单位化得
0
得分
4= 5，2，4, 10T ,求该向量组的秩以及一个最大无关组，并将其余向量用该最大
无关组线性表示.
解：
1 1 3 5
1 1 3 5
1,
2,
3,
4
2 0
4 2
3 1
2 4
r2 2 r1
r4 2r1
0 0
6 2312Fra bibliotek1 4

福州大学至诚学院高等数学期末试卷B卷

福州⼤学⾄诚学院⾼等数学期末试卷B卷福州⼤学⾄诚学院期末考试试卷 2017—2018 学年第⼀学期考试⽇期： 2018 年 1 ⽉注意事项：答题前，考⽣在试卷及答题卡上务必⽤直径0.5毫⽶⿊⾊签字笔写上⾃⼰的姓名、准考证号等信息。

考⽣务必将答案抄到答题卡上，在试卷上作答⽆效。

考⽣务必在答题卡密封线内作答。

⼀、单项选择题(1-8题，每⼩题3分，共24分)1.设函数f(x)=xsinx，则f ′( π2)=( )A.1/2B. 1C.π/2D. 2π2. limx→∞(1+1x)2x=( )A. e?2B. e?1C. eD. e23.∫x2e x3dx=( )A.13x2e x3+C B. 3x2e x3+C C.13e x3+C D.3e x3+C4.设⼆元函数z=x2y+xsiny,则x=( )A.2xy+sinyB. x2+xcosyC.2xy+xsinyD.x2y+siny5.设球⾯⽅程(x?1)2+(y+2)2+(z+3)2=4,则该球⾯的球⼼坐标与半径分别为( )A.(-1,2,3);2B.(-1,2,-3);4C.(1,-2,-3);2 D(1,-2,3);36.已知f(x)在x0处可导，且f′(x0)= 2，则lim→0f(x0+2?)?f(x0)=( )A.2B. 1/2C.1D.47.⽅程(y ′)3+y ′′?y 4=x 是( )阶微分⽅程A.4B.3C.2D.1 8.设f(x)=x (x-1) (x-2) (x-3) (x-4) (x-5) ，则f ′(1)=( )A.24B.-24C.12D.-12⼆、填空题;(9-14 ⼩题，每⼩题4分,共24分) 9.设limx→0sin2x x=10.曲线y=√x 在点(1,1)处的切线⽅程是，法线⽅程是 11.设y= (2x 3+5)4,求y ′= 12. ∫sinx π0dx= 13.设z = x y ，则zx= ，z y ??=14.过点(1,0,1)且与平⾯x-y+2z+1=0 垂直的直线⽅程为三、解答题：15-21题，共52分15．(本题满分8分)设f (x )={ x 3 , x ≤1 ;ax +b, x ＞1 ;在x =1处连续且可导，求a ，b 的值16.(本题满分7分) 计算lim x→0x2e 1x 217（本题满分7分）求y=x cosx的导数18 （本题满分8分）求函数f(x)= x3?3x+2 的极值点与极值19（本题满分7分）计算∫(lnx)2xd x20.（本题满分7分）求微分⽅程y′′+2y′?3y=2e x的通解21（本题满分8分）dxdy其中，D是由直线 y=x、x=2与 y=0 所围成的区域。

XXX2017-2018学年第一学期期末考试高一数学试卷

XXX2017-2018学年第一学期期末考试高一数学试卷XXX2017-2018学年第一学期期末考试高一年级数学试卷第I卷(选择题共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知向量a=(2,1),b=(λ−1,2),若a+b与a−b共线,则λ=（）A.−2B.−1C.1D.2改写：向量a=(2,1)，向量b=(λ-1,2)，若a+b和a-b共线，则λ=（） A。

-2 B。

-1 C。

1 D。

22.已知3sinα+4cosα=2，则1-sinαcosα-cos2α的值是() A。

- B。

C。

-2 D。

2改写：已知3sinα+4cosα=2，求1-sinαcosα-cos2α的值，答案为() A。

- B。

C。

-2 D。

23.已知在△ABC中，AB=AC=1，BC=3，则AB·AC=() A。

1/33 B。

- C。

-2 D。

-改写：在△ABC中，AB=AC=1，BC=3，求XXX的值，答案为() A。

1/33 B。

- C。

-2 D。

-4.在△ABC中，若AB2=AB·AC+BA·BC+CA·CB，则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定改写：在△ABC中，如果AB2=AB·AC+BA·BC+CA·CB，则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定5.已知△ABC中，内角A,B,C所对边的边长分别为a,b,c,且c=7/11，a+b=22/3，XXX-tanA-tanB=3，则△ABC的面积为() A。

3/33 B。

- C。

3 D。

33/2改写：已知△ABC中，内角A,B,C所对边的边长分别为a,b,c，且c=7/11，a+b=22/3，XXX-tanB=3，求△ABC的面积，答案为() A。

3/33 B。

- C。

【5套打包】淄博市小学一年级数学上期末考试单元综合练习题及答案

人教版一年级数学上册期末试卷及答案一、填空题（共10题；共55分）1.按顺序填数：________，14，________ 16，________，________。

2.18由________个十和________个一组成。

3.9前面的第一个数是________，9后面的第一个数是________。

4.1个十和4个一组成的数是________。

________7.填“<”、“>"、“=”。

7________9 18________8 9________11 17-7________17-718-6________8 16________8+8 19-7________7+0 15-4________7+48.找规律填数。

（完整word版）小学数学一年级上册数学试卷可直接打印

（完整word版）⼩学数学⼀年级上册数学试卷可直接打印⼩学数学⼀年级上册数学试卷（时间：40分钟）⼀、计算：1、⼝算：24%7+7= 9+5= 3+13= 14+0+4=6－2= 0+10= 5+7= 13+5－2=15－3= 18－8= 19-0= 2+11－3=12+7= 2+13= 6+12= 17-10+8=16－6= 9+6= 8+7= 0+9+2=9－9= 6+8= 6+4= 11+3+2=⼆、填空：1、填数：8%2、概念：10%(1)个位上是0，⼗位上是2，这个数是（）。

20⾥⾯有（）个⼗。

(2)18⾥有（）个⼀和（）个⼗。

12⾥有（）个⼀。

(3)13这个数，⼗位上是（），个位上是（）。

(4)（）个⼀和（）个⼗合起来是17。

(5)10个⼀是（）。

3、○⾥填上>、<或=：8%20○8 5+7○8 4+4○18-18 19-2○11+312○13 10-4○13 8+4○9+8 2+3○9-8+144、在○⾥填上+或-：8%3○7=10 7○4=11 13○2=11 7○6=1314○5=19 0○9=9 14○14=0 ８○８=165、填□：8%□+7=19 □+5=8 □+4=12 □-3 < 49+□=18 16-□=12 8+□=10 9 < □+56、18、8、10三个数，写出四个算式：4%□+□=□□+□=□□-□=□□-□=□三、讲讲算算：16%1、和⑧共有17个2、红花10朵黄花6朵有5个 , ⑧有⼏个？红花和黄花⼀共有多少朵？__________________ __________________⼝答：⑧有_____个。

⼝答：红花和黄花⼀共有___朵。

3、停车场有14辆，开⾛了3辆4、△△△▲▲▲▲还剩⼏辆？△△△▲▲▲▲__________________ _________________⼝答：还剩____辆。

5、⼩军和⼩⽅⼀共剪了18颗星。

10北京市清华附中2017-2018学年高一上学期期末考试数学试卷 Word版含解析

北京市清华附中2017-2018学年第一学期高一期末数学试题一、选择题（本大题共8小题，共40.0分）1.下列各角中，与50°的角终边相同的角是（）A. B. C. D.【答案】D【解析】【分析】写出与50°的角终边相同的角的集合，取k＝﹣1得答案．【详解】与50°的角终边相同的角的集合为{α|α＝50°+k•360°，k∈Z}．取k＝﹣1，可得α＝﹣310°．∴与50°的角终边相同的角是﹣310°．故选：D．【点睛】本题考查终边相同角的概念，是基础题．2.设向量，则的夹角等于（）A. B. C. D.【答案】A【解析】试题分析：∵，∴，∴的夹角等于，故选A考点：本题考查了数量积的坐标运算点评：熟练运用数量积的概念及坐标运算求解夹角问题是解决此类问题的关键，属基础题3.已知角α的终边经过点P（4，-3），则的值为（）A. B. C. D.【答案】C【解析】【分析】利用任意角函数的定义求出cosα，利用三角函数的诱导公式化简求出值．【详解】∵角α的终边经过点P（4，﹣3），∴p到原点的距离为5∴sinα，cosα∴故选：C．【点睛】本题考查三角函数的定义，考查诱导公式，属于基础题.4.为了得到函数y=cos（2x-）的图象，只需将函数y=cos2x的图象（）A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】B【解析】【分析】由条件利用函数y＝A sin（ωx+φ）的图象变换规律可得结论．【详解】函数cos2（x），故把函数y＝cos2x的图象向右平移个单位长度，可得函数的图象，故选：B．【点睛】本题主要考查函数y＝A sin（ωx+φ）的图象变换规律，属于中档题．5.已知非零向量与满足=且，则△ABC为（）A. 三边均不相等的三角形B. 直角三角形C. 等腰非等边三角形D. 等边三角形【答案】D【解析】【分析】根据得出B＝C，得出A，由此判断△ABC是等边三角形．【详解】△ABC中，，∴，∴cos，cos，，∴B＝C，△ABC是等腰三角形；又，∴1×1×cos A，∴cos A，A，∴△ABC是等边三角形．故选：D．【点睛】本题考查了平面向量的数量积运算问题，也考查了三角形形状的判断问题，是基础题．6.同时具有性质“①最小正周期为π；②图象关于直线x=对称；③在[，]上是增函数”的一个函数是（）A. B.C. D.【答案】C【解析】【分析】根据三角函数的图象与性质，判断满足条件的函数即可．【详解】“①最小正周期是π，可得ω＝2，排除选项A；②图象关于直线x对称，可得：2，cos，排除选项B，2，cos，排除选项D；对于C，函数y＝sin（2x），最小正周期为π，且2，sin1，函数图象关于x对称；x∈[，]时，2x∈[，]，∴y＝sin（2x）是单调增函数，C满足条件．故选：C．【点睛】函数的性质(1) .(2)周期(3)由求对称轴(4)由求增区间;由求减区间.7.定义在R上的偶函数f（x）满足f（x+2）=f（x），且在[1，2]上是减函数，若α，β是锐角三角形的两个内角，则（）A. fB. fC. fD. f【答案】A【解析】【分析】根据题意，分析可得f（﹣x）＝f（x+2），即函数f（x）的图象关于直线x＝1对称，据此分析可得f（x）在区间[0，1]上是增函数，由α，β是锐角三角形的两个内角便可得出sinα＞cosβ，从而根据f（x）在（0，1）上是增函数即可得出f（sinα）＞f（cosβ），即可得答案．【详解】根据题意，定义在R上的偶函数f（x）满足f（x+2）＝f（x），则有f（﹣x）＝f（x+2），即函数f（x）的图象关于直线x＝1对称，又由函数f（x）在[1，2]上是减函数，则其在[0，1]上是增函数，若α，β是锐角三角形的两个内角，则α+β，则有αβ，则有sinα＞sin（β）＝cosβ，又由函数f（x）在[0，1]上是增函数，则f（sinα）＞f（cosβ）；故选：A．【点睛】本题考查函数的奇偶性、周期性与周期性的综合应用，注意分析函数在（0，1）上的单调性．8.若定义[-2018，2018]上的函数f（x）满足：对任意x1，x2∈[-2018，2018]有f（x1+x2）=f（x1）+f（x2）-2017，且当x＞0时，有f（x）＞2017，设f（x）的最大值、最小值分别为M，m，则M+m的值为（）A. 0B. 2018C. 4034D. 4036【答案】C【解析】【分析】计算f（0）＝2017，构造函数g（x）＝f（x）﹣2017，判断g（x）的奇偶性得出结论．【详解】令x1＝x2＝0得f（0）＝2f（0）﹣2017，∴f（0）＝2017，令x1＝﹣x2得f（0）＝f（﹣x2）+f（x2）﹣2017＝2017，∴f（﹣x2）+f（x2）＝4034，令g（x）＝f（x）﹣2017，则g max（x）＝M﹣2017，g min（x）＝m﹣2017，∵g（﹣x）+g（x）＝f（﹣x）+f（x）﹣4034＝0，∴g（x）是奇函数，∴g max（x）+g min（x）＝0，即M﹣2017+m﹣2017＝0，∴M+m＝4034．故选：C．【点睛】本题考查了奇偶性的判断与性质，考查函数的最值求法，注意运用赋值法，属于中档题．二、填空题（本大题共6小题，共30.0分）9.若θ为第四象限的角，且，则cosθ=______；sin2θ=______．【答案】(1). (2). -【解析】【分析】由已知利用同角三角函数基本关系式可求cosθ，进而利用二倍角的正弦函数公式可求sin2θ的值．【详解】∵θ为第四象限的角，且，∴cosθ，sin2θ＝2sinθcosθ＝2×（）．故答案为：，．【点睛】本题主要考查了同角三角函数基本关系式，二倍角的正弦函数公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．10.已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若，则△ABC的面积为______．【答案】【解析】【分析】利用三角形的内角和解出B，使用余弦定理解出c，代入三角形的面积公式计算．【详解】∵A+C＝2B，A+B+C＝π，∴B，由余弦定理得cos B，解得c＝2或c＝﹣1（舍）．∴S△ABC sin B．故答案为：．【点睛】本题考查了余弦定理在解三角形中的应用，三角形的面积公式，属于中档题．11.已知tanx=2，则cos2x+sin（π+x）cos（+x）=______【答案】【解析】【分析】利用诱导公式，同角三角函数的基本关系，求得cos2x+sin（π+x）cos（x）的值．【详解】∵tan x＝2，则cos2x+sin（π+x）cos（x）＝cos2x﹣sin x•（﹣sin x），故答案为：．【点睛】本题主要考查诱导公式，同角三角函数的基本关系，属于基础题．12.已知α∈（0，π）且sin（α+）=，则cos（α+）=______；sinα=______【答案】(1). (2).【解析】【分析】直接利用同角三角函数基本关系式求cos（α）；再由sinα＝sin[（）]，展开两角差的正弦求解．【详解】∵α∈（0，π），∴α∈（），又sin（α），∴cos（α）；则sinα＝sin[（）]＝sin（）cos cos（）sin．故答案为：；．【点睛】本题考查两角和与差的三角函数，考查同角三角函数基本关系式的应用，是基础题．13.如图，在直角梯形中，，若分别是线段和上的动点，则的取值范围是__________．【答案】【解析】以AB为x轴，BC为y轴建立直角坐标系，则A(-3,0),C(0,2),设F(0,m)，E(n，2)故=2m-3n-4，由图可知：，所以2m-3n-4点睛：对于向量问题，最容易解答的办法就是将问题的点转化为坐标求解写表达式，然后再根据题意范围求解结果14.已知函数f（x）=2sin2x-2sin2x-a．①若f（x）=0在x∈R上有解，则a的取值范围是______；②若x1，x2是函数y=f（x）在[0，]内的两个零点，则sin（x1+x2）=______【答案】(1). [，](2).【解析】【分析】①利用三角函数的公式化简，f（x）＝0在x∈R上有解，转化为两个函数图象有交点问题即可求解；②x1，x2是函数y＝f（x）在[0，]内的两个零点，即么x1，x2是关于在[0，]内的对称轴是对称的．即可求解【详解】f（x）＝2sin2x﹣2sin2x﹣a＝2sin2x﹣（1﹣cos2x）﹣a＝2sin2x+cos2x﹣1﹣a1﹣a．其中tanθ①f（x）＝0在x∈R上有解，则sin（2x+θ）＝a+1有解，∵∴a+1．则a的取值范围是[，]，故答案为：[，]②∵x1，x2是函数y＝f（x）在[0，]内的两个零点，那么x1，x2是关于在[0，]内的对称轴是对称的．由f（x）1﹣a．其中tanθ其对称轴2x+θkπ，k∈Z．x1，x2是关于在[0，]内的对称轴是对称的．又[0，]，且tanθ∴对称轴x∴x1+x2．则sin（x1+x2）＝sin（）＝cosθ．∵tanθ，即，∴cosθ，则sin（x1+x2）．故答案为：．【点睛】本题主要考查了三角函数的图象及性质的应用，同角三角函数间的基本关系式，属于中档题．三、解答题（本大题共6小题，共80.0分）15.已知函数f（x）=4sinxcos（x+）+1．（1）求f（）的值；（2）求f（x）的最小正周期；（3）求f（x）在区间[0，]上的最大值和最小值．【答案】（1）；（2）；（3）最小值为-1，最大值为2.【解析】【分析】（1）根据两角和的余弦公式、二倍角公式及辅助角公式将f（x）化简为f（x）＝2sin（2x），即可计算；（2）根据周期公式求解即可；（3）由x在[0，]上，求解内层函数的范围，结合三角函数的性质可得最值．【详解】函数f（x）=4sinx（cosxcos-sinxsin）+1，=2sinxcosx-2sin2x+1，=sin2x+cos2x，=2sin（2x+），（1）f（）=2sin（+）=2sin=（2）周期T=；（3）由x在[0，]上，∴2x+∈[，]，当2x+=，即x=，f（x）取得最小值为-1；当2x+=，即x=，f（x）取得最大值为2．【点睛】本题考查三角函数的恒等变换，三角函数的性质，属于中档题16.已知不共线向量，满足．（1）求；（2）是否存在实数λ，使与共线？（3）若，求实数k的值．【答案】（1）；（2）；（3）k=.【解析】【分析】（1）直接利用向量的数量积的应用求出结果；（2）利用向量的共线求出λ的值；（3）利用向量垂直的充要条件求出结果．【详解】（1）不共线向量，满足||=3，||=5，（ -3）•（2+）=20．所以：，解得：，所以：•（-）=．（2）存在实数使λ+与（-2）共线由于：λ+与（-2）共线故：，所以：．（3）若（k2）⊥（k-2），则：，整理得：，∴k=.【点睛】本题考查的知识要点：向量的数量积的应用，向量垂直和共线的充要条件的应用．17.设锐角三角形的内角A，B，C的对边分别为a、b、c，且sinA-cosC=cos（A-B）．（1）求B的大小；（2）求cosA+sinC的取值范围．【答案】（1）；（2）（，）.【解析】【分析】（1）利用诱导公式，两角和差的三角公式，化简所给的式子，求得sin B的值，可得B的值．（2）化简要求的式子sin（A），根据A∈（，），利用正弦函数的定义域和值域，求得cos A+sin C的取值范围．【详解】（1）设锐角三角形中，sinA-cosC=cos（A-B），即sinA+cos（A+B）=cos（A-B），即sinA+cosAcosB-sinAsinB=cosAcosB+sinAsinB，即sinA=2sinAsinB，,∴sinB=，锐角三角形中B=．（2）cosA+sinC=cosA+sin（π-A-B）=cosA+sin（-A）=cosA+sin（+A）=cosA+cosA+sinA=sin（A+）．∵B=，∴A∈（，），A+∈（，），∴sin（A+）∈（，），∴sin（A+）∈（，），即cosA+sinC的取值范围为（，）．【点睛】本题主要考查诱导公式，两角和差的三角公式，正弦函数的定义域和值域，属于中档题．18.已知向量=（cosθ，sinθ），=（cosβ，sinβ）．（1）若，求的值；（2）若记f（θ）=，θ∈[0，]．当1≤λ≤2时，求f（θ）的最小值．【答案】（1）1 ；（2）--1.【解析】【分析】（1）根据向量的坐标运算和向量的模以及两角和差即可求出答案；（2）根据向量的数量积和二倍角公式化简得到f（θ）＝2cos2（θ）﹣2λcos（θ）﹣1，令t＝cos（θ），根据二次函数的性质即可求出．【详解】（1）∵向量=（cosθ，sinθ），=（cosβ，sinβ），∴-=（cosθ-cosβ，sinθ-sinβ），∴|-|2=（cosθ-cosβ）2+（sinθ-sinβ）2=2-2cos（θ-β）=2-2cos=2-1=1，∴|-|=1；（2）•=cosθcosβ+sinθsinβ=cos（θ-β）=cos（2θ-），∴|+|==2|cos（θ-）|=2cos（θ-），∴f（θ）=cos（2θ-）-2λcos（θ-）=2cos2（θ-）-2λcos（θ-）-1令t=cos（θ-），则t∈[，1]，∴f（t）=2t2-2λt-1=2（t-）2--1，又1≤λ≤2，≤≤1，∴t=时，f（t）有最小值--1，∴f（θ）的最小值为--1．【点睛】本题考查了向量的坐标运算和向量的数量积以及三角函数的化简，以及二次函数的性质，属于中档题．19.借助计算机（器）作某些分段函数图象时，分段函数的表示有时可以利用函数，例如要表示分段函数g（x）=总可以将g（x）表示为g（x）=xh （x-2）+（-x）h（2-x）．（1）设f（x）=（x2-2x+3）h（x-1）+（1-x2）h（1-x），请把函数f（x）写成分段函数的形式；（2）已知G（x）=[（3a-1）x+4a]h（1-x）+log a x⋅h（x-1）是R上的减函数，求a的取值范围；（3）设F（x）=（x2+x-a+1）h（x-a）+（x2-x+a+1）h（a-x），求函数F（x）的最小值．【答案】（1）f（x）=；（2）≤a＜；（3）当a≤-时，最小值为-a+；当a≥时，最小值为为a+；当-＜a＜时，最小值为F（a）=a2+1．【解析】【分析】（1）分当x＞1、当x＝1和当x＜1时3种情况加以讨论，分别根据函数的对应法则代入，可得f（x）相应范围内的表达式，最后综合可得函数f（x）写成分段函数的形式；（2）运用分段函数形式表示G（x），再由一次函数、对数函数的单调性，可得a的范围；（3）由题意，讨论x＞a，x＝a，x＜a，求得F（x）的解析式，再结合二次函数的图象与性质，分a、a和a的4种情况进行讨论，最后综合可得F（x）的最小值．【详解】（1）当x＞1时，x-1＞0，1-x＜0，可得f（x）=（x2-2x+3）+0•（1-x2）=x2-2x+3；当x=1时，f（x）=2；当x＜1时，x-1＜0，1-x＞0，可得f（x）=1-x2．即有f（x）=；（2）G（x）=[（3a-1）x+4a]h（1-x）+log a x⋅h（x-1）=，由y=G（x）是R上的减函数，可得，解得≤a＜；（3）F（x）=（x2+x-a+1）h（x-a）+（x2-x+a+1）h（a-x），当x＞a时，x-a＞0，可得F（x）=x2+x-a+1；若a≥-，可得F（x）在x＞a递增，可得F（x）＞F（a）=a2+1；若a＜-，可得F（x）的最小值为F（-）=-a；当x=a时，可得F（x）=2（a2+1）；当x＜a时，x-a＜0，a-x＞0，则F（x）=x2-x+a+1．若a≥，可得F（x）在x＜a的最小值为F（）=a+；若a＜，可得F（x）在x＜a递减，即有F（x）＞F（a）=a2+1．①当a≥时，F（x）在区间（-∞，-）上单调递减，在区间（-，a）上单调递增，在区间（a，+∞）上单调递增，可得F（-）为最小值，且为-+a+1=a+；②当-＜a＜时，F（x）在区间（-∞，a）上单调递减，在区间（a，+∞）上单调递增．F（x）的最小值为F（a）=a2+1；③当a≤-时，在区间（-∞，a）上单调递减，在区间（a，-）上单调递减，在区间（-，+∞）上单调递增．所以F（x）的最小值为F（-）=-a+；综上所述，得当a≤-时，F（x）的最小值为-a+；当a≥时，F（x）的最小值为为a+；当-＜a＜时，F（x）的最小值为F（a）=a2+1．【点睛】本题以分段函数和含有字母参数的二次函数为载体，讨论函数的单调性与最小值，着重考查了基本初等函数的图象与性质、函数解析式的求解及常用方法和单调性的综合等知识，属于难题．20.一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“保三角形函数”．（1）判断f1（x）=x，f2（x）=log2（6+2sinx-cos2x）中，哪些是“保三角形函数”，哪些不是，并说明理由；（2）若函数g（x）=lnx（x∈[M，+∞））是“保三角形函数”，求M的最小值；（3）若函数h（x）=sinx（x∈（0，A））是“保三角形函数”，求A的最大值．【答案】（1）见解析；（2）2 ；（3）.【解析】【分析】（1）不妨设a≤c，b≤c，由函数的值域，即可得到结论；（2）要利用“保三角形函数”的概念，求M的最小值，首先证明当M≥2时，函数h（x）＝lnx （x∈[M，+∞））是保三角形函数，然后证明当0＜M＜2时，h（x）＝lnx（x∈[M，+∞））不是保三角形函数，从而求出所求；（3）A的最大值是，讨论①当A时；②当A时；结合新定义和三角函数的恒等变换，即可得到最大值．【详解】（1）不妨设a≤c，b≤c，由a+b＞c，可得f1（a）+f1（b）＞f1（c），即有f1（x）=x为“保三角形函数”；由6+2sinx-cos2x=sin2x+2sinx+5=（sinx+1）2+4∈[4，8]，可得f2（x）∈[2，3]，即有2+2＞3，可得f2（x）为“保三角形函数”；（2）M的最小值为2（i）首先证明当M≥2时，函数h（x）＝lnx（x∈[M，+∞））是保三角形函数．对任意一个三角形三边长a，b，c∈[M，+∞），且a+b＞c，b+c＞a，c+a＞b，则h（a）＝lna，h（b）＝lnb，h（c）＝lnc．因为a≥2，b≥2，a+b＞c，所以（a﹣1）（b﹣1）≥1，所以ab≥a+b＞c，所以lnab＞lnc，即lna+lnb＞lnc．同理可证明lnb+lnc＞lna，lnc+lna＞lnb．所以lna，lnb，lnc是一个三角形的三边长．故函数h（x）＝lnx（x∈[M，+∞），M≥2），是保三角形函数…13分（ii）其次证明当0＜M＜2时，h（x）＝lnx（x∈[M，+∞））不是保三角形函数，h（x）＝lnx （x∈[M，+∞））不是保三角形函数因为0＜M＜2，所以M+M＝2M＞M2，所以M，M，M2是某个三角形的三条边长，而lnM+lnM＝2lnM＝lnM2，所以lnM，lnM，lnM2不能为某个三角形的三边长，所以h（x）＝lnx不是保三角形函数．所以，当M＜2时，h（x）＝lnx（x∈[M，+∞））不是保三角形函数．综上所述：M的最小值为2（3）A的最大值是．①当A＞时，取a==b，c=，显然这3个数属于区间（0，A），且可以作为某个三角形的三边长，但这3个数的正弦值、、1显然不能作为任何一个三角形的三边，故此时，h（x）=sinx，x∈（0，A）不是保三角形函数．②当A=时，对于任意的三角形的三边长a、b、c∈（0，），若a+b+c≥2π，则a≥2π-b-c＞2π--=，即a＞，同理可得b＞，c＞，∴a、b、c∈（，），∴sina、sinb、sinc∈（，1]．由此可得sina+sinb＞+=1≥sinc，即sina +sinb＞sinc，同理可得sina+sinc＞sinb，sinb+sinc＞sina，故sina、sinb、sinc 可以作为一个三角形的三边长．若a+b+c＜2π，则+＜π，当≤时，由于a+b＞c，∴0＜＜≤，∴0＜sin＜sin≤1．当＞时，由于a+b＞c，∴0＜＜＜，∴0＜sin＜sin＜1．综上可得，0＜sin＜sin≤1．再由|a-b|＜c＜，以及y=cosx在（ 0，π）上是减函数，可得cos=cos＞cos＞cos＞0，∴sina+sinb=2sin cos＞2sin cos=sinc，同理可得sina+sinc＞sinb，sinb+sinc＞sina，故sina、sinb、sinc 可以作为一个三角形的三边长．故当A=时，h（x）=sinx，x∈（0，A）是保三角形函数，故A的最大值为．【点睛】要想判断f（x）为“保三角形函数”，要经过严密的论证说明f（x）满足“保三角形函数”的概念，但要判断f（x）不为“保三角形函数”，仅须要举出一个反例即可，属于创新题．。

福州市2017-2018学年第一学期高三期末考试文科数学试卷(有答案)

福州市2017-2018学年第一学期高三期末考试文科数学试卷(有答案)福州市2017-2018学年第一学期高三期末考试文科数学试卷（有答案）本试题卷共23题，分为第I卷和第II卷，共计150分，考试时间120分钟。

第I卷一、选择题（共12小题，每小题5分，共60分）1.已知集合A={x(x-6)(x+1)0}，则A∩B=（C）。

2.若复数z=a1为纯虚数，则实数a=（B）。

3.已知a=(12)，b=(-1,1)，c=2a-b，则|c|=（B）。

4.3cos15°-4sin215°cos15°=（D）。

5.已知双曲线C的两个焦点F1F2都在x轴上，对称中心为原点，离心率为3，若点M在C 上，且MF1MF2M到原点的距离为3，则C的方程为（C）。

6.已知圆柱的高为2，底面半径为3，若该圆柱的两个底面的圆周都在同一个球面上，则这个球的表面积等于（B）。

7.右面的程序框图的算法思路源于我国古代著名的《孙子剩余定理》。

图中的Mod(N,m)=n表示正整数N除以正整数m后的余数为n，例如Mod(10,3)=1.执行该程序框图，则输出的i等于（C）。

8.将函数y=2sinx+cosx的图象向右平移1个周期后，所得图象对应的函数为（D）。

二、填空题（共3小题，每小题10分，共30分）9.已知函数y=ln(1-x)，则y''=（B）。

10.已知函数f(x)=x+sinx，则f'(π)的值为（C）。

11.已知函数f(x)=x+sinx，则f(x)在[0,π]上的最小值为（A）。

三、解答题（共8小题，每小题10分，共80分）12.解方程log2(x+1)+log2(x-1)=1.13.已知函数f(x)=x^3-3x^2+2x+1，求f(x)的单调递减区间。

14.已知函数f(x)=x^3-3x^2+2x+1，求f(x)的极值和极值点。

15.已知函数f(x)=x^3-3x^2+2x+1，求f(x)的图象在点(1,1)处的切线方程。

2017级第一学期数学试题

2017级第一学期期末考试数学试卷注意事项：1、考试时间：90分钟2、请首先按要求在试卷的标封处填写姓名、身份证号码。

3、请仔细阅读各种题目的回答要求，在规定的位置填写答案。

4、不要在试卷上乱写乱画，不要在标封区填写无关内容。

一、填空题（10X2=20）（1）不等式|X+2|≧0的解集为。

（2）已知A={1，2，3，4，5，6}，B={2，5，6}，则A ∩B= 。

（3）已知全集U={1，2，3，4，5}，A={1，2，3}，则CuA= 。

（4）已知集合M={a,0},N={1,2}，M ∩N={1}，则a= 。

（5）设A=（-5，4），B=[1,8]，则A ∪B= 。

（6）集合{X|X ≧-2}用区间表示为。

（7）设A=（-1、3]，B=[3、6），求A ∩B= 。

（8）集合{X|-2<X ≦3}用区间表示为。

（9）不等式|3X|<4的解集用区间表示为。

（10）△ABC 的每一个内角都是60° △ABC 为等边三角形。

用（⇔⇐⇒,,）填空二、选择题（20X20=40）1、下列对象能组成集合的是（）A 、大于5的自然数B 、一切很大的数C 、班上个子很高的同学D 、班上考试得分很高的同学 2、绝对值等于3 的所有整数组成的集合是（） A 、3 B 、{3，-3} C 、{3} D 、3，-33、不等式|X+3|≧0的解集为（）A 、∅B 、{-3}C 、（-∞、-3）∪（-3、+∞）D 、R 4、不等式|X+1|<1的解集是（） A 、[-2、0） B 、（-2、0） C 、（-∞、-2）∪（0、+∞） D 、R5、设x,y 为定数,则x 2=y 2的充要条件是( )A,x=y B,x=-y C,x 3=y 3D,｜x ｜=｜y ｜6、设全集u={0,1,2,3,4,5,6,7},A={2，3，4，5，6}则CuA=( ) A 、{0，2，3，4，5，6，} B 、{2，3，4，5，6} C 、{0，1，7} D 、∅7、不等式|X-1|<3的解集为（）A 、[-2、4]B 、（-2、4）C 、（-∞、-2）∪（4、+∞）D 、R 8、设A=（2、5），B=[3、6），则A ∩B=（） A 、（2、5） B 、[3、6） C 、（3、5） D 、[3、5） 9、不等式|X+2|>2的解集为（） A 、∅ B 、（0、+∞） C 、（-∞、-4）∪（0、+∞） D 、R10、 x 2+6x+( )=(x+3)2A 、6B 、8C 、9D 、1011、设全集为R ，若C A =(-1、+∞)，则A=（） A 、[-1、+∞) B 、( -∞、-1] C 、（-∞、-1）D 、（-1、-∞） 12、不等式-2X<10的解集是（） A 、[-2、5] B 、（5、+∞） C 、（-∞、-2）∪（5、+∞） D 、（-5、+∞）13、下列集合中不是集合{1，2，3}的真子集是（） A 、{1，2，3} B 、{1、2} C 、{2、3} D 、φ 14、集合{1，2}的子集有（）个。

人教版2017~2018学年度初三第一学期期末考试数学试题附详细答案

E D CBA2017-2018学年第一学期期末测试卷初三数学一、选择题（本题共30分，每小题3分）1．⊙O 的半径为R ，点P 到圆心O 的距离为d ，并且d ≥ R ，则P 点 A.在⊙O 内或圆周上 B.在⊙O 外C.在圆周上D.在⊙O 外或圆周上2. 把10cm 长的线段进行黄金分割，则较长线段的长（236.25≈, 精确到0.01）是A ．3.09cmB ．3.82cmC ．6.18cmD ．7.00cm 3．如图，在△ABC 中，DE ∥BC ，DE 分别与AB 、AC 相交于点D 、E ，若AD =4，DB =2，则AE ︰EC 的值为 A . 0.5 B . 2 C . 32 D . 23 4. 反比例函数xky =的图象如图所示,则K 的值可能是 A .21B . 1C . 2D . -1 5. 在Rt △ABC 中，∠C =90°，BC =1，那么AB 的长为A ．sin AB ．cos AC ．1cos AD ． 1sin A6．如图，正三角形ABC 内接于⊙O ，动点P 在圆周的劣弧AB 上，且不与A,B 重合，则∠BPC 等于A .30︒B .60︒ C. 90︒ D. 45︒ 7．抛物线y=21x 2的图象向左平移2个单位，在向下平移1个单位，得到的函数表达式为 A . y =21x 2+ 2x + 1 B ．y =21x 2+ 2x - 2C . y =21x 2 - 2x - 1 D. y =21x 2- 2x + 18. 已知二次函数)0(2≠++=a c bx ax y 的图象如图所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ； ④ b c 32<； ⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有 A. 2个 B. 3个C. 4个D. 5个9. 如图所示，在正方形ABCD 中，E 是BC 的中点，F 是CD 上的一点，AE ⊥EF ，下列结论：①∠BAE ＝30°；②CE 2＝AB·CF ；③CF ＝31FD ；④△ABE ∽△AEF .其中正确的有A. 1个B. 2个C. 3个D. 4个10．如图，已知△ABC 中，BC =8，BC 边上的高h =4，D 为BC 边上一个动点，EF ∥BC ，交AB 于点E ，交AC 于点F ，设E 到BC 的距离为x ，△DEF 的面积为y ，则y 关于x 的函数图象大致为A. B. C. D.二、填空题（本题共18分, 每小题3分） 11．若5127==b a ，则32ba -= ． 12. 两个相似多边形相似比为1:2,且它们的周长和为90,则这两个相似多边形的周长分别是 , ． 13.已知扇形的面积为15πcm 2,半径长为5cm ,则扇形周长为 cm ．14. 在Rt △ABC 中，∠C =90°，AC =4, BC =3,则以2.5为半径的⊙C 与直线AB 的位置关系是．15. 请选择一组你喜欢的a,b,c 的值，使二次函数)0(2≠++=a c bx ax y 的图象同时满16. 点是 17.18.如图：在Rt△ABC中，∠C=90°，BC=8，∠B=60°, 解直角三角形.19.已知反比例函数x 1k y -=图象的两个分支分别位于第一、第三象限．（1）求k的取值范围；（2）取一个你认为符合条件的K值，写出反比例函数的表达式，并求出当x=﹣6时反比例函数y的值；20.已知圆内接正三角形边心距为2cm，求它的边长.24.密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物，是美国最高的独自挺立的纪念碑，如图．拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，求拱门的最大高度．25. 如图，已知⊙O 是△ABC 的外接圆，AB 是⊙O 的直径， D 是AB 的延长线上的一点，AE ⊥DC 交DC 的延长线于点E ，且AC 平分∠EAB ．求证：DE 是⊙O 的切线．26. 已知：抛物线y=x 2+bx+c 经过点（2，-3）和（4，5）（1）求抛物线的表达式及顶点坐标；（2）将抛物线沿x 轴翻折，得到图象G ，求图象G 的表达式；（3）在（2）的条件下，当-2<x <2时，直线y =m 与该图象有一个公共点，求m 的值或取值范围.27. 如图，已知矩形ABCD 的边长3cm 6cm AB BC ==，．某一时刻，动点M 从A 点出发沿AB 方向以1c m /s 的速度向B 点匀速运动；同时，动点N 从D 点出发沿DA 方向以2c m /s 的速度向A 点匀速运动，问：（1）经过多少时间，AMN △的面积等于矩形ABCD 面积的19？（2）是否存在时刻t ，使以A,M,N 为顶点的三角形与ACD △相似？若存在，求t 的值；若不存在，请说明理由．()28.（1）探究新知：如图1，已知△ABC 与△ABD 的面积相等，试判断AB 与CD 的位置关系，并说明理由．（2）结论应用：① 如图2，点M ，N 在反比例函数xky =（k ＞0）的图象上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，垂足分别为E ，F ．试证明：MN ∥EF ．② 若①中的其他条件不变，只改变点M ，N 的位置如图3所示，请判断 MN 与 EF 是否平行？请说明理由.29. 设a ,b 是任意两个不等实数，我们规定：满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间，表示为[a ,b ]．对于一个函数，如果它的自变量x 与函数值y 满足：当m ≤x ≤n 时，有m ≤y ≤n ,我们就称此函数是闭区间[m .n ]上的“闭函数”．如函数4y x =-+，当x =1时，y =3；当x =3时，y =1，即当13x ≤≤时，有13y ≤≤，所以说函数4y x =-+是闭区间[1,3]上的“闭函数”．（1）反比例函数y =x 2016是闭区间[1,2016]上的“闭函数”吗？请判断并说明理由；（2）若二次函数y =22x x k --是闭区间[1,2]上的“闭函数”，求k 的值；（3）若一次函数y =kx +b (k ≠0)是闭区间[m ,n ]上的“闭函数”，求此函数的表达式（用含 m ，n 的代数式表示）．图 3一、选择题：（本题共30分，每小题3分）二、填空题（本题共18分, 每小题3分）三、计算题：（本题共72分，第17—26题，每小题5分，第27题7分，第28题7分，第29题8分）17. 4sin 304560︒︒︒．解：原式=33222214⨯+⨯-⨯--------------------- 4分 =2-1+3 =4--------------------- 5分18. 解：∵在Rt △ABC 中，∠C =90°，∠B =60°∵∠A=90°-∠B =30°--------------------- 1分∴AB==16--------------------- 3分∴AC=BCtanB=8．--------------------- 5分19. 解：（1）∵反比例函数图象两支分别位于第一、三象限，∴k ﹣1＞0，解得：k ＞1；---------------- 2分（2）取k=3，∴反比例函数表达式为x2y = ---------------- 4分当x=﹣6时，3162x 2y -=-==；---------------------5分（答案不唯一）20. 解: 如图:连接OB,过O 点作OD ⊥BC 于点D ---------------- 1分在Rt △OBD 中,∵∠BOD =︒︒=606360---------------- 2分 ∵ BD=OD ·tan60°---------------- 3分 =23---------------- 4分 ∴BC=2BD=43∴三角形的边长为43 cm ---------------- 5分B21.证明∵△ABC ∽△ADE ，∴∠BAC ＝∠DAE ，∠C ＝∠E ，---------------- 1分 ∴∠BAC －∠DAC ＝∠DAE －∠DAC ，∴∠1＝∠3， ------------------------------ 2分又∵∠C ＝∠E ，∠DOC ＝∠AOE ，∴△DOC ∽△AOE ，----------------------------3分 ∴∠2＝∠3 ， ----------------------------4分 ∴∠1＝∠2＝∠3． ----------------------------5分22. 解：过P 作PD ⊥AB 于D ，---------------- 1分在Rt △PBD 中，∠BDP ＝90°，∠B ＝45°， ∴BD ＝PD ． ---------------- 2分在Rt △PAD 中，∠ADP ＝90°，∠A ＝30°， ∴AD ＝PD ＝PD＝3PD ，--------------------3分 ∴PD ＝13100+≈36.6＞35，故计划修筑的高速公路不会穿过保护区．----------------------------5分23.解：（1）不同类型的正确结论有：①BE=CE ；②BD=CD ；③∠BED=90°；④∠BOD=∠A ；⑤AC//OD ；⑥AC ⊥BC ；⑦222OE +BE =OB ；⑧OE BC S ABC ∙=∆；⑨△BOD 是等腰三角形；⑩ΔBOE ΔBAC ~；等等。

湖南四大名校内部资料高一年级数学长郡高一2017—2018—1期末数学考试试卷

长郡中学20182017-学年度高一第一学期期末考试数学命题人：肖伟军审题人：曾卫国时量：120分钟满分：100分得分：一、选择题（本大题共15个小题，每小题3分，共45分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1. 设集合{}3,1=A ，集合{}5,4,2,1=B ，则集合=B A （） A. {}5,4,2,1,3,1 B. {}1 C. {}5,4,3,2,1 D. {}5,4,3,2 2. 已知3tan -=α，παπ<<2，则αsin 的值为（）A.21 B. 23 C. 21- D. 23-3.4=3=，且a 与b 不共线，若向量b k a +与b k a -互相垂直，则k 的值为（）A. 34±B. 43± C. 332± D. 23±4，如果奇函数()x f 在区间[]8,2上是减函数且最小值为6，则()x f 在区间[]2,8--上是（） A. 增函数且最小值为6- B. 增函数且最大值为6-C. 减函数且最小值为6-D. 减函数且最大值为6- 5. 方程0732=-+x x的解所在的区间为（）A. ()0,1-B. ()1,0C. ()2,1D. ()3,26. ABC ∆中，内角A ，B ，C 所对边的长分别是a ，b ，c ，若ab b c a =+-222，则=C （） A. ︒30 B. ︒60 C. ︒120 D. ︒60或︒120 7. ABC ∆中，内角A ，B ，C 所对边的长分别是a ，b ，c ，若abB A =cos cos ，则ABC ∆为（） A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰三角形或直角三角形8. 已知集合⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<⎪⎭⎫ ⎝⎛=--12162x x x A ，(){}1log 4<+=a x x B ，若φ=B A ，则实数a 的取值范围为（）A. 21<<aB. 21≤≤aC. φD. 21≤<a9. 设α是第二象限角，()4,x P 为其终边上的一点，且x 51cos =α，则=αtan （） A. 34 B. 43 C. 43- D. 34-10. 化简()()()()()⎪⎭⎫⎝⎛+----⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛++-απαπαπαπαπαπαπαπ29sin sin 3sin cos 211cos 2cos cos 2sin 的结果为（）A. αtan -B. αtanC. αtan 1-D. αtan 111. 先把函数()⎪⎭⎫⎝⎛-=6sin πx x f 的图象上各点的横坐标变为原来的21（纵坐标不变），再把新得到的图象向右平移3π个单位，得到()x g y =的图象，当⎥⎦⎤⎢⎣⎡∈43,4ππx 时，函数()x g 的值域为（） A. ⎥⎦⎤⎢⎣⎡-1,23 B. ⎥⎦⎤⎢⎣⎡-1,21 C. ⎥⎦⎤⎢⎣⎡-23,23 D. [)0,1- 12. 设()x f 是定义在R 上的周期为2的偶函数，已知[]3,2∈x 时，()x x f =，则[]0,2-∈x 时，()x f 的解析式为（）A. ()4+=x x fB. ()x x f -=2C. ()13+-=x x fD. ()12+-=x x f 13. 若函数()x x x f ωωcos 3sin -=，R x ∈，又()21=x f ，()02=x f ，且21x x -的最小值为23π，则ω的的值为（） A.31 B. 32 C. 34D. 2 14. 如图，正三角形ABC 的中心位于点()1,0G ，()2,0A ，动点P 从点A 出发沿ABC ∆的边界按逆时针方向运动，设x AGP =∠（π20≤≤x ），向量OP 在()0,1=a 方向上的射影为y （O 为坐标原点），则y 关于x 的函数()x f y =的图象大致为（）A. B.C. D.15. 已知定义在R 上的奇函数()x f ，当0>x 时，()()⎪⎩⎪⎨⎧>-≤<-=-2,22120,121x x f x x f x ，则关于x 的方程()[]()0162=--x f x f 的实根个数为（）A. 6B. 7C. 8D. 9二、填空题（本大题共5小题，每小题3分，共15分，把答案填写在题中的横线上.） 16. =++05lg 2lg π ； 17. 已知3tan =α，则=+-ααααsin 3cos cos sin 2 ；18. 已知向量a ，b2=，a 与b 的夹角为︒60，则b 在a 上的投影是；19. 若函数()322--=kx x x f 在区间[]4,2-上具有单调性，则实数k 的取值范围是；20. 在ABC ∆中，9=⋅AC AB ，C A B sin cos sin ⋅=，6=∆ABC S ，P 为线段AB上一点，且CB y CA x CP +=yx 11+的最小值为 .三、解答题（本大题共5小题，每小题8分，共40分，要求写出必要的文字说明、证明过程或演算步骤.）21. （小题满分8分）已知集合()(){}023≤-+=x x x A ，{}41≤≤=x x B . （1）求B A ；（2）求()B A C R .22. （本小题满分8分）设ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，且3cos sin =Ba Ab .（1）求角B 的大小；（2）若32=b ，A C sin 2sin =，求a ，c 的值.23. （本小题满分8分）已知函数()23cos cos sin 32+-=x x x x f . （1）求()x f 的单调递增区间；（2）若角α，β的终边不共线，且()()βαf f =，求()βα+tan 的值.24. （本小题满分8分）已知向量()ααsin ,cos =a ，()ββsin ,cos =b 552=. （1）求()βα-cos ；（2）若20πα<<，02<<-βπ，且135sin -=β，求αsin .25. （本小题满分8分）已知二次函数()x x x f +=2，若不等式()()x x f x f 2≤+-的解集为C .（1）求集合C ；（2）若函数()()111--=+x xaa f x g （0>a 且1≠a ）在集合C 上存在零点，求实数a 的取值范围.。

2017-2018学年第一学期期末考试一年级数学试卷

高一数学期末(A卷)-答案

人教版小学一年级上册数学期末测试卷精品(历年真题)

【5套打包】济宁市小学一年级数学上期末考试单元测试卷(含答案)(1)

2017--2018学年度第一学期期末测评小学一年级数学试卷

2017-2018学年度第一学期期中质量检测一年级数学试卷及答案

河南省新乡市一中 2017-2018学年上期初一年级第一次月考数学试卷无答案

复旦大学《线性代数I》2017-2018学年第一学期期末考试试卷A卷

福州大学至诚学院高等数学期末试卷B卷

XXX2017-2018学年第一学期期末考试高一数学试卷

【5套打包】淄博市小学一年级数学上期末考试单元综合练习题及答案

（完整word版）小学数学一年级上册数学试卷可直接打印

10北京市清华附中2017-2018学年高一上学期期末考试数学试卷 Word版含解析

福州市2017-2018学年第一学期高三期末考试文科数学试卷(有答案)

2017级第一学期数学试题

人教版2017~2018学年度初三第一学期期末考试数学试题附详细答案

湖南四大名校内部资料高一年级数学长郡高一2017—2018—1期末数学考试试卷

最新人教版小学一年级上册数学黄冈真题考卷20200120