公式汇总(word版)
(完整word版)最全小学数学公式大全(最新版)

最全小学数学公式大全一、小学数学几何形体周长面积体积计算公式:长方形的周长=(长+宽)×2 C=(a+b)×2正方形的周长=边长×4 C=4a长方形的面积=长×宽S=ab正方形的面积=边长×边长S=a.a= a三角形的面积=底×高÷2 S=ah÷2平行四边形的面积=底×高S=ah梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2直径=半径×2 d=2r 半径=直径÷2 r= d÷2圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr圆的面积=圆周率×半径×半径三角形的面积=底×高÷2。
公式S= a×h÷2正方形的面积=边长×边长公式S= a×a长方形的面积=长×宽公式S= a×b平行四边形的面积=底×高公式S= a×h梯形的面积=(上底+下底)×高÷2 公式S=(a+b)h÷2内角和:三角形的内角和=180度。
长方体的体积=长×宽×高公式:V=abh长方体(或正方体)的体积=底面积×高公式:V=abh正方体的体积=棱长×棱长×棱长公式:V=aaa圆的周长=直径×π 公式:L=πd=2πr圆的面积=半径×半径×π 公式:S=πr2圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
(完整word版)小、初、高中数学公式大全

目录一、初中代数 (2)二、高中代数 (5)2.1、函数 (5)2.1.1不等式 (9)2.1.1数列 (11)2.1.1三角函数 (12)2.1.1复数 (15)2.2排列、组合 (16)2.3平面几何 (18)2.3.1直线与角 (18)2.3.2三角形 (19)2.4立体几何 (20)2.4.1直线与平面 (20)2.4.2多面体、棱柱、棱锥 (23)2.5解析几何 (24)2.5.1方程与曲线 (24)2.5.2直线 (25)2.5.3圆 (27)2.5.4椭圆 (28)2.5.5双曲线 (28)2.5抛物线 (30)2.6向量部分 (31)2.6.1空间向量 (31)2.6.2平面向量 (32)三、常用公式 (33)3.1常用公式 (33)3.2几何图形及计算公式 (35)四、坐标几何和二维、三维图形 (38)4.1坐标几何 (38)4.2二维图形 (40)4.3三维图形 (41)小学数学公式大全1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径 S=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积 =长×宽×高 V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高 V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷319、长方体(正方体、圆柱体)的体1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、 1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数目录一、初中代数 (4)二、高中代数 (7)2.1、函数 (7)2.1.1不等式 (11)2.1.1数列 (13)2.1.1三角函数 (14)2.1.1复数 (17)2.2排列、组合 (18)2.3平面几何 (20)2.3.1直线与角 (20)2.3.2三角形 (21)2.4立体几何 (22)2.4.1直线与平面 (22)2.4.2多面体、棱柱、棱锥 (25)2.5解析几何 (26)2.5.1方程与曲线 (26)2.5.2直线 (27)2.5.3圆 (29)2.5.4椭圆 (30)2.5.5双曲线 (30)2.5抛物线 (32)2.6向量部分 (33)2.6.1空间向量 (33)2.6.2平面向量 (34)三、常用公式 (35)3.1常用公式 (35)3.2几何图形及计算公式 (37)四、坐标几何和二维、三维图形 (40)4.1坐标几何 (40)4.2二维图形 (42)4.3三维图形 (43)一、初中代数二、高中代数2.1、函数,2.1.1不等式2.1.1数列名称定义通项公式前n项的和公式其它数列按照一定次序排成一列的数叫做数列,记为{an}如果一个数列{an}的第n项an与n之间的关系可以用一个公式来表示,这个公式就叫这个数列的通项公式等差数列等比数列数列前n项和与通项的关系:无穷等比数列所有项的和:数学归纳法适用范围证明步骤注意事项只适用于证明与自然数n有关的数学命题设P(n)是关于自然n的一个命题,如果(1)当n取第一个值n0(例如:n=1或n=2)时,命题成立(2)假设n=k时,命题成立,由此推出n=k+1时成立。
(完整word版)高中必背88个数学公式

高中必背88个数学公式——圆的公式1、圆体积=4/3(π)(r^3)2、面积=(π)(r^2)3、周长=2(π)r4、圆的标准方程(x-a)2+(y-b)2=r2【(a,b)是圆心坐标】5、圆的一般方程x2+y2+dx+ey+f=0【d2+e2-4f>0】高中必背88个数学公式——椭圆公式1、椭圆周长公式:l=2πb+4(a-b)2、椭圆周长定理:椭圆的周长等于该椭圆短半轴,长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差.3、椭圆面积公式:s=πab4、椭圆面积定理:椭圆的面积等于圆周率(π)乘该椭圆长半轴长(a)与短半轴长(b)的乘积。
以上椭圆周长、面积公式中虽然没有出现椭圆周率t,但这两个公式都是通过椭圆周率t推导演变而来。
高中必背88个数学公式——两角和公式1、sin(a+b)=sinacosb+cosasinbsin(a-b)=sinacosb-sinbcosa2、cos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinb3、tan(a+b)=(tana+tanb)/(1-tanatanb)tan(a-b)=(tana-tanb)/(1+tanatanb)4、ctg(a+b)=(ctgactgb-1)/(ctgb+ctga)ctg(a-b)=(ctgactgb+1)/(ctgb-ctga)高中必背88个数学公式——倍角公式1、tan2a=2tana/(1-tan2a)ctg2a=(ctg2a-1)/2ctga2、cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a高中必背88个数学公式——半角公式1、sin(a/2)=√((1-cosa)/2)sin(a/2)=-√((1-cosa)/2)2、cos(a/2)=√((1+cosa)/2)cos(a/2)=-√((1+cosa)/2)3、tan(a/2)=√((1-cosa)/((1+cosa))tan(a/2)=-√((1-cosa)/((1+cosa))4、ctg(a/2)=√((1+cosa)/((1-cosa))ctg(a/2)=-√((1+cosa)/((1-cosa))高中必背88个数学公式——和差化积1、2sinacosb=sin(a+b)+sin(a-b)2cosasinb=sin(a+b)-sin(a-b)2、2cosacosb=cos(a+b)-sin(a-b)-2sinasinb=cos(a+b)-cos(a-b)3、sina+sinb=2sin((a+b)/2)cos((a-b)/2cosa+cosb=2cos((a+b)/2)sin((a-b)/2)4、tana+tanb=sin(a+b)/cosacosbtana-tanb=sin(a-b)/cosacosb5、ctga+ctgbsin(a+b)/sinasinb-ctga+ctgbsin(a+b)/sinasinb高中必背88个数学公式——等差数列1、等差数列的通项公式为:an=a1+(n-1)d (1)2、前n项和公式为:Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2(2)从(1)式可以看出,an是n的一次数函(d≠0)或常数函数(d=0),(n,an)排在一条直线上,由(2)式知,Sn是n的二次函数(d≠0)或一次函数(d=0,a1≠0),且常数项为0.在等差数列中,等差中项:一般设为Ar,Am+An=2Ar,所以Ar为Am,An的等差中项.且任意两项am,an的关系为:an=am+(n-m)d它可以看作等差数列广义的通项公式.3、从等差数列的定义、通项公式,前n项和公式还可推出:a1+an=a2+an-1=a3+an-2=…=ak+an-k+1,k∈{1,2,…,n}若m,n,p,q∈N*,且m+n=p+q,则有am+an=ap+aqSm-1=(2n-1)an,S2n+1=(2n+1)an+1Sk,S2k-Sk,S3k-S2k,…,Snk-S(n-1)k…或等差数列,等等.和=(首项+末项)*项数÷2项数=(末项-首项)÷公差+1首项=2和÷项数-末项末项=2和÷项数-首项项数=(末项-首项)/公差+1高中必背88个数学公式——等比数列1、等比数列的通项公式是:An=A1*q^(n-1)2、前n项和公式是:Sn=[A1(1-q^n)]/(1-q)且任意两项am,an的关系为an=am·q^(n-m)3、从等比数列的定义、通项公式、前n项和公式可以推出:a1·an=a2·an-1=a3·an-2=…=ak·an-k+1,k∈{1,2,…,n}4、若m,n,p,q∈N*,则有:ap·aq=am·an,等比中项:aq·ap=2ar ar则为ap,aq等比中项.记πn=a1·a2…an,则有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1另外,一个各项均为正数的等比数列各项取同底数数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列.在这个意义下,我们说:一个正项等比数列与等差数列是“同构”的.性质:①若m、n、p、q∈N,且m+n=p+q,则am·an=ap*aq;②在等比数列中,依次每k项之和仍成等比数列.“G是a、b的等比中项”“G^2=ab(G≠0)”.在等比数列中,首项A1与公比q都不为零.高中必背88个数学公式——抛物线1、抛物线:y=ax*+bx+c就是y等于ax的平方加上bx再加上c。
数学公式大全(word版-)

高等数学公式导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin ududx x tg u u u x u u x +==+-=+=, , , 一些初等函数: 两个重要极限:ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(μμμxxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxx x x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑ΛΛΛ中值定理与导数应用:拉格朗日中值定理。
(完整word版)八九年级物理公式汇总

八九年级物理公式 班别 姓名一、八年级物理公式1.速度:v =ts 2.密度:V m =ρ3.重力:G =mg4.压强:p=SF 5.液体的压强:p=ρ液g h (此公式也适合竖直放置的柱形固体)6.物体沉浮条件:漂浮:ρ物<ρ液 G 物=F 浮上浮:ρ物<ρ液 G 物<F 浮 悬浮:ρ物=ρ液 G 物=F 浮 下沉(沉底):ρ物>ρ液 G 物>F 浮7.浮力的计算:原因法:F 浮=F 向上—F 向下原理法:F 浮=G 排=ρ液gV 排平衡法:F 浮=G 物(只适合漂浮和悬浮)称量法:在上面拉物体:F 浮=G 物—F 拉在下面拉物体:F 浮=G 物 + F 拉8.功:W=Fs=Gh 9.功率:P=tW=Fv 10.杠杆平衡条件:F 1L1=F 2L2 11.机械效率:η=总有W W滑轮组的机械效率:η=总有W W =nF G Fs h G 物=物=动有有W W W +=动物物G G G +斜面的机械效率:η=Fsh G 物 12.滑轮组绳子自由端的拉力F 与物体重G 物、动滑轮重G 动的关系:(下面的n 为拉着动滑轮的绳子数)考虑动滑轮重但不计摩擦时:F=nG G 动物+13.滑轮组绳子自由端移动的距离s 与物体提升高度h 的关系:s=n h 14.斜面:Gh =FL (不计摩擦)二、九年级物理公式1. 吸热:Q 吸 =c m ( t – t o )=cm ⊿t2. 放热:Q 放 =c m ( t o – t )=cm ⊿t 3 热平衡方程(放出的热量全部被吸收):Q 吸=Q 放 4. 燃烧燃料放出的热量:Q 放 =q m 或 Q 放 =qV5.炉子效率:mq Q QQ 吸放吸==η6. 热机效率:mqW QW 有放有==η7. 串联电路:开关:控制所有用电器,开关位置改变,控制作用不变。
电流:I =I 1=I 2 电压:U =U 1+U 2 电阻:R 总=R 1+R 2n 个相同的电阻R 串联的总电阻:R 总=nR 8.并联电路:开关:干路开关控制所有的用电器,支路开关控制该条支路的用电器。
高中物理公式大全(word版)

高中物理公式总结一、质点的运动(1)------直线运动1)匀变速直线运动1.平均速度V平=s/t(定义式)2.有用推论Vt2-Vo2=2as3.中间时刻速度Vt/2=V平=(Vt+Vo)/24.末速度Vt=Vo+at5.中间位置速度Vs/2=[(Vo2+Vt2)/2]1/26.位移s=V平t=Vot+at2/2=Vt/2t7.加速度a=(Vt-Vo)/t{以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}8.实验用推论Δs=aT2 {Δs为连续相邻相等时间(T)内位移之差}9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
注:(1)平均速度是矢量;(2)物体速度大,加速度不一定大;(3)a=(Vt-Vo)/t只是量度式,不是决定式;(4)其它相关内容:质点、位移和路程、参考系、时间与时刻〔见第一册P19〕/s--t图、v--t图/速度与速率、瞬时速度〔见第一册P24〕。
2)自由落体运动1.初速度Vo=02.末速度Vt=gt3.下落高度h=gt2/2(从Vo位置向下计算)4.推论Vt2=2gh注:(1)自由落体运动是初速度为零的匀加速直线运动,遵循匀变速直线运动规律;(2)a=g=9.8m/s2≈10m/s2(重力加速度在赤道附近较小,在高山处比平地小,方向竖直向下)。
3)竖直上抛运动1.位移s=Vot-gt2/22.末速度Vt=Vo-gt (g=9.8m/s2≈10m/s2)3.有用推论Vt2-Vo2=-2gs4.上升最大高度Hm=Vo2/2g(抛出点算起)5.往返时间t=2Vo/g (从抛出落回原位置的时间)注:(1)全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值;(2)分段处理:向上为匀减速直线运动,向下为自由落体运动,具有对称性;(3)上升与下落过程具有对称性,如在同点速度等值反向等。
(完整版)行测数量关系常用公式汇总(可编辑修改word版)

公务员考试行测数学常用公式汇总大全(行测数学秒杀实战方法)目录一、基础代数公式 (2)二、等差数列 (2)三、等比数列 (2)四、不等式 (3)五、基础几何公式 (3)六、工程问题 (4)七、几何边端问题 (4)八、利润问题 (5)九、排列组合 (5)十、年龄问题 (5)十一、植树问题 (6)十二、行程问题 (6)十三、钟表问题 (7)十四、容斥原理 (7)十五、牛吃草问题 (8)十六、弃九推断 (8)十七、乘方尾数 (8)十八、除以“7”乘方余数核心口诀 (8)十九、指数增长 (9)二十、溶液问题 (9)二十二、减半调和平均数 (10)二十三、余数同余问题 (10)二十四、星期日期问题 (10)二十五、循环周期问题 (10)二十六、典型数列前N 项和 (11)二、等差数列三、等比数列1. 平方差公式:(a +b )·(a -b )=a 2-b 22. 完全平方公式:(a±b)2=a 2±2ab+b 23. 完全立方公式:(a±b)3=(a±b)(a 2ab+b 2)4. 立方和差公式:a 3+b 3=(a ± b)(a 2+ ab+b 2) 5. a m·a n=a m +na m ÷a n =a m -n (a m )n =a mn (ab)n =a n ·b nn ⨯(a 1 + a n )1(1)s n ==na 1+ n(n-1)d ;22(2)a n =a 1+(n -1)d ;(3) 项数 n =a n - a 1+1;d(4) 若 a,A,b 成等差数列,则:2A =a+b ; (5) 若 m+n=k+i ,则:a m +a n =a k +a i ;(6)前 n 个奇数:1,3,5,7,9,…(2n —1)之和为 n 2(其中:n 为项数,a 1 为首项,a n 为末项,d 为公差,s n 为等差数列前 n 项的和)(1)a n =a 1q n -1;a (· 1-q n) (2)s n = 1(q ≠ 1)1 - q(3) 若 a,G,b 成等比数列,则:G 2=ab ; (4) 若 m+n=k+i ,则:a m ·a n =a k ·a i ; (5) a m -a n =(m-n)d (6) a m =q (m-n)a n一、基础代数公式- b + b 2 - 4ac - b - b 2 - 4ac = 1 四、不等式五、基础几何公式(其中:n 为项数,a 1 为首项,a n 为末项,q 为公比,s n 为等比数列前 n 项的和)(1) 一元二次方程求根公式:ax 2+bx+c=a(x-x 1)(x-x 2)其中:x 1= ;x 2= (b 2-4ac ≥ 0)2a2abc根与系数的关系:x 1+x 2=- ,x 1·x 2= a a (2) a + b ≥ 2 ( a + b )2 2≥ ab a 2 + b 2 ≥ 2ab ( a + b + c )33≥ abc(3) a 2 + b 2 + c 2 ≥ 3abca +b +c ≥ 33推广: x 1 + x 2 + x 3 +... + x n ≥ n n x 2 ...x n(4)一阶导为零法:连续可导函数,在其内部取得最大值或最小值时,其导数为零。
(完整word版)高数公式大全

高等数学公式·平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1—tanα·tanβ)tan(α-β)=(tanα—tanβ)/(1+tanα·tanβ)·三角和的三角函数:sin(α+β+γ)=s inα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ—sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1—tanα·tanβ-tanβ·tanγ—tanγ·tanα)·辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B·倍角公式:·三倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα) sin(3α)=3sinα—4sin^3(α)cos(2α)=cos^2(α)—sin^2(α)=2cos^2(α)-1=1—2sin^2(α)cos(3α)=4cos^3(α)-3cosαtan(2α)=2tanα/[1-tan^2(α)]·半角公式:sin(α/2)=±√((1—cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)—sin(α—β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=—(1/2)[cos(α+β)-cos(α—β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α—β)/2]sinα—sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα—cosβ=—2sin[(α+β)/2]sin[(α—β)/2]·推导公式tanα+cotα=2/sin2αtanα—cotα=—2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n—1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角函数的角度换算[编辑本段]公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)部分高等内容[编辑本段]·高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)—e^(-ix)]/(2i) cosx=[e^(ix)+e^(—ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(—ix)]泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…此时三角函数定义域已推广至整个复数集。
(完整word版)统计学常用公式

公式一1. 众数【MODE 】(1) 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。
(2) 组距分组数据众数的计算对于组距分组数据,先找出出现次数最多的变量值所在组,即为众数所在组,再根据下面的公式计算计算众数的近似值。
下限公式: 1012M =L++i ∆⨯∆∆ 式中:0M 表示众数;L 表示众数的下线;1∆表示众数组次数与上一组次数之差;2∆表示众数组次数与下一组次数之差;i 表示众数组的组距。
上限公式:2012M =U-+i ∆⨯∆∆ 式中:U 表示众数组的上限。
2.中位数【MEDIAN 】(1)未分组数据中中位数的计算根据未分组数据计算中位数时,要先对数据进行排序,然后确定中位数的位置。
设一组数据按从小到大排序后为12N X X X ,,…,,中位数e M ,为则有:e N+M =X1()2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数(2)分组数据中位数的计算分组数据中位数的计算时,要先根据公式N / 2 确定中位数的位置,并确定中位数所在的组,然后采用下面的公式计算中位数的近似值:N=1m-1e m-S 2M =L+ii fd f ⨯∑式中:e M 表示中位数;L 表示中位数所在组的下限;m-1S 表示中位数所在组以下各组的累计次数;m f 表示中位数所在组的次数;d 表示中位数所在组的组距。
3.均值的计算【A VERAGE 】(1)未经分组均值的计算未经分组数据均值的计算公式为: 112n ++==nii x x x x x n n=∑…(2)分组数据均值计算分组数据均值的计算公式为: 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4.几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根,计算公式为:式中:G 表示几何平均数;∏表示连乘符号。
(完整word版)excel表格公式大全

1、查找重复内容公式:=IF(COUNTIF(A:A,A2)>1,"重复","")。
2、用出生年月来计算年龄公式:=TRUNC((DAYS360(H6,"2009/8/30",FALSE))/360,0)。
3、从输入的18位身份证号的出生年月计算公式:=CONCATENATE(MID(E2,7,4),"/",MID(E2,11,2),"/",MID(E2,13,2))。
4、从输入的身份证号码内让系统自动提取性别,可以输入以下公式:=IF(LEN(C2)=15,IF(MOD(MID(C2,15,1),2)=1,"男","女"),IF(MOD(MID(C2,17,1),2)=1,"男","女"))公式内的“C2”代表的是输入身份证号码的单元格。
1、求和:=SUM(K2:K56) ——对K2到K56这一区域进行求和;2、平均数:=AVERAGE(K2:K56) ——对K2 K56这一区域求平均数;3、排名:=RANK(K2,K$2:K$56) ——对55名学生的成绩进行排名;4、等级:=IF(K2>=85,"优",IF(K2>=74,"良",IF(K2>=60,"及格","不及格")))5、学期总评:=K2*0.3+M2*0.3+N2*0.4 ——假设K列、M列和N列分别存放着学生的“平时总评”、“期中”、“期末”三项成绩;6、最高分:=MAX(K2:K56) ——求K2到K56区域(55名学生)的最高分;7、最低分:=MIN(K2:K56) ——求K2到K56区域(55名学生)的最低分;8、分数段人数统计:(1)=COUNTIF(K2:K56,"100") ——求K2到K56区域100分的人数;假设把结果存放于K57单元格;(2)=COUNTIF(K2:K56,">=95")-K57 ——求K2到K56区域95~99.5分的人数;假设把结果存放于K58单元格;(3)=COUNTIF(K2:K56,">=90")-SUM(K57:K58) ——求K2到K56区域90~94.5分的人数;假设把结果存放于K59单元格;(4)=COUNTIF(K2:K56,">=85")-SUM(K57:K59) ——求K2到K56区域85~89.5分的人数;假设把结果存放于K60单元格;(5)=COUNTIF(K2:K56,">=70")-SUM(K57:K60) ——求K2到K56区域70~84.5分的人数;假设把结果存放于K61单元格;(6)=COUNTIF(K2:K56,">=60")-SUM(K57:K61) ——求K2到K56区域60~69.5分的人数;假设把结果存放于K62单元格;(7)=COUNTIF(K2:K56,"<60") ——求K2到K56区域60分以下的人数;假设把结果存放于K63单元格;说明:COUNTIF函数也可计算某一区域男、女生人数。
高中物理公式大全(word版)

高中物理公式总结一、质点的运动(1)------直线运动1)匀变速直线运动1.平均速度V平=s/t(定义式)2.有用推论Vt2-Vo2=2as3.中间时刻速度Vt/2=V平=(Vt+Vo)/24.末速度Vt=Vo+at5.中间位置速度Vs/2=[(Vo2+Vt2)/2]1/26.位移s=V平t=Vot+at2/2=Vt/2t7.加速度a=(Vt-Vo)/t{以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}8.实验用推论Δs=aT2 {Δs为连续相邻相等时间(T)内位移之差}9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
注:(1)平均速度是矢量;(2)物体速度大,加速度不一定大;(3)a=(Vt-Vo)/t只是量度式,不是决定式;(4)其它相关内容:质点、位移和路程、参考系、时间与时刻〔见第一册P19〕/s--t图、v--t图/速度与速率、瞬时速度〔见第一册P24〕。
2)自由落体运动1.初速度Vo=02.末速度Vt=gt3.下落高度h=gt2/2(从Vo位置向下计算)4.推论Vt2=2gh注:(1)自由落体运动是初速度为零的匀加速直线运动,遵循匀变速直线运动规律;(2)a=g=9.8m/s2≈10m/s2(重力加速度在赤道附近较小,在高山处比平地小,方向竖直向下)。
3)竖直上抛运动1.位移s=Vot-gt2/22.末速度Vt=Vo-gt (g=9.8m/s2≈10m/s2)3.有用推论Vt2-Vo2=-2gs4.上升最大高度Hm=Vo2/2g(抛出点算起)5.往返时间t=2Vo/g (从抛出落回原位置的时间)注:(1)全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值;(2)分段处理:向上为匀减速直线运动,向下为自由落体运动,具有对称性;(3)上升与下落过程具有对称性,如在同点速度等值反向等。
(完整word版)高考数学公式大全

高考数学公式大全 一、集合1.集合的运算符号:交集“ ”,并集“ ”补集“C ”子集“⊆”2.非空集合的子集个数:n 2(n 是指该集合元素的个数)3.空集的符号为∅ 二、函数1.定义域(整式型:R x ∈;分式型:分母0≠;零次幂型:底数0≠;对数型:真数0>;根式型:被开方数0≥)2.偶函数:)()(x f x f -= 奇函数:0)()(=-+x f x f 在计算时:偶函数常用:)1()1(-=f f奇函数常用:0)0(=f 或0)1()1(=-+f f3.单调增函数:当在x 递增,y 也递增;当x 在递减,y 也递减 单调减函数:与增函数相反4.指数函数计算:nm nmaa a +=⋅;nm n m aa a -=÷;nm n m aa ⋅=)(;m n mn a a=;10=a指数函数的性质:x a y =;当1>a 时,x a y =为增函数; 当10<<a 时,x a y =为减函数 指数函数必过定点)1,0(5.对数函数计算:1l o g =aa ;0log 1=a ;nm ana ma ⋅=+log log log ;nma na m a log log log =-; ma m an nl o g l o g =;ma mannlog 1log =对数的性质:xa y log = ;当10<<a 时,xa y log =为减函数.当1>a 时,xa y log =为增函数对数函数必过定点)0,1( 6.幂函数:a x y =7.函数的零点:①)(x f y =的零点指0)(=x f②)(x f y =在),(b a 内有零点;则0)()(<∙b f a f三、三角函数①计算:1cos sin 22=+αα;θθθtan cos sin = ②正负符号判断:“一全正,二正弦,三切,四余弦” ③和差公式:βαβαβαsin cos cos sin )sin(±=± βαββαsin sin cos cos )cos( a =± βαβαβαtan tan 1tan tan )tan(∙±=±④二倍角公式:αααcos sin 22sin ∙=;ααααα2222sin cos sin 211cos 22cos -=-=-=ααα2tan 1tan 2)2tan(-=;⑤特殊角00 030 045 060 0900120 0135 0150 0180sin0 212223 123 22 21 0 cos1 2322 21 0 21-22-23-1-tan0 3313不存在3-1-33- 0⑥诱导公式口诀“奇变偶不变;符号看象限。
(完整word版)excel表格公式大全

1 、查找重复内容公式:=IF(COUNTIF(A:A,A2)>1," 重复","")2 、用出生年月来计算年龄公式:=TRUNC((DAYS360(H6,"2009/8/30",FALSE))/360,0) 。
3 、从输入的18 位身份证号的出生年月计算公式:=CONCATENATE(MID(E2,7,4),"/",MID(E2,11,2),"/",MID(E2,13,2)) 。
4 、从输入的身份证号码内让系统自动提取性别,可以输入以下公式:=IF(LEN(C2)=15,IF(MOD(MID(C2,15,1),2)=1,"男","女"),IF(MOD(MID(C2,17,1),2)=1,"男","女))公式内的“C代表的是输入身份证号码的单元格。
1、求和:=SUM(K2:K56) ――对K2到K56这一区域进行求和;2、平均数:=AVERAGE(K2:K56)――对K2 K56 这一区域求平均数;3、排名:=RANK(K2,K$2:K$56)――对55 名学生的成绩进行排名;4、等级:=IF(K2>=85,"优',IF(K2>=74," 良",IF(K2>=60,"及格","不及格")))5、学期总评:=K2*0.3+M2*0.3+N2*0.4 ——设K列、M列和N列分别存放着学生的平时总评"、期中” 期末"三项成绩;6、最高分:=MAX(K2:K56)――求K2到K56区域(55名学生)的最高分;7、最低分:=MIN(K2:K56) ――求K2 到K56 区域( 55 名学生)的最低分;8、分数段人数统计:(1) =COUNTIF(K2:K56,"100")――求K2到K56区域100分的人数;假设把结果存放于K57单元格;( 2) =COUNTIF(K2:K56,">=95")—K57 ――求K2到K56区域95〜99.5分的人数;假设把结果存放于K58单元格;( 3) =COUNTIF(K2:K56,">=90") -SUM(K57:K58)――求K2到K56区域90〜94.5分的人数;假设把结果存放于K59单元格;( 4) =COUNTIF(K2:K56,">=85") -SUM(K57:K59)――求K2到K56区域85-89.5分的人数;假设把结果存放于K60单元格;( 5) =COUNTIF(K2:K56,">=70") -SUM(K57:K60)――求K2到K56区域70-84.5分的人数;假设把结果存放于K61单元格;( 6) =COUNTIF(K2:K56,">=60") -SUM(K57:K61)――求K2到K56区域60-69.5分的人数;假设把结果存放于K62单元格;( 7) =COUNTIF(K2:K56,"<60") ――求K2 到K56 区域60 分以下的人数;假设把结果存放于K63 单元格;说明:COUNTIF函数也可计算某一区域男、女生人数。
(完整版)初中数学各种公式(完整版)(可编辑修改word版)

-b b 2 - 4ac n 数学各种公式及性质1. 乘法与因式分解①(a +b )(a -b )=a 2-b 2;②(a ±b )2=a 2±2ab +b 2;③(a +b )(a 2-ab +b 2)=a 3+b 3; ④(a -b )(a 2+ab +b 2)=a 3-b 3;a 2+b 2=(a +b )2-2ab ;(a -b )2=(a +b )2-4ab 。
2. 幂的运算性质①a m ×a n =a m +n ;②a m ÷a n =a m -n ;③(a m )n =a mn ;④(ab )n =a n b n ;⑤( a)n =a;bb n⑥a -n = 1a n ,特别:( )-n =( )n ;⑦a 0=1(a ≠0)。
3. 二次根式 ①( )2=a (a ≥0);② =丨a 丨;③ = × ;④ =(a >0,b ≥0)。
4. 三角不等式|a|-|b|≤|a±b|≤|a|+|b|(定理);加强条件:||a|-|b||≤|a±b|≤|a|+|b|也成立,这个不等式也可称为向量的三角不等式(其中 a ,b 分别为向量 a 和向量 b )|a+b|≤|a|+|b|;|a-b|≤|a|+|b|;|a|≤b<=>-b≤a≤b ; |a-b|≥|a|-|b|; -|a|≤a≤|a|; 5. 某些数列前 n 项之和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2;1+3+5+7+9+11+13+15+…+(2n -1)=n 2 ;2+4+6+8+10+12+14+…+(2n)=n(n+1); 12+22+32+42+52+62+72+82+…+n 2=n(n+1)(2n+1)/6; 13+23+33+43+53+63+…n 3=n 2(n+1)2/4; 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3; 6. 一元二次方程对于方程:ax 2+bx +c =0:① x △ b 2 4ac求根公式是 =,其中 = - 2a 叫做根的判别式。
(完整word版)大学物理公式大全(大学物理所有的公式应有尽有)

第一章 质点运动学和牛顿运动定律1.1平均速度 v =t △△r1.2 瞬时速度 v=lim△t →△t △r =dtdr1. 3速度v=dtds ==→→lim lim△t 0△t △t△r 1.6 平均加速度a =△t △v1.7瞬时加速度(加速度)a=lim△t →△t △v =dtdv1.8瞬时加速度a=dt dv =22dt rd1.11匀速直线运动质点坐标x=x 0+vt 1.12变速运动速度 v=v 0+at 1.13变速运动质点坐标x=x 0+v 0t+21at 2 1.14速度随坐标变化公式:v 2-v 02=2a(x-x 0) 1.15自由落体运动 1.16竖直上抛运动⎪⎩⎪⎨⎧===gy v at y gtv 22122 ⎪⎪⎩⎪⎪⎨⎧-=-=-=gyv v gt t v y gt v v 221202200 1.17 抛体运动速度分量⎩⎨⎧-==gt a v v av v yx sin cos 001.18 抛体运动距离分量⎪⎩⎪⎨⎧-•=•=20021sin cos gt t a v y t a v x 1.19射程 X=gav 2sin 21.20射高Y=gav 22sin 201.21飞行时间y=xtga —ggx 21.22轨迹方程y=xtga —av gx 2202cos 21.23向心加速度 a=Rv 21.24圆周运动加速度等于切向加速度与法向加速度矢量和a=a t +a n1.25 加速度数值 a=22n t a a +1.26 法向加速度和匀速圆周运动的向心加速度相同a n =Rv 21.27切向加速度只改变速度的大小a t =dtdv1.28 ωΦR dtd R dt ds v ===1.29角速度 dt φωd =1.30角加速度 22dt dtd d φωα== 1.31角加速度a 与线加速度a n 、a t 间的关系a n =222)(ωωR RR R v == a t =αωR dtd R dt dv ==牛顿第一定律:任何物体都保持静止或匀速直线运动状态,除非它受到作用力而被迫改变这种状态。
小学数学公式大全(WORD完全版)

小学数学公式大全(完全版)1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径?=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积=长×宽×高V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷319、长方体(正方体、圆柱体)的体1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1 、正方形C周长S面积a边长周长=边长×4 C=4a 面积=边长×边长S=a×a2 、正方体V:体积a:棱长表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3 、长方形C周长S面积a边长周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4 、长方体V:体积s:面积a:长b: 宽h:高(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5 三角形s面积a底h高面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形s面积a底h高面积=底×高s=ah7 梯形s面积a上底b下底h高面积=(上底+下底)×高÷2 s=(a+b)×h÷28 圆形S面积C周长∏d=直径r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9 圆柱体v:体积h:高s;底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10 圆锥体v:体积h:高s;底面积r:底面半径体积=底面积×高÷3 总数÷总份数=平均数和差问题(和+差)÷2=大数(和-差)÷2=小数和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1 非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1) 株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1 全长=株距×(株数+1) 株距=全长÷(株数+1)2 封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100% 涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1) 利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%) 时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒积=底面积×高V=Sh 第一部分:概念1、加法交换律:两数相加交换加数的位置,和不变。
(完整word版)资料分析公式汇总
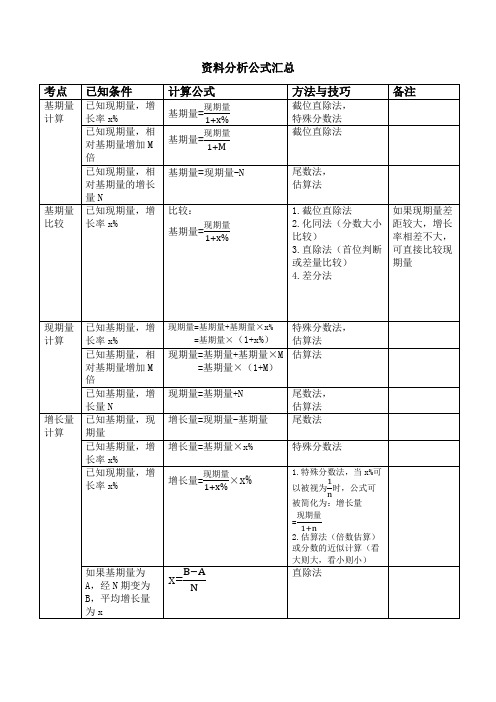
资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础一、稿酬计算公式1.图书稿酬的计算方法:1)版税方式:稿酬=版税=图书定价×发行数×版税率提示:还可以“图书批发价”代替“图书定价”;以“印数”或“实际销售数”代替“发行2)基本稿酬加印数稿酬方式:稿酬=基本稿酬+印数稿酬=稿费标准×字数+(稿费标准×字数)×1%×印数÷1000提示:①稿酬标准(原创及注释,(30~100)/千字;改编,(10~50)/千字;汇编,(3~10)/千字;翻译,(20~80)/千字));②不足一千字的,按一千字计算;③原创和演绎作品重印稿酬按基本稿酬的1%计算。
3)一次性付酬方式:付酬标准和计算方式可参照基本稿酬。
2.报纸、期刊稿酬的计算方法:只适用一次性付酬方式,付酬标准和计算方式可参照基本稿酬。
提示:不足五百字的按五百字计算;超过五百字不足一千字的,按一千字计算。
二、增值税计算公式:1. 当期不含税销售额:当期不含税销售额=当期含税销售额÷(1+增值税率)2.当期增值税销项税额:当期增值税销项税额=当期不含税销售额×增值税率提示:除挂历的销售收入使用17%外,其他出版物的销售收入采用13%的低税率。
考试试题中会明确给出。
3.当期应纳增值税税额:当期应纳增值税税额=当期增值税销项税额-当期累计进项增值税额4.推导公式:应纳增值税额=[销售总额÷(1+增值税率)]×增值税率-进项增值税额提示:若值为正,则需交纳税额;若为负值则无须交纳税额,多余进项税额后期抵扣。
三、营业税计算公式:应纳营业税额=有关营业收入额×税率提示:税率通常为5%。
四、所得税计算公式:1.企业所得税:企业所得税应纳税额=应纳税所得额×税率提示:现行企业所得税税率为25%。
2.个人所得税计算公式:1)稿酬总额大于或等于4000元时:个人所得税=稿酬总额×(1-20%)×20%×(1-30%)2)稿酬总额小于4000元时:个人所得税=(稿酬总额-800)×20%×(1-30%)提示:这里稿酬总额,无论是一次性获得,还是分几次获得,都要合并累计在一起计征个人所得税。
因此要根据稿酬总额选择相应的公式。
五、附加税费计算公式:应纳税额=当期应纳增值税税额(或营业税税额)×税率提示:若计算城市维护建设税,则税率为7%;若计算教育费附加,则税率为3%。
实务一、版面字数计算公式(2011 年修改了系数):1.每行字数与版心宽度:字数=版心宽度÷(0.35×文字磅数)版心宽度=0.35×文字磅数×字数2.每面行数与版心高度:行数=(版心高度-0.35×文字磅数)÷(0.35×文字磅数+0.35×行距磅数)+1版心高度=0.35×文字磅数×行数+0.35×行距磅数×(行数-1)3.版面字数与书脊宽度:胶版纸书脊宽度≈0.0006 毫米×纸张定量×总页面数轻质纸书脊宽度≈面数÷2×纸张定量×纸张系数/1000二、印刷用纸量计算公式:1.印张与令重1)印张:印张数=总面数÷开数推导公式:总面数=印张数×开数总页数=(印张数×开数)÷2提示:面数=页数×2;1 张全张纸的一半两面印刷后为 1 个印张。
2)令重:令重=单张纸面积[纸张的长度×宽度(将毫米换算成米)]×定量(纸张重量)×500÷1000 提示:令重单位为 kg;500张全张纸为1令,1令合 1000个印张。
2.用纸吨数:用纸吨数=令重×用纸令数÷10003.纸张费用:纸张费用=用纸吨数×纸张每吨单价纸张费用=吨价÷1000×令重×令数4.书刊用纸量:1)正文(即书心)用纸总量:书心用纸令数=单册面数×印数÷开数÷1000×(1+加放数)提示:图书中的正文、目录等应是另页起排的,紧挨其前的部件如果页面数为单数,就应该加上1个空白面;图书的最后页码为单数,也应加1个空白面。
2)环衬、书名页和插页用纸总量:提示:公式同上,但因用纸种类不同,因此需要分别计算用纸量;1个环衬有4面,前后环衬就有8面。
3)封面用纸总量:①首先根据书刊的开本大小和书脊宽度以及有无勒口确定封面用纸开数:封面纸的开数=(纸张的一边长÷图书成品净尺寸的一边长)×(另边长÷净另边长)×2纸张的长边=(图书净尺寸短边+勒口宽度+3)×2+书脊厚度纸张的短边=图书净尺寸长边+6提示:若非特殊注明,一般取材切多的;其中纸张的一边长是需要剪掉叼口量的。
②然后计算封面用纸令数:封面用纸令数=印数÷封面纸开数÷500×(1+加放数)4)护封用纸总量:护封用纸令数=印数÷护封纸开数÷500×(1+加放数)提示:原则上与封面用纸计算相同。
不同之处在于的净尺寸须根据书壳的幅面净尺寸和书脊宽度计算。
三、书刊印制计算公式:1.印张与书页数:书页数=印张数/折算系数提示:全张纸幅面的一半两面印刷后为1个印张;折算系数是开数倒数的2倍。
实例:2.色令:色令数=纸张令数×印刷面数×印刷色数提示:1令纸=500张全张纸;1令纸单面印刷1次为1色令;1 令纸=1000 印张书心用纸令数=单册印张数×印数÷1000×(1+加放数)书心色令数=单册印张数×印数÷1000×印刷面数×印刷色数封面用纸令数=印数÷封面开数÷500×(1+加放数)封面色令数=印数÷封面开数÷500×印刷面数×印刷色数3.令和方:1 令=500张全张纸=1000张对开纸=1000方四、书刊印制费用计算公式:1.制版费用:1)制版费用:制版费用=输入输出费+晒上版费2)输入输出费:输入输出费=文字录入排版费+图片输入费+图文编辑费+胶片输出费+打样费3)晒上版费:晒上版费=单价×单册印张数×2×印刷色数2.印刷费用:1)色令制计价法:书心印刷费用=色令单价×单册印张数×印数÷1000×印刷面数×印刷色数封面印刷费用=色令单价×印数÷封面开数÷500×印刷面数×印刷色数2)印张制计价法:书心印刷费用=印张单价×单册印张数×印数×印刷色数封面印刷费用=印张单价×单册印张数×印数×印刷色数提示:单册印张数不足0.5按0.5计;超过0.5不足1的,按1印张计算。
3.装订费用:1)装订费:装订费=(书心帖数+封面帖数+n1+n2+n3+…)×单价×印数提示:n1、n2、n3…代表其他部件帖数,有几个,就根据录入的个数计算。
封面一般计 2帖;书心部分一般是1印张合1帖,不足 1 印张的按1帖计;单页型插页计1帖;前后环衬,环衬计2帖;只有前环衬,计1帖。
2.表面整饰加工费:表面整饰加工费=覆膜费+热固化上光费+局部紫外线固化上光费五、本量利分析计算公式:1.基本概念公式:单位销售收入=定价×发行折扣率÷(1+增值税率)销售收入总额=单位销售收入×生产数量单位销售税金=[定价×发行折扣率÷(1+销项增值税率)×销项增值税率-该出版物进项增值税总额÷生产数量]×(城市维护建设税率+教育费附加率)销售税金总额=单位销售税金×生产数量单位变动成本=变动成本总额÷生产数量单位固定成本=固定成本总额÷生产数量2.本量利分析基本公式:利润=销售收入总额-销售税金总额-变动成本总额-固定成本总额利润=(单位销售收入-单位销售税金-单位变动成本)×生产数量-固定成本总额3.保本点测算:保本生产数量=固定成本总额÷(单位销售收入-单位销售税金-单位变动成本)4.预期利润测算:目标利润=(单位销售收入-单位销售税金-单位变动成本)×生产数量-固定成本总额5.目标销售量测算:目标销售量(生产数量)=(固定成本总额+利润)÷(单位销售收入-单位销售税金-单位变动成本)七、出版物定价法计算公式:1.成本定价法:①已知单位销售税金条件下的计算公式:定价=[(固定成本总额+利润)÷生产数量+单位销售税金+单位变动成本] ÷发行折扣率×(1+增值税率)★在稿酬支付采取版税方式时:定价=[(固定成本总额+利润)÷生产数量+单位销售税金+单位变动成本] ÷[发行折扣率- 版税率×(1+增值税率)]×(1+增值税率)②未知单位销售税金条件下的经验算式:定价=[固定成本总额+利润÷生产数量+单位变动成本]÷发行折扣率×[1+增值率×(1+城市维护建设税率+教育费附加率)]★在稿酬支付采取版税方式时:定价=[(固定成本总额+利润÷生产数量+单位变动成本]÷{发行折扣率-版税率×[1+增值率×(1+城市维护建设税率+教育费附加率)]}×[1+增值率×(1+城市维护建设税率+教育费附加率)]提示:成本定价法公式 2011 年有重大变动,复习时一定要掌握并学会运用。
2.印张定价法:定价=正文印张价格标准×正文印张数+封面价格+插页 1价格标准×插页 1 数量+插页 2价格标准×插页2数量+……+插页n价格标准×插页 n数量提示:“正文印张价格标准”单位是元/印张;“插页价格标准”单位是元/页;如有护封、函套等,其价格可事先加入封面价格。
出版合同范本编辑甲方(权利人):_____地址:_____乙方(出版者):_____地址:_____作品名称:_____作者姓名:_____甲乙双方就出版上述作品达成协议如下:第一条甲方授予乙方在_____地区独家出版发行该作品之_____版本的权利。
未经对方许可,任何一方不得将上述权利在合同有效期内授予第三方。
