方,矩,三角,锯齿波频谱分析实验
多种波形发生器实验分析报告

多种波形发生器实验分析报告目录一、实验概述 (2)1. 实验目的 (2)2. 实验设备与材料 (3)3. 实验原理 (4)二、实验内容与步骤 (5)1. 波形发生器设计与搭建 (6)1.1 设计要求与方案选择 (7)1.2 波形发生器硬件搭建 (9)1.3 波形发生器软件编程 (10)2. 多种波形合成与输出 (12)2.1 合成波形的设计与实现 (12)2.2 波形输出设置与调整 (13)2.3 实时监控与数据分析 (15)3. 实验测试与结果分析 (16)3.1 测试环境搭建与准备 (17)3.2 实验数据采集与处理 (18)3.3 结果分析与讨论 (19)三、实验结果与讨论 (20)1. 实验结果展示 (21)2. 结果分析 (22)2.1 各波形参数对比分析 (23)2.2 性能评估与优化建议 (24)3. 问题与改进措施 (25)四、实验总结与展望 (26)1. 实验成果总结 (27)2. 存在问题与不足 (28)3. 后续研究方向与展望 (29)一、实验概述本次实验旨在研究和分析多种波形发生器的性能特点,包括产生信号的频率、幅度、波形稳定性等方面。
实验中采用了多种类型的波形发生器,如正弦波、方波、三角波、梯形波等,并对其输出波形进行了详细的测量和分析。
实验过程中,我们首先对各种波形发生器的基本功能进行了测试,确保其能够正常工作。
我们对不同波形发生器产生的波形进行了对比分析,重点关注了波形的频率、幅度和波形稳定性等关键指标。
我们还对波形发生器的输出信号进行了频谱分析和噪声测试,以评估其性能表现。
通过本次实验,我们获得了丰富的实验数据和经验,为进一步优化波形发生器的设计提供了有力支持。
实验结果也为我们了解各种波形发生器在实际应用中的性能表现提供了重要参考。
1. 实验目的本次实验的主要目的是深入研究和理解多种波形发生器的原理及其在实际应用中的表现。
通过搭建实验平台,我们能够模拟和观察不同波形(如正弦波、方波、三角波等)的产生与特性,进而探究其各自的优缺点以及在不同场景下的适用性。
锯齿波发生电路实验报告

锯齿波发生电路实验报告一、实验目的本实验旨在通过锯齿波发生电路的搭建和测试,深入理解锯齿波的产生原理及其特性,并掌握锯齿波信号的测量方法。
二、实验原理锯齿波是一种周期性信号,其波形类似于锯齿形,因此得名。
它在时间轴上的变化呈现出逐渐上升或下降的趋势,并在达到峰值或谷值时突然反转。
锯齿波发生电路主要由一个三角形波发生器和一个比较器组成。
三角形波发生器输出一个周期性变化的三角形波信号,而比较器则将这个三角形波信号与一个直流电压进行比较,从而产生锯齿波信号。
具体来说,当三角形波信号上升到与直流电压相等时,比较器会输出高电平;当三角形波下降到与直流电压相等时,比较器会输出低电平。
这样就可以通过不断重复这个过程来产生连续的锯齿波信号。
三、实验步骤1. 准备实验所需材料:555计时器芯片、电容、电阻、比较器芯片等。
2. 按照电路图搭建锯齿波发生电路,注意连接正确性。
3. 接通电源,调节电位器使得比较器的输出波形为锯齿波。
4. 用示波器测量锯齿波的频率和幅值,并记录下来。
四、实验结果分析通过实验测量得到的锯齿波信号频率为1kHz左右,幅值为2V。
这与理论预计相符合,说明实验搭建正确,并且锯齿波发生电路能够正常工作。
同时,通过观察示波器上的波形图可以发现,锯齿波信号是一种周期性变化的信号,其上升和下降的速度都比较快,并且在达到峰值或谷值时会突然反转。
这些特点使得锯齿波信号在一些特定场合下具有重要应用价值。
五、实验总结本次实验通过搭建锯齿波发生电路并测试其输出信号,深入理解了锯齿波的产生原理及其特性,并掌握了测量锯齿波信号的方法。
同时,实验结果也验证了理论预计,说明实验精度较高。
通过本次实验,我们不仅学习了电路搭建和调试的技巧,更重要的是加深了对锯齿波信号的理解和应用。
这对于今后进行相关领域的研究和开发都具有重要意义。
信号与线性系统实验报告2

实验二连续系统频域分析一、实验目的1.通过观察信号的分解与合成过程,理解利用傅利叶级数进行信号频谱分析的方法。
2.了解波形分解与合成原理。
3.掌握带通滤波器有关特性的设计和测试方法。
4.了解电信号的取样方法与过程以及信号恢复的方法。
5.观察连续时间信号经取样后的波形图,了解其波形特点。
6.验证取样定理并恢复原信号。
二、实验内容1.用示波器观察方波信号的分解,并与方波的傅利叶级数各项的频率与系数作比较。
2.用示波器观察三角波信号的分解,并与三角波的傅利叶级数各项的频率与系数作比较。
3.用示波器观察方波信号基波及各次谐波的合成。
4.用示波器观察三角波信号基波及各次谐波的合成。
5.用示波器观察不同的取样频率抽样得到的抽样信号。
6.用示波器观察各取样信号经低通滤波器恢复后的信号并验证抽样定理。
三、实验仪器1.信号与系统实验箱一台2.信号系统实验平台3.信号的分解与合成模块(DYT3000-69)一块4.信号的取样与恢复模块(DYT3000-68)一块5.同步信号源模块(DYT3000-57)(选用)6.20MHz双踪示波器一台7.连接线若干四、实验原理1、信号的分解与合成任何电信号都是由各种不同频率、幅度和初始相位的正弦波跌加而成的。
对周期信号由它的傅利叶级数展开式可知,各次谐波为基波频率的整数倍。
而非周期信号包含了从零到无穷大的所有频率成份,每一频率成份的幅度均趋向无穷小,但其相对大小是不同的。
通过一个选频网络可以将电信号中所包含的某一频率成份提取出来。
本实验采用性能较好的有源带通滤波器作为选频网络。
对周期信号波形分解的方案框图如图2-1所示。
实验中对周期方波、三角波、锯齿波信号进行信号的分解。
方波信号的傅利叶级数展开式为411()(sin sin 3sin 5)35Af t t t t ωωωπ=+++…;三角波信号的傅利叶级数展开式为2811()(sin sin 3sin 5)925A f t t t t ωωωπ=-+-…;锯齿波信号的傅利叶级数展开式为11()(sin sin 2sin 3)223A A f t t t t ωωωπ=-+++…,其中2T πω=为信号的角频率。
实验:典型信号频谱分析

实验3.2典型信号频谱分析实验目的1. 在理论学习的基础上,通过本实验熟悉典型信号的波形和频谱特征,并能够从信号频谱中读取所需的信息。
2. 了解信号频谱分析的基本方法及仪器设备。
实验原理1. 典型信号及其频谱分析的作用正弦波、方波、三角波和白噪声信号是实际工程测试中常见的典型信号,这些信号时域、频域之间的关系很明确,并且都具有一定的特性,通过对这些典型信号的频谱进行分析,对掌握信号的特性,熟悉信号的分析方法大有益处,并且这些典型信号也可以作为实际工程信号分析时的参照资料。
本次实验利用DRVI 快速可重组虚拟仪器平台可以很方便的对上述典型信号作频谱分析。
2. 频谱分析的方法及设备信号的频谱可分为幅值谱、相位谱、功率谱、对数谱等等。
对信号作频谱分析的设备主要是频谱分析仪,它把信号按数学关系作为频率的函数显示出来,其工作方式有模拟式和数字式二种。
模拟式频谱分析仪以模拟滤波器为基础,从信号中选出各个频率成分的量值;数字式频谱分析仪以数字滤波器或快速傅立叶变换为基础,实现信号的时一频关系转换分析。
傅立叶变换是信号频谱分析中常用的一个工具,它把一些复杂的信号分解为无穷多个相互之间具有一定关系的正弦信号之和,并通过对各个正弦信号的研究来了解复杂信号的频率成分和幅值。
信号频谱分析是采用傅立叶变换将时域信号x(t)变换为频域信号X(f),从而帮助人们从另一个角度来了解信号的特征。
时域信号x(t)的傅氏变换为:X(f) x(t)e j2ft dt式中X(f)为信号的频域表示,x(t)为信号的时域表示,f为频率。
3. 周期信号的频谱分析周期信号是经过一定时间可以重复出现的信号,满足条件:x ( t ) = x ( t + nT )从数学分析已知,任何周期函数在满足狄利克利( Dirichlet)条件下,可以展开成正交函数线性组合的无穷级数,如正交函数集是三角函数集(sinn 3 0t,cosn达式:利用三角函数的和差化积公式,周期信号的三角函数展开式还可写如下形a n ,b n ,A n , n 为信号的傅立叶系数,表示信号在频率 f n 处的成分大小。
实验五 三角波-方波(锯齿波-矩形波)发生器实验报告
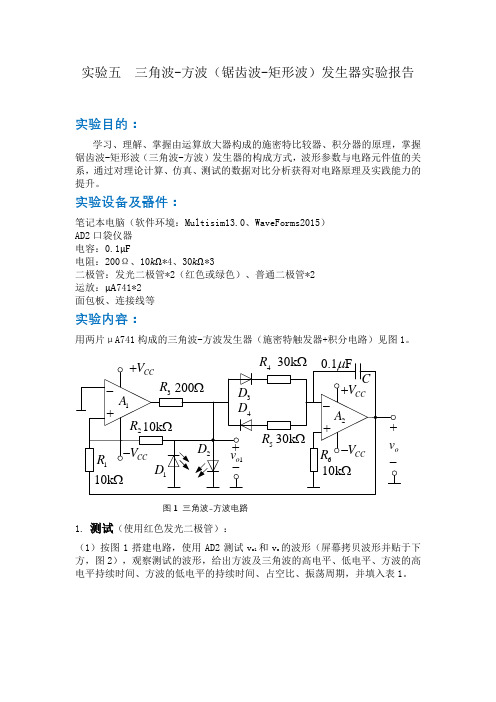
实验五三角波-方波(锯齿波-矩形波)发生器实验报告实验目的:学习、理解、掌握由运算放大器构成的施密特比较器、积分器的原理,掌握锯齿波-矩形波(三角波-方波)发生器的构成方式,波形参数与电路元件值的关系,通过对理论计算、仿真、测试的数据对比分析获得对电路原理及实践能力的提升。
实验设备及器件:笔记本电脑(软件环境:Multisim13.0、WaveForms2015)AD2口袋仪器电容:0.1μF电阻:200Ω、10kΩ*4、30kΩ*3二极管:发光二极管*2(红色或绿色)、普通二极管*2运放:μA741*2面包板、连接线等实验内容:用两片μA741构成的三角波-方波发生器(施密特触发器+积分电路)见图1。
图1 三角波-方波电路1.测试(使用红色发光二极管):(1)按图1搭建电路,使用AD2测试vo1和vo的波形(屏幕拷贝波形并贴于下方,图2),观察测试的波形,给出方波及三角波的高电平、低电平、方波的高电平持续时间、方波的低电平的持续时间、占空比、振荡周期,并填入表1。
图2 三角波-方波电路的测试波形(2)令图1中的R4=10 kΩ,其他器件参数不变,构成锯齿波-矩形波发生器,使用AD2测试vo1和vo2的波形(屏幕拷贝波形并贴于下方,图3),通过波形给出锯齿波及矩形波的高电平、低电平、矩形波的高电平持续时间、矩形波的低电平的持续时间、占空比、振荡周期,并填入表2。
图3 锯齿波-矩形波电路的测试波形2.计算(1)利用测试(1)所得的方波高电平和低电平值(输出vo1,也就是发光二极管在该工作条件下的正向压降,计算周期时可使用正负峰值的平均值计算),并根据电路器件参数,理论计算三角波输出端(vo)的高电平和低电平值、方波高电平持续时间、方波低电平的持续时间、占空比、振荡周期,并填入表1。
(计算时需要考虑D3、D4二极管正向压降的影响,鉴于选用二极管的特性及实验中流过D 3、D4二极管的电流只有100μA左右,取正向压降为0.5V)。
三角波-方波(锯齿波-矩形波)发生器实验报告

三角波-方波(锯齿波-矩形波)发生器实验报告一、实验背景及目的在电子技术中,经常需要产生特定频率和形态的波形信号。
三角波-方波(锯齿波-矩形波)发生器可以产生多种波形信号,因此应用广泛。
本实验的目的是学习如何设计和制作三角波-方波(锯齿波-矩形波)发生器,并且深入理解相关电路的工作原理。
二、实验原理本实验中,我们使用反相输入放大器作为比较器。
比较器会将输入的连续波形信号与阈值进行比较,若输入信号高于阈值,则输出高电平;反之,则输出低电平。
通过将两个反相输入放大器连接形成反馈环路,可以得到三角波和锯齿波的信号。
通过在反馈环路中添加开关管,可以将三角波信号转化为矩形波信号。
三、实验器材1. 实验板2. 集成电路 LM3583. 可变电阻4. 电容5. 二极管6. 开关管四、实验步骤1. 将 LM358 集成电路插入实验板正确位置。
2. 连接反馈电路:将时序电容和可变电阻串联,连接到反相输入端口。
将电容和电阻的另一端连接到非反相输入端口。
3. 连接反馈电路:将正输入端口连接到负电源的直流电压。
4. 连接输出端口:将反相输出端口连接到非反相输入端口。
5. 连接输出端口:将输出端口连接到输出负载电阻。
6. 添加电容:将一个电容连接到输出负载电阻的另一端,并将其连接到微调电器。
7. 连接矩形波开关管:将开关管连接到反馈环路中,通过它进行转换。
8. 连接锯齿波开关管:将开关管连接到反馈环路中,通过它进行转换。
9. 测试电路:检查电路是否连接正确。
10. 调节电阻:根据需要调节可变电阻以产生不同的波形信号。
五、实验结果在实验中,我们成功地设计和制作了三角波-方波(锯齿波-矩形波)发生器,并且得到了以下结果:1. 通过调节电阻,我们可以产生不同的波形信号,包括三角波、锯齿波和矩形波。
2. 我们发现,当添加了矩形波开关管时,产生的矩形波信号的占空比由电阻决定。
3. 我们发现,在添加锯齿波开关管时,电容和电阻的值将会影响锯齿波的斜率。
非周期信号(方波,锯齿波,三角波)的合成分解以及频谱分析的MATLAB实现

1.2 主要功能
1.数值分析 2.数值和符号计算 3.工程与科学绘图 4.控制系统的设计与仿真 5.数字图像处理 6.数字信号处理 7.通讯系统设计与仿真 8.财务与金融工程
2
连续周期信号的傅立叶级数分析及其 MATLAB 实现
2 连续周期信号的傅立叶级数
频域分析法即傅里叶分析法,它是变换域分析法的基石。其中,傅里叶级数 是变换域分析法的理论基础,傅里叶变换作为频域分析法的重要数学工具,具有 明确的物理意义,在不同的领域得到广泛的应用。
2.1 连续时间周期信号的分解
以高等数学的知识,任何周期为 T 的周期函数,在满足狄里赫利条件时,则 该周期信号可以展开成傅里叶级数。傅里叶级数有三角形式和指数形式两种。
(3-2)
2
2
3
MATLAB 实现程序:
n=7;
6
连续周期信号的傅立叶级数分析及其 MATLAB 实现
T0=2;A=2; T1=2; tn_i=1; for tn=0:0.01:T1*T0
y_t(tn_i)=A* rem (tn,T0)/T0; t_t(tn_i)=tn; tn_i=tn_i+1; end; t=0:0.01:T1*T0; x=A/2; pi=3.1415926; w0=2*pi/T0; for i=1:n fw(i)=i*w0; a(i)=-A/(pi*i); y(i,:)=a(i)*sin(fw(i)*t); x=x+y(i,:); end; subplot(1,3,1); plot(t_t,[y_t;x]); title('锯齿波、锯齿波合成图') subplot(1,3,2); plot(t,[x; y]); title('0-n 次谐波及合成图') subplot(1,3,3); stem(fw,a); title('锯齿波频谱图') 生成图形:
实验一:典型信号的波形和频谱分析
典型信号的波形和频谱分析一. 实验目的1. 在理论学习的基础上,通过本实验熟悉典型信号的频谱特征,并能够从信号频谱中读取所需的信息。
2. 了解信号频谱分析的基本原理和方法,掌握用频谱分析提取测量信号特征的方法。
二. 实验原理频谱分析可用于识别信号中的周期分量,是信号分析中最常用的一种手段。
信号频谱分析是采用傅里叶变换将时域信号x(t)变换为频域信号X(f),从而帮助人们从另一个角度来了解信号的特征。
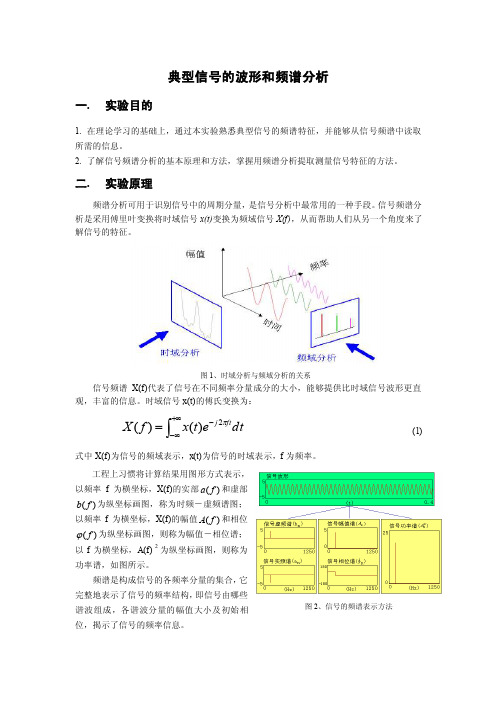
图1、时域分析与频域分析的关系信号频谱X(f)代表了信号在不同频率分量成分的大小,能够提供比时域信号波形更直观,丰富的信息。
时域信号x(t)的傅氏变换为:dt e t x f X ft j ⎰+∞∞--=π2)()( (1) 式中X(f)为信号的频域表示,x(t)为信号的时域表示,f 为频率。
工程上习惯将计算结果用图形方式表示,以频率f 为横坐标,X(f)的实部)(f a 和虚部)(f b 为纵坐标画图,称为时频-虚频谱图;以频率f 为横坐标,X(f)的幅值)(f A 和相位)(f ϕ为纵坐标画图,则称为幅值-相位谱;以f 为横坐标,A(f) 2为纵坐标画图,则称为功率谱,如图所示。
频谱是构成信号的各频率分量的集合,它完整地表示了信号的频率结构,即信号由哪些谐波组成,各谐波分量的幅值大小及初始相位,揭示了信号的频率信息。
图2、信号的频谱表示方法三. 实验内容白噪声信号、正弦波信号、方波信号、三角波信号和正弦波信号+白噪声信号的幅值谱特性和频谱参数识别方法。
用频谱分析方法对工业测量信号、声卡采集的音频信号、MP3音乐文件中的信号进行分析,给出它们的频谱。
四. 实验步骤图3是信号频谱分析实验界面,改变信号的频率、幅值和相位,观察信号频谱的变化。
选择白噪声、正弦波、方波等不同的典型信号,观察信号的频谱特征。
图3信号频谱分析实验环境五. 实验报告要求1.简述实验目的和原理。
2.拷贝实验系统运行界面,插入到实验报告中。
频谱分析实验报告

频谱分析实验报告篇一:典型信号的频谱分析实验报告贵州大学实验报告学院:专业:班级:1.正弦波信号的频谱特性:2.方波信号的频谱特性:3.三角波信号的频谱特性:4.正弦信号加白噪声信号的频谱特性:篇二:信号发生及频谱分析实验报告基于LABVIEW的信号发生及频谱分析的设计课程设计:虚拟仪器系统设计专业名称:电子信息工程2013年11月25日基于虚拟仪器的信号发生及频谱分析的设计摘要虚拟仪器是将仪器技术、计算机技术、总线技术和软件技术紧密的融合在一起,利用计算机强大的数字处理能力实现仪器的大部分功能,打破了传统仪器的框架,形成的一种新的仪器模式。
本设计采用USB6211数据采集卡,将虚拟仪器技术用于信号发生器的设计。
该系统具有生成正弦波、方波、三角波、锯齿波及PWM波的功能。
本文首先概述了信号发生器及虚拟仪器技术在国内外的发展及趋势,然后介绍了信号发生器的相关理论,给出了信号发生器的基本原理框图,并探讨了虚拟仪器的总线及其标准、框架结构、LABVIEW开发平台。
在分析本系统功能需求的基础上,介绍了数据采集卡、LABVIEW的编程模式等设计中所涉及到的硬件和技术。
本设计是虚拟仪器模拟真实仪器的尝试。
实践证明虚拟仪器是一种优秀的解决方案,能够实现各种硬件可以完成的任务。
关键词虚拟仪器,数据采集卡,信号发生器,LABVIEWSignal based on virtual instrument and the design of the frequency spectrum analysisAbstractVirtual instrument is formed by the instrument technology, computer technology, bus technology and software technology. Powerful digital processing’s ability of computer is used to achieve the main functions of instrument. Virtual instrument broke the framework of the traditional instruments, and built a new device model. This design uses USB6211 data acquisition card. The virtual instrument technology has been utilized in the design of signal generator. The system has ability to produce sine wave, square wave, and triangle wave, saw tooth wave and PWM wave. This article summarizes the development and trend of the signalgenerator and virtual instrument at home and abroad at first. And then introduces the theory of signal generator, gives a basic block diagram of signal generator, also the frame structure and LABVIEW development platform of the virtual instrument with the inquiry of the bus’s standard. Based on the analysis of this system’s functional requirements, this article introduces the hardware and technology which involved in design of the data acquisition card and the LABVIEW’s programming design is an attempt of virtual instrument to simulate the reality instrument. It shows the virtual instrument is an excellent solution to achieve the task which is achieved by traditional hardware in the past.Key Words: Virtual Instruments,Data Acquisition Cards,Signal Generators,LABVIEW目录1. 实验相关问题............................................................... .. (1)实验目的............................................................... .. (1)实验内容............................................................... .. (1)实验要求............................................................... .. (1)2. 实验方案选择............................................................... .. (1)仿真波形的产生............................................................... .. (1)白噪声的产生............................................................... (1)仿真信号频谱分析............................................................... . (1)3. 系统总体的设计及实现............................................................... (1)系统设计及程序框图流程............................................................... . (1)系统具体应用程序............................................................... . (2)程序框图的具体设计步骤............................................................... . (2)虚拟正弦波发生器的设计............................................................... (2)虚拟方波发生器的设计............................................................... .. (3)虚拟锯齿波发生器的设计............................................................... .. (3)虚拟三角波发生器的设计............................................................... .. (4)4. 系统调试............................................................... ..................................................................... (1)调试步骤............................................................... .. (1)调试结果............................................................... .. (1)1. 实验相关问题实验目的1. 学习LabVIEW 软件特点及工作环境。
频谱分析实验报告

基于Matlab 的频谱分析一、实验目的1.频谱分析的基本概念及应用;2.常用信号的频谱:余弦信号、方波信号、三角波信号; 3.应用DFT 进行频谱分析,MATLAB 编程仿真 (1)整周期采样、非整周期采样→频谱泄漏; (2)填零运算→高密度频谱; (3)非整周期采样时,加窗改进; 4.应用频谱分析仪测量常用信号的频谱。
二、实验原理1、利用DFT 计算连续信号的频谱分析过程从图中看出,这是一次近似过程,首先,用离散采样信号的 DTFT ()j X e ω来近似连续信号()a x t 的傅立叶变换()a X j Ω,其次,将()x n 截短,这一过程等效于用一矩形序列()R N n 与()x n 相乘,其DTFT 为()()*()j j j NN XeX eR eωωω=最后,再对截短的信号作DFT 2、频谱分析的近似过程出现问题及解决办法 (1)混叠①混叠现象对连续信号x(t)进行数字处理前,要进行采样()()()a n x n T x t t n T δ∞=-∞=-∑采样序列的频谱是连续信号频谱的周期延拓,周期为fs ,如采样率过低,不满足N采样定理,fs<2fh ,则导致频谱混迭,使一个周期内的谱对原信号谱产生失真,无法恢复原信号,进一步的数字处理失去依据。
另外,干扰信号的频率高于折叠频率/2s f 的也会产生频谱混叠。
②对于干扰信号的频率高于/2s f 产生频谱混叠的解决办法:在采样前加一抗混叠滤波器,滤除高于折叠频率/2s f 的频率成分。
(2) 泄漏①产生原因处理实际信号序列 x (n )时,一般总要将它截断为一有限长序列,长为N 点,相当于乘以一个矩形窗 w(n)=RN(n)。
矩形窗函数,其频谱有主瓣,也有许多副瓣,窗口越大,主瓣越窄,当窗口趋于无穷大时,就是一个冲击函数。
我们知道,时域的乘积对应频域的卷积,所以,加窗后的频谱实际是原信号频谱与矩形窗函数频谱的卷积,卷积的结果使频谱延伸到了主瓣以外,且一直延伸到无穷。
波形发生电路实验报告

姓名: 学号:班级:实验十波形发生电路实验目的1.掌握波形发生电路的结构特点和分析、计算、测试方法2.熟悉波形发生器的设计方法实验仪器双踪示波器数字万用表交流毫伏表直流电源预习要求1.分析下图中电路的工作原理,并根据电路参数画出输出Uo和Uc的波形。
2.图5-10-2电路如何使输出波形占空比变大?画出电路原理图。
实验原理非正弦波产生电路,一般由电子开关(电压比较器),外加反馈网络构成闭环电路形成。
常用的波形发生电路有方波、三角波、锯齿波发生器等。
1.方波发生器电路如图所示,集成运放和电阻R2、R3、R4构成滞回电压比较器,作为电子开关使用,R1、C相串联作为具有延迟作用的反馈网络,整个电路是一个闭环电路。
设电路刚加电时,Uc=0,且滞回比较器的输出电压为Uz,则集成运放同相输入端此时的电位为U﹢=R2*Uz/(R2+R3)同时Uz通过R1向C充电,Uc由零逐渐上升,当Uc﹥U+时,Uo从Uz跳变为-Uz,则U+=-R2*Uz/(R2+R3)同时,电容C通过R1放电,使Uc逐渐下降,小于U+时,Uo又跳变为Uz,回到初始状态,如此周而复始,产生振荡,输出方波。
该方波发生器输出的方波振荡周期 T=2R1*C*㏑(1+2R2/R3)2.占空比可调的矩形波发生电路通常将矩形波高电平的时间与周期时间之比称为占空比。
方波的占空比为50%。
如果需要产生占空比小于或大于50%的矩形波,则应设法使方波发生电路中电容的充电时间常数与放电时间常数不相等。
下图电路中利用二极管的单向导电性可以构成占空比可调的矩形波发生电路。
该电路发生的矩形波振荡周期 T=(Rw +2R1)C㏑(1+2R2/R3)占空比T1/T=(R′w+R1)/( Rw+2R1)调节电位器Rw可使输出矩形波的占空比变化。
3.三角波发生电路上述方波发生器中Uc的波形近似三角形,但其线性度比较差。
下图电路可以产生线性度比较高的三角波,它包含两部分电路,前一部分为滞回电压比较器,后一部分为积分电路。
方,矩,三角,锯齿波频谱分析实验

Im(k ) , 函数 Complex To Polar 可直接得 2* Re 2 (k ) + Im 2 (k ) ,相位谱为 ϕ (k ) = arctan Re(k ) 2
到复数的模和相位角。 再把用弧度表示的相位转换为角度。 使用两个图形控件显示幅度谱和 相位谱。 程序面板如下图所示:
五、实验步骤:
1.设计 DFT 变换程序,求取仿真信号的幅值频谱和相位谱。 (要求仅采用基本数学 函数实现) 。 分析:DFT 计算公式为: X (k ) = ∑ x(n)e
n =0 N −1 −j 2π nk N
其中
k = 0,1,2..., N − 1 ,采用双循环, n = 0,1,2..., N − 1
先固定 k,内循环累加求和,计算 ∑ x(n)e
n =0
N −1
−j
2π nk N
,再改变 k,外循环。最后将 X(k)转换为幅
度谱和相位谱。设计中要用到数值运算子模板中的 Complex Functions 复数处理函数。 (1)产生仿真信号。打开 3.5 节第 2 个实验内容的程序,它能够产生频率、幅值和 直流偏值可调的正弦、方波、三角波、锯齿波信号,还可叠加高斯噪声信号,并且采样率和 采样点可选。 (2)计算 = n 0,1, 2..., N − 1 ,结果为 1 个数组,见图
2) 3) 4)
各节点之间的频率间隔由时间长度 N 和采样频率 fs 决定: 第 k 个节点对应的频率值为 有一半数据有意义。
f (k ) = k ⋅ fs N 。
FFT形成的频谱相对于折叠频率f S /2 对称,FFT的输出频率范围为 0~f S /2。实际只
用 DFT 进行测试信号频域特性分析存在主要误差有量化误差、混叠误差、频谱泄漏和 栅栏效应等,减少计算误差的办法有,增加 A/D 的有效位数,提高采样频率,增加采样时 间和采样点数,整周期采样或加窗处理等。
信号测试实验报告——基本信号分析实验报告
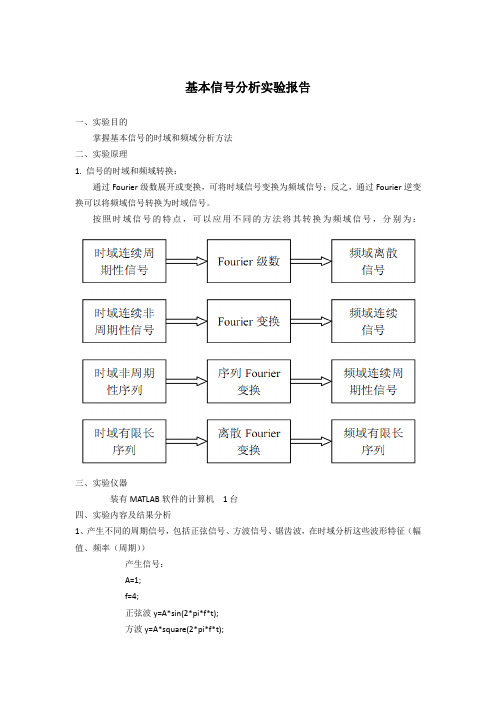
基本信号分析实验报告一、实验目的掌握基本信号的时域和频域分析方法二、实验原理1. 信号的时域和频域转换:通过Fourier级数展开或变换,可将时域信号变换为频域信号;反之,通过Fourier逆变换可以将频域信号转换为时域信号。
按照时域信号的特点,可以应用不同的方法将其转换为频域信号,分别为:三、实验仪器装有MATLAB软件的计算机1台四、实验内容及结果分析1、产生不同的周期信号,包括正弦信号、方波信号、锯齿波,在时域分析这些波形特征(幅值、频率(周期))产生信号:A=1;f=4;正弦波y=A*sin(2*pi*f*t);方波y=A*square(2*pi*f*t);锯齿波y=A*sawtooth(2*pi*f*t);由时域图也可看出三种信号的幅值均为A=1V,频率为f=4Hz。
2、在Matlab中产生随机噪声、阶跃信号t=0:0.001:3y=randn(size(t));幅值杂乱无绪,为噪声特征。
syms t;f=heaviside(t);ezplot(f,[-1,1]);幅值为A=1V,t<0时为0。
3、对产生的信号进行Fourier级数展开、Fourier变换,从频域分析信号的特征,并说明方波信号和锯齿波信号的带宽。
fs=1000;det=1/fs; t=0:det:6; f=50; A=1;y=A*sin(2*pi*f*t); Y1=fft(y,512); Y2=abs(Y1); Y=Y2/256*4/pi; ff=fs*(0:256)/512; subplot(4,1,1); plot(ff,Y(1:257));分析:正弦波、方波、锯齿波均为时域连续周期性信号,故通过Fourier 级数展开。
正弦信号的Fourier 级数展开为其本身。
在频谱图的正半轴上,正弦波在时,产生一个尖峰,该尖峰的幅值等于正弦函数的幅值。
其他频率上无尖峰。
方波信号的Fourier 级数展开形式为()()004A 1A(f)[sin 2πf t sin 3*2πf t ]π3=++,其幅频谱只包含基波及奇次谐波的频率分量,各次谐波的幅值以1n的规律收敛。
基本通信信号的时频特性认识

基本通信信号的时频特性认识一、实验目的1. 观察基本通信信号的时域波形,包括正弦信号、方波信号、三角波、锯齿波、SINC信号、exp rise、exp fall、noise、burst及调制的AM信号和FM信号;2. 利用傅里叶变化从频域分析基本模拟通信信号的频谱成分及带宽情况。
二、实验内容1.熟悉示波器的基本使用方法包括时间轴及幅度的手动和自动调整、run/stop、math menu、measrue、course等;2.熟悉函数信号发生器对各种波形的产生方法,包括正弦信号、方波信号(调节占空比)、三角波、锯齿波、任意波形(SINC信号、exp_rise、exp_fall等)、noise、burst及调制的AM信号(Fre及DEPTH)和FM信号。
3.熟悉并认识示波器数据采集软件wavestar的存储和使用方法。
4.使用函数信号发生器产生不同的信号,用示波器分别观察这些信号的时域波形及频谱成分。
5.设置函数信号发生器,改变其产生信号的不同参数,用示波器观察这些参数对时域信号波形的影响。
6.用数据采集软件采集不同参数的各种信号,存储相应的数据文件和波形文件,以便进行后期的数据处理。
数据采集过程中应注意使用奈奎斯特采样定理,并观察示波器(即:模拟-数字转换器)示波器是如何设定采样频率(采样间隔)的。
7.使用Matlab等仿真、分析软件,对采集到的各种信号进行频谱分析,并举例说明各种信号的带宽情况。
8.选取1~3种信号,写出其时域的数学表达式和对应的傅里叶变换表达式,将理论结果与实验结果进行对比验证,并分析之。
三、实验步骤1. 利用信号发生器产生相应的信号,并在示波器上观察信号的时域波形,并利用wavestar对时域波形进行保存;2. 利用示波器得到信号的频域波形,观察频域波形并保存;3. 设置函数信号发生器,改变一些信号波形的不同参数,用示波器观察这些参数对时域信号波形的影响;4. 对实验要求的几种信号依次进行上述操作,对于不同信号进行观察、分析。
信号与系统实验手册

信号与系统实验指导手册通信教研室编河南师范大学计算机与信息技术学院二O一O年三月目录实验1 实验仪表使用练习 (1)实验2 基于MATLAB的信号时域表示 (2)实验3 阶跃响应与冲激响应 (3)实验4 用MATLAB实现连续信号卷积 (6)实验5 信号卷积实验 (7)实验6 矩形脉冲信号的分解 (11)实验7 矩形脉冲信号的合成 (15)实验8 谐波幅度对波形合成的影响 (17)实验9 谐波相位对波形合成的影响 (20)实验10 抽样定理与信号恢复 (21)实验11 数字滤波器的设计 (28)实验12 用MATLAB进行信号频谱分析 (29)实验1 实验仪表使用练习一、实验目的1.了解课程中所使用的RZ8663信号与系统模块组成,及各部件的基本功能。
2.了解示波器在信号检测方面的使用方法,及频率计的使用方法。
二、实验内容熟悉信号与系统实验中所使用到的实验模块功能,熟练使用示波器观察信号波形。
三、实验步骤①打开RZ8663实验箱,观察其模块组成,了解各模块功能。
②给示波器加上电源,对自检信号进行校正。
③ J702置于“三角”,选择输出信号为“三角波”,拨动开关K701选择“函数”。
④默认输出信号频率为2KHz,按下S702使输出频率为500Hz。
⑤示波器的CH1接于TP702,观察信号源输出信号的波形。
⑥调整信号源输出信号的频谱及信号类型,重新在示波器上观察信号波形。
四、实验报告要求1.描绘频率为500Hz,2KHz下正弦波和三角波的波形,标明信号幅度A、周期T。
2.调整信号源,观察占空比为1/2的方波信号并画出其波形。
五、实验设备1. 双踪示波器1台2. 信号系统实验箱1台3. 导线若干实验2 基于MATLAB 的信号时域表示一、实验目的利用 MATLAB 实现信号的时域表示以及图形表示。
二、实验内容连续信号的MA TLAB 描述:列出单位冲激函数、单位阶跃函数、复指数函数的MATLAB 表达式。
正弦波方波三角波

课程设计名称:设计制作一个方波\三角波\正弦波\锯齿波发生器摘要函数信号发生器是一种能够产生多种波形,如三角波、锯齿波、矩形波(含方波)、正弦波的电路。
该电路可为实验室提供波形频率范围为0.02Hz~20kHz,幅值2v的稳定信号源。
大大降低了实验成本,有效的简化了实验的操作步骤,是实验室小型电路信号发生器的理想所选,具有广泛的应用价值。
此信号发生器采用模块化结构,主要由以下三个模块组成,即正弦波发生器模块、方波发生器模块、三角波发生器模块。
在设计此函数信号发生器时,采用模块化的设计思想,使设计起来更加简单、容易、条理清晰。
同时调试起来也更容易。
经过一系列的分析、准备,本次设计除在美观方面处理得不够得当之外,完成了全部的设计要求。
关键词:函数信号发生器、 LM324、集成运算放大器、晶体管差分放大目录前言 (4)第一章函数发生器的设计要求 (5)1.1 波形发生器的特点及应用 (5)1.2 设计任务及要求 (5)第二章电路设计原理及单元模块 (6)2.1 设计原理 (6)2.1 单元模块 (6)2.1.1 RC选频振荡模块 (6)2.1.2 过零比较器 (8)2.3.3 产生三角波模块 (9)第三章安装与调试 (12)3.1 电路的安装 (12)3.2 电路的调试 (12)3.2 电路的分析 (13)结论 (14)参考文献 (14)附录一 (15)附录二 (16)前言科学技术是第一生产力。
三次工业革命使我们的社会发生了翻天覆地的变化,使我们由手工时代进入了现代的电器时代。
同时科技在国家的国防事业中发挥了重要的作用,只有科技发展了才能使一个国家变得强大。
而作为二十一世纪的主义,作为一名大学生,不仅仅要将理论知识学会,更为重要的是要将所学的知识用于实际生活之中,使理论与实践能够联系起来。
波形发生器在实际生活中有很重要的作用,影响着科技的发展,在当今社会又好又快的生活方式是人们所向往的,因此作为一名学习知识的青年,应该学好基础知识,设计出是人民满意的东西,产出人性化和自能化的电子产品,另一方面电子产品不断的更新,需要我们更加扎实的基础。
实验三:波形产生电路

四、 实验内容
2) 对图 3.5.4 电路进行修改,使之变成矩形 波和锯齿波振荡电路,即 vO1为矩形波, vO2 为锯齿波。要求锯齿波的逆程(电压 下降段)时间大约是正程(电压上升段) 时间的20%左右。观测vO1、vO2的波形, 记录它们的幅度、周期(频率)等参数。
下次实验内容
题目:晶体管输出特性测试电路:
1)电阻R3= R4=10K,测出下面情况时vo 的波形 电位器RW阻值依次为0 , 10K, 15K, 20K
2) 调整电位器RW使vo 为正弦波(不能失真)且 幅值最大,用示波器测出vo 的频率和峰值。并 测出电位器 RW 的阻值,分析电路的振荡条件。 3)将两个二极管断开,观察输出波形有什么变化。
实验三 波形产生电路
一 、 实验目的
1.
通过实验掌握由运放构成的正弦波振荡 电路的原理与设计方法。 2. 通过实验掌握由运放构成的方波(矩形 波)和三角波(锯齿波)振荡电路的原理 与设计方法。 3*.了解运放摆率对振荡波形跳变沿的影 响。
二、 实验任务
正弦波、三角波及脉冲方波的产生。 实验要求: (1)正弦波振荡电路的内容, 起评分70分 ( 2 )在( 1 )的基础上另作多谐振荡电路的方波 及三角波的产生 起评分85分 (3)在(2)的基础上另作多谐振荡电路的矩形 波及锯齿波的产生 起评分100分
三、实验电路在实验性上的位置
实验用元件为两只A741,已经插在实验向上。
四、 实验内容
1. RC桥氏正弦振荡电路
R2 16k R1 16k C2 0.01F D1 D2
vf
C1 0.01F
+ A
-
vo
a
R3 10k
RW b 47k
R4 10k
实验三 周期信号的频谱分析

实验三 周期信号的频谱分析一、实验目的1、掌握连续时间周期信号的傅里叶级数的物理意义和分析方法;2、观察截短傅里叶级数而产生的“Gibbs 现象”,了解其特点以及产生的原因;3、掌握各种典型的连续时间非周期信号的频谱特征 二、原理说明:1、连续时间周期信号的傅里叶级数分析任何一个周期为T 1的正弦周期信号,只要满足狄利克利条件,就可以展开成傅里叶级数。
其中三角傅里叶级数为:∑∞=++=1000)]sin()cos([)(k k k t k b t k a a t x ωω 2.1或: ∑∞=++=100)cos()(k k kt k ca t x ϕω 2.2其中102T πω=,称为信号的基本频率(Fundamental frequency ),k k b a a ,和,0分别是信号)(t x 的直流分量、余弦分量幅度和正弦分量幅度,k k c ϕ、为合并同频率项之后各正弦谐波分量的幅度和初相位,它们都是频率0ωk 的函数,绘制出它们与0ωk 之间的图像,称为信号的频谱图(简称“频谱”),k c -0ωk 图像为幅度谱,k ϕ-0ωk 图像为相位谱。
三角形式傅里叶级数表明,如果一个周期信号x(t),满足狄里克利条件,那么,它就可以被看作是由很多不同频率的互为谐波关系(harmonically related )的正弦信号所组成,其中每一个不同频率的正弦信号称为正弦谐波分量 (Sinusoid component),其幅度(amplitude )为k c 。
也可以反过来理解三角傅里叶级数:用无限多个正弦谐波分量可以合成一个任意的非正弦周期信号。
指数形式的傅里叶级数为:∑∞-∞==k tjk kea t x 0)(ω 2.3其中,k a 为指数形式的傅里叶级数的系数,按如下公式计算:⎰--=2/2/1110)(1T T tjk k dt et x T a ω 2.4指数形式的傅里叶级数告诉我们,如果一个周期信号x(t),满足狄里克利条件,那么,它就可以被看作是由很多不同频率的互为谐波关系(harmonically related )的周期复指数信号所组成,其中每一个不同频率的周期复指数信号称为基本频率分量,其复幅度(complex amplitude )为k a 。
示波器的使用学生实验报告

广州大学学生实验报告
,左端为一电子枪,电子枪加热后发出一束电子,电子经电场加速以高速打在右
,屏上的荧光物发光形成一亮点。
亮点在偏转板电压的作用下,
在一定范围内,亮点的位移与偏转板上所加电压成正比。
图扫描的作用及其显示
Y轴偏转板上加正弦电压,而X轴偏转板不加任何电压,则电子束的亮点在纵方向随时间作正弦式振荡,在横方向不动。
我们看到的将是一条垂直的亮线,如图
如果在Y轴偏转板上加正弦电压,又在X轴偏转板上加锯齿形电压,则荧光屏上的亮点将同时进行方向互相垂直的两种位移,其合成原理如图所示,描出了正弦图形。
如果正弦波与锯齿
如果已知f x,则由李萨如图形可求出f y。
4 A 模式,水平轴为时间轴
4 XY 模式,显示李萨如图形
5 单次扫描
5 非自动扫描 5 自动扫描
6 时间分度,按下为微调状态
8 打开通道1
9 纵轴分度,表示纵轴上一格代表多大电压
10 波形上下移动
11 输入信号。
fft谱分析实验报告

fft谱分析实验报告FFT谱分析实验报告引言:谱分析是一种常用的信号处理方法,它可以将信号在频率域上进行分析。
傅里叶变换是一种常见的谱分析方法,而快速傅里叶变换(FFT)是一种高效的傅里叶变换算法。
本实验旨在通过使用FFT算法对不同信号进行谱分析,探究其在信号处理领域的应用。
实验目的:1. 了解FFT算法的原理和基本步骤;2. 掌握使用FFT算法进行信号谱分析的方法;3. 分析不同信号的频谱特征,探索信号处理的应用。
实验仪器和材料:1. 个人计算机;2. MATLAB软件。
实验步骤:1. 准备信号样本:选择不同类型的信号样本,如正弦信号、方波信号和三角波信号,并将其存储为.mat格式的文件。
2. 打开MATLAB软件,并载入信号样本文件。
3. 对信号样本进行FFT变换:使用MATLAB中的fft函数对信号样本进行FFT变换,得到信号的频谱。
4. 绘制频谱图:使用MATLAB中的plot函数将信号的频谱绘制出来,可以选择使用线性坐标或对数坐标进行展示。
5. 分析频谱特征:观察频谱图中的峰值位置、幅值大小等特征,分析不同信号的频谱特征。
实验结果与分析:1. 正弦信号的频谱特征:正弦信号在频谱上呈现出单个峰值,峰值位置对应着信号的频率,峰值的幅值表示信号的强度。
2. 方波信号的频谱特征:方波信号在频谱上呈现出多个峰值,峰值位置对应着信号的谐波频率,峰值的幅值表示谐波的强度。
3. 三角波信号的频谱特征:三角波信号在频谱上呈现出多个峰值,峰值位置对应着信号的谐波频率,峰值的幅值表示谐波的强度。
结论:通过本实验,我们了解了FFT算法的原理和基本步骤,并掌握了使用FFT算法进行信号谱分析的方法。
通过对不同信号样本的频谱分析,我们发现不同信号在频谱上呈现出不同的特征。
正弦信号的频谱呈现单个峰值,方波信号和三角波信号的频谱呈现多个峰值。
这些频谱特征可以帮助我们了解信号的频率分布和强度分布,对信号处理和信号识别具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、实验原理:
1.非正弦周期函数的傅立叶分解 (1).定义 如果给定的周期函数 f (t ) 满足狄里赫利条件(函数在任意有限区间内,具有有限个极 值点与不连续点) ,则该周期函数定可展开为一个收敛的正弦函数级数,如下式:
∞
f (t ) = a 0 + = A0 +
2 T 2 T
∫
T 2 T − 2
f (t ) cos(kωt )dt =
1 2π 1 π f (t ) cos(kωt )d (ωt ) = ∫− π f (t ) cos(kωt )d (ωt ) ∫ 0 π π
bk =
T
f (t ) sin( kωt )dt =
∫−2T
T
f (t ) sin( kωt )dt =
Re 2 (k ) + Im 2 (k ) ,相位谱为 ϕ (k ) = arctan
Im(k ) 。计算出的频谱为峰值 Re(k )
频谱,对周期信号而言,谱线的高度仅为付氏频谱谱线高度的一半。当用有效值
X (k ) 。 (RMS)表示幅值频谱时, X (k ) = RMS 2
f ∆f = s N 。
1 T f (t )e − jkωt dt , c 0 = a 0 T 0 2).幅度频谱与相位频谱
∫
体现| c k |与频率之间的关系的谱线,称为幅度频谱。 由于指数级数中的 k 可以分别取相应的正负值,因此幅度频谱关于 Y 轴对称;而其谱 线的高度仅为付氏频谱谱线高度的一半。例如方波
Akm
f(t) A t
f(t) A t T 图 3 锯齿波 2T 3T
f (t ) =
A A 1 1 1 2π + (sin ωt + sin 2ωt + sin 3ωt + sin 4ωt + ) ,其中 ω = 2 π 2 3 4 T
2.频谱 (1).非正弦周期函数的频谱 对某函数以频率为横轴, 各个频率对应的正弦函数的幅值为纵轴所绘出的线段系称为该 函数的频谱。 对于周期函数而言,其频谱为一系列谱线。如 方波
3.使用上面设计的程序,分别选择波形为正弦、方波、三角波、锯齿波,改变信号 频率和幅度,选择适当的采样率和采样点,分析正弦、方波、三角波、锯齿波信号的频谱, 并与理论计算值比较。 4.被测信号叠加噪声后,再进行测量和分析误差。
4.在 LabVIEW 中的频谱分析 VI
在 LabVIEW 中实现频谱分析计算的 3 个层次的 VI 分别为 Express Ⅵ中的 Spectral Measurements.vi ,波形 VI 中的 FFT Spectrum (Mag-Phase).vi 和 FFT Spectrum
(Real-Im).vi ,基本函数 VI 的 Amplitude and Phase Spectrum.vi。 (1)Express Ⅵ中的 Spectral Measurements.vi 到达途径为 Functions → Signal Analysis,主要参数有:①选择不同的谱分析种类(Spectral Measurement):峰值频谱,均 方值(RMS)频谱,功率谱和功率谱密度。②幅度单位:线性还是分贝 dB。③窗函数 Window 的类型。 ④平均 Averaging 参数: 有平均模式 Mode、 平均权重 Weighting、 平均次数 Numbers of averages 和平均输出类型 Produce spectrum。⑤相位谱输出的变换:反卷及将弧度转换 为度。 ( 2 ) 波 形 VI 中 的 FFT Spectrum(Mag-Phase).vi 的 参 数 设 置 及 定 义 与 Spectral Measurements.vi 的相似,其输入输出端口如下所示。
2) 3) 4)
各节点之间的频率间隔由时间长度 N 和采样频率 fs 决定: 第 k 个节点对应的频率值为 有一半数据有意义。
f (k ) = k ⋅ fs N 。
FFT形成的频谱相对于折叠频率f S /2 对称,FFT的输出频率范围为 0~f S /2。实际只
用 DFT 进行测试信号频域特性分析存在主要误差有量化误差、混叠误差、频谱泄漏和 栅栏效应等,减少计算误差的办法有,增加 A/D 的有效位数,提高采样频率,增加采样时 间和采样点数,整周期采样或加窗处理等。
2π N −1 −j nk N X ( k ) = ∑ x ( n )e k = 0,1,2..., N − 1 n =0 DFT 和 IDFT: 2π N −1 n = 0,1,2..., N − 1 j nk x ( n) = 1 N x k e ( ) ∑ N n =0 为了方便显示,做归一化处理,用 X ( k ) N 来表示频谱。此外,由上式计算出的频谱
−j 2π n N −
。再用
(其实部为零) 。
(3)采用双循环,计算 X(k),见图。 。 。的左上部分。内外循环的循环次数都为 N。内 循环改变 n,累加求和,计算 ∑ x(n)e
n =0 N −1 −j 2π nk N
,累加求和需要使用移位寄存器。先使用 Index
Array 函数从数组中得到第 n 个元素,再相乘。外循环中再改变 k。 ( 4 ) 将 X(k) 转 换 为 幅 度 谱 和 相 位 谱 。 计 算 公 式 为 : 有 效 值 幅 度 谱 为
先固定 k,内循环累加求和,计算 ∑ x(n)e
n =0
N −1
−j
2π nk N
,再改变 k,外循环。最后将 X(k)转换为幅
度谱和相位谱。设计中要用到数值运算子模板中的 Complex Functions 复数处理函数。 (1)产生仿真信号。打开 3.5 节第 2 个实验内容的程序,它能够产生频率、幅值和 直流偏值可调的正弦、方波、三角波、锯齿波信号,还可叠加高斯噪声信号,并且采样率和 采样点可选。 (2)计算 = n 0,1, 2..., N − 1 ,结果为 1 个数组,见图
图 DFT 计算频谱的程序
2.使用 LabVIEW 提供的频谱分析函数:波形 VI 中的 FFT Spectrum(Mag-Phase).vi, 分析仿真信号的频谱。 提示:仍然使用 3.5 节第 2 个实验内容的程序产生仿真信号。频谱计算采用 FFT Spectrum(Mag-Phase).vi 。 把 鼠 标 放 在 FFT 函 数 的 输 入 端 口 右 击 , 在 弹 出 窗 口 中 选 择 “Create->Control”即产生窗函数类型选择和平均参数选择控件,在用控件选择幅度显示单 位和相位的显示。参考程序入图所示。前面板如下图所示:
0.5T
4A/π
|ck | 2A/π 2A/π
4A/5π 4A/7π 7ω ω
4A/3π ω
-A T
2A/7 π 2A/5π 2A/3π ω ω ω ω ω
2A/3π 3ω
2A/5π 2A/7π 5ω 7ω ω
3 ω 5ω
图 7(a) 方波的傅立叶频谱
图 7 方波及其傅立叶频谱、幅度谱
3.信号的离散傅立叶变换(DFT) 模拟信号x(t)经采样后变为离散时间序列x(n),T S 为采样周期,采样频率fs=1/T S 。计算 机中的处理的信号是有限长度的离散信号x(n),对应的离散频谱为X(k)。时域与频域转换使 用的算法是离散傅里叶变换(DFT)和反变换(IDFT) ,计算公式如下:
∑ (a
k =1 ∞
k
cos kωt + bk sin kωt ) cos(kωt + ψ k )
∑A
k =1
km
其中,上式中的各个系数的计算公式为:
a0 =
1 T 2 T 2 T
∫0
T
f (t )dt =
1 T
∫
T 2 T − 2
f (t )dt
T 为信号的周期。
ak =
∫0 ∫0
T
f (t ) cos(kωt )dt =
O ω
A/2π A/3π A/4π 2ω 3ω 4ω ω
图 6 锯齿波的傅立叶频谱
(3). 傅立叶变换与频谱函数 1).周期函数的傅立叶级数的指数形式
= k 1= k 1
f (t ) = a0 + ∑ (ak cos kωt + bk sin kωt ) = a0 + ∑ [ak (
∞ (a − jbk )e jkωt −∞ (ak − jbk )e jkωt = a0 + ∑ k +∑ 2 2 k =1 k = −1
−j 2π n N
的右下部分。采样点数
2π N
N 从仿真波形产生函数的采样信息簇得到,使用簇 cluster 子模板中的 Unbundle 函数实现。 采用一个循环次数为 N 的 For 循环产生元素为 0,1,…,N-1 的 1 维数组,乘以 复数处理函数中的 Re/Im To Complex,组合为复数
f(t) A t
0.5T
-A T 图 1 方波
f (t ) =
2)三角波
4A 1 1 1 2π (sin ωt + sin 3ωt + sin 5ωt + sin 7ωt + ) ,其中的 ω = π 3 5 7 T
f(t) A t T -A 图 2 三角波
f (t ) =
3)锯齿波
8A 1 1 1 2π (sin ωt − sin 3ωt + sin 5ωt − cos 7ωt + ) ,其中的 ω = 2 π 9 25 49 T
五、实验步骤:
1.设计 DFT 变换程序,求取仿真信号的幅值频谱和相位谱。 (要求仅采用基本数学 函数实现) 。 分析:DFT 计算公式为: X (k ) = ∑ x(n)e
