力矩-转动定律-转动惯量知识
合集下载
力距 转动定律 转动惯量

r dr
+
0
t
1 0 2 0 0t ( )t t 2 t 2
0 t
r R
3 R0 t 0 4 mg
2
例2
一质量为
m 、长为 l
的均匀细长棒,求
通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
r
dr
dr l 2 O´
O´
l
解 设棒的线密度为 ,取一距离转轴 OO´ 为 2 2 处的质量元 dm dr dI r dm r dr
r
I 2
l/2
0
1 3 r dr l 12
例 一根长为l、质量为m的均匀细直棒,其一端有一固定 的光滑水平轴,因而可以在竖直平面内转动。最初棒静止 在水平位置,求它由此下摆θ角时的角加速度和角速度。 (已知棒对O轴的转动惯量为 I 1 ml 2)
解:(1)计算棒所受重力对O轴的力矩
棒在下摆任意θ角时,质元dm所受重 力对O轴的力矩大小是 xdmg 棒所受重力对O轴的力矩
因与L无关,所以该式也是均质圆环对oz 的转动惯量。
1 2 2 I z m( R1 R2 ) 2
讨论:
(1)若内半径R1 =0,得均质实心圆柱体对oz 的转动惯量:
1 2 I z mR2 2
均质圆盘对oz 的转动惯量
(2)若圆筒壁很薄R1≈ R2 = R, 得薄圆筒对oz 的转动惯量:
薄圆柱壳的体积 薄圆柱壳的质量
dV 2rdrL, dm dV
2 3
薄圆柱壳对oz 的转动惯量
dI z r dm r 2 rdrL L 2 r dr
2
o
力矩转动定律转动惯量解析课件

02
CATALOGUE
转动惯量基础概念
转动惯量的定义
转动惯量
描述刚体绕固定轴转动的惯性大 小的物理量。
定义公式
I = Σ(m * r^2),其中m为刚体的 质量,r为刚体上任意质点到转动 轴的距离。
转动惯量的性质
转动惯量只与刚体的质量分布 和转动轴的位置有关,与刚体 的运动状态无关。
对于同一刚体,不同的转动轴 位置,其转动惯量可能不同。
力矩转动定律转动 惯量解析课件
contents
目录
• 力矩转动定律概述 • 转动惯量基础概念 • 力矩与转动惯量的关系 • 转动惯量的计算方法 • 转动惯量的应用实例
01
CATALOGUE
力矩转动定律概述
力矩的定义
力矩是描述力的转动效果的物理量,其大小等于力和力臂的乘积。
力矩是一个向量,其大小等于力和力臂的乘积。力臂是从转动轴到力的垂直距离 。在二维平面中,力矩可以表示为M=F×r,其中F是力,r是力臂。
CATALOGUE
转动惯量的应用实例
飞轮的设计与优化
飞轮的设计
飞轮是利用转动惯量储存能量的重要 装置,其设计需要考虑转动惯量的大 小、质量分布、转速等因素。
飞轮的优化
为了提高飞轮的储能效率和稳定性, 需要对飞轮进行优化设计,如采用轻 质高强度的材料、优化飞轮的形状和 尺寸等。
陀螺仪的设计与优化
陀螺仪的设计
陀螺仪是利用角动量守恒原理工作的惯性导 航和姿态测量器件,其设计需要考虑转动轴 的稳定性、转动惯量的大小和分布等因素。
陀螺仪的优化
为了提高陀螺仪的测量精度和稳定性,需要 对陀螺仪进行优化设计,如采用高性能的轴 承材料、减小摩擦力矩等。
电机转子的设计与优化
一,刚体的定轴转动(运动)二,力矩,刚体定轴转动的转动定律,转动惯量

二、刚体定轴转动的转动定律
~利用力矩定义+牛顿第二定律,研究刚体作定 轴转动的动力学规律。 设:oz为定轴, 为 P 刚体中任一质点 i ,其 质量为 ∆ m i。质点 iv ur 受外力 F i ,内力 F i ′ 的作用,均在与 O z 轴 相垂直的同一平面内。 ①牛顿第二定律: ur r v F i + Fi ′ = ∆ m i a i 建立自然坐标:切向、法向;
三、转动惯量 J 1.转动惯量的物理意义: 当以相同的力矩分别作用于两个绕定轴转动的不同 刚体时,它们所获得的角加速度一般是不一样的,转 动惯量大的刚体所获得的角加速度小,即角速度改变 得慢,也就是保持原有转动状态的惯性大;反之,转 动惯量小的刚体所获得的角加速度大,即角速度改变 得快,也就是保持原有转动状态的惯性小。因此,转 动惯量是描述刚体在转动中的惯性大小的物理量。 2.与转动惯量有关的因素:①刚体的质量;②转轴的 位置;③刚体的形状。 实质与转动惯量有关的只有前两个因素。形状即质量 分布,与转轴的位置结合决定转轴到每个质元的矢径。
R 3
例3、求长为L、质量为m的均匀细棒对图中不同轴的 转动惯量。 B 解:取如图坐标,dm=λdx A
J
A
=
∫
∫
L
0
x 2 λ dx = mL 2 / 3
A
x λ dx = mL
2 2
JC =
L 2 L − 2
L C L/2 L/2
X B X
/ 12
例4. 求质量 m ,半径 R 的球壳对直径的转动惯量 解:取离轴线距离相等的点的 集合为积分元
F i t ri + F i t′ ri = ∆ m i ri 2 α
外力矩 内力矩
③对所有质元的同样的式子求和:
定轴转动刚体的转动定律度力矩角动量转动惯量

Iz Ix Iy
z
定理证明:
对于质量平面分布的刚体, 绕 x 轴的转动惯量为:
o
yy
Ix y2dm
x
dm
绕 y 轴的转动惯量为:
I y x2dm
x
绕 z 轴的转动惯量为:
19
z
Iz z2dm (x 2 y2 )dm
y2dm x 2dm I x I y 证毕
o
yy
x z dm
0
M
绕圆环质心轴的转动惯量为
dm
oR
I MR2
例2:在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的 质点,可绕 o 轴转动,求:质点系的转动惯量I。
解:由转动惯量的定义
I
2
mi ri 2
2mb 2
m
(3b)2
11mb 2
i 1
9
例3: 如图所示,一质量为m、长为l的均质空心圆柱
体(即圆筒圆筒)其内、外半径分别为R1和R2。试求
的质元受阻力矩大,
细杆的质量密度 m
l
质元质量 dm dx
o
xl dm m dx
x
质元受阻力矩:
dM 阻 dmgx
细杆受的阻力矩
m l
M阻
dM
阻
0l
gxdx
1 2
gl 2
1 2
mgl
4
二、定轴转动刚体的角动量
1 .质点对点的角动量
L
r
P
r
mv
作圆周运动的质点的角动量L=rmv;
l
x2dm
L
x2dx
1 L3
0
1 mL2
0
3
A
力矩、转动定律、角动量守恒

mgl 1 mgl 1 mv2 v gl 4g
2
2
l
P24 1-6: As shown in below figure, the body A is connected to the body B by the light rope which is through uniform solid cylinder(圆柱体) with a mass Mand a radius R. The body A has a mass of m1 and the mass of B is m2.There is not relative motion between the rope and cylinder. Find the tension force between the solid cylinders with
a R
(4)以上三式联立,可得物体 下落的加速度和张力:
a
m2
m2
m1 2
g
T m1m2 g 2m2 m1
m2 R(m2
m1 ) 2
g
o m1
m2 x
P34.习题19 质量为m、长为L的均质细杆可绕水平光滑轴O在竖直 平面内转动。若使杆从水平位置开始由静止释放,试求杆转至铅垂
T=?
J 1 MR2 2
M,R
m1 A
B m2
解:⑴ 研究对象:A、B和圆柱体; ⑵ 受力分析如图:
A向上运动,有加速度aA,B向下运动,加速 度aB,圆柱体顺时针转动。
T
T
T
A
B
T
m1g m2g
T
T1
T2
T2
(3)列方程:
4-2 力矩 转动定律 转动惯量
19
物理学 第六版
4-2 力矩 转动定律 转动惯量
解 (1) 用隔离法分 别对各物体作受力分析, 取如图所示坐标系.
A
mA
FN
mA FT1
PA
O
x
C
mC
mB B
FT1
FC
PC
FT2
FT2
O
mB
PB y
第四章 刚体转动与流体运动
20
物理学 第六版
4-2 力矩 转动定律 转动惯量
第四章 刚体转动与流体运动
1
物理学 第六版
4-2 力矩 转动定律 转动惯量
讨论
(1)若力
F
不在转动平面内,把力分
解为平行 和垂 直于 转轴方向的两个分量
F
Fz
F
其中 Fz对转 轴的
力矩为零,故 F 对转
轴的力矩 M zk
r
F
z
F
k
O rFz
F
M z rF sin
索跨过一半径为R、质量为mC的圆柱形滑轮 C,并系在另一质量为mB 的物体B上,B 竖 直悬挂.滑轮与绳索间无滑动, 且滑轮与
轴承间的摩擦力可略去不计.(1)两物体的 线加速度为多少? 水平和竖直两段绳索的
张力各为多少?(2) 物体 B 从静止落下距 离 y 时,其速率是多少?
第四章 刚体转动与流体运动
4
物理学 第六版
4-2 力矩 转动定律 转动惯量
解 设水深h,坝长L,在坝面上取面积 元 dA Ldy ,作用在此面积元上的力
dF pdA pLdy
转动定律、转动惯量讲解
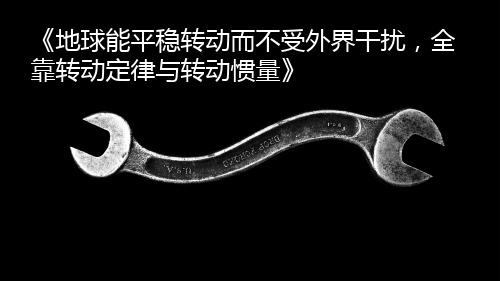
Fit*ri+Fit'*ri= Δmi*(ri^2)*α
这是一个质点的规律,如果把所有的质点加起来,即∑Fit*ri+∑Fit'*ri= ∑Δmi*(ri^2)*α,因为刚体内部质点间的合力对转轴的力矩为零,即∑Fit'*ri= 0, 于是就有∑Fit*ri = ∑Δmi*(ri^2)*α,等式左边表示刚体所有质点所受外力对转轴 的力矩,也就是合力矩M;
《地球能平稳转动而不受外界干扰,全 靠转动定律与转动惯量》
上一章讲了刚体的定轴转动与角速度和角加速度的概念,如果有外力作用在刚体 上,那么刚体会发生什么变化呢?这就是本章要讲到的力矩、转动定律以及转动 惯量等概念。
首先来说力矩,在如图1所示的坐标系中,有一外力F作用在刚体内的P点,刚体 相对于原点的位置矢量为r,显然力F不经过原点O,于是把从O点到力F延长线的 垂直距离d叫做力F对转轴的力臂,其大小d=rsinθ ,而力F的大小和力臂d的乘积 Frsinθ 就叫做F对转轴的力矩,用大写字母M表示,力矩除了有小外,也有方向,
为了深刻理解转动惯量,以地球的转动惯量公式Je = (2mR^2)/5为例子,将地 球质量和半径带入式子可知,地球在转动时转动惯量非常大,根据转动定律可知, 需要非常大的力矩才能使地球加速或者减速,对于地球表面的所有物体而言,没 有哪个物体可以提供这样的力矩,这也就是地球平稳转动的原因。
讲完了转动定律,下一章《芭蕾舞演员的旋转加速秘诀-角动量守恒》将继续讲 解角动量。
而等式右边表示的量只与刚体的形状、质量、刚体的转轴有关。这个量就叫做转 动惯量,用大写字母J表示。于是等式可以表示为:M=J *α。这就是刚体的转动 定律,它的形式对应牛顿第二定律,其物理意义就是在同一力矩下,转动惯量大 的刚体,获得的角加速度就小,转动惯量小的刚体获得的角加速度就大。
这是一个质点的规律,如果把所有的质点加起来,即∑Fit*ri+∑Fit'*ri= ∑Δmi*(ri^2)*α,因为刚体内部质点间的合力对转轴的力矩为零,即∑Fit'*ri= 0, 于是就有∑Fit*ri = ∑Δmi*(ri^2)*α,等式左边表示刚体所有质点所受外力对转轴 的力矩,也就是合力矩M;
《地球能平稳转动而不受外界干扰,全 靠转动定律与转动惯量》
上一章讲了刚体的定轴转动与角速度和角加速度的概念,如果有外力作用在刚体 上,那么刚体会发生什么变化呢?这就是本章要讲到的力矩、转动定律以及转动 惯量等概念。
首先来说力矩,在如图1所示的坐标系中,有一外力F作用在刚体内的P点,刚体 相对于原点的位置矢量为r,显然力F不经过原点O,于是把从O点到力F延长线的 垂直距离d叫做力F对转轴的力臂,其大小d=rsinθ ,而力F的大小和力臂d的乘积 Frsinθ 就叫做F对转轴的力矩,用大写字母M表示,力矩除了有小外,也有方向,
为了深刻理解转动惯量,以地球的转动惯量公式Je = (2mR^2)/5为例子,将地 球质量和半径带入式子可知,地球在转动时转动惯量非常大,根据转动定律可知, 需要非常大的力矩才能使地球加速或者减速,对于地球表面的所有物体而言,没 有哪个物体可以提供这样的力矩,这也就是地球平稳转动的原因。
讲完了转动定律,下一章《芭蕾舞演员的旋转加速秘诀-角动量守恒》将继续讲 解角动量。
而等式右边表示的量只与刚体的形状、质量、刚体的转轴有关。这个量就叫做转 动惯量,用大写字母J表示。于是等式可以表示为:M=J *α。这就是刚体的转动 定律,它的形式对应牛顿第二定律,其物理意义就是在同一力矩下,转动惯量大 的刚体,获得的角加速度就小,转动惯量小的刚体获得的角加速度就大。
4-2-力矩-转动定律-转动惯量jm

方向: 服从右手螺旋法则
2、刚体的定 轴 转动定律
M J
d: 力臂
Z
R Om
40
二 转动惯量
➢ 离散质点系 J miri2 ➢ 连续质点系 J r 2dm
* r: 质点到转轴的垂直距离
➢ 平行轴定理 J Jc md 2
41
➢ 常用的转动惯量公式
m质点:J r2m 圆盘(圆柱): J 1 mR2
7
(2)刚体内作用力和反作用力的力矩 互相抵消.
刚体对转轴的合内力矩为零。
Mij 0
Z
M
O
rj
i
j F
d ri F
M
Mij M M Fd Fd 0
8
5、求合力矩
M rF
M Frsin Fd
R+ T
r
R
T1
T2
对转轴:M TR 转对轴:M T2R T1r
9
FT1
2L
o d
26
➢ 转动定律应用 M J
说明
(1) M J , 与 M 方向相同
(2) 为瞬时关系
(3) 转动中M J与平动中F ma
地位相同
27
例: 一定滑轮的质量为 m ,半径为 r ,一轻绳
两边分别系 m1 和 m2 两物体挂于滑轮上,绳不伸
长,绳与滑轮间无相对滑动。不计轴的摩擦,初角 速度为零,求滑轮转动角速度随时间变化的规律。
圆环:J mR 2 更稳定ຫໍສະໝຸດ 飞轮的质量为什么 大都分布于外轮缘?
定轴转动定理
M J
M / J
25
定轴转动定理 M J
细棒绕其一端 J 1 mL2
竿 子
3
长
大学物理-力矩、转动定律、转动惯量

gh
yLdy
1 2
p0 Lh 2
1 6
gLh2
h
y
o
L
dA
x
dy
y
Q
dy
x
二、转动定律
质点的动力学问题 刚体的动力学问题
F ma
M
设刚体有n个质点组成,
先取任一质点i来研究
mi ri
外力:Fi 内力:Fi
由牛 顿第二定律得: Fi Fi miai
切线方向:Fit Fit miait
X
dV r2dZ (R2 Z 2 )dZ
其质量:dm dV (R2 Z 2 )dZ
其转动惯量:dJ 1 r 2dm 1 (R2 Z 2 )2 dZ
2
2
dJ 1 r 2dm 2
1 (R2 Z 2 )2 dZ
2
Z r dZ
O
R
Y
J dJ
X
R 1 (R2 Z 2 )2 dZ
比较
牛顿第二定律 F m a
转动定律
M J
三、转动惯量 J miri2 (4 9)
对质量连续分布的刚体 J r 2dm (4 11)
转动惯量的单位:kg m2
影响转动惯量得因素
注意:
(1)、刚体的质量(材料) (2)、刚体质量的分布
质点也有转动惯量
J mr2
(3)、转轴的位置
对质量不连续分布的刚体 J m 2
R 2
8 R5 2 mR2
m 4 R3
3
15
5
例3)求一质量为m的均匀实心球对其一条直径
为轴的转动惯量。
Z x
解:方法二 在球上取一体积元
dV
dV dxdydz
7-31 刚体定轴转动的力矩 转动定律 转动惯量
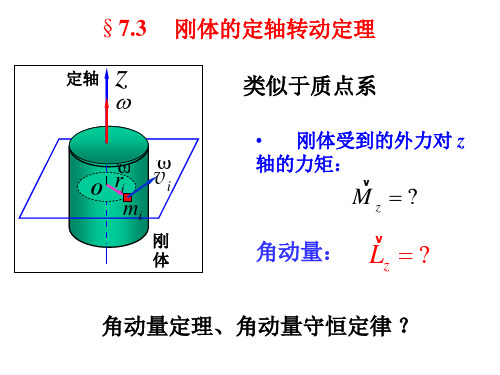
r dr
dm 2 rdr
对转动惯量的贡献为: 所以有:
m
2
R
dI r dm 2 r dr
0
I 2
1 2 r dr mR 2
3
常用的几个转动惯量:
质 点:
C R m
I mr 2
均匀圆环:
C R
m
I c mR
2
均匀圆盘: 均匀杆:
I c垂直
1 2 mR 2
3、绕一端轴,杆的转动惯量
x dx
例2、均质细圆环的转动惯量 任取线元dl , dm=dl,距离轴 r
ω m r
I r dm r
2
2
dm m r
2
例3、质量为m,半径为R 的均质圆盘的转动惯量 可看作由半径不同的圆环构成,盘面 m 单位面积的质量为
ω
R
3
0
R2
任取面元ds(离r 远处dr 宽细环)
1 2 I A ml 3
A
C l 2 l 2
m
1 2 I c ml 12
另外一些参见P224表7.1。
3、计算 I 的几条规律:
1)对同一轴 I 具有可叠加性
JC C d J m 2)平行轴定理 平行
I Ii
I Ic md
2
d --两平行轴距离
2) 平行轴定理 质量为 m 的刚体,如果对 其质心轴的转动惯量为 J C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量
(m1 m2 ) gR M f 1 (m1 m2 m) R 2 2
不计轴上摩擦、不计滑轮质量(Mf = 0, m = 0)
T1 T2
§4.2 力矩 转动惯量 转动定律
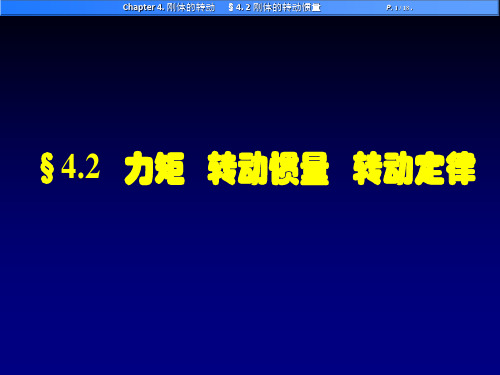
Fi
3. Mz、J、皆对同一轴而言。
fi
n
ri Fi ri fi ( miri2)
i
i
i 1
o ri
f
i
mi
Fi
n
ri Fi J i1
Mz J ( 转动定律 )
Chapte作r 4者. 刚:体杨的茂转田作动者:§杨4.茂2 田刚体的转动惯量
P. 27 / 18 .
1. Mz J 反映了力矩 Mz与角加速度 间的瞬时关系。
P. 29 / 18 .
例 已知细杆长l、质量 m,初角速度为0,细杆与桌面
间有摩擦,经 t0 时间后杆静止,求摩擦力矩 M阻。
解:细杆只受摩擦力矩,且为恒力矩,由 Mz J 可
知,细杆作匀变速转动:
m, l
而 J 1 ml 2 3
0 t
0 t0 0
0
t0
M阻 J
ml 2 3t 0
i 1
二、转动惯量
n
J miri2 i 1
mi
m3
ri
r3
r2
r1 m1
m2
1 2
(
n i1
mi ri2
) 2
Ek
1( 2
n i1
mi ri2
) 2
Chapte作r 4者. 刚:体杨的茂转田作动者:§杨4.茂2 田刚体的转动惯量
P. 9 / 18 .
n
可知: 一定时, miri2越大,刚体转动动能亦越大。
i 1
n
ri Fi J i1
Mz J
Fi fi
o ri
F ma
f
i
mi
Fi
( 转动定律 )
Chapte作r 4者. 刚:体杨的茂转田作动者:§杨4.茂2 田刚体的转动惯量
力矩转动定律转动惯量jm汇总课件

力矩的物理意义
总结词
力矩描述了力使物体绕某点转动的趋势或转动效果。
详细描述
力矩决定了物体绕某点转动的趋势或转动效果,其方向与力和力臂的乘积方向 相同。力矩越大,物体转动的趋势或转动效果越明显。
力矩的计算方法
总结词
力矩的大小等于力和力臂的乘积,计中力臂是从转动轴(或转动中心)到力的垂 直距离。计算公式为 M=FL,其中 M 为力矩,F 为力,L 为力臂。同时,力矩的 方向与力和力臂的乘积方向相同。
转动惯量的大小决定了物体旋转运动 的加速度、角速度和角动量等参数的 变化规律,进而影响物体的运动状态 和稳定性。
转动惯量的计算方法
转动惯量的计算方法主要包括平行轴定理和垂直轴定理。
平行轴定理指出,对于一个质量分布均匀的刚体,其相对于某固定轴的转动惯量,等于该刚体的质量乘以质心到该轴的距离 的平方,再加上所有相对于此轴的离散质量的转动惯量之和。垂直轴定理则说明,一个质量分布均匀的刚体相对于任一垂直 于其对称平面的轴的转动惯量,等于该刚体的质量乘以其对称轴到质心的距离的平方。
车辆工程
在车辆工程中,力矩转动定律用于分析车辆动力学和稳定性 问题。例如,通过分析车轮的力矩,可以研究车辆的操控性 能和行驶稳定性。
力矩转动定律在科研中的应用
物理学研究
力矩转动定律是物理学中分析转 动问题的基本原理,广泛应用于 分析天体运动、刚体动力学等问 题。
生物学研究
在生物学研究中,力矩转动定律 用于分析生物体的运动和平衡机 制,如动物的行走、飞行等。
动惯量。
实验步骤
2. 将刚体安装到实验装置上 ,调整力矩计和角位移传感
器的位置和角度。
1. 准备实验器材:刚体、力 矩计、角位移传感器、数据
42力矩转动定律转动惯量
dm ——质量线密度 dl
dm r dl
r1
m1
J mr 2
m2
(2)质量离散分布刚体的转动惯量 J m j rj2 m1r12 m2r22 (3)质量连续分布刚体的转动惯量
J r 2 dm
j
r2
r3m3转轴来自dm:质量元15
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
F :垂直于转轴的分力;
F F F
k
O
F
F
r
P
F
M r F 大小: M rF sin rd
方向: 右手螺旋法则
4
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
对于作定轴转动的刚体,一般规定: 如力矩使刚体沿逆时针方向转动,力矩为正; 如力矩使刚体沿顺时针方向转动,力矩为负; 讨论 1 力矩的三要素: (1)力的大小和方向; (2)力的作用点; (3)转轴位置 . 2. 若力F不在转动平面内: z
j
转动定律
M J
2 J m r jj 刚体的转动惯量:
刚体定轴转动的角 加速度与它所受的合外 力矩成正比 ,与刚体的 转动惯量成反比.
11
三 转动惯量 1. 物理意义 转动惯量与物体的惯性质量物理意义一致, 是物体转动惯性大小的量度。 2. 与转动惯量有关的因素: (3)转轴的位置; (2)质量分布; (1)刚体的总质量; 对所有质点求和:
j
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
m2
2
r3
m3
(3)质量连续分布刚体的转动惯量
J r 2 dm
转轴
dm:质量元
力矩-转动定律资料

N
解: (1) 棒在任意位置时的重力矩
o
M L d M L ld gcm osL ldgc l oL到s C转为轴质的心距
0
0
0
离
l
•c
d
dm
1 2L 2gco s mL 2g co s mC g co Ls
mg
(2)MI1m2 L, 3g cos
3
2L
ddtd d ddtd d
a2
T2
T2
m2
m2
a1
T1
g
T2
a22mm1m 1m1(2m gm1m22m 122121m2)gm 1mm333g
2m1m2g m1 m2
1 2
m2m3g
1 2
m3
谢谢!
应用于刚体 => 转动定律
F
dp
dt
dL
M外 dt
问题归结为确定刚体的角动量。
1. 定轴转动刚体的角动量 (a) 质点对点的角动量
作圆周运动质点的角动量 L= rmv (b) 定轴转动刚体的角动量
Lrprm v Z
在以角速度ω作定轴转动的刚体内, 取质元 mi , 则其对OZ 轴的角动量为
T m1g
N r
m2g
由(2)式:
I
T=T’= r
代入(1)式: m1g -
I = m1a
r
所以:
m1g -
I = m1r
r
m1gr
= m1r2+I
m1g - T= m1a….(1)
T’r=I…(2) T’
a = r …(3)
T=T’ …(4)
I 1 mr 2 2
m1gr
4-2力矩转动定律转动惯量

J r2dm
图1
图2
J1 J2
➢ 常用的转动惯量 (P110 表)
21
四 平行轴定理
质量为m 的刚体,
如果对其质心轴的转动 惯量为 JC ,则对任一与
该轴平行,相距为 d 的
转轴的转动惯量
JO JC md 2
d
C mO
J Jc
22
J Jc md2
圆盘对P 轴的转动惯量 P R O m
Fit Fit miait miri
11
➢ 质元绕Z轴转动的力矩
M i ri Fit ri Fit miri2
➢ 刚体绕Z轴转动的力矩
z
Fi内
Fi外
r O i m i 质量元
Mi riFit riFit
mi ri 2
M
r
F
M Frsin Fd
5
4、一对力偶的力矩
M Fd
F
F
o
l
F 0 M 0
M F l F l Fl
22
ro
F'
F
F 0
M 0
M Fr Fr 0
6
讨论
(1)若力 F不在转动平面内,把力分
解为平行和垂直于转轴方向的两个分量
41
➢ 常用的转动惯量公式
m质点:J r2m 圆盘(圆柱): J 1 mR2
2
杆:
Jc
1 12
mL2
J
端
1 3
mL2
R Om
O1
O1’
d=L/2
力矩 转动定律 转动惯量
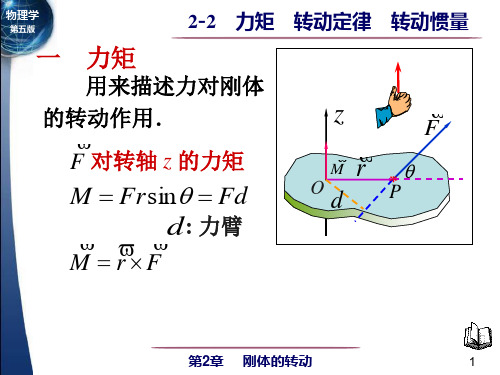
解 应用转动定律
L
M J 求β L M mg cos 2 1 2 J mL 3 3g cos 2L
第2章 刚体的转动
mg
35
物理学
第五版
2-2 力矩
转动定律 转动惯量
6 一轻绳绕在有水平轴的定滑轮上,滑 轮质量为m,绳下端挂一物体,物体所受重 力为G, 滑轮的角加速度为β 1 ,若将物体去 掉而以与G相等的力直 接向下拉绳子,滑轮 β2 β1 R R 的角加速度β 2 将 (A) 不变 (C) 变大 (D) 无法判断
说明 刚体的转动惯量与以下三个因素有关: (1)与刚体的体密度 有关. (2)与刚体的几何形状及体密度 的分 布有关. (3)与转轴的位置有关.
第2章 刚体的转动
11
物理学
第五版
2-2 力矩
转动定律 转动惯量
四 平行轴定理
质量为m 的刚体, 如果对其质心轴的转动 惯量为 J C ,则对任一与 该轴平行,相距为 d 的 转轴的转动惯量
(mA mC 2)mB g FT2 mA mB mC 2
注意:
FT1 FT2
第2章 刚体的转动
26
物理学
第五版
2-2 力矩
转动定律 转动惯量
如令 mC 0 ,可得
mA mB g FT1 FT2 mA mB
mA mB g FT1 mA mB mC 2 (mA mC 2)mB g FT2 mA mB mC 2
第2章 刚体的转动
28
物理学
第五版
2-2 力矩
转动定律 转动惯量
解 细杆受重力和 铰链对细杆的约束力FN 作用,由转动定律得
m,l O
大学物理-力矩-转动定律-转动惯量
F
p
18
2 – 5 刚体的定轴转动
第二章 动力学基础
解 (1) Fr J
Fr 98 0.2 39.2 rad/s2
J 0.5
mg T ma
(2) Tr J
a r
两者区别?
rO
F T
T
J
mgr mr 2
98 0.2 0.5 10 0.22
i
J r2dm
9
2 – 5 刚体的定轴转动
第二章 动力学基础
四. J 的计算
质量连续分布刚体的转动惯量
J mjrj2 r2dm dm :质量元 j
对质量线分布的刚体: dm dl
:质量线密度
对质量面分布的刚体:
:质量面密度
对质量体分布的刚体:
在圆规迹切线方向
mk ak mk rk Fk fk
两边乘以rk,并对整个刚体求和
第二章 动力学基础
z
o
vk
mk
( mk rk2 ) Fk rk fk rk
k
k
k
5
2 – 5 刚体的定轴转动
第二章 动力学基础
( mk rk2 ) Fk rk fk rk
17
2 – 5 刚体的定轴转动
第二章 动力学基础
四、转动定律的应用举例
例1 一轻绳绕在半径 r =20 cm 的飞轮边缘, 在绳端施以F=98 N 的拉力,飞轮的转动惯量 J=0.5 kg·m2,飞轮与转轴间的摩擦不计 。
rO
求: (1) 飞轮的角加速度。
(2) 如以重量P =98 N的物体挂在 绳端,试计算飞轮的角加速度。
(完整版)转动定律讲解
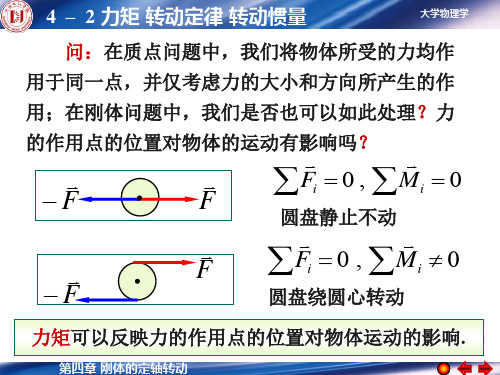
d力臂:转轴到力作用线的垂直距离
方向: r F 的方向 单位: N m
对于定轴转动;
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1)与转轴平行的力对转轴不产生力矩;
2)与转 轴垂直但通过转轴的力对转轴不产生力矩; 3)若力 F 不在转动平面内,把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零,故 F 对转轴的
力矩
M r F
M z rF sin
4)合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动:(规定转动 正方向)
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
方向: r F 的方向 单位: N m
对于定轴转动;
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1)与转轴平行的力对转轴不产生力矩;
2)与转 轴垂直但通过转轴的力对转轴不产生力矩; 3)若力 F 不在转动平面内,把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零,故 F 对转轴的
力矩
M r F
M z rF sin
4)合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动:(规定转动 正方向)
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量
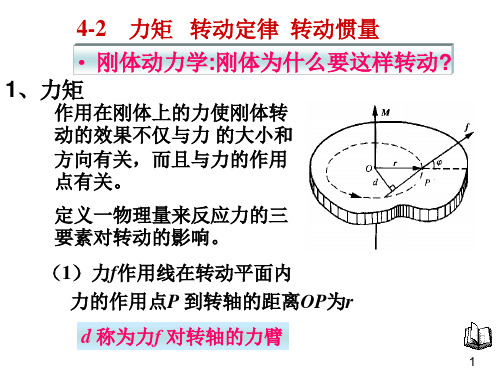
} ⇒ω
} ⇒θ
2、 M = Jα
F = ma
}⇒
17
m反映质点的平动惯性,J 反映刚体的转动惯性。 反映质点的平动惯性, 反映刚体的转动惯性。 反映质点的平动惯性
三 转动惯量
J 的计算方法 质量离散分布
J = ∑ ∆m r
j
2 j j
J = ∑ ∆m r = (∆m )r + (∆m2 )r + L+ (∆mN )r
质量为m,长为L的细棒绕其一端的 的细棒绕其一端的J 质量为 ,长为 的细棒绕其一端的
1 2 J c = mL 12
O1
O1’
L2 1 2 J = J c + m( ) = mL 2 3
d=L/2
O2 O2’
20
竿 子 长 些 还 是 短 些 较 安 全 ?
飞轮的质量为什么 大都分布于外轮缘? 大都分布于外轮缘?
(3) )
1 2 对M: T2 r − T1r = J α = M r α : 2
4、运动学: 运动学:
rα = a
(4) )
26
解以上四个联立方程式, 解以上四个联立方程式 可得
1 T2 ' ≠ T 、
原因: 原因:
' 1
' (1)若:T2 ' = T T2 ' r −T ' r = Jα v 1 1 FN v 1 T 1 ⇒ J = mr2 = 0 ⇒m = 0 2 m
21
例1(补充例题):一个转动惯量为2.5 kg⋅m2 、 (补充例题) 一个转动惯量为 ⋅ 例题 直径为60cm 的飞轮,正以 的飞轮,正以130 rad⋅s−1 的角速度旋转。 直径为 ⋅ 的角速度旋转。 现用闸瓦将其制动, 现用闸瓦将其制动 如果闸瓦对飞轮的正压力为 500 N, 闸瓦与飞轮之间的摩擦系数为0.50。求: 闸瓦与飞轮之间的摩擦系数为 。
力矩转动定律转动惯量

二. 转动定律
Fit (mi )at mri
M i ri Fit (mi )atri
at ri
Mi (mi )ri2
z
Fit
O ri mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量 转动定律
J miri2
M J
M J 转动定律
J miri2
J miri2
i
适用于离散分布刚体转动惯量的计算
J r2dm m
适用于连续分布刚体转动惯量的计算
在国际单位制(SI)中,转动惯量的单位 为千克二次方米,即 k.g m2
例: 1.求长为L ,质量为m 的均匀细棒AB
的转动惯量.
(1)对于通过棒的一端与棒垂直的轴;
(2)对于通过棒的中点与棒垂直的轴.
2
l
5. 一长为 质l 量为 匀m质细杆竖直放置,其下
端与一固定铰链 O 相接,可绕其转动.由于此竖直放 置的细杆处于非稳定平衡状态,当其受到微小扰动时, 细杆将在重力作用下由静止开始绕铰链 O 转动.试计
算细杆转动到与竖直线成 角时的角加速度和角速度.
解 细杆受重力和
铰链对细杆的约束力
FN
作用,由转动定律得
T2
mM
Gm
a2 GM
(2M m)mg mM阻
T1 m( g a)
2
R
M m m
2
(2m m)Mg MM阻
T2 M ( g a)
2
R
M m m
2
注意:当不计滑轮的质量和摩擦阻力矩时, 此时有 -T-1---T(2中学的情况)
4.一根长l质量为m 的均匀直棒,其一端固定在光滑的水平轴O,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令大气压为 p0 ,则 p p0 g(h y)
dF PdA [ p0 g(h y)]Ldy
h
F 0 [ p0 g(h y)]Ldy
p0Lh
1 2
gLh2
y
dA
代入数据,得
hy
dy
F 5.911010 N
O
L
x
第四章 刚体的转动
6
物理学
第五版
4-2 力矩 转动定律 转动惯量
过大坝基点 Q 且与 x 轴平行的力矩 .
y
y
x
h
O
Q
x
O
L
第四章 刚体的转动
4
物理学
第五版
4-2 力矩 转动定律 转动惯量
解 设水深h,坝长L,在坝面上取面积 元 dA Ldy ,作用在此面积元上的力
dF pdA pLdy
y
y
dA
x
dy
hy
x
O
Q
O
L
第四章 刚体的转动
5
物理学
第五版
4-2 力矩 转动定律 转动惯量
第四章 刚体的转动
物理学
第五版
4-2 力矩 转动定律 转动惯量
三 转动惯量
J mjrj2 J r2dm j
➢ 转动惯量的单位:kg·m2
➢ J 的意义:转动惯性的量度 .
第四章 刚体的转动
13
物理学
第五版
4-2 力矩 转动定律 转动惯量
➢ J 的计算方法
❖ 质量离散分布
J mjrj2 m1r12 m2r22 mjrj2
dF [ p0 g(h y)]Ldy
dF对通过点Q的轴的力矩 dM ydF
h
M 0 y[ p0 g(h y)]Ldy
y
1 2
p0 Lh2
1 6
gLh3
h dF O
dy 代入数据,得:
y
M 2.14 1012 N m
Q
第四章 刚体的转动
7
物理学
第五版
4-2 力矩 F
不在转动平面内,把力分
解为平行 和垂 直于 转轴方向的两个分量
F Fz F
其中 Fz对转 轴的
力矩为零,故 F 对转
轴的力矩 M zk
r
F
z
F
k
O Fz r
F
M z rF sin
第四章 刚体的转动
2
物理学
第五版
4-2 力矩 转动定律 转动惯量
(2)合力矩等于各分力 矩的矢量和 M M1 M2 M3
圆盘对P 轴的转动惯量 P R O m
JP
1 2
mR2
mR2
质量为m,长为L的细棒绕其一端的J
Jc
1 12
mL2
O1
O1’
J
Jc
m( L)2 2
1 3
mL2
d=L/2
O2
O2’
第四章 刚体的转动
17
物理学
第五版
4-2 力矩 转动定律 转动惯量
竿
子
长
些
还
是
短
些
较
安
飞轮的质量为什么
全 ?
大都分布于外轮缘?
物理学
第五版
4-2 力矩 转动定律 转动惯量
解 (1) 用隔离法分 别对各物体作受力分析, 取如图所示坐标系.
A
mA
FN
PmA AO
FT1
x
C
mC
mB B
FT1
FC
PC
FT2
FT2
O
mB PB y
第四章 刚体的转动
21
物理学
第五版
4-2 力矩 转动定律 转动惯量
z
O rj
Fej
m j
Fij
Mej Mij mjrj2
j
j
Mij M ji Mij 0
j
第四章 刚体的转动
9
物理学
第五版
4-2 力矩 转动定律 转动惯量
Mej ( mjrj2 )α
j
定义转动惯量
J mjrj2 J r2dm j
z
O rj
Fej
m j
Fij
转动定律 M J
物理学
第五版
一
力矩
4-2 力矩 转动定律 转动惯量
用来描述力对刚体
的转动作用.
M Frsin Fd
d: 力臂
F 对 转轴 z的力矩
M rF
F
F
Fi 0, M i 0
z
M
r
Od
F
P*
F
Fi 0,
F
Mi 0
i
i
i
i
第四章 刚体的转动
1
物理学
第五版
4-2 力矩 转动定律 转动惯量
二 转动定律 (1)单个质点 m
与转轴刚性连接
Ft mat mr
M rF sin θ
z
M
Ft
F
O
r
m
Fn
M rFt mr 2 M mr2
第四章 刚体的转动
8
物理学
第五版
4-2 力矩 转动定律 转动惯量
(2)刚体
质量元受外力
内力
Fij
Fej,
Mej Mij mjrj2
外力矩 内力矩
第四章 刚体的转动
15
物理学
第五版
4-2 力矩 转动定律 转动惯量
四 平行轴定理
质量为m 的刚体,
如果对其质心轴的转动
惯量为 JC ,则对任一与
该轴平行,相距为 d 的
转轴的转动惯量
d
C mO
JO JC md 2
第四章 刚体的转动
16
物理学
第五版
4-2 力矩 转动定律 转动惯量
J Jc md2
❖ 质量连续分布
J mjrj2 r2dm j
r2dV V
dm:质量元 dV :体积元
第四章 刚体的转动
14
物理学
第五版
4-2 力矩 转动定律 转动惯量
说明
刚体的转动惯量与以下三个因素有关:
(1)与刚体的体密度 有关. (2)与刚体的几何形状(及体密度 的分
布)有关.
(3)与转轴的位置有关.
索跨过一半径为R、质量为mC的圆柱形滑轮 C,并系在另一质量为mB 的物体B上,B 竖 直悬挂.滑轮与绳索间无滑动, 且滑轮与
轴承间的摩擦力可略去不计.(1)两物体的 线加速度为多少? 水平和竖直两段绳索的
张力各为多少?(2) 物体 B 从静止落下距 离 y 时,其速率是多少?
第四章 刚体的转动
20
第四章 刚体的转动
18
物理学
第五版
4-2 力矩 转动定律 转动惯量
➢ 转动定律应用 M J
说明
(1) M J , 与 M 方向相同.
(2) 为瞬时关系.
(3) 转动中M J与平动中F ma
地位相同.
第四章 刚体的转动
19
物理学
第五版
4-2 力矩 转动定律 转动惯量
例2 质量为mA的物体A 静止在光滑水 平面上,和一质量不计的绳索相连接,绳
刚体定轴转动的角加速度与它所受的合 外力矩成正比,与刚体的转动惯量成反比.
第四章 刚体的转动
10
物理学
第五版
4-2 力矩 转动定律 转动惯量
转动定律 M J 讨论 (1) M
J (2) M J J d
dt
(3)M 0, ω=常量
第四章 刚体的转动
11
物理学
第五版
4-2 力矩 转动定律 转动惯量
(3)刚体内作用力和反作用力的力矩 互相抵消.
M ij
rj
j
O
d ri
i Fji
Fij
M ji
第四章 刚体的转动
Mij M ji
3
物理学
第五版
4-2 力矩 转动定律 转动惯量
例1 有一大型水坝高110 m、长1 000 m ,
水深100m,水面与大坝表面垂直,如图所
示. 求作用在大坝上的力,以及这个力对通
