四边形及周长的认识练习题
三角形四边形看图形周长面积专项练习30题(有答案)ok
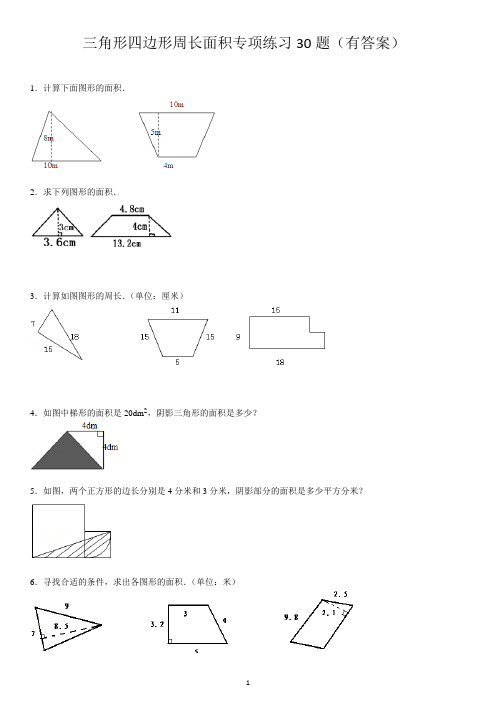
三角形四边形周长面积专项练习30题(有答案)1.计算下面图形的面积.2.求下列图形的面积.3.计算如图图形的周长.(单位:厘米)4.如图中梯形的面积是20dm2,阴影三角形的面积是多少?5.如图,两个正方形的边长分别是4分米和3分米,阴影部分的面积是多少平方分米?6.寻找合适的条件,求出各图形的面积.(单位:米)7.算出下面图形的面积.8.求阴影部分面积.单位:厘米.9.图形王国展风采.(求下面图形的周长,单位:厘米.)10.找准所需条件,计算下列图形的面积.(单位:米)11.求下面图形的面积.12.如图:三角形ABC的面积是6cm2,AB长4cm,求AB边上的高CD的长.13.如图所示,BC长为5,求画阴影线的两个三角形的面积之和.14.找准所需条件,计算下列图形的面积.(单位:米)15.如图,直角三角形的三条边分别长3cm、4cm、5cm,求最长边上的高为多少厘米.16.17.选择合适的数据计算下面图形的面积.18.求下面图形的面积.(单位:厘米)请同学们先写出每个图形的面积计算字母公式,然后再进行计算.19.计算下面图形或阴影部分的面积.(单位:cm)20.找出如图所需数据再求出面积.(单位:cm)21.一个三角形的底长是5m,如果底边延长1m,那么面积就增加1.5m2,请你求出原来三角形的面积是多少平方米?22.三角形ABC是一个正三角形,求这个图形的周长.23.求下面图形中阴影部分的面积.24.求下面各图形中涂色部分的面积25.如图,长方形的长是12cm,宽是5cm,三角形①的面积是24cm2,阴影部分面积是多少?26.求下面图形的面积.(单位:厘米)27.28.下面平行四边形中,涂色部分的面积是10平方分米求空白部分的面积.(单位:分米)29.30.如图数字分别表示两个长方形和一个直角三角形的面积,另一个三角形面积是_________.参考答案:1.三角形的面积:10×8÷2=80÷2,=40(m2);梯形的面积:(4+10)×5÷2=14×5÷2,=35(m2);答:三角形的面积为40(m2);梯形的面积为35(m2).2.(1)3.6×3÷2=5.4(平方厘米);(2)(4.8+13.2)×4÷2,=18×4÷2,=36(平方厘米);答:三角形的面积是5.4平方厘米,梯形的面积是36平方厘米3.①7+15+18=40(厘米);②5+11+15×2,=16+30,=46(厘米);③(18+9)×2=27×2,=54(厘米).答:三角形的周长是40厘米,等腰梯形的周长是46厘米,六边形的周长是54厘米.4.20﹣4×4÷2,=20﹣8,=12(平方分米),答:阴影三角形的面积是12平方分米.5.(4+3)×3÷2﹣(3×3﹣×3.14×32),=7×3÷2(9﹣7.065),=10.5﹣1.935,=8.565(平方分米);答:阴影部分的面积是8.565平方分米6.(1)三角形的面积:7×8.5÷2,=59.5÷2,=29.75(平方米);(2)梯形的面积:(3+5)×3.2÷2,=8×3.2÷2,=25.6÷2,=12.8(平方米);(3)平行四边形的面积:9.8×2.1=20.58(平方米);答:三角形的面积是29.75平方米,梯形的面积是12.8平方米,平行四边形的面积是20.58平方米7.(1)3.6×2.5÷2=4.5(平方厘米);(2)(1.4+4.6)×3.2÷2=6×3.2÷2=9.6(平方分米);(3)6.2×3.5=21.7(平方米);答:三角形的面积是4.5平方厘米;梯形的面积是9.6平方分米;平行四边形的面积是21.7平方米.8.12×12×=36(平方厘米);答:阴影部分的面积为36平方厘米.9.①6+7+9=22(厘米);②(13+24)×2=37×2,=74(厘米);③7+8+6+5+3+4=33(厘米);④32×4=128(厘米);答:三角形的周长是22厘米,长方形的周长是74厘米,六边形的周长是33厘米,正方形的周长是128厘米.10.(1)6×8÷2=24(平方米);(2)(14+24)×10÷2,=38×10÷2,=190(平方米);答:三角形的面积是24平方米;梯形的面积是190平方米11.(1)2.4×0.9÷2=1.08(平方厘米);(2)2.2×1.2+2.2×0.8÷2,=2.64+0.88,=3.52(平方分米);答:甲图形的面积是1.08平方厘米,乙图形的面积是3.52平方分米.12.6×2÷4,=12÷4,=3(cm);答:AB边上的高CD的长为3厘米.13.(5×5÷2﹣5×2÷2)×2,=(12.5﹣5)×2,=7.5×2,=15,答:阴影线的两个三角形的面积之和是15.14.三角形的面积:3×4÷2,=12÷2,=6(平方米);梯形的面积:(8+12)×10÷2,=20×10÷2,=200÷2,=100(平方米);组合图形的面积:6.3×4×2,=25.2×2,=50.4(平方米);答:三角形的面积是6平方米,梯形的面积是100平方米,组合图形的面积是50.4平方米15.3×4÷2×2÷5,=12÷5,=2.4(厘米),答:这个三角形最长边上的高2.4厘米,16.(27×2÷9)×5÷2,=(54÷9)×5÷2,=6×5÷2,=30÷2,=15(平方米);答:阴影部分的面积是15平方米.17.(1)30×40÷2,=1200÷2,=600(平方厘米),答:三角形的面积是600平方厘米;(2)15×8=120(平方分米),答:平行四边形的面积是120平方分米;(3)(8+15)×10÷2,=23×10÷2,=230÷2,=115(平方厘米),答:梯形的面积是115平方厘米.18.S△=ah÷2,=8×6÷2,=48÷2,=24(平方厘米);S▱=ah,=12×15,=180(平方厘米);S梯形=(a+b)h÷2,=(10+18)×12÷2,=28×12÷2,=336÷2,=168(平方厘米);答:三角形、平行四边形和梯形的面积分别是24平方厘米、180平方厘米和168平方厘米19.(1)12×4.5÷2,=4.5×6,=27(平方厘米),(2)8×8=64(平方厘米),(3)42×2÷15=5.6(厘米),(4.5+15)×5.6÷2,=19.5×5.6÷2,=54.6(平方厘米).20.(1)20×22÷2=220(平方厘米);答:三角形的面积是220平方厘米.(2)(18+12)×10÷2,=30×10÷2,=150(平方厘米);答:图形的面积是150平方厘米.(3)10×8=80(平方厘米);答:平行四边形的面积是80平方厘米21.原三角形的高:1.5×2÷1=3(米),原三角形的面积:5×3÷2=7.5(平方米);答:原来三角形的面积是7.5平方米.22.6×2+3.14×6×,=12+9.42,=21.42(厘米),答:这个图形的周长是21.42厘米.23.14×12÷2=84(平方厘米);答:阴影部分的面积是84平方厘米.24.(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米25.阴影部分的面积:12×5﹣24=36(平方厘米);答:阴影部分的面积是36平方厘米.26.(1)8×6÷2,=48÷2,=24(平方厘米);(2)12×15=180(平方厘米);(3)(10+18)×12÷2,=28×12×,=28×6,=168(平方厘米),答:三角形的面积是24平方厘米,平行四边形的面积是180平方厘米,梯形的面积是168平方厘米.27.8×5÷2,=40÷2,=20,答:阴影部分是面积是20.28.因为空白部分的高=阴影部分的高,所以空白部分梯形的高为:10×2÷5=4(分米);空白部分的面积:(3+3+5)×4÷2,=11×4÷2,=44÷2,=22(平方分米);答:空白部分的面积是22平方分米.29.7×4﹣7×4÷2,=28﹣14,=14(平方厘米).答:阴影部分的面积是14平方厘米.30.因为AO×OD=15,OC×OE=12,所以AO×OD×OC×OE=15×12,而OD×OE=5×2=10,所以OA×OC=15×12÷10=18,所以另一个三角形面积是:18÷2=9,答:另一个三角形面积是9,故答案为:9。
四年级数学上册《平行四边形和梯形》求周长应用题,考试必考

《平行四边形和梯形》求周长应用题1、一个平行四边形的一条边长14厘米,它的邻边比它短2厘米,这个四边形的周长是多少厘米?解:(14+2+14) X2=30X2=60厘米答:它的周长是60厘米。
2、一个等腰梯形的上底是2厘米,下底是4厘米,它的周长是12厘米,等腰梯形的腰是多少厘米?解:[12-(2+4)]÷2=3 (厘米)答:等腰梯形的腰是3厘米。
3、已知一个平行四边形的周长是38厘米,其中一条边长10厘米,另外三条边长分别是多少厘米?解:如下图的平行四边形中,AD=BC=10 厘米38÷2-10=19-10=9 (厘米)答:平行四边形另外三条边分别是10厘米,9厘米,9厘米。
《平行四边形和梯形》求周长应用题4、一个等腰梯形的上底是4厘米,下底是6厘米,它的周长是20厘米,等腰梯形的腰长多少厘米?解: (20-4-6)÷2=10÷2=5 (厘米)答:等腰梯形的腰长是5厘米。
5、一个等腰梯形的腰长是15厘米,上底长6厘米,下底长12厘米,这个等腰梯形的周长是多少?解: 15X2+6+12=30+6+12=48 (厘米)答:这个等腰梯形的周长是48厘米。
6、一个等腰梯形的下底比上底长8厘米,上底和一条腰一共长36厘米,这个梯形的周长是多少?解: 36+8+36=44+36=80 (厘米)答:这个梯形的周长是80厘米。
《平行四边形和梯形》求周长应用题7、一个等腰梯形的上底是6厘米,下底是上底的2倍,腰和下底相等。
这个等腰梯形的周长是多少厘米?解:下底6X2=12 (厘米)6+12+12+12=42 (厘米)答:这个等腰梯形的周长是42厘米。
8、一个平行四边形的一条边是14厘米,它的邻边比它少4厘米,这个平行四边形的周长是多少厘米?解:(14+14-4) X2=24X2=48 (厘米)答:这个平行四边形的周长是48厘米。
9、张大爷有一块等腰梯形的菜地。
它的上底长15米,下底长20米,腰比下底短4米,这块菜地的周长是多少?腰长: 20-4=16米周长: 15+20+16X2=35+32=67米答:这块菜地的周长是67米。
小升初专题一三角形四边形圆周长面积习题含答案解析

专题一三角形、四边形、圆周长及面积选择题(共30小题)1.(2013秋•临泉县校级期末)下面()组中两个图形的周长相等.A.B.C.2.(2012春•简阳市期末)在周长相等的情况下,下面的图形中()的面积最大.A.长方形B.正方形C.圆D.三角形3.(2012•祥云县模拟)将一个长方形的铁丝框,拉成一个平行四边形,它的周长()比原来的长方形周长.A.大于B.小于C.等于4.(2015•西安校级模拟)一个长方形框架拉成平行四边形后,面积()A.不变B.减小C.增大 D.既可能减小又可能增大5.如图所示,把一个正方形木框拉成一个平行四边形,它的面积()A.变大B.变小C.不变6.(2012•北京自主招生)一个边长4cm的正方形,把4个角各减去边长为1cm的小正方形,那么它的周长()A.减少16cm B.增加8cm C.减少8cm D.不变7.(2010•南通校级模拟)如图的周长是()分米.A.22 B.20 C.18 D.288.(2014秋•吴中区校级期末)下图中的几个图形,()是三角形面积的2倍.A.A B.B C.C D.D9.(2012•宁波)用同样长的四根铁丝分别围成长方形、正方形、平行四边形、圆形,其中面积最大的是()A.正方形B.圆形C.平行四边形 D.长方形10.(2012秋•石林县校级期中)一个长方形,长是15dm,宽是长的,求面积的算式是()A.15×B.15×(15×)C.(15+)×211.(2008秋•绵阳校级期末)图中平行四边形底边a上的高是()厘米.A.4 B.6 C.512.(2005•让胡路区校级自主招生)平行四边形的底边扩大6倍,高缩小2倍,所得的新平行四边形比原平行四边形的面积()A.减少2倍B.增加2倍C.减少3倍D.增加3倍13.一个平行四边形的底扩大10倍,高缩小10倍,它的面积()A.扩大100倍B.缩小100倍C.扩大10倍D.大小不变14.(2015秋•泸西县校级期末)底和高相等的两个三角形()A.形状相同B.周长相等C.面积相等15.(2012•海门市)三角形斜边上的高是()厘米.A.20 B.24 C.2816.(2011•海港区)如图有甲乙丙三个面积相等的平行四边形,它们阴影部分的面积相比较()A.甲大B.乙大C.丙大D.相等17.(2010秋•海安县校级期中)面积相等的两个三角形,形状()A.相同B.不相同C.不一定相同18.一个三角形和一个平行四边形的面积相等,高也相等,已知平行四边形的底是9分米,三角形的底是()分米.A.18 B.4.5 C.919.与面积是24平方厘米的平行四边形等第等高的三角形的面积是()平方厘米.A.8 B.12 C.24 D.4820.如图中阴影部分面积相当于长方形面积()A.B.C.21.如图,平行四边形的面积是30平方分米,甲、乙、丙三个三角形的面积的比是()A.6:3:5 B.2:4:6C.5:3:8D.2:1:322.(2010•宜昌)在一个面积为40平方厘米的平行四边形中画一个最大的三角形,这个三角形的面积是()平方厘米.A.40 B.30 C.20 D.1023.(2015•库尔勒市模拟)要画一个周长是18.84厘米的圆,那么圆规两脚之间应取()A.2厘米B.3厘米C.4厘米24.(2015•寿阳县模拟)大圆和小圆的半径比是3:2,那么小圆和大圆的面积比是()A.2:3 B.3:2 C.9:3 D.4:925.(2015•长沙)在一个长8分米,宽6分米的长方形中画一个最大的圆,圆的半径是()分米.A.8 B.6 C.4 D.326.(2014秋•萧县期中)半圆的周长()A.πr+r B.πr+2r C.πr+r27.(2014•白下区)圆的半径扩大2倍后,它的面积与原来比()A.扩大2倍B.扩大4倍C.不变28.(2013秋•寿光市校级期末)已知梯形的面积是45dm2,上底是4dm,下底是6dm,它的高是()dm.A.9 B.4.5 C.2.25 D.4529.(2012•遵义县校级模拟)一堆钢管,最下层有6根,最上层有2根,每相邻两层间相差一根,这对钢管共有()根.A.16 B.12 C.2030.两个完全一样的梯形拼成一个平行四边形,平行四边形的面积是12平方厘米,那么其中一个梯形的面积是()A.6平方厘米B.12平方厘米C.24平方厘米专题一三角形、四边形、圆周长及面积参考答案与试题解析一.选择题(共30小题)1.(2013秋•临泉县校级期末)下面()组中两个图形的周长相等.A.B.C.【考点】长方形的周长.【专题】平面图形的认识与计算.【分析】根据封闭图形的周长等于围成这个封闭图形的所有线段的长度之和进行判断即可.【解答】解:A.第一个长方形的周长<第二个图形的周长;B.第一个图形的周长都等于8个正方形的边长之和;第二个图形的周长等于12个正方形的边长之和;C.经测量长方形的长和宽分别等于平行四边形的相邻两边的长,所以长方形的周长等于平行四边形的周长.故选:C.【点评】解决本题关键是明确封闭图形的周长的意义.2.(2012春•简阳市期末)在周长相等的情况下,下面的图形中()的面积最大.A.长方形B.正方形C.圆D.三角形【考点】长方形的周长;正方形的周长;圆、圆环的周长;长方形、正方形的面积;三角形的周长和面积;圆、圆环的面积.【分析】完成本题可根据这四种几何图形的面积公式进行推理.【解答】解:根据三角形面积推导公式可知,周长相等的情况下,三角形面积一定小于正方形和长方形;由此再比较圆、正方形及长方形在周长相等的情况下,哪种图形面积最大;设一个圆的半径是1,它的周长是6.28,面积是3.14,和它周长相等的正方形的面积是:(6.28÷4)2=2.4649,和它周长相等的长方形的面积是:6.28÷2=3.14,设这个长方形的长、宽分别为a、b:取一些数字(0.1,3.04),(0.5,2.64),(1,2.14),…(2.14,1),(2.64,0.5),(3.04,0.1)可以发现长方形的长和宽越接近,面积就越大,当长和宽相等时,也就是变成正方形了,所以这个长方形的面积一定小于正方形的面积.所以在周长相等的情况下,面积:圆>正方形>长方形>三角形.故选:C.【点评】在周长相等的情况下,在所有几何图形中,圆的面积最大,应当做常识记住.3.(2012•祥云县模拟)将一个长方形的铁丝框,拉成一个平行四边形,它的周长()原来的长方形周长.A.大于B.小于C.等于【考点】长方形的周长;平行四边形的特征及性质.【分析】将一个长方形的铁丝框,拉成一个平行四边形,铁丝的长度没有发生变化,所以平行四边形的周长等于长方形的周长.【解答】解:因为在将一个长方形的铁丝框,拉成一个平行四边形的过程中,铁丝的长度没有发生变化,只是形状发生变化,所以平行四边形的周长等于长方形的周长.故选:C.【点评】本题主要考查了周长的意义;注意在将一个长方形的铁丝框,拉成一个平行四边形,它的面积发生变化.4.(2015•西安校级模拟)一个长方形框架拉成平行四边形后,面积()A.不变B.减小C.增大D.既可能减小又可能增大【考点】长方形、正方形的面积;平行四边形的面积.【分析】长方形是特殊的平行四边形,一个长方形框架,把它拉成平行四边形,周长不变,面积变小.由此解答【解答】解:因为把长方形框架拉成平行四边形,由于平行四边形的高小于长方形的宽,所以面积变小.故选:B.【点评】此题主要考查长方形和平行四边形之间的关系,长方形是特殊的平行四边形,它们的周长相等时,平行四边形的面积小于长方形的面积.由此解决问题.5.如图所示,把一个正方形木框拉成一个平行四边形,它的面积()A.变大B.变小C.不变【考点】平行四边形的面积.【专题】综合题;平面图形的认识与计算.【分析】正方形的面积=边长×边长,平行四边形的面积=底×高,把一个正方形木框拉成一个平行四边形,底不变,高变了,正方形的一条边长成了平行四边形的斜边,高变矮了,所以面积也就变小了;据此解答.【解答】解:正方形的面积=边长×边长,平行四边形的面积=底×高,把一个正方形木框拉成一个平行四边形,底不变,高变矮了,面积变小了,所以把一个正方形木框拉成一个平行四边形,它的面积变小;故选:B.【点评】此题是考查正方形和平行四边形面积的认识理解,以及它们之间的区别联系.6.(2012•北京自主招生)一个边长4cm的正方形,把4个角各减去边长为1cm的小正方形,那么它的周长()A.减少16cm B.增加8cm C.减少8cm D.不变【考点】正方形的周长;图形的拆拼(切拼).【分析】分别向外平移正方形4个角上的线段,可知把4个角各减去边长为1cm的小正方形后图形的周长=边长4cm的正方形的周长,根据周长公式计算即可求解.【解答】解:根据平移的知识可知:两种图形的周长都为4×4=16(cm),即不变.故选:D.【点评】考查了图形的拆拼(切拼)和正方形的周长.正方形的周长公式:C=4a.7.(2010•南通校级模拟)如图的周长是()分米.A.22 B.20 C.18 D.28【考点】长方形的周长.【分析】由图意可知:利用平移的方法,则图形的周长就等于长是5分米,宽是4分米的长方形的周长,从而利用长方形的周长公式即可求解.【解答】解:(4+5)×2,=9×2,=18(分米);故选:C.【点评】解答此题的关键是明白:图形的周长就等于长是5分米,宽是4分米的长方形的周长.8.(2014秋•吴中区校级期末)下图中的几个图形,()是三角形面积的2倍.A.A B.B C.C D.D【考点】长方形、正方形的面积;平行四边形的面积;三角形的周长和面积;梯形的面积.【分析】三角形的面积等于和它等底等高的平行四边形面积的一半,进而得出结论.【解答】解:三角形的面积等于和它等底等高的平行四边形面积的一半,由图知:三角形的底为3,高为3,和它等底等高的平行四边形是C;故选:C.【点评】解答此题应结合题意,根据三角形和平行四边形的面积计算进行分析解答.9.(2012•宁波)用同样长的四根铁丝分别围成长方形、正方形、平行四边形、圆形,其中面积最大的是()A.正方形B.圆形C.平行四边形 D.长方形【考点】长方形、正方形的面积;平行四边形的面积;圆、圆环的面积.【分析】在平面图形中,若周长一定,所围成的图形越接近圆形,其面积就越大,据此即可求解.【解答】解:因为在平面图形中,若周长一定,所围成的图形越接近圆形,其面积就越大,所以用同样长的四根铁丝分别围成长方形、正方形、平行四边形、圆形,其中面积最大的是圆形;故答案为:B.【点评】解答此题的主要依据是:在平面图形中,若周长一定,所围成的图形越接近圆形,其面积就越大.10.(2012秋•石林县校级期中)一个长方形,长是15dm,宽是长的,求面积的算式是()A.15×B.15×(15×)C.(15+)×2【考点】长方形、正方形的面积.【专题】平面图形的认识与计算.【分析】由“宽是长的,”得出的单位“1”是长,用乘法列式求出宽,再根据长方形的面积公式S=ab求出长方形的面积.【解答】解:15×(15×),=15×12,=180(平方分米),答:面积是180平方分米;故选:B.【点评】本题主要是利用长方形的面积公式S=ab解决问题.11.(2008秋•绵阳校级期末)图中平行四边形底边a上的高是()厘米.A.4 B.6 C.5【考点】平行四边形的面积.【专题】平面图形的认识与计算.【分析】根据平行四边形的面积公式S=ah,把底8厘米,高3厘米代入公式求出平行四边形的面积,再用面积除以4就是平行四边形底边a上的高.【解答】解:3×8÷4,=24÷4,=6(厘米),答:平行四边形底边a上的高是6厘米;故选:B.【点评】本题主要是灵活利用平行四边形的面积公式S=ah解决问题,注意一定是底和对应的高相乘.12.(2005•让胡路区校级自主招生)平行四边形的底边扩大6倍,高缩小2倍,所得的新平行四边形比原平行四边形的面积()A.减少2倍B.增加2倍C.减少3倍D.增加3倍【考点】平行四边形的面积.【分析】平行四边形的面积=底×高,设其底边为a,高为h,则变化后的平行四边形的底为6a,高为h,分别表示出二者的面积,即可求得面积的变化情况.【解答】解:设原平行四边形的底为a,高为h,则则变化后的平行四边形的底为6a,高为h,新平行四边形的面积=6a×h=3ah,原平行四边形的面积=ah,所以3ah÷ah=3倍;3﹣1=2倍;答:所得的新平行四边形比原平行四边形的面积增加2倍,故选:B.【点评】此题主要考查平行四边形的面积计算方法的灵活应用.13.一个平行四边形的底扩大10倍,高缩小10倍,它的面积()A.扩大100倍B.缩小100倍C.扩大10倍D.大小不变【考点】平行四边形的面积.【专题】平面图形的认识与计算.【分析】根据平行四边形的面积=底×高,再根据积的不变的性质,一个因数扩大10倍,另一个因数缩小10倍,积不变.据此解答.【解答】解:由分析得:一个平行四边形的底扩大10倍,高缩小10倍,它的面积大小不变.故选:D.【点评】此题考查的目的是理解掌握平行四边形的面积公式和积不变的性质.14.(2015秋•泸西县校级期末)底和高相等的两个三角形()A.形状相同B.周长相等C.面积相等【考点】三角形的周长和面积.【专题】平面图形的认识与计算.【分析】根据三角形的面积=底×高÷2,若三角形的底和高相等,则面积相等,由此做出选择.【解答】解:因为三角形的面积=底×高÷2,若三角形的底和高相等,则面积相等;故选:C.【点评】本题主要是灵活利用三角形的面积公式S=ah÷2解决实际问题.15.(2012•海门市)三角形斜边上的高是()厘米.A.20 B.24 C.28【考点】三角形的周长和面积.【专题】压轴题;平面图形的认识与计算.【分析】直角三角形的面积等于两条直角边的乘积的一半,由此求出直角三角形的面积,再乘2除以斜边就是斜边上的高.【解答】解:30×40÷2×2÷50,=1200÷50,=24(厘米);答:三角形斜边上的高是24厘米.故选:B.【点评】本题主要是灵活利用三角形的面积公式S=ah÷2解决问题;注意在直角三角形中,一条直角边作为底,另一条直角边就是高.16.(2011•海港区)如图有甲乙丙三个面积相等的平行四边形,它们阴影部分的面积相比较()A.甲大B.乙大C.丙大D.相等【考点】三角形的周长和面积;平行四边形的面积.【分析】由甲图可知:阴影部分的面积是平行四边形面积的一半;由乙图可知:阴影部分的面积是平行四边形面积的一半;由丙图可知:阴影部分的面积是平行四边形面积的一半;因为甲乙丙是三个面积相等的平行四边形,所以三个图中阴影部分的面积都相等;进而选择即可.【解答】解:由分析知:各个图形中阴影部分的面积都是平行四边形面积的一半,各图中阴影部分的面积相比较,一样大;故选:D.【点评】解答此题的关键是进行分别分析,进而得出结论.17.(2010秋•海安县校级期中)面积相等的两个三角形,形状()A.相同B.不相同C.不一定相同【考点】三角形的周长和面积.【专题】平面图形的认识与计算.【分析】根据三角形的面积=底×高÷2,可知面积相等的三角形,形状不一定相同,例如:底和高分别是6和2的三角形与底和高分别是4和3的三角形面积相等,但形状就不同.【解答】解:面积相等的三角形,形状不一定相同.故选:C.【点评】此题考查面积相等的三角形,形状不一定相同,因为三角形的面积与底和高有关.18.一个三角形和一个平行四边形的面积相等,高也相等,已知平行四边形的底是9分米,三角形的底是()分米.A.18 B.4.5 C.9【考点】三角形的周长和面积.【专题】平面图形的认识与计算.【分析】根据三角形的面积公式S=ah÷2,知道a1=2S÷h,根据平行四边形的面积公式S=ah,知道a2=S÷h,所以三角形的底是平行四边形的底的2倍,即a1=2a2,由此求出三角形的底.【解答】解:9×2=18(分米).答:三角形的底是18分米.故选:A.【点评】此题主要考查了利用三角形的面积公式与平行四边形的面积公式推导出三角形与平行四边形的面积相等,高也相等时底的关系,由此解决问题.19.与面积是24平方厘米的平行四边形等第等高的三角形的面积是()平方厘米.A.8 B.12 C.24 D.48【考点】三角形的周长和面积.【专题】平面图形的认识与计算.【分析】三角形的面积=×底×高,平行四边形的面积=底×高,若平行四边形和三角形等底等高,则三角形的面积是平行四边形面积的一半,据此即可求解.【解答】解:24÷2=12(平方厘米);答:与它等底等高的三角形的面积是12平方厘米.故选:B.【点评】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.20.如图中阴影部分面积相当于长方形面积()A.B.C.【考点】三角形的周长和面积;长方形、正方形的面积.【分析】由于三角形的高与长方形的宽相等,由三角形的底与长方形的长之间的关系即可得出阴影部分面积与长方形面积之间的关系.【解答】解:因为三角形的高与长方形的宽相等,三角形的底是长方形的长的,故阴影部分面积相当于长方形面积的÷2=.故选:C.【点评】考查了三角形的面积,长方形的面积.本题得到三角形的高与长方形的宽相等以及三角形的底是长方形的长的是解题的关键.21.如图,平行四边形的面积是30平方分米,甲、乙、丙三个三角形的面积的比是()A.6:3:5 B.2:4:6C.5:3:8D.2:1:3【考点】三角形的周长和面积;平行四边形的面积.【分析】由图可知:甲和乙等高不等底,则其面积比就等于对应底的比,而丙的面积是甲和乙的面积和,据此即可求出三者的面积比.【解答】解:S甲:S乙:S丙,=4:2:(4+2),=4:2:6,=2:1:3;答:甲、乙、丙三个三角形的面积的比2:1:3.故选:D.【点评】解答此题的主要依据是:等高不等底的三角形,面积比等于对应底的比.22.(2010•宜昌)在一个面积为40平方厘米的平行四边形中画一个最大的三角形,这个三角形的面积是()平方厘米.A.40 B.30 C.20 D.10【考点】三角形的周长和面积;平行四边形的面积.【专题】平面图形的认识与计算.【分析】根据“在一个面积为40平方厘米的平行四边形中画一个最大的三角形,”知道所画的三角形必须与平行四边形等底等高,由此根据等底等高的三角形的面积是平行四边形面积的一半,列式解答即可.【解答】解:40÷2=20(平方厘米),答:这个三角形的面积是20平方厘米.故选:C.【点评】关键是知道要画的三角形的面积必须与平行四边形等底等高,再根据根据等底等高的三角形的面积与平行四边形面积的关系解决问题.23.(2015•库尔勒市模拟)要画一个周长是18.84厘米的圆,那么圆规两脚之间应取()A.2厘米B.3厘米C.4厘米【考点】圆、圆环的周长.【专题】平面图形的认识与计算.【分析】根据题意,圆规两脚之间的距离即是所画圆的半径,可利用圆的周长公式进行计算,列式解答即可得到答案.【解答】解:18.84÷3.14÷2=6÷2=3(厘米);答:圆规两脚之间的距离应是3厘米.故选:B.【点评】此题主要考查的是圆的周长公式的使用.24.(2015•寿阳县模拟)大圆和小圆的半径比是3:2,那么小圆和大圆的面积比是()A.2:3 B.3:2 C.9:3 D.4:9【考点】圆、圆环的周长.【分析】要求小圆和大圆的面积比是多少,应根据圆的面积计算公式“s=πr2”,分别用公式表示出来,然后根据题意进行比即可.【解答】解:S大=πR2,S小=πr2,S小:S大=πr2:πR2=r2:R2=22:32=4:9;故选:D.【点评】此题属于考查圆的面积和半径的关系,应明确:圆的半径比,即圆的周长比,直径比;圆的面积比即半径的平方的比.25.(2015•长沙)在一个长8分米,宽6分米的长方形中画一个最大的圆,圆的半径是()分米.A.8 B.6 C.4 D.3【考点】圆、圆环的周长.【分析】当圆的直径等于长方形的宽6分米时,此时圆最大,否则,圆就会超出长方形的边界.【解答】解:一个长8分米,宽6分米的长方形中画一个最大的圆,圆的半径是3分米.故选:D.【点评】解答此题要注意:长方形中画一个最大的圆,是以宽边作圆的直径.26.(2014秋•萧县期中)半圆的周长()A.πr+r B.πr+2r C.πr+r【考点】圆、圆环的周长;用字母表示数.【专题】平面图形的认识与计算.【分析】一个半圆的周长是圆周长的一半加上直径,根据圆的周长公式:c=πd或c=2πr,求出圆周长的一半再加直径.【解答】解:圆的周长的一半是:2πr÷2=πr,一个半圆的周长是:πr+2r;故选:B.【点评】此题主要考查一个半圆的周长的计算,关键是理解半圆的周长与圆周长的一半不是同一个概念.根据圆的周长的计算方法解答.27.(2014•白下区)圆的半径扩大2倍后,它的面积与原来比()A.扩大2倍B.扩大4倍C.不变【考点】圆、圆环的周长.【分析】根据圆的面积公式,把扩大后的2倍半径代入,求出结果和原公式对比即可.【解答】解:根据S=πr2;半径扩大2倍后为2r,所以得:S扩=π(2r)2,=4πr2;所以面积扩大为原来的4倍;故选:B.【点评】此题考查了圆的面积公式.28.(2013秋•寿光市校级期末)已知梯形的面积是45dm2,上底是4dm,下底是6dm,它的高是()dm.A.9 B.4.5 C.2.25 D.45【考点】梯形的面积.【专题】平面图形的认识与计算.【分析】根据梯形的面积公式:s=(a+b)×h÷2,那么h=s×2÷(a+b),据此列式解答.【解答】解:45×2÷(4+6)=90÷10=9(分米)答:它的高是9分米.故选:A.【点评】此题主要考查梯形面积公式的灵活运用.29.(2012•遵义县校级模拟)一堆钢管,最下层有6根,最上层有2根,每相邻两层间相差一根,这对钢管共有()根.A.16 B.12 C.20【考点】梯形的面积.【专题】简单应用题和一般复合应用题.【分析】根据题意,最上层有2根,最下层有6根,相邻两层相差1根,这堆钢管的层数是(6﹣2+1)层,根据梯形的面积计算方法进行解答.【解答】解:(2+6)×(6﹣2+1)÷2=8×5÷2=20(根);答:这堆钢管一共有20根.故选:C.【点评】此题主要考查梯形的面积计算方法,能够根据梯形的面积计算方法解决有关的实际问题.30.两个完全一样的梯形拼成一个平行四边形,平行四边形的面积是12平方厘米,那么其中一个梯形的面积是()A.6平方厘米B.12平方厘米C.24平方厘米【考点】梯形的面积;平行四边形的面积.【专题】平面图形的认识与计算.【分析】两个完全一样的梯形可以拼成一个平行四边形.这个平行四边形的面积是原来两个梯形面积的和,即为每个梯形面积的2倍,可用平行四边形的面积除以2进行计算即可得到每个梯形的面积,据此解答即可.【解答】解:12÷2=6(平方厘米)答:其中一个梯形的面积是6平方厘米.故选:A.【点评】两个完全一样的平面图形拼成一个图形,其面积就等于原图形的面积的2倍.。
四边形测试题(含答案)

八年级数学试题(考试时间:90分钟 满分:100分)一、填空:(每小题2分,共24分)1、对角线_____平行四边形是矩形。
2、如图⑴已知O 是□ABCD 的对角线交点,AC =24,BD =38,AD =14,那么△OBC 的周长等于_____。
3、在平行四边形ABCD 中,∠C =∠B+∠D,则∠A =___,∠D =___。
4、一个平行四边形的周长为70cm ,两边的差是10cm ,则平行四边形各边长为____cm 。
5、已知菱形的一条对角线长为12cm ,面积为30cm 2,则这个菱形的另一条对角线长为__________cm 。
6、菱形ABCD 中,∠A =60o ,对角线BD 长为7cm ,则此菱形周长_____cm 。
7,那么它的面积______。
8、如图2矩形ABCD 的两条对角线相交于O,∠AOB =60o ,AB =8,则矩形对角线的长___。
9、如图3,等腰梯形ABCD 中,AD ∥BC ,AB ∥DE ,BC =8,AB =6,AD =5则△CDE 周长___。
10、正方形的对称轴有___条11、如图4,BD 是□ABCD 的对角线,点E 、F 在BD 上,要使四边形AECF 是平行四边形,还需增加的一个条件是______12、要从一张长为40cm ,宽为20cm 的矩形纸片中,剪出长为18cm ,宽为12cm 的矩形纸片,最多能剪出______张。
二、选择题:(每小题3分,共18分)13、在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )A 、1:2:3:4B 、1:2:2:1C 、2:2:1:1D 、2:1:2:1 14、菱形和矩形一定都具有的性质是( ) A 、对角线相等 B 、对角线互相垂直 C 、对角线互相平分 D 、对角线互相平分且相等 15、下列命题中的假命题是( )A 、等腰梯形在同一底边上的两个底角相等B 、对角线相等的四边形是等腰梯形C 、等腰梯形是轴对称图形D 、等腰梯形的对角线相等16、四边形ABCD 的对角线AC 、BD 交于点O ,能判定它是正方形的是( ) A 、AO =OC ,OB =OD B 、AO =BO =CO =DO ,AC ⊥BD C 、AO =OC ,OB =OD ,AC ⊥BD D 、AO =OC =OB =OD 17、给出下列四个命题⑴一组对边平行的四边形是平行四边形 ⑵一条对角线平分一个内角的平行四边形是菱形⑶两条对角线互相垂直的矩形是正方形 ⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形。
人教版小学三年级上册数学第三单元四边形练习题
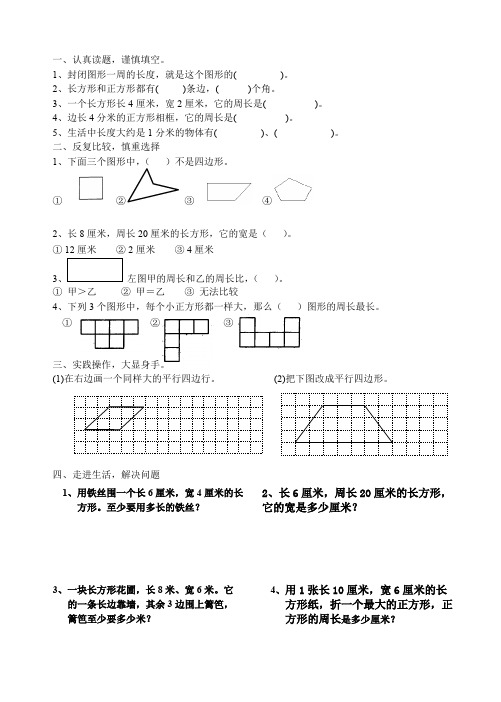
1、封闭图形一周的长度,就是这个图形的(
Байду номын сангаас
)。
2、长方形和正方形都有( )条边,(
)个角。
3、一个长方形长 4 厘米,宽 2 厘米,它的周长是(
4、边长 4 分米的正方形相框,它的周长是(
)。
5、生活中长度大约是 1 分米的物体有(
)、(
二、反复比较,慎重选择
1、下面三个图形中,( )不是四边形。
(2)把下图改成平行四边形。
四、走进生活,解决问题
1、用铁丝围一个长 6 厘米,宽 4 厘米的长 方形。至少要用多长的铁丝?
2、长 6 厘米,周长 20 厘米的长方形, 它的宽是多少厘米?
3、一块长方形花圃,长 8 米、宽 6 米。它 的一条长边靠墙,其余 3 边围上篱笆, 篱笆至少要多少米?
4、用 1 张长 10 厘米,宽 6 厘米的长 方形纸,折一个最大的正方形,正 方形的周长是多少厘米?
)。 )。
①
②
③
④
2、长 8 厘米,周长 20 厘米的长方形,它的宽是( )。 ① 12 厘米 ② 2 厘米 ③ 4 厘米
3、 ① 甲>乙
左图甲的周长和乙的周长比,( )。 ② 甲=乙 ③ 无法比较
4、下列 3 个图形中,每个小正方形都一样大,那么( )图形的周长最长。
①
②
③
三、实践操作,大显身手。 (1)在右边画一个同样大的平行四边行。
四边形的周长计算练习题

四边形的周长计算练习题在几何学中,四边形是指拥有四个边的多边形。
它是一种常见的图形,包括正方形、长方形、菱形以及各种不规则四边形等。
计算四边形的周长是几何学中的基本问题之一,下面将提供几道四边形周长计算的练习题,供读者们进行实践和巩固知识。
练习题一:已知一个矩形,其长为5 cm,宽为3 cm。
请计算该矩形的周长。
解答一:矩形的周长可通过公式计算:周长 = 2 × (长 + 宽)。
根据题意,长为5 cm,宽为3 cm。
将这些值代入公式中,我们可以计算得到:周长 = 2 × (5 cm + 3 cm) = 2 × 8 cm = 16 cm。
因此,给定矩形的周长为16 cm。
练习题二:给定一个正方形,已知其边长为10 cm。
请计算该正方形的周长。
解答二:正方形的周长可以直接计算:周长 = 4 ×边长。
根据题意,正方形的边长为10 cm。
将这个值代入公式中,我们可以计算得到:周长 = 4 × 10 cm = 40 cm。
因此,给定正方形的周长为40 cm。
练习题三:现有一个菱形,已知其对角线长度分别为6 cm和8 cm。
请计算该菱形的周长。
解答三:菱形的周长无法直接通过公式计算,但我们可以利用其对角线长度来求得。
根据菱形的性质,其对角线相交于正中心,并将菱形分为四个等边三角形。
可以观察到,菱形的周长等于四个等边三角形的周长之和。
首先,我们可以使用勾股定理计算菱形两个直角三角形的斜边长度。
其中,对角线分别为6 cm和8 cm,因此有:斜边1 = √(6 cm/2)^2 + (√(8 cm/2)^2 = √9 cm^2 + 16 cm^2 = √25 cm^2 = 5 cm。
斜边2 = 斜边1 = 5 cm。
接下来,我们可以计算等边三角形的周长。
由于等边三角形的三条边长均相等,我们只需求得其中一条边长,然后乘以3即可。
等边三角形的边长 = 斜边1 = 斜边2 = 5 cm。
《四边形的认识》综合练习题

《四边形的认识》综合练习题
四边形的认识综合练题
问题一
请问以下哪些图形是四边形?
a) 正方形
b) 圆形
c) 梯形
d) 三角形
答案:a) 正方形, c) 梯形
问题二
四边形具有哪些特点?
答案:四边形是一个有四条边的几何图形。
它的特点包括:
- 有四个角
- 相邻两边不共线
- 相邻两边不重叠
- 对角线相交于一点
- 对角线长度相等
问题三
下面哪些陈述是关于平行四边形的?
a) 对角线相等
b) 对边平行
c) 有一个直角
d) 有两条边相等
答案:b) 对边平行
问题四
计算下面平行四边形的面积:
________________
/ /
/ /
/______________/
已知底边长度为 10cm,高度为 5cm。
答案:面积 = 底边长度 ×高度 = 10cm × 5cm = 50cm²
问题五
请问矩形和正方形是什么关系?
答案:矩形是一种特殊的四边形,它的特点是拥有四个直角。
正方形是一种特殊的矩形,它的特点是拥有四个相等的边和四个直角。
问题六
如果一个四边形有两个相等的边,这个四边形是什么形状?答案:如果一个四边形有两个相等的边,它是一个梯形。
中考数学四边形专题训练50题含参考答案
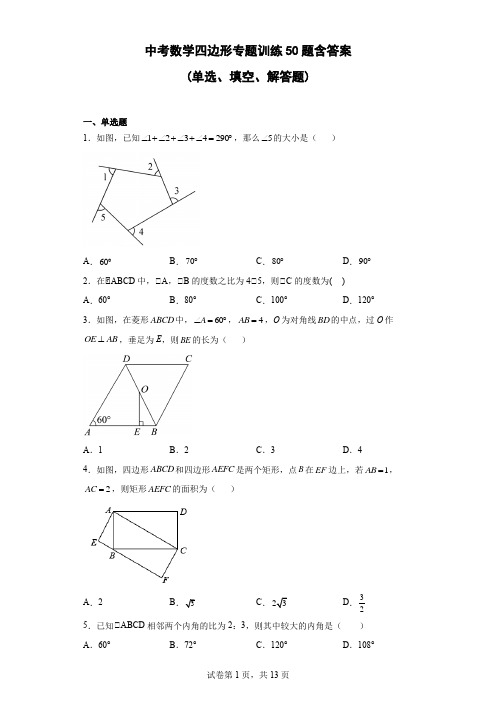
中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.如图,已知1234290∠+∠+∠+∠=︒,那么5∠的大小是( )A .60︒B .70︒C .80︒D .90︒ 2.在▱ABCD 中,∠A ,∠B 的度数之比为4∠5,则∠C 的度数为( )A .60°B .80°C .100°D .120° 3.如图,在菱形ABCD 中,60A ∠=︒,4AB =,O 为对角线BD 的中点,过O 作OE AB ⊥,垂足为E ,则BE 的长为( )A .1B .2C .3D .4 4.如图,四边形ABCD 和四边形AEFC 是两个矩形,点B 在EF 边上,若1AB =,2AC =,则矩形AEFC 的面积为( )A .2 BC .D .32 5.已知∠ABCD 相邻两个内角的比为2:3,则其中较大的内角是( ) A .60° B .72° C .120°D .108°6.如图,将长方形ABCD 沿对角线BD 折叠,使点C 落在点C ′处,BC ′交AD 于E ,AD =8,AB =4,则重叠部分(即BDE △)的面积为( )A .6B .7.5C .10D .207.如图,在矩形ABCD 中,6cm,8cm AB BC ==,点E 是BC 的中点,点F 是边CD 上一动点,当AEF △的周长最小时,则DF 的长为( )A .1B .2C .3D .48.如图,在四边形ABCD 中,110C ∠=︒,与BAD ∠,ABC ∠相邻的外角都是120°,则α∠的值为( )A .50°B .55°C .60°D .65° 9.如图,点E 为正方形ABCD 外一点,且ED CD =,连接AE ,交BD 于点F .若38CDE ∠=︒,则BFC ∠的度数为( )A .71︒B .72︒C .81︒D .82︒ 10.在平行四边形ABCD 中,点E 在DC 边上,连接AE ,交BD 于点F ,若DE ∠EC =3:2,则∠DEF 的面积与∠BAF 的面积之比为( )A.3:5B.9:4C.9:25D.3:211.如图,四边形ABCD是正方形,直线a、b、c分别经过A、D、C三点,且a b c∥∥.若a与b之间的距离是2,b与c之间的距离是3,则正方形ABCD的面积是()A.12B.13C.14D.1512.如图,在∠ABC中,点D在边BC上,过点D作DE∠AC,DF∠AB,分别交AB,AC于E,F两点.则下列说法不正确的是()A.四边形AEDF是平行四边形B.若∠B+∠C=90°,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若BD=AD=DC,则四边形AEDF是矩形13.小明在计算某多边形的内角和时,由于马虎漏掉了一个角,结果得到970°,则原多边形是一个()A.七边形B.八边形C.九边形D.十边形14.如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接OE,则OE的长为()A.10B.52C.5D.415.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是()∠平行四边形;∠菱形;∠任意四边形;∠对角线互相垂直的四边形A.∠∠B.∠∠C.∠∠D.∠∠16.如图,已知点O为∠ABC的AC边上的中点,连接BO并延长到D,使得OD=OB,要使四边形ABCD为矩形,∠ABC中需添加的条件是()A.AB=BC B.∠ABC=90°C.∠BAC=45°D.∠BCA=45°17.如图,在矩形ABCD中,AB=10,BC=12,点M,N分别在AD,BC上,且=,3AM BN=,E为BC边上一动点,连接DE,将DCEAD AM∆沿DE所在直线折叠得到∠DC E',当C'点恰好落在线段MN上时,NE的长为()A.B.5C.3D.18.如图,菱形ABCD中,∠ABC=60°,AB=4,对角线AC、BD交于点O,E是线段BO上一动点,F是射线DC上一动点,若∠AEF=120°,则线段EF的长度的整数值的个数有()A.1个B.2个C.3个D.4个19.如图,正方形ABCD边长为4,E,F分别为线段AD,BC上一点,且1AE=,CF=,AC与DF相交于H,I为线段AH上一点(不与端点重合),J为线段DH上1+的最小值为()一点(不与端点重合),则EI IJA B C D二、填空题20.如图,已知点A的坐标是(-2),点B的坐标是(1-,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是______.21.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA∠CA交DB的延长线于点E,若AB=3,BC=4,则OAAE的值为__________.22.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,若∠E=20°,则∠ADB=______.23.如图,□ABCD的对角线交于点O,且AB=4,∠OCD的周长为13,则□ABCD的两条对角线长度之和为________.24.一个多边形的内角和等于它外角和的7倍,则这个多边形的边数为_________. 25.如图,在矩形ABCD 中,5AB =,7BC =,点E 为BC 上一动点,把ABE 沿AE 折叠,当点B 的对应点B '落在ADC ∠或DAB ∠的角平分线上时,则点B '到BC 的距离为______________.26.如图,在平行四边形ABDC 中,点M 是CD 的中点,AM 与BC 相交于点N ,那么:ACN S △S 四边形BDMN 等于_______.27.如图,在周长为16,面积为6的矩形纸片ABCD 中,E 是AD 的中点.F 是AB 上一动点,将AEF ∆沿直线EF 折叠,点A 落在点'A 处.在EF 上任取一点G ,连接'GA ,GC ,则'A G GC +的最小值为___________.28.如图,∠ABC 中∠ACB =90°,BC =2,AC =4,若正方形DEFG 的顶点D 在AB 上,顶点F 、G 都在AC 上,射线AE 交BC 边于点H ,则CH 长为___.29.如图,在矩形ABCD 中,AB =6,AD =10,H 是CD 边上一点,现将BCH ∆沿BH 折叠,点C 的对应点C '正好落在AD 边上,点E 、F 分别是AD 、BH 边上的动点,再将四边形ABHD 沿EF 折叠,若点A 的对应点A '正好落在线段BH 上,且4BA HA ''=,则线段AE 的长为______.30.如图,在矩形ABCD 中,6cm AB =,BC =,点P 从点A 出发沿AB 以2cm /s 的速度向点B 移动,若出发t 秒后,2PA PC =,则t =_________秒.31.如图,已知菱形ABCD 的对角线AC=2,∠BAD=60°,BD 边上有2013个不同的点122013,,,p p p ⋯,过(1,2,,2013)i p i =⋯作i i PE AB ⊥于i E ,i i PFAD ⊥于i F ,111122222013201320132013PE PF P E P F P E P F ++++⋯++的值为_______________32.“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图∠是由边长10cm 的正方形薄板分成7块制作成的“七巧板”图∠是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______cm (结果保留根号).33.在面积为15的平行四边形ABCD 中,过点A 作AE 垂直于直线BC 于点E ,作AF 垂直于直线CD 于点F ,若AB =5,BC =6,则CE +CF 的值为_________________. 34.在菱形ABCD 的纸板中画O ,随意向其投掷一枚飞镖.若4AB =,60A ∠=,则飞镖落在O 中的概率的最大值为______.35.如图,在ABC ∆中,D 为BC 边中点,P 为AC 边中点,E 为BC 上一点且27BE CE =,连接AE ,取中点Q 并连接QD ,取QD 中点G ,延长PG 与BC 边交于点H ,若9BC =,则HE =_________.36.如图所示,AE 是▱ABCD 的∠DAB 的平分线,且交BC 于点E ,EF ∠AB 交AD 于点F ,则四边形ABEF 一定是____________.37.如图,在矩形ABCD 中,点M 在AB 边上,把∠BCM 沿直线CM 折叠,使点B 落在AD 边上的点E 处,连接EC ,过点B 作BF ∠EC ,垂足为F ,若2CD =,4CF =,则线段AE 的长为______.38.如图,在矩形ABCD 中,3AB =,BC a =,点E 在边BC 上,且3.5BE a =连接AE ,将ABE 沿AE 折叠,若点B 的对应点B '落在矩形ABCD 的边上,则a 的值为______ .39.如图,Rt∠ABC ,AB =3,AC =4,点D 在以C 为圆心3为半径的圆上,F 是BD 的中点,则线段AF 的最大值是_____.三、解答题40.如图,四边形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在线段OA ,OC 上,且OB OD =,12∠=∠,AE=CF .(1)证明;BEO DFO ≌;(2)证明:四边形ABCD 是平行四边形.41. 如图.在Rt ∠ABC 中,∠B =90°,AC =60cm ,∠A =60°,点D 从点A 出发沿AC 方向以4cm ∕秒的速度向点C 匀速运动,同时点E 从点B 出发沿BA 方向以2cm ∕秒的速度向点A 匀速运动,设点D 、E 运动的时间是t 秒(0<t <15),过点D 作DF ∠BC 于点F ,连接DE 、EF .(1)求证:四边形AEFD 是平行四边形;(2)当t 为何值时,动点D 恰好在AF 的垂直平分线上;(3)点D 、F 在运动过程中是否存在t 的值,使∠DEF 是直角三角形,若存在求出t 的值,若不存在,说明理由.42.如图,在Rt ABC 中,90ACB ∠=︒,D ,E 分别是AB ,AC 的中点,连接CD ,过点E 作EF ∥CD ,交BC 的延长线于点F .(1)求证:四边形DCFE 是平行四边形;(2)若四边形DCFE 的周长是18,AC 的长为6,求线段AB 、 BC 的长.43.知:如图,n 边形12345n A A A A A A .(1)求证:n 边形12345n A A A A A A 的内角和等于()2180n -⋅︒;(2)在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°,求这个多边形的内角和;(3)粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°,这个多加的外角度数为 ,多边形的边数为 .44.如图,在ABCD 中,对角线AC ,BD 交于点O ,E 是AD 上任意一点,连接EO 并延长,交BC 于点F ,连接AF ,CE .(1)求证:四边形AFCE 是平行四边形;(2)若60DAC ︒∠=,15ADB ∠=°,4AC =.∠直接写出ABCD 的边BC 上的高h 的值;∠当点E 从点D 向点A 运动的过程中,下面关于四边形AFCE 的形状的变化的说法中,正确的是A .平行四边形→矩形→平行四边形→菱形→平行四边形B .平行四边形→矩形→平行四边形→正方形→平行四边形C .平行四边形→菱形→平行四边形→菱形→平行四边形D .平行四边形→菱形→平行四边形→矩形→平行四边形45.如图,在∠ABC 中,AB =AC ,D 为BC 中点.四边形ABDE 是平行四边形.求证:四边形ADCE 是矩形46.已知正方形OABC 在直角坐标系中(如图),A (1,﹣3),求点B 、C 的坐标.47.如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连结BG ,DE .(正方形四条边都相等,四个角都是直角)1.我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系:(1)猜想图1中线段BG 和线段DE 的长度和位置关系:______________.(2)将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度a ,得到如图2.如图3情形.请你通过观察、测量等方法判断上述猜想是否仍然成立:_______(成立、不成立)若成立,请你选取图2或图3中的一种情况说明你的判断.48.在矩形ABCD 中,点P 是射线BC 上一动点,点B 关于直线AP 的对称点为E ,直线PE 与直线CD 交于点F .(1)如图1,当A ,C ,E 共线时,若30ACB ∠=︒,判断∠ACF 的形状,并证明;(2)若当点P 在线段BC 上的某个位置时(不与B ,C 重合),有45PAF ∠=︒,求证:当点P 在BC 延长线上任意位置时,都有45PAF ∠=︒.49.【教材呈现】下图是华师版数学教材的部分内容探索如图24.2.1,画Rt ABC ,并画出斜边AB 上的中线CD ,量一量,看看CD 与AB 有什么关系.相信你与你的伙伴一定会发现:CD 恰好是AB 的一半,下面让我们演绎推理证明这一猜想.已知:如图24.2.2,在Rt ABC ,90ACB ∠=,CD 是斜边AB 上的中线.求证:12CD AB =.【证明】请根据教材图24.2.2的提示,完成直角三角形的性质“直角三角形斜边中线等于斜边一半”的证明【延伸】如图∠,在四边形ABCD 中,90ADC ∠=︒,AB AC =,点E 、F 分别为AC ,BC 的中点,连结EF 、DE ,则线段DE 与EF 的数量关系是___________.【应用】(1)如图∠,在【延伸】的条件下,当AC 平分BAD ∠,90DEF ∠=时,则BAD ∠的大小为______.(2)如图∠,在【延伸】的条件下,当2AB =,四边形CDEF 是菱形时,直接写出四边形ABCD 的面积.参考答案:1.B【分析】根据多边形外角和为360︒度进行求解即可.【详解】解:∠1234290∠+∠+∠+∠=︒,12345360∠+∠+∠+∠+∠=︒,∠()5360123470=︒-∠+∠+∠+∠=︒∠,故选B .【点睛】本题主要考查了多边形外角和,熟知多边形外角和为360︒是解题的关键. 2.B【分析】根据平行四边形邻角互补,即可将角A 和角B 的度数求出,再利用对角相等即可求出角C.【详解】∠四边形ABCD 为平行四边形,∠∠A+∠B=180°,∠∠A ,∠B 的度数之比为4∠5 ∠∠A=180°49⨯=80°, 即∠C=80°,故选B.【点睛】本题考查了平行四边形的性质,属于简单题,熟悉平行四边形的性质是解题关键. 3.A【分析】先求出OB 的长和∠BOE 的度数,再根据30°角所对的直角边等于斜边的一半,即可求出BE 的值.【详解】解:在菱形ABCD 中,AB =AD ,60A ∠=︒,ABD ∴是等边三角形,4BD AB ∴==,O 为BD 的中点,122OB BD ∴==, 60OE AB ABD ⊥∠=︒,,30BOE ∴∠=︒,112BE OB ∴==. 故选A .【点睛】本题考查了等边三角形的判定和直角三角形30°角所对的直角边等于斜边的一半,熟练掌握等边三角形的判定和直角三角形30°角所对的直角边等于斜边的一半是解题的关键.4.B【分析】根据勾股定理可求出BC 的长度,再求解∠ACB 的度数,进而求出CF 的长度,最后用矩形面积公式求解即可.【详解】∠四边形ABCD 和四边形AEFC 是两个矩形,∠∠ABC =90°,在Rt ∠ABC 中,由勾股定理可得:BC连接BD 交AC 于点O ,∠四边形AEFC 是矩形,∠BD =AC =2,∠CO =DO =12BD =1, ∠CD =1,∠∠CDO 为等边三角形,∠∠ACD =60°,∠∠ACB =30°,∠四边形AEFC 是矩形,∠AC EF ∥,∠∠CBF =∠ACB =30°,∠CF =12BC∠矩形AEFC 的面积=AC ×CF故选:B 【点睛】本题主要考查了矩形的性质,含有30°角的直角三角形,等边三角形的判定与性质,以及勾股定理,熟练地掌握相关内容是解题的关键.5.D【分析】根据平行四边形邻角互补的性质及题意,可得出较大内角的度数.【详解】解:∠平行四边形ABCD∠相邻内角和为108o∠相邻内角的比为2:3∠较大内角度数是:3180=1085o o ⨯ 故答案是:D.【点睛】本题主要考查平行四边形邻角互补,准确应用平行四边形的性质是解题的关键. 6.C【分析】由折叠结合矩形的性质先证明,BE DE =设,BE DE x == 则8,AE x =- 再利用勾股定理求解,x 从而可得BDE △的面积. 【详解】解: 长方形ABCD ,8,4,AD AB ==//,AD BC ∴,ADB CBD ∴∠=∠由对折可得:,CBD C BD '∠=∠,ADB C BD '∴∠=∠,BE DE ∴=设,BE DE x == 则8,AE x =-由222,BE AB AE =+()22248,x x ∴=+-1680,x ∴=5,x ∴= 5,DE BE ∴==115410.22BDE S DE AB ∴==⨯⨯=故选:.C【点睛】本题考查的是矩形与折叠问题,勾股定理的应用,矩形的性质,掌握以上知识是解题的关键.7.D【分析】作点E 关于直线CD 的对称点E',连接AE'交CD 于点F ,再根据CE F BE A ∽即可求出CF 的长,进而得出DF 的长.【详解】解:如图所示:作点E 关于直线CD 的对称点E',连接AE'交CD 于点F ,此时,∠AEF 的周长最小, ∠在矩形ABCD 中,AB =6,BC = 8,点E 是BC 中点,∠'4BE CE CE ,∠CF AB ∥,∠CE F BE A ''∽, ∠CE CF BE AB ='' ,即4846CF , 解得:2CF =, ∠624DF CD CF ;故选:D .【点睛】本题考查的是轴对称最短路线问题及相似三角形的判定与性质,根据题意作出E 点关于直线CD 的对称点E',再根据轴对称的性质求出CE'的长,利用相似三角形的对应边成比例即可得出结论,熟练应用轴对称和相似的判定与性质相关知识解决问题是解题的关键.8.A【分析】先求出∠ABC =∠BAD =60°,再根据四边形的内角和等于360°,可得∠ADC =130°,即可求解.【详解】解:∠与BAD ∠,ABC ∠相邻的外角都是120°, ∠∠ABC =∠BAD =60°,∠∠ADC =360°-∠ABC -∠BAD -∠BCD =130°,∠18050ADC ∠=︒-∠=︒α.故选:A.【点睛】本题主要考查了四边形的内角和定理、邻补角,熟练掌握四边形的内角和等于360°是解题的关键.9.A【分析】根据正方形的性质,得AD CD =,90ADC ∠=︒,得45ADB CDB ∠=∠=︒;根据ED CD =,得AD DE =;根据等边对等角,38CDE ∠=︒,可求出DAE ∠;根据三角形的内角和,得AFD ∠;根据ADF △和CDF 全等,得AFD CFD ∠=∠,即可求出BFC ∠的角度.【详解】∠四边形ABCD 正方形∠AD CD =,90ADC ∠=︒∠45ADB CDB ∠=∠=︒∠ED CD =∠AD DE =∠DAE DEA ∠=∠∠38CDE ∠=︒∠9038128ADE ∠=︒+︒=︒∠26DAE DEA ∠=∠=︒∠在ADF △中,180DAF AFD ADF ∠+∠+∠=︒∠2645180AFD ︒+∠+︒=︒∠109AFD ∠=︒∠在ADF △和CDF 中AD CD ADF CDF DF DF =⎧⎪∠=∠⎨⎪=⎩∠ADF CDF ≅∠109AFD CFD ∠=∠=︒∠180180109BFC AFD ∠=︒-∠=︒-︒故选:A.【点睛】本题考查正方形和三角形的知识,解题的关键是掌握正方形的性质,全等三角形的性质和判定,等边对等角.10.C【分析】先判断∠DEF∠∠BAF,根据相似三角形的面积比等于相似比的平方计算即可.【详解】解:∠四边形ABCD是平行四边形,∠DC∠AB,DC=AB,∠∠DEF∠∠BAF,∠2DEFBAFS DES AB⎛⎫= ⎪⎝⎭.又∠DE:EC=3:2,∠3==5 DE DE DEAB DC DE EC=+,∠2239==525 DEFBAFS DES AB⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭△△.故选C.【点睛】本题考查平行四边形的性质、相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.11.B【分析】先作辅助线AE∠直线b于点E,CF∠直线b于点F,然后根据题目中的条件,可以证明△AED和△DFC全等,即可得到DF=AE,然后根据勾股定理,即可得到CD的长,从而可以得到正方形ABCD的面积.【详解】解:作AE∠直线b于点E,作CF∠直线b于点F,则AE=2,CF=3,∠四边形ABCD是正方形,∠AD =DC ,∠ADC =90°,∠∠ADE +∠CDF =90°,∠AE ∠直线b ,CF ∠直线b ,∠∠AED =∠DFC =90°,∠∠ADE +∠DAE =90°,∠∠DAE =∠CDF ,在△AED 和△DFC 中,AED DFC DAE CDF AD DC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠AED ∠∠DFC (AAS ),∠AE =DF ,∠AE =2,CF =3,∠CFD =90°,∠DF =2,∠CD∠正方形ABCD13,故选:B .【点睛】本题考查正方形的性质、全等三角形的判定与性质、勾股定理,平行线之间的距离,解答本题的关键是明确题意,利用数形结合的思想解答.12.C【分析】根据平行四边形、矩形及菱形的判定方法分别判断后即可确定正确的选项.【详解】解:∠DE ∠AC ,DF ∠AB ,∠四边形AEDF 是平行四边形,故A 选项正确;∠四边形AEDF 是平行四边形,∠B +∠C =90°,∠∠BAC =90°,∠四边形AEDF 是矩形,故B 选项正确;若BD =CD ,则四边形AEDF 是平行四边形,不一定是菱形,故C 选项错误;∠BD =AD =DC ,∠∠DBA =∠DAB ,∠DAC =∠DCA ,∠∠DAB +∠DAC =90°,即∠BAC =90°,∠四边形AEDF 是矩形,故选C .【点睛】本题考查了命题与定理的知识,解题的关键是了解平行四边形、矩形及菱形的判定方法,难度不大.13.B【分析】根据n 边形的内角和是(n -2)•180°,少计算了一个内角,结果得970度.则内角和(n -2)•180°与970°的差大于0度,且(n -2)•180°小于970°+180°.因而可以解不等式()9702180970180n <-⨯<+,多边形的边数n 一定是最小的整数值即可.【详解】解:设多边形的边数是n ,依题意有:()9702180970180n <-⨯<+ 解得:77781818n <<, ∠则多边形的边数n =8;故选B .【点睛】本题主要考查了多边形的内角和定理,正确确定多边形的边数是解题的关键. 14.B【分析】根据菱形的性质得到OA =12AC =3,OD =12BD =4,AC ∠BD ,利用勾股定理求出AD ,再根据直角三角形斜边中线的性质求出OE 即可.【详解】∠四边形ABCD 为菱形,∠OA =12AC =3,OD =12BD =4,AC ∠BD ,∠AD 5,∠点E 是边AD 的中点,∠OE =12AD =52, 故选:B .【点睛】此题考查了菱形的性质,勾股定理,直角三角形斜边中线的性质,熟记菱形的性质是解题的关键.15.D【分析】根据中点四边形为平行四边形,当四边形的对角线互相垂直时则平行四边形为矩形,即可得到答案.【详解】解:顺次连接一个四边形的各边中点,得到的四边形是平行四边形,若四边形的对角线互相垂直,则所得平行四边形为矩形,则满足条件的是∠∠, 故选:D .【点睛】此题考查中点四边形的判定,矩形的判定,熟记判定定理是解题的关键. 16.B【分析】由题意可证四边形ABCD 是平行四边形,由矩形的判定可求解.【详解】解:∠点O 为∠ABC 的AC 边上的中点,∠AO =CO ,且OD =OB ,∠四边形ABCD 是平行四边形,∠有一个角为直角的平行四边形是矩形,对角线相等的平行四边形是矩形,∠添加条件为∠ABC =90°,故选B .【点睛】本题考查了矩形的判定,平行四边形的判定,熟练掌握矩形的判定是本题的关键.17.A【分析】设CE =x ,则C ′E =x ,证明四边形MNCD 是矩形,由矩形的性质得出∠DMN =∠MNC =90°,MN =CD =10,由折叠的性质得出C ′D =CD =10,求出6MC '=,则4NC '=,在Rt NEC '中,由勾股定理得出222(8)4x x --=,解方程可得出答案.【详解】解:设CE =x ,则C ′E =x ,∠矩形ABCD 中,AB =10,∠CD =AB =10,AD =BC =12,AD∥BC ,∠点M ,N 分别在AD ,BC 上,且3AM =AD ,BN =AM ,∠DM =CN =8,∠四边形CDMN 为平行四边形,∠∠NCD =90°,∠四边形MNCD 是矩形,∠∠DMN =∠MNC =90°,MN =CD =10,由折叠知,C ′D =CD ,10,∠6MC '==,∠1064CN '=-=,∠EN =CN -CE =8-x ,∠C ′E 2-NE 2=C ′N 2,∠222(8)4x x --=,解得,5x =,即853NE CN CE =-=-=.故选:C .【点睛】本题主要考查了矩形的性质与判定,勾股定理,一元一次方程的应用,折叠的性质,熟练掌握折叠的性质是解题的关键.18.C【分析】连结CE ,根据菱形的性质和全等三角形的判定可得∠ABE ∠∠CBE ,根据全等三角形的性质可得AE =CE ,设∠OCE =a ,∠OAE =a ,∠AEO =90°﹣a ,可得∠ECF =∠EFC ,根据等角对等边可得CE =EF ,从而得到AE =EF ,在Rt∠ABO 中,根据含30°的直角三角形的性质得到AO =2,可得2≤AE ≤4,从而得到EF 的长的整数值可能是2,3,4.【详解】解:如图,连结CE,∠在菱形ABCD 中,AB =BC ,∠ABE =∠CBE =30°,BE =BE ,∠∠ABE ∠∠CBE ,∠AE =CE ,设∠OCE =a ,∠OAE =a ,∠AEO =90°﹣a ,∠∠DEF =120°﹣(90°﹣a )=30°+a ,∠∠EFC =∠CDE +∠DEF =30°+30°+a =60°+a ,∠∠ECF=∠DCO+∠OCE=60°+a,∠∠ECF=∠EFC,∠CE=EF,∠AE=EF,∠AB=4,∠ABE=30°,∠在Rt∠ABO中,AO=2,∠OA≤AE≤AB,∠2≤AE≤4,∠AE的长的整数值可能是2,3,4,即EF的长的整数值可能是2,3,4.故选C.【点睛】考查了菱形的性质,全等三角形的判定与性质,等角对等边,根据含30°的直角三角形的性质,解题的关键是添加辅助线,证明∠ABE∠∠CBE.19.C有最小值,如下【分析】作点E关于AC的对称点K,EI+IJ=KI+KJ,当EJ∠DF时EI IJ图所示,延长KJ交DC于N点,过N作NM∠AD,得到∠KMN∠∠FCD,再由∠DJ0N∠∠DCF求出J0N,最后KN减去J0N即为所求.【详解】解:如图,作点E关于AC的对称点K,当EJ∠DF时EI+IJ有最小值为KJ0,此时设KN与DF、CD的交点分别为J0和N点,过N点作MN∠AD交AB于点M.∠∠KND+∠FDC=90°,∠DFC+∠FDC=90°∠∠KND=∠DFC又∠AB∠CD∠∠MKN=∠KND=∠DFC在∠MKN 和∠CFD 中90∠=∠⎧⎪∠=∠=⎨⎪=⎩MKN CFD KMN FCD MN DC ,∠∠MKN∠∠CFD(AAS)∠1,112=====+=KM CF KN DF DN AM ,又∠DJ 0N∠∠DCF ∠0=J N DN CF DF,代入数据:01J N,得0J∠00=-==KJ KN J N 故答案为:C.【点睛】本题考查了正方形的性质、相似三角形的性质和判定、线段最值问题等,两条折线段的最值问题一般通过平移、对称等转移到一条线段上去,然后再根据两点之间线段最短或点到直线的距离垂线段最短求解即可.20.(1【分析】根据菱形具有的平行四边形基本性质,对角线互相平分,且交点为坐标原点,则B ,D 关于原点对称, 因此在直角坐标系中两点的坐标关于原点对称,横坐标与横坐标互为相反数,纵坐标与纵坐标互为相反数便可得.【详解】∠四边形ABCD 是菱形,对角线相交于坐标原点O∠根据平行四边形对角线互相平分的性质,A 和C ; B 和D 均关于原点O 对称 根据直角坐标系上一点(),x y 关于原点对称的点为()--x,y 可得已知点B的坐标是(-1, ,则点D的坐标是( .故答案为:(.【点睛】本题旨在考查菱形的基本性质及直角坐标系中关于原点对称点的坐标的知识点,熟练理解掌握该知识点为解题的关键.21.724 【分析】过点A 作AH BD ⊥于点H ,分别利用勾股定理和等面积法求出AH 和OH 的长度,从而可结合正切函数求出tan AOE ∠,进而结合题意可得出AE AO,即可得出结论.【详解】解:在Rt ABC 中,∠3,4AB BC ==,∠5AC =, ∠115222AO AC BD ===, 如解图,过点A 作AH BD ⊥于点H , ∠1122ABD S BD AH AB AD =⋅=⋅, ∠534AH =⨯, ∠125AH =,∠在Rt AOH 中,710OH ==, ∠tan 247AH OH AOE ==∠, 又∠EA CA ⊥,∠在Rt EAO △中,tan 247AE AO AOE ==∠, ∠724AO AE =, 故答案为:724.【点睛】本题考查矩形的性质,正切函数的定义等,理解矩形的基本性质,掌握正切函数的定义是解题关键.22.40°【分析】连接AC ,由矩形性质可得∠E =∠DAE 、BD =AC =CE ,知∠E =∠CAE ,而∠E =20°,可得∠ADB 度数.【详解】解:连接AC ,∠四边形ABCD是矩形,∠AD∠BE,AC=BD,且∠E=20°,∠∠E=∠DAE,又∠BD=CE,∠CE=CA,∠∠E=∠CAE,∠∠ADB=∠CAD=∠CAE+∠DAE=2∠E=40°,故答案为:40°.【点睛】本题主要考查矩形性质,熟练掌握矩形对角线相等且互相平分、对边平行是解题关键.23.18【详解】由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线看作一个整体.解:∠四边形ABCD是平行四边形,∠AB=CD=4,∠∠OCD的周长是13,∠OD+OC=13-4=9,∠BD=2DO,AC=2OC,∠平行四边形的两条对角线的和=BD+AC=2(DO+OC)=18故选A.“点睛”本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形的基本性质:∠平行四边形两组对边分别平行;∠平行四边形两组对边分别相等;∠平行四边形的两种对角分别相等;∠平行四边形的对角线互相平分.24.16【详解】设多边形的边数为n,依题意,得:(n−2)⋅180°=7×360°,解得n=16,故答案为16.25.2或1或52- 【分析】过点B '作B M AD '⊥于M ,延长MB '交BC 于点H ,则MH BC ⊥于点H ,则MH BC ⊥,5MH AB ==,分点B 的对应点B '落在ADC ∠的角平分线上和点B 的对应点B '落在DAB ∠的角平分线两种情况,利用勾股定理列方程,即可求得答案. 【详解】解:四边形ABCD 是矩形,5,7,90,AB CD AD BC ADC AD BC ∥,过点B '作B M AD '⊥于M ,延长MB '交BC 于点H ,则MH BC ⊥于点H ,则MH BC ⊥,5MH AB ==,∠当点B 的对应点B '落在ADC ∠的角平分线上时,连接B D ',45,ADB MB D,DM B M∠设DM B M x '==,则7AM x =-,又由折叠的性质知5AB AB '==,∠在直角AMB '△中,由勾股定理得到:222AM AB B M ,即()22275x x -=-, 解得:1234,x x ==,则点B '到BC 的距离为532MH B M '-=-=或541MH B M '-=-=.∠当点B 的对应点B '落在DAB ∠的角平分线上时,45,B AMMB A ,AM B M∠设AM m B M '==,又由折叠的性质知5AB AB '==,∠在直角AMB '△中,由勾股定理得到:222AB AM B M ,即2225m m =+,解得:12m m ==(不合题意,舍去),则点B '到BC 的距离为5MH B M '-=-故答案为:2或1或5- 【点睛】本题考查的是翻折变换的性质、勾股定理、矩形的性质、解一元二次方程等知识点,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.26.2:5【详解】试题分析:根据平行四边形的性质可得∠ABN∠∠MCN ,再结合点M 是CD 的中点,根据相似三角形的性质及三角形的面积公式求解即可.∠平行四边形ABDC∠∠ABN∠∠MCN∠点M 是CD 的中点∠AN=2MN∠∠CAN 的面积是∠MCN 的面积的2倍,∠BCD 的面积是∠MCN 的面积的6倍 ∠四边形BDMN 是∠MCN 的面积的5倍∠:ACN BDMN S S ∆四边形=2:5.考点:平行四边形的性质,相似三角形的判定和性质,三角形的面积公式点评:平行四边形的性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.27.【分析】连接AC 交EF 于H ,连接A ′H ,当点G 与点H 重合时,此时A 'G +GC 的值最小,由勾股定理求出AC 的长,则可得出答案.【详解】解:连接AC 交EF 于H ,连接A ′H ,当点G 与点H 重合时,此时A 'G +GC 的值最小,设AB =x ,BC =y ,∠矩形ABCD 的周长为16,面积为6,∠2()166x y xy +=⎧⎨=⎩, ∠22x y +52=,∠AC ==∠A 'G +GC 的最小值为故答案为:【点睛】本题考查翻折变换,矩形的性质,轴对称最短问题等知识,解题的关键是学会用转化的思想思考问题.28.43【分析】根据题意可知1tan =2BC DG BAC AC AG ==∠,tan =EF CH HAC AF AC=∠再利用正方形的性质求解即可.【详解】解:∠四边形DEFG 是正方形,∠DG=G F =EF ,∠DGF =∠EF A =90°,∠∠DGA =90°, ∠tan =DG BAC AG ∠,tan =EF HAC AF ∠ ∠∠ACB =90°,BC =2,AC =4, ∠1tan ==2BC BAC AC ∠,tan =CH HAC AC ∠ ∠1tan =2BC DG BAC AC AG==∠, ∠2AG DG =,∠3=3AF DG EF = ∠1tan =3EF CH HAC AF AC ==∠, ∠433AC CH ==, 故答案为:43【点睛】本题主要考查了正方形的性质和解直角三角形,解题的关键在于能够熟练掌握解直角三角形的相关知识.29.16936【分析】过点A 作MN ∠BC ,分别交BC 于M ,交AD 于N ,则四边形ABMN 是矩形,AM =AN ,MN =AB =6,然后证明A MB HCB '△∽△,得到485AN BM BC ===,45A M HC '=,再由折叠的性质可得10BC BC '==,AE A E '=,CH C H '=,则可由勾股定理得到8AC '=,则2C D AD AC ''=-=,从而可以求得103CH =,得到8=3A M ',则10=3A N MN A M ''=-,设=AE A E y '=,则8EN y =-,由222A E A N EN ''=+,得到()2221083y y ⎛⎫=+- ⎪⎝⎭,解方程即可. 【详解】解:如图所示,过点A 作MN ∠BC ,分别交BC 于M ,交AD 于N ,∠四边形ABCD 是矩形,∠=90A ABM BMN C ∠=∠=∠=︒∠ ,CD ∠BC ,∠四边形ABMN 是矩形,∠AM =AN ,∠A M BC '⊥,CD BC ⊥,∠A M CH '∥,∠A MB HCB '△∽△, ∠BA BM A M BH BC HC''==, ∠4BA HA ''=,∠5BH HA '=, ∠4=5BA BM A M BH BC HC ''==,∠485AN BM BC ===,45A M HC '=, 由折叠的性质可得10BC BC '==,AE A E '=,CH C H '=,∠8AC '=,∠2C D AD AC ''=-=,设C H CH x '==,则6DH x =-,∠222C H DH C D ''=+,∠()2264x x =-+, 解得103x =, ∠103CH =, ∠8=3A M ', ∠10=3A N MN A M ''=-, 设=AE A E y '=,则8EN y =-,∠222A E A N EN ''=+, ∠()2221083y y ⎛⎫=+- ⎪⎝⎭, 解得16936y =, ∠16936AE =, 故答案为:16936.【点睛】本题主要考查了矩形的性质与判定,折叠的性质,勾股定理,解题的关键在于能够熟练掌握矩形的性质与判定.30.【分析】根据矩形的性质和勾股定理,用含t 的代数式表示出P A ,PC ,再列出方程,即可求解.【详解】解:∠在矩形ABCD 中,6cm AB =,BC =,点P 从点A 出发沿AB 以2cm /s 的速度向点B 移动,∠P A =2t ,PC ∠2PA PC =,∠2t =t 1t 2, 故答案是:【点睛】本题主要考查矩形的性质,勾股定理,二次根式,一元二次方程,用用含t 的代数式表示出P A ,PC ,是解题的关键.31.2013【详解】试题分析:在菱形ABCD 中,BD∠AC ,BD 与AC 互相平分,因为∠BAD=60°,所以∠BAC=30°,又因为AC=2,设BD 的一半为x ,则AB=2x ,根据勾股定理,得1AP ,因为i i PE AB ⊥于i E ,i i PF AD ⊥于i F ,利用等面积法,得12·AD·1P F +12·AB·1P E =12·BD·12AC 1P F +1P E )1P F +1P E =1,同理可得,111122222013201320132013PE PF P E P F P E P F ++++⋯++=2013×1=2013.考点:菱形的相关性质和等面积法的应用点评:该题主要考查学生对菱形性质的理解和掌握程度,同时要求学生提高对题目的观察能力,找出其中的规律.32.2【分析】由题目中第一个图可到小正方形的边长与小等腰三角形的直角边相等,与平行四边形的短边相等,所以大正方形的对角线长度为4倍小正方形边长,设出小正方形边长,利用大正方形面积列出方程,解出方程即可【详解】设小正方形边长为a ,由题目中第一个图可到小正方形的边长与小等腰三角形的直角边相等,与平行四边形的短边相等, 所以大正方形对角线长4a ,S 大正方形=442a a ⨯。
人教新课标三年级上册数学试题-四边行—长方形的周长 人教新课标

长方形的周长
基础训练
一、填空题
(1)、(),是它的周长。
(2)、长方形()边相等,四个角都是()。
(3)、一个长方形的长是4厘米,宽是2厘米,它的周长是()厘米。
列式:()
二、计算下面各图形的周长。
三、你认为下面的说法正确吗?
1、长方形的对边相等。
()
5、下面两个图形的周长相等。
()
三、自已画出一个周长是10厘米的长方形。
能力提升
解决问题,你能行!
1、如果一个长方形的周长是18厘米,你认为它的长和宽可能分别是多少厘米?(请写出算式,至少写3种)
2、王爷爷有一块长方形菜地,长6米,宽3米。
课外拓展
你会求下面图形的周长吗?(单位:米)。
四边形及周长的认识练习题

四边形及周长的认识练习题一、填空。
)
角。
)个角,而且都是(()条边,、长方形和
正方形都有(1。
)(短边的长叫做长方形的,)
(长方形的长边的长叫做长方形的、2)(一个长
方形有)条宽。
条长和()边都相等。
)边
相等,正方形的(、长方形和正方形的不同之处
就是,长方形的(3 )、正方形每条边的
长叫做(4 )相等。
)形,它(这个图形
是(、5)(这个正方形的边长是厘米的长方
形纸上剪掉一个最大的正方形,8宽厘米、10在一张
长、6 )厘米。
)厘米,宽是(厘米,剩下的
长方形的长是()根。
)根;摆一个正方形至少
用(、用同样的小棒摆图形:摆一个长方形至少用
(7 二、选择题。
)、当一个四边形四条边都相
等,四个角都相等时,这个四边形是(1 长方形
C.正方形 B.平行四边形A. )个最大的正方
形。
、下面的长方形,最多可以截(2 4 B.3 C.2 . A 、甲<乙C 乙=、甲B 、下面
两个图形的周长(、甲>乙A 3 )乙
甲 ,( )的周长最短(厘米的正方形拼成下面的
图形。
1、用四个边长4 )的周长最长。
A B C (先编号再填序号)三、下面哪些图形
是四边形、长方形、正方形。
正方形:长方形:四边形:四、画一画,在方格纸中画出一个长方形,一个正方形和一个平行四边形。
五、描出下列图形的周长,并选两个量出长度计算周长。
六、七、你会求下面图形的周长吗?(单位:厘米)。
初中数学四边形专题训练50题含答案

中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.平行四边形不一定具有的性质是( )A .对角线互相垂直B .对边平行且相等C .对角线互相平分D .对角相等 2.如图,在MON ∠的两边.上分别截取,OA OB ,使OA OB =;分别以点A ,B 为圆心,OA 长为半径作弧,两弧交于点C ;连接,,,AC BC AB OC .若2AB =,四边形OACB 的面积为4.则OC 的长为( )A .2B .3C .4D .5 3.在ABCD 中,下列结论错误的是( )A .//AB CD B .B D ∠=∠C .AC BD =D .180C D ∠+∠=︒ 4.如图,在平行四边形ABCD 中,E 是AB 延长线上的一点,若∠A=60°,则∠1的度数为( )A .120°B .60°C .45°D .30° 5.若平行四边形中两个内角的度数比为1∠2,则其中较大的内角是( ) A .100° B .60° C .120° D .90° 6.如图,正方形OABC 与正方形ODEF 是位似图形,点O 为位似中心,位似比为2:3,点B 、E 在第一象限.若点A 的坐标为()1,0,则点E 的坐标是( )A .0)B .33,22⎛⎫ ⎪⎝⎭C .D .(2,2) 7.四边形ABCD 中,对角线AC ,BD 交于点O ,AD//BC ,为了判定四边形是平行四边形,还需一个条件,其中错误..的是( ) A .AB//CD B .∠A=∠C C .AB=CD D .AO=CO 8.一个多边形的内角和等于外角和,则这个多边形的边数为( )A .10B .8C .6D .49.顺次连接等腰梯形各边中点所围成的四边形是( )A .平行四边形B .矩形C .菱形D .正方形 10.已知平行四边形ABCD 的周长为32,AB =4,则BC 的长为( )A .4B .12C .24D .48 11.如图,四边形ABCD 是矩形,,把矩形沿直线AC 折叠,点B 落在点E处,连结DE,则的值是( )A .B .C .8D .7:25 12.如图,在平行四边形ABCD 中,AB=4,CE 平分∠BCD 交AD 边于点E ,且AE=3,则BC 的长为( )A .4B .6C .7D .813.如图,在矩形ABCD ,对角线AC 与BD 相交于点O ,EO AC ⊥于点O ,交BC 于点E ,若ABE ∆的周长为8,3AB =,则AD 的长为 ( )A .2B .5.5C .5D .414.如图,矩形ABCD 中,4AB =,2BC =.点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则BE 的长是( )A .B C .2.5 D .1.5 15.如图,在平行四边形ABCD 中,过点P 作直线EF 、GH 分别平行于AB 、BC ,那么图中共有( )平行四边形.A .4个B .5个C .8个D .9个 16.如图,已知直线PQ CD ⊥于点P ,B 是CPQ ∠内部一点,过点B 作BA PQ ⊥于点A ,BC CD ⊥于点C ,四边形PABC 是边长为8cm 的正方形,N 是AB 的中点,动点M 从点P 出发,以2cm/s 的速度,沿P A B C →→→方向运动,到达点C 停止运动,设运动时间为()s t ,当CM PN =时,t 等于( )A .2B .4C .2或4D .2或617.如图,在菱形中,,,是的中点.过点作,垂足为.将沿点到点的方向平移,得到.设、分别是、的中点,当点与点重合时,四边形的面积为A .B .C .D . 18.如图,点EF 、分别是菱形ABCD 的边AD 、DC 的中点,如果阴影部分的面积和是10,则菱形对角线AC 与BD 的乘积AC BD ⋅等于( )A .10B .32C .20D .1619.如图,在正方形1ABCB 中,AB =AB 与直线l 所夹锐角为60,延长1CB 交直线l 于点1A ,作正方形1112A B C B ,延长12C B 交直线l 于点2A ,作正方形2223A B C B ,延长23C B 交直线l 于点3A ,作正方形3334A B C B ⋯,依次规律,则线段20212022A A =( )A .20192⨯⎝⎭B .20202⨯⎝⎭C .20212⨯⎝⎭D .20222⨯⎝⎭20.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,添加一个条件使平行四边形ABCD 为矩形的是( )A .AD AB = B .AB AD ⊥C .AB AC =D .CA BD ⊥二、填空题21.如图,这个图案是用形状、大小完全相同的等腰梯形密铺而成的,则这个图案中的等腰梯形的底角(指锐角)是_________度.22.如图,点E 在矩形ABCD 的对角线BD 上,EF BC ⊥于点F ,连接AF ,若5BC =,2EF =,则ABF △的面积为_________.23.已知菱形的两条对角线长分别为3和4,则菱形的面积为______.24.有一个边长为50cm 的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为_____.25.如图,Rt ABC 中,90C BC AC ∠=︒>,,以AB BC AC ,,三边为边长的三个正方形面积分别为1S ,2S ,3S .若ABC 的面积为7,140S =,则32S S -的值等于______.26.如图,将长方形ABCD沿AE折叠,已知50∠=︒,则BADCED'∠'的大小是_____27.如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为CC',则图中阴影部分的面积为__.28.用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是______.29.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为_____.30.如图,将四边形ABCD沿BD、AC剪开,得到四个全等的直角三角形,已知,OA =4,OB=3,AB=5将这四个直角三角形拼为一个没有重叠和缝隙的四边形,则重新拼成的四边形的周长为_____.31.在长方形ABCD中,10AB=,将长方形ABCD折叠,折痕为EF.AD=,8(1)如图1,当A'与B重合时,EF=_______;(2)如图1,当直线EF过点D时,点A的对应点A'落在线段BC上,则线段EF的长为______.32.如图,P 是▱ABCD 内的任意一点,连接P A 、PB 、PC 、PD ,得到△P AB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论:∠S 1+S 3=S 2+S 4,∠若S 3=2S 1,则S 2=2S 4,∠若S 1+S 3=5,则ABCD 的面积为10;∠S 1+S 2=S 3+S 4.其中正确的结论的序号是____________(把所有正确结论的序号都填在横线上).33.如图, 直线l 是四边形ABCD 的对称轴,若AB CD =,有下面的结论:∠AB BC ⊥;∠AC BD ⊥;∠//AB CD ;∠AO OC =.其中正确的结论有__.34.如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形,恰好能拼成这样一个“勾股圆方图”,则该矩形与拼成的正方形的周长之比为________.35.如图,平行四边形ABCD 中,45B ∠=︒,7BC =,CD =E ,F 分别是边AB ,BC 的中点,连接CE ,DF ,取CE ,DF 的中点G ,H ,连接GH ,则GH 的长度为__________.36.如图,正方形ABCD的边长为1,AC,BD是对角线,将∠DCB绕着点D顺时针旋转45°得到∠DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:∠DE平分∠ADB;∠BE∠四边形AEGF是菱形;∠BC+FG=1.5.其中结论正确的序号是_______.37.如图,点E、F是平行四边形ABCD的边AB、DC上的点,F与DE相交于点P,BF与CE相交于点Q若S△APD=14cm2,S△BCQ=16cm2,四边形PEQF的面积为______.38.如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为_____.39.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为__________.三、解答题40.□ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F ,四边形AFCE 是否是菱形?为什么?41.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,延长CD 到E ,使DE CD =,连接AE .(1)求证:四边形ABDE 是平行四边形;(2)连接OE ,若60ABC ∠=︒,且8AD DE ==,求OE 的长.42.如图,点E 、F 分别在ABCD 的边AB 、CD 的延长线上,且BE =DF ,连接AC 、EF 、AF 、CE ,AC 与EF 交于点O .(1)求证:AC 、EF 互相平分;(2)若EF 平分∠AEC ,判断四边形AECF 的形状并证明.43.正方形ABCD 的对角线交点为O ,连AE 交BC 于E ,交OB 于F ,2EC FO =,求证:AE 平分BAC ∠.44.如图,在三角形ABC 中,90C ∠=︒,四边形DEFC 是边长为4的正方形,且D 、E 、F 分别在边AC AB BC 、、上.把三角形ADE 绕点E 逆时针旋转一定的角度.(1)当点D 与点F 重合时,点A 的对应点G 落在边BC 上,此时四边形ACGE 的面积为___________;(2)当点D 的对应点1D 落在线段BE 上时,点A 的对应点为点1A ,在旋转过程中点A 经过的路程为1l ,点D 经过的路程为2l ,且12:3:2l l =,求线段1AD 的长. 45.如图所示,已知四边形ABCD 是平行四边形,在AB 的延长线上截取BE=AB ,BF=BD ,连接CE ,DF ,相交于点M .求证:CD=CM .46.如图,在直角梯形ABCD 中,AD ∠BC ,AD ∠CD ,M 为腰AB 上一动点,联结MC 、MD ,AD =10,BC =15,cot B 512=.(1)求线段CD 的长.(2)设线段BM 的长为x ,∠CDM 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域.47.在Rt ABC 与Rt BDE 中,90ABC DBE ∠=∠=︒,AB BC =,BD BE =.(1)如图1,若点D ,B ,C 在同一直线上,连接AD ,CE ,则AD 与CE 的关系为_________;(2)如果将图1中的BDE △绕点B 在平面内顺时针旋转到如图2的位置,那么请你判断AD 与CE 的关系,并说明理由;(3)如图3,若6AB =,2BD =,连接AE ,分别取DE ,AE ,AC 的中点M ,P ,N ,连接MP ,NP ,MN ,将BDE △绕点B 在平面内顺时针旋转一周,请直接写出旋转过程中MPN△面积的最小值和最大值.48.如图,在矩形ABCD中,AD=4,CD=3,点E为AD的中点.连接CE,将∠CDE 沿CE折叠得∠CFE,CE交BD于点G,交BA的延长线于点M,延长CF交AB于点N.(1)求DG的长;(2)求MN的长.49.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED 的边长;如果不存在,请说明理由.参考答案:1.A【分析】结合平行四边形的性质即可判定.【详解】结合平行四边形的性质可知选项B、C、D均正确,但平行四边形的对角线不垂直,则A不正确.故选A.【点睛】本题考查了平行四边形的性质,熟练掌握平行四边形的性质是正确解题的关键.2.C【分析】根据作法判定出四边形OACB是菱形,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.【详解】解:根据作图,AC=BC=OA,∠OA=OB,∠OA=OB=BC=AC,∠四边形OACB是菱形,∠AB=2,四边形OACB的面积为4,∠12AB•OC=12×2×OC=4,解得OC=4.故选:C.【点睛】本题主要考查菱形的性质与判定,熟练掌握菱形的性质与判定是解题的关键.3.C【分析】根据平行四边形的性质逐项判断即可.【详解】解:A、由平行四边形行两组对边分别平行可得//AB CD,故A正确;B、由平行四边形对角相等可得B D∠=∠,故B正确;C、AC、BD为平行四边形对角线,平行四边形对角线互相平分,但不一定相等,故C错误;D、由平行四边形行两组对边分别平行可得//AD BC,两直线平行同旁内角互补,可得180C D∠+∠=︒,故D正确.故选:C.【点睛】本题主要考查平行四边形的性质及其推论,熟练掌握平行四边形的性质是解题关键.4.B【详解】解:∠四边形ABCD 是平行四边形,∠AD∠BC ,∠∠1=∠A=60°.故选B .5.C【分析】据平行四边形的性质得出AB //CD ,推出∠B +∠C =180°,根据∠B :∠C =1:2,求出∠C 即可.【详解】解:∠四边形ABCD 是平行四边形∠AB //CD ,∠∠B +∠C =180°,∠∠B :∠C =1:2,∠∠C =23×180°=120°,故选:C .【点睛】本题考查了平行线的性质和平行四边形的性质的应用,能熟练地运用性质进行计算是解此题的关键,题目比较典型,难度不大.6.B【分析】由题意可得:2:3OA OD =,又由点A 的坐标为()1,0,即可求得OD 的长,又由正方形的性质,即可求得E 点的坐标.【详解】解:∠正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为2:3, ∠:2:3OA OD =,∠点A 的坐标为()1,0,即1OA =, ∠32OD =, ∠四边形ODEF 是正方形,∠32 DE OD==.∠E点的坐标为:33,22⎛⎫ ⎪⎝⎭.故选:B.【点睛】此题考查了位似变换的性质与正方形的性质.此题比较简单,注意理解位似变换与相似比的定义是解此题的关键.7.C【分析】根据平行四边形的判定定理逐项判断即可.【详解】解:A.根据两组对边分别平行可判定是平行四边形,不符合题意;B.根据平行线性质可得另一对内角相等,根据两组对角分别相等可判定是平行四边形,不符合题意;C.不能判定是平行四边形,可能是等腰梯形,符合题意;D.可通过全等证对角线互相平分,能判定是平行四边形,不符合题意;故选:C.【点睛】本题考查了平行四边形的判定,解题关键是熟知平行四边形的判定定理,准确进行判断.8.D【分析】设这个多边形的边数为n,根据内角和等于外角和列方程解答即可.【详解】解:设这个多边形的边数为n,则()2180360n-⨯︒=︒,解得4n=,故选:D.【点睛】此题考查了多边形内角和与外角和的计算,熟练掌握多边形内角和公式及外角和是解题的关键.9.C【分析】由E、F、G、H分别为AB、BC、CD、DA的中点,得出EF,HG,FG,EH是中位线,再得出四条边相等,根据“四条边都相等的四边形是菱形”进行证明.【详解】解:如图所示,因为E、F、G、H分别为AB、BC、CD、DA的中点,连接AC、BD,因为E、F分别是AB、BC的中点,所以EF=12AC ,且EF∠AC同理可得HG=12AC ,且HG∠AC , FG=12BD ,且FG∠BD , EH=12BD ,且EH∠BD , ∠EF∠HG ,HE ∠FG ,∠四边形EFGH 是平行四边形,又因为等腰梯形的对角线相等,即AC=BD ,因此有EF=FG=GH=HE ,所以连接等腰梯形各中点所得四边形为菱形.故选:C【点睛】此题考查三角形中位线的性质,解题的关键是掌握三角形的中位线定理及菱形的判定.10.B【详解】由题意得:2()32,4,12AB BC AB BC +===得: .故选B.11.D【详解】试题分析:从D,E 处向AC 作高DF,EH .设AB=4k,AD=3k,则AC=5k .由∠AEC的面积=4k×3k=5k×EH,得EH=95k k;根据勾股定理得CH=,∠四边形ACED是等腰梯形,∠CH=AF=95 k,所以DE=5k﹣95k×2=75k.所以DE:AC=75k:5k=7:25.故选D.考点:翻折变换.12.C【分析】由平行四边形的性质可得AD∠BC,且AD=BC,结合角平分线的性质可求得DE=DC=AB=4,则可求得AD的长,可求得答案.【详解】解:∠四边形ABCD为平行四边形,∠AB=CD=4,AD∠BC,AD=BC,∠∠DEC=∠BCE.∠CE平分∠BCD,∠∠DCE=∠BCE,∠∠DEC=∠DCE,∠DE=DC=4.∠AE=3,∠AD=BC=3+4=7.故选C.【点睛】本题主要考查平行四边形的性质,利用平行线的性质及角平分线的性质求得DE=DC是解题的关键.13.C【分析】由矩形的性质可得AO=CO,由线段垂直平分线的性质可得AE=EC,即可求解.【详解】解:∵四边形ABCD是矩形,∴AO=CO,BC=AD,∵EO⊥AC,∴AE=EC,∵△ABE的周长为8,∴AB+AE+BE=8,∴3+BC=8,∴AD =BC =5,故选:C .【点睛】本题考查了矩形的性质,线段垂直平分线的性质,掌握矩形的性质是本题的关键.14.D【分析】由矩形ABCD 中,四边形EGFH 是菱形,易证得()COF AOE AAS ≌,即可得OA OC =,然后由勾股定理求得AC 的长,继而求得OA 的长,又由AOE ABC ∽△△,利用相似三角形的对应边成比例,即可求得答案.【详解】解:如图,连接EF ,交AC 于O ,∠四边形EHFG 是菱形,EF AC OE OF ∴⊥=,,∠四边形ABCD 是矩形,90B D ∴∠=∠=︒,AB CD ∥,ACD CAB ∴∠=∠,在COF 与AOE △中,FCO OAE FOC AOE OF OE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()COF AOE AAS ∴≌,AO CO ∴=,AC AB ==12AO AC ∴==, 90CAB CAB AOE B ∠=∠∠=∠=︒,,AOE ABC ∴∽,∠AO AE AB AC=,=, 2.5AE ∴=,1.5BE ∴=,故选:D .【点睛】本题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质,准确作出辅助线是解此题的关键.15.D【详解】∠AD∠BC 、AB∠CD ,EF∠AB ,GH∠BC ,∠AB∠EF∠DC ,AD∠GH∠BC ,∠共有9个平行四边形,如平行四边形AGPE ,平行四边形BGPF ,平行四边形PEDH ,平行四边形PFCH ,平行四边形ABFE ,平行四边形EFCD ,平行四边形AGHD ,平行四边形BGHC ,平行四边形ABCD ,故选D.16.D【分析】分点M 是AP 的中点和点M 与点N 重合两种情况讨论,由全等三角形的性质和正方形的性质即可求解.【详解】解:当点M 是AP 的中点时,∵四边形P ABC 是正方形,∴PC =P A =AB ,∠CP A =∠P AN =90°,∵N 是AB 的中点,点M 是AP 的中点,∴PM =AN =4,在△CPM 和△P AN 中,PA CP CPA PAN PM AN =⎧⎪∠=∠⎨⎪=⎩∴△CPM ≌△P AN (SAS ),∴PN =CM ,∴t 42==2, 当点M 与点N 重合时,由正方形的对称性可得PN =CM ,∴t842+==6,故选:D【点睛】本题考查了正方形的性质,全等三角形的性质,利用分类讨论思想解决问题是解题的关键.17.A【详解】试题分析:作在菱形中,,,是的中点是的中点,故答案选A.考点:平行四边形的面积,三角函数.18.B【分析】设EF交BD于G,AC交BD于O,由三角形中位线的性质可得EF=12AC,EF//AC,可得EG为∠AOD的中位线,可得DG=12OD,根据菱形的性质可得BG=34BD,根据菱形的面积公式列方程即可得答案.【详解】设EF交BD于G,AC交BD于O,∠点E F 、分别是菱形ABCD 的边AD 、DC 的中点, ∠EF=12AC ,EF//AC ,∠EG 为∠AOD 的中位线, ∠OG=12OD ,∠四边形ABCD 是菱形, ∠OD=OB=12BD ,BD∠AC , ∠BG=34BD ,BG∠EF , ∠S 菱形ABCD =S 阴影+S △BEF ,阴影部分的面积和是10, ∠12AC·BD=10+12EF·BG=10+12·12AC·34BD , 解得:AC·BD=32.故选:B【点睛】本题考查菱形的性质、三角形中位线的性质及菱形的面积公式,菱形的对角线互相垂直且平分;菱形的面积等于两条对角线乘积的一半;三角形的中位线平行于第三边且等于第三边的一半;熟练掌握相关性质及公式是解题关键.19.C【分析】利用特殊角的三角函数值分别求出11A B 、22A B 、33A B ,以此类推找到规律求出20222022A B ,最后根据202120222022Rt A A B 中20212022202290A B A ∠=︒,20222021202230A A B ∠=︒,即可求解.【详解】解:∠AB 与直线l 所夹锐角为60︒,且1BAB ∠是正方形1ABCB 的一个顶角, ∠11180609030B AA ∠=︒-︒-︒=︒,又∠1190AB A ∠=︒,∠在11Rt AB A △中,11111tan A B AB A AB =⨯∠,∠正方形1ABCB 的边长AB∠11111tan A B AB A AB =⨯∠同理可求得: 222A B =⎝⎭,333A B =⎝⎭,以此类推可知: 20222021202120222022A B ===⎝⎭⎝⎭⎝⎭,∠202120222022Rt A A B 中20212022202290A B A ∠=︒,20222021202230A A B ∠=︒,∠2021202120222022202222A A A B ==⨯⎝⎭,故C 正确.故选:C . 【点睛】本题主要考查了正方形的性质、含特殊角的锐角三角函数等知识,含30°的直角三角形的性质.利用从特殊到一般寻找规律是解题的关键.20.B【分析】根据矩形的判定和平行四边形的性质分别对各个选项进行判断即可.【详解】解: A 、AD AB =时,平行四边形ABCD 是菱形,故选项A 不符合题意; B 、AB AD ⊥时,∠BAD =90°,则平行四边形ABCD 是矩形,故选项B 符合题意; C 、AB AC =时,平行四边形ABCD 不一定是矩形,故选项C 不符合题意;D 、CA BD ⊥时,平行四边形ABCD 是菱形,故选项D 不符合题意;故选:B .【点睛】此题考查的是平行四边形的性质、矩形的判定以及等腰三角形的判定等知识;熟练掌握矩形的判定和平行四边形的性质是解答此题的关键.21.60°【分析】根据图案的特点,可知密铺的一个顶点处的周角,由3个完全相同的等腰梯形的较大内角组成,即可求出等腰梯形的较大内角的度数,进而即可得到答案.【详解】由图案可知:密铺的一个顶点处的周角,由3个完全相同的等腰梯形的较大内角组成,∠等腰梯形的较大内角为360°÷3=120°,∠等腰梯形的两底平行,∠等腰梯形的底角(指锐角)是:180°-120°=60°.故答案是:60°.【点睛】本题主要考查等腰梯形的性质以及平面镶嵌,掌握平面镶嵌的性质是解题的关键.22.5【分析】证明∠BEF∠∠BCD,由相似三角形的性质求得BF•CD,即求得BF•AB,进而由三角形的面积公式求得结果.【详解】解:∠四边形ABCD是矩形,∠AB=CD,∠ABC=∠BCD=90°,∠EF∠BC,∠EF∠CD,∠∠BEF∠∠BDC,∠BF EF BC CD=,∠BC=5,EF=2,∠BF•CD=BC•EF=5×2=10,∠BF•AB=10,∠∠ABF的面积=12BF•AB=5,故答案为:5.【点睛】本题主要考查了矩形的性质,相似三角形的判定与性质,三角形的面积计算,关键是由相似三角形求得BF•AB的值.23.6【分析】根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.【详解】解:∠菱形的两条对角线长分别为3和4,∠菱形的面积为134=6 2⨯⨯故答案为:6【点睛】本题考查了菱形的性质,菱形的面积通常有两种求法,可以用底乘以高,也可以用对角线乘积的一半求解,计算时要根据具体情况灵活运用.24.【分析】根据圆与其内切正方形的关系,易得圆盖的直径至少应为正方形的对角线的长,已知正方形边长为50cm,进而由勾股定理可得答案.【详解】解:根据题意,知圆盖的直径至少应为正方形的对角线的长;再根据勾股定理,50故答案为:.【点睛】题主要考查正多边形和圆的相关知识;注意:熟记等腰直角三角形的斜边是直角边的 倍,可以给解决此题带来方便.25.【分析】结合正方形面积公式,平方差公式,勾股定理,三角形面积公式,可知()()2223S S BC AC BC AC BC AC -=-=+-,2240BC AC +=,14BC AC ⋅=,然后运用完全平方公式()2222a b a b ab ±=+±求解即可.【详解】解:根据题意,2140S AB ==,22S BC =,23S AC = ∠()()2223S S BC AC BC AC BC AC -=-=+-在Rt ABC 中,根据勾股定理,222BC AC AB +=∠2240BC AC +=∠7Rt ABC S = ∠172BC AC ⋅⋅= ∠14BC AC ⋅=∠BC AC +==BC AC -====∠()()BC AC BC AC +-==即23S S -=故答案为:【点睛】本题考查勾股定理与三角形、正方形的面积,完全平方公式与平方差公式的灵活应用,掌握并熟练应用勾股定理和各类公式是解题的关键.26.40【详解】试题分析:先根据折叠的性质求得、的度数,即可求得、的度数,再根据长方形的性质求解即可.∠50CED ∠='︒,AE 为折痕∠∠∠BAD ∠'. 考点:折叠的性质点评:折叠的性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.27.342π+【分析】根据菱形的性质以及旋转角为30°,连接CD ′和BC ',可得A 、D′、C 及A 、B 、C′分别共线,求出扇形的面积,再根据AAS 证得两个小三角形全等,求得面积,最后根据扇形ACC '的面积-两个小的三角形的面积即可.【详解】解:连接CD ′和BC '∠∠DAB =60°∠30DAC CAB ∠=∠=︒∠30C AB ∠''=︒∠A 、D′、C 及A 、B 、C′分别共线∠AC =∠扇形ACC′的面积为:2303604ππ⨯=∠AC =AC ′,AD′=AB在OCD OC B ''和中CD BC ACD AC D COD C OB '='⎧⎪∠=∠''⎨⎪∠'=∠'⎩∠()OCD OC B AAS ''≌∠OB =OD′,CO =C′O又∠60,30CBC BC O ︒∠'∠=='︒∠90BOC ∠'=︒在Rt BOC '中,())22211BO BO +-=解得13,22BO C O ='=∠S △OCB=12BO C O '⨯⨯=,∠322442C B AC OC S S Sππ''=-=-=+阴影扇形 故答案为:342π+ 【点睛】本题考查了旋转的性质,菱形的性质,扇形的面积公式,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.28.18或16【分析】首先由直角边分别为3和4,求得其斜边,然后分别从以边长为3,4,5的边为对角线拼成一个平行四边形(非矩形),去分析求解即可求得答案. 【详解】解:直角边分别为3和4,∴5=,若以边长为3的边为对角线,则所得的平行四边形的周长是:2(54)18⨯+=; 若以边长为4的边为对角线,则所得的平行四边形的周长是:2(53)16⨯+=;若以边长为5的边为对角线,则所得的平行四边形的周长是:2(34)14⨯+=(此时是矩形,舍去);综上可得:所得的平行四边形的周长是:16或18.故答案为:16或18.【点睛】此题考查了平行四边形的性质以及勾股定理.注意掌握分类讨论思想的应用是解此题的关键.29【分析】如图,连接BD交AC于E,由四边形ABCD是菱形,推出AC∠BD,AE=EC,在Rt△EOD中,利用勾股定理求出DE,在Rt△ADE中利用勾股定理求出AD即可.【详解】如图,连接BD交AC于E.∠四边形ABCD是菱形,∠AC∠BD,AE=EC,∠OA=2OC,AC=3,∠CO=DO=2EO=1,AE=32,∠EO=12,DE=EB==,∠AD=【点睛】本题考查菱形的性质、勾股定理等知识,解题的关键是灵活应用勾股定理解决问题.30.20,22,26,28【分析】以直角三角形边长相等的边为公共边,拼接四边形,再计算周长;【详解】解:∠如图周长=20;∠如图周长=22;∠如图周长=26;∠如图周长=28;∠如图周长=22;∠四边形的周长为:20,22,26,28;故答案为:20,22,26,28.【点睛】本题考查了图形的拼接,四边形的周长;作出拼接图形是解题关键.31.10【分析】(1)根据题意结合图形直接写出答案即可解决问题;(2)根据勾股定理首先求出A C'的长度;再次利用勾股定理求出AE的长度,即可解决问题.【详解】解:(1)如图1,当A'与B重合时,EF=10;(2)如图2,设AE=x,则BE=8-x;∠四边形ABCD为矩形,∠BC=AD=10,DC=AB=8;∠B=∠C=90°;由题意得:=A D AD '=10;由勾股定理得:222A C A D DC 1006436''=-=-=∠A C 6BA 1064''==-=, ,在Rt∠A BE '中,由勾股定理得:222(8)4x x =-+解得:x=5,由勾股定理得:222EF =10+5=125∠EF =【点睛】该命题主要考查了翻折变换及其应用问题;能根据翻折变换的性质准确找出命题图形中隐含的等量关系是解题的关键.32.∠∠【分析】根据平行四边形的的性质可以得到AB =CD ,AD =BC ,设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4,然后利用三角形的面积公式列式整理判断即可得到答案.【详解】解:∠四边形ABCD 是平行四边形,∠AB =CD ,AD =BC ,设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4,hAB 、hBC 分别为平行四边形的AB 边和BC 边的高则S 1=12AB •h 1,S 2=12BC •h 2,S 3=12CD •h 3,S 4=12AD •h 4,hAB = h 1+h 3,hBC =h 2+h 4 ∠12AB •h 1+12CD •h 3=12AB •hAB ,12BC •h 2+12AD •h 4=12BC •hBC ,又∠S 平行四边形ABCD =AB •hAB =BC •hBC ,∠S 2+S 4=S 1+S 3,故∠正确;根据S 3=2S 1只能判断h 3=2h 1,不能判断h 2=2h 4,即不能得出S 2=2S 4,故∠错误; 根据S 1+S 3=S 2+S 4,S 1+S 3=5,能得出ABCD 的面积为5×2=10,故∠正确;由题意只能得到S 2+S 4=S 1+S 3无法得到S 1+S 2=S 3+S 4,故∠错误;故答案为:∠∠.【点睛】本题主要考查了平行四边形的性质,三角形的面积,用平行四边形的面积表示出相对的两个三角形的面积是解题的关键.33.∠∠∠【分析】根据轴对称的性质得到直线l 垂直平分BD ,则根据线段垂直平分线的性质得AB AD =,CD CB =,由于AB=CD ,则AB BC CD BC ===,于是可判断四边形ABCD 为菱形,然后根据菱形的性质对4个结论进行判断.【详解】证明:∠直线l 是四边形ABCD 的对称轴,∴直线l 垂直平分BD ,AB AD ∴=,CD CB =,AB CD =,AB BC CD BC ∴===,∴四边形ABCD 为菱形,AC BD ∴⊥,//AB CD ,OA OC =,所以∠∠∠正确 .故答案为∠∠∠.【点睛】本题考查了轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.也考查了菱形的判定与性质.34.35)【分析】设图2的矩形分割成四个全等三角形的两直角边为a 、b (a >b ),由图1与图2的两个小正方形相同,得出a 与b 的关系,再求出矩形的边长和大正方形的边长,应用周长公式求得其周长,最后便可求得其比值.【详解】解:设图2的矩形分割成四个全等三角形的两直角边为a 、b (a >b ),小正方形的边长为a-b ,矩形的长为2a+a-b=3a-b ,宽为b ,∠矩形的周长为:2(3a-b+b )=6a ,由图2知,中间小正方形的边长为b ,∠a-b=b ,∠a=2b ,∠大正方形的周长为,==∠该矩形与拼成的正方形的周长之比:=故答案为:3:5).【点睛】本题主要考查了勾股定理,矩形的性质,正方形的性质,关键是根据图形求得全等直角三角形的两直角边与矩形和大正方形的边长的关系.35.134【分析】连接DG 并延长,交于AB 延长线于点M ,过点M 作MN ∠CB ,交于CB 延长线于点N ,首先根据平行四边形的性质证明(),CGD EGM AAS ≅得出,DG GM =即可得出1,2HG FM =再利用勾股定理求出FM ,即可求得答案. 【详解】连接DG 并延长,交于AB 延长线于点M ,过点M 作MN ∠CB ,交于CB 延长线于点N ,如图,∠四边形ABCD 为平行四边形,∠CD ∠AB,AB CD ==∠CDG EMG ∠=∠又∠G 为CE 中点,∠,CG GE =在CGD △和EGM 中∠CDG EMG DGC MGE CG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩∠(),CGD EGM AAS ≅∠,DG GM = ,CD EM = ∠1,2HG FM = AB EM =, ∠,AE BM =∠点E 为AB 的中点,∠1,2AE EB AB ==∠12EB BM AB ===, 又∠45,B ∠=︒∠45,MBN ∠=︒∠,BN MN =设,BN MN x ==在Rt BMN 中,∠222,BN MN BM +=∠222x x +=, 解得,5,2x = 即5,2BN MN == ∠点F 为BC 的中点, ∠17,22BF BC == ∠75622FN BF BN =+=+=, 在Rt MNF △中,∠222,NF MN MF +=∠13,2MF = ∠113,24HG FM == 故填:134. 【点睛】本题考查平行四边形的性质,全等三角形的判定与性质,三角形中位线定理,勾股定理,解题关键是熟练掌握平行四边形的性质和三角形中位线定理.36.∠∠∠【分析】根据旋转的性质可知,∠DGH ∠∠DCB ,进而得知DH =DB ,∠H =∠CBD =45°,∠DGH =∠DCB =90°,DG =DC =AD ,之后可证∠ADF ∠∠GDF ,四边形AEGF 是菱形,再根据勾股定理可知AE 的长度,进而可以一一判断选出答案.【详解】解:根据旋转的性质可知,∠DGH ∠∠DCB ,∠DH =DB ,∠H =∠CBD =45°,∠DGH =∠DCB =90°,DG =DC =AD ,在Rt ∠AED 与Rt ∠GED 中,AD =DG ,ED =ED∠Rt ∠AED ∠Rt ∠GED (HL )∠∠ADE =∠GDE ,即DE 平分∠ADB ,故∠正确;在∠ADF 和∠GDF 中,AD =DG ,∠ADF =∠GDF ,DF =DF ,∠∠ADF ∠∠GDF (SAS )∠AF =GF ,∠DAF =∠DGF =45°又∠∠ABD =45°∠FG ∠AE∠∠DAC =45°,∠∠DAC =∠H ,∠AF ∠EG∠四边形AEGF 是平行四边形,又∠AF =GF∠平行四边形AEGF 是菱形,故∠正确;∠∠H =45°,∠HAE =90°∠AE =AH∠AE =AF =HD -AD =BD -AD∠正方形ABCD 的边长为1,根据勾股定理可知BD ==即HD∠AE 1∠BE =)11=2-∠正确; ∠四边形AEGF 是菱形∠FG =AE 1∠BC +FG =1∠错误;综上答案为:∠∠∠.【点睛】本题考查的是正方形的性质,菱形的判定与性质,勾股定理和直角三角形的性质,是一道综合性较强的题,能够充分调动所学知识是解题的关键.37.30cm 2。
四边形的面积与周长的综合练习题

四边形的面积与周长的综合练习题四边形是平面几何中常见的一种图形,它具有四个边和四个角。
面积和周长是描述四边形特征的重要概念,通过练习题我们可以更好地理解四边形的性质和计算方法。
本文将提供一些综合练习题,帮助读者巩固对四边形面积与周长的理解。
题目一:某个长方形的周长是28 cm,面积是72 cm²,求长方形的长和宽分别是多少。
解答:设该长方形的长为a cm,宽为b cm,则根据长方形周长的计算公式,有:2a + 2b = 28 (1)根据长方形面积的计算公式,有:ab = 72 (2)根据方程组(1)和(2),可以求解出长方形的长和宽。
题目二:一个梯形的上底为3 cm,下底为7 cm,高为4 cm,求梯形的面积和周长分别是多少。
解答:根据梯形的计算公式,梯形的面积可以计算为上底与下底平均值乘以高的结果:面积 = (3 + 7) × 4 ÷ 2 = 20 cm²梯形的周长可以通过计算各边的长度之和得出:周长 = 上底 + 下底 + 斜边1 + 斜边2= 3 + 7 + 斜边1 + 斜边2(注:由于未给出斜边的具体长度,无法计算周长的具体值。
)题目三:一个菱形的对角线分别为8 cm和10 cm,求菱形的面积和周长分别是多少。
解答:菱形的面积可以通过对角线的乘积除以2得出:面积 = (8 × 10) ÷ 2 = 40 cm²菱形的周长可以通过计算四条边的长度之和得出,由于菱形的四条边相等,可以简化计算:周长 = 4 ×边长(注:由于未给出边长的具体值,无法计算周长的具体值。
)题目四:一个正方形的一条边长为6 cm,求正方形的面积和周长分别是多少。
解答:正方形的面积可以通过边长的平方得出:面积 = 边长 ×边长= 6 × 6 = 36 cm²正方形的周长可以通过计算四条边的长度之和得出,由于正方形的四条边相等,可以简化计算:周长 = 4 ×边长= 4 × 6 = 24 cm通过以上综合练习题,我们对四边形的面积与周长的计算方法有了更深入的理解。
四边形测试卷及答案

四边形测试卷一.选择题(共11小题)1.如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为()A.2cm B.3cm C.4cm D.3cm2.以不在一条直线上的三点A、B、C为顶点的平行四边形共有()A.1个B.2个C.3个D.4个3.如图,在周长为20cm的▱ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE 的周长为()A.4cm B.6cm C.8cm D.10cm4.下列命题中错误的是()A.平行四边形的对边相等B.两组对边分别相等的四边形是平行四边形C.矩形的对角线相等D.对角线相等的四边形是矩形5.正方形具有而菱形不具有的性质是()A.四条边都相等B.对角线相等C.对角线平分一组对角D.对角线垂直且互相平分6.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个7.如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,其面积是()A.bc﹣ab+ac+c2B.ab﹣bc﹣ac+c2C.a2+ab+bc﹣ac D.b2﹣bc+a2﹣ab8.如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为()A.1 B.C.D.29.点A、B、C、D在同一平面内,若从①AB∥CD②AB=CD③BC∥AD④BC=AD这四个条件中选两个,不能推导出四边形ABCD是平行四边形的选项是()A.①②B.①④C.②④D.①③10.要从一张长40cm,宽20cm的矩形纸片中剪出长为18cm,宽为12cm的矩形纸片则最多能剪出()A.1张B.2张C.3张D.4张11.给出五种图形:①矩形;②菱形;③等腰三角形(腰与底边不相等);④等边三角形;⑤平行四边形(不含矩形,菱形).其中,能用完全重合的含有30°角的两块三角板拼成的图形是()A.②③B.②③④C.①③④⑤D.①②③④⑤二.填空题(共7小题)12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是_________cm.13.在四边形ABCD中,E、F、G、H分别是四条边的中点,要使四边形EFGH为菱形,四边形ABCD 应具备的条件是_________.14.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长为_________.15.如图,延长正方形ABCD边BC延长至E,使CE=AC,则∠AFC=_________.16.如图,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为_________cm(结果不取近似值).17.在矩形ABCD中,M是BC的中点,MA⊥MD,若矩形的周长为48cm,则矩形ABCD的面积为______cm2.18.如图,梯形ABCD中,AD∥BC,且AD:BC=3:5,梯形ABCD的面积是8cm2,点M、N分别是AD和BC上一点,E、F分别是BM、CM的中点,则四边形MENF的面积是_________cm2.三.解答题(共9小题)19.如图,田村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大核桃树.田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形的形状,请问田村能否实现这一设想?若能,请你设计并画出图形;若不能,请说明理由(画图要保留痕迹,不写画法).20.将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.21.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE 交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由.22.如图,正方形ABCD的对角线AC和BD相交于点O,O又是正方形A1B1C1O的一个顶点,O A1交AB于点E,OC1交BC于点F.(1)求证:△AOE≌△BOF;(2)如果两个正方形的边长都为a,那么正方形A1B1C1O绕O点转动,两个正方形重叠部分的面积等于多少?为什么?23.已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(1)求证:BE=DF;(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM,FM,判断四边形AEMF是什么特殊四边形?并证明你的结论.24.如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.(1)求证:△PDQ是等腰直角三角形;(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.25.如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.(1)当点E坐标为(3,0)时,试证明CE=EP;(2)如果将上述条件“点E坐标为(3,0)”改为“点E坐标为(t,0)(t>0),结论CE=EP是否成立,请说明理由;(3)在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,用t表示点M的坐标;若不存在,说明理由.26.已知:如图,E为▱ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.27.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D,过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.(1)①当α=_________度时,四边形EDBC是等腰梯形,此时AD的长为_________;②当α=_________度时,四边形EDBC是直角梯形,此时AD的长为_________;(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.答案与评分标准一.选择题(共11小题)1.(2010•菏泽)如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为()A.2cm B.3cm C.4cm D.3cm考点:菱形的性质;勾股定理;三角形中位线定理。
小学数学四边形周长计算练习题

小学数学四边形周长计算练习题题1:计算四边形的周长A. 计算四边形ABCD的周长,已知AB = 5cm,BC = 7cm,CD = 6cm,AD = 4cm。
B. 计算四边形EFGH的周长,已知EF = 8cm,FG = 9cm,GH =7.5cm,HE = 5cm。
C. 计算四边形IJKL的周长,已知IJ = 12cm,JK = 5.2cm,KL =8.6cm,LI = 6cm。
题2:判断四边形类型并计算周长A. 判断四边形MNOP是否具有相等的对边和对角线,并计算其周长。
已知MN = 5cm,NO = 8cm,OP = 5cm,PM = 8cm。
B. 判断四边形QRST是否具有两对平行边和四个相等的角,并计算其周长。
已知QR = 6cm,RS = 9cm,ST = 6cm,TQ = 9cm。
C. 判断四边形UVWX是否具有四个相等的边长和四个直角,并计算其周长。
已知UV = 4cm,VW = 4cm,WX = 4cm,XU = 4cm。
题3:应用四边形周长计算A. 一个长方形的宽为3cm,周长为16cm,求长方形的长度。
B. 一个正方形的周长为32cm,求正方形的边长。
C. 一个梯形的上底长为5cm,下底长为10cm,两个斜边长分别为6cm和8cm,求梯形的周长。
题4:四边形周长综合运用A. 一个菱形的周长为20cm,已知两个相邻边长分别为6cm和8cm,求另外两个边长。
B. 一个平行四边形的周长为50cm,已知两个相邻边长分别为12cm和15cm,求另外两个边长。
C. 一个任意四边形的周长为22cm,已知三个相邻边长分别为4cm,6cm和7cm,求第四个边长。
题5:四边形周长与计算器应用A. 使用计算器计算一个特殊四边形ABCD的周长,已知AB =18.5cm,BC = 15.2cm,CD = 13.7cm,DA = 16.4cm。
B. 使用计算器计算一个不规则四边形EFGH的周长,已知EF =23.6cm,FG = 28.4cm,GH = 19.9cm,HE = 21.3cm。
四边形练习题及答案

四边形练习题及答案一、选择题1. 以下哪个不是四边形的性质?A. 四边形的内角和为360度B. 四边形的对角线互相平分C. 四边形的对边平行D. 四边形的对角线相等答案:C2. 在平行四边形中,下列说法正确的是:A. 对角线相等B. 对角线互相垂直C. 对角线互相平分D. 对边相等答案:C3. 菱形的四个角的度数之和是多少?A. 180度B. 360度C. 540度D. 720度答案:B4. 矩形的对角线具有什么性质?A. 相等B. 互相垂直C. 互相平分D. 互相垂直且相等答案:D5. 梯形中,以下哪个说法是错误的?A. 只有一组对边平行B. 非平行边相等的梯形是等腰梯形C. 梯形的对角线相等D. 梯形的内角和为360度答案:C二、填空题1. 四边形ABCD中,若AB平行于CD,则四边形ABCD是________。
答案:梯形2. 若四边形ABCD的对角线互相平分,则四边形ABCD是________。
答案:平行四边形3. 菱形的对角线互相________。
答案:垂直4. 矩形的四个角都是________度。
答案:905. 等腰梯形的两个非平行边相等,且两底平行,其对角线________。
答案:相等三、简答题1. 请简述矩形和正方形的共同性质。
答案:矩形和正方形都是平行四边形,它们的共同性质包括:对边平行且相等,对角线互相平分且相等,四个角都是直角。
2. 什么是等腰梯形?请简述其性质。
答案:等腰梯形是两腰相等的梯形。
其性质包括:两腰相等,两底平行,底角相等,对角线相等。
四、计算题1. 已知四边形ABCD是平行四边形,AB=5cm,BC=7cm,∠ABC=60度,求对角线AC的长度。
答案:由于ABCD是平行四边形,AB平行于CD,BC平行于AD。
根据平行四边形的性质,我们可以知道∠ACD=∠ABC=60度。
由于AB=5cm,BC=7cm,我们可以将三角形ABC视为一个30-60-90度的特殊三角形,其中AC是斜边,根据30-60-90度三角形的性质,斜边AC=AB*√3=5√3cm。
四边形练习题(含答案)

四边形练习题(含答案)1、阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:(1)菱形的“二分线”可以是。
(2)三角形的“二分线”可以是。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.2、用配方法解方程时,原方程可变形为()A. B.C. D.3、用两块边长为a的等边三角形纸片拼成的四边形是【】A.等腰梯形 B.菱形 C.矩形 D.正方形4、在下面图形中,每个大正方形网格都是由边长为1的小正方形组成,则图中阴影部分面积最大的是()5、下列命题中错误的是()A.两组对边分别相等的四边形是平行四边形B.对角线相等的平行四边形是矩形C.一组邻边相等的平行四边形是菱形D.一组对边平行的四边形是梯形6、如图,每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )A. B.2 C. D.7、将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形.将纸片展开,得到的图形是()8、如下图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP 的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是A.10 B.16 C.18 D.209、如图,在梯形ABCD中,AD//BC,AD=2,AB=3,BC=6,沿AE翻折梯形ABCD,使点B落在AD的延长线上,记为B′,连接B′E交CD于F,则的值为( )A. B. C. D.10、用任意两个全等的直角三角形拼下列图形:①平行四边形②矩形③菱形④正方形⑤等腰三角形⑥等边三角形其中一定能够拼成的图形是_______(只填题号).11、某陶瓷市场现出售的有边长相等的正三角形、正方形、正五边形的地板砖,某顾客想买其中的镶嵌着铺地板,则他可以选择的是.12、在一张三角形纸片中,剪去其中一个50°的角,得到如图所示的四边形,则图中∠1+∠2的度数为______________。
一年级数学应用题认识多边形的周长的应用题

一年级数学应用题认识多边形的周长的应用题在数学学科中,多边形是一个非常重要的概念。
它不仅具有基本的几何属性,还在日常生活中具有广泛的应用。
本文将通过一系列应用题的形式,来帮助一年级学生更好地认识多边形的周长及其应用。
1. 题目一:小明有一个正方形的花坛,每条边长为3米,他想用绳子将花坛围起来,请问他需要多长的绳子?解析:正方形是一种特殊的多边形,它有四条边,而且四条边长度相等。
题目中已经给出了边长,我们需要计算出周长。
周长=每条边的长度×边的数量根据题目,每条边的长度为3米,边的数量为4条,所以周长=3米×4=12米。
小明需要12米的绳子将花坛围起来。
2. 题目二:一张矩形的桌子,长为2米,宽为1.5米,需要用围栏将其围起来,围栏每米需要花费8元,请问需要多少钱?解析:矩形也是一种常见的多边形,它有四条边,且相邻两条边长度相等。
题目给出了长和宽,我们需要计算出周长,并据此计算所需费用。
周长=长+宽+长+宽根据题目,长为2米,宽为1.5米,所以周长=2米+1.5米+2米+1.5米=7米。
围栏每米需要花费8元,所以需要的总费用=周长×每米花费=7米×8元/米=56元。
小明需要支付56元才能将桌子围起来。
3. 题目三:小红的房间是一个不规则四边形,其中两条边长分别为2米和4米,另外两条边长分别为3米和5米,她想计算出房间的周长。
解析:题目中描述的不规则四边形是一种特殊的多边形,它的四条边可以有不同的长度。
我们需要计算出这个不规则四边形的周长。
周长=边1长度+边2长度+边3长度+边4长度根据题目,边1长度为2米,边2长度为4米,边3长度为3米,边4长度为5米,所以周长=2米+4米+3米+5米=14米。
小红的房间周长为14米。
4. 题目四:一条跑道是一个由9个等边三角形组成的多边形,每个三角形的边长为8米,那么跑道的周长是多少?解析:跑道是由多个等边三角形组成的多边形,每个三角形的边长相等。
小学数学四边形及周长练习题

小学数学四边形及周长练习题四边形及周长练习题是小学数学的重要内容之一。
通过练习题的训练,学生能够熟练掌握四边形的特点和计算周长的方法。
本文将为您提供一系列的练习题,帮助您更好地理解和运用相关知识。
练习题一:矩形的周长问题:一个矩形的长是8cm,宽是5cm,求它的周长是多少?解析:矩形的周长等于两个相邻边的长度之和的两倍。
根据题目给出的数据,我们可以得到矩形的周长为:(8 + 5) × 2 = 26(cm)。
练习题二:正方形的周长问题:一个正方形的边长是6cm,求它的周长是多少?解析:正方形的周长等于边长的四倍。
根据题目给出的数据,我们可以得到正方形的周长为:6 × 4 = 24(cm)。
练习题三:菱形的周长问题:一个菱形的对角线长分别为10cm和6cm,求它的周长是多少?解析:菱形的周长等于其对角线长度的两倍。
首先,我们需要求出菱形的边长。
根据菱形的性质可知,菱形的对角线相交垂直且平分对方角,因此可以将菱形划分为四个直角三角形。
通过勾股定理,我们可以求得菱形的边长为8cm。
然后,根据边长的长度,我们可以得到菱形的周长为:8 × 4 = 32(cm)。
练习题四:平行四边形的周长问题:一个平行四边形的底边长为10cm,高度为4cm,求它的周长是多少?解析:平行四边形的周长等于底边长的两倍与高度的两倍之和。
根据题目给出的数据,我们可以得到平行四边形的周长为:(10 × 2) + (4 × 2) = 28(cm)。
练习题五:不规则四边形的周长问题:一个不规则四边形的四条边长分别为5.2cm、7.9cm、4.6cm 和9.3cm,求它的周长是多少?解析:不规则四边形的周长等于四条边长的和。
根据题目给出的数据,我们可以得到不规则四边形的周长为:5.2 + 7.9 + 4.6 + 9.3 = 27(cm)。
通过以上的练习题,我们可以看到四边形的周长计算方法是相对简单的,只需要将相邻边长相加即可。
四年级平行四边形和梯形的周长应用题练习题一

四年级平行四边形和梯形的周长应用题练习题一姓名:1)一个平行四边形的一条边是14厘米;它的邻边比它短2厘米;这个平行四边形的周长是多少厘米?2)一个等腰梯形的上底是2厘米;下底是4厘米;它的周长是12厘米;那么等腰梯形的腰长是多少厘米?3)已知平行四边形的周长是38厘米;其中一条边是10厘米;另外3条边分别是多少厘米?4)一个平行四边形的一条边是12厘米;它的邻边比它短2厘米;这个平行四边形的周长是多少厘米?5)已知平行四边形的周长是60厘米;其中一条边是20厘米;另外3条边分别是多少厘米?6)一个等腰梯形的上底是22厘米;下底是24厘米;它的周长是66厘米;那么等腰梯形的腰长是多少厘米?7)一个平行四边形的一条边是12厘米;它的邻边比它长2厘米;这个平行四边形的周长是多少厘米?8)一个等腰梯形的上底是15厘米;下底是26厘米;它的腰长是12厘米;它的周长是多少厘米?9)一个平行四边形的邻边分别是9厘米和13厘米;它的周长是多少厘米?10)一个梯形的上底是16厘米;下底比上底少8厘米;两腰分别长9厘米、7厘米。
这个梯形的周长是多少厘米?11)一个等腰梯形的上底是32厘米;下底比上底长7厘米;腰长是26厘米;这个梯形的周长是多少厘米?12)一个平行四边形的一条边长23分米;比另一条边长6分米。
它的周长是多少厘米?13)一个长方形的长是67厘米;宽是45厘米;它的周长和面积分别是多少?14)一个正方形的周长是60厘米;它的面积是多少?15)一个正方形的边长是20厘米;它的周长和面积分别是多少?16)把2个边长都是30厘米的正方形拼成一个长方形;这个长方形的周长和面积分别是多少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四边形及周长的认识练习题
一、填空。
1、长方形和正方形都有()条边,()个角,而且都是()角。
2、长方形的长边的长叫做长方形的(),短边的长叫做长方形的()。
一个长方形有()条长和()条宽。
3、长方形和正方形的不同之处就是,长方形的()边相等,正方形的()边都相等。
4、正方形每条边的长叫做()
5、这个图形是()形,它()相等。
6、在一张长10厘米、宽8厘米的长方形纸上剪掉一个最大的正方形,这个正方形的边长是()厘米,剩下的长方形的长是()厘米,宽是()厘米。
7、用同样的小棒摆图形:摆一个长方形至少用()根;摆一个正方形至少用()根。
二、选择题。
1、当一个四边形四条边都相等,四个角都相等时,这个四边形是()
A.平行四边形
B.正方形
C.长方形
2、下面的长方形,最多可以截()个最大的正方形。
A.4 B.3 C.2
3、下面两个图形的周长()A、甲>乙B、甲=乙C、甲<乙
甲乙
4、用四个边长1()的周长最短,( )的周长最长。
A B C
三、下面哪些图形是四边形、长方形、正方形。
(先编号再填序号)
四边形:长方形:正方形:
四、画一画,在方格纸中画出一个长方形,一个正方形和一个平行四边形。
五、描出下列图形的周长,并选两个量出长度计算周长。
六、
七、你会求下面图形的周长吗?(单位:厘米)。
