吴振顺《控制工程基础》王积伟第二版课后习题解答
机械控制工程基础第二版课后答案

机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c?(idt2?i1)dt得到:cr2du2?(1?r2r1)u2?cr2du1dt?r2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1c?idt消去i得到:(r1?r2)一阶微分方程du2dt?u2c?r2du1dt?u1c第二章2-2解:1)确定输入、输出变量f(t)、x2f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f?f?m2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44?(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33?(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22?(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?1?1s?22e?t?e?2t (4)199s?4e?4t?19119s?1?t?1123(s?1)?t?e?13te1(s?1)2(5)?2(s?2)?2(s?1)??2e?2t?2e?t?te?t (6)?0.25?2ss?42?0.5?2?2s?42?2s?1?2.5s?t?0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,?1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程??mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图??mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x??2x?2x (2) ???2x??2tx?2x xxxoooioooi??2x?2x(4) ???2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》第二版课后习题答案
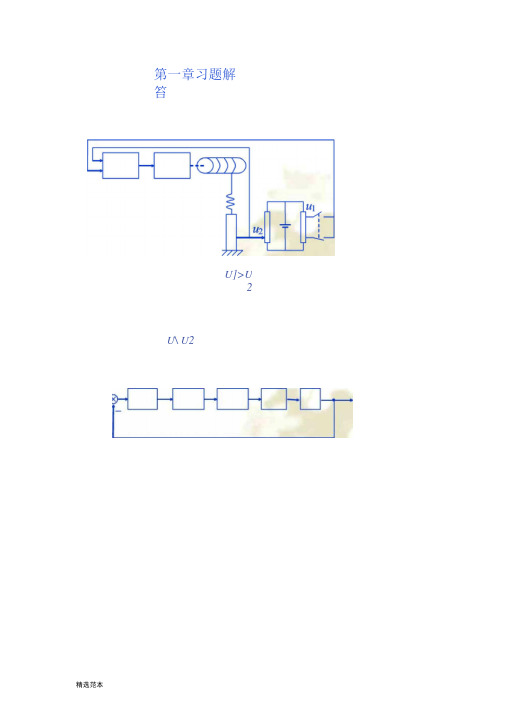
第一章习题解笞U]>U2 U\ U2第二章习题解答2-1a) b)d)f)L^f| 忙d)f\ — fl =^2X O严(f)=$(M+E ⑴虑 如(f) =iQ)RRC^-u o (t)^u o (t) = RC^-u^t) at at fs (r)=B 低[xi (f) -曲(幼 j/B (t)=fK (t) = KXo(t) B dB d 『八10602斤不%()+%©二斤击可()占dR^c —% (0+ (*i + 心)% ⑴=邛应 ~u i (0+ R 2u t (0 atati =i R +,C u o =IR?:R R 严冃3宙 % =gR\ +u oa)=K ](旳一兀)+」:dx o ](J?l + J?2)C —«c (!)+ %("■ R Q C — Wj(O + tti (Oat at(K[ + K2)B — x o (t)+ K\K2X o (t)= K\R 〒曲(f)+ 琦心再(f)dt at10602a) b) c) Q © f)U Q —1/?2 + — j icit— Z/?| + iR-f H —J idte)dxK\% K i (兀 _ %) = K 》(兀)—x)=号二dtoB 2+ (®K° ++ B'B? + 场*3 + 水2〃?)& 2+ (K }B 2+K }B 3 + 心汝 + KM 巴2 + K }K 2X 2 dt3J S + 2用 + 8S-丘($ + 2)($戈+2$十4)广、■炉+ 5,2+9用+7E ($+恥 + 2)乡一rn\fU2K 2rdx { dx 2< dt dt ;/(O™-坷罕~_叭 dtdxj … 一 —- - K?x^ = m dtdx l dx 2dt dt护d 2x 2 2~d^ k,用典2+ (的+创坷+用2创+加2*3);?7皿乔对)13173 G($)= --------------- —(£+。
《控制工程基础》(王积伟 吴振顺)课后习题答案 高等教育出版社
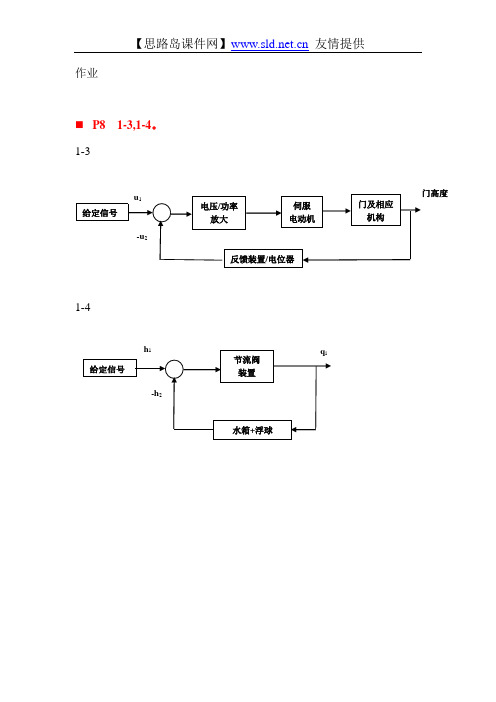
作业P81-3,1-4。
1-31-4(P72)2-1,2-2。
2-1-a22,u u u u u u i c i c -==+dt du dt du c RC RC R i u i22-==dt du dt du i RC u RC =+222-1-b221Kx B B dt dx dt dx =-dt dx dt dx B Kx B 122=+2-1-c2u u u i c -=2212()(1212R C C R i i u R u R u dt du dt du R c i i -+-=+=i dt du dt du u R C R R u R R C R R i 22121221)(2+=++2-1-d22211121x K x K x K B B dt dx dt dx =-+-1122112)(x K B x K K B dt dx dt dx +=++2-1-e1211R u R u R ii -=⎰⎰⎰-+-=+=dt u dt u u u dt i R i u C R i C R R R i R R R CR 211211212111212i dt du dt du u C R u C R R i +=++22212)(⏹ (P72)2-1,2-2 2-1-fdt dy B y K X K y K x K x K x K =--=-2222222111,122121)1(x x y K K K K -+= dt dx K BK dt dx K K B x K x K K x K 121221)1()(1122122-+=-+- 111212112)(x K BK x K K K B dt dx dtdx +=++ 2-22222212121212222311311)(,)()(dt x d dtdx dtdx dtdx dt x d dtdx dtdx dtdx mBx K B mBB x K t f =---=----22322322221)(x K B B m Bdt dx dtx d dtdx +++=313222212113311)()(dt x d dt x d dt x d dtdx dtt df m B B B K=++--22222223233312222313232222322)(])([])([dt x d dtdx dt x d dt x d B B B dtdx dt x d B K dtt df B KB B m x K B B m ++++-+++-+2223213233321424321)(dt x d B K m dt x d B B B m dt x d B m m ++=+222323424][)(12323121213212312121dt x d dt x d dt x d K m B B B B B B K m B m B m B m B m m m +++++++++dt t df dtdx B x K K B B K B B K )(32213213122)]()([=+++++⏹ (P72)2-3:-2)、-4)、-6);2-4:-2)。
《控制工程基础》王积伟第二_课后习题解答完整
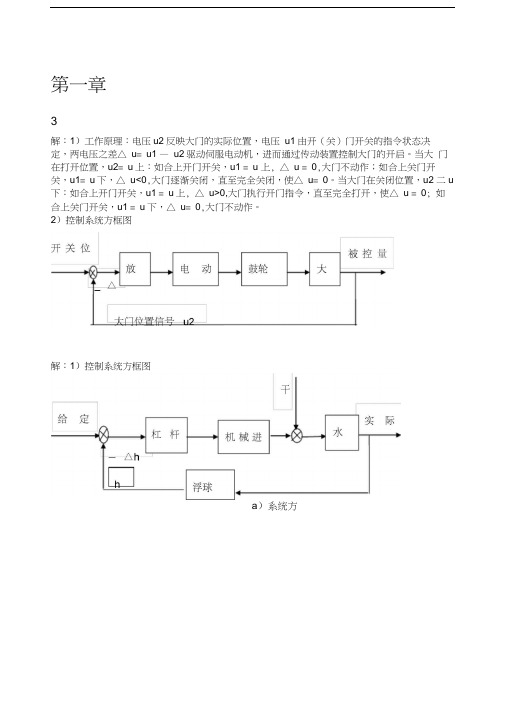
第一章3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△ u= u1 —u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2= u上:如合上开门开关,u1 = u 上, △ u = 0,大门不动作;如合上关门开关,u1= u下,△ u<0,大门逐渐关闭,直至完全关闭,使△ u= 0。
当大门在关闭位置,u2 二u 下:如合上开门开关,u1 = u上, △ u>0,大门执行开门指令,直至完全打开,使△ u = 0; 如合上关门开关,u1 = u下,△ u= 0,大门不动作。
2)控制系统方框图解:1)控制系统方框图a)系统方a )水箱是控制对象,水箱的水位是被控量,水位的给定值 h '由浮球顶杆的长度给定,杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是 进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随 之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制 系统。
b )水箱是控制对象,水箱的水位是被控量,水位的给定值 h '由浮球拉杆的长度给定。
杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后, 在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水 位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离 散控制系统。
2-1 解:(c )确定输入输出变量(u1,u2)得到:CR 2dU 1(1 匹)u 2 =CR 2dU 1-R2u 1 dt R 1 dt R一阶微分方程(e )确定输入输出变量(u1,u2)消去i 得到:(& R 埒汁2牛亡 一阶微分方程第二章2- 2解:1)确定输入、输出变量f (t ) 、X 2□2)工作原理:b )系统方框图干f(t)-fK1⑴-fB 1⑴-fBMF^d^- - 1 -(s 2) (s 1) (s 1)2M(s)=0, 4) D(s)=0,得到极点:一1, M(s)=0, 得到零点:2) 对各元件列微分方程:2f f f _ d X 2(t)fB3 ~'T K2-'T B 2= m 2K1B3 dt 2=K 1X 1; f B1 = B 1 -- -dt B d (x 1 - x2) =B 3 甬;fK2 = K 2X23)4) 5) 拉氏变换.F(s)—KX(s)—B 1SX1G)—B3$(X 1(s) —X 2(s)] = gs 2X 1(s) 叉'B 3S[X 1(s) -X 2(s)] -K 2X2G)-B 2SX2G ) = m 2S 2X 2(s) 消去中间变量: 拉氏反变换:mi|m 2 d 4X d 3X d 2X$ (B 1m 2 七2口1 B s mh B s mJ $(B 1B 3 B 1B 2 B s B ?心口2 ^心)/dt dt dt 2_3(K 1B 2 K 1B 3 K 2B 1 K 2B 3)等 K 1g 弋詈解:(2) (4)1 1 11 1 1 — 29 s 49 s 13 (s 1)(5)(6)-0.25 2s 0.5 2 22 2.5 s2- 5解:1)D(s)=0, M(s)=0,2) D(s)=0, M(s)=0,得到极点:0,0,-2,-5得到零点:一 1 , ' 得到极点:一 2, — 1, —2 得到零点:0 , 0 , — 1+ □0 +oci3) D(s)=O, 得到极点:0,得到零点:一2,2- 8解:1) a )建立微分方程b) 拉氏变换 c) 画单元框图(略) d) 画系统框图mx o (t) = f k (t) f Bl (t) - f B2(t) f k (t)二 k(X i (t) —x °(t))ms 2X o (s) = F k (s) F BI (S ) -F B 2(S )b) 拉氏变换:F k (s )=k (X i (s )-X o (s))F Bi (s)=B i S (X j (s)—X o (s))F B 2(S )工 B 2S X O (S )c) 绘制单元方框图(略)4)绘制系统框图Fi ( s )2)a)建立微分方程:f B1(t) B id (N (t)-")) dtf B2 (t)=B 2 dX o (t) dt由于扰动产生的输出为:要消除扰动对输出的影响,必须使 X o2(S )=0 得到:QK 2K 3G o (s) -K 3K 4S =0第三章3- 1解:1)法一:一阶惯性环节的调整时间为 4T ,输出达稳态值的98%故: 4T = 1min ,得到:T = 15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
《控制工程基础》王积伟_第二版_课后习题解答

d)画系统框图
2)a)建立微分方程:
b)拉氏变换:
c)绘制单元方框图(略)
4)绘制系统框图
2-11
解:a)
b)
2-14
解:(1)
(2)由于扰动产生的输出为:
要消除扰动对输出的影响,必须使
得到:
得到:
第三章
3-1
解:1)法一:一阶惯性环节的调整时间为4T,输出达稳态值的98%,故:
3-8
解:闭环传递函数
1)K=200:
最大超调量
峰值时间
调整时间
上升时间
振动次数
2)K=150,得到:
依次得到的动态性能指标:0、54,0037s,0、175s,0、02s,2、34。
3)K=13、5,得到:
此时,系统为过阻尼系统,为两个惯性环节串联。
4)对于二阶系统传递函数化为标准形式后,只要 不变,系统调整时间ts不变;随着 增大,过渡过程在缩短(tp,tr),但总过渡时间(调整时间ts)不变;而随着 的减小,振动幅度在加剧,振动次数N、超调量Mp都在加大。
3)单位加速度输入稳态误差;
法二:
3-11
解:开环传递函数 ,此系统为 型系统。
1)稳态误差系数
2)输入信号为阶跃信号、速度信号与加速度信号的组合,它们的系数分别为:
根据信号线性叠加的原理,系统的稳定误差为:
a)当 时,
b)当 时,
c)当 时,
3-12
解:
1)仅有输入信号作用下的稳态误差
偏差传递函数
4T=1min,得到:T=15s
法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
2)法一:输入信号 ,就是速度信号;
吴振顺《控制工程基础》王积伟_第二版_课后习题解答

第一章3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u<0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u>0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c )确定输入输出变量(u1,u2) 22111R i R i u += 222R i u =⎰-=-dt i i Cu u )(11221得到:1121221222)1(u R R dt du CR u R R dt du CR +=++一阶微分方程(e )确定输入输出变量(u1,u2)⎰++=idtC iR iR u 1211Ru u i 21-=消去i 得到:Cudt du R C u dt du R R 1122221)(+=++一阶微分方程第二章2-2解:1)确定输入、输出变量f(t)、x 22)对各元件列微分方程:222213311111122222232121311;)(;)()()()()()(x K f dtx x d B f dtdxB f x K f dt t x d m f f f dt t x d m t f t f t f t f K B B K B K B B B K =-====--=---3)拉氏变换:)()()()]()([)()]()([)()()(22222222131212131111s X s m s sX B s X K s X s X s B s X s m s X s X s B s sX B s X K s F =---=----4)消去中间变量:)()()()(23223232131123s X sB s m s B K s B s m s B K s B s sX B s F ++++++=+5)拉氏反变换:dtdfB x K K dt dx B K B K B K B K dtx d K m m K B B B B B B dt x d m B m B m B m B dt x d m m s s 3221232123121222212122131323132122142421)()()(=++++++++++++++2-3解:(2)2112+-+s stt e e 22---(4)2)1(13111914191+++-+s s st t t te e e ---+-3191914(5)2)1(1)1(2)2(2+-+++-s s s tt t te e e ----+-222(6)s s s s s 5.2124225.04225.022++-+⨯⨯-+⨯-5.222sin 2cos 5.0+----t e t t 2-5解:1)D(s)=0,得到极点:0,0,-2,-5M(s)=0,得到零点:-1,,,∞+∞+∞+ 2) D(s)=0,得到极点:-2,-1,-2 M(s)=0,得到零点:0,0,-1 3) D(s)=0,得到极点:0,,231j +-231j --M(s)=0,得到零点:-2,,∞+∞+4) D(s)=0,得到极点:-1,-2,∞- M(s)=0,得到零点:∞+ 2-8解:1)a )建立微分方程dtt dx Bt f t f t x t x k t f t x k t f t f bat f t f t f t f t x m B k k k i k k )()()())()(()()()()()()()()()(202201121==-===--=∙∙b)拉氏变换)()())()(()()()()()()()()()(20220112102s BsX s F s X s X k s F s X k s F s F bas F s F s F s F s X ms k k k i k k =-===--= c)画单元框图(略) d)画系统框图2)a)建立微分方程:dt t dx B t f dt t x t x d B t f t x t x k t f t f t f t f t x m oB o i B i k B B k )()())()(()())()(()()()()()(22110210=-=-=-+=∙∙ b)拉氏变换:)()())()(()())()(()()()()()(02211212s sX B s F s X s X s B s F s X s X k s F s F s F s F s X ms B o i B o i k B B k o =-=-=-+= c)绘制单元方框图(略) 4)绘制系统框图2-11解:a)1212321232141H G G H G G H G G G G G -+++b)))((1)(214321214321H G G G G H G G G G G G -++++2-14解:(1)321232132132101111)()(K K K s Ts K K K TsK s K K Ts K s K K s X s X i i ++=+++==φ321243032132132103402)(111)(1)()()(K K K s Ts s K K s G K K K TsK s K K Ts K s K K s G Ts K K s N s X s n ++-=+++++-==φ(2)由于扰动产生的输出为: )()()()()(321243032102s N K K K s Ts sK K s G K K K s N s s X n ++-==φ要消除扰动对输出的影响,必须使0)(02=s X 得到:0)(430321=-s K K s G K K K得到:2140)(K K s K s G =第三章3-1解:1)法一:一阶惯性环节的调整时间为4T ,输出达稳态值的98%,故: 4T =1min ,得到:T =15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
