《信息论基础》试卷(期末)(B卷)
信息基础试题及答案

01 B 1按照现代教育技术的观点,教师的主要任务是传授知识。
正确错误02 B 1学习资源是学习过程中所要利用的环境和条件,包括教学人员、教学媒体、教学环境和教学方法。
正确错误03 A 1现代教育思想的重大转变是:以教为中心转向以学为中心、从传授知识转向发展学生学习能力。
正确错误04 A 1现代教育技术的发展经历了五个发展阶段,而多媒体网络教育系统是20世纪90年代以后才进入教育领域。
正确错误05 B 1纵观教育技术理论的发展,现代教学理论为教育技术的形成和发展奠定了坚实的基础。
正确错误06 A 1认知主义学习理论认为学习不是刺激与反应的直接联结,而是认知结构的重新组织。
正确错误07 B 1按照“经验之塔”理论,角色扮演属于“观察的经验”。
正确错误08 A 1行为主义学习理论强调外在环境对学习的影响,故而在教育上主张奖励与惩罚。
正确错误09 A 1按照建构主义学习理论的观点,知识来之于人们与环境的交互作用。
正确错误010 A 1教育传播的主要手段是利用媒体来传播知识,并注重教学过程中的双向性交流。
正确错误011 B 1教育最优化是指学习到最多的知识,取得最佳的学习成绩。
正确错误012 C 2教育技术是学习过程和学习资源的______五个领域的理论与实践。
开发、应用、购置、建构、设计组织、设计、试验、管理、辅导设计、开发、应用、管理、评价远程教育、电化教育、学习管理、开发、评价013 D 2现代教育技术的研究对象包括哪两个方面?学习过程和学习方法教学过程和教学手段教学过程和教学方法学习过程和学习资源014 D 2学习过程是学习者通过与信息和环境的相互作用而得到新知识和掌握新技能的______过程。
建立分析感应认知015 D 2学习资源是学习过程中所要利用的环境和条件,包括以下的哪项内容?教学环境教学媒体教学人员以上都是016 B 2现代教育思想提倡从以“______”为中心转向以“______”为中心。
《信息论基础》试卷(期末)(B卷)

《信息论基础》试卷(期末)(B卷)重庆邮电⼤学2007/2008学年2学期《信息论基础》试卷(期末)(B 卷)(半开卷)⼀、填空题(共20分,每空1分)1、通信系统中,编码的主要⽬的有两个,分别是和。
2、离散⽆记忆信源存在剩余度的原因是。
3、当时,信源熵为最⼤值。
⼋进制信源的最⼤熵为,最⼩熵为。
4、⽆失真信源编码的平均码长最⼩理论极限制为。
5、⼀个事件发⽣概率为0.125,则⾃相关量为。
6、根据信原输出随机序列中随机变量前后之间有⽆统计依赖性,信原可以分为和。
7、噪声瞬时值的概率密度函数服从分布,同时功率谱密度为的噪声称为⾼斯⽩噪声。
8、当时,信源与信道达到匹配。
9、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是⾼斯分布或正态分布或时,信源具有最⼤熵,其值为值。
9、在下⾯空格中选择填⼊数学符号“,,,=≥≤>”或“?” (1)H(XY) H(Y)+H(X|Y) H(Y)+H(X)(2)假设信道输⼊⽤X 表⽰,信道输出⽤Y 表⽰。
在有噪⽆损信道中, H(X/Y) 0, H(Y/X) 0, I(X;Y) H(X)。
⼆、(6分)若连续信源输出的幅度被限定在【1,3】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
三、(16分)已知信源12345S P 0.250.20.20.20.15s s s s s =(1)⽤霍夫曼编码法编成⼆进制变长码;(4分)(2)计算平均码长—L ;(4分)(3)计算编码信息率R ';(4分)(4)计算编码后信息传输率R ;(2分)(5)计算编码效率η。
(2分)四、(12分)已知⼀个平均功率受限的连续信号,通过带宽W 10MHz =的⾼斯⽩噪声信道,试计算(1)若信噪⽐为10,信道容量为多少?(4分)(2)若信道容量不变,信噪⽐降为5,信道带宽为多少?(4分)(3)若信道通频带减为5MHz 时,要保持相同的信道容量,信道上的信号与噪声的平均功率⽐值应等于多少?(4分)五、(16分)某个信息源发出符号的概率为:12()(),P a P a =3()0.4,P a =假设该信息源发出的符号前后有关联,其依赖关系为:112122321333312133(|);(|);(|);(|);(|);(|);443344P a a P a a P a a P a a P a a P a a ======(1)画出状态转移图(4分)(2)计算稳态概率(4分)(3)计算信源的极限熵(4分)(4)计算稳态下H1,H2及其对应的剩余度。
《信息管理学基础》期末考试试题#优选、

黔南民族师范学院 2017—2018学年度第二学期试卷:(B卷)考试方式:(闭)卷校区:本部课程名称:《信息管理学基础》考试用时:120 分钟一、填空题(每空2分,共20分)1、事物存在的方式和运动状态的表现方式,这指的是_____层次的信息。
2、主体所感或表述的事物存在的方式和运动状态,这指的是_____层次论的信息。
3、布拉德福定律的两个基本要点:一是_________,形成主体来源(期刊)的有序目录;二是指确定相关论文再主体来源中的分布规律。
4、文献的半衰期,是指某学科领域现时尚在利用的全部文献中的_______是在多长一段时间内发表的。
5、结构化开发方法的基本思想是,在系统分析与设计阶段是_______,______。
6、《中图法》一般以_____标志大类,采用______方式标识其二级类,其余类目均采用数字标志,所有数字按_____对待,为使号码醒目,规定______一点。
二、选择题(10分)1、信息链中最高级别的环节是(D、智能)2、信息分布的“富集”和“贫集”现象实际上是人类社会特有的_____机制支配结果。
(B、选择)3、普莱斯指数,即某一学科领域内,对发展年限不超过___年的文献的引用次数与总的引用次数之比值。
(C、5)4、信宿可以是(A、人,物,也可以包括机器)5、信息论的创始人是(A、香农)三、简答题(每小题10分,共50分)1、请结合实例,解释以下转化关系:数据+背景=信息,信息+经验=知识。
2、信息分布中的“核心趋势”和“集中取向”有什么不同?3、试分析马太效应的正面作用和负面作用。
4、其夫定律。
5、面向对象方法按系统开发的一般过程分为几个阶段?四、论述题(每小题10分,共20分)1、论述搜索引擎的工作原理。
2、说明互联网搜索和移动搜索的区别。
填空题答案:1、本体论;2、认识论;3频次等级排序4、一半;5、自项向下,逐层分解;6、大写字母,双字母,小数,每三位。
最新文件仅供参考已改成word文本。
信息论基础B卷及答案
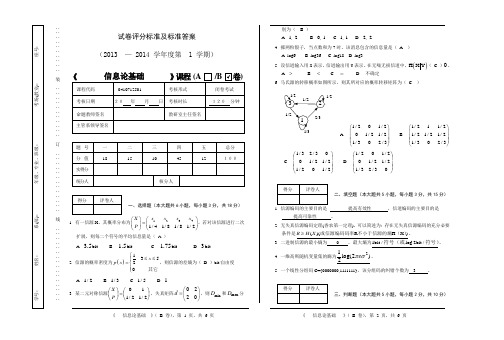
∶∶∶∶∶∶∶∶∶∶装∶∶∶∶∶∶∶∶∶∶∶订∶∶∶∶∶∶∶∶∶∶∶∶∶线∶∶∶∶∶∶∶∶∶∶∶∶∶∶∶∶试卷评分标准及标准答案(2013 — 2014 学年度第 1 学期)《课程(A 卷)一、选择题(本大题共6小题,每小题3分,共18分)1. 有一信源X,其概率分布为12341/41/81/81/2X x x x xP⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,若对该信源进行二次扩展,则每二个符号的平均信息量是(A )A. 3.5bitB. 1.5bitC. 1.75bitD. 3bit2. 信源的概率密度为()1352xp x⎧≤≤⎪=⎨⎪⎩其它,则信源的差熵为(D )bit/自由度.A.1/2B.1/3C.1/5D.13. 某二元对称信源011/21/2XP⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,失真矩阵0220d⎛⎫⎪⎝⎭=,则minD和maxD分别为( B )A. 1, 2B. 0, 1C. 1, 1D. 2, 24. 掷两粒骰子,当点数和为7时,该消息包含的信息量是(A )A. log6B. log36C. log18D. log35. 设信道输入用X表示,信道输出用Y表示。
在无噪无损信道中,()H X Y(C )0。
A. >B. <C. =D. 不确定6. 马氏源的转移概率如图所示,则其所对应的概率转移矩阵为(C )1/2A.1/201/201/21/21/302/3⎛⎫⎪⎪⎪⎝⎭B.1/211/21/21/21/21/302/3⎛⎫⎪⎪⎪⎝⎭C.1/32/3001/21/21/201/2⎛⎫⎪⎪⎪⎝⎭D.1/201/201/21/21/32/30⎛⎫⎪⎪⎪⎝⎭二、填空题(本大题共5小题,每小题3分,共15分)1. 信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2. 无失真信源编码定理(香农第一定理),可以简述为:存在无失真信源编码的充分必要条件是R H X()()R H X≥或信源编码码率不小于信源的熵()。
信息论与编码期末考试题(全套)

1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为 bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= Hr(S))。
七、信道编码(21分)
现有生成矩阵
1.求对应的系统校验矩阵Hs。(2分)
2求该码字集合的最小码字距离d、最大检错能力 、最大纠错能力tmax。(3分)
2.填写下面的es表 (8分)
e
s
0000000
0000001
0000010
0000100
0001000
0010000
0100000
1000000
4.现有接收序列为 ,求纠错译码输出 。(4分)
2.设对称离散信道矩阵为 ,求信道容量C。(10分)
3.有一稳态马尔可夫信源,已知转移概率为p(S1/S1)=2/3,p(S1/S2)=1。求:
(1)画出状态转移图和状态转移概率矩阵。
(2)求出各状态的稳态概率。
(3)求出信源的极限熵。
(20分)
(五)
一、(11’)填空题
(1)1948年,美国数学家香农发表了题为"通信的数学理论”的长篇论文,从而创立了信息论。
(1)信息就是一种消息。 ()
(2)信息论研究的主要问题是在通信系统设计中如何实现信息传输、存储和处理的有效性和可靠性。 ()
(3)概率大的事件自信息量大。 ()
(4)互信息量可正、可负亦可为零。 ()
(5)信源剩余度用来衡量信源的相关性程度,信源剩余度大说明信源符号间的依赖关系较小。 ()
(整理)信息论期末考试试题1.doc

安徽大学2011—2012学年第1学期 《信息论》考试试卷(AB 合卷)院/系 年级 专业 姓名 学号一、填空题1、接收端收到y 后,获得关于发送的符号是x 的信息量是 。
2、香农信息的定义 。
3、在已知事件z Z ∈的条件下,接收到y 后获得关于事件x 的条件互信息(;|)I x y z 的表达式为 。
4、通信系统模型主要分成五个部分分别为: 。
5、研究信息传输系统的目的就是要找到信息传输过程的共同规律,以提高信息传输的可靠性、有效性、 和 ,使信息传输系统达到最优化。
6、某信源S 共有32个信源符号,其实际熵H ∞=1.4比特/符号,则该信源剩余度为 。
7、信道固定的情况下,平均互信息(;)I X Y 是输入信源概率分布()Px 的 型凸函数。
信源固定的情况下,平均互信息(;)I X Y 是信道传递概率(|)P y x 的 型凸函数。
8、当信源与信道连接时,若信息传输率达到了信道容量,则称此信源与信道达到匹配。
信道剩余度定义为 。
9、已知信源X 的熵H (X )=0.92比特/符号,则该信源的五次无记忆扩展信源X 5的信息熵5()H X = 。
10、将∞H ,6H ,0H ,4H ,1H 从大到小排列为 。
11、根据香农第一定理,对于离散无记忆信源S ,用含r 个字母的码符号集对N 长信源符号序列进行变长编码,总能找到一种无失真的唯一可译码,使每个信源符号所需平均码长满足: 。
12、多项式剩余类环[]())q F x f x 是域的充要条件为 。
13、多项式剩余类环[](1)n q F x x -的任一理想的生成元()g x 与1n x -关系为 。
14、有限域122F 的全部子域为 。
15、国际标准书号(ISBN )由十位数字12345678910a a a a a a a a a a 组成(诸i a ∈11F ,满足:1010(mod11)ii ia=≡∑),其中前九位均为0-9,末位0-10,当末位为10时用X 表示。
《信息论》期末考试试题( 卷)标准答案

2.(共 10 分)有两枚硬币,第一枚是正常的硬币,它的一面是国徽,另一面是 面值;第二枚是不正常的硬币,它的两面都是面值。现随机地抽取一枚硬币,进 行 2 次抛掷试验,观察硬币朝上的一面,其结果为:面值、面值。
1)求该试验结果与事件“取出的是第一枚硬币”之间的互信息;(4 分)
=
E( XS + αS 2 ) σ SσU
=
αQ σ SσU
I (U ; S) = H (U ) + H (S ) − H (US )
=
1 2
log
2πe σ
2 U
+
1 2
log
2πeσ
2 S
+
log 2πeσUσ S
1− ρ2
=
1 2
log
σ
σ σ2 2
SU
σ2 2
US
− (αQ)
2
=
1 log P + α 2Q
2 1 d = 1 0 7)若失真矩阵为 3 1 ,输入等概,则 Dmin = 2/3 , Dmax = 2/3 。
三、简答题(6 分)
1.仙农第二定理指出了“高效率、高可靠性”的信道编码存在性,
1)“高效率”的含义是什么?
(1 分)
2)“高可靠性” 的含义是什么?
(1 分)
3)存在这种信道编码的必要条件是什么?
1− ρ2
=
1 log
σ
2 U
σ
2 Y
2
σ
2 U
σ
2 Y
−
(P
+ αQ)2
=
1 log
(P + Q + N )(P + α 2Q)
精选2020年大学《信息技术基础》期末模拟考试(含参考答案)

2020年大学《信息技术基础》期末考试188题[含答案]一、单选题1.1876年由()发明的电话使得人们长距离通信成可能,从而开辟了近代通信的历史。
A、爱迪生B、麦克斯韦C、贝尔D、莫尔斯2.通信系统模型中信息由信源发出,经过信道而达到接收者。
接收方需要经过()把信号转换成原有的消息形式。
A、编码B、解码C、调制D、加密3.TCP/IP 是一组应用于()的网络协议。
A、局域网B、互联网C、无线网D、电信网4.在一个采用八进制脉冲的通信系统中,每个脉冲所含的信息量是二进制脉冲的()倍。
A、1B、2C、3D、45.物联网的实现应该具备3个基本条件:即全面感知、可靠传递和()。
A、底层处理B、模糊处理C、数据处理D、智能处理6.下列度量单位中,用来度量计算机网络数据传输速率(比特率)的是()。
B、MIPSC、GHzD、Mbps7.为了解决目前IP地址空间局限性的问题,提出的下一代IP协议是()。
A、IPv4B、IPv5C、IPv6D、IPv78.在一个二元数字传输无噪声通信系统中,带宽为B赫兹信道所能承载的最大数据传输速率是()。
A、B/2B、BC、2BD、Blog29.在有线宽带接入中,传输速率最快的是接入方式是()。
A、ADSLB、以太网C、铜缆接入D、光纤10.已知某个有扰通信系统可用频带最高频率为H(Hz),最低频率为L(Hz),并且已知,则该信道的容量为()。
A、L×mB、H×mC、(H-L)×mD、(H-L)11.按通信距离和覆盖范围来分,Internet属于()。
A、对等网B、局域网C、城域网D、广域网12.Internet上各种网络和各种不同类型的计算机相互通信的基础是()协议。
B、TCP/IPC、OSID、DNS13.在程序流程图中为了表示输入输出,我们一般用()框表示。
A、菱形B、平行四边形C、三角形D、矩形第七单元测验114.超文本传输协议的英文简称是()。
信息技术基础——期末测试题(满分100分)

信息技术基础——期末测试题(满分100分)一、单选题(40分)1、在浏览网页时把自己喜爱并且经常浏览的网站地址,存放在浏览器的( D )。
A、工具栏B、存储器C、记录本D、收藏夹2、在Excel表格中,D5单元格位于( B )。
A、第4行第5列B、第5行第4列C、第4行第4列D、第5行第5列3、历史上的典故:“明修栈道,暗渡陈仓”主要体现了信息的哪个特征?(B )A、共享性B、真伪性C、价值性D、载体依附性4、我国首次界定计算机犯罪的法律是(B )。
A、1991年《计算机软件保护条例》B、1997年《中华人民共和国刑法》C、《中华人民共和国著作权法》D、《中华人民共和国技术合同法》5、信息技术给人们带来积极影响的有下列选项中的哪一项。
(D )A、信息泛滥B、信息污染C、信息犯罪D、计算机辅助学习6、下列关于信息资源管理方法的描述,正确的是( D )。
A、数据库管理完全可以取代人工管理B、人工管理完全可以取代数据库管理C、文件管理只能通过″资源管理器″来管理D、人工管理、文件管理、数据库管理都有其适用的场合7、我们发现同一航班的飞机票在全国各地的售票点都能买到,因此可以断定飞机票的销售系统一定使用了(C)。
A、手工管理系统B、文件管理系统C、数据库管理系统D、分散管理系统8、在Excel中,下列选项中的哪一项是降序排列的按钮。
( D )A、B、C、D、9、Excel文件的扩展名默认为(D )。
A、.pptB、.docC、.htmD、.xls10、如今我们可以不去电影院而在家里通过网络看电影,这主要体现了(A )。
A、信息技术改变了我们的生活方式B、信息技术对个人就业产生影响C、信息技术促使人们思想观念发生变化D、信息技术对科学研究产生了影响11、我要在上海买房子,但现在我却收到一条成都售房的短信,我应以下列选项中的哪一项作为鉴别此信息的重点。
( C )A、多样性B、时效性C、适用性D、共享性12、人与人之间可以通过语言交流信息,此时语言是信息的(A )。
信息论复习题期末答案

信息论复习题期末答案1. 信息论的创始人是谁?答案:信息论的创始人是克劳德·香农。
2. 信息熵的概念是什么?答案:信息熵是衡量信息量的一个指标,它描述了信息的不确定性或随机性。
在信息论中,熵越高,信息的不确定性越大。
3. 请简述信源编码定理。
答案:信源编码定理指出,对于一个具有确定概率分布的离散无记忆信源,存在一种编码方式,使得信源的平均编码长度接近信源熵的值,且当信源长度趋于无穷大时,编码长度与信源熵之间的差距趋于零。
4. 什么是信道容量?答案:信道容量是指在特定的通信信道中,能够以任意小的错误概率传输信息的最大速率。
它是信道的最大信息传输率,通常用比特每秒(bps)来表示。
5. 香农公式是如何定义信道容量的?答案:香农公式定义信道容量为信道输入和输出之间的互信息量的最大值,可以表示为C = B log2(1 + S/N),其中C是信道容量,B是信道带宽,S是信号功率,N是噪声功率。
6. 差错控制编码的目的是什么?答案:差错控制编码的目的是为了检测和纠正在数据传输过程中可能发生的错误,以提高数据传输的可靠性。
7. 什么是线性码?答案:线性码是一种特殊的编码方式,其中任意两个合法编码的线性组合仍然是一个合法编码。
线性码通常可以用生成矩阵和校验矩阵来表示。
8. 卷积码和块码有什么区别?答案:卷积码和块码都是差错控制编码的类型,但它们的主要区别在于编码的结构和处理方式。
卷积码是连续的,其编码过程是按时间序列进行的,而块码是离散的,其编码过程是针对数据块进行的。
9. 什么是信道编码定理?答案:信道编码定理指出,对于任何给定的信道和任何小于信道容量的错误概率,都存在一种编码方式,可以使得错误概率趋近于零。
10. 请解释什么是信道编码的译码算法。
答案:信道编码的译码算法是一种用于从接收到的编码信号中恢复原始信息的方法。
常见的译码算法包括维特比算法、最大似然译码和最小均方误差译码等。
这些算法旨在最小化译码错误的概率。
新版精选2020年大学《信息技术基础》考核复习题库完整版(含参考答案)

2020年大学《信息技术基础》期末考试188题[含答案]一、单选题1.计算机网络中广域网和局域网的分类通常是以()来划分的。
A、信息交换方式B、网络工作模式C、网络覆盖与连接距离D、网络终端2.1876年由()发明的电话使得人们长距离通信成可能,从而开辟了近代通信的历史。
A、爱迪生B、麦克斯韦C、贝尔D、莫尔斯3.超文本传输协议的英文简称是()。
A、TCPB、IPC、WWWD、HTTP4.为使网内计算机之间的通信可靠有效,通信双方必须共同遵守的规则和约定称为()。
A、语法B、合约C、协议D、文法5.2009年诺贝尔物理学奖被授予华裔科学家高锟,以表彰他在()基础理论与应用方面所做出的杰出贡献。
A、电耦合器件(CCD)B、集成电路C、光纤通信D、计算机芯片6.图中网络结构属于()拓扑结构。
A、总线型B、星型C、环型D、网状型7.局域网中通常采用的工作模式不包括()。
A、浏览器/服务器模式B、主机/终端模式C、客户机/服务器模式D、对等网络模式8.目前发展迅速的()是一种新的计算模式,它将计算、数据、应用等资源作为服务提供给用户的一种计算机集群的计算模式。
A、云计算B、量子计算C、分布计算D、服务计算9.以下()不是目前Internet上常用的搜索引擎。
A、TencentB、GoogleC、YahooD、Baidu10.下列选项中,哪个是正确的E-mail地址()。
A、210.34.224.246B、jeri@C、D、11.以下特性()不属于信息系统安全构架的信息安全特性。
A、验证性B、可控性C、完整性D、不可抵赖性12.在OSI/RM的七层参考模型中,中继器和路由器分别工作在()。
A、物理层和应用层B、物理层和传输层C、传输层和网络层D、物理层和网络层13.在有线宽带接入中,传输速率最快的是接入方式是()。
A、ADSLB、以太网C、铜缆接入D、光纤14.为提高信道利用率,采用多路复用技术,其中不包括()。
《信息论基础》模拟试题.doc
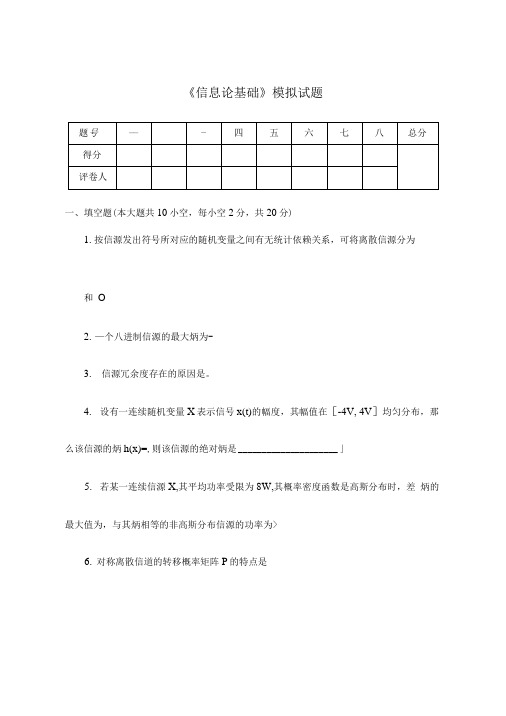
《信息论基础》模拟试题一、填空题(本大题共10小空,每小空2分,共20分)1.按信源发出符号所对应的随机变量之间有无统计依赖关系,可将离散信源分为和O2.—个八进制信源的最大炳为-3.信源冗余度存在的原因是。
4.设有一连续随机变量X表示信号x(t)的幅度,其幅值在[-4V, 4V]均匀分布,那么该信源的炳h(x)=,则该信源的绝对炳是_____________________ 」5.若某一连续信源X,其平均功率受限为8W,其概率密度函数是高斯分布时,差炳的最大值为,与其炳相等的非高斯分布信源的功率为>6.对称离散信道的转移概率矩阵P的特点是二、掷两粒骰子,各面出现的概率都是1/6,计算信息量:1.两骰子面朝上点数之和为2,该消息包含的信息量是多少?(3分)2.两骰子而朝上点数之和为8时,该消息包含的信息量是多少?(3分)3.两骰子血朝上点数是3和4,该消息包含的信息量是多少?(3分)三、设X,Y是二个相互统计独立的二元随机变量,其取-1或1的概率相等。
定义另一个二元随机变量Z,取Z=X+Y。
试计算:1.H(Y)、H(Z); (6 分)2.H (XY) ; (3 分)3.I (X;Y), I (Y;Z). (8 分) 四、一阶马尔可夫链信源有3个符号{a,b.c),转移概率为:P (a/a)二1/2, p (b/a)=1/4, p (c/a) =1 /4, p (a/b) =1 /2, p (b/b)二0, p (c/b) =1/2, p (a/c) =1/2, p (b/c) =1/2, p (c/c)=0。
1.画出状态图;写出转移概率矩阵;(6分)2.求出各符号稳态概率;(6分)3.计算其极限滴;(4分)五、在干扰离散对称信道上传输符号1和0,已知p(0)=1/4,p(1)=3/4,试求:1该信道的转移概率矩阵P(3分)2该信道的信道容量及其输入概率分布(7分)0.6六、某信道的转移矩阵p().50.30.30.2().5 00.2试求:该信道的信道容量及最佳输入概率分布o (6分)七、设在平均功率受限高斯可加波形信道中,信道宽带为5KH 乙乂设信 噪比为20db 1 肖H •耸'该隹1首的隹1首恣晶.分)2若功率信嬴比降或lOdbi 达到相同的最大信息传输率,信道带宽应是 多少? (3分)八、信源符号 X 有 6 种字母,概率为 0.25 , 0.2, 0.16, 0.15 , 0.1, 0.07 , 0.04 , 0.03. 用霍夫曼编码法编成二进制变长码,写出编程过程并计算:(共16分)1. 编码前信源X 的信源剩余度,2. 平均码长3. 编码效率。
最新2020年大学《信息技术基础》期末完整考试复习题库(含答案)

2020年大学《信息技术基础》期末考试188题[含答案]一、单选题1.超文本传输协议的英文简称是()。
A、TCPB、IPC、WWWD、HTTP2.在模拟传输系统中,电话信号的频率范围在300~3300 Hz之间,它的带宽是()Hz。
A、300B、3000C、3300D、36003.通信系统模型中信息由信源发出,经过信道而达到接收者。
接收方需要经过()把信号转换成原有的消息形式。
A、编码B、解码C、调制D、加密4.物联网的实现应该具备3个基本条件:即全面感知、可靠传递和()。
A、底层处理B、模糊处理C、数据处理D、智能处理5.为了解决目前IP地址空间局限性的问题,提出的下一代IP协议是()。
A、IPv4B、IPv5C、IPv6D、IPv76.不属于无线宽带接入技术的()。
A、ADSLB、WIFIC、卫星接入D、蓝牙7.在一个二元数字传输无噪声通信系统中,带宽为B赫兹信道所能承载的最大数据传输速率是()。
A、B/2B、BC、2BD、Blog28.在有线宽带接入中,传输速率最快的是接入方式是()。
A、ADSLB、以太网C、铜缆接入D、光纤9.关于“互联网+”的内涵,最恰当的表述是()。
A、“互联网+”就是“互联网+IT行业”。
B、“互联网+”是让互联网与各个传统行业进行深度融合,创造经济社会发展新形态。
C、“互联网+”将是经济社会创新发展的重要驱动力量。
D、“互联网+”就是“互联网+人工智能”。
10.国家“十三五”规划中指出:“要构建现代化通信骨干网络,推进宽带接入光纤化进程。
在以光纤作为传输介质的系统中,传输的信号形式是()。
A、电信号B、磁信号C、光信号D、声波信号11.为提高信道利用率,采用多路复用技术,其中不包括()。
A、频分多路复用B、分组多路复用C、时分多路复用D、波分多路复用第八单元测验112.1876年由()发明的电话使得人们长距离通信成可能,从而开辟了近代通信的历史。
A、爱迪生B、麦克斯韦C、贝尔D、莫尔斯13.在程序流程图中为了表示输入输出,我们一般用()框表示。
信息论考试卷与答案..

考试科目名称:信息论一. 单选(每空2分,共20分)1.一个m位的二进制数的自信息量为(A )A.m bitB.1 bitC.m2mD.22.信源编码的目的是(A )A.提高通信有效性B.提高信息传输的可靠性C.提高通信系统的安全性D.压缩信源的冗余度3.下面属于最佳变长编码的是(C )A.算术编码和游程编码B.香农编码和游程编码C.哈夫曼编码和费诺编码D.预测编码和香农编码4.表中符合即时码的是(A )和(D )5.下列各量可能为负值的是(B )A.自信息量B.互信息量C.信息熵D.平均互信息量6.联合熵H(XY)与熵H(X)及条件熵H(X/Y)之间存在关系错误的是(D )A.H(XY)=H(X)+H(Y/X)B.若X和Y相互独立,H(Y)=H(Y/X)C.H(XY)=H(Y)+H(X/Y)D.H(XY)=H(X)+H(X/Y)7.已知发送26个英文字母(包括空格),其最大信源熵(发送概率相等)为H0 = log27 = 4.76比特/符号;在字母发送概率不等时,其信源熵为H1 = 4.03比特/符号;考虑字母之间相关性时,其信源熵为H2 = 3.32=1.4比特/符号。
问若用一般传送比特/符号;以此类推,极限熵H∞方式,冗余度γ为( B )A.0.58B.0.71C.0.65D.0.298. 某信道传递矩阵为,其信道容量为( D )A .)41log 4143log 43()81,81,41,21(4log ++-=H C B .)41log 4343log 41()81,81,41,21(2log +--=H C C .)41log 4143log 43()81,81,41,21(4log +--=H CD .)41log 4143log 43()81,81,41,21(2log +--=H C9. 下列各图所示信道是对称信道的是( C )A .B .C .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8181214181814121PD.二. 综合(共80分)1.(10分)试画出通信系统的模型,并叙述各部分的定义和作用。
信息论期末考试试题 答案

安徽大学2011—2012学年第1学期 《信息论》考试试卷参考答案(AB 合卷)一、 填空题 1、()(;)log()()p xy I x y p x p y =;2、事物运动状态或存在方式的不确定性的描述;3、(|)log(|)(|)p xy z p x z p y z ;4、信源 编码器 信道 译码器 信宿;5、保密性 认证性;6、0.72;7、 , ;8、(;)C I X Y - ;9、4.6 ; 10、0H ≥1H ≥4H ≥6H ≥∞H ; 11、()()1log log N L H S H S r N r N≤<+; 12、()f x 在q F 上不可约; 13、()g x |1n x -; 14、2F 、22F 、32F 、42F 、62F 、122F ; 15、8,4.二、判断题1、╳2、√3、√4、╳5、╳6、√7、√8、╳9、 ╳三、计算题 1、解:1111()log log 12222H X =--=1()log24H Y =-= 1()log 38H Z =-=当Z Y X ,,为统计独立时:()()()()1236H XYZ H X H Y H Z =++=++=2、解:二次扩展信源为2111213212223313233,,,,,,,,411111111,,,,,,,,9999363693636x x x x x x x x x x x x x x x x x x X P ⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦信源熵:22HX H X =()()22112log 2log )3366=-+⨯(=2log3-2/3比特/二符号 3、解:1)信道到矩阵为1/31/61/31/61/61/31/61/3P ⎛⎫= ⎪⎝⎭,故此信道为对称信道1111log 4(,,,)3636C H =-5l o g 33=-(比特/符号)相应的最佳输入概率分布为等概率分布。
(2)信道到矩阵为1/21/31/61/61/21/31/31/61/2P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,故此信道为对称信道111l o g 3(,,)236C H =-12log 323=- (比特/符号) 相应的最佳输入概率分布为等概率分布。
信息论基础(含习题与解答)

信息论基础(含习题与解答)
1.习题
(1)解码的定义是什么?
解码是指从消息中分离出编码信息,并将其转换为原始消息的过程。
(2)什么是哈夫曼编码?
哈夫曼编码是一种熵编码方案,它把出现频率最高的信息单位用最短的码字表示,从而有效地压缩了信息。
(3)请解释索引信息论。
索引信息论是一种认知科学,它研究了使用多个索引信息对信息资源进行管理和协作的方法。
它重点研究的是如何将信息可视化,以便用户可以快速找到需要的信息,同时有效地利用多个索引信息。
2.答案
(1)解码的定义是什么?
解码是指从消息中分离出编码信息,并将其转换为原始消息的过程。
(2)什么是哈夫曼编码?
哈夫曼编码是一种熵编码方案,它把出现频率最高的信息单位用最短的码字表示,从而有效地压缩了信息。
(3)请解释索引信息论。
索引信息论是一种认知科学,它研究了使用多个索引信息对信息资源进行管理和协作的方法。
它主要专注于通过设计有效的用户界面来提高信
息的有用性,实现信息的检索和可视化,以实现快速了解和分析信息资源。
它强调以用户为中心,基于支持知识管理和协作的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆邮电大学2007/2008学年2学期《信息论基础》试卷(期末)(B 卷)(半开卷)一、填空题(共20分,每空1分)1、通信系统中,编码的主要目的有两个,分别是 和 。
2、离散无记忆信源存在剩余度的原因是 。
3、当 时,信源熵为最大值。
八进制信源的最大熵为 ,最小熵为 。
4、无失真信源编码的平均码长最小理论极限制为 。
5、一个事件发生概率为0.125,则自相关量为 。
6、根据信原输出随机序列中随机变量前后之间有无统计依赖性,信原可以分为 和 。
7、噪声瞬时值的概率密度函数服从 分布,同时功率谱密度为 的噪声称为高斯白噪声。
8、当 时,信源与信道达到匹配。
9、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是高斯分布或正 态分布或 时,信源具有最大熵,其值为值 。
9、在下面空格中选择填入数学符号“,,,=≥≤>”或“〈” (1)H(XY) H(Y)+H(X|Y) H(Y)+H(X)(2)假设信道输入用X 表示,信道输出用Y 表示。
在有噪无损信道中, H(X/Y) 0, H(Y/X) 0, I(X;Y) H(X)。
二、(6分)若连续信源输出的幅度被限定在【1,3】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
三、(16分)已知信源12345S P 0.250.20.20.20.15s s s s s ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用霍夫曼编码法编成二进制变长码;(4分) (2)计算平均码长—L ;(4分)(3)计算编码信息率R ';(4分)(4)计算编码后信息传输率R ;(2分)(5)计算编码效率η。
(2分)四、(12分)已知一个平均功率受限的连续信号,通过带宽W 10MHz =的高斯白噪声信道,试计算(1)若信噪比为10,信道容量为多少?(4分)(2)若信道容量不变,信噪比降为5,信道带宽为多少?(4分)(3)若信道通频带减为5MHz 时,要保持相同的信道容量,信道上的信号与噪声的平均功率比值应等于多少?(4分)五、(16分)某个信息源发出符号的概率为:12()(),P a P a =3()0.4,P a =假设该信息源发出的符号前后有关联,其依赖关系为:112122321333312133(|);(|);(|);(|);(|);(|);443344P a a P a a P a a P a a P a a P a a ======(1) 画出状态转移图(4分) (2) 计算稳态概率(4分)(3) 计算信源的极限熵(4分)(4) 计算稳态下H1,H2及其对应的剩余度。
(4分)六、(8分)同时掷两个正常的股子,也就是各面呈现的概率都是16,计算(1)“3和4同时出现”事件的自信息量;(2分)(2)两个点数中至少有一个是1的自信息;(2分) (3)两个点数中之和为3的自信息;(2分) (4)两个点数的各种组合(无序对)的熵。
(2分)七、(22分)设离散无记忆信源的概率空间为120.750.75X x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,通过二进制对称信道,其概率转移矩阵为2/31/31/32/3⎡⎤⎢⎥⎣⎦,信道输出端的接受符号集为12[]Y y y =(1)计算信源熵()H X ;(4分) (2)损失熵(|)H X Y ;(4分) (3)噪声熵(|)H Y X ;(4分)(4)受到消息Y 后获得的平均互信息量(:)I Y X (4分) (5)该信道的信道容量(4分)(6)说明该信道达到信道容量时的输入概率分布。
(2分)《信息论基础》试卷答案一、填空题(共20分,每空1分)1、通信系统中,编码的主要目的有两个,分别是提高有效性和可靠性。
2、离散无记忆信源存在剩余度的原因是分布不等概。
3、当信源各符号无相关性、等概分布时,信源熵为最大值。
八进制信源的最大熵为3/bit 符号,最小熵为0/bit 符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H r (S))。
5、一个事件发生概率为0.125,则自相关量为3bit 。
6、根据信原输出随机序列中随机变量前后之间有无统计依赖性,信原可以分为有记忆信源和无记忆信源。
7、噪声瞬时值的概率密度函数服从高斯分布,同时功率谱密度为均匀分布的噪声称为高斯白噪声。
8、当R=C 或(信道剩余度为0)时,信源与信道达到匹配。
9、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是高斯分布或正22x -21log 22e πσ。
9,,,=≥≤>”或“〈”(1)()H XY =H(Y)+H(X|Y)H(Y)+H(X)≤(2)假设信道输入用X 表示,信道输出用Y 表示。
在有噪无损信道中, H(X/Y)= 0, H(Y/X)>0,I(X;Y)=H(X)。
二、(6分)若连续信源输出的幅度被限定在【1,3】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
解:该信源的相对熵:()h(X)=log b-a log(31)1bit =-= 绝对熵为+∞ 三、(16分)已知信源12345S P 0.250.20.20.20.15s s s s s ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用霍夫曼编码法编成二进制变长码;(4分) (2)计算平均码长—L ;(4分)(3)计算编码信息率R ';(4分)(4)计算编码后信息传输率R ;(2分) (5)计算编码效率η。
(2分)解:(1)霍夫曼编码后的二进制变长码:S1:10, S2:00, S3:00, S4:110, S5:111,S1 0.25S2 0.2S3 0.2S4 0.2S5 0.151.00.40.351100.61(2)平均码长:I=0.35*3+0.65*2=2.35码元/符号; (3)编码信息率:R '=—L *logr=2.35*1=2.35 bit/信源符号 (4)编码后信息传输率:111110.25log 0.2log 0.2log 0.2log 0.15log H(s)0.250.20.20.20.15R=2.35L0.50.6*2.3220.15*2.7370.982.35++++=+==—(5)编码效率:η =H(s)L—=98%四、(12分)已知一个平均功率受限的连续信号,通过带宽W 10MHz =的高斯白噪声信道,试计算(1)若信噪比为10,信道容量为多少?(4分)(2)若信道容量不变,信噪比降为5,信道带宽为多少?(4分)(3)若信道通频带减为5MHz 时,要保持相同的信道容量,信道上的信号与噪声的平均功率比值应等于多少?(4分) 解: (1)根据香农公式:()()67Wlog 1SNR 1010log 110 3.4610C =+=⨯⨯+=⨯(2)当SNR 5=,()()7Wlog 1SNR Wlog 15 3.4610C =+=+=⨯则 773.4610W 1.33810Hz 2.585⨯==⨯ (3)当带宽减为5MHz ,()()67Wlog 1SNR 510log 1SNR 3.4610+=⨯⨯+=⨯SNR =120五、(16分)某个信息源发出符号的概率为:12()(),P a P a =3()0.4,P a =假设该信息源发出的符号前后有关联,其依赖关系为:112122321333312133(|);(|);(|);(|);(|);(|);443344P a a P a a P a a P a a P a a P a a ======(5) 画出状态转移图(4分) (6) 计算稳态概率(4分)(7) 计算信源的极限熵(4分)(8) 计算稳态下H1,H2及其对应的剩余度。
(4分) 解:(1)1 0.25 S2 0.2S3 0.2S4 0.2S5 0.151.00.40.35110.61(2)由3113221123323123()()(|)31()()()4421()()()()()()13413()()()344()113()114()11i i i iiP E P E P E EP a P a P aP a P a P a P a P a P aP a P a P aP aP aP a=⋅⎧=+⎪⎪⎪=+++=⎨⎪⎪=+⎪⎩===∑得另:联立得:(3)该信源的极限熵:332()(|)log(|)431321413***bit/114411331144i i i i ii iH H P E P E E P E EH H H∞==-⋅⋅⋅=∑∑(,)+(,)+(,)=0.839 符号3121(4) H()log() 1.572/H0.839/H0.008HH20.47Hi iiP a P a bitbitηη=-⋅====∑12符号符号对应的剩余度:=1-=1-六、(8分)同时掷两个正常的股子,也就是各面呈现的概率都是16,计算(1)“3和4同时出现”事件的自信息量;(2分) (2)两个点数中至少有一个是1的自信息;(2分) (3)两个点数中之和为3的自信息;(2分) (4)两个点数的各种组合(无序对)的熵。
(2分) 解:(1)P (3和4同时出现)=1123618⨯= 1log4.169918I bit ∴=-= (2)P (1,1 or1,j or i,1)=1551136363636++=11log 1.710536I bit ∴=-=(3) P (1,2 or2,1)=1123618⨯=1log 4.169918I bit ∴=-=(4) 相同点出现的概率为136,共6种组合不同点出现的概率为118,共15种组合其熵为:116log3615log18 4.34/3618H bit =⨯⨯+⨯⨯=事件七、(22分)设离散无记忆信源的概率空间为120.750.75X x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,通过二进制对称信道,其概率转移矩阵为2/31/31/32/3⎡⎤⎢⎥⎣⎦,信道输出端的接受符号集为12[]Y y y =(1)计算信源熵()H X ;(4分) (2)损失熵(|)H X Y ;(4分) (3)噪声熵(|)H Y X ;(4分)(4)受到消息Y 后获得的平均互信息量(:)I Y X (4分) (5)该信道的信道容量(4分)(6)说明该信道达到信道容量时的输入概率分布。
(2分) 解(1)()(0.75,0.25)0.811/H X H bit ==符号;2211111121221(2) (|Y)(,)log (|)217()()(|)()(|)0.75*0.25*331275()1()1121275()(,)0.98bit/1212(|X)(x )(|)log (|)0.918/(i i i i i j i j i j i iiH X P x y P x y P y P x P x y P x P y x P y P y H Y H H Y P P y x P y x bit H ===-⋅=⋅+⋅=+==-=-====-⋅⋅⋅=∑∑∑∑符号符号2112XY)(X)(|X) 1.729/(|Y)(XY)()0.749/DMC C=log log 0.0821(x )(x )2ij i j j H H Y bit H X H H Y bit P P P P ==-==-=====∑2符号符号(4)I(X:Y)=H(x)-H(X|Y)=0.062bit/符号(5)该信道为对称信道,故bit/符号(6)这时的输入信号概率分布为:。
