高二数学选择进修2-2第二章推理与证明
_高中数学第二章推理与证明2

跟踪练习
(2014~2015·合肥一六八中高二期中)观察下题的解答过
程:
已知正实数 a、b 满足 a+b=1,求 2a+1+ 2b+1的最
大值.
解:∵
2a+1· 2≤
2a+12+ 2
22=a+32,
2b+1· 2
≤
2b+12+ 2
22=b+32,
相 加 得 2a+1 · 2 + 2b+1 · 2 = 2 ( 2a+1 + 2b+1)≤a+b+3=4.
综合法: ∵a、b、c∈R+,∴(a-b)2+(b-c)2+(c-a)2≥0, ∴2(a2+b2+c2)≥(ab+bc+ac), ∴3(a2+b2+c2)≥a2+b2+c2+2ab+2bc+2ac, ∴3(a2+b2+c2)≥(a+b+c)2, ∴ a2+b32+c2≥a+3b+c.
人教版 选修2-2
第二章 推理与证明
2.2 直接证明与间接证明
2.2.1 综合法和分析法
目标导航
• 了解综合法与分析法的特点,熟练应用分析法与综合法证明 命题.
重点难点
• 重点:综合法和分析法的概念及思考过程、特点. • 难点:综合法和分析法的应用.
新知导学
1.综合法证明不等式
• 1.定义 • 利用___已__知__条__件___和某些数学__定__义____、__定__理____、
、已知的重要不等式和逻辑推理的基本理论;
• (2)适用范围:对于一些条件复杂,结构简单的不等式的证明 ,经常用综合法.而对于一些条件简单、结论复杂的不等式 的证明,常用分析法;
• (3)思路方法:分析法证明不等式的思路是从要证的不等式出 发,逐步寻求使它成立的充分条件,最后得到的充分条件是 已知(或已证)的不等式;
高二数学选修2-2(B版)_总结归纳:推理与证明

推理与证明对于数学的学习,应具备“能力”,其中本章的“推理与证明”就是一种重要的“逻辑思维”能力形式.通过本章的复习,要有着扎实的推理、论证能力,以增强对问题的敏锐的观察,深刻的理解、领悟能力.一.推理部分1.知识结构:2.和情推理:归纳推理与类比推理统称为和情推理.①归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或有个别事实概括出一般结论的推理,称为归纳推理.②类比推理:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.③定义特点;归纳推理是由特殊到一般、由部分到整体的推理;而类比推理是由特殊到特殊的推理;都能由已知推测、猜想未知,从而推理结论.但是结论的可靠性有待证明.例如:已知2()53f n n n =-+-,可以(1)10f =>,(2)30,f =>(3)30,(4)10f f =>=>,于是推出:对入任何n N *∈,都有()0f n >;而这个结论是错误的,显然有当5n =时,(5)30f =-<.因此,归纳法得到的结论有待证明.例如:“在平面内与同一条直线垂直的两条直线平行”;类比线与线得到:“在空间与同一条直线垂直的两条直线平行“;显然此结论是错误的”.类比线与面得到:在空间与同一个平面垂直的两个平面平行;显然此结论是错误的.④推理过程:从具体问题出发 观察、分析、比较、联想 归纳、类比 猜想.3.演绎推理:从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理(逻辑推理).①定义特点:演绎推理是由一般到特殊的推理;②数学应用:演绎推理是数学中证明的基本推理形式;推理模式:“三段论”:ⅰ大前提:已知的一般原理(M 是P );ⅱ小前提:所研究的特殊情况(S 是M );ⅲ结论:由一般原理对特殊情况作出判断(S 是P );集合简述:ⅰ大前提:x ∈M 且x 具有性质P ;ⅱ小前提:y ∈S 且S ⊆M ;ⅲ结论: y 也具有性质P ;例题1.若定义在区间D 上的函数()f x 对于D 上的n 个值12,,n x x x ,总满足[]12121()()()()n n x x x f x f x f x f n n ++++++≤,称函数()f x 为D 上的凸函数;现已知()sin f x x =在(0,)π上是凸函数,则ABC ∆中,sin sin sin A B C ++的最大值是 .解答:由[]12121()()()()n n x x x f x f x f x f n n ++++++≤(大前提)因为()sin f x x =在(0,)π上是凸函数 (小前提)得()()()3()3A B C f A f B f C f ++++≤ (结论)即sin sin sin 3sin 3A B C π++≤=因此,sin sin sin A B C ++的最大值是2 注:此题是一典型的演绎推理“三段论”题型4.和情推理与演绎推理的关系:①和情推理是由特殊到一般的推理,演绎推理是由一般到特殊的推理;②它们又是相辅相成的,前者是后者的前提,后者论证前者的可靠性;例2.设()2x x a a f x -+=,()2x xa a g x --=(其中0a >且1a ≠) (1)5=2+3请你推测(5)g 能否用(2),(3),(2),(3)f f g g 来表示;(2)如果(1)中获得了一个结论,请你推测能否将其推广.解答:(1)由(3)(2)(3)(2)f g g f +=332a a -+222a a --+332a a --222a a -+ =552a a -- 又(5)g =552a a -- 因此,(5)g =(3)(2)(3)(2)f g g f +(2)由(5)g =(3)(2)(3)(2)f g g f +即(23)g +=(3)(2)(3)(2)f g g f +于是推测()g x y +=()()()()f x g y g x f y + 证明:因为:()2x x a a f x -+=,()2x xa a g x --=(大前提) 所以()g x y +=2x y x ya a ++-, ()g y =2y y a a --,()f y =2y ya a -+,(小前提及结论) 所以()()()()f x g y g x f y +=2x x a a -+2y y a a --+2x x a a --2y ya a -+ =2x y x ya a ++-=()g x y + 解题评注:此题是一典型的由特殊到一般的推理,构造(23)g +=(3)(2)(3)(2)f g g f +是此题的一大难点,要经过观察、分析、比较、联想而得到;从而归纳推出一般结论()g x y +=()()()()f x g y g x f y +.二.证明部分1.知识结构2.综合法与分析法①综合法;利用已知条件和某些数学定义、公理、定理等出发,经过一系列推理论证,推导出所要证明的结论成立.②分析法:从要证明的结论出发逐步寻求使它成立的充分条件,直至把要证明的结论归结为判别一个明显成立的条件为止.③综合应用:在解决问题时,经常把综合法与分析法和起来使用;使用分析法寻找成立的条件,再用综合法写出证明过程.例3.已知:0a b >>,求证:22()()828a b a b a b ab a b-+-<-< 证明:因为0a b >> 所以22()()828a b a b a b ab a b-+-<< ⇔222()()()44a b a b a b a b--<< ⇔|22a b a b<< ⇔2a b a b a b<< ⇔121b a a b < ⇔1b a a b<又由已知0a b >>1b a a b<<成立. 由于以上分析步步等价,因此步步可逆.故结论成立.解题评注:(1)以上解答采用恒等变形,其实质从上往下属于分析法,反之属于综合法.(2)1b a a b<,(0a b >>)是结论成立的充要条件,当然找到了结论成立的充分条件就可以了.例4.求证抛物线22(0)y px p =>,以过焦点的弦为直径的圆必与2p x =-相切. 证明:(如图)作AA /、BB /垂直准线,取AB 的中点M ,作MM /垂直准线. 要证明以AB 为直径的圆与准线相切只需证|MM /|=12|AB | 由抛物线的定义:|AA /|=|AF |,|BB /|=|BF |所以|AB |=|AA /|+|BB /|因此只需证|MM /|=12(|AA /|+|BB /|) 根据梯形的中位线定理可知上式是成立的. 所以以过焦点的弦为直径的圆必与2p x =-相切. 以上解法同学们不难以综合法作出解答.解题评注:分析法是从结论出发寻找证题思路的一种重要的思维方法,特别是题设和结论相结合,即综合法与分析法相结合,可使很多较为复杂的问题得到解决.3.数学归纳法一般地,证明一个与正整数n有关的命题的步骤如下:(1)(归纳奠基)证明当n取第一个值n0时命题成立;(2)(归纳递推)假设n=k (0(,)k n k n ≥∈*时命题成立,证明当1n k =+ 时命题也成立。
高二数学选修2-2第二章 推理与证明

§2.1.1 合情推理学习目标1. 结合已学过的数学实例,了解归纳推理的含义;2. 能利用归纳进行简单的推理,体会并认识归纳推理在数学发现中的作用.学习过程一、课前准备(预习教材P 70~ P77,找出疑惑之处) 在日常生活中我们常常遇到这样的现象:(1)看到天空乌云密布,燕子低飞,蚂蚁搬家,推断天要下雨; (2)八月十五云遮月,来年正月十五雪打灯.以上例子可以得出推理是 的思维过程.二、新课导学探究任务一:考察下列示例中的推理问题:因为三角形的内角和是180(32)︒⨯-,四边形的内角和是180(42)︒⨯-,五边形的内角和是180(52)︒⨯-……所以n 边形的内角和是新知1:从以上事例可一发现: 叫做合情推理。
归纳推理和类比推理是数学中常用的合情推理。
探究任务二:问题1:在学习等差数列时,我们是怎么样推导首项为1a ,公差为d 的等差数列{a n }的通项公式的?新知 2 归纳推理就是根据一些事物的 ,推出该类事物的 的推理归纳是 的过程 例子:哥德巴赫猜想:观察 6=3+3, 8=5+3, 10=5+5, 12=5+7, 14=7+7, 16=13+3, 18=11+7, 20=13+7, ……,50=13+37, ……, 100=3+97,猜想: .归纳推理的一般步骤1 。
2 。
※ 典型例题例1用推理的形式表示等差数列1,3,5,7……2n-1,……的前n 项和S n 的归纳过程。
例2设2()41,f n n n n N +=++∈计算(1),(2),(3,)...(10)f f f f 的值,同时作出归纳推理,并用n=40验证猜想是否正确。
练1. 观察圆周上n 个点之间所连的弦,发现两个点可以连一条弦,3个点可以连3条弦,4个点可以连6条弦,5个点可以连10条弦,由此可以归纳出什么规律?三、总结提升※ 学习小结 1.归纳推理的定义. 2. 归纳推理的一般步骤:①通过观察个别情况发现某些相同的性质; ②从已知的相同性质中推出一个明确表述的一般性命题(猜想). ※ 当堂检测(时量:5分钟 满分:10分)计分: 1.下列关于归纳推理的说法错误的是( ). A.归纳推理是由一般到一般的一种推理过程 B.归纳推理是一种由特殊到一般的推理过程 C.归纳推理得出的结论具有或然性,不一定正确 D.归纳推理具有由具体到抽象的认识功能2. 已知2()(1),(1)1()2f x f x f f x +==+ *x N ∈(),猜想(f x )的表达式为( ).A.4()22x f x =+B.2()1f x x =+C.1()1f x x =+D.2()21f x x =+3.111()1()23f n n N n +=+++⋅⋅⋅+∈,经计算得357(2),(4)2,(8),(16)3,(32)222f f f f f =>>>>猜测当2n ≥时,有__________________________.4 已知1+2=3,1+2+3=6,1+2+3+4=10,……1+2+3+……+n=(1)2n n +,观察下列立方和: 13,13+23,13+23+33,13+23+33+43,…… 试归纳出上述求和的一般公式。
最新人教版高中数学选修2-2第二章《推理与证明》本章小结
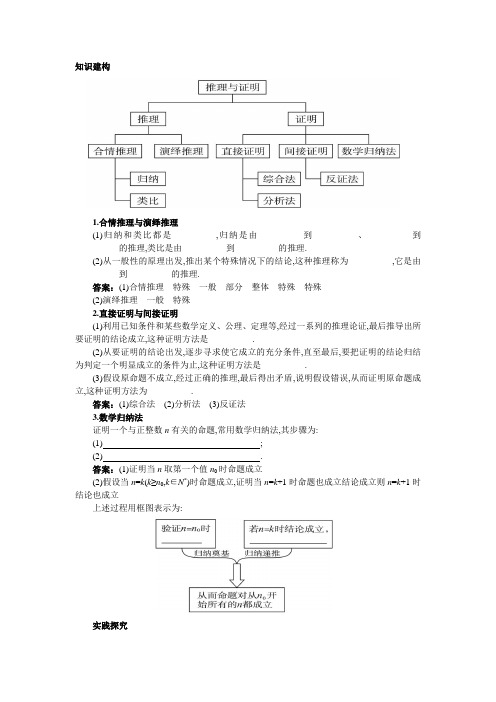
知识建构1.合情推理与演绎推理(1)归纳和类比都是__________,归纳是由__________到__________、__________到__________的推理,类比是由__________到__________的推理.(2)从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为__________,它是由__________到__________的推理.答案:(1)合情推理特殊一般部分整体特殊 特殊(2)演绎推理一般特殊2.直接证明与间接证明(1)利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法是__________.(2)从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,要把证明的结论归结为判定一个明显成立的条件为止,这种证明方法是__________.(3)假设原命题不成立,经过正确的推理,最后得出矛盾,说明假设错误,从而证明原命题成立,这种证明方法为__________.答案:(1)综合法(2)分析法(3)反证法3.数学归纳法证明一个与正整数n有关的命题,常用数学归纳法,其步骤为:(1);(2).答案:(1)证明当n取第一个值n0时命题成立(2)假设当n=k(k≥n0,k∈N*)时命题成立,证明当n=k+1时命题也成立结论成立则n=k+1时结论也成立上述过程用框图表示为:实践探究1.下图中的三角形称为希尔宾斯基(S ierpi n s k i)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式__________.思路分析:如题图,这4个三角形中着色三角形的个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.猜想这个数列的一个通项公式是a n =3n -1.答案:a n =3n -1温馨提示:(1)上面数列的递推关系为a n +1=3a n .(2)通项公式可用数学归纳法证明.2.若数列{a n }是一个等差数列,则{na a a n 21+++ }是一个等差数列.类比这条性质,若数列{b n }是一个等比数列,则有__________是一个等比数列.思路分析:在等差数列{a n }与等比数列{b n } 中,有{a n } {b n }和 a 1+a 2+…+a n积 b 1b 2…b n算术平均数{n a a a n 21+++ }等差几何平均数{n n 21b b b }等比证明:设数列{b n }的首项为b 1,公比为q, 则n 1)-(n 2111n n 211n 1n n211n 1n 21q b q b b b b b b b ++++++++++= =2121n 12n 1n 21)n(n n 11n 21)n (n 1n 1q q b q b q b q b --+++=(常数),∴数列{n n 21b b b }为等比数列. 答案:{ n n 21b b b }3.已知O 是△A B C 内任意一点,连结A O 、BO 、C O 并延长交对边于A′、B ′、C′,则1C C C O B B B O A A A O =''+''+''.这是平面几何中的一道题,其证明常采用“面积法”: C C C O B B B O A A A O ''+''+''=ABCABC ABC OAB ABC OCA ABC OBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=1. 运用类比,猜想对于空间中的四面体A —B CD,存在什么类似的结论?并用“体积法”证明. 猜想:已知点O 为四面体A —B CD 内任意一点,连结A O 、BO 、C O 、D O 并延长交相对面于A′、B ′、C′、D′,则有OD D O OC C O OB B O OA A O '+'+'+'=1. 证明:设点A 、O 到平面B CD 的距离分别为h 、h′,则OA A O h h '=', ∴OA A O h h h S 31h S 31V V BCD BCD BCD A BCDO '='=⋅'⋅=∆∆--. 同理,ACDB ACD O V V OB B O --=', ABDC ABD O V V OC C O --=', ,V V OD D O ABCD ABC O --=' ∴OD D O OC C O OB B O OA A O '+'+'+'=BCDA BCD A V V --=1.。
高二数学第二章推理与证明章末小结新人教A版选修2-2

1 1 a+ b 只要证 a+ b + ab ≥ 8,
11 11 只要证 a+ b + b+ a ≥ 8,
11 即证 a+ b≥ 4.
也就是证
a+ a
b+a+b
b ≥
4.
ba 即证 a+ b≥ 2,
ba 由基本不等式可知,当 a>0, b>0 时, a+ b≥ 2 成立,
所以原不等式成立.
知识点三 反证法
反证法的理论基础是互为逆否命题的等价性,从逻辑角度看,命题“若
p,则 q”的否
定是“若 p,则?q”,由此进行推理,如果发生矛盾,那么就说明“若
p,则?q”为假,从
而可以导出“若 p,则 q”为真,从而达到证明的目的.反证法反映了“正难则反”的解题
思想.
一般以下题型用反证法: ①当“结论”的反面比“结论”本身更简单、 更具体、 更明确;
推得所求结果,则用综合法,若从条件出发,应用相关的公理、定理、公式、结论难以推得
所求结果,则可以考虑使用分析法. (3) 解题反思,回顾解题过程,对所得结果和解题步骤进行检查,确保解题的严谨性和
完备性.
11 1 设 a>0, b>0, a+ b= 1,求证: a+ b+ ab≥ 8.
证明: 方法一 综合法 因为 a>0, b>0, a+ b= 1,
圆
球
(1) 圆心与弦 ( 非直径 ) 中点的连线垂直于弦
球心与截面圆 ( 非轴截面 ) 圆心的连线垂直于 截面
(2) 与圆心距离相等的两条弦长相等 (3) 圆的周长 c=π d
与球心距离相等的两个截面圆面积相等 球的表面积 S=π d2
(4) 圆的面积 S= πd2 4
球的体积 V= π d3 6
高中数学合情推理(一)

通俗地说,合情推理是指“合乎情理”的推理。
合情推理的应用
数学研究中,得到一个新结论之前,合情推理 常常能帮助我们猜测和发现结论。
证明一个数学结论之前,合情推理常常能为我 们提供证明的思路和方向
在印度,有这么一个古老的传说:在世界 中心贝拿勒斯(在印度北部)的圣庙里,一块 黄铜板上插着三根宝石针。印度教的主神梵天 在创造世界的时候,在其中一根针上从下到上 地穿好了由大到小的64片金片,这就是所谓 的汉诺塔。不论白天黑夜,总有一个僧侣在按 照下面的法则移动这些金片:一次只移动一片 ,不管在哪根针上,小片必须在大片上面。僧 侣们预言,当所有的金片都从梵天穿好的那根 针上移到另外一根和众生也都将针上时,世界 就将在一声霹雳中消灭,而梵塔、庙宇同归于 尽。
目前最佳的结果是中国数学家陈景润於1966年证明的, 称为陈氏定理(Chen‘s Theorem) “任何充份大的偶数都 是一个质数与一个自然数之和,而後者仅仅是两个质数 的乘积。” 通常都简称这个结果为大偶数可表示为 “1 + 2 ”的形式。
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
观察可得:数列的前4项都等于相应项数的倒数。
1 由此猜想(归纳)这个数列的通项公式为: an n
归纳推理的一般步骤:
⑴ 对有限的资料进行观察、分析、 归纳整理; ⑵ 提出带有规律性的结论,即猜想; ⑶ 检验猜想。
练 根据图中5个图形及相应点的个数的变化规律, 习 试猜测第n个图形中有 n2 n 1 个点.
歌尼斯堡七桥猜想
18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的 普莱格尔河上有7座桥,将河中的两个岛和河 岸连结,如图所示。城中的居民经常沿河过桥 散步,于是提出了一个问题:能否一次走遍7 座桥,而每座桥只许通过一次,最后仍回到起多面体的 欧拉定理、四色问题等都是拓扑学发展史的重要 问题。拓扑学的英文名是Topology,直译是地志 学, 拓扑学是几何学的一个分支,但是这种几何 学又和通常的平面几何、立体几何不同。通常的 平面几何或立体几何研究的对象是点、线、面之 间的位置关系以及它们的度量性质。拓扑学对于 研究对象的长短、大小、面积、体积等度量性质 和数量关系都无关。
高二数学选修2-2:第二章 推理与证明

【例 3】 一直线与△ABC 的边 AB,AC 分别相交于 E,F,则SS△△AABECF =AABE··AACF.将平面上的三角形与空间中的三棱锥进行类比,试 推理三棱锥的性质,并给出证明. 解 在三棱锥 S-ABC 中,平面 α 与侧棱 SA,SB,SC 分别相 交于 D,E,F. 则VVSS--DABECF=SSDA··SSBE··SSCF. 证明如下:
则当 n=k+1 时,2+2 1·4+4 1·…·2k2+k 1·22kk++31
> k+1·22kk++31=22kk++31.
要证当 n=k+1 时结论成立,
只需证 2
2k+k+3 1>
k+2成立,
只需证:4k2+12k+9>4k2+12k+8 成立,显然成立,
∴当 n=k+1 时,2+2 1·4+4 1·…·2k2+k 1·22kk++31> k+1+1成立, 综合①②可知不等式b1b+1 1·b2b+2 1·…·bnb+n 1> n+1成立.
从而只需证 2
a2+a12≥ 2 a+1a,
只要证 4a2+a12≥2a2+2+a12,
即 a2+a12≥2,而上述不等式显然成立,故原不等式成立.
【例5】 如图,在四面体B-ACD中,CB=CD,AD⊥BD,且E,F 分别是AB,BD的中点,求证: (1)直线EF∥平面ACD; (2)平面EFC⊥平面BCD.
∴AB∥EN. 又AB∥CD∥EF, ∴EN∥EF, 这与EN∩EF=E矛盾,故假设不成立. ∴ME与BN不共面,即它们是异面直线.
专题四 数学归纳法 1.数学归纳法事实上是一种完全归纳的证明方法,它适用于与自
然数有关的问题.两个步骤、一个结论缺一不可,否则结论不 成立;在证明递推步骤时,必须使用归纳假设,必须进行恒等 变换. 2.探索性命题是近几年高考试题中经常出现的一种题型,此类问 题未给出问题的结论,需要由特殊情况入手,猜想、证明一般 结论,它的解题思路是:从给出条件出发,通过观察、试验、 归纳、猜想、探索出结论,然后再对归纳,猜想的结论进行证 明.
(人教版)高中数学选修2-2课件:第2章 推理与证明2.2.1

数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
分析法
1.分析法的定义 从要证明的结_论__出__发____,逐步寻求使它成立的充_分__条__件____, 直至最后,把要证明的结论归结为判定一个明显成立的条件( 已知条件、定理、定义、公理等)为止,这种证明方法叫做分 析法.
1.综合法证明问题的步骤 第一步:分析条件,选择方向.仔细分析题目的已知条 件(包括隐含条件),分析已知与结论之间的联系与区别,选择 相关的公理、定理、公式、结论,确定恰当的解题方法.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
第二步:转化条件,组织过程.把题目的已知条件,转 化成解题所需要的语言,主要是文字、符号、图形三种语言之 间的转化.组织过程时要有清晰的思路,严密的逻辑,简洁的 语言.
3.已知a,b,c∈ R且不全相等, 求证:a2+b2+c2>ab+bc+ca. 证明: 证法一:(分析法) 要证a2+b2+c2>ab+bc+ca, 只需证2(a2+b2+c2)>2(ab+bc+ca), 只需证(a2+b2-2ab)+(b2+c2-2bc)+(c2+a2-2ca)>0, 只需证(a-b)2+(b-c)2+(c-a)2>0,
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
(人教版)高中数学选修2-2课件:第2章 推理与证明2.3

第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
2.3 数学归纳法
数学 选修2-2
第二章 推理与证明
Hale Waihona Puke 自主学习 新知突破合作探究 课堂互动
高效测评 知能提升
自主学习 新知突破
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
(2)应用数学归纳法应注意: ① 数学归纳法仅适用于与正整数n有关的数学命题的证 明. ② 验证是证明的基础,递推是证明的关键,二者缺一不 可; ③在证 明n=k+1命题成立时,必须使用归纳假设的结 论,否则就不是数学归纳法.
数学 选修2-2
第二章 推理与证明
合作探究 课堂互动
高效测评 知能提升
“观察—归纳—猜想—证明”模式的题目的解
法
(1)观察:由已知条件写出前几项;
(2)归纳:找出前几项的规律,找到项与项数的关系;
(3)猜想:猜想出通项公式;
(4)证明:用数学归纳法证明猜想的形式,因为猜想不
一定正确,所以要通过数学归纳法给出证明.
数学 选修2-2
证明: ①当n=1时,左边=1,右边=1,命题成立. ②假设n=k(k≥1,k∈N*)时,命题成立, 即1+5+9+…+(4k-3)=k(2k-1). 则当n=k+1时,左边=1+5+9+…+(4k-3)+(4k+1) =k(2k-1)+(4k+1)=2k2+3k+1=(2k+1)(k+1) =[2(k+1)-1](k+1)=右边, ∴当n=k+1时,命题成立. 由①②知,对一切n∈N*,命题成立.
高中数学教案选修2-2《第2章 推理与证明》

目标定位:1.推理与证明是数学的基本思维过程,也是人们学习和生活中经常使用的思维方法.和过去的教学内容(例如函数)相比,在本章中是把基本的数学(思维)方法(而不是某个数学对象)作为正面研究对象的.因此,本章的学习过程,是中学生第一次对数学活动过程的正面的系统的审视——这就是我们对本章教学活动的定位.2.推理方法与证明方法是从思维活动中抽象出来的,是由数学思维过程凝缩而成的“对象”.我们不能离开数学思维活动来谈论数学思维方法,不能满足于把数学方法看成是既定的程序、步骤和规则,不能满足于对方法做静态的逻辑的分析(这正是过去传统的教材中所强调的),而应当从(数学)活动本身,特别是从数学活动的过程来考察推理方法和证明方法建构的过程,以及这些方法是如何被运用到数学活动中成为“活”的方法的?应当着重于体会方法的特点、联系和作用(这正是传统教材中忽略的,而在苏教版教材中特别强调的).这样一来,考察和研究数学思维过程就应该成为本模块学习的出发点和归宿了.3.与数学知识(如概念)的建构不同,在数学方法建构的过程中,数学思维活动过程本身就是被考察的对象并提供了抽象的原型.例如,在本章的引言中,教材就是通过对“摸球中的思维过程”的分析,抽象出推理、证明方法的.在这里,摸球中的思维过程本身就成为抽象的原型!正是这样的特点,决定了在有关“方法”的教学必须建立在对数学思维活动做“正面”考察的基础之上.4.课程标准明确指出:设置本模块的目的是让学生结合已学过的数学实例和生活中的实例,对合情推理、演绎推理以及数学证明的方法进行概括与总结,进一步体会合情推理、演绎推理以及两者之间的联系与差异;体会数学证明的特点,了解数学证明的基本方法,感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯,提高数学思维能力,形成对数学较为完整的认识.课程标准的上述要求.决定了本章中对思维过程的考察与分析应该是系统的,因为只有进行系统的考察才能让学生形成对数学较为完整的认识,才能通过对各种方法的比较,掌握各种方法的特点、作用以及它们之间的关系,更好地把它们运用到数学活动中去.5.本章具体的教学目标是:(1)结合已经学过的数学实例和生活中的实例,了解合情推理的含意,能利用归纳和类比等进行简单的推理,体会并认识合情推理在数学发现中的作用.(2)结合已经学过的数学实例和生活中的实例,了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单的推理.(6)通过对实例的介绍(如欧基里德《几何原本》、马克思《资本论》、杰弗逊《独立宣言》、牛顿三定律),体会公理化思想.(7)了解计算机在自动推理领域和数学证明中的作用.教材解读:1.根据对本章教学的基本定位,为了帮助学生对数学思维过程作系统的正面的考察,教材做了如下的工作:(1)教科书为学习活动设置了数学探索发现活动的大背景,大框架.(注意引言的作用),在分别阐述了归纳、类比、演绎等推理方法以后,又专门设置了一节“推理案例赏析”所有这些,都为对思维过程进行系统的考察提供了条件.(2)教科书充分地利用案例,通过案例(这些案例大多是从学生学习过的材料中选取的)提供数学思维活动的素材,把案例当成学习活动的出发点和载体,把案例分析看成是教学活动的主要形式.因为惟有如此,才能使学生进行深刻的思考(反思),对思维活动过程做“正面的”审视.(3)教科书注意对思维活动过程做适度的形式化概括.因为惟有如此,才能把对思维过程分析的成果固定下来,形成数学方法并运用到思维活动中去.以上各点可以从第一节〈合情推理与演绎推理〉的展开框图中看出:2.和其他模块相比,在本章中,案例分析更具有举足轻重的作用.因为除了案例分析,我们实在找不到更好的方法为学生提供“数学活动过程”,让学生参与到数学活动中来体验数学方法发现的过程,看到活生生的数学方法.因此,案例分析应该成为本模块教学的出发点和载体,为考察和分析数学活动过程提供素材和讨论的平台,同时,案例分析也应该是教学活动的主要手段.教学方法与教学建议:1.在教学中不仅要重视对推理方法和证明方法的特点进行(静态)分析,更要重视这些方法被抽象出来的过程,通过对数学活动过程的分析来认识它们的特点和作用(即对它们做动态的考察).从而正确地理解和运用这些方法,达到从整体上提高数学思维能力的目的.2.本章所学习的大部分内容如:合情推理、演绎推理、证明方法(包括反证法)都是学生熟悉的,他们早就在自觉或不自觉地把这些方法运用于学习与生活当中了.在教学中要注意从学生已学过的数学实例和生活中的实例出发,唤起学生的经验,找到知识的生长点,这是学生学习和理解本章内容的基础.3.在教学中,要通过对学生真实的思维过程和数学发现活动的典型案例的分析,让学生形成反思的意识,养成反思的良好习惯.4.教学的重点应该是对基本的数学方法的理解和运用.首先是对“推理”和“证明”在数学发现活动中的作用.这就要求学生从整体上认识本章所介绍的数学方法.如在“合情推理和演绎推理”的教学中,应通过实例,引导学生运用合情推理去探索、猜测一些数学结论,并用演绎推理确认所得结论的正确性,或者用反例推翻错误的猜想.教学的重点在于通过具体实例理解合情推理与演绎推理(它们的作用、特点、关系),理解数学发现过程,而不必追求对概念的抽象表述.在证明方法的教学中,应通过实例,引导学生认识各种证明方法的特点,掌握这些方法的思考过程,体会证明的必要性,而对证明的技巧性不宜作过高的要求.5.数学的推理方法和证明方法,不仅运用在数学中,而且在生活中的其它领域都有广泛的应用.在教学中要引用生活中和其它学科中的例子,让学生体会数学和生活的联系,体会数学应用的广泛性,认识数学的文化价值.6.公理化思想和机器证明体现了数学的文化价值.在教学中要让学生体会公理化思想中蕴涵的理性精神,和机器化证明中的算法思想.下面是具体的教学建议,供参考.引言1.华罗庚教授“摸球”的例子,为推理与证明的学习提供了一个大的背景.它具有丰富的教学意义.在教学中不仅应该让学生体会到,“推理”与“证明”是构成探索活动的两个最基本的环节,让学生体会到,探索活动是一个不断的“提出猜想——验证猜想——再提出猜想——再验证猜想”的过程,而且应当让学生体会到永不休止的探索精神正是理性精神的表现!而数学家就是通过不断地提出猜想、证明猜想来进行探索活动的!2.引言中提出的两个问题(我们怎样进行推理?我们怎样验证(证明)结论?)是本大节的中心问题.本节的教学内容就是依据它展开的.2.1 合情推理与演绎推理1.合情推理和演绎推理是数学活动中常用的两种推理形式,它们具有不同的形式、特点和作用.本节先分别研究它们的特点和作用,然后再通过对具体的数学发现过程的分析,进一步体会它们之间的联系,在具体的数学思维过程中感受它们的作用.2.演绎、归纳、类比是学生熟悉的推理方式.教材列举了3个例子,开始了对这些推理形式的考察.教学中可以让学生举出更多的例子.3.通过揭示三个推理案例的共同点概括出“推理”的概念.并根据它们在结构上的不同特点,进行分类研究,这个过程虽然简单,却体现了案例分析是本章教学的主要形式的特点.2.1.1 合情推理1.合情推理是由G·波利亚提出的概念.他通过对数学发现活动的分析注意到数学活动是由“猜想”和“论证”两个环节构成的,相应地在这两个不同的环节里使用着不同的思维方法,即合情推理与论证推理(教科书中称为演绎推理).G·波利亚并没有为合情推理下定义.实际上,在教学中,只要让学生把合情推理看成是提出猜想的推理而演绎推理是可以给出证明的推理就行了.据此,教科书按照G·波利亚的思路,编写了引言,突出了对探索活动的分析,突出了“猜想”和“证明”两个重要的思维环节,而对合情推理的定义作淡化处理(只在阅读材料中提了一下)(《课程标准》给合情推理作了如下定义:合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等)、实验和实践的结果,以及个人的经验和直觉等推测某地结果的推理过程.)2.归纳、类比是合情推理的两种常用的形式,除此以外,合情推理还有其他的多种形式,如:联想、想象、直觉等等.2.1.1.1 归纳推理1.归纳推理是学生熟悉的推理方式.和过去不同,在本节中,我们专注于推理的形式,而不关注推理的内容,即专门对推理的形式进行考察,考察的重点则是归纳推理的特点和它的作用.2.归纳推理的一般模式为:S具有P,1S具有P,2……S n具有P(S,S2,…,S n是A类事物的对象)1——————————————————————————所以,A类事物具有P.教学中可以介绍给学生.3.“思考”要求列举更多的有关归纳推理的例子,下面的例子可供参考.(1)观察:1 = 12,1 + 3 = 22,1 + 3 + 5 = 32,1 + 3 + 5 +7 = 42,由此猜想:1 + 3 + 5 + 7 + …+ (2n1) = n2.(2)1640年,费马在给友人的信中谈到:220+ 1 = 3,221+ 1 = 5,222+ 1 = 17,223+ 1 = 257,224+ 1 = 65 537都是素数,由此,他猜想:任何形如22n+ 1(n N)的数(通常称为费马数,记作F n)都是素数.此后,一直未有人怀疑过这个结论.直到1732年,欧拉发现F= 225+ 1 = 4 294 967 297 = 641 6 700 417并不是素数,才推翻费马的猜5想.此例还说明,在归纳推理中,根据同一个前提,可以推出不同的结论:当n > 1时,F n的末位数字是7(猜想).2.要让学生体会到归纳不仅是一种方法,而且体现了一种态度.欧拉说:把归纳看成是一种机会,“以便证明它或推翻它”,这就是我们对待归纳的态度,而归纳的价值就在于“在这两种情况之中我们都会学到一些有用的东西.”可以看出,归纳的态度就是探索的态度,这一点在华罗庚的“摸球”游戏中也得到了充分的体现.要让学生体会到,探索活动是在猜想的推动下进行的,没有猜想就没有探索!而归纳的价值就在于它是提出猜想的一种方法!3.在归纳推理中,根据同一个的前提,往往可以推出不同的结论.例如从例4中的推理前提出发,也可以得到当n>1时,F n的末位数字是7的结论(猜想).4.完全归纳法(和数学归纳法类似)实质上是一种演绎推理,它是一种必然性推理,是数学证明的工具,因此它不属于合情推理.2.1.1.2 类比推理1.类比推理是学生熟悉的推理方式.和过去不同,在本节中,我们专注于推理的形式,而不关注推理的内容,即专门对推理的形式进行考察.2.类比推理的一般模式为:A类事物具有性质a,b,c,d,B类事物具有性质a',b',c',(a,b,c与a',b',c'相似或相同)————————————————所以,B类事物可能具有性质d'.教学中可以介绍给学生.3.例1是根据等式的性质类比不等式的性质.4.例2可以看成是系统间的类比.用现代数学的角度来看,类比就是两个具有同构关系的模型间的推理.数学(科学)发现活动中的类比绝大多数都是这类类比.在教学中要注意对类比过程的分析.5.类比可以看成是从已知的相似性,推断未知的相似性的推理.在教学中要引导学生对类比的过程进行分析,弄清在推理中究竟是从哪些已知的“相似性”推出什么样的未知的“相似性”的.6.在运用类比推理时,首先要找出两类对象之间可以确切表述的相似性(或一致性);然后,再用一类对象的性质去推测另一类对象的性质,从而得出一个猜想;最后,检验这个猜想.在教学中不要满足于对对象相似性的模糊认识,要坚持把它们的相似性用语言确切地表述出来.只有这样,才能把类比和“比喻”区别开来.2.1.2 演绎推理1.演绎推理是一种重要的推理形式,通过数学学习,学生已经在广泛地使用它,在教学中,要让学生体会到演绎推理是严格按照逻辑法则进行的推理,是必然性推理的特点.2.三段论是演绎推理的主要形式.三段论有多种格式,教科书介绍了其中常用的一种,其用意在于让学生体会到演绎推理是一种形式化程度相当高的推理,而不是正面讲“三段论”,因此,在教学中不必拓展补充.3.除了三段论以外,演绎推理还有直接推理,关系推理、联言推理、假言推理、选言推理等多种形式.4.三段论也有多种形式,三段论的依据是不言自明的三段论公理:一类事物的全部是什么或不是什么,那么这类事物的部分也是什么或不是什么.对此教科书中用集合论的语言和图形作了说明,其目的是帮助学生理解三段论.(教学中不必提出三段论公理)5.三段论推理在数学中有重要的应用,特别是在理论初建或概念性质运用的初期.但是数学推理过程不全是三段论组合,直接用三段论推理的并不多,有些数学证明过程(如教科书中例2),虽然可以归结为三段论的组合,但却太为繁琐了,所以并不实用.6.数学并不等同于逻辑,它已独自发展几千年,尤其是它的符号系统,使得它有自身的一套简单的推理形式或规则,尽管它能用三段论解释,但大可不必去追溯它的三段论本源.因而在数学中,直接选定了若干演绎推理的规则.如:“如果q P ⇒,P 真,则q 真”、“如果b c ,,a b ⇒⇒,则c a ⇒”(三段论的“数学形式”)等等.(如课本中例2的证明就使用了这些规则)应该告诉学生,数学中的运算也是演绎推理的一种形式.7.在数学中学习演绎推理,并不等同于学习形式逻辑或数理逻辑,课程标准规定,本小节的学习目标是,“体会演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单的推理”,相信注意到这些,就可以理解教科书的编写意图,并掌握教学的分寸了.8.在叙述演绎推理的特点时,要和归纳、类比的特点对照,让学生理解它们是两类不同的推理.9.教科书中说“演绎推理是一种收敛性的思维方法,它较少创造性”,这并不是说,演绎推理就完全没有发现功能,更不是说演绎推理在数学发现活动中没有作用.为了让学生全面认识演绎推理在发现活动中的作用,教科书提供了阅读材料:“海王星的发现和探索性演绎法”,这个材料对全面准确地理解演绎推理在探索活动中的作用是很有帮助的.2.1.3 推理案例赏析1.《推理案例赏析》是推理方法的综合应用,是对推理方法更深层次的考察.这样,教科书就为推理的教学提供了一个“总——分——总”的结构,而本小节正是后一个“总”.它引导学生在前面学习的基础上,对各种推理方法做综合的动态的考察,帮助学生体会不同推理方法的特点和联系,感受它们在数学思维过程中的作用.2.在教学中,要注意对思维过程的分析.课本中提供的思维过程只是几种典型的解决问题的思路.面对着这些问题,学生可能会有更多的想法,应该鼓励学生谈谈自己的想法,并对课本中的思考过程做出评价.3.关于例1的教学.(1)“提出问题”是数学发现活动中重要的环节.教学中要注意分析提出问题的过程.在例1和例2中,都是通过类比提出研究课题的.(2)课本中的思路1是“归纳的方案”,总的说,它是通过归纳提出猜想的.但是应该注意到,作为归纳基础的“表”中的每个数据都是由运算提供的,也就是说,演绎提供了归纳的基础.所以说:在数学发现活动中,演绎起到了类似“实验”的作用,在这里演绎为归纳提供了前提.(3)在“归纳的方案”中,解题者原本希望从表2-1-5中归纳出一般结论,可是却失败了,但是正是失败引导他尝试计算S1(n)和S2(n)的比,找到了通向成功的路.要让学生体会到发现活动都是具有尝试的性质的,失败是经常会遇到的,所以常说“失败是成功之母”.通过教学要让学生体会到,对思维过程进行调控的重要性.对此,在“思路2”和例2中,都有体现.教学中,要让学生体会到发现过程是一个曲折的艰苦的过程,认识到思维调控的重要性.(4)尝试计算S1(n)和S2(n)的比,是导致发现的关键,这个念头是由“联想”激发的.联想也是合情推理的一种方法.(5)思路2是一个“演绎的方案”,但这并不是说,在这个方案中没有使用合情推理的方法,相反地,应该说合情推理在这个方案中同样起了关键的作用.比如,这个方案中的“初始念头”——“尝试用直接相加的方法求出自然数的平方和”就是由合情推理提供的.(6)在思路2的教学中,设置了“(2)从失败中汲取有用的信息,进行新的尝试”的环节,是为了让学生体会到思维调控的重要性,注意对思维过程的分析,进而养成反思的习惯.(7)“既然能用上面的方法求出S1(n),那么我们也应该可以用类似的方法求出S2(n)”,这也是一个猜想,它是由类比得到的.4.关于例2的教学.(1)例2通过具体的问题对类比推理的方法做了更深入的介绍.类比在数学发现活动中具有十分重要的作用,应该让学生学会自觉地科学地把类比方法运用到发现活动中去.(2)把棱台和梯形类比,开始只是模糊的念头,通过分析,清晰地认识到它们之间的“相似性”,这时才会有科学的“类比推理”.因此,“确定类比对象”和“对类比对象的进一步分析”都是重要的思维环节,是进行类比推理的前提.学生在使用类比时,经常忽略这些环节.(3)验证猜想的过程也是对猜想做调整的过程.在这个过程中,合情推理仍然发挥着重要的作用.教学中请注意合情推理在“验证猜想”中的作用.(4)从美感出发做出的判断,可以称为审美推断.本例在“验证猜想”的环节中,使用了这种方法.审美推断也是一种合情推理的方法,在科学发现活动中具有重要的价值.通过案例的分析,应该让学生体会到审美在发现活动中的作用.(5)在公式(猜想)的调整过程中,实际上使用的是“探索性演绎法”(即在猜想的基础上进行的演绎推理),这可以让学生更好地体会到“演绎推理”在数学发现活动中所具有的类似于“实验”的功能.5.关于实习作业.学生可以通过查找资料来完成实习作业.例如可以引用本书提到的数学史中的例子:如欧拉公式、哥德巴赫猜想等,也可以从教科书中选取案例如:“正弦定理的发现”、“余弦定理的发现”、“和差化积公式的推导”等等.通过反思,对自己的思维活动进行分析(如你是怎样解决某个问题的).6.在思考以及实习作业中,教材反复提出了相同的问题,其用意是希望为学生分析思维活动时提供一个反思的框架.2.2 直接证明与间接证明教学的重点是让学生了解直接证法与间接证法的特点,知道证明的一般步骤,能使用它们证明问题,在教学中不要拘泥于“概念”,在“概念”上下功夫.2.1 直接证明1.课本中选用的两个例子都是学生熟知的,在《数学(必修5)》的基本不等式中就采用了这两个证明.现在教科书把它用作讨论综合法和分析法的素材,是为了让学生能集中精力关注这两种证明方法形式结构上的特点和区别,进而展开对证明方法的研究.2.一般地,分析法和综合法是两种常见的思维方法,人们利用它们来寻求证明问题的思路.在教科书中是把它们看成两种证明方法的(指呈现出来的证明过程).思维方法和证明方法当然有微妙的差别,但是如果把“证明”看成是思维过程,这样做也就没有什么不可以.3.综合法,从条件出发,“由因导果”,分析法,紧抓证题目标,“执果索因”.在实际的解题活动中,总是把两者结合起来使用的.2.2 间接证明1.反证法是一种重要的间接证法(同一法也是一种重要的间接证法).在教学中应先让学生弄清直接证明和间接证明的区别,然后再转入反证法.2.学生在学习立体几何初步时,已经使用反证法,因此他们是有经验的,但当时并没有正面介绍反证法.3.反证法的逻辑依据是矛盾律和排中律.反证法的实质在于:若肯定定理的假设而否定其结论,就会导致矛盾.具体地说,反证法不直接证明命题“若p则q”,而是从原题的反论题“既p又┐q”入手,由p与┐q合乎逻辑地推出一个矛盾结果;根据矛盾律,两个互相矛盾的判断,不能同真,必有一假,断定反论题“既p又┐q”为假;进而再根据排中律,两个互相矛盾的判断,不能同假,必有一真.由此肯定命题“若p则q”为真.虽然学生没有学过排中律和矛盾律,但是由于这两个定律的“准公理性”,学生还是能理解反证法的思想的,因而在教学中没有必要提出排中律和矛盾律.2.3 公理化思想1.公理化思想体现了数学中的理性精神和求真意识.为了确保命题真实性,数学对命题提出了演绎证明的要求,这种要求直接导致公理化产生.教学中要让学生体会到这一点.2.公理是“公认正确而不需证明的命题”,是“证明其它一切命题的基础”,是“选定”和“设置”的,都体现了现代公理法的思想,在教学中不要过多地强调公理是“经过长期的实践证明的”说法.3.可以建议有兴趣的学生阅读《数学史初步》中有关非欧几何的材料.教学案例:归纳推理执教:高建国(扬州大学附属中学)点评:张乃达(江苏省扬州中学)1.概念、技能、能力、态度我们可以从不同的层面来看归纳.第一种是把它看成一个概念,这要弄清什么是推理?什么是归纳推理?这是从知识层面来看归纳的;第二种是把归纳看成是一种方法,这就要弄清怎样进行归纳?归纳有哪几步?第一步怎么做?第二步又怎么做?等等,这是从技能层面来看归纳的.第三种是把归纳看成是一种能力,提高学生的归纳能力——归纳的能力实质上就是分析,分析到位了,思维能力提高了,归纳才能得到有价值的东西.这是从能力的层面看归纳的.长期以来,我们的教师大都习惯于从上面三个层次看归纳,并以此确定本节课的教学内容和重点,这正是习惯于从知识与能力的层面看待数学教育的体现!其实,如果从文化的视角来分析,就可以看到归纳还可以被看成是一种态度,一种对待事物的态度.归纳的态度实际上就是探究的态度,它总是用探究者的眼光来看世界——看到某些现象,总想从中归纳出某种规律!促使哥德巴赫提出那个著名的猜想的正是这种态度,向中学生介绍哥德巴赫猜想的目的也正是让他们学习这种态度!这种态度正是理性精神的表现!也是这节课中最有教育价值的东西!通过上面的分析,对这节课应该怎么上就清楚了.通过这节课当然应该让学生知道什么是推理?什么是归纳?怎样进行归纳?但是这并不是重点,其实学生早就在使用归纳的方法了,现在只要正面的小结一下就可以了!提高归纳的能力也不是这节课能够实现的目标,归纳的能力,是思维能力的体现,它不能独立于思维能力之外,也不是通过这节课就能实现的目标!这节课的重点应该是归纳态度的培养和探究精神的激发!在本节课中,执教老师对课的定位是比较准确的,较好地处理了概念、技能、能力和态度的关系.渗透了归纳态度的培养,探求欲望的激发,让学生体会到,在我们的周围,到处都存在着值得探索的问题,到处都可以运用归纳的方法来提出猜想,进而展开探索的活动,这对学生理性精神的形成是很有意义的.2.用数学(家)的眼光看世界。
高二数学人教A版选修2-2课件:第二章 推理与证明 整合

专题一
专题二
专题三
专题四
(2)要证原等式成立,只需证:
2cos(α-β)sin α-sin(2α-β)=sin β.
①
因为①式左边=2cos(α-β)sin α-sin[(α-β)+α]
=2cos(α-β)sin α-sin(α-β)cos α-cos(α-β)sin α
=cos(α-β)sin α-sin(α-β)cos α
当
n=k+1
时,������2������
+1
=1+1
2
+
1 3
+…+21������
+
2������1+1+…+2������1+1>1+���2���
+
1 2������ +1
+
2������1+2+…+2������1+1>1+���2���
+
2������ 2������ +2������
=1+���2���
专题一
专题二
专题三
专题四
(所1)以 解:f因 '(x为 )=xf+'(x������������)≥ =x0+在������������,且 区间 f(x[)1在 ,e]区 上间 恒[成 1,e立]上,即是a增≥函-x数 2 在, 区间[1,e]上恒
成立.所以 a≥-1.
(2)证明:当 a=1 时,f(x)=12x2+ln x,x∈[1,e]. 令 F(x)=f(x)-23x3=12x2+ln x-23x3, 又 F'(x)=x+1������-2x2=(1-������)(1+������������+2������2)≤0,
人教版高中数学高二选修2-2第二章《推理与证明》章末复习导学案

第二章《推理与证明》章末复习导学案考试要求1.了解合情推理的思维过程;2.掌握演绎推理的一般模式3.会灵活运用直接证明和间接证明的方法,证明问题;4.掌握数学归纳法的整体思想. 典例精析精讲例1 如图,已知□ABCD ,直线BC ⊥平面ABE ,F 为CE 的中点. (1)求证:直线AE ∥平面BDF ;(2)若90AEB ∠=,求证:平面BDF ⊥平面BCE .例2 已知数列{}n a 的前n 项和11()22n n n S a -=--+(n 为正整数).(Ⅰ)令2nn n b a =,求证数列{}n b 是等差数列,并求数列{}n a 的通项公式;(Ⅱ)令1n n n c a n +=,12........n n T c c c =+++试比较n T 与521nn +的大小,并予以证明.例3 设数列{}n a 的前n 项和为n S ,对任意的正整数n ,都有51n n a S =+成立,记例1图A.C可能是线段AB的中点5.(2011湖南理16)对于*n N ∈,将n 表示12100121222...22k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯,当0i =时,1i a =,当1i k ≤≤时,1a 为0或1.记()I n 为上述表示中ai 为0的个数(例如:021012,4120202I =⨯=⨯+⨯+⨯),故(1)0I =, (4)2I =),则(1)(12)I =________________;(2) ()12mI n n =∑________________.6.(2011北京理8)设()0,0A ,()4,0B ,()4,4C t +,()(),4D t t R ∈.记()N t 为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的值域为A .{}9,10,11B .{}9,10,12C .{}9,11,12D .{}10,11,127.(2011江西理7)观察下列各式:55=3125,65=15625,75=78125,…则20115的末四位数字为A .3125B .5625C .0625D .81258.(2011广东理8)设S 是整数集Z 的非空子集,如果,,a b S ∀∈有ab S ∈,则称S关于数的乘法是封闭的.若T,V 是Z 的两个不相交的非空子集,,T U Z ⋃=且,,,a b c T ∀∈有;,,,abc T x y z V ∈∀∈有xyz V ∈,则下列结论恒成立的是A .,T V 中至少有一个关于乘法是封闭的B .,T V 中至多有一个关于乘法是封闭的C .,T V 中有且只有一个关于乘法是封闭的D .,T V 中每一个关于乘法都是封闭的9.(2011江西理10)如右图,一个直径为l 的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M 和N 是小圆的一条固定直径的两个端点.那么,当小圆这样滚过大圆内壁的一周,点M ,N 在大圆内所绘出的图形大致是10.(2011安徽理15)在平面直角坐标系中,如果x 与y 都是整数,就称点(,)x y 为整点,下列命题中正确的是_____________(写出所有正确命题的编号).①存在这样的直线,既不与坐标轴平行又不经过任何整点 ②如果k 与b 都是无理数,则直线y kx b =+不经过任何整点 ③直线l 经过无穷多个整点,当且仅当l 经过两个不同的整点④直线y kx b =+经过无穷多个整点的充分必要条件是:k 与b 都是有理数 ⑤存在恰经过一个整点的直线11.(2011四川理16)函数f x ()的定义域为A ,若1212x x A f x =f x ∈,且()()时总有12x =x f x ,则称()为单函数.例如,函数f x ()=2x+1(x R ∈)是单函数.下列命题:①函数f x ()=2x (x ∈R )是单函数;②若f x ()为单函数,121212x x A x x f x f x ∈≠≠,且,则()();③若f :A →B 为单函数,则对于任意b ∈B ,它至多有一个原象; ④函数f (x )在某区间上具有单调性,则f (x )一定是单函数. 其中的真命题是 .(写出所有真命题的编号)12.(2011山东理15)设函数()(0)2xf x x x =>+,观察:1()(),2xf x f x x ==+21()(()),34xf x f f x x ==+ 32()(()),78xf x f f x x ==+)知,FG解:解:(b=于是1n()2122n +综合(1)(2)可知1+∴-=n n a a∴当n 为偶数时,设∴1(n R b =(b +4k ≥成立. )16n +λ⎡⎣即证:(a(21)2n n x -+(1)(n +++。
高中数学选修22推理与证明2
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
类比推理
如图所示,在△ABC中,射影定理可体现为a= b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边, 类比上述定理,写出对空间四周体性质的猜想.
[思路点拨] 这是一种由平面图形到空间图形的类比, 于是联想到:边长→面积,平面角→二面角,边的射影→面的 射影等.
方法二:5件首饰的珠宝颗数依次为:1,1+5,1+5+ 9,1+5+9+13,1+5+9+13+17,则第6件首饰上的珠宝 颗数为1+5+9+13+17+21=66,即每件首饰上的珠宝数 是以1为首项,4为公差的等差数列的前n项和,故第n件首饰 的珠宝颗数为1+5+9+…+(4n-3)=2n2-n.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
2.在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36, 45,55,…这些数叫做三角形数,这是由于这些数目的点能够排 成正三角形(如图所示),则三角形数的普通体现式f(n)=( )
A.n+2 C.n-12n+2
高效测评 知能提升
[问题2] 蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟 是用肺呼吸的,蜥蜴是用肺呼吸的,蛇,鳄鱼,海龟,蜥蜴都 是爬行动物,全部的爬行动物都是用肺呼吸的吗?
[提示2] 是.全部的爬行动物都是用肺呼吸的.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
人教版高二数学选修2-2(B版)全册PPT课件

3.1.1 实数系
3.1.3 复数的几何意义
3.2.2 复数的乘法
பைடு நூலகம்
本章小节
附录 部分中英文词汇对照表
第一章 导数及其应用
人教版高二数学选修2-2(B版)全册 PPT课件
1.2 导数的运算
1.2.1 常数函数与冥函数的导
1.2.3 导数的四则运算法则
1.3.2 利用导数研究函数的极值
1.4 定积分与微积分基本定理
1.4.1 曲边梯形
本章小结
第二章 推理与证明
2.1.2 演绎推理
2.2.2 反证法
2.3.2 数学归纳法应用举例
阅读与欣赏
《原本》与公理化思想
3.1 数系的扩充与复数的概念
人教版高二数学选修2-2(B版)全 册PPT课件目录
0002页 0036页 0087页 0156页 0219页 0238页 0254页 0282页 0336页 0371页 0418页 0458页 0460页 0495页 0555页 0598页 0600页
第一章 导数及其应用
1.1.2 瞬时速度与导数
教师版-高中数学知识手册:选修2-2(2)推理证明

- 51 - 选修2-2数学知识点 选修2-2—第2章 推理证明第2章 推理证明1.归纳推理:从个别事实中推演出一般性的结论. 【归纳推理是由部分到整体,由特殊..到一般..的推理】 2.类比推理:由两个(两类)对象之间在某些方面的相似或相同,推演出他们在其他方面也相似或相同.【类比推理是由特殊..到特殊..的推理】 注:归纳推理与类比推理都属于合情推理,两种推理所得的结论未必是正确的.3.演绎推理:由一般性的命题推演出特殊性命题的推理方法.【演绎推理是由一般..到特殊..的推理】 (1)只要前提是真实的,推理的形式是正确的,那么结论必定是真实的.(2)“三段论”推理是演绎推理的一般模式,它包括:① 大前提:已知的一般性推理. 大前提:M 是P② 小前提:所研究的特殊情况. 小前提:S 是M③ 结论:根据一般原理,对特殊情况做出的判断. 结论:S 是P .注:(1)集合表示:若集合M 的所有元素都具有性质P ,S 是M 的子集,则S 中所有元素都具有性质P .(2)三段论的论断基础:“凡肯定(或否定)了某一类对象的全部,也就肯定(或否定)了这一类对象的各部分或个体.”简言之,“全体概括个体.”4.直接证明: 综合法 “执因导果”; 分析法“执果导因”(1)综合法的特点:从“已知”看“可知”,逐步推向“未知”,其逐步推理,是寻找它的必要条件.综合法的格式:“∴, ”或“⇒”(2)分析法的特点:从“未知”看“需知”,逐步靠拢已知,其逐步推理,是寻找它的充分条件.分析法的格式:“要证…只要证”5.间接证明:反证法(1)定义:一般地,假设原命题的结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.(2)用反证法导出的矛盾主要有:① 与数学公理、定理、定义、公式或与已知条件矛盾;② 与假设矛盾;及自相矛盾.(3)步骤:① 反设——假设命题的结论不成立,即假定原结论的反面为真;② 归谬——从反设(把反设作为新条件)和原命题的已知条件出发,应用正确的推理,得出矛盾结果; ③ 存真——由矛盾结果,断定反设不真,从而肯定原结论成立.6.数学归纳法公理:对于某些与正整数有关的数学命题,常采用数学归纳法证明:(1)当n 取第一个值0n 时结论正确;(2)假设当),(0*n k N k k n ≥∈=时结论正确,证明当1+=k n 时结论也正确. 那么,命题对于从0n 开始的所有正整数n 都成立.①第1步中0n n =时,0n 不一定是1,根据题目要求,也可能是2,3等.②第2步证明当1+=k n 时结论是否正确时,必须利用“假设当k n =时成立”作为条件,根据有关定理、定义、公式、性质,推证出当1+=k n 时成立,不能直接代入,否则1+=k n 时也成假设了.。
(人教版)高中数学选修2-2课件:第2章 推理与证明2.2.2

自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
反证法常见的矛盾类型
反证法的关键是在正确的推理下得出矛盾,这个矛盾可 以是与_已__知__条__件___矛盾,或与假__设______矛盾,或与_定__义____、 公理、定理、事实矛盾等.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
90°. 上述步骤的正确顺序为________.
解析: 由反证法的一般步骤可知,正确的顺序应为 ③①②.
答案: ③①②
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
2.用反证法证明命题:“a,b∈ N,ab可被5整除,那 么a,b中至少有一个能被5整除”时,假设的内容应为( )
A.a,b都能被5整除 B.a,b都不能被5整除 C.a,b不都能被5整除 D.a不能被5整除 解析: “至少有一个”的否定是“一个也没有”,即 “a,b 都不能被5整除”. 答案: B
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
人教A版数学高二选修2-2检测第二章推理与证明单元质量评估(二)

单元质量评估(二)(第二章)(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2017·郑州高二检测)下列表述正确的是( )①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.A.①②③B.②③④C.②④⑤D.①③⑤【解析】选 D.归纳推理由部分到整体,特殊到一般,演绎推理由一般到特殊,类比推理由特殊到特殊,故①③⑤正确.2.(2017·石家庄高二检测)下列推理是归纳推理的是( )A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆B.由a1=1,a n=3n-1,求出S1,S2,S3,猜想出数列的前n项和S n的表达式C.由圆x2+y2=r2的面积πr2,猜出椭圆+=1的面积S=πabD.科学家利用鱼的沉浮原理制造潜艇【解析】选B.从S1,S2,S3猜想出数列的前n项和S n,是从特殊到一般的推理,所以B是归纳推理.3.已知a<b<0,下列不等式中成立的是( )A.a2<b2B.<1C.a<4-bD.<【解析】选C.令a=-2,b=-1,满足a<b<0,则a2>b2,=2>1,>,故A,B,D 都不成立.4.已知c>1,a=-,b=-,则正确的结论是( )A.a>bB.a<bC.a=bD.a,b大小关系不定【解析】选B.因为a=,b=,所以a<b.5.(2017·平顶山高二检测)有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线b⊄平面α,直线a⊂平面α,直线b∥平面α,则直线b∥直线a”的结论显然是错误的,这是因为( )A.大前提错误B.小前提错误C.推理形式错误D.非以上错误【解析】选 A.推理过程中,“直线平行于平面,则平行于平面内所有直线”是错误的.6.(2017·太原高二检测)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(-3,4),且法向量为n=(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系中,经过点A(1,2,3),且法向量为m=(-1,-2,1)的平面的方程为( )A.x+2y-z-2=0B.x-2y-z-2=0C.x+2y+z-2=0D.x+2y+z+2=0 【解析】选 A.类比直线方程求法得平面方程为(-1)×(x-1)+(-2)×(y-2)+1×(z-3)=0,即x+2y-z-2=0.【补偿训练】在平面直角坐标系xOy中,二元一次方程Ax+By=0(A,B 不为0)表示过原点的直线.类似地:在空间直角坐标系Oxyz中,三元一次方程Ax+By+Cz=0(A,B,C不为0)表示________.【解析】Ax+By=0表示一条直线.Ax+By+C=0中的C=0说明截距为0,即当y=0时,解得x=0,所以当然过原点.同理,Ax+By+Cz=0,当z=0时,Ax+By=0,它是平面xOy中的一条过原点的直线,所以Ax+By+Cz=0是过原点的一个平面.答案:过原点的平面7.已知f(x+1)=,f(1)=1(x∈N*),猜想f(x)的表达式为( )A.f(x)=B.f(x)=C.f(x)=D.f(x)=【解析】选B.由已知得,f(2)==,f(3)===,f(4)==,因而,猜想f(x)=.8.分析法又叫执果索因法,若使用分析法证明:“设a>b>c,且a+b+c=0,求证:<a”,则最终的索因应是( )A.a-b>0B.a-c>0C.(a-b)(a-c)>0D.(a-b)(a-c)<0【解析】选A.因为a>b>c,且a+b+c=0,所以3c<a+b+c<3a,即a>0,c<0.要证<a,只需证b2-ac<3a2,只需证(-a-c)2-ac<3a2,只需证2a2-ac-c2>0,只需证(a-c)·(2a+c)>0,只需证2a+c>0(a>0,c<0,则a-c>0),只需证a+c+(-b-c)>0,即证a-b>0,这显然成立.【补偿训练】已知f(x)=x3+x,a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )A.一定大于零B.一定等于零C.一定小于零D.正负都有可能【解析】选A.f(x)=x3+x是奇函数,且在R上是增函数,由a+b>0得a>-b,所以f(a)>f(-b),即f(a)+f(b)>0,同理f(a)+f(c)>0,f(b)+f(c)>0,所以f(a)+f(b)+f(c)>0.9.数列{a n}中,a1=1,S n表示前n项和,且S n,S n+1,2S1成等差数列,通过计算S1,S2,S3,猜想当n≥1时,S n= ( )A. B.C. D.1-【解析】选B.由题意知,2S n+1=2S1+S n,则S1=1,S2=,S3=,则S n=.10.(2017·武汉高二检测)已知a>0,b>0,a,b的等差中项为,且m=a+,n=b+,则m+n的最小值为( )A.3B.4C.5D.6【解析】选 C.由已知,得a+b=1,m+n=a++b+=1++=1++=3++≥3+2=5. 11.(2017·枣庄高二检测)将正奇数按如图所示的规律排列,则第21行从左向右的第5个数为( )13 5 79 11 13 15 1719 21 23 25 27 29 31…A.809B.853C.785D.893【解析】选A.前20行共有正奇数1+3+5+…+39=202=400个,则第21行从左向右的第5个数是第405个正奇数,所以这个数是2×405-1=809.12.在等差数列{a n}中,若a n>0,公差d>0,则有a4·a6>a3·a7,类比上述性质,在等比数列{b n}中,若b n>0,公比q>1,则b4,b5,b7,b8的一个不等关系是( )A.b4+b8>b5+b7B.b4+b8<b5+b7C.b4+b7>b5+b8D.b4+b7<b5+b8【解析】选A.在等差数列{a n}中,由于4+6=3+7时有a4·a6>a3·a7,所以在等比数列{b n}中,由于4+8=5+7,所以应有b4+b8>b5+b7或b4+b8<b5+b7.因为b4=b1q3,b5=b1q4,b7=b1q6,b8=b1q7,所以(b4+b8)-(b5+b7)=(b1q3+b1q7)-(b1q4+b1q6)=b1q6·(q-1)-b1q3(q-1)=(b1q6-b1q3)(q-1)=b1q3(q3-1)(q-1).因为q>1,b n>0,所以b4+b8>b5+b7.【补偿训练】(2017·西安高二检测)设f(x)=(x-a)(x-b)(x-c)(a,b,c是两两不等的常数),则++的值是____________. 【解题指南】利用导数的运算法则分别计算f′(a),f′(b),f′(c),再代入式子++计算.【解析】f′(x)=(x-b)(x-c)+(x-a)(x-c)+(x-a)(x-b),f′(a)=(a-b)(a-c),f′(b)=(b-a)(b-c),f′(c)=(c-a)(c-b),++=++==0.答案:0二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中的横线上)13.(2017·沈阳高二检测)一同学在电脑中打出如下若干个圈:若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的的个数是________.【解析】将圆分组:第一组○●,2个第二组○○●,3个第三组○○○●,4个所以每组图总个数构成一个等差数列,前n组圆的总个数为S n=2+3+4+…+(n+1)=·n=.令S n=120,得n≈14.1.即包含了14整组.答案:1414.(2017·济南高二检测)从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16= -(1+2+3+4),…,推广到第n个等式为________.【解析】因为1=1=(-1)1+1·1,1-4=-(1+2)=(-1)2+1·(1+2),1-4+9=1+2+3=(-1)3+1·(1+2+3),1-4+9-16=-(1+2+3+4)=(-1)4+1·(1+2+3+4),所以1-4+9-16+…+(-1)n+1·n2=(-1)n+1·(1+2+…+n).答案:1-4+9-16+…+(-1)n+1·n2=(-1)n+1(1+2+…+n)15.(2017·北京高考)某学习小组由学生和教师组成,人员构成同时满足以下三个条件:(i)男学生人数多于女学生人数;(ii)女学生人数多于教师人数;(iii)教师人数的两倍多于男学生人数.①若教师人数为4,则女学生人数的最大值为________;②该小组人数的最小值为________.【解析】设男学生人数、女学生人数、教师人数分别为a,b,c,则有2c>a>b>c,且a,b,c∈Z.①当c=4时,b的最大值为6;②当c=3时,a的值为5,b的值为4,此时该小组人数的最小值为12.答案:①6 ②1216.(2017·泸州高二检测)对于命题“如果O是线段AB上一点,则||·+||·=0”将它类比到平面的情形是:若O是△ABC 内一点,有S△OBC·+S△OCA·+S△OBA·=0,将它类比到空间的情形应为:若O 是四面体ABCD内一点,则有________.【解析】根据类比的特点和规律,所得结论形式上一致,由线段类比平面,平面类比到空间,由线段长类比为三角形面积,再类比成四面体的体积,故可以类比为V O-BCD·+V O-ACD·+V O-ABD·+V O-ABC·=0. 答案:V O-BCD·+V O-ACD·+V O-ABD·+V O-ABC·=0【补偿训练】现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为________.【解析】平面内类比到空间=.答案:三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设函数f(x)=ax2+bx+c(a≠0)中,a,b,c均为整数,且f(0),f(1)均为奇数.求证:f(x)=0无整数根.【证明】假设f(x)=0有整数根n,则an2+bn+c=0(n∈Z),而f(0),f(1)均为奇数,即c为奇数,a+b为偶数,则a,b,c同时为奇数或a,b同时为偶数,c为奇数,当n为奇数时,an2+bn为偶数;当n为偶数时,an2+bn 也为偶数,即an2+bn+c为奇数,与an2+bn+c=0矛盾.所以f(x)=0无整数根.【补偿训练】(2017·中山高二检测)已知函数f(x)=a x+(a>1).(1)证明:函数f(x)在(-1,+∞)上为增函数.(2)用反证法证明方程f(x)=0没有负数根.【证明】(1)f′(x)=a x lna+,因为a>1,x∈(-1,+∞),所以a x lna>0,>0,所以f′(x)=a x lna+>0,所以函数f(x)在(-1,+∞)上为增函数.(2)假设方程f(x)=0存在负数根x0,即x0<0(x0≠-1),则+=0,即=-.因为a>1,所以0<<1,所以0<-<1,即<x0<2,与假设x0<0相矛盾,故方程f(x)=0没有负数根.【拓展延伸】适宜用反证法证明的命题有:(1)结论本身是以否定形式出现的命题.(2)关于唯一性,存在性的命题.(3)结论是以“至多”“至少”等形式出现的命题.(4)结论的反面比原结论更具体,更容易研究的命题.18.(12分)已知在△ABC中,有一个内角不小于120°,求证:最长边与最短边之比不小于.【解题指南】设最大角为A,最小角为C,因为A≥120°,所以B+C≤60°,C≤30°,再利用正弦定理和二倍角公式求出的范围,即得所证.【证明】设最大角为A,最小角为C,则最大边为a,最小边为c.因为A ≥120°,所以B+C≤60°,且C≤B,所以2C≤B+C≤60°,C≤30°.所以==≥=2cosC≥.【补偿训练】已知f(x)=ax3+3x2-x+1,a∈R.(1)若f(x)的曲线在x=1处的切线与直线y=x+1垂直,求a的值及切线方程.(2)若对任意x∈R不等式f′(x)≤4x恒成立,求实数a的取值范围. 【解析】(1)f′(x)=3ax2+6x-1,因为曲线在x=1处的切线与直线y=x+1垂直,所以f′(1)=3a+5=-1⇒a=-2,此时切点为(1,1),切线方程为x+y-2=0.(2)因为对任意x∈R不等式f′(x)≤4x恒成立,所以3ax2+2x-1≤0恒成立,所以⇒a≤-.19.(12分)(2017·南昌高二检测)已知△ABC的三边a,b,c的倒数成等差数列,试分别用分析法和综合法证明B为锐角.【证明】分析法:要证明B为锐角,只需证cosB>0,又因为cosB=,所以只需证明a2+c2-b2>0,即a2+c2>b2.因为a2+c2≥2ac,所以只需证明2ac>b2.由已知=+,即2ac=b(a+c),所以只需证明b(a+c)>b2,即只需证明a+c>b.而a+c>b显然成立,所以B为锐角.综合法:由题意:=+=,则b=,所以b(a+c)=2ac.因为a+c>b,所以b(a+c)=2ac>b2.又a2+c2≥2ac,所以cosB=≥>0.又因为0<B<π,所以0<B<,即B为锐角.【补偿训练】(2016·杭州高二检测)已知:0<b<a<e,其中e是自然对数的底数.(1)试猜想a b与b a的大小关系.(2)证明你的结论.【解析】(1)取a=2,b=1可知:a b>b a,又当a=1,b=时,a b>b a,由此猜测a b>b a对一切0<b<a<e成立.(2)要证a b>b a对一切0<b<a<e成立,需证lna b>lnb a,需证blna>alnb,需证>,设函数f(x)=,x∈(0,e),f′(x)=,当x∈(0,e)时,f′(x)>0恒成立.所以f(x)=在(0,e)上单调递增,所以f(a)>f(b),即blna>alnb,所以a b>b a.20.(12分)已知x,y∈N*,下列不等式成立.①x2+y2≥;②x2+y2≥;③x2+y2≥.根据上述不等式,请你推出一般的结论,并证明你的结论.【解析】一般的结论是:已知x,y∈N*,a,b都是正数,且a+b=1,则ax2+by2≥(ax+by)2.证明:因为a+b=1,所以a=1-b>0,b=1-a>0.所以(ax2+by2)-(ax+by)2=(a-a2)x2-2abxy+(b-b2)y2=a(1-a)x2-2a(1-a)xy+a(1-a)y2=a(1-a)(x2-2xy+y2)=a(1-a)(x-y)2.又a>0,1-a>0,(x-y)2≥0,所以(ax2+by2)-(ax+by)2≥0.所以ax2+by2≥(ax+by)2成立.21.(12分)用数学归纳法证明(n2-12)+2·(n2-22)+…+n(n2-n2)=n2(n-1)(n+1)(n∈N*).【证明】(1)当n=1时,左边=1·(12-12)=0,右边=·12·0·2=0,所以左边=右边,n=1时等式成立.(2)假设当n=k(k∈N*)时等式成立,即1·(k2-12)+2·(k2-22)+…+k·(k2-k2)=k2(k-1)(k+1).则当n=k+1时,1·[(k+1)2-12]+2·[(k+1)2-22]+…+k·[(k+1)2-k2]+(k+1)[(k+1)2-(k+1)2]=[1·(k2-12)+2·(k2-22)+…+k·(k2-k2)]+[1·(2k+1)+2(2k+1)+…+k(2k+1)]=k2(k-1)(k+1)+·(2k+1)=k(k+1)[k(k-1)+2(2k+1)]=k(k+1)(k2+3k+2)=(k+1)2k(k+2),即当n=k+1时等式成立.由(1)(2)知对一切n∈N*,等式成立.【拓展延伸】数学归纳法的两点关注(1)关注点一:用数学归纳法证明等式问题是数学归纳法的常见题型,其关键点在于“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始n0是多少.(2)关注点二:由n=k到n=k+1时,除等式两边变化的项外还要利用n=k 时的式子,即利用假设,正确写出归纳证明的步骤,从而使问题得以证明.22.(12分)(2017·兰州高二检测)如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P,Q分别在棱DD1,BC上,BQ=4.(1)若DP=DD1,证明:PQ∥平面ABB1A1.(2)若P是D1D的中点,证明:AB1⊥平面PBC.【证明】(1)在AA1上取一点N,使得AN=AA1,连接PN,BN. 因为DP=DD1,且A1D1=3,AD=6,所以PN AD,又BQ AD,所以PN BQ,所以四边形BQPN为平行四边形,所以PQ∥BN.因为BN⊂平面ABB1A1,PQ⊄平面ABB1A1,所以PQ∥平面ABB1A1.(2)如图所示,取A1A的中点M,连接PM,BM.因为A1A,D1D是梯形的两腰,P是D1D的中点,所以PM∥AD,于是由AD∥BC知,PM∥BC,所以P,M,B,C四点共面.由题设可知,BC⊥AB,BC⊥A1A,所以BC⊥平面ABB1A1,所以BC⊥AB1,因为tan∠ABM====tan∠A1AB1,所以∠ABM=∠A1AB1,所以∠ABM+∠BAB1=∠A1AB1+∠BAB1=90°, 所以AB1⊥BM,又因为BC∩BM=B,知AB1⊥平面PBC.。
高中数学 第二章 推理与证明练习 新人教A版选修2-2-新人教A版高二选修2-2数学试题

第二章 推理与证明(时间:120分钟,满分:150分)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.证明:n +22<1+12+13+14+…+12n<n +1(n >1),当n =2时,中间式子等于( ) A.1 B.1+12C.1+12+13D.1+12+13+14解析:选D.n =2时中间式子的最后一项为14,所以中间式子为1+12+13+14.2.用反证法证明命题:“若函数f (x )=x 2+px +q ,那么|f (1)|,|f (2)|,|f (3)|中至少有一个不小于12”时,反设正确的是( )A.假设|f (1)|,|f (2)|,|f (3)|都不小于12B.假设|f (1)|,|f (2)|,|f (3)|都小于12C.假设|f (1)|,|f (2)|,|f (3)|至多有两个小于12D.假设|f (1)|,|f (2)|,|f (3)|至多有一个小于12解析:选B.“|f (1)|,|f (2)|,|f (3)|中至少有一个不小于12”的反设为“|f (1)|,|f (2)|,|f (3)|都小于12”.3.设x >0,则不等式x +1x ≥2,x +4x 2≥3,x +27x 3≥4,…,推广到x +axn ≥n +1,则a=( )A.2nB.2nC.n 2D.n n解析:选D.结合已知的三个不等式可以发现第二个加数的分子是分母x 的指数的指数次方,可得a =n n.4.下面是一段“三段论”推理过程:若函数f (x )在(a ,b )内可导且单调递增,则在(a ,b )内,f ′(x )>0恒成立.因为f (x )=x 3在(-1,1)内可导且单调递增,所以在(-1,1)内,f ′(x )=3x 2>0恒成立.以上推理中( )A.大前提错误B.小前提错误C.结论正确D.推理形式错误解析:选A.f (x )在(a ,b )内可导且单调递增,则在(a ,b )内,f ′(x )≥0恒成立,故大前提错误,故选A.5.用数学归纳法证明:1+11+2+11+2+3+…+11+2+3+…+n =2nn +1时,由n =k 到n =k +1左边需要添加的项是( )A.2k (k +2)B.1k (k +1)C.1(k +1)(k +2)D.2(k +1)(k +2)解析:选D.由n =k 到n =k +1时,左边需要添加的项是11+2+3+…+(k +1)=2(k +1)(k +2).故选D.6.分析法又称执果索因法,若用分析法证明:“设a >b >c ,且a +b +c =0,求证 b 2-ac <3a ”索的因应是( )A.a -b >0B.a -c <0C.(a -b )(a -c )>0D.(a -b )(a -c )<0解析:选C.要证明 b 2-ac <3a ,只需证b 2-ac <3a 2,只需证(a +c )2-ac <3a 2,只需证-2a 2+ac +c 2<0,即证2a 2-ac -c 2>0,即证(a -c )(2a +c )>0,即证(a -c )(a -b )>0.7.若sin A a =cos B b =cos C c,则△ABC 是( )A.等边三角形B.有一个内角是30°的直角三角形C.等腰直角三角形D.有一个内角是30°的等腰三角形解析:选C.因为sin A a =cos B b =cos C c,由正弦定理得,sin A a =sin B b =sin Cc,所以sin B b =cos B b =cos C c =sin C c.所以sin B =cos B ,sin C =cos C , 所以∠B =∠C =45°,所以△ABC 是等腰直角三角形.8.已知f (x )=x 3+x ,a ,b ,c ∈R ,且a +b >0,a +c >0,b +c >0,则f (a )+f (b )+f (c )的值一定( )A.大于0B.等于0C.小于0D.正负都可能解析:选A.f (x )为奇函数,也是增函数,因此由a +b >0可得a >-b ,所以f (a )>f (-b ),即f (a )>-f (b ),于是f (a )+f (b )>0,同理,f (a )+f (c )>0,f (b )+f (c )>0,所以f (a )+f (b )+f (c )>0.9.我们把平面中的结论“到定点的距离等于定长的点的轨迹是圆”拓展至空间中为“到定点的距离等于定长的点的轨迹是球”,类似可得:已知A (-1,0,0),B (1,0,0),则点集{P (x ,y ,z )||PA |-|PB |=1}在空间中的轨迹描述正确的是( )A.以A ,B 为焦点的双曲线绕轴旋转而成的旋转曲面B.以A ,B 为焦点的椭球体C.以A ,B 为焦点的双曲线单支绕轴旋转而成的旋转曲面D.以上都不对解析:选C.在平面中,点集{P (x ,y )||PA |-|PB |=1}是以A ,B 为焦点的双曲线的一支,点集{P (x ,y ,z )||PA |-|PB |=1}在空间中的轨迹是以A ,B 为焦点的双曲线单支绕轴旋转而成的旋转曲面,故选C.10.我国古代数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”是高,“幂”是截面积.意思是:如果两个等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等.类比祖暅原理,如图所示,在平面直角坐标系中,区域①是一个形状不规则的封闭图形,区域②是一个上底长为1、下底长为2的梯形,且当实数t 取[0,3]上的任意值时,直线y =t 被区域①和区域②所截得的两线段长总相等,则区域①的面积为( )A.4B.92 C.5D.112解析:选B.根据题意,由祖暅原理分析可得①的面积等于②的面积,又②是一个上底长为1、下底长为2的梯形,所以①的面积为(1+2)×32=92.11.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )A.(7,5)B.(5,7)C.(2,10)D.(10,2)解析:选B.依题意,把“整数对”的和相同的分为一组,不难得知第n 组中每个“整数对”的和均为n +1,且第n 组共有n 个“整数对”,这样的前n 组一共有n (n +1)2个“整数对”,注意到10×(10+1)2<60<11×(11+1)2,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为:(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).12.如果△A 1B 1C 1的三个内角的余弦值分别等于△A 2B 2C 2的三个内角的正弦值,则( ) A.△A 1B 1C 1和△A 2B 2C 2都是锐角三角形 B.△A 1B 1C 1和△A 2B 2C 2都是钝角三角形C.△A 1B 1C 1是钝角三角形,△A 2B 2C 2是锐角三角形D.△A 1B 1C 1是锐角三角形,△A 2B 2C 2是钝角三角形解析:选D.因为三角形内角的正弦值是正值,所以△A 1B 1C 1的三个内角的余弦值均大于0.因此△A 1B 1C 1是锐角三角形.假设△A 2B 2C 2也是锐角三角形,并设cos A 1=sin A 2,则cos A 1=cos (90°-∠A 2), 所以∠A 1=90°-∠A 2.同理设cos B 1=sin B 2,cos C 1=sin C 2, 则有∠B 1=90°-∠B 2,∠C 1=90°-∠C 2. 又∠A 1+∠B 1+∠C 1=180°,所以(90°-∠A 2)+(90°-∠B 2)+(90°-∠C 2)=180°, 即∠A 2+∠B 2+∠C 2=90°. 这与三角形内角和等于180°矛盾,所以原假设不成立.若△A 2B 2C 2是直角三角形,不妨设A 2=π2,则sin A 2=1=cos A 1,而A 1在(0,π)内无解.故选D.二、填空题:本题共4小题,每小题5分.13.补充下列证明过程: 要证a 2+b 2+c 2≥ab +bc +ac (a ,b ,c ∈R ),即证,即证W. 因为a ,b ,c 为实数,上式显然成立,故命题结论成立. 答案:2(a 2+b 2+c 2)≥2ab +2bc +2ac (a -b )2+(b -c )2+(a -c )2≥014.已知a =5-12,函数f (x )=a x,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为W.解析:因为当0<a <1时,函数f (x )=a x为减函数,a =5-12∈(0,1),所以函数f (x )=(5-12)x为减函数.故由f (m )>f (n )得m <n .答案:m <n15.有三X 卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一X 卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是W.解析:为方便说明,不妨将分别写有1和2,1和3,2和3的卡片记为A ,B ,C .从丙出发,由于丙的卡片上的数字之和不是5,则丙只可能是卡片A 或B ,无论是哪一X ,均含有数字1,再由乙与丙的卡片上相同的数字不是1可知,乙所拿的卡片必然是C ,最后由甲与乙的卡片上相同的数字不是2,知甲所拿的卡片为B ,此时丙所拿的卡片为A .答案:1和316.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n 行有n 个数且两端的数均为1n (n ≥2),每个数是它下一行左右相邻两数的和,如11=12+12,12=13+16,13=14+112,…,则第7行第4个数(从左往右数)为W. 11 1212 131613 14112112141512013012015…解析:由“第n 行有n 个数且两端的数均为1n ”可知,第7行第1个数为17,由“每个数是它下一行左右相邻两数的和”可知,第7行第2个数为16-17=142.同理易知,第7行第3个数为130-142=1105,第7行第4个数为160-1105=1140.答案:1140三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)定义在[-1,1]上的奇函数f (x ),当a ,b ∈[-1,1],a +b ≠0时,有f (a )+f (b )a +b>0.证明:函数f (x )的图象上不存在两个不同的点A ,B ,使直线AB 恰好与y 轴垂直.证明:假设函数f (x )的图象上存在两个不同的点A ,B ,使直线AB 恰好与y 轴垂直,则A ,B 两点的纵坐标相同.设它们的横坐标分别为x 1和x 2,x 1<x 2,且x 1,x 2∈[-1,1],则f (x 1)=f (x 2). 又f (x )是奇函数,所以f (x 1)-f (x 2)=f (x 1)+f (-x 2)=f (x 1)+f (-x 2)x 1+(-x 2)[x 1+(-x 2)].又由题意,得f (x 1)+f (-x 2)x 1+(-x 2)>0,且x 1+(-x 2)<0,所以f (x 1)+f (-x 2)<0,即f (x 1)-f (x 2)<0, 这与f (x 1)=f (x 2)矛盾,故假设不成立,即函数f (x )的图象上不存在两个不同的点A ,B ,使直线AB 恰好与y 轴垂直. 18.(本小题满分12分)已知:A ,B 都是锐角,且A +B ≠90°,(1+tan A )(1+tan B )=2.求证:A +B =45°.证明:因为(1+tan A )(1+tan B )=2, 展开化简为tan A +tan B =1-tan A tan B . 因为A +B ≠90°,tan (A +B )=tan A +tan B 1-tan A tan B =1.又因为A ,B 都是锐角,所以0°<A +B <180°.所以A +B =45°.19.(本小题满分12分)已知a >0,b >0,2c >a +b ,求证:c -c 2-ab <a <c +c 2-ab . 证明:要证c -c 2-ab <a <c +c 2-ab . 只需证-c 2-ab <a -c <c 2-ab , 即证|a -c |<c 2-ab ,只需证(a -c )2<(c 2-ab )2, 只需证a 2-2ac +c 2<c 2-ab ,即证2ac >a 2+ab ,因为a >0,所以只需证2c >a +b .因为2c >a +b 已知, 所以原不等式成立.20.(本小题满分12分)如图,在直三棱柱ABC A 1B 1C 1中,A 1B 1=A 1C 1,D ,E 分别是棱BC ,CC 1上的点(点D 不同于点C ),且AD ⊥DE ,F为B 1C 1的中点.求证:(1)平面ADE ⊥平面BCC 1B 1; (2)直线A 1F ∥平面ADE .证明:(1)因为ABC A 1B 1C 1是直三棱柱, 所以CC 1⊥平面ABC .因为AD ⊂平面ABC ,所以CC 1⊥AD .因为AD ⊥DE ,CC 1,DE ⊂平面BCC 1B 1,CC 1∩DE =E , 所以AD ⊥平面BCC 1B 1. 因为AD ⊂平面ADE , 所以平面ADE ⊥平面BCC 1B 1.(2)因为A 1B 1=A 1C 1,F 为B 1C 1的中点, 所以A 1F ⊥B 1C 1,因为CC 1⊥平面A 1B 1C 1,且A 1F ⊂平面A 1B 1C 1, 所以CC 1⊥A 1F .因为CC 1,B 1C 1⊂平面BCC 1B 1,CC 1∩B 1C 1=C 1, 所以A 1F ⊥平面BCC 1B 1. 由(1)知AD ⊥平面BCC 1B 1, 所以A 1F ∥AD .因为AD ⊂平面ADE ,A 1F ⊄平面ADE , 所以A 1F ∥平面ADE .21.(本小题满分12分)设函数f (x )=x 3+11+x ,x ∈[0,1].证明:(1)f (x )≥1-x +x 2;(2)34<f (x )≤32.证明:(1)因为1-x +x 2-x 3=1-(-x )41-(-x )=1-x 41+x,由于x ∈[0,1],有1-x 41+x ≤1x +1,即1-x +x 2-x 3≤1x +1,所以f (x )≥1-x +x 2.(2)由0≤x ≤1得x 3≤x ,故f (x )=x 3+1x +1≤x +1x +1=x +1x +1-32+32=(x -1)(2x +1)2(x +1)+32≤32,所以f (x )≤32.由第一问得f (x )≥1-x +x 2=⎝ ⎛⎭⎪⎫x -122+34≥34,又因为f (12)=1924>34,所以f (x )>34.综上,34<f (x )≤32.22.(本小题满分12分)在各项为正的数列{a n }中,数列的前n 项和S n 满足S n =12⎝ ⎛⎭⎪⎫a n +1a n .(1)求a 1,a 2,a 3;(2)由(1)猜想数列{a n }的通项公式,并用数学归纳法证明你的猜想. 解:(1)易求得a 1=1,a 2=2-1,a 3=3- 2. (2)猜想a n =n -n -1(n ∈N *)证明:①当n =1时,a 1=1-0=1,命题成立. ②假设n =k (k ≥1,k ∈N *)时,a k =k -k -1成立, 则n =k +1时,a k +1=S k +1-S k =12⎝⎛⎭⎪⎫a k +1+1a k +1-12⎝⎛⎭⎪⎫a k +1ak=12⎝ ⎛⎭⎪⎫a k +1+1a k +1-12⎝ ⎛⎭⎪⎫k -k -1+1k -k -1 =12⎝ ⎛⎭⎪⎫a k +1+1a k +1-k ,所以,a 2k +1+2ka k +1-1=0,所以a k +1=k +1-k .即n =k +1时,命题成立. 由①②知,n ∈N *时,a n =n -n -1.。
2-2第二章归纳推理 (1)

5
,
.(用n表示)
f (3) f (2) 2 f (4) f (3) 3 f (5) f (4) 4
f (n) f (n 1) n 1 累加得: f (n) f (2) 2 3 4 ( n 1)
例6:数一数图中的凸多面体的面数F、顶
哥德巴赫猜想 (Goldbach Conjecture)
目前最佳的结果是中国数学家陈景润于 1966年证明的,称为陈氏定理 .“任何充分大 的偶数都是一个质数与一个自然数之和,而後 者仅仅是两个质数的乘积。” 通常都简称这 个结果为大偶数可表示为 “1 + 2 ”的形式.
例题解析:
例1 蛇是用肺呼吸的, 鳄鱼是用肺呼吸的, 海龟也是用肺呼吸的, 蜥蜴是用肺呼吸的, 蛇、鳄鱼、海龟、蜥蜴都是爬行动物. 所以,所有的爬行动物都是用肺呼吸的.
(1810 ) (310 ) 6 10 (年)( 6000 亿年)
18 7 11
例5(2005年广东)设平面内有n条直线(n≥3),其中有 且仅有两条直线互相平行,任意三条直线不过同一 点.若用f(n)表示这n条直线交点的个数,f(4)=
1 ( n 2)( n 1) 当n>4时,f(n)= 2 f(n)=f(n-1)+n-1
n=1时, n=2时, n=3时,
2
1
3
f (1) 1 f (2) 3 f (3) 7 f (2) 1 f (2) n=4时, f (4) 15 f (3) 1 f (3) n1 1, 归纳: f ( n) 2 f (n 1) 1, n 2
n 1 n
例3 在印度北部的佛教圣地贝拿勒斯的圣庙里有三根木桩,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学选修2-2第二章推理与证明1、 下列表述正确的是( ).①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理. A .①②③; B .②③④; C .②④⑤; D .①③⑤.2、下面使用类比推理正确的是 ( ). A.“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =” B.“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅”C.“若()a b c ac bc +=+” 类推出“a b a bc c c+=+ (c ≠0)” D.“n n a a b =n (b )” 类推出“n n a a b +=+n(b )”3、 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线b ⊆/平面α,直线a ≠⊂平面α,直线b ∥平面α,则直线b ∥直线a ”的结论显然是错误的,这是因为 ( )A.大前提错误B.小前提错误C.推理形式错误D.非以上错误4、用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )。
(A)假设三内角都不大于60度; (B) 假设三内角都大于60度;(C) 假设三内角至多有一个大于60度; (D) 假设三内角至多有两个大于60度。
5、在十进制中01232004410010010210=⨯+⨯+⨯+⨯,那么在5进制中数码2004折合成十进制为 ( ) A.29 B. 254 C. 602 D. 20046、利用数学归纳法证明“1+a +a 2+…+a n +1=aan --+112, (a ≠1,n ∈N)”时,在验证n=1成立时,左边应该是 ( )(A)1 (B)1+a (C)1+a +a 2 (D)1+a +a 2+a 37、某个命题与正整数n 有关,如果当)(+∈=N k k n 时命题成立,那么可推得当1+=k n 时命题也成立. 现已知当7=n 时该命题不成立,那么可推得 ( )A .当n=6时该命题不成立B .当n=6时该命题成立C .当n=8时该命题不成立D .当n=8时该命题成立8、用数学归纳法证明“)12(212)()2)(1(-⋅⋅⋅⋅=+++n n n n n nΛΛ”(+∈N n )时,从 “1+==k n k n 到”时,左边应增添的式子是 ( )A .12+kB .)12(2+kC .112++k k D .122++k k 9、已知n 为正偶数,用数学归纳法证明 )214121(2114131211nn n n +++++=-++-+-ΛΛ时,若已假设2(≥=k k n 为偶 数)时命题为真,则还需要用归纳假设再证( )A .1+=k n 时等式成立B .2+=k n 时等式成立C .22+=k n 时等式成立D .)2(2+=k n 时等式成立10、数列{}n a 中,a 1=1,S n 表示前n 项和,且S n ,S n+1,2S 1成等差数列,通过计算S 1,S 2,S 3,猜想当n ≥1时,S n = ( )A .1212-+n nB .1212--n nC .nn n 2)1(+ D .1-121-n11、一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 。
12、从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,推广到第n 个等式为_________________________.13、设平面内有n条直线(3)n ≥,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用()f n 表示这n条直线交点的个数,则(4)f = ; 当n>4时,()f n = (用含n 的数学表达式表示)。
14、求证:(1)223)a b ab a b ++≥+; (2) 6+7>22+5。
15、设a ,b ,x ,y ∈R ,且错误!未找到引用源。
16、若a,b,c均为实数,且错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,求证:a,b,c中至少有一个大于0。
17、数学归纳法证明:错误!未找到引用源。
能被错误!未找到引用源。
整除,错误!未找到引用源。
.18、观察以下各等式:①110tan 60tan 60tan 20tan 20tan 10tan 0=⋅+⋅+⋅②15tan 75tan 75tan 10tan 10tan 5tan 0=⋅+⋅+⋅分析上述各式的共同特点,写出能反映一般规律的等式,并对你的结论进行证明。
19、 已知数列{}n a 的前n 项和为n S ,且)(,121N n a n S a n n ∈==,(1)试计算4321,,,S S S S ,并猜想n S 的表达式; (2) 证明你的猜想,并求出n a 的表达式。
17、用数学归纳法证明:(Ⅰ))12(2)1()12)(12(532311222++=+-++⋅+⋅n n n n n n Λ;20、已知数列{a n}满足S n+a n=2n+1, (1) 写出a1, a2, a3,并推测a n的表达式;(2) 用数学归纳法证明所得的结论。
(12分)第四十一中学高二数学选修2-2《推理与证明测试题》答案一、选择题:本大题共10小题,每小题3分,共30分.DCABB CABBB二、填空题:本大题共4小题,每小题3分,共12分.11、1412、错误!未找到引用源。
13、错误!未找到引用源。
14、 5 ;错误!未找到引用源。
三、解答题:本大题共6题,共58分。
15、证明:(1)∵222+≥,a b ab23a+≥,23b+≥;将此三式相加得222++≥++,a b ab(3)2∴223)++≥+.a b ab a b(2)要证原不等式成立,只需证(6+7)2>(22+5)2,∵上式显然成立, ∴原不等式成立.16、可以用综合法与分析法---略17、可以用反证法---略18、(1)可以用数学归纳法---略 (2)当1+=k n 时,左边+≤-+++-+++=+k k k k )12121()121211(1ΛΛ (k k k 212121+++Λ)1212+=⋅+=k k k k =右边,命题正确19、可以用数学归纳法---略2k 项20、解:(1) a 1=23, a 2=47, a 3=815, 猜测 a n =2-n 21(2) ①由(1)已得当n =1时,命题成立;②假设n =k 时,命题成立,即 a k =2-k 21,当n =k +1时, a 1+a 2+……+a k +a k +1+a k +1=2(k +1)+1,且a 1+a 2+……+a k =2k +1-a k∴2k +1-a k +2a k +1=2(k +1)+1=2k +3,∴2a k +1=2+2-k 21, a k +1=2-121 k ,即当n =k +1时,命题成立.根据①②得n ∈N + , a n =2-n 21都成立例2.设在R 上定义的函数)(x f ,对任意实数x 都有5lg 3lg )2(,2lg 3lg )1(),()1()2(+=-=-+=+f f x f x f x f 且,试求归纳出)2001(f 的值。
练习:1.从222576543,3432,11=++++=++=中, 得出一般性结论是2)12()23()1(-=-+⋅⋅⋅+++n n n n 2. 已知函数21)(xx x f +=,则[]{}4434421fn x f f f 个)(....=21nxx +3.)(131211)(+∈+⋅⋅⋅+++=N n nn f ,经计算的27)32(,3)16(,25)8(,2)4(,23)2(>>>>=f f f f f ,推测当2≥n 时,有____________________.(22)2(+>n f n) 4.已知:23150sin 90sin 30sin 222=++οοο, 23125sin 65sin 5sin 222=++οοο 通过观察上述两等式的规律,请你写出一般性的命题:23)120(sin )60(sin sin 222=++++οοααα 5.考察下列一组不等式:,5252522233⋅+⋅>+,5252523344⋅+⋅>+ ,5252523344⋅+⋅>+ ΛΛ,525252322355⋅+⋅>+.将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是()0,,,0,>≠>+>+++n m b a b a b a b a b a m n n m n m nm6.观察下列不等式:121⋅≥2111⋅,⎪⎭⎫ ⎝⎛+⋅31131≥⎪⎭⎫ ⎝⎛+⋅412121 ,⎪⎭⎫ ⎝⎛++⋅5131141≥⎪⎭⎫ ⎝⎛++⋅61412131,...,由此猜测第n 个不等式为 .(*n ∈N ) ++++51311(11n ...)121-+n ≥+++614121(1n (21)+ 7.在ABC Rt ∆中,若,,,900a BCb AC C ===∠则三角形ABC 的外接圆半径222b a r +=,把此结论类比到空间,写出类似的结论 。
(取空间三条侧棱互相垂直的四面体,三条侧棱长分别为c b a ,,,则此三棱锥外接球的半径是2222c b a r ++=。
)8.已知命题:平面上一矩形ABCD 的对角线AC 与边AB 和AD 所成角分别为βα、,则1cos cos 22=+βα。
若把它推广到空间长方体中,试写出相应的命题形式:_____________(长方体1111D C B A ABCD -中,对角线C A 1与棱11111D A B A A A 、、所成的角分别为γβα、、,则1cos cos cos 222=++γβα,2sin sin sin 222=++γβα。
或是:长方体1111D C B A ABCD -中,对角线C A 1与平面D A C A B A 1111、、所成的角分别为γβα、、,则2cos cos cos 222=++γβα,1sin sin sin 222=++γβα。
或是:长方体C A 1中,对角面11ACC A 与平面1111ADD A ABB A 、所成的二面角分别为βα、,则1cos cos 22=+βα。
) 9.若AB 是过二次曲线中心的任一条弦,M 是二次曲线上异于A 、B 的任一点,且AM 、BM均与坐标轴不平行,则对于椭圆12222=+b y a x 有22ab K K BM AM -=⋅。
