数值分析第五版计算实习题复习进程
数值分析计算实习题二

《数值分析》计算实习题二算法设计方案1.主要计算步骤:计算函数f(x,y)在拟合所需的节点处的函数值。
将各拟合节点(x i,y j)分别带入非线性方程组0.5 cos t + u + v + w – x = 2.67t + 0.5 sin u + v + w – y = 1.070.5t + u + cos v + w – x =3.74t + 0.5u + v + sin w – y =0.79解非线性方程组得解向量(t ij,u ij,v ij,w ij)。
对数表z(t,u)进行分片二次代数插值,求得对应(t ij,u ij)处的值,即为f(x i,y j) 的值。
对上述拟合节点分别进行x,y最高次数为k(k=0,1,2,3…)次的多项式拟合。
每次拟合后验证误差大小,直到满足要求。
2.求解非线性方程组选择Newton迭代法,迭代过程中需要求解线性方程组,选择选主元的Doolittle分解法。
3.对z(t,u)进行插值选择分片二次插值。
4.拟合基函数φr(x)ψs(y)选择为φr(x)=x r,ψs(y)=y s。
拟合系数矩阵c通过连续两次解线性方程组求得。
一.源程序#include "stdio.h"#include "stdlib.h"#include "math.h"void Doolittle(double *A,int n,int *M)//功能说明:对n阶矩阵A进行选主元的Doolittle分解//参数说明:A:欲进行分解的方阵,同时也是返回参数,分解后的结果// 存储于A中// n:方阵A的维数// M;(返回参数)n维向量,记录选主元过程中行交换的次序{int i,j,k,t;double *s;double Maxs,temp;s=(double*) calloc(n,sizeof(double));for(k=0;k<n;k++){for(i=k;i<n;i++){s[i]=A[i*n+k];for(t=0;t<k;t++) s[i]-= A[i*n+t] * A[t*n+k];}Maxs=abs(s[k]); M[k]=k;for(i=k+1;i<n;i++){if(Maxs<abs(s[i])){Maxs=abs(s[i]);M[k]=i;}}if(M[k]!=k){for(t=0;t<n;t++){temp=A[k*n+t];A[k*n+t]=A[M[k]*n+t];A[M[k]*n+t]=temp;}temp=s[k];s[k]=s[M[k]];s[M[k]]=temp;}if(Maxs<(1e-14)){s[k]=1e-14;printf("%.16e方阵奇异\n",Maxs);}A[k*n+k]=s[k];for(j=k+1;(j<n)&&(k<n-1);j++){for(t=0;t<k;t++) A[k*n+j]-=A[k*n+t]*A[t*n+j];A[j*n+k]=s[j]/A[k*n+k];}}}void Solve_LUEquation(double* A,int n,double* b,double* x) //功能说明:解方程LUx=b,其中L、U共同存储在A中//参数说明:A:经Doolittle分解后的方阵// n:方阵A的维数// b:方程组的右端向量// x:(返回参数)方程组的解向量{int i,t;for(i=0;i<n;i++){x[i]=b[i];for(t=0;t<i;t++) x[i]-=A[i*n+t]*x[t];}for(i=n-1;i>-1;i--){for(t=i+1;t<n;t++) x[i]-=A[i*n+t]*x[t];x[i]/=A[i*n+i];}}void Transpose(double *A,int m,int n,double* AT)//功能说明:求m×n阶矩阵A的转置AT//参数说明:A:已知m×n阶矩阵// m:A的行数// n:A的列数// AT:(返回参数)A的转置矩阵(n×m){int i,j;for(i=0;i<m;i++)for(j=0;j<n;j++) AT[j*m+i]=A[i*n+j];}void Solve_LEquation(double* A,int n,double* B,double* x,int m) //功能说明:解线性方程组Ax=B,该函数可对系数矩阵相同// 而右端向量不同的多个方程组同时求解。
数值分析计算实习题

数值分析计算实习题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN《数值分析》计算实习题姓名:学号:班级:第二章1、程序代码Clear;clc;x1=[ ];y1=[ ];n=length(y1);c=y1(:);for j=2:n %求差商for i=n:-1:jc(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1));endendsyms x df d;df(1)=1;d(1)=y1(1);for i=2:n %求牛顿差值多项式df(i)=df(i-1)*(x-x1(i-1));d(i)=c(i-1)*df(i);endP4=vpa(sum(d),5) %P4即为4次牛顿插值多项式,并保留小数点后5位数pp=csape(x1,y1, 'variational');%调用三次样条函数q=;q1=q(1,:)*[^3;^2;;1];q1=vpa(collect(q1),5)q2=q(1,:)*[^3;^2;;1];q2=vpa(collect(q2),5)q3=q(1,:)*[^3;^2;;1];q3=vpa(collect(q3),5)q4=q(1,:)*[^3;^2;;1];q4=vpa(collect(q4),5)%求解并化简多项式2、运行结果P4 =*x - *(x - *(x - - *(x - *(x - *(x - - *(x - *(x - *(x - *(x - + q1 =- *x^3 + *x^2 - *x +q2 =- *x^3 + *x^2 - *x + q3 =- *x^3 + *x^2 - *x + q4 =- *x^3 + *x^2 - *x +3、问题结果4次牛顿差值多项式4()P x = *x - *(x - *(x - - *(x - *(x - *(x - - *(x - *(x - *(x - *(x - +三次样条差值多项式()Q x0.10.20.30.40.50.60.70.80.910.40.50.60.70.80.911.1323232321.33930.803570.40714 1.04,[0.2,0.4]1.3393 1.60710.88929 1.1643,[0.4,0.6]1.3393 2.4107 1.6929 1.4171,[0.6,0.8]1.3393 3.21432.8179 1.8629,[0.8,1.0]x x x x x x x x x x x x x x x x ⎧-+-+∈⎪-+-+∈⎪⎨-+-+∈⎪⎪-+-+∈⎩第三章1、程序代码Clear;clc; x=[0 1]; y=[1 ];p1=polyfit(x,y,3)%三次多项式拟合 p2=polyfit(x,y,4)%四次多项式拟合 y1=polyval(p1,x);y2=polyval(p2,x);%多项式求值plot(x,y,'c--',x,y1,'r:',x,y2,'y-.')p3=polyfit(x,y,2)%观察图像,类似抛物线,故用二次多项式拟合。
数值分析第五版第5章学习资料

n
即 de(A t) aijAij (i1,2,,n), j1
其中 A ij 为 a ij 的代数余子式,Aij(1)ijMij, M ij 为元素 a ij 的余子式.
行列式性质:
( ad ) ( A e ) d t B ( A e )d ( t B )A e , ,B t R n n .
有非零解,故系数行列式 deIt (A)0,记
a11 a12 p()det(I A) a21 a22
a1n a2n
(1.3)
an1 an2 ann n c1n1cn1cn 0.
p()称为矩阵 A的特征多项式,方程(1.3)称为矩阵 A的特
征方程.
9
因为 n次代数方程 p() 在复数域中有 n个根
其中用 ri 表示矩阵的第 i行. 由此看出,用消去法解方程组的基本思想是用逐次消
去未知数的方法把原方程组 Axb化为与其等价的三角 形方程组,而求解三角形方程组可用回代的方法.
上述过程就是用行的初等变换将原方程组系数矩阵化 为简单形式(上三角矩阵),从而将求解原方程组(2.1)的 问题转化为求解简单方程组的问题.
n
n
trA aii i.
i1
i1
(1.4) (1.5)
称 trA为 A的迹.
A的特征值 和特征向量 x还有一下性质:
(1) AT 与 A有相同的特征值 及特征向量 .
(2)若 A非奇异,则 A1 的特征值为 1,特征向量为 x.
(3)相似矩阵 BS1AS有相同的特征多项式.
11
例1 求 A的特征值及谱半径
4x2x3 5,
2x3 6.
显然,方程组(2.6)是容易求解的,解为
x (1,2,3)T.
数值分析(第五版)计算实习题第五章作业教学资料

>> format compact
>> A=[3.01 6.03 1.99;1.27 4.16 -1.23;0.987 -4.81 9.34];
>> b=[1;1;1];
>> [RA,RB,n,X]=liezhu(A,b),h=det(A),C=cond(A)
输出:
请注意:因为RA=RB,所以方程组有唯一解
ans =
-9.5863 18.3741 -3.2258 3.5240
xX =
10.4661
jxX =
0.9842
Xgxx =
22.7396
xAb =
0.0076
xAbj =
0.0076
Acp =
2.9841e+03
第四题:
(1)输入:
建立m文件:
forn=2:6
a=hilb(n);
pnH(n-1)=cond(a,inf);
RA =
3
RB =
3
n =
3
X =
1.0e+03 *
1.5926
-0.6319
-0.4936
h =
-0.0305
C =
3.0697e+04
(2)输入:
>> A=[3.00 6.03 1.99;1.27 4.16 -1.23;0.990 -4.81 9.34];
>> b=[1;1;1];
>> [RA,RB,n,X]=liezhu(A,b),h=det(A)
>> r=b-H*X,deltax=X-x
输出:
X =
数值分析-复习及习题选讲

5、线性方程组的数值解法
1.了解Gauss消元法的基本思想,知道适用范围 顺序Gauss消元法:矩阵A的各阶顺序主子式都不为零. 主元Gauss消元法:矩阵A的行列式不为零. 2.掌握矩阵的直接三角分解法。
会对矩阵进行Doolittle分解(LU)、Crout分解及Cholesky分解。
熟练掌握用三角分解法求方程组的解。 了解平方根法和追赶法的思想。 3.了解向量和矩阵的范数的定义,会判定范数(三要素非负性、齐 次性、三角不等式);会计算几个常用的向量和矩阵的范数; 了解范数的等价性和向量矩阵极限的概念。 4.了解方程组的性态,会计算简单矩阵的条件数。
k n
f
( n 1)
(2)记(t)=(t-x)k,则yj=(xj)=(xj-x)k, j=0,1,…,n.于是
n ( t ) k (t x) k f (t ) y j l j (t ) n 1 (t ) ( x j x) l j (t ) j 0 j 0 (n 1)! 取t=x,则有 n ( x j x) k l j ( x) 0
收敛于(x)在I上的唯一不动点x*.
都收敛于方程的唯一根x*.
推论 若(x)在x*附近具有一阶连续导数,且|(x*)|<1, 则对充分接近 x*的初值x0,迭代法xk+1=(xk)收敛. 3. 了解迭代法收敛阶的概念,会求迭代法收敛的阶.了解Aitken加速 技巧.
xk 1 C (1) xkp阶收敛于x*是指: lim k x p k
7.设(x)=x4+2x3+5, 在区间[-3,2]上, 对节点x0= -3, x1=-1,求出(x)的
三次Hermite插值多项式在区间[x0,x1]上的表达式及误差公式.
数值分析第五版计算实习题

弟二草插值法3.卜列数据点的插值可以得到平方根函数的近似,在区间064]上作图。
(1〉用这9个点做8次多项式插值Q x)。
(2)用三次样条(第一边界条件)程岸求S(X)。
从得到结果石在[0.64] 1:・哪个插值更粘确:在区间[0,1] I:•两种插值哪个更精确?(1) 8次多项式插值:(1)8次多项式插值:首先建立新的M-file:输入如卜代码(此为拉格朗口插值的功能函数)并保存function f=Language(x,y,x0)%求Li知数据点的拉格朗Fl插值多项式%己知数据点的x坐标向量:x%已知数据点的y坐标向量:y%插值的x坐标:x0%求得的拉格朗H插值多项式或在X0处的插值:fsyms t;ifi(lcngth(x)=length(y))n=length(x);elsedisp(*x和y的维数不相等!);return;end %检错tbr(i=l:n)i=y(i);fbr(j=1:i-l)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i-M:n)end;for(j=i+l:n) l=l*(t-x(j))/(x(i)-x(j)); end;simplify(f);if(i==n) if|nargin=3)f=subs(C't\xO);else f=collcct(f);f=vpa(f,6);endendend再建立新的M-file:输入:clear;x=[0 1 49 16 25 36 49 64];y=[0:l:8];%计算拉格朗口基丞数%计算拉格朗ri插值函数%化简%计算插值点的曲数值%将插值多项式展开%将插值多项式的系数化成6位精度的小数f=Uinguage(x,y) 运行得到f=1.32574*1-381410*t A2+.604294e-1 *t A3+.222972e-3 *t A5-.542921 e-5*t A6+.671268e・7T7・.328063e・9T8・.498071 e-2*t A4 这就是8次多项式插值L s(x)= 1.32574怜.381410*t A2+.604294e-1 *t A3+.222972e-3 *t A5-.542921 e-5*t A6+.671268e-7*t A7-.328063e-9*t A8-.498071 e-2*t A4. (2)三次样条插值:建立新的M-filc:输入:clear;x=[0 I 49 1625 36 4964];尸[0:8];t=[0:0.1:64];Y=t.A(0.5);O=Language(x,y)f= 1,32574*t-.381410*t.A2+.604294e-1 *t.A3+.222972e-3*t.A5-.542921 e・5*(. W+.671268e-7*t.A7-.328063e-9*t.A8-.498071 e-2 *t.A4;S=interp l(x,y,t.'spline,);plol(x,y,o;(・YY.lf.'b'」S'g:');grid;运行程序得到如下图:从结果屮很明显可以看出在[0.64].上.三次样条插值更精确,儿乎与原函数帀合。
数值分析第五版计算实习题

数值分析计算实习题第二章2-1程序:clear;clc;x1=[0.2 0.4 0.6 0.8 1.0];y1=[0.98 0.92 0.81 0.64 0.38];n=length(y1);c=y1(:);for j=2:n %求差商for i=n:-1:jc(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1));endendsyms x df d;df(1)=1;d(1)=y1(1);for i=2:n %求牛顿差值多项式df(i)=df(i-1)*(x-x1(i-1));d(i)=c(i)*df(i);enddisp('4次牛顿插值多项式');P4=vpa(collect((sum(d))),5) %P4即为4次牛顿插值多项式,并保留小数点后5位数pp=csape(x1,y1, 'variational');%调用三次样条函数q=pp.coefs;disp('三次样条函数');for i=1:4S=q(i,:)*[(x-x1(i))^3;(x-x1(i))^2;(x-x1(i));1];S=vpa(collect(S),5)endx2=0.2:0.08:1.08;dot=[1 2 11 12];figureezplot(P4,[0.2,1.08]);hold ony2=fnval(pp,x2);x=x2(dot);y3=eval(P4);y4=fnval(pp,x2(dot));plot(x2,y2,'r',x2(dot),y3,'b*',x2(dot),y4,'co');title('4次牛顿插值及三次样条');结果如下:4次牛顿插值多项式P4 = - 0.52083*x^4 + 0.83333*x^3 - 1.1042*x^2 + 0.19167*x + 0.98三次样条函数x∈[0.2,0.4]时, S = - 1.3393*x^3 + 0.80357*x^2 - 0.40714*x + 1.04 x∈[0.4,0.6]时,S = 0.44643*x^3 - 1.3393*x^2 + 0.45*x + 0.92571x∈[0.6,0.8]时,S = - 1.6964*x^3 + 2.5179*x^2 - 1.8643*x + 1.3886 x∈[0.8,1.0]时,S =2.5893*x^3 - 7.7679*x^2 + 6.3643*x - 0.80571输出图如下2-3(1)程序:clear;clc;x1=[0 1 4 9 16 25 36 49 64];y1=[0 1 2 3 4 5 6 7 8];%插值点n=length(y1);a=ones(n,2);a(:,2)=-x1';c=1;for i=1:nc=conv(c,a(i,:));endq=zeros(n,n);r=zeros(n,n+1);for i=1:n[q(i,:),r(i,:)]=deconv(c,a(i,:));%wn+1/(x-xk) end 三次样条插值曲线4次牛顿插值曲线Dw=zeros(1,n);for i=1:nDw(i)=y1(i)/polyval(q(i,:),x1(i));%系数endp=Dw*q;syms x L8;for i=1:nL8(i)=p(n-i+1)*x^(i-1);enddisp('8次拉格朗日插值');L8=vpa(collect((sum(L8))),5)xi=0:64;yi=polyval(p,xi);figureplot(xi,yi,x1,y1,'r*');hold ontitle('8次拉格朗日插值');结果如下:8次拉格朗日插值L8 =- 3.2806e-10*x^8 + 6.7127e-8*x^7 - 5.4292e-6*x^6 + 0.00022297*x^5 - 0.0049807*x^4 + 0.060429*x^3 - 0.38141*x^2 + 1.3257*x输出图如下:第五章4-1(3)程序:clc;clear;y= (x)sqrt(x).*log(x);a=0;b=1;tol=1e-4;p=quad(y,a,b,tol);fprintf('采用自适应辛普森积分结果为: %d \n', p); 结果如下:采用自适应辛普森积分结果为: -4.439756e-01第九章9-1(a)程序:clc;clear;a=1;b=2;%定义域h=0.05;%步长n=(b-a)/h;y0=1;%初值f= (x,y) 1/x^2-y/x;%微分函数Xn=linspace(a,b,n+1);%将定义域分为n等份Yn=zeros(1,n);%结果矩阵Yn(1)=y0;%赋初值%以下根据改进欧拉公式求解for i=1:nxn=Xn(i);xnn=Xn(i+1);yn=Yn(i);yp=yn+h*f(xn,yn);yc=yn+h*f(xnn,yp);yn=(yp+yc)/2;Yn(i+1)=yn;endXn=Yn;%以下根据经典四阶R-K法公式求解for i=1:nxn=Xn(i);yn=Yn(i);k1=f(xn,yn);k2=f(xn+h/2,yn+h/2*k1);k3=f(xn+h/2,yn+h/2*k2);k4=f(xn+h,yn+h*k3);yn=yn+h/6*(k1+2*k2+2*k3+k4);Yn(i+1)=yn;enddisp(' 改进欧拉法四阶经典R-K法'); disp([Xn' Yn'])结果如下:改进欧拉法四阶经典R-K法1 10.99887 0.998850.99577 0.99780.99114 0.996940.98532 0.996340.97857 0.996030.97111 0.996060.96311 0.996450.9547 0.997230.94598 0.998410.93705 10.92798 1.0020.91883 1.00440.90964 1.00730.90045 1.01060.89129 1.01430.88218 1.01840.87315 1.02290.86421 1.02780.85538 1.03310.84665 1.0388(b)程序:clc;clear;a=0;b=1;%定义域H=[0.1 0.025 0.01];%步长y0=1/3;%初值f= (x,y) -50*y+50*x^2+2*x;%微分函数xi=linspace(a,b,11);Y=1/3*exp(-50*xi)+xi.^2;%准确解Ym=zeros(1,11);for j=1:3h=H(j);n=(b-a)/h;Xn=linspace(a,b,n+1);%将定义域分为n等份Yn=zeros(1,n);%结果矩阵Yn(1)=y0;%赋初值for i=1:nxn=Xn(i);yn=Yn(i);k1=f(xn,yn);k2=f(xn+h/2,yn+h/2*k1);k3=f(xn+h/2,yn+h/2*k2);k4=f(xn+h,yn+h*k3);yn=yn+h/6*(k1+2*k2+2*k3+k4);Yn(i+1)=yn;endfor k=1:11m=0.1/h;Ym(k)=Yn(1+(k-1)*m);enddelta=Ym-Y;fprintf('步长为: %d \n', h);disp(' 四阶经典R-K法准确解误差'); disp([Ym' Y' delta'])end结果如下:步长为: 1.000000e-01四阶经典R-K法准确解误差0.33333 0.33333 04.6055 0.012246 4.593263.062 0.040015 63.022864.05 0.09 863.9611844 0.16 118431.6235e+05 0.25 1.6235e+052.2256e+06 0.36 2.2256e+063.0509e+07 0.49 3.0509e+074.1823e+08 0.64 4.1823e+085.7333e+09 0.81 5.7333e+097.8594e+10 1 7.8594e+10步长为: 2.500000e-02四阶经典R-K法准确解误差0.33333 0.33333 00.013015 0.012246 0.000768940.040063 0.040015 4.82e-050.090037 0.09 3.6857e-050.16004 0.16 3.6723e-050.25004 0.25 3.6722e-050.36004 0.36 3.6722e-050.49004 0.49 3.6722e-050.64004 0.64 3.6722e-050.81004 0.81 3.6722e-051 1 3.6722e-05步长为: 1.000000e-02四阶经典R-K法准确解误差0.33333 0.33333 00.012256 0.012246 9.5673e-060.040016 0.040015 7.8252e-070.090001 0.09 6.6347e-070.16 0.16 6.6226e-070.25 0.25 6.6225e-070.36 0.36 6.6225e-070.49 0.49 6.6225e-070.64 0.64 6.6225e-070.81 0.81 6.6225e-071 1 6.6225e-07由结果可知,步长越小,结果越精确。
李庆扬-数值分析第五版第5章和第7章习题答案解析复习课程

李庆扬-数值分析第五版第 5 章和第7 章习题答案解析第5章复习与思考题习题Ta iicii 1、设A 是对称阵且a n 0,经过高斯消去法一步后,A 约化为,证明A 2是对A 2称矩阵。
证明:所以A2为对称矩阵。
A (a j ))n i ;证明:(I )A 的对角元素—a H °(i I2|||,n) ; (2)A 2是对称正定矩阵;即A 是对称矩阵。
3、设L k 为指标为k 的初等下三角矩阵(除第~~k 列对角元以下元素外, L k 和单位阵I 相 同),即a ii °I2. 1.. a in设对称矩阵ai2A i2a22. …% 2aina2 n. 1.. a nn a iiai2.. .ai2a22 —a i 2 ..an2A ⑴ aiiaiia22annaiia inan2a ^aina ii所以a Ta n2 —a i2..a ii[ai2...a n2]a nn — amaiiai23|ian2耳2 aiiai nannai n aiiOl n2、设A 是对称正定矩阵,经过高斯消去法一步后,A 约化为A (a j ) n ,其中A (O j )n ,(i )依次取 X i (0,0, ,0,i,0,所以有a iiX T A X0。
,0)T , i i,2,,n ,则因为A 是对称正定矩阵, (2) A 2中的元素满足a (2)aja i冋(i,jaii2,3, ,n),又因为A 是对称正定矩阵,满足a j a ji , i, ji,2,,n ,所以 a (2)aja ii ai jaiiajia iiaji(2)----- aji ■)a,则经过1次高斯校区法后,有0 a 2n亚 %a l1a i nai111m k i,k 1m^k 1求证当i,j k时,L k I ij L k I ij也是一个指标为k的初等下三角矩阵,其中I j为初等置换矩阵。
4、试推导矩阵A的Crout分解A=LU的计算公式,其中L为下三角矩阵,U为单位上三角矩阵。
数值分析习题汇总复习过程

数值分析习题汇总第一章 引论(习题)2.证明:x 的相对误差约等于x 的相对误差的1/2.证明 记 x x f =)( ,则)()(***x x x x x xx x f E r +-=-=)(21**x E x x x x x xr ≈-⋅+=. □3.设实数a 的t 位β进制浮点机器数表示为)(a fl . 试证明 tb a b a fl -≤+*=*121||),1/()()(βδδ, 其中的记号*表示+、-、⨯、/ 中一种运算. 证明: 令: )()()(b a fl b a fl b a **-*=δ可估计: 1|)(|-≥*c b a fl β (c 为b a *阶码), 故:121||--≤c t c ββδt -=121β 于是: )1()()(δ+*=*b a b a fl . □4.改变下列表达式使计算结果比较精确: (1) ;1||,11211<<+--+x xxx 对(2);1,11>>--+x xx xx 对(3)1||,0,cos 1<<≠-x x xx对.解 (1) )21()1(22x x x ++. (2) )11(2x x x x x-++.(3) xxx x x x x cos 1sin )cos 1(sin cos 12+≈+=-. □6.设937.0=a 关于精确数x 有3位有效数字,估计a 的相对误差. 对于x x f -=1)(,估计)(a f 对于)(x f 的误差和相对误差.解 a 的相对误差:由于 31021|)(|-⋅≤-=a x x E . xa x x E r -=)(, 221018110921)(--⋅=⨯≤x E r . (1Th ) )(a f 对于)(x f 的误差和相对误差. |11||)(|a x f E ---==()25.021011321⨯⋅≤-+---ax x a =310-33104110|)(|--⨯=-≤a f E r . □9.序列}{n y 满足递推关系:1101.100-+-=n n n y y y . 取01.0,110==y y 及01.0,101150=+=-y y ,试分别计算5y ,从而说明该递推公式对于计算是不稳定的.解 递推关系: 1101.100-+-=n n n y y y (1) 取初值 10=y , 01.01=y 计算可得: 11001.10022-⨯=-y 10001.1-=410-= 6310-=y , 8410-=y , 10510-=y , …(2) 取初值 50101-+=y , 2110-=y ,记: n n n y y -=ε,序列 {}n ε ,满足递推关系,且 5010--=ε , 01=ε1101.100-+-=n n n εεε, 于是: 5210-=ε,531001.100-⨯=ε, 55241010)01.100(---⨯=ε,55351002.20010)01.100(--⨯-⨯=ε,可见随着 n ε 的主项 5210)01.100(--⨯n 的增长,说明该递推关系式是不稳定的.第二章 多项式插值 (习 题)1. 利用Lagrange 插值公式求下列各离散函数的插值多项式(结果要简化):(1(2解(2):方法一. 由 Lagrange 插值公式)30)(20)(10()3)(2)(1()(0x x x x x x x x x x x x x l ------=,)()()()()(332211003x l f x l f x l f x l f x L ⋅+⋅+⋅+⋅=)1)((31)2)()(1()1)(()(2123210---=-----=x x x x x x x l , ))(1(2)1)()(1()(21221211--=--+=x x x x x x l ,x x x x x x l )1()()1()1!()(2382121232--=-⋅⋅-+=, )()1(12)()1()(2121213-+=⋅⋅-+=x x x x x x x l . 可得: )21()(23-=x x x L 方法二. 令)()21()(3B Ax x x x L +-= 由 23)1(3-=-L , 21)1(3=L , 定A ,B (称之为待定系数法) □2. 设)(,),(),(10x l x l x l n 是以n x x x ,,,10 为节点的n 次多项式插值问题的基函数.(1)证明.,,2,1,0,)(0n k x x l x ni k i k i ==∑=(2)证明+----+--+=))(())((1)(2010101000x x x x x x x x x x x x x l)())(()())((02010110n n x x x x x x x x x x x x ------+- .证明(1) 由于 j i j i x l ,)(δ= 故: =)(x L n ∑=ni i k i x l x)( , 当 j x x = 时有: k j j n x x L =)( ,n j ,,1,0 =)(x L n 也即为 k x 的插值多项式,由唯一性,有: ∑==ni k i ki x x l x)( , n k ,,1,0 =证明(2):利用Newton 插值多项式)(],[)()(0100x x x x f x f x N n -+=)()(],,[100---++n n x x x x x x f )()()()()()(00101x l x x x x x x x x x f n n =----=差商表:f(x) 一阶 二阶 … n 阶差商0x 11x 0101x x - 0)()(11020x x x x --n x 0 0)()(1010n x x x x --代入)(*式有:)()()()()(1)(020*******n n n x x x x x x x x x x x x x x x N -----++--+=- . )(0x l 为n 次代数多项式,由插值多项式的唯一性: 有 )()(0x N x l n ≡. □4. 设a b b a C x f -<<∈ε0],,[)(3.考虑以b a a ,,ε+为节点的Lagrange 插值公式当0→ε时的极限.证明成立公式)()()(x R x p x f +=. 其中)()()2)(()(2a f ab a b x x b x p --+-=),()()()())((22b f a b a x a f a b x b a x --+'---+ )()()(61)(2ξf b x a x x R '''--=,),(b a ∈ξ 并计算)(),(),(a p b p a p '.解 作)(x f 以b a a ,,ε+为节点的Lagrange 插值多项式,有: )()()(22x R x L x f +=, 其中:)()()()()()()()()()(2εεεεε+-+--+-----=a fb a b x a x a f b a b x a x x L)()()()()(b f a b a b a x a x εε------+, )()()(!3)()(2b x a x a x f x R ----'''=εζ , b a <<ζ 令: 0→ε 有)()(6)()()(22b x a x f x R x R --'''=→ζ, 又: )()()()([)()(2a f a b ax a f a b a x x b x L εεεεε----+----= )]()()()()(a f a b a x a f a b a x -------+εεεε )()()()()(b f a b a b a x a x εε------+)()()2()(2a f ab a b x x b --+-→)()()()(a f a b a x x b '---+ )()()()(22x P b f a b a x =--+故当 0→ε 时,成立公式: )()()(x R x P x f +=. □5. 给出13)(4+-=x x x f 的数值表解:因为34)(3'-=x x f ,2''12)(x x f = )(x f 为凹函数.又从数值表可见:1)当]5.0,1.0[∈x 时,)(x f 单调下降.有反函数)(1y f x -=2)x 于3.0及4.0之间有一个根)(y f的Newton 插值多项式:)17440.0)(10810.0)(40160.0)(70010.0(01225.0)10810.0)(40160.0)(70010.0(01531.0)40160.0)(70010.0(0096436.0)70010.0(33500.01.0)(4+---+------+--=y y y y y y y y y y y N.337.0)0(4*≈=N x □7、若 1)(37++=x x x f ,问:?]2,,2,2[710= f ; ?]2,,2,2[810= f .解 1)(37++=x x x f .有:=]2,,2,2[71f !7)()7(ξf =1, !8)(]2,,2,2[)8(810ηf f = 0=. □9.证明下列关系的正确性:(1) i i i i i i f g g f g f ∆+∆=⋅∆+1)((2) 1/)()/(+∆-∆=∆i i i i i i i i g g g f f g g f(3) )()(/!)1()/1(nh x h x x h n x n n n ++-=∆ 证明:(1) =⋅-⋅=⋅∆++i i i i i i g f g f g f 11)(i i i i i i i i g f g f g f g f ⋅-⋅+⋅-⋅++++1111i i i i f g g f ∆+∆=+1.(3) n x n n )1()1(-=∆!)()(nh x h x x h n++此题可利用数学归纳法:设 k n = 成立,证明 1+=k n 成立.又 1=n 时是成立的. □10. 利用差分性质证明:2333]2/)1([21)(+=+++=n n n n g .[提示:考虑差分)()1()(n g n g n g -+=∆,并利用差分和函数值可互相表示] 证明: 记: 2]2/)1([)(+=n n n f ,33321)(n n g +++= 有: 3)1()()1()(+=-+=∆n n f n f n f 故: ∑-=∆=10)()(n k k f n g ∑-=-+=1)]()1([n k k f k f2]2/)1([)0()(+=-=n n f n f . □13、求次数4≤的多项式)(x P ,满足1)1()0()1(===-P p P ,2)1()1(='=-'P P解 作重节点差商的Newton 插值公式 )1(]1,1[)1()(+--+-=x f f x P22)1(]1,0,1,1[)1(]0,1,1[+--++--+x x f x f )1()1(]1,1,0,1,1[2-+--+x x x f 重节点差商表:i x i f 一阶 二阶 三阶 四阶10-=x 110-=x 1 201=x 1 0 -212=x 1 0 0 112=x 1 2 2 1 0得 22)1()1(2)1(21)(+++-++=x x x x x P 13+-=x x . □17、 设 ]1,0[)(2C x f ∈ ,并且 0)0(=f ,1)1()21(==f f求证 ⎰≥''1212))((dx x f证: 取 ,00=x 211=x , 12=x , 21=h00=f , 11=f , 12=f 记: )(i i x s M ''= , 2,1,0=i有 h x x M h x x M x S 01101)(-+-=''x M x M 102)21(2+-= )21(2)1(2)(212-+-=''x M x M x S 又三弯矩方程为:( 2],,[210-=x x x f )244210-=++M M M , )24(41201M M M ++-=.分段积分: ⎰⎰+''=''∆121221)]([)]([dx x s dx x s ⎰''12221)]([dx x s ⎰+-+=210201)]21([4dx x M x M ⎰-+-121221)]21()1([4dx x M x M⎰⎰-+-+-+-=121121221201)]21()1([4)]1()21([4dx x M x M dx x M x M由于 ⎰=-1212241)21(dx x , ⎰=-1212241)1(dx x , ⎰=--121481)1()21(dx x x ,于是: ⎰++++=''∆1022212110202]2[61))((M M M M M M M dx x S 又: )24(41201M M M ++-=记 =),(20M M I ⎰∆''12))((dx x S=)()24(41[6120202220M M M M M M +++-+ ])24(81220M M +++由00=∂∂M I , 02=∂∂M I. 得: ⎩⎨⎧=+-=-07072020M M M M 即当: 020==M M 时, ),(20M M I 达最小故: ⎰=⋅⋅≥''∆12212)24(8161))((dx x S ,由最小模原理: ⎰≥''1212)]([dx x f . □20.已知插值条件为求相应的三次插值样条函数.解 利用三弯矩方法 )(i i x s M ''= , 2,1,0=i 10=x , 22=x , 32=x⎪⎩⎪⎨⎧-=+=++=+542364622121010M M M M M M M解得: 70-=M , 201=M , 372-=M]2,1[∈x 72431729)(231-+-=x x x x s ]3,2[∈x 105229367219)(232+-+-=x x x x s . □第四章 数值积分方法与数值微分 (习 题)1.直接验证梯形公式(1.2)与中矩形公式(1.3)具有1次代数精度,而辛甫生公式(1.4)则具有3次代数精度. 解梯形公式: ⎰+-≈ba b f a f ab dx x f )]()([2)(.矩形公式: ⎰+-≈b a ba f ab dx x f )2()()(. 以上两求积公式以 ,1)(=x f x 代入公式两边,结果相等,而以2)(x x f =代入公式两边,其结果不相等.故梯形公式的代数精度等于1. Simpson 公式:⎰+++-≈b a b f ba f a f ab dx x f )]()2(4)([6)(. 容易验证:以2,,1)(x x x f =分别代入Simpson 公式两边,结果相等。
计算方法与实习第五版-习题答案

绪论
习题1——10:设 f ( x) 8x5 0.4x4 4x3 9x 1 用秦九韶法求f(3)。 解:
8
0.4
24
4
0
9
1
x3
8
70.8
74.8
224.4
224.4
673.2 664.2
1992.6
1993.6
23.6
∴ f(3)=1993.6
第一章 绪论 练习
f ( xk )(xk xk 1 ) xk 1 xk f ( xk ) f ( xk 1 )
习题2——11:用割线法求方程x3-2x-5=0的根,要 求精确到4位有效数字,取x0=2, x1=2.2。
解: x0=2.0 x1=2.2
1.248* (2.2 2) x2 2.2 2.089 1.248 (1) 0.0621 * (2.089 2.2) x3 2.089 2.094 0.0621 1.248 0.0036 * (2.094 2.089 ) x4 2.094 2.095 0.0036 0.0621 0.00001 * (2.095 2.094 ) x5 2.095 2.095 0.00001 0.00361
150591收敛045571收敛方程求根方程求根141421不收敛方程求根方程求根方程求根方程求根10在15附近有一根将方程写成如下不同的等价形式判断是否满足迭代收敛的条件并选择一种最好的迭代格式以x15为初值求方程的根要求精确到4位有效数字
计算方法(数值分析)
习题答案——第一、二章
教师:马英杰 成都理工大学 核自学院
解:计算根 1)迭代公式: xk 1
数值分析计算实习第一题

直接用定义: ������������(������������)2 = ‖������������‖2‖������������−1‖2
求 A 的条件数很繁琐,需要先进行化简:
首先:
由于 A 是对称矩阵,
‖������������‖2 = �������������max(������������������������������������)
说明 :
1. 在所用的算法中,凡是要给出精度水平的ε,都取 ������������=10−12。
2. 选择算法的时候应使矩阵 A 的所有零元素都不存储。
3. 打印以下内容:
(1)算法设计方案和思路。
(2)全部源程序。
(3)特征值������������1,������������501,������������������������,������������������������������������(������������=1,2,⋯,39)以及������������������������������������������������(������������)2, det������������的值(采用 e 型输出实型数,并 至少显示 12 位有效数字)。
λi[16] -2.533970311130E+00 λi[38] 8.648666065193E+00
λi[17] -2.003230769563E+00 λi[39] 9.254200344575E+00
λi[18] -1.503557611227E+00 cond(A)2 1.925204273903E+03
λi[19] -9.935586060080E-01 det(A) 2.772786141752E+118
数值分析(第五版)计算实习题第四章作业

第四章:1、(1):复合梯形建立m文件:function t=natrapz(fname,a,b,n)h=(b-a)/n;fa=feval(fname,a);fb=feval(fname,b); f=feval(fname,a+h:h:b-h+0.001*h); t=h*(0.5*(fa+fb)+sum(f));输入:>> syms x>> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,10)输出:ans =-0.417062831779470输入:>> syms x>> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,100)输出:ans =-0.443117908008157输入:>> syms x>> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,1000)输出:ans =-0.444387538997162复合辛普森建立m文件:function t=comsimpson(fname,a,b,n)h=(b-a)/n;fa=feval(fname,a);fb=feval(fname,b);f1=feval(fname,a+h:h:b-h+0.001*h);f2=feval(fname,a+h/2:h:b-h+0.001*h);t=h/6*(fa+fb+2*sum(f1)+4*sum(f2));输入:>> syms x>> f=inline('sqrt(x).*log(x);');>> format long;>>comsimpson(f,eps,1,10)输出:ans =-0.435297890074689输入:>>syms x>>f=inline('sqrt(x).*log(x);');>>comsimpson(f,eps,1,100)输出:ans =-0.444161178415673输入:>>syms x>>f=inline('sqrt(x).*log(x);');>>comsimpson(f,eps,1,1000)输出:ans =-0.444434117614180(2)龙贝格建立m文件:function [RT,R,wugu,h]=Romberg(fun,a,b,wucha,m) %RT是龙贝格积分表%R是数值积分值%wugu是误差估计%h是最小步长%fun是被积函数%a b是积分下、上限%m是龙贝格积分表中行最大数目%wucha是两次相邻迭代值的绝对误差限n=1;h=b-a;wugu=1;x=a;k=0;RT=zeros(4,4);RT(1,1)=h*(feval(fun,a)+feval(fun,b))/2;while((wugu>wucha)&(k<m)|(k<4))k=k+1;h=h/2;s=0;for j=1:nx=a+h*(2*j-1);s=s+feval(fun,x);endRT(k+1,1)=RT(k,1)/2+h*s;n=2*n;for i=1:kRT(k+1,i+1)=((4^i)*RT(k+1,i)-RT(k,i))/(4^i-1);endwugu=abs(RT(k+1,k)-RT(k+1,k+1));endR=RT(k+1,k+1);输入:>>fun=inline('sqrt(x).*log(x)');>> [RT,R,wugu,h]=Romberg(fun,eps,1,1e-5,13)输出:RT =1 至5 列-0.000000268546145 0 0 0-0.245064670140209 -0.326752804004897 0 0-0.358104125949240 -0.395783944552250 -0.400386020588741 0 0-0.408090073087781 -0.424752055467295 -0.426683262861631 -0.427100679405645 0-0.429474601629505 -0.436602777810080 -0.437392825966266 -0.437562819031419 -0.437603847029951-0.438389494461832 -0.441361125405941 -0.441678348578999 -0.441746372747455 -0.4417627788404596 列-0.441766844267449R =-0.441766844267449wugu =4.065426989774412e-06h =0.031250000000000(3)自适应辛普森输入:>> f=inline('sqrt(x).*log(x)');>> q=quad(f,0,1,1e-4)输出:q =-0.4439755729517282.(1)复合辛普森建立m文件function q=combinesimpson2(F,x0,a,b,n)%复合Simpson多元求积公式%F—被积函数%x0—被积函数自变量%[a,b]积分区间%n—区间份数x=linspace(a,b,n+1);q=0;for k=1:nq=q+subs(F,x0,x(k))+4*subs(F,x0,(x(k)+x(k+1))/2)+subs(F,x0,x(k+1)); endq=q*(b-a)/n/6;输入:>> clear>> syms x y;>> F=exp(-x.*y);>> s=combinesimpson2(combinesimpson2(F,'x',0,1,4),'y',0,1,4)输出:s =exp(-1)/576 + exp(-1/2)/144 + exp(-1/4)/72 + exp(-3/4)/144 + exp(-1/8)/36 +exp(-3/8)/36 + exp(-5/8)/72 + exp(-7/8)/72 + (5*exp(-1/16))/144 + exp(-3/16)/24 + exp(-5/16)/36 + exp(-7/16)/36 + exp(-9/16)/144 + exp(-1/32)/36 + exp(-3/32)/18 + exp(-5/32)/36 + exp(-7/32)/36 + exp(-9/32)/36 + exp(-15/32)/36 + exp(-21/32)/36 + exp(-1/64)/36 + exp(-3/64)/18 + exp(-5/64)/18 + exp(-7/64)/18 + exp(-9/64)/36 + exp(-15/64)/18 + exp(-21/64)/18 + exp(-25/64)/36 + exp(-35/64)/18 + exp(-49/64)/36 + 47/576>> double(s)ans =0.796599967946203高斯求积公式function q=gaussquad(F,x0,a,b,n)%Gauss求积公式%F—被积函数%x0—被积函数自变量%[a,b]积分区间%n—节点个数syms t;F=subs(F,x0,(b-a)/2*t+(a+b)/2);[x,A]=gausspoints(n);q=(b-a)/2*sum(A.*subs(F,t,x));输入:>> clear>> syms x y;F=exp(-x.*y);>> s=gaussquad(gaussquad(F,x,0,1,4),y,0,1,4)输出:s =0.7966(2)复合辛普森输入:>> syms x y;>> f=exp(-x.*y);>> s=combinesimpson2(combinesimpson2(f,y,0,sqrt(1-x^2),4),x,0,1,4)输出:s =(3^(1/2)*(exp(-3^(1/2)/4) + 2*exp(-3^(1/2)/8) + 2*exp(-3^(1/2)/16) + 2*exp(-(3*3^(1/2))/16) + 4*exp(-3^(1/2)/32) + 4*exp(-(3*3^(1/2))/32) + 4*exp(-(5*3^(1/2))/32) + 4*exp(-(7*3^(1/2))/32) + 1))/576 + (7^(1/2)*(exp(-(3*7^(1/2))/16) + 2*exp(-(3*7^(1/2))/32) + 2*exp(-(3*7^(1/2))/64) + 2*exp(-(9*7^(1/2))/64) + 4*exp(-(3*7^(1/2))/128) + 4*exp(-(9*7^(1/2))/128) + 4*exp(-(15*7^(1/2))/128) + 4*exp(-(21*7^(1/2))/128) + 1))/1152 + (15^(1/2)*(exp(-15^(1/2)/16) + 2*exp(-15^(1/2)/32) + 2*exp(-15^(1/2)/64) + 2*exp(-(3*15^(1/2))/64) + 4*exp(-15^(1/2)/128) + 4*exp(-(3*15^(1/2))/128) + 4*exp(-(5*15^(1/2))/128) + 4*exp(-(7*15^(1/2))/128) + 1))/1152 + (15^(1/2)*(exp(-(7*15^(1/2))/64) + 2*exp(-(7*15^(1/2))/128) + 2*exp(-(7*15^(1/2))/256) + 2*exp(-(21*15^(1/2))/256) + 4*exp(-(7*15^(1/2))/512) + 4*exp(-(21*15^(1/2))/512) + 4*exp(-(35*15^(1/2))/512) + 4*exp(-(49*15^(1/2))/512) + 1))/1152 + (39^(1/2)*(exp(-(5*39^(1/2))/64) + 2*exp(-(5*39^(1/2))/128) + 2*exp(-(5*39^(1/2))/256) + 2*exp(-(15*39^(1/2))/256) + 4*exp(-(5*39^(1/2))/512) + 4*exp(-(15*39^(1/2))/512) + 4*exp(-(25*39^(1/2))/512) + 4*exp(-(35*39^(1/2))/512) + 1))/1152 + (55^(1/2)*(exp(-(3*55^(1/2))/64) + 2*exp(-(3*55^(1/2))/128) + 2*exp(-(3*55^(1/2))/256) + 2*exp(-(9*55^(1/2))/256) + 4*exp(-(3*55^(1/2))/512) + 4*exp(-(9*55^(1/2))/512) + 4*exp(-(15*55^(1/2))/512) + 4*exp(-(21*55^(1/2))/512) + 1))/1152 + (63^(1/2)*(exp(-63^(1/2)/64) + 2*exp(-63^(1/2)/128) + 2*exp(-63^(1/2)/256) + 2*exp(-(3*63^(1/2))/256) + 4*exp(-63^(1/2)/512) + 4*exp(-(3*63^(1/2))/512) + 4*exp(-(5*63^(1/2))/512) + 4*exp(-(7*63^(1/2))/512) + 1))/1152 + 1/24>> double(s)ans =0.670113633359095。
数值分析报告(第五版)计算实习的题目第三章

数值分析计算实习题第三章第二次作业:题一:x=-1:0.2:1;y=1./(1+25.*x.^2);f1=polyfit(x,y,3)f=poly2sym(f1)y1=polyval(f1,x)x2=linspace(-1,1,10)y2=interp1(x,y,x2)plot(x,y,'r*-',x,y1,'b-')hold onplot(x2,y2,'k')legend('数据点','3次拟合曲线','3次多项式插值')xlabel('X'),ylabel('Y')输出:f1 =0.0000 -0.5752 0.0000 0.4841f =(4591875547102675*x^3)/81129638414606681695789005144064 - (3305*x^2)/5746 + (1469057404776431*x)/20282409603651670423947251286016 + 4360609662300613/9007199254740992y1 =-0.0911 0.1160 0.2771 0.3921 0.4611 0.4841 0.4611 0.3921 0.2771 0.1160 -0.0911x2 =-1.0000 -0.7778 -0.5556 -0.3333 -0.1111 0.1111 0.3333 0.5556 0.7778 1.0000y2 =0.0385 0.0634 0.1222 0.3000 0.7222 0.7222 0.3000 0.1222 0.0634 0.0385题二:X=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];Y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];p1=polyfit(X,Y,3)p2=polyfit(X,Y,4)Y1=polyval(p1,X)Y2=polyval(p2,X)plot(X,Y,'r*',X,Y1,'b-.',X,Y2,'g--')p3=polyfit(X,Y,2)Y3=polyval(p3,X)f1=poly2sym(p1)f2=poly2sym(p2)f3=poly2sym(p3)plot(X,Y,'r*',X,Y1,'b-.',X,Y2,'g--',X,Y3,'m--')legend('数据点','3次多项式拟合','4次多项式拟合','2次多项式拟合') xlabel('X轴'),ylabel('Y轴')输出:p1 =-6.6221 12.8147 -4.6591 0.9266p2 =2.8853 -12.3348 16.2747 -5.2987 0.9427Y1 =0.9266 0.5822 0.4544 0.5034 0.9730 2.0103 2.4602Y2 =0.9427 0.5635 0.4399 0.5082 1.0005 1.9860 2.4692p3 =3.1316 -1.2400 0.7356Y3 =0.7356 0.6429 0.6128 0.6454 0.8984 1.7477 2.6271f1 =- (7455778416425075*x^3)/1125899906842624 + (1803512222945435*x^2)/140737488355328 - (40981580032809*x)/8796093022208 + 8345953784399011/9007199254740992f2 =(1624271450198125*x^4)/562949953421312 - (3471944732519173*x^3)/281474976710656 + (4580931990070659*x^2)/281474976710656 - (1491459232922115*x)/281474976710656 + 1061409433081293/1125899906842624f3 =(18733*x^2)/5982 - (74179*x)/59820 + 73337/99700题三:建立三角插值函数的m文件function [A,B,Y1,Rm]=sanjiaobijin(X,Y,X1,m)%A B分别是m阶三角多项式Tm (x)的系数aj,bj(j=1,2,...,m)的系数矩阵,Y1是Tm(x)在X1处的值,X Y 数据点 ,Rm为均方误差n=length(X)-1;max1=fix((n-1)/2);if m>max1m=max1;endA=zeros(1,m+1);B=zeros(1,m+1);Ym=(Y(1)+Y(n+1))/2;Y(1)=Ym;Y(n+1)=Ym;A(1)=2*sum(Y)/n;for i=1:mB(i+1)=sin(i*X)*Y';A(i+1)=cos(i*X)*Y';endA=2*A/n;B=2*B/n;A(1)=A(1)/2;Y1=A(1);for k=1:mY1=Y1+A(k+1)*cos(k*X1)+B(k+1)*sin(k*X1);Tm=A(1)+A(k+1).*cos(k*X)+B(k+1).*sin(k*X);k=k+1;endY,Tm,Rm=(sum(Y-Tm).^2)/n输出:>> X=-pi:2*pi/33:pi;>> Y=X.^2.*cos(X);[A,B,Y1,Rm]=sanjiaobijin(X,Y,X1,16)输出:A =1 至 12 列-0.1397 4.4002 -2.8326 1.2355 -0.9128 0.7914 -0.7319 0.6982 -0.6773 0.6635 -0.6541 0.647413 至 17 列-0.6426 0.6393 -0.6370 0.6355 -0.6348B =1.0e-15 *1 至 12 列0 -0.0194 -0.0150 -0.0044 -0.0300 0.0105 0.0627 -0.0821 -0.0599 -0.0133 -0.0211 0.029713 至 17 列0.0178 0.0962 -0.1049 0.0328 -0.0122即可得16插值多项式的值X1=-pi:0.001:pi;[A,B,Y1,Rm]=sanjiaobijin(X,Y,X1,16)plot(X,Y,'r*',X1,Y1,'b-.')legend('数据点','16次三角插值多项式')xlabel('X轴'),ylabel('Y轴')。
p178-179 实习题答案(数值分析(第五版))

1.列主元法(178页实习1题)函数liezhu(A,b).m的头文件的程序如下:n=length(b);detA=det(A);d=0;x=zeros(n,1);c=zeros(1,n);if abs(det(A))<=epserror('系数矩阵是奇异的'); %所求方程组系数矩阵必须是是非奇异的!return;end%按列选主元for i=1:n-1max=abs(A(i,i));m=i;for j=i+1:nif max<abs(A(j,i))max=abs(A(j,i));m=j;endend%换行if m~=ifor k=i:nc(k)=A(i,k);A(i,k)=A(m,k);A(m,k)=c(k);endd=b(i);b(i)=b(m);b(m)=d;end%消元for k=i+1:nfor j=i+1:nA(k,j)=A(k,j)-A(i,j)*A(k,i)/A(i,i);endb(k)=b(k)-b(i)*A(k,i)/A(i,i);A(k,i)=0;endEnd%回代求解x(n)=b(n)/A(n,n);for i=n-1:(-1):1sum=0;for j=i+1:nsum=sum+A(i,j)*x(j);endx(i)=(b(i)-sum)/A(i,i);endend其结果如下:>> A=[10,-7,0,1;-3,2.099999,6,2;5,-1,5,-1;2,1,0,2];>> b=[8;5.900001;5;1];>> [x,detA]=liezhu(A,b)x =0.0000-1.00001.00001.0000detA =-762.00012.LU分解法:(178页实习1题)LUFJ.m文件中函数LUFJ(A,b)的程序如下:function LUFJ(A,b) %A为系数矩阵,b为右端项矩阵%UNTITLED2 Summary of this function goes here% Detailed explanation goes here[m,n]=size(A); %初始化矩阵A,b,L和Un=length(b);L=eye(n,n);U=zeros(n,n);U(1,1:n)=A(1,1:n); %开始进行LU分解L(2:n,1)=A(2:n,1)/U(1,1);for k=2:nU(k,k:n)=A(k,k:n)-L(k,1:k-1)*U(1:k-1,k:n);L(k+1:n,k)=(A(k+1:n,k)-L(k+1:n,1:k-1)*U(1:k-1,k))/U(k,k); endL %输出L矩阵U %输出U矩阵y=zeros(n,1); %开始解方程组Ux=yy(1)=b(1);for k=2:ny(k)=b(k)-L(k,1:k-1)*y(1:k-1);endx=zeros(n,1);x(n)=y(n)/U(n,n);for k=n-1:-1:1x(k)=(y(k)-U(k,k+1:n)*x(k+1:n))/U(k,k); endfor k=1:nfprintf('x[%d]=%f\n',k,x(k));endend运行结果如下:>> A=[10,-7,0,1;-3,2.099999,6,2;5,-1,5,-1;2,1,0,2];>> b=[8;5.900001;5;1];>> LUFJ(A,b)L =1.0e+006 *0.0000 0 0 0-0.0000 0.0000 0 00.0000 -2.5000 0.0000 00.0000 -2.4000 0.0000 0.0000U =1.0e+007 *0.0000 -0.0000 0 0.00000 -0.0000 0.0000 0.00000 0 1.5000 0.57500 0 0 0.0000x[1]=-0.000000x[2]=-1.000000x[3]=1.000000x[4]=1.0000003.雅可比迭代法:(179页实习3题)Jacobi.m文件中函数Jacobi(A,b,eps)的程序如下:function Jacobi(A,b,eps) %A为系数矩阵,b为后端项矩阵,epe为精度[m,n]=size(A);D=diag(diag(A)); %求矩阵DL=D-tril(A); %求矩阵LU=D-triu(A); %求矩阵Utemp=1;x=zeros(m,1);k=0;while abs(max(x)-temp)>epstemp=max(abs(x));k=k+1; %记录循环次数x=-inv(D)*(L+U)*x+inv(D)*b; %雅克比迭代公式endfor k=1:nfprintf('x[%d]=%f\n',k,x(k));end运行结果如下:>> A=[10 -1 2 0;0 8 -1 3;2 -1 10 0;-1 3 -1 11];>> b=[-11;-11;6;25];>> Jacobi(A,b,0.00005)x[1]=-1.466538x[2]=-2.358692x[3]=0.657438x[4]=2.8424524 .Gauss-Seidel迭代程序(179页实习3题)Gauss-Seidel.m文件中函数Gauss-Seidel(A,b,eps)的程序如下:function Gauss_Seidel(A,b,eps) %A为系数矩阵,b为后端项矩阵,epe为精度[m,n]=size(A);D=diag(diag(A)); %求矩阵DL=D-tril(A); %求矩阵LU=D-triu(A); %求矩阵Utemp=1;x=zeros(m,1);k=0;while abs(max(x)-temp)>epstemp=max(abs(x));k=k+1; %记录循环次数x=inv(D-L)*U*x+inv(D-L)*b; %Gauss_Seidel的迭代公式endfor k=1:nfprintf('x[%d]=%f\n',k,x(k));end其运行结果如下:>> A=[10 -1 2 0;0 8 -1 3;2 -1 10 0;-1 3 -1 11];>> b=[-11;-11;6;25];>> Gauss_Seidel(A,b,0.005) x[1]=-1.466538x[2]=-2.358692x[3]=0.657438x[4]=2.842452。
数值分析计算实习题目一
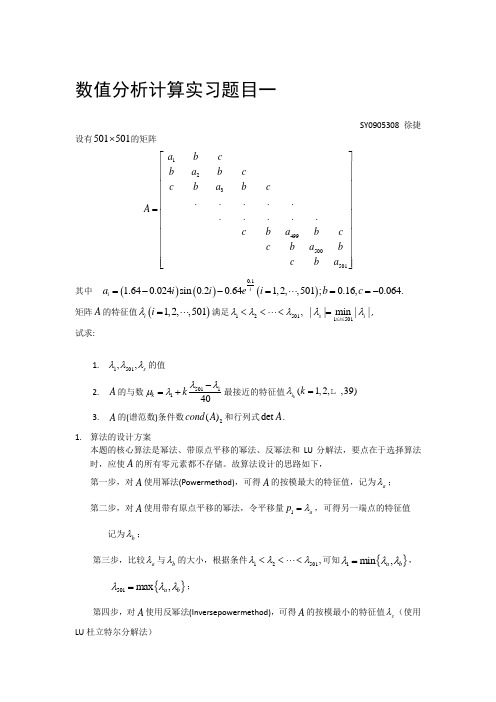
数值分析计算实习题目一SY0905308 徐捷设有501501⨯的矩阵123499500501..........a b c b a b c c b a b c A cb a bc cb a b cba ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其中()()()0.11.640.024sin 0.20.641,2,,501;0.16,0.064.ii a i i ei b c =--=⋅⋅⋅==-矩阵A 的特征值()1,2,,501i i λ=⋅⋅⋅满足12501,λλλ<<⋅⋅⋅<1501||min ||s i i λλ≤≤=, 试求:1.1501,,s λλλ的值2. A 的与数5011140k kλλμλ-=+最接近的特征值(1,2,,39)k i k λ=3. A 的(谱范数)条件数2()cond A 和行列式det A .1. 算法的设计方案本题的核心算法是幂法、带原点平移的幂法、反幂法和LU 分解法,要点在于选择算法时,应使A 的所有零元素都不存储。
故算法设计的思路如下,第一步,对A 使用幂法(Powermethod),可得A 的按模最大的特征值,记为a λ; 第二步,对A 使用带有原点平移的幂法,令平移量1a p λ=,可得另一端点的特征值记为b λ;第三步,比较a λ与b λ的大小,根据条件12501,λλλ<<⋅⋅⋅<可知{}1min ,a b λλλ=,{}501max ,a b λλλ=;第四步,对A 使用反幂法(Inversepowermethod),可得A 的按模最小的特征值s λ(使用LU 杜立特尔分解法)第五步,根据5011140k kλλμλ-=+计算出k μ,然后利用带有原点平移的反幂法求得k i λ,其中平移量k k p μ=,反幂法运算39次,可得2239,,,i i i λλλ ;第六步, 根据定义,非奇异的实对称矩阵A 的谱范数条件数()12||ncond A λλ=,其中1n λλ和分别是矩阵A 的模为最大和模为最小的特征值,对于本题,则有{}15012|max ||,|||()||s cond A λλλ=;第七步,由LU 分解可知,A LU =,可得5011det det()det()det()(1501)n iii A LU L U u i ====⋅=≤≤∏。
数值分析计算实习题(二)

数值分析计算实习题(二)数值分析计算实习题(二)SY1004114 全昌彪一:算法设计方案概述:本题采用fortran90语言编写程序,依据题目要求,采用带双步位移QR分解法求出所给矩阵的所有特征值,并求出相应于其实特征值的特征向量,以及相关需要给出的中间结果。
1、矩阵的A的初始化(赋值):利用子函数initial(a,n)来实现,返回n×n 维二维数组a。
2、A矩阵的拟上三角化:利用子函数hessenberg(a,n),在对矩阵进行QR分解前进行拟上三角化,这样可以提高计算效率,减少计算量,返回A矩阵的相似矩阵Hessenberg阵A(n-1)。
3、对A(n-1)进行带双步位移QR分解得出Cm及A矩阵的所有特征值,这一步利用了两个子函数eigenvalue(a,n,lamda,lamdai)和qrresolve(b,c,m)带双步位移QR分解可以加速收敛。
每次QR分解前先进行判断,若可以直接得到矩阵的特征值,则对矩阵直接降阶处理;若不可以,则进行QR分解,这样就进一步减少了计算量,提高了计算效率。
考虑到矩阵A可能有复特征值,采用两个一维数组lamda(n)及lamdai(n)分别存储其实部和虚部。
在双步位移处理及降阶过程中,被分解的矩阵Ak(m ×m)及中间矩阵M k(m×m)的维数随m不断减少而降阶,于是引入了动态矩阵C(m×m)和B(m×m)分别存储,在使用前,先声明分配内存,使用结束后立即释放内存。
返回A(n-1)经双步位移QR分解后的矩阵及A矩阵的所有特征值。
4、特征向量的求解:采用子函数eigenvector(a,lamda)实现求解A矩阵的属于实特征值的特征向量。
核心算法为高斯列主元消去法,(A-λI)x=b,b=0,回代过程令x(10)=1,即可求出对应于每一实特征值的特征向量的各个元素。
5、相关输出结果:所有数据均采用e型输出,数据保留到小数点后12位。
计算方法与实习第五版期末复习资料

《计算机在材料科学中的应用》习题课第一章 误差等概念1. 误差来源:模型误差、观测误差、截断误差、舍入误差2. 绝对误差(限):e=x*-x ,|e|=|x*-x|≤ε3. 相对误差(限):e r =(x*-x)/x ,|e r |=|x*-x|/|x|≤εr4. 有效数字:|e|≤m-n 11025. 防止误差的危害:避免两相近数相减,多数作乘数或小数作除数,大数“吃”小数第二章 方程求根1. 根的存在及隔离2. 二分法:误差是()k+11b-a 23. 迭代法:'1x (x)|(x)|1 ||k k x x ϕϕε+=<-<, ,4. 加速法:'()L x ϕ≈取, 1111() L 1Lk k k k k k x x x x x x ϕ-+--+++⎧⎪⎨+-⎪⎩-==() 5. 牛顿迭代法:1000''1'111111'f()f()f ()0f ()f() f ()=c f()-f()f()()f ()=f()-f()f() f ()k k k k k k k k k k k k k k k k k k k k k k k x x x x x x x x x x x c x x x x x x x x x x x x x x x x λλ++--+--+->-----''=, 选取时使得简化牛顿法:,=拟牛顿法(割线法): ,=牛顿下山法:=, 选取下山因子使得1|f()|<|f()|k k x x +⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩第三章 方程组求解1. 消去法:高斯消去法,列主元消去法,高斯-约当法,消元因子 ()()k ikik k kka l a =消元公式 (k+1)(k)(k)ij ij ik kj (k+1)(k)(k)i i ik k a =a -l a (i,j=k+1,k+2,...,n)b =b -l b (i=k+1,k+2,...,n)⎧⎪⎨⎪⎩ 回代公式 kjn(k)(k)kjj=k+1k (k)kkb - a x x =(k=n,...,1)a∑2. 矩阵直接分解:紧凑格式3. 追赶法4. 迭代法:收敛条件1||||nii ij j j ia a =≠>∑①雅可比法迭代格式:ji n(k)i ij j=1j i(1)iib -a x x =(i=1,2,...,n) a k ≠+∑②高斯-赛德尔法迭代格式:jji i-1n(k+1)(k)i ij ij j=1j=i+1(1)iib -a x -a x x =(i=1,2,...,n)a k +∑∑第四章 插值法1. 插值多项式2012j j j j (1)n+1 ()()... , (x )= f( x )= y (j=0,1,...,n) x [a,b],() ()=()-()=()(n+1)!n n n n f x P x a a x a x a x P f R x f x P x x ξω+≈=++++=插值条件,插值节点,插值区间插值余项2. 拉格朗日插值: 插值基函数 n 001 () L ()()0 n nji j i i j i j j ix x i j l x x y i jx x ==≠-=⎧==⎨≠-⎩∑∏,3. 差商:10011002010122101k-2k 01k-2k-101k k k-1f(x )-f(x )f[x ,x ]=x -x f[x ,x ]-f[x ,x ]f[x ,x ,x ]=x -x f[x ,x ,...,x ,x ]-f[x ,x ,...,x ,x ]f[x ,x ,...,x ]=x -x 一阶差商二阶差商k 阶差商4. 牛顿插值公式f(x)=f(x 0)+f[x 0,x 1](x-x 0)+f[x 0,x 1,x 2](x-x 0)(x-x 1)+… +f[x 0,x 1,…,x n ](x-x 0)(x-x 1)…(x-x n-1) 5. 差分(等间距节点)111122111 = () , () -() -() - - k k k k k k k k k k k k k k m m m k k k x x kh x x f f x f x x h f f f f x x h f f f f x x h f f fm f f f δ+-+---+=+-∆≡∇≡≡∆=∆∆k 0k+1k 等距节点时,(k=0,1,...,n ),h=记则在处以为步长的向前差分:在处以为步长的向后差分:在处以为步长的中心差分:同样也有各自的阶差分111111122- -m m m k k k m m m k k k f f f f f fδδδ-----+-∇=∇∇=6. 牛顿前插公式20000001012nf f f ()=()+(-)()()....()...()()h 2!h n!h n n n f x f x x x x x x x x x x x R x -∆∆∆+--++--+7. 样条插值:三次样条插值,要求光滑、连续第五章 曲线拟合最小二乘原理2012n2i 01m j j j=1n (j=1,2,...,n),[]()...a (i=0,1,..., m),• (a ,...,a )= [P(x ) - y ] (x)(x,y ) m m p x a a x a x a x p n ϕ=++++∑j j 1n 有对数据(x ,y )在x ,x 上求一个m 次多项式适当选取使得,a 为最小值,则称为最小二乘拟合多项式是间的经验公式。
数值分析第五版上机实验答案实验一~实验六

实验一Lagrange插值算法实验目的:掌握拉格朗日(Lagrange)插值算法的基本原理,理解插值基函数的性质,掌握基本的误差概念。
学习用计算机语言编写程序实现算法。
[参考程序]#include "stdio.h"//定义插值节点及所求点数据,根据题目不同而修改double x[]={0.32,0.34,0.36};double y[]={0.314567,0.333487,0.352274};double xx=0.3367;// Lagrange插值算法函数,利用循环计算具有对称性的基函数和最终结果double Lagrange(double xxx,int n){int i;double result=0,temp;for(i=0;i<=n;i++){temp=1;for(int j=0;j<= n;j++){if(j!=i){temp=temp*(xxx-x[j])/(x[i]-x[j]);}}result=result+temp*y[i];}return result;}void main(){int n;printf("Please input n:");scanf("%d",&n);printf("Sin(%f) = %f \n",xx,Lagrange(xx,n));}实验二Newton均差插值算法实验目的:掌握Newton均差插值算法的基本原理,理解均差的概念,掌握均差表的计算方法。
学习用计算机语言编写程序实现算法。
[参考程序]#include "stdio.h"#define N 10double f[N][N];//定义插值节点及所求点数据,根据题目不同而修改double x[]={0.4,0.55,0.65,0.80,0.90,1.05};double y[]={0.41075,0.57815,0.69675,0.88811,1.02652,1.25382};double fx(int i,int j);double S(int start,int end,double xx);main(){int loopi,loopj,n;double result,xx;scanf("%d",&n);scanf("%lf",&xx);for(loopi=0;loopi<=n;loopi++){//零阶均差作为均差表二维数组的第0列f[loopi][0]=y[loopi];}//循环计算均差表中的所有数据for(loopi=1;loopi<=n;loopi++){for(loopj=1;loopj<=loopi;loopj++){f[loopi][loopj]=fx(loopi,loopj);}}result=S(0,n,xx);printf("Result is: %f",result);return 1;}//求均差的函数double fx(int i,int j){if(j==0){return f[i][j];}else{//这种表示方法需要注意两个x的下标return (fx(i,j-1)-fx(i-1,j-1))/(x[i]-x[i-j]);}}//用秦九韶算法计算插值多项式结果double S(int start,int end,double xx){if(start==end){return f[end][end];}else{return (S(start+1,end,xx)*(xx-x[start])+f[start][start]);}}实验三Newton差分插值算法实验目的:掌握Newton差分插值算法的基本原理,理解差分的概念,掌握差分表的计算方法。
数值分析计算实习题列主元高斯消去法解线性方程组

数值分析计算实习题第5章解线性方程组的直接方法【选题列主元高斯消去法解线性方程组。
书上的计算实习题1、2、3都要求用列主元高斯消去法解线性方程组,所以考虑写一个普适的程序来实现。
对于线性方程组Ax二b,程序允许用户从文件读入矩阵数据或直接在屏幕输入数据。
文件输入格式要求:(1)第一行为一个整数n (2<=n<=100),表示矩阵阶数。
(2)第2~n+l行为矩阵A各行列的值。
(3)第n+2~n+n+2行为矩阵b各行的值。
屏幕输入:按提示输入各个数据。
输出:A. b、det(A).列主元高斯消去计算过程、解向量X。
【算法说明】设有线性方程组Ax=b,其中设A为非奇异矩阵。
方程组的增广矩阵为«12«21[Nb] =第1步(k=l ):首先在A的第一列中选取绝对值最大的元素®I,作为第一步的主元素:«|| H0然后交换(A, b)的第1行与第I行元素,再进行消元计算。
设列主元素消去法已经完成第1步到第k・l步的按列选主元,交换两行,消元计算得到与原方程组等价的方程组 A(k)x=b(k)4? …4;)…唸)•忒••輕■[A.b]T[A ⑹,b")] = ••■咲■■■■■* *■〃伏)・• - %■第k步计算如下: 对于 k=l, 2, •…,0-1(1)按列选主元:即确定t使(2)如果tHk,则交换[A, b]第t行与第k行元素。
(3)消元计算54* J 叫=一鱼(=^ + 1,…,H)% 吗 <-«y + 〃如伽 (fJ = R + l,…/)b- <-勺+加汝仇, (i = /c + l,…,《)消元乘数mik 满足:n (%-D 内)X1 < ------ -- ---- 9(j = « 一 1,«一2■…J)tk M 1,(,=斤 +1, •••,«)fet e(4)回代求解【程序】/*【普适列主元消去法解线性方程组】对于线性方程组:Ax=b 输入:[选择屏幕直接输入]1.A的行阶数n(l <= 11<= 100)2.A的值3.b的值[选择读取文件1文件名(和主程序同级文件夹下)输出:I.A2・b3・ det(A)4解向疑X */#inciude <stdio.h>#include <stdlibJi>#include <niath.h> double A[1051(J05LA_B[I05][105Lb[105].x[105];double det A:int n.mark = 1;〃读入数据void input(){int ij:char ch[20],name[ 100];HLE *f;printf("\iv-An是否从文件读取数据(Y/N):”); scanf(”%st&ch);if(ch[0] = Y II ch[0] = y)( prinif(“请输入文件名(包括扩展需):"); scanf("%s".name):f = fop cn(namc「T');fscanfCf/'%d'\&n);ford = 0:i < n;i 卄) for(j = 0;j < nJ ++) fscanf(f,'*%ir\&A[i]|j)):for(i = 0:i < n;i卄)fscanf(「%F・&b[i]);else{prin氓”请输入A的阶数:”);scanf( '%d %d\&n): prinifC请输入A的值:”);for(i = 0:i V n:i ++)for(j = 0;j < n:j ++) scanf("%lf\&A[i]U]);phnifC请输入b的值:”);for(i = 0:i < n;i 卄)scanf(''%lf\&b[i]):〃讣算行列式的值double det{double s[105](105] jni m){int z.jkdouble b[105][105Klotal = 0.r; /*b[Nl[N]用于存放,在矩阵s[Nl[N冲元素s[0]的余子式灯if(m>2){for(z = 0:z V m:z++){for(j = 0;j V m ・ 1 j ++)for(k = 0:k vn卜l;k ++)if(k >= z)bUKk] = sU+l](k+l];elsebLi][k] = s[j+l][k];if(z % 2==0)r=s[0)⑵ * dcKb.m - 1):/*递归调用制elser= (-1) * s[0](z] * det(b.m -1);total = total + r;else if(m == 2)total = s[0][0] *s(l][l]-s[0](l] *s[l][01:else if(m == 1)total =s[0][0];return total;// 输出A^llb和dcl(A)void ouipui_l(){ int i j;primlTAW);for(i = 0;i < n:i ++){ for(j = 0:j < n:j ++)p rintf('-%15.4f\A[i]lj]);prinif(W);prinlf(5b = \rf);for{i = 0;i < n:i ++)prinif("%15.4l\iV\b[i]):printf("\ndet(A) = %・4f\n”・dclA);//主il•算函数void couni_x(){int ij,k:int max; double tmpjnik;〃构造增广矩阵for{i = 0;i<n:i++){for。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值分析计算实习题第二章2-1程序:clear;clc;x1=[0.2 0.4 0.6 0.8 1.0];y1=[0.98 0.92 0.81 0.64 0.38];n=length(y1);c=y1(:);for j=2:n %求差商for i=n:-1:jc(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1));endendsyms x df d;df(1)=1;d(1)=y1(1);for i=2:n %求牛顿差值多项式df(i)=df(i-1)*(x-x1(i-1));d(i)=c(i)*df(i);enddisp('4次牛顿插值多项式');P4=vpa(collect((sum(d))),5) %P4即为4次牛顿插值多项式,并保留小数点后5位数pp=csape(x1,y1, 'variational');%调用三次样条函数q=pp.coefs;disp('三次样条函数');for i=1:4S=q(i,:)*[(x-x1(i))^3;(x-x1(i))^2;(x-x1(i));1];S=vpa(collect(S),5)endx2=0.2:0.08:1.08;dot=[1 2 11 12];figureezplot(P4,[0.2,1.08]);hold ony2=fnval(pp,x2);x=x2(dot);y3=eval(P4);y4=fnval(pp,x2(dot));plot(x2,y2,'r',x2(dot),y3,'b*',x2(dot),y4,'co');title('4次牛顿插值及三次样条');结果如下:4次牛顿插值多项式P4 = - 0.52083*x^4 + 0.83333*x^3 - 1.1042*x^2 + 0.19167*x + 0.98三次样条函数x∈[0.2,0.4]时, S = - 1.3393*x^3 + 0.80357*x^2 - 0.40714*x + 1.04 x∈[0.4,0.6]时,S = 0.44643*x^3 - 1.3393*x^2 + 0.45*x + 0.92571x∈[0.6,0.8]时,S = - 1.6964*x^3 + 2.5179*x^2 - 1.8643*x + 1.3886 x∈[0.8,1.0]时,S =2.5893*x^3 - 7.7679*x^2 + 6.3643*x - 0.80571输出图如下2-3(1)程序:clear;clc;x1=[0 1 4 9 16 25 36 49 64];y1=[0 1 2 3 4 5 6 7 8];%插值点n=length(y1);a=ones(n,2);a(:,2)=-x1';c=1;for i=1:nc=conv(c,a(i,:));endq=zeros(n,n);r=zeros(n,n+1);for i=1:n[q(i,:),r(i,:)]=deconv(c,a(i,:));%wn+1/(x-xk) end 三次样条插值曲线4次牛顿插值曲线Dw=zeros(1,n);for i=1:nDw(i)=y1(i)/polyval(q(i,:),x1(i));%系数endp=Dw*q;syms x L8;for i=1:nL8(i)=p(n-i+1)*x^(i-1);enddisp('8次拉格朗日插值');L8=vpa(collect((sum(L8))),5)xi=0:64;yi=polyval(p,xi);figureplot(xi,yi,x1,y1,'r*');hold ontitle('8次拉格朗日插值');结果如下:8次拉格朗日插值L8 =- 3.2806e-10*x^8 + 6.7127e-8*x^7 - 5.4292e-6*x^6 + 0.00022297*x^5 - 0.0049807*x^4 + 0.060429*x^3 - 0.38141*x^2 + 1.3257*x输出图如下:第五章4-1(3)程序:clc;clear;y= @(x) sqrt(x).*log(x);a=0;b=1;tol=1e-4;p=quad(y,a,b,tol);fprintf('采用自适应辛普森积分结果为: %d \n', p); 结果如下:采用自适应辛普森积分结果为: -4.439756e-01第九章9-1(a)程序:clc;clear;a=1;b=2;%定义域h=0.05;%步长n=(b-a)/h;y0=1;%初值f= @(x,y) 1/x^2-y/x;%微分函数Xn=linspace(a,b,n+1);%将定义域分为n等份Yn=zeros(1,n);%结果矩阵Yn(1)=y0;%赋初值%以下根据改进欧拉公式求解for i=1:nxn=Xn(i);xnn=Xn(i+1);yn=Yn(i);yp=yn+h*f(xn,yn);yc=yn+h*f(xnn,yp);yn=(yp+yc)/2;Yn(i+1)=yn;endXn=Yn;%以下根据经典四阶R-K法公式求解for i=1:nxn=Xn(i);yn=Yn(i);k1=f(xn,yn);k2=f(xn+h/2,yn+h/2*k1);k3=f(xn+h/2,yn+h/2*k2);k4=f(xn+h,yn+h*k3);yn=yn+h/6*(k1+2*k2+2*k3+k4);Yn(i+1)=yn;enddisp(' 改进欧拉法四阶经典R-K法'); disp([Xn' Yn'])结果如下:改进欧拉法四阶经典R-K法1 10.99887 0.998850.99577 0.99780.99114 0.996940.98532 0.996340.97857 0.996030.97111 0.996060.96311 0.996450.9547 0.997230.94598 0.998410.93705 10.92798 1.0020.91883 1.00440.90964 1.00730.90045 1.01060.89129 1.01430.88218 1.01840.87315 1.02290.86421 1.02780.85538 1.03310.84665 1.0388(b)程序:clc;clear;a=0;b=1;%定义域H=[0.1 0.025 0.01];%步长y0=1/3;%初值f= @(x,y) -50*y+50*x^2+2*x;%微分函数xi=linspace(a,b,11);Y=1/3*exp(-50*xi)+xi.^2;%准确解Ym=zeros(1,11);for j=1:3h=H(j);n=(b-a)/h;Xn=linspace(a,b,n+1);%将定义域分为n等份Yn=zeros(1,n);%结果矩阵Yn(1)=y0;%赋初值for i=1:nxn=Xn(i);yn=Yn(i);k1=f(xn,yn);k2=f(xn+h/2,yn+h/2*k1);k3=f(xn+h/2,yn+h/2*k2);k4=f(xn+h,yn+h*k3);yn=yn+h/6*(k1+2*k2+2*k3+k4);Yn(i+1)=yn;endfor k=1:11m=0.1/h;Ym(k)=Yn(1+(k-1)*m);enddelta=Ym-Y;fprintf('步长为: %d \n', h);disp(' 四阶经典R-K法准确解误差'); disp([Ym' Y' delta'])end结果如下:步长为: 1.000000e-01四阶经典R-K法准确解误差0.33333 0.33333 04.6055 0.012246 4.593263.062 0.040015 63.022864.05 0.09 863.9611844 0.16 118431.6235e+05 0.25 1.6235e+052.2256e+06 0.36 2.2256e+063.0509e+07 0.49 3.0509e+074.1823e+08 0.64 4.1823e+085.7333e+09 0.81 5.7333e+097.8594e+10 1 7.8594e+10步长为: 2.500000e-02四阶经典R-K法准确解误差0.33333 0.33333 00.013015 0.012246 0.000768940.040063 0.040015 4.82e-050.090037 0.09 3.6857e-050.16004 0.16 3.6723e-050.25004 0.25 3.6722e-050.36004 0.36 3.6722e-050.49004 0.49 3.6722e-050.64004 0.64 3.6722e-050.81004 0.81 3.6722e-051 1 3.6722e-05步长为: 1.000000e-02四阶经典R-K法准确解误差0.33333 0.33333 00.012256 0.012246 9.5673e-060.040016 0.040015 7.8252e-070.090001 0.09 6.6347e-070.16 0.16 6.6226e-070.25 0.25 6.6225e-070.36 0.36 6.6225e-070.49 0.49 6.6225e-070.64 0.64 6.6225e-070.81 0.81 6.6225e-071 1 6.6225e-07由结果可知,步长越小,结果越精确。
9-3主程序:clc;clear;options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-4]); [X,Y] = ode45(@rigid,[0 0.004],[1 1 0],options);subplot(1,2,1);plot(X,Y(:,1),'-',X,Y(:,2),'-.',X,Y(:,3),'.');title('四阶R-K方法');legend('y1', 'y2','y3');[X,YY] = ode23t(@rigid,[0 0.004],[1 1 0],options); subplot(1,2,2);plot(X,YY(:,1),'-',X,YY(:,2),'-.',X,YY(:,3),'.'); title('梯形法');legend('y1', 'y2','y3');rigid函数function dy = rigid (~,y)dy = zeros(3,1); % a column vectordy(1) = -0.013*y(1)-1000*y(1)*y(2);dy(2) = -2500*y(2) * y(3);dy(3) =-0.013*y(1)-1000*y(1)*y(2)-2500*y(2) * y(3);结果如图:。
