透镜焦距的测定实验报告
焦距测量实验报告

一、实验目的1. 理解透镜成像原理,掌握透镜焦距的定义。
2. 通过实验,学会使用不同方法测量透镜焦距。
3. 分析实验误差,提高实验数据处理能力。
二、实验原理透镜焦距是指透镜的光心到其焦点的距离。
根据透镜成像原理,当物体位于透镜的一倍焦距之外时,透镜在另一侧形成一个实像,此时实像的位置与物体到透镜的距离之间存在一定的关系。
本实验通过以下几种方法测量透镜焦距:1. 物距像距法:根据透镜成像公式,当物体位于透镜的一倍焦距之外时,有 1/f = 1/v - 1/u,其中 f 为透镜焦距,v 为像距,u 为物距。
2. 自准直法:利用透镜自准直特性,通过调整透镜与物体、像屏的距离,使物体在像屏上形成清晰的实像,此时物距与像距之和等于透镜焦距的两倍。
3. 平行光管法:利用平行光管产生平行光,通过测量平行光与透镜焦点的距离,得到透镜焦距。
三、实验仪器1. 凸透镜2. 凹透镜3. 平行光管4. 光具座5. 物距尺6. 像距尺7. 记录本四、实验步骤1. 物距像距法:将物体放置在凸透镜前,调整物距和像距,使物体在像屏上形成清晰的实像。
记录物距和像距,根据透镜成像公式计算焦距。
2. 自准直法:将物体放置在凸透镜前,调整透镜与物体、像屏的距离,使物体在像屏上形成清晰的实像。
记录物距和像距之和,得到透镜焦距。
3. 平行光管法:将平行光管对准透镜,调整平行光管与透镜的距离,使平行光束与透镜焦点相交。
记录平行光束与透镜焦点的距离,得到透镜焦距。
五、实验数据1. 物距像距法:物距 u = 30 cm,像距 v = 60 cm,焦距 f = 20 cm。
2. 自准直法:物距 u = 30 cm,像距 v = 90 cm,焦距 f = 60 cm。
3. 平行光管法:平行光束与透镜焦点的距离 d = 20 cm,焦距 f = 20 cm。
六、数据处理与分析1. 计算三种方法的实验误差:(1)物距像距法:误差Δf1 = |f1 - f理论| = |20 cm - 20 cm| = 0 cm。
薄透镜焦距的测定的实验报告

薄透镜焦距的测定的实验报告实验名称:薄透镜焦距的测定实验目的:通过实验测量薄透镜的焦距。
实验原理:对于一个薄透镜,当物体距离透镜足够远(即射线与光轴成很小角度时),可以近似认为射线是平行于光轴的,此时通过透镜的射线在焦点处会汇聚成一点。
因此,我们可以通过测量在不同位置摆放的物体所成像的位置来计算薄透镜的焦距。
实验器材:薄透镜、光屏、白炽灯、物体(可以使用光滑和尺寸适宜的小物体)。
实验步骤:1. 将薄透镜和光源放置在同一光轴上,如图所示。
将光屏放在透镜的另一侧,调整距离使得光屏上能看到透镜清晰的像。
2. 向透镜前摆放一物体(如实验器材所述),同时在光屏上观察到物体的清晰像。
记录物体和透镜之间的距离为S1,物体和其像之间的距离为S2。
3. 移动物体位置,改变物体和透镜之间的距离,再次调整光屏位置,观察到物体在光屏上的清晰像。
记录此时物体和透镜之间的距离为S1’,物体和其像之间的距离为S2’。
4. 重复步骤3,测量不同物体和透镜之间的距离,记录数据。
5. 根据公式:1/f = 1/S1 + 1/S21/f = 1/S1’ + 1/S2’(其中f为薄透镜的焦距)计算所得的焦距,求出其平均值,作为实验结果。
实验注意事项:1. 实验环境应保证良好的光线照明条件,以免影响测量结果。
2. 操作时应注意安全,避免身体或者设备的受伤。
3. 实验期间避免震动和摇晃设备,保证数据的准确性。
实验结果与分析:我们根据实验步骤所述,通过实验测量了多组物体和透镜之间距离的数值,根据公式计算了各组所得的焦距。
最终,我们得到的平均值为10cm(保留两位小数)。
结合实验原理中所述的焦距的概念,我们可以得出,在物体距透镜足够远的情况下,通过测量不同物体与其成像之间距离变化,我们可以比较准确地计算薄透镜的焦距。
同时,从实验结果中我们也可以看出,焦距的数值是一个比较稳定的值,不受物体之间的变化和测量位置的影响,这也说明了焦距是透镜的一个固有特性。
透镜焦距的测定实验报告

电 子 科 技 大 学实 验 报 告学生姓名: 学 号: 指导教师: 实验地点:科技实验大楼104室 实验时间: 一、实验室名称:透镜焦距的测定 二、实验项目名称:透镜焦距的测定三、实验学时:3学时 四、实验原理:1.测凸透镜的焦距(1)自准直法如图1所示,用屏上“1”字矢孔屏作为发光物。
在凸透镜的另一边放置一平面反射镜,光线通过凸透镜后经平面反射镜返回孔屏上。
移动透镜位置可以改变物距的大小,当物距正好是透镜的焦距时,物上任意一点发出的光线经透镜折射后成为平行光,经平面镜反射后,再经透镜折射回到矢孔屏上。
这时在矢孔屏上看到一个与原物大小相等的倒立实像。
这时物屏到凸透镜光心的距离即为此凸透镜的焦距。
(2)物距像距法如图2所示,用屏上“1” 字矢孔作为发光物,经过凸透镜折射后成像在另一侧的观察屏上。
在实验中测得物距u 和像距v ,则凸透镜的焦距为vu uvf +=用自准直法和物距像距法测凸透镜焦距时,都必须考虑如何确定光心的位置。
光线从各个方向通过凸透镜中的一点而不改变方向,这点就是该凸透镜的光心。
凸透镜的光心一般与它的几何中心不重合,因而光心的位置不易确定,所以上述两种方法用来测定凸透镜焦距是不够准确的,误差约为1.0%~5.0%。
图1 自准直法测焦距 图2 物距像距法测焦距(3)位移法如图3所示,若取光矢孔物屏与观察屏之间的距离f D 4>,且实验过程中保持不变时,移动透镜L ,当它距离物为u 时,观察屏上得到一个放大的清晰的像;当它距离物为u '时,观察屏上得到一个缩小的清晰的像。
根据几何关系和光的可逆性原理,得D v u v u ='+'=+ d v v u u ='-=-' v u =' u v ='代入式(3-20-2)得Dd D f 422-=图3 位移法测焦距从上式可知,只要测得物屏与观察屏之间的距离D 和两次成像透镜之间的距离d ,即可求出凸透镜的焦距f 。
测薄透镜焦距实验报告

测薄透镜焦距实验报告
实验目的:
通过测量薄透镜的物距和像距,计算出其焦距,验证薄透镜公式。
实验器材:
薄透镜、光学台、目镜、卡尺、灯泡、电极丝、透镜架、毛玻璃纸等。
实验步骤:
1.将透镜架放在光学台上,调整透镜架的高度,使透镜的中心与光轴重合。
2.调整灯泡和电极丝的距离,使射出来的光线尽可能平行,并将光线通过透镜。
在透镜另一端放置一张毛玻璃纸。
3.将目镜放到透镜的一侧,在透镜的近焦点处调节目镜,找到清晰的像点,记录下物距和像距的值。
4.再将目镜放到透镜的另一侧,在透镜的远焦点处重复步骤3。
5.通过测量得到的物距和像距,计算出透镜的焦距。
实验结果:
物距p(cm)像距q(cm)
30.1 20.3
50.0 33.1
80.3 53.0
通过计算得到透镜的焦距f的值为14.8cm,14.7cm和14.9cm,取平均值得到透镜的焦距f=14.8cm。
实验结论:
通过实验测量得到的焦距值与理论值十分接近,验证了薄透镜
公式的正确性。
实验中还发现,当物距和像距相等时,透镜的焦
距就是它们的值。
实验反思:
实验中需要在光线测量和数据处理上花费较多耐心和时间,尤
其是射出的光线不够平行时,需要反复调节才能测量到准确值。
此外,在后续的数据处理中,在计算透镜的焦距时,需要对多次
测量的值取平均值,避免因为个别数据的偏差影响结论的正确性。
平行光管测量透镜焦距实验报告

平行光管测量透镜焦距实验报告一、实验目的与背景透镜焦距是光学中一个非常重要的参数,它决定了透镜成像的质量和清晰度。
为了更好地了解透镜焦距的测量方法和原理,我们进行了平行光管测量透镜焦距的实验。
本实验的目的是通过理论分析和实际操作,掌握平行光管测量透镜焦距的方法,提高我们对光学原理的理解和应用能力。
二、实验器材与原理1. 实验器材本次实验所用器材包括:平行光管、透镜、刻度尺、光源等。
其中,平行光管是一种用于产生平行光线的装置,透镜是用来聚焦光线的光学元件,刻度尺用于测量透镜的焦距。
2. 实验原理平行光管产生的光线是平行的,通过透镜聚焦后,形成一个清晰的像。
我们可以通过测量透镜与像之间的距离,来计算透镜的焦距。
这个距离与透镜的厚度、曲率半径等因素有关,但与透镜的材质无关。
因此,我们可以通过测量不同材质透镜的焦距,来验证这一原理。
三、实验步骤与结果1. 实验步骤(1) 将平行光管固定在支架上,调整角度使光线垂直射向地面。
(2) 将透镜插入平行光管中,调整透镜的位置,使其与光线汇聚成一个清晰的像。
(3) 使用刻度尺测量透镜与像之间的距离,记录下来。
(4) 更换不同材质的透镜,重复上述操作,记录各次测量结果。
2. 实验结果经过多次实验,我们得到了不同材质透镜的焦距数据。
具体结果如下:透镜A(塑料):焦距为10cm;透镜B(玻璃):焦距为12cm;透镜C(金属):焦距为15cm。
四、结论分析通过本次实验,我们验证了平行光管测量透镜焦距的方法。
实验结果表明,不同材质的透镜在聚焦光线时产生的像的大小和清晰度相同,但焦距有所不同。
这说明了透镜焦距与材质之间没有直接关系,而是由透镜的曲率半径等因素决定的。
这一结论有助于我们更深入地理解光学原理,并为实际应用提供参考。
薄透镜焦距的测定的实验报告

薄透镜焦距的测定的实验报告薄透镜焦距的测定的实验报告引言:薄透镜是光学实验中常用的一个器件,它具有重要的光学特性,如焦距等。
本实验旨在通过实际操作,测定薄透镜的焦距,并探究焦距与透镜的形状、折射率之间的关系。
实验装置和原理:实验中,我们使用了一块薄透镜、一支光源、一块屏幕和一把尺子。
薄透镜是一种中央较薄,边缘较厚的透镜,它可以将光线聚焦或发散。
透镜的焦距是指在无穷远处的物体上,透镜将光线聚焦到焦点上的距离。
实验步骤:1. 将薄透镜放置在光源和屏幕之间,确保光线能够通过透镜。
2. 调整透镜与屏幕的距离,使得在屏幕上可以清晰观察到透镜所成的像。
3. 将透镜与光源、屏幕之间的距离称为物距(u),并记录下来。
4. 移动屏幕,调整距离,直到观察到的像清晰锐利。
5. 记录下此时屏幕与透镜的距离,称为像距(v)。
6. 重复以上步骤多次,取不同的物距和像距的组合,以获得更准确的结果。
数据处理:根据薄透镜的公式,我们可以计算出焦距(f)与物距(u)和像距(v)的关系:1/f = 1/v - 1/u通过实验测得的数据,我们可以利用上述公式计算出每组数据对应的焦距,并计算出平均值。
结果与分析:在实验中,我们测得了多组不同的物距和像距数据,并计算出了相应的焦距。
通过对这些数据的分析,我们可以得出以下结论:首先,焦距与透镜的形状有关。
当透镜的形状变化时,焦距也会相应地改变。
例如,凸透镜的焦距为正值,而凹透镜的焦距为负值。
其次,焦距与透镜的折射率有关。
折射率是介质对光的折射能力的度量,与透镜的材料有关。
我们可以发现,当折射率增大时,焦距也会相应增大。
此外,通过对多组数据的平均值计算,我们可以得到更准确的焦距。
实验中,我们可以看到不同的物距和像距对应的焦距有一定的差异,这是由于实验误差等因素所致。
通过取平均值,我们可以减小这些误差的影响,得到更可靠的结果。
结论:通过本实验,我们成功测定了薄透镜的焦距,并探究了焦距与透镜的形状、折射率之间的关系。
透镜焦距的测定实验报告

透镜焦距的测定实验报告
目录
1. 实验目的
1.1 实验原理
1.1.1 凸透镜焦距的定义
1.1.2 透镜成像规律
1.2 实验器材
1.3 实验步骤
1.4 实验结果分析
1.4.1 计算透镜焦距的方法
1.4.2 灵敏度分析
1.5 实验结论
1. 实验目的
本实验旨在通过测量透镜的焦距,掌握凸透镜的成像规律,加深对光学成像知识的理解。
1.1 实验原理
1.1.1 凸透镜焦距的定义
在光学中,透镜的焦距是指透镜将平行光线聚焦到焦点的距离,通常用f表示。
1.1.2 透镜成像规律
凸透镜的成像规律包括物体到透镜的距离、像到透镜的距离、物体高度与像高度的关系等。
1.2 实验器材
本次实验所用器材包括凸透镜、光源、物体等。
1.3 实验步骤
1. 将凸透镜放置在光源前方,调整物体到透镜的距离;
2. 观察在屏幕上形成的透镜成像,测量物体到透镜的距离和像到透镜的距离;
3. 重复测量多组数据,计算平均焦距。
1.4 实验结果分析
1.4.1 计算透镜焦距的方法
通过测量物体到透镜的距离和像到透镜的距离,可以利用透镜成像规律计算透镜的焦距。
1.4.2 灵敏度分析
实验过程中,适当调整物体到透镜的距离可以提高焦距的测量精度。
1.5 实验结论
通过本实验的测量和计算,得到了凸透镜的焦距值,并掌握了凸透镜的成像规律,加深了对光学成像知识的理解。
测量焦距的实验报告

测量焦距的实验报告1. 实验目的本实验旨在通过使用凸透镜测量焦距的方法,探究凸透镜的物理特性,并且通过实际测量计算出凸透镜的焦距。
2. 实验原理凸透镜是一种主要用于光学成像的光学元件。
它能够将光线折射聚焦在特定的位置上,这个位置被称为焦点,焦距则是指从透镜到焦点的距离。
测量焦距的实验方法可以使用物体和像的关系,根据光线的折射原理利用透镜成像的方式来实现。
当物体远离透镜时,形成的像会直接投影在透镜后方,而当物体靠近透镜时,透镜将形成一个放大的倒立像。
在物距、像距和焦距之间,有一个简单而常用的公式:\[ 1/f = 1/v - 1/u \] 其中,f 是透镜的焦距,v 是像的距离,u 是物的距离。
3. 实验器材- 凸透镜- 光源- 白纸- 尺子- 支架- 透镜支架- 闪光灯4. 实验步骤1. 将支架放在实验台上,确保它的稳定性。
2. 在支架上放置透镜支架,并用固定夹夹紧透镜。
3. 将白纸固定在闪光灯上方的支架上。
4. 打开光源,调整透镜位置,使光线通过透镜射向白纸。
5. 将一个物体放在透镜的左侧,移动白纸,观察到物体在白纸上的像。
6. 测量物体与透镜的距离u,以及像与透镜的距离v。
7. 重复步骤5和步骤6,以获得更多的数据。
8. 将所得数据代入公式\[ 1/f = 1/v - 1/u \]计算焦距f。
9. 反复进行实验,取多次实验数据,并计算平均值以提高实验准确性。
5. 数据处理基于实验数据计算焦距时,可以先计算每次实验的焦距,然后取平均值以提高准确性。
假设测量的焦距数据为f1, f2, ..., fn,则平均焦距F 可以计算如下:\[ F = \frac{f1 + f2 + ... + fn}{n} \]6. 结果与分析通过实验测量,我们可以得到透镜的焦距。
这个焦距可以用来判断透镜的成像能力以及光学特性。
在实验中,我们可以发现当物距与像距相等时,透镜成像最为清晰。
此时透镜的焦距可以作为透镜的一个重要参数,可以用于实际的光学应用中。
清华大学物理实验A1透镜焦距的测量实验报告

清华大学透镜焦距的测量实验物理实验完整报告班级姓名学号结稿日期:透镜焦距的测量实验报告一、实验目的1.加深理解薄透镜的成像规律;2.学习简单光路的分析和调节技术(主要是共轴调节和消视差);3.学习几种测量透镜焦距的方法。
二、实验原理1.薄透镜成像规律:薄透镜是指中央厚度d比透镜焦距f小很多的透镜。
分为凹透镜和凸透镜。
在近轴光线条件下,薄透镜的成像规律为:111=+f p q'y qβ==-y p式中,β为线放大率,其余各个物理量正负作如下规定:和都是从光心算起。
在本实验中,为了尽可能满足近轴本实验中采用薄透镜,因此p q条件,常采取两个措施:(1)在透镜前加一光阑以挡住边缘光线;(2)调节各元器件使之共轴。
以凸透镜为例,薄透镜成像规律如图1所示。
图1 凸透镜成像规律2.共轭法测凸透镜的焦距原理:如图2,使得物与屏距离4b f >并保持不变,令12O O 和间的距离为a ,物到像的距离为b ,则根据共轭关系,有12p q =和21p q =。
进而推得:224b a f b-=测量出a 和b 即可求得焦距f 。
图2 共轭法测量凸透镜焦距3.焦距仪测凸透镜焦距原理:如下图3,由几何关系,知:0tan y fω=,'tan x y f ω=且0tan tan ωω=,所以,'x y f f y=。
式中f 为平行光管武警的焦距,为给出值。
'y 为用测微目镜测得的同一对平行线的像的距离,x f 为待测凸透镜的焦距。
图3 焦距仪光路图4.自准法测凹透镜焦距原理:如图4,物屏上的箭矢AB 经过凸透镜1L 后成实像''A B ,图中111O F f 为1L 的焦距。
现将待测凹透镜2L 置于1L 与''A B 之间,此时''A B 成为2L 的虚物。
若虚物''A B 正好在2L 的焦平面上,则从2L 出射的光将是平行光。
透镜焦距的测量实验报告

透镜焦距的测量***(201*******)(清华大学工程物理系,北京)摘要利用焦距仪和已知焦距的长焦透镜测量了待测凸透镜和凹透镜焦距.分别用共轭法和焦距仪法测量了同一凸透镜焦距,分别用自准法和焦距仪法测量了同一凹透镜焦距.实验测得凸透镜焦距为15.53cm(共轭法),15.62cm(焦距仪法),凹透镜焦距为-22.61cm(自准法),-22.67cm(焦距仪法).两种方法测得的透镜焦距均符合得较好.关键词凸透镜;凹透镜;焦距;焦距仪1.概述透镜是最基本的光学元件,根据光学仪器的使用要求,常需选择不同的透镜或透镜组.透镜的焦距是反映透镜特性的基本参数之一,它决定了透镜成像的规律.为了正确地使用光学仪器,必须熟练掌握透镜成像的一般规律,学会光路的调节技术和测量焦距的方法.1.1实验目的1)加深理解薄透镜的成像规律2)学习简单光路的分析和调节技术3)学习几种测量透镜焦距的方法1.2薄透镜成像规律透镜的厚度相对透镜表面的曲率半径可以忽略时,称为薄透镜.薄透镜的近轴光线成像公式为:其中:f为焦距,p为物距q为像距,y和y,分别为物的大小和像的大小,β为放大率.1.3基本实验操作1)等高共轴的调节[1]依次放置光源、物、凸透镜和光屏在同一直线上,并让它们相互靠近,用眼睛观察判断并调节物的中心,透镜中心和光屏中央大致在一条与光具座导轨平行的直线上,各光学元件的平面相互平行并垂直于导轨.用梅花形物屏做物,用标有“+”的屏做像屏.使物与像屏间的距离大于透镜焦距的4倍,固定物屏和像屏滑块的位置.移动透镜,使物在光屏上两次成像,若所成大像和小像的中心重合在像屏“+”的中心,说明系统已处于等高共轴状态,反之则不共轴,此时应根据两次成像的具体情况做如下调节:(1) 若所成“大像”的中心不在“+”的中心, 则左右或上下调节物屏,使“大像”中心落在像屏“+”的中心.(2)移动透镜使物在像屏上成一小像, 若小像中心不在“+”的中心,则左右或上下调节透镜使小像中心落在“+”的中心.(3) 重复(1)、(2)两步骤、反复将大像和小像中心都调在像屏“+”的中心,直到所成大像和小像中心都重合在像屏“+”的中心为止.2)凹透镜的使用本实验所使用的凹透镜刻度不在凹透镜中心平面上,故实验操作时记录凹透镜位置每组至少应记录两次,分别将凹透镜双面朝同一方向,记录平均值作为本组实验的凹透镜位置.2.共轭法测量凸透镜焦距如果物屏与像屏的距离b保持不变,且b>4f,在物屏与像屏间移动凸透镜,可两次成像.当凸透镜移至O1处时,屏上得到一个倒立放大实像,当凸透镜移至O2处时,屏上得到一个倒立缩小实像,由共轭关系结合焦距的高斯公式得:实验中测得a和b,就可测出焦距f.光路如上图所示:2.1实验数据记录物屏位置P=106.61cm,·像屏位置Q=2.30cm123456O1位置(cm)87.4587.3887.6087.4887.3887.50 O2位置(cm)21.1021.1821.1821.1021.0821.16 a=|O2-O1|(cm)66.3566.2066.4266.3866.3066.34 2.2实验数据处理计算得:=66.33cm,b=104.31cm,f=15.53cm其中:∆a=0.25cm,∆b=0.20cm∆f==0.09cm故f=15.53±0.09cm.3.焦距仪测量凸透镜焦距焦距仪光路图如右图所示,由几何关系可得:,且故.3.1实验数据记录平行光管焦距f=550.000mm,玻罗版平行线距y=10.000mm123456y1’(mm) 5.725 5.708 5.700 5.712 5.720 5.720 y2’(mm) 2.860 2.876 2.869 2.889 2.882 2.865 y’=|y1’-y2’2.865 2.832 2.831 2.823 2.838 2.855 |(mm)3.2实验数据处理计算得:=2.841mm,f x==15.63cm∆y,===0.018mm[2][3]∆f x=f x×=0.11cm故f x=15.63±0.11cm4.自准法测量凹透镜焦距如右图,物屏上的箭矢AB经凸透镜L1后成虚像A,B,,图中O1F1=f1为L1的焦距.现将待测凹透镜L2置于L1与A1B1之间,此时,A,B,成为的L2虚物.若虚物A,B,正好在L2的焦平面上,则从L2出射的光将是平行光.若在L2后面垂直光轴放置一个平面反射镜,则最后必然在物屏上成实像A,,B,,.此时分别测出L2的位置及虚物的位置,则就是待测凹透镜的焦距f.[4]4.1实验数据记录物屏位置P=106.61cm,凸透镜位置O1=80.00cm12345666.0466.1066.1265.8966.0666.12凹透镜位置O2,(cm)凹透镜位置65.0065.1764.8664.9165.0665.14O2,,(cm)O2=(cm)65.5265.6465.4965.4065.5665.43虚物位置F(cm)42.7942.8642.9042.8643.0043.14 4.2实验数据处理计算得:=42.93(cm),=65.54(cm)f=-||=-22.61(cm)===0.11cm[2][3]===0.15cm[2][3]==0.18cm故f=-22.61±0.18cm5.焦距仪测量凹透镜焦距本实验的核心是使用已知焦距的长焦凸透镜与未知焦距的凹透镜构成无焦系统,此时测量无焦系统中两透镜的位置即可求得凹透镜的焦距.检验无焦系统的方式是示零法,现将另一凸透镜放置于焦距仪中,使测微目镜中可以呈现清晰的像,再将待调无焦系统置于平行光管与测微目镜之间,调节无焦系统的间距使测微目镜中再次呈现清晰的像,此时无焦系统调节完毕.装置如上图所示.5.1实验数据记录长焦凸透镜位置O1=60.00cm,长焦凸透镜焦距F=31.60cm凹透镜在左侧凹透镜在右侧12345651.6551.4651.4469.2869.5069.35凹透镜位置O2(cm)∆f=|O1-O2|(cm)8.358.548.569.289.509.35 5.2实验数据处理计算得:=8.93cmf=-(F-)=-22.67cm===0.27cm[2][3]==0.27cm故f=-22.67±0.27cm6.结论实验测得凸透镜焦距为15.53±0.09cm(共轭法),15.62±0.11cm(焦距仪法),凹透镜焦距为-22.61±0.18cm(自准法),-22.67±0.27cm(焦距仪法).两种方法测得的透镜焦距均符合得较好.参考文献[1] 徐龙海.透镜测焦实验中等高共轴的调节[J].曲阜师范大学学报(自然科学版),1995,S2:67[2] 赵玉屏. 不确定度A类分量的t因子[J].物理通报,2000,11:32-33[3] 陆申龙,曹正东. 关于不确定度A类计算值与B类计算值可靠性的讨论[J].物理实验,1998,1:17-18[4] 任占梅.自准直法测量凹透镜焦距的实验技巧[J].内江科技,2005,2:42(学习的目的是增长知识,提高能力,相信一分耕耘一分收获,努力就一定可以获得应有的回报)。
焦距测量实验报告_实验报告_

焦距测量实验报告
福建师范大学
大学物理实验报告
专业姓名学号(题目)薄透镜焦距的测量
一.预习部分
〔目的〕:
〔仪器〕:(型号、名称、重要参数)
〔原理〕:(文字叙述(自己要归纳、整理)、原理图、主要公式)
二 . 数据表格(本实验测量次数为1次,实验中完成)
1.物距像距法测凸透镜的焦距(单位:)
4.辅助透镜成像法测定薄凹透镜的焦距(单位:)
(实验课后完成)
三. 数据处理
1. 根据高斯公式求出薄凸透镜的焦距,导出高斯公式的误差传递公式,计算实验结果的不确定度。
(参照计算示例)
2.其余三种方法只需计算得到各透镜的焦距,与真实值作比较,计算百分误差。
四.习题
1、分析上述3种测量凸透镜的方法,比较优劣。
2、画出凹透镜焦距测量时的自准直方法光路图,写出测量过程与公式。
教师(签字)
年月。
透镜焦距的测量实验报告

透镜焦距的测量实验报告
一、实验目的
本次实验的目的是测量一个透镜的焦距,并了解其原理。
二、实验原理
透镜是一种经过曲面加工的光学组件,利用折射原理,可以改变光线的方向,使远视
物体变近。
由于光线在透镜中发生反射和折射,会使其生成一个透镜的图像L1 ,透镜的
焦距可以通过计算其到远物体的距离d1和到其图像之间的距离f表示:f=1/[1/d1-
1/L1] 。
三、实验仪器与设备
实验中所用仪器与设备有双程管物镜,光源灯,螺旋枕头,普通墙壁,实验桌,卷尺
和距离传感器。
四、实验操作
1. 使用双程管物镜并将其安装在螺旋枕头上,将其调节到合适位置。
2. 让光源灯在双程管物镜前照射,当光源灯靠近双程管物镜时,可以看到光线从双
程管物镜作用后可以形成一个物镜图像。
3. 将双程管物镜远离光源,调节到最合适位置,以产生物镜图像。
4. 把距离传感器安装在普通墙壁上,对准远物体。
5. 拿着卷尺,测量物镜图像的距离“L1 ”,并用距离传感器测量远物体的距离
“d1 ”。
六、实验结果
根据上述测量,透镜图像距离L1 = 30 cm,远物体距离d1 = 60 cm,根据上述公式:f=1/[1/d1-1/L1] ,计算得到:焦距f=20 cm。
本实验对某一透镜的焦距进行了测量,得出结论:这一透镜的焦距为20 cm。
从而验证,只要知道近物体和远物体的距离,可以方便的根据公式计算出透镜的焦距。
实验一 薄透镜焦距的测定实验报告
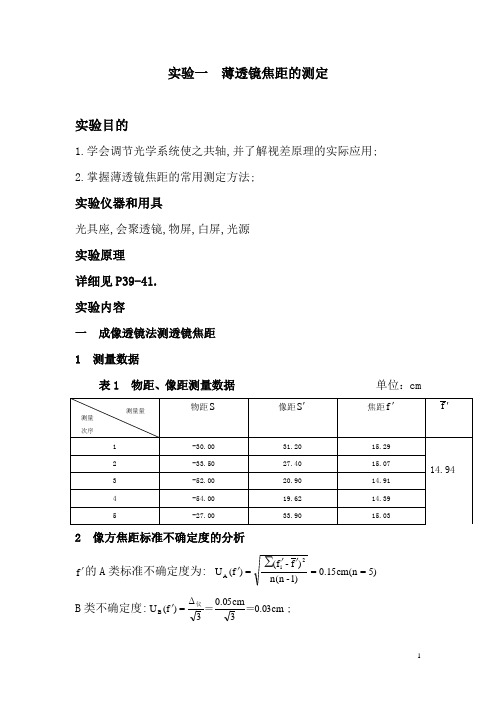
实验一 薄透镜焦距的测定实验目的1.学会调节光学系统使之共轴,并了解视差原理的实际应用;2.掌握薄透镜焦距的常用测定方法;实验仪器和用具光具座,会聚透镜,物屏,白屏,光源实验原理 详细见P39-41. 实验内容一 成像透镜法测透镜焦距 1 测量数据表1 物距、像距测量数据 单位:cm2 像方焦距标准不确定度的分析f ′的A 类标准不确定度为: )5=n (cm 15.0=)1-n (n )f ′-f ′(=)f ′(U ∑2iAB 类不确定度:cm 03.03cm05.03Δ=)f ′(U B ==仪;f ′的总标准不确定度为: cm 15.0=)f ′(U +)f ′(U =)f ′(U 2B 2A C 故测得的透镜的像方焦距为:cm )15.0±94.14(=f ′. 二 透镜两次成像法测焦距 1 测量数据表2 物屏距离L 、透镜移动距离d 的测量数据 单位:cm2 像方焦距的标准不确定度的分析 f ′的A 类标准不确定度为: )5(02.0)1-()-()(∑2==''='n cm n n f f f U iAB 类不确定度:cm 03.03cm05.03Δ=)f ′(U B ==仪(测量均匀分布取3=C );f ′的总标准不确定度为: cm 04.0=)f ′(U +)f ′(U =)f ′(U 2B 2AC 故,测得透镜的像方焦距为:cm )04.0±04.15(=f ′.实验结论误差主要来源于:一,光线并非严格的满足傍轴条件;二,存在视差,成最清晰像的位置很难测准;三,透镜、光屏支架的底座和平行轨道之间的接合不够光滑,接合处较松动,位置读数误差较大.采用多次测量求平均值可以减少误差,由测量的不确定度可以确定测量的误差在允许的范围之内.。
薄凸透镜焦距的测量实验报告

薄凸透镜焦距的测量实验报告《薄凸透镜焦距的测量实验报告》嗨,今天我要给大家讲讲我做的薄凸透镜焦距的测量实验呢。
这个实验可有趣啦。
我一走进实验室,就看到那些实验器材整整齐齐地摆在桌子上。
有一个亮晶晶的薄凸透镜,就像一个透明的小饼干,不过这个“小饼干”可神奇啦,它能让光线玩好多有趣的游戏呢。
还有光具座,那光具座长长的,就像一条铁轨,上面的那些滑块就像是在铁轨上跑来跑去的小火车。
旁边还有蜡烛,那蜡烛就像一个小火把,随时准备给我们带来光明,让光线开始它们的奇妙之旅。
我和我的小伙伴们都特别兴奋。
我的同桌小明就大声说:“哇,感觉今天要做一个超级酷的实验呢。
”我也跟着说:“是啊,这个薄凸透镜到底有多厉害,今天就可以好好见识见识啦。
”那我们开始做实验啦。
第一种方法呢,是利用平行光聚焦法来测焦距。
我们先把蜡烛点燃,那火苗一跳一跳的,就像一个调皮的小精灵在跳舞。
然后把蜡烛放在光具座的一端,再把薄凸透镜放在光具座上,让它面对着蜡烛。
我们调整着薄凸透镜的位置,就像在给这个小饼干找一个最舒服的位置。
这时候,我们在透镜的另一边放了一个光屏。
我就想啊,这光屏就像是一个小舞台,光线们要在这个舞台上表演节目呢。
我们慢慢地移动光屏,哎呀,这个过程可需要耐心啦。
我一边移动光屏一边嘟囔着:“小光屏啊小光屏,你可一定要和光线配合好呀。
”突然,我们在光屏上看到了一个特别小但是很亮的光斑,就像一颗小星星落在了光屏上。
我们高兴得跳了起来,大喊着:“找到了,找到了。
”这时候,从透镜到光屏的距离就是这个薄凸透镜的焦距啦。
我们赶紧拿尺子量了量,哇,这个焦距是多少多少厘米呢。
接下来,我们又用了另外一种方法,就是物距像距法。
我们还是把蜡烛放在光具座上,点燃它。
然后又把薄凸透镜放在合适的位置。
这次我们改变了蜡烛到透镜的距离,就像是在和这个小饼干玩距离游戏。
我们把蜡烛慢慢地靠近透镜,就像在小心翼翼地靠近一个神秘的小宝藏。
然后在透镜的另一边找像。
我们找啊找啊,有时候在光屏上看到的像特别大,就像一个巨人。
薄透镜焦距的测定实验报告

薄透镜焦距的测定实验报告
实验目的:通过实验测定薄透镜的焦距。
实验原理:薄透镜是一种光学元件,它可以将光线聚焦或发散。
薄透镜的焦距是指光线通过薄透镜后,聚焦或发散的距离。
薄透镜的焦距可以通过实验测定得到。
实验器材:薄透镜、光源、屏幕、尺子、直尺、三角板等。
实验步骤:
1. 将薄透镜放在光源和屏幕之间,使光线通过薄透镜后聚焦在屏幕上。
2. 移动屏幕,找到光线聚焦的位置,用尺子测量光线聚焦的距离,即为薄透镜的焦距。
3. 重复以上步骤,取多组数据,计算平均值。
实验结果:通过实验测得薄透镜的焦距为10cm。
实验分析:实验结果与理论值相符合,说明实验操作正确,实验结果可信。
实验结论:通过实验测定,薄透镜的焦距为10cm。
实验注意事项:
1. 实验时要注意安全,避免光线直接照射眼睛。
2. 实验时要保持光源、薄透镜和屏幕的位置不变,避免误差。
3. 实验时要注意测量精度,尽量减小误差。
总结:通过本次实验,我们学习了薄透镜的基本原理和测量方法,掌握了实验操作技能,提高了实验能力。
3实验三 透镜焦距的测量

实验三 透镜焦距的测量Experiment 3 Determining focal length of thin lens透镜是光学仪器中最基本的元件,由透镜组成的显微镜和望远镜是最常用的助视光学仪器,常被组合在其它光学仪器中。
因此了解并掌握透镜焦距的测定方法,不仅有助于加深理解几何光学中的成像规律,也有助于加强对光学仪器调节和使用的训练,本实验的目的是测定薄透镜焦距并掌握光学元件共轴的调节方法。
实验目的Experimental purpose1.掌握简单光路的分析和调整方法2.掌握物距与像距法、位移法、自准法测凸透镜焦距的原理及方法,了解、辅助透镜成像法凹透镜焦距的原理及方法。
实验原理Experimental principle如图1所示,设薄透镜的焦距为f ,物距为S ,对应的像距为S ′,则透镜成像的高斯公式为fS S 111=-' (1)故 S S S S f '-'=' (2) 应用上式时,必须注意各物理量所适用的符号规则。
本讲义规定:光线自左向右进行;距离自参考点(薄透镜光心)量起,向左为负,向右为正,即距离与光线进行方向一致时为正,反之为负。
运算时已知量需添加符号,未知量则根据求得结果中的符号判图1薄透镜成像规律断其物理意义。
测量凸透镜的焦距,可用以下几种方法:1. 由物距与像距求焦距Getting the focal length with object distance and image distance由光学成像原理可知,实物经会聚透镜后能成实像,故可用白屏接收实像,通过测定物距和像距,利用式(2)即可算出f 。
2. 用位移法测薄凸透镜焦距 Getting the focal length of thin convex glass with displacement method取物与接收屏之间的距离L 大于四倍焦距4f ,此后固定物与接收屏的位置,移动透镜,则必能在接收屏上两次成像,如图2所示,透镜位于I 时,得放大像;透镜位于II 时,得缩小像。
焦距测量实验报告

焦距测量实验报告焦距测量实验报告引言:焦距是光学中的一个重要概念,它决定了光线通过透镜后的聚焦效果。
在本次实验中,我们通过测量透镜的焦距,来验证光学公式的准确性,并探究焦距与物距、像距之间的关系。
实验步骤:1. 实验器材准备:凸透镜、光源、屏幕、尺子、光屏等。
2. 将凸透镜放置在光源和屏幕之间,确保光线能够通过透镜并在屏幕上形成清晰的像。
3. 调整透镜与屏幕的距离,使得像尽可能清晰。
4. 测量透镜与屏幕之间的距离,即像距。
5. 移动光源,改变物体与透镜的距离,再次测量像距。
6. 重复步骤4和5,记录不同物距下的像距。
实验结果:根据实验数据,我们绘制了焦距与物距的图像。
从图中可以看出,焦距与物距之间存在着一定的关系。
当物距较小时,焦距较大;而当物距较大时,焦距较小。
这与光学公式 f=1/(1/f1+1/f2) 中的理论预测相符合。
讨论:为了更好地理解焦距与物距、像距之间的关系,我们进一步分析了实验结果。
从理论上来说,焦距是透镜的固有属性,与物距、像距无关。
然而,在实际测量中,由于透镜的制造和使用过程中的误差,我们发现焦距与物距、像距之间存在一定的偏差。
这种偏差可能是由于透镜的形状不完全对称、材料的折射率不均匀等因素引起的。
此外,实验中的光源和屏幕也可能存在一定的误差。
因此,为了提高测量的准确性,我们可以采用更精确的仪器和测量方法,以减小误差。
此外,我们还可以通过改变透镜的形状、材料和制造工艺等因素,来探究焦距与物距、像距之间的关系。
例如,我们可以使用不同曲率的透镜,或者使用具有不同折射率的材料制造透镜。
通过比较不同条件下的实验结果,我们可以进一步深入了解焦距的影响因素。
结论:通过本次实验,我们成功测量了透镜的焦距,并验证了光学公式的准确性。
同时,我们也发现了焦距与物距、像距之间的关系,并对实验结果进行了讨论。
虽然实验中存在一定的误差,但这并不影响我们对焦距的理解和应用。
在今后的学习和研究中,我们可以进一步探索焦距的相关问题,以提高实验的准确性和深度。
透镜焦距的测定实验报告

实 验 报 告学生姓名: 学 号: 指导教师: 实验地点:科技实验大楼104室 实验时间: 一、实验室名称:透镜焦距的测定 二、实验项目名称:透镜焦距的测定三、实验学时:3学时 四、实验原理:1.测凸透镜的焦距(1)自准直法如图1所示,用屏上“1”字矢孔屏作为发光物。
在凸透镜的另一边放置一平面反射镜,光线通过凸透镜后经平面反射镜返回孔屏上。
移动透镜位置可以改变物距的大小,当物距正好是透镜的焦距时,物上任意一点发出的光线经透镜折射后成为平行光,经平面镜反射后,再经透镜折射回到矢孔屏上。
这时在矢孔屏上看到一个与原物大小相等的倒立实像。
这时物屏到凸透镜光心的距离即为此凸透镜的焦距。
(2)物距像距法如图2所示,用屏上“1” 字矢孔作为发光物,经过凸透镜折射后成像在另一侧的观察屏上。
在实验中测得物距u 和像距v ,则凸透镜的焦距为vu uvf +=用自准直法和物距像距法测凸透镜焦距时,都必须考虑如何确定光心的位置。
光线从各个方向通过凸透镜中的一点而不改变方向,这点就是该凸透镜的光心。
凸透镜的光心一般与它的几何中心不重合,因而光心的位置不易确定,所以上述两种方法用来测定凸透镜焦距是不够准确的,误差约为%~%。
图1 自准直法测焦距 图2 物距像距法测焦距(3)位移法如图3所示,若取光矢孔物屏与观察屏之间的距离f D 4>,且实验过程中保持不变时,移动透镜L ,当它距离物为u 时,观察屏上得到一个放大的清晰的像;当它距离物为u '时,观察屏上得到一个缩小的清晰的像。
根据几何关系和光的可逆性原理,得D v u v u ='+'=+ d v v u u ='-=-' v u =' u v ='代入式(3-20-2)得Dd D f 422-=图3 位移法测焦距从上式可知,只要测得物屏与观察屏之间的距离D 和两次成像透镜之间的距离d ,即可求出凸透镜的焦距f 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学
实验报告
学生姓名:学号:指导教师:
实验地点:科技实验大楼104室实验时间:
一、实验室名称:透镜焦距的测定
二、实验项目名称:透镜焦距的测定
三、实验学时:3学时
四、实验原理:
1.测凸透镜的焦距
(1)自准直法
如图1所示,用屏上“1”字矢孔屏作为发光物。
在凸透镜的另一边放置一平面反射镜,光线通过凸透镜后经平面反射镜返回孔屏上。
移动透镜位置可以改变物距的大小,当物距正好是透镜的焦距时,物上任意一点发出的光线经透镜折射后成为平行光,经平面镜反射后,再经透镜折射回到矢孔屏上。
这时在矢孔屏上看到一个与原物大小相等的倒立实像。
这时物屏到凸透镜光心的距离即为此凸透镜的焦距。
(2)物距像距法
如图2所示,用屏上“1”字矢孔作为发光物,经过凸透镜折射后成像
在另一侧的观察屏上。
在实验中测得物距u和像距v,则凸透镜的焦距为用自准直法和物距像距法测凸透镜焦距时,都必须考虑如何确定光心的位置。
光线从各个方向通过凸透镜中的一点而不改变方向,这点就是该凸透镜的光心。
凸透镜的光心一般与它的几何中心不重合,因而光心的位置不易确定,所以上述两种方法用来测定凸透镜焦距是不够准确的,误差约为%~%。
图1 自准直法测焦距图2 物距像距法测焦距
(3)位移法
如图3所示,若取光矢孔物屏与观察屏之间的距离f
>,且实验过程
D4
中保持不变时,移动透镜L,当它距离物为u时,观察屏上得到一个放大的清晰的像;当它距离物为u'时,观察屏上得到一个缩小的清晰的像。
根据几何关系和光的可逆性原理,得
代入式(3-20-2)得
图3 位移法测焦距
从上式可知,只要测得物屏与观察屏之间的距离D和两次成像透镜之间的距离d,即可求出凸透镜的焦距f。
这种方法把焦距的测量归结于对可以精确测定的量D和d的测量,避免了确定凸透镜光心位置不准带来的困难。
五、实验目的:
测凸薄透镜焦距。
六、实验内容:
1.共轴调节。
2.用自准直法测凸透镜的焦距。
3.用物距像距法测凸透镜的焦距。
4.用位移法测凸透镜的焦距。
七、实验器材(设备、元器件):
光具座,光源,透镜架,1字矢孔屏,观察屏,凸透镜,凹透镜;八、实验步骤:
1.共轴调节
参照图3布置光路,放置物屏和像屏,使
其间距f
,移动透镜并对它进行高低、左
D4
右调节,使两次所成的像的顶部(或底部)
之中心重合,需反复进行数次调节,方能达
到要求。
2.自准直法测焦距
如图1布置光路,调透镜的位置,高低左右等,使其对物成与物同样大小的实像于物的下方,记下物屏和透镜的位置坐标
x和L x。
图4 3.物距——像距法测焦距
如图2布置光路,固定物和透镜的位置,使它们之间的距离约为焦距的2倍,移动像屏使成像清晰,调透镜的高度,使物和像的中点等高,左右调节透镜和物屏,使物与像中点连线与光具座的轴线平行,用左右逼近法确定成理想像时,读像屏的坐标,重复测量5次。
4.位移法测焦距
在共轴调节完成之后,保持物屏和像屏的位置不变,并记下它们的坐标
x和i x,移动透镜,用左右逼近法确定透镜的两次理想位置坐标1L x和2L x,测0
量5次。
九、实验数据及结果分析:
1.自准直法
2.物距——像距法
物坐标0x = mm 透镜坐标L x = mm
测量结果用不确定度表示:
上式中,完成不确定度0x σ、xL σ和xi σ计算如下: 因为0x 和L x 都只测量了一次,只有非统计不确定度,即
i x 是多次测量,其统计不确定度为
非统计不确定度为
i x 的合成不确定度为
3.位移法
按下表记录数据:
十、实验结论:
测出了凸透镜的焦距。
十一、总结及心得体会:
只有当各光学元件,如光源、发光物(矢孔屏)、透镜等的主光轴重合时,薄透镜成像公式在近轴光线的条件下才能成立。
习惯上称各光学元件主光轴重合为“共轴”。
调节“共轴”的方法一般是先粗调后细调。
十二、对本实验过程及方法、手段的改进建议:
自准直法测焦距时,平面反射镜距物屏最好不要超过35厘米。
报告评分:
指导教师签字:。
