著名机构讲义秋季18-8年级数学拓展版--直角三角形的判定、性质和推论-课后作业学生版

合集下载

北师大版八年级数学下册课件.1直角三角形的性质与判定课件

第1章三角形的证明
1.2 直角三角形
第1课时直角三角形的性质与判定
教学目标
1.了解直角三角形两锐角互余及互逆命题的转化 2.运用勾股定理逆定理判定直角三角形
重难点
1.熟练掌握勾股定理逆定理的证明方法 2.互逆命题的真假性判定
提出问题，导入新课
问题1 直角三角形的定义是什么？有一个是直角的三角形叫直角三角形.
归纳新知
勾股定理：直角三角形两条直角边的平方和等于斜边的平方．
定理：如果一个三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形．
条件和结论互换
上面两个定理的条件和结论有什么关系吗？与同伴交流.
探求新知
再视察下面三组命题：
如果两个角是对顶角，那么它们相等；如果两个角相等，那么它们是对顶角.
知识回顾
勾股定理：直角三角形两条直角边的平方和等于斜边的平方. 即 a2 + b2 = c2. 勾股定理在西方文献中又称为毕达哥拉斯定理.
a
c
b
勾
弦
股
提出问题探求新知
勾股定理是一个真命题，那么把这个命题的条件和结论颠倒过来，形成一个新的命题：
如果一个三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形．
解：（1）多边形是四边形.原命题是真，逆命题是假.（2）同旁内角互补，两直线平行.原命题是真，逆命题是真.（3）如果那么 a = 0， b = 0，那么 ab = 0.原命题是假，逆命题是真.
课堂小结
角的性质
直角三角形
边的性质
定理1：直角三角形的两个锐角互余定理2：有两个角互余的三角形是直角三角形
如果小明患了肺炎，那么他一定会发烧；如果小明发烧，那么他一定患了肺炎.

湘教版八年级数学下册《1.1直角三角形的性质和判定》公开课精品课件

腰三角形“三线合一”的性质解题．
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判有两个角互余的三定角形是直角三角形
直角三角形斜边上的中线等于斜边的一半.
第1章直角三角形
1.1 直角三角形的性质和判定（Ⅰ）
第2课时含30°角的直角三角形的性质及其应用
学习目标
1.理解和掌握有关30°角的直角三角形的性质和应用; （重点）
总结归纳
有两个角互余的三角形是直角三角形.
A
应用格式：
在△ABC 中，
∵ ∠A +∠B =90°，
∴ △ABC 是直角三角形．B
C
典例精析例3 如图，∠C=90 °, ∠1= ∠2，△ADE是直角三
角形吗？为什么？
解：在Rt△ABC中，
∠2+ ∠A=90 °. ∵ ∠1= ∠2,
∴∠1 + ∠A=90 °. 即△ADE是直角三角形.
可得BC=CD=
1 2
AB.
B
C
D
证法1
证明：取线段AB的中点D，连接CD.
∵CD为Rt△ABC斜边AB上的中线，
CD

1 2
AB =
BD
C
∵∠BCA =90°，且∠A=30°，
∴∠B=60°，
B
∴△CBD为等边三角形，
BC
=
BD

1 2
AB.
证明方法：中线法
30° A D
证法2
证明：在△ABC 中， ∵ ∠C =90°，∠A =30°, ∴ ∠B =60°．
第1章直角三角形
1.1直角三角形的性质和判定（Ⅰ）

著名机构讲义秋季20-8年级数学拓展版--期末复习-教师版

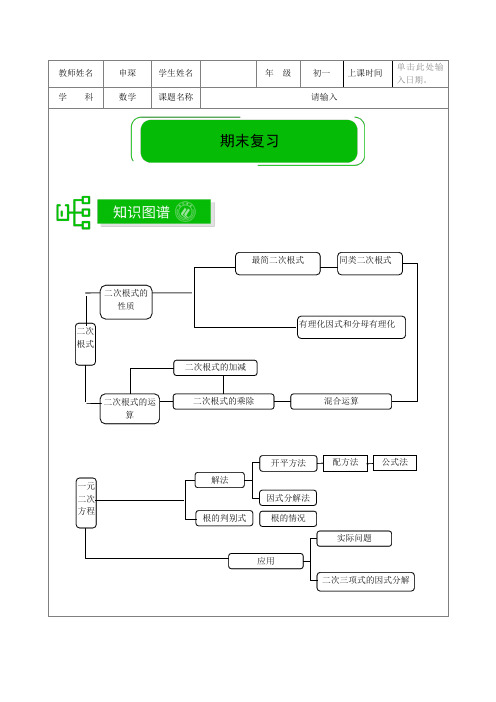
教师姓名申琛学生姓名年级初一上课时间单击此处输入日期。

学科数学课题名称请输入二次根式的性质解法二次三项式的因式分解配方法平行向量因式分解法实际问题应用二次根式的加减二次根式的乘除混合运算最简二次根式有理化因式和分母有理化同类二次根式二次根式二次根式的运算一元二次方程开平方法公式法平行向量根的判别式根的情况期末复习一、选择题【练习1】下列二次根式中，最简二次根式是（）A ．15 B ．5C ．0.5D ．50【答案】B 【解析】5551=；22215.0==；2550=．函数的定义域和求函数值定义依据函数勾股定理的逆定理直角三角形的性质演绎推理几何证明勾股定理直角三角形全等的判定线段的垂直平分线定理及逆定理角的平分线定理及逆定理正比例函数概念、图像和性质反比例函数概念、图像和性质正反比例函数综合运用命题实际问题变量与常量点的轨迹函数的常用表示法：解析法列表法图像法公理定理逆命题逆定理【解析】解：令018 42= -+xx ，由()08014482>=-⨯⨯-=∆由公式法得：12252522x x+-=-=-，；所以225254814(225)(225)22x x x x x x⎛⎫⎛⎫+-+-=++=+++-⎪⎪⎪⎪⎝⎭⎝⎭，故选C．【练习12】已知函数()0y kx k=≠中y随x的增大而增大，那么它和函数()0ky kx=≠在同一直角坐标系平面内的大致图像可能是（）．【答案】D【解析】Θ函数()0≠=kkxy中y随x的增大而增大；0>∴k∴函数()0≠=kkxy和函数()0≠=kxky的图像都在一、三象限，故D正确．【练习13】如图，A、C是函数1yx=的图象上任意两点，过点A作y轴的垂线，垂足为B，过点C作y轴的垂线，垂足为D，记AOBRt△的面积为1S，CODRt△的面积为2S，则1S和2S的大小关系是（）．A．21SS>B．21SS<EDBCAC ．1S =2SD ．由A 、C 两点的位置确定【答案】C【解析】Θ点A 和点C 都在反比例函数图像上，212121===∴xy S S ，故选C ．【练习14】如图，有一块直角三角形纸片，两直角边AC =6cm ，BC =8cm ，现将直角边AC 沿直线AD折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）A ．2cmB ．3cmC ．4cmD ．5cm【答案】B【解析】解：在ABC Rt ∆中，由勾股定理得：cm AB 10=，再由折叠的性质可得6CD DE AE AC cm===，，所以cm AE AB BE 4=-=，且AB DE ⊥；设CD 为x ，则x BD -=8，x DE =，在DEB Rt ∆中，有222BD DE BE =+，即()22284x x -=+，解得：cm x 3=．故B 项正确【练习15】在△ABC 中，AB =15，AC =13，BC 边上的高AD =12，则△ABC 的周长是（） A ．42B ．32C ．42或32D ．37或33【答案】A【解析】ΘBC AD ⊥，∴在ADC Rt ∆中，由勾股定理得：222AD AC CD -=，所以5=CD ，同理可得：222AD AB BD -=，所以9=BD ．当△ABC 为锐角三角形时，1495=+=+=CD BD BC ，则△ABC 的周长42151413=++=；当△ABC 为钝角三角形时，954BC BD CD =-=-=，则△ABC 的周长1341532=++=；故选C二、填空题【练习16】（1）若211()x x x y ---=+，则x -y 的值为_______；（2）使(2)(1)21x x x x -+=-⋅+成立的条件是______；（3）二次根式m n +的有理化因式是__________．_______________；（2）某厂计划今年的产值为a 比前年翻一番，且这两年的增长率相同，则这三年的总产值是_____________．【答案】（1）()960001760002=+x ；（2）3222a a +．【解析】根据平均增长率问题的方程类型()b x a n=±1来列方程：（1）()960001760002=+x ；（2）设增长率为x ，则2(1)2x +=，解得：21x =-，故这三年的总产值为：1132(121)2222a a a a a ++-+=+．【练习23】（1）在实数范围内分解因式：2361x x -+=________________；（2）若一元二次方程2210mx x +-=在实数范围内有实数根，则m 的取值范围是___________________．【答案】（1）⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+-3633633x x ；（2）01≠-≥m m 且．【解析】（1）令01632=+-x x ，由()2643240∆=--⨯=>，所以由公式法得：12363633x x +-==，，故⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+-=+-36336331632x x x x ．（2）由题意得：044≥+=∆m 且0≠m ；解得：01≠-≥m m 且．【练习24】计算：113185044252⎛⎫+-÷ ⎪ ⎪⎝⎭=____________．【答案】2．【解析】()22422229242145051183=÷-+=÷⎪⎪⎭⎫ ⎝⎛-+．【练习25】如图，Rt ABC ∆中，9040ACB A D ∠=∠=o o ，，为AB 中点，CE AB ⊥，则DCE ∠=_____．C【答案】ο10．【解析】οΘ90=∠ACB ，D 为AB 中点，CD AD =∴，ο40=∠=∠∴A ACD ，AB CE ⊥Θ，∴οοο5090180=∠--=∠A ACE ， οοο104050=-=∠-∠=∠∴ACD ACE DCE ．【练习26】（1）如果正比例函数y = kx （k ≠0）的自变量取值增加7，函数值相应减少4，那么当x =4时，y =_________；（2）若x 与-3y 成反比例函数关系，y 与-4z 成反比例函数关系，则x 与z 成__________比例函数．【答案】（1）716-；（2）反．【解析】（1）由题意得：()()74+=-x k y ，即k kx y 74+=-，代入kx y =中，解得：74-=k ，所以正比例函数为x y 74-=，故当4=x 时，716-=y ．（2）由题意得：1234k kx y y z =-=-，，所以1122433()4k k x z k k z=-=⋅-，故x 与z 成反比例函数．【练习27】（1）如图，已知在△ABC 中，CD 平分∠ACD ，∠A =2∠B ，BC =a ，AD =b ，则AC =________（用含a 、b 的代数式表示）；（2）在△ABC ，AB =BC ，BD =DC ，BC =CE ，则图中一定相等的角（小于平角)有______对．【答案】（1）b a -；（2）3．【解析】（1）如图所示，在BC 上截取CE ，使得AC CE =，连接DE ΘCD 平分ACD ∠，∴ECD ACD ∠=∠，又ΘCD CD CE AC ==，，ECD ACD ∆≅∆∴，ABCD （1）EABCD（2）CED A b DE AD ∠=∠==∴；，又ΘEDB B CED B A ∠+∠=∠∠=∠，2，EDB B ∠=∠∴，b AD DE BE ===∴，又Θ，a BC = b a BE BC CE AD -=-==∴．（2）BCA BAC ∠=∠；BEA BAD ∠=∠；CAE DAC ∠=∠．【练习28】（1）如图，在Rt △ABC 中，∠C =90度，BC =24cm ，∠BAC 的平分线AD 交BC 于点D ，BD ：DC =5：3，则点D 到AB 的距离为_______cm ；（2）等腰直角三角形ABC 的斜边BC =4，△DBC 为等边三角形，那么A 、D 两点的距离是____________；（3）在矩形ABCD 中，AB :AD =1:2，将点A 沿折痕DE 对折，使点A 落在BC 上的F 点，则∠ADE =______度．【答案】（1）9；（2）232232+-或；（3）15．【解析】（1）作AB DE ⊥于E ，Θcm BC DC BD 243:5:==，，cm DC 9=∴， ΘAD 是BAC ∠的平分线，AB DE C ⊥=∠，ο90， cm DC DE 9==∴．（2）分两种情况：①连接AD ，交BC 于E ，ΘDBC ∆为等边三角形，4===∴BC CD BD ，AC AB =Θ，∴AD 垂直平分BC ，12902AE BC DEB ∴==∠=o ，，322422=-=∴DE ，232+=+=∴AE DE AD ； ②如图示，由①得：32=DE ，2=AE ， 232-=-=∴AE DE AD ；所以2-32232或+=AD ．（3）如图所示：由题意可得2:1:=AD AB ，由翻折性质AD DF =，则在中CDF Rt ∆2:1:=CF DC ，故ο30=∠DFC ；在矩形ABCD 中，CF AD //，所以ο30=∠=∠DFC ADF ，故ο1521=∠=∠=∠ADF EDC ADE ．【练习29】一元二次方程()21230k x kx k -+++=有两个不相等的实数根，求k 的最大整数值____________．【答案】0．【解析】由题意得：()()()012831422>+-=+--=∆k k k k ，解得：23<k 且10k -≠，即1≠k ，所以k 的取值范围为23<k 且1≠k ．所以k 的最大整数值为0．【练习30】方程()012017201520162=-⨯-x x 的较大根m ，方程22015201610x x -+=较小根为n ，则m -n 的值_______________．【答案】20152014．【解析】Θ()012017201520162=-⨯-x x ，∴()()()01120161201620162=-+--x x ， ∴()012016201622=-+-x x x ，即()()01120162=-+-x x x ，∴()()01201612=+-x x ，解得：122112016x x ==-，， 1=∴m ，又Θ01201620152=+-x x ，∴()()0112015=--x x ，解得：12112015x x ==，，∴20151=n ，故20152014201511=-=-n m ．【练习31】 △AOC 与△DCE 均为等边三角形，点A 、D 均在双曲线3(0)y x x=>上，点O 为坐标原点，点C 、E 在x 轴上，A 、D 的坐标分别是______________．【答案】()13A ，；()2163D+-，．【解析】如图，过点A 作x AH ⊥轴于点H ，过点D 作x DF ⊥轴于点F ．AOC ∆Θ为等边三角形，∴设()3A a a ，AOC DEyxH F又Θ点A 在双曲线()03>=x xy 上， ∴332=a ，解得：1=a 或1-=a （舍），则点A 的坐标为()13，；同理，设()()32D b b -，，则()323=-b b ，解得：12+=b （负值舍去），则点D 的坐标为()2163+-，．【练习32】已知三角形ABC 为等腰直角三角形，且A （2，3），B 、C 分别在坐标轴上，则点B 的坐标分别是______________．【答案】见解析．【解析】如图所示：()110B -，；()220B ，；()350B ，；()405B ，；()503B ，；()601B ，．三、解答题【练习33】（1）已知212a =-，求224421a a a a -+-+的值；（2）已知：52321x x y -+-=+，求x y +的值．【答案】（1）224-；（2）1．【解析】（1）()0212212<+-=-=a Θ，【答案】见解析【解析】解：设每件售价定为x 元()10>x ，由题意得：()()[]{}6405.010102008=÷---x x 化简得：0192282=+-x x ，解得：121216x x ==，当12=x 时，()[]{}1605.01010200=÷--x ；当16=x 时，()[]{}805.01010200=÷--x ．所以售价定为12元时每天可售160件，售价定为16元时每天可售80件，利润可达每天640元．【练习37】已知正比例函数()11y k x =+的图像经过()()242A B m -，、，两点．（1）求m 的值；（2）如果点B 在反比例函数()220k y k x=≠的图像上，求反比例函数的解析式．【答案】（1）1-=m ；（2）xy 2-=．【解析】（1）因为正比例函数图像经过()42-，A ，所以()4121-=+k ，解得：31-=k ，所以正比例函数解析式为x y 2-=，由题意得，当2=y 时，22=-m ，得：1-=m ；（2）由点B 在反比例函数图像，得：2212-=⨯-=k ，所以反比例函数解析式为xy 2-=．【练习38】如图，在△ABC 中，∠C =90度，AC =BC ，AD 平分∠CAB ，AB =20cm ．求AC +CD 的长．【答案】20cm ．【解析】过D 作AB DE ⊥，垂足为点E ，Θο90=∠C ，DEA C ∠=∠∴．ΘAD 平分CAB ∠，EAD CAD ∠=∠∴．在ACD ∆和AED ∆中，⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD DAE CAD AED C ，ABCD EAED ACD ∆≅∆∴，AC AE CD DE ∴==，．又90AC BC ACB =∠=o Q ，，ABC ∆∴是等腰直角三角形， ο45=∠=∠∴CAB B ，οοο454590180=--=∠∴BDE ， ∴B EDB ∠=∠，∴EB DE CD ==， ∴cm AB EB AE CD AC 20==+=+．【练习39】如图：在四边形ABCD 中，∠C =90°，=3=412=13BC CD AD AB =，，，，求四边形ABCD的面积．【答案】36．【解析】Θο90=∠C ，43==CD BC ，，∴由勾股定理得：522=+=DC BC BD ，Θ1213==AD AB ，，∴222AB BD AD =+，ο90=∠∴ADB ， ∴四边形ABCD 的面积36125214321=⨯⨯+⨯⨯=+=∆∆ABD BCD S S S ．【练习40】小智和小方沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米，小智骑自行车，小方步行，当小智从原路回到学校时，小方刚好到达图书馆，图中折现O ——A ——B ——C 和线段OD 分别表示两人离学校的路程y （千米）与所经过的时间x （分钟）之间的函数关系，请根据图像回答下列问题：（1）小智在图书馆查阅资料的时间为_______分钟，小智返回学校的速度为_________千米/分钟；（2）请你求出小方离开学校的路程y （千米）与所经过的时间x （分钟）之间的函数关系．【答案】（1）15，154；（2）()450454≤≤=x x y ．【解析】（1）1515-30=（分钟），154154=÷（min /km ），所以小智在图书馆查阅资料的时间为15分钟，ABCDx （分钟）y （千米） 15 3045AB小智 O 小方4C D小智返回学校的速度为154千米/分钟．（2）由图像可知，y 是x 的正比例函数，设所求函数的解析式为()0≠=k kx y ，代入()454，，得：k 454=，解得：454=k ，所以y 与x 的函数关系式为：()450454≤≤=x x y ．【练习41】如图，在四边形ABCD 中，∠ABC =∠ADC =90°，对角线AC 与BD 相交于点O ，M 、N 分别是边AC 、BD 的中点．（1）求证：MN BD ⊥；（2）当∠BCA =15°，AC =8cm ，OB =OM 时，求MN 的长．【答案】见解析．【解析】（1）证明：连接DM BM 、．Θο90=∠=∠ADC ABC ，点M 、点N 分别是边BD AC 、的中点，∴AC DM BM 21==． ΘN 是BD 的中点，∴BD MN ⊥．（2）ΘAC CM BM BCA 2115===∠，ο， ∴ο15=∠=∠CBM BCA ，ο30=∠∴BMA ．OM OB =Θ，ο30=∠=∠∴BMA OBM ， 182AC BM AC ==Q ，， 4=∴BM ．在BMN Rt ∆中，οο3090=∠=∠NBM BNM ，，221==∴BM MN ．ABCD NMO【练习42】已知：如图()a ，在等腰三角形ABC 中，∠C =90°，AD 是∠CAB 的平分线．（1）求证：AB =AC +CD ；（2）把原题中的“∠C =90°”改为“∠C =100°”，其余条件不变，如图()b ，请说出AB 、AD 、CD 之间的数量关系，并证明．【答案】见解析．【解析】（1）在边AB 上截取AC AE =；ΘAD 是CAD ∠的角平分线，∴DAB CAD ∠=∠， AC AE AD AD ==，Θ，AED ACD ∆≅∆∴， ο90=∠=∠=∴C AED DE CD ，，AC AB =Θ，ο45=∠=∠∴B CAB ，ο45=∠=∠∴B BDE ， CD BE DE ==∴，∴CD AC BE AE AB +=+=；（2）CD AD AB +=．证明：在AB 上截取AD AF AC AE ==，， 100AC BC C =∠=o Q ，，ο40=∠=∠∴B BAC ，又ΘAD 平分CAB ∠，∴ο20=∠=∠BAD CAD ，由（1）得AED ACD ∆≅∆，∴ο100=∠=∠=C AED CD DE ，，∴ο80=∠DEB ， Θο20=∠=FAD AD AF ，，∴ο80=∠=∠AFD ADF ，∴CD DE DF ==， Θοο40100=∠=∠B BFD ，，∴ο40=∠FDB ，则CD DF FB ==， ∴CD AD BF AF AB +=+=．ABCD（图a ）ABCD（图b ）EE F【练习43】已知：在△ABC 中，AB =AC ，AD ⊥BC ，垂足为D ，BE ⊥AC ，垂足为E ，M 为AC 的中点，联结DE ，DM 设C α∠=．（1）当△ABC 时锐角三角形时（如图），试用α表示∠EDM ；（2）当△ABC 时钝角三角形时，请画出相应的图形，并用α表示∠EDM （可直接写出）．【答案】（1）ο1803-=∠αEDM ；（2）α3180-=∠οEDM ．【解析】（1）ΘAB AC AD BC =⊥，，CD BD =∴，ΘAC BE ⊥，∴BC DE CD 21==，∴α21802180-=∠-=∠οοC CDE ，又ΘBC AD ⊥，M 为AC 中点，∴AC DM CM 21==，∴α=∠=∠C CDM ，∴()οο18032180-=--=∠-∠=∠αααCDE CDM EDM ．（2）如图，同（1）可得：α21802180-=∠-=∠οοC CDE ，α=∠=∠C CDM ，∴ααα31802180-=--=∠-∠=∠οοCDM CDE EDM ．【练习44】如图，在气象站台A 的正西方向240千米的B 处有一台风中心，该台风中心以每小时20千米的速度沿北偏东60°的BD 方向移动，在距离台风中心130千米内的地方都要受其影响．（1）台风中心在移动的过程中，与气象台A 的最短距离是多少?（2）台风中心在移动的过程中，气象台将受台风的影响，求台风影响气象台的时间会持续多长?【答案】（1）km 120；（2）5小时．【解析】（1）如图，过点A 作BD AE ⊥于E ， Θ台风中心在BD 上移动，AB CD EMABC D 东北60.0°E∴AE 就是气象台距离台风中心的最短距离，在ABE Rt ∆中，24030AB km ABE =∠=o ，， ∴km AB AE 12021==，所以台风中心在移动过程中，与气象台A 的最短距离为km 120；（2）由题意得：线段CD 就是气象台A 受到台风影响的路程，在ACE Rt ∆中，km AE km AC 120,130==，∴km AE AC CE 501201302222=-=-=，ΘAC AD AE CD =⊥，，km ED CE 50==∴，∴km CD 100=，∴台风影响气象台的时间会持续520100=÷（小时）．【练习45】如图，在平面直角坐标系中，已知第一象限内的点A 的坐标为（1，m ）OA =2，正比例函数3x y m=和反比例函数1k y x -=的图像都经过点A ，过点A 作OA 的垂线交x 轴于点B ．（1）求m 和k 的值；（2）求点B 的坐标．【答案】（1）3=m ；13+=k ；（2）()40B ，．【解析】（1）Θ第一象限内的点A 的坐标为()1m ，，在正比例函数mxy 3=的图像上，∴mm 13⨯=，解得：3±=m ， Θ正比例函数经过第一、三象限，∴3=m ，则()13A ，，代入xk y 1-=，解得：13+=k ．（2）由（1）得()13A ，，设点B 的坐标为()0a ，， ∴()23122=+=AO ，a BO =，()()2231+-=a AB ，由题意得：OA BA ⊥．则在OAB Rt ∆中，由勾股定理：222BO AO AB =+，所以()22431a a =++-，解得：4=a ，A BOxy所以()40B ，．【练习46】如图，细心观察，认真分析各式，如何解答问题：211(1)122S +== 222(2)132S +== 233(3)142S +==．．．．．．．．．．．．（1）用含有n （n 是正整数）的等式表述上述的变化规律；（2）推算出10OA 的长；（3）求出222212310...S S S S ++++的值．【答案】（1）()N n nS n ∈=2；（2）1010=OA ；（3）455．【解析】（1）由已知式子可得：()112+=+n n ，()N n nS n ∈=2；（2）由图可得：11=OA ，22222=⨯=OA ，32323=⨯=OA ，所以1010=OA ；（3）由（1）、（2）得：()45510 (2141)...210232221=+++=++++S S S S ．【练习47】如图，在平面直角坐标系中，已知△AOB 是等边三角形，点A 的坐标是A 1 A 2A 3A 4A 5A 6S 5OS 1S 2S 3S 4（0，3），点B 在第一象限，点P 是x 轴正半轴上的一个动点，连接AP ，并把△AOP 绕着点A 按逆时针方向旋转，使边AO 与AB 重合，得到△ABD ．（1）当点P 运动到点30（，）时，求此时DP 的长及点D 的坐标；（2）若△OPD 的面积等于34，请求出符合条件的点P ．【答案】（1）32=DP ，D ()233，；（2）7302P ⎛⎫- ⎪ ⎪⎝⎭，．【解析】（1）ΘAOB ∆是等边三角形，∴ο60=∠OAB ， ΘAOP ∆绕着点A 按逆时针方向旋转边AO 与AB 重合，∴旋转角ο60=∠=∠=PAD OAB ，AP AD =， ∴APD ∆是等边三角形，∴AP DP =．Θ()()0330A P，，，，∴()323322=+=AP ，∴3023OAP DP AP ∠===o ，， ∴ο90=∠+∠=∠PAD OAP OAD ．∴点D 坐标为()233，，32=DP ．（2）过点D 作DH ⊥x 轴于点H ，连接OD ，设点(0)P x ，，因为点P 是x 轴正半轴上的一个动点，所以OP x =，易证3322DH x =+，Θ12OPD S OP DH =⋅⋅V ， ∴1333()2224x x ⋅⋅+=，解得：372x -±=，Θ0x >， ∴732x -=．故P 点坐标为7302P ⎛⎫- ⎪ ⎪⎝⎭，．【练习48】已知：在△ABC 中，AB =6，AC =5，∠A 为锐角，△ABC 的面积为9，点P 为ABP DO xyH边AB 上动点，过点B 作BD ∥AC ,交CP 的延长线于点D ，∠ACP 的的平分线交AB 于点E ．（1）如图1，当CD ⊥AB 时，求PE 的长；（2）如图2，当点E 为AB 中点时，请猜想并证明：线段AC 、CD 、DB 的数量关系．【答案】（1）23=PE ；（2）BD CD AC +=．【解析】（1）过点E 作EF ⊥AC 于点FΘAB CD ⊥，∴921=⋅=∆CP AB S ABC ， 6=AB Θ， ∴3=CP ．在ACP Rt ∆中，由勾股定理得：222CP AP AC +=， 5=AC Θ，4=∴AP ．ΘCE 平分ACP ∠，CD ⊥AB ，EF ⊥AC ， ∴PE EF =易证CPE CFE ≅V V ， 3CF CP ∴==， 2AF ∴=．在Rt AEF V 中，222AF EF AE +=Q ，2222(4)PE PE ∴+=-， 23=∴PE ；（2）连接DE 并延长交AC 于点F ，Θ//BD AC BE EA =，，∴DE EF DEB FEA =∠=∠，， ∴FEA DEB ∆≅∆，∴DB AF =，又ΘFC AF AC +=，FC BD AC +=∴， EF DE =Θ，CE 平分FCD ∠， ∴DF CE ⊥，∴CD FC =， BD CD AC +=∴．【练习49】如图，已知点()34A ，，AB ⊥X 轴，垂足为点B ，将△AOB 绕点O 逆时针旋转90°，得到''AOB△．（1）在图中画出''AOB △，并直接写出''A B 、的坐标；A BCDE P 图1P ABCDE图2F（2）求'OA 的长；（3）在y 轴上是否存在点C ，使得△'AOC 为等腰三角形，如果存在，请求出所有符合条件的点C的坐标；如果不存在，请说明理由．【答案】见解析．【解析】（1）()43A '-，；()03B '，．（2）()53422=+-='A O ．（3）存在，①1C 为以A '为圆心，O A '为半径与y 轴的交点，即C A O A '='，则()106C ，； ②2C 、3C 为以O 为圆心，O A '为半径与y 轴的交点，即OC A O ='，则()502，C ，()305C -，； ③4C 为线段A O '垂直平分线与y 轴的交点，即CO A C ='，设()40C a ，，则322D ⎛⎫- ⎪⎝⎭，，在4ODC Rt ∆中，由勾股定理得： 24242OC DC OD =+，故625=a ，所以42506C ⎛⎫ ⎪⎝⎭，．【练习50】已知：如图，在△ABC 中，∠C =90°，∠B =30°，AC =3，点D 、E 、F 分别在边BC 、AC 、AB 上（点E 、F 与△ABC 顶点不重合），AD 平分∠CAB ，EF ⊥AD ，垂足为H ．（1）求证：AE =AF ；（2）设CE =x ，△BDF 的面积为y ，求y 与x 之间的函数解析式，并写出定义域；（3）当△DEF 是直角三角形时，求出BF 的长．xyAB C【答案】见解析．【解析】（1）证明：ΘAD 平分CAB ∠，AD EF ⊥，ο30=∠B ，ο90=∠C ， ο30=∠=∠∴FAD EAD ，又ΘAH AH =， ∴AFH AEH ∆≅∆，∴AF AE =；（2）过点F 作BC FO ⊥于O ，在ABC ∆中，90303C B AC ∠=∠==o o ，，，6=∴AB ， ΘAD 平分CAB ∠，ο30=∠=∠∴DAB CAD ， ∴ο30=∠=∠B DAB ，DB AD =∴，又在ACD Rt ∆中，ο303=∠=CAD AC ，，由勾股定理322==CD AD ，32=∴BD ，又x AE AB AF AB BF +=-=-=3，则在BFO Rt ∆中，2321xBF FO +==，233321xFO BD S BDF +=⋅⋅=∴∆，即23323+=x y ， Θ点E 不与C A 、重合，30<<∴x ．（3）由（1）得AF AE =，AD AD =Θ， AFD AED ∆≅∆∴，AFD AED ∠=∠∴，BFD CED ∠=∠∴． AD EF ⊥Θ，而使DEF ∆为直角三角形， ο90=∠∴EDF ，ο90=∠+∠∴BDF CDE ．又Θο90=∠C ，ο90=∠+∠∴CED CDE ，∴CED BDF ∠=∠，ABC D E FD ABC又ΘDFB CED ∠=∠，∴DFB BDF ∠=∠，∴BD BF =．由（2）得：3=CD ，即322===CD AD BF ．所以当32=BF 时，DEF ∆为直角三角形．【练习51】已知，梯形ABCD 中，AB ∥CD ，BC ⊥AB ，AB =AD ，连接BD 如图1所示，点P 沿梯形的边，从A -B -C -D -A 移动，设点P 移动的距离是x ，BP =y ．（1）求证：∠A =2∠CBD ；（2）当点P 从A 移动到点C 时，y 与x 的函数关系如图2中的折线MNQ 所示，求CD 的长；（3）在（2）的情况下，点P 从点A -B -C -D -A 移动的过程中，△BDP 是否可能为等腰三角形？若能，请求出所有能使△BDP 为等腰三角形的x 的值；若不能，请说明理由．【答案】见解析．【解析】（1）证明：ΘAD AB =，ABD ∆∴为等腰三角形．又ο90=∠CBA ，CBD ABD ∠-=∠∴ο90， Θο1802=∠+∠A ABD ，CBD A ∠=∠2；（2）由函数图像可知：53AB BC ==，，过点D 作DF ⊥AB ，那么DF 与AB 平行且相等，由勾股定理，可得4AF =，所以1CD BF ==；（3）要使BDP ∆为等腰三角形，分以下几种情况讨论：①当点P 在AB 边上时，如果PB PD =，那么点P 在BD 的中垂线上，故作BD 中垂线，由于AB =AD ，则点A 必在中垂线上，即点P 与点A 重合，此时0x =；如果DB DP =（如图一），过点P 作PF ⊥AB 于点F ，由等腰三角形性质可得：1PF BF ==，所以3x AP ==；如果BP BD =，此时，510x AB BP =-=-；②当点P 在BC 边上时，只有PB PD =（如图二）．设PB PD a ==，则3CP a =-，在Rt CDP V 中，由勾股定理，得：O85 MN图2xy 图1A BCDF DAB CPF图一 DABC 图二P222CD CP PD +=，即221(3)a a +-=，解得：53a =，所以520533AP =+=； ③当点P 在CD 上时，没有满足条件的点；④当点P 在DA 上时（如图三），如果BP BD =，过点B 作BG ⊥AD 于点G ，则AG AD DG =-．因为222(10)BG DG =-，222AB AG BG =+，解得：1DG =．此时11x AB BC CD DP =+++=；如果DB DP =，那么10DP =，此时910x AB BC CD DP =+++=+；如果PB PD =，那么P 点与A 点重合，此时14x AB BC CD DA =+++=，综上所述，当△BDP 为等腰三角形时，x 的值为0或3或510-或203或11或910+或14．DABC图三PG。

学而思初二数学秋季班第11讲.特殊三角形之直角三角形.提高班.教师版

1初二秋季·第11讲·提高班·教师版满分晋级漫画释义三角形12级成比例线段三角形11级特殊三角形之直角三角形三角形10级勾股定理与逆定理 11特殊三角形之直角三角形2初二秋季·第11讲·提高班·教师版有一个角是直角的三角形叫做直角三角形，这是初中阶段研究的一个特殊三角形，它的性质和判定是常考内容，也是解决初中几何问题的常用手段．一、直角三角形1. 直角三角形的性质：⑴ 两锐角互余；⑵ 三边满足勾股定理；⑶ 斜边上的中线等于斜边的一半；⑷ 30︒角所对的直角边等于斜边的一半．另外，直角三角形中还有一个重要的结论：两直角边的乘积等于斜边与斜边上高的乘积，即ab ch =．2. 直角三角形的判定：⑴ 有一个角是直角；⑵ 两锐角互余；⑶ 勾股定理的逆定理；⑷ 一条边上的中线等于这条边的一半．二、等腰直角三角形等腰直角三角形是集等腰三角形和直角三角形为一体的特殊图形，除具备等腰三角形和直角三角形的所有性质以外，它的底边中线也同时具备了“三线合一”和“斜边中线”的共同特点，可谓“集大成者”．另外，等腰直角三角形还可以看成是正方形的“半成品”，因此“还原正方形”也是等腰直角三角形常用的辅助线做法之一．思路导航知识互联网题型一：直角三角形的性质及判定3初二秋季·第11讲·提高班·教师版【引例】如图，正方形ABCD 的边长为4，E F 、分别在BC CD 、上，且3BE CF ==，AE BF 、相交于M ，求BM 的长．【解析】 ∵ABCD 是正方形，∴4AB BC ==，90ABC C ∠=∠=︒，∵3BE CF ==，∴ABE BCF △≌△， ∴BAE CBF ∠=∠，∴90BME ∠=︒ 又由勾股定理可知5AE =，在Rt ABE △中，BM AE ⊥， ∴AB BE AE BM ⋅=⋅，∴125AB BE BM AE ⋅==．【例1】 1. 在ABC △中，若35A ∠=︒，55B ∠=︒，则这个三角形是__________三角形．2. 如图，在ABC △中，90ACB ∠=︒，CD AB ⊥，若28A ∠=︒，则B ∠=_______，ACD ∠=________，BCD ∠=________．3. 如图，已知图中每个小正方形的边长为1，则点C 到AB 所在直线的距离等于．（十三中分校期中）4. 如图，在四边形ABCD 中，∠A ＝60°，∠B ＝∠D ＝90°，BC ＝2，CD ＝3，则AB ＝．EABCDDCBA5. 已知Rt △ABC 中，∠C ＝90°，AB 边上的中线长为2，且AC ＋BC ＝6，则S △ABC ＝．【解析】 1. 直角典题精练例题精讲图2图1AMFDE FMDCBADCBAABC4初二秋季·第11讲·提高班·教师版2. 62︒；62︒；28︒3. 24. 833．通过向外补形，将四边形问题转化为三角形问题来解决．5. ∵AB 边上的中线长为2，∴AB =4，∴AC 2+BC 2=AB 2=16 ∵AC ＋BC ＝6，∴()236AC BC +=，即AC 2+BC 2+2AC BC =36 ∴1S 52ABC AC BC ==△【例2】若直角三角形的两条直角边长为a b 、，斜边为c ，斜边上的高为h ，求证：⑴ 222111a b h+=；⑵ a b c h +<+．【解析】 ⑴ ∵222a b c +=，ab ch =，∴abc h=，代入得22222a b a b h +=，∴222111a b h+=． ⑵ 由222a b c +=，ab ch =，则22222a ab b c ch ++=+，∴222222a ab b c ch h ++<++，即()()22a b c h +<+， ∴a b c h +<+．特殊的直角三角形是指()306090︒︒︒，，和()454590︒︒︒，，的直角三角形，它们的三条边之间有特殊的比例关系，分别是1:3:2和1:1:2，熟练运用这种特殊的比例关系，能够在解题过程中大幅提高解题的速度与正确率．【引例】已知，Rt ABC △中，90C ∠=︒，30A ∠=︒，6AC =，求BC AB 、的长．例题精讲思路导航题型二：特殊直角三角形的边角关系5初二秋季·第11讲·提高班·教师版【解析】解法一：∵90C ∠=︒，30A ∠=︒，∴12BC AB =，设BC x =，则2AB x =，那么()()22262x x +=，解得2x =（舍负）∴2BC =，22AB =．解法二：∵90C ∠=︒，30A ∠=︒，∴::1:3:2BC AC AB =， ∴6233AC BC ===，∴222AB BC ==．【例3】 ⑴ 在ABC △中，a b c 、、分别是A B C ∠∠∠、、的对边，且::1:2:3A B C ∠∠∠=，则a 与c 的关系是____________．⑵ 如图，把两块相同的含30︒角的三角尺如图放置，若66AD =cm ，则三角尺的最长边长为．（四中期中）⑶ 如图，以等腰直角三角形AOB 的斜边为直角边向外作第2个等腰直角三角形1ABA ，再以等腰直角三角形1ABA 的斜边为直角边向外作第3个等腰直角三角形11A BB ，…，如此作下去，若1OA OB ==，则第8个等腰直角三角形的面积是．【解析】 ⑴ 2c a =；⑵ 12cm ；⑶ 64．【例4】如图，点D 、E 是等边△ABC 的BC 、AC 上的点，且CD ＝AE ，AD 、BE 相交于P 点，BQ ⊥AD 。

【最新】湘教版八年级数学下册第一章《直角三角形的性质和判定(Ⅱ)》公开课课件.ppt

• 10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 7:11:48 PM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 • 12、越是无能的人，越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 • 13、志不立，天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
。2020年12月16日星期三2020/12/162020/12/162020/12/16
• 15、会当凌绝顶，一览众山小。2020年12月2020/12/162020/12/162020/12/1612/16/2020
• 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2020/12/162020/12/16December 16, 2020
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
图形面积的两个基本性质

著名机构讲义秋季18-8年级数学拓展版--直角三角形的判定、性质和推论-教师版

教师姓名申琛学生姓名年级初一上课时间单击此处输入日期。

学科数学课题名称请输入模块一：直角三角形全等的判定1、直角三角形全等的判定方法：（1）直角三角形是特殊的三角形，对于一般三角形全等的判定方法，直角三角形都适用；（2）直角三角形还有一个特殊的判定方法：有一条直角边和斜边对应相等的两个直角三角形全等（简记“H ．L ”）．【例1】如图，∠D =∠C =90°，请添加一个条件，使得△ABC ≌△BAD ，并在括号内写出判定的依据．（1）AD =__________( )；（2）∠DAB =_________ ()．【答案】BC ，.H L ；CBA ，..A A S ．【解析】（1）有一条直角边和斜边对应相等的两个直角三角形全等；（2）两角及其中一角的对边对应相等的两个三角形全等．直角三角形的全等判定及性质BACD【例2】已知：如图，EF ⊥AD ，BC ⊥AD ，AG =DH ，AF =DC ，那么图中全等的三角形共有______对．【答案】3对．【解析】AFG DCH V V ≌；ACB DFE V V ≌；EOG BOH V V ≌．【例3】下列命题中，正确的个数是()①两条边分别相等的两个直角三角形全等； ②斜边和直角边对应相等的两个直角三角形全等； ③斜边相等的两个等腰直角三角形全等． A ．3B ．2C ．1D ．0【答案】B【解析】①错误；②、③正确．【例4】已知：如图，AC ⊥BC ，AD ⊥BD ，AD =BC ，CE ⊥AB ，DF ⊥AB ，垂足分别是E 、F ，求证：CE =DF ．【答案】见解析．【解析】Q AC ⊥BC ，AD ⊥BD ，90ACB BDA ∴∠=∠=︒在RT ACB V 和RT BDA V 中， AB BABC AD =⎧⎨=⎩RT ACB ∴V ≌RT BDA V （.H L ）CAB DBA ∴∠=∠（全等三角形对应角相等），AC BD =（全等三角形对应边相等） Q CE ⊥AB ，DF ⊥AB 90AEC BFD ∴∠=∠=︒ 在RT AEC V 和RT BFD V 中AEC BFD CAB DBA AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩， RT AEC ∴V ≌RT BFD V （..A A S ）CE DF ∴=（全等三角形对应边相等）【例5】如图，已知：Rt △ABC 中，∠ACB 是直角，D 是AB 上一点，BD =BC ，过D 作AB 的垂线交ACABCDEFG OH E ABCDF BD于E ，求证：CD ⊥BE ．【答案】见解析．【解析】90ACB DE AB ∠=︒⊥Q ，，90ECB EDB ∠∴∠==︒．在RT BEC V 和RT BED V 中，BE BEBC BD=⎧⎨=⎩，RT BEC ∴V ≌RT BED V （.H L ） EC ED ∴=（全等三角形对应边相等）E ∴在CD 的垂直平分线上（垂直平分线逆定理）又BC BD =Q （已知），B ∴也在CD 的垂直平分线上（垂直平分线逆定理） BE ∴垂直平分CD （两点确定一条直线），即CD ⊥BE ．【例6】如图，△ABC 中，AB ⊥BC ，AD 平分∠BAC ，DF ⊥AC ，ED =CD ．求证：AC =AE +2BE ．【答案】见解析．【解析】Q AD 平分∠BAC ，且AB ⊥BC ，DF ⊥ACBD FD ∴=（角平分线性质定理）在RT BED V 和RT FCD V 中，ED CD BD FD =⎧⎨=⎩， RT BED ∴V ≌RT FCD V （.H L ）BE FC ∴=（全等三角形对应边相等）同理可证：RT ABD V ≌RT AFD V （.H L ），AB AF ∴=（全等三角形对应边相等）AC AF FC AB AE BE =+=+Q ，，2AC AE BE ∴=+．【例7】如图1，点A 、E 、F 、C 在一条直线上，AE =CF ，过E 、F 分别作DE ⊥AC ，BF ⊥AC ．若AB =CD ，（1）BD 与EF 有什么关系?为什么?（2）若变为图2所示位置，结论是否仍然成立?请说明理由．AB CD EFABCEFG【答案】（1）BD 与EF 互相平分；（2）成立．【解析】（1）提示：证 RT ABF V ≌RT CDE V （.H L ）；RT DEG V ≌RT BFG V （..A A S ）得：EG FG DG BG ==，（全等三角形对应边相等）（2）同理可证，结论成立．【例8】在直角△ABC 中，AB =AC ，∠BAC =90°，直线l 为经过点A 的任一直线，BD ⊥l 于点D ，CE ⊥l于点E ，若BD >CE ，试问：（1） AD 与CE 的大小关系如何?请说明理由；（2）线段BD 、DE 、CE 之间的数量关系如何?你能说明清楚吗?试一试．【答案】（1）AD CE =；（2）BD CE DE =+．【解析】（1）90BAC ∠=︒Q ，90BAD CAE ∴∠+∠=︒，BD l CE l ⊥⊥Q ，， 90BDA AEC ∴∠=∠=︒，90DBA BAD ∴∠+∠=︒， DBA EAC ∴∠=∠在RT ABD V 和RT CAE V 中，BDA AECAB CA DBA EAC∠=∠⎧⎪=⎨⎪∠=∠⎩， RT ABD ∴V ≌RT CAE V （..A S A ）AD CE ∴=（全等三角形对应边相等）（2）BD CE DE =+AD CE =Q ，又AE AD DE =+Q ， AE CE DE ∴=+RT ABD Q V ≌RT CAE V， BD AE ∴= BD CE DE ∴=+．【例9】如图，在△ABC 中，AB =AC ，DE 是过点A 的直线，BD ⊥DE 于D ，CE ⊥DE 于E ．（1）若BC 在DE 的同侧（如图1），且AD =CE ，求证：AB ⊥AC ．（2）若BC 在DE 的两侧（如图2），其他的条件不变，问AB 与AC 仍垂直吗?若是，请予以证明，若不是，请说明理由．AB CD ElCDE【答案】见解析．【解析】（1）证明：Q BD ⊥DE ，CE ⊥DE90BDA AEC ∴∠=∠=︒．在RT BDA V 和RT AEC V 中，AB CA AD CE=⎧⎨=⎩， RT ABD ∴V ≌RT CAE V （.H L ）， DAB ECA ∴∠=∠．90AEC ∠=︒Q ， 90CAE ECA ∴∠+∠=︒， 90CAE DAB ∴∠+∠=︒， 90BAC ∴∠=︒ ，∴AB ⊥AC ．（2）AB ⊥AC ．同理可证： RT ABD V ≌RT CAE V，则可证90BAC ∠=︒，即AB ⊥AC ．【例10】如图，在△ABC 中，∠ACB =90°，CD 是斜边AB 上的高，在AB 上截取AE =AC ，过点E 作EF∥CD 、交BC 边于点F ，EG 垂直BC 于点G ，求证：DE=EG ．【答案】见解析．【解析】联结CEQ AE =AC ，ACE AEC ∴∠=∠90ACB ∠=︒Q ， 90ACE ECG ∴∠+∠=︒ CD AB ⊥Q ， 90AEC ECD ∴∠+∠=︒ ECD ECG ∴∠=∠又Q CD AB ⊥，EG BC ⊥DE GE ∴=模块二：直角三角形的性质2、两个性质：（1）直角三角形的两个锐角互余；（2）在直角三角形中，斜边的中线等于斜边的一半．如果有直角三角形，作斜边的中线这条辅助线，可达到解决问题的目的．ABCDEFG【例11】如图，在△ABC 中，∠ACB =90°，CD ⊥AB 于D ：（1）若∠B =55°，则∠A =________；（2）若∠B -∠A =10°，则∠B =_________；（3）图中与∠A 互余的角有_________，与∠A 相等的角有_________．【答案】（1）35︒；（2）50︒；（3）B ∠、ACD ∠；BCD ∠．【解析】直角三角形的两个锐角互余，题目中有三个直角三角形ABC V 、ACD V 、BCD V ．【例12】如图，已知，四边形ABCD 中，∠ABC =∠ADC =90°，M 、N 分别是AC 、BD 中点．求证：MN⊥BD ．【答案】见解析．【解析】联结MD 、MB ．Q 90ABC ADC ∠=∠=︒，M 分别是AC 中点1122BM AC DM AC ∴==，（直角三角形斜边上中线等于斜边的一半）BM DM ∴=， N Q 是BD 中点， MN BD ∴⊥（等腰三角形三线合一）．【例13】如图，在Rt △ABC 中，∠C =90°，AB 的中垂线交AB 于E 、AC 于D ，BD 、CE 交于F ，设∠A =y ，∠DFC =x ，（1）求证：∠CDB =∠CEB ；（2）用x 的代数式表示y ．【答案】（1）略；（2）1603y x =︒-．【解析】（1）90C ∠=︒Q ，AB 的中垂线交AB 于E12AE BE AB ∴==、12CE AB =（直角三角形斜边中线等于斜边一半） AE CE ∴=，A ACE ∴∠=∠，2CEB A ∴∠=∠．又Q AB 的中垂线交AB 于E ， AD DB ∴=（垂直平分线的性质）A ABD ∴∠=∠，2CDB A ∴∠=∠， CDB CEB ∴=∠（2）A y DFC x ∠=∠=Q ，，A ACE ∠=∠，A ABD ∠=∠ 又2CDB A ABD CDB y ∠=∠+∠∴∠=Q ，ACE y ∠=180ACE CDB DFC ∴∠+∠+∠=︒．即3180x y +=︒，1603y x ∴=︒-ABCD EAB CDMN【例14】如图ABC ∆中，AD 是BC 边上的高，CF 是AB 边的中线，BF DC =，P 是CF 中点．求证：（1）DP FC ⊥；（2）2B BCF ∠=∠．【答案】略【解析】（1）联结DFQ AD 是BC 边上的高，CF 是AB 边的中线， 12BF AB ∴=∵DF 是直角ABD V 斜边上的中线， 12DF AB ∴=， BF DF ∴=．BF DC =Q ， DC DF ∴=，又Q P 是CF 中点， DP CF ∴⊥．（2）BF DF =Q ， B BDF ∴∠=∠， DF DC =Q ， BCF DFC ∴∠=∠．2BDF BCF DFC BCF ∠=∠+∠=∠Q ， 2B BCF ∴∠=∠．【例15】如图，AB ，CD 交于点O ，且BD=BO ，CA =CO ，E 、F 、M 分别是OD 、OA 、BC 的中点，求证：ME MF =．【答案】略【解析】联结BE CF ， BD BO CA CO ==Q ，，E 、F 分别是OD 、OA 的中点BE DO CF AO ∴⊥⊥，M Q 是BC 的中点1122EM BC FM BC ∴==，（直角三角形斜边上的中线等于斜边的一半）EM MF ∴=【例16】如图，在梯形ABCD 中，AD //BC ，M 、N 分别是AD 、BC 的中点，若∠B 与 ∠C 互余，则MN 与(BC -AD )的关系是什么? 【答案】()12MN BC AD =-．【解析】过点M 分别作////ME AB MF DC ，，交BC 于点E 、FB MEFC MFE ∴∠=∠∠=∠，， Q ∠B 与∠C 互余， 90MEF MFE ∴∠+∠=︒，90EMF ∴∠=︒，即MEF V 为直角三角形．AB CDPFABCDEFO MABCDMNEFQ 在梯形ABCD 中，AD //BC ，////ME AB MF DC ，，AM BE DM CF ∴==，， Q M 、N 分别是AD 、BC 的中点， AM DM BN CN ∴==， ()BC AD BC BE CF EF ∴-=-+=，EN FN =12MN EF ∴=， ()12MN BC AD ∴=-．【例17】如图，已知在钝角∆ABC 中，AC 、BC 边上的高分别是BE 、AD ，BE 、AD 的延长线交于点H ，点F 、G 分别是BH 、AC 的中点．（1）求证：∠FDG =90°；（2）连结FG ，试问∆FDG 能否为等腰直角三角形?若能，试确定∠ABC 的度数，并写出你的推理过程；若不能，请简要说明理由．【答案】见解析．【解析】（1）证明：Q AC 、BC 边上的高分别是BE 、AD ，又Q 点F 、G 分别是BH 、AC 的中点，12DG CG AC ∴==，12DF BF BH ∴==（斜边中线等于斜边的一半）GDC GCD BCE ∴∠=∠=∠，DBF BDF ∴∠=∠GDC BDF BCE DBF ∴∠+∠=∠+∠，又AE BH ⊥Q ，90BCE DBF ∴∠+∠=︒ 90GDC BDF ∴∠+∠=︒，即90FDG ∠=︒（2）能，45ABC ∠=︒．若GDF V 为直角等腰三角形，则GD FD =，AC BH ∴=， ACD ∴V ≌BHD V （..A A S ），AD BD ∴=，45ABC ∴∠=︒．【例18】如图，等腰直角三角形ABC 中，∠ACB ＝90°，AD 为腰CB 上的中线，CE ⊥AD 交AB 于E ．求证：∠CDA ＝∠EDB ．【答案】见解析．【解析】过点C 作CH AB ⊥于点H ，交AD 于点F ．Q 等腰直角三角形ABC 中，90ACB ∠︒＝，45B ∴∠=︒．CH AB ⊥Q ，45ACH BCH ∴∠=∠=︒， ACF BCH B ∴∠=∠=∠又CE AD ⊥Q ， 12∴∠=∠．B EFHD AGC AB C DE1 2H F在ACF V 和CBE V 中， 12ACF B AC CB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ACF ∴V ≌CBE V （..A S A ）， CF BE ∴=．Q AD 为腰CB 上的中线，CD BD ∴=．在CFD V 和BED V 中， CF BE DCF B CD BD =⎧⎪∠=∠⎨⎪=⎩， CFD ∴V ≌BED V （..S AS ）CDF BDE ∴∠=∠，即CDAEDB ∠∠＝．【例19】如图，点A 、B 、C 在同一直线上，在直线AC 的同侧作△ABE 和△BCF ，连接AF 、CE ，取AF 、CE 的中点M 、N ，连接MB 、NB 、NM ．（1）若△ABE 和△FBC 是等腰直角三角形，且∠ABE =∠FBC =90°，如图1所示，则△MBN 是_____________三角形；（2）若△ABE 和△FBC 中，BA =BE ，BC =BF ，且∠ABE =∠FBC =α，如图2所示，则△MBN 是_____________三角形，且∠MBN =_______；（3）若（2）中的△ABE 绕点B 旋转一定的角度，如图3，其他的条件不变那么（2）中的结论是否成立?若成立，给出你的证明，若不成立，写出正确的结论并给出证明．【答案】（1）等腰直角；（2）等腰，α；（3）结论仍然成立．【解析】（1）易证ABF V ≌EBC V ， AF EC ∴=，BM BN ∴=，∴AMB V ≌ENB V ，MBA NBE ∴∠=∠ 90MBA MBF ∠+∠=︒Q ，90MBF NBE ∴∠+∠=︒ 即90MBN ∠=︒，MBN ∴V 为等腰直角三角形（2）根据题意，可知ABF V ≌EBC V ，BM BN ∴= 即MBN V 为等腰三角形，ABM EBN ∠=∠QABE MBN α∴∠=∠=，MBN α∴∠=MEFAB CNEFM图1（3）∵ABF V ≌EBC V ，AF CE AFB ECB ∴=∠=∠，FM CN ∴=， MFB ∴V ≌NCB V BM BN ∴=，MBF NBC ∠=∠MBN MBF FBN FBN NBC FBC α∴∠=∠+∠=∠+∠=∠=【例20】已知，如图，在△ABC 中，边AB 上的高CF 、边BC 上的高AD 与边CA 上的高BE 交于点H ，连接EF ，AH 和BC 的中点为N 、M ．求证：MN 是线段EF 的中垂线．【答案】见解析．【解析】连接FM 、EM 、FN 、EN∵︒=∠90BFC ，M 为BC 的中点， ∴BC FM 21= ∵︒=∠90BEC ，M 为BC 的中点，∴BC EM 21=，∴ME FM =∵︒=∠90AFH ，N 为AH 的中点，∴AH FN 21= ∵︒=∠90AEH ，N 为AH 的中点，∴AH EN 21=， ∴EN FN =， ∵ME FM =，EN FN = ∴MN 是线段EF 的中垂线．模块三：直角三角形性质的推论3、推论：（1）在直角三角形中，30°所对的直角边等于斜边的一半；（2）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°．ABCDE FNHM【例21】 △ABC 中，AB =AC =6，∠B =30°，则BC 边上的高AD =________；（2）△ABC 中，AB =AC ，AB 上的高CD =12AB ，则顶角∠BAC =_______．【答案】（1）3；（2）30︒或150︒．【解析】（1）在RT ABD V 中，30B ∠=︒，则132AD AB ==；（2）要分两种情况考虑，△ABC 可能是锐角三角形，也可能是钝角三角形；当△ABC 是锐角三角形时，30BAC ∠=︒；当△ABC 是钝角三角形时，150BAC ∠=︒．【例22】如图，在矩形ABCD 中，AB =2BC ，在CD 上取一点E ，使AE =AB ，则∠EBC 的度数为__________．【答案】15︒．【解析】过点E 作EH AB ⊥，垂足为H ，则EH BC =．又2AB BC =Q ，AE AB =，2AE EH ∴=，30EAB ∴∠=︒ 75ABE ∴∠=︒， 15EBC ∴∠=︒【例23】已知：如图，在△ABC 中，BA =BC ，∠B =120°，AB 的垂直平分线MN 交AC 于D ，求证：12AD DC =．【答案】见解析．【解析】连接BD∵BA =BC ，∠B =120°， ∴︒=∠=∠30C A ∵AB 的垂直平分线MN 交AC 于D ，∴DB AD =， ∴︒=∠=∠30DBA A∵∠B =120°，∴︒=︒-︒=∠9030120DBC∵︒=∠30C ，︒=∠90DBC ，∴DC BD 21=∵DB AD =，∴DC AD 21=A BCDEH AB CDNM【例24】已知：如图，Rt △ABC 和Rt △ABD 中，DA =DB ，∠ADB =90°，BC =12AB ， ∠ACB =90°，DE ⊥AB ，联结DC ，求∠EDC 的大小．【答案】75°．【解析】连接CE∵DA =DB ，DE ⊥AB ，∴EB AE =∵Rt △ABC ，BC =12AB ，∴︒=∠30CAB∵Rt △ABC ，EB AE =，∴CE AE =∴ACE CAB ∠=∠，∴︒=∠+∠=∠60ACE CAB CEB ∵DE ⊥AB ，∴︒=︒-︒=∠306090DEC ∵Rt △ABC 和Rt △ABD ，EB AE =∴AB CE AB DE 21,21==，∴CE DE =∵︒=∠30DEC ，∴︒=︒-︒=∠75230180EDC【例25】已知如图，在直角△ABC 中，∠ACB =90°，∠A =30°，D 为AB 上一点，且BD =14AB ．求证：CD ⊥AB ．【答案】见解析【解析】取AB 的中点E ，连接CE∵AB BE 21=，BD =14AB ，∴BE BD =2，∴DB ED = ∵∠ACB =90°，∠A =30°，∴AB BC 21= ∵∠ACB =90°，EB AE =，∴AB CE 21=，∴CE BC = ∵CE BC =，DB ED =，∴CD ⊥AB ．EDCBAABCDE【例26】已知等边△ABC 中，D 、E 分别是BC 、AC 上的点，且AE =CD ，AD 与BE 相交于点F ，过点B作BG ⊥AD ，垂足为G ，（1）求FG ：BF 的值；（2）若D 、E 分别在BC 、CA 的延长线上，其他条件都不变，上述结论是否仍然成立，请说明理由．【答案】（1）1：2；（2）见解析．【解析】（1）∵BAE ACD ∠=∠，AE =CD ，AB =CA ，∴CAD ABE ≌△△，∴ABE CAD ∠=∠∵︒=∠+∠60BAF CAD ，∴︒=∠+∠60BAF ABE ∴︒=∠60BFG ，∴︒=∠30FBG∵BG ⊥AD ，∴BF FG 21=，即FG ：BF=1：2；（2）若D 、E 分别在BC 、CA 的延长线上，其他条件都不变，也可以用同样的方法证明出两个三角形全等，进而得到结论．【例27】在△ABC 中，已知∠A=60°，BE ⊥AC 于E ，CF ⊥AB 于F ，点D 是BC 中点. （1）如果AB=AC ，求证△DEF 为等边三角形；（2）如果AB≠AC ，试猜想△DEF 是不是等边三角形，若是，请加以证明，若不是，请说明理由；（3）如果CM =4，FM =5，求BE 的长度．【答案】（1）见解析；（2）是，理由见解析；（3）12．【解析】（1）∵BE ⊥AC ，点D 是BC 中点，∴BC DC DE 21==∵CF ⊥AB ，点D 是BC 中点，∴BC BF DF 21==，∴DF DE =∵∠A =60°，AB =AC ，∴△ABC 是等边三角形，∴︒=∠=∠60ACB ABC ∵DC DE =，︒=∠60ACB ，∴△DEC 是等边三角形，∴︒=∠60EDC ∵DB DF =，︒=∠60ABC ，∴△BFD 是等边三角形，∴︒=∠60FDB ∴︒=︒-︒-︒=∠606060180FDE ∵DF DE =，∴△DEF 为等边三角形（2）∵BE ⊥AC ，点D 是BC 中点，∴BC DC DE 21== ABCDEFGABCDE FM∵CF ⊥AB ，点D 是BC 中点，∴BC BF DF 21==，∴DF DE = ∵∠A =60°，∴︒=∠+∠120ACB ABC ， ∵DC DE =，∴ACB DEC ∠=∠ ∵DB DF =，∴ABC DFB ∠=∠， ∴180FDE FDB EDC ∠=︒-∠-∠()()180********ABC ACB =︒-︒-∠-︒-∠ ()218060ABC ACB =∠+∠-︒=︒ ∵DF DE =，∴△DEF 为等边三角形（3）∵∠A =60°，BE ⊥AC 于E ，CF ⊥AB ，∴︒=∠=∠30ECM FBM∴1122FM BM EM CM ==，∵CM =4，FM =5，∴102==BM EM ，， ∴12210=+=+=ME BM BE【例28】已知∠MAN ，AC 平分∠MAN ，（1）在图1中，若∠MAN =120°，∠ABC =∠ADC =90°，求证：AB +AD =AC .（2）在图2中，若∠MAN =120°，∠ABC +∠ADC =180°，则(1)中的结论是否仍然成立?若成立，请给出证明；若不成立，请说明理由．【答案】见解析【解析】(1)∵∠MAN =120°，AC 平分∠MAN ，∴︒=∠=∠60CAB CAD∵∠ABC =∠ADC =90°，∴∠ACD =∠ACB =30°，∴AC AB 21=，AC AD 21=∴AC AC AC AD AB =+=+2121；（2）过C 作CE ⊥AM ，过C 作CF ⊥AN ，垂足分别为E 、F ∵AC 平分∠MAN ，CE ⊥AM ，CF ⊥AN ， ∴CF CE =∵∠ABC +∠ADC =180°，∠MDC +∠ADC =180°， ∴∠EDC =∠ABCABCD M NNABCD MEF∵∠EDC =∠ABC ，CF CE =，CFB CED ∠=∠ ∴CBF CED ≌△△，∴BF ED =∴AF AE BF AF DE AE AB AD +=++-=+ ∵∠MAN =120°，AC 平分∠MAN ， ∴︒=∠=∠60CAB CAD ∵∠ABC =∠ADC =90°， ∴∠ACE =∠ACF =30°，∴AC AE 21=，AC AF 21=∴AC AC AC AD AB =+=+2121【练习1】下列条件不可以判定两个直角三角形全等的是（）．A 、两条直角边对应相等B 、斜边一个锐角对应相等C 、一条直角边和一条斜边对应相等D 、一条边和一个角对应相等【答案】D【解析】A 的理由是S A S ..；B 的理由是S A A ..，C 的理由是L H .【练习2】如图在△ABC 中，∠ACB =90°，在AB 上截取AE =AC ，BD =BC ，则∠DCE =_________．【答案】45°【解析】180DCE CDE CED ∠=︒-∠-∠ 180********B A︒-∠︒-∠=︒--452A B∠+∠==︒．【练习3】如图在△ABC 中，∠ACB =90°，CD ⊥AB 于点D ，∠A =30°，则AD =_____AB【答案】43．【解析】∵︒=∠+∠90ACD A ，︒=∠+∠90ACD BCD ， ∴︒=∠=∠30A BCD∵︒=∠90ACB ，∠A =30°，∴AB BC 21=∵︒=∠90BDC ，︒=∠30BCD ，∴BC BD 21=，∴AB BD 41=，∴AB AD 43=【练习4】如图，在直角△ABC 在，∠ACB =90°，AB =8cm ，D 为AB 的中点，DE ⊥AC 于E ，∠A =30°，求BC 、CD 和DE 的长．【答案】BC =4cm ，CD=4cm ，DE=2cm ．【解析】∵∠ACB = 90°，AB = 8cm ，D 为AB 的中点，∠A =30°，∴421421====AB BC AB CD ，∵DE ⊥AC ，∠A =30°，∴221==AD DE ．【练习5】如图，△ABC 中，AD ⊥BC 于点D ，BE ⊥AC 于点E ，交AD 于点H ，且AD=BD ，AC=BH ，连接CH ．求证：∠ABC=∠BCH ．【答案】见解析【解析】∵ADC BDH ∠=∠90=o ，AC =BH ，BD AD =∴ACD BHD ≌△△， ∴DC DH = ∵AD ⊥BC ， ∴︒=∠=∠45BCH CHD∵BD AD =，BC AD ⊥，∴︒=∠=∠45BAD ABC ， ∴∠ABC =∠BCH ．【练习6】如图，已知，在锐角三角形ABC 中，∠ABC =2∠C ，AD ⊥BC 于点D ，E 为AC的中点，ED 的延长线交AB 的延长线于点F ，求证：BF =BD ．【答案】见解析．ABC DABCDEABCDEABCDEH【解析】∵AD ⊥BC ，E 为AC 的中点，∴AC EC DE 21==，∴EDC C ∠=∠∵BDF EDC ∠=∠，∴BDF C ∠=∠ ∵∠ABC =2∠C ，∴BDF ABC ∠=∠2∵F BDF ABC ∠+∠=∠，∴F BDF ∠=∠，∴BF =BD ．【练习7】如图，在△ABC 中，BE ⊥AC 于点E ，CF ⊥AB 于点F ，D 是边BC 的中点，连接DF 、EF 、DE ．（1）求证：ED =DF ；（2）若△DEF 是等边三角形，则△ABC 应满足什么条件? 【答案】见解析．【解析】（1）∵BE ⊥AC ，点D 是BC 中点，∴BC DC DE 21==∵CF ⊥AB ，点D 是BC 中点，∴BC BD DF 21==，∴DF DE =；（2）︒=∠60A 时，△DEF 是等边三角形． ∵BE ⊥AC ，点D 是BC 中点，∴BC DC DE 21== ∵CF ⊥AB ，点D 是BC 中点，∴BC BF DF 21==，∴DF DE =∵∠A =60°，∴︒=∠+∠120ACB ABC ， ∵DC DE =，∴ACB DEC ∠=∠ ∵DB DF =，∴ABC DFB ∠=∠， ∴180FDE FDB EDC ∠=︒-∠-∠()()180********ABC ACB =︒-︒-∠-︒-∠ ()218060ABC ACB =∠+∠-︒=︒AC BEFD∵DF DE =， ∴△DEF 为等边三角形【练习8】如图，AD ∥BC ，且BD ⊥CD ，BD = CD ，AC = BC ．求证：AB = BO ．【答案】见解析．【解析】过A 作AE ⊥BC 垂足为E ，过D 作DF ⊥BC ，垂足为F∵BD ⊥CD ，BD = CD ，DF ⊥BC ，∴BC DF 21=∵AE ⊥BC ，DF ⊥BC ，AD ∥BC ， ∴四边形AEFD 是长方形，∴DF AE =∵BC DF 21=，DF AE =，AC = BC∴AC AE 21=，∴︒=∠30ACB ∵AC = BC ，∴︒=∠=∠75ABC BAO∵BD ⊥CD ，BD = CD ，∴︒=∠45DBC ，∴︒=∠30ABD ∵︒=∠75BAO ，∴︒=∠75AOB ∴AOB BAO ∠=∠，∴AB = BO【练习9】已知：如图在△ABC 中，AD 是BC 边上的高，CE 是AB 上的中线，DC =BE ，DG ⊥CE ，垂足为点G ．求证：∠AEC =3∠DCE ．【答案】见解析【解析】联结ED∵AD 是BC 边上的高，CE 是AB 上的中线，∴AB BE ED 21==∵DC =BE ，∴DC DE =，∴DEC DCE ∠=∠ABDOCE FABCDEG∴DCE DEC DCE EDB ∠=∠+∠=∠2∵ED BE =，∴EDB B ∠=∠，∴DCE B ∠=∠2 ∴DCE DCE B AEC ∠=∠+∠=∠3【练习10】如图，在等边三角形ABC 中，D 、E 分别是BC 、AC 上的一点，且AE =CD ，AD 与BE 相交于点F ，CF ⊥BE . 求AF ：BF 的值．【答案】1:2．【解析】过B 作BK ⊥AD 的垂线，垂足为K∵AC AB =，ACD BAE ∠=∠，AE =CD ， ∴CAD ABE ≌△△， ∴ABE DAC ∠=∠∴︒=∠+∠=∠+∠=∠60BAF DAC BAF ABE BFD ∵︒=∠60BFD ，BK ⊥AD ，∴︒=∠30FBK ，∴BF FK 21=∵CBF BAK ∠=∠，BFC AKB ∠=∠，BC AB = ∴BCF ABK ≌△△∴BF AK =，即BF FK AF =+∴BF BF AF =+21∴AF BF 2=，即AF ：BF=1:2ABCDFE K【练习11】如图，在直角三角形ABC 中，∠BAC =90°，AB =AC ，以AB 为边向外作等边三角形ABD ，AE ⊥BD 于点E ，AE 交CD 于点M . （1）线段DM 与线段BC 有怎样的数量关系?并证明；（2）若△ABC 于△ABD 在AB 的同侧，CD 的延长线与AE 的延长线交于点M ，请在图2 中画出△ABD 与点M ；线段DM 与BC 仍有（1）中的数量关系吗?并证明．【答案】见解析．【解析】（1）∵直角三角形ABC 中，∠BAC =90°，AB =AC ，等边三角形ABD ，∴︒=∠150CAD ，AC=AD∴()︒=∠-︒=∠1518021CAD ADC∵︒=∠60ADB ，∴︒=∠45CDB∵AE ⊥BD ，∴△DME 是等腰直角三角形 ∴DE DM 2=∵等边三角形ABD ，AE ⊥BD 于点E ∴DB DE 21=，∴DB DM 22= ∵直角三角形ABC 中，∠BAC =90°，AB =AC ， ∴AB BC 2=∵AB DB =，∴DB BC 2= ∵DB DM 22=，∴DM BC 2= （2）成立．理由同（1）一样．ABCDME图1ABC图2。

部审湘教版八年级数学下册课堂同步教学课件1.1第1课时直角三角形的性质和判定

典例精析
例已知：如图，CD是△ABC的AB边上的中线求，证且：△CADBC12是AB直. 角三角形.
证明：因所为以C∠D1=∠12AA，B(=等BD边=对A等D，角)
∠2=∠B .
根据三角形内角和性质，有
∠A+∠B+∠ACB =180°，即得∠A+∠B+∠1+∠2=180°，
2(∠A+∠B)=180°.
这节课我们一起探索直角三角形的判定与性质.
讲授新课
一直角三角形的两个锐角互余
如图1-1，在Rt△ABC中， ∠C=90°，两锐角的和等于多少呢？
在Rt△ABC中，因为 ∠C=90°，由三角形内角和定理，可得∠A +∠B=90°.
图1-1
结论
由此得到：
直角三角形的两个锐角互余.
二有两个锐角互余的三角形是直角三角形
1.在Rt△ABC中，斜边上的中线CD=2.5cm ，则斜边 AB的长是多少？
解: AB=2CD=2×2.5=5(cm).
2.如图，AB∥CD，∠BAC和∠ACD的平分线相交于H 点，E为AC的中点，EH=2. 那么△AHC是直角三角形吗？为什么？若是，求出AC的长.
解: 因为 AB∥CD，所以 ∠BAC+∠DCA=180°.
图1-4
又∵ ∠A +∠B=90° ， DCA+DCB 90 ，
∴ BDCB.
∴ CD= BD.
故得
CD=
AD=
BD=
1 2
AB.
∴ 点D是斜边上的中点，即 CD 是斜边 AB的中线.
从而 CD与CD重合，且 CD 1 AB. 2
图1-4

八年级数学下册第1章直角三角形1.1直角三角形的性质和判定(Ⅰ)第2课时教学课件新版湘教版

1.1 直角三角形的性质和判定(Ⅰ)
第2课时
1.掌握“直角三角形斜边上的中线等于斜边的一半”的性质定理以及应用. 2.巩固利用添辅助线证明有关几何问题的方法.
3.通过图形的变换，引导学生发现并提出新问题，进行类比联想，促使学生的思维向多层次多方位发散，从而培养学生的创新精神和创造能力. 4.从生活的实际问题出发，引发学生学习数学的兴趣，从而培养学生发现问题和解决问题的能力.
（一）直角三角形的性质[3条]： 1.直角三角形的两个锐角互余. 2.直角三角形斜边上的中线等于斜边的一半. 3.直角三角形中，30度角所对的直角边等于斜边的一半.
（二）直角三角形的判定[2条]： 1.有两个角互余的三角形是直角三角形. 2.在三角形中，若一边上的中线等于该边的一半，那么这个三角形是直角三角形.
证明：连结CM，
∵∠ACB=90°，BC=AC，
∴∠A=∠B=45°.
∵M是AB的中点，
∴CM平分∠BCA（等腰三角形顶角的平分线和底边
上的中线重合），
∴∠MCE=∠MCB=45°，
BD CE
在△BDM和△CEM中B MCE,
BM CM
B
D M
∴△BDM≌△CEM（SAS），∴MD=ME，
D是AB的中点，CD=4cm，则AB=
cm.
【答案】8
【规律方法】直角三角形中的边角关系，利用角的互余，直角三角形斜边上的中线等于斜边的一半，等腰直角三角形的性质，构造全等三角形是证明角、线段相等的常用方法.
谢谢观看ຫໍສະໝຸດ 北60° BF
东 A
【解析】过A点作AD ⊥ BF，
由已知可得：
∠FBA=30°
北
∴ AD= 1AB=150km，

八年级数学直角三角形教师讲义带答案

直角三角形一、直角三角形的性质重点：直角三角形的性质定理与其推论：①直角三角形的性质，在直角三角形中，斜边上的中线等于斜边的一半;②推论：〔1〕在直角三角形中，假如一个锐角等于30°，那么它所对的直角边等于斜边的一半;〔2〕在直角三角形中，假如一条直角边等于斜边的一半，那么这条直角边所对的角为30°.难点：1.性质定理的证明方法.2.性质定理与其推论在解题中的应用.二、直角三角形全等的推断重点：驾驭直角三角形全等的断定定理：斜边、直角边公理：斜边和一条直角边对应相等的两个直角三角形全等〔HL〕难点：创立全等条件与三角形中各定理联络解综合问题。

三、角平分线的性质定理：角平分线上的点到这个角的两边的间隔相等.定理的数学表示：如图4，∵ OE是∠AOB的平分线，F是OE上一点，且CF⊥OA于点C，DF⊥OB于点D，∴ CF＝DF.定理的作用：①证明两条线段相等；②用于几何作图问题；角是一个轴对称图形，它的对称轴是角平分线所在的直线.2.关于三角形三条角平分线的定理：〔1〕关于三角形三条角平分线交点的定理：图4三角形三条角平分线相交于一点，并且这一点到三边的间隔相等.定理的数学表示：如图6，假如AP 、BQ 、CR 分别是△ABC 的内角∠BAC 、 ∠ ABC 、∠ACB 的平分线，那么： ① AP 、BQ 、CR 相交于一点I ；② 假设ID 、IE 、IF 分别垂直于BC 、CA 、AB 于点D 、E 、F ，那么DI ＝EI ＝FI. 定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题. 〔2〕三角形三条角平分线的交点位置与三角形形态的关系：三角形三个内角角平分线的交点肯定在三角形的内部.这个交点叫做三角形的内心〔即内切圆的圆心〕.3.关于线段的垂直平分线和角平分线的作图：〔1〕会作线段的垂直平分线；〔2〕会作角的角平分线；〔3〕会作与线段垂直平分线和角平分线有关的简洁综合问题的图形. 四、勾股定理的证明与应用１．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：假如直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c +=勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五〞形式的勾股定理，后来人们进一步发觉并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方勾股定理的证明方法许多，常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会变更 ②依据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理cba HG FEDCBA常见方法如下：方法一：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证３.勾股定理的适用范围勾股定理提示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因此在应用勾股定理时，必需明了所考察的对象是直角三角形４.勾股定理的应用①直角三角形的随意两边长，求第三边在ABC ∆中，90C ∠=︒，那么c，b，a =②知道直角三角形一边，可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题假如三角形三边长a ，b ，c 满意222a b c +=，那么这个三角形是直角三角形，其中c 为斜边①勾股定理的逆定理是断定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形〞来确定三角形的可能形态，在运用这肯定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较，假设它们相等时，以a ，b ，c 为三边的三角形是直角三角形；假设222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；假设222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 与222a b c +=只是一种表现形式，不行认为是唯一的，如假设三角形三边长a ，b ，c 满意222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边③勾股定理的逆定理在用问题描绘时，不能说成：当斜边的平方等于两条直角边的平方和时，bacbac cabcaba bcc baE D CBA这个三角形是直角三角形①可以构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以进步解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数： 221,2,1n n n -+〔2,n ≥n 为正整数〕；2221,22,221n n n n n ++++〔n 为正整数〕2222,2,m n mn m n -+〔,m n >m ，n 为正整数〕７．勾股定理的应用勾股定理可以扶植我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在运用勾股定理时，必需把握直角三角形的前提条件，理解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进展计算，应设法添加协助线〔通常作垂线〕，构造直角三角形，以便正确运用勾股定理进展求解．８.．勾股定理逆定理的应用勾股定理的逆定理能扶植我们通过三角形三边之间的数量关系推断一个三角形是否是直角三角形，在详细推算过程中，应用两短边的平方和与最长边的平方进展比较，切不行不加思索的用两边的平方和与第三边的平方比较而得到错误的结论．９.勾股定理与其逆定理的应用勾股定理与其逆定理在解决一些实际问题或详细的几何问题中，是密不行分的一个整体．通常既要通过逆定理断定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．常见图形：AB C30°D C BA ADB C10、互逆命题的概念假如一个命题的题设和结论分别是另一个命题的结论和题设，这样的两个命题叫做互逆命题。

著名机构讲义秋季18-8年级数学拓展版--直角三角形的判定、性质和推论-课后作业教师版

【作业1】下列命题中，正确的有()个①腰长及底边上的高对应相等的两个等腰三角形全等 ②有一直角边和斜边对应相等的两个直角三角形全等 ③有两边和其中一边上的高对应相等的两个三角形全等 A ．0B ．1C ．2D ．3【答案】C【解析】（1）（2）对，（3）错误，满足条件的三角形可以是锐角三角形也可以是钝角三角形．【作业2】（1）直角△ABC 中，∠C = 90°，CD ⊥AB ，点E 是AB 的中点，∠ACD =25°，则∠ECB =__________；（2）直角△ABC 中，∠C =90°，CD ⊥AB ，点E 是AB 的中点，∠DCE =10°，则∠B =______________．【答案】（1）25°；（2）40°．【解析】利用直角三角形斜边上的中线等于斜边的一半的角度之间的关系可得到答案．【作业3】如图，ABC ∆中，AB AC =，DB DC =，DE AC ⊥，2AC AD =，8AB =，则AD =________，AE =____________．【答案】4；2．【解析】∵AB AC =，DB DC =，∴BC AD ⊥∵2AC AD =，∴︒=∠30C ，∴42121===AB AC AD∵DE AC ⊥，∴︒=∠=∠30B ADE ，∴221==AD AE ．直角三角形的全等判定及性质DABCEAB CD E【作业4】（1）等腰三角形底角是75°，腰长为9，则此三角形的面积是_______；（2）等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的顶角的度数是_____________．【答案】（1）481；（2）30°或150°．【解析】（1）∵等腰三角形底角是75°，∴顶角为30度，则腰上的高为29，则三角形的面积为48129921=⨯⨯；（2）注意分锐角三角形和钝角三角形两种情况分类讨论．【作业5】已知：AB ⊥BC ，DC ⊥BC ，点E 在BC 上，且AE =AD ，AB =BC ，求证：CE =CD ．【答案】见解析．【解析】过D 作DF ⊥AB ，垂足为F∵AB ⊥BC ，DC ⊥BC ，DF ⊥AB ， ∴四边形BCDF 是长方形， ∴BC DF =，CD BF = ∵BC AB =，∴DF AB = ∵DF AB =，AE=AD ， ∴EBA AFD ≌△△， ∴BE AF =∵BC AB =，∴BF CE = ∵CD BF =，∴CD CE =【作业6】已知：如图，△ABC 中，∠B =40°，∠C =20°，DA ⊥CA ，求证：CD=2AB ．【答案】见解析【解析】取CD 的中点E ，联结AE∵DA ⊥CA ，ED CE =∴CD CE AE 21==∴︒=∠=∠20CAE C ∴︒=∠+∠=∠40CAE C AEB∵︒=∠40B ，∴B AEB ∠=∠，∴AB AE =∵CD AE 21=，∴CD AB 21=，即AB CD 2=【作业7】如图，已知：△ABC 中，AB =AC ，∠A=60°，BD =CD ，BE ∥AC ，DE ⊥BE ，求证：4BE=AC .ABCDE FABCDE【答案】见解析．【解析】连接AD∵AB =AC ，∠A=60°，∴△ABC 是等边三角形，∴BC =AC∵AB =AC ，BD =CD ，∴BC AD ⊥∵︒=∠=∠3021BAC DAC ，BC AD ⊥，∴AC DC 21=∵BD =CD ，∴AC BD 21=∵BE ∥AC ，∴︒=∠=∠60C DBE∵DE ⊥BE ，∴BD BE 21=∵AC BD 21=，∴AC BE 41=，即4BE=AC ．【作业8】在等腰直角△ABC 中，D 是斜边AB 的中点，E 、F 分别在直线AC 、BC 上，且AE =CF ，联结DE 、DF 、EF ，试判断△DEF 的形状，并加以证明．【答案】等腰直角三角形．证明见解析．【解析】等腰直角三角形．联结CD∵等腰直角△ABC 中，D 是斜边AB 的中点， ∴AB CD ⊥，︒=∠=∠=∠=∠45ACD BCD B A ，DB AD CD ==∵DB CD =，ACD B ∠=∠，AE =CF ，∴FBD ECD ≌△△ ∴DF DE =，BDF CDE ∠=∠∵︒=∠+∠90BDF CDF ，∴︒=∠+∠90CDE CDF ，即︒=∠90EDF ∵DF DE =，∴△DEF 是等腰直角三角形．【作业9】已知：如图，在四边形ABCD 中，∠ABC =∠ADC =90°，AC 、BD 相交于点O ，M 、N 分别为AC 、BD 的中点．（1）求证：MN ⊥BD ；A BC D EFA（2）当∠BAC =15°，AC =10，OB =OM 时，求MN 的长．【答案】见解析．【解析】（1）联结BM ，MD∵∠ABC =∠ADC =90°，M 分别为AC 的中点∴1122BM AC DM AC ==，， ∴MD BM =∵N 分别为BD 的中点， ∴MN ⊥BD ；（2）∵∠BAC =15°，AM BM =，∴︒=∠30BMC ∵OB =OM ，∴︒=∠=∠30MBO BMC∵MN ⊥BD ，∴BM MN 21=由（1）可得：521==AC BM ，∴25=MN【作业10】已知：等腰直角△ABC 中，O 是斜边AC 的中点，P 是斜边AC 上的一个动点，D 是线段BC 上的一点，且BP =PD ，过点D 作AC 边上的高DE ，求证：PE =BO ．【答案】见解析．【解析】∵等腰直角△ABC 中，∴︒=∠45C∵O 是斜边AC 的中点，∴︒=∠45OBC ∴OBC C ∠=∠∵BP =PD ，∴PDB PBD ∠=∠∵C DPE PDB OBC PBO PBD ∠+∠=∠∠+∠=∠， ∴DPE PBO ∠=∠∵DPE PBO ∠=∠，POB PED ∠=∠，BP =PD ， ∴PED BOP ≌△△ ∴PE =BO ．【作业11】如图1，已知点D 在AC 上，△ABC 和△ADE 都是等腰直角三角形，点M 为 EC 的中点．（1）求证：△BMD 为等腰直角三角形；（2）将△ADE 绕点A 逆时针旋转45°，如图2所示，（1）中的结论是否仍然成立，请说明理由；AB CD PEO（3）将△ADE 绕点A 逆时针旋转135°，（1）中的结论是否仍然成立，请说明理由．【答案】见解析．【解析】（1）联结DM∵︒=∠90ABC ，点M 为EC 的中点．∴EC BM 21=，BCM BME ∠=∠2∵︒=∠90EDC ，点M 为EC 的中点． ∴EC DM 21=，DCM EMD ∠=∠2，∴DM BM =∴22BMD BME EMD BCM DCM ∠=∠+∠=∠+∠ ()2290BCM DCM BCD =∠+∠=∠=︒ ∴△BMD 为等腰直角三角形；（2）延长DM 与BC 交于点N ∵AB DE ⊥，AB CB ⊥∴BC DE ∥，∴MCN DEM ∠=∠ ∵NMC EMD ∠=∠，MC EM =∴CNM EDM ≌△△，∴MN DM =，CN ED = ∵ED AD =，∴CN AD = ∵BC AB =，∴BN BD =∵MN DM =，∴DM BM ⊥，DM BM = ∴△BMD 为等腰直角三角形；（3）过C 作CN ∥ED 交DM 的延长线于N ∵CN ∥ED ，∴MED MCN ∠=∠∵MED MCN ∠=∠，DME CMN ∠=∠，MC EM = ∴CNM EDM ≌△△，∴MN DM =，CN ED = ∵ED AD =，∴CN AD =∵BC AB =，BAD BCN ∠=∠，CN AD =∴BCN BAD ≌△△，∴BN BD =，CBN DBA ∠=∠∵︒=∠+∠90CBN ABN ，∴︒=∠+∠90DBA ABN ，即︒=∠90DBN ∵MN DM =，∴DM BM ⊥，DM BM = ∴△BMD 为等腰直角三角形．图1 AB CDEMA BCDE图2M N。

八年级数学下册第1章直角三角形1.2直角三角形的性质和判定(Ⅱ)第1课时教学课件新版湘教版

1.2 直角三角形的性质和判定(Ⅱ)
第1课时
1.掌握勾股定理的内容. 2.理解勾股定理的证明. 3.应用勾股定理进行有关计算与证明.
星期日老师带领初二全体学生去凌峰山风景区游玩,同学们看到山势险峻,查看景区示意图得知:凌峰山主峰高约为900 米,如图:为了方便游人,此景区从主峰A处向地面B处架了一条缆车线路,已知山底端C处与地面B处相距1200米, ∠ACB=90°, 请问缆车路线AB长应为多少？
4.(广东·中考）如图（1），已知小正方形ABCD的面积
为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2（如图（2））；···以此下去，则正方形A4B4C4D4的面积为__________.
C2
C1
D1 D C A B B1
aA
bB
c
C
SA+SB=SC a2+b2=c2
这是2002年国际数学家大会会标
cb a
赵爽弦图
∵ 1 ab×4+(b-a)²=c²， 2
即2ab+（b²-2ab+a²）=c²， ∴a²+b² =c².
结论：
直角三角形中，两条直角边的平方和，等于斜边的
平方. B
在Rt△ABC中，∠C=90° ，
边BC，AC，AB所对应的边分别为a，b，c,则存在下列关系，勾 a
A的面积 B的面积 C的面积
图1 16
9
25
图2 4
9
13
你是怎样得到表中的结果的？与同伴交流交流．
C A
B
C
图1 A
B
图2
议一议

中学优质公开课教学课件精选直角三角形的性质与判定

∵AC2+BC2=AB2 (已知),
A′C′=AC,B′C′=BC (作图),
B′
∴ AB2=A′B′2 ∴ AB=A′B′
(等式性质). (等式性质).
c a
∴ △ABC≌ △A′B′C′ (SSS).
C′
b
∴ ∠C=∠C′＝ 90° (全等三角形的对应角角形 (直角三角形意义).
A
A′
观察刚才两个命题, 它们的条件与结论之间有怎样的关系? 与同伴交流.
直角三角形两直角边的平方和等于斜边的平方.
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
再观察下面三组命题:
如果两个角是对顶角, 那么它们相等, 如果两个角相等, 那么它们是对顶角;
如果小明患了肺炎, 那么他一定会发烧, 如果小明发烧, 那么他一定患了肺炎;
观察这两个定理你能分别指出它的条件和结论吗？（积分抢答）
（性质）定理：直角三角形的两个锐角互余.
（判定）定理：有两个角互余的三角形是直角三角形.
这是从角的角度研究直角三角形的性质和判定，那从边的角度研究都有哪些定理呢？
直角三角形中的勾股定理
如果直角三角形两直角边分别为a、b，斜边为c，那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方. 勾股定理在西方文献中又称为毕达哥拉斯定理
（pythagoras theorem）.
c a
弦勾
b
股
你能分别指出它的条件和结论吗？
你会证明勾股定理吗？回忆一下都有哪些方法？条件作为已知，结论作为求证。
勾股定理的证明有很多方法，例如拼图计算、割补法、赵爽的弦图、总统证法、青朱出入图、折纸法、拼图计算等，下面我们来回忆其中一个的“总统证法”.

著名机构讲义秋季18-8年级数学提升版--直角三角形的判定、性质和推论-课后作业教师版

【作业1】下列命题中，正确的有()个①腰长及底边上的高对应相等的两个等腰三角形全等 ②有一直角边和斜边对应相等的两个直角三角形全等 ③有两边和其中一边上的高对应相等的两个三角形全等 A ．0B ．1C ．2D ．3【答案】C【解析】（1）（2）对，（3）错误，满足条件的三角形可以是锐角三角形也可以是钝角三角形．【作业2】（1）直角△ABC 中，∠C = 90°，CD ⊥AB ，点E 是AB 的中点，∠ACD =25°，则∠ECB =__________；（2）直角△ABC 中，∠C =90°，CD ⊥AB ，点E 是AB 的中点，∠DCE =10°，则∠B =______________．【答案】（1）25°；（2）40°．【解析】利用直角三角形斜边上的中线等于斜边的一半的角度之间的关系可得到答案．【作业3】如图，ABC ∆中，AB AC =，DB DC =，DE AC ⊥，2AC AD =，8AB =，则AD =________，AE =____________．【答案】4；2．【解析】∵AB AC =，DB DC =，∴BC AD ⊥∵2AC AD =，∴︒=∠30C ，∴42121===AB AC AD∵DE AC ⊥，∴︒=∠=∠30B ADE ，∴221==AD AE ．直角三角形的全等判定及性质DABCEAB CD E【作业4】（1）等腰三角形底角是75°，腰长为9，则此三角形的面积是_______；（2）等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的顶角的度数是_____________．【答案】（1）481；（2）30°或150°．【解析】（1）∵等腰三角形底角是75°，∴顶角为30度，则腰上的高为29，则三角形的面积为48129921=⨯⨯；（2）注意分锐角三角形和钝角三角形两种情况分类讨论．【作业5】已知：AB ⊥BC ，DC ⊥BC ，点E 在BC 上，且AE =AD ，AB =BC ，求证：CE =CD ．【答案】见解析．【解析】过D 作DF ⊥AB ，垂足为F∵AB ⊥BC ，DC ⊥BC ，DF ⊥AB ， ∴四边形BCDF 是长方形， ∴BC DF =，CD BF = ∵BC AB =，∴DF AB = ∵DF AB =，AE=AD ， ∴EBA AFD ≌△△， ∴BE AF =∵BC AB =，∴BF CE = ∵CD BF =，∴CD CE =【作业6】已知：如图，△ABC 中，∠B =40°，∠C =20°，DA ⊥CA ，求证：CD=2AB ．【答案】见解析【解析】取CD 的中点E ，联结AE∵DA ⊥CA ，ED CE =∴CD CE AE 21==∴︒=∠=∠20CAE C ∴︒=∠+∠=∠40CAE C AEB∵︒=∠40B ，∴B AEB ∠=∠，∴AB AE =∵CD AE 21=，∴CD AB 21=，即AB CD 2=【作业7】如图，已知：△ABC 中，AB =AC ，∠A=60°，BD =CD ，BE ∥AC ，DE ⊥BE ，求证：4BE=AC .ABCDE FABCDEA【答案】见解析．【解析】连接AD∵AB =AC ，∠A=60°，∴△ABC 是等边三角形，∴BC =AC∵AB =AC ，BD =CD ，∴BC AD ⊥∵︒=∠=∠3021BAC DAC ，BC AD ⊥，∴AC DC 21=∵BD =CD ，∴AC BD 21=∵BE ∥AC ，∴︒=∠=∠60C DBE∵DE ⊥BE ，∴BD BE 21=∵AC BD 21=，∴AC BE 41=，即4BE=AC ．【作业8】在等腰直角△ABC 中，D 是斜边AB 的中点，E 、F 分别在直线AC 、BC 上，且AE =CF ，联结DE 、DF 、EF ，试判断△DEF 的形状，并加以证明．【答案】等腰直角三角形．证明见解析．【解析】等腰直角三角形．联结CD∵等腰直角△ABC 中，D 是斜边AB 的中点， ∴AB CD ⊥，︒=∠=∠=∠=∠45ACD BCD B A ，DB AD CD ==∵DB CD =，ACD B ∠=∠，AE =CF ，∴FBD ECD ≌△△ ∴DF DE =，BDF CDE ∠=∠∵︒=∠+∠90BDF CDF ，∴︒=∠+∠90CDE CDF ，即︒=∠90EDF ∵DF DE =，∴△DEF 是等腰直角三角形．【作业9】已知：如图，在四边形ABCD 中，∠ABC =∠ADC =90°，AC 、BD 相交于点O ，M 、N 分别为AC 、BD 的中点．（1）求证：MN ⊥BD ；A BCDEFA DM（2）当∠BAC =15°，AC =10，OB =OM 时，求MN 的长．【答案】见解析．【解析】（1）联结BM ，MD∵∠ABC =∠ADC =90°，M 分别为AC 的中点∴1122BM AC DM AC ==，， ∴MD BM =∵N 分别为BD 的中点， ∴MN ⊥BD ；（2）∵∠BAC =15°，AM BM =，∴︒=∠30BMC ∵OB =OM ，∴︒=∠=∠30MBO BMC∵MN ⊥BD ，∴BM MN 21=由（1）可得：521==AC BM ，∴25=MN【作业10】已知：等腰直角△ABC 中，O 是斜边AC 的中点，P 是斜边AC 上的一个动点，D 是线段BC 上的一点，且BP =PD ，过点D 作AC 边上的高DE ，求证：PE =BO ．【答案】见解析．【解析】∵等腰直角△ABC 中，∴︒=∠45C∵O 是斜边AC 的中点，∴︒=∠45OBC ∴OBC C ∠=∠∵BP =PD ，∴PDB PBD ∠=∠∵C DPE PDB OBC PBO PBD ∠+∠=∠∠+∠=∠， ∴DPE PBO ∠=∠∵DPE PBO ∠=∠，POB PED ∠=∠，BP =PD ， ∴PED BOP ≌△△ ∴PE =BO ．ABCDPEO。