初中数学竞赛几何证明题综合训练
精选初中数学几何证明经典试题(含答案)

十二周培优精选如图, 0是半圆的圆心,C 、E 是圆上的两点,CD 丄AB ,CD = GF . 2、已知:如图, P 是正方形 ABCD 内点,/ PAD = Z PDA = 15°. 求证:△PBC 是正三角形.3、设P 是正方形 ABCD 一边BC 上的任一点,PF 丄AP , CF 平分/ DCE . 求证:PA = PF .(初二) A经典题41、已知:△ ABC 是正三角形,P 是三角形内一点, 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/ PBA = Z PDA . 求证:/ PAB = Z PCB .4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与BCF 相交于P ,且CAE = CF .求证:/ DPA =Z DPC .( P <1•如下图做GH 丄AB,连接EO 。
由于GOFE 四点共圆,所以/ GFH =Z OEG,即貝GHF s\ OGE ,可得®0 = GO GF GH又CO=EO ,所以CD=GF 得证。
2.如下图做厶DGC 使与△ ADP 全等,可得△ PDG 为等边△,从而可得△ DGC ◎△ APD CGP,得出 PC=AD=DC,和/ DCG= / PCG = 15°已知: 求证: 如图, 求证: 如图, 求证: 如图,在四边形 ABCD 中,AD = BC , M 、N 分别是AB 、 / DEN = Z F . 四边形 ABCD 为正方形,DE // AC , AE = AC , AE 与CD 相交于F . D CE = CF .(初二) CD 的中点,AD 、 四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于 AE = AF .(初二) FMN E 、F 已知: 求证: EF 丄AB , EG 丄 CO . CPA = 3, PB = 4, PC = 5.B CO所以/ DCP=30°,从而得出△ PBC是正三角形4.如下图连接AC并取其中点Q,连接QN和QM所以可得/ QMF= / F,/ QNM= / DEN和/ QMN= / QNM , 从而得出/DEN = / F。
初中数学几何证明经典试题(含答案)
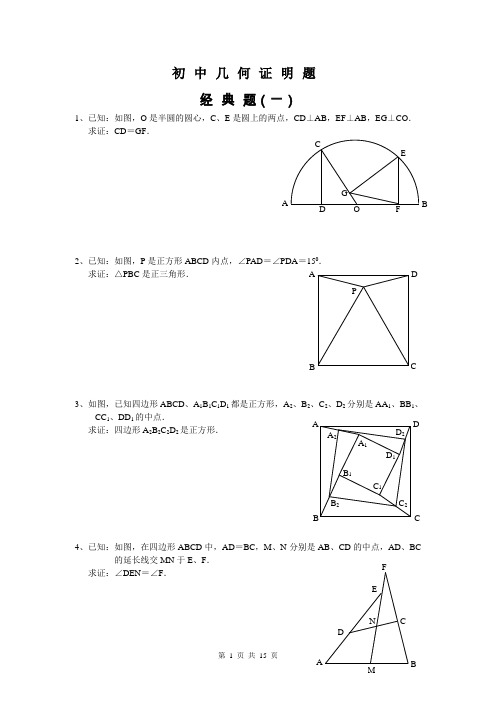
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .3、设P 是正方形ABCD 一边求证:PA =PF .4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF B、D .求证:AB =DC ,BC =AD .经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.2、设P是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
数学初中竞赛大题训练:几何专题(包含答案)

数学初中竞赛大题训练:几何专题1.阅读理解:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”.证明“四点共圆”判定定理有:1、若线段同侧两点到线段两端点连线夹角相等,那么这两点和线段两端点四点共圆;2、若平面上四点连成的四边形对角互补,那么这四点共圆.例:如图1,若∠ADB=∠ACB,则A,B,C,D四点共圆;或若∠ADC+∠ABC=180°,则A,B,C,D四点共圆.(1)如图1,已知∠ADB=∠ACB=60°,∠BAD=65°,则∠ACD=55°;(2)如图2,若D为等腰Rt△ABC的边BC上一点,且DE⊥AD,BE⊥AB,AD=2,求AE 的长;(3)如图3,正方形ABCD的边长为4,等边△EFG内接于此正方形,且E,F,G分别在边AB,AD,BC上,若AE=3,求EF的长.解:(1)∵∠ADB=∠ACB=60°,∴A,B,C,D四点共圆,∴∠ACD=∠ABD=180°﹣∠ADB﹣∠BAD=180°﹣60°﹣65°=55°,故答案为:55°;(2)在线段CA取一点F,使得CF=CD,如图2所示:∵∠C=90°,CF=CD,AC=CB,∴AF=DB,∠CFD=∠CDF=45°,∴∠AFD=135°,∵BE⊥AB,∠ABC=45°,∴∠ABE=90°,∠DBE=135°,∴∠AFD=∠DBE,∵AD⊥DE,∴∠ADE=90°,∵∠FAD+∠ADC=90°,∠ADC+∠BDE=90°,∴∠FAD=∠BDE,在△ADF和△DEB中,,∴△ADF≌△DEB(ASA),∴AD=DE,∵∠ADE=90°,∴△ADE是等腰直角三角形,∴AE=AD=2;(3)作EK⊥FG于K,则K是FG的中点,连接AK,BK,如图3所示:∴∠EKG=∠EBG=∠EKF=∠EAF=90°,∴E、K、G、B和E、K、F、A分别四点共圆,∴∠KBE=∠EGK=60°,∠EAK=∠EFK=60°,∴△ABK是等边三角形,∴AB=AK=KB=4,作KM⊥AB,则M为AB的中点,∴KM=AK•sin60°=2,∵AE=3,AM=AB=2,∴ME=3﹣2=1,∴EK===,∴EF===.2.问题再现:如图1:△ABC 中,AF 为BC 边上的中线,则S △ABF =S △ACP =S △ABC由这个结论解答下列问题:问题解决:问题1:如图2,△ABC 中,CD 为AB 边上的中线,BE 为AC 边上的中线,则S △BOC =S 四边形ADOE .分析:△ABC 中,CD 为AB 边上的中线,则S △BCD =S △ABC ,BE 为AC 边上的中线,则S △ABE =S △ABC∴S △BCD =S △ABE∴S △BCD ﹣S △BOD =S △ABE ﹣S △BOD又∵S △BOC =S △BCD ﹣S △BOD ,S 四边形ADOE =S △ABE ﹣S △BOD即S △BOC =S 四边形ADOE问题2:如图3,△ABC 中,CD 为AB 边上的中线,BE 为AC 边上的中线,AF 为BC 边上的中线.(1)S △BOD =S △COE 吗?请说明理由.(2)请直接写出△BOD 的面积与△ABC 的面积之间的数量关系:S △BOD =S △ABC .问题拓广:(1)如图4,E 、F 分别为四边形ABCD 的边AD 、BC 的中点,请直接写出阴影部分的面积与四边形ABCD 的面积之间的数量关系:S 阴= S 四边形ABCD . (2)如图5,E 、F 、G 、H 分别为四边形ABCD 的边AD 、BC 、AB 、CD 的中点,请直接写出阴影部分的面积与四边形ABCD 的面积之间的数量关系:S 阴= S 四边形ABCD .(3)如图6,E 、F 、G 、H 分别为四边形ABCD 的边AD 、BC 、AB 、CD 的中点,若S △AME =1、S △BNG =1.5、S △CQF =2、S △DPH =2.5,则S 阴= 7 .解:问题2:S △BOD =S △COE 成立,理由:∵△ABC 中,CD 为AB 边上的中线,∴S △BCD =S △ABC ,∵BE 为AC 边上的中线,∴S △CBE =S △ABC∴S △BCD =S △CBE∵S △BCD =S △BOD +S △BOC ,S △CBE =S △COE +S △BOC∴S △BOD =S △COE(2)由(1)有S △BOD =S △COE ,同(1)方法得,S △BOD =S △AOD ,S △COE =S △AOE ,S △BOF =S △COF ,∴S △BOD =S △COE =S △AOE =S △AOD ,∵点O 是三角形三条中线的交点,∴OA =2OF ,∴S △AOC =2S △COF =S △AOE +S △COE =2S △COE ,∴S △COF =S △COE ,∴S △BOD =S △COE =S △AOE =S △AOD =S △BOF =S △COF ,∴S △BOD =S △ABC ,故答案为问题拓广:(1)如图4:连接BD,由问题再现:S△BDE =S△ABD,S△BDF =S△BCD,∴S阴影=S四边形ABCD,故答案为,(2)如图5:连接BD,由问题解决:S△BMD =S△ABD,S△BDN=S△BCD,∴S阴影=S四边形ABCD,故答案为;(3)如图6,设四边形的空白区域分别为a,b,c,d,∵S△AME =1、S△BNG=1.5、S△CQF=2、S△DPH=2.5,由(1)得出:a+1+2.5=a+3.5=S△ACD①,c+1.5+2=c+3.5=S△ACB②,b +1+1.5=b +2.5=S △ABD ③,d +2+2.5=d +4.5=S △BCD ④,①+②+③+④得,a +3.5+c +3.5+b +2.5+d +4.5=a +b +c +d +14=S 四边形ABCD ⑤而S 四边形ABCD =a +b +c +d +7+S 阴影⑥∴S 阴影=7,故答案为7.3.如图,在△ABC 中,AB >AC ,内切圆⊙I 与边BC 切于点D ,AD 与⊙I 的另一个交点为E ,⊙I 的切线EP 与BC 的延长线交于点P ,CF ∥PE 且与AD 交于点F ,直线BF 与⊙I 交于点M 、N ,M 在线段BF 上,线段PM 与⊙I 交于另一点Q .证明:∠ENP =∠ENQ .证明:如图,设⊙I 与AC 、AB 分别切于点S 、T ,连接ST 、AI 、IT ,设ST 与AI 交于点G .则IE ⊥PE ,ID ⊥PD ,故I 、E 、P 、D 四点共圆,∵AS 2=AE •AD =AG •AI ,∵∠EAG =∠DAI ,∴△AEG ∽△AID ,∴∠AGE=∠AID,∴E,G,D,I四点共圆,∴I、G、E、P、D五点共圆,∴∠IGP=∠IEP=90°,即IG⊥PG,∴P、S、T三点共线,对直线PST截△ABC,由梅涅劳斯定理知,∵AS=AT,CS=CD,BT=BD,∴,设BN的延长线与PE交于点H,对直线BFH截△PDE,由梅涅劳斯定理知,∵CF∥BE,∴,∴,∴PH=HE,∴PH2=HE2=HM•HN,∴,∴△PHN∽△MHP,∴∠HPN=∠HMP=∠NEQ,∵∠PEN=∠EQN,∴∠ENP=∠ENQ.4.如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足,直线ED交外接圆于点M.求证:∠AMH=90°.证明:作高BP,CQ.连结MB、MC、MP、MQ、PQ.===•①=•=•②由①②得:=,又∵∠MBA=∠MCA,∴△MBQ∽△MCP,∴点M、A、P、Q四点共圆,即点M、A、P、Q、H五点共圆,又AH为直径,∴∠AMH=90°.5.如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD 和AC交于点N.求证:OH⊥MN.证明:∵A 、C 、D 、F 四点共圆,∴∠BDF =∠BAC又∵∠OBC =(180°﹣∠BOC )=90°﹣∠BAC ,∴OB ⊥DF .∵CF ⊥MA ,∴MC 2﹣MH 2=AC 2﹣AH 2(①)∵BE ⊥NA ,∴NB 2﹣NH 2=AB 2﹣AH 2 (②)∵DA ⊥BC ,∴BD 2﹣CD 2=BA 2﹣AC 2 (③)∵OB ⊥DF ,∴BN 2﹣BD 2=ON 2﹣OD 2 (④)∵OC ⊥DE ,∴CM 2﹣CD 2=OM 2﹣OD 2,①﹣②+③+④﹣⑤,得NH 2﹣MH 2=ON 2﹣OM 2 MO 2﹣MH 2=NO 2﹣NH 2∴OH ⊥MN .6.在图1到图4中,已知△ABC 的面积为m .(1)如图1,延长△ABC 的边BC 到点D 使CD =BC ,连接DA ,若△ACD 的面积为S 1,则S 1= m .(用含m 的式子表示)(2)如图2,延长△ABC 的边BC 到点D ,延长边CA 到点E ,使CD =BC ,AE =CA ,连接DE .若△DEC 的面积为S 2,则S 2= 2m .(用含a 的代数式表示)(3)如图3,在图2的基础上延长AB 到点F ,使BF =AB ,连接FD 于E ,得到△DEF ,若阴影部分的面积为S 3,则S 3= 6m .(用含a 的代数式表示)(4)可以发现将△ABC 各边均顺次延长一倍,连接所得端点,得到△DEF ,如图3,此时,我们称△ABC 向外扩展了一次.可以发现扩展一次后得到的△DEF 的面积是原来△ABC 面积的 7 倍.(5)应用上面的结论解答下面问题:去年在面积为15平方面的△ABC 空地上栽种了各种花卉,今年准备扩大种植规模,把△ABC 内外进行两次扩展,第一次由△ABC 扩展成△DEF ,第二次由△DEF 扩展成△MGH ,如图4,求这两次扩展的区域(即阴影部分)面积共为多少平方米?解:(1)∵CD =BC ,∴△ABC 和△ACD 的面积相等(等底同高),故得出结论S 1=m .(2)连接AD ,,∵AE =CA ,∴△DEC 的面积S 2为△ACD 的面积S 1的2倍,故得出结论S 2=2m .(3)结合(1)(2)得出阴影部分的面积为△DEC 面积的3倍, 故得出结论则S 3=6m .(4)S △DEF =S 阴影+S △ABC=S 3+S △ABC=6m +m=7m=7S △ABC故得出结论扩展一次后得到的△DEF 的面积是原来△ABC 面积的7倍.(5)根据(4)结论可得两次扩展的区域(即阴影部分)面积共为(7×7﹣1)×15=720(平方米),答:求这两次扩展的区域(即阴影部分)面积共为720平方米. 7.(1)如图①,AD 是△ABC 的中线,△ABD 与△ACD 的面积有怎样的数量关系?为什么?(2)若三角形的面积记为S ,例如:△ABC 的面积记为S △ABC ,如图②,已知S △ABC =1,△ABC 的中线AD 、CE 相交于点O ,求四边形BDOE 的面积.小华利用(1)的结论,解决了上述问题,解法如下:连接BO ,设S △BEO =x ,S △BDO =y ,由(1)结论可得:S,S △BCO =2S △BDO =2y ,S △BAO =2S △BEO =2x . 则有,即.所以.请仿照上面的方法,解决下列问题: ①如图③,已知S △ABC =1,D 、E 是BC 边上的三等分点,F 、G 是AB 边上的三等分点,AD 、CF 交于点O ,求四边形BDOF 的面积.②如图④,已知S △ABC =1,D 、E 、F 是BC 边上的四等分点,G 、H 、I 是AB 边上的四等分点,AD 、CG 交于点O ,则四边形BDOG 的面积为 .解:(1)S △ABD =S △ACD .∵AD 是△ABC 的中线,∴BD =CD ,又∵△ABD 与△ACD 高相等,∴S △ABD =S △ACD .(2)①如图3,连接BO ,设S △BFO =x ,S △BDO =y ,S △BCF =S △ABD =S △ABC =S △BCO =3S △BDO =3y ,S △BAO =3S △BFO =3x .则有,即,所以x +y =,即四边形BDOF 的面积为;②如图,连接BO ,设S △BDO =x ,S △BGO =y ,S△BCG =S△ABD=S△ABC=,S△BCO =4S△BDO=4x,S△BAO =4S△BGO=4y.则有,即,所以x+y=,即四边形BDOG的面积为,故答案为:.8.我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.【提出问题】如何用表示几何图形面积的方法推证:13+23=32?【解决问题】A表示1个1×1的正方形,即:1×1×1=13B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.由此可得:13+23=32【递进探究】请仿用上面的表示几何图形面积的方法探究:13+23+33=62.要求:自己构造图形并写出详细的解题过程.【推广探究】请用上面的表示几何图形面积的方法探究:13+23+33+…+n3=.(参考公式:)注意:只需填空并画出图形即可,不必写出解题过程.【提炼运用】如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,如图(1)中,共有1个小立方体,其中1个看的见,0个看不见;如图(2)中,共有8个小立方体,其中7个看的见,1个看不见;如图(3)中,共有27个小立方体,其中19个看的见,8个看不见;求:从第(1)个图到第(101)个图中,一切看不见的棱长为1的小立方体的总个数.解:【递进探究】如图,A表示一个1×1的正方形,即:1×1×1=13,B、C、D表示2个2×2的正方形,即:2×2×2=23,E、F、G表示3个3×3的正方形,即:3×3×3=33,而A、B、C、D、E、F、G恰好可以拼成一个大正方形,边长为:1+2+3=6,,∵S A+S B+S C+S D+S E+S F+S G=S大正方形∴13+23+33=62;【推广探究】由上面表示几何图形的面积探究知,13+23+33+…+n3=(1+2+3+…+n)2,又∵1+2+3+…+n=,∴13+23+33+…+n3=()2=.【提炼运用】图(1)中,共有1个小立方体,其中1个看的见,0=(1﹣1)3个看不见;如图(2)中,共有8个小立方体,其中7个看的见,1=(2﹣1)3个看不见;如图(3)中,共有27个小立方体,其中19个看的见,8=(3﹣1)3个看不见;…,从第(1)个图到第(101)个图中,一切看不见的棱长为1的小立方体的总个数为:(1﹣1)3+(2﹣1)3+(3﹣1)3+…+(101﹣1)3=03+13+23+…+1003=50502=25502500.故一切看不见的棱长为1的小立方体的总个数为25502500.故答案为:62;.9.问题引入:如图,在△ABC中,D是BC上一点,AE=AD,求:尝试探究:过点A作BC的垂线,垂足为F,过点E作BC的垂线,垂足为G,如图所示,有=,=,.类比延伸:若E为AD上的任一点,如图所示,试猜S四边形ABEC 与S△ABC的比是图中哪条线段的比,并加以证明.拓展应用:如图,E为△ABC内一点,射线AE于BC于点D,射线BE交AC于点F,射线CE交AB于点G,求的值.解:问题引入:∵在△ABC中,D是BC上一点,AE=AD,∴,,∴==;尝试探究:∵AE=AD,∴=,∵AF⊥BC,EG⊥BC,∴AF∥EG,∴△EDG∽△ADB,∴=;∵===,∴=1﹣=;故答案为:,,;类比延伸:=,∵E为AD上的一点,∴=,=,∴==;拓展应用:∵==,同理:=,=,∴==2.10.如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD 的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.证明:连接AP、BP,取AP的中点E,取BP的中点F,连接DE、ME、QE、CF、QF、MF,如图.∵E为AP的中点,F为BP的中点,M为AB的中点,∴EM∥BP,EM=BP,MF∥AP,MF=AP.∵E为AP的中点,F为BP的中点,∠ADP=∠BCP=90°,∴DE=AE=EP=AP,FC=PF=BF=BP,∴DE=MF,EM=FC.在△DEM和△MFC中,,∴△DEM≌△MFC(SSS),∴∠DEM=∠MFC.∵EM∥BP,MF∥AP,∴四边形PEMF是平行四边形,∴∠PEM=∠PFM.又∵∠DEM=∠MFC,∴∠DEP=∠CFP.∵DE=AE,FC=BF,∴∠DAE=∠ADE=∠DEP,∠FBC=∠FCB=∠CFP,∴∠DAE=∠FBC,即∠DAP=∠PBC.∵∠ADP=∠AQP=90°,E为AP中点,∴ED=EA=EQ=EP=AP,∴D、A、Q、P四点共圆,∴∠PQD=∠DAP.同理可得:∠PQC=∠PBC,∴∠PQD=∠PQC.11.如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.解:连接OC,如图.∵MC与⊙O相切,∴OC⊥MC.∵CM⊥AD,∴OC∥AM.∵CE∥AB,∴四边形AOCE是平行四边形,∴OA=CE=7,∴AB=14.∵点C是弧BD的中点,∴BC=CD=6.∵AB是⊙O的直径,∴∠ACB=90°,∴AC===4.∵CE∥AB,∴△CGE∽△AGB,∴===,∴AG=AC=.在Rt△ACB中,cos∠BAC===.∵点C是弧BD的中点,∴∠BAC=∠CAD,即∠BAC=∠EAG,∴cos∠EAG=.在△EAG中,cos∠EAG=.∴=.∵AG=,AE=CE=7,∴=.整理得:GE2=.∵GE>0,∴GE=.∴EG的长为.12.如图,圆内接四边形ABCD的边AB、DC的延长线交于E,AD、BC延长线交于F,EF中点为G,AG与圆交于K.求证:C、E、F、K四点共圆.证明:延长AG到H,使得GH=AG,连接EH、FH、CK,如图所示.∵GH=AG,EG=FG,∴四边形AEHF是平行四边形,∴∠EAG=∠GHF,∠GAF=∠GHE.∵A、B、C、K四点共圆,∴∠KCF=∠EAG,∴∠KCF=∠GHF,∴K、C、H、F四点共圆.∵K、C、A、D四点共圆,∴∠KCD=∠KAF,∴∠KCD=∠GHE,∴K、C、E、H四点共圆,∴K、C、E、H、F五点共圆,∴C、E、F、K四点共圆.13.在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.证明:连接CK,BK,BC,如图所示.∵AB是⊙O直径,∴∠ACB=90°,∴∠OAC+∠ABC=90°.∵A、B、C、D四点共圆,∴∠BDC=∠BAC.∵A、O、C、K四点共圆,∴∠CKO=∠OAC.∵D、O、B、K四点共圆,∴∠BKO=∠BDO.∴∠BKC=∠BKO﹣∠CKO=∠BDO﹣∠OAC.∵OB=OD,∴∠ABD=∠BDO.∴∠BMC=∠ABD﹣∠BDC=∠BDO﹣∠BAC=∠BKC.∴B、C、K、M四点共圆.∴∠ABC=∠MKC.∴∠MKO=∠MKC+∠CKO=∠ABC+∠OAC=90°.14.已知,在△ABC中,AC>AB,BC边的垂直平分线与∠BAC的外角∠PAC的平分线相交于E,与BC相交点D,DE与AC相交于点F.(1)如图1,当∠ABC=3∠ACB时,求证:AB=AE;(2)如图2,当∠BAC=90°,∠ABC=2∠ACB,过点D作AC的垂线,垂足为点H,并延是点D关于直线AC的对长DH交射线AE于点M,过点E作BP的垂线,垂足为点G,点D1称点,试探究AG和MD之间的数量关系,并证明你的结论.1解:(1)证明:连接BF,如图1.设∠A CB=x,则∠ABC=3x,∵FD垂直平分BC,∴FB=FC,∴∠FBC=∠FCB=x,∴∠ABF=∠AFB=2x,∴AB=AF,∠PAC=4x.∵AE平分∠PAC,∴∠EAC=2x.∵∠AFE=∠DFC=90°﹣x,∴∠AEF=180°﹣∠EAF﹣∠AFE=180°﹣2x﹣(90°﹣x)=90°﹣x,∴∠AEF=∠AFE,∴AE=AF,∴AB=AE..(2)AG=MD1证明:作EN⊥AC于N,取EC中点O,、NM、MC、MO、NO、EB、EC,如图2.连接AD1∵AE平分∠PAC,EN⊥AC,EG⊥AP,∴EG=EN,∠EGA=∠ENA=90°.∵∠BAC=90°,∴∠EGA=∠ENA=∠BAC=90°,∴四边形EGAN是矩形.∵EG=EN,∴矩形EGAN是正方形,∴AG=AN,∠EAN=45°,∠GEN=90°.∵ED垂直平分BC,∴EB=EC.在Rt△BEG和Rt△CEN中,,∴Rt△BEG≌Rt△CEN(HL),∴∠GBE=∠NCE,∠GEB=∠NEC,∴∠GEN=∠BEC=90°∵EB=EC,∴∠ECB=∠EBC=45°.∵∠BAC=90°,∠ABC=2∠ACB,∴∠ABC=60°,∠ACB=30°,∴∠ABE=∠ACE=15°.∵∠BAC=90°,点D为BC中点,∴AD=CD,∴∠DAC=∠DCA=30°.∵点D与点D关于AC对称,1AC=∠DAC=30°,∴∠D1=45°﹣30°=15°.∴∠MAD1∵DA=DC,DM⊥AC,∴DM垂直平分AC,∴MA=MC,∴∠CMH=∠AMH=90°﹣45°=45°,∴∠AMC=90°,∴∠ENC=∠AMC=90°.∵点O为EC中点,∴ON=OM=OE=OC=EC,∴E、N、C、M四点共圆,∴∠EMN=∠ECN=15°,∴∠MAD=∠EMN=15°,1中,在△AMN和△MAD1,,∴△AMN≌△MAD1,∴AN=MD1.∴AG=MD115.在平面直角坐标系中,已知A(2,2),AB⊥y轴于B,AC⊥x轴于C.(1)如图1,E为线段OB上一点,连接AE,过A作AF⊥AE交x轴于F,连EF,ED平分∠OEF交OA于D,过D作DG⊥EF于G,求DG+EF的值;(2)如图2,D为x轴上一点,AC=CD,E为线段OB上一动点,连接DA、CE、F是线段CE的中点,若BF⊥FK交AD于K,请问∠KBF的大小是否变化?若不变,求其值;若改变,求其变化范围.解:(1)∵AB⊥y轴于B,AC⊥x轴于C,∴∠ABO=∠ACO=90°.∵∠BOC=90°,∴四边形ABOC是正方形,∴AB=AC=BO=CO=2,OA平分∠BOC,∠BAC=90°.∵AF⊥AE,∴∠EAF=90°,∴∠BAC=∠EAF,∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,即∠BAE=∠CAF.在△ABE和△ACF中,,∴△ABE≌△ACF(ASA),∴AE=AF,BE=CF.设BE=CF=t,OE=2﹣t,OF=2+t.∵ED平分∠OEF,∴点D是△OEF的内心.如图1,作DM⊥OB于M,作DH⊥OF于H,且DG⊥EF于G,∴DG=DM=DH,∴四边形MOHD是正方形,∴MO=HO=DM=DG.设DG=MO=x,∴x=,∴x=,∴EF=4﹣2x,∴WF=2﹣x.∴DG+EF=x+2﹣x=2.即DG+EF的值为2;(2)∠KBF的大小不变,∠KBF=45°如图2,延长BF交AC于G,连接KG,作KM⊥AB于M,KN⊥AC于N,∵四边形ABOC是正方形,∴O B∥AC.∴∠EBF=∠CGF,∠BEF=∠GCF.∵F是CE的中点,∴EF=CF.在△BEF和△GCF中,,∴△BEF≌△GCF(AAS),∴BF=GF.∵BF⊥FK,∴∠BFK=∠GFK=90°.在△BFK和△GFK中,,∴△BFK≌△GFK(SAS)∴BK=GK.∵AC=CD,∠ACD=90°,∴△ACD是等腰直角三角形,∴∠CAD=45°.∵KN⊥AC,∴∠ANK=90°,∴∠AKN=45°,∴AN=KN.∵KM⊥AB,∴四边形AMKN是正方形,∴KM=KN.∠M=∠GNK=90°AM∥KN.在Rt△BKM和Rt△GKN中,,∴Rt△BKM≌Rt△GKN(HL),∴∠MBK=∠NGK.∠GKN=∠BKM.∵AM∥KN,∴∠BKN=∠MBK.∵∠BKM+∠BKN=90°,∴∠GKN+∠BKN=90°,即∠BKG=90°.∵BK=GK,∴△BKG是等腰直角三角形.∴∠KBF=45°,∴∠KBF的大小不变,∠KBF=45°.16.如图,已知⊙O1与⊙O2相交于A,B两点,直线MN⊥AB于A,且分别与⊙O1,⊙O2交于M、N,P为线段MN的中点,又∠AO1Q1=∠AO2Q2,求证:PQ1=PQ2.解:连接MQ1、BQ1、BQ2、NQ2,过点P作PH⊥Q1B于H,如图所示.则由圆内接四边形的性质可得:∠Q1MA+∠ABQ1=180°,∠ABQ2+∠ANQ2=180°,∠MAB=∠BQ2N.由圆周角定理可得:∠ABQ 1=∠AO 1Q 1,∠ANQ 2=∠AO 2Q 2. ∵∠AO 1Q 1=∠AO 2Q 2,∴∠ABQ 1=∠ANQ 2,∴∠ABQ 2+∠ABQ 1=∠ABQ 2+∠ANQ 2=180°, ∴Q 1、B 、Q 2三点共线.由圆内接四边形的性质可得:∠ABQ 1=∠ANQ 2, ∴∠Q 1MA +∠ANQ 2=∠Q 1MA +∠ABQ 1=180°, ∴MQ 1∥NQ 2.∵AB ⊥MN ,∴∠MAB =90°,∴∠Q 1Q 2N =∠MAB =90°.∵PH ⊥Q 1B ,即∠Q 1HP =90°,∴∠Q 1HP =∠Q 1Q 2N ,∴PH ∥NQ 2,∴MQ 1∥PH ∥NQ 2.∵P 为线段MN 的中点,∴H 为线段Q 1Q 2的中点,∴PH 垂直平分Q 1Q 2,∴PQ 1=PQ 2.。
全国初中数学竞赛试题汇编---几何解答题及答案

全国初中数学竞赛试题汇编---几何解答题1、如图,圆O 与圆D 相交于,A B 两点,BC 为圆D 的切线,点C 在圆O 上,且AB BC =.(1)证明:点O 在圆D 的圆周上.(2)设△ABC 的面积为S ,求圆D 的的半径r 的最小值.解:(1)连,,,OA OB OC AC ,因为O 为圆心,AB BC =,所以△OBA ∽△OBC ,从而OBA OBC ∠=∠.因为,OD AB DB BC ⊥⊥,所以9090DOB OBA OBC DBO ∠=°−∠=°−∠=∠,所以DB DO =,因此点O 在圆D 的圆周上.(2)设圆O 的半径为a ,BO 的延长线交AC 于点E ,易知BE AC ⊥.设2AC y =(0)y a <≤,OE x =,AB l =,则222a x y =+,()S y a x =+,22222222()2222()aSl y a x y a ax x a ax a a x y=++=+++=+=+=.因为22ABC OBA OAB BDO ∠=∠=∠=∠,AB BC =,DB DO =,所以△BDO ∽△ABC ,所以BD BO AB AC =,即2r a l y =,故2alr y=.所以22223222()4422a l a aS S a Sr y y y y ==⋅=⋅≥,即r ≥其中等号当a y =时成立,这时AC 是圆O 的直径.所以圆D 的的半径r .2、如图,给定锐角三角形ABC ,BC CA <,AD ,BE 是它的两条高,过点C 作△ABC 的外接圆的切线l ,过点D ,E 分别作l 的垂线,垂足分别为F ,G .试比较线段DF 和EG 的大小,并证明你的结论.解法1:结论是DF EG =.下面给出证明.因为FCD EAB ∠=∠,所以Rt △FCD ∽Rt △EAB .于是可得CD DF BE AB =⋅.同理可得CEEG AD AB=⋅.又因为tan AD BEACB CD CE ∠==,所以有BE CD AD CE ⋅=⋅,于是可得DF EG =.解法2:结论是DF EG =.下面给出证明连接DE ,因为90ADB AEB ∠=∠=°,所以A ,B ,D ,E 四点共圆,故CED ABC ∠=∠.又l 是⊙O 的过点C 的切线,所以ACG ABC ∠=∠.所以,CED ACG ∠=∠,于是DE ∥FG ,故DF =EG .3、是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角2倍的△ABC ?证明你的结论.解:存在满足条件的三角形.当△ABC 的三边长分别为6=a ,4=b ,5=c 时,B A ∠=∠2.………………5分如图,当B A ∠=∠2时,延长BA 至点D ,使b AC AD ==.连接CD ,则△ACD 为等腰三角形.因为BAC ∠为△ACD 的一个外角,所以2BAC D ∠=∠.由已知,2BAC B ∠=∠,所以D B ∠=∠.所以△CBD 为等腰三角形.又D ∠为△ACD 与△CBD 的一个公共角,有△ACD ∽△CBD ,于是BDCDCD AD =,即cb aa b +=,所以()c b b a +=2.而264(45)=×+,所以此三角形满足题设条件,故存在满足条件的三角形.………………15分说明:满足条件的三角形是唯一的.若B A ∠=∠2,可得()c b b a +=2.有如下三种情形:(i )当b c a >>时,设1+=n a ,n c =,1−=n b (n 为大于1的正整数),代入()c b b a +=2,得()()()21121n n n +=−−,解得5=n ,有6=a ,4=b ,5=c ;(ⅱ)当b a c >>时,设1+=n c ,n a =,1−=n b (n 为大于1的正整数),代入()c b b a +=2,得()n n n 212⋅−=,解得2=n ,有2=a ,1=b ,3=c ,此时不能构成三角形;(ⅲ)当c b a >>时,设1+=n a ,n b =,1−=n c (n 为大于1的正整数),代入()c b b a +=2,得()()1212−=+n n n ,即0132=−−n n ,此方程无整数解.所以,三边长恰为三个连续的正整数,且其中一个内角等于另一个内角的2倍的三角形存在,而且只有三边长分别为4,5,6构成的三角形满足条件.4、△ABC 的三边长,,,,,BC a AC b AB c a b c === 都是整数,且,a b 的最大公约数是2.点G和点I 分别为△ABC 的重心和内心,且90oGIC ∠=,求△ABC 的周长.解:如图,连结GA ,GB ,过G ,I 作直线交BC 、AC 于点E 、F ,作△ABC 的内切圆I ,切BC 边于点D 。
初中数学竞赛几何证明题综合训练

第 1 页 共6 页 几何证明题综合训练1. 线段或角相等的证明(1) 利用全等△或相似多边形;利用全等△或相似多边形;(2) 利用等腰△;利用等腰△;(3) 利用平行四边形;利用平行四边形; (4) 利用等量代换;利用等量代换;(5) 利用平行线的性质或利用比例关系利用平行线的性质或利用比例关系 (6) 利用圆中的等量关系等。
利用圆中的等量关系等。
2. 线段或角的和差倍分的证明(1) 转化为相等问题。
如要证明a=b±c ,可以先作出线段p=b±c ,再去证明a=p ,即所谓“截长补短”,角的问题仿此进行。
,角的问题仿此进行。
(2) 直接用已知的定理。
例如:中位线定理,Rt △斜边上的中线等于斜边的一半;△的外角等于不相邻的内角之和;圆周角等于同弧所对圆心角的一半等等。
△的外角等于不相邻的内角之和;圆周角等于同弧所对圆心角的一半等等。
3. 两线平行与垂直的证明(1) 利用两线平行与垂直的判定定理。
利用两线平行与垂直的判定定理。
(2) 利用平行四边形的性质可证明平行;利用等腰△的“三线合一”可证明垂直。
(3) 利用比例关系可证明平行;利用勾股定理的逆定理可证明垂直等。
利用比例关系可证明平行;利用勾股定理的逆定理可证明垂直等。
【竞赛例题剖析】【例【例11】从⊙】从⊙O O 外一点P 向圆引两条切线PA PA、、PB 和割线PCD PCD。
从。
从A 点作弦AE 平行于CD CD,连结,连结BE 交CD 于F 。
求证:求证:BE BE 平分CD CD。
【分析1】构造两个全等△。
】构造两个全等△。
连结ED ED、、AC AC、、AF AF。
CF=DF CF=DF←△←△←△ACF ACF ACF≌△≌△≌△EDF EDF EDF←←←ïïîïïíìîí쬬Ð=ÐÐ=Ð=ЬÐ=ЬþýüÐ=Ð=四点共圆、、、P B F A ABP AFC ABPAEF EFD EFD AFC CD //AE EDF ACF ED AC ←∠←∠PAB=PAB=PAB=∠∠AEB=AEB=∠∠PFB【分析2】利用圆中的等量关系。
初中数学几何证明试题(含答案)
第 6 页 共 15 页
4.如下图连接 AC 并取其中点 Q,连接 QN 和 QM,所以可得∠QMF=∠F,∠QNM=∠
DEN 和∠QMN=∠QNM,从而得出∠DEN=∠F。
经 典 题(二)
1.(1)延长 AD 到 F 连 BF,做 OG⊥AF,
又∠F=∠ACB=∠BHD, 可得 BH=BF,从而可得 HD=DF, 又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ,即 AD•BC=BE•AC,
①
BC AC
又∠ACB=∠DCE,可得△ABC∽△DEC,既得
AB = DE ,即 AB•CD=DE•AC,
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
第 11 页 共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB,OC,既得∠BOC=1200,
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页 共 15 页
3.作 OF⊥CD,OG⊥BE,连接 OP,OA,OF,AF,OG,AG,OQ。 由于 AD = AC = CD = 2FD = FD , AB AE BE 2BG BG
(2)过 P 点作 BC 的平行线交 AB,AC 与点 D,F。
由于∠APD>∠ATP=∠ADP,
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得:最大 L< 2 ;
全国各地初中(九年级)数学竞赛《几何》真题大全 (附答案)

全国各地初中(九年级)数学竞赛专题大全竞赛专题7 几何一、单选题 1.(2021·全国·九年级竞赛)某种产品由甲、乙、丙三种元件构成,如图为生产效率最高,在表示工人分配的扇形图中,生产甲、乙、丙元件的工人数量所对应的扇形圆心角的大小依次是( ).A .120,180,60︒︒︒B .108,144,108︒︒︒C .90,180,90︒︒︒D .72,216,720︒︒︒2.(2021·全国·九年级竞赛)如图所示,一次函数y kx b =+的图象过点(1,4)P 且与x 轴和y 轴的正半轴交于AB 、两点,点O 为坐标原点,当AOB 的面积最小时,k ,b 的值为( )A .4k =-,8b =B .4k =-,4b =C .2k =-,4b =D .2k =-,2b =3.(2021·全国·九年级竞赛)如图,已知DEF 的边长分别为3,2,正六边形网格由24个边长为2的正三角形组成,以这些正三角形的顶点画ABC ,使得ABC DEF ∽△△,相似比为ABk DE=,那么k 的不同值共有( )个.A .1B .2C .3D .4二、填空题4.(2021·全国·九年级竞赛)如图所示,正方形ABCD 的边长为10cm ,点E 在边CB 的延长线上且10cm EB =,点P 在边CD 上运动,EP 与AB 的交点为F .设cm DP x =,EFB △与四边形AFPD 的面积和为2cm y ,那么y 与x 之间的函数关系式是________.5.(2021·全国·九年级竞赛)把两个半径为5及一个半径为8的圆形纸片放在桌面上,使它们两两外切.若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于________. 6.(2021·全国·九年级竞赛)由一次函数2,2y x y x =+=-+和x 轴围成的三角形与圆心在(1,1)、半径为1的圆构成的图形覆盖的面积等于______.7.(2021·全国·九年级竞赛)某广场地面铺满了边长为36cm 的正六边形地砖,现向上抛掷半径为3cm 的圆碟,圆碟落地后与地面不相交的概率大约是_________. 三、解答题8.(2021·全国·九年级竞赛)平面上7个点,它们之间可以连一些线段,使7个点中任意三点必存在两点有线段相连.问最少要连几条线段?证明你的结论.9.(2021·全国·九年级竞赛)在直径为5的圆内放入10个点,证明其中必有两点的距离小于2.10.(2021·全国·九年级竞赛)设1M 是凸五边形12345A A A A A ,将1M 沿1i A A 方向平移,使1A 移到i A 得到凸五边形(2,3,4,5)i M i =.证明:12345,,,,M M M M M 中至少有两个图形,它们有公共内点.11.(2021·全国·九年级竞赛)在圆周上任取21个点,证明:以这些点为端点的弧中至少存在100条不超过120︒的弧.12.(2021·全国·九年级竞赛)两人A 和B 相约在12点与下午1点之间在某地会面,先到的人要等候另一人20分钟,过时就可以离开.如果每人可在指定的一小时内任何时刻到达,并且两人到达的时刻是彼此独立的(即一人到达的时刻与另一人到达的时刻没有影响),试计算两人能会面的概率.13.(2021·全国·九年级竞赛)平面上给出n个不全共线的点,求证:存在一条直线l,它恰通过其中两个点.14.(2021·全国·九年级竞赛)已知A,B,C,D为平面上两两距离不超过1的任意4点,今欲作一圆覆盖这4点(即A,B,C,D在圆内或圆周上)问圆的半径最小该是多少?试证明之.15.(2021·全国·九年级竞赛)任意凸四边形ABCD中总存在一条对角线和一条边,以它们为直径的两个圆可以覆盖这个四边形.16.(2021·全国·九年级竞赛)设甲是边长为1的正三角形纸片,乙是边长为1的正方形纸片,丙是边长为1的正五边形纸片,丁是边长为1的正六边形纸片.证明:(1)不能用甲、乙、丙合起来盖住一个半径为1的圆;(2)能用甲、乙、丙、丁合起来盖住一个半径为1的圆.17.(2021·全国·九年级竞赛)在一个半径等于6的圆内任意放入六个半径等于1的小圆.证明:其中总还有一块空位置,可以完整地放入一个半径为1的小圆.18.(2021·全国·九年级竞赛)将4张圆形纸片放在桌面上,使得其题中任何3张圆形纸片都有公共点,那么这4张圆形纸片是否一定有公共点?证明你的结论.19.(2021·全国·九年级竞赛)平面上给定了若干个圆,它们覆盖的面积为1.证明:从中可选出若干个两两不重叠的圆,使它们覆盖的面积不小于19.20.(2021·全国·九年级竞赛)证明:一个边长为5的正方形可以被3个边长为4的正方形所覆盖.21.(2021·全国·九年级竞赛)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).(1)当30α=︒时,通过计算说明此溶液是否会溢出;(2)现需要倒出不少于33000cm的溶液,当α等于60︒时,能实现要求吗?通过计算说明理由.22.(2021·全国·九年级竞赛)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头停泊,它们在一昼夜内到达的时间是等可能的,如果甲的停泊时间是1小时,乙的停泊时间是2小时,求它们中任何一艘都不需要等候码头空出的概率(精确到0.001).23.(2021·全国·九年级竞赛)把长为a 的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.24.(2022·福建·九年级竞赛)如图,四边形ABCD 是平行四边形,∠DAC =45°,以线段AC 为直径的圆与AB 和AD 的延长线分别交于点E 和F ,过点B 作AC 的垂线,垂足为H .求证:E ,H ,F 三点共线.竞赛专题7 几何答案解析一、单选题 1.(2021·全国·九年级竞赛)某种产品由甲、乙、丙三种元件构成,如图为生产效率最高,在表示工人分配的扇形图中,生产甲、乙、丙元件的工人数量所对应的扇形圆心角的大小依次是( ).A .120,180,60︒︒︒B .108,144,108︒︒︒C .90,180,90︒︒︒D .72,216,720︒︒︒【答案】B 【详解】解 设分配生产甲、乙、丙3种元件的人数分别为x 人,y 人,z 人,于是每小时生产甲、乙、丙三种元件的个数分别为50,30,20x y z .为了提高效率应使生产出来的元件全部组成成品而没有剩余.设共可组成k 件成品,则503020504020x y z k ===,即4,,3x k y k z k ===,从而4::1::13:4:33x y z ==.设在扇形图中生产甲、乙、丙三种元件的圆心角分别为,,αβγ,则3336036036010834310x x y z α=⨯︒=⨯︒=⨯︒=︒++++,4436036036014434310y x y z β=⨯︒=⨯︒=⨯︒=︒++++,3336036036010834310z x y z γ=⨯︒=⨯︒=⨯︒=︒++++.故应选B .2.(2021·全国·九年级竞赛)如图所示,一次函数y kx b =+的图象过点(1,4)P 且与x 轴和y 轴的正半轴交于A B 、两点,点O 为坐标原点,当AOB 的面积最小时,k ,b 的值为( )A .4k =-,8b =B .4k =-,4b =C .2k =-,4b =D .2k =-,2b =【答案】A 【详解】解 因函数y kx b =+的图象过点(1,4)P ,所以4,4k b b k =+=-,于是(4)y kx k =+-. 令0y =得4,0k A k -⎛⎫⎪⎝⎭. 令0x =得(0,4)B k -.连OP ,得 114122OABOAP OPBSSSOA OB =+=⨯⨯+⨯⨯ 14141(4)22k k k -=⨯⨯+⨯⨯- 11642k k ⎛⎫=-+ ⎪⎝⎭.显然0k <.令k u =-,则0u >,于是116116442822OABSu u u u⎛⎫=++≥+⨯⨯= ⎪⎝⎭.等号成立当且仅当16(0)u u u=>,即4u =,这时4,48k b k =-=-=. 故选A .注:OAB 的面积也可用114(4)22OABk SOA OB k k-=⨯⨯=⨯⨯-算出. 3.(2021·全国·九年级竞赛)如图,已知DEF 的边长分别为3,2,正六边形网格由24个边长为2的正三角形组成,以这些正三角形的顶点画ABC ,使得ABC DEF ∽△△,相似比为ABk DE=,那么k 的不同值共有( )个.A .1B .2C .3D .4【答案】C 【详解】作图知与DEF 相似的三角形,而相似比不同的三角形只有如图所示的三种,故选C .二、填空题4.(2021·全国·九年级竞赛)如图所示,正方形ABCD 的边长为10cm ,点E 在边CB 的延长线上且10cm EB =,点P 在边CD 上运动,EP 与AB 的交点为F .设cm DP x =,EFB △与四边形AFPD 的面积和为2cm y ,那么y 与x 之间的函数关系式是________.【答案】550(010)y x x =+<< 【详解】解 由DP x =得10PC x =-. 又12BF BE PC EC ==,即11(10),10(10)22BF x AF BF x =-=-=+, 所以EFBAFPD y SS =+四边形11()22BE BF AF DP AD =⨯⨯++⨯ 111110(10)(10)102222x x x ⎡⎤=⨯⨯-+++⨯⎢⎥⎣⎦550(010)x x =+<<. 故应填550(010)y x x =+<<.5.(2021·全国·九年级竞赛)把两个半径为5及一个半径为8的圆形纸片放在桌面上,使它们两两外切.若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于________. 【答案】1133.【详解】如图,设1O 的半径为8,2O ,3O 的半径为5,切点为A .由对称性,能盖住这3个圆的最小圆形纸片的中心O 在对称轴1O A 上,且与已知三个圆内切.若设这个圆形纸片的半径为r ,则在12Rt O O A 中22221122(85)512O A OO O A =-=+-=,在2Rt OO A 中,25OO r =-,1112(8)OA O A OO r =-=--,25O A =,于是,由22222OO O A OA =+得222(5)5(128)r r -=+-+,由此解出4011333r ==,即所求圆形纸片的最小半径等于1133.6.(2021·全国·九年级竞赛)由一次函数2,2y x y x =+=-+和x 轴围成的三角形与圆心在(1,1)、半径为1的圆构成的图形覆盖的面积等于______. 【答案】42π+【详解】如图,所覆盖面积2 114214222ABCS S S ππ=+=⨯⨯+⋅=+半圆.故答案为:42π+.7.(2021·全国·九年级竞赛)某广场地面铺满了边长为36cm 的正六边形地砖,现向上抛掷半径为3cm 的圆碟,圆碟落地后与地面不相交的概率大约是_________. 【答案】49【详解】解 要使圆碟与地砖的边缘不相交的条件是落地后圆碟的中心到正六边形地砖ABCDEF 的任何一边的距离不小于圆的半径63cm ,也就是圆碟的中心必落在与地砖ABCDEF 同中心且边与地砖边彼此平行、距离为63111111A B C D E F 内(图6-1).作OG AB ⊥于G ,交11A B 于1G 且163cm GG =,所以33336183OG AB ====1118363123OG OG GG =-==而113OG =,所以1132433OA ===,故11124A B OA ==. 设正六边形ABCDEF 和111111A B C D E F 的面积分别为S 和1S ,则所求概率为22211122224243639S A B p S AB =====.故应填49. 三、解答题8.(2021·全国·九年级竞赛)平面上7个点,它们之间可以连一些线段,使7个点中任意三点必存在两点有线段相连.问最少要连几条线段?证明你的结论.【答案】9条,见解析 【详解】解法一:设最少要连n 条线段,如图4-3中7个点之间共连有9条线段,其中任意三点间必有两点连有线段,故9n ≤.另一方面,我们证明9n ≥,下面分4种情形讨论: (1)若7点中存在一点1A 不与其他6点237,,,A A A 连线,则依题意1A ,i A ,j A (27)i j ≤<≤中必有2点连线,于是只可能i A 与j A 连有线,即237,,,A A A 这6点中任意两点连有线,图中一共连了65152⨯=条线. (2)若7点中存在一点1A 只连出一条线段,设1A 仅与2A 连有线而与其余5点3A ,4A ,5A ,6A ,7A ,没有连线,则同(1)可知3A ,4A ,5A ,6A ,7A 这5点中任意两点连有线,至少连有54102⨯=条线.(3)若每点出发至少连出2条线,且有一点恰连出2条线.设该点为1A ,它连出的两条线为12A A ,13A A ,则不与1A 相连的4个点每两点连有线,要连4362⨯=条线,而2A 连出的线段至少2条,除21A A 外,至少还有一条,所以此时至少要连6219++=条线. (4)若每点至少连出3条线,则至少要连73102⨯>条线. 综上所述,最少要连9条线段.解法二:设7点中从1A 出发所连的线段最少,只有k 条,设它们是121311,,,k A A A A A A +,其余6k -个点126,,,k B B B -都与1A 没有连线,于是对任意2点i B ,j B (16)i j k ≤<≤-,由已知条件知1A ,i B ,j B 中必有2点连有线,而1A 与i B ,1A 与j B 没有连线,故只可能i B 与j B 连有线,即16,,k B B -中每点与其余5k -点连有线,于是从各点连出的线段数的总和不少于(1)(6)(5)k k k k ++--221030k k =-+.但上述计数中每条线段计算了2次,故图中所连线段至少为()21210302k k -+=22551522k ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭22151522⎛⎫⎛⎫≥+- ⎪ ⎪⎝⎭⎝⎭1569=-=,即至少要连9条线段. 另一方面,如图4-3中,7点中连有9条线段时满足题设条件. 综上所述,最少要连9条线段.9.(2021·全国·九年级竞赛)在直径为5的圆内放入10个点,证明其中必有两点的距离小于2. 【答案】见解析 【详解】分析 把圆等分为9个扇形显然不行(虽然必有一扇形内至少有2点,但不保证它们的距离小于2),因此,我们先作一个与已知圆同心的小圆(其直径必须小于2,但不能太小),然后将余下的圆环部分8等分. 证明 设O 是已知圆心,如图,以O 为圆心作半径为0.9的圆,再将余下的圆环8等分,于是将已知圆面分成了9个部分,由抽屉原理知其中必有一部分内至少有已知10点中的101129-⎡⎤+=⎢⎥⎣⎦点,M N ,若,M N 在小圆内,则220.9 1.82MN OC ≤=⨯=<. 若,M N 同在一个扇面形内,则由余弦定理,有222cos45MN AC OC OA OC OA ≤+-⋅︒0.81 6.2520.9 2.50.7 3.912+-⨯⨯⨯<.从例2可以看出,分割图形制造“抽屉”时,可能不是将图形等分为几部分,而是要求分割的每一部分图形都具有所需要的性质(例2中每一部分图形内任意两点的距离都小于2),读者应用这种方法解题时,应该注意到这一点.10.(2021·全国·九年级竞赛)设1M 是凸五边形12345A A A A A ,将1M 沿1i A A 方向平移,使1A 移到i A 得到凸五边形(2,3,4,5)i M i =.证明:12345,,,,M M M M M 中至少有两个图形,它们有公共内点.【答案】见解析 【详解】证明 如图,以1A 为位似中心,以2:1为相似比作1M 的位似图形M ,则M 仍为凸五边形且1M 在M 内.下面我们证明2345,,,M M M M 都在M 内,例如先证4M 在M 内.设P 是4M 内任意一点,它是1M 内的点Q 经过平移得到的,于是14QP A A ∥,故14A A PQ 为平行四边形,又R 是14A A PQ 的两条对角线的交点,因Q 和4A 属于1M ,且1M 是凸五边形,故R 属于M ,而111,:2:1A R RP A P A R ==,故P 属于M .又P 是M ,内任意一点,所以4M 包含在M 之内,同理235,,M M M 都包含在M 内,设12345,,,,M M M M M 及M 的面积分别为12345,,,,S S S S S 及S ,则2123451152S S S S S S S S ++++=>⋅=.于是,由图形重叠原理知,12345,,,,M M M M M 中至少有两个图形,它们有公共内点.11.(2021·全国·九年级竞赛)在圆周上任取21个点,证明:以这些点为端点的弧中至少存在100条不超过120︒的弧.【答案】见解析 【详解】证明:我们称不超过120︒的弧为好弧.不妨设以1A 为端点的好弧最少,并且设它只有1n -条,它们是12131,,,n A A A A A A ,从而以231,,,n A A A -为端点的好弧都至少有1n -条,故以这n 个点为端点的好弧至少有1(1)2n n ⋅-条,除这n 个点外,其余21n -个点记为1221,,,n n A A A ++,从中任取两点,(121)i j A A n i j +≤<≤.因1i j A A A ,至少有一个内角不超过60︒,故11,,i j i j A A A A A A 中至少有一条弧不超过260120⨯︒=︒,根据1A 的取法,这条弧不能是1i A A 和1j A A ,而只能是j i A A ,即j i A A 是好弧.可见以1221,,,n n A A A ++中任意两点,(121)i j A A n i j +≤<≤为端点的弧都为好弧.这样的好弧有1(21)(20)2n n ⋅--条.综上所述知好弧至少有2211213991399(1)(21)(20)100222424y n n n n n ⎛⎫⎛⎫=⋅-+⋅--=-+≥+= ⎪ ⎪⎝⎭⎝⎭条.当10n =或11时,y 取到最小值100,于是结论成立.12.(2021·全国·九年级竞赛)两人A 和B 相约在12点与下午1点之间在某地会面,先到的人要等候另一人20分钟,过时就可以离开.如果每人可在指定的一小时内任何时刻到达,并且两人到达的时刻是彼此独立的(即一人到达的时刻与另一人到达的时刻没有影响),试计算两人能会面的概率. 【答案】59 【详解】解 我们用,x y 分别表示,A B 到达的时刻,而两人能会面的充分必要条件为20x y -≤,其中060,060x y ≤≤≤≤.我们用平面直角坐标系中的点(),x y 表示,A B 到达的时刻(从中午12点以后算起,以分为单位),于是所有可能结果是一个边长为60的正方形OABC .代表能够会面的点都落在图中画有阴影线的区域H 内(图6-2),于是21260240402H ADE OABC S S S =-⨯=-⨯⨯⨯正方形 226040=-,故两人能会面的概率为22226040251()6039HOABC S p S -===-=正方形. 答:两人能会面的概率等于59. 13.(2021·全国·九年级竞赛)平面上给出n 个不全共线的点,求证:存在一条直线l ,它恰通过其中两个点.【答案】见解析【详解】证明:平面上只有有限点,过每两点作一直线只有有限点直线,每条直线与不在这条直线上的点(由已知条件知这样的点必存在)配成对,则这样的点只有有限个,每个点线对中都有该点到直线的距离,记这些距离最小的点对为(,)P l ,则l 为所求.实际上,设l 上有不少于3个给定的已知点,则过P 作PA l ⊥于A (如图),则在l 上A 的某一侧(包括A )必有2个已知点,设为,M N (M 可能与A 重合,连PN ,并M 作MQ PN ⊥于Q ,过A 作AR PN ⊥于R ,则MQ AR AP d ≤<=,这与AP d =最小矛盾,于是结论得证.注 本题是英国著名数学家希尔维斯特(J.J. Sylvester)在其逝世前不久提出的一个有趣的问题.这个貌似简单的问题,当时困扰过不少的数学家,并且这状况持续350年之久,直到1933年,伽莱(T. Callai)给出了一个非常复杂的证明.不久以后,凯里(L. M. Kelly) 才给出上述很简单的证明,其证法的关键就是利用极端原理.14.(2021·全国·九年级竞赛)已知A ,B ,C ,D 为平面上两两距离不超过1的任意4点,今欲作一圆覆盖这4点(即A ,B ,C ,D 在圆内或圆周上)问圆的半径最小该是多少?试证明之. 3 【详解】注意最不利的情形点A 、B 、C 、D 中有3点构成边长等于1的正三角形,覆盖此三角形的圆的半径不小33 (1)A 、B 、C 、D 共线,这时4点在一条长度不超过1的线段内,结论显然成立;(2)A 、B 、C 、D 中有3点(例如A 、B 、C )构成一个三角形,第4点D 在此三角形内,不妨设60C ∠≥︒,以AB 为弦作圆O ,使AB 所对的弓形弧(含C 的一侧)为60︒,则此圆O 覆盖A 、B 、C 、D 4点.作此圆直径2AE R =,则22222(2)1R R AE BE AB -=-=≤,即3R ≤,故A 、B 、C 、D 4点被一个半径不大3 (3)A 、B 、C 、D 是一个凸四边形的4个顶点,则A C ∠+∠,B D ∠+∠中必有一个不小于180︒,不妨设180B D ∠+∠≥︒,同(2)可证ABC 的外接圆半径3≤180B D ∠+∠≥︒知D 点也在这个圆内或圆周上,故A 、B 、C 、D 3 315.(2021·全国·九年级竞赛)任意凸四边形ABCD 中总存在一条对角线和一条边,以它们为直径的两个圆可以覆盖这个四边形.【答案】见解析【详解】四边形的4个内角中至少有一个90≥︒,不妨设90A ∠≥︒,以对角BD 为直径的圆O 必覆盖ABD △.若90C ∠≥︒,圆O 覆盖四边形ABCD 结论成立,若90C ∠>︒,则C 在圆外,圆O 与CD 、CB 中至少一条线段相交,不妨设圆O 与CD 交于E ,于点分别以BD 、BC 为直径的两个圆覆盖四边形ABCD .16.(2021·全国·九年级竞赛)设甲是边长为1的正三角形纸片,乙是边长为1的正方形纸片,丙是边长为1的正五边形纸片,丁是边长为1的正六边形纸片.证明:(1)不能用甲、乙、丙合起来盖住一个半径为1的圆;(2)能用甲、乙、丙、丁合起来盖住一个半径为1的圆.【答案】(1)见解析;(2)见解析【详解】(1)因为对于半径为1的圆,边长为1的正三角形至多盖住60︒的弧,边长为1的正方形至多盖住90︒的弧,边长为1的正五边形至多盖住120︒的弧(因边长为1的正五边形对角线的长<边长为1的正六边形对角线的长3=,而6090120360︒+︒+︒<︒,所以甲、乙、丙合起来不得盖住半径为1的圆.(2)如图所示,用甲、乙、丙、丁合起来可盖住半径为1的圆.17.(2021·全国·九年级竞赛)在一个半径等于6的圆内任意放入六个半径等于1的小圆.证明:其中总还有一块空位置,可以完整地放入一个半径为1的小圆.【答案】见解析【详解】分析 与证明设半径为6的大圆O 内任意放入6个半径为1的小圆,则小圆圆心都在以O 为中心,615-=为半径的圆内.如果大圆内无论怎样再放入一个半径为1的小圆7O ,都要与6个小圆中某个(16)i O i ≤≤重叠,那么7112i O O ≤+≤,即半径为5的圆将被6个半径为2的圆所覆盖.由图形重叠原理知6个小圆的总面积将不小于半径为5的圆的面积.但实际上226224255ππππ⋅=<=⋅,得到矛盾,于是命题得证.注:本例的证题关键是将外圆缩小,而将里圆扩大,这是解决嵌入问题的一种技巧,即收缩与膨胀技巧或裁边与镶边技巧.18.(2021·全国·九年级竞赛)将4张圆形纸片放在桌面上,使得其题中任何3张圆形纸片都有公共点,那么这4张圆形纸片是否一定有公共点?证明你的结论.【答案】见解析.【解析】【分析】【详解】设4张圆形纸片是(1,2,3,4)k O k ,其中1O ,2O ,3O 有公共点1A ,1O ,2O ,4O 有公共点2A ,1O ,3O ,4O 有公共点3A ,2O ,3O ,4O 公共点4A .(1)若1A ,2A ,3A ,4A 共线(如图顺序),因为1A ,3A 都是圆形纸片1O 与3O 的公共点,故线段13A A 在圆形纸片1O 与2O 的公共部分内,又24A A 都是圆形纸片2O 与4O 的公共点,故线段24A A 在圆形纸片2O 与4O 的公共部分内,所以线段23A A 上任意一点都是这4张圆形纸片的公共点.(2)若1A ,2A ,3A ,4A 中有一点在以其余3点为顶点的三角形的边界上或内部(如图).因为1A ,2A ,3A 都在1O 内,故123A A A △被圆形纸片1O 所覆盖,从而4A 在圆形纸片1O 内,而4A 是圆形纸片2O ,3O ,4O 的公共点,所以4A 是这张圆形纸片的公共点.(3)若1A ,2A ,3A ,4A 是一个凸四边形的4个顶点(如图),同上可知线段13A A 在圆形纸片1O 与3O 的公共部分内,线段24A A 在圆形纸片2O 与4O 的公共部分内,所以13A A 与24A A 的交点是这4张圆形纸片的公共点.总之,这4张圆形纸片一定有公共点.19.(2021·全国·九年级竞赛)平面上给定了若干个圆,它们覆盖的面积为1.证明:从中可选出若干个两两不重叠的圆,使它们覆盖的面积不小于19. 【答案】见解析.【解析】【分析】【详解】从给定圆中选出半径最大的圆1O ,其半径为1r ,面积为1S ,则与圆1O 有重叠的圆连同圆1O 一起覆盖的面积()211139M r S π≤=,即1119S M ≥.然后去掉与圆1O 重叠的圆,再从剩下的圆(圆1O 除外)选出半径最大的圆2O ,其半径为2r ,并将与圆2O 有重叠的圆去掉.这样经过有限步可得有限个两两不重叠的圆1O ,2O ,…k O ,它们覆盖的面积为()12121199k k S S S M M M ++⋅⋅⋅+≥++⋅⋅⋅+=. 20.(2021·全国·九年级竞赛)证明:一个边长为5的正方形可以被3个边长为4的正方形所覆盖.【答案】见解析.【解析】【分析】【详解】设正方形ABCD 的边长为5,先放置一个边长为4的正方形CEFG ,其中C 为原正方形ABCD 的一个顶点,E 在边CD 上,F 在正方形ABCD 内,G 在边CB 上.连AF ,再放置第二个边长为4的正方形111AB C D ,其中A 是原正方形的一个顶点,且使D 在射线11D C 上(如图),由勾股定理有:2211D D AD AD =-2211543D C =-=<.故D 在线段11D C 内,且1111431C D D C D D =-=-=.设11B C 与CD 交于H ,则1541DE CD CE DC DH =-=-==<,故E 在线段DH 内,从而E 被正方形111AB C D 覆盖.又11145B AD B AC FAD ∠>∠=︒=∠,即AF 在1B AD 内,且1224AF DE AB ==,故F 也被正方形111AB C D 覆盖,这就证明了梯形AFED 可以被一个边长为4的正方形111AB C D 所覆盖.同理,梯形AFGB 也可以被一个边长为4的正方形222AB C D 所覆盖,于是正方形ABCD 可被3个边长为4的正方形所覆盖. 21.(2021·全国·九年级竞赛)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm 的正方形,高为30cm ,内有20cm 深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).(1)当30α=︒时,通过计算说明此溶液是否会溢出;(2)现需要倒出不少于33000cm 的溶液,当α等于60︒时,能实现要求吗?通过计算说明理由.【答案】(1)不会溢出,理由见解析;(2)不能实现要求,见解析.【解析】【分析】【详解】(1)当30α=︒时,如图a ,过C 作//CF BP 交AD 所在直线于F .在Rt CDF △中,20330,20cm,30cm FCD CD DF ∠=︒==<,所以点F 在线段AD 上,20330AF =此时容器内能容纳的溶液量为()3 ()203320203030201040003cm 2ABCF AF BC AB S ⎛⎫⎛+⋅=⋅=⋅⋅= ⎪ ⎪ ⎝⎭⎝⎭梯形.而容器中原有溶液量为()32020208000cm ⨯⨯=.因为3400038000⎛> ⎝⎭,所以当30α=︒时溶液不会溢出. (2)如图b ,当60α=︒时,过C 作//CF BP 交AB 所在直线于F .在Rt CBF △中,30cm 30BC BCF =∠=︒,,10320cm BF =<,所以点F 在线段AB 上,故溶液纵截面为Rt BFC △.因211503cm 2BFC S BC BF =⨯⨯=,容器内溶液量为315032030003cm =,倒出的溶液量为3(80003)3000cm -<,所以不能实现要求. 22.(2021·全国·九年级竞赛)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头停泊,它们在一昼夜内到达的时间是等可能的,如果甲的停泊时间是1小时,乙的停泊时间是2小时,求它们中任何一艘都不需要等候码头空出的概率(精确到0.001).【答案】0.879.【解析】【分析】【详解】设自当天零时算起,甲、乙两船到达码头的时刻分别是x 和y ,则必须024,024x y ≤≤≤≤.我们视(),x y 为平面直角坐标系内的点,于是点(),x y 落在一个面积为224S =的正方形OABC 的内部或边界上(如下图).如果轮船不需要等候码头空出,那么当船甲先到时,船乙应迟来1个小时以上,即1y x -≥,即1y x ≥+;当船乙先到时,船甲应迟来2个小时以上,即2x y -≥,即2y x ≤-,即点(),x y 应在直线1y x =+的上方且在直线2y x =-的下方,也就是点(),x y 应在如图所示的两个三角形ADE 和CFG △中某一个的内部或边界上,故所求概率ADE CFGABCD S S p S +=四边形.而24123,24222CG CF AD AE ==-===-=,所以211222223231103220.879241152p ⨯⨯+⨯⨯===. 答:两船中任何一艘都不需要等候码头空出的概率为0.879.23.(2021·全国·九年级竞赛)把长为a 的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.【答案】14【解析】【分析】【详解】解 设其中两条线段的长为,x y ,则第3条线段的长为()a x y -+,于是,x y 的取值范围是0,0,0,0,0()0.x a x a y a y a a x y a x y a ⎧<<<<⎧⎪⎪<<⇔<<⎨⎨⎪⎪<-+<<+<⎩⎩ ① 要使3条线段构成一个三角形的3条边,其充要条件是其中任意一条线段的长度小于其余两条线段的长度之和.这等价于每条线段的长度都小于2a ,即 0,0,220,0,220().22a a x x a a y y a a a x y x y a ⎧⎧<<<<⎪⎪⎪⎪⎪⎪<<⇔<<⎨⎨⎪⎪⎪⎪<-+<<+<⎪⎪⎩⎩ ②将(),x y 视为平面直角坐标系的坐标,则满足条件①的点(),x y 在以()()()0,0,,0,0,O A a B a 为顶点的OAB 内.而满足条件②的点(),x y 在以(,),(0,),,0()2222a a a a C D E 为顶点的CDE △内,故所求概率为11222142CDE OAB a a CD DE Sp S a a OA OB ⨯⨯⨯====⨯⨯⨯.答:3条线段能构成一个三角形的三边的概率为14. 24.(2022·福建·九年级竞赛)如图,四边形ABCD 是平行四边形,∠DAC =45°,以线段AC 为直径的圆与AB 和AD 的延长线分别交于点E 和F ,过点B 作AC 的垂线,垂足为H .求证:E ,H ,F 三点共线.【答案】见解析【解析】【分析】如图:证明P ,A ,B ,C 四点共圆.可得CBE APC ∠=∠.①,证明C ,E ,B ,H 四点共圆,可得CHE CBE ∠=∠.②,证明C ,H ,F ,P 四点共圆,可得180APC CHF ∠=︒-∠.③,由①②③代换可得180CHE CHF ∠+∠=︒.可得结论;【详解】如图,延长BH 与直线AD 相交于点P ,连接CP .因为45DAC ∠=︒,BP AC ⊥,所以45BPA ∠=︒.又45BCADAC∠=∠=︒,所以BPA BCA ∠=∠,于是P ,A ,B ,C 四点共圆.所以CBE APC ∠=∠.①连接CE ,由AC 为圆直径,得90CEA CHB ∠=︒=∠,所以C ,E ,B ,H 四点共圆,于是CHE CBE ∠=∠.②连接CF ,由AC 为圆直径,得90CFP CHP ∠=︒=∠,所以C ,H ,F ,P 四点共圆,于是180APC CHF ∠=︒-∠.③由②,①,③,得180CHE CBE APC CHF ∠=∠=∠=︒-∠,所以180CHE CHF ∠+∠=︒.所以E ,H ,F 三点共线.【点睛】本题考查了圆内接罩边形的判断及性质,难度较大,解题的关键是构造圆内接四边形.。
初中数学几何证明经典试题含答案

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HE OF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初三经典几何证明练习题(含答案)

初三几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P是正方形ABCD内部的一点,∠PAD=∠PDA=15°。
求证:△PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OP⊥BC求证:BC=2OP证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE =CF .证明:连接BD 交AC 于O 。
过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75°∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .证明:连接BD ,过点E 作EG ⊥AC 于G ∵ABCD 是正方形∴BD ⊥AC ,又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)证明:过点F 作FG ⊥CE 于G ,FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF ∵AP ⊥FP ∴∠APB+∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BAP 设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴∠CAE=∠CEA=21∠GCE=15°在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AFB ∴△FGP ∽△PBA ∴FG :PB=PG :AB4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC ,BC =AD .(初三)证明:过点E 作EK ∥BD ,分别交AC 、AF 于M 、K ,取EF 的中点H , 连接OH 、MH 、EC ∵EH=FH∴OH ⊥EF ,∴∠PHO=90° 又PC ⊥OC ,∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO 又EK ∥BD ,∴∠HPO=∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针方向旋转60°得△BCQ ,连接PQ 则△BPQ 是正三角形∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)证明:过点P 作AD 的平行线,过点A 作PD 两平行线相交于点E ,连接BE ∵PE ∥AD ,AE ∥PD∴ADPE 是平行四边形∴PE=AD ,又ABCD 是平行四边形∴AD=BC∴PE=BC又PE ∥AD ,AD ∥BC ∴PE ∥BC ∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相平分 ∴ABCD 是平行四边形 ∴AB=DC ,BC=AD 又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB∴∠ADP=∠AEP3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证明:在BD 上去一点E ,使∠BCE=∠∵CD⌒ =CD ⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC∴ACBCAD BE = ∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD∵BC⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC ∴CDACDE AB = ∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)证明:过点D 作DG ⊥AE 于G ,作DH ⊥FC 于H ,连接DF 、DE ∴S △ADE =12AE ·DG ,S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA =∠DPC经典题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:3≤L <2. 证明:(1)将△BPC 绕B 点顺时针旋转60°的△BEF ,连接PE , ∵BP=BE ,∠PBE=60° ∴△PBE 是正三角形。
七年级几何证明题训练(含答案)

1. 已知:如图11所示,∆ABC 中,∠=C 90于E ,且有AC AD CE ==。
求证:DE =122. 已知:如图 求证:BC =3. 已知:如图13所示,过∆ABC 的顶点A ,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ 。
设M 为BC 的中点。
求证:MP =MQ4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++14【试题答案】1. 证明:取AC ADAF CDAFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390,∴∠=∠=∴≅∴=∴=4312AC CEACF CED ASA CF EDDE CD∆∆()2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截CB CE BCD ECD CD CD CBD CEDB EBAC B BAC E=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==ADE E AD AEBC CE ,3. 证明:延长PM CQ AP BP BP CQ PBM ⊥∴∴∠=∠,// 又BM CM =,∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线AD BC AD AEBC AE AD⊥∴<∴=>,22()AB AC BCBC AB AC BC AD AB AC BC AD AB AC BC +>∴<++∴<++∴<++2414。
初中数学几何证明经典题(含答案)
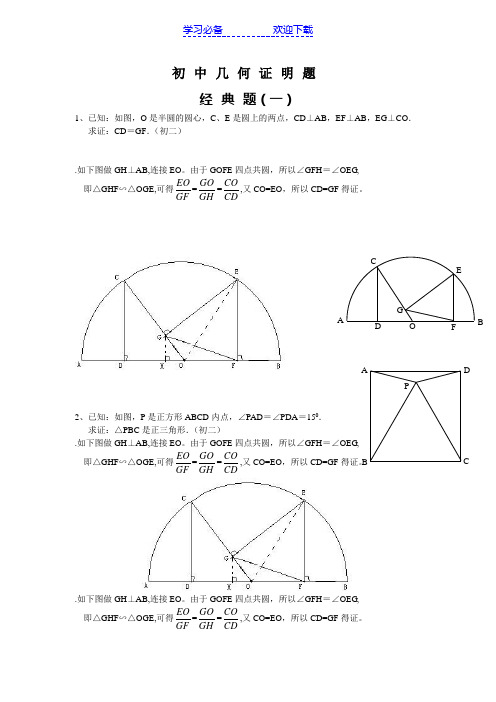
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初三证明几何练习题和答案

初三证明几何练习题和答案在初三的数学学习中,证明几何是一个重要的内容。
通过证明几何的练习,不仅可以提高学生的逻辑思维和推理能力,还能加深对几何概念的理解。
本文将提供一些初三常见的证明几何练习题和答案,以供学生参考。
1. 设AO和BO是直线段垂直平分线,点C在直线AB上。
证明:∠ACO = ∠BCO。
解答:首先,根据直线段垂直平分线的定义,AO和BO互相垂直且平分直线段AB。
设∠ACO的度数为x,∠BCO的度数为y。
则根据垂直平分线的性质可知∠COA = ∠COB = 90°。
再根据直线上的角平分线性质可知∠COA = ∠AOC = x/2,∠COB= ∠BOC = y/2。
又由于∠COA = 90°,则x/2 + y/2 = 90°,即x + y = 180°。
因此,根据等量关系可得∠ACO = ∠BCO,证明完成。
2. 在△ABC中,垂直平分线BD交边AC于点E,证明:AE = EC。
解答:根据垂直平分线的定义,BD是边AC的垂直平分线,即BD垂直于AC且平分边AC。
设AE的长度为x,EC的长度为y。
根据垂直平分线的性质可知∠BDE = ∠BDE = 90°,∠BED =∠CED。
由于△BDE和△BEC中∠BDE = ∠BEC = 90°,则两个三角形中的另外两个角也相等,即∠BDE = ∠BEC。
又由于∠BDE = ∠BEC,三角形内角和为180°,则∠BED + ∠BDE + ∠BEC = 180°。
代入角度的数值可得∠BED + 90° + ∠BED = 180°,即∠BED = 45°。
进一步,根据角平分线的性质可知∠AEB = ∠BEC,即∠AEB = 45°。
因为∠AEB为三角形△AEB的内角,所以△AEB的另外两个角之和也为180°。
因此,180° = 45° + x + 45°,化简得180° = x + 90°,即x = 90°,即AE的长度为90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明题综合训练1. 线段或角相等的证明(1) 利用全等△或相似多边形; (2) 利用等腰△; (3) 利用平行四边形; (4) 利用等量代换;(5) 利用平行线的性质或利用比例关系 (6) 利用圆中的等量关系等。
2. 线段或角的和差倍分的证明(1) 转化为相等问题。
如要证明a=b±c ,可以先作出线段p=b±c ,再去证明a=p ,即所谓“截长补短”,角的问题仿此进行。
(2) 直接用已知的定理。
例如:中位线定理,Rt △斜边上的中线等于斜边的一半;△的外角等于不相邻的内角之和;圆周角等于同弧所对圆心角的一半等等。
3. 两线平行与垂直的证明(1) 利用两线平行与垂直的判定定理。
(2) 利用平行四边形的性质可证明平行;利用等腰△的“三线合一”可证明垂直。
(3) 利用比例关系可证明平行;利用勾股定理的逆定理可证明垂直等。
【竞赛例题剖析】【例1】从⊙O 外一点P 向圆引两条切线PA 、PB 和割线PCD 。
从A 点作弦AE 平行于CD ,连结BE 交CD 于F 。
求证:BE 平分CD 。
【分析1】构造两个全等△。
连结ED 、AC 、AF 。
CF=DF ←△ACF ≌△EDF ←←⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧←←∠=∠∠=∠=∠←∠=∠←⎭⎬⎫∠=∠=四点共圆、、、P B F A ABP AFC ABP AEF EFD EFD AFC CD //AE EDF ACF ED AC←∠PAB=∠AEB=∠PFB【分析2】利用圆中的等量关系。
连结OF 、⎪⎩⎪⎨⎧=∠←=∠←=、、、P B F O 90OBP 90OFP DF CF 0←∠PFB=∠POB ←←⎩⎨⎧←∠=∠←∠=∠是切线、PB PA AEB POB CD//AE AEB PFB注:连结OP 、OA 、OF ,证明A 、O 、F 、P 四点共圆亦可。
【例2】△ABC 内接于⊙O ,P 是弧 AB 上的一点, 过P 作OA 、OB 的垂线,与AC 、BC 分别交于S 、T , AB 交于M 、N 。
求证:PM=MS ⇔PN=NT 。
【分析】只需证NPTNMS PM =, PM ²PN=MS ²NT 。
(∠1=∠2,∠3=∠4)→△APM ∽△PBN →PNAMBN PM =→PM ²PN=AM ²BN (∠BNT=∠AMS ,∠BTN=∠MAS )→△BNT ∽△SMA →NTAMBN MS =→MS ²NT=AM ²BN【例3】已知A 为平面上两半径不等的圆O 1和O 2的一个交点,两外公切线P 1P 2、Q 1Q 2分别切两圆于P 1、P 2、Q 1、Q 2,M 1、M 2分别为P 1Q 1、P 2Q 2的中点。
求证:∠O 1AO 2=∠M 1AM 2。
【分析】设B 为两圆的另一交点,连结并延长BA 交P 1P 2于C ,交O 1O 2于M ,则C 为P 1P 2的中点,且P 1M 1∥CM ∥P 2M 2,故CM 为M 1M 2的中垂线。
在O 1M 上截取MO 3=MO 2,则∠M 1AO 3=∠M 2AO 2。
故只需证∠O 1AM 1=∠O 3AM 1,即证311131O M M O AO A O =。
由△P 1O 1M 1∽P 2O 2M 2,M 1O 3=M 2O 2,O 1P 1=O 1A ,O 2P 2=O 2A 可得。
【例4】在△ABC 中,AB>AC ,∠A 的外角平分线交△ABC 的外接圆于D ,DE ⊥AB 于E ,求证:AE=2ACAB -。
【分析】方法1、2AE=AB-AC← 在BE 上截取EF=AE ,只需证BF=AC ,连结DC 、DB 、DF ,从而只需证△DBF ≌△DCA ← DF=DA ,∠DBF=∠DCA ,∠DFB=∠DAC ←∠DFA=∠DAF=∠DAG 。
方法2、延长CA 至G ,使AG=AE ,则只需证BE=CG← 连结DG 、DC 、DB ,则只需证△DBE ≌△DCG ← DE=DG ,∠DBE=∠DCG ,∠DEB=∠DGC=Rt ∠。
【例5】∠ABC 的顶点B 在⊙O 外,BA 、BC 均与⊙O 相交,过BA 与圆的交点K 引∠ABC 平分线的垂线,交⊙O 于P ,交BC 于M 。
求证:线段PM 为圆心到∠ABC 平分线距离的2倍。
【分析】若角平分线过O ,则P 、M 重合,PM=0,结论显然成立。
若角平分线不过O ,则延长DO 至D',使OD'=OD ,则只需证DD'=PM 。
连结D'P 、DM ,则只需证DMPD'为平行四边形。
过O 作m ⊥PK ,则D −−→−)(m S D',K −−→−)(m S P ,∴∠D'PK=∠DKP BL 平分∠ABC ,MK ⊥BL →BL 为MK 的中垂线→∠DKB=∠DMK∴∠D'PK=∠DMK ,∴D'P ∥DM 。
而D' D ∥PM ,∴DMPD'为平行四边形。
【例6】在△ABC 中,AP 为∠A 的平分线,AM 为BC 边上的中线,过B 作BH ⊥AP 于H ,AM 的延长线交BH 于Q ,求证:PQ ∥AB 。
【分析】方法1、结合中线和角平分线的性质,考虑用比例证明平行。
倍长中线:延长AM 至M',使AM=MA',连结BA',如图6-1。
PQ ∥AB ←MA QM MB PM =←QM MA QM MA PM MB PM MB -+=-+←/QA AQPC BP = ←⎪⎪⎩⎪⎪⎨⎧∠=∠←===BQ A ABQ B A BA QAAQ B A AC ,ACBAPC BP ////∠A'BQ=180°-(∠HBA+∠BAH+∠CAP)= 180°-90°-∠CAP=90°-∠BAP=∠ABQ方法2、结合角平分线和BH ⊥AH 联想对称知识。
延长BH 交AC 的延长线于B',如图6-2。
则H 为BB'的中点,因为M 为BC 的中点,连结HM ,则HM ∥B /C 。
延长HM 交AB 于O ,则O 为AB 的中点。
延长MO 至M',使OM'=OM ,连结M'A 、M'B ,则AM'BM 是平行四边形,∴MP ∥AM',QM ∥BM'。
于是,QB HQ'MM HM PA HP ==,所以PQ ∥AB 。
【例7】菱形ABCD 的内切圆O 与各边分别切于E 、F 、G 、H ,在EF 与GH 上分别作⊙O 的切线交AB 于M ,交BC 于N ,交CD 于P ,交DA 于Q 。
求证:MQ ∥NP 。
(95年全国联赛二试3)B'D D【分析】由AB ∥CD 知:要证MQ ∥NP ,只需证∠AMQ=∠CPN ,结合∠A=∠C 知,只需证△AMQ ∽△CPN ←CNCPAQ AM =,AM ²CN=AQ ²CP 。
连结AC 、BD ,其交点为内切圆心O 。
设MN 与⊙O 切于K ,连结OE 、OM 、OK 、ON 、OF 。
记∠ABO=φ,∠MOK=α,∠KON=β,则∠EOM=α,∠FON=β,∠EOF=2α+2β=180°-2φ。
∴∠BON=90°-∠NOF-∠COF=90°-β-φ=α∴∠CNO=∠NBO+∠NOB=φ+α=∠AOE+∠MOE=∠AOM又∠OCN=∠MAO ,∴△OCN ∽△MAO ,于是CNAOCO AM =, ∴AM ²CN=AO ²CO同理,AQ ²CP=AO ²CO 。
【例8】ABCD 是圆内接四边形,其对角线交于P ,M 、N 分别是AD 、BC 的中点,过M 、N 分别作BD 、AC 的垂线交于K 。
求证:KP ⊥AB 。
【分析】延长KP 交AB 于L ,则只需证∠PAL+∠APL=90°, 即只需证∠PDC+∠KPC=90°,只需证∠PDC=∠PKF , 因为P 、F 、K 、E 四点共圆,故只需证∠PDC=∠PEF ,即EF ∥DC 。
CPDP FC DE =←CN 2DM2CB DA FC DE ==←CNDM FC DE =←△DME ∽△CNF【例9】以△ABC 的边BC 为直径作半圆,与AB 、AC 分别交于点D 、E 。
过D 、E 作BC 的垂线,垂足分别是F 、G ,线段DG 、EF 交于点M 。
求证:AM ⊥BC 。
【分析】连结BE 、CD 交于H ,则H 为垂心,故AH ⊥BC 。
(同一法) 设AH ⊥BC 于O ,DG 、AH 交于M 1,EF 、AH 交于M 2。
下面证M 1、M 2重合。
OM 1∥DF →GF GO DF OM 1=→OM 1=FG DFOG ∙。
OM 2∥EG →GF FO EG OM 2=→OM 2=FGOFEG ∙。
只需证OG ²DF=EG ²OF ,即DFEGOF OG =←Rt △OEG ∽Rt △ODF ←∠DOF=∠DHB=∠EHC=∠EOG 。
