初中数学所有几何证明定理
初中几何证明的所有公理和定理

初中几何证明的所有公理和定理几何学是数学的一个分支,研究平面和空间中的图形、形状、大小以及它们之间的关系。
在几何学中,有一些基本的公理和定理被广泛应用于证明其他几何结论。
以下是初中几何中常用的公理和定理。
一、公理1.尺规公理:任意两点可以用直尺连接,任意一点可以用剪刀间距来复原。
2.同位角公理:同位角互等。
3.平行公理:通过点外一条直线的直线,与这条直线平行的直线只有唯一一条。
4.直线偏转公理:过直线和不在直线上的一点,有且只有一条直线与该直线相交。
二、定理1.垂直平分线定理:平分一条线段的直线必垂直于该线段。
2.三角形内角和定理:三角形内角的和为180°。
3.直角三角形定理:在直角三角形中,两个直角三角形的边长和斜边相等。
4.点到直线的距离定理:点到直线的距离等于点到该直线上垂线的距离。
5.等腰三角形定理:等腰三角形的底边中点到顶点的距离等于底边的一半。
6.等边三角形定理:等边三角形的三条边相等。
7.三角形外角定理:三角形外角等于其对应内角的和。
8.直角三角形的勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方。
9.海伦公式:已知三角形的三边长,可以通过海伦公式求解其面积。
10.等周定理:等周的两角相等,反之亦成立。
11.三角形中位线定理:三角形两边中点连线中位线,且平分第三边。
12.周长定理:四边形周长等于各边长的和。
13.三角形周长定理:三角形的周长等于三边长的和。
14.三角形中线定理:三角形中线等分中位线,且平分第三边。
15.三角形终边定理:一个角的终边上的点,到另一个角所在的直线的距离永远相等。
16.五边形内角和定理:五边形的内角和是540°。
17.钝角三角形的边长关系:钝角三角形两边长的平方和小于斜边长的平方。
18.三角形的相似性定理:对应角等价、对应边成比例的两个三角形为相似三角形。
19.平行线的性质定理:平行条边分别过枚角且长度成正比,则连线为平行线。
20.重叠三角形定理:如果两个角和一个边分别相等,则两个三角形相等。
初中数学几何定理大全

( 2)N边形的内角和:( n -2)× 180° .
( 3)任意多边形的外角和都为 360°
28、平行四边形的性质:
( 1)平行四边形的对边平行且相等;
( 2)平行四边形的对角相等;
( 3)平行四边形的对角线互相平分。
-可编辑修改 -
29、平行四边形的判定 : ( 1)两组对边分别平行的四边形是平行四边形; ( 2)一组对边平行且相等的四边形是平行四边形; ( 3)两组对边分别相等的四边形是平行四边形; ( 4)两组对角分别相等的四边形是平行四边形; ( 5)对角线互相平分的四边形是平行四边形 . 30、矩形的性质: ( 1)具有平行四边形的所有性质 ( 2)矩形的四个角都是直角; ( 3)矩形的对角线相等且互相平分 . 31、矩形的判定: ( 1)有一个角是直角的平行四边形是矩形。 ( 2)有三个角是直角的四边形是矩形 . ( 3)对角线相等的平行四边形是矩形。 32、菱形的性质: ( 1)具有平行四边形的所有性质 ( 2)菱形的四条边都相等; ( 3)菱形的对角线互相垂直平分,并且每一条对角线平分 一组对角 . 33、菱形的判定: ( 1)四条边相等的四边形是菱形 . ( 2)一组邻边相等的平行四边形是菱形。 ( 3)对角线互相垂直的平行四边形是菱形。 34、正方形的性质: ( 1)具有矩形、菱形的所有性质 ( 2)正方形的四个角都是直角; ( 3)正方形的四条边都相等; ( 4)正方形的两条对角线相等,且互相垂直平分,每一条 对角线平分一组对角 . 35、正方形的判定:(证明既是矩形又是菱形) ( 1)有一个角是直角的菱形是正方形; ( 2)有一组邻边相等的矩形是正方形 . ( 3)对角线相等的菱形是正方形 ( 4)对角线互相垂直的矩形是正方形 36、等腰梯形的判定: ( 1)同一条底边上的两个内角相等的梯形是等腰梯形; ( 2)两条对角线相等的梯形是等腰梯形 . 37、等腰梯形的性质: ( 1)等腰梯形的同一条底边上的两个内角相等; ( 2)等腰梯形的两条对角线相等 . 38、梯形的中位线平行于梯形的两底边,并且等于两底和 的一半 . 四、相似形与全等形 39、全等多边形的对应边、对应角分别相等 . 40、全等三角形的判定: ( 1)如果两个三角形的三条边分别对应相等,那么这两个 三角形全等( SSS.) . ( 2)如果两个三角形有两边及其夹角分别对应相等,那么 这两个三角形全等.( SAS.) ( 3)如果两个三角形的两个角及其夹边分别对应相等,那 么这两个三角形全等 (ASA). ( 4)有两个角及其中一个角的对边分别对应相等的两个三 角形全等( AAS.) ( 5)如果两个直角三角形的斜边及一条直角边分别对应相 等,那么这两个直角三角形全等 . ( H.L. ) 41、相似三角形的性质:对应边、周长、对应线段的比均 等于相似比,面积比等于相似比的平方 42、相似三角形的判定:(类似于全等判定) ( 1)平行于三角形的一边的直线和其他两边相交所构成的 三角形与原三角形相似。 ( 2)如果一个三角形的两角分别与另一个三角形的两角对 应相等,那么这两个三角形相似;
初中数学9大几何模型(证明结论及推导)
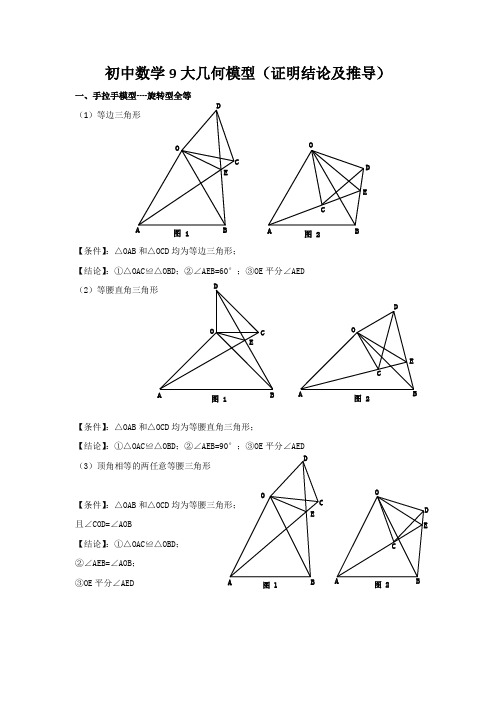
初中数学9大几何模型(证明结论及推导)一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CDO ABCDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
中考数学证明角相等

一.证明角相等
1.余角、补角的性质:同角(或等角)的余角 (补角)相等.
2
1
3
∠1+∠2=90º ∠1+∠3=90º
∠2 =∠3
1.余角、补角的性质:同角(或等角)的余角 (补角)相等. 2.对顶角相等. 3.平行线的性质:两直线平行同位角(内错角)相等. 4.三角形外角定理:三角形外角等于和它 不相邻的内角之和. 5.全等三角形的性质:全等三角形对应角相等. 6.等腰三角形的性质:等边对等角;三线合一. 7.直角三角形的性质:在直角三角形中,如果一条直角边是斜
角都等于它的内对角. 16.弦切角定理:弦切角等于所夹弧所对的圆周角 17:两个弦切角所夹的弧相等,这两个弦切角相等. 18.三角形的内心的性质:三角形的内心与角顶点的连线平分这个角.
19.正多边形的性质:正多边形的外角等于它的中心角.
例1:已知 I 为ABC的内心,延长AI 交BC于D,作IE ⊥BC. 求证:∠BID=∠CIE
边的一半,则这条直角边所对的角是 30°.
8.角平分线的性质定理的逆定理:到一个角两边距离相等的 点在这个角的平分 线上.
9.平行四边形的性质:平行四边形的对角 相等.
10.菱形的性质:菱形的对角线互相垂直平 分,并且每一条对 角线平分一组对角.
11.等腰梯形的性质定理:等腰梯形同一底上 的两个角相等.
例4:AB是 ⊙O的直径,弦CD⊥AB于E,M是上任意 一点。延长AM与DC的延长线交于F。求证: ∠FMC=∠AMD
分析:
已知条件有直径与弦互相垂直, 可考虑用垂径定理。
要证∠FMC=∠AMD 而∠FMC 是圆内接四边形ABCM的外角, 所以∠FMC=∠ABC
∠AMD与∠ABC所对的弧
初中数学所有几何证明定理

初中数学所有几何证明定理初中数学中的几何证明定理有很多,下面列举一些较为常见和重要的:1.垂线定理:如果两条直线相交,且其中一条直线垂直于另一条直线,那么相交的两条直线分成的两对相邻角互为互补角。
证明:假设直线AB与直线CD相交于点O,且直线AB垂直于直线CD,那么∠AOC和∠BOD构成一对互补角,同时∠AOD和∠BOC构成一对互补角。
2.同位角定理:如果两条平行线被一条横截线相交,那么相交的各对同位角相等。
证明:假设平行线AB与CD被平行于它们的条横截线EF相交于点O,那么∠AEO和∠COF,∠FEO和∠DOF互相等。
3.对顶角定理:如果两条直线AB和CD相交,那么由相交而分成的四个角中的相邻角互为对顶角。
证明:假设直线AB与直线CD相交于点O,那么∠AOB和∠COD、∠BOC和∠AOD互为对顶角。
4.垂直角定理:如果两条直线AB和CD相交,那么由相交而分成的四个角中的互为相对角的两对角中,有一对互为垂直角。
证明:假设直线AB与直线CD相交于点O,那么∠AOC和∠BOC互为相对角,如果直线AB与直线CD垂直,那么∠AOC和∠BOC互为垂直角。
5.三角形的内角和定理:一个三角形的内角的和等于180°。
证明:假设三角形的三个顶点为A、B、C,以AB为边作一个封闭的三角形ABC,再以BC为边作一个封闭的三角形ACB。
根据同位角定理,∠BAC+∠BCE=∠ACB+∠ACD,即∠BAC+∠ACB+∠BCE=∠ACB+∠ACD+∠BCE,因此∠BAC+∠ACB+∠BCE=∠ACB+∠ACB,即∠BAC+∠ACB+∠ACB=180°。
6.线段的三等分定理:对于线段AB上的任意一点C,如果AC与CB 的长度相等,那么AC与CB将线段AB分为三个相等的部分。
证明:利用数学归纳法,首先取一点D在线段AB上,并且AD的长度为BD的两倍,那么根据线段的加法性质,我们有AB=AD+BD=AD+AD=2AD。
初中数学定理最全整理归纳

初中数学定理大全初中数学点、线、角的定理点的定理:过两点有且只有一条直线点的定理:两点之间线段最短角的定理:同角或等角的补角相等角的定理:同角或等角的余角相等直线定理:过一点有且只有一条直线和已知直线垂直直线定理:直线外一点与直线上各点连接的所有线段中,垂线段最短几何平行定理平行定理:经过直线外一点,有且只有一条直线与这条直线平行推论:如果两条直线都和第三条直线平行,这两条直线也互相平行证明两直线平行定理:同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行两直线平行推论:两直线平行,同位角相等初中数学定理:三角形内角定理定理:三角形两边的和大于第三边推论:三角形两边的差小于第三边三角形内角和定理:三角形三个内角的和等于180°推论1:直角三角形的两个锐角互余推论2:三角形的一个外角等于和它不相邻的两个内角的和推论3:三角形的一个外角大于任何一个和它不相邻的内角全等三角形判定定理定理:全等三角形的对应边、对应角相等边角边定理(SAS):有两边和它们的夹角对应相等的两个三角形全等角边角定理(ASA):有两角和它们的夹边对应相等的两个三角形全等推论(AAS):有两角和其中一角的对边对应相等的两个三角形全等边边边定理(SSS):有三边对应相等的两个三角形全等斜边、直角边定理(HL):有斜边和一条直角边对应相等的两个直角三角形全等角的平分线定理定理1:在角的平分线上的点到这个角的两边的距离相等定理2:到一个角的两边的距离相同的点,在这个角的平分线上角的平分线是到角的两边距离相等的所有点的集合等腰三角形性质定理等腰三角形的性质定理:等腰三角形的两个底角相等(即等边对等角)推论1:等腰三角形顶角的平分线平分底边并且垂直于底边等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合推论3:等边三角形的各角都相等,并且每一个角都等于60°等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)推论1:三个角都相等的三角形是等边三角形推论2有一个角等于60°的等腰三角形是等边三角形初中数学公式定理对称定理定理:线段垂直平分线上的点和这条线段两个端点的距离相等逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上线段的垂直平分线可看作和线段两端点距离相等的所有点的集合定理1:关于某条直线对称的两个图形是全等形定理2:如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线定理3:两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上逆定理:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称直角三角形定理定理:在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半判定定理:直角三角形斜边上的中线等于斜边上的一半勾股定理:直角三角形两直角边a、b的平方和、等于斜边c 的平方,即a^2+b^2=c^2勾股定理的逆定理:如果三角形的三边长a、b、c有关系a^2+b^2=c^2,那么这个三角形是直角三角形多边形内角和定理定理:四边形的内角和等于360°四边形的外角和等于360°多边形内角和定理:n边形的内角的和等于(n-2)×180°推论:任意多边的外角和等于360°平行四边形定理平行四边形性质定理1:平行四边形的对角相等平行四边形性质定理2:平行四边形的对边相等推论:夹在两条平行线间的平行线段相等平行四边形性质定理3:平行四边形的对角线互相平分平行四边形判定定理1:两组对角分别相等的四边形是平行四边形平行四边形判定定理2:两组对边分别相等的四边形是平行四边形平行四边形判定定理3:对角线互相平分的四边形是平行四边形平行四边形判定定理4:一组对边平行相等的四边形是平行四边形矩形的定理矩形性质定理1:矩形的四个角都是直角矩形性质定理2:矩形的对角线相等矩形判定定理1:有三个角是直角的四边形是矩形矩形判定定理2:对角线相等的平行四边形是矩形菱形定理菱形性质定理1:菱形的四条边都相等菱形性质定理2:菱形的对角线互相垂直,并且每一条对角线平分一组对角菱形面积=对角线乘积的一半,即S=(a×b)÷2菱形判定定理1:四边都相等的四边形是菱形菱形判定定理2:对角线互相垂直的平行四边形是菱形正方形定理正方形性质定理1:正方形的四个角都是直角,四条边都相等正方形性质定理2:正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角中心对称定理定理1:关于中心对称的两个图形是全等的定理2:关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分逆定理:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称等腰梯形性质定理等腰梯形性质定理:1.等腰梯形在同一底上的两个角相等2.等腰梯形的两条对角线相等等腰梯形判定定理:1.在同一底上的两个角相等的梯形是等腰梯形2.对角线相等的梯形是等腰梯形平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰推论2:经过三角形一边的中点与另一边平行的直线,必平分第三边中位线定理三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2S=L×h相似三角形定理相似三角形定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似相似三角形判定定理1:两角对应相等,两三角形相似(ASA)直角三角形被斜边上的高分成的两个直角三角形和原三角形相似判定定理2:两边对应成比例且夹角相等,两三角形相似(SAS)判定定理3:三边对应成比例,两三角形相似(SSS)相似直角三角形定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似性质定理1:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比性质定理2:相似三角形周长的比等于相似比性质定理3:相似三角形面积的比等于相似比的平方三角函数定理任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值初中数学圆的定理1.2不共线的三点确定一个圆经过一点可以作无数个圆经过两点也可以作无数个圆,且圆心都在连结这两点的线段的垂直平分线上定理:过不共线的三个点,可以作且只可以作一个圆推论:三角形的三边垂直平分线相交于一点,这个点就是三角形的外心三角形的三条高线的交点叫三角形的垂心1.3垂径定理圆是中心对称图形;圆心是它的对称中心圆是周对称图形,任一条通过圆心的直线都是它的对称轴定理:垂直于弦的直径平分这条弦,并且评分弦所对的两条弧推论1:平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧推论2:弦的垂直平分弦经过圆心,并且平分弦所对的两条弧推论3:平分弦所对的一条弧的直径,垂直评分弦,并且平分弦所对的另一条弧1.4弧、弦和弦心距定理:在同圆或等圆中,相等的弧所对的弦相等,所对的弦的弦心距相等圆与直线的位置关系2.1圆与直线的位置关系如果一条直线和一个圆没有公共点,我们就说这条直线和这个圆相离如果一条直线和一个圆只有一个公共点,我们就说这条直线和这个圆相切,这条直线叫做圆的切线,这个公共点叫做它们的切点定理:经过圆的半径外端点,并且垂直于这条半径的直线是这个圆的切线定理:圆的切线垂直经过切点的半径推论1:经过圆心且垂直于切线的直线必经过切点推论2:经过切点且垂直于切线的直线必经过圆心如果一条直线和一个圆有两个公共点,我们就说,这条直线和这个圆相交,这条直线叫这个圆的割线,这两个公共点叫做它们的交点直线和圆的位置关系只能由相离、相切和相交三种2.2三角形的内切圆如果一个多边形的各边所在的直线,都和一个圆相切,这个多边形叫做圆的外切多边形,这个圆叫做多边形的内切圆定理:三角形的三个内角平分线交于一点,这点是三角形的内心三角形一内角评分线和其余两内角的外角评分线交于一点,这一点叫做三角形的旁心。
初中数学几何证明的公式

初中数学几何证明的公式由于ABCD菱形所以AD=DC 角cdb=角adb由于AP=AP所以DCP全等 DAP所以PC=PA AP=PC 角DCP=角DAP2由于ABCD菱形所以DF平行ap所以角BAP=角F由于角DCP=角DAP所以角PCE=角BAP所以角F=角PCE由于角CPE=角 CPF所以三角形PCE相像于三角形PFC由于PC=AP所以AP2=PE*PF2CE=EF=4证明:由于:CE⊥AD所以:由于:AD平分∠CAB所以:在三角形AEC和三角形AEF中AE=AE所以:三角形AEC全等于三角形AEF所以:CE=EF由于,∠ACB=90°,CE⊥AD所以:三角形ACE相像于三角形DEC所以:CE*CE=AE*AD=16所以:CE=4所以:CE=EF=43D是RtΔABC的斜边BC上一点,且ΔABD与ΔACD的.内切圆相等,S表示RtΔABC的面积,中学几何证明。
求证:S=AD^2。
对于任意ΔABC,D是边BC上一点,假如ΔABD与ΔACD 的内切圆相等,那么有AD^2=[(CA+AB)^2-BC^2]/4 (1)下面先证这一命题,证明范文《中学几何证明》。
设AD=*,那么BD/CD=S(ABD)/S(ACD)=(AB+*+BD)/(CA+*+CD) (2)由余弦定理得:BD/CD=(*^2-AB^2+BD^2)/(-*^2+CA^2-CD^2) (3)又BD+CD=BC (4)依据以上三式,可推得(1)式.由于ΔABC是直角三角形,BC为斜边,由勾股定理得: BC^2=CA^2+AB^2, (5)又RtΔABC的面积S=CA*AB/2。
(6)依据(1),(5),(6)式得:AD^2=[(CA+AB)^2-BC^2]/4=CA*AB/2=S4证明设S1,S2分别表示ΔABD与ΔACD的面积.作DE⊥AB于E,DF⊥CA于F。
设AB=c,CA=b,BD=n,CD=m。
由相像三角形知:DE=nb/(n+m), DF=mc/(n+m),在RtΔADE中,由勾股定理得:AD^2=(n^2*b^2+m^2*c^2)/(n+m)^2。
(完整版)初中常见定理证明

初中常有定理的证明一、三角形1、运用你所学过的三角形全等的知识去证明定理:有两个角相等的三角形是等腰三角形.(用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依照)2、证明定理:等腰三角形的两个底角相等.(画出图形、写出已知、求证并证明)3、表达并证明三角形内角和定理.要求写出定理、已知、求证,画出图形,并写出证明过程4、我们知道,证明三角形内角和定理的一种思路是力求将三角形的三个内角转变到同一个极点的三个相邻的角,从而利用平角定义来得到结论,你能想出多少种不同样的方法呢?同学之间可相互交流.5、三角形中位线定理,是我们特别熟悉的定理.① 请你在下面的横线上,完满地表达出这个定理:② 依照这个定理画出图形,写出已知和求证,并对该定理给出证明.6、定理“直角三角形斜边上的中线等于斜边的一半”的逆命题是,这个命题正确吗?若正确,请你证明这个命题,若不正确请说明原由.7、用所学定理、定义证明命题证明:直角三角形斜边上的中线等于斜边的一半.8、同学们,这学期我们学过很多定理,你还记得“在直角三角形中,若是一个锐角等于 30 度,那么它所对的直角边等于斜边的一半”,请你写出它的抗命题,并证明它的真假.解:原命题的抗命题为:在直角三角形中,若是一条直角边等于斜边的一半,那么这条直角边所对的角是 30°.9、利用图( 1)或图( 2 )两个图形中的有关面积的等量关系都能证明数学中一个十分出名的定理,这个定理称为是,该定理的结论其数学表达式.10、利用图中图形的有关面积的等量关系都能证明数学中一个十分出名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“ 总统” 证法.这个定理称为,该定理的结论其数学表达式是.11 、 [ 定理表述 ]请你根据图 1 中的直角三角形,写出勾股定理内容;[ 试一试证明 ]以图 1 中的直角三角形为基础,可以构造出以 a、 b 为底,以 a+b 为高的直角梯形(如图 2),请你利用图 2,验证勾股定理.定理表述:直角三角形中,两直角边的平方和等于斜边的平方.ab c2证明:∵ S 四边形ABCD =S△ABE +S△AED +S△CDE= 22 212 、如图,△ ABC 中,① AB=AC,② ∠ BAD=∠ CAD,③ BD=CD,④AD⊥BC.请你选择其中的两个作为条件,另两个作为结论,证明等腰三角形的“ 三线合一” 性质定理.13、课本指出:公认的真命题称为公义,除了公义外,其他的真命题(如推论、定理等)的正确性都需要经过推理的方法证实.( 1)表达三角形全等的判断方法中的推论 AAS;( 2)证明推论 AAS.要求:表达推论用文字表达;用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依照.14 、在数学课外活动中,某学习小组在谈论“导学案”上的一个作业题:已知:如图, OA均分∠ BAC,∠1=∠2.求证: AO⊥ BC.同学甲说:要作辅助线;同学乙说:要应用角均分线性质定理来解决:同学丙说:要应用等腰三角形“ 三线合一” 的性质定理来解决.若是你是这个学习小组的成员,请你结合同学们的谈论写出证明过程.15、证明:勾股定理逆定理已知:在 ABC中, AB=c,AC=b,BC=a ,若 c2 =a 2 + b 2求证:∠ C = 90 度证明:作 RT DEF,使∠ E=RT∠, DE=b ,EF=a在 RT2 2 2= a2 2 DEF中, DF = ED + EF +b因为 c2 =a 2 + b 2所以 DF =c所以 DF=AB,DE=AC,EF=BC所以 RT DFE≌Δ ABC(SSS)所以∠ C=∠E = RT∠二、四边形(一)梯形1、定理证明:“等腰梯形的两条对角线相等” .2、用两种方法证明等腰梯形判判定理:在同一底上的两个角相等的梯形是等腰梯形(要求:画出图形,写出已知、求证、证明).3、在梯形 ABCD中,如图所示, AD∥ BC,点 E、 F 分别是 AB、 CD的中点,连接 EF,EF 叫做梯形的中位线.观察 EF 的地址,联想三角形的中位线定理,请你猜想: EF 与 AD、 BC 有怎样的地址和数量关系并证明你的猜想.4、采用如图所示的方法,可以把梯形ABCD折叠成一个矩形EFNM(图中EF, FN, EM 为折痕),使得点 A 与 B、 C 与 D 分别重合于一点.请问,线段 EF 的位置如何确定;经过这种图形变化,你能看出哪些定理或公式(至少三个)?证明你的所有结论.解:可以看出梯形的中位线定理、面积公式、平行线的性质定理等.(二)平行四边形1、定理证明:一组对边平行且相等的四边形是平行四边形.2、定理求证:对角线互相均分的四边形是平行四边形.3、我们在几何的学习中能发现,很多图形的性质定理与判判定理之间有着一定的联系.例如:菱形的性质定理“ 菱形的对角线互相垂直” 和菱形的判判定理“ 对角线互相垂直的平行四边形是菱形” 就是这样.但是课本中对菱形的别的一个性质“ 菱形的对角线平分一组对角” 却没有给出近似的判判定理,请你利用如图所示图形研究一下这个问题.要求:若是有近似的判判定理,请写出已知、求证并证明.若是没有,请举出反例.(三)圆证明:一条弧所对圆周角等于它所对圆心角的一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学所有几何证明定理
证明题的思路
很多几何证明题的思路往往是填加辅助线,分析已知、求证与图形,探索证明。
对于证明题,有三种思考方式:
(1)正向思维。
对于一般简单的题目,我们正向思考,轻而易举可以做出,这里
就不详细讲述了。
(2)逆向思维。
顾名思义,就是从相反的方向思考问题。
在初中数学中,逆向思
维是非常重要的思维方式,在证明题中体现的更加明显。
同学们认真读完一道题的题干后,不知道从何入手,建议你从结论出发。
例如:
可以有这样的思考过程:要证明某两条边相等,那么结合图形可以看出,只要
证出某两个三角形相等即可;要证三角形全等,结合所给的条件,看还缺少什
么条件需要证明,证明这个条件又需要怎样做辅助线,这样思考下去……这样
我们就找到了解题的思路,然后把过程正着写出来就可以了。
(3)正逆结合。
对于从结论很难分析出思路的题目,可以结合结论和已知条件认
真的分析。
初中数学中,一般所给的已知条件都是解题过程中要用到的,所以可以从已知
条件中寻找思路,比如给我们三角形某边中点,我们就要想到是否要连出中位线,或者是否要用到中点倍长法。
给我们梯形,我们就要想到是否要做高,或
平移腰,或平移对角线,或补形等等。
正逆结合,战无不胜。
证明题要用到哪些原理?
要掌握初中数学几何证明题技巧,熟练运用和记忆如下原理是关键。
下面归类一下,多做练习,熟能生巧,遇到几何证明题能想到采用哪一类型原理来解决问题。
一、证明两线段相等
1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
12.两圆的内(外)公切线的长相等。
13.等于同一线段的两条线段相等。
二、证明两个角相等
1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等。
三、证明两条直线互相垂直
1.等腰三角形的顶角平分线或底边的中线垂直于底边。
2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3.在一个三角形中,若有两个角互余,则第三个角是直角。
4.邻补角的平分线互相垂直。
5.一条直线垂直于平行线中的一条,则必垂直于另一条。
6.两条直线相交成直角则两直线垂直。
7.利用到一线段两端的距离相等的点在线段的垂直平分线上。
8.利用勾股定理的逆定理。
9.利用菱形的对角线互相垂直。
10.在圆中平分弦(或弧)的直径垂直于弦。
11.利用半圆上的圆周角是直角。
四、证明两直线平行
1.垂直于同一直线的各直线平行。
2.同位角相等,内错角相等或同旁内角互补的两直线平行。
3.平行四边形的对边平行。
4.三角形的中位线平行于第三边。
5.梯形的中位线平行于两底。
6.平行于同一直线的两直线平行。
7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。
五、证明线段的和差倍分
1.作两条线段的和,证明与第三条线段相等。
2.在第三条线段上截取一段等于第一条线段,证明余下部分等于第二条线段。
3.延长短线段为其二倍,再证明它与较长的线段相等。
4.取长线段的中点,再证其一半等于短线段。
5.利用一些定理(三角形的中位线、含30度的直角三角形、直角三角形斜边上的中线、三角形的重心、相似三角形的性质等)。
六、证明角的和差倍分
1.与证明线段的和、差、倍、分思路相同。
2.利用角平分线的定义。
3.三角形的一个外角等于和它不相邻的两个内角的和。
七、证明线段不等
1.同一三角形中,大角对大边。
2.垂线段最短。
3.三角形两边之和大于第三边,两边之差小于第三边。
4.在两个三角形中有两边分别相等而夹角不等,则夹角大的第三边大。
5.同圆或等圆中,弧大弦大,弦心距小。
6.全量大于它的任何一部分。
八、证明两角的不等
1.同一三角形中,大边对大角。
2.三角形的外角大于和它不相邻的任一内角。
3.在两个三角形中有两边分别相等,第三边不等,第三边大的,两边的夹角也大。
4.同圆或等圆中,弧大则圆周角、圆心角大。
5.全量大于它的任何一部分。
九、证明比例式或等积式
1.利用相似三角形对应线段成比例。
2.利用内外角平分线定理。
3.平行线截线段成比例。
4.直角三角形中的比例中项定理即射影定理。
5.与圆有关的比例定理---相交弦定理、切割线定理及其推论。
6.利用比利式或等积式化得。
十、证明四点共圆
1.对角互补的四边形的顶点共圆。
2.外角等于内对角的四边形内接于圆。
3.同底边等顶角的三角形的顶点共圆(顶角在底边的同侧)。
4.同斜边的直角三角形的顶点共圆。
5.到顶点距离相等的各点共圆。
