电力系统节点矩阵与环网求解
高等电力系统分析-第二章-电力系统网络矩阵

第二章电力系统网络矩阵作业:2-1, 2-6, 2-722.1 节点导纳矩阵Y●N 个节点(不含地),b 条支路●A 0-(N+1)×b 阶, y b -b ×b 阶●则(N+1)×(N+1)阶节点不定导纳矩阵为:T 00b 0Y A y A2.1.1 Y 的性质、特点及物理意义(1)节点不定导纳矩阵0Y301bT k k kk y ===∑Y M M k kkky y yy --想象:透明胶片的叠加4节点方程1,11,21,1,1112,12,22,2,122,1,2,,1`1,11,21,1,111N N N N N N N N N N N N N N N NN N N N Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I ++++++++++⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦参考节点6节点不定导纳矩阵Y 0的性质性质1:无移相器时,Y 0对称:=T 00b 0Y A Y A中的每个非零元都是实数,而Y b 是对角线矩阵。
0A 由于=T 00Y Y8性质3:Y 0是奇异矩阵,并有0Y 1=0证明:=T 00b 0Y A Y A01bT k k kk y =∴==∑Y M M k k kky y y y --011()()b bT T k k kk k kk k y y ==∴==∑∑Y 1M M 1M M 10T k=M 1而9◆齐次方程存在非零解,所以Y 0奇异(数学上的理解);◆所有节点电位相同时,支路无电流(物理意义上的理解);0Y 1=0怎样理解?10T ∴1I = 0∴T1Y =0 V 0Y 1=00T1Y =0对任意节点电压都成立13241I 2I 3I 4I 1,11,21,31,4112,12,22,32,4223,13,23,33,4334,14,24,34,444Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦12340I I I I +++= N=3, N+1=411如果电力网络无接地支路,这时是一个浮空网:13241I 2I 3I 4I 40I = 1230I I I ++= N 个节点的网络Y 0奇异此时不独立3I 例12(2)节点定导纳矩阵Y选地为参考节点,排在N+1位置,参考电压是零T Iy = V 0o T oo o y I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦Y y I y V 是地节点电流平衡方程是网络方程,不含地节点Y =IV 不独立1313241I 2I 3I 4I 1,11,21,31,4112,12,22,32,4223,13,23,33,4334,14,24,34,440Y Y Y Y I V Y Y Y Y I V Y Y Y Y I V Y Y Y Y I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦1,11,21,3112,12,22,3223,13,23,333Y Y Y V I Y Y Y V I Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦节点不定导纳矩阵节点定导纳矩阵例Y =IV14433Y V 411Y V 14,14,24,3243V Y Y Y V I V ⎡⎤⎢⎥⎡⎤=⎣⎦⎢⎥⎢⎥⎣⎦4411422433I Y V Y V Y V =++ 13241I 2I 3I 4I 422Y V 411y V 4141Y y =-地节点电流平衡方程4123I I I I =--- 各节点接地支路电流•天网上节点注入电流之和=接地支路电流之和的负值=流出地节点电流TI y = V15节点定导纳矩阵的性质性质1:无移相器支路时,Y 是N ×N 阶对称矩阵Tb Y =Ay A性质2:Y 是稀疏矩阵对Y 的贡献k k kky y y y --iky j16[]T lm l l k T mk ky y yy ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦M M M M T T T Tl l ll m kk m lk k ky y y y =+++M M M M M M M M1l m lm m k mk z z y y z z y y -⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ilz jpkz qmz 两条支路有互感时,它们对应的支路导纳子矩阵是:对节点导纳矩阵的贡献是17l m l m m k m k l m l m mkmki p j q y y y y i y y y y p y y y y j y y y y q ⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦对节点导纳矩阵的贡献是ijpq新增耦合等值支路ilz jpkz qmz ijpqm y -my -my my l y ky18性质3:有接地支路时,Y非奇异,Y每行元素之和等于该节点接地导纳13241I 2I 3I 4I 1,11,21,32,12,22,33,13,23,3Y Y Y Y Y Y Y Y Y ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦节点4不包括在内如果节点接地支路的导纳较小时,Y接近奇异例19121310121321122320233132132330y y y y y y y y y y y y y y y ++--⎡⎤⎢⎥=-++-⎢⎥⎢⎥--++⎣⎦Y N =3,b =6,N +1=41321I 2I 3I 0I 节点定导纳矩阵的形态例21(3)Y 的物理意义表示短路参数:在节点i 接单位电压源,其余节点短路接地,流入节点i 的电流数值为自导纳Y ii ,流入节点j 的电流数值为互导纳Y ji32Y 12312Y 22Y +_1[]1222321Y Y Y ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦Y2213222112I Y y ==- 111121310I Y y y y ==++ 12y 33113I Y y ==- 13y 10y 1+_ 示例例(自导纳)(互导纳)(互导纳)242.1.3 Y 的修改◆支路追加和移去T l l ly '=±Y Y M M◆节点合并(母联开关合上)注意移去连支、树支、桥支路的情况行相加(电流之和等于总电流)1,11,21,3112,12,22,3223,13,23,333Y Y Y V I Y Y Y V I Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2V 3V 23V V = 23I I I +=列相加(节点电压相等)251,11,21,3112,12,22,3223,13,23,323Y Y Y V I Y Y Y V I Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦1,11,21,3112,12,22,3223,13,23,33Y Y Y I V Y Y Y I V Y Y Y I ⎡⎤⎡⎤+⎡⎤⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥+⎣⎦⎣⎦1,11,21,3112,13,12,22,33,23,3232Y Y Y I V Y Y Y Y Y Y I I V +⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥+++++⎣⎦⎣⎦⎣⎦23V V = 23I I I +=26节点p消去n p T p pp Y ⎡⎤⎢⎥⎣⎦Y Y Y p T ppp Y ⎡⎤⎢⎥⎣⎦Y Y 1T n n p pp pY -=-Y Y Y Y 1T p pp pY --Y Ypp擦除增加27◆某节点s 电压给定,V s 是已知量,求其余节点的电压n s n n T sss s s Y V I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦Y Y ΙY V n n n s sV =-Y ΙY V 把节点s的电压源变成电流源减少一个待求量,方程减少一阶和s 相连的节点,注入电流有一个增量28◆变压器变比变化时的修正变比由变成tt '[]111/1/l y tt ⎡⎤⎢⎥⎢⎥=-⎢⎥-⎢⎥⎣⎦Y []111/1/l y t t ⎡⎤⎢⎥⎢⎥''=-'⎢⎥-⎢⎥⎣⎦Y '∆=-Y Y Y可在原网络上贴◆支路参数变化时的修正l y l y '参数由变成在原网络上贴y y y'∆=-变压器支路对导纳矩阵的贡献29(1)以地为参考节点的Z ,N ⨯N 阶(有接地支路)2.2 节点阻抗矩阵Z1-=Z Y2.2.1 Z 的性质、特点及其物理意义.Z I = V(2)Z 元素的物理意义开路参数(3)Z 矩阵的性质Z矩阵对称(互易定理)Z是非奇异的满阵(为什么非奇异?为什么满阵?)对纯感性支路组成的无源网,节点自阻抗更大,即| Z ii|≥| Z ij|对纯感性支路组成的无源网,节点对的自阻抗更大,| Z ij,ij|≥| Z ij,kl|节点对的自阻抗| Z ij,ij|≠0,除非ij端口存在短路。
电力系统分析第四章《电力网络的数学模型》课件精选全文

网络接线的改变
4-3 节点阻抗矩阵
节点电压方程
YV=I
定义
Y–1=Z
则有 网络方程的通式 对角元 Zkk ——自阻抗.
V= Y–1I=ZI
n
Vi Zij Iij j 1
非对角元 Zik ——互阻抗. 一、节点阻抗矩阵元素的物理意义
Z kk
Vk Ik
I j 0, jk
自阻抗:从节点k看进去的对地内阻抗.
电力系统基础
第四章 电力网络的数学模型
▪ 4-1 节点导纳矩阵 ▪ 4-2 网络方程的解法 ▪ 4-3 节点阻抗矩阵 ▪ 4-4 节点编号顺序的优化
一、节点方程
4-1 节点导纳矩阵
准备:举例形成最简单型等值电路的节点导纳矩阵详细过程,n个节点可以简单 类推。电路求解方法中,节点法最适合于计算机处理。
(i,
j
1,2,
已有p 个节点
(a)
已有p 个节点
追加变压器(b树) 支和连支
, p)
节点阻抗矩阵的特点: 1. 对称阵; 2. 满矩阵; 3. 不能直观形成与修改。
(网络方程的求解,略)
填空则:修在改节后点的i与导j纳之矩间阵增Y加的一元条素支为路_的__导__纳_。为yij,
(1)Yij=Yij+yij, Yii=Yii+yij, Yjj=Yjj+yij (2)Yij=Yij–yij, Yii=Yii–yij, Yjj=Yjj–yij (3)Yij=Yij–yij, Yii=Yii+yij, Yjj=Yjj+yij (4)Yij=Yij+yij, Yii=Yii–yij, Yjj=Yjj–yij
阻抗为 zkm 的连支。由于不增加新节点,故阻 抗矩阵的阶次不变。
电力系统环网详细讲解

Z]?匚 + z 巧(I a - Z 3) + Z 31 (I a - Z 2 - I 3) = 0 假设全网各节点均为UNZ0°,则:* 4巾 ” -S3丽7和 3 " Vsu?s令流经Z 12的功率为-,可以得到: i 訂 H V3U WK> 出 來 嘟 半 拿3.4环网潮流计算第3章 简单电力系统的潮流计算3.4.1环网中的初步功率分布令流经乙2的电流为 则根据 KVL(Kirchhoff Voltage Law) 流经Z 31的电流为',流经乙3的电流为 可以列出:无你+ Z 迫I 苦§ +為厶=0如果节点2、3与负荷对应的电流分别为 ,则:Z]2S卄 Z石(久一S2~) + Z^S.-S2-S3)二020+i5MVA -2-ilMVA18+14MVAS115+jlOM 17+jllMV4冷 〔厶2 +2石+Z31)同理* S —"彳23十目十z 口S) b (Z^ + 2加+2引)可以理解为用力矩法求梁的反作用力:这两个公式可以推广到2节点、4节点 在求得S 和S bi 后,便可求得环网中各段的功率,即不包括线路功率损耗的功率 分布,这称为环网中的初步功率分布。
g 1 15+jlOMVA 2— 17+订 1MVA如果支路功率由两个方向实际流入一个节点, 则该节点称为功率分点,可以标为AF1 A 1 F218+j4MVA有时有功功率分点和无功功率分点不一致,可以分别表示为A、二3.4.2环网的实际功率分布和电压降落从功率分点将环网解开成两个开式网,然后分别对两个开式网计算功率分布和电压降落。
如果有功功率分点和无功功率分点不一致,则多以无功功率分点解开环网成为两个开式网。
[例3-5]如图系统,U=115kV,头二20 + J13.88A/E4S3 =10 + /9.038A/E4乙2=13.2+j17.16 Q,乙3=9.9+j12.87 Q =N,(1)试求功率分布。
电力系统网络矩阵

i
Yii
+
N
YNi
-
节点导纳矩阵表示短路参数。
在网络中节点i 接单位电压源,其余 节点都短路接地,此时流入节点i 的
电流数值上是Yii,流入节点j的电流
数值上是Yij。
注意:只有和节点i有支路相连的节点才有 电流,因此导纳矩阵是稀疏矩阵。节点导 纳矩阵的元素只包含网络的局部信息。
2011-1-1
高等电力网络分析
C2Z(0)C1
yaa1
zaa
za 0 z01z0a
2011-1-1
高等电力网络分析
14
3、追加树支支路
增加新节点q
部i 分 网
络j
a p
q 前 A0
A
A0 0T
ep 1q
后 y0
Y
A0 0T
ep y0
1
ya
0
y0a A0T
yaa
eTp
0 1
整理后可得
Z
Z(0) C2Z(0)
(Yn YpYpp1YpT )Vn In YpYpp1Ip
Y Yn YpYpp1YpT
i p
2011-1-1
j
i
k
j
消去节点p,只需对Y阵
中和p有支路相连的节
点之间的元素进行修正,
k
其他节点之间的元素不
需要修正。
高等电力网络分析
8
4、节点电压给定的情况
Yn YsT
Ys Yss
Vn Vs
部i
分
追加前:
网
a
络j
Y(0) A0z01A0T
追加后: Y A0
辅助矩阵求逆定理
M a
y0
1 电力网络的数学模型及求解方法

An An
a1(1) n (2) a2 n (3) a3 n 1
(1) a1, n 1 (2) a2, n 1 (3) a3, n 1 (n) an ,n 1
(1) (1) x1 a12 x2 a13 x3 (2) x2 a23 x3
Y jj yij
Yij Y ji yij
3)在原有网络节点i 和节点j 间切除一条支路
节点导纳阵阶数不变; 与节点i、j有关的元素修正为 Yii yij Y jj yij
Yij Y ji yij
4)原有网络节点i 和节点j 间支路参数发生改变
相当于切除一条原参数的支路,再增加一条新参数的支路
则由节点方程式可知
以之前的简单电力网络说明节点导纳阵各元素的具体意义
y1
4 2
y4
y3
3
y5
y2
5
1
V1 1
y6
Y的特点: 对称性、稀疏性、可逆性
y4 y5 y6 y4 y5 0 0
y4 y1 y3 y4 y3 y1 0
y5 y3 y2 y3 y5 0 y2
AX = B
a11 a A A B 21 an1 a12 a22 an 2 a1n a2 n ann b1 a11 a21 b2 bn an1 a12 a22 an 2 a1n a2 n ann a1,n1 a2,n1 an ,n1
ib
5
根据基尔霍夫电流定律, 可列出各节点的电流方程
1
y6
y4 (V2 V1 ) y5 (V3 V1 ) y6V1 0 y1 (V4 V2 ) y3 (V2 V3 ) y4 (V2 V1 ) 0 y2 (V5 V3 ) y3 (V2 V3 ) y5 (V3 V1 ) 0 y1 (V4 V2 ) ia y2 (V5 V3 ) ib
第二章 电力系统网络矩阵20110409讲解

2.2 节点阻抗矩阵
性质3:对纯电阻性或纯感性支路组成的电 网,|Zii|≥|Zij| 对这两种网络,节点i注入单位电流时,节 点i的电位最高,其它节点电位不会高于节 点i的电位,由节点阻抗矩阵元素的物理意 义,故上述结论成立.对于既含感性又含 容性支路的电网,情况比较复杂,上述结 论不能保证成立。
完全 网络
2.2 节点阻抗矩阵
假定部分网络的原始支路阻抗矩阵是z0,关联
支
矩阵是A0,相对应的节点阻抗矩阵和节点导纳 矩阵是Z(0)和Y(0),则有:
ym yk ym
q
ym i
yk p
ym j
yk q
2.1 节点导纳矩阵
性质3:当存在接地支路时,Y是非奇异的,Y的每行元素 之和等于该行所对应节点上的接地支路的导纳。这里非标 准变比变压器支路用π等值模型表示。
Y0U 0 I0
Y0 1 0
节点不定导纳矩阵的特点:连通网络的公共参考点与连 通网络之间没有支路相关联,全网各节点电位不定,节点 导纳矩阵不可逆。
2.1 节点导纳矩阵
2.节点定导纳矩阵 选地节点为电压参考点,将它排在第N+1号,令参考节点 电位为零,则可将不定导纳矩阵表示的网络方程写成分块 形式:
2.2 节点阻抗矩阵
节点阻抗矩阵的形成方法: (1)导纳矩阵求逆 (2)支路追加法 (3)连续回代法
2.2 节点阻抗矩阵
2.2.2 用支路追加法建立节点阻抗矩阵
•部分网络:是一个连通网络,它由要分析的电 网的部分或全部母线和部分支路组成。
电力系统分析第4章 电力网络的数学模型

Vn
I2(1)
•
•
Y (1) n2
V2
Y (1) nn
Vn
I2(1)
式中
Y (1) ij
Yij
Yi1Yj1 Y11
; Ii(1)
I
Yi1 Y11
I1
第四章电力网络的数学模型
4.2 网络方程的解法
➢ 对方程式再作一次消元,其系数矩阵便演变为
Y11
Y (2)
Y12 Y13 Y1n
Y (1) 22
第四章电力网络的数学模型
4.1 节点导纳矩阵
➢一般地,对于有n个独立节点地网络,可以列写n个 节点方程
•
•
•
Y11 V1 Y12 V2 Y1n Vn
•
I1
•
•
•
Y21 V1 Y22 V2 Y2n Vn
•
I2
•
•
• •
Yn1 V1 Yn2 V2 Ynn Vn In
(4-3)
4.1 节点导纳矩阵
➢上述方程经过整理可以写成
•
•
Y11 V1 Y12 V2
0
•
•
•
•
Y21 V1 Y22 V2 Y23 V3 Y24 V4 0
•
•
•
Y32 V2 Y33 V3 Y34 V4 0
•
•
•
Y42 V2 Y43 V3 Y44 V4
•
I
4
(4-2)
第四章电力网络的数学模型
4.1 节点导纳矩阵
➢将电势源和阻抗的串联变 换成电流源和导纳的并联,得 到的等值网络如图所示,其中:
•
•
I 1 y10 E1
节点导纳矩阵及潮流计算

目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2.1节点导纳矩阵 (3)2.2牛顿-拉夫逊法 (4)2.2.1牛顿-拉夫逊法基本原理 (4)2.2.2牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算,它的任务是对给定的运行条件确定系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件:如图所示电网。
1∠002阵Y;2+j13)给出潮流方程或功率方程的表达式;4)当用牛顿-拉夫逊法计算潮流时,给出修正方程和迭代收敛条件。
2原理介绍2.1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取,也可根据电路知识中找出改网络的关联矩阵,在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道,在利用电子数字计算机计算电力系统运行情况时,多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组:nn Y n +V (2-1) 由此可以得到n 个节点导纳矩阵:nn Y ⎫⎪⎪⎪⎪⎭它反映了网络的参数及接线情况,因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
由导纳短阵所了解的节点方程式是电力网络广泛应用的一种数学模型。
通过上面的讨论,可以看出节点导纳矩阵的有以下特点:(1)导纳矩阵的元素很容易根据网络接线图和支路参数直观地求得,形成节点导纳矩阵的程序比较简单。
(3)导纳矩阵是稀疏矩阵。
它的对角线元素一般不为零,但在非对角线元素中则存在不少零元素。
1第一章 电力网络的数学模型及求解方法

第1章电力网络的数学模型及求解方法电力网络的数学模型是现代电力系统分析的基础。
例如,正常情况下的电力潮流和优化潮流分析、故障情况下短路电流计算以及电力系统静态安全分析和动态稳定性的评估,都离不开电力网络的数学模型。
这里所谓电力网络,是指由输电线路、电力变压器、并(串)联电容器等静止元件所构成的总体[1]。
从电气角度来看,无论电力网络如何复杂,原则上都可以首先做出它的等值电路,然后用交流电路理论进行分析计算。
本章所研究的电力网络均由线性的集中参数元件组成,适用于电力系统工频状态的分析。
对于电磁暂态分析问题,当涉及到高额现象及波过程时,需要采用分布参数的等值电路。
电力网络通常是由相应的节点导纳矩阵或节点阻抗矩阵来描述的[2,3]。
在现代电力系统分析中,我们需要面对成干上万个节点及电力网络所连接的电力系统。
对电力网络的描述和处理往往成为解决有关问题的关键[4]。
电力网络的导纳矩阵具有良好的稀疏特性,可以用来高效处理电力网络方程,是现代电力系统分析中广泛应用的数学模型。
因此。
电力网络节点导纳矩阵及其稀疏特性是本章讨论的核心内容。
节点阻抗矩阵的概念在处理电力网络故障时有广泛应用,将在1.4节中介绍。
此外,虽然关于电力网络的等值电路在一般输配电工程的教科书中都有论述,但在建立电力网络数学模型时,关于变压器和移相器的处理却有一些特点,因此1.1节中首先介绍这方面的内容。
1.1 基础知识1.1.1 节点方程及回路方程通常分析交流电路有两种方法,即节点电压法和回路电流法[3]。
这两种方法的共同特点是把电路的计算归结为一组联立方程式的求解问题;其差别是前者采用节点方程,后者采用回路方程。
目前在研究电力系统问题时,采用节点方程比较普遍,但有时以回路方程作为辅助工具。
以下首先以简单电力网络为例,说明利用节点方程计算电力网络的原理和持点。
图1—1表示了一个具有两个电源和一个等值负荷的系统。
该系统有5个节点和6条支路,y 1-y 6为各支路的导纳。
第二章电力系统网络矩阵0409

有一元件α,其自阻抗为zαα,它和部分网络各元件的互
阻抗z0α,则部分网络和支路α一起构成的原始网络元件
支 方程可用阻抗形式写成:
路 追
U.bo U.ba
z0
z
ao
z z
oa aa
I I
.
bo .
ba
加 法
IIbbo
y0 y 0
y0 y
UUbbo
注:Ibo,Ubo是 不包括支路α的部 分网络元件的电流 和电压列矢量, Ibα,Ubα是元件α 的电流和电压。
Yp Ypp
U. U.
n p
I.n
.
Ip
.
.
.
消去节点p:
Yn
YpY
Y 1 T
pp p
Un In YpYpp1 I p
消去节点p后的导纳矩阵为:
Y
Yn
YpY
Y 1 T
pp p
Yij
Yij
YipYpj Ypp
.
I
n
YpYpp1
.
I
p
为消去节点p 后的注入电流
消去节点后可能 产生注入元。
2.1 节点导纳矩阵
2.节点合并
两节点合并,相当于令两节点电压相等,新节点注入电流等 于原两个节点注入电流之和。 例:节点p,q 合并,合并后节点称为p,则:
U p U p Uq Ip Ip Iq
相当于把导纳矩阵第q行加到第p行上,将第q列加到第p列 上,节点合并不改变导纳矩阵的奇异性。
2.1 节点导纳矩阵
变成 ,此t时 ,节点导纳矩阵中Yii不变,只有三个元素将发
生变化. 其中非对角元素将由Yij变成 Yij, 变化量是△Yij
电力网节点导纳矩阵计算例题与程序
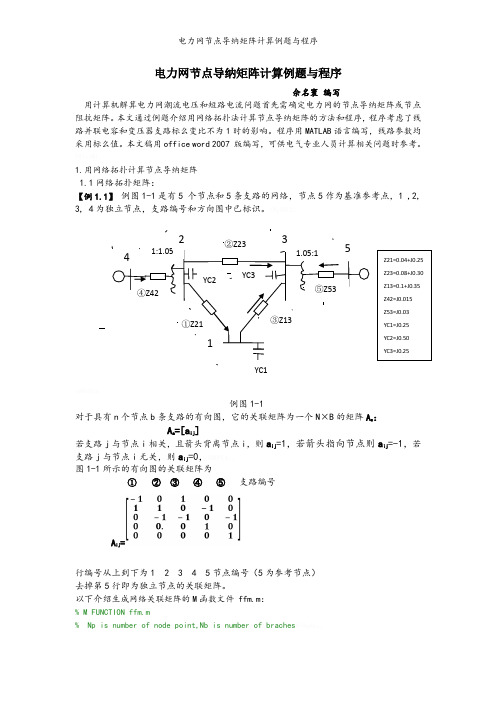
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0,图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1.051.05:142315Z21=0.04+J0.25 Z23=0.08+J0.30 Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25 YC2=J0.50 YC3=J0.25% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
节点导纳矩阵及潮流计算

目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2.1节点导纳矩阵 (3)2.2牛顿-拉夫逊法 (4)2.2.1牛顿-拉夫逊法基本原理 (4)2.2.2牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (10)4结果分析 (14)5总结 (15)参考资料 (16)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算,它的任务是对给定的运行条件确定系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件: 如图所示电网。
其元件导纳参数为:y 12=0.5-j3, y 23=0.8-j4, y 13=0.75-j2.5任务及要求:1)根据给定的运行条件,确定图2所示电力系统潮流计算时各节点的类型和待求量;1∠002+j12)求节点导纳矩阵Y ;3)给出潮流方程或功率方程的表达式;4)当用牛顿-拉夫逊法计算潮流时,给出修正方程和迭代收敛条件。
2原理介绍2.1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取,也可根据电路知识中找出改网络的关联矩阵,在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道,在利用电子数字计算机计算电力系统运行情况时,多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组:11112211211222221122n n n n nn n Y Y Y n Y Y Y n Y Y Y n +++=⎫⎪+++=⎪⎬⎪⎪+++=⎭V V V I V V V I V V V I L L L L (2-1)由此可以得到n 个节点导纳矩阵:111212212212n n n n nn Y Y Y Y Y Y Y Y Y Y ⎛⎫⎪ ⎪= ⎪⎪⎝⎭LL L L(2-2)它反映了网络的参数及接线情况,因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
电力网节点导纳矩阵计算例题与程序

电力网节点导纳矩阵计算例题与程序————————————————————————————————作者:————————————————————————————————日期:电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0, 图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m②③①YYY④⑤1:1 1.042315Z21=0.04+J0.25Z23=0.08+J0.30Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
电力系统计算与仿真分析 第一章 节点网络方程

小结
当电力网络结构或元件参数发生局 部变化时,可以在原有的节点导纳矩 阵基础上进行修改得到新的节点导纳 矩阵。节点导纳矩阵和节点阻抗矩阵 互为逆矩阵。节点网络方程也可以节 点阻抗矩阵形式描述。
感谢聆听!
物理意义:当电网络中节点i接入单 位电压源,其他节点都接地时,自导 纳Yii在数值上等于节点i注入网络的 电流。
一、节点电压方程
节点阻抗矩阵Z: 两边同乘Y-1: 即:
Z Y 1 Y 1YU = Y 1 I
ZI = U
节点网络方程的另一种形式
二、节点导纳矩阵的形成
节点导纳矩阵可以根据降阶节点—支路关联矩阵A(简称关联矩阵)来形成。 对于n个独立节点、b条支路的网络,A的阶次为n×b。
Yii Yii yij yij
Yjj
Yjj
yij
yij
Yij Yji Yij yij yij Yji yij yij
四、小结
本章详细地介绍了以节点导纳矩阵
形式描述的节点网络方程。节点导纳 矩阵Y可以根据关联矩阵A以及支路导 纳所组成的对角矩阵YB形成。关联矩 阵A可以表示节点与支路的联系,矩 阵A反映了电力网络的拓扑约束。矩 阵YB反映了电力网络的支路特性约束
电力系统计算与仿真分析
第一章 节点网络方程
提纲
Outline
一 节点电压方程 二 节点导纳矩阵的形成 三 节点导纳矩阵的修改 四 小结
一、节点电压方程
广泛应用
一、节点电压方程
对于具有n个独立节点的网络,可以列出以下方程:
YY1211UU11
Y12U 2 Y22U 2
Y1kU k Y2kU k
自导纳发Y生 变Y化: y
ii
ii
Lesson-02节点导纳矩阵及节点网络方程的解法

Vi 1, Vj 0, j 1, 2, , n, j i
Y11V1 Y12V2
Y1nVn
I1
Y21V1 Y22V2
Y2nVn
I
2
...
Yn1V1 Yn2V2 YnnVn In
I1
Y1i
I2 Y2i
Ii Yii
i7
y24
1 y12 i5 2 i6 y23
3
y34 i8 4
I1
i1
i2
y10
y20
i3
i4
y30
y40
I4
导纳形式的节点方程
y10V1 y12 (V1 V2 ) I1
y12 (V2
V1 )
y20V2
y23 (V2
V3 )
y24 (V2
V4 )
0
y23 (V3 V2 ) y34 (V3 V4 ) y30V3 0
李长松 Spring 2016
电力系统计算机辅助分析
稳定性计算
第5/6章
发电机组和 负荷数学模型
第4章
潮流计算
第2章
电力网络 数学模型
第1章
短路计算
第3章
什么是“数学模型”
• A mathematical model is a description for property or behavior of a system (or a process or a phenomenon) using mathematical concepts and language.
Y21V1 Y22V2
Y2nVn
I
2
1第一章电力网络的数学模型及求解方法

第1章电力网络的数学模型及求解方法电力网络的数学模型是现代电力系统分析的基础。
例如,正常情况下的电力潮流和优化潮流分析、故障情况下短路电流计算以及电力系统静态安全分析和动态稳定性的评估,都离不开电力网络的数学模型。
这里所谓电力网络,是指由输电线路、电力变压器、并(串)联电容器等静止元件所构成的总体[1]。
从电气角度来看,无论电力网络如何复杂,原则上都可以首先做出它的等值电路,然后用交流电路理论进行分析计算。
本章所研究的电力网络均由线性的集中参数元件组成,适用于电力系统工频状态的分析。
对于电磁暂态分析问题,当涉及到高额现象及波过程时,需要采用分布参数的等值电路。
电力网络通常是由相应的节点导纳矩阵或节点阻抗矩阵来描述的[2,3]。
在现代电力系统分析中,我们需要面对成干上万个节点及电力网络所连接的电力系统。
对电力网络的描述和处理往往成为解决有关问题的关键[4]。
电力网络的导纳矩阵具有良好的稀疏特性,可以用来高效处理电力网络方程,是现代电力系统分析中广泛应用的数学模型。
因此。
电力网络节点导纳矩阵及其稀疏特性是本章讨论的核心内容。
节点阻抗矩阵的概念在处理电力网络故障时有广泛应用,将在1.4节中介绍。
此外,虽然关于电力网络的等值电路在一般输配电工程的教科书中都有论述,但在建立电力网络数学模型时,关于变压器和移相器的处理却有一些特点,因此1.1节中首先介绍这方面的内容。
1.1 基础知识1.1.1 节点方程及回路方程通常分析交流电路有两种方法,即节点电压法和回路电流法[3]。
这两种方法的共同特点是把电路的计算归结为一组联立方程式的求解问题;其差别是前者采用节点方程,后者采用回路方程。
目前在研究电力系统问题时,采用节点方程比较普遍,但有时以回路方程作为辅助工具。
以下首先以简单电力网络为例,说明利用节点方程计算电力网络的原理和持点。
图1—1表示了一个具有两个电源和一个等值负荷的系统。
该系统有5个节点和6条支路,y1-y6为各支路的导纳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(0)
Yij
(5)在原有网络的节点i、j 之间变压器的
变比由k*改变为k*'
ZⅠ i k :1 * ZT j ZⅡ
ZⅠ
yT 1 k* 2 k*
i
yT/k*
j
yT
ZⅡ
k* 1 k*
yT 1 k* yT 1 k* Yii ( yT ) ( yT ) 2 2 k* k* k* k* 1 1 ( 2 2 ) yT k* k*
第四章 复杂电力系统潮流的计算机算法
1. 建立数学模型:节点电压方程、导纳矩阵的形成 2. 功率方程、节点分类及约束条件 3. 迭代法计算潮流
功率方程的非线性性质 高斯—塞德尔法 用于潮流计算———速度慢、易于收敛
与修改
4. 牛顿—拉夫逊法计算潮流
原理:局部线性化 直角座标法、极座标法、PQ分解法 用于潮流计算———速度快、但注意初值选择
1 理想变压器的引用
目标:端部条件与实际电路中的值相等(参数不再 需要归算)的等值电路 理想变压器 1、双绕组
I 1:k
, 1
I
2
I
2
, 1
1
I RT jXT
1
1:k I
2
2
U
1
U
U
1
-jBT
GT
1’
,
U
2
2’
I I 推导目的:等值电路中端部条件( U , ) ( U , )不变 变压器参数受变比影响
I 1 U 1 y10 (U 1 U 2) y12 (U 1 U 3) y13 I 2 U 2 y 20 (U 2 U 1) y 21 (U 2 U 3) y 23 0 U 3 y 30 (U 3 U 1) y 31 (U 3 U 2) y 32
20
4.1.3 节点导纳矩阵的修改
不同的运行状态,(如不同结线方式下的运行状
况、变压器的投切或变比的调整等)
改变一个支路的参数或它的投切只影响该支 路两端节点的自导纳和它们之间的互导纳,因此 仅需对原有的矩阵作某些修改。
Y Y
( 0)
Y
Yij Y
( 0) ij
Yij
电力网
Y11 Y 21 Yi 1 (0) Y Y j1 Yn1
(c)注入功率和注入电流
1
U1
y12
U2
2
I1 IG1 IL1
I2 IG2 IL2
y10 y20 —
~ ~ ~ S1 SG1 SL1
—
~ ~ ~ S2 SG2 SL2
~ ~ S1和S2为节点 和2的注入功率, 1 规定注入网络功率为正
实际电力系统已知条件为节点注入功率和 部分节点电压,用功率代替电流得:
y30
-
I 2 U2 y12 U2 y23 U2 y20
Y22 y12 y23 y20
自导纳:对角元数值上等于与该节点所连导纳的 总和
1 U1
y12 y13
U3 3
2 y23 y20
+
I2
U2
I1
y10 I3
y30
-
I1 Y12 U 2 (U1 U3 0)
自 导 纳
互 导 纳
Y12 Y21 y12 Y23 Y32 y23 Y13 Y31 y13
Y11 y10 y12 y13 Y22 y20 y21 y23 Y33 y30 y32 y33
2
Y 矩阵元素的物理意义
(1)自导纳
Ii Yii U i (U 0, j i ) j Yii yi 0 y ij
§4.1 电力网络方程
• 电力网络方程指将网络的有关参数和变量及其
相互关系归纳起来组成的,反映网络特性的数 学方程式组。如节点电压方程、回路电流方程, 割集电压方程。相应有: • (1)节点导纳矩阵
• (2)节点阻抗矩阵
• (3)回路阻抗矩阵
4.1.1 节点电压方程
~
电力网
网络元件:恒定参数
代数方程
j
Ui 1 其余节点j: 全部接地 Uj 0
节点i: 加单位电压
节点 i 注入网络电流 Yii≠0
(2)互导纳
if j i Ij Y ji U i
(U j 0, j i )
Ui 1 其余节点j: 全部接地 Uj 0
节点i: 加单位电压
1 1 2 2
17
推导过程:从1-1’,2-2’之间等值,将导纳支路拿出去
ZT 1:k
1
U
1
I
1
ห้องสมุดไป่ตู้
1:k ZT
I
2
2
2
U
I 1 I k U U I Z k
1 2 2 1 1
I I
1
T
2
U U (y y ) y U U k Z Z U U y (y y ) U U k Z k Z
1 2 1 10 12 2 12 T T 1 2 2 1 12 2 20 12 T T
T 12
1’
2’
如果双端口网络用π型表示(且YT=1/ZT) y Y y12 I I k
1 2
U y10
1
y20
U
2
k 1 YT y10 k
1 k YT 2 y20 k
yT k* 1 yT k* 1 Y jj ( yT ) ( yT )0 k* k* k* k*
yT yT Yij Yij ( ) k* k*
4.1.4 基本方程和节点的分类
1、功率方程
(a)简单系统
等值电源功率 G
~ ~ SG1 PG1 jQG1 SG 2 PG 2 jQG 2
YU I
6
Y 节点导纳矩阵,U节点电压相量,I节点电流列相量
展开式:
Y11U 1 Y12U 2 Y1nU n I 1 Y21U 1 Y22U 2 Y2 nU n I 2 Yn1U 1 Yn 2U 2 Ynn U n I n
发电机:电压源或电流源 负荷:恒定阻抗
n 个独立节点的网络,n 个节点电压方程
Y11 Y12 Y Y22 21 Yn1 Yn 2
矩阵形式:
Y1n U1 I1 Y2 n U 2 I 2 Ynn U n I n
(1)从原网络引出一条支路增加一个节点
Y 增加一行一列(n+1)×(n+1)
i yik k
电力网
Ykk y ik Yik Yki y ik Yii y ik Yii Yii
(0)
Yii
(2)在原有网络节点i、j 之间增加一条支路
i
Y 阶次不变
电力网
j
Yii Y jj yij
18
等值电路支路以阻抗表示:
kZ T
k ZT k 1
k2 ZT 1 k
1
I ZT
1
k:1 I
2
2
试推导:
U
1
U
2
1’
2’
19
2
用直接法形成节点导纳矩阵
1)节点导纳矩阵是方阵,其阶数就等于网络中除参考节点外 的节点数。 2)节点导纳矩阵是稀疏矩阵,其各行非对角元非零元素的个 数等于与该行相对应节点所连接的不接地的支路数。 3)节点导纳矩阵的对角元就等于各该节点所连接导纳的和。 4)节点导纳矩阵的非对角元等于连接节点i、j支路导纳的负 值。 5)节点导纳矩阵是对称阵,以对角元为轴,上三角元和下三 角元对应相等,因此,一般只求上三角或下三角部分元素。 6)网络中的变压器可采用“理想变压器”,用π型等值电路。
I YU
( Pi jQi )*
. . . . . . . . . . .
.
.
.
.
.
.
整理后:
I 1 ( y 10 y12 y 13 ) U 1 y 12 U 2 y 13 U 3 Y 11 U 1 Y 12 U 2 Y 13 U 3 I 2 y 21 U 1 ( y 20 y 21 y 23 ) U 2 y 23 U 3 Y 21 U 1 Y 22 U 2 Y 23 U 3 0 y 31 U 1 y 32 U 2 ( y 30 y 31 y 32 ) U 3 Y 31 U 1 Y 32 U 2 Y 33 U 3
Yii Yij 节点i的自导纳 节点i、j间的互导纳
7
1 以母线电压作为待求量,列出节点电压方程
1 2
~
电力系统结线图
~
3
注意: 零电位是 不编号的
负荷用阻抗表示 1
2
3
E1
电力系统等值网络
E2
电压源变为电流源
1 y13 I1 y10 y12 3 y30 y23 y20 I2 2
以零电位作为参考,根据基尔霍夫电流定律
. . . . . . . . . . . . . . . .
.
.
.
.
其中:
Y11 Y12 Y13 U1 I1 Y Y U I Y23 2 2 21 22 Y31 Y32 Y33 U 3 I 0
